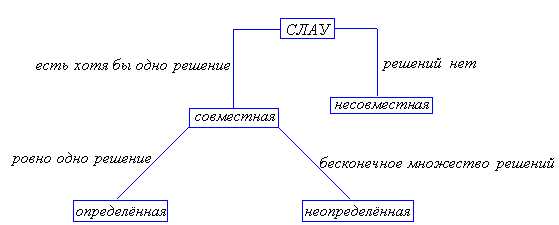
Матрица совместная – Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.
Система линейных алгебраических уравнений. Основная и расширенная матрица. Совместная, несовместная и однородная системы уравнений.
⇐ ПредыдущаяСтр 8 из 8Система линейных алгебраических уравнений, содержащая уравнений и неизвестных имеет следующий вид:
(1)
Обозначим матрицу-столбец из неизвестных через X и матрицу-столбец из свободных членов через B.
– столбец неизвестных, – столбец свободных членов.
Тогда систему (1) можно записать в виде: , (2)
где – основная матрица системы.
Уравнение (2) называется матричным уравнением. Перепишем уравнение (2) следующим образом .
Тогда получим решение матричного уравнения в виде: (3)
Матрицу называют расширенной матрицей системы.
Определение.Система линейных алгебраических уравнений называется прямоугольной, если , и квадратной, если .
Определение.Система линейных алгебраических уравнений называется однородной, если , т.е., если столбец свободных членов состоит из одних нулей.
Определение. Система линейных алгебраических уравнений называется неоднородной, если .
Определение. Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Определение. Совместная система линейных алгебраических уравнений называется определенной, если она имеет только одно решение, и неопределенной, если она имеет более одного решения.
Определение.Две системы называются эквивалентными, если любое решение одной из них является решением и другой системы. Заметим, что все несовместные системы являются эквивалентными.
Элементарные преобразования системы линейных уравнений:
1. перестановка любых двух уравнений;
2. умножение обеих частей одного уравнения на любое число отличное от нуля;
3. прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.
Элементарные преобразования переводят данную систему в эквивалентную.
mykonspekts.ru
Совместная, несовместная СЛАУ.
Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется
Определённая, неопределённая СЛАУ.
Если СЛАУ имеет решение и при том единственное, то её называют определённой а если решение неединственное – то неопределённой.
МАТРИЧНЫЕ УРАВНЕНИЯ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов
Найдем произведение
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
или короче A∙X=B.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: . Поскольку A-1A = E и
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных.
Формулы Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А : D = det (ai j) и n вспомогательных определителей D i (i= ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид: D × x
Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: x i = D i / D.
Если главный определитель системы D и все вспомогательные определители D i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Теорема (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца .
Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и .
Наконец несложно заметить, что
Таким образом, получаем равенство: . Следовательно, .
Аналогично выводятся равенства и , откуда и следует утверждение теоремы.
Теорема Кронекера — Капелли.
Система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы .
Доказательство: Оно распадается на два этапа.
1. Пусть система имеет решение. Покажем, что .
Пусть набор чисел является решением системы. Обозначим через -ый столбец матрицы , . Тогда , то есть столбец свободных членов является линейной комбинацией столбцов матрицы . Пусть . Предположим, что . Тогда по . Выберем в базисный минор . Он имеет порядок . Столбец свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы . Столбец свободных членов в миноре является линейной комбинацией столбцов матрицы . В силу свойств определителя , где — определитель, который получается из минора заменой столбца свободных членов на столбец . Если столбец проходил через минор M, то в , будет два одинаковых столбца и, следовательно, . Если столбец не проходил через минор , то будет отличаться от минора порядка r+1 матрицы только порядком столбцов. Так как , то . Таким образом, , что противоречит определению базисного минора. Значит, предположение, что , неверно.
2. Пусть . Покажем, что система имеет решение. Так как , то базисный минор матрицы является базисным минором матрицы . Пусть через минор проходят столбцы . Тогда по теореме о базисном миноре в матрице столбец свободных членов является линейной комбинацией указанных столбцов:
| (1) |
Положим , , , , остальные неизвестные возьмем равными нулю. Тогда при этих значениях получим
В силу равенства (1) . Последнее равенство означает, что набор чисел является решением системы. Существование решения доказано.
В рассмотренной выше системе , и система является совместной. В системе , , и система является несовместной.
Замечание:Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить и , ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.
Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)
Пусть дана система линейных уравнений с неизвестными . Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя и к методу нахождения ранга матрицы. Предлагаемый алгоритм называется
Выпишем расширенную матрицу системы
Назовем элементарными операциями следующие действия с матрицами:
1. перестановка строк;
2. умножение строки на число, отличное от нуля;
3. сложение строки с другой строкой, умноженной на число.
Цель алгоритма — с помощью применения последовательности элементарных операций к матрице добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице . Пусть это будет столбец с номером . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице уже произведена, то есть . Тогда ко второй строке прибавим первую, умноженную на число , к третьей строке прибавим первую, умноженную на число , и т.д. В результате получим матрицу
(Первые нулевые столбцы, как правило, отсутствуют.)
Если в матрице встретилась строка с номером k, в которой все элементы равны нулю, а , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что -ое уравнение будет иметь вид
Этому уравнению не удовлетворяет ни один набор чисел .
Матрицу можно записать в виде
где
По отношению к матрице выполняем описанный шаг алгоритма. Получаем матрицу
где , . Эту матрицу снова можно записать в виде
и к матрице снова применим описанный выше шаг алгоритма.
Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее.
Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида
Далее выполняется так называемый обратный ход метода Гаусса. По матрице составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть . Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.
Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы Ax=b. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин (в частности, просто произвольной величиной ). Эта запись и будет общим решением системы.
Если система была однородной, то получим общее решение однородной системы. Коэффициенты при , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при — второе решение и т.д.
Способ 2: Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одной переменной, перенесенной в правую часть, нужно присвоить значение 1, а остальным — нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другой переменной в правой части значение 1, а остальным — нули, получим второе решение из фундаментальной системы и т.д.
Определение:система называется совместной, если она имеет хотя бы одно решение, и несовместной — в противном случае, то есть в случае, когда решений у системы нет. Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных. Например, система из трех уравнений с двумя неизвестными
имеет решение , и даже имеет бесконечно много решений, а система из двух уравнений с тремя неизвестными
решений не имеет, то есть является несовместной.
Определение: Расширенной матрицей системы линейных уравнений называется матрица , отличающаяся от матрицы системы наличием дополнительного столбца из свободных членов:
Следствие: Ранг расширенной матрицы либо равен рангу матрицы системы A, либо больше его на единицу.
Доказательство: Так как любая линейно независимая система столбцов матрицы A является линейно независимой системой столбцов матрицы , то в силу предложения 14.26 (Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему) .
Пусть . Предположим, что , . Тогда в матрице есть линейно независимая система из r+k столбцов. Среди этих столбцов может быть только один, не принадлежащий матрице A. Тогда подсистема остальных r+k-1 столбцов, принадлежащих матрице A , должна быть линейно независимой. Следовательно, . Получили противоречие. Предположение, что k>1, неверно.
Квадратные системы с невырожденной матрицей.
Система называется квадратной, если число m ее уравнений равно числу n неизвестных, то есть когда ее матрица A — квадратная матрица.
Решение СЛАУ:Пусть дана СЛАУ
A11x1 + … + a1nxn = 0
……. … ……
Am1x1 + … + amnxn = 0
Данная система всегда совместна так как имеет тривиальное решение х1=…=хn=0
Для существования нетривиальных решений необходимо и достаточно выполнение
словия r = r(A) < n , что равносильно условию det(A)=0, когда матрица А – квадратная.
ThСовокупность решений СЛАУ образует линейное пространство размерности (n-r). Это означает, что произведение ее решения на число, а также сумма и линейная комбинация конечного числа ее решений является решениями этой системы. Линейное пространство решений любой СЛАУ является подпространством пространства Rn.
Любая совокупность (n-r) линейно независимых решений СЛАУ (являющаяся базисом в пространстве решений) называется фундаментальной совокупностью решений(ФСР).
Пусть х1,…,хr — базисные неизвестные, хr+1,…,хn – свободные неизвестные. Свободным переменным дадим поочередно следующие значения:
хr+1=1 хr+1=0 хr+1=0
хr+2=0 хr+2=1 хr+2=0
…… …… ……
хn=0 хn=0 хn=1
Определив значения базисных переменных, соответствующие каждому набору значений свободных переменных, получим решения:
Х1 (1) Х1 (2) Х1 (n-r)
…… …… …….
Х(1) = Хr (1), Х(2) = Хr (2),…,Х(n-r) = Хr (n-r)
1 0 0
0 1 0
0 0 1
Построенная таким образом система решений системы уравнений называется нормальнойфундаментальной совокупностью решений.
Теорема. Множество всех решений однородной системы уравнений
A11x1 + … + a1nxn = 0
……. … ……
Am1x1 + … + amnxn = 0
Образует линейное пространство S (пространство решений), которое является подпространством в Rn (n – число неизвестных), причем dims=k=n-r, где r- ранг системы. Базис в пространстве решений{x (1),…, x (k)} называется фундаментальной системой решений, и общее решение имеет вид:
X=c1x (1) + … + ckx (k), c (1),…, c (k) ? R
infopedia.su
17 Системы линейных уравнений
§1. Системы линейных уравнений.
Система вида
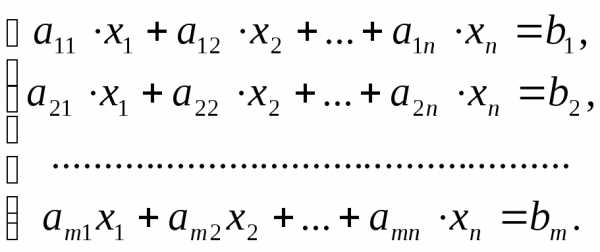 (1)
(1)
называется системой mлинейных уравнений сnнеизвестными.
Здесь  — неизвестные,
— неизвестные, — коэффициенты при неизвестных,
— коэффициенты при неизвестных, — свободные члены уравнений.
— свободные члены уравнений.
Если все свободные члены уравнений
равны нулю, система называется однородной.Решениемсистемы называется
совокупность чисел ,
при подстановке которых в систему вместо
неизвестных все уравнения обращаются
в тождества. Система называетсясовместной, если она имеет хотя бы
одно решение. Совместная система, имеющая
единственное решение, называетсяопределенной. Две системы называютсяэквивалентными, если множества их
решений совпадают.
,
при подстановке которых в систему вместо
неизвестных все уравнения обращаются
в тождества. Система называетсясовместной, если она имеет хотя бы
одно решение. Совместная система, имеющая
единственное решение, называетсяопределенной. Две системы называютсяэквивалентными, если множества их
решений совпадают.
Система (1) может быть представлена в матричной форме с помощью уравнения
(2)
где
.
§2. Совместность систем линейных уравнений.
Назовем расширенной матрицей системы (1) матрицу

Теорема Кронекера — Капелли. Система (1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:
.
§3. Решение систем n линейных уравнений с n неизвестными.
Рассмотрим неоднородную систему nлинейных уравнений сnнеизвестными:
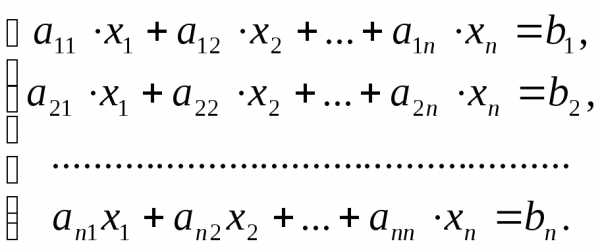 (3)
(3)
Теорема Крамера. Если главный
определитель системы (3)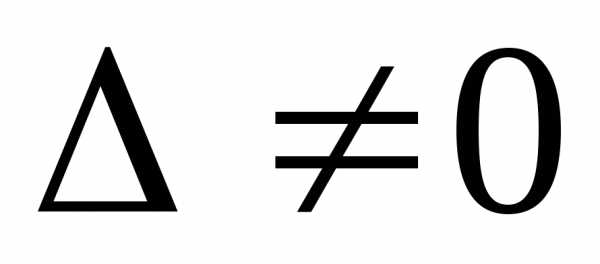 ,
то система имеет единственное решение,
определяемое по формулам:
,
то система имеет единственное решение,
определяемое по формулам:
т.е. ,
где  — определитель, получаемый из определителя
— определитель, получаемый из определителя заменой
заменой -го
столбца на столбец свободных членов.
-го
столбца на столбец свободных членов.
Если 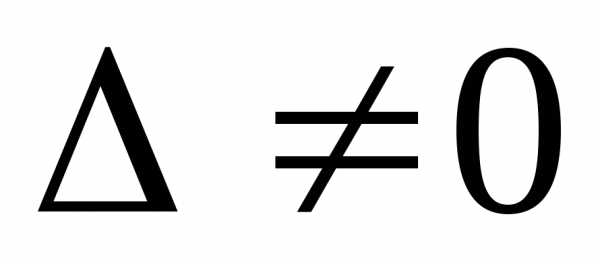 ,
а хотя бы один из
,
а хотя бы один из ≠0,
то система решений не имеет.
≠0,
то система решений не имеет.
Если , то система имеет бесконечно много решений.
Систему (3) можно решить, используя ее
матричную форму записи (2). Если ранг
матрицы Аравенn,
т.е.,
то матрицаАимеет обратную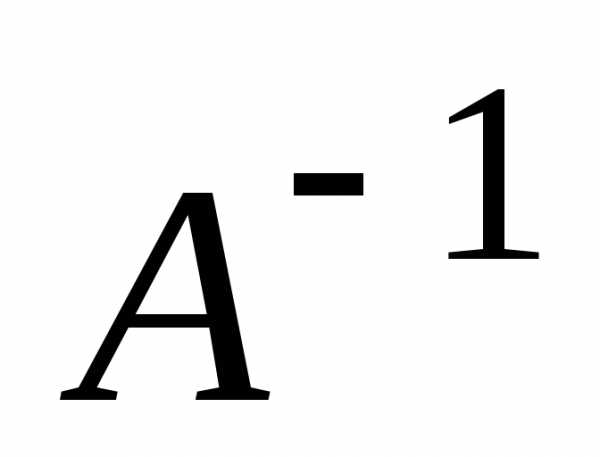 .
Умножив матричное уравнениена матрицу
.
Умножив матричное уравнениена матрицу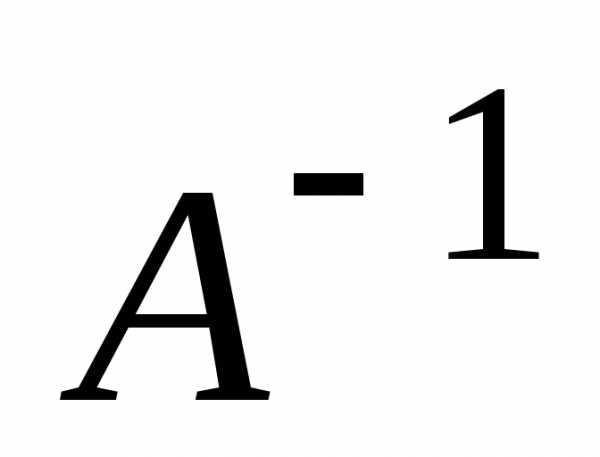 слева, получим:
слева, получим:
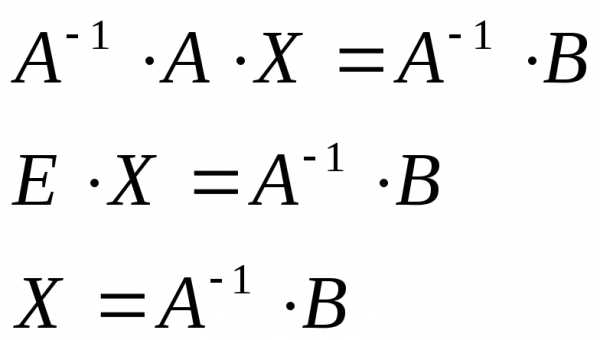 .
.
Последнее равенство выражает способ решения систем линейных уравнений с помощью обратной матрицы.
Пример. Решить систему уравнений с помощью обратной матрицы.
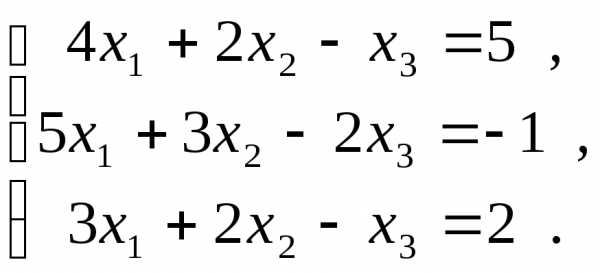
Решение. Матрица невырожденная, так как
невырожденная, так как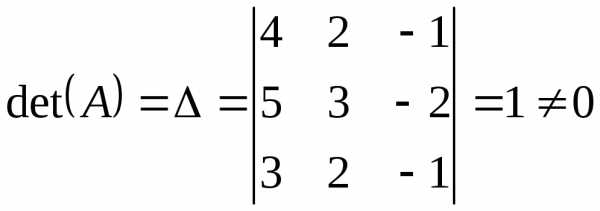 ,
значит, существует обратная матрица.
Вычислим обратную матрицу:
,
значит, существует обратная матрица.
Вычислим обратную матрицу: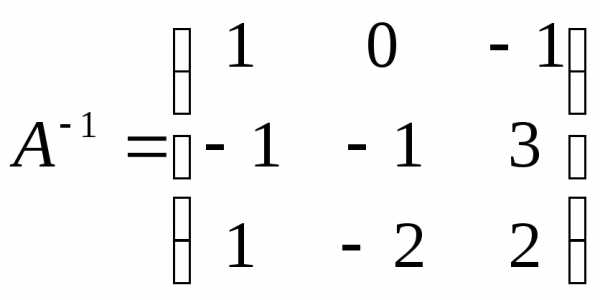 .
.
Тогда
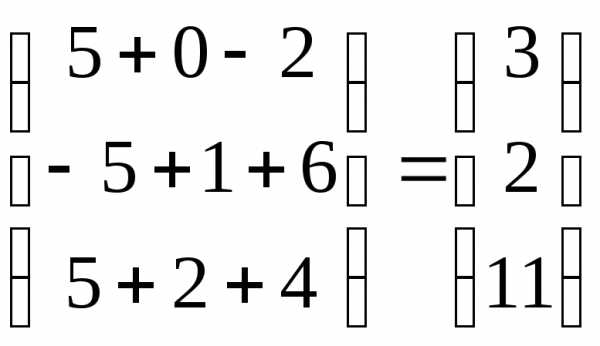 ,
,
т.е. .
Задание. Решить систему методом Крамера.
§4. Решение произвольных систем линейных уравнений.
Пусть дана неоднородная система линейных уравнений вида (1).
Предположим, что система совместна,
т.е. выполнено условие теоремы
Кронекера-Капелли:
.
Если ранг матрицы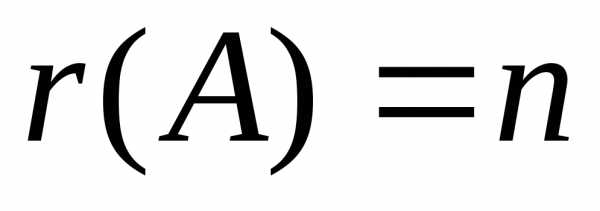 (числу неизвестных), то система имеет
единственное решение. Если
(числу неизвестных), то система имеет
единственное решение. Если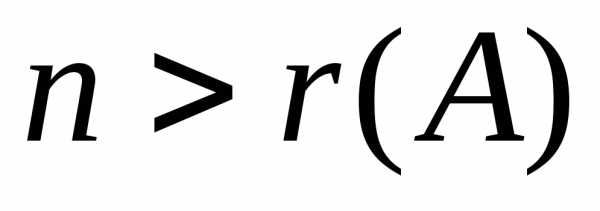 ,
то система имеет бесконечно много
решений. Поясним.
,
то система имеет бесконечно много
решений. Поясним.
Пусть ранг матрицы r(A)=r<n. Поскольку, то существует некоторый ненулевой минор порядкаr. Назовем его базисным минором. Неизвестные, коэффициенты которых образуют базисный минор, назовем базисными переменными. Остальные неизвестные назовем свободными переменными. Переставим уравнения и перенумеруем переменные так, чтобы этот минор располагался в левом верхнем углу матрицы системы:
 .
.
Первые rстрок линейно независимы, остальные выражаются через них. Следовательно, эти строки (уравнения) можно отбросить. Получим:
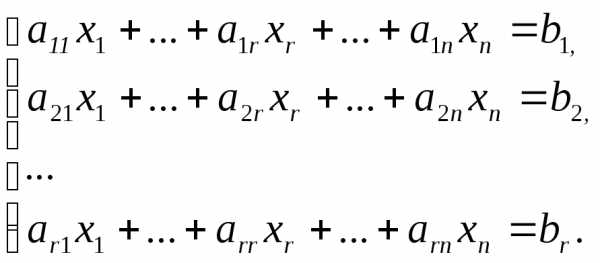
Дадим свободным переменным произвольные числовые значения: . Оставим в левой части только базисные переменные, свободные перенесем в правую часть.
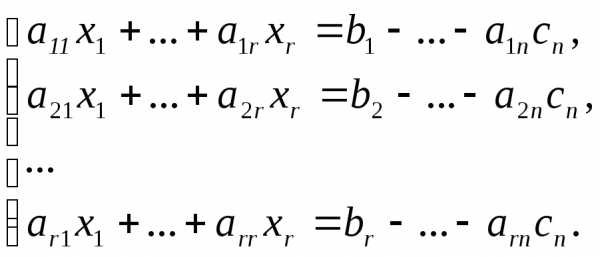
Получили систему rлинейных уравнений сrнеизвестными, определитель которой отличен от 0. Она имеет единственное решение.
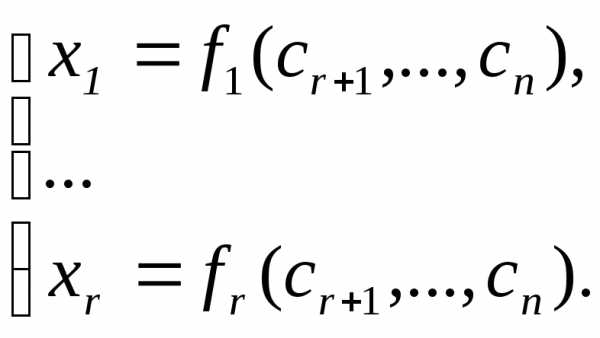
Эта система называется общим решением
системы линейных уравнений (1). Иначе:
выражение базисных переменных через
свободные называется общим решениемсистемы. Из него можно получить бесконечное
множествочастных решений, придавая
свободным переменным произвольные
значения. Частное решение, полученное
из общего при нулевых значениях свободных
переменных называетсябазисным
решением. Число различных базисных
решений не превосходит .
Базисное решение с неотрицательными
компонентами называетсяопорнымрешением системы.
.
Базисное решение с неотрицательными
компонентами называетсяопорнымрешением системы.
Пример.
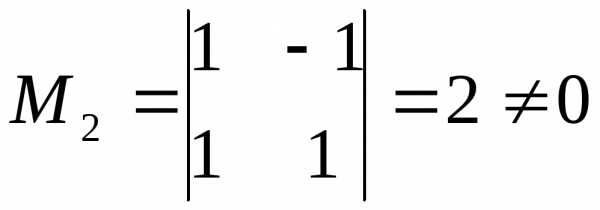 ,r=2.
,r=2.
Переменные 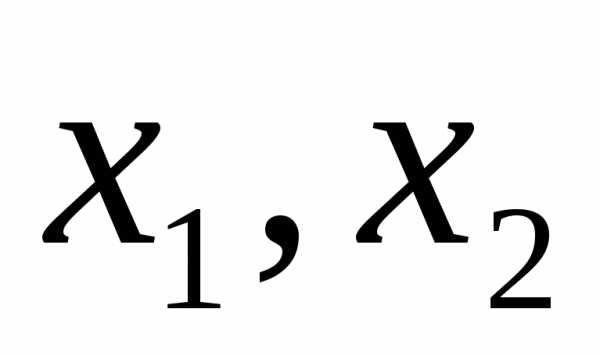 — базисные,
— базисные,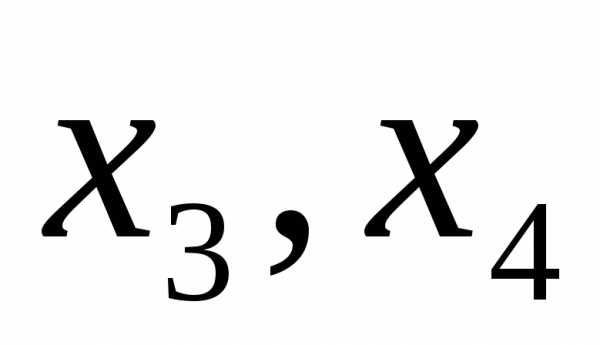 — свободные.
— свободные.
Сложим уравнения; выразим  через
через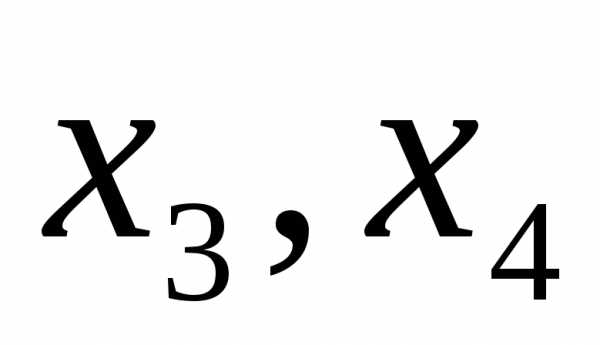 :
:
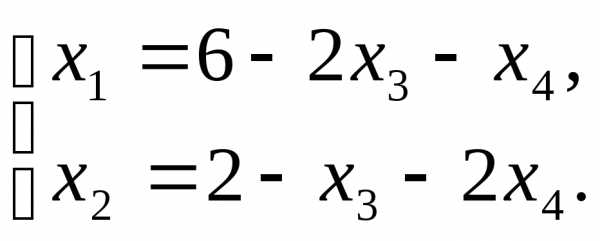 — общее решение.
— общее решение.
— частное решение при.
— базисное решение, опорное.
§5. Метод Гаусса.
Метод Гаусса — это универсальный метод исследования и решения произвольных систем линейных уравнений. Он состоит в приведении системы к диагональному (или треугольному) виду путем последовательного исключения неизвестных с помощью элементарных преобразований, не нарушающих эквивалентности систем. Переменная считается исключенной, если она содержится только в одном уравнении системы с коэффициентом 1.
Элементарными преобразованиямисистемы являются:
— умножение уравнения на число, отличное от нуля;
— сложение уравнения, умноженного на любое число, с другим уравнением;
— перестановка уравнений;
— отбрасывание уравнения 0 = 0.
Элементарные преобразования можно совершать не над уравнениями, а над расширенными матрицами получающихся эквивалентных систем.
Пример.
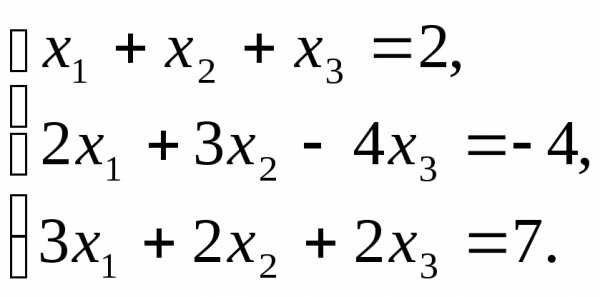
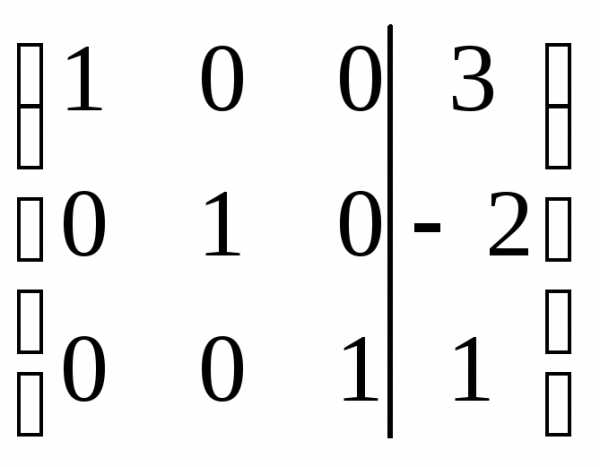
Решение.Выпишем расширенную матрицу системы:
 .
.
Выполняя элементарные преобразования, приведем левую часть матрицы к единичному виду: на главной диагонали будем создавать единицы, а вне ее — нули.
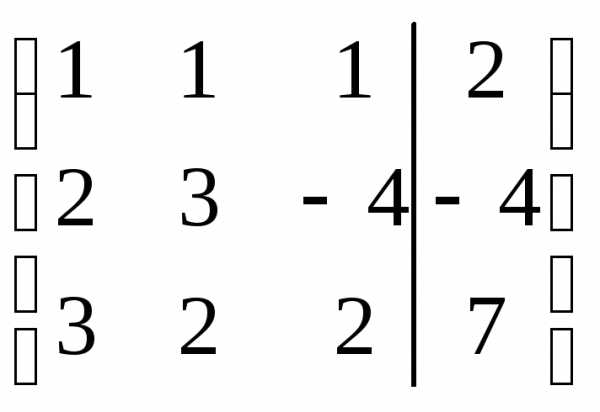



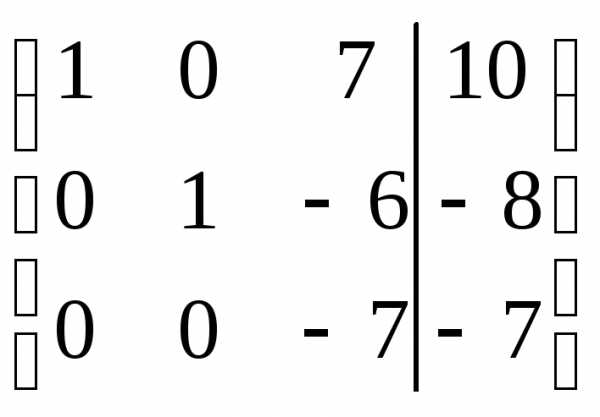




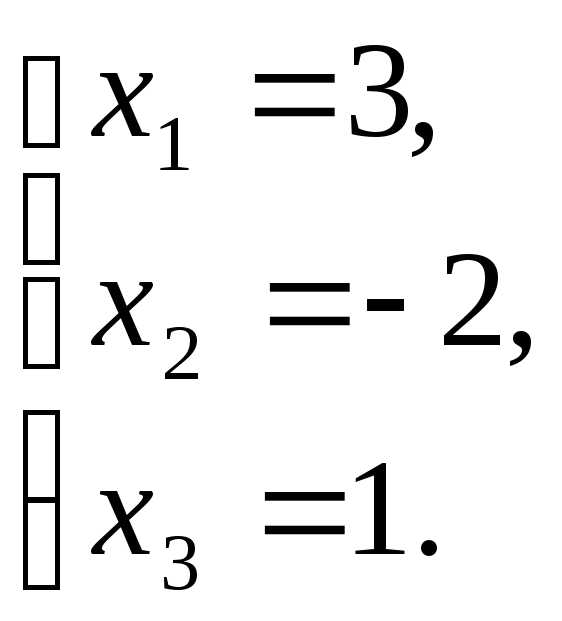
Замечание. Если при выполнении
элементарных преобразований получено
уравнение вида 0= к (где к 0), то система несовместна.
0), то система несовместна.
Решение систем линейных уравнений методом последовательного исключения неизвестных можно оформлять в виде таблицы.
Левый столбец таблицы содержит информацию об исключенных (базисных) переменных. Остальные столбцы содержат коэффициенты при неизвестных и свободные члены уравнений.
В исходную таблицу записывают расширенную матрицу системы. Далее приступают к выполнению преобразований Жордана:
1. Выбирают переменную  ,
которая станет базисной. Соответствующий
столбец называют ключевым. Выбирают
уравнение, в котором эта переменная
останется, будучи исключенной из других
уравнений. Соответствующую строку
таблицы называют ключевой. Коэффициент
,
которая станет базисной. Соответствующий
столбец называют ключевым. Выбирают
уравнение, в котором эта переменная
останется, будучи исключенной из других
уравнений. Соответствующую строку
таблицы называют ключевой. Коэффициент ,
стоящий на пересечении ключевой строки
и ключевого столбца, называют ключевым.
,
стоящий на пересечении ключевой строки
и ключевого столбца, называют ключевым.
2. Элементы ключевой строки делят на ключевой элемент.
3. Ключевой столбец заполняют нулями.
4. Остальные элементы вычисляют по правилу прямоугольника. Составляют прямоугольник, в противоположных вершинах которого находятся ключевой элемент и пересчитываемый элемент; из произведения элементов, стоящих на диагонали прямоугольника с ключевым элементом, вычитают произведение элементов другой диагонали, полученную разность делят на ключевой элемент.
Пример. Найти общее решение и базисное решение системы уравнений:
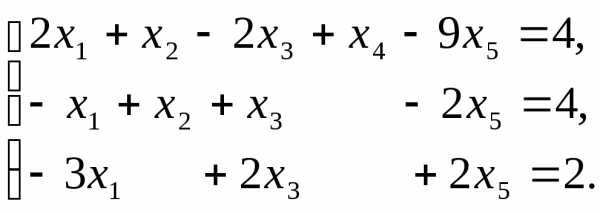
Решение.
Базис | | | | | | |
| 2 -1 -3 | 1 1 0 | -2 1 2 | 1 0 0 | -9 -2 2 | 4 4 2 |
| 3 -1 -3 | 0 1 0 | -3 1 2 | 1 0 0 | -7 -2 2 | 0 4 2 |
| -1,5 0,5 -1,5 | 0 1 0 | 0 0 1 | 1 0 0 | -4 -3 1 | 3 3 1 |
Общее решение системы :
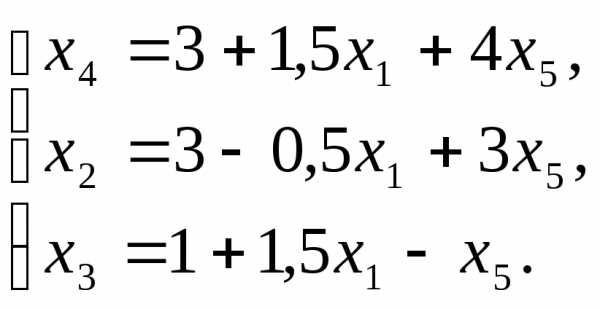
Базисное решение: .
Перейти от одного базиса системы к другому позволяет преобразование однократного замещения: вместо одной из основных переменных в базис вводят одну из свободных переменных. Для этого в столбце свободной переменной выбирают ключевой элемент и выполняют преобразования по указанному выше алгоритму.
§6. Нахождение опорных решений
Опорным решением системы линейных уравнений называется базисное решение, не содержащее отрицательных компонент.
Опорные решения системы находят методом Гаусса при выполнении следующих условий.
1. В исходной системе все свободные члены
должны быть неотрицательны: 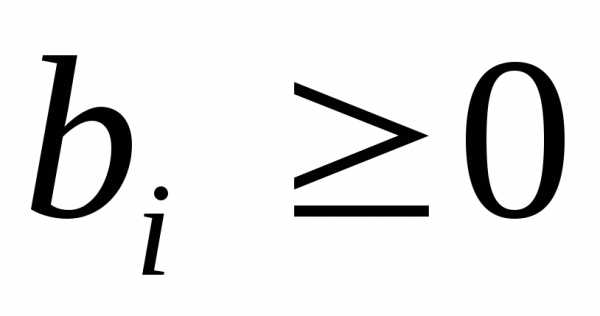 .
.
2. Ключевой элемент выбирают среди положительных коэффициентов.
3. Если при переменной, вводимой в базис, имеется несколько положительных коэффициентов, то в качестве ключевой строки берется та, в которой отношение свободного члена к положительному коэффициенту будет наименьшим.
Замечание 1. Если в процессе исключения
неизвестных появится уравнение, в
котором все коэффициенты неположительны,
а свободный член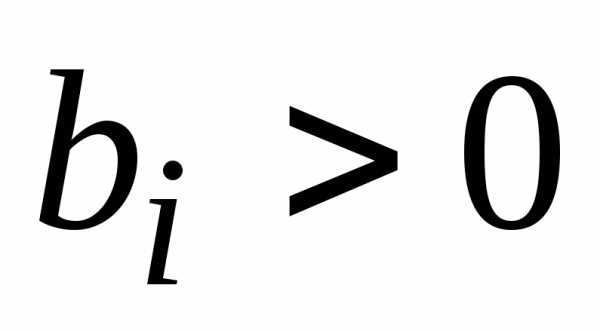 ,
то система не имеет неотрицательных
решений.
,
то система не имеет неотрицательных
решений.
Замечание 2. Если в столбцах коэффициентов при свободных переменных нет ни одного положительного элемента, то переход к другому опорному решению невозможен.
Пример.
базис | | | | | | | | |
| 11 -6 -8 | 4 -1 -3 | -39 11 29 | 3 -5 -5 | 0 1 0 | -1 1 1 | 0 15 1 | min |
| 3 2 -8 | 1 2 -3 | -10 -18 29 | -2 0 -5 | 0 1 0 | 0 0 1 | 1 14 1 | min |
| 3 -4 1 | 1 0 0 | -10 2 -1 | -2 4 -11 | 0 1 0 | 0 0 1 | 1 12 4 | min ; |
| 1 0 0 | | | | 0 1 0 | 0 0 1 | | . |
studfiles.net
Система линейных алгебраических уравнений
Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.
Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.
Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему
содержащую m уравнений и n неизвестных (x1,x2,…,xn). Прилагательное «линейных» означает, что все неизвестные (их еще называют переменными) входят только в первой степени.
Параметры aij называют коэффициентами, а bi – свободными членами СЛАУ. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «m×n система линейных уравнений», – тем самым указывая, что СЛАУ содержит m уравнений и n неизвестных.
Если все свободные члены bi=0 то СЛАУ называют однородной. Если среди свободных членов есть хотя бы один, отличный от нуля, СЛАУ называют неоднородной.
Решением СЛАУ (1) называют всякую упорядоченную совокупность чисел (α1,α2,…,αn), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных x1,x2,…,xn, обращают каждое уравнение СЛАУ в тождество.
Любая однородная СЛАУ имеет хотя бы одно решение: нулевое (в иной терминологии – тривиальное), т.е. x1=x2=…=xn=0.
Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной, если же решений нет – несовместной. Если совместная СЛАУ имеет ровно одно решение, её именуют определённой, если бесконечное множество решений – неопределённой.
Матричная форма записи систем линейных алгебраических уравнений.
С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:
Матрица A называется матрицей системы. Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.
Матрица A˜ называется расширенной матрицей системы. Её получают добавлением к матрице системы столбца, содержащего свободные члены b1,b2,…,bm. Обычно этот столбец отделяют вертикальной чертой, – для наглядности.
Матрица-столбец B называется матрицей свободных членов, а матрица-столбец X – матрицей неизвестных.
Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: A⋅X=B.
Примечание
Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. rangA=rangA˜.
Система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если rangA=rangA˜, то решение есть; если rangA≠rangA˜, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква n, которая равна количеству переменных заданной СЛАУ.
Следствие из теоремы Кронекера-Капелли
Если rangA≠rangA˜, то СЛАУ несовместна (не имеет решений).
Если rangA=rangA˜<n, то СЛАУ является неопределённой (имеет бесконечное количество решений).
Если rangA=rangA˜=n, то СЛАУ является определённой (имеет ровно одно решение).
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения нет, а если существуют – то сколько.
Методы решения СЛАУ
Метод Крамера
Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода Крамера можно выразить в трёх пунктах:
Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. Δ≠0.
Для каждой переменной xi необходимо составить определитель Δ Xi, полученный из определителя Δ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
Найти значения неизвестных по формуле xi= Δ Xi /Δ
Решение систем линейных алгебраических уравнений с помощью обратной матрицы.
Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:
Записать три матрицы: матрицу системы A, матрицу неизвестных X, матрицу свободных членов B.
Найти обратную матрицу A-1.
Используя равенство X=A-1⋅B получить решение заданной СЛАУ.
Метод Гаусса. Примеры решения систем линейных алгебраических уравнений методом Гаусса.
Метод Гаусса является одним из самых наглядных и простых способов решения систем линейных алгебраических уравнений (СЛАУ): как однородных, так и неоднородных. Коротко говоря, суть данного метода состоит в последовательном исключении неизвестных.
Преобразования, допустимые в методе Гаусса:
Смена мест двух строк;
Умножение всех элементов строки на некоторое число, не равное нулю.
Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
Вычеркивание строки, все элементы которой равны нулю.
Вычеркивание повторяющихся строк.
Насчет последних двух пунктов: повторяющиеся строки можно вычёркивать на любом этапе решения методом Гаусса, – естественно, оставляя при этом одну из них. Например, если строки №2, №5, №6 повторяются, то можно оставить одну из них, – например, строку №5. При этом строки №2 и №6 будут удалены.
Нулевые строки убираются из расширенной матрицы системы по мере их появления.
studfiles.net
Лекция 6. Системы линейных уравнений
Системы линейных уравнений. Лекция 6.
Системы линейных уравнений.
Основные понятия.
Система видa
называется системой — линейных уравнений снеизвестными.
Числа ,,называютсякоэффициентами системы.
Числа ,называютсясвободными членами системы, –переменными системы. Матрица
называется основной матрицей системы, а матрица
– расширенной матрицей системы. Матрицы — столбцы
и — соответственноматрицами свободных членов и неизвестных системы. Тогда в матричной форме систему уравнений можно записать в виде .Решением системы называется значений переменных, при подстановке которых, все уравнения системы обращаются в верные числовые равенства. Всякое решение системы можно представить в виде матрицы — столбца. Тогда справедливо матричное равенство.
Система уравнений называется совместной если она имеет хотя бы одно решение и несовместной если не имеет ни одного решения.
Решить систему линейных уравнений это значит выяснить совместна ли она и в случае совместности найти её общее решение.
Система называется однородной если все её свободные члены равны нулю. Однородная система всегда совместна, так как имеет решение
.
Теорема Кронекера – Копелли.
Ответ на вопрос существования решений линейных систем и их единственности позволяет получить следующий результат, который можно сформулировать в виде следующих утверждений относительно системы линейных уравнений снеизвестными
(1)
Теорема 2. Система линейных уравнений (1) совместна тогда и только тогда когда ранг основной матрицы равен рангу расширенной (.
Теорема 3. Если ранг основной матрицы совместной системы линейных уравнений равен числу неизвестных, то система имеет единственное решение.
Теорема 4. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.
Правила решения систем.
Находят ранги основной и расширенной матрицы и если то система не совместна.
Если , то система совместна, в этом случае находят какой-нибудь базисный минор- того порядка и берут соответствующие ему- уравнений системы, отбрасывая остальные. Те переменные, коэффициенты которых входят в базисный минор, называются главными, остальныепеременных называют свободными. Выражения со свободными переменными переносят в правую часть.
3. Находят выражение главных переменных через свободные и получают общее решение системы.
4. Придавая свободным переменным произвольные значения получают все значения главных переменных.
Методы решения систем линейных уравнений.
Метод обратной матрицы.
Пусть дана система линейных уравнений снеизвестными
причем , т. е. система имеет единственное решение. Запишем систему в матричном виде
,
где ,,.
Умножим обе части матричного уравнения слева на матрицу
.
Так как , то получаем, откуда получаем равенство для нахождения неизвестных
.
Пример 27. Методом обратной матрицы решить систему линейных уравнений
Решение. Обозначим через основную матрицу системы
.
Пусть , тогда решение найдем по формуле.
Вычислим .
Так как , тои система имеет единственное решение. Найдем все алгебраические дополнения
, ,
, ,
, ,
, ,
Таким образом
.
Сделаем проверку
.
Обратная матрица найдена верно. Отсюда по формуле , найдем матрицу переменных.
.
Сравнивая значения матриц, получим ответ: .
Метод Крамера.
Пусть дана система линейных уравнений снеизвестными
причем , т. е. система имеет единственное решение. Запишем решение системы в матричном видеили
Отсюда
Обозначим
. . . . . . . . . . . . . . ,
Таким образом, получаем формулы для нахождения значений неизвестных, которые называются формулами Крамера.
Пример 28. Решить методом Крамера следующую систему линейных уравнений .
Решение. Найдем определитель основной матрицы системы
.
Так как , то, система имеет единственное решение.
Найдем остальные определители для формул Крамера
,
,
.
По формулам Крамера находим значения переменных
Ответ:
Метод Гаусса.
Метод заключается в последовательном исключении переменных.
Пусть дана система линейных уравнений снеизвестными.
Процесс решения по методу Гаусса состоит из двух этапов:
На первом этапе расширенная матрица системы приводится с помощью элементарных преобразований к ступенчатому виду
,
где , которой соответствует система
После этого переменные считаются свободными и в каждом уравнении переносятся в правую часть.
На втором этапе из последнего уравнения выражается переменная , полученное значение подставляется вуравнение. Из этого уравнения
выражается переменная . Этот процесс продолжается до первого уравнения. В результате получается выражение главных переменныхчерез свободные переменные.
Пример 29. Решить методом Гаусса следующую систему
Решение. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду
.
Так как больше числа неизвестных, то система совместна и имеет бесконечное множество решений. Запишем систему для ступенчатой матрицы
Определитель расширенной матрицы этой системы, составленный из трех первых столбцов не равен нулю, поэтому его считаем базисным. Переменные
, будут базисными а переменная – свободной. Перенесем ее во всех уравнениях в левую часть
Из последнего уравнения выражаем
Подставив это значение в предпоследнее второе уравнение, получим
откуда . Подставив значения переменныхив первое уравнение, найдем. Ответ запишем в следующем виде
Ответ:
32
studfiles.net
9. Свойства определителей.
Определение. Транспонирование матрицы – такое преобразование матрицы, при котором строки становятся столбцами с сохранением порядка следования.
Свойства определителей.
При транспонировании матрицы определитель не меняется.
При перестановке любых двух строк (столбцов) определитель меняет только знак.
При умножении строки (столбца) на некоторое число определитель умножается на это число.
Если все соответствующие элементы квадратных матриц одного порядка одинаковы, за исключением элементов одной i—ой строки, то
.
Величина определителя не изменяется, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженной на некоторое число.
Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
Определитель равен нулю, если
все элементы некоторой строки (столбца) равны нулю,
две строки (столбца) одинаковы,
две строки (столбца) определителя пропорциональны.
Методы вычисления определителей.
Разложение по строке или столбцу.
Метод обращения в нуль всех (кроме одного) элементов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), зануляются все элементы выбранной строки (столбца) кроме одного, принадлежащего вычитаемому столбцу (строке).
Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, используется для последовательного зануления всех элементов первой строки (столбца) кроме одного, второй строки (столбца) – всех кроме двух и т.д. В итоге определитель преобразуется к треугольному виду. Величина такого определителя равна произведению элементов главной диагонали.
Вычисление с использованием теоремы Лапласа, согласно которой определитель
 —
го порядка равен сумме произведений
всех его миноров
—
го порядка равен сумме произведений
всех его миноров —
го порядка, стоящих в выделенных
—
го порядка, стоящих в выделенных строках
(столбцах), на их алгебраические
дополнения.
строках
(столбцах), на их алгебраические
дополнения.
Примеры.
1. Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:
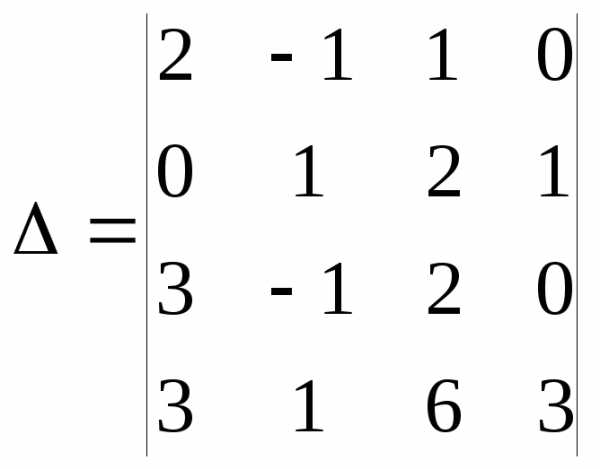
Решение. Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец. Итак, имеем
Полученные в итоге
два определителя третьего порядка
вычислим тем же методом. В определителе  нулевых элементов нет, поэтому можно
выбрать для разложения любой из столбцов,
например, первый. В
нулевых элементов нет, поэтому можно
выбрать для разложения любой из столбцов,
например, первый. В единственный нулевой элемент находится
на пересечении первого столбца со второй
строкой. Для разнообразия будем разлагать
единственный нулевой элемент находится
на пересечении первого столбца со второй
строкой. Для разнообразия будем разлагать по второй строке:
по второй строке:
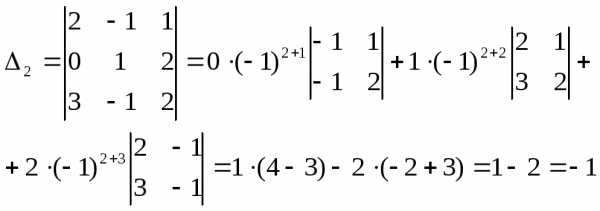
Таким образом, окончательно получим .
10. Система линейных алгебраических уравнений. Основная и расширенная матрица. Совместная, несовместная и однородная системы уравнений.
Система линейных
алгебраических уравнений, содержащая 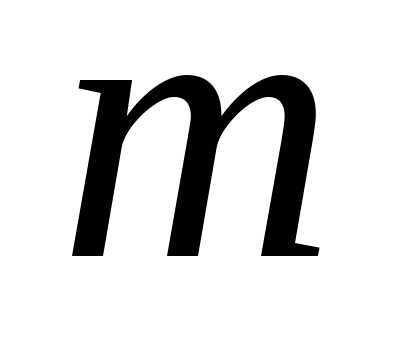 уравнений и
уравнений и 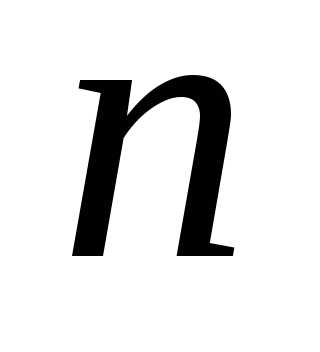 неизвестных имеет следующий вид:
неизвестных имеет следующий вид:
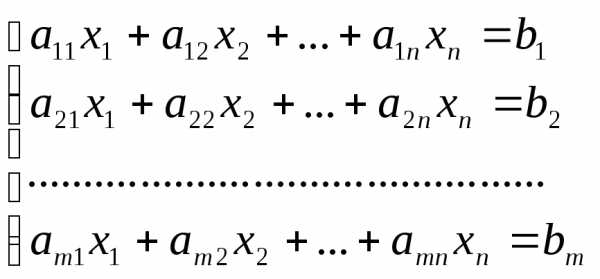 (1)
(1)
Обозначим матрицу-столбец из неизвестных через Xи матрицу-столбец из свободных членов черезB.
 –столбец
неизвестных,
–столбец
неизвестных, 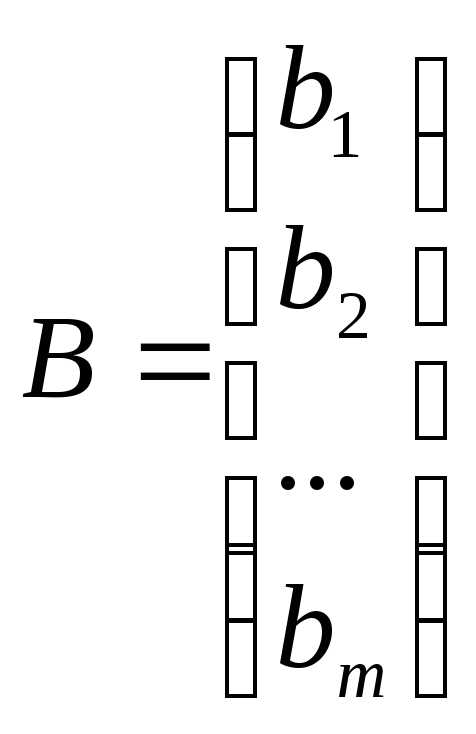 – столбец свободных членов.
– столбец свободных членов.
Тогда систему (1) можно записать в виде: , (2)
где –основная матрицасистемы.
–основная матрицасистемы.
Уравнение (2) называется матричным уравнением. Перепишем уравнение (2) следующим образом .
Тогда получим решение матричного уравнения в виде: (3)
Матрицу  называютрасширенной матрицейсистемы.
называютрасширенной матрицейсистемы.
Определение. Система линейных алгебраических
уравнений называетсяпрямоугольной,
если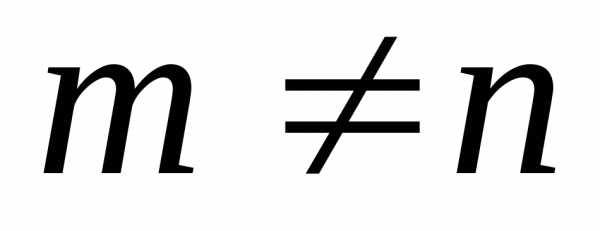 ,
иквадратной, если
,
иквадратной, если .
.
Определение. Система линейных алгебраических
уравнений называетсяоднородной,
если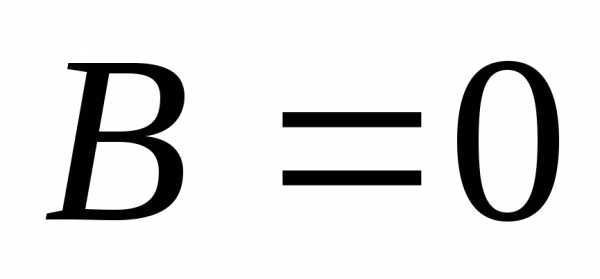 ,
т.е., если столбец свободных членов
состоит из одних нулей.
,
т.е., если столбец свободных членов
состоит из одних нулей.
Определение.Система линейных алгебраических
уравнений называетсянеоднородной,
если .
.
Определение.Система линейных алгебраических уравнений называетсясовместной, если она имеет хотя бы одно решение, инесовместной, если она не имеет ни одного решения.
Определение.Совместная система линейных алгебраических уравнений называетсяопределенной, если она имеет только одно решение, инеопределенной, если она имеет более одного решения.
Определение. Две системы называютсяэквивалентными, если любое решение одной из них является решением и другой системы. Заметим, что все несовместные системы являются эквивалентными.
Элементарные преобразования системы линейных уравнений:
перестановка любых двух уравнений;
умножение обеих частей одного уравнения на любое число отличное от нуля;
прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.
Элементарные преобразования переводят данную систему в эквивалентную.
19
studfiles.net
Критерий совместности системы линейных уравнений.
⇐ ПредыдущаяСтр 6 из 18Следующая ⇒
Критерий совместности системы линейных уравнений даёт теорема Кронекера-Капелли.
Леопольд Кронекер (1823 – 1891 гг.) ─ немецкий математик. Теорема, о которой пойдёт речь, содержалась в его лекциях, читавших в Берлинском университете в 1883 – 1891 гг.
Альфред Капели (1858 – 1916) ─ итальянский математик. Он, по-видимому, впервые дал формулировку теоремы с использованием термина «ранг матрицы» в своей работе в 1892г.
Теорема Кронекера-Капелли.
Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.
Пример. Исследовать систему на совместность
Решение. Приведение матрицы системы и расширенной матрицы системы к ступенчатому виду будем выполнять одновременно.
Ранг матрицы системы равен 2, а ранг расширенной матрицы системы равен 3. По теореме Кронекера-Капелли система несовместна.
Метод Гаусса решения системы линейных уравнений.
Метод Гаусса применяется для произвольной системы линейных уравнений. Нам понадобится
Определение. Систему линейных уравнений будем называть ступенчатой, если матрица этой системы ступенчатая.
При решении системы линейных уравнений применим следующий алгоритм:
1. Записываем расширенную матрицу системы (1) и приводим её к ступенчатому виду,
определяем ранги матрицы и расширенной матрицы системы.
2. Если найденные ранги не равны, то система несовместна.
3. Ранг матрицы системы равен рангу расширенной матрицы системы и равен числу r. В
этом случае система совместна и надо найти её решение.
4. Используя ступенчатый вид расширенной матрицы системы, записываем соответствующую ступенчатую систему.
5. Если число r равно числу неизвестных n, то ступенчатая система имеет вид
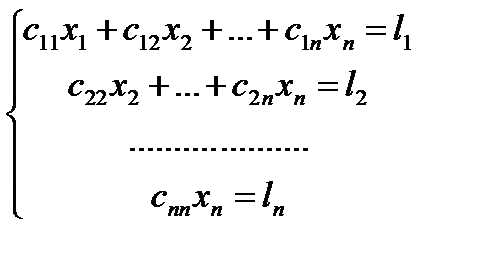 (2)
(2)
Из системы (2) последовательно находим значения для х1, х2,…, хт, начиная с последнего уравнения. В этом случае система (1) имеет единственное решение.
6. Если число r меньше числа неизвестных, то ступенчатая система имеет вид
 (3)
(3)
В системе (3) r уравнений и n неизвестных. Неизвестные х1,…,хj1, которые первыми встречаются в уравнениях системы (3), назовём главными неизвестными, остальные ─ свободными неизвестными. Из системы (3) последовательно выражаем главные неизвестные через свободные, начиная с последнего уравнения. Свободные неизвестные могут принимать любые значения. В этом случае система имеет бесконечно много решений.
Примеры.
1). Ответ: (2;-3;-1).
2) Ответ: нет решений.
3) Ответ: бесконечно много решений.
Правило Крамера решения систем линейных уравнений.
Габриэль Крамер (1704 – 1752) ─ швейцарский математик, который в 1750 г. нашёл метод решения систем линейных уравнений, названный впоследствии правилом Крамера.
Определение. Система линейных уравнений называется крамеровской,если тело уравнений равно числу неизвестных и определитель матрицы системы отличен от нуля.
Теорема 7.1. Крамеровская система имеет единственное решение, которое находится по формулам
где ─ определитель матрицы системы, ─ определитель, полученный из , заменой столбца коэффициентов при на столбец свободных членов.
Доказательство. Пусть дана крамеровская система
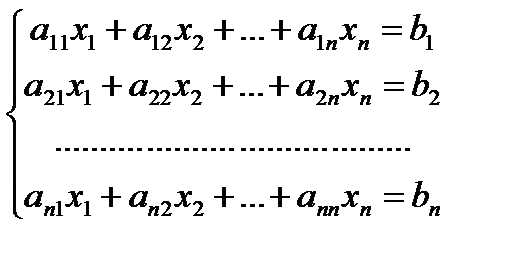 (4)
(4)
Тогда
│А│= ∆ =  ¹ 0.
¹ 0.
По теореме 3 лекции 6 матрица системы А имеет обратную матрицу А-1.
Запишем крамеровскую систему (4) в матричном виде
АХ = В (5)
где
А =  , Х = , В = .
, Х = , В = .
Умножим обе части матричного уравнения (5) слева на А-1:
А-1(АХ) = А-1В,
Ввиду ассоциативности умножения матриц имеем
А-1(АХ) = (А-1А)Х = ЕТХ = Х.
Таким образом,
Х = А-1В ─ решение системы.
1) Покажем, что такое решение единственно. Предположим, что Х1 и Х2 ─ два решения матричного уравнения (5). Тогда АХ1 = В и АХ2 = В, откуда АХ1 = АХ2. Умножая обе чисти равенства на А-1 слева, имеем
А-1(АХ1) = А-1(АХ2),
(А-1А)Х1 = (А-1А)Х2,
ЕnХ1 = ЕnХ2,
Х1 = Х2.
Следовательно, система (4) имеет единственное решение.
2) Найдём решение системы (4). Из равенства Х = А-1В имеем:
= 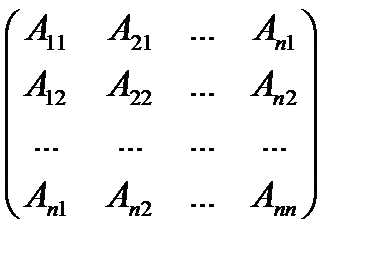 ,
,
откуда
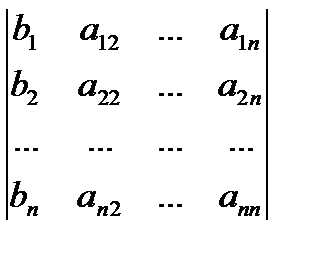 ,
,
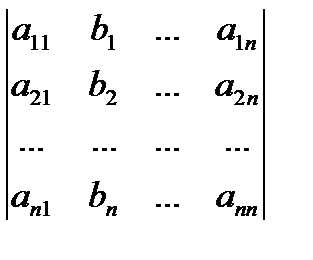 ,
,
……………………………………………………..
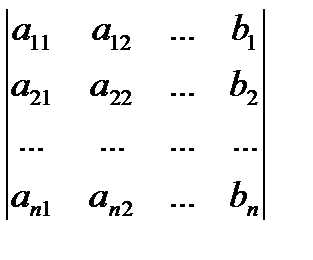 .
.
Обозначая определители в правой части равенств соответственно, получим формулы .
Пример. Решить систему уравнений по правилу Крамера
Ответ: (1;1;1).
Рекомендуемые страницы:
lektsia.com

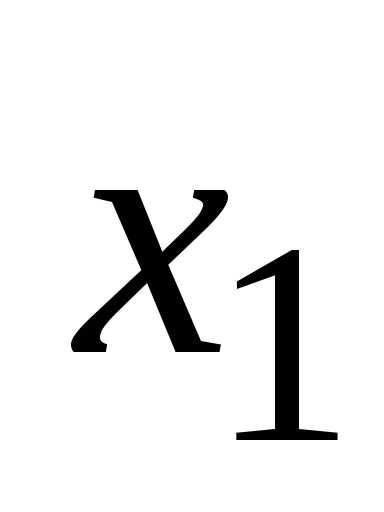
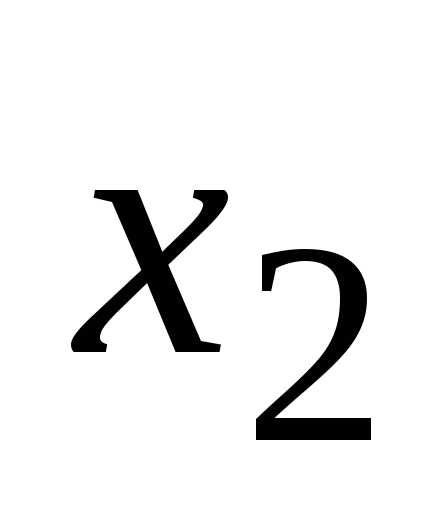

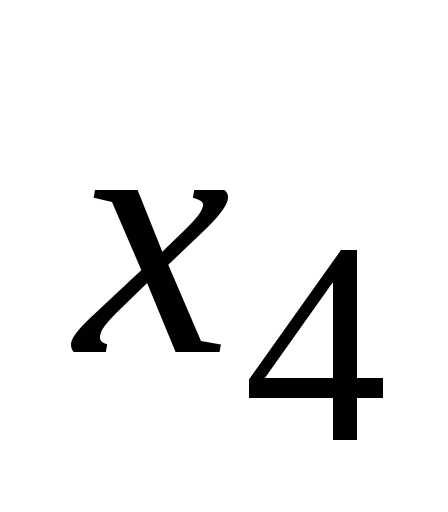


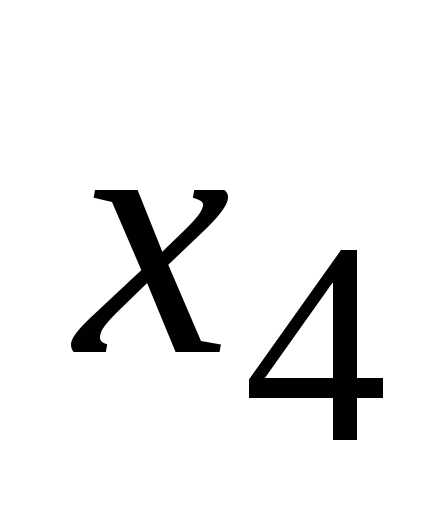
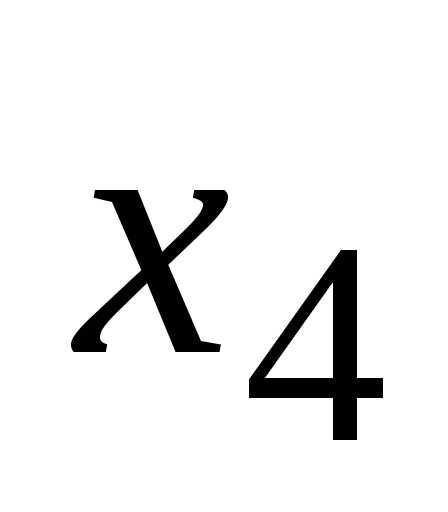
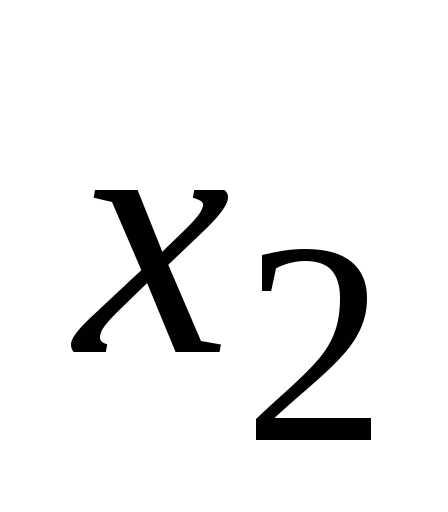
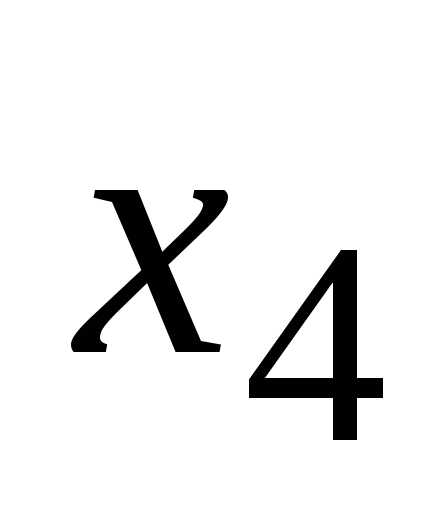

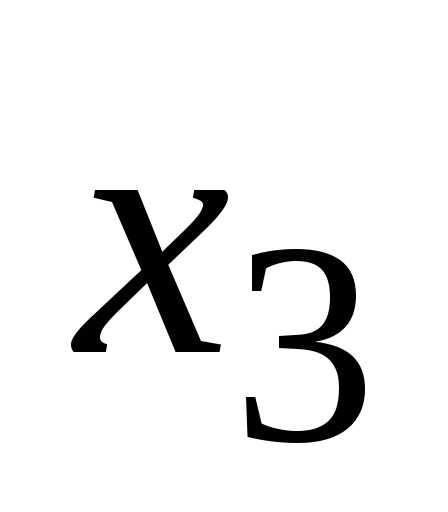
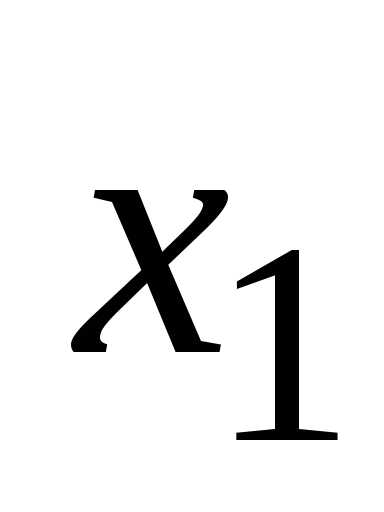
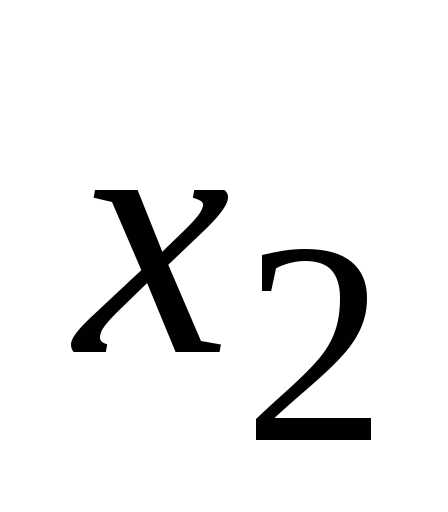
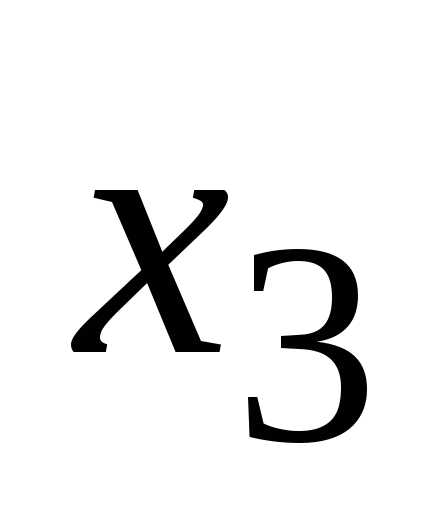
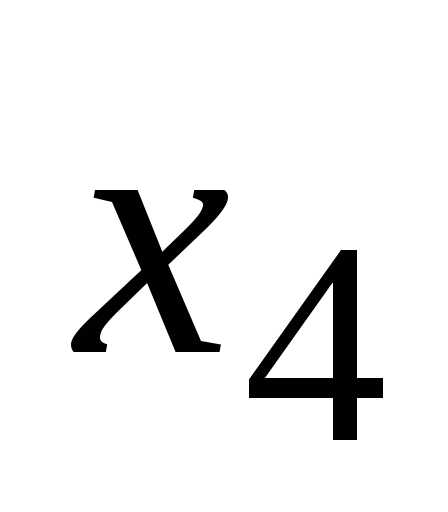
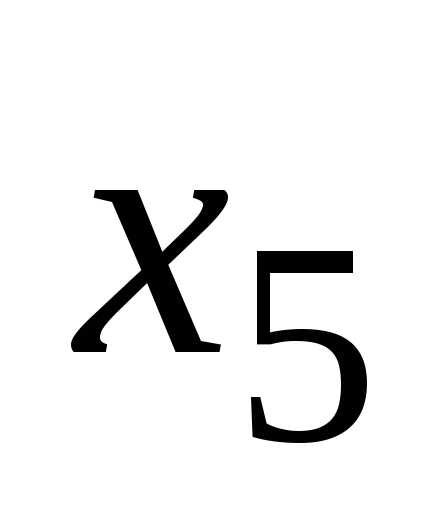
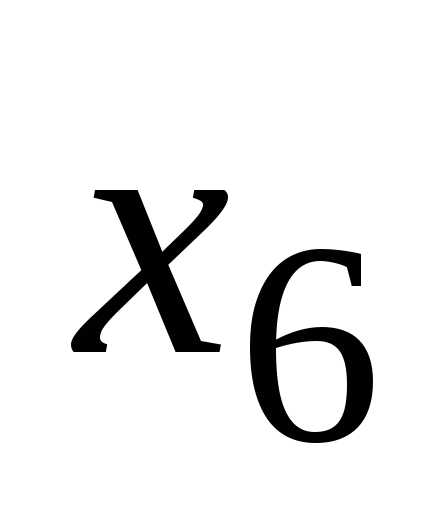
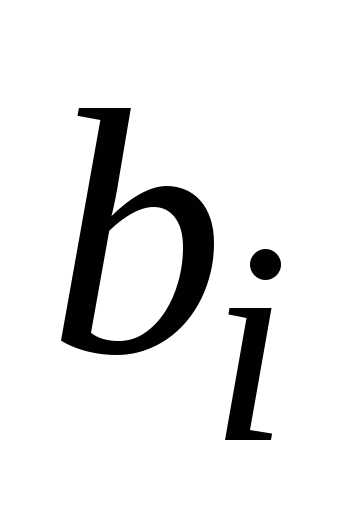
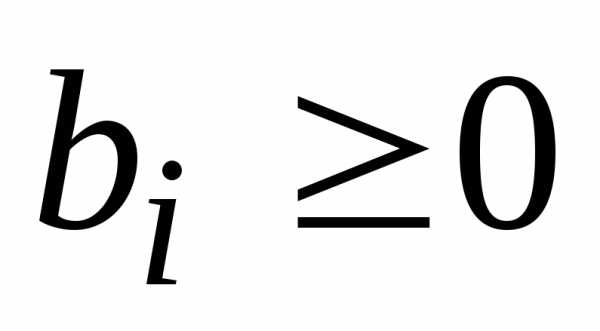 ;
;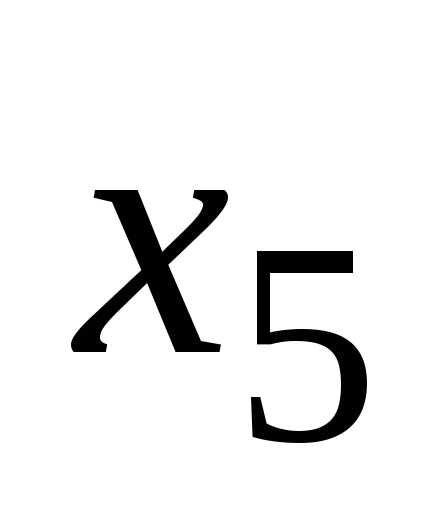
 ;
;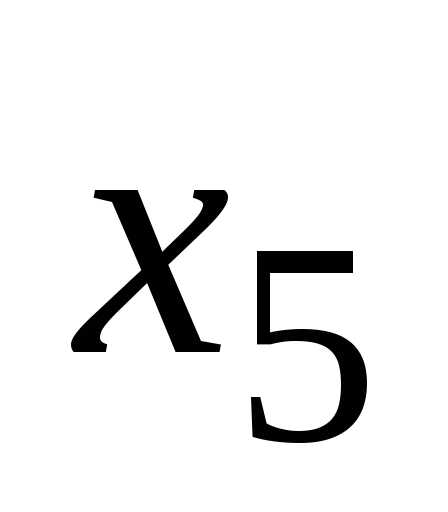
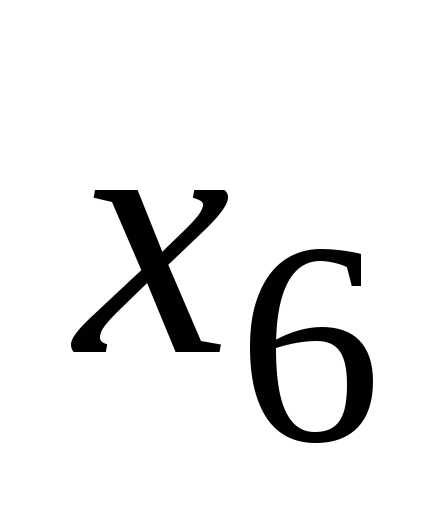
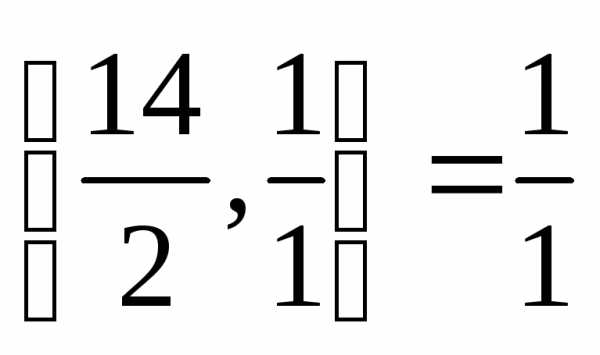 ;
;
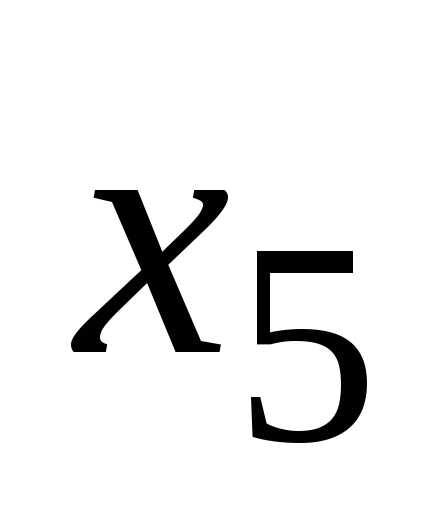
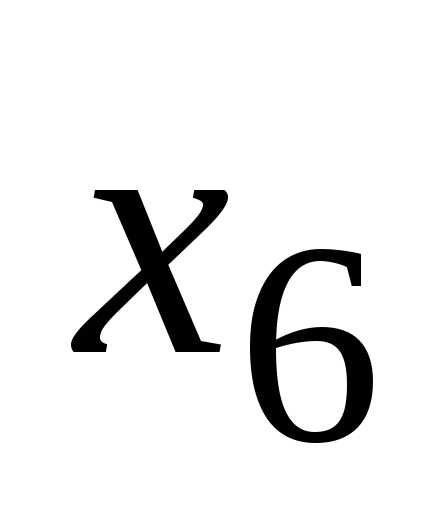
 ;
;
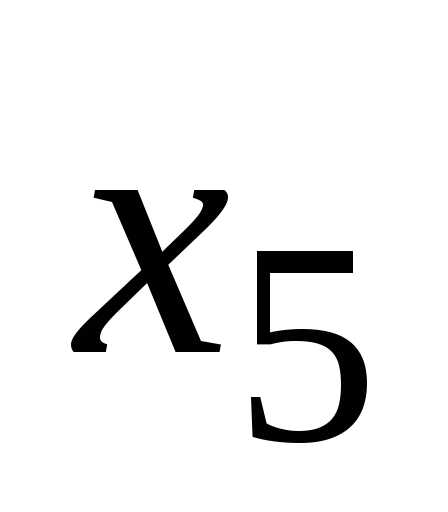
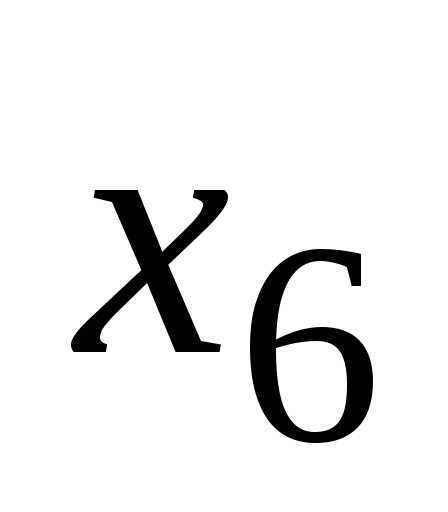
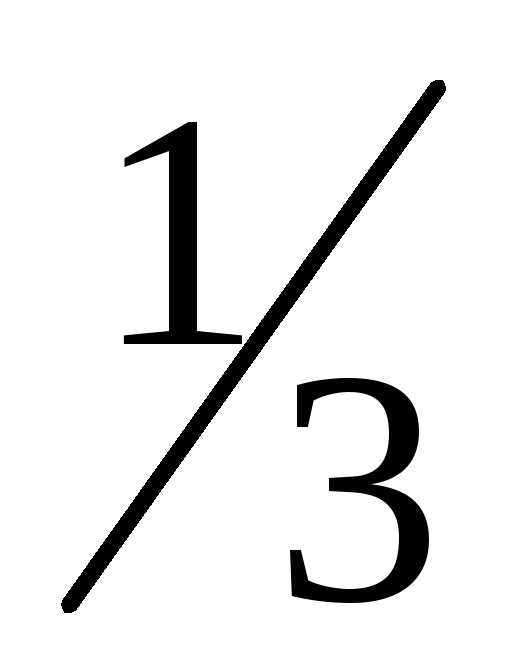

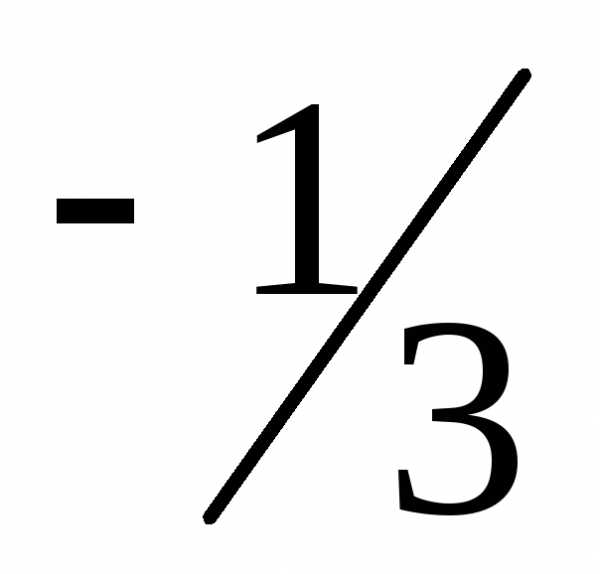
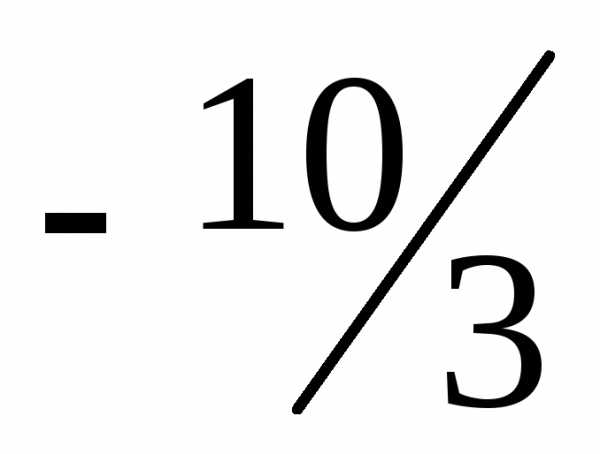

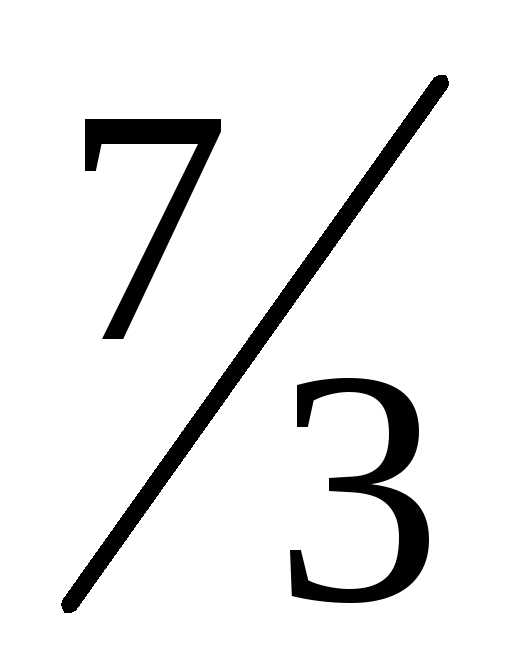


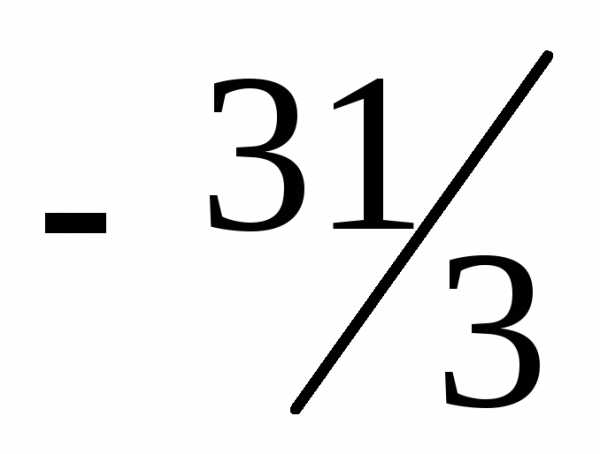
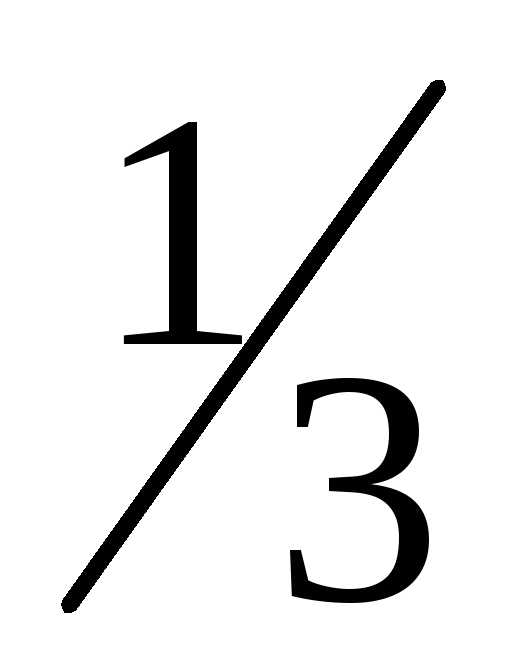
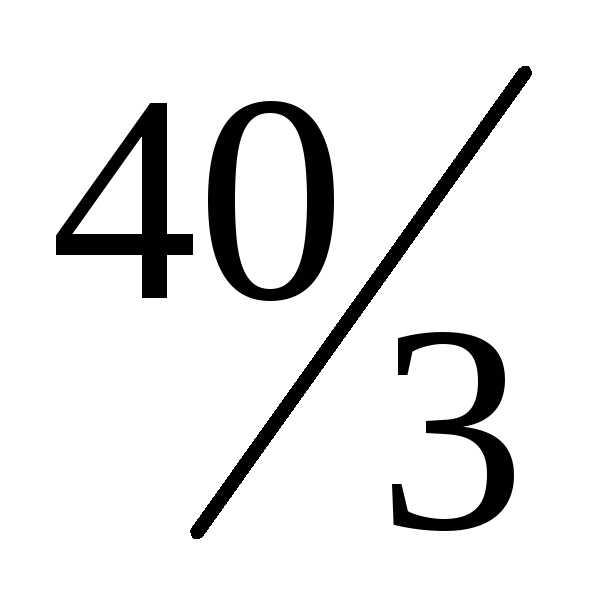
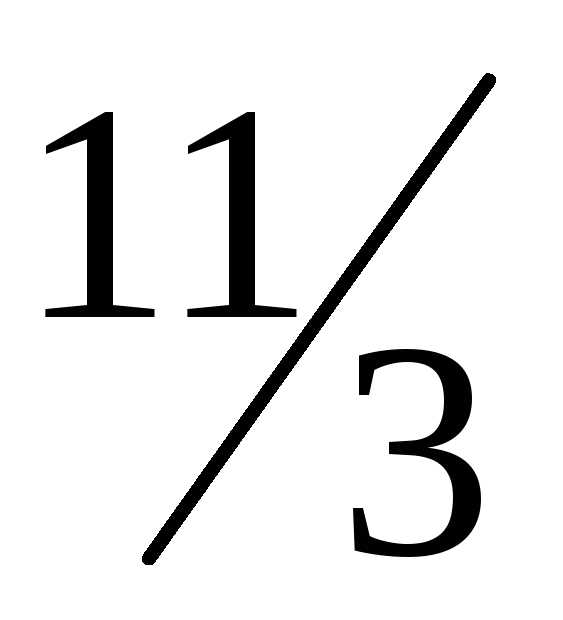
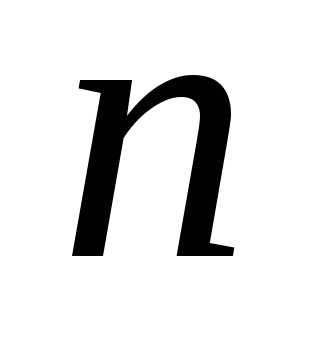 —
го порядка равен сумме произведений
всех его миноров
—
го порядка равен сумме произведений
всех его миноров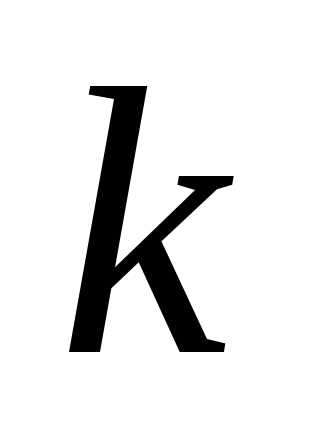 —
го порядка, стоящих в выделенных
—
го порядка, стоящих в выделенных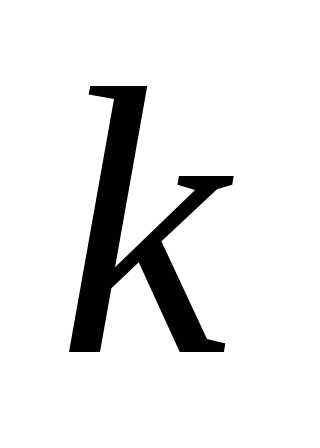 строках
(столбцах), на их алгебраические
дополнения.
строках
(столбцах), на их алгебраические
дополнения.