Математическая модель в экономике – Экономико-математическая модель — это… Что такое Экономико-математическая модель?

Содержание

Математические модели в экономике

МПС Российской федерации

Уральский Государственный Университет Путей Сообщения

Челябинский Институт Путей Сообщения

КУРСОВАЯ РАБОТА

по курсу: “Экономико-математическое моделирование»

Тема: “Математические модели в экономике»

Выполнил:

Шифр:

Адрес:

Проверил:

Челябинск 200_ г.

План

Введение

Часть № 1 «Исследование математической модели»

Составление математической модели

Создание и сохранение отчетов

Анализ найденного решения. Ответы на вопросы

Выводы

Часть № 2 «Расчет экономико-математической модели межотраслевого баланса

Решение задачи на компьютере

Межотраслевой баланс производства и распределения продукции

Выводы

Литература

Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХ в. Однако, методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться роль моделирования как универсального метода научного познания.

Термин «модель» широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Рассмотрим только такие «модели», которые являются инструментами получения знаний.

Модель — это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.

Под моделированием понимается процесс построения, изучения и применения моделей. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез.

Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания.

Необходимость использования метода моделирования определяется тем, что многие объекты (или проблемы, относящиеся к этим объектам) непосредственно исследовать или вовсе невозможно, или же это исследование требует много времени и средств.

Моделирование — циклический процесс. Это означает, что за первым четырехэтапным циклом может последовать второй, третий и т.д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта и ошибками в построении модели, можно исправить в последующих циклах. В методологии моделирования, таким образом, заложены большие возможности саморазвития.

Целью математического моделирования экономических систем является использование методов математики для наиболее эффективного решения задач, возникающих в сфере экономики, с использование, как правило, современной вычислительной техники.

Процесс решения экономических задач осуществляется в несколько этапов:

Содержательная (экономическая) постановка задачи. Вначале нужно осознать задачу, четко сформулировать ее. При этом определяются также объекты, которые относятся к решаемой задаче, а также ситуация, которую нужно реализовать в результате ее решения. Это — этап содержательной постановки задачи. Для того, чтобы задачу можно было описать количественно и использовать при ее решении вычислительную технику, нужно произвести качественный и количественный анализ объектов и ситуаций, имеющих к ней отношение. При этом сложные объекты, разбиваются на части (элементы), определяются связи этих элементов, их свойства, количественные и качественные значения свойств, количественные и логические соотношения между ними, выражаемые в виде уравнений, неравенств и т.п. Это — этап системного анализа задачи, в результате которого объект оказывается представленным в виде системы.

Следующим этапом является математическая постановка задачи, в процессе которой осуществляется построение математической модели объекта и определение методов (алгоритмов) получения решения задачи. Это — этап системного синтеза (математической постановки) задачи. Следует заметить, что на этом этапе может оказаться, что ранее проведенный системный анализ привел к такому набору элементов, свойств и соотношений, для которого нет приемлемого метода решения задачи, в результате приходится возвращаться к этапу системного анализа. Как правило, решаемые в экономической практике задачи, стандартизованы, системный анализ производится в расчете на известную математическую модель и алгоритм ее решения, проблема состоит лишь в выборе подходящего метода.

Следующим этапом является разработка программы решения задачи на ЭВМ. Для сложных объектов, состоящих из большого числа элементов, обладающих большим числом свойств, может потребоваться составление базы данных и средств работы с ней, методов извлечения данных, нужных для расчетов. Для стандартных задач осуществляется не разработка, а выбор подходящего пакета прикладных программ и системы управления базами данных.

На заключительном этапе производится эксплуатация модели и получение результатов.

Таким образом, решение задачи включает следующие этапы:

1. Содержательная постановка задачи.

2. Системный анализ.

3. Системный синтез (математическая постановка задачи)

4. Разработка или выбор программного обеспечения.

5. Решение задачи.

Последовательное использование методов исследования операций и их реализация на современной информационно-вычислительной технике позволяет преодолеть субъективизм, исключить так называемые волевые решения, основанные не на строгом и точном учете объективных обстоятельств, а на случайных эмоциях и личной заинтересованности руководителей различных уровней, которые к тому же не могут согласовать эти свои волевые решения.

Системный анализ позволяет учесть и использовать в управлении всю имеющуюся информацию об управляемом объекте, согласовать принимаемые решения с точки зрения объективного, а не субъективного, критерия эффективности. Экономить на вычислениях при управлении то же самое, что экономить на прицеливании при выстрелах. Однако ЭВМ не только позволяет учесть всю информацию, но и избавляет управленца от ненужной ему информации, а всю нужную пускает в обход человека, представляя ему только самую обобщенную информацию, квинтэссенцию. Системный подход в экономике эффективен и сам по себе, без использования ЭВМ, как метод исследования, при этом он не изменяет ранее открытых экономических законов, а только учит, как их лучше использовать.

Сложность процессов в экономике требует от человека, принимающего решения, высокой квалификации и большого опыта. Это, однако, не гарантирует ошибок, дать быстрый ответ на поставленный вопрос, провести экспериментальные исследования, невозможные или требующие больших затрат и времени на реальном объекте, позволяет математическое моделирование.

Математическое моделирование позволяет принять оптимальное, то есть наилучшее решение. Оно может незначительно отличаться от грамотно принятого решения без применения математического моделирования (около 3%). Однако при больших объемах производства такая «незначительная» ошибка может привести к огромным потерям.

Excel и Mathcad имеются средства, позволяющие провести математический анализ и найти оптимальное решение.

Постановка задачи.

На предприятии имеется возможность выпуска продукции 4-х видов. Для выпуска единицы продукции каждого вида необходимо затратить определенное количество трудовых, финансовых, сырьевых ресурсов. В наличии имеется ограниченное количество каждого ресурса. Реализация единицы продукции приносит прибыль. Значения параметров приведены в таблице 1. Дополнительное условие: финансовые затраты на производство продукций №2 и №4 не должны превышать 50р. (каждого вида).

На основе математического моделирования средствами Excel

определить, какую продукцию и в каких количествах целесообразно произвести с точки зрения получения наибольшей прибыли, проанализировать результаты, ответить на вопросы, сделать выводы.

Таблица 1.

mirznanii.com

Математические методы в экономике — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 марта 2017; проверки требуют 7 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 марта 2017; проверки требуют 7 правок.

Эта статья или раздел описывает ситуацию применительно лишь к одному региону, возможно, нарушая при этом правило о взвешенности изложения.

Вы можете помочь Википедии, добавив информацию для других стран и регионов.

Математические методы в экономике — научное направление в экономике, посвящённое исследованию экономических систем и процессов с помощью математических моделей. Включают в себя^{[источник не указан 472 дня]}:

Математические методы являются важнейшим инструментом анализа экономических явлений и процессов, построения теоретических моделей, позволяющих отобразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику. Математическое моделирование становится языком современной экономической теории, одинаково понятным для учёных всех стран мира^[1].

Математика как основа теории принятия решений широко применяется для управления (планирования, прогнозирования, контроля) экономическими объектами и процессами. Например, прогнозы социально-экономического развития РФ, разрабатываемые МЭРТ, основаны на математическом анализе ретросп

ru.wikipedia.org

Классификация математических моделей, используемых в экономике и менеджменте

Курсовая работа

Классификация математических моделей, используемых в экономике и менеджменте

Содержание

Введение

1. Математические модели в экономике и менеджменте

1.1 Классификация экономико-математических моделей

2. Оптимизационное моделирование

2.1 Линейное программирование

2.1.1 Линейное программирование как инструмент математического моделирования экономики

2.1.2 Примеры моделей линейного программирования

2.2 Динамическое программирование

2.2.1 Модель динамического программирования

2.2.2 Принцип оптимальности и уравнение Беллмана

2.2.3 Общее описание процесса моделирования и построения вычислительной схемы динамического программирования

2.2.4 Оптимальное распределение ресурсов

2.2.5 Оптимальное управление запасами

2.2.6 Задача о замене

Заключение

Современная математика характеризуется интенсивным проникновением в другие науки, во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Математика стала для многих отраслей знаний не только орудием количественного расчёта, но также методом точного исследования и средством предельно чёткой формулировки понятий и проблем. Без современной математики с её развитым логическим и вычислительным аппаратом был бы не возможен прогресс в различных областях человеческой деятельности.

Экономика как наука об объективных причинах функционирования и развития общества пользуется разнообразными количественными характеристиками, а поэтому вобрала в себя большое число математических методов.

Актуальность данной темы состоит в том, что в современной экономике используются оптимизационные методы, которые составляют основу математического программирования, теории игр, сетевого планирования, теории массового обслуживания и других прикладных наук.

Изучение экономических приложений математических дисциплин, составляющих основу актуальной экономической математики, позволяет приобрести некоторые навыки решения экономических задач и расширить знания в этой области.

Целью данной работы является изучение некоторых оптимизационных методов, применяемых при решении экономической задач.

Математические модели в экономике. Широкое использование математических моделей является важным направлением совершенствования экономического анализа. Конкретизация данных или представление их в виде математической модели помогает выбрать наименее трудоёмкий путь решения, повышает эффективность анализа.

Все экономические задачи, решаемые с применением линейного программирования отличаются альтернативностью решения и определенными ограничивающими условиями. Решить такую задачу — значит выбрать из всех допустимо возможных (альтернативных) вариантов лучший, оптимальный. Важность и ценность использования в экономике метода линейного программирования состоят в том, что оптимальный вариант выбирается из достаточно значительного количества альтернативных вариантов.

Самыми существенными моментами при постановке и решении экономических задачах в виде математической модели являются:

· адекватность экономико-математической модели действительности;

· анализ закономерностей, соответствующих данному процессу;

· определение методов, с помощью которых можно решить задачу;

· анализ полученных результатов или подведение итога.

Под экономическим анализом понимается прежде всего факторный анализ.

Пусть y=f(x_i ) — некоторая функция, характеризующая изменение показателя или процесса; x₁ ,x₂ ,…,x_n — факторы, от которых зависит функция y=f(x_i ). Задана функциональная детерминированная связь показателя y с набором факторов . Пусть показатель y изменился за анализируемый период. Требуется определить, какой частью численное приращение функции y=f(x₁ ,x₂ ,…,x_n ) обязано приращению каждого фактора.

Можно выделить в экономическом анализе — анализ влияния производительности труда и численности работающих на объем произведенной продукции; анализ влияния величины прибыли основных производственных фондов и нормируемых оборотных средств на уровень рентабельности; анализ влияния заемных средств на маневренность и независимость предприятия и т. п..

В экономическом анализе, кроме задач, сводящихся к разбиению его на составляющие части, существует группа задач, где требуется функционально увязать ряд экономических характеристик, т.е. построить функцию, содержащую в себе основное качество всех рассматриваемых экономических показателей.

В этом случае ставится обратная задача- так называемая задача обратного факторного анализа.

Пусть имеется набор показателей x₁ ,x₂ ,…,x_n , характеризующих некоторый экономический процесс F. Каждый из показателей характеризует этот процесс. Требуется построить функцию f(x_i ) изменения процесса F, содержащую основные характеристики всех показателей x₁ ,x₂ ,…,x_n

Главный момент в экономическом анализе — определение критерия, по которому будут сравниваться различные варианты решения.

Математические модели в менеджменте. Во всех сферах человеческой деятельности большую роль играет принятие решений. Для постановки задачи принятия решения необходимо выполнить два условия:

· наличие выбора;

· выбор варианта по определенному принципу.

Известны два принципа выбора решения: волевой и критериальный.

Волевой выбор, наиболее часто используемый, применяют при отсутствии формализованных моделей как единственно возможный.

Критериальный выбор заключается в принятии некоторого критерия и сравнении возможных вариантов по этому критерию, Вариант, для которого принятый критерий принимает наилучшее решение, называют оптимальным, а задачу принятия наилучшего решения – задачей оптимизации.

Критерий оптимизации называют целевой функцией.

Любую задачу, решение которой сводится к нахождению максимума или минимума целевой функции, называют экстремальной задачей.

Задачи менеджмента связаны с нахождением условного экстремума целевой функции при известных ограничениях, накладываемых на ее переменные.

В качестве целевой функции при решении различных оптимизационных задач принимают количество или стоимость выпускаемой продукции, затрат на производство, сумму прибыли и т.п. Ограничения обычно касаются людских материальных, денежных ресурсов.

Оптимизационные задачи менеджмента, различные по своему содержанию и реализуемые с использованием стандартных программных продуктов, соответствуют тому или иному классу экономико-математических моделей.

Рассмотрим классификацию некоторых основных задач оптимизации, реализуемых менеджментом на производстве.

Классификация задач оптимизации по функции управления:

Сочетание различных элементов модели приводит к различным классам задач оптимизации:

Существует значительное разнообразие видов, типов экономико-математических моделей, необходимых для использования в управлении экономическими объектами и процессами. Экономико-математические модели подразделяются на макроэкономические и микроэкономические в зависимости от уровня моделируемого объекта управления, динамические, которые характеризуют изменения объекта управления во времени, и статические, которые описывают взаимосвязи между разными параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в моделях, выделяются экономико-статистические, модели линейного и нелинейного программирования, матричные модели, сетевые модели.

mirznanii.com

Математические модели в экономике

Факультет дистанционного обучения

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)
Кафедра экономики
Контрольная работа № 1

по дисциплине «математические модели в экономике »

выполнена по методике М.Г. Сидоренко «математические модели в экономике»

Вариант-1
Выполнил:

студент ФДО ТУСУР

гр.: з-828-Б

специальности 080105

Афонина Ю.В,

1 декабря 2010 г.
Г. Нефтеюганск

2010г

Задание 1
В пространстве трех товаров рассмотрите бюджетное множество при векторе цен P и доходе Q. Описать его и его границу с помощью обычных и векторных неравенств и равенств, изобразите бюджетное множество и его границу графически. В ответ дать число, равное объему бюджетного множества.

Вариант	1
Данные	P = (1,3,4) Q = 24

Цена товара , товара, товара и бюджетное множество есть пирамида ОАВС. Точка А имеет координату , точка В имеет координату , точка С имеет координату .

Бюджетное множество B(P,Q) и его граница G(P,Q) зависят от цен и дохода.

Бюджетное множество и его границу можно определить с помощью обычных неравенств и равенств так:

и с помощью векторных равенств и неравенств

Объем бюджетного множества равен объему построенной пирамиды ОАВС.

Объему пирамиды ОАВС равен одной трети произведения площади основания на высоту:

где S – площадь основания, H – высота пирамиды.

В рассматриваемом случае высота Н равна 24.

Площадь основания равна Ѕ АВ умножить на ВС и на синус угла между ними.

Задание 2
Даны зависимости спроса D и предложения S от цены. Найдите равновесную цену, при которой выручка максимальна и эту максимальную выручку.

Вариант	Данные
1	D = 1000 – 10p; S = 100 +10p

Решение:

Точка равновесия характеризуется равенством спрос и предложения, т.е. 1000 – 10p = 100+10p. Равновесная цена p^* = 45 и выручка при равновесной цене W(p^*) = p^** D(p^*) = p^** S(p^*) = 24750.

При цене p > p^* объем продаж и выручка определяется функцией спроса, при p < p^* — предложения. Необходимо найти цену , определяющую максимум выручки:

p*(1000 – 10p) – функция имеет максимум в точке 50, W(50)=25000

p*(100 — 10p) –функция максимальна в точке 5, W(5)=250

Таким образом, максимальная выручка W(р) =25000 достигается не при равновесной цене.

Задание 3
Найдите решение матричной игры (оптимальные стратегии и цену игры).

Вариант	Игра
1

Сначала необходимо проверить наличие седловой точки. Седловой точки нет.

Обозначим стратегию Первого , искомую оптимальную стратегию Второго .

Выигрыш Первого есть случайная величина с таким рядом распределения:

W(x,y):	2	-3	-2	2
W(x,y):	xy	x(1-y)	(1-x)y	(1-x) (1-y)

Находим средний выигрыш за партию Первого – математическое ожидание случайной величины W(x,y):

M(x,y)=2xy-3x(1-y)-2(1-x)y+2(1-x)(1-y)=2xy-3x+3xy-2y+2xy+2-2x-2y+2xy=9xy-5x-4y+2=9x(y-5/9)-4(y-5/9)+6/9=9(y-5/9)(x-4/9)+6/9
Для нахождения оптимальных стратегий игроков необходимо, чтобы M(x,y^*)≤ M(x^*,y^*)≤ M(x^*,y). Это выполняется при x^*=4/9 и y^*=5/9, так как именно в этом случае M(x , 5/9) = M(4/9 , 5/9) = M(4/9 , y) = 6/9.

Следовательно, оптимальная стратегия первого игрока есть
,
Второго — . Цена игры по определению равна v=M(P^*,Q^*)=6/9
Задание 4
Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции. Найти коэффициенты полных материальных затрат двумя способами (с помощью формул обращения невырожденных матриц и приближенно), заполнить схему межотраслевого баланса.

Вариант	Данные
1

1. определим матрицу коэффициентов полных материальных затрат по второму способу, учитывая косвенные затраты до 2-го порядка включительно. Запишем матрицу коэффициентов косвенных затрат 1-го порядка:

матрицу коэффициентов второго порядка:

Таким образом, матрица коэффициентов полных материальных затрат приближенно равна:

3. определим матрицу коэффициентов полных материальных затрат с помощью формул обращения невыраженных матриц (первый способ).

А) находим матрицу (Е — А):

Б) вычисляем определитель этой матрицы:

В) транспонируем матрицу (Е — А):

Г) находим алгебраические дополнения для элемента матрицы :

Таким образом, присоединенная к матрице (Е – А) матрица имеет вид:

Д) используя формулу (7.14), находим матрицу коэффициентов полных материальных затрат:

Элементы матрицы В, рассчитанные по точным формулам обращения матриц, больше соответствующих элементов матрицы, рассчитанных по второму приближенному способу без учета косвенных материальных затрат порядка выше 2-го.

1. найдем величины валовой продукции трех отраслей (вектор Х), используя формулу (7.9)

2. для определения элементов первого квадрата материального межотраслевого баланса воспользуемся формулой, вытекающей из формулы (7.4): . Из этой формулы следует, что для получения первого столбца первого квадрата нужно элементы первого столбца заданной матрицы А умножить на величину ; элементы второго столбца матрицы А умножить на ; элементы третьего столбца матрицы А умножить на .

Составляющие третьего квадранта (условно чистая продукция) находятся с учетом формулы (7.1) как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.

Четвертый квадрант в нашем примере состоит из одного показателя и служит, в частности, для контроля правильности расчета: сумма элементов второго квадранта должна в стоимостном материальном балансе совпадать с суммой элементов третьего квадранта. Результаты расчета приведены в таблице.

Производящие отрасли	Потребляющие отрасли
Производящие отрасли	1	2	3	Конечная продукция	Валовая продукция
1 2 3	476.76 397.3 158.92	118.04 59.02 59.02	0 33.76 0	200 100 120	794.6 590.2 337.6
Условно чистая продукция	-238.38	354.12	303.84	420
Валовая продукция	794.6	590.2	337.6		1722.4

Задание 5
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящей средней с интервалом сглаживания 3, методом экспоненциального сглаживания (=0,1), представить результаты сглаживания графически, определите для ряда трендовую модель в виде полинома первой степени (линейную модель), дайте точечный и интервальный прогноз на три шага вперед.

Вариант	Ряд данных
1	у = 12, 10, 11, 13, 14, 15, 14, 13, 15, 16

Найдем среднее арифметическое

Среднее квадратическое отклонение

t	1	2	3	4	5	6	7	8	9	10
	—	1.06	0.53	1,06	0.53	0.53	0.53	0.53	1.06	0.53

Аномальный уровень отсутствует.
Методом простой скользящей средней с интервалом сглаживания 3

Для вычисления сглаженных уровней ряда применяется формула:

где при нечетном m, в нашем случае m = 3, следовательно

y(t)	12	10	11	13	14	15	14	13	15	16
	—	—	11	11.3	12.7	14	14.3	14	14	14.7

Методом экспоненциального сглаживания (=0,1)

Экспоненциальное сглаживание осуществляется по формуле:, где — параметр сглаживания. В нашем случае = 0,1.

y(t)	12	10	11	13	14	15	14	13	15	16
	11.1	10.99	2.2	3.28	4.35	5.42	6.29	6.96	7.76	8.58

Графическое представление результатов сглажевания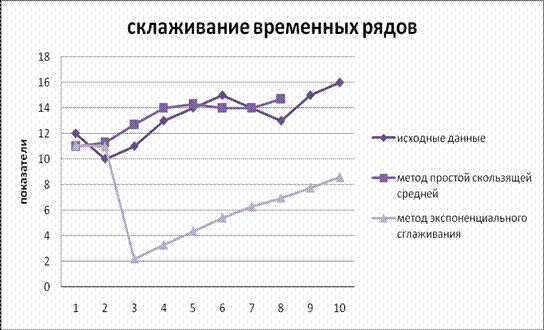

Ниже в таблице приведены исходный ряд данных yt и сглаженные двумя способами уровни исходного ряда. При этом при сглаживании при помощи метода простой скользящей средней использовался интервал сглаживания m = 3.

При сглаживании экспоненциальным методом был доведён параметр сглаживания а = 0,1
Соответственно, числовая последовательность весов имела вид:

t	yt	методом простой скользящей средней	_ методом y экспоненциального сглаживания
1	12	—	11.1
2	10	11	10.99
3	11	11.3	2.2
4	13	12.7	3.28
5	14	14	4.35
6	15	14.3	5.42
7	14	14	6.29
8	13	14	6.96
9	15	14.7	7.76
10	16	—	8.58

Чтобы правильно подобрать лучшую кривую роста для моделирования и прогнозирования экономического явления, необходимо знать особенности каждого вида кривых в экономике часто используется полиномиальная кривая роста, как кривая с полиномом первой степени.

Параметр a1 называют линейным приростом. Для полинома первой степени характерен постоянный закон роста. Если посчитать первые приросты по формуле

ut
=
yt
–
yt
-1,
t = 2,3,…,n,
то они будут постоянной величиной и равны а 1.

Значения прироста для полиномов любого порядка не зависят от значений самой функции .

Полиномные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня. Исходный временной ряд предварительно сглаживается методом простой скользящей средней.

Необходимо оценить адекватность и точность построения модели, т.е. необходимо выполнение следующих условий:

a) проверка случайности колебаний уровней остаточной последовательности:

Проверку случайности уровней ряда проведем по критерию пиков, должно выполняться:

Фактическое

Расчётное

Отклонение

Точки пиков

10.99

11.51

12.03

12.55

13.07

13.59

14.11

14.63

15.15

15.67

1.01

-1.51

-1.03

0.45

0.93

1.41

-0.11

-1.63

-0.15

0.33

—

133

133.3

—

a) проверка соответствия распределения случайной компоненты нормальному закону распределения:

В соответствии с характером изменения средних приростов и производных показателей выбирается вид кривой роста для исходного временного ряда.

Необходимые условия:

Если эти условия выполняются одновременно, то гипотеза о характере распределения случайной компоненты принимается, если выполняется хотя бы одно из следующих неравенств:

то гипотеза о нормальном распределении отвергается, трендовая модель признаётся неадекватной.
1)

2)
Таким образом, одно из неравенств не выполняется, трендовая модель неадекватна, значит, дальнейшее исследование не имеет смысла, но попробуем.

Прогнозирование экономических показателей на основе трендовых моделей основано на распространении закономерностей, связей и соотношений, действующих в изучаемом периоде, за его пределами. Достоверный прогноз возможен лишь относительно таких объектов и явлений, которые в значительной степени детерминируются прошлым и настоящим. При прогнозировании лучше задавать интервалы значений, в которых с достаточной долей уверенности можно ожидать появления прогнозируемой величины. Установление такого интервала называется интервальным прогнозом.

Прогноз на основании трендовых моделей (кривых роста) содержит два элемента: точечный и интервальный прогнозы.

Для полинома первой степени адекватная линейная модель

coolreferat.com

Экономико-математическая модель — это… Что такое Экономико-математическая модель?

Экономико-математическая модель [economic model, economico-mathematical model] — математическое описание экономического процесса или объекта, произведенное в целях их исследования и управления ими: математическая запись решаемой экономической задачи (поэтому часто термины “модель” и “задача” употребляются как синонимы). Существует еще несколько вариантов определения этого термина.

В самой общей форме модель — условный образ объекта исследования, сконструированный для упрощения этого исследования. При построении модели предполагается, что ее непосредственное изучение дает новые знания о моделируемом объекте (см. Моделирование). Все это полностью относится и к Э.-м.м.

В принципе в экономике применимы не только математические (знаковые), но и материальные модели. Например, гидравлические (в которых потоки воды имитируют потоки денег и товаров, а резервуары отождествляются с такими экономическими категориями, как объем промышленного производства, личное потребление и др.) и электрические (в США была известна модель «Эконорама», представлявшая собой сложную электрическую схему, в которой имитировались экономические процессы). Но все эти попытки имели лишь демонстрационное применение, а не служили средством изучения закономерностей экономики. С развитием же электронно-вычислительной техники потребность в них, по-видимому, и вовсе отпала.

Э.-м.м. оказывается в этих условиях основным средством модельного исследования экономики. Модель может описывать либо внутреннюю структуру объекта, либо, если структура неизвестна, — его поведение, т.е. реакцию на воздействие известных факторов (принцип «черного ящика«). Один и тот же объект может быть описан различными моделями в зависимости от исследовательской или практической потребности, возможностей математического аппарата и т.п. Поэтому всегда необходима оценка модели и области, в которой выводы из ее изучения могут быть достоверны.

Во всех случаях необходимо, чтобы модель содержала достаточно детальное описание объекта, позволяющее, в частности, осуществлять измерение экономических величин и их взаимосвязей, чтобы были выделены факторы, воздействующие на исследуемые показатели. Например, формула, по которой определяется на заводе потребность в материалах, исходя из норм расхода, есть Э.-м.м.

Если количество видов изделий обозначить через n, нормативы расхода — a_i , количество изделий каждого вида — x_i , то модель запишется так:

где i = 1, 2, …, n. Кроме того, полезно записать условия, в которых она действительна, т.е. ограничения модели (например, лимиты на те или иные материалы). Строго говоря, расчет по такой формуле не даст точного результата: потребность в материалах может зависеть также от случайных изменений в размерах брака и отходов, от страховых запасов и т.д. Но в общем, она зависит именно от указанных двух видов величин: норм расхода материала и объемов выпуска продукции. Первые из них в данном случае называются параметрами модели, вторые — переменными модели.

Такая модель называется описательной, или дескриптивной; она описывает зависимость расхода (потребности в материале), от двух факторов: количества изделий и расходных норм. Большое значение в экономике имеют оптимизационные модели (или оптимальные). Они представляют собой системы уравнений, равенств и неравенств, которые кроме ограничений (условий) включают также особого рода уравнение, называемое функционалом или критерием оптимальности. С помощью такого критерия находят решение, наилучшее по какому-либо показателю, например, минимум затрат на материалы при заданном объеме продукции, или, наоборот, максимум продукции (или прибыли) при заданных ограничениях по ресурсам и т.д.

Например, можно попытаться найти такой план работы цеха, который при заданном объеме материалов (т.е. их расход не должен быть больше какой-то величины, допустим, B) гарантирует наибольший объем продукции. Единственное, что надо при этом знать дополнительно — цену единицы продукции — p_i. Тогда модель будет записываться так

при условии

Кроме того, обязательно надо учесть, что искомые величины объемов производства каждого изделия не должны быть отрицательными:

x_i ≥ 0, i = 1, 2, …, n.

Мы получили элементарную оптимизационную модель, относящуюся к типу моделей линейного программирования. Решив эту модель, т.е. узнав значения всех x_i от 1-го до n-го, мы получим искомый план.

Важное свойство Э.-м.м. — их применимость к разным, на первый взгляд непохожим ситуациям. Например, если в приведенном примере через a_i обозначить нормы внесения удобрений, а через x_i — размеры участков, то та же самая формула покажет общий объем потребности в удобрениях. Точно такую же формулу можно применить к расчету затрат семьи на покупку разных продуктов, и во многих других случаях.

Модель может быть сформулирована тремя способами: в результате прямого наблюдения и изучения некоторых явлений действительности (феноменологический способ), вычленения из более общей модели (дедуктивный способ), обобщения более частных моделей (индуктивный способ).

Подобные модели, в которых описывается моментное состояние экономики, называются статическими (от слова «статика»). Те же, которые показывают развитие объекта моделирования, — динамическими. Модели могут строиться не только в виде формул, как рассмотренные здесь (это называется аналитическое представление модели; см. Аналитическая модель), но и в виде числовых примеров (численное представление) и в форме таблиц (матричное представление), и в форме особого рода графов (сетевое представление модели). Соответственно различают модели числовые, аналитические, матричные, сетевые.

Экономическая наука давно пользуется моделями. Одной из первых была модель воспроизводства, разработанная французским ученым Ф.Кенэ еще в XYIII в. А в XX в. первая общая модель развивающейся экономики была сконструирована Дж. фон Нейманом. Значительный опыт построения э.-м. моделей накоплен учеными СССР, применявшими их для анализа экономических процессов, прогнозирования и планирования во всех звеньях и на всех уровнях экономики, вплоть до планирования развития народного хозяйства страны в целом, особенно — перспективного.

Принято подразделять Э-м.м. на две большие группы:

модели, отражающие преимущественно производственный аспект экономики;

модели, отражающие преимущественно социальные аспекты экономики.

Разумеется, такое деление в значительной степени условно, поскольку в каждой из моделей в той или иной степени сочетаются производственный и социальный аспекты.

Из моделей первой группы можно назвать: модели долгосрочного прогноза сводных показателей экономического развития; межотраслевые модели; отраслевые модели оптимального планирования и размещения производства, а также модели оптимизации структуры производства в отраслях.

Из моделей второй группы наиболее разработаны модели, связанные с прогнозированием и планированием доходов и потребления населения, демографических процессов.

Существует большое число классификаций типов Э.-м.м., которые, однако, носят фрагментарный характер. И это, по-видимому, неизбежно, так как нереально охватить все многообразие социально-экономических задач, объектов и процессов, описываемых различными моделями.

Представленные в нашем словаре модели можно условно классифицировать следующим образом

1. Наиболее общее деление моделей — по способу отражения действительности:

Аналоговая модель

Иконическая модель (то же: портретная модель)

Концептуальная модель

Структурная модель

Функциональная модель.

2. По предназначению (цели создания и применения) модели:

Балансовая модель

Дескриптивная модель (то же: Описательная)

Имитационная модель

Информационная модель

Нормативная модель (то же: Прескриптивная модель),

в т.ч. Оптимальная модель (то же: Оптимизационная модель).

3. По способу логико-математического описания моделируемых экономических систем:

Аналитическая модель

Вероятностная модель (то же: Стохастическая модель)

Детерминированная модель

Дискретная модель

Линейная модель

Математико-статистическая модель

Матричная модель

Нелинейная модель

Непрерывная модель

Модель равновесия

Неравновесная модель

Регрессионная модель

Сетевая модель

Числовая модель

Эконометрическая модель.

— дискретного выбора

— непрерывной длительности (выживания)

-логит-иодель

-пробит-модель

— тобит-модель..

4. По временному и пространственному признаку:

Гравитационная модель

Динамическая модель (см . Динамические модели экономики)

Модели с «бесконечным временем»

Статическая модель

Точечная модель

Трендовая модель и др..

5. По уровню моделируемого объекта в хозяйственной иерархии:

Глобальная модель

Макроэкономическая модель (то же: Агрегатная модель)

Модели мезоэкономики

Микроэкономическая модель

6. По внутренней структуре модельного описания системы:

Автономная модель

Закрытая модель

Комплекс моделей

Многосекторная модель (многоотраслевая, многопродуктовая)

Однопродуктовая модель

Открытая модель

Система моделей (в том числе многоуровневая или многоступенчатая).

7.. По сфере применения .

Выше было указано на необозримость областей применения Э.-м.м.; поэтому мы не даем здесь их перечисления, а отсылаем к соответствующим статьям словаря: например, о прогнозных моделях — к статье Прогнозирование, об отраслевых — к статье Отраслевые задачи оптимального планирования развития и размещения производства, и т.д.

Наиболее развитая типология социально-экономических задач и моделей представлена в кн.: Вилкас Э.Й., Майминас Е.З. Решения: теория, информация, моделирование. — М.: “Радио и связь”, 1981.При разработке приведенной выше условной классификации учитывались материалы этой книги.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

economic_mathematics.academic.ru

Математические модели в экономике и программировании (Реферат)

Математические модели в экономике и программировании

1. Детерминированные и вероятностные математические модели в экономике. Преимущества и недостатки

Методы исследования экономических процессов базируются на использовании математических — детерминированных и вероятностных — моделей, представляющих изучаемый процесс, систему или вид деятельности. Такие модели дают количественную характеристику проблемы и служат основой для принятия управленческого решения при поисках оптимального варианта. Насколько обоснованы эти решения, являются ли они лучшими из возможных, учтены ли и взвешены все факторы, определяющие оптимальное решение, каков критерий, позволяющий определить, что данное решение действительно наилучшее, — таков круг вопросов, имеющих большое значение для руководителей производства, и ответ на которые можно найти с помощью методов исследования операций [Чесноков С. В. Детерминационный анализ социально-экономических данных. — М.: Наука, 1982, стр. 45].

Одним из принципов формирования системы управления является метод кибернетических (математических) моделей. Математическое моделирование занимает промежуточное положение между экспериментом и теорией: нет необходимости строить реальную физическую модель системы, ее заменит математическая модель. Особенность формирования системы управления заключается в вероятностном, статистическом подходе к процессам управления. В кибернетике принято, что любой процесс управления подвержен случайным, возмущающим воздействиям. Так, на производственный процесс оказывают влияния большое количество факторов, учесть которые детерминированным образом невозможно. Поэтому считается, что на производственный процесс воздействуют случайные сигналы. В силу этого планирование работы предприятия может быть только вероятностным.

По этим причинам часто, говоря о математическом моделировании экономических процессов, имеют в виду именно вероятностные модели.

Опишем каждый из типов математических моделей.

Детерминированные математические модели характеризуются тем, что описывают связь некоторых факторов с результативным показателем как функциональную зависимость, т. е. в детерминированных моделях результативный показатель модели представлен в виде произведения, частного, алгебраической суммы факторов, или в виде любой другой функции. Данный вид математических моделей наиболее распространен, поскольку, будучи достаточно простыми в применении (по сравнению вероятностными моделями), позволяет осознать логику действия основных факторов развития экономического процесса, количественно оценить их влияние, понять, какие факторы и в какой пропорции возможно и целесообразно изменить для повышения эффективности производства.

Вероятностные математические модели принципиально отличаются от детерминированных тем, что в вероятностных моделях взаимосвязь между факторами и результирующим признаком вероятностная (стохастическая): при функциональной зависимости (детерминированные модели) одному и тому же состоянию факторов соответствует единственное состояние результирующего признака, тогда как в вероятностных моделях одному и тому же состоянию факторов соответствует целое множество состояний результирующего признака [Толстова Ю. Н. Логика математического анализа экономических процессов. — М.: Наука, 2001, с. 32-33].

Преимущество детерминированных моделей в простоте их применения. Основной недостаток — низкая адекватность реальной действительности, т. к., как было отмечено выше, большинство экономических процессов носит вероятностный характер.

Достоинством вероятностных моделей является то, что они, как правило, больше соответствуют реальной действительности (более адекватны), чем детерминированные. Однако, недостатком вероятностных моделей является сложность и трудоемкость их применения, так что во многих ситуациях достаточно бывает ограничиться детерминированными моделями.

2. Постановка задачи линейного программирования на примере задачи о пищевом рационе

Впервые постановка задачи линейного программирования в виде предложения по составлению оптимального плана перевозок; позволяющего минимизировать суммарной километраж, была дана в работе советского экономиста А. Н. Толстого в 1930 году.

Систематические исследования задач линейного программирования и разработка общих методов их решения получили дальнейшее развитие в работах российских математиков Л. В. Канторовича, В. С. Немчинова и других математиков и экономистов. Также методам линейного программирования посвящено много работ зарубежных и, прежде всего, американских ученых.

Задача линейного программирования состоит в максимизации (минимизации) линейной функции.

, где

при ограничениях

(*)

причем все

Замечание. Неравенства могут быть и противоположного смысла. Умножением соответствующих неравенств на (-1) можно всегда получить систему вида (*).

Если число переменных системы ограничений и целевой функции в математической модели задачи равно 2, то её можно решить графически.

Итак, надо максимизировать функцию к удовлетворяющей системе ограничений.

Обратимся к одному из неравенств системы ограничений.

С геометрической точки зрения все точки, удовлетворяющие этому неравенству, должны либо лежать на прямой , либо принадлежать одной из полуплоскостей, на которые разбивается плоскость этой прямой. Для того чтобы выяснить это, надо проверить какая из них содержит точку ().

Замечание 2. Если , то проще взять точку (0;0).

Условия неотрицательности также определяют полуплоскости соответственно с пограничными прямыми . Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы — это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую (где h — некоторая постоянная). Чаще всего берется прямая . Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции.

Вектор в каждой точке перпендикулярен прямой , поэтому значение f будет возрастать при перемещении прямой в направлении градиента (убывать в направлении антиградиента). Для этого параллельно прямой проводим прямые, смещаясь в направлении градиента (антиградиента).

Эти построения будем продолжать до тех пор, пока прямая не пройдет через последнюю вершину многоугольника решений. Эта точка определяет оптимальное значение.

Итак, нахождение решения задачи линейного программирования геометрическим методом включает следующие этапы:

Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

Находят полуплоскости, определяемые каждым из ограничений задачи.

Находят многоугольник решений.

Строят вектор .

Строят прямую .

Строят параллельные прямые в направлении градиента или антиградиента, в результате чего находят точку, в которой функция принимает максимальное или минимальное значение, либо устанавливают неограниченность сверху (снизу) функции на допустимом множестве.

Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.

Задача о рациональном питании (задача о пищевом рационе)

Постановка задачи

Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П1, П2, П3, П4; стоимость единицы каждого продукта равна соответственно С1, С2, С3, С4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее b1 единиц; углеводов — не менее b2 единиц; жиров — не менее b3 единиц. Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице, где aij (i=1,2,3,4; j=1,2,3) — какие-то определённые числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры).

продукт

элементы

белки

углеводы

жиры

П1

П2

П3

П4

A11

A21

A31

A41

A12

A22

A32

A42

A13

A23

A33

A43

Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

Математическая модель

Обозначим x1, x2, x3, x4 количества продуктов П1, П2, П3, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать, — стоимость рациона (обозначим её L): она линейно зависит от элементов решения x1, x2, x3, x4.

Целевая функция:

Система ограничений:

a11x1+a21x2+a31x3+a41x4 больше или равно b1

a12x1+a22x2+a32x3+a42x4 больше или равно b2

a13x1+a23x2+a32x3+a43x4 больше или равно b3

Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения x1, x2, x3, x4.

Таким образом, поставленная задача сводится к следующему: найти такие неотрицательные значения переменных x1, x2, x3, x4, чтобы они удовлетворяли ограничениям — неравенствам и одновременно обращали в минимум линейную функцию этих переменных:

Список литературы

Гончаров В. В. Важнейшие понятия и концепции в современном управлении. — М.: МНИИПУ, 2002, 341 с.

История экономических учений. // Под ред. Н. А. Хохлова. — СПб: Питер, 2002, 324 с.

Казаков А. П., Минаев Н. В. Экономика. Курс лекций. Упражнения. Тесты и тренинги. — М.: Изд-во ЦИПКК АП, 1999, 359 с.

Макроэкономика. Учебное пособие. // Под ред. А. М. Бункина. — М.: Инфра-М, 1995, 337 с.

Нуриев, Розанова. Поведение потребителя в рыночной экономике. // Вопросы экономики, 2003, № 1, с. 4-9.

Социально-экономическая статистика. // Под ред. Г. Л. Громыко. — М.: Изд-во МГУ, 1999, 350 с.

Толстова Ю. Н. Логика математического анализа экономических процессов. — М.: Наука, 2001, 160 с.

Ховард К., Эриашвили Н. Д., Никитин А. М. Экономическая теория. — М, 2000, 564 с.

Чесноков С. В. Детерминационный анализ социально-экономических данных. — М.: Наука, 1982, 259 с.

Для подготовки данной работы были использованы материалы с сайта http://www.matematika-r.info/

topref.ru

Математические модели в экономике 2

МПС Российской федерации

Уральский Государственный Университет Путей Сообщения

Челябинский Институт Путей Сообщения
КУРСОВАЯ РАБОТА

по курсу: “Экономико-математическое моделирование»

Тема: “Математические модели в экономике»
Выполнил:

Шифр:

Адрес:

Проверил:
Челябинск 200_ г.

План
Введение

Часть № 1 «Исследование математической модели»

Составление математической модели

Создание и сохранение отчетов

Анализ найденного решения. Ответы на вопросы

Выводы

Часть № 2 «Расчет экономико-математической модели межотраслевого баланса

Решение задачи на компьютере

Межотраслевой баланс производства и распределения продукции

Выводы

Литература

_{Введение}

Процесс решения экономических задач осуществляется в несколько этапов:

На заключительном этапе производится эксплуатация модели и получение результатов.

Таким образом, решение задачи включает следующие этапы:

1. Содержательная постановка задачи.

2. Системный анализ.

3. Системный синтез (математическая постановка задачи)

4. Разработка или выбор программного обеспечения.

5. Решение задачи.

Математические методы, применяемые для анализа математической модели и принятия оптимального решения, весьма сложны и их реализация без применения ЭВМ затруднительна. В составе программ Excel и Mathcad имеются средства, позволяющие провести математический анализ и найти оптимальное решение.

coolreferat.com

РубрикаПолезно знать

Математическая модель в экономике – Экономико-математическая модель — это… Что такое Экономико-математическая модель?

Математические модели в экономике

Математические методы в экономике — Википедия

Классификация математических моделей, используемых в экономике и менеджменте

Математические модели в экономике

Экономико-математическая модель — это… Что такое Экономико-математическая модель?

Математические модели в экономике и программировании (Реферат)

Математические модели в экономике 2

Введение

Добавить комментарий Отменить ответ

_{Введение}