Квадратный график – Квадратичная функция и ее график

Квадратичная функция и ее график

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где  называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:

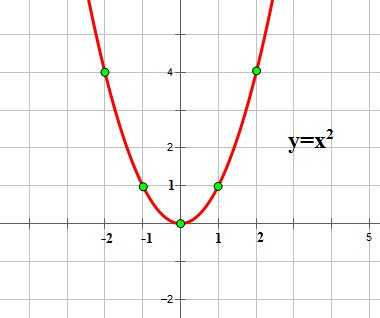
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.

График  функции  имеет вид:

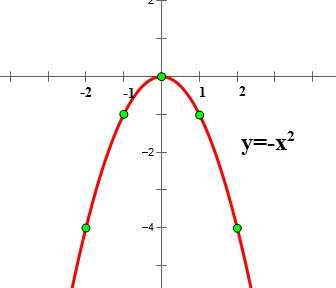
Для нахождения координат базовых точек составим таблицу:

 

Обратите внимание, что график функции  симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика  функции — значения х, в которых функция равна нулю, или нули функции

. На графике нули функции  — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты  точек  пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции  нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

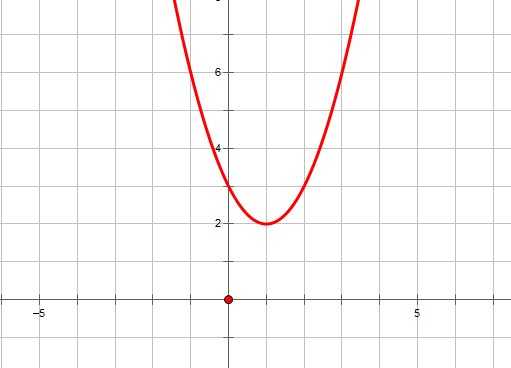
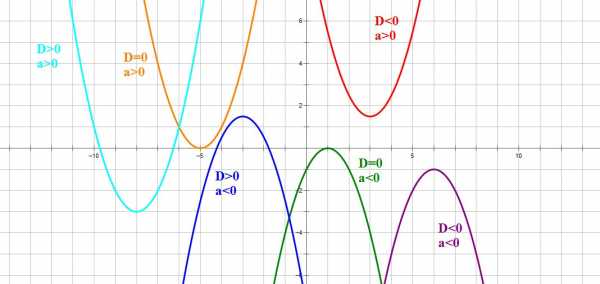
1. Если ,то уравнение  не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

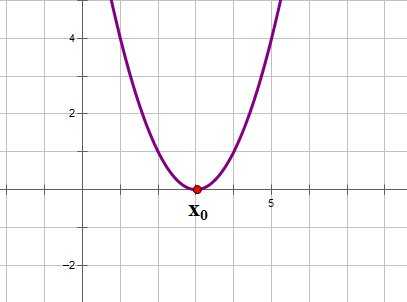
2. Если ,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола   имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

3.  Если ,то уравнение  имеет два решения, и, следовательно, квадратичная парабола   имеет две точки пересечения с осью ОХ:

,  

Если ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

 

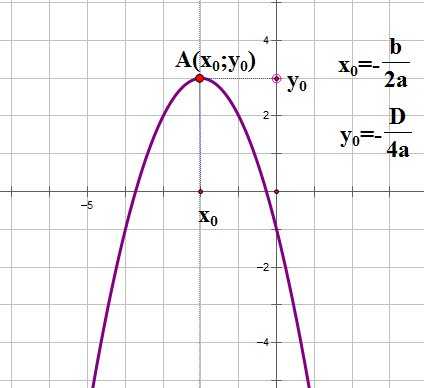
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы  с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

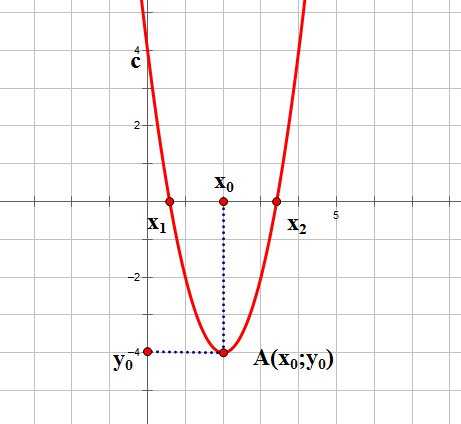
Итак, основные параметры графика квадратичной функции показаны  на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

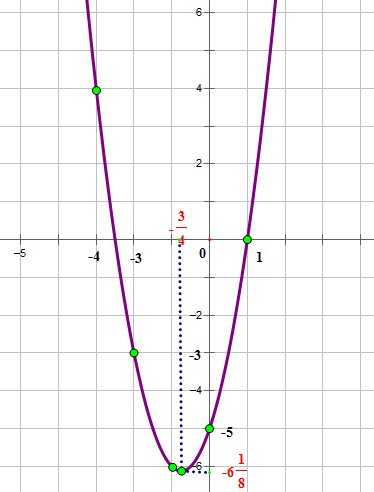
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 

1. Направление ветвей параболы.

Так как ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена 

 

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение: 

,  

3.   Координаты  вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные  слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы  соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их  в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2.  Уравнение квадратичной функции имеет вид  — в этом уравнении — координаты вершины параболы

или в уравнении квадратичной функции  , и второй коэффициент — четное число.

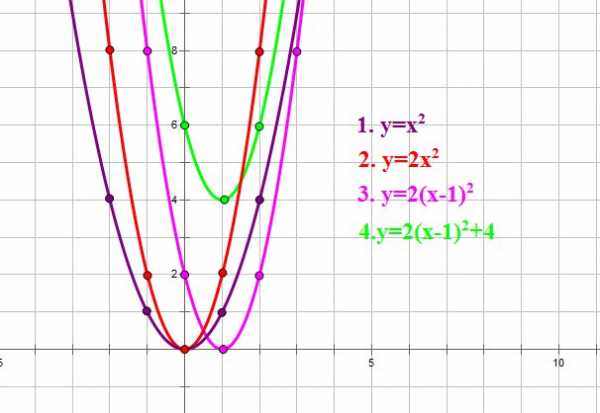
Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

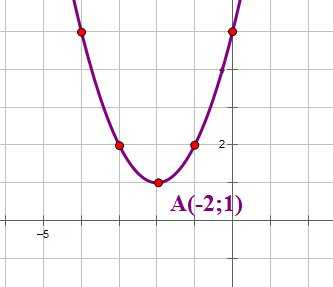
Теперь рассмотрим построение  графика функции . В уравнении этой функции , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат: 

Следовательно,  координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3.  Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда 

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на  координатную плоскость и построим график:

 

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения  ,

— сдвига графика функции вдоль оси от значения  
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Квадратичная функция, ее свойства, примеры и график

Функция y = ax² + bx + c, где a, b и c — заданные числа, a ≠ 0, x — переменная, называется квадратичной функцией. Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.

При этом многочлен ax² + bx + c называют квадратным трехчленом. Числа a, b и c называются коэффициентами квадратного трехчлена: a — первым коэффициентом, b — вторым,                        c — свободным членом. Значения x, при которых квадратный трехчлен обращается в нуль, называются корнями квадратного трехчлена.

Для нахождения корней квадратного трехчлена нужно решить квадратное уравнение                 

ax² + bx + c = 0. Рассмотрим пример, найдем корни квадратного трехчлена x² — x — 2. Решая уравнение x² — x — 2 = 0, получаем: x₁ = -1, x₂ = 2.

Число корней квадратного уравнения ax² + bx + c = 0 зависит от знака его дискриминанта                     D = b² — 4ac, а значит и квадратный трехчлен:

• имеет два различных корня, если D > 0;
• имеет один корень (два равных корня), если D = 0;
• не имеет действительных корней, если D < 0.

Рассмотрим пример, квадратный трехчлен 3x² — 8x + 

5 имеет два различных корня, так как          D = 8² — 4* 3*5 = 4 > 0, корни этого трехчлена: x₁ = 5/3,  x₂ = 1.

Квадратный трехчлен 4x² — 4x + 1 имеет один корень, так как D = 4² — 4*4*1 = 0, корень этого трехчлена  х = 1/2.

Квадратный трехчлен 2x² — 5x + 6 не имеет действительных корней, так как                                       D = 5² — 4*2*6 = — 23 < 0.

График квадратичной функции

Рассмотрим самую простую квадратичную функцию y = x², т. е. функцию y = ax² + bx + c, при a = 1, b = c = 0. Для построения графика этой функции составим таблицу ее значений.

х	-2	-1	0	1	2
у	4	1	0	1	4

Отметим точки на координатной плоскости и соединим их плавной линией.

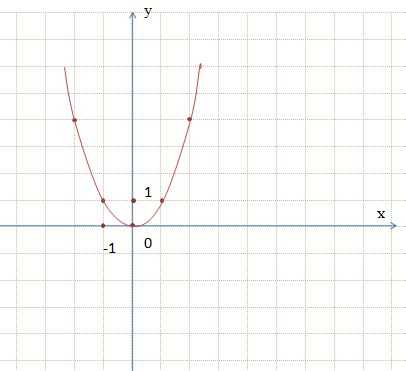
Кривая, являющаяся графиком функции y = x², называется параболой. Ось ординат является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы y = x² является начало координат.

Рассмотрим функцию вида y = 2x², чтобы построить график составим таблицу значений.

x	-2	-1	0	1	2
y	8	2	0	2	8

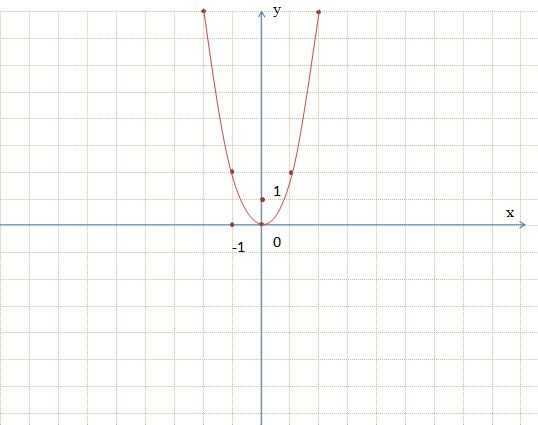
Сравним графики функций y = 2х² и y = х². При одном и том же х значение функции y = 2х² в 2 раза больше значения функции y = х². Это значит, что каждую точку графика y = 2х² можно получить из точки графика функции y = х² с той же абсциссой увеличением ее ординаты в 2 раза. Говорят, что график функции y = 2х² получается растяжением графика функции y = х² в 2 раза вдоль оси ординат.

Рассмотрим функцию вида y = 1/2x², чтобы построить график составим таблицу значений.

х	-2	-1	0	1	2
y	2	0.5	0	0.5	2

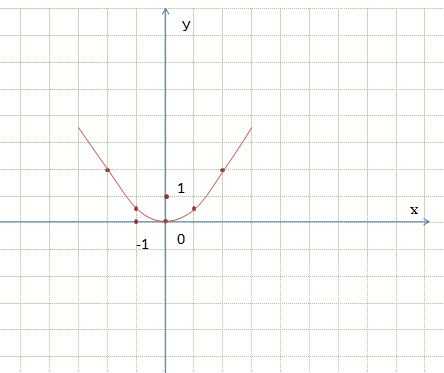
Сравним графики функций y = 1/2x² и y = х². Каждую точку графика y = 1/2x² можно получить из точки графика функции  y = х² с той же абсциссой уменьшением ее ординаты в 2 раза. Говорят, что график функции y = 1/2x² получается сжатием графика функции y = х² в 2 раза вдоль оси ординат.

Рассмотрим функцию вида y = —x²,  и сравним с функцией y = х². При одном и том же значении х значения этих функций равны по модулю и противоположны по знаку. Следовательно, график функции y = —x² можно получить симметрией относительно оси абсцисс графика функции  y = х². Составим таблицу значений.

х	-2	-1	0	1	2
у	-4	-1	0	-1	-4

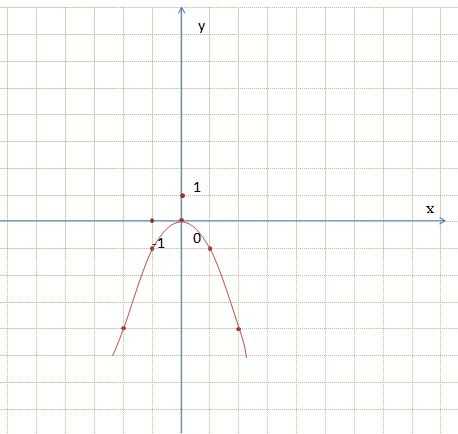
Говорят, что ветви параболы y = х² направлены вверх, а ветви параболы y = —x² направлены вниз. Аналогично график функции y = -2х² симметричен графику функции y = 2х² относительно оси абсцисс. График функции y = -1/2х² симметричен графику функции y = 1/2х² относительно оси абсцисс. График функции y = ах² при любом а ≠ 0 также называют параболой. При а > 0 ветви параболы направлены вверх, а при а < 0 вниз.

Рассмотрим функцию вида y = x² — 2х — 3, чтобы построить график составим таблицу значений.

х	-2	-1	0	1	2	3	4
у	5	0	-3	-4	-3	0	5

 

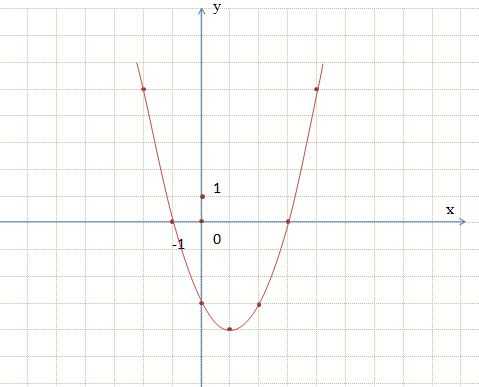
Вообще, графиком функции y = ax² + bx + c является парабола, получаемая сдвигом параболы      y = ax² вдоль координатных осей. Равенство y = ax² + bx + c называют уравнением параболы.

Автор публикации

0 Комментарии: 3Публикации: 79Регистрация: 04-09-2015

prostoi-sovet.ru

Квадратичная функция. Как построить параболу?

Квадратичная функция – это функция вида \(y=ax^2+bx+c\). График квадратичной функции – парабола.

Примеры:

\(y= x^2+6x+5\)		\(y=x^2-4x+5\)
\(y=-2x^2-4x+4\)		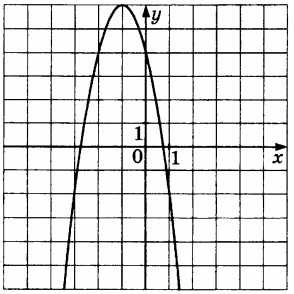\(y=-3x^2+21x-34\)

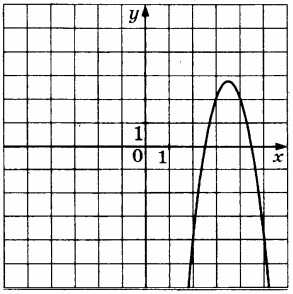«Анатомия» квадратичной функции:

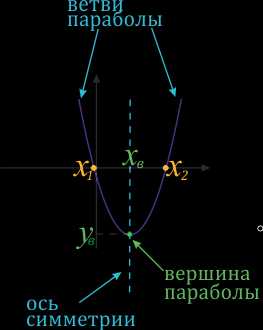
\(x_в\) и \(y_в\) – координаты вершины параболы. \(x_в\) можно найти с помощью формулы: \(x_в=\frac{-b}{2a}\). \(y_в\) можно найти подставив в формулу квадратичной функции вместо \(x\) значение \(x_в: y_в=ax_в^2+bx_в+с\)
Ось симметрии проходит через вершину параболы и параллельна оси \(y\) (ординат). \(x_1\) и \(x_2\) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.

3 параметра позволяющих сопоставить формулу квадратичной функции и график:

1.	\(a>0\) — ветви параболы направлены вверх
	\(a<0\) — ветви параболы направлены вниз
2.	\(c\) равна ординате точки пересечения графика с осью \(y\)
3.	координата вершины параболы \(x_в=-\frac{b}{2a}\)

Пример (задание из ОГЭ). На рисунке изображён график квадратичной функции \(y=ax^2+bx+c\)

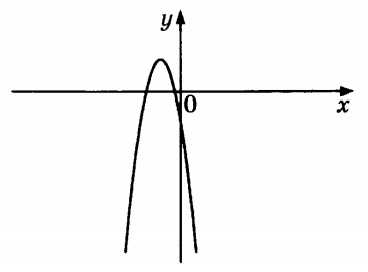
Какие знаки параметров \(a\) и \(c\)?

Решение:

Ветви параболы направлены вниз, значит \(a<0\)
График функции пересекает ось \(y\) в точке лежащий ниже оси \(x\), значит \(c<0\)

Ответ: \(a<0\),\(c<0\)

Пример (задание из ОГЭ). Установите соответствие между квадратичными функциями и их графиками:

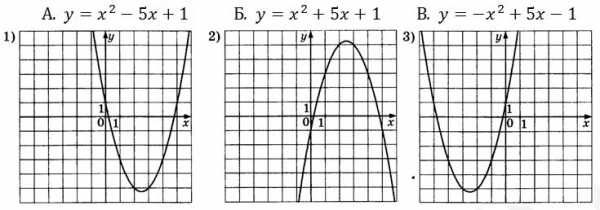
Решение:
Во втором графике ветви параболы направлены вниз, значит \(a<0\). Под этот график подходит только функция под буквой В.
Во втором и третьем графике \(a>0,c=1\) – по этим параметрам нам определить их функции. Тогда найдем \(x_в\) функций под буквой А и Б:

А. \(y=x^2-5x+1\)      \(x_в=\frac{5}{2}=2,5\) так же как на графике 1
Б. \(y=x^2+5x+1\)      \(x_в= \frac{-5}{2}=-2,5\) так же как на графике 3

Ответ:  

Как построить график квадратичной функции (параболу)?

Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно.

1. Найдите координаты вершины параболы. Поставьте точку вершины на координатной плоскости и проведите через неё ось симметрии параболы.
2. Найдите точку пересечения графика с осью \(y\): \(x=0;y=c\). Постройте точку симметричную точке \((0;c)\) относительно оси параболы.
3. Найдите координату целой точки, лежащей вблизи оси параболы.  Отметьте  симметричную ей точку на плоскости.


4. Соедините точки плавной линией.

\(a=2\), \(b=8\), \(c=2\) 1. \(x_в=\frac{-b}{2a}=\frac{-8}{2 \cdot 2}=-2\) \(y_в=2 \cdot (-2)^2+8 \cdot (-2)+2=2 \cdot 4-16+2=-6\)
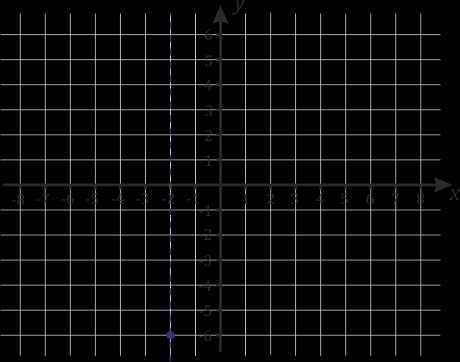
2. \(x=0, y=2\)
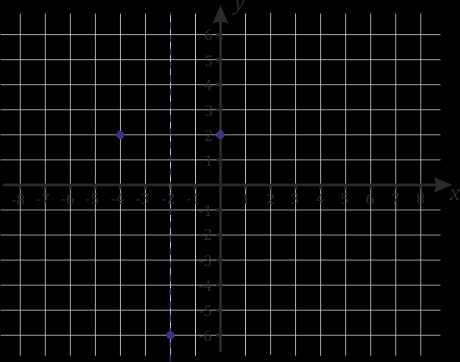3. При \(x=-3\), \(y=2 \cdot (-3)^2+8 \cdot (-3)+2=2 \cdot 9-24+2=20-24=-4\)
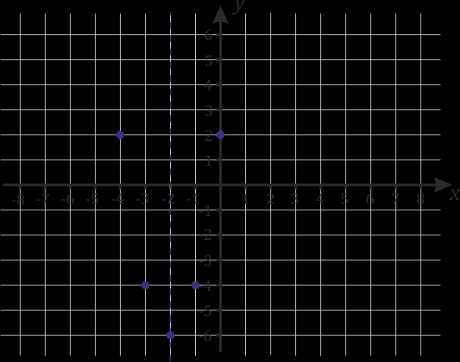
Готово!

Связь квадратичной функции и квадратных уравнений:

Давайте сравним общий вид квадратичной функции и общий вид квадратного уравнения:

\(y=ax^2+bx+c\)

\(ax^2+bx+c=0\)

И там, и там есть квадратный трехчлен \(ax^2+bx+c\). Разница в том, что в функции мы исследуем все возможные значения трехчлена, а в уравнении мы ищем \(x\), при которых значение трехчлена будет равно нулю или при каких \(x\), \(y=0\). Поэтому по графику функции \(y=ax^2+bx+c\) легко определить корни уравнения \(ax^2+bx+c=0\).

Пример:

\(y=x^2+6x+5\)	\(y=x^2-4x+5\)
Судя по графику, корнями уравне- ния \(x^2+6x+5=0\) будут \(x_1=-5\) и \(x_2=-1\)	У уравнения \(x^2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\))

Смотрите также:
Линейная функция
Виды графиков функций
Квадратные неравенства

Скачать статью

cos-cos.ru

Квадратичная функция, парабола, график, свойства: нули, вершина, ось симметрии, промежутки возрастания, убывания. Тесты

Тестирование онлайн

• Квадратичная функция

Определение. График

Квадратичной (квадратной) функцией называется функция вида

где a, b, с — числа.

Графиком квадратичной функции является парабола.

Парабола имеет вершину, ось, проведенная через вершину и параллельная оси Оу, делит параболу на две симметричные части. Вершиной параболы называется точка

Если коэффициент а>0, то ветви параболы направлены вверх, если a, то ветви параболы направлены вниз.

Свойства квадратичной функции y=x²

1) Областью определения функции является множество всех действительных чисел, т.е.

2) Множеством значений функции является промежуток

3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.

4) Функция является четной, график симметричен относительно оси Оу.

5) Функция непериодическая.

6)Парабола имеет с осями координат единственную общую точку (0;0) — начало координат.

7) Значение аргумента x=0 является нулем функции.

8) На промежутке функция убывающая, а на промежутке — возрастающая.

9) Функция принимает положительные значения на множестве , т.е. все точки параболы, кроме начала координат.

Преобразование параболы

Функция y=x² — частный случай квадратичной функции.

Квадратичную функцию всегда можно привести у виду , а затем построить параболу с помощью ее геометрических преобразований.

Для построения параболы необходимо:

1) Найти координаты вершины

2) Построить ось симметрии, проанализировать куда направлены ветви параболы

3) Найти точки пересечения параболы с осью Ox (нули), если они есть, решив уравнение

4) Найти точку пересечения с осью Оу, решив уравнение

fizmat.by

Квадратичная функция

•Квадратичной функцией называется функция вида y=ax²+bx+c, где a,b,c — числа, причем a≠0.
•Графиком квадратичной функции является парабола.

Чтобы построить график функции y=x² составим таблицу значений

и построим график, используя полученные точки:

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции y=x² при любых значениях остальных коэффициентов.
График функции y=-x² имеет вид:

Итак:
•Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
•Если старший коэффициент a

Второй этап построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции y=f(x) с осью ОХ, нужно решить уравнение f(x)=0.

В случае квадратичной функции y=ax²+bx+c нужно решить квадратное уравнение ax²+bx+c=0.

В процессе решения квадратного уравнения мы находим дискриминант: D=b²-4ac, который определяет число корней квадратного уравнения.

И здесь возможны три случая:
1. Если D2+bx+c=0 не имеет решений, и, следовательно, парабола y=ax²+bx+c не имеет точек пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:

2. Если D=0 ,то уравнение ax²+bx+c=0 имеет одно решение, и, следовательно, парабола y=ax²+bx+c имеет одну точку пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:

3.Если D>0, то уравнение ax²+bx+c=0 имеет два решения, и, следовательно, парабола y=ax²+bx+c имеет две точки пересечения с осью ОХ: ,
Если a>0, то график функции выглядит примерно так:

Значит, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный этап построения графика квадратичной функции – координаты вершины параболы:

Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один этап построения графика функции – точка пересечения параболы y=ax²+bx+c с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы y=ax²+bx+c с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c.

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные моменты построения графика квадратичной функции показаны на рисунке:

www.tofmal.ru

Построение графика квадратичной функций: алгоритм и примеры

 

Квадратичной функцией называется функция вида: 
y=a*(x^2)+b*x+c,
где а – коэффициент при старшей степени неизвестной х,
b – коэффициент при неизвестной х,
а с — свободный член.
Графиком квадратичной функции является кривая, называемая параболой. Общий вид параболы представлен на рисунке ниже.

Рис.1 Общий вид параболы.

Есть несколько различных способов построения графика квадратичной функции. Мы рассмотрим основной и самый общий из них.

Алгоритм построения графика квадратичной функции y=a*(x^2)+b*x+c

1. Построить систему координат, отметить единичный отрезок и подписать координатные оси.

2. Определить направление ветвей параболы (вверх или вниз).
Для этого надо посмотреть на знак коэффициента a. Если плюс — то ветви направлены вверх, если минус — то ветви направлены вниз.

3. Определить координату х вершины параболы.
Для этого нужно использовать формулу Хвершины = -b/2*a.

4. Определить координату у вершины параболы.
Для этого подставить в уравнение Увершины = a*(x^2)+b*x+c вместо х, найденное в предыдущем шаге значение Хвершины.

5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу.

6. Найти точки пересечения графика с осью Ох.
Для этого требуется решить квадратное уравнение a*(x^2)+b*x+c = 0 одним из известных способов. Если в уравнение не имеет вещественных корней, то график функции не пересекает ось Ох.

7. Найти координаты точки пересечения графика с осью Оу.
Для этого подставляем в уравнение значение х=0 и вычисляем значение у. Отмечаем эту и симметричную ей точку на графике.

8. Находим координаты произвольной точки А(х,у)
Для этого выбираем произвольное значение координаты х, и подставляем его в наше уравнение. Получаем значение у в этой точке. Нанести точку на график. А также отметить на графике точку, симметричную точке А(х,у).

9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика.

Пример построения графика

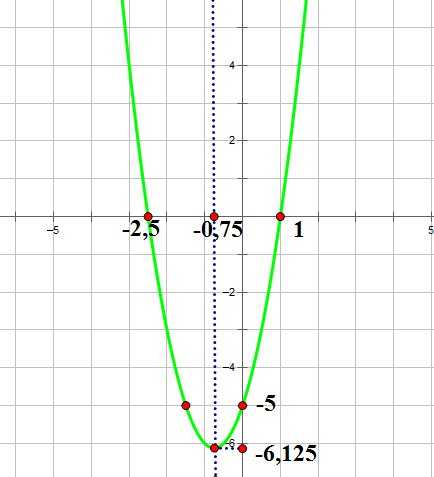
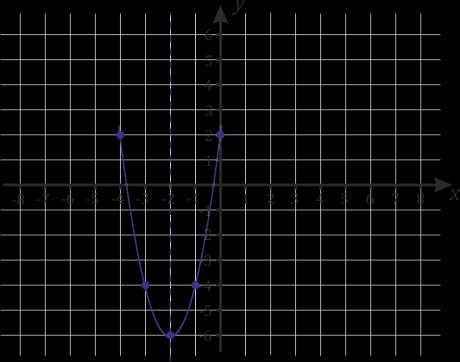
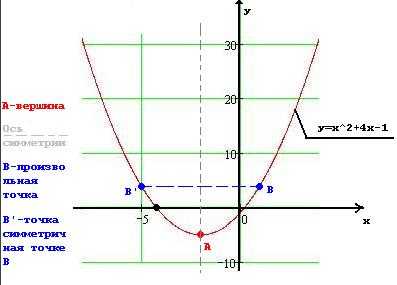
В качестве примера, построим график квадратичной функции заданной уравнением y=x^2+4*x-1
1. Рисуем координатные оси, подписываем их и отмечаем единичный отрезок.
2. Значения коэффициентов а=1, b=4, c= -1. Так как а=1, что больше нуля ветви параболы направлены вверх.
3. Определяем координату Х вершины параболы Хвершины = -b/2*a = -4/2*1 = -2.
4. Определяем координату У вершины параболы
Увершины = a*(x^2)+b*x+c = 1*((-2)^2) + 4*(-2) – 1 = -5.
5. Отмечаем вершину и проводим ось симметрии.
6. Находим точки пересечения графика квадратичной функции с осью Ох. Решаем квадратное уравнение x^2+4*x-1=0.
х1=-2-√3 х2 = -2+√3. Отмечаем полученные значения на графике.
7. Находим точки пересечения графика с осью Оу.
х=0; у=-1
8. Выбираем произвольную точку B. Пусть она имеет координату х=1.
Тогда у=(1)^2 + 4*(1)-1= 4.
9. Соединяем полученные точки и подписываем график.

В результате получится такой график.

Нужна помощь в учебе?

Предыдущая тема: Графики функции: от чего зависит вид графика функции
Следующая тема:&nbsp&nbsp&nbspРешение неравенств второй степени с одной переменной: приводим примеры

Все неприличные комментарии будут удаляться.

www.nado5.ru

2.Квадратичная функция y=x² — Функции и их графики

В уравнении квадратичной функции:

a – старший коэффициент

b – второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:

 Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.

График  функции  имеет вид:

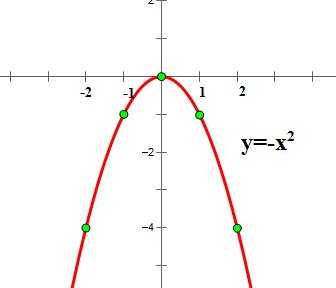
Для нахождения координат базовых точек составим таблицу:

 

Обратите внимание, что график функции  симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика  функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты  точек  пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции  нужно решить квадратное уравнение 

sites.google.com