Квадратные уравнения формула – Квадратное уравнение — Википедия
Формула корней квадратного уравнения. Теорема Виета. Формула корней квадратного уравнения.
О.Уравнение вида,
где – переменная,
– переменная,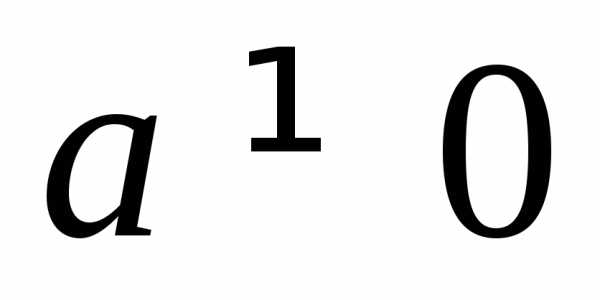 называетсяквадратным.
называетсяквадратным.
О.Если ,
то уравнение называетсяприведенным
квадратным уравнением.
,
то уравнение называетсяприведенным
квадратным уравнением.
О.Квадратное уравнение, в котором хотя
бы один из коэффициентов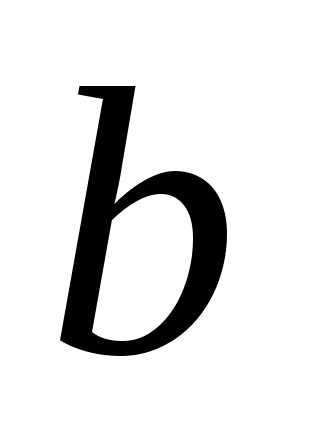 или
или равен
равен ,
называетсянеполным квадратным
уравнением
,
называетсянеполным квадратным
уравнением
Выведем формулу корней квадратного уравнения в общем случае:
, 
Поделим
обе части уравнения на 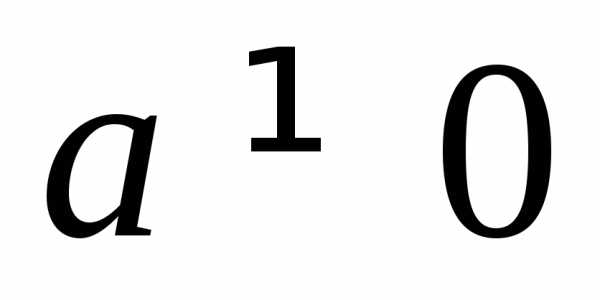 .
При этом корни уравнения не изменятся(почему?).
.
При этом корни уравнения не изменятся(почему?).

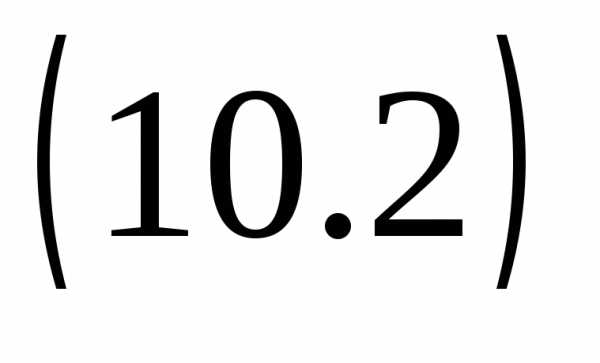
Выделим полный квадрат:
О.Выражение:
 ,
тогда уравнение можно записать так:
,
тогда уравнение можно записать так:
Возможны следующие 3 случая:
Если
 ,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения:
,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения:



То есть

 или
или 

 или
или 
Эти две формулы можно объединить в следующую:
 —
эта формула
называется формулой
корней квадратного уравнения
—
эта формула
называется формулой
корней квадратного уравнения
Если
 ,
то уравнение
,
то уравнение  примет вид:
примет вид:
В этом случае уравнение имеет один корень.
Замечание: можно также сказать, что в этом случае квадратное уравнение имеет два совпадающих корня.
Если

 ,
поэтому уравнение
,
поэтому уравнение  ,
а значит и уравнение
,
а значит и уравнение  не
имеет корней (почему?).
не
имеет корней (почему?).
Таким образом,
Если  ,
то уравнение
,
то уравнение 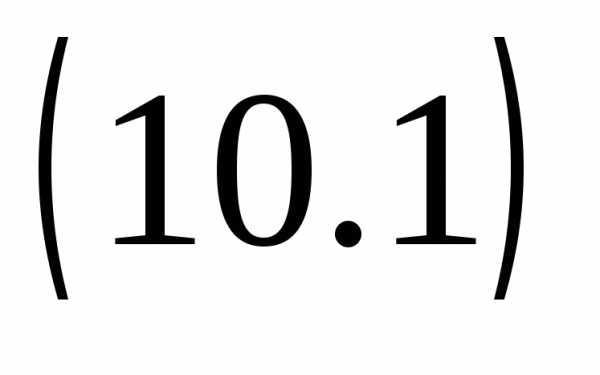 имеет 2 различных корня:
имеет 2 различных корня: 
 ,
то уравнение
,
то уравнение  имеет 2 совпадающих корня:
имеет 2 совпадающих корня: 
Если  ,
то уравнение
,
то уравнение 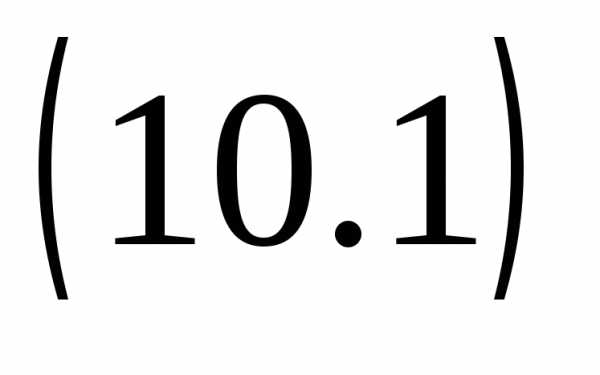 корней не имеет.
корней не имеет.
Теорема Виета.
Пусть
дано уравнение
, 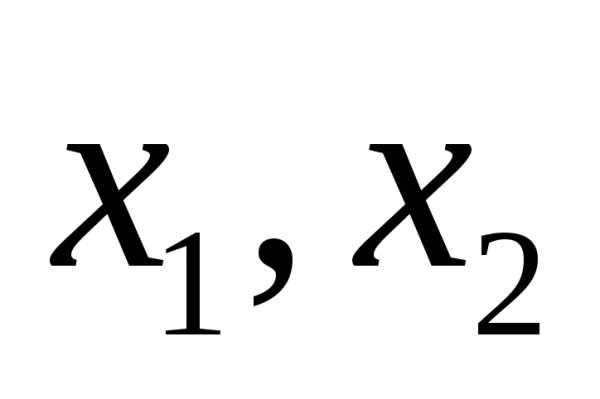 – корни уравнения, тогда
– корни уравнения, тогда

Доказательство:
Пусть
уравнение
имеет 2 различных корня ( ):
):


Итак,
действительно 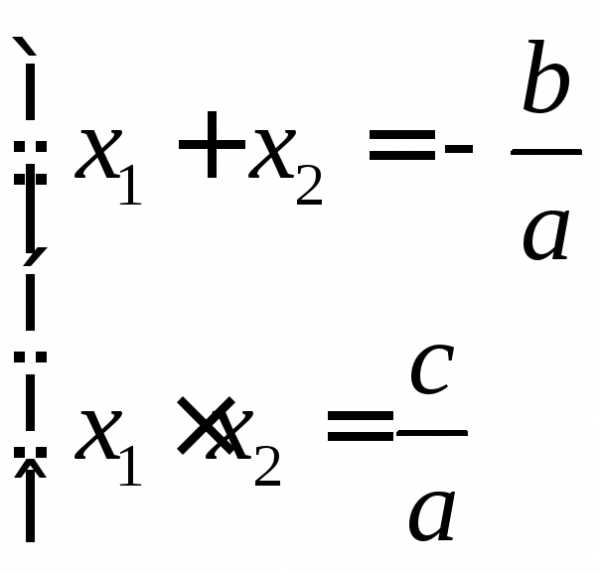

Замечание:
Если рассмотреть приведенное квадратное
уравнение
,
то формулы Виета будут выглядеть так: 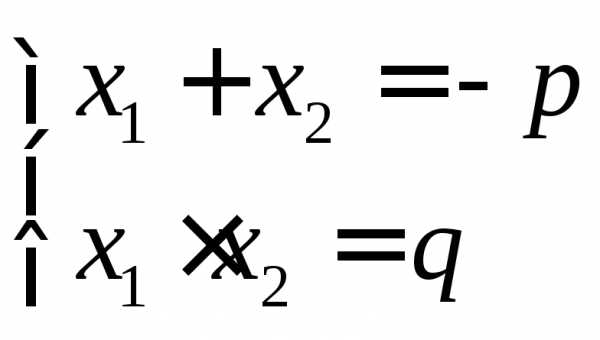
В школьном курсе математики чаще всего формулы Виета применяются именно для приведенного квадратного уравнения.
Имеет место теорема, обратная теореме Виета:
Если
числа  и
и таковы, что
таковы, что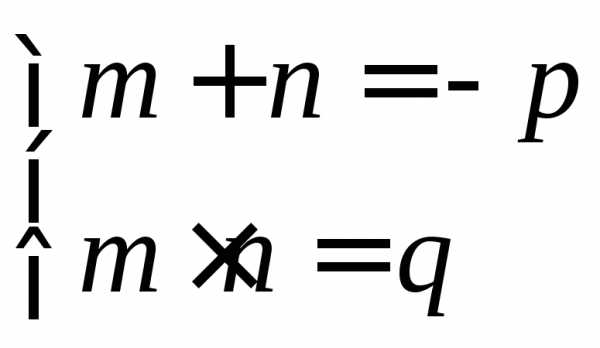
То эти числа являются корнями уравнения
Доказательство:
Значит,
числа  и
и действительно являются корнями уравнения
.
действительно являются корнями уравнения
. 
Замечание: теорема, обратная теореме Виета, позволяет составлять квадратные уравнения по его корням.
Например, если , то, тогда эти числа являются корнями уравнения
Разложение квадратного трехчлена на линейные множители
 – переменная,
– переменная,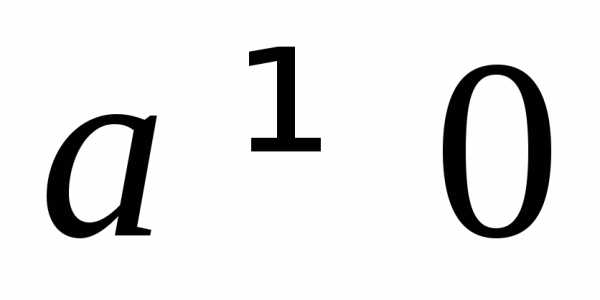 называетсяквадратным трехчленом.
называетсяквадратным трехчленом.О.Корнемквадратного трехчлена называется значение переменной, при которой значение этого трехчлена равно нулю.
Теорема.
Если  и
и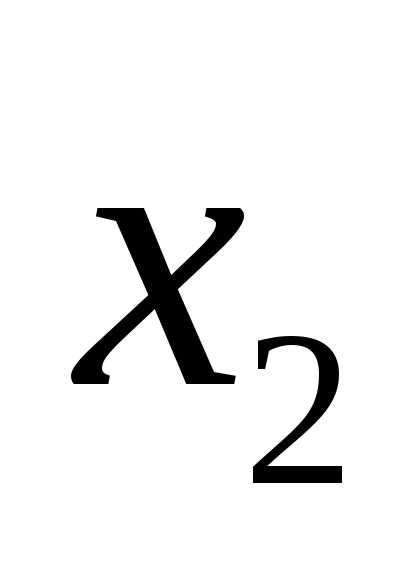 – корни квадратного трёхчлена
– корни квадратного трёхчлена
Доказательство:
Вынесем за скобки
в многочлене множительа. Получим:.
Так как корни квадратного трёхчленаявляются корнями квадратного уравнения,
то, по теореме Виета, ,
, .
.
Поэтому
Итак, 
Если квадратный
трёхчлен имеет один корень (два
совпадающих корня), то формула 
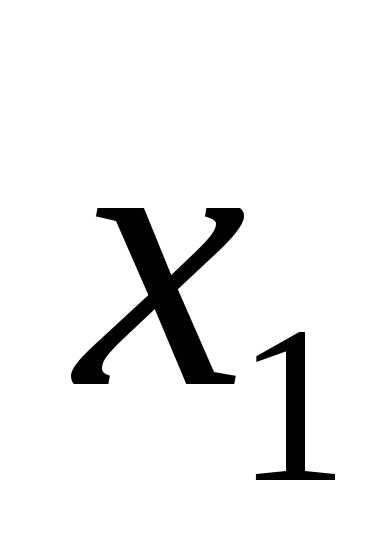 — корень квадратного трёхчлена.
— корень квадратного трёхчлена.Заметим, что если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
studfiles.net
Формулы корней квадратных уравнений | Учеба-Легко.РФ
Пусть дано квадратное уравнение ах2 + bх + с = 0.
Применим к квадратному трехчлену ах2 + bх + с те же преобразования, которые мы выполняли в § 13, когда доказывали теорему о том, что графиком функции у = ах
Имеем
Обычно выражение b2 — 4ас обозначают буквой D и называют дискриминантом квадратного уравнения ах2 + bх + с = 0 (или дискриминантом квадратного трехчлена ах + bх + с).
Таким образом
Значит, квадратное уравнение ах2 + их + с = О можно переписать в виде
Любое квадратное уравнение можно преобразовать к виду (1), удобному, как мы сейчас убедимся, для того, чтобы определять число корней квадратного уравнения и находить эти корни.
Доказательство. Если D < 0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.
Пример 1. Решить уравнение 2x2 + 4х + 7 = 0.
Решение. Здесь а = 2, b = 4, с = 7,
D = b2-4ac = 42. 4. 2. 7 = 16-56 = -40.
Так как D < 0, то по теореме 1 данное квадратное уравнение не имеет корней.
Доказательство. Если D = 0, то уравнение (1) принимает вид
— единственный корень уравнения.
Замечание 1. Помните ли вы, что х = — — абсцисса вершины параболы, которая служит графиком функции у = ах2 + их + с? Почему именно это
значение оказалось единственным корнем квадратного уравнения ах2 + их + с — 0? «Ларчик» открывается просто: если D — 0, то, как мы установили ранее,
Графиком же функции является парабола с вершиной в точке (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число.

Пример 2. Решить уравнение 4x2 — 20x + 25 = 0.
Решение. Здесь а = 4, b = -20, с = 25, D = b2 — 4ас = (-20)2 — 4 • 4 • 25 = 400 — 400 = 0.
Так как D = 0, то по теореме 2 данное квадратное уравнение имеет один корень. Этот корень находится по формуле
Ответ: 2,5.
Замечание 2. Обратите внимание, что 4х2 — 20х +25 — полный квадрат: 4х2 — 20х + 25 = (2х — 5)2.
Если бы мы это заметили сразу, то решили бы уравнение так: (2х — 5)2 = 0, значит, 2х — 5 = 0, откуда получаем х = 2,5. Вообще, если D = 0, то
ах2 + bх + с = — это мы отметили ранее в замечании 1.
Если D > 0, то квадратное уравнение ах2 + bх + с = 0 имеет два корня, которые находятся по формулам
Доказательство. Перепишем квадратное уравнение ах2 + Ьх + с = 0 в виде (1)
Положим
По условию, D > 0, значит, правая часть уравнения положительное число. Тогда из уравнения (2) получаем, что

Итак, заданное квадратное уравнение имеет два корня:
Замечание 3. В математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое
понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отноше-
ние к различным пюдям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.
Пример 3. Решить уравнение Зх2 + 8х — 11 = 0.
Решение. Здесь а = 3, b = 8, с = — 11,
D = b2 — 4ас = 82 — 4 • 3 • (-11) = 64 + 132 = 196.
Так как D > 0, то по теореме 3 данное квадратное уравнение имеет два корня. Эти корни находятся по формулам (3)
Фактически мы с вами выработали следующее правило:
Правило решения уравнения
ах2 + bх + с = 0

Это правило универсально, оно применимо как к полным, так и к неполным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому правилу не решают, их удобнее решать так, как мы это делали в предыдущем параграфе.
Пример 4. Решить уравнения:
а) х2 + Зх — 5 = 0; б) — 9x2 + 6х — 1 = 0; в) 2х2-х + 3,5 = 0.
Р е ш е н и е. а) Здесь а = 1, b = 3, с = — 5,
D = b2 — 4ас = З2 — 4 • 1 • (- 5) = 9 + 20 = 29.
Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находим по формулам (3)
б) Как показывает опыт, удобнее иметь дело с квадратными уравнениями, у которых старший коэффициент положителен. Поэтому сначала умножим обе части уравнения на -1, получим
9x2 — 6x + 1 = 0.
Здесь а = 9, b = -6, с = 1, D = b2 — 4ас = 36 — 36 = 0.
Так как D = 0, то данное квадратное уравнение имеет один корень. Этот корень находится по формуле х = — . Значит,
Это уравнение можно было решить по-другому: так как
9х2 — 6x + 1 = (Зх — IJ, то получаем уравнение (Зх — I)2 = 0, откуда находим Зх — 1 = 0, т. е. х = .
в) Здесь а = 2, b = — 1, с = 3,5, D = b2 — 4ас = 1 — 4 • 2 • 3,5= 1 — 28 = — 27. Так как D < 0, то данное квадратное уравнение не имеет корней.
Математики — люди практичные, экономные. Зачем, говорят они, пользоваться таким длинным правилом решения квадратного уравнения, лучше сразу написать общую формулу:
Если окажется, что дискриминант D = b2 — 4ас — отрицательное число, то записанная формула не имеет смысла (под знаком квадратного корня находится отрицательное число), значит, корней нет. Если же окажется, что дискриминант равен нулю, то получаем
т. е. один корень (говорят также, что квадратное уравнение в этом случае имеет два одинаковых корня:
Наконец, если окажется, что b2 — 4ас > 0, то получаются два корня х1и х2, которые вычисляются по тем же формулам (3), что указаны выше.
Само число в этом случае положительно (как всякий квадратный корень из положительного числа), а двойной знак перед ним означает, что в одном случае (при отыскании х1 ) это положительное число прибавляется к числу — b, а в другом случае (при отыскании х2) это положительное число вы-
читается из числа — b.
У вас есть свобода выбора. Хотите —- решайте квадратное уравнение подробно, используя сформулированное выше правило; хотите — запишите сразу формулу (4) и с ее помощью делайте необходимые выводы.
Пример 5. Решить уравнения:
Решение, а) Конечно, можно использовать формулы (4) или (3), учитывая, что в данном случае Но зачем выполнять действия с дробями, когда проще и, главное, приятнее иметь дело с целыми числами? Давайте освободимся от знаменателей. Для этого нужно умножить обе части уравнения на 12, т. е. на наименьший общий знаменатель дробей, служащих коэффициентами уравнения. Получим
откуда 8х2 + 10x — 7 = 0.
А теперь воспользуемся формулой (4)
б) Мы снова имеем уравнение с дробными коэффициентами: а = 3, b = — 0,2, с = 2,77. Умножим обе части уравнения на 100, тогда получим уравнение с целыми коэффициентами:
300x2 — 20x + 277 = 0.
Далее воспользуемся формулой (4):
Простая прикидка показывает, что дискриминант (подкоренное выражение) — отрицательное число. Значит, уравнение не имеет корней.
Пример 6. Решить уравнение
Решение. Здесь, в отличие от предыдущего примера, предпочтительнее действовать по правилу, а не по сокращенной формуле (4).
Имеем а = 5, b = -, с = 1, D = b2 — 4ас = (- ) 2 — 4 • 5 • 1 = 60 — 20 = 40. Так как D > 0, то квадратное уравнение имеет два корня, которые будем искать по формулам (3)
Пример 7. Решить уравнение
х2 — (2р + 1)x +(р2+р-2) = 0
Решение. Это квадратное уравнение отличается от всех рассмотренных до сих пор квадратных уравнений тем, что в роли коэффициентов выступают не конкретные числа, а буквенные выражения. Такие уравнения называют уравнениями с буквенными коэффициентами или уравнениями с параметрами. В данном случае параметр (буква) р входит в состав второго коэффициента и свободного члена уравнения.
Найдем дискриминант:
Пример 8. Решить уравнение рx2 + (1 — р) х — 1 = 0.
Решение. Это также уравнение с параметром р, но, в отличие от предыдущего примера, его нельзя сразу решать по формулам (4) или (3). Дело в том, что указанные формулы применимы к квадратным уравнениям, а про заданное уравнение мы этого пока сказать не можем. В самом деле, а вдруг р = 0? Тогда
уравнение примет вид 0 • x2+ (1-0)x- 1 = 0, т. е. х — 1 = 0, откуда получаем х = 1. Вот если точно известно, что , то можно применять формулы корней квадратного уравнения:
uclg.ru
Формулы корней квадратного уравнения / Открытый урок
Цели урока:
Образовательная:
— знакомство с формулой корней квадратного уравнения, дискриминанта и формирование первичных умений применения ее при решении квадратных уравнений;
— определять количество корней квадратного уравнения в зависимости от знака дискриминанта.
Развивающая:
— развитие математической речи, критического и объективного мышления;
Воспитательная:
формирование познавательного интереса, умения планировать свою работу, формирование объективной самооценки и взаимооценки.
Тип урока: урок изучения нового материала.
Вид урока: урок с применением ИКТ.
Оборудование:
- компьютер;
- мультимедийный проектор;
- презентация,
- раздаточный материал
- «Алгоритм решения квадратного уравнения»
Структура урока
- Организационный момент (1мин)
- Проверка домашнего задания (3мин)
- Устная работа (6 мин)
- Изучение нового материала (15мин)
- Первичное закрепление материала (3мин)
- Странички истории (1мин)
- Физкультминутка (1мин)
- Работа по учебнику (7 мин)
- Самостоятельная работа (5мин)
- Итог урока (2мин)
- Домашнее задание (1мин)
Ход урока
1. Организационный момент.
Ребята! Сегодня тема урока: «Формула корней квадратного уравнения». (Записывается тема урока, слайд ) Эпиграфом нашего урока служат слова двух великих математиков:
Эпиграф к уроку:
Уравнения, как растения, могут иметь корни, а могут и не иметь
А для начала проверим домашнее задание
2. Проверка домашнего задания
Работа 1 ученика показывается с помощью документ-камеры, проверяется всем классом. Остальные проверяют свои решения по своим тетрадям, ошибки исправляют.
3. Актуализация
Устный опрос.
Вопрос 1. Какие уравнения называются квадратными?
(Уравнения вида ax²+bx + c = 0 , где a,b, c – некоторые числа называется квадратным.)
Вопрос 2 . Что значит решить уравнение?
(Решить уравнение – это значит найти все его корни или доказать, что их нет.)
Вопрос 3. Какие из них называются полными, а какие неполными квадратными уравнениями?
(Если коэффициенты b, c отличны от нуля, то уравнение называется полным квадратным уравнением. Если хотя бы один из коэффициентов b, c равен нулю, то уравнение называется неполным.)
Вопрос 4. Перечислите виды неполных квадратных уравнений и расскажите о способах их решения и числе возможных корней уравнений.
|
(Виды неполных квадратных уравнений
|
||
|
ax² = 0 |
ax²+bx = 0 |
ax²+ c = 0 |
|
Способы решения
|
||
|
Уравнение всегда имеет один корень, х = 0. |
Уравнение решается разложением на множители, вынесением общего множителя за скобки. Всегда имеет два корня, один из которых равен нулю. |
Уравнение решается разложением на множители по формуле разность квадратов, если c < 0 и имеет два противоположных корня. Если c > 0, то уравнение не имеет корней.) |
Вопрос 5. Практический. Установите соответствие между уравнением и ответом, не решая уравнения.
|
Уравнение |
|
Ответ |
|
1. х² — 4 = 0 |
|
А. нет корней |
|
2. х² + 5х = 0 |
|
Б. 0 |
|
3. х² + 25 = 0 |
|
В. ± 2 |
|
4.2х² — 6х = 0 |
|
Г. – 5; 0 |
|
5. 5х² = 0 |
|
Д. ± 3 |
|
6. 9 – х² = 0 |
|
Е. 0; 3 |
Вопрос 6. Сколько корней может иметь квадратное уравнение?
1. Назовите вид данного уравнения.
2. Назовите его коэффициенты. (12, 72, 108)
4. Изучение нового материала
Мы повторили пройденный материал о неполных квадратных уравнениях, перейдем к полным.
Вопрос 7.
Какие способы решения полных квадратных уравнений вы знаете на данный момент? (Графический способ и способ выделения полного квадрата.)
Какие недостатки этих способов были нами отмечены ранее? (Графический способ не всегда дает точный результат, а способ выделения полного квадрата достаточно сложный и трудоемкий)
А теперь скажите, могли ли математики спать спокойно, если бы для таких нужных и важных уравнений не было бы более простого и универсального способа решения?
Таким образом, цель нашего урока???????
(рассмотреть универсальную формулу для решения квадратных уравнений и научиться ее применять)
Итак, приступим.
Квадратное уравнение имеет видax²+bx + c = 0.
Объясняется на примерах.
ПРИМЕРЫ
Решим три уравнения.
Пример 1.Пример 2.
Пример 3.
Для решения квадратных уравнений используется такое понятие как дискриминант, которое обозначается буквой Д и вычисляется по формуле
D= b2— 4ас
Давайте вычислим для каждого уравнений Д.
Пример 1. Д=49
Пример 2. Д=0
Пример 3. Д<0
ЗНАЧИТ (на доске писать)
Для каждого варианта есть свои формулы для нахождения корня уравнения
|
Д>0 |
Д=0 |
Д<0 |
|
Х=
|
Нет решения |
Давайте найдем для каждого уравнения корни.
Пример 1.
Д=49
Х1=0,5
Х2=-3
Ответ пишем в порядке возрастания. -3; 0,5
Пример 2.
Пример 3.
Пишем в тетрадях (на слайде)
Алгоритм решения квадратных уравнений.
 5. Первичное закрепление материала
5. Первичное закрепление материала
1.Решите уравнения. Задания ОГЭ
Решение у доски (1ученик) —15х+14=0
- 1 вариант 2- 5х +2=0
- 2 вариант -8х — 84=0
Обмениваются тетрадями и взаимопроверка.
6. Странички истории (слайд)
1. Франсуа Виет (1540-1603)
Знаменитый французский ученый. Он впервые установил зависимость между корнями и коэффициентами квадратного уравнения.
3. Кристиан Вольф
Впервые ввёл термин «квадратное уравнение» немецкий философ Кристиан Вольф знаменитый немецкий философ.
4. Сильвестр Джеймс Джозеф английский математик, Сильвестр Джеймс Джозеф, который ввёл термин «дискриминант».
7. Физкультминутка для глаз.
8. Работа по учебнику.
А теперь мы перейдем к работе по учебнику
№25.1 Найти дискриминант квадратного уравнения
№25.3 Определите число корней квадратного уравнения
№25.5 (аб) Решите полное квадратное уравнение
(Учебник Мордкович А.Г.)

9. Самостоятельная работа (на листочках, выполняем с копировкой). Проверяем с помощью Документ-камеры.
Решаем самостоятельно.
|
1 вариант |
2 вариант |
|
7-5х-2=0 |
9-12х+4=0 |
Ответы: 1 вариант : -2/7 и 1
2 вариант : 2/3
10. Итоги урока
Давайте подведем итоги нашего урока.
Что же мы сегодня на уроке узнали? (Мы узнали новую формулу для корней квадратного уравнения)
Чему научились? (Мы научились вычислять дискриминант квадратного уравнения и решать его с помощью дискриминанта)
Таким образом, цель нашего урока достигнута. Мы узнали универсальную формулу решения квадратных уравнений, в ее универсальности мы еще не раз убедимся.
Каков алгоритм решения квадратного уравнения?
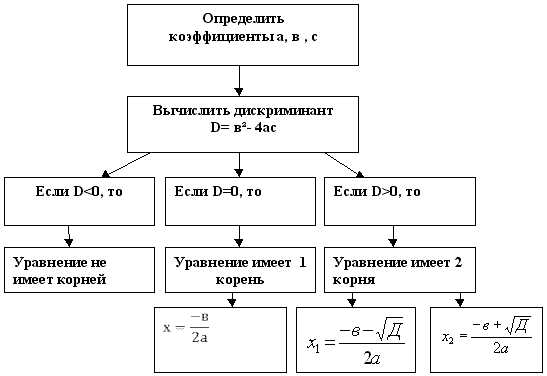
11.Домашнее задание объясняется.
№ 25.2 Найти дискриминант квадратного уравнения
№ 25.4 Определите число корней квадратного уравнения
№ 25.5(в,г) Решите полное квадратное уравнение
open-lesson.net

 ,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения:
,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения: ,
то уравнение
,
то уравнение  примет вид:
примет вид: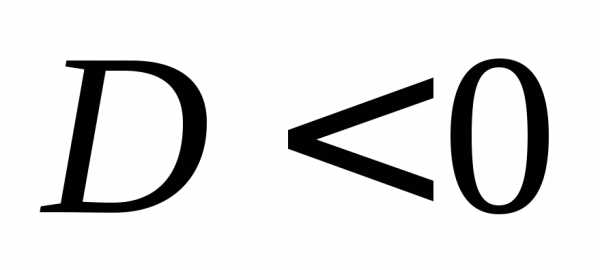
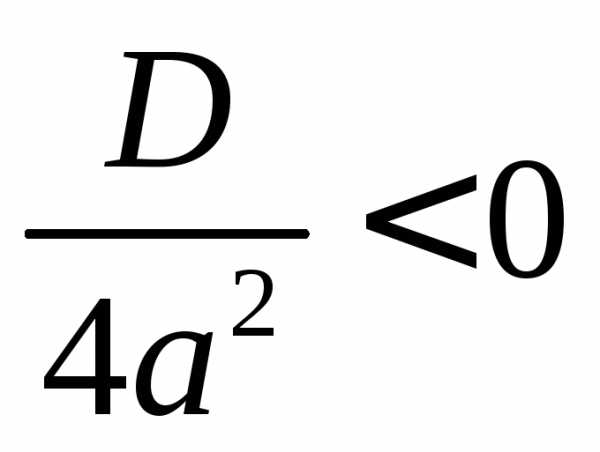 ,
поэтому уравнение
,
поэтому уравнение  ,
а значит и уравнение
,
а значит и уравнение  не
имеет корней (почему?).
не
имеет корней (почему?).