Квадратная формула – Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.
формулы вычисления. Формула нахождения корней квадратного уравнения
Некоторые задачи в математике требуют умения вычислять значение корня квадратного. К таким задачам относится решение уравнений второго порядка. В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
Что такое квадратный корень?
В математике этому понятию соответствует символ √. Исторические данные говорят, что он начал использоваться впервые приблизительно в первой половине XVI века в Германии (первый немецкий труд по алгебре Кристофа Рудольфа). Ученые полагают, что указанный символ является трансформированной латинской буквой r (radix означает «корень» на латыни).

Корень из какого-либо числа равен такому значению, квадрат которого соответствует подкоренному выражению. На языке математики это определение будет выглядеть так: √x = y, если y2 = x.
Корень из положительного числа (x > 0) является также числом положительным (y > 0), однако если берут корень из отрицательного числа (x < 0), то его результатом уже будет комплексное число, включающее мнимую единицу i.
Приведем два простых примера:
√9 = 3, поскольку 32 = 9; √(-9) = 3i, поскольку i2 = -1.
Итерационная формула Герона для нахождения значений корней квадратных
Приведенные выше примеры являются очень простыми, и вычисление корней в них не представляет никакого труда. Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.
Во всех вышеназванных случаях следует применять специальный метод вычисления корня квадратного. В настоящее время таких методов известно несколько: например разложение в ряд Тейлора, деление столбиком и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский способ определения квадратных корней (существуют свидетельства, что древние вавилоняне применяли ее в своих практических вычислениях).
Пусть необходимо определить значение √x. Формула нахождения квадратного корня имеет следующий вид:
an+1 = 1/2(an+x/an), где limn->∞(an) => x.
Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a0 (оно может быть произвольным, однако для быстрого получения результата следует выбирать его таким, чтобы (a0)2 было максимально близко к x. Затем подставить его в указанную формулу вычисления квадратного корня и получить новое число a1, которое уже будет ближе к искомому значению. После этого необходимо уже a1 подставить в выражение и получить a2. Эту процедуру следует повторять до получения необходимой точности.
Пример применения итерационной формулы Герона
Описанный выше алгоритм получения корня квадратного из некоторого заданного числа для многих может звучать достаточно сложно и запутанно, на деле же оказывается все гораздо проще, поскольку эта формула сходится очень быстро (особенно если выбрано удачное число a0).
Приведем простой пример: необходимо вычислить √11. Выберем a0 = 3, так как 32 = 9, что ближе к 11, чем 42 = 16. Подставляя в формулу, получим:
a1 = 1/2(3 + 11/3) = 3,333333;
a2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
a3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Дальше нет смысла продолжать вычисления, поскольку мы получили, что a2 и a3 начинают отличаться лишь в 5-м знаке после запятой. Таким образом, достаточно было применить всего 2 раза формулу, чтобы вычислить √11 с точностью до 0,0001.
В настоящее время широко используются калькуляторы и компьютеры для вычисления корней, тем не менее отмеченную формулу полезно запомнить, чтобы иметь возможность вручную вычислять их точное значение.
Уравнения второго порядка
Понимание того, что такое корень квадратный, и умение его вычислять используется при решении квадратных уравнений. Этими уравнениями называют равенства с одной неизвестной, общий вид которых приведен на рисунке ниже.
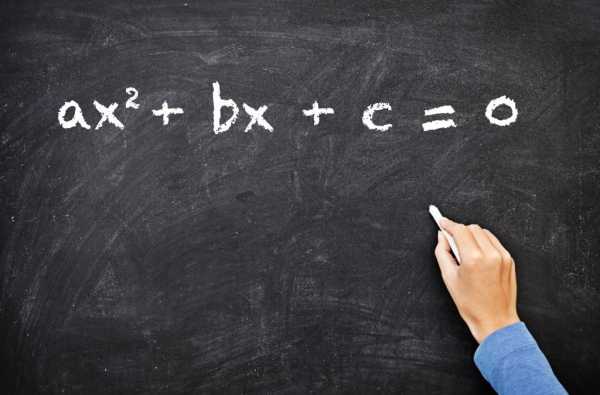
Здесь c, b и a представляют собой некоторые числа, причем a не должно равняться нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.
Любые значения икса, удовлетворяющие указанному на рисунке равенству, называются его корнями (следует не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x2), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.
Нахождения корней квадратного уравнения (формула)
Этот способ решения рассматриваемого типа равенств также называется универсальным, или методом через дискриминант. Его можно применять для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:
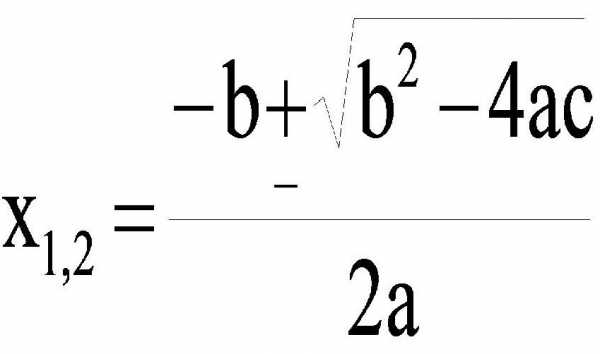
Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление x1 отличается от расчета x2 только знаком перед корнем квадратным. Подкоренное выражение, которое равно b2 — 4ac, является не чем иным, как дискриминантом рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, поскольку он определяет число и тип решений. Так, если он равен нулю, то решение будет всего одно, если он положительный, то уравнение обладает двумя действительными корнями, наконец, отрицательный дискриминант приводит к двум комплексным корням x1 и x2.
Теорема Виета или некоторые свойства корней уравнений второго порядка
В конце XVI века один из основоположников современной алгебры француз Франсуа Виет, изучая уравнения второго порядка, смог получить свойства его корней. Математически их можно записать так:
x1 + x2 = -b / a и x1 * x2 = c / a.
Оба равенства легко может получить каждый, для этого необходимо лишь выполнить соответствующие математические операции с корнями, полученными через формулу с дискриминантом.

Совокупность этих двух выражений можно по праву назвать второй формулой корней квадратного уравнения, которая предоставляет возможность угадывать его решения, не используя при этом дискриминант. Здесь следует оговориться, что хотя оба выражения справедливы всегда, применять их для решения уравнения удобно только в том случае, если оно может быть разложено на множители.
Задача на закрепление полученных знаний
Решим математическую задачу, в которой продемонстрируем все приемы, обсуждаемые в статье. Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.

Это условие сразу напоминает о теореме Виета, применяя формулы суммы квадратных корней и их произведения, записываем:
x1 + x2 = -b / a = 4;
x1 * x2 = c / a = -13.
Если предположить, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:
x2 — 4x — 13 = 0.
Воспользуемся формулой с дискриминантом, получим следующие корни:
x1,2 = (4 ± √D)/2, D = 16 — 4 * 1 * (-13) = 68.
То есть задача свелась к нахождению числа √68. Заметим, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получим: √68 = 2√17.
Теперь воспользуемся рассмотренной формулой квадратного корня: a0 = 4, тогда:
a1 = 1/2(4 + 17/4) = 4,125;
a2 = 1/2(4,125 + 17/4,125) = 4,1231.
В вычислении a3 нет необходимости, поскольку найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставляя его в формулу для x1,2, получим:
x1 = (4 + 8,246)/2 = 6,123 и x2 = (4 — 8,246)/2 = -2,123.
Как видим, сумма найденных чисел действительно равна 4, если же найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.
fb.ru
Квадрат. Формулы
Квадрат и окружность – две простые фигуры геометрии свойства которых должны знать все. Квадрат является частным случаем четырехугольников, прямоугольников, параллелограммов, ромбов, а отличается от них равными сторонами и прямыми углами.
Квадрат наиболее симметричная фигура среди всех четырехугольников.
Свойства квадрата
Свойства квадрата — это основные признаки которые позволяют распознать его среди прямоугольников, ромбов, четырехугольников:
- В квадрата все стороны и углы равны AB=BC=CD=AD.
- Противоположные стороны параллельны между собой
- Углы между соседними сторонами прямые.
- Диалонали квадрата равны и пересекаются под прямым углом.
- Диагонали является одновременно биссектрисами углов квадрата.
- Точка в которой пересекаются диагонали является центром квадрата, кроме этого — центром вписанной и описанной окружности.
- Диагонали делят квадрат на четыре одинаковые равнобедренные прямоугольные треугольники .
Площадь квадрата
Больше примеров в школьном курсе при изучении квадрату связано с вычислением его площади и периметра. Вам может показаться что для вычисления площади достаточно знать одну формулу S=a*a и этого хватит для всех задач, однак это не так. Поскольку быстро информация воспринимается и изучается визуально, то мы объединили все величины квадрата которые Вам придется вычислять и нарисовали простые и понятные рисунки с формулами. Их без трудностей можете скачать по ссилке внизу статьи.
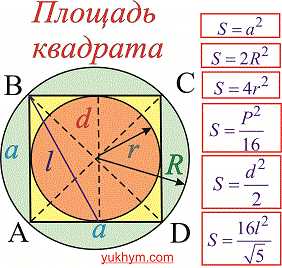
Большинство обозначений Вам понятна, но повторим их снова
a– сторона квадрата;
d– диагональ;
P– периметр;
S– площадь;
R– радиус описанной окружности;
r– радиус вписанной окружности;
l– отрезок изображен на рисунке (часто используется в сложных примерах).
Формулы площади квадрата которые приведены ниже дают возможность вычислять ее через периметр, сторону, диагонали, радиусы .
Они не слишком сложные и каждая из них может Вам пригодиться для вычисления площади квадрата.
Периметр квадрата
Что может быть проще вычисления периметра квадрата если конечно известно его стороны. Однако, если задана только диагональ, площадь, радиус то нахождение периметра не так очевидно. Приведенный ниже рисунок содержит самые необходимые формулы для вычисления параметра
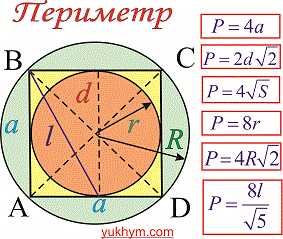
Сами же формулы периметру от различных параметров квадрату привидены ниже
Диагональ квадрата
Диагональ квадрата может бить выражена через радиусы вписанной, описанной окружностей, сторону, периметр, площадь следующими формулам.
В качестве справочника формул диагонали квадрата можете использовать следующий рисунок.
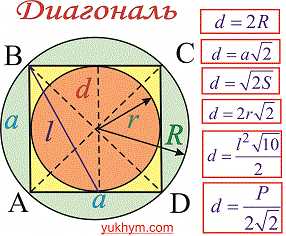
Радиус описанной окружности
Простейшая для вычислений формула радиуса описанной окружности R=d/2, т.е. радиус равен половине диагонали квадрата. Все последующие формулы которые помогут определить радиус описанной окружности содержат корни, однако при вычислениях незаменимы.
Ниже изображен вспомогательный рисунок с приведенным всеми формулами.

Радиус вписанной окружности в квадрат
Радиус вписанной окружности из рисунка равный половине его стороны.
Также он равной одной восьмой части периметра. Зависимости для нахождения радиуса вписанной окружности через площадь, диагональ, радиус описанной окружности содержат иррациональности. Однако и в условиях примеров величины, известные для вычисления радиуса, как правило, заданны с корнями или такими которые легко упрощаются (например ).
Черновик-подсказка формул радиуса вписанной в квадрат окружности приведена ниже
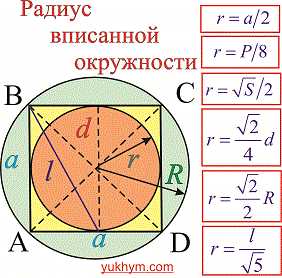
Если же задано диаметр вписанной или описанной окружности то делим пополам (чтобы получить радиус) и можем применять в приведенных формулах. Это Вы думаю помните.
Бонус для всех школьников и студентов. Все цветные графики с формулами площади квадрата, его периметра, диагонали, радиусов вписанной и описанной окружности Вы можете скачать по ссылке внизу.
Распечатывайте формулы и пользуйтесь в обучении.
{jd_file file==18}
Понравился материал — поделись ссылкой с друзьями.
Посмотреть материалы:
{jcomments on}
yukhym.com
Корни квадратного уравнения | Формулы с примерами
Нахождение корней квадратного уравнения 8 класс
ФормулаКорни квадратного уравнения ax2 + bx + c = 0 можно найти по
формуле: , где — дискриминант
квадратного уравнения.
Возможны три правила:
Правило 11. D > 0. Тогда уравнение имеет 2 различных корня: Пример
2x2 + 7x — 4 = 0;
a = 2, b = 7, c = -4.
D = 72 — 4 • 2 • (- 4) = 81 > 0,
x1 = -7 — ? 812 • 2 = — 4;
x2 = -7 + ? 812 • 2 = 12.
Правило 22. D = 0. Тогда уравнение имеет единственный корень. Пример
x2 — 4x + 4 = 0.
D = (-4)2 — 4 • 1 • 4 = 0, x = — -4 2 • 1 = 2.
Заметим, что x2 — 4x + 4 = 0 x = 2.
Правило 3
3. D . Тогда уравнение не имеет корней, так как не существует ? D.
3x2 — x + 7 = 0.
D = (-1)2 — 4 • 3 • 7 = -83
С четным вторым коэффициентом
Правило, формулыЕсли b = 2k, то корни уравнения ax2 + 2kx + c = 0 находятся по формуле:
Где:
Пример 11. x2 + 18x + 32 = 0.
a = 1; b = 18 => k = b2 = 9; c = 32.
D1 = D4 = ( 182)2 — 1 • 32 = 49 > 0, значит уравнение имеет 2 корня:
x1 = -9 -? 491 = -16, x2 = -9 + 7 = -2.
Пример 22. 3x2 + 2x + 1 = 0.
a = 3; b2 = 1; c = 1.
D
3. 196x2 + 28x + 1 = 0.
a = 196; b2 = -14; c = 1.
D1 = D4 = (- 14)2 — 196 = 0, значит уравнение имеет один корень.
x = 14 196 = 1 14.
Формулы по алфавиту:
© 2018 Все права защищеныПри использовании материалов данного сайта обязательно указывать ссылку на источник
Все формулы стороны квадрата
1. Формула стороны квадрата через диагональ
a — сторона квадрата
d — диагональ квадрата
Формула стороны квадрата, (a):
2. Формула стороны квадрата через радиус вписанной окружности
a — сторона квадрата
R — радиус вписанной окружности
D — диаметр вписанной окружности
Формула стороны квадрата, (a):
3. Формула стороны квадрата через радиус описанной окружности
a — сторона квадрата
R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула стороны квадрата, (
4. Формула стороны квадрата через площадь и периметр
a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
Формула стороны квадрата, (a):
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a — сторона квадрата
C — линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
www-formula.ru
Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.
Квадратным уравнением называется уравнение вида
,
где
x — переменная,
a,b,c — постоянные (числовые) коэффициенты.
В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
| Формула дискриминанта: |
. |
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
- D>0 — уравнение имеет 2 различных вещественных корня
- D=0 — уравнение имеет 2 совпадающих вещественных корня
- D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)
В общем случае корни уравнения равны:
.
Очевидно, в случае с нулевым дискриминантом, оба корня равны
.
Если коэффициент при х
В таком случае корни уравнения вычисляются по формуле:
Теорема Виета.
Приведенным квадратным уравнением называется уравнение вида
,
то есть квадратное уравнение с единичным коэффициентом при старшем члене.
В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:
.
Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х2.
tehtab.ru
Квадратная формула • ru.knowledgr.com
В основной алгебре квадратная формула — решение квадратного уравнения. Есть другие способы решить квадратное уравнение вместо того, чтобы использовать квадратную формулу, такую как факторинг, заканчивая квадрат или изображение в виде графика. Используя квадратную формулу часто наиболее удобный способ.
Общее квадратное уравнение —
:
Здесь x
Происхождение формулы
Как только студент понимает, как закончить квадрат, они могут тогда получить квадратную формулу. По этой причине происхождение иногда оставляют как осуществление для студента, который может, таким образом, испытать повторное открытие этой важной формулы. Явное происхождение следующие.
Разделите квадратное уравнение на a, который позволен потому что отличного от нуля:
:
Вычтите c/a из обеих сторон уравнения, уступив:
:
Квадратное уравнение находится теперь в форме, к которой может быть применен метод завершения квадрата. Таким образом добавьте константу к обеим сторонам уравнения, таким образом, что левая сторона становится полным квадратом:
:
который производит
:.
Соответственно, после реконструкции условий справа, чтобы иметь общего знаменателя, мы получаем это:
:
Квадрат был таким образом закончен. Пущение квадратного корня обеих сторон приводит к следующему уравнению:
:
Изоляция x дает квадратную формулу:
:
Плюс — минус символ «±» указывает на это оба
:
решения квадратного уравнения. Есть много альтернатив для этого происхождения с незначительными различиями, главным образом относительно манипуляции.
Некоторые источники, особенно более старые, используют альтернативную параметризацию квадратного уравнения такой как или, где у b есть величина одна половина более общей. Они приводят к немного отличающимся формам для решения, но иначе эквивалентны.
Историческое развитие
Самые ранние методы для решения квадратных уравнений были геометрическими. Вавилонские клинообразные таблетки содержат проблемы, приводимые к решению квадратных уравнений. Египетский Берлинский Папирус, относясь ко времени Среднего Королевства (2050 до н.э к 1650 до н.э), содержит решение квадратного уравнения с двумя терминами.
Греческий математик Евклид (приблизительно 300 до н.э) использовал геометрические методы, чтобы решить квадратные уравнения в Книге 2 его Элементов, влиятельного математического трактата. Правила для квадратных уравнений появляются в китайцах Эти Девять Глав по Математическому Искусству приблизительно 200 до н.э. В его работе Arithmetica греческий математик Диофант (приблизительно 250 до н.э) решил квадратные уравнения с методом, более узнаваемо алгебраическим, чем геометрическая алгебра Евклида. Его решение дает только один корень, даже когда оба корня положительные.
Индийский математик Брэхмэгапта (597–668 н. э.) явно описал квадратную формулу в своем трактате Brāhmasphuṭasiddhānta, изданный в 628 н. э., но написанный в словах вместо символов. Его решение квадратного уравнения было следующие: «К абсолютному числу, умноженному на четыре раза [коэффициент] квадрат, добавьте квадрат [коэффициент] средний член; квадратный корень того же самого, меньше [коэффициент] средний член, разделенный на дважды [коэффициент] квадрат, является стоимостью».
Это эквивалентно:
:
Персидский математик 9-го века al-Khwārizmī, под влиянием более ранних греческих и индийских математиков, решил квадратные уравнения алгебраически. Квадратная формула, покрывающая все случаи, была сначала получена Саймоном Стевином в 1594. В 1637 Рене Декарт издал La Géométrie, содержащий квадратную формулу в форме, которую мы знаем сегодня. Первое появление общего решения в современной математической литературе появилось в газете 1896 года Генри Хитона.
Важность этого решения
Среди многих уравнений, с которыми каждый сталкивается, изучая алгебру, квадратная формула — один из самых важных, и считается самым полезным методом решения квадратных уравнений. В отличие от некоторых других методов решения, таких как факторинг, квадратная формула может использоваться, чтобы решить любое квадратное уравнение. Много уравнений, которые, первоначально кажется, не являются квадратными, могут быть помещены в квадратную форму и решили использование квадратной формулы. По этим причинам это часто запоминается.
Завершение квадрата также допускает решение всего quadratics, поскольку это математически эквивалентно, но квадратная формула дает результат без потребности в таком большом количестве алгебраической манипуляции. Также, это обычно считают более практичным, чтобы использовать формулу. Завершение квадрата очень полезно для других целей, таково как помещение уравнений для конических секций в стандартную форму.
Другие происхождения
Много альтернативных происхождений квадратной формулы могут быть найдены в литературе. Эти происхождения или (a) более просты, чем стандарт, заканчивающий квадратный метод, (b) представляют интересные применения других часто используемых методов в алгебре или (c) понимание предложения других областей математики.
Дополнительный метод завершения квадрата
Значительное большинство текстов алгебры, изданных за прошлые несколько десятилетий, учит, что завершение квадрата, используя последовательность представило ранее: (1) делят каждую сторону на a, (2) перестраивают, (3) тогда добавляют квадрат половины b/a.
Как указано Ларри Хоеном в 1975, заканчивая квадрат может быть достигнут различной последовательностью, которая приводит к более простой последовательности средних сроков: (1) умножают каждую сторону на 4a, (2) перестраивают, (3) тогда добавляют.
Другими словами, квадратная формула может быть получена следующим образом:
:
ax^2+bx+c &= 0 \\
4 a^2 x^2 + 4abx + 4 акра &= 0 \\
4 a^2 x^2 + 4abx &=-4ac \\
4 a^2 x^2 + 4abx + b^2 &= b^2 — 4 акра \\
(2ax + b) ^2 &= b^2 — 4 акра \\
2ax + b &= \pm \sqrt {b^2-4ac} \\
2ax &=-b \pm \sqrt {b^2-4ac} \\
x &= \frac {-b\pm\sqrt {b^2-4ac}} {2a} \\
Это фактически представляет древнее происхождение квадратной формулы, и по крайней мере еще было известно индуистам 1 025 н. э. По сравнению с происхождением в стандартном использовании это дополнительное происхождение короче, связало меньше вычислений с буквальными коэффициентами, избегает частей до последнего шага, имеет более простые выражения и использует более простую математику. Как Хоен заявляет, «легче ‘добавить квадрат b‘, чем это должно ‘добавить квадрат половины коэффициента термина x‘».
Заменой
Другая техника — решение заменой. В этой технике мы занимаем место в квадратное, чтобы добраться:
:
Расширение результата и затем сбор полномочий продуктов:
:
Мы еще не наложили второе условие на и, таким образом, мы теперь выбираем m так, чтобы средний член исчез. Таким образом, или. Вычитание постоянного термина с обеих сторон уравнения (чтобы переместить его в правую сторону) и затем деление на давание:
:
Замена дает:
:
Поэтому; замена обеспечивает квадратную формулу.
При помощи алгебраических тождеств
Позвольте корням стандартного квадратного уравнения быть и. В этом пункте мы вспоминаем идентичность:
:
Пуская квадратный корень с обеих сторон, мы получаем
:
Начиная с коэффициента ≠ 0, мы можем разделить стандартное уравнение на, чтобы получить квадратный полиномиал, имеющий те же самые корни. А именно,
:
От этого мы видим, что суммой корней стандартного квадратного уравнения дают, и продукт тех корней дан
Следовательно идентичность может быть переписана как:
:
Теперь,
:
С тех пор, если мы берем тогда, мы получаем и если мы вместо этого берем тогда, мы вычисляем, что, Объединяя эти результаты при помощи стандартной стенографии, у нас есть это, решениями квадратного уравнения дают:
:
Лагранж resolvents
Альтернативный способ получить квадратную формулу через метод Лагранжа resolvents, который является началом теории Галуа.
Этот метод может быть обобщен, чтобы дать корни кубических полиномиалов и биквадратных полиномиалов, и приводит к теории Галуа, которая позволяет понимать решение алгебраических уравнений любой степени с точки зрения группы симметрии их корней, группы Галуа.
Этот подход сосредотачивает на корнях больше, чем при реконструкции оригинального уравнения.
Учитывая monic квадратный полиномиал
:
предположите что это факторы как
:
Расширение урожаев
:
где и.
Так как заказ умножения не имеет значения, можно переключиться и и ценности p, и q не изменится: каждый говорит, что p и q — симметричные полиномиалы в и. Фактически, они — элементарные симметричные полиномиалы – любой симметричный полиномиал в и могут быть выражены с точки зрения и подход теории Галуа к анализу, и решение полиномиалов: учитывая коэффициенты полиномиала, которые являются симметричными функциями в корнях, может один «разрыв симметрия» и возвращать корни? Таким образом решая полиномиал степени n связан со способами перестроить («перестановка») n условия, который называют симметричной группой на n письмах и обозначают Для квадратного полиномиала, единственный способ перестроить два условия состоит в том, чтобы обменять их («переместите» их), и таким образом решение квадратного полиномиала просто.
Найти корни и рассмотреть их сумму и различие:
:
r_1 &= \alpha + \beta \\
r_2 &= \alpha — \beta.
Их называют Лагранжем resolvents полиномиала;
заметьте, что один из них зависит от заказа корней, который является ключевым пунктом.
Можно возвратить корни от resolvents, инвертировав вышеупомянутые уравнения:
:
\alpha &= \textstyle {\\frac {1} {2} }\\уехал (r_1+r_2\right) \\
\beta &= \textstyle {\\frac {1} {2} }\\уехал (r_1-r_2\right).
Таким образом решение для resolvents дает оригинальные корни.
Формально, resolvents называют дискретным Фурье преобразовывает (DFT) приказа 2, и преобразование может быть выражено матрицей с обратной матрицей, матрицу преобразования также называют матрицей DFT или матрицей Vandermonde.
Теперь симметричная функция в и таким образом, она может быть выражена с точки зрения p и q, и фактически, как отмечено выше. Но не симметрично, начиная с переключения и урожаев (формально, это называют действиями группы симметричной группы корней). С тех пор не симметрично, это не может быть выражено с точки зрения полиномиалов p и q, поскольку они симметричны в корнях, и таким образом так любое многочленное выражение, вовлекающее их. Изменение заказа корней только изменяется фактором, и таким образом квадрат симметричный в корнях и таким образом выразимый с точки зрения p и q. Используя уравнение
:
урожаи
:
и таким образом
:
Если Вы пускаете положительный корень, ломая симметрию, каждый получает:
:
r_1 &=-p \\
r_2 &= \sqrt {p^2 — 4q }\
и таким образом
:
\alpha &= \textstyle {\\frac {1} {2} }\\уехал (-p +\sqrt {p^2 — 4q }\\право) \\
\beta &= \textstyle {\\frac {1} {2} }\\уехал (-p-\sqrt {p^2 — 4q }\\право)
Таким образом корни —
:
который является квадратной формулой. Замена приводит к обычной форме для того, когда квадратным не является monic. resolvents может быть признан как являющийся вершиной и является дискриминантом (monic полиномиала).
Подобный, но более сложный метод работает на кубические уравнения, где у каждого есть три resolvents и квадратное уравнение («полиномиал решения») связь и который может решить квадратным уравнением, и так же для биквадратного (степень 4) уравнение, решение которого полиномиала является кубическим, которое может в свою очередь быть решено. Тот же самый метод для quintic уравнения приводит к полиномиалу степени 24, который не упрощает проблему, и фактически решения quintic уравнений в целом не могут быть выражены, используя, только коренится.
См. также
- Фундаментальная теорема алгебры
Внешние ссылки
- Квадратный калькулятор формулы
- Квадратный калькулятор формулы Онлайн
- Альтернативная формула (Вольфрам)
ru.knowledgr.com
Квадратичная формула — Циклопедия
Квадратичная формула Математика — Выделение полного квадрата // Skill upКвадратичная формула — В элементарной алгебре, квадратичная формула является решением квадратного уравнения. Существуют разные способы решения квадратного уравнения не используя квадратичную формулу, такие как факторизация, выделение полного квадрата, или график функции. Использование квадратичной формулы чаще всего, является намного удобным способом решения.
Квадратное уравнение общего вида
- [math]ax^2+bx+c=0.[/math]
Здесь [math]x[/math] является неизвестным. Постоянные [math]a[/math], [math]b[/math], [math]c[/math] являются коэффициентами, причем [math]\quad a \ne 0.[/math] Каждый из значений, которое выдает квадратичная формула, называется корнем квадратного уравнения. Можно проверить что квадратичная формула удовлетворяет квадратному уравнению, с помощью подстановки значения [math]x[/math] в само квадратное уравнение.
Геометрически, эти корни показывают значения [math]x[/math] при котором, любая парабола, в явном виде [math]y=ax^2+bx+c[/math], пересекает ось абсцисс. Данное пересечение ещё называют «нулями функции».
[править] Происхождение формулы
После того, как ученик понимает, метод выделения полного квадрата, он может самостоятельно открыть квадратичную формулу.[1][2] По этой причине, при изучении квадратичной формулы сам метод нахождения, опускают.
- ↑ Rich, Barnett & Schmidt, Philip (2004), «Schaum’s Outline of Theory and Problems of Elementary Algebra», The McGraw–Hill Companies, ISBN 0-07-141083-X, <http://books.google.com/?id=8PRU9cTKprsC> , Chapter 13 § 4.4, p. 291
- ↑ Li, Xuhui. An Investigation of Secondary School Algebra Teachers’ Mathematical Knowledge for Teaching Algebraic Equation Solving, p. 56 (ProQuest, 2007): «The quadratic formula is the most general method for solving quadratic equations and is derived from another general method: completing the square.»
cyclowiki.org
