Куб разности правило – Решение уравнений. Формулы приведения для полиномов. Разность квадратов, квадрат разности, квадрат суммы, разность и сумма кубов, куб разности и суммы. Они же «формулы сокращенного умножения».

Содержание

Разность квадратов, сумма и разность кубов

Разность квадратов

Выведем формулу разности квадратов $a^2-b^2$.

Для этого вспомним следующее правило:

Если к выражению прибавить любой одночлен и вычесть такой же одночлен, то мы получим верное тождество.

Прибавим к нашему выражению и вычтем из него одночлен $ab$:

Вынесем за скобки общие множители:

Вынесем за скобки $\left(a+b\right)$:

Итого, получим:

То есть, разность квадратов двух одночленов равна произведению их разности на их сумму.

Пример 1

Представить в виде произведения ${4x}^2-y^2$

Данное выражение можно переписать в следующем виде:

\[{4x}^2-y^2={(2x)}^2-y^2\]

Используя формулу разности квадратов, получим:

\[{(2x)}^2-y^2=\left(2x-y\right)(2x+y)\]

Сумма кубов

Выведем формулу суммы кубов $a^3+b^3$.

Для этого будем пользоваться тем же правилом, что и выше.

Прибавим к нашему выражению и вычтем из него одночлены $a^2b\ и\ {ab}^2$:

Вынесем за скобки общие множители:

Вынесем за скобки $\left(a+b\right)$:

Итого, получим:

То есть, сумма кубов двух одночленов равна произведению их суммы на неполный квадрат их разности.

Пример 2

Представить в виде произведения ${8x}^3+y^3$

Данное выражение можно переписать в следующем виде:

\[{8x}^3+y^3={(2x)}^3+y^3\]

Используя формулу разности квадратов, получим:

\[{(2x)}^3+y^3=\left(2x+y\right)(4x^2-2xy+y^2)\]

Разность кубов

Выведем формулу разность кубов $a^3-b^3$.

Для этого будем пользоваться тем же правилом, что и выше.

Прибавим к нашему выражению и вычтем из него одночлены $a^2b\ и\ {ab}^2$:

Вынесем за скобки общие множители:

Вынесем за скобки $\left(a-b\right)$:

Итого, получим:

То есть, разность кубов двух одночленов равна произведению их разности на неполный квадрат их суммы.

Пример 3

Представить в виде произведения ${8x}^3-y^3$

Данное выражение можно переписать в следующем виде:

\[{8x}^3-y^3={(2x)}^3-y^3\]

Используя формулу разности квадратов, получим:

\[{(2x)}^3-y^3=\left(2x-y\right)(4x^2+2xy+y^2)\]

Пример задач на использование формул разности квадратов и суммы и разности кубов

Пример 4

Разложить на множители.

а) ${(a+5)}^2-9$

б) $8-x^3y^3$

в) $-x^3+\frac{1}{27}$

Решение:

а) ${(a+5)}^2-9$

Запишем данное выражение в виде:

\[{{(a+5)}^2-9=(a+5)}^2-3^2\]

Применяя формулу разности квадратов, получим:

\[{(a+5)}^2-3^2=\left(a+5-3\right)\left(a+5+3\right)=\left(a+2\right)(a+8)\]

б) $8+x^3y^3$

Запишем данное выражение в виде:

\[8+x^3y^3=2^3+{(xy)}^3\]

Применим формулу кумы кубов:

\[2^3+{(xy)}^3=\left(2+xy\right)(4-2xy+x^2y^2)\]

в) $-x^3+\frac{1}{27}$

Запишем данное выражение в виде:

\[-x^3+\frac{1}{27}={\left(\frac{1}{3}\right)}^3-x^3\]

Применим формулу кумы кубов:

\[{\left(\frac{1}{3}\right)}^3-x^3=\left(\frac{1}{3}-x\right)\left(\frac{1}{9}+\frac{x}{3}+x^2\right)\]

spravochnick.ru

правила применения формул сокращенного умножения

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, сумма кубов приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·( а² — ас + с²).

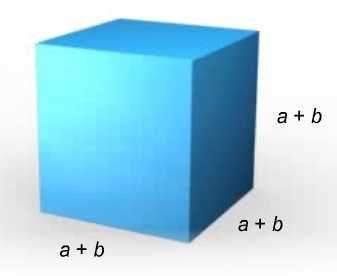
Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а³– с³= (а – с)(а²+ ас + с²).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Материалы по теме:

Интересные статьи

autogear.ru

Урок по теме «Куб суммы и куб разности двух выражений»

Краткосрочный план урока № 56 Зам.дир.по УР 24.01.2018

7.5А Формулы сокращенного умножения

Школа: КГУ ШГ № 118

Дата: 24.01.2018

ФИО учителя: Липова Н.А.

Класс: 7а,б,в,г,д,е

Предмет:

алгебра

Тема урока:

Куб суммы и куб разности двух выражений

Тип урока

Урок изучения нового материала

Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)

Учащийся:

7.2.1.18 знать и применять формулы сокращённого умножения

Цели урока

Ознакомить учащихся с формулами «куб разности» и «куб суммы»;

Научить применять формулы сокращённого умножения в упрощениях и преобразованиях выражений.

Критерии оценивания

Учащиеся умеют:

знать и применять формулы сокращенного умножения;
применять формулы сокращенного умножения при упрощении алгебраических выражений;
применять формулы сокращенного умножения при разложении многочлена на множители

Языковые цели

давать словесную формулировку формул сокращённого умножения;
записывать формулы сокращенного умножения по словесной формулировке;
аргументировать выбор способа разложения многочлена на множители;

объяснять выполнение разложения многочлена на множители.

Лексика и терминология, специфичная для предмета:

формулы сокращенного умножения;
разность квадратов двух выражений;
квадрат суммы двух выражений;
квадрат разности двух выражений;
разность кубов двух выражений;
наибольший общий множитель;
куб разности двух выражений;

удвоенное произведение;
утроенное произведение;
куб суммы двух выражений;
разложение на множители;
сумма кубов двух выражений
общий множитель;
способ группировки;
полный квадрат;
неполный квадрат.

Серия полезных фраз для диалога/письма

разность квадратов двух выражений равна…;
квадрат суммы (разности) двух выражений равен….;
куб суммы (разности) двух выражений равен….;
сумма (разность) кубов двух выражений равна…;
чтобы вынести общий множитель за скобки…;
наибольший общий делитель коэффициентов…;
данное выражение можно записать в виде…;
чтобы разложить многочлен на множители.…;
произведение множителей равно нулю, если…;
сгруппируем члены многочлена (выражения), имеющие …;
чтобы представить данный многочлен в виде произведения, используем …;
чтобы в данном выражении выделить квадрат суммы (разности)….

Привитие ценностей

Уважение, сотрудничество, открытость.

Привитие ценностей осуществляется посредством/через парную и групповую виды работ.

Навыки использования ИКТ

Применение интерактивной доски.

Предварительные знания

Умение выполнять действия с одночленами и многочленами. Знание ФСУ квадрат суммы и разности, разность квадратов.

Ход урока

Запланированные этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

2 мин

Орг. момент. Приветствие.

Создание благоприятного психологического климата в классе.

Стратегия «Комплимент». Учащиеся говорят друг другу комплимент.

мяч

Актуализация знаний

5 мин

Стратегия «Соответствие».

Для каждого выражения из левого столбца подберите ему тождественно равное в правом:

1		а
2		б
3		в
4		г
5		д
6		е
7		ж
8		з
9		и

Ответы:
Самопроверка по ключу. Ключ: 1г, 2д, 3ж, 4и, 5з, 6а, 7е, 8в, 9б.

Рефлексия этапа:

Были сложности в выполнении задания?
Какие?
Все ли пары вы нашли? Какая пара является для Вас новой?
Как Вы думаете, формула ли это?

Приложение 1

Проблемный вопрос

2 мин

Пара 7е составляет ли равенство?

Можно ли назвать её ФСУ? Почему?

Выход на тему урока

2 мин

Совместный вывод формулы для объёма куба.

Диалоговое обучение.

Приложение 2

Формулировка темы и целей урока

1 мин

Учащиеся формулируют тему урока и его цели.

— По выполненным заданиям как вы думаете, что будет являтся предметом нашего исследования на уроке?

Самостоятельное изучение нового материалы

10 мин

Мини исследование

Вывод ФСУ

Куб разности

Диалоговое обучение.

Учитель: Вспомним, как умножить многочлен на многочлен?

Ученик: При умножении многочлена на многочлен каждый член одного многочлена умножают на каждый член другого.

Учитель: Однако в некоторых случаях умножение многочленов можно выполнить короче, воспользовавшись формулами сокращённого умножения.

Учитель: Зная формулы квадрата суммы и квадрата разности, нетрудно вывести формулы куба суммы и куба разности.

Именно эти преобразования были выполнены выше.

Работа в группах. Стратегия «Соседи по партам». Учащиеся объединяются в группы по 4 человека по номеру парт (1-2), (3-4), (5-6) и так далее.

Самостоятельно докажите ФСУ «куб разности» и сформулируйте устно.

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

Защита работы группы.

Листы А3, маркеры

Закрепление.

17 мин

Закрепление с попутным обсуждением.

Отработка формул.

№1. Представить выражение в виде многочлена:

б)

в)

г)

№2. Представьте в виде многочлена:

а) (2а²+3в²)³

в) (10х⁴–6у²)³

№3. Представьте многочлен в виде куба двучлена:

а) (8р³–27q³+54pq²–36p²q)

в) (х³у³+6х²у²+12ху+8)

№ 5.111, №5.109

Рефлексия этапа:

Если ли сложности с решением заданий?
Какие?
Есть ли вопросы, которые требуют дополнительного разъяснения?

Приложение 3

учебник

Рефлексия

1 мин

Учащиеся дополняют следующие предложения:

Сегодня я узнал…
Было интересно…
Было трудно…
Я выполнял задания…
Теперь я могу…
Урок дал мне для жизни…

Домашнее задание

1 мин

Выучить теоретический материал. Уметь выводить ФСУ

№ 5.100(3 ст), № 5.103

Учебник

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Дифференциация может быть выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в оказании индивидуальной поддержки учащемуся, в подборе учебного материала и ресурсов с учетом индивидуальных способностей учащихся (Теория множественного интеллекта по Гарднеру).

Дифференциация может быть использована на любом этапе урока с учетом рационального использования времени.

Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.

Здоровьесберегающие технологии.

Используемые физминутки и активные виды деятельности.

Пункты, применяемые из Правил техники безопасности на данном уроке.

Рефлексия по уроку

Были ли цели урока/цели обучения реалистичными?

Все ли учащиеся достигли ЦО?

Если нет, то почему?

Правильно ли проведена дифференциация на уроке?

Выдержаны ли были временные этапы урока?

Какие отступления были от плана урока и почему?

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках

kopilkaurokov.ru

Правило куба суммы и куба разности — Ваше право

Статьи по естественным наукам и математике

Куб суммы двух выражений равен сумме кубов этих выражений, сложенной с утроенным произведением квадрата первого выражения на второе и утроенным произведением квадрата второго выражения на первое.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Здесь (a + b) 3 — куб суммы, a 3 + b 3 — сумма кубов, 3a 2 b — утроенное произведение квадрата первого выражения на второе, 3ab 2 — утроенное произведение квадрата второго выражения на первое.

Вывести эту формулу можно путем умножения многочленов:

(a + b) 3 = (a + b) 2 (a + b) = (a 2 + 2ab + b 2 )(a + b) = a 3 + a 2 b + 2a 2 b + 2ab 2 + ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Куб разности двух выражений равен разности кубов этих выражений минус утроенное произведение квадрата первого выражения на второе и плюс утроенное произведение квадрата второго выражения на первое.

(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3 .

Вывести эту формулу можно путем умножения многочленов:

(a – b) 3 = (a – b) 2 (a – b) = (a 2 – 2ab + b 2 )(a – b) = a 3 – a 2 b – 2a 2 b + 2ab 2 + ab 2 – b 3 = a 3 – 3a 2 b + 3ab 2 – b 3 .

Обратите внимание, что минус там, где b в нечетной степени.

scienceland.info

Урок математики по теме «Формулы куба суммы и куба разности»

Цели:

закрепить умения и навыки учащихся по данной теме;

развитие умений преодолевать трудности при решении тождеств с использованием формул сокращенного умножения;

воспитание у учащихся настойчивости, целеустремленности в учебе.

Ход урока.

I. Орг. момент.

II. Мотивация урока.

Формулы сокращенного умножения имеют широкое применение в математике. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений.

Наша цель – систематизировать знания по теме «Формулы сокращенного умножения», показать знание этих формул и умение применять их в различных математических ситуациях.

III. Актуализация опорных знаний.

Проверка словесной формулировки формул сокращенного умножения.

1. Квадрат суммы двух выражений равен.

Квадрату первого выражения, плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

2. Квадрат разности двух выражений равен.

Квадрату первого выражения, минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

3. Разность квадратов двух выражений равна.

Произведению разности этих выражений и их суммы.

4. Куб суммы двух выражений равен.

Кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

5. Куб разности двух выражений равен.

Кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

Работа в парах. У каждой пары имеется лист с заданием. Установите принцип соответствия и заполните таблицу.

videouroki.net

Куб разности и разность кубов: правила применения формул сокращенного умножения

Квадрат суммы

Квадрат разности

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a? — с? = (a + с)·(a – с).

Куб суммы

Сумма кубов

Если значения сторон небольшие, то выполнить вычисления просто.

Куб разности

Разность кубов

fb.ru

Формулы сокращённого умножения

При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.

Следует также помнить, что вместо « a » и « b » в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

a 2 ? b 2 = (a ? b)(a + b)

15 2 ? 2 2 = (15 ? 2)(15 + 2) = 13 · 17 = 221
9a 2 ? 4b 2 с 2 = (3a ? 2bc)(3a + 2bc)

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(a + b) 2 = a 2 + 2ab + b 2

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:

Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.
112 = 100 + 1
Запишем сумму чисел в скобки и поставим над скобками квадрат.
112 2 = (100 + 12) 2
Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 · 100 · 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.

(8a + с) 2 = 64a 2 + 16ac + c 2

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

(a ? b) 2 = a 2 ? 2ab + b 2

Также стоит запомнить весьма полезное преобразование:

Формула выше доказывается простым раскрытием скобок:

(a ? b) 2 = a 2 ?2ab + b 2 = b 2 ? 2ab + a 2 = (b ? a) 2

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Запомнить эту «страшную» на вид формулу довольно просто.

Выучите, что в начале идёт « a 3 ».
Два многочлена посередине имеют коэффициенты 3 .
Вспомним, что любое число в нулевой степени есть 1 . (a 0 = 1, b 0 = 1) . Легко заметить, что в формуле идёт понижение степени « a » и увеличение степени « b ». В этом можно убедиться:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a ? b) 3 = a 3 ? 3a 2 b + 3ab 2 ? b 3

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков « + » и « ? ». Перед первым членом « a 3 » стоит « + » (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять « ? », затем опять « + » и т.д.

(a ? b) 3 = + a 3 ? 3a 2 b + 3ab 2 ? b 3 = a 3 ? 3a 2 b + 3ab 2 ? b 3

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a 3 + b 3 = (a + b)(a 2 ? ab + b 2 )

Сумма кубов — это произведение двух скобок.

Первая скобка — сумма двух чисел.
Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
(a 2 ? ab + b 2 )
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.

Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

a 3 ? b 3 = (a ? b)(a 2 + ab + b 2 )

Будьте внимательны при записи знаков.

Применение формул сокращенного умножения

Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.

a 2 + 2a + 1 = (a + 1) 2
(aс ? 4b)(ac + 4b) = a 2 c 2 ? 16b 2

Таблицу со всеми формулами сокращённого умножения вы можете скачать в разделе «Шпаргалки».

math-prosto.ru

Открытый урок «Куб суммы и разности двух выражений»

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Алгебра 7 класс Урок №

Тема урока: Куб суммы и разности двух выражений

Организ ация деятельност и учащихся по усвоению:

знаний понятий: формул сокращённого умножения ;

умений применять их при возведении в квадрат и куб суммы или разности двух выражений;

навыков работы с выражениями.

Ознакомление учащихся с формулами куба суммы и разности двух выражений.

Образовательная: формировать знания учащихся о формулах сокращенного умножения: куб суммы и разности двух выражений, повторить ранее изученные формулы сокращенного умножения, применение их при раскрытии скобок;

Развивающая: развивать математическую речь при чтении формул, мышление при анализе нового материала;

Воспитательная: воспитание дисциплинированности, умение оценивать свою работу.

I Организационный момент

Чтобы спорилось нужное дело,

Чтобы в жизни не знать неудач,

В путешествие отправимся смело,

В мир примеров и разных задач

Эта история произошла давным – давно. В древнем городе жил добрый мудрец и злой человек, который завидовал славе мудреца. И решил он придумать такой вопрос, чтобы мудрец не смог на него ответить. Пошёл он на луг, поймал бабочку, сжал между сомкнутыми ладонями и подумал: « Спрошу – ка я: о, мудрейший, какая у меня бабочка – живая или мертвая? Если он скажет, что мертвая, я раскрою ладони – бабочка улетит, а если скажет, что живая, я сомкну ладони, и бабочка умрёт». Так завистник и сделал. Поймал бабочку, посадил между ладоней, отправился к мудрецу и спросил его: «Какая у меня бабочка живая или мертвая»? Мудрец ответил: «Всё в твоих руках!»

Как часто, ребята, нам кажется, что ничего не понимаю, ничего не знаю, ничего не решу! Но я хочу повторить слова мудреца «все в твоих руках». Пусть эти слова будут девизом нашего урока.

III Актуализация знаний

Фронтальная работа с классом

Найдите квадраты выражений с; -8; 5а; 6х 2 ; у 3 ; ху

Найдите произведение: 2х и 6с; 5у и 2х; 4а и 3у; 2х 2 и 3х

5у+2х — возведите в куб второе выражение

— возведите в квадрат первое выражение

-найдите удвоенное(утроенное) произведение первого и второго

Используя термины «разность», «сумма», «квадрат», «куб» прочитать выражения: с+у; (х+а) 2 , х-у, (с-а) 3 , с 2 +х 2 , у 2 -х 2

— к каким выражениям можем применить формулы сокращенного умножения

Работа в парах: Восстановить формулы сокращенного умножения

Формулы сокращенного умножения

IV Изучение нового материала

— Приступаем к изучению новых формул

— Зная формулы квадрата суммы и квадрата разности, нетрудно вывести формулы куба суммы и куба разности.

-Что означает третья степень

Ученик должен дописать её до конца, т.е.

Данное тождество называют формулой куба суммы.

Учитель: аналогично можно получить, что (выводят самостоятельно)

Данное тождество называют формулой куба разности.

Пример: (2х+3у) 3 =(2х) 3 +3•(2х) 2 •3у+3•2х•(3у) 2 +(3у) 3 =8х 3 +36х 2 у+54ху 2 +27у 3

Задание 1. Выполните возведение в куб

infourok.ru

pred64.ru

правила применения формул сокращенного умножения

Образование 8 мая 2013

Квадрат суммы

Квадрат разности

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a – с).

Куб суммы

Сумма кубов

Если значения сторон небольшие, то выполнить вычисления просто.

Куб разности

Разность кубов

Источник: fb.ru Образование
Сумма кубов и их разность: формулы сокращенного умножения

Математика – одна из тех наук, без которых невозможно существование человечества. Практически каждое действие, каждый процесс сопряжены с использованием математики и ее элементарных действий. Многие великие учен…

Красота
Глазурирование волос: состав и выбор следства, правила применения, влияние на кожу головы и волосы, плюсы использования, рекомендации и отзывы

Инновационные методы ухода за волосами не оставляют равнодушными даже самых ярых приверженцев натуральных средств. Кто бы что ни говорил, но в тех условиях, в которых мы проживаем, омовение волос ромашковым раствором …

Красота
Масло-спрей для волос: обзор магазинных и домашних средств, правила применения, отзывы

Польза масел для волос известна многим женщинам. Они способствуют улучшению внутренней структуры прядей, их внешнего вида. Но не все считают такие средства удобными в использовании. Именно поэтому производители выпуск…

Домашний уют
Водостойкий силиконовый герметик: особенности и правила применения

При проведении домашнего ремонта, а также в области профессионального строительства никак не обойтись без использования силиконового герметика. Этот материал заменил самодельные мастики, битумные смеси и всевозможные …

Домашний уют
Клей плиточный «Юнис». Свойства и правила применения.

Многие профессиональные строители и любители самостоятельно выполнять ремонтные работы в квартире отдают предпочтение специализированным продуктам, которые помогают достичь максимального эффекта.Среди многообра…

Домашний уют
Герметик для дерева: разновидности и правила применения.

Важным этапом в процессе строительства деревянного дома является его утепление. Грамотно выполненный, этот вид работ обеспечит комфортный климат в помещении и снизит затраты на отопление. В качестве утеплителя из совр…

Домашний уют
Двойной суперфосфат: применение, формула и цена удобрения

Минеральные удобрения — основа современного сельского хозяйства. Они позволяют значительно повышать плодородие даже совсем бедных почв, что дает возможность выращивать богатые урожаи практически во всех регионах…

Еда и напитки
Зеленый кофе с имбирем: отзывы врачей, характеристика и правила применения средства для похудения

Зеленый кофе — сравнительно новый на рынке БАДов продукт, стремительно…

Закон
Огнетушитель ранцевый: правила применения и выбор

Огнетушитель ранцевый, как и другие подобные устройства, обладает особенностями эксплуатации. Этот прибор является одним из удобных, поскольку у него есть наплечные ремни. При необходимости устройство позволит устрани…

Здоровье
Раствор для линз «Авизор»: правила применения и достоинства

«Авизор» — препарат, предназначенный для очистки контактных линз. За годы применения он доказал свою эффективность. Торговое название этого раствора — «Авизор Уника Сенситив». Он прекрасно подх…

monateka.com

Куб разности и разность кубов: правила применения формул сокращенного умножения

Квадрат суммы

Квадрат разности

Разность квадратов

Куб суммы

Сумма кубов

Если значения сторон небольшие, то выполнить вычисления просто.

Куб разности

Разность кубов

4u-pro.ru

РубрикаПолезно знать

Разность квадратов, сумма и разность кубов

Разность квадратов

Сумма кубов

Разность кубов

Пример задач на использование формул разности квадратов и суммы и разности кубов

правила применения формул сокращенного умножения

Материалы по теме:

Интересные статьи

Урок по теме «Куб суммы и куб разности двух выражений»

Правило куба суммы и куба разности — Ваше право

Статьи по естественным наукам и математике

Урок математики по теме «Формулы куба суммы и куба разности»

Куб разности и разность кубов: правила применения формул сокращенного умножения

Формулы сокращённого умножения

Применение формул сокращенного умножения

Открытый урок «Куб суммы и разности двух выражений»

правила применения формул сокращенного умножения

Куб разности и разность кубов: правила применения формул сокращенного умножения

Добавить комментарий Отменить ответ