Косинус пи 2 – Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
cos (pi / 2 + x)
Задача.
Упростить выражение .
Решение.
Чтобы упростить заданное выражение, выполним его анализ. Итак, выражение содержит тригонометрическую функцию косинус, под знаком которой находится сумма двух аргументов.
Как известно, в тригонометрии используются формулы сложения аргументов, независимо от того, какие значения стоят на их месте.
Эти формулы удобнее всего использовать, когда на месте одного из аргументов стоит конкретное (постоянное) число.
К примеру, в заданном примере на месте первого аргумента стоит постоянное число , а на месте второго — неизвестная переменная х. В таком случае при использовании формулы значение тригонометрической функции от постоянного числа можно найти, вследствие чего выражение станет намного проще.
Итак, чтобы упростить заданное выражение, будем использовать формулу косинуса сложения аргументов:
Получили выражение, которое содержит тригонометрические функции, вычислить значение которых можно при помощи таблицы тригонометрических функций. Запишем найденные значения в полученное выражение.
Итак, заданное выражение после упрощения приняло вид .
Ответ. .
ru.solverbook.com
cos (3 / 2 Пи)
Существует несколько вариантов вычисления значения выражения cos (3 / 2 Пи).
Первый вариант. Использование таблицы тригонометрических функций
Этот вариант самый легкий и простой и заключается в том, что в таблице нужно найти соответствующие значения.

Существует много разновидностей таблицы, в некоторых из них аргументы представлены только в виде радиан, в других — в градусах, а некоторые содержат значения и радиан, и градусов.
Иногда все же полезно перевести значение угла в градусы, чтобы легче воспринять значение косинуса. Но не запрещается использовать таблицу с градусами и радианами )).
Из таблицы определим значение косинуса от 3 Пи / 2 — это 0.
Математическая запись:
Второй вариант. Тригонометрическая окружность.
Удобный вариант, если недоступна таблица тригонометрических функций. Здесь значение тригонометрической функции можно определить с помощью тригонометрической окружности.

На тригонометрической окружности (или круге) на оси абсцисс расположены значения функции косинус.
Согласно заданию аргумент функции равен 3 Пи / 2. На окружности это значение находится на оси ординат в самом низу. Чтобы вычислить значение заданной функции нужно опустить перпендикуляр на ось Ох, после чего получим значение 0. Таким образом, косинус от 3 Пи / 2 равен 0.
Третий вариант. Использование графика косинуса.
Если нет таблицы, а по тригонометрической окружности ориентироваться сложно, то полезно использовать график косинуса, по которому также можно определить значение.
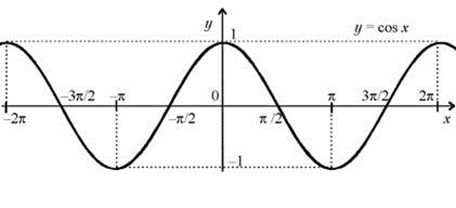
ru.solverbook.com
Таблица косинусов (полная, градусы и значения)
В данной таблице представлены значения косинусов от 0° до 360°. Таблица косинусов нужна, чтобы узнать, чему равен косинус угла. Нужно только найти его в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-kosinusov — uchim.org
Таблица косинусов для 0°-180°
|
|
|
Таблица косинусов для 181°-360°
|
|
|
Как легко запомнить таблицу косинусов (видео)
Существуют также следующие таблицы тригонометрических функций: таблица синусов, таблица тангенсов и таблица котангенсов.
Всё для учебы » Математика в школе » Таблица косинусов (полная, градусы и значения)
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-kosinusov
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
uchim.org
Формулы приведения тригонометрических функций
Формулы приведения тригонометрических функций
Формулы привидения тригонометрических функций представлены в виде таблицы. Ниже находятся некоторые формулы приведения в табличном виде. Еще ниже эти формулы приведения расписаны для некоторых тригонометрических функций в виде тригонометрических тождеств.Таблицы значений тригонометрических функций находятся на другой странице.
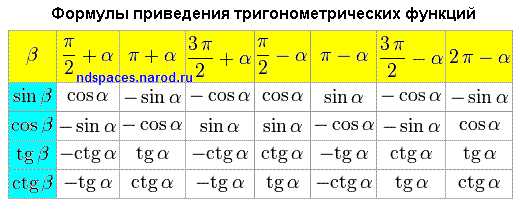
Формулы привидения для синуса выглядят так:
sin (π/2 + α) = cos α
sin (π + α) = — sin α
sin (3π/2 + α) = — cos α
sin (π/2 — α) = cos α
sin (π — α) = sin α
sin (3π/2 — α) = — cos α
sin (2π — α) = — sin α
Формулы приведения для тригонометрической функции синус будут следующие. Синус угла пи пополам (пи/2) плюс или минус угол альфа равняется косинусу угла альфа. Синус угла пи плюс угол альфа или угла два пи минус альфа по формуле приведения будет равен минус синусу угла альфа. Синус угла три вторых пи (3пи/2) плюс или минус альфа равен минус косинусу альфа. Если угол равняется пи минус альфа, то синус такого угла равняется синусу угла альфа. Тригонометрия формулы и тригонометрические тождества. Перевод синуса в косинус.
Тригонометрические формулы привидения для косинуса приобретают такой вид:
cos (π/2 + α) = — sin α
cos (π + α) = — cos α
cos (3π/2 + α) = sin α
cos (π/2 — α) = sin α
cos (π — α) = — cos α
cos (3π/2 — α) = — sin α
cos (2π — α) = cos α
Для косинуса формулы приведения имеют следующий вид. Косинус угла пи пополам (пи/2) плюс угол альфа и косинус три вторых пи минус альфа равняются минус синусу угла альфа. Косинус угла пи плюс или минус угол альфа в результате равен минус косинусу альфа. Формула приведения для косинуса угла (3пи/2) три вторых пи плюс угол альфа и пи пополам минус альфа равняется синусу угла альфа. Тригонометрическая функция косинус пи пополам (1/2 пи) минус альфа равняется тригонометрической функции косинус угла альфа. Тригонометрия формулы. Перевод косинуса в синусы.
Тригонометрическая функция тангенс имеет следующие формулы привидения:
tg (π/2 + α) = — ctg α
tg (π + α) = tg α
tg (π/2 — α) = ctg α
tg (π — α) = — tg α
tg (3π/2 — α) = ctg α
tg (2π — α) = tg α
Тригонометрические формулы приведения функции тангенс tg. Тангенс угла пи деленное на два плюс альфа и угла три вторых пи плюс альфа приравниваются минус котангенсу угла альфа. Тригонометрическая функция тангенс угла пи на два или три пи деленное на два (3/2 пи) минус альфа равна котангенсу альфа. Тангенс угла пи минус альфа равен минус тангенсу угла альфа. Формулы приведения для тангенса пи плюс альфа и тангенса два пи минус альфа равняются тангенсу угла альфа. Тригонометрические тождества. Перевод тангенса в котангенсы.
Тригонометрическая функция тангенс имеет следующие формулы привидения:
ctg (π/2 + α) = — tg α
ctg (π + α) = ctg α
ctg (3π/2 + α) = — tg α
ctg (π/2 — α) = tg α
ctg (π — α) = — ctg α
ctg (3π/2 — α) = tg α
ctg (2π — α) = ctg α
Формулы приведения функции котангенс ctg угла. Для угла 1/2 пи плюс альфа и угла 3/2 пи плюс альфа котангенс равняется минус тангенсу -tg угла альфа. Если в этих же выражениях угол альфа не прибавляется, а вычитается, тогда котангенс такого угла равняется тангенсу угла альфа. Функция котангенс пи минус альфа равна минус котангенсу угла альфа. Котангенс угла пи плюс альфа и 2 пи минус альфа будет равен котангенсу угла альфа. Тригонометрические тождества и формулы тригонометрия. Перевод котангенсов в тангенсы.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
17 января 2010 года — 28 февраля 2017 года..
© 2006 — 2017 Николай Хижняк. Все права защишены.
ndspaces.narod.ru
Таблица косинусов
Таблица косинусовГлавная > к >
Таблица косинусов для основных углов: 0°, 90°, 180°, 270°, 360°.
| Угол х (в градусах) |
0° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|
| Угол х (в радианах) |
0 | ||||
| cos x | 1 | 0 | -1 | 0 | 1 |
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) |
0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) |
0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) |
√2/2 (0,7071) |
1/2 (0,5) |
0 | -1/2 (-0,5) |
-√2/2 (-0,7071) |
-√3/2 (-0,8660) |
-1 | -√3/2 (-0,8660) |
-√2/2 (-0,7071) |
-1/2 (-0,5) |
0 | 1/2 (0,5) |
√2/2 (0,7071) |
√3/2 (0,8660) |
1 |
Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°.
Таблица косинусов — это посчитанные значения косинусов от 0° до 360°.
Если не под рукой калькулятора — таблица косинусов может пригодиться.
Для того, чтобы узнать чему равен косинус от нужного Вам угла достаточно найти его в таблице:
| cos 1° | = 0,9998 | cos 91° | = -0,0175 | cos 181° | = -0,9998 | cos 271° | = 0,0175 |
|---|---|---|---|---|---|---|---|
| cos 2° | = 0,9994 | cos 92° | = -0,0349 | cos 182° | = -0,9994 | cos 272° | = 0,0349 |
| cos 3° | = 0,9986 | cos 93° | = -0,0523 | cos 183° | = -0,9986 | cos 273° | = 0,0523 |
| cos 4° | = 0,9976 | cos 94° | = -0,0698 | cos 184° | = -0,9976 | cos 274° | = 0,0698 |
| cos 5° | = 0,9962 | cos 95° | = -0,0872 | cos 185° | = -0,9962 | cos 275° | = 0,0872 |
| cos 6° | = 0,9945 | cos 96° | = -0,1045 | cos 186° | = -0,9945 | cos 276° | = 0,1045 |
| cos 7° | = 0,9925 | cos 97° | = -0,1219 | cos 187° | = -0,9925 | cos 277° | = 0,1219 |
| cos 8° | = 0,9903 | cos 98° | = -0,1392 | cos 188° | = -0,9903 | cos 278° | = 0,1392 |
| cos 9° | = 0,9877 | cos 99° | = -0,1564 | cos 189° | = -0,9877 | cos 279° | = 0,1564 |
| cos 10° | = 0,9848 | cos 100° | = -0,1736 | cos 190° | = -0,9848 | cos 280° | = 0,1736 |
| cos 11° | = 0,9816 | cos 101° | = -0,1908 | cos 191° | = -0,9816 | cos 281° | = 0,1908 |
| cos 12° | = 0,9781 | cos 102° | = -0,2079 | cos 192° | = -0,9781 | cos 282° | = 0,2079 |
| cos 13° | = 0,9744 | cos 103° | = -0,225 | cos 193° | = -0,9744 | cos 283° | = 0,225 |
| cos 14° | = 0,9703 | cos 104° | = -0,2419 | cos 194° | = -0,9703 | cos 284° | = 0,2419 |
| cos 15° | = 0,9659 | cos 105° | = -0,2588 | cos 195° | = -0,9659 | cos 285° | = 0,2588 |
| cos 16° | = 0,9613 | cos 106° | = -0,2756 | cos 196° | = -0,9613 | cos 286° | = 0,2756 |
| cos 17° | = 0,9563 | cos 107° | = -0,2924 | cos 197° | = -0,9563 | cos 287° | = 0,2924 |
| cos 18° | = 0,9511 | cos 108° | = -0,309 | cos 198° | = -0,9511 | cos 288° | = 0,309 |
| cos 19° | = 0,9455 | cos 109° | = -0,3256 | cos 199° | = -0,9455 | cos 289° | = 0,3256 |
| cos 20° | = 0,9397 | cos 110° | = -0,342 | cos 200° | = -0,9397 | cos 290° | = 0,342 |
| cos 21° | = 0,9336 | cos 111° | = -0,3584 | cos 201° | = -0,9336 | cos 291° | = 0,3584 |
| cos 22° | = 0,9272 | cos 112° | = -0,3746 | cos 202° | = -0,9272 | cos 292° | = 0,3746 |
| cos 23° | = 0,9205 | cos 113° | = -0,3907 | cos 203° | = -0,9205 | cos 293° | = 0,3907 |
| cos 24° | = 0,9135 | cos 114° | = -0,4067 | cos 204° | = -0,9135 | cos 294° | = 0,4067 |
| cos 25° | = 0,9063 | cos 115° | = -0,4226 | cos 205° | = -0,9063 | cos 295° | = 0,4226 |
| cos 26° | = 0,8988 | cos 116° | = -0,4384 | cos 206° | = -0,8988 | cos 296° | = 0,4384 |
| cos 27° | = 0,891 | cos 117° | = -0,454 | cos 207° | = -0,891 | cos 297° | = 0,454 |
| cos 28° | = 0,8829 | cos 118° | = -0,4695 | cos 208° | = -0,8829 | cos 298° | = 0,4695 |
| cos 29° | = 0,8746 | cos 119° | = -0,4848 | cos 209° | = -0,8746 | cos 299° | = 0,4848 |
| cos 30° | = 0,866 | cos 120° | = -0,5 | cos 210° | = -0,866 | cos 300° | = 0,5 |
| cos 31° | = 0,8572 | cos 121° | = -0,515 | cos 211° | = -0,8572 | cos 301° | = 0,515 |
| cos 32° | = 0,848 | cos 122° | = -0,5299 | cos 212° | = -0,848 | cos 302° | = 0,5299 |
| cos 33° | = 0,8387 | cos 123° | = -0,5446 | cos 213° | = -0,8387 | cos 303° | = 0,5446 |
| cos 34° | = 0,829 | cos 124° | = -0,5592 | cos 214° | = -0,829 | cos 304° | = 0,5592 |
| cos 35° | = 0,8192 | cos 125° | = -0,5736 | cos 215° | = -0,8192 | cos 305° | = 0,5736 |
| cos 36° | = 0,809 | cos 126° | = -0,5878 | cos 216° | = -0,809 | cos 306° | = 0,5878 |
| cos 37° | = 0,7986 | cos 127° | = -0,6018 | cos 217° | = -0,7986 | cos 307° | = 0,6018 |
| cos 38° | = 0,788 | cos 128° | = -0,6157 | cos 218° | = -0,788 | cos 308° | = 0,6157 |
| cos 39° | = 0,7771 | cos 129° | = -0,6293 | cos 219° | = -0,7771 | cos 309° | = 0,6293 |
| cos 40° | = 0,766 | cos 130° | = -0,6428 | cos 220° | = -0,766 | cos 310° | = 0,6428 |
| cos 41° | = 0,7547 | cos 131° | = -0,6561 | cos 221° | = -0,7547 | cos 311° | = 0,6561 |
| cos 42° | = 0,7431 | cos 132° | = -0,6691 | cos 222° | = -0,7431 | cos 312° | = 0,6691 |
| cos 43° | = 0,7314 | cos 133° | = -0,682 | cos 223° | = -0,7314 | cos 313° | = 0,682 |
| cos 44° | = 0,7193 | cos 134° | = -0,6947 | cos 224° | = -0,7193 | cos 314° | = 0,6947 |
| cos 45° | = 0,7071 | cos 135° | = -0,7071 | cos 225° | = -0,7071 | cos 315° | = 0,7071 |
| cos 46° | = 0,6947 | cos 136° | = -0,7193 | cos 226° | = -0,6947 | cos 316° | = 0,7193 |
| cos 47° | = 0,682 | cos 137° | = -0,7314 | cos 227° | = -0,682 | cos 317° | = 0,7314 |
| cos 48° | = 0,6691 | cos 138° | = -0,7431 | cos 228° | = -0,6691 | cos 318° | = 0,7431 |
| cos 49° | = 0,6561 | cos 139° | = -0,7547 | cos 229° | = -0,6561 | cos 319° | = 0,7547 |
| cos 50° | = 0,6428 | cos 140° | = -0,766 | cos 230° | = -0,6428 | cos 320° | = 0,766 |
| cos 51° | = 0,6293 | cos 141° | = -0,7771 | cos 231° | = -0,6293 | cos 321° | = 0,7771 |
| cos 52° | = 0,6157 | cos 142° | = -0,788 | cos 232° | = -0,6157 | cos 322° | = 0,788 |
| cos 53° | = 0,6018 | cos 143° | = -0,7986 | cos 233° | = -0,6018 | cos 323° | = 0,7986 |
| cos 54° | = 0,5878 | cos 144° | = -0,809 | cos 234° | = -0,5878 | cos 324° | = 0,809 |
| cos 55° | = 0,5736 | cos 145° | = -0,8192 | cos 235° | = -0,5736 | cos 325° | = 0,8192 |
| cos 56° | = 0,5592 | cos 146° | = -0,829 | cos 236° | = -0,5592 | cos 326° | = 0,829 |
| cos 57° | = 0,5446 | cos 147° | = -0,8387 | cos 237° | = -0,5446 | cos 327° | = 0,8387 |
| cos 58° | = 0,5299 | cos 148° | = -0,848 | cos 238° | = -0,5299 | cos 328° | = 0,848 |
| cos 59° | = 0,515 | cos 149° | = -0,8572 | cos 239° | = -0,515 | cos 329° | = 0,8572 |
| cos 60° | = 0,5 | cos 150° | = -0,866 | cos 240° | = -0,5 | cos 330° | = 0,866 |
| cos 61° | = 0,4848 | cos 151° | = -0,8746 | cos 241° | = -0,4848 | cos 331° | = 0,8746 |
| cos 62° | = 0,4695 | cos 152° | = -0,8829 | cos 242° | = -0,4695 | cos 332° | = 0,8829 |
| cos 63° | = 0,454 | cos 153° | = -0,891 | cos 243° | = -0,454 | cos 333° | = 0,891 |
| cos 64° | = 0,4384 | cos 154° | = -0,8988 | cos 244° | = -0,4384 | cos 334° | = 0,8988 |
| cos 65° | = 0,4226 | cos 155° | = -0,9063 | cos 245° | = -0,4226 | cos 335° | = 0,9063 |
| cos 66° | = 0,4067 | cos 156° | = -0,9135 | cos 246° | = -0,4067 | cos 336° | = 0,9135 |
| cos 67° | = 0,3907 | cos 157° | = -0,9205 | cos 247° | = -0,3907 | cos 337° | = 0,9205 |
| cos 68° | = 0,3746 | cos 158° | = -0,9272 | cos 248° | = -0,3746 | cos 338° | = 0,9272 |
| cos 69° | = 0,3584 | cos 159° | = -0,9336 | cos 249° | = -0,3584 | cos 339° | = 0,9336 |
| cos 70° | = 0,342 | cos 160° | = -0,9397 | cos 250° | = -0,342 | cos 340° | = 0,9397 |
| cos 71° | = 0,3256 | cos 161° | = -0,9455 | cos 251° | = -0,3256 | cos 341° | = 0,9455 |
| cos 72° | = 0,309 | cos 162° | = -0,9511 | cos 252° | = -0,309 | cos 342° | = 0,9511 |
| cos 73° | = 0,2924 | cos 163° | = -0,9563 | cos 253° | = -0,2924 | cos 343° | = 0,9563 |
| cos 74° | = 0,2756 | cos 164° | = -0,9613 | cos 254° | = -0,2756 | cos 344° | = 0,9613 |
| cos 75° | = 0,2588 | cos 165° | = -0,9659 | cos 255° | = -0,2588 | cos 345° | = 0,9659 |
| cos 76° | = 0,2419 | cos 166° | = -0,9703 | cos 256° | = -0,2419 | cos 346° | = 0,9703 |
| cos 77° | = 0,225 | cos 167° | = -0,9744 | cos 257° | = -0,225 | cos 347° | = 0,9744 |
| cos 78° | = 0,2079 | cos 168° | = -0,9781 | cos 258° | = -0,2079 | cos 348° | = 0,9781 |
| cos 79° | = 0,1908 | cos 169° | = -0,9816 | cos 259° | = -0,1908 | cos 349° | = 0,9816 |
| cos 80° | = 0,1736 | cos 170° | = -0,9848 | cos 260° | = -0,1736 | cos 350° | = 0,9848 |
| cos 81° | = 0,1564 | cos 171° | = -0,9877 | cos 261° | = -0,1564 | cos 351° | = 0,9877 |
| cos 82° | = 0,1392 | cos 172° | = -0,9903 | cos 262° | = -0,1392 | cos 352° | = 0,9903 |
| cos 83° | = 0,1219 | cos 173° | = -0,9925 | cos 263° | = -0,1219 | cos 353° | = 0,9925 |
| cos 84° | = 0,1045 | cos 174° | = -0,9945 | cos 264° | = -0,1045 | cos 354° | = 0,9945 |
| cos 85° | = 0,0872 | cos 175° | = -0,9962 | cos 265° | = -0,0872 | cos 355° | = 0,9962 |
| cos 86° | = 0,0698 | cos 176° | = -0,9976 | cos 266° | = -0,0698 | cos 356° | = 0,9976 |
| cos 87° | = 0,0523 | cos 177° | = -0,9986 | cos 267° | = -0,0523 | cos 357° | = 0,9986 |
| cos 88° | = 0,0349 | cos 178° | = -0,9994 | cos 268° | = -0,0349 | cos 358° | = 0,9994 |
| cos 89° | = 0,0175 | cos 179° | = -0,9998 | cos 269° | = -0,0175 | cos 359° | = 0,9998 |
| cos 90° | = 0 | cos 180° | = -1 | cos 270° | = -0 | cos 360° | = 1 |
comments powered by HyperComments
tab.wikimassa.org
Таблица косинусов — 2mb.ru
Таблица косинусов является одной из основных таблиц, которые используются в геометрии.
В ней представлены косинусы углов от 0 до 360 градусов. Таблица позволяет решать математические задачи, в которых необходимо использовать тригонометрические данные без применения расчетов и калькулятора.
Таблица косинусов 0° — 180°.
|
|
|
Таблица косинусов 180° — 360°.
|
|
|
2mb.ru
