Кос график – Учебно-методические документы по инженерной графике. Комплект контрольно-оценочных средств (КОС), рабочая программа и календарно-тематический план.
График косинуса | Алгебра
Как построить график функции y=cos x? Начнём строить график косинуса с промежутка [-π/2;π/2].
В качестве единичного берём отрезок длиной 2 клеточки тетради. Для удобства округлим число π до целого
Так как единица изображается отрезком длиной 2 клеточки, то числ π — 6 клеточками. Соответственно, π/2 — это отрезок в 3 клеточки, π/3 — 2 клеточки. По оси Ox будем отмечать не единичные отрезки, а отрезки длиной π/2 (то есть разбиваем ось абсцисс на отрезки через каждые 3 клеточки).
Составим таблицу значений косинуса на промежутке [-π/2;π/2]:
Полученные точки отмечаем на координатной плоскости:

Продолжим рассмотрение графика косинуса вправо, на промежутке [π/2;3π/2]:
2π/3 — дважды по π/3 — 4 клеточки; 4π/3 — 8 клеточек:
Так как y=cos x — периодическая функция с периодом T=2π, то график функции, взятый на на промежутке [-π/2;3π/2], повторяется вправо и влево, на плюс бесконечность и на минус бесконечность:
График функции y=cos x
График функции y=cos x также можно получить параллельным переносом на π/2 влево из графика функции y=sin x.
Графики тригонометрических функций рассматривают не только в алгебре. Они находят практическое применение в других дисциплинах (в физике, биологии и других).
www.algebraclass.ru
График косинуса, с примерами построения
График косинуса имеет вид как показано на рисунке 1. Кривая, задающая график косинуса, называется косинусоидой.

Рис. 1
График функции пересекает ось в точках Максимальные значения, равные функция принимает в точках а минимальные, равные – при График функции возрастает при и убывает при
Примеры решения задач
ПРИМЕР 1| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси ординат вверх на 1 единицу (рис. 2)
 Рис. 2 |
| Задание | Построить график функции |
Искомый график получается из графика функции в результате параллельного переноса вдоль оси абсцисс вправо на (рис. 3).
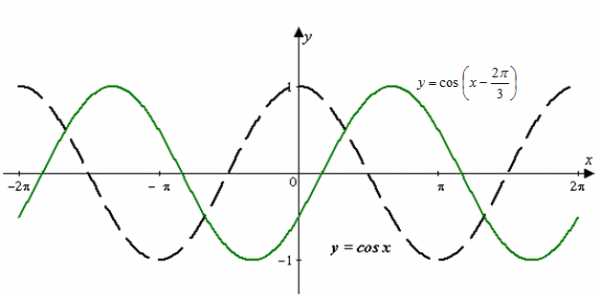 Рис. 3 |
| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции Сначала графика функции растянем вдоль оси ординат в три раза (увеличим расстояния от каждой точки графика до оси абсцисс в три раза), получим график функции (рис. 4).
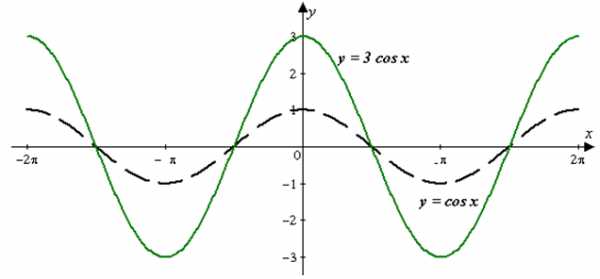 Рис. 4 Затем, отразим график функции симметрично относительно оси абсцисс, получим искомый график (рис. 5). 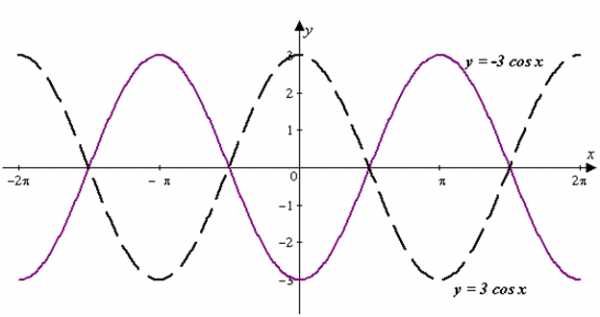 Рис. 5 |
Разность косинусов
Косинус суммы
Сумма синусов
Таблица брадиса косинусы
Косинус умножить на косинус (Произведение косинусов)
Тригонометрический круг (окружность)
ru.solverbook.com
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции (синусоида)
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).
Рис.1.
Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции
Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.
Синус — периодическая функция с наименьшим положительным периодом : , таким образом, через промежутки длиной вид графика функции повторяется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние , где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение , то есть график функции проходит через начало координат.
На оси значение . Поэтому необходимо найти такие значения , при которых , то есть ордината соответствующей точки единичной окружности, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при (см. рис. 1).
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, при всех , а также, учитывая период, при всех .
Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому при .
Промежутки возрастания и убывания. Учитывая периодичность функции с периодом , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 3, а), то при увеличении аргумента ордината соответствующей точки единичной окружности увеличивается (то есть , следовательно, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков
Рис.2 Рис.3
Если (рис.3,б), то при увеличении аргумента ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , например на промежутке . Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке . Учитывая нечетность функции (ее график симметричен относительно начала координат), для построения графика на промежутке отображаем полученную кривую симметрично относительно начала координат (рис. 5).
Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который называется синусоидой .(Рис.6)
Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой . Такие процессы называют
График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным переносом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой , где А — амплитуда
колебания, — частота, — начальная фаза, — период колебания.
СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число).
- Область значений:
-
Функция четная:
(график симметричен относительно оси ).
- Функция периодическая с периодом :
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:
.
Рис.7
Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции . Это можно записать так: .
Как видим, наибольшее значение функции равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .
Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при .
Косинус — четная функция: , поэтому ее график симметричен относительно оси .
Косинус — периодическая функция с наименьшим положительным периодом : . Таким образом, через промежутки длиной вид графика функции повторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .
Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 0 при , а также, учитывая период, при всех .
Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому при
Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 9, а), то при увеличении аргумента абсцисса соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .
Если (рис. 9, б), то при увеличении аргумента абсцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков .
Рис.8 Рис.9
Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу
Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также
абсциссы и ординаты этих точек. Так как , то при повороте
прямоугольника около точки на угол — против часовой стрелки он перейдет в прямоугольник . Но тогда . Следовательно, 00.
Укажем также формулы, которые нам понадобятся далее:.
Тогда,
Таким образом, .
Учитывая, что , график функции можно получить из графика функции его параллельным переносом вдоль оси на (рис. 11). Полученный график называется косинусоидой (рис. 12).
Рис.11
Рис.12
График функции (тангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
ya-znau.ru
Тригонометрические функции | Математика | FANDOM powered by Wikia
Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические фу́нкции — математические функции от угла. Они безусловно важны при изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. Более современные определения выражают тригонометрические функции через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на произвольные вещественные числа и даже на комплексные числа.
В настоящее время выделяют шесть основных тригонометрических функций, указанных ниже вместе с уравнениями, связывающими их друг с другом. Для последних четырёх функций, эти соотношения часто называют определениями этих функций, однако можно определять эти функции геометрически или как-нибудь по-другому. Кроме того, существуют другие функции, такие как $ \operatorname{versin} $ и $ \operatorname{exsec} $, но они в настоящее время редко используются (см. Редко используемые тригонометрические функции). С тригонометрическими функциями тесно связаны обратные им функции (см. Обратные тригонометрические функции)
| Функция | Обозначение | Соотношение |
|---|---|---|
| Си́нус | $ \sin $ | $ \sin x=\cos\left(\frac{\pi}{2}-x\right) $ |
| Ко́синус | $ \cos $ | $ \cos x=\sin\left(\frac{\pi}{2}-x\right) $ |
| Та́нгенс | $ \operatorname{tg} $ или $ \tan $ | $ \operatorname{tg}\; x=\frac{\sin x}{\cos x}=\operatorname{ctg}\; \left(\frac{\pi}{2}-x\right)=\frac{1}{\operatorname{ctg}\; x} $ |
| Кота́нгенс | $ \operatorname{ctg} $ или $ \cot $ | $ \operatorname{ctg}\; x=\frac{\cos x}{\sin x}=\operatorname{tg}\; \left(\frac{\pi}{2}-x\right)=\frac{1}{\operatorname{tg}\; x} $ |
| Се́канс | $ \sec $ | $ \sec x=\frac{1}{\cos x}=\csc\left(\frac{\pi}{2}-x\right) $ |
| Косе́канс | $ \operatorname{cosec} $ или $ \csc $ | $ \operatorname{cosec}\; x=\frac{1}{\sin x}=\sec\left(\frac{\pi}{2}-x\right) $ |
Тригонометрические функции в прямоугольном треугольнике Править
Чтобы определить тригонометрические функции произвольного угла $ \alpha, $ возьмём произвольный прямоугольный треугольник, содержащий угол $ \alpha $. Стороны этого треугольника мы будем называть так:
- Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона $ c. $
- Противолежащий катет — катет, лежащий напротив угла. Например, катет $ a $ — противолежащий по отношению к углу $ A. $
- Прилежащий катет — катет, являющийся стороной угла. Например, катет $ b $ — прилежащий по отношению к углу $ A. $
Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна $ \pi. $ Это означает, что углы между катетами и гипотенузой лежат между $ 0 $ и $ \frac{\pi}{2}. $ Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.
Си́нус угла — отношение противолежащего катета к гипотенузе: $ \sin\alpha=\frac{a}{c}. $ Это отношение не зависит от выбора треугольника $ {ABC} $, содержащего угол $ \alpha, $ так как все такие треугольники подобны.
Ко́синус угла — отношение прилежащего катета к гипотенузе: $ \cos\alpha=\frac{b}{c}. $ Так как $ \sin\beta=\frac{b}{c}, $ синус одного острого угла в треугольнике равна косинусу второго, и наоборот.
Та́нгенс угла — отношение противолежащего катета к прилежащему: $ \operatorname{tg}\,\alpha=\frac{a}{b}. $
Кота́нгенс угла — отношение прилежащего катета к противолежащему: $ \operatorname{ctg}\,\alpha=\frac{b}{a}. $ Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.
Се́канс угла — отношение гипотенузы к прилежащему катету: $ \sec\alpha=\frac{c}{b}. $
Косе́канс угла — отношение гипотенузы к противолежащему катету: $ \operatorname{cosec}\,\alpha=\frac{c}{a}. $
Из определений тригонометрических функций следует:
- $ a=c\sin\alpha\,, $
- $ b=c\cos\alpha\,, $
- $ a=b\,\operatorname{tg}\,\alpha, $
- $ b=a\,\operatorname{ctg}\,\alpha, $
- $ c=b\sec\alpha\,, $
- $ c=a\,\operatorname{cosec}\,\alpha, $
и симметрично:
- $ b=c\sin\beta\,, $
- $ a=c\cos\beta\,, $
- $ b=a\,\operatorname{tg}\,\beta, $
- $ a=b\,\operatorname{ctg}\,\beta, $
- $ c=a\sec\beta\,, $
- $ c=b\,\operatorname{cosec}\,\beta. $
Определение тригонометрических функций через окружность Править
Пусть на плоскости задана прямоугольная система координат с началом в точке $ O $ и с осями $ {OX} $ и $ {OY} $ . Возьмём в этой системе координат окружность с центром в точке $ O $ и радиусом, равным единице. Пусть отрезок $ {OA} $ поворачивается на произвольный угол $ \vartheta $ вокруг центра $ O. $
Синусом угла $ \vartheta $ называется отношение ординаты точки $ A $ к длине отрезка $ {OA}. $ Обозначают $ \sin\vartheta=\frac{AC}{OA}. $ Так как длина отрезка $ {OA} $ равна $ 1 $, то $ \sin\vartheta={AC}. $
Косинусом угла $ \vartheta $ называется отношение абсциссы точки $ A $ к длине отрезка $ {OA}. $ Обозначают $ \cos\vartheta=\frac{OC}{OA}. $ Так как длина отрезка $ {OA} $ равна 1, то $ \cos\vartheta={OC}. $
Тангенсом угла $ \vartheta $ называется отношение ординаты точки $ A $ к абсциссе точки $ A $. Обозначают $ \operatorname{tg}\,\vartheta=\frac{AC}{OC} $ (в англоязычной литературе $ \tan\vartheta ). $ Так как $ {AC}=\sin \vartheta $ и $ {OC}=\cos\vartheta, $ то $ \operatorname{tg}\,\vartheta=\frac{\sin\vartheta}{\cos\vartheta}. $
Котангенсом угла $ \vartheta $ называется отношение абсциссы точки $ A $ к ординате точки $ A $. Обозначают $ \operatorname{ctg}\,\vartheta=\frac{OC}{AC} $ (в англоязычной литературе $ \cot\vartheta ). $ Так как $ {AC}=\sin\vartheta $ и $ {OC}=\cos\vartheta, $ то $ \operatorname{ctg}\,\vartheta=\frac{\cos\vartheta}{\sin\vartheta}. $ Котангенс равен обратному значению тангенса: $ \operatorname{ctg}\,\vartheta=\frac{1}{\operatorname{tg}\,\vartheta}. $
Секансом угла $ \vartheta $ называется отношение длины отрезка $ {OA} $ к абсциссе точки $ A $. Обозначают $ \sec\vartheta=\frac{OA}{OC}. $ Так как длина отрезка $ {OA} $ равна 1, то $ \sec\vartheta=\frac{1}{OC}. $ Секанс равен обратному значению косинуса: $ \sec\vartheta=\frac{1}{\cos\vartheta}. $
Косекансом угла $ \vartheta $ называется отношение длины отрезка $ {OA} $ к ординате точки $ A $. Обозначают $ \operatorname{cosec}\,\vartheta=\frac{OA}{AC} $ (в англоязычной литературе $ \csc\vartheta ). $ Так как длина отрезка $ {OA} $ равна $ 1 $, то $ \operatorname{cosec}\,\vartheta=\frac{1}{AC}. $ Косеканс равен обратному значению синуса: $ \operatorname{cosec}\,\vartheta=\frac{1}{\sin\vartheta}. $
Из определения следует: если косинус угла равен нулю, то тангенс и секанс этого угла не существуют. Аналогично для котангенса и косеканса: если синус угла равен нулю, то котангенс и косеканс этого угла не существуют.
Определение тригонометрических функций через ряды Править
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенных рядов:
- $ \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}+\cdots = \sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{(2n+1)!}, $
- $ \cos x=1-\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}+\cdots = \sum_{n=0}^\infty\frac{(-1)^nx^{2n}}{(2n)!}. $
Пользуясь этими формулами, а также уравнениями $ \operatorname{tg}\,x=\frac{\sin x}{\cos x}, $ $ \operatorname{ctg}\,x=\frac{\cos x}{\sin x}, $ $ \sec x=\frac{1}{\cos x} $ и $ \operatorname{cosec}\,x=\frac{1}{\sin x}, $ можно найти разложения в ряд Тейлора и других тригонометрических функций:
- $ \operatorname{tg}\,x=x+\frac{x^3}{3} + \frac{2x^5}{15} + \frac{17x^7}{315} + \frac{62x^9}{2835} + \cdots = \sum_{n=1}^\infty\frac{(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}}{(2n)!}x^{2n-1} \quad \left(-\frac{\pi}{2}<x<\frac{\pi}{2}\right), \quad $ где $ B_n $ — числа Бернулли.
- $ \sec x=1+\frac{x^2}{2}+\frac{5x^4}{24}+\frac{61x^6}{720}+\frac{277x^8}{8064}+\cdots = \sum_{n=0}^\infty\frac{(-1)^nE_{2n}}{(2n)!}x^{2n}, $ где $ E_n $ — числа Эйлера.
Значения тригонометрических функций для некоторых углов Править
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
| $ \alpha \,\! $ | 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) |
|---|---|---|---|---|---|---|---|
| $ \sin \alpha \,\! $ | $ {0} \,\! $ | $ \frac{1}{2}\,\! $ | $ \frac{ \sqrt{2}}{2}\,\! $ | $ \frac{ \sqrt{3}}{2}\,\! $ | $ {1}\,\! $ | $ {0}\,\! $ | $ {-1}\,\! $ |
| $ \cos \alpha \,\! $ | $ {1} \,\! $ | $ \frac{ \sqrt{3}}{2}\,\! $ | $ \frac{ \sqrt{2}}{2}\,\! $ | $ \frac{1}{2}\,\! $ | $ {0}\,\! $ | $ {-1}\,\! $ | $ {0}\,\! $ |
| $ \mathop{\mathrm{tg}}\, \alpha \,\! $ | $ {0} \,\! $ | $ \frac{1}{ \sqrt{3}}\,\! $ | $ {1}\,\! $ | $ \sqrt{3}\,\! $ | $ \infty \,\! $ | $ {0}\,\! $ | $ \infty \,\! $ |
| $ \mathop{\mathrm{ctg}}\, \alpha \,\! $ | $ \infty \,\! $ | $ \sqrt{3}\,\! $ | $ {1} \,\! $ | $ \frac{1}{ \sqrt{3}}\,\! $ | $ {0}\,\! $ | $ \infty \,\! $ | $ {0}\,\! $ |
| $ \sec \alpha \,\! $ | $ {1} \,\! $ | $ \frac{2}{ \sqrt{3}}\,\! $ | $ \sqrt{2}\,\! $ | $ {2}\,\! $ | $ \infty \,\! $ | $ {-1}\,\! $ | $ \infty \,\! $ |
| $ \operatorname{cosec}\, \alpha \,\! $ | $ \infty \,\! $ | $ {2}\,\! $ | $ \sqrt{2}\,\! $ | $ \frac{2}{ \sqrt{3}}\,\! $ | $ {1}\,\! $ | $ \infty \,\! $ | $ {-1}\,\! $ |
Значения тригонометрических функций нестандартных углов Править
$ \sin \frac{\pi}{10} = \sin 18^\circ = \frac{\sqrt{5}-1}{4} $$ \operatorname{tg} \frac{\pi}{120}= \operatorname{tg} 1.5^\circ =\sqrt{\frac{8-\sqrt{2(2-\sqrt{3})(3-\sqrt{5})} — \sqrt{ 2(2+\sqrt{3})(5+\sqrt{5})}}{8+\sqrt{2(2-\sqrt{3})(3-\sqrt{5})}+\sqrt{2(2+\sqrt{3})(5+\sqrt{5})} }} $
$ \cos \frac{\pi}{240}=\frac{1}{16}\left(\sqrt{2-\sqrt{2+\sqrt{2}}} \left(\sqrt{2(2+\sqrt{5})}+\sqrt{3}-\sqrt{15} \right) + \sqrt{\sqrt{2+\sqrt{2}}+2} \left (\sqrt{6(5+\sqrt{5})}+\sqrt{5} — 1 \right) \right) $
$ \cos \frac{\pi}{17} = \frac{1}{8} \sqrt{2 \left( \sqrt{2\sqrt{\frac{17(17-\sqrt{17})}{2}}-\sqrt{\frac{17-\sqrt{17}}{2}}-4\sqrt{34+2\sqrt{17}} + 3\sqrt{17}+17}+\sqrt{34-2\sqrt{17}}+\sqrt{17}+15 \right)} $
Свойства тригонометрических функций Править
Функция y = cos x — чётная. Функции: y = sin x, y = tg x, y = ctg x — нечётные, то есть:
- $ \sin \left( — x \right) = — \sin x\,, $
- $ \cos \left( — x \right) = \cos x\,, $
- $ \mathop{\mathrm{tg}}\, \left( — x \right) = — \mathop{\mathrm{tg}}\, x\,, $
- $ \mathop{\mathrm{ctg}}\, \left( — x \right) = — \mathop{\mathrm{ctg}}\, x\,. $
Для острых углов $ \alpha < \frac{ \pi}{2}\,\! $ справедливо:
- $ \sin \left( \frac{ \pi}{2} — \alpha \right) = \cos \alpha\,, $
- $ \cos \left( \frac{ \pi}{2} — \alpha \right) = \sin \alpha\,, $
- $ \mathop{\mathrm{tg}}\, \left( \frac{ \pi}{2} — \alpha \right) = \mathop{\mathrm{ctg}}\, \alpha\,, $
- $ \mathop{\mathrm{ctg}}\, \left( \frac{ \pi}{2} — \alpha \right) = \mathop{\mathrm{tg}}\, \alpha\,. $
Для углов $ 0 < \alpha < \pi \,\! $ справедливо:
- $ \sin \left( \pi — \alpha \right) = \sin \alpha\,, $
- $ \cos \left( \pi — \alpha \right) = — \cos \alpha\,, $
- $ \mathop{\mathrm{tg}}\, \left( \pi — \alpha \right) = — \mathop{\mathrm{tg}}\, \alpha, \qquad \alpha \ne \frac{ \pi}{2}\,. $
Рассмотрим треугольник ABO (см. Рис. 1). По теореме Пифагора:
- $ \left(AB \right)^2 + \left(BO \right)^2 = \left(OA \right)^2 \,, $
если OA = 1, то AB = sin α и OB = cos α, то есть
- $ \sin^2 \alpha + \cos^2 \alpha = 1. \qquad \qquad (1)\, $
Если разделить выражение (1) на $ \cos^2 \alpha \,, $ то получим следующее тождество:
- $ 1 + \mathop{\mathrm{tg}}\,^2 \alpha = \frac{1}{ \cos^2 \alpha}. \qquad \qquad (2) \, $
Если разделить выражение (1) на $ \sin^2 \alpha \,, $ то получим следующее тождество:
- $ 1 + \frac{1}{ \mathop{\mathrm{tg}}\,^2 \alpha} = \frac{1}{ \sin^2 \alpha}, \qquad \qquad (3) \, $
или
- $ 1 + \mathop{\mathrm{ctg}}\,^2 \alpha = \frac{1}{ \sin^2 \alpha}. \qquad \qquad (4) \, $
Производные и интегралы Править
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
$ ( \sin x )’ = \cos x \,, $
$ ( \cos x )’ = -\sin x \,, $
$ ( \mathop{\mathrm{tg}}\, x )’ = \frac{1}{\cos ^2 x}, $
$ ( \mathop{\mathrm{ctg}}\, x )’ = -\frac{1}{\sin ^2 x}. $
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. «tangens» — касающийся) и «секанс» (лат. «secans» — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
- GonioLab: Проясненная Единичная Окружность, Тригонометрические и Гиперболические функции (Java Web Start)
ar:تابع مثلثي ast:Función trigonométrica bg:Тригонометрична функция bs:Trigonometrijske funkcije ca:Funció trigonomètrica cs:Goniometrická funkce da:Trigonometrisk funktiongl:Función trigonométrica io:Trigonometriala funciono is:Hornafallksh:Sinus nl:Goniometrische functie pl:Funkcje trygonometrycznesimple:Trigonometric function sl:Trigonometrična funkcija sr:Тригонометријске функције sv:Trigonometrisk funktion tg:Функсияҳои тригонометрӣ th:ฟังก์ชันตรีโกณมิติ uk:Тригонометричні функції vi:Hàm lượng giáczh-classical:三角函數
ru.math.wikia.com
Функция y=cos t, её основные свойства и график. Рабочие материалы
Дополнительные сочиненияНа этом уроке мы подробно рассмотрим функцию у = cos х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = cost на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=cost, её основные свойства и график
1. Тема урока, введение
Функцией называется закон, по которому каждому значению независимого аргумента ставится в соответствие единственное значение функции.
2. Определение функции y=cost, её график
Вспомним определение функции Пусть t – любое действительное число. Ему соответствует единственная точка M на числовой окружности. У точки M есть единственная абсцисса. Она и называется косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
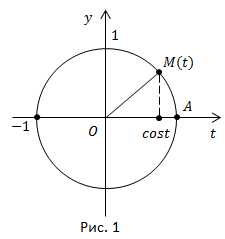
Центральный угол численно равен величине дуги в радианах, т. е. числу Поэтому аргументом может быть и действительное число, и угол в радианах.
Если мы умеем для каждого значения определить то можем построить график функции
Можно получить график функции и другим способом. По формулам приведения поэтому график косинуса – это синусоида, сдвинутая по оси x на влево (рис.2).

3. Основные свойства функции y=cost
Свойства функции
1) Область определения:
2) Область значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции: .
13) Точки максимума:
14) Максимум функции:
4. Вывод, заключение
Мы рассмотрели основные свойства и график функции Далее они будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебраический тренажер.-К.: А. С.К., 1997.
7. Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А. П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
1. Математика .
2. Интернет-портал Problems. ru .
3. Образовательный портал для подготовки к экзаменам .
dp-adilet.kz
Арксинус, арккосинус — свойства, графики, формулы
Арксинус, arcsin
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений –π/2 ≤ y ≤ π/2.
sin(arcsin x) = x
arcsin(sin x) = x
Арксинус иногда обозначают так:
.
График функции арксинус
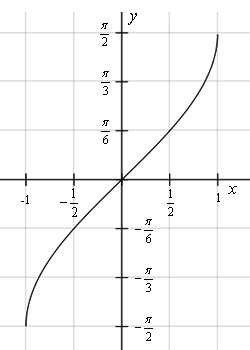
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
cos(arccos x) = x
arccos(cos x) = x
Арккосинус иногда обозначают так:
.
График функции арккосинус

График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков:
,
где – многочлен степени . Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin t. Интегрируем по частям, учитывая что –π/2 ≤ t ≤ π/2, cos t ≥ 0:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| < 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Тригонометрические функции, их свойства и графики.
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода , где Т — период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Функция синус y = sin(x).
Изобразим график функции синус, его называют «синусоида».
Свойства функции синус y = sinx.
Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
Наименьший положительный период функции синуса равен двум пи: .
Функция обращается в ноль при , где , Z – множество целых чисел.
Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .
Функция синус — нечетная, так как .
Функция убывает при , возрастает при .
Функция синус имеет локальные максимумы в точках , локальные минимумы в точках .
Функция y = sinx вогнутая при , выпуклая при .
Координаты точек перегиба .
Асимптот нет.
Функция косинус y = cos(x).
График функции косинус (его называют «косинусоида») имеет вид:
Свойства функции косинус y = cosx.
Функция тангенс y = tg(x).
График функции тангенс (его называют «тангенсоида») имеет вид:

Свойства функции тангенс y = tgx.
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют «котангенсоида»):

Свойства функции котангенс y = ctgx.
studfiles.net
