Корреляция примеры – Основы корреляционного анализа. Примеры анализа прямолинейной связи при парной корреляции

Метод корреляционного анализа: пример. Корреляционный анализ

В научных исследованиях часто возникает необходимость в нахождении связи между результативными и факторными переменными (урожайностью какой-либо культуры и количеством осадков, ростом и весом человека в однородных группах по полу и возрасту, частотой пульса и температурой тела и т.д.).

Вторые представляют собой признаки, способствующие изменению таковых, связанных с ними (первыми).

Понятие о корреляционном анализе

Существует множество определений термина. Исходя из вышеизложенного, можно сказать, что корреляционный анализ — это метод, применяющийся с целью проверки гипотезы о статистической значимости двух и более переменных, если исследователь их может измерять, но не изменять.

Есть и другие определения рассматриваемого понятия. Корреляционный анализ — это метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. Корреляционный анализ — это метод по изучению статистической зависимости между случайными величинами с необязательным наличием строгого функционального характера, при которой динамика одной случайной величины приводит к динамике математического ожидания другой.

Понятие о ложности корреляции

При проведении корреляционного анализа необходимо учитывать, что его можно провести по отношению к любой совокупности признаков, зачастую абсурдных по отношению друг к другу. Порой они не имеют никакой причинной связи друг с другом.

В этом случае говорят о ложной корреляции.

Задачи корреляционного анализа

Исходя из приведенных выше определений, можно сформулировать следующие задачи описываемого метода: получить информацию об одной из искомых переменных с помощью другой; определить тесноту связи между исследуемыми переменными.

Корреляционный анализ предполагает определение зависимости между изучаемыми признаками, в связи с чем задачи корреляционного анализа можно дополнить следующими:

• выявление факторов, оказывающих наибольшее влияние на результативный признак;
• выявление неизученных ранее причин связей;
• построение корреляционной модели с ее параметрическим анализом;
• исследование значимости параметров связи и их интервальная оценка.

Связь корреляционного анализа с регрессионным

Метод корреляционного анализа часто не ограничивается нахождением тесноты связи между исследуемыми величинами. Иногда он дополняется составлением уравнений регрессии, которые получают с помощью одноименного анализа, и представляющих собой описание корреляционной зависимости между результирующим и факторным (факторными) признаком (признаками). Этот метод в совокупности с рассматриваемым анализом составляет метод корреляционно-регрессионного анализа.

Условия использования метода

Результативные факторы зависят от одного до нескольких факторов. Метод корреляционного анализа может применяться в том случае, если имеется большое количество наблюдений о величине результативных и факторных показателей (факторов), при этом исследуемые факторы должны быть количественными и отражаться в конкретных источниках. Первое может определяться нормальным законом — в этом случае результатом корреляционного анализа выступают коэффициенты корреляции Пирсона, либо, в случае, если признаки не подчиняются этому закону, используется коэффициент ранговой корреляции Спирмена.

Правила отбора факторов корреляционного анализа

При применении данного метода необходимо определиться с факторами, оказывающими влияние на результативные показатели. Их отбирают с учетом того, что между показателями должны присутствовать причинно-следственные связи. В случае создания многофакторной корреляционной модели отбирают те из них, которые оказывают существенное влияние на результирующий показатель, при этом взаимозависимые факторы с коэффициентом парной корреляции более 0,85 в корреляционную модель предпочтительно не включать, как и такие, у которых связь с результативным параметром носит непрямолинейный или функциональный характер.

Отображение результатов

Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.

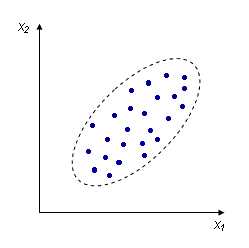
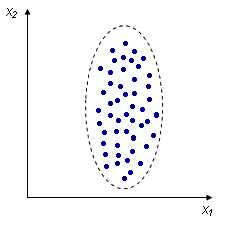
При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.

Трехмерное представление диаграммы разброса (рассеивания)

Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.

Также используется матрица диаграммы рассеивания, которая отображает все парные графики на одном рисунке в матричном формате. Для n переменных матрица содержит n строк и n столбцов. Диаграмма, расположенная на пересечении i-ой строки и j-ого столбца, представляет собой график переменных Xi по сравнению с Xj. Таким образом, каждая строка и столбец являются одним измерением, отдельная ячейка отображает диаграмму рассеивания двух измерений.

Оценка тесноты связи

Теснота корреляционной связи определяется по коэффициенту корреляции (r): сильная — r = ±0,7 до ±1, средняя — r = ±0,3 до ±0,699, слабая — r = 0 до ±0,299. Данная классификация не является строгой. На рисунке показана несколько иная схема.

Пример применения метода корреляционного анализа

В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.

Исходные данные для корреляционного анализа

Профессиональная группа	курение	смертность
Фермеры, лесники и рыбаки	77	84
Шахтеры и работники карьеров	137	116
Производители газа, кокса и химических веществ	117	123
Изготовители стекла и керамики	94	128
Работники печей, кузнечных, литейных и прокатных станов	116	155
Работники электротехники и электроники	102	101
Инженерные и смежные профессии	111	118
Деревообрабатывающие производства	93	113
Кожевенники	88	104
Текстильные рабочие	102	88
Изготовители рабочей одежды	91	104
Работники пищевой, питьевой и табачной промышленности	104	129
Производители бумаги и печати	107	86
Производители других продуктов	112	96
Строители	113	144
Художники и декораторы	110	139
Водители стационарных двигателей, кранов и т. д.	125	113
Рабочие, не включенные в другие места	133	146
Работники транспорта и связи	115	128
Складские рабочие, кладовщики, упаковщики и работники разливочных машин	105	115
Канцелярские работники	87	79
Продавцы	91	85
Работники службы спорта и отдыха	100	120
Администраторы и менеджеры	76	60
Профессионалы, технические работники и художники	66	51

Начинаем корреляционный анализ. Решение лучше начинать для наглядности с графического метода, для чего построим диаграмму рассеивания (разброса).

Она демонстрирует прямую связь. Однако на основании только графического метода сделать однозначный вывод сложно. Поэтому продолжим выполнять корреляционный анализ. Пример расчета коэффициента корреляции представлен ниже.

С помощью программных средств (на примере MS Excel будет описано далее) определяем коэффициент корреляции, который составляет 0,716, что означает сильную связь между исследуемыми параметрами. Определим статистическую достоверность полученного значения по соответствующей таблице, для чего нам нужно вычесть из 25 пар значений 2, в результате чего получим 23 и по этой строке в таблице найдем r критическое для p=0,01 (поскольку это медицинские данные, здесь используется более строгая зависимость, в остальных случаях достаточно p=0,05), которое составляет 0,51 для данного корреляционного анализа. Пример продемонстрировал, что r расчетное больше r критического, значение коэффициента корреляции считается статистически достоверным.

Использование ПО при проведении корреляционного анализа

Описываемый вид статистической обработки данных может осуществляться с помощью программного обеспечения, в частности, MS Excel. Корреляционный анализ в Excel предполагает вычисление следующих парамет­ров с использованием функций:

1. Коэффициент корреляции определяется с помощью функции КОРРЕЛ [CORREL](массив1; массив2). Массив1,2 — ячейка интервала значений результативных и факторных переменных.

Линейный коэффициент корреляции также называется коэффициентом корреляции Пирсона, в связи с чем, начиная с Excel 2007, можно использовать функцию ПИРСОН (PEARSON) с теми же массивами.

Графическое отображение корреляционного анализа в Excel производится с помощью панели «Диаграммы» с выбором «Точечная диаграмма».

После указания исходных данных получаем график.

2. Оценка значимости коэффициента парной корреляции с использованием t-критерия Стьюдента. Рассчитанное значение t-критерия _{сравнивается с табличной (критической) величиной данного показателя из соответствующей таблицы значений рассматриваемого параметра с учетом заданного уровня значимости и числа степеней свободы. Эта оценка осуществляется с использованием функции СТЬЮДРАСПОБР (вероятность; степени_свободы).}

3. Матрица коэффициентов парной корреляции. Анализ осуществляется с помощью средства «Анализ данных», в котором выбирается «Корреляция». Статистическую оценку коэффициентов парной корреляции осуществляют при сравнении его абсолютной величины с табличным (критическим) значением. При превышении расчетного коэффициента парной корреляции над таковым критическим можно говорить, с учетом заданной степени вероятности, что нулевая гипотеза о значимости линейной связи не отвергается.

В заключение

Использование в научных исследованиях метода корреляционного анализа позволяет определить связь между различными факторами и результативными показателями. При этом необходимо учитывать, что высокий коэффициент корреляции можно получить и из абсурдной пары или множества данных, в связи с чем данный вид анализа нужно осуществлять на достаточно большом массиве данных.

После получения расчетного значения r его желательно сравнить с r критическим для подтверждения статистической достоверности определенной величины. Корреляционный анализ может осуществляться вручную с использованием формул, либо с помощью программных средств, в частности MS Excel. Здесь же можно построить диаграмму разброса (рассеивания) с целью наглядного представления о связи между изучаемыми факторами корреляционного анализа и результативным признаком.

fb.ru

Корреляция — Википедия

Материал из Википедии — свободной энциклопедии

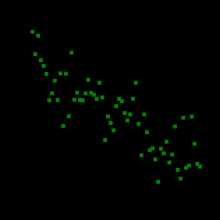Для графического представления корреляционной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определённого символа. Такой график называется диаграммой рассеяния.

Корреля́ция (от лат. correlatio «соотношение, взаимосвязь») или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.^[1]

Математической мерой корреляции двух случайных величин служит корреляционное отношение η{\displaystyle \mathbf {\eta } }^[2] либо коэффициент корреляции R{\displaystyle \mathbf {R} } (или r{\displaystyle \mathbf {r} })

[1]. В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической^[3].

Впервые в научный оборот термин корреляция ввёл французский палеонтолог

ru.wikipedia.org

Корреляционный анализ

1) корреляционный анализ как средство получения информации;

2) особенности процедур определения коэффициентов линейной и ранговой корреляции.

Корреляционный анализ(от лат. «соотношение», «связь») применяется для проверки гипотезы о статистической зависимости значений двух или нескольких переменных в том случае, если исследователь может их регистрировать (измерять), но не контролировать (изменять).

Когда повышение уровня одной переменной сопровождается повышением уровня другой, то речь идет о положительнойкорреляции. Если же рост одной переменной происходит при снижении уровня другой, то говорят об

отрицательнойкорреляции. При отсутствии связи переменных мы имеем дело снулевойкорреляцией.

При этом переменными могут быть данные тестирований, наблюдений, экспериментов, социально-демографические характеристики, физиологические параметры, особенности поведения и т. д. К примеру, использование метода позволяет нам дать количественно выраженную оценку взаимосвязи таких признаков, как: успешность обучения в вузе и степень профессиональных достижений по его окончании, уровень притязаний и стресс, количество детей в семье и качества их интеллекта, черты личности и профессиональная ориентация, продолжительность одиночества и динамика самооценки, тревожность и внутригрупповой статус, социальная адаптированность и агрессивность при конфликте…

В качестве вспомогательных средств, процедуры корреляции незаменимы при конструировании тестов (для определения валидности и надежности измерения), а также как пилотажные действия по проверке пригодности экспериментальных гипотез (факт отсутствия корреляции позволяет отвергнуть предположение о причинно-следственной связи переменных).

Усиление интереса в психологической науке к потенциалу корреляционного анализа обусловлено целым рядом причин. Во-первых, становится допустимым изучение широкого круга переменных, экспериментальная проверка которых затруднена или невозможна. Ведь по этическим соображениям, к примеру, нельзя провести экспериментальные исследования самоубийств, наркомании, деструктивных родительских воздействий, влияния авторитарных сект. Во-вторых, возможно получение за короткое время ценных обобщений данных о больших количествах исследуемых лиц. В-третьих, известно, что многие феномены изменяют свою специфику во время строгих лабораторных экспериментов. А корреляционный анализ предоставляет исследователю возможность оперировать информацией, полученной в условиях, максимально приближенных к реальным. В-четвертых, осуществление статистического изучения динамики той или иной зависимости нередко создает предпосылки к достоверному прогнозированию психологических процессов и явлений.

Однако следует иметь в виду, что применение корреляционного метода связано и с весьма существенными принципиальными ограничениями.

Так, известно, что переменные вполне могут коррелировать и при отсутствии причинно-следственной связи между собой.

Это иногда возможно в силу действия случайных причин, при неоднородности выборки, из-за неадекватности исследовательского инструментария поставленным задачам. Такая ложная корреляция способна стать, скажем, «доказательством» того, что женщины дисциплинированнее мужчин, подростки из неполных семей более склонны к правонарушениям, экстраверты агрессивнее интровертов и т. п. Действительно, стоит отобрать в одну группу мужчин, работающих в высшей школе, и женщин, предположим, из сферы обслуживания, да еще и протестировать тех и других на знание научной методологии, то мы получим выражение заметной зависимости качества информированности от пола. Можно ли доверять такой корреляции?

Еще чаще, пожалуй, в исследовательской практике встречаются случаи, когда обе переменные изменяются под влиянием некоей третьей или даже нескольких скрытых детерминант.

Если мы обозначим цифрами переменные, а стрелками — направления от причин к следствиям, то увидим целый ряд возможных вариантов:

1234

1234

1234

1234 и т. д.

Невнимание к воздействию реальных, но неучтенных исследователями факторов позволило представить обоснования того, что интеллект — сугубо наследуемое образование (психогенетический подход) или, напротив, что он обусловлен лишь влиянием социальных составляющих развития (социогенетический подход). В психологии, следует заметить, нераспространены феномены, имеющие однозначную первопричину.

Кроме того, факт наличия взаимосвязи переменных не дает возможности выявить по итогам корреляционного исследования причину и следствие даже в тех случаях, когда промежуточных переменных не существует.

Например, при изучении агрессивности детей было установлено, что склонные к жестокости дети чаще сверстников смотрят фильмы со сценами насилия. Означает ли это, что такие сцены развивают агрессивные реакции или, наоборот, подобные фильмы привлекают самых агрессивных детей? В рамках корреляционного исследования дать правомерный ответ на этот вопрос невозможно.

Необходимо запомнить: наличие корреляций не является показателем выраженности и направленности причинно-следственных отношений.

Другими словами, установив корреляцию переменных, мы можем судить не о детерминантах и производных, а лишь о том, насколько тесно взаимосвязаны изменения переменных и каким образом одна из них реагирует на динамику другой.

При использовании данного метода оперируют той или иной разновидностью коэффициента корреляции. Его числовое значение обычно изменяется от -1 (обратная зависимость переменных) до +1 (прямая зависимость). При этом нулевое значение коэффициента соответствует полному отсутствию взаимосвязи динамики переменных.

Например, коэффициент корреляции +0,80 отражает наличие более выраженной зависимости между переменными, чем коэффициент +0,25. Аналогично, зависимость между переменными, характеризуемая коэффициентом -0,95, гораздо теснее, чем та, где коэффициенты имеют значения +0,80 или + 0,25 («минус» указывает нам только на то, что рост одной переменной сопровождается уменьшением другой).

В практике психологических исследований показатели коэффициентов корреляции обычно не достигают +1 или -1. Речь может идти только о той или иной степени приближения к данному значению. Часто корреляция считается выраженной, если ее коэффициент выше 0,60. При этом недостаточной корреляцией, как правило, считаются показатели, располагающиеся в интервале от -0,30 до +0,30.

Однако, сразу следует оговорить, что интерпретация наличия корреляции всегда предполагает определение критических значений соответствующего коэффициента. Рассмотрим этот момент более подробно.

Вполне может получиться так, что коэффициент корреляции равный +0,50 в некоторых случаях не будет признан достоверным, а коэффициент, составляющий +0,30, окажется при определенных условиях характеристикой несомненной корреляции. Многое здесь зависит от протяженности рядов переменных (т. е. от количества сопоставляемых показателей), а также от заданной величины уровня значимости (или от принятой за приемлемую вероятность ошибки в расчетах).

Ведь, с одной стороны, чем больше выборка, тем количественно меньший коэффициент будет считаться достоверным свидетельством корреляционных отношений. А с другой стороны, если мы готовы смириться со значительной вероятностью ошибки, то можем посчитать за достаточную небольшую величину коэффициента корреляции.

Существуют стандартные таблицы с критическими значениями коэффициентов корреляции. Если полученный нами коэффициент окажется ниже, чем указанный в таблице для данной выборки при установленном уровне значимости, то он считается статистически недостоверным.

Работая с такой таблицей, следует знать, что пороговой величиной уровня значимости в психологических исследованиях обычно считается 0,05 (или пять процентов). Разумеется, риск ошибиться будет еще меньше, если эта вероятность составляет 1 на 100 или, еще лучше, 1 на 1000.

Итак, не сама по себе величина подсчитанного коэффициента корреляции служит основанием для оценки качества связи переменных, а статистическое решение о том, можно ли считать вычисленный показатель коэффициента достоверным.

Зная это, обратимся к изучению конкретных способов определения коэффициентов корреляции.

Значительный вклад в разработку статистического аппарата корреляционных исследований внес английский математик и биолог Карл Пирсон (1857-1936), занимавшийся в свое время проверкой эволюционной теории Ч. Дарвина.

Обозначение коэффициента корреляции Пирсона(r) происходит от понятия регрессии — операции по сведению множества частных зависимостей между отдельными значениями переменных к их непрерывной (линейной) усредненной зависимости.

Формула для расчета коэффициента Пирсона имеет такой вид:

,

где x, y— частные значения переменных,-(сигма) — обозначение суммы, а 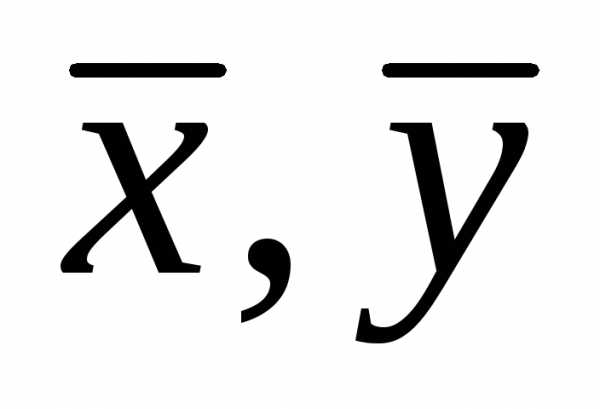— средние значения тех же самых переменных. Рассмотрим порядок использования таблицы критических значений коэффициентов Пирсона. Как мы видим, в левой ее графе указано число степеней свободы. Определяя нужную нам строчку, мы исходим из того, что искомая степень свободы равнаn-2, гдеn— количество данных в каждом из коррелируемых рядов. В графах же, расположенных с правой стороны, указаны конкретные значения модулей коэффициентов.

Число степеней «свободы» (n-2)	Уровни значимости
	0, 05	0, 02	0, 01	0,001
1	0,99692	0, 99951	0, 99988	0, 9999988
2	0,9500	0, 9800	0, 9900	0, 9990
3	0,878	0, 9343	0, 9587	0,9911
4	0,811	0, 882	0, 9172	0, 9741
5	0,754	0, 833	0, 875	0,9509
6	0,707	0, 789	0, 834	0, 9249
7	0,666	0, 750	0, 798	0, 898
8	0,632	0, 715	0, 765	0, 872
9	0,602	0, 685	0, 735	0,847
10	0,576	0, 658	0, 708	0, 823
11	0,553	0, 634	0, 684	0, 801
12	0,532	0, 612	0, 661	0, 780
13	0,514	0, 592	0, 641	0, 760
14	0,497	0, 574	0, 623	0, 742
15	0,482	0, 558	0, 606	0, 725
16	0,468	0, 543	0, 590	0, 708
17	0,456	0, 529	0, 575	0, 693
18	0,444	0, 5) 6	0, 561	0, 679
19	0,433	0, 503	0, 549	0, 665
20	0,423	0, 492	0, 537	0, 652
25	0,381	0, 445	0, 487	0, 597
30	0,349	0, 409	0, 449	0, 554
35	0,325	0, 381	0, 418	0,519
40	0,304	0, 358	0, 393	0, 490
45	0,288	0, 338	0, 372	0, 465
50	0,273	0, 322	0, 354	0, 443
60	0,250	0, 295	0, 325	0, 408
70	0,232	0, 274	0, 302	0, 380
80	0,217	0, 257	0, 283	0, 357
90	0,205	0, 242	0, 267	0, 338
100	0,195	0, 230	0, 254	0, 321

Причем, чем правее расположен столбик чисел, тем выше достоверность корреляции, увереннее статистическое решение о её значимости.

Если у нас, например, коррелируют два ряда цифр по 10 единиц в каждом из них и получен по формуле Пирсона коэффициент, равный +0,65, то он будет считаться значимым на уровне 0,05 (так как больше критического значения в 0,632 для вероятности 0,05 и меньше критического значения 0,715 для вероятности 0,02). Такой уровень значимости свидетельствует о существенной вероятности повторения данной корреляции в аналогичных исследованиях.

Теперь приведем пример вычисления коэффициента корреляции Пирсона. Пусть в нашем случае необходимо определить характер связи между выполнением одними и теми же лицами двух тестов. Данные по первому из них обозначены как x, а по второму — какy.

Для упрощения расчетов введены некоторые тождества. А именно:

При этом мы имеем следующие результаты испытуемых (в тестовых баллах):

Испытуемые	x	y	x2	y2	xy
Первый	1	2	1	4	2
Второй	2	4	4	16	8
Третий	3	5	9	25	15
Четвертый	3	3	9	9	9
Пятый	4	6	16	36	24
Шестой	4	6	16	36	24
Седьмой	5	8	25	64	40
Восьмой	6	9	36	81	54
Девятый	7	9	49	81	63
Десятый	9	10	81	100	90
Одиннадцатый	9	11	81	121	99
Двенадцатый	10	12	100	144	120
	63	85	427	717	548

;

;

Заметим, что число степеней свободы равно в нашем случае 10. Обратившись к таблице критических значений коэффициентов Пирсона, узнаем, что при данной степени свободы на уровне значимости 0,999 будет считаться достоверным любой показатель корреляции переменных выше, чем 0,823. Это дает нам право считать полученный коэффициент свидетельством несомненной корреляции рядов xиy.

Применение линейного коэффициента корреляции становится неправомерным в тех случаях, когда вычисления производятся в пределах не интервальной, а порядковой шкалы измерения. Тогда используют коэффициенты ранговой корреляции. Разумеется, результаты при этом получаются менее точными, так как сопоставлению подлежат не сами количественные характеристики, а лишь порядки их следования друг за другом.

Среди коэффициентов ранговой корреляции в практике психологических исследований довольно часто применяют тот, который предложен английским ученым Чарльзом Спирменом (1863-1945), известным разработчиком двухфакторной теории интеллекта.

Используя соответствующий пример, рассмотрим действия, необходимые для определения коэффициента ранговой корреляции Спирмена.

Формула его вычисления выглядит следующим образом:

;

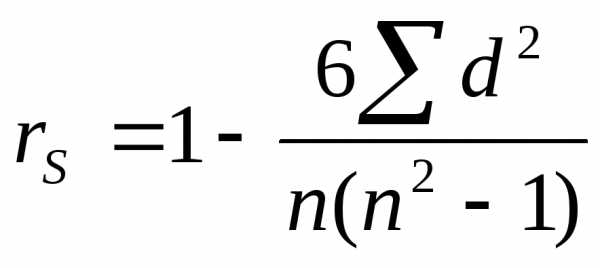где d -разности между рангами каждой переменной из рядовxиy,

n— число сопоставляемых пар.

Пусть xиy— показатели успешности выполнения испытуемыми некоторых видов деятельности(оценки индивидуальных достижений). При этом мы располагаем следующими данными:

Испытуемые	x	ранг x	y	ранг y	d	d2
Первый	10	1	25	5	4	16
Второй	11	2,5	25	5	2,5	6,25
Третий	11	2,5	25	5	2,5	6,25
Четвертый	12	4	24	3	1	1
Пятый	13	5	26	7,5	2,5	6,25
Шестой	15	6,5	26	7,5	1	1
Седьмой	15	6,5	27	9	2,5	6,25
Восьмой	18	8	28	10	2	4
Девятый	20	9	23	2	7	49
Десятый	21	10	22	1	9	81

Заметим, что вначале производится раздельное ранжирование показателей в рядах xиy. Если при этом встречается несколько равных переменных, то им присваивается одинаковый усредненный ранг.

Затем осуществляется попарное определение разности рангов. Знак разности несущественен, так как по формуле она возводится в квадрат.

В нашем примере сумма квадратов разностей рангов 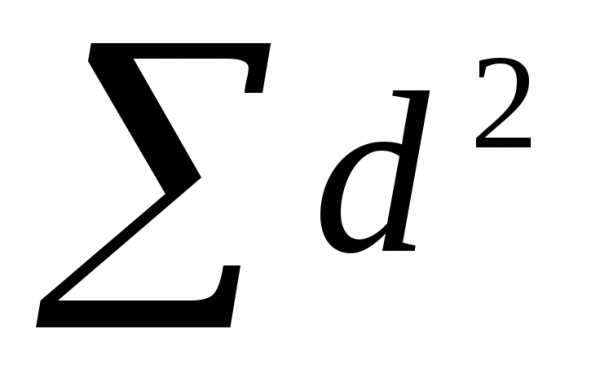равна 178. Подставим полученное число в формулу:

Как мы видим, показатель коэффициента корреляции в данном случае составляет ничтожно малую величину. Тем не менее, сопоставим его с критическими значениями коэффициента Спирмена из стандартной таблицы.

n-2	0.05	0.01	n-2	0.05	0.01	n-2	0.05	0.01
5	0,94		17	0,48	0,62	29	0,37	0,48
6	0,85		18	0,47	0,60	30	0,36	0,47
7	0,78	0,94	19	0,46	0,58	31	0,36	0,46
8	0,72	0,88	20	0,45	0,57	32	0,36	0,45
9	0,68	0,83	21	0,44	0,56	33	0,34	0,45
10	0,64	0,79	22	0,42	0,54	34	0,34	0,44
11	0,61	0,76	23	0,42	0,53	35	0,33	0,43
12	0,58	0,73	24	0,41	0,52	36	0,33	0,43
13	0,56	0,70	25	0,40	0,51	37	0,33	0,42
14	0,54	0,68	26	0,39	0,50	38	0,32	0,41
15	0,52	0,66	27	0,38	0,49	39	0,32	0,41
16	0,50	0,64	28	0,38	0,48	40	0,31	0,40

Вывод: между указанными рядами переменных xиyкорреляция отсутствует.

Надо заметить, что использование процедур ранговой корреляции предоставляет исследователю возможность определять соотношения не только количественных, но и качественных признаков, в том, разумеется, случае, если последние могут быть упорядочены по возрастанию выраженности(ранжированы).

Нами были рассмотрены наиболее распространенные, пожалуй, на практике способы определения коэффициентов корреляции. Иные, более сложные или реже применяемые разновидности данного метода при необходимости можно найти в материалах пособий, посвященных измерениям в научных исследованиях.

ОСНОВНЫЕ ПОНЯТИЯ:корреляция; корреляционный анализ; коэффициент линейной корреляции Пирсона; коэффициент ранговой корреляции Спирмена; критические значения коэффициентов корреляции.

Вопросы для обсуждения:

1. Каковы возможности корреляционного анализа в психологических исследованиях? Что можно и что нельзя выявить с помощью данного метода?

2. Какова последовательность действий при определении коэффициентов линейной корреляции Пирсона и ранговой корреляции Спирмена?

Упражнение 1:

Установите, являются ли статистически достоверными следующие показатели корреляции переменных:

а) коэффициент Пирсона +0,445 для данных двух тестирований в группе, состоящей из 20 испытуемых;

б) коэффициент Пирсона -0,810 при числе степеней свободы равном 4;

в) коэффициент Спирмена +0,415 для группы из 26 человек;

г) коэффициент Спирмена +0,318 при числе степеней свободы равном 38.

Упражнение 2:

Определите коэффициент линейной корреляции между двумя рядами показателей.

Ряд 1: 2, 4, 5, 5, 3, 6, 6, 7, 8, 9

Ряд 2: 2, 3, 3, 4, 5, 6, 3, 6, 7, 7

Упражнение 3:

Сделайте выводы о статистической достоверности и степени выраженности корреляционных отношений при числе степеней свободы равном 25, если известно, что составляет: а) 1200; б) 1555; в) 2300

Упражнение 4:

Выполните всю последовательность действий, необходимых для определения коэффициента ранговой корреляции между предельно обобщёнными показателями успеваемости школьников («отличник», «хорошист» и т.д.) и характеристиками выполнения ими теста умственного развития (ШТУР). Сделайте интерпретацию полученных показателей.

Упражнение 5:

С помощью коэффициента линейной корреляции рассчитайте показатели ретестовой надежности имеющегося в вашем распоряжении теста интеллекта. Выполните исследование в студенческой группе с интервалом времени между тестированиями в 7-10 дней. Сформулируйте выводы.

studfiles.net

Корреляции в дипломных работах по психологии

Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.

Материалы по корреляциям в сети слишком научны. Неспециалисту трудно разобраться в формулах. В то же время понимание смысла корреляций необходимо маркетологу, социологу, медику, психологу – всем, кто проводит исследования на людях.

В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.

 

Содержание

 

Что такое корреляция
Численное выражение корреляционной связи

Корреляционный анализ в психологии
Коэффициенты корреляции Пирсона и Спирмена
Как рассчитать коэффициент корреляции

Использование корреляционного анализа в дипломных работах по психологии 

Что такое корреляция

Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.

Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».

Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).

Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?

Правильно,  между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.

В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.

 

Численное выражение корреляционной зависимости

Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.

Например, изучается роль чтения в жизни людей. Исследователи взяли группу из 40 человек и измерили у каждого испытуемого два показателя: 1) сколько времени он читает в неделю; 2) в какой мере он считает себя благополучным (по шкале от 1 до 10). Ученые занесли эти данные в два столбика и с помощью статистической программы рассчитали корреляцию между чтением и благополучием. Предположим, они получили следующий результат -0,76. Но что значит это число? Как его проинтерпретировать? Давайте разбираться.

Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:

1. Знак «+» или «-»  отражает направление зависимости.
2. Величина коэффициента отражает силу зависимости.

 

Прямая и обратная

Знак плюс перед коэффициентом указывает на то, что связь между явлениями или показателями прямая. То есть, чем больше один показатель, тем больше и другой. Выше оклад — выше продажи. Такая корреляция называется прямой, или положительной.

Если коэффициент имеет знак минус, значит, корреляция обратная, или отрицательная. В этом случае чем выше один показатель, тем ниже другой. В примере с чтением и благополучием мы получили -0,76, и это значит, что, чем больше люди читают, тем ниже уровень их благополучия.

 

Сильная и слабая

Корреляционная связь в численном выражении – это число в диапазоне от -1 до +1. Обозначается буквой «r». Чем выше число (без учета знака), тем корреляционная связь сильнее.

Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.

Максимально возможная сила зависимости  – это 1 или -1. Как это понять и представить?

Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.

Испытуемый	IQ	Успеваемость (баллы)
1	90	4,0
2	91	4,1
3	92	4,2
4	93	4,3
5	94	4,4
6	95	4,5
7	96	4,6
8	97	4,7
9	98	4,8
10	99	4,9

 

Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.

Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость  между интеллектом и успеваемостью равна 1.

Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).

Испытуемый	IQ	Успех в общении с противоположным полом (баллы)
1	90	10
2	91	9
3	92	8
4	93	7
5	94	6
6	95	5
7	96	4
8	97	3
9	98	2
10	99	1

 

Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.

Это пример полной согласованности изменения двух показателей в группе — максимально возможная отрицательная взаимосвязь. Корреляционная связь между IQ и успешностью общения с противоположным полом равна -1.

А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.

Испытуемый	IQ	Длина прыжка с места (м)
1	90	2,5
2	91	1,2
3	92	2,0
4	93	1,7
5	94	1,9
6	95	1,3
7	96	1,7
8	97	2,3
9	98	1,1
10	99	2,6

 

Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.

Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:

• если коэффициент больше 0,70 – связь между показателями сильная;
• от 0,30 до 0,70 – связь умеренная,
• меньше 0,30 – связь слабая.

Если оценить по этой шкале полученную нами выше корреляцию между чтением и благополучием, то окажется, что эта зависимость  сильная и отрицательная -0,76. То есть, наблюдается сильная отрицательная связь между начитанностью и благополучием. Что еще раз подтверждает библейскую мудрость о соотношении  мудрости и печали.

Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.

Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).

 

Корреляционный анализ в психологии

Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?

В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.

В психологии иная ситуация. Например, психологи публикуют данные о связи теплых отношений в детстве с родителями и уровня креативности во взрослом возрасте. Означает ли это, что любой из испытуемых с очень теплыми отношениями с родителями в детстве будет иметь очень высокие творческие способности? Ответ однозначный – нет. Здесь нет закона, подобного физическому. Нет механизма влияния детского опыта на креативность взрослых. Это наши фантазии! Есть согласованность данных (отношения – креативность), но за ними нет закона. А есть лишь корреляционная связь. Психологи часто называют выявляемые взаимосвязи психологическими закономерностями, подчеркивая их вероятностный характер — не жесткость.

Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:

1. Анализ взаимосвязи между психологическими показателями. В нашем примере IQ и успешность общения с противоположным полом – это психологические параметры. Выявление корреляции между ними расширяет представления о психической организации человека, о взаимосвязях между различными сторонами его личности – в данном случае между интеллектом и сферой общения.
2. Анализ взаимосвязей IQ с успеваемостью и прыжками – пример связи психологического параметра с непсихологическими. Полученные результаты раскрывают особенности влияния интеллекта на учебную и спортивную деятельность.

Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:

1. Выявлена значимая положительная зависимость интеллекта студентов и их успеваемости.
2. Существует отрицательная значимая взаимосвязь IQ с успешностью общения с противоположным полом.
3. Не выявлено связи IQ студентов с умением прыгать с места.

Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.

Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.

Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.

 

Коэффициенты Пирсона и Спирмена

Рассмотрим два метода расчета.

Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:

1. Берутся значения двух параметров в группе испытуемых (например, агрессии и перфекционизма).
2. Находятся средние значения каждого параметра в группе.
3. Находятся разности параметров каждого испытуемого и среднего значения.
4. Эти разности подставляются в специальную форму для расчета коэффициента Пирсона.

Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:

1. Берутся значения двух индикаторов в группе испытуемых.
2. Находятся ранги каждого фактора в группе, то есть место в списке по возрастанию.
3. Находятся разности рангов, возводятся в квадрат и суммируются.
4. Далее разности рангов подставляются в специальную форму для вычисления коэффициента Спирмена.

В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.

В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.

Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.

 

Как рассчитать коэффициент корреляции

Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.

Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.

 

Расчет с помощью электронных таблиц Microsoft Excel

Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.

Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».

Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.

 

Далее нажимаем галочку (то есть, рассчитать) и получаем значение , в нашем случае 0,038. Как видим, коэффициент не равен нулю, хотя и очень близок к нему.

В таблицах Excel реализована формула расчета только коэффициента Пирсона.

 

Расчет с помощью программы STATISTICA

Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.

 

Как видно, расчет  дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.

 

Использование корреляционного анализа в дипломных работах по психологии (пример)

Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах).

Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:

• «Взаимосвязь субъективного ощущения одиночества и самоактуализации у женщин зрелого возраста»;
• «Особенности влияния жизнестойкости менеджеров на успешность их взаимодействия с клиентами в конфликтных ситуациях»;
• «Личностные факторы стрессоустойчивости сотрудников МЧС».

Таким образом, слова «взаимосвязь», «влияние» и «факторы» — верные признаки того, что методом анализа данных в эмпирическом исследовании должен быть корреляционный анализ.

Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков».

1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом:

• каждая строка содержит данные на одного испытуемого;
• каждый столбец содержит показатели по одной шкале для всех испытуемых.

№ испытуемого	Личностная тревожность	Агрессивность
1	12	24
2	14	25
3	11	13
4	17	19
5	21	29
6	26	29
7	13	16
8	16	20
8	13	24
9	18	21
10	23	31

2. Необходимо решить, какой из двух типов коэффициентов — Пирсона или Спирмена — будет использоваться. Напоминаем, что Пирсон дает более точный результат, но он чувствителен к выбросам в данных Коэффициенты  Спирмена могут использоваться с любыми данными (кроме номинативной шкалы), поэтому именно они чаще всего используют в дипломах по психологии.

3. Заносим таблицу сырых данных в статистическую программу.

 

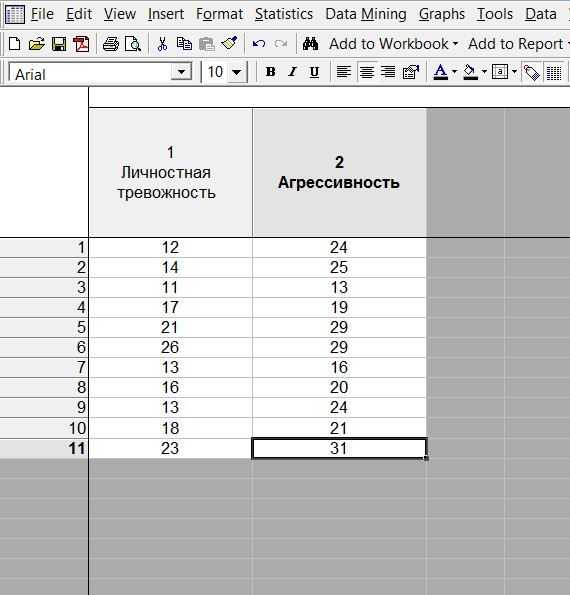
4. Рассчитываем значение.

5. На следующем этапе важно определить, значима ли взаимосвязь. Статистическая программа подсветила результаты красным, что означает, что корреляция статистически значимы при уровне значимости 0,05 (указано выше).

Однако полезно знать, как определить значимость вручную. Для этого понадобится таблица критических значений Спирмена.

Таблица критических значений коэффициентов Спирмена

	Уровень статистической значимости
Число испытуемых	р=0,05	р=0,01	р=0,001
5	0,88	0,96	0,99
6	0,81	0,92	0,97
7	0,75	0,88	0,95
8	0,71	0,83	0,93
9	0,67	0,8	0,9
10	0,63	0,77	0,87
11	0,6	0,74	0,85
12	0,58	0,71	0,82
13	0,55	0,68	0,8
14	0,53	0,66	0,78
15	0,51	0,64	0,76

Нас интересует уровень значимости 0,05 и объем нашей выборки 10 человек. На пересечении этих данных находим значение критического Спирмена: Rкр=0,63.

Правило такое: если полученное эмпирическое значение Спирмена больше либо равно критическому, то он статистически значим. В нашем случае: Rэмп (0,66) > Rкр (0,63), следовательно, взаимосвязь между агрессивностью и тревожностью в группе подростков статистически значима.

5. В текст дипломной нужно вставлять данные в таблице формата word, а не таблицу из статистической программы. Под таблицей описываем полученный результат и интерпретируем его.

Таблица 1

Коэффициенты Спирмена агрессивности и тревожности в группе подростков

	Агрессивность
Личностная тревожность	0,665*

* — статистически достоверна (р≤0,05)

Анализ данных, приведенных в таблице 1, показывает, что существует статистически значимая положительная связьмежду агрессивностью и тревожностью подростков. Это означает, что чем выше личностная тревожность подростков, тем выше уровень их агрессивности. Такой результат дает основание предположить, что агрессия для подростков выступает одним из способов купирования тревожности. Испытывая неуверенность в себе, тревогу в связи с угрозами самооценке, особенно чувствительной в подростковом возрасте, подросток часто использует агрессивное поведение, таким непродуктивным способом снижая тревогу.

6. Можно ли при интерпретации связей говорить о влиянии? Можно ли сказать, что тревожность влияет на агрессивность? Строго говоря, нет. Выше мы показали, что корреляционная связь между явлениями носит вероятностный характер и отражает лишь согласованность изменений признаков в группе. При этом мы не можем сказать, что эта согласованность вызвана тем, что одно из явлений является причиной другого, влияет на него. То есть, наличие корреляции между психологическими параметрами не дает оснований говорить о существовании между ними причинно-следственной связи. Однако практика показывает, что термин «влияние» часто используется при анализе результатов корреляционного анализа.

© СтудентуПсихологу.рф

xn--c1abdmpkibfqehdkeh3a.xn--p1ai

Корреляции для начинающих / Хабрахабр

Апдейт для тех, кто сочтет статью полезной и занесет в избранное. Есть приличный шанс, что пост уйдет в минуса, и я буду вынужден унести его в черновики. Сохраняйте копию!

Краткий и несложный материал для неспециалистов, рассказывающий в наглядной форме о различных методах поиска регрессионных зависимостей. Это все и близко не академично, зато надеюсь что понятно. Прокатит как мини-методичка по обработке данных для студентов естественнонаучных специальностей, которые математику знают плохо, впрочем как и автор. Расчеты в Матлабе, подготовка данных в Экселе — так уж повелось в нашей местности

Введение

Зачем это вообще надо? В науке и около нее очень часто возникает задача предсказания какого-то неизвестного параметра объекта исходя из известных параметров этого объекта (предикторов) и большого набора похожих объектов, так называемой учебной выборки. Пример. Вот мы выбираем на базаре яблоко. Его можно описать такими предикторами: красность, вес, количество червяков. Но как потребителей нас интересует вкус, измеренный в попугаях по пятибалльной шкале. Из жизненного опыта нам известно, что вкус с приличной точностью равен 5*красность+2*вес-7*количество червяков. Вот про поиск такого рода зависимостей мы и побеседуем. Чтобы обучение пошло легче, попробуем предсказать вес девушки исходя из ее 90/60/90 и роста.

Исходные данные

В качестве объекта исследования возьму данные о параметрах фигуры девушек месяца Плейбоя. Источник — www.wired.com/special_multimedia/2009/st_infoporn_1702, слегка облагородил и перевел из дюймов в сантиметры. Вспоминается анекдот про то, что 34 дюйма — это как два семнадцатидюймовых монитора. Также отделил записи с неполной информацией. При работе с реальными объектами их можно использовать, но сейчас они нам только мешают. Зато их можно использовать для проверки адекватности полученных результатов. Все данные у нас непрерывные, то есть грубо говоря типа float. Они приведены к целым числам только чтобы не загромождать экран. Есть способы работы и с дискретными данными — в нашем примере это например может быть цвет кожи или национальность, которые принимают одно из фиксированного набора значений. Это больше имеет отношение к методам классификации и принятия решений, что тянет еще на один мануал. Data.xls В файле два листа. На первом собственно данные, на втором — отсеянные неполные данные и набор для проверки нашей модели.

Обозначения

W — вес реальный
W_p — вес, предсказанный нашей моделью
S — бюст
T — талия
B — бедра
L — рост
E — ошибка модели

Как оценить качество модели?

Задача нашего упражнения — получить некую модель, которая описывает какой-либо объект. Способ получения и принцип работы конкретной модели нас пока не волнует. Это просто функция f(S, T, B, L), которая выдает вес девушки. Как понять, какая функция хорошая и качественная, а какая не очень? Для этого используется так называемая fitness function. Самая классическая и часто используемая — это сумма квадратов разницы предсказанного и реального значения. В нашем случае это будет сумма (W_p — W)^2 для всех точек. Собственно, отсюда и пошло название «метод наименьших квадратов». Критерий не лучший и не единственный, но вполне приемлемый как метод по умолчанию. Его особенность в том, что он чувствителен по отношению к выбросам и тем самым, считает такие модели менее качественными. Есть еще всякие методы наименьших модулей итд, но сейчас нам это пока не надо.

Простая линейная регрессия

Самый простой случай. У нас одна переменная-предиктор и одна зависимая переменная. В нашем случае это может быть например рост и вес. Нам надо построить уравнение W_p = a*L+b, т.е. найти коэффициенты a и b. Если мы проведем этот расчет для каждого образца, то W_p будет максимально совпадать с W для того же образца. То есть у нас для каждой девушки будет такое уравнение:
W_p_i = a*L_i+b
E_i = (W_p-W)^2

Общая ошибка в таком случае составит sum(E_i). В результате, для оптимальных значений a и b sum(E_i) будет минимальным. Как же найти уравнение?

Матлаб

Для упрощения очень рекомендую поставить плагин для Excel под названием Exlink. Он в папке matlab/toolbox/exlink. Очень облегчает пересылку данных между программами. После установки плагина появляется еще одно меню с очевидным названием, и автоматически запускается Матлаб. Переброс информации из Экселя в Матлаб запускается командой «Send data to MATLAB», обратно, соответственно, — «Get data from MATLAB». Пересылаем в Матлаб числа из столбца L и отдельно из W, без заголовков. Переменные назовем так же. Функция расчета линейной регрессии — polyfit(x,y,1). Единица показывает степень аппроксимационного полинома. У нас он линейный, поэтому единица. Получаем наконец-то коэффициенты регрессии: regr=polyfit(L,W,1). a мы можем получить как regr(1), b — как regr(2). То есть мы можем получить наши значения W_p: W_p=L*repr(1)+repr(2). Вернем их назад в Эксель.

Графичек

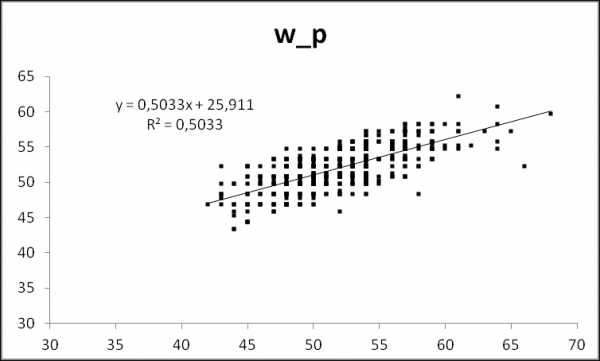
Мда, негусто. Это график W_p(W). Формула на графике показывает связь W_p и W. В идеале там будет W_p = W*1 + 0. Вылезла дискретизация исходных данных — облако точек клетчатое. Коэффициент корреляции ни в дугу — данные слабо коррелированы между собой, т.е. наша модель плохо описывает связь веса и роста. По графику это видно как точки, расположенные в форме слабо вытянутого вдоль прямой облака. Хорошая модель даст облако растянутое в узкую полосу, еще более плохая — просто хаотичный набор точек или круглое облако. Модель необходимо дополнить. Про коэффициент корреляции стоит рассказать отдельно, потому что его часто используют абсолютно неправильно.

Расчет в матричном виде

Можно и без всяких полифитов справиться с построением регрессии, если слегка дополнить столбец с величинами роста еще одним столбцом, заполненным единицами: L(:,2)=1. Двойка показывает номер столбца, в который пишутся единицы. Тогда коэффициенты регрессии можно будет найти по такой формуле: repr=inv(L'*L)*L'*W. И обратно, найти W_p: W_p=L*repr. Когда осознаешь магию матриц, пользоваться функциями становится неприкольно. Единичный столбец нужен для расчета свободного члена регрессии, то есть просто слагаемого без умножения на параметр. Если его не добавлять, то в регрессии будет всего один член: W_p=a*L. Достаточно очевидно, что она будет хуже по качеству, чем регрессия с двумя слагаемыми. В целом, избавляться от свободного члена надо только в том случае, если он точно не нужен. По умолчанию он все-таки присутствует.

Мультилинейная регрессия

В русскоязычной литературе прошлых лет упоминается как ММНК — метод множественных наименьших квадратов. Это расширение метода наименьших квадратов для нескольких предикторов. То есть у нас в дело идет не только рост, но и все остальные, так сказать, горизонтальные размеры. Подготовка данных точно такая же: обе матрицы в матлаб, добавление столбца единиц, расчет по той же самой формуле. Для любителей функций есть b = regress(y,X). Эта функция также требует добавления столбца единиц. Повторяем расчет по формуле из раздела про матрицы, пересылаем в Эксель, смотрим.

Попытка номер два

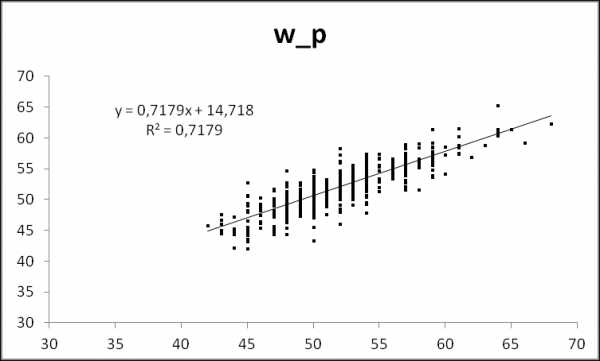
А так получше, но все равно не очень. Как видим, клетчатость осталась только по горизонтали. Никуда не денешься, исходные веса были целыми числами в фунтах. То есть после конверсии в килограммы они ложатся на сетку с шагом около 0.5. Итого финальный вид нашей модели:

W_p = 0.2271*S + 0.1851*T + 0.3125*B + 0.3949*L — 72.9132

Объемы в сантиметрах, вес в кг. Поскольку у нас все величины кроме роста в одних единицах измерения и примерно одного порядка по величине (кроме талии), то мы можем оценить их вклады в общий вес. Рассуждения примерно в таком духе: коэффициент при талии самый маленький, равно как и сами величины в сантиметрах. Значит, вклад этого параметра в вес минимален. У бюста и особенно у бедер он больше, т.е. сантиметр на талии дает меньшую прибавку к массе, чем на груди. А больше всего на вес влияет объем задницы. Впрочем, это знает любой интересующийся вопросом мужчина. То есть как минимум, наша модель реальной жизни не противоречит.

Валидация модели

Название громкое, но попробуем получить хотя бы ориентировочные веса тех девушек, для которых есть полный набор размеров, но нет веса. Их 7: с мая по июнь 1956 года, июль 1957, март 1987, август 1988. Находим предсказанные по модели веса: W_p=X*repr

Что ж, по крайней мере в текстовом виде выглядит правдоподобно. А насколько это соответствует реальности — решать вам

Применимость

Если вкратце — полученная модель годится для объектов, подобных нашему набору данных. То есть по полученным корреляциям не стоит считать параметры фигур женщин с весом 80+, возрастом, сильно отличающимся от среднего по больнице итд. В реальных применениях можно считать, что модель пригодна, если параметры изучаемого объекта не слишком отличаются от средних значений этих же параметров для исходного набора данных. Могут возникнуть (и возникнут) проблемы, если у нас предикторы сильно коррелированы между собой. То есть, например это рост и длина ног. Тогда коэффициенты для соответствующих величин в уравнении регрессии будут определены с малой точностью. В таком случае надо выбросить один из параметров, или воспользоваться методом главных компонент для снижения количества предикторов. Если у нас малая выборка и/или много предикторов, то мы рискуем попасть в переопределенность модели. То есть если мы возьмем 604 параметра для нашей выборки (а в таблице всего 604 девушки), то сможем аналитически получить уравнение с 604+1 слагаемым, которое абсолютно точно опишет то, что мы в него забросили. Но предсказательная сила у него будет весьма невелика. Наконец, далеко не все объекты можно описать мультилинейной зависимостью. Бывают и логарифмические, и степенные, и всякие сложные. Их поиск — это уже совсем другой вопрос.

Планы на будущее

Если хорошо пойдет, то постараюсь в том же стиле изложить метод главных компонент для снижения размерности данных, регрессию на главные компоненты, метод PLS, начала кластерного анализа и методов классификации объектов. Если хабрапублика не очень хорошо примет, то буду стараться учесть замечания. Если вообще никак — то забью на просвещение ширнармасс вообще, мне и своих студентов хватит. До новых встреч!

habr.com

Виды корреляции

Виды корреляционной связи между измеренными переменными могут быть различны: так корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна, если с увеличением или уменьшением одной переменной, вторая переменная также растёт, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами (полиномиальная, гиперболическая).

Если повышение уровня одной переменной сопровождается повышением уровня другой, то речь идет о положительной корреляции. Чем выше личностная тревожность, тем больше риск заболеть язвой желудка. Возрастание громкости звука сопровождается ощущением повышения его тона.

Если рост уровня одной переменной сопровождается снижением уровня другой, то мы имеем дело с отрицательной корреляцией. По данным Зайонца, число детей в семье отрицательно коррелирует с уровнем их интеллекта. Чем боязливей особь, тем меньше у нее шансов занять доминирующее положение в группе. Нулевой называется корреляция при отсутствии связи переменных.

Отрицательная и положительная корреляция

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция—корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным;положительная корреляцияв таких условиях —корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным. В практической деятельности, когда число коррелируемых пар признаков Х и Y невелико, то при оценке зависимости между показателями используется следующую градацию: 1) высокая степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,7 до 0,99; 2) средняя степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,5 до 0,69; 3) слабая степень взаимосвязи – значения коэффициента корреляции находится от 0,2 до 0,49.

3. Самостоятельное вычисление корреляции

Интересно было посмотреть, зависит ли каким-либо образом количество медалистов от заработной платы преподавателей школ в субъектах РФ. Чтобы это посмотреть, нужно самостоятельно вычислить корреляции. Процесс вычисления можно упростить, воспользовавшись Microsoft Excel: достаточно лишь ввести численные данные различных стран по уровню доходов и уровню рождаемости за какой-либо период и воспользоваться специальной функцией.

Опишем процесс подсчета корреляции. Для начала соберем численные данные интересующих нас показателей и сгруппируем их в таблицу, состоящую из двух столбцов. Первый из них содержит данные о средней заработной плате преподавателей, а второй — об количественном соотношении числа медалистов к числу всех выпускников. Каждая строка таблицы будет соответствовать определенному субъекту РФ. В конце столбцов в пустой ячейке впишем «=КОРРЕЛ». Затем выделим данные в одном столбце, поставим знак “;” и выделим второй столбец. Полученная цифра соответствует искомому значению корреляции.

studfiles.net

Пример корреляционного анализа

Поиск Лекций Корреляционный анализ   Корреляция – связь между двумя или несколькими исследуемыми событиями, явлениями или величинами. Так, в химической технологии достаточно продуктивно используется корреляционный анализ для установления влияния состава исходного сырья, руд, потоков на технологические и технико-экономические показатели производства (степень превращения в продукт, степень извлечения ценных компонентов из руд, качество продукта, себестоимость получения продукта и т.п.). Он позволяет также выявить влияние условий работы оборудования, технологических коллективов и факторов, изменяющихся случайным образом (содержание примесей, колебания расходов потоков, переходные режимы работы оборудования, аварийные остановки и т.п.) на основные показатели, что необходимо для оптимизации режимов производства. Корреляционный анализ используется, когда отсутствуют теоретические зависимости, когда связь между явлениями только предполагается и носит вероятностный характер. Методами корреляционного анализа исследуют наличие случайных связей между независимыми переменными, сам факт существования или статистическую гипотезу о наличии или отсутствии связи. Результат корреляционного анализа также носит вероятностный характер, так как заключение о наличии или отсутствии связи принимается с некоторой наперед заданной доверительной вероятностью. Корреляционный анализ заключается в определении и анализе коэффициентов корреляции, путем сравнения найденных коэффициентов корреляции с критическими значениями, указывающими на существование значимой корреляционной связи. Качественную оценку между двумя исследуемыми величинами Х1 и Х2 можно представить графически (рис.5.3). При наличии строго определенной (детерминированной) линейной связи между величинами Х1 и Х2 график зависимости Х2=f(X1) выглядит в виде прямой линии, на которой каждому значению Х1 соответствуют величины Х2, отсутствует случайное рассеяние точек. Такой график описывается уравнением: Х2=а+вХ1 (1) где а — свободный коэффициент; в — тангенс угла наклона прямой линии Х2 к оси Х1. При наличии вероятностной линейной зависимости Х2 от Х1, носящей случайный характер, график изображается в виде совокупности точек, лежащих вблизи прямой линии (рис.5.4-5.5). Величина отклонения экспериментальных точек от прямой линии указывает на величину корреляции между величинами Х1 и Х2. Чем сильнее корреляционная связь между Х1 и Х2, тем меньше отклонения точек от прямой линии. При отсутствии корреляционной связи между Х1 и Х2 точки на графике можно представить в виде области, имеющей форму круга (рис.5.6). В этом случае между точками можно провести бесчисленное количество прямых линий.             Рис.5.3. Детерминированная линейная связь между Х1 и Х2   Рис.5.4. Положительная связь Х1 с Х2 Рис.5.5. Отрицательная связь Х1 с Х2 Рис.5.6. Отсутствие связи между случайными величинами Х1 и Х2   Количественной оценкой корреляционной связи между величинами Х и У является коэффициент корреляции rxy. Он измеряет силу линейной связи между Y и X и может принимать значения от -1 до 1. При положительной величине коэффициента корреляции (положительная корреляционная связь) росту величины Х соответствует возрастание величины У. При отрицательной величине коэффициента корреляции (отрицательная корреляционная связь) росту величины Х соответствует уменьшение величины У. Если величины X и Y независимы, то коэффициент корреляции rxy=0. Коэффициент корреляции rxyвычисляют по величине ковариации: rxy= cov (X,Y)/SxSy (2)   где cov (X,Y)= å(Хi-X)(Yi-Y)/(n-1) — ковариация; Sx— среднее квадратическое отклонение величин Х; Sy— среднее квадратическое отклонение величин У. Коэффициент корреляции является случайной величиной, поскольку вычисляется из случайных величин. Две случайные величины X и Y являются коррелированными, если их коэффициент корреляции отличен от нуля. Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайно, то отсюда еще нельзя заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля. Возникает необходимость проверить гипотезу о значимости (существенности) выборочного коэффициента корреляции (или о равенстве нулю коэффициента корреляции генеральной совокупности). Если гипотеза о равенстве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции значим, а величины X и Y коррелированны; если гипотеза принята, то выборочный коэффициент корреляции незначим, а величины X и Y некоррелированы. Для того чтобы при заданном уровне значимости проверить гипотезу о равенстве нулю генерального коэффициента корреляции нормально распределенной случайной величины необходимо вычислить наблюдаемое значение критерия tнабл:   (3)   где rxy — значение коэффициента корреляции, вычисленное по формуле (2). По таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы f=n-2 найти критическую точку tкр(;f) для двусторонней критической области. Затем производится сравнение абсолютной величины |tнабл| и tкр. Если |tнабл|<tкр –коэффициент корреляции незначим, а если |tнабл|>tкр — выборочный коэффициент корреляции значимо отличается от нуля и случайные величины коррелированны. Значимость коэффициента корреляции также можно определить /21/ по формуле: (4) Вычисленную величину ξ сравнивают с табличным значением коэффициента Стьюдента t(Р=0.95;f= )=1.96. Если тестовая статистика ξ больше табличного значения коэффициента Стьюдента t, то коэффициент корреляции значимо отличается от нуля. Значимость отличия между двумя коэффициентами корреляции определяют по тестовой статистике /21/: (5) Вычисленную величину ξ сравнивают с табличным значением коэффициента Стьюдента t(Р=0.95;f= )=1.96. Если статистика ξ больше табличного значения коэффициента Стьюдента t, то коэффициенты корреляции значимо отличается. Пример корреляционного анализа При получении 98%-го хлорида калия, важно знать между какими компонентами существует корреляционная связь, с какими примесями в сильвинитовой руде ассоциируется бромид-ион. В связи с этим проводят корреляционный анализ и выявляют корреляционные связи содержания компонентов в составе сильвинитовой руды. Состав сильвинитовой руды Березниковского калийного рудоуправления №1 приведен в табл.5.9. Таблица 5.9 Состав компонентов сильвинитовой руды ствола №3, БКРУ-1 (данные за 2006 г.)   № Месяц н.о. KCl NaCl MgCl2 CaSO4 Br— январь 1,9 27,6 0,17 2,1 0,062   1,7 27,3 68,5 0,18 2,11 0,062   27,2 68,3 0,23 2,20 0,064 февраль 1,8 67,8 0,14 1,94 0,064   1,8 27,7 68,1 0,15 1,99 0,065   1,5 26,2 69,9 0,13 1,98 0,062 март 1,7 27,5 68,7 0,16 1,83 0,066   1,7 68,8 0,15 2,07 0,061   1,8 27,7 68,3 0,09 1,96 0,063 апрель 1,6 27,9 68,3 0,12 1,78 0,064   1,4 68,7 0,11 1,78 0,067   1,7 67,9 0,11 1,96 0,064 май 1,5 27,5 68,7 0,23 1,89 0,065   1,9 27,3 68,2 0,18 1,95 0,061   1,7 27,3 68,8 0,15 1,83 0,063 июнь 1,9 28,3 67,5 0,14 1,96 0,063   1,8 27,5 68,7 0,14 1,91 0,064   1,8 27,5 68,5 0,18 1,94 0,063 июль 1,8 26,7 69,4 0,13 1,89 0,063   1,7 27,7 68,3 0,13 1,94 0,061   1,7 27,2 68,6 0,16 2,02 0,062 август 1,8 27,2 68,8 0,14 1,86 0,065   1,8 28,4 67,2 0,11 2,18 0,062   1,9 67,6 0,17 2,01 0,063 сентябрь 1,8 27,5 68,3 0,19 1,92 0,063   1,7 27,2 68,8 0,14 1,85 0,064   1,9 27,5 0,21 2,00 0,064 октябрь 1,9 27,4 68,5 0,15 1,94 0,063   1,7 27,4 68,5 0,17 2,01 0,063   1,7 27,5 68,6 0,11 1,98 0,063 ноябрь 1,7 27,7 68,3 0,13 1,99 0,064   1,7 27,6 68,4 0,14 1,90 0,063   1,9 68,8 0,13 2,07 0,061 Примечание: но – нерастворимый в воде остаток.   Для проведения корреляционного анализа используем прикладной пакет «Анализ данных» программы Microsoft Excel. Для этого копируем данные табл.1 в программу Microsoft Excel, сохраняя в памяти компьютера файл под определенным именем. Далее, в меню программы Microsoft Excel выберем кнопку “Сервис”, после нажатия на которую выберем кнопку “Анализ данных”. Если пакет “Анализ данных” не установлен в программе Microsoft Excel, то для его установки выполняют указанные в разделе Статистический анализ операции. В пакете “Анализ данных” выбирают инструмент “Корреляция” и нажимают “ОК”. В программе появляется окно запроса входного интервала анализируемых данных. С помощью мышки выделяют входной интервал анализируемых данных (имя и содержание столбцов, начиная с первого столбца “н.о.”). В меню “Корреляция” указывают группирование – (по столбцам или по строкам), выбирают – “По столбцам”. Для идентификации столбцов в выводимой таблице ставим метку в строке “Метки в первой строке”. В параметрах вывода данных ставят метку напротив строки – “Новый рабочий лист”. При этом, данные расчетов коэффициентов корреляции выведутся на новый рабочий лист программы Microsoft Excel в виде табл.5.10. Таблица 5.10 Значения коэффициентов корреляции компонентов сильвинитовой руды БКРУ-1 н.о. KCl NaCl MgCl2 CaSO4 Br- Н.о.           KCl 0,093357         NaCl -0,4618 -0,87199       MgCl2 0,273002 -0,19928 -0,04059     CaSO4 0,495106 -0,03191 -0,33646 0,25169   Br- -0,32867 0,282824 0,019446 0,029904 -0,53145   Для оценки значимости вычисленных коэффициентов корреляции используем выражение: Для приведенного примера n=33. Вычисленные по этой формуле величины tнабл приведены в табл.5.11. Таблица 5.11 Значения коэффициентов tнабл   н.о. KCl NaCl MgCl2 CaSO4 Br- Н.о.             KCl 0,52207           NaCl -2,8988 -9,91788         MgCl2 1,580031 -1,13225 -0,22618       CaSO4 3,172802 -0,17776 -1,98931 1,447964     Br- -1,9376 1,641726 0,108291 0,166573 -3,4931     Величину tкр находят по статистической таблице или по функции: =СТЬЮДРАСПОБР(0,05;32), принимая уровень значимости a=0.05, число степеней свободы f=n-1= 32. Отсюда, найдено критическое значение tкр=2,036933. Сравнение |tнабл | и tкр показало, что к значимым коэффициентам регрессии относятся только четыре выделенных в табл. 2 коэффициента корреляции. Из анализа данных табл.5.11 следует, что значимая корреляционная связь существует между: 1) содержанием нерастворимого остатка и содержанием NaC1 и СаSO4; 2) содержанием КС1 и NaC1; 3) содержанием СаSO4 и бромид-ионом. По знаку коэффициентов корреляции можно заключить, что чем меньше содержание в сильвинитовой руде хлорида натрия и выше содержание сульфата кальция, тем больше содержание в руде нерастворимого остатка. Содержание основного вещества КС1 в руде возрастает при снижении содержания примеси хлорида натрия. Содержание примеси бромид-иона снижается при увеличении в руде примеси сульфата кальция. По величине коэффициента корреляции можно заключить, что наибольшая корреляционная связь существует между основными компонентами сильвинитовой руды – хлоридами КС1 и NaC1 (r=-0.872). Найденные зависимости полезны для оптимизации работы флотационных и галургических производств, перерабатывающих сильвинитовые руды.   Рекомендуемые страницы:



poisk-ru.ru