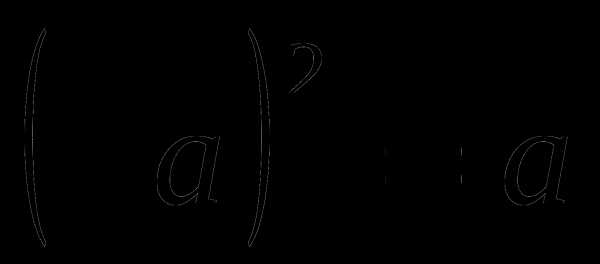Корни в каком классе проходят – Помогите…. 7-й класс!!! — запись пользователя Олеся (Lesenok1980) в сообществе Дети от шести и старше в категории Средняя (5-9 классы)

Содержание

Урок по алгебре на тему «Квадратный корень из произведения» в 8 классе

Тип урока: изучение новой темы

Цели урока:

— создать условия для вывода обучающимися утверждения = и применения его для вычисления квадратных корней;

— способствовать развитию логики, умения проводить анализ и делать выводы;

— продолжать воспитание устойчивого интереса к математике.

ХОД УРОКА:

I. Организационный момент

II. Мотивация

Сегодняшний урок я хотела бы начать со слов Фридриха Адольфа Вильгельма Дистервега — немецкого педагога, политика «Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь». (слайд 2)

Миниатюра, которую разыгрывают ученики.

За столом сидит ученик, он в роли учителя математики. К столу прикреплен плакат «Экзамен по математике».

Вбегает ученик.

— Извлекать корни умеешь? – спрашивает экзаменатор.

Ученик:

— Да. Конечно. Нужно потянуть за стебель растения посильнее, и корень его извлечется из почвы.

— Нет, я имела в виду другой корень, например, из девяти.

— Это будет «девя», так как в слове «девять» суффиксом является «ть».

— Ты меня не совсем понял, я имела в виду корень квадратный.

— Квадратных корней не бывает. Они бывают мочковатые и стержневые.

— Арифметический квадратный корень из девяти?

— А, тогда три, так как три в квадрате равно девяти.

При этом ученик берет со стола плакат с записью =3 и показывает его аудитории.

Сегодня на уроке мы продолжим изучение квадратных корней, мы будем учиться извлекать квадратный корень из произведения.

(слайд 3)

Знания, полученные по этой теме, помогут вам в дальнейшем изучении математики, а именно при изучении темы « Преобразования выражений, содержащих квадратные корни». А также при сдаче государственного экзамена в 9 классе за курс основной школы.

Я вас попрошу поставить на полях своих тетрадей ту оценку, которую вы хотели бы получить за урок.

Цели урока: (слайд 4)

Повторить определение арифметического квадратного корня.
Вывести правило вычисления квадратного корня из произведения.
Научиться находить квадратный корень из произведения.
Проверить знания и умения с помощью самостоятельной работы.

План урока: (слайд 5)

Теоретический опрос
Устная работа.
Мини лабораторная работа.
Практическая работа.
Самостоятельная работа.
Подведение итогов.
Задание на дом.

III. Актуализация опорных знаний.

Теоретический опрос.

(слайд 6)

Как читается выражение ?
При каком значении а выражение имеет смысл?
Что называется арифметическим квадратным корнем из числа а?
Когда равенство =b является верным?
При каком значении а выполняется равенство
?

Устная работа: (слайд 7)

1. Вычислите:

2. Сравните:

IV. Изучение нового материала. (слайды 8, 9)

Мини лабораторная работа.

Разбейте тетрадный лист на три вертикальные части. В первый столбец запишите квадратные корни и вычислите их.
Во второй столбец запишите квадратные корни и вычислите их. (корень из произведения) Какой порядок действий при вычислениях?
В третий столбец запишите выражения и найдите их значения. Какой порядок действий при вычислениях? (произведение корней)
Посмотрите внимательно на решения во всех трех столбцах. Какой вывод можно сделать?

— В каких столбцах вычисления для вас были легкими?

— Объясните, почему? Чем вы пользовались при вычислениях?

— Почему во втором столбце вычисления было сделать труднее?

— Сравните подкоренные выражения во всех трех столбиках. Какой вывод можно сделать?

(Учитель выслушивает различные варианты ответов учащихся и подводит под правило)

(слайд 10)

— Кто может сформулировать правило вычисления квадратного корня из произведения?

— Это правило справедливо для любых множителей?

— Запишите правило в общем виде, с помощью букв.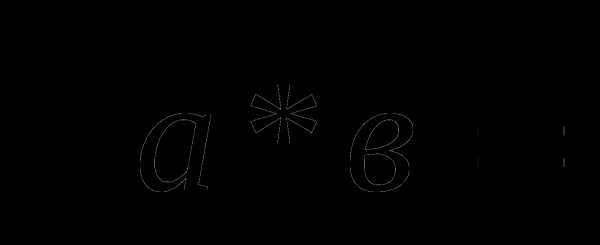

Работа с учебником.

На стр. 84-85 учебника прочитайте текст, найдите правило и сравните с тем, которое вы сформулировали. Рассмотрим пример 1

Учитель:

— Можно ли применить правило для трех и более множителей? (слайд 11)

Закрепление изученного.

Практическая работа.

Вычислите значение квадратного корня, используя теорему о корне из произведения. (слайды 12, 13)

Учащиеся комментируют, а учитель у доски показывает оформление.

Эту формулу можно использовать и для быстрых вычислений. (слайд 14)

Как бы вы стали вычислять значение следующего выражения?

– ?

Учащиеся предлагают два способа:

Iспособ:

II способ:

Второй способ более изящный, мы применили формулу разности квадратов: а²-в²=(а-в)(а+в) и воспользовались свойством квадратных корней.

Гимнастика для глаз (слайды 15,16)

Сейчас я покажу вам решение некоторых примеров.

(слайд 17)

4. Самостоятельная работа. (слайд 18 )

1 вариант

2 вариант

Критерии оценивания – слайд 19

5. Применение изученных свойств квадратных корней в других областях. (слайды20, 21)

Мы находимся на первой ступени преобразования квадратных корней.
Квадратные корни применяются при многих расчетах.

Так, например, в физике при определении первой космической скорости

G-гравитационная постоянная:
M-масса Земли;
R-радиус Земли.

Расчетами первой космической скорости вы будете заниматься в 10 классе.
При броуновском движении средняя квадратичная скорость молекул газа находится по формуле.

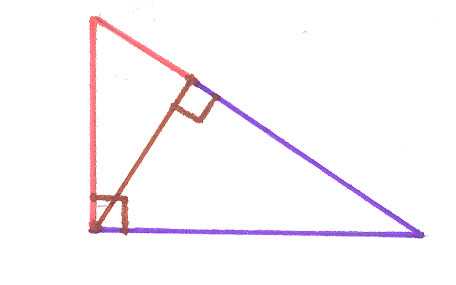
В геометрии часто встречаются средние значения, например катет прямоугольного треугольника равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу. А высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое проекций катета на гипотенузу.

Также площадь треугольника можно вычислить по формуле Герона:

Итог урока. (слайд 22)

1. Сформулируйте теорему о квадратном корне из произведения.

2. Верно ли, что значения указанных квадратных корней можно найти по свойству квадратного корня из произведения?

а)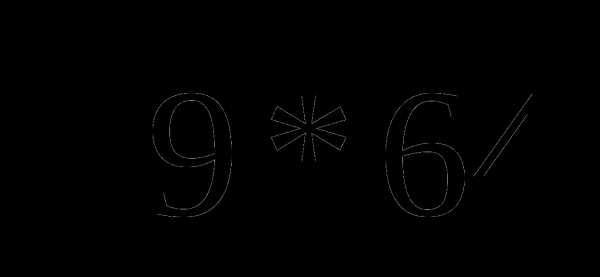

б)

в)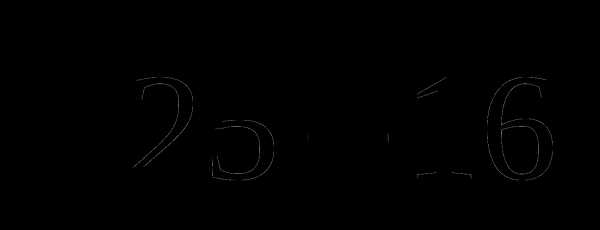

Ученик вычислил значение и получил два варианта ответа 1 и 5. Какой из них верный? Объясните.

Согласно словам Дистервега: «Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь», проведите самоанализ, ответив на вопросы на бланке.

Как я знаю и применяю материал по теме: «Квадратный корень из произведения»:

а)на отлично;
б) хорошо;
в) удовлетворительно;
г) совсем не знаю и не могу применять.

Поднимите, пожалуйста, руки те, кто достиг своих поставленных целей.
Поднимите руки те, кто получил оценку выше той, которую поставил себе на полях в начале урока.
А теперь поднимите руки те, кто не достиг тех результатов, которые намечал в начале урока.
Что еще нужно подучить, над чем нужно поработать?

Домашнее задание П.16, №№369(б,г,е), 374(б,г,е,з), 376(б,г,е) (слайд 23)

Слайд 24 На этом уроке вы, ребята, познакомились с теоремой об извлечении квадратного корня из произведения, а также рассмотрели её применение. Вам были предложены упражнения для решения и вы могли проверить себя. Я только хочу вам напомнить, что при решении задач, примеров надо искать рациональные подходы и применять разнообразные способы.

МОБУ СОШ с. Железнодорожный

Открытый урок алгебры в 8 классе

по теме:

«Квадратный корень из произведения»

Провела: учитель математики Гольман Л.М.

2014-2015 учебный год

infourok.ru

Урок по теме: Квадратные корни.

МКОУ Новобелянская средняя общеобразовательная школа

Урок по теме
«Квадратные корни.

Арифметический квадратный корень»

Подготовила: Куприкова Н.И.

учитель математики

2016

Тема: «Квадратные корни. Арифметический квадратный корень».

Цели: ввести понятия квадратного корня и арифметического квадратного корня; сформировать умение извлекать квадратные корни; развиватьлогическое мышление, смекалку.

Оборудование: компьютер, презентация

План урока:

Организационный момент.
Устная работа.
Объяснение нового материала.
Формирование умений и навыков.
Итоги урока.
Домашнее задание.

Ход урока:

Организационный момент.

Сообщение темы и целей урока.

(слайд 1)

Устная работа.

Вычислите:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) .

(слайд 2)

1. Объяснение нового материала.

Введение понятия квадратного корня.

Рассмотрим задачу о нахождении стороны квадрата по его площади.

Пусть площадь квадрата равна 64 . Чему равна длина стороны этого квадрата?

Обозначим длину стороны квадрата (в сантиметрах) буквой х. Тогда площадь квадрата будет см². По условию площадь равна 64 см², значит х²=64.

Корнями уравнения х²=64 являются числа: 8 и — 8. Действительно, 8²=64 и (-8)²=64. Так как длина не может выражаться отрицательным числом, тоусловию задачи удовлетворяет только один из корней — число 8. Итак, длина стороны квадрата равна 8 см.

Корни уравнения х²=64, т.е. Числа, квадраты которых равны 64, называют квадратными корнями из числа 64.

(слайд 3)

Задание. Вместо пустых клеточек поставьте числа так, чтобы равенства были верными:

‪²=16 ‪²= ‪²=100

Определение. Квадратным корнем из числа а называют число, квадрат которого равен а.

Задание: выяснить, является ли число n квадратным корнем из числа m, если:

а) n=5, m=25; в) n=0,3, m=0,9;

б) n= — 7, m=49; г) n=6, m= — 36.

(слайд 4)

Введение понятия арифметического квадратного корня.

Учащиеся должны усвоить существенный признак данного понятия — арифметический квадратный корень является неотрицательным числом (то естьнеобходимо знание того, что равенство означает одновременно выполнение двух условий: b²=a и b≥0).

Число 8 — неотрицательный корень уравнения х²=64 — называют арифметическим квадратным корнем из 64. Иначе говоря, арифметический квадратный корень из 64 — это неотрицательное число, квадрат которого равен 64.

Определение. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.

Задание: определить, является ли число n арифметическим квадратным корнем из числа m, если:

а) n=8, m=64; в) n=0,2, m=0,4;

б) n= — 3, m=9; г) n=0,4, m=0,16.

(слайд 5)

Физкультминутка. Гимнастика для глаз: быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5 (повторить 4–5 раз).

Историческая справка.

Обратим внимание на совпадение в терминах — квадратный корень и корень уравнения. Это совпадение неслучайно. Уравнения вида х²=а исторически были первыми сложными уравнениями, и их решения были названы корнями по метафоре, что из стороны квадрата, как из корня, вырастает сам квадрат. В дальнейшем термин «корень» стал употребляться и для произвольных уравнений.

Название «радикал» тоже связано с термином «корень»: по-латыне корень — radix (он же редис — корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа √ связывают с написанием латинской буквы r.

(слайд 6)

Основное свойство арифметического квадратного корня.

Вычислите значения следующих выражений:

, , .

Сформулируйте вывод:

, если а≥0

(слайд 7)

Формирование умений и навыков.

Найдите значение арифметического квадратного корня:

а) ; б) ; в) ; г) ; д) ; е) .

Найдите значение выражения:

а) ; б) ; в) ; г) .

Укажите натуральные значения n, при которых является натуральным числом значение выражения

(Решение: чтобы значение выражения являлось натуральным числом, подкоренное выражение должно быть равно 1, 4 или 9. Получаем 3 случая:

11 — n=1 11 — n=4 11 — n=9

n=10 n=7 n=2

Эти же значения можно было найти подбором.

Ответ: 2, 7, 10.)

(слайд 8)

Итоги урока.

Что называется квадратным корнем из числа а?
Сколько квадратных корней может быть из числа а?
Что такое арифметический квадратный корень из числа а?
Имеет ли смысл запись ? Почему?

(слайд 9)

6. Домашнее задание:

Найдите значение выражения:

а) ; б) ; в) .

(слайд 10)

infourok.ru

Работа над составом слова в начальных классах. Понятие корень, однокоренные слова

Разделы: Начальная школа

Вводный урок

Чтобы полнее использовать все возможности темы “Состав слова”, учителю с самого начала надо помнить, что мы в школе занимаемся не этимологическим анализом слов, а морфологическим. В чём же между ними разница? При этимологическом анализе мы выясняем происхождение того или иного слова, отмечаем, какие изменения произошли в данном слове в процессе развития языка.

Морфологический анализ слова заключается в выявлении живых языковых связей, поэтому слово можно членить только до тех пор, пока оставшаяся часть имеет какое-то значение.

Главное состоит в том, чтобы разбор слов по составу не проходил механически, чтобы не сводить всю работу по составу слова к одному умению — выделять корень только потому, что похожий звуковой комплекс слышится и в других словах. Конечно, корень – это та часть слова, которая легче всего осознаётся в слове и поэтому естественно желание учителя научить учеников выделять в слове сразу корень. Однако проводить эту работу надо осторожно. После того, как у учеников сформировали понятие о родственных словах, дальнейшую работу по составу слова лучше всего проводить на парах слов. Ученикам предлагаются два родственных слова, из которых одно непроизводное, состоящее только из корня, а второе – непосредственно образовано от первого, например, соль и солонка. Сначала ученики устанавливают, что это родственные слова, затем в производном слове выделяют корень. При этом рассуждения учеников должны выглядеть приблизительно так: соль и солонка – родственные слова. Слово солонка образовано от слова соль, так как солонка – это посуда для соли. Соль – это корень слова, так как дальше его разделить нельзя. Этот корень встречается и в других родственных словах: солёный, солить, засолить.

При выделении корня важно подбирать слова разных частей речи: слова — предметы, слова - признаки предметов, слова – действия предметов. Например, чтобы выделить корень в слове белый, ученики подбирают слова: беленький, белить, белок, белизна. Этот ряд слов помогает уточнить значение корня и точнее его выделить, но не объясняет полностью семантики всего слова. Решить эту задачу поможет подбор слов одной словообразовательной модели, например, краснеть, чернеть, алеть, желтеть и др. Корень у всех этих слов разный, но все они образованы от основы качественных прилагательных с помощью суффикса - е-ть и имеют общее значение “становиться каким-то”. Привлечение к анализу слов одной модели не только обеспечит членение слова, но и даст возможность лучше определить значение слов. Кроме того, в сознании ученика отложится определённая модель, по которой он без труда в нужных случаях образует такие глаголы, как свирепеть, голубеть, грубеть, лиловеть и т.п., независимо от того, встречался он с этими словами раньше или нет. Задача начальных классов заключается в том, чтобы показать, как значение одного слова зависит от значения другого, и сформировать понятие о значении некоторых словообразовательных моделей. Например, значение лица в русском языке передаётся суффиксом – ист (тракторист, связист), —тель (учитель, водитель), —ник (плотник, дворник), —чик (лётчик, учётчик). Значение конкретного предмета вносят суффиксы – ниц-а (сахарница, хлебница,), —ин-а (-инк-а) (горошина, изюминка), — этот суффикс употребляется в языке со значением единичности.

Существительные с суффиксом – б-а и – к-а имеют значение отвлечённого действия (ходьба, мойка).

Среди суффиксов имён прилагательных заслуживают внимание следующие: —н-ый, —ов-ый, —ск-ий, —еск-ий, —ист-ый, —оват-лив-ый, —еньк-ий и др. Первые три суффикса обычно образуют имена прилагательные от существительных и имеют значение “относящийся к кому-чему-либо”, “такой, как у кого-то”. Суффикс – ист — употребляется либо со значением “похожий на что-то” (серебристый, волнистый), либо со значением “обладающий чем-то в большом количестве” (душистый, голосистый). Суффикс – оват — употребляется со значением “обладающий слегка каким-то качеством” (розоватый, беловатый). Суффикс – еньк — употребляется с уменьшительно-ласкательным значением (светленький, славненький). Суффикс –лив— показывает склонность предмета к какому-нибудь действию (говорливый, слезливый). Значение всех перечисленных суффиксов довольно конкретно и потому доступно младшим школьникам.

Несколько труднее глагольные суффиксы, поскольку большинство из них имеет чисто грамматическое значение, поэтому при анализе глаголов целесообразнее раскрывать словообразующую роль приставок. Значение глагольных приставок усваивается довольно легко, например, приставка –в— показывает направление действия внутрь: влететь, вписать; приставка –вы— омонимична приставке –в-: она показывает направление действия наружу, например, вылететь, выписать. Указание на достижение действия содержит в себе приставка –до-: добежать, доделать.

Учитель в начальной школе должен помочь формированию у учащихся более отчётливых представлений о существовании в языке определённых словообразовательных моделей, которым свойственна словообразовательная общность и общность значения. Главный упор должен быть сделан на смысловую зависимость слов друг от друга. Это не только будет способствовать развитию речи, но и обеспечит правильный подбор родственных слов для проверки трудных орфограмм.

Для знакомства с понятием “Корень” во 2 классе предлагаю урок-знакомство с данным понятием и первичным закреплением этого понятия на практике.

Цели: способствовать формированию понятия корень, как главной значимой части однокоренных родственных слов; способствовать развитию умений учащихся выделять в словах корень, подбирать однокоренные слова; способствовать расширению словарного запаса учащихся, развитию внимания.

Материал:

1. Учебник. Русский язык. Р.Н.Бунеев, Е.В.Бунеев, О.В.Пронина.

2. П.А.Грушникова. работа над словом на уроках русского языка в начальных классах.

3. Наглядный материал:

плакат с однокоренными словами к слову воз;
карточки с корнями земл, звер, вод;
плакат со словами:

Лес, лесок, лесной, лесник.
Цвет, цветок, цветной, цветник.
Лётчик, самолёт, полёт.
Ледяной, ледовый, лёд.

плакат со словами:

Сад, посадка, посадил.
Род, родители, родил.
Ходит, выходка, ходы.
Трудовой, трудись, труды.

плакат со словами:

Белка, беленький, белить.
Водяной, вода, водить.
Лист, лиса, лисёнок.
Лось, лоскут, лосёнок.
Горный, горка, городок.
Пёс, песочный, песок.

4. Раздаточный материал:

— карточки со словами: земляк, вода, землемер, зверёк, водолаз, землячка, озвереть, водоём, земляной, звериный, водяной, приземлить, зверюшка, зверь, водитель.
карточки с пословицами:

Незнайка лежит, а Знайка далеко бежит.

Все знания бог человеку не дал.

Знайка дорожкой бежит, Незнайка на печке лежит.

5. Школьный словообразовательный словарь русского языка. Под редакцией А.Тихонова.

Методы: фронтальный, индивидуальный, групповой (работа в парах).

Ход урока

I. Проверка домашнего задания.

II. Сообщение темы урока.

— Всё на свете из чего-нибудь состоит: облака – из множества водяных капелек, лес – из деревьев. Речь состоит из предложений, а предложения из слов. Слова сделаны из своего “строительного” материала. И каждый из “кирпичиков” вносит в слово свою часть смысла – “смыслиночку”. А может кто-нибудь из вас уже знает и скажет, как называется “главный кирпичик” слова – главная его часть? (Корень)

— Правильно. Корень. Но слово корень – многозначное. Где в жизни вы уже встречались с этим словом? (Подземная часть растений, внутренняя часть зуба, волоса, ногтя.)

— У всех этих слов есть общее значение – они важная часть своих предметов. А мы будем говорить о корне как части слова.

III. Наблюдение над однокоренными словами, значением корня.

1. Работа с наглядным материалом.

— Много-много лет тому назад появилось одно слово. Нашли его люди и думают: “Что с ним делать?” А слово это и говорит: “Посадите меня, и я разрастусь в большое красивое дерево”.

— Посадили люди слово, и стало оно расти. Сначала один росток пустило, потом второй, третий. Много ростков появилось от этого слова. Все они на него похожи, но и своё в каждом есть. Вот такое дерево выросло! (На доске открывается плакат)

— Прочитайте внимательно слова, посмотрите, может быть, вы мне сами назовёте общую часть этих слов, из которой выросли все эти слова? (Ответы детей)

— Правильно (открывается корень воз). Эта часть ВОЗ. И вот тогда решили люди назвать общую часть слов корнем. Потом на глаза им попался ещё один маленький корешок ХОД, такой грустный, но уже очень юркий. И попросил он людей его тоже посадить в землю, пообещав разрастись в большое дерево. Не поверили люди, но всё же посадили его, не пропадать же ему совсем. Много, очень много ростков появилось от одного маленького корешка ХОД, и все они были чем-то похожи на своего предка. Попробуйте угадать и назвать эти слова.

— Записываем слова на доске и в тетрадях. (Вход, выход, походка, переход, ходить…)

— Чем же похожи эти слова? Какая часть в этих словах будет корнем? (Ход.)

— Правильно, корень ход и выделяется корень дугой. (Выделяем.)

— А попробуйте прочитать только корень. (Читают.)

— Вы поняли, что означает это слово? (Да.)

— А попробуйте закрыть корень и прочитать оставшиеся части. (Читают.)

— Ясен ли смысл слов? (Нет.)

— Какой же мы сделаем вывод, что такое корень? (Ответы детей.)

— Правильно, корень – это главная часть слова. В корне заключён смысл слова. От него “растут” другие слова.

— А теперь прочитаем в учебнике о корне на стр. 75. (Чтение правила вслух.)

— Кто понял и сможет рассказать, что такое корень? (Ответы детей.)

2. Дидактическая игра “Найди свой дом”.

— А сейчас мы поиграем. У меня три домика. В первом живёт корень земл, во втором – звер, в третьем – вод. У вас на столах карточки со словами. Прочитайте внимательно и найдите домик для своего слова.

— Начинаем заселять дома: (Дети по очереди прикрепляют свои слова.)

земл	звер	вод
земляк	зверь	вода
землемер	зверёк	водолаз
землячка	озвереть	водоём
земляной	звериный	водяной
приземлить	зверюшка	водитель

— Внимательно посмотрите и скажите, все ли слова в каждом столбике одинаковые по смыслу? (Находят лишнее.)

— Верно, слово водитель “лишнее”. Значит однокоренные слова – это какие слова? (Ответы детей.)

— Верно, однокоренные слова имеют общий корень и одинаковое значение, смысл.

— А как написан корень в однокоренных словах? (Ответы детей.)

— Правильно, корень в однокоренных словах пишется одинаково.

— А чтобы “лишнему” слову не было скучно, подберём ему однокоренные слова и запишем их, корень выделим. (Письмо с комментированием учителя. Дети называют слова, учитель пишет на доске и проговаривает, дети пишут в тетрадях: водитель, приводить, проводник, проводы.)

— Взаимопроверка.

3. Упражнение в выделении корня в однокоренных словах. (На доске два плаката.)

— Так же, как и кустов,
Корень слова есть у слов.
удь внимателен к словам,

Отыщи в них корень сам.

— Спишите слова, выделите корень:

1 вариант:

Лес, лесок, лесной, лесник.
Цвет, цветок, цветной, цветник.
Лётчик, самолёт, полёт.
Ледяной, ледовый, лёд.

2 вариант:

Сад, посадка, посадил.
Род, родители, родил.
Ходит, выходка, ходы.
Трудовой, трудись, труды.

— Выделим корень на доске. (По одному ученику от каждого варианта.)

— Правильно ли выделили корень? У кого не было ошибок?

— Самопроверка.

IV. Физкультминутка.

V. Закрепление изученного материала.

— А сейчас я посмотрю, хорошо ли вы поняли сегодняшнюю тему.

1. Упражнение в подборе однокоренных слов.

— Подобрать однокоренные слова. Слова записать в столбик. Работаем в парах. (Корни на листах прикреплены на доске)

1 ряд – мороз.

2 ряд – груз.

3 ряд – мор.

— Проверка (Дети читают цепочкой):

1 ряд	2 ряд	3 ряд
мороз	груз	море
заморозки	грузчик	моряк
морозный	грузовой	приморье
заморозить	грузить	морской
морозильник	погрузка	мореход

— А у кого из вас встретилось словарное слово? (Ответы.)

— Верно, это слово мороз. Ещё раз запомните, как оно пишется.

2. Работа со словарём.

— Мы с вами пользуемся двумя словарями: “Орфографический словарь” и “Толковый словарь”. А сегодня я покажу вам новый словарь. Если у вас будут трудности в подборе однокоренных слов, вам поможет “Школьный словообразовательный словарь русского языка” под редакцией А.Тихонова.

— Попробуйте по словарю подобрать однокоренные слова к слову газ. (Ответы детей.)

3. Игра “Найди лишнее слово”.

— А сейчас словесная игра на внимательность. В каждой строке есть “лишнее” слово. Вы должны его назвать и объяснить свой выбор.

На доске:

Белка, беленький, белить.
Водяной, вода, водить.
Лист, лиса, лисёнок.
Лось, лоскут, лосёнок.
Горный, горка, городок.
Пёс, песочный, песок.

— Молодцы! А теперь на слух: Моряки, морской, моржи.

Корень, корневой, коржи.
Холод, холмик, холодок.
Носик, носит, носок.
Семя, семечко, семья.
Вдруг, подруга, друзья.

— Хорошо!

VI. Творческая работа.

— Объясните смысл пословиц:

Незнайка лежит, а Знайка далеко бежит.

Все знания бог человеку не дал.

Знайка дорожкой бежит, Незнайка на печке лежит.

VII. Итог урока.

— Что нового вы узнали на уроке? (Ответы детей.)

— Что же такое корень? (Главная часть однокоренных родственных слов.)

— Как пишется корень в однокоренных словах? (Одинаково.)

— Вы сегодня очень хорошо работали. Как вы думаете, кто сегодня работал на отлично, чётко и ясно отвечал на вопросы и можно ему поставить “5”?

— А кто немножко ошибся и ему можно поставить “4”?

— Молодцы! Всем спасибо! Урок окончен.

VIII. Домашнее задание.

— Придумать сказку про корень и выучить правило на странице 75.

xn--i1abbnckbmcl9fb.xn--p1ai

Начальная школа. Разбор слова по составу: arteschool

Разбираем слово по составу

По-моему, в 1 классе детей учили писать. Ну, и на том спасибо. Хотя, честно говоря, я так и не понял, почему мало внимания уделялось отработке навыка написания, почему цифру «5» мой ребенок начинал рисовать с хвостика, цифру «8» рисовал «зеркально», а в тетрадях не было косой линовки. Сам я с огромным трудом пишу от руки, предпочитая для заметок использовать что-то вроде скорописи. Для официальных документов у меня есть собственный шрифт, в котором буквы пишутся по наикратчайшей траектории. В связи с этим я не чувствую себя способным помочь ребенку научиться писать «по-школьному».

А вот с орфографией помочь можно. И, как свидетельствует мой опыт общения с нынешними студентами, помогать нужно.

Из-за чего возникают орфографические ошибки? Вовсе не из-за того, что правила русского языка излишне сложны и требуют упрощения. Русский язык куда проще английского, где за века накопилось множество исключений. А большая часть орфографических ошибок есть результат неумения видеть состав слова. Если ребенок умеет выделять корень и знает то небольшое число исключений, когда меняется корневая гласная, значит, он не будет делать ошибки при написании корня. Если ребенок видит суффиксы и понимает значение суффиксов (то есть, представляет, для чего нужен тот или иной суффикс), значит, он не будет делать ошибок при их написании.

В школе разбор слова по составу дается как самостоятельная тема. И, даже умея разбирать слово, редкий ученик может связать разбор с той массой разрозненных правил по написанию суффиксов и приставок, которые ему предлагается запомнить. Ведь «дом» орфографии строится не с фундамента – с умения видеть структуру слова, а как-то хаотично, когда сначала изучают корень и учат ставить его под ударение, а потом удивляются, почему это вдруг ребенок пытается поставить под ударение суффикс. В конечном счете, многие правила просто не нанизываются на единый связующий стержень, остаются отголосками разрозненной информации, а школьники пишут все менее и менее грамотно.

Если хотите помочь своему ребенку, научите его разбирать слова по составу в самом раннем возрасте. Мы начали изучать это сегодня – на каникулах после окончания первого класса.

Технология такая.

1. Научите выделять окончание. Если кто-то не помнит, то окончание – это изменяемая часть слова. Возьмите слово и начните задавать для него разные вопросы.

Например, «тумбочка». Это что? Тумбочка. У меня нет чего? Тумбочки. Покажите ребенку, какая часть слова меняется, выделите ее значком окончания.

Для прилагательных не забывайте ставить слово в разные роды, чтобы ребенок видел, что окончание состоит не из одной, а из нескольких букв.

Он какой? Красный. Нет какого? Красного. Оно какое? Красное.

Когда я учился в начальной школе, я думал, что у слова «стол» нет окончания. В четвертом классе нам рассказали, что окончание есть, но оно «нулевое». Обозначается, соответственно, пустым квадратиком после слова. Не знаю, как учат в современной начальной школе, но, думаю, будет правильнее сразу показать ребенку, что окончание может быть нулевым. (Это, в частности, нужно потому, что у наречий нет окончаний, поэтому, чтобы в будущем не возникала путаница, лучше сразу определить, что у существительного окончание имеется, хотя иногда и не представлено буквами.)

2. Выделив окончание, покажите ребенку основу слова. И научите ее значку.

3. Теперь научите видеть корень и обозначать его значком.

В традиционных грамматиках корнем называют неизменяемую часть слова. По-моему, понять такое определение ребенку сложно.

Поэтому, объясняя понятие корня, попробуйте показать ребенку, что корень – это прежде всего самая важная частичка слова, несущая сам смысл предмета, восходящая к тому праслову, от которого пошли все другие слова с данным корнем.

Мне объяснение давалось проще, т.к. ранее я уже показывал Юле примеры того, как слово приходит из одного общего языка в другие языки и живет в них в разном виде.

Когда разберетесь с корнями, не забудьте показать ребенку, что есть слова, кажущиеся однокоренными, но на деле таковыми не являющиеся. Например, «горе» и «гора».

4. Далее выделите приставку. И покажите ее значок. Очень хорошо, если вы сразу поясните ребенку значение некоторых приставок.

5. И теперь остается самое сложное – суффиксы.

Суффикс – это часть слова, которая путешествует из одного слова в другое. Когда в слове появляется суффикс, оно меняет значение. Начните разбор со слов, где есть уменьшительно-ласкательные суффиксы. В русском языке таковых много. Можете показать, как «ДОМ» превращается в «домИК» из-за суффикса «-ик». «Макс» становится «МаксИКом».

С суффиксами есть одна сложность, которая связана с тем, что в начальной школе и средней школе суффиксы могут выделяться по-разному. Там, где в начальной школе обычно видят один суффикс, в средней могут различить сразу два. Это не должно вас пугать. Вы же учите ребенка разбирать слово не для олимпиад, а для того, чтобы он писал грамотнее. Поэтому оставьте учителям заниматься схоластикой и выяснять, сколько суффиксов рекомендуют выделять в слове последние инструкции Министерства всеобщего недообразования.

Научите ребенка видеть суффиксы. Выделив суффикс, сразу обсудите с ребенком его значение. Всегда обсуждайте значение суффикса! Это поможет ребенку запомнить основные суффиксы, и через какое-то время он не только будет видеть их самостоятельно, но будет безошибочно их писать.

И последнее замечание. Когда будете разбирать сложные слова, например, «пароход», помните, что «о» и «е» не являются частью слова. Их называют соединительными гласными. Когда я учился в школе, их просто подчеркивали.

Рассказав ребенку про соединительную гласную в сложных словах (и сделав несколько упражнений со сложными словами), вы избавите ребенка от ошибок в будущем.

==
А если пройдете по этой ссылке http://russian-pages.newmail.ru/traditional/suffiksy/exercises.html , то найдете интересный материал про суффиксы для себя, а также несколько упражнений, выполняя которые, ребенок научится лучше видеть суффиксы в словах.

arteschool.livejournal.com

Урок математики в 11-м классе «Расположение корней квадратного уравнения в зависимости от параметра»

Разделы: Математика

Цель:

формировать умение распознавать положение квадратной параболы на плоскости в зависимости от параметра,
развивать логическое мышление,
умение работать в проблемной ситуации.

Ход урока

Проверка домашнего задания.

Объяснение нового материала.

Решение многих задач с параметрами, предлагаемых на экзаменах, в частности, на ЕГЭ по математике, требует умения правильно формулировать необходимые и достаточные условия, соответствующие различным случаям расположения корней квадратного трёхчлена на числовой оси.

Пусть квадратный трёхчлен f(x) = ax² + bx + с имеет корни x₁и_x₂, — абсцисса вершины параболы y = ax² + bx + с, d — заданное число. Рассмотрим ряд утверждений, связанных с взаимным расположением x₁,_x₂и числа d.

Теорема 1. Для того чтобы оба корня квадратного трёхчлена были больше числа d, (рис.1) необходимо и достаточно выполнение условий.

Пример:

При каких значениях параметра а корни уравнения ax²—(2а + 1)х + 3а — 1 = 0 больше единицы?

Решение: 1. При а = 0 х = -1 — не удовлетворяет требованию задачи.

2. При а

Ответ:

Теорема 2. Для того чтобы оба корня квадратного трёхчлена были меньше числа d, (рис.2) необходимо и достаточно выполнение условий

Рассмотрим задачи на применение этих теорем, обращая внимание на алгоритм получения необходимых и достаточных условий, соответствующих данному случаю расположения корней квадратного трёхчлена на числовой оси. Учащиеся должны научиться составлять эти условия, а не пытаться механически их запомнить.

Задачи для самостоятельного решения.

Найдите значение параметра m, при которых уравнение имеет два отрицательных решения.

Ответ: при уравнение имеет два отрицательных решения.

Найти все значения параметра , при которых уравнение имеет два положительных различных решения.

Ответ: при уравнение имеет два положительных различных решения

При каких значениях параметра а корни уравнения больше 1?

Ответ: при корни уравнения больше 1.

При каких значениях параметра а оба корня уравнения меньше 1?

Ответ: при оба корня уравнения меньше 1.

При каких значениях параметра p оба корня квадратного трехчлена отрицательны?

Ответ: при оба корня квадратного трехчлена отрицательны.

Найдите все значения параметра а, при которых оба корня уравнения больше 1?

Ответ: не существует таких значений параметра а, при которых оба корня уравнения больше 1.

Теорема 3. Для того чтобы число d было расположено между корнями квадратного трёхчлена, (рис.3) необходимо и достаточно выполнение условий

Задача для самостоятельного решения

Найти все значения параметра , при которых только один корень квадратного трехчлена больше 2.

Ответ: или .

При каком значении параметра один корень уравнения больше 1, а другой — меньше 1?

Ответ: при один корень уравнения больше 1, а другой — меньше 1.

При каких значениях параметра число 2 находится между корнями квадратного уравнения ?

Ответ: при один корень уравнения больше 2, а другой — меньше .

Найти все значения параметра , при которых только один корень уравнения удовлетворяет неравенству .

Ответ: или .

Теорема 4. Для того чтобы оба корня квадратного трёхчлена лежали в интервале (d: p), (рис.4) необходимо и достаточно выполнение условий

(4)

Пример. При каких значениях параметра а оба корня уравнения удовлетворяют условию 1<x<3?

Решив систему, получим ответ

Задачи для самостоятельного решения

При каких значениях параметра а оба корня уравнения удовлетворяют условию ?

Ответ: .

При каких значениях параметра а, все решения уравнения удовлетворяют условию .

Ответ: при все решения уравнения удовлетворяют условию .

При каких значениях параметра а все решения уравнения удовлетворяют условию ?

Ответ: при все решения уравнения удовлетворяют условию .

При каких значениях параметра корни уравнения принадлежат промежутку (-1; 1)?

Ответ: при корни уравнения лежат на промежутке (-1; 1).

Найти все значения параметра при которых оба корня квадратного уравнения по модулю не превосходят 2.

Ответ: при корни уравнения не превосходят по модулю 2.

При каких значениях параметра все решения уравнения удовлетворяют условию .

Ответ: при или .

Определите все значения параметра k, чтобы один из корней уравнения был меньше нуля, а другой — больше 1?

Ответ: при .

При каких значениях параметра корни уравнения принадлежат промежутку (-1; 1)?

Ответ: при корни уравнения лежат на промежутке (-1; 1).

Найти все значения параметра , при которых оба корня квадратного уравнения по модулю не превосходят 2.

Ответ: при корни уравнения не превосходят по модулю 2.

При каких значениях параметра все решения уравнения удовлетворяют условию .

Ответ: при или .

Теорема 5 . Для того чтобы отрезок [d; p] лежал в интервале (x₁; x₂), (рис.5) необходимо и достаточно выполнение условий

или (5)

Задачи для самостоятельного решения

Найти все значения параметра , при которых один корень уравнения меньше 1, а другой больше 2.

Ответ: при один корень уравнения меньше 1, а другой больше 2.

Найти все значения параметра при которых корни квадратного уравнения удовлетворяют условию .

Ответ: при .

При каких значениях параметра корни уравнения не находятся на промежутке [-1; 1]?

Ответ: при корни уравнения не лежат на промежутке [-1; 1].

Определите все значения параметра k, чтобы один из корней уравнения был меньше нуля, а другой — больше 1?

Ответ: при .

Домашнее задание.

Выбрать и решить пять уравнений из разных разделов.
xn--i1abbnckbmcl9fb.xn--p1ai

РубрикаПолезно знать