Корень в степени 3 – Корень в степени 3 — как решить корень из 8 в степени 2/3. Мне нужно подробное решение. — 22 ответа

Корни и степени. Квадратный корень, кубический корень.

Степенью называется выражение вида .

Здесь  — основание степени,  — показатель степени.

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

По определению, .

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

.

Возвести число в куб — значит умножить его само на себя три раза.

.

Возвести число в натуральную степень  — значит умножить его само на себя раз:

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

По определению,

.

Это верно для . Выражение  не определено.

Определим также, что такое степень с целым отрицательным показателем.

Конечно, все это верно для , поскольку на ноль делить нельзя.

Например,

Заметим, что при возведении в минус первую степень дробь переворачивается.

Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где  — целое,  — натуральное.

Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.

Арифметический квадратный корень

Уравнение  имеет два решения:  и .

Это числа, квадрат которых равен .

А как решить уравнение ?

Если мы нарисуем график функции , то увидим, что и у этого уравнения есть два решения, одно из которых положительно, а другое отрицательно.

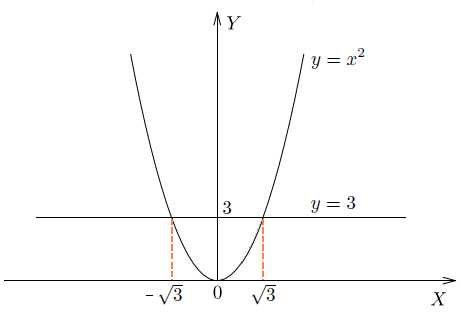
Но эти решения не являются целыми числами. Более того, они не являются рациональными. Для того чтобы записать эти решения, мы вводим специальный символ квадратного корня.

Арифметический квадратный корень из числа  — это такое неотрицательное число, квадрат которого равен .

Запомните это определение.

Арифметический квадратный корень обозначается .

Например,

Обратите внимание:

1) Квадратный корень можно извлекать только из неотрицательных чисел

2) Выражение всегда неотрицательно. Например, .

Перечислим свойства арифметического квадратного корня:

1.

2.
3.

Запомним, что выражение не равно . Легко проверить:

— получился другой ответ.

Кубический корень

Аналогично, кубический корень из  — это такое число, которое при возведении в третью степень дает число .

Например, , так как ;

, так как ;

, так как .

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Теперь мы можем дать определение корня -ной степени для любого целого .

Корень -ной степени

Корень -ной степени из числа  — это такое число, при возведении которого в -ную степень получается число .

Например,

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.

По определению,

в общем случае .

Сразу договоримся, что основание степени больше .

Например,

Выражение по определению равно .

При этом также выполняется условие, что больше .

Например,

Запомним правила действий со степенями:

— при перемножении степеней показатели складываются

— при делении степени на степень показатели вычитаются

— при возведении степени в степень показатели перемножаются

Ты нашел то, что искал? Поделись с друзьями!

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

1.

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

2.

3.

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Решение корней в онлайн калькуляторе

Решение корней — одна из многих функций, которой обладает бесплатный калькулятор, размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.

Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени калькулятор онлайн посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.д.

Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.

Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.

Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.

Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице кнопки калькулятора онлайн.

Извлечение квадратного корня

Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.

Пример решения квадратных корней в калькуляторе:

Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.

Квадратный корень из отрицательного числа:

Корень третьей степени

Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).

Корень 3 степени:

Корень степени n

Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).

Корень 4 степени:

Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.

Корень 5 степени с приблизительным результатом:

Корень из дроби

Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.

Квадратный корень из дроби:

Корень из корня

В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.

Пример, как извлечь корень из корня:

Степень в корне

Выполняя извлечение корня степени, следует помнить, что по свойству корней степень самого корня и степень под корнем по возможности сокращаются на наибольший общий делитель (НОД). Кстати, функционал калькулятора включает также нахождение НОД, подробнее на странице дополнительные функции.

Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.

Квадратный корень из степени:

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Решение корней в онлайн калькуляторе was last modified: Март 3rd, 2016 by Admin

compuzilla.ru

Возведение в степень и извлечение корня из числа онлайн.

Корень нечётной степени из положительного числа

В результате вычисления корня нечётной степени из положительного числа будет положительное число: .

Пример Вычислим корни нечётной степени из 8, 27, 125, 243

Корни 3 степени также называют кубическими корнями.

В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.

Корень нечётной степени из отрицательного числа

В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .

Пример Найдем корни 3 и 5 степеней из отрицательных чисел.

Корень четной степени из положительного числа

Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .

Пример Вычислим корни 2 и 4 степени.

Корень 2-й степени называют квадратный корнем.

Корень четной степени из отрицательного числа

Корень четной степени из отрицательного числа не существует для вещественных чисел.

Корень любой степени из нуля

calcs.su

Корень в 3 степени из 81. Сколько будет?

Действие, в результате которого находится/отыскивается корень, называется извлечением корня. Извлечение корня обратно возведению в степень, так как посредством этого действия отыскивается то, что дано при возведении в степень — основание степени, а дано то, что при возведении в степень отыскивается — сама степень. Потому правильность извлечения корня проверяется возведением в степень.

число n, означающее, какой степени находится корень, называется показателем корня. То есть: выражение b возведенное в степень n равняется выражению a, где b и a неотрицательные числа.

число а, стоящее под знаком корня/радикала, называется подкоренным выражением

число b, искомое число, называется арифметическим корнем n-ой степени

Корень 3/третьей степени называется кубическим корнем.

Очень просто найти значение корней, воспользовавшись онлайн калькуляторами , указав в окошечках показателя степени и подкоренного выражения заданные значения. Там же есть и таблицы, с помощью которых так же просто найти значение корня по заданным степени и числу

Онлайн калькулятор: koreniz.ru

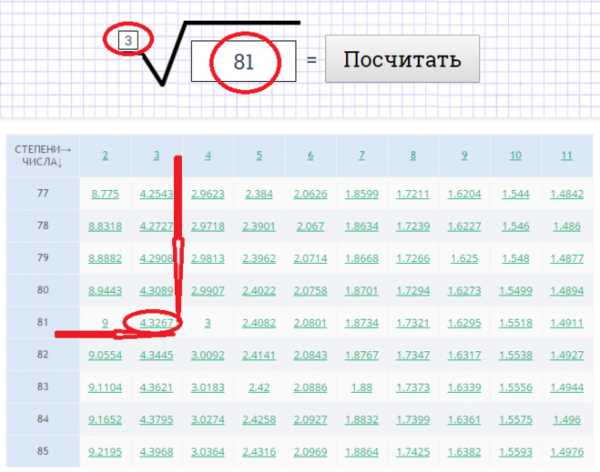
Онлайн калькулятор: vsekorni.ru

В данном случае:

число 81 — подкоренное число

число 3 — показатель степени корня

число 4,3267487 — корень

Для того, чтобы найти это значение, можно воспользоваться 2 свойствами корней:

1) подкоренное выражение можно разлагать на множители.

2) значения корня любого множителя можно выносить за знак радикала.

---

Вот, что получится:

куб. из 81 = куб. из 3*3*3*3 = куб. из 27*3.

27 — это куб числа 3, соответственно куб. из 27 = 3 и его можно вынести за знак корня.

Осталось найти кубический корень из числа 3.

Можно воспользоваться специальным калькулятором, таблицами Брадиса или обычным подбором.

куб. из 3 будет равен числу 1,442.

Соответственно, искомое значение равно следующему произведению:

куб. из 81 = куб. из 27 * куб. из 3 = 3*1,442 = 4,32.

info-4all.ru

Корень степени n

15 января 2017

Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)

У вас тоже так? Читайте дальше — и всё поймёте

Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)

Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.

Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:

Корни бывают чётной степени (наш любимый $\sqrt{a}$, а также всякие $\sqrt[4]{a}$ и даже $\sqrt[116]{a}$ ) и нечётной степени (всякие $\sqrt[3]{a}$, $\sqrt[7]{a}$ и т.д.). И определение корня нечётной степени несколько отличается от чётной.

Вот в этом грёбаном «несколько отличается» скрыто, наверное, 95% всех ошибок и недопонимания, связанного с корнями. Поэтому давайте раз и навсегда разберёмся с терминологией:

Определение. Корень чётной степени n из числа $a$ — это любое неотрицательное число $b$ такое, что ${{b}^{n}}=a$. А корень нечётной степени из того же числа $a$ — это вообще любое число $b$, для которого выполняется всё то же равенство: ${{b}^{n}}=a$.

В любом случае корень обозначается вот так:

\[b=\sqrt[n]{a}\]

Число $n$ в такой записи называется показателем корня, а число $a$ — подкоренным выражением. В частности, при $n=2$ получим наш «любимый» квадратный корень (кстати, это корень чётной степени), а при $n=3$ — кубический (степень нечётная), который тоже часто встречается в задачах и уравнениях.

Примеры. Классические примеры квадратных корней:

\[\begin{align} & \sqrt{4}=2; \\ & \sqrt{81}=9; \\ & \sqrt{256}=16. \\ \end{align}\]

Кстати, $\sqrt{0}=0$, а $\sqrt{1}=1$. Это вполне логично, поскольку ${{0}^{2}}=0$ и ${{1}^{2}}=1$.

Кубические корни тоже часто встречаются — не надо их бояться:

\[\begin{align} & \sqrt[3]{27}=3; \\ & \sqrt[3]{-64}=-4; \\ & \sqrt[3]{343}=7. \\ \end{align}\]

Ну, и парочка «экзотических примеров»:

\[\begin{align} & \sqrt[4]{81}=3; \\ & \sqrt[5]{-32}=-2. \\ \end{align}\]

Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!

А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.

Зачем вообще нужны корни?

Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?

Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:

\[\begin{align} & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end{align}\]

Ну и так далее. Ладно, ладно: последние две строчки я считал на калькуляторе.:)

Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:

\[5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625\]

Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:

\[5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5={{5}^{6}}=15\ 625\]

Это же очень удобно! Все вычисления сокращаются в разы, и можно не тратить кучу листов пергамента блокнотиков на запись какого-нибудь 5¹⁸³. Такую запись назвали степенью числа, у неё нашли кучу свойств, но счастье оказалось недолгим.

После грандиозной пьянки, которую организовали как раз по поводу «открытия» степеней, какой-то особо упоротый математик вдруг спросил: «А что, если нам известна степень числа, но неизвестно само число?» Вот, действительно, если нам известно, что некое число $b$, допустим, в 5-й степени даёт 243, то как нам догадаться, чему равно само число $b$?

Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. Потому что выяснилось, что для большинства «готовых» степеней таких «исходных» чисел нет. Судите сами:

\[\begin{align} & {{b}^{3}}=27\Rightarrow b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & {{b}^{3}}=64\Rightarrow b=4\cdot 4\cdot 4\Rightarrow b=4. \\ \end{align}\]

А, что если ${{b}^{3}}=50$? Получается, что нужно найти некое число, которое будучи трижды умноженное само на себя даст нам 50. Но что это за число? Оно явно больше 3, поскольку 3³ = 27 < 50. С тем же успехом оно меньше 4, поскольку 4³ = 64 > 50. Т.е. это число лежит где-то между тройкой и четвёркой, но чему оно равно — фиг поймёшь.

Именно для этого математики и придумали корни $n$-й степени. Именно для этого ввели значок радикала $\sqrt{*}$. Чтобы обозначить то самое число $b$, которое в указанной степени даст нам заранее известную величину

\[\sqrt[n]{a}=b\Rightarrow {{b}^{n}}=a\]

Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.

Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:

\[\sqrt{2}=1,414213562…\]

Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:

\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]

Или вот ещё пример:

\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]

Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).

Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.

Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.

Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.

Пример.

\[\begin{align} & \sqrt{2+\sqrt[3]{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt[3]{\sqrt[5]{-32}}=\sqrt[3]{-2}\approx -1,2599… \\ \end{align}\]

Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. Впрочем, можно, посчитать на калькуляторе, но даже самый совершенный калькулятор дат нам лишь несколько первых цифр иррационального числа. Поэтому гораздо правильнее записать ответы в виде $\sqrt{5}$ и $\sqrt[3]{-2}$.

Именно для этого их и придумали. Чтобы удобно записывать ответы.

Почему нужны два определения?

Внимательный читатель уже наверняка заметил, что все квадратные корни, приведённые в примерах, извлекаются из положительных чисел. Ну, в крайнем случае из нуля. А вот кубические корни невозмутимо извлекаются абсолютно из любого числа — хоть положительного, хоть отрицательного.

Почему так происходит? Взгляните на график функции $y={{x}^{2}}$:

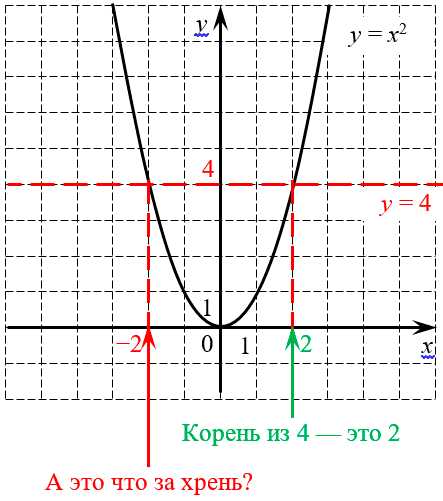График квадратичной функции даёт два корня: положительный и отрицательный

Попробуем с помощью этого графика посчитать $\sqrt{4}$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:${{x}_{1}}=2$ и ${{x}_{2}}=-2$. Это вполне логично, поскольку

\[x=\pm 2\Rightarrow {{x}^{2}}=4\]

С первым числом всё понятно — оно положительное, поэтому оно и есть корень:

\[\sqrt{4}=2\]

Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)

В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.

Подобная проблема возникает у всех корней с чётным показателем:

1. Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
2. Из отрицательных чисел корень с чётным $n$ вообще не извлекается.

Именно поэтому в определении корня чётной степени $n$ специально оговаривается, что ответ должен быть неотрицательным числом. Так мы избавляемся от неоднозначности.

Зато для нечётных $n$ такой проблемы нет. Чтобы убедиться в этом, давайте взглянем на график функции $y={{x}^{3}}$:

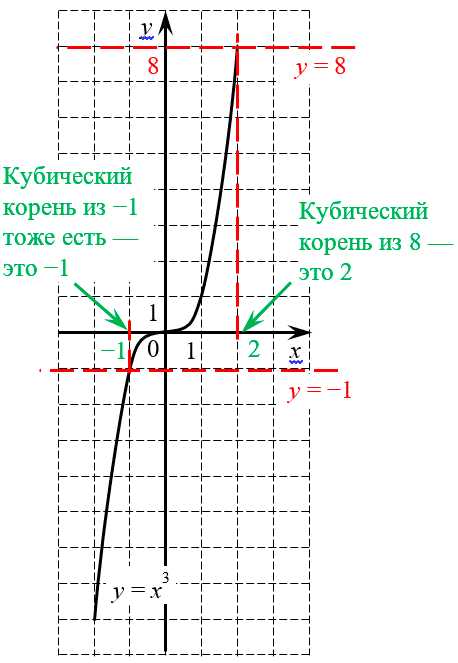Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа

Из этого графика можно сделать два вывода:

1. Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
2. Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).

Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.

Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.

Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.

А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:

1. Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
2. А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.

Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.

Основные свойства и ограничения

У корней много странных свойств и ограничений — об этом будет отдельный урок. Поэтому сейчас мы рассмотрим лишь самую важную «фишку», которая относится лишь к корням с чётным показателем. Запишем это свойство в виде формулы:

\[\sqrt[2n]{{{x}^{2n}}}=\left| x \right|\]

Другими словами, если возвести число в чётную степень, а затем из этого извлечь корень той же степени, мы получим не исходное число, а его модуль. Это простая теорема, которая легко доказывается (достаточно отдельно рассмотреть неотрицательные $x$, а затем отдельно — отрицательные). О ней постоянно талдычат учителя, её дают в каждом школьном учебнике. Но как только дело доходит до решения иррациональных уравнений (т.е. уравнений, содержащих знак радикала), ученики дружно забывают эту формулу.

Чтобы детально разобраться в вопросе, давайте на минуту забудем все формулы и попробуем посчитать два числа напролом:

\[\sqrt[4]{{{3}^{4}}}=?\quad \sqrt[4]{{{\left( -3 \right)}^{4}}}=?\]

Это очень простые примеры. Первый пример решит большинство людишек, а вот на втором многие залипают. Чтобы без проблем решить любую подобную хрень, всегда учитывайте порядок действий:

1. Сначала число возводится в четвёртую степень. Ну, это как бы несложно. Получится новое число, которое даже в таблице умножения можно найти;
2. И вот уже из этого нового числа необходимо извлечь корень четвёртой степени. Т.е. никакого «сокращения» корней и степеней не происходит — это последовательные действия.

Раберёмся с первым выражением: $\sqrt[4]{{{3}^{4}}}$. Очевидно, что сначала надо посчитать выражение, стоящее под корнем:

\[{{3}^{4}}=3\cdot 3\cdot 3\cdot 3=81\]

Затем извлекаем корень четвёртой степени из числа 81:

\[\sqrt[4]{81}=3\]

Теперь сделаем то же самое со вторым выражением. Сначала возводим число −3 в четвёртую степени, для чего потребуется умножить его само на себя 4 раза:

\[{{\left( -3 \right)}^{4}}=\left( -3 \right)\cdot \left( -3 \right)\cdot \left( -3 \right)\cdot \left( -3 \right)=81\]

Получили положительное число, поскольку общее количество минусов в произведении — 4 штуки, и они все взаимно уничтожится (ведь минус на минус даёт плюс). Дальше вновь извлекаем корень:

\[\sqrt[4]{81}=3\]

В принципе, эту строчку можно было не писать, поскольку и ежу понятно, что ответ получится один и тот же. Т.е. чётный корень из той же чётной степени «сжигает» минусы, и в этом смысле результат неотличим от обычного модуля:

\[\begin{align} & \sqrt[4]{{{3}^{4}}}=\left| 3 \right|=3; \\ & \sqrt[4]{{{\left( -3 \right)}^{4}}}=\left| -3 \right|=3. \\ \end{align}\]

Эти вычисления хорошо согласуются с определением корня чётной степени: результат всегда неотрицателен, да и под знаком радикала тоже всегда стоит неотрицательное число. В противном случае корень не определён.

Замечание по поводу порядка действий

Прежде чем мы двинемся дальше, хотел бы отметить, что выражения $\sqrt{{{a}^{2}}}$ и ${{\left( \sqrt{a} \right)}^{2}}$, столь похожие на первый взгляд, на самом деле имеют принципиально разный смысл. Судите сами:

1. Запись $\sqrt{{{a}^{2}}}$ означает, что мы сначала возводим число $a$ в квадрат, а затем извлекаем из полученного значения квадратный корень. Следовательно, мы можем быть уверены, что под знаком корня всегда сидит неотрицательное число, поскольку ${{a}^{2}}\ge 0$ в любом случае;
2. А вот запись ${{\left( \sqrt{a} \right)}^{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.

Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.

Впрочем, все эти проблемы актуальны лишь для чётных показателей.

Вынесение минуса из-под знака корня

Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:

\[\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}\]

Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:

\[\begin{align} & \sqrt[3]{-8}=-\sqrt[3]{8}=-2; \\ & \sqrt[3]{-27}\cdot \sqrt[5]{-32}=-\sqrt[3]{27}\cdot \left( -\sqrt[5]{32} \right)= \\ & =\sqrt[3]{27}\cdot \sqrt[5]{32}= \\ & =3\cdot 2=6. \end{align}\]

Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.

И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!

Арифметический корень

Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?

А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них.

Определение. Арифметическим корнем $n$-й степени из неотрицательного числа $a$ называется такое неотрицательное число $b$, что ${{b}^{n}}=a$.

Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.

Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:

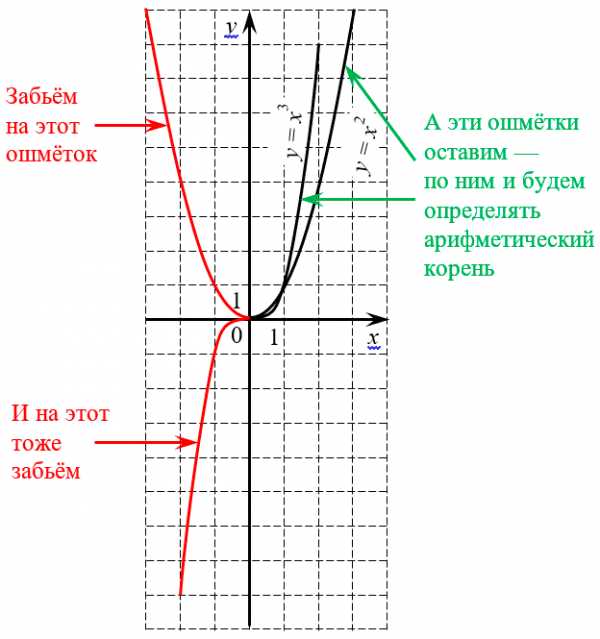Область поиска арифметического корня — неотрицательные числа

Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.

Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»

Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. Например, правило возведения в степень:

\[\sqrt[n]{a}=\sqrt[n\cdot k]{{{a}^{k}}}\]

Обратите внимание: мы можем возвести подкоренное выражение в любую степень и одновременно умножить на эту же степень показатель корня — и в результате получится то же самое число! Вот примеры:

\[\begin{align} & \sqrt[3]{5}=\sqrt[3\cdot 2]{{{5}^{2}}}=\sqrt[6]{25} \\ & \sqrt{2}=\sqrt[2\cdot 4]{{{2}^{4}}}=\sqrt[8]{16} \\ \end{align}\]

Ну и что в этом такого? Почему мы не могли сделать это раньше? А вот почему. Рассмотрим простое выражение: $\sqrt[3]{-2}$ — это число вполне нормальное в нашем классическом понимании, но абсолютно недопустимо с точки зрения арифметического корня. Попробуем преобразовать его:

$\begin{align} & \sqrt[3]{-2}=-\sqrt[3]{2}=-\sqrt[3\cdot 2]{{{2}^{2}}}=-\sqrt[6]{4} \lt 0; \\ & \sqrt[3]{-2}=\sqrt[3\cdot 2]{{{\left( -2 \right)}^{2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$

Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.

WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.

Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.

Алгебраический корень: для тех, кто хочет знать больше

Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному.

Так вот: помимо «классического» определения корня $n$-й степени из числа и связанного с ним разделения на чётные и нечётные показатели есть более «взрослое» определение, которое вообще не зависит от чётности и прочих тонкостей. Это называется алгебраическим корнем.

Определение. Алгебраический корень $n$-й степени из числа любого $a$ — это множество всех чисел $b$ таких, что ${{b}^{n}}=a$. Для таких корней нет устоявшегося обозначения, поэтому просто поставим чёрточку сверху:

\[\overline{\sqrt[n]{a}}=\left\{ b\left| b\in \mathbb{R};{{b}^{n}}=a \right. \right\}\]

Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:

1. Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
2. Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
3. Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.

Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.

Пример. Вычислите выражения:

\[\overline{\sqrt{4}};\quad \overline{\sqrt[3]{-27}};\quad \overline{\sqrt[4]{-16}}.\]

Решение. С первым выражением всё просто:

\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]

Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.

\[\overline{\sqrt[3]{-27}}=\left\{ -3 \right\}\]

Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.

Наконец, последнее выражение:

\[\overline{\sqrt[4]{-16}}=\varnothing \]

Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.

Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt[4]{-16}$, и многие другие странные вещи.

Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».

На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)

Смотрите также:

1. Как умножать корни с произвольными показателями?
2. Сложные иррациональные уравнения — что с ними делать и как их решать?
3. Тест к уроку «Простые проценты» (легкий)
4. Сводный тест по задачам B12 (2 вариант)
5. Репетитор по математике как психолог
6. Тест по задачам B14: легкий уровень, 1 вариант

www.berdov.com

Как извлечь корень третьей степени

Операции извлечения корня, в которых показателем служат числа два и три имеют собственные названия — квадратный и кубический корни. Если у вас есть возможность пользоваться компьютером, то наиболее простой способ извлечения из произвольного числа корня третьей степени (кубического) — задействовать программный калькулятор ОС.

Инструкция

• Нажмите кнопку win, чтобы раскрыть главное меню операционной системы. Пункт, нужный для запуска искомого приложения («Калькулятор»), может присутствовать в главном разделе этого меню. Если же вы его там не увидите, то раскройте подраздел «Все программы», а в нем папку «Стандартные». В этой папке есть вложенная папка «Служебные» — откройте ее и выберите этот самый пункт «Калькулятор».
• Есть другие способы запуска этого приложения. Например, в ОС Windows 7 вы можете открыть главное меню и набрать «кальк» в поле «Найти программы и файлы», а затем выбрать строку «Калькулятор» среди результатов поиска. В любой версии Windows можно нажать сочетание клавиш win + r, чтобы открыть стандартный диалог запуска программ, ввести команду calc и нажать клавишу enter или щелкнуть по кнопке OK.
• В зависимости от версии используемой операционной системы в калькуляторе может существовать два варианта вычисления кубического корня. В более ранних (например, Windows XP) вам необходимо переключить интерфейс калькулятора в «научный» или «инженерный» вариант, выбрав соответствующий пункт в разделе «Вид» меню калькулятора. Затем введите подкоренное выражение и поставьте отметку в поле с надписью Inv — этот чекбокс отвечает за инвертирование функций, обозначенных на управляющих кнопках интерфейса приложения. Кликните по кнопке возведения в третью степень (x^3) и вычислитель рассчитает и покажет результат обратной операции — извлечения кубического корня из введенного числа.
• В более поздних версиях ОС (например, Windows 7) достаточно ввести число, из которого следует извлечь корень третьей степени, и кликнуть по соответствующей кнопке на экране — на ней есть надпись ³√x. Переключать калькулятор в «инженерный» интерфейс здесь не требуется.

completerepair.ru