Корень квадратный корень кубический – Квадратный, кубический и другие корни в Excel с примерами — MS Office Excel — Работа на компьютере: инструкции и советы — Образование, воспитание и обучение

Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.

Алгоритм извлечения кубического корня

Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.

1. Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
2. Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
3. Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a²× x+30× a × x²+x³ такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
4. Запишите под нижним числом результат вычисления по формуле 300 × a² × x+30 × a × x²+x
   3 и произведите вычитание. Перейдите к пункту 3.

wpcalc.com

Простые и не очень способы того, как вычислить кубический корень :: SYL.ru

Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.

Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.

Что нужно знать о корне произвольной степени?

Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».

Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.

Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.

Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.

Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.

Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «аⁿ».

В-третьих, для них справедливы все действия со степенями.

• Их можно перемножать. Тогда показатели степеней складываются.
• Корни можно разделить. Степени нужно будет вычесть.
• И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.

В чем сходства и различия квадратного и кубического корней?

Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.

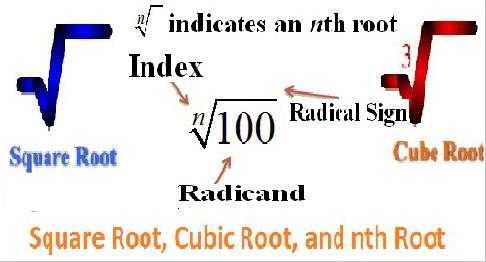
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.

Извлечение кубического корня на калькуляторе

Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?

На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.

А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».

Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

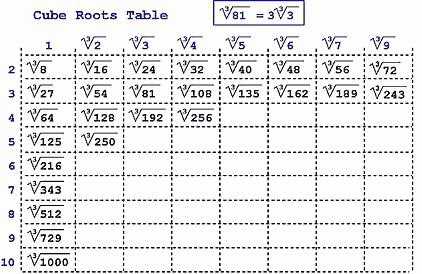
В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.

1. Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
2. Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
3. Выполнить вычитание.
4. К остатку приписать первую группу цифр после запятой.
5. В черновике записать выражение: а² * 300 * х + а * 30 * х² + х³. Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
6. Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
7. Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.

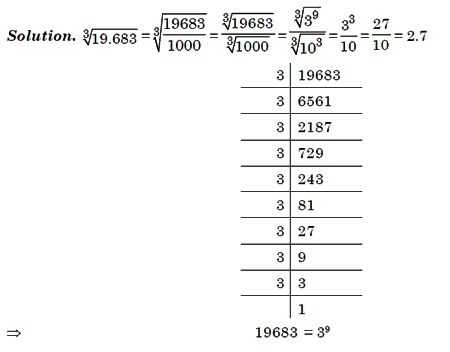
Наглядный пример вычисления кубического корня

Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.

Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.

1. 15> 2³, значит под целой частью записана 8, а над корнем 2.
2. После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
3. а = 2. Поэтому: 2² * 300 * х +2 * 30 * х² + х³ < 7000, или 1200 х + 60 х² + х³< 7000.
4. Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
5. Вычитание дает 1176, а над корнем появилось число 4.
6. Приписать к остатку три нуля.
7. а = 24. Тогда 172800 х + 720 х² + х³< 1176000.
8. х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
9. Снова приписать нули.
10. а = 246. Неравенство получается таким: 18154800х + 7380х² + х³< 113064000.
11. х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.

Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.

Необычный способ извлечения кубического корня

Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.

К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.

Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.

Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.

www.syl.ru

Кубический корень

  Кубический корень. Как извлечь квадратный корень из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:

Совсем немного, а если потренируетесь  два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.

*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.

Мы знаем, что:

Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):

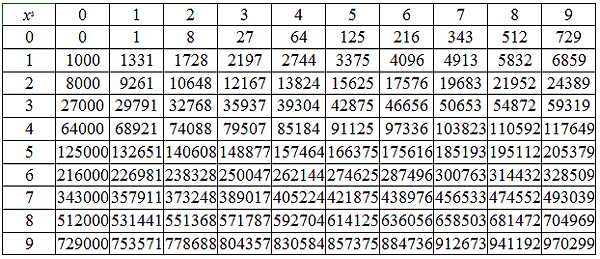
Вы без труда  сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?

1. Это кубы чисел кратных десяти:

Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.

2. Это свойство чисел при произведении.  

Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?

Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.

1³ = 1,   11³ = 1331,   21³ = 9261,   31³ = 26791,   41³ = 68921   …

То есть, при возведении в куб числа с единицей на конце в результате  у нас всегда получится число с единицей в конце.

При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.

Покажем соответствие в табличке для всех чисел:

Знания представленных двух моментов вполне достаточно.

Рассмотрим примеры:

Извлечь кубический корень из 21952.

Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.

Извлечь кубический корень из 54852.

Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.

Извлечь кубический корень из 571787.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.

Извлечь кубический корень из 614125.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.

Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.

Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.

После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉

На самом ЕГЭ задач с такими «страшненькими» корнями  нет. Например, в Задаче 27125 требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.

Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Извлечение кубического корня в столбик

Я уже писала здесь, как можно извлекать в столбик квадратный корень. Однако практически такой же алгоритм, напоминающий деление столбиком (или арабский способ деления) работает и для извлечения корней более высоких степеней. Рассмотрим, как извлекать кубический корень с произвольной точностью, определяя на каждом шаге по одной цифре этого корня. Как и для квадратных корней, буду описывать алгоритм пошагово, и каждый шаг будет сопровождаться примером.

Итак, давайте для примера будем извлекать кубический корень из .

1. Разобьем цифры исходного числа на группы по три цифры в каждой. При этом разбиение начинаем от десятичной запятой, двигаясь влево и вправо.

Пример. В нашем случае разбиение выглядит таким образом: .

2. Извлечем кубический корень из первой слева группы цифр. Разумеется, точно корень может не извлекаться, поэтому возьмем наибольшее число, куб которого меньше числа, образованного данной группой цифр.

Пример. В нашем случае первая слева группа цифр , поэтому первая цифра кубического корня — . Действительно, , а вот уже равно .

3. Возводим найденное число в куб и вычитаем из первой слева группы цифр, к разности приписываем справа следующие три цифры (т.е. цифры следующей группы).

Пример. В нашем случае получаем:

4. Теперь нужно подобрать следующую цифру корня. Для этого квадрат числа, образованного уже имеющимися цифрами, умножаем на и выбираем цифру, при умножении на которую получится число, меньшее, чем число, образованное всеми цифрами разности, кроме двух последних, но достаточно близкое к нему. Однако следует иметь в виду, что если при очередном вычитании получилось отрицательное число, нужно последнюю вычисленную цифру уменьшить на единицу.

Пример. Имеем: , поэтому выбираем цифру (в самом деле, , а ).

5. Умножаем полученное ранее произведение на выбранную цифру, потом еще на , прибавляем к полученному числу квадрат выбранной цифры, умноженный на число, образованное уже найденными цифрами корня, домноженное на , после чего прибавляем еще куб выбранной цифры.

Пример. У нас получится
.

6. Из полученной на шаге 3 разности вычитаем число, полученное на шаге 5.

Пример. В нашем случае это будет .

7. Переходим к шагу 4.

Продолжаем данную последовательность шагов алгоритма до тех пор, пока корень не вычислен с требуемой точностью.

Пример. В нашем случае мы возводим в квадрат и умножаем его на : . Теперь подберем цифру, при умножении на которую числа получим близкое к , но меньшее его число. Эта цифра (). Теперь из числа (разность, полученная на предыдущем шаге и приписанная справа следующая группа цифр) нужно вычесть следующую сумму:

Тем самым, разность будет равна нулю, и корень, который оказался точным, извлечен — это .

Теперь приведу запись, которая при этом получается (разумеется, при реальных вычислениях все скорее всего будет не столь красиво и аккуратно ).

Алгоритм основан на формуле куба суммы: .

Для тех же, кому интересно извлечение корней высших степеней, даю ссылку (правда, материал на английском): http://en.wikipedia.org/wiki/Shifting_nth-root_algorithm.

hijos.ru

Корень из числа: определения, примеры

Квадратный корень, арифметический квадратный корень

Чтобы понять определение корня из числа, и квадратного корня в частности, нужно иметь представление о степени с натуральным показателем. В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.

Начнем с определения квадратного корня

Определение

Квадратный корень из числа a — это число, квадрат которого равен a.

Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (5²=5·5=25, (−0,3)²=(−0,3)·(−0,3)=0,09, (0,3)²=0,3·0,3=0,09 и 0²=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.

Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.

Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.

Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля. Это следует из очевидного равенства 0

Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b²=0, что невозможно, так как при любом отличном от нуля b значение выражения b² является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.

Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b. Допустим, что существует число c, которое тоже является квадратным корнем из a. Тогда по определению квадратного корня справедливы равенства b

Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.

Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.

Определение

Арифметический квадратный корень из неотрицательного числа a – это неотрицательное число, квадрат которого равен a.

Для арифметического квадратного корня из числа a принято обозначение . Знак называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.

Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.

При чтении слово «арифметический» часто опускается, например, запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о положительном квадратном корне из числа.

В свете введенного обозначения из определения арифметического квадратного корня следует, что и для любого неотрицательного числа a.

Квадратные корни из положительного числа a с помощью знака арифметического квадратного корня записываются как и . Например, квадратные корни из числа 13 есть и . Арифметический квадратный корень из нуля равен нулю, то есть, . Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишены смысла выражения и .

На базе определения квадратного корня доказываются свойства квадратных корней, которые часто применяются на практике.

Нахождение квадратных корней заслуживает детального изучения, этой теме посвящена отдельная статья извлечение квадратных корней.

В заключение этого пункта заметим, что квадратные корни из числа a являются решениями квадратного уравнения вида x²=a относительно переменной x.

К началу страницы

www.cleverstudents.ru

Кубический корень — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Куби́ческий ко́рень из a, обозначающийся как <math>\sqrt[3]{a}</math> или как a^1/3 — это число <math>x,</math> куб которого равен <math>a.</math> Другими словами, это решение уравнения <math>x^3 = a</math> (обычно подразумеваются вещественные решения).

Вещественный корень

Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат):

<math>\sqrt[3]{-x} = -\sqrt[3]{x}</math>

Комплексный корень

Кубический корень из комплексного числа (из любого числа) <math>c</math> имеет ровно три значения (частный случай свойства корня n-ой степени):

<math>\sqrt[3]{c} = \sqrt[3]{\left|c\right|} \left( \cos{\frac{\phi + 2k\pi}{3}} + i \sin{\frac{\phi + 2k\pi}{3}} \right), \quad k = 0, 1, 2, \quad \phi = \arg {c}.</math>

Здесь под <math>\sqrt[3]{\left|c\right|}</math> понимается арифметический корень из положительного числа <math>\left|c\right|.</math>

В частности

<math>\sqrt[3]{1} = \begin{cases} 1 \\ \cos{\frac{2\pi}{3}} + i \sin{\frac{2\pi}{3}} = — \frac{1}{2} + i \frac{\sqrt{3}}{2} \\ \cos{\frac{2\pi}{3}} — i \sin{\frac{2\pi}{3}} = — \frac{1}{2} — i \frac{\sqrt{3}}{2} \end{cases}</math>

<math>\sqrt[3]{-1} = \begin{cases} -1 \\ \cos{\frac{\pi}{3}} + i \sin{\frac{\pi}{3}} = \frac{1}{2} + i \frac{\sqrt{3}}{2} \\ \cos{\frac{\pi}{3}} — i \sin{\frac{\pi}{3}} = \frac{1}{2} — i \frac{\sqrt{3}}{2} \end{cases}</math>

Два комплексных значения кубического корня получаются из вещественных по формуле:

<math>\sqrt[3]{x}_{2,3} = \sqrt[3]{x}\left( -\frac{1}{2} \pm i \frac{\sqrt{3}}{2}\right).</math>

Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.

Показательная форма

Корень из комплексных чисел можно определить так:

<math>x^{1/3} = \exp ( \tfrac13 \ln{x} )</math>

Где ln — главная ветвь натурального логарифма.

Если представить <math>x</math> как

<math>x = r \exp(i \theta)</math>

то формула кубического числа такова:

<math>\sqrt[3]{x} = \sqrt[3]{r}\exp ( \tfrac13 i\theta ).</math>

Это геометрически означает, что в полярных координатах мы берем кубический корень радиуса и делим полярный угол на три, для того, чтобы определить кубический корень. Значит, если <math>x</math> комплексное, то <math>\sqrt[3]{-8}</math> будет обозначать не <math>-2</math>, а будет <math>1 + i\sqrt{3}.</math>

Интересные факты

Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.

При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26 %) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.

Способы вычисления

Столбиком

Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.

Алгоритм таков:

1. Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
2. Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
3. Далее найденный промежуточный ответ заменим буквой <math>a</math>. Вычислите по формуле <math>300\times a^2\times x+30\times a\times x^2+x^3</math> такое число <math>x</math>, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное <math>x</math> справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
4. Запишите под нижним числом результат вычисления по формуле <math>300\times a^2\times x+30\times a\times x^2+x^3</math> и произведите вычитание. Перейдите к пункту 3.

См. также

Напишите отзыв о статье «Кубический корень»

Литература

• Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 32—33.

Отрывок, характеризующий Кубический корень

К девяти часам утра, когда войска уже двинулись через Москву, никто больше не приходил спрашивать распоряжений графа. Все, кто мог ехать, ехали сами собой; те, кто оставались, решали сами с собой, что им надо было делать.
Граф велел подавать лошадей, чтобы ехать в Сокольники, и, нахмуренный, желтый и молчаливый, сложив руки, сидел в своем кабинете.
Каждому администратору в спокойное, не бурное время кажется, что только его усилиями движется всо ему подведомственное народонаселение, и в этом сознании своей необходимости каждый администратор чувствует главную награду за свои труды и усилия. Понятно, что до тех пор, пока историческое море спокойно, правителю администратору, с своей утлой лодочкой упирающемуся шестом в корабль народа и самому двигающемуся, должно казаться, что его усилиями двигается корабль, в который он упирается. Но стоит подняться буре, взволноваться морю и двинуться самому кораблю, и тогда уж заблуждение невозможно. Корабль идет своим громадным, независимым ходом, шест не достает до двинувшегося корабля, и правитель вдруг из положения властителя, источника силы, переходит в ничтожного, бесполезного и слабого человека.
Растопчин чувствовал это, и это то раздражало его. Полицеймейстер, которого остановила толпа, вместе с адъютантом, который пришел доложить, что лошади готовы, вошли к графу. Оба были бледны, и полицеймейстер, передав об исполнении своего поручения, сообщил, что на дворе графа стояла огромная толпа народа, желавшая его видеть.
Растопчин, ни слова не отвечая, встал и быстрыми шагами направился в свою роскошную светлую гостиную, подошел к двери балкона, взялся за ручку, оставил ее и перешел к окну, из которого виднее была вся толпа. Высокий малый стоял в передних рядах и с строгим лицом, размахивая рукой, говорил что то. Окровавленный кузнец с мрачным видом стоял подле него. Сквозь закрытые окна слышен был гул голосов.
– Готов экипаж? – сказал Растопчин, отходя от окна.
– Готов, ваше сиятельство, – сказал адъютант.
Растопчин опять подошел к двери балкона.
– Да чего они хотят? – спросил он у полицеймейстера.
– Ваше сиятельство, они говорят, что собрались идти на французов по вашему приказанью, про измену что то кричали. Но буйная толпа, ваше сиятельство. Я насилу уехал. Ваше сиятельство, осмелюсь предложить…
– Извольте идти, я без вас знаю, что делать, – сердито крикнул Растопчин. Он стоял у двери балкона, глядя на толпу. «Вот что они сделали с Россией! Вот что они сделали со мной!» – думал Растопчин, чувствуя поднимающийся в своей душе неудержимый гнев против кого то того, кому можно было приписать причину всего случившегося. Как это часто бывает с горячими людьми, гнев уже владел им, но он искал еще для него предмета. «La voila la populace, la lie du peuple, – думал он, глядя на толпу, – la plebe qu’ils ont soulevee par leur sottise. Il leur faut une victime, [„Вот он, народец, эти подонки народонаселения, плебеи, которых они подняли своею глупостью! Им нужна жертва“.] – пришло ему в голову, глядя на размахивающего рукой высокого малого. И по тому самому это пришло ему в голову, что ему самому нужна была эта жертва, этот предмет для своего гнева.
– Готов экипаж? – в другой раз спросил он.
– Готов, ваше сиятельство. Что прикажете насчет Верещагина? Он ждет у крыльца, – отвечал адъютант.
– А! – вскрикнул Растопчин, как пораженный каким то неожиданным воспоминанием.
И, быстро отворив дверь, он вышел решительными шагами на балкон. Говор вдруг умолк, шапки и картузы снялись, и все глаза поднялись к вышедшему графу.
– Здравствуйте, ребята! – сказал граф быстро и громко. – Спасибо, что пришли. Я сейчас выйду к вам, но прежде всего нам надо управиться с злодеем. Нам надо наказать злодея, от которого погибла Москва. Подождите меня! – И граф так же быстро вернулся в покои, крепко хлопнув дверью.
По толпе пробежал одобрительный ропот удовольствия. «Он, значит, злодеев управит усех! А ты говоришь француз… он тебе всю дистанцию развяжет!» – говорили люди, как будто упрекая друг друга в своем маловерии.

wiki-org.ru

Кубический корень из числа

Практически каждый человек мечтает совершенствоваться, идти к чему-то более серьёзному и сложному. Все делают это по-своему. Одни ищут работу, на которой, со временем займут руководящие места, другие жаждут просто заработать побольше денег. Всегда считалось, что чем умнее человек, тем больших успехов он добьётся. Но есть и те, которые совершенствуют свой ум и оттачивают искусство вычисления. Кубический корень (его вычисление) – один из распространенных способов “привести мозги в порядок”.

Издревле считалось, что тренировка ума — это путь к обретению мудрости. Древние греки, которые достигли огромных высот в математике, говорили, что ”каждый человек рожден мудрецом, но не каждый его может отыскать внутри себя”. В последнее время стало очень популярно развивать умение проводить сложные, а иногда и громоздские вычисления в уме. Кубический корень, вычислить который не так просто, если число достаточно большое – один из способов. Существует несколько распространенных вариантов, как извлечь кубический корень из числа. Рассмотрим парочку.

Способ номер 1

Иногда можно встретить афиши, гласящие, что один человек проводит в уме сложнейшие вычисления, в том числе и вычисления кубического корня. Какое-то время, было непонятно, как это делается, но вот алгоритм вычисления известен, и каждый может блеснуть своими умениями.

Извлечение кубического корня проводится путем “отсечения от числа”. Сначала нужно запомнить одну простую закономерность: последние цифры и результат возведения в куб, для некоторых чисел, а именно 1, 4, 5, 6 и 9 одинаковы. Давайте рассмотрим конкретный пример. Предположим, нам нужно извлечь кубический корень из числа 85 184. Рассмотрим самую большую группу в данном числе – тысячи, это 85. Какое число, в кубе даст наиболее близкое значение к 85 но при этом не превзойдет его? Это число 4. Теперь рассмотрим оставшиеся числа 184. Заметьте, что оно заканчивается на 4. Единственное однозначное число, которое дает при возведении в 3-ю степень 4-ку в конце многозначного числа, это число 4. Выходит, что ответом на вопрос является число 44. Умножаем его на самого себя 2 раза (44x44x44) и получаем 85184.

Способ номер 2

Кубический корень можно извлечь и с помощью разложения числа в ряд Тейлора. Однако этот вариант намного сложнее, чем предыдущий. Нам понадобится чёткое знание формулы разложения, и все операции нужно будет вычислять уже не в уме, а на бумаге. Так как кубический корень — это возведение числа в степень 1/3, то проведем вычисления с возведением числа 5. Разложив это число в ряд Тейлора, получим ответ, с мизерной погрешностью. Однако вычислений пришлось проводить немало. Поэтому такой способ не самый выгодный с точки зрения экономии времени. Ведь если число очень большое, то потребуется приложить много усилий для решения

Есть конечно ещё один способ, калькулятор. На инженерных калькуляторах есть возможность одним нажатием кнопки извлечь корень кубический из числа. Как уже было сказано выше, способов извлечения кубического корня из числа очень много. И все время находятся энтузиасты, которые пробуют все новые и новые варианты. Сейчас, при желании, можно найти таблицы со значением кубических корней всех чисел. Вы можете сами, забавы ради или для «разминки мозгов», составить свою таблицу. Конечно, это дело не одного дня, однако подобное времяпрепровождение можно превратить в интересное и достаточно редкое хобби. Ведь счет, неважно какой, — это очень хорошая тренировка для ума. Самое главное — это не то, как и что вы считаете, а то делаете ли вы это вообще. Все люди уникальны, существуют уникумы, которые в уме производят все сложнейшие вычисления. Дар этот у них от природы. Все же остальные могут развивать в себе эти способности. Старайтесь, и быть может вы следующим, кто придумает очередной способ того, как вычислить кубический корень из числа.

fb.ru