Корень из степени числа – CGI script error

Содержание

Лекция 7. Корни натуральной степени из числа.

Корнем степени n из действительного числа a, где n — натуральное число, называется такое действительное число x, n-ая степень которого равна a.

Корень степени n из числа a обозначается символом . Согласно этому определению .

Нахождение корня n-ой степени из числа a называется извлечением корня. Число аназывается подкоренным числом (выражением), n — показателем корня. При нечетном n существует корень n-ой степени для любого действительного числа a. При четном n существует корень n-ой степени только для неотрицательного числаa. Чтобы устранить двузначность корня n-ой степени из числа a, вводится понятие арифметического корня n-ой степени из числа a.

Понятие арифметического корня степени N

Если и n

— натуральное число, большее 1, то существует, и только одно, неотрицательное число х, такое, что выполняется равенство . Это число хназывается арифметическим корнем n-й степени из неотрицательного числа а и обозначается . Число а называется подкоренным числом, n — показателем корня.

Итак, согласно определению запись , где , означает, во-первых, что и, во-вторых, что , т.е. .

Понятие степени с рациональным показателем

Степень с натуральным показателем: пусть а — действительное число, а n — натуральное число, большее единицы, n-й степенью числа а называют произведение n множителей, каждый из которых равен а, т.е. . Число а — основание степени,

n — показатель степени. Степень с нулевым показателем: полагают по определению, если , то . Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если и n — натуральное число, то . Степень с дробным показателем: полагают по определению, если и n — натуральное число, m — целое число, то .

Операции с корнями.

Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и одновременно возвести в n-ую степень подкоренное число, то значение корня не изменится:

5. Если уменьшить степень корня в n раз и одновременно извлечь корень n-ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.

Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной величине отрицательного показателя:

Теперь формула a ^m : a ⁿ = a ^{m — n}может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .

П р и м е р . a⁴ : a⁷ = a ^{4 — 7} = a ^-3 .

Если мы хотим, чтобы формула a ^m : a ⁿ = a ^m^{— n} была справедлива при m = n , нам необходимо определение нулевой степени.

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы . 2 ⁰ = 1, ( – 5 )⁰ = 1, ( – 3 / 5 ) ⁰= 1.

Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n–ой степени из m-ой степени этого числа а :

О выражениях, не имеющих смысла. Есть несколько таких выражений.

Случай 1.

где a ≠ 0 , не существует.

В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит условию: a ≠ 0

Случай 2.

— любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x, то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x, что и требовалось доказать.

Случай 3

Если считать, что правила действий со степенями распространяются и на степени с нулевым основанием, то 0 ⁰ — любое число.

Действительно,

Р е ш е н и е . Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует, что x – любое число; но принимая во внимание, что внашем случае x > 0 , ответом является x > 0 ;

3) при x < 0 получаем: – x / x = 1, т.e. –1 = 1, следовательно,

в этом случае нет решения. Таким образом, x > 0.

[Билет 33] Корень n-й степени из числа. Алгебраический и арифметический корни. Функция √

Корень n-й степени из числа.

Определение корня. Безусловно, все так или иначе знакомы с интуитивным понятием квадратного корня — это такое число, квадрат которого равен a. Аналогично определяется корень n-й степени из числа a, где n — положительное число.

Определение. Корнем n-й степени из числа a называется такое число, n-я степень которого равна a.

Согласно данному определению корень n-й степени из числа а — это решение уравнения xn=a. Число корней этого уравнения зависит от n и от а.

Рассмотрим функцию f(x)=x^n. Как известно, на промежутке [0; ∞) эта функция при любом n возрастает и принимает все значения промежутка [0; inf). По теореме о корне уравнение xn=a для любого а, принадлежащего промежутку [0; ∞), имеет неотрицательный корень и только один. Его называют арифметическим корнем n-й степени из числа n и обозначают n√a Число n называют показателем корня, а само число a — подкоренным выражением. Знак корня √ так же называют радикалом.

Алгебраический и арифметический корни.

Арифметическим корнем n–й степени из неотрицательного числа a называется неотрицательное число, n–я степень которого равна a .

Алгебраическим корнем n–й степени из данного числа называется множество всех корней из этого числа. Алгебраический корень чётной степени имеет два значения: положительное и отрицательное, например:

Функция √

Квадратный корень из числа a — это такое число, квадрат которого (результат умножения на себя) равен a, то есть решение уравнения x² = aотносительно переменной x

Квадратный корень как элементарная функция

График функции y=x Квадратным корнем называют также функцию x вещественной переменной x, которая каждому x0 ставит в соответствие арифметическое значение корня. Свойства функции y=x
Свойства функции y=3x
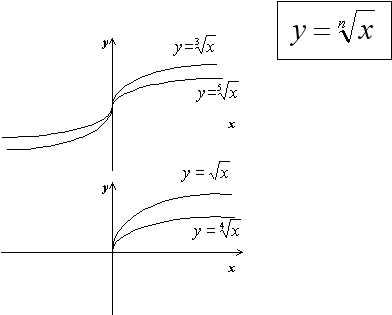
Функция y=nx .

Степенная функция с положительным дробным показателем.

Степенная функция с положительным дробным показателем это функция, заданная формулой y = x^r, где r — положительная несократимая дробь.

Свойства функции y = x^r:

Область определения — луч [о;+) .
Функция общего вида, т.е. ни четная, ни нечетная.
Функция y = x^r возрастает на [о;+) .

На пример график функции y = x^5/2, заключен между графиками функций y = x² и y = x³, заданных на промежутке
[о;+) .
Подобный вид имеет любой график функции вида y = x^r, где r > 1, а график любой степенной функции y = x^r, где 0r y = x^2/3.

Степенная функция с отрицательным дробным показателем.

Степенная функция с отрицательным дробным показателем это функция, заданная формулой y = x ^{— r},
где r — положительная несократимая дробь.

Свойства функции y = x ^{— r}:

Облать определения — промежуток (о;+) .
Функция общего вида, т.е. ни четная, ни нечетная.
Функция y = x ^{— r} убывает на (о;+) .
График функции y = x ^{— r} подобен ветке гиперболы, построенной на положительных значениях аргумента функции.

fizmatinf.blogspot.com

Как представить корень в виде степени

Как представить корень в виде степени?

Для этого нужно от корня перейти к степени с дробным показателем:

В частности,

Например,

Во многих случаях преобразование выражений с корнями проще выполнять, представив корни в виде степеней.

www.algebraclass.ru

Определение корня n-ой степени: извлечение корня

Рассмотрим следующий пример. x⁴=16. Мы можем записать это уравнение в следующем виде:

или используя формулу разности квадратов так:

Произведение двух сомножителей равно нулю, если хотя бы один из них равен нулю.

Выражение x² +4 не может равняться нулю, следовательно, остается только (x²-4)=0.

Решаем его, получаем два ответа.

Ответ: x=-2 и x=2.

Получили, что уравнение x⁴=16 имеет только 2 действительных корня. Это корни четвертой степени из числа 16. Причем положительный корень, называют арифметическим корнем 4 степени из числа 16. И обозначают 4√16. То есть 4√16=2.

Определение

Арифметическим корнем натуральной степени n>=2 из неотрицательного числа а называется некоторое неотрицательное число, при возведении которого в степень n получается число а.

Можно доказать, что для любого неотрицательного а и натурального n уравнение xⁿ=a будет иметь один единственный неотрицательный корень. Именно этот корень и называют арифметическим корнем n-ой степени из числа а.

Арифметический корень n-ой степени из числа а обозначается следующим образом n√a.

Число а в данном случае называется подкоренным выражением.

В случае когда n=2, двойку не пишут, а записывают просто √а.

Арифметические корни второй и третей степени имеют свои специальные названия.

Арифметический корень второй степени называется квадратным корнем, а арифметический корень третей степени – кубическим корнем.

Используя только ишь определение арифметического корня, можно доказать, что n√a равен b. Для этого нужно показать, что:

1. b больше либо равно нулю.
2. bⁿ =a.

Например, 3√(64) = 4, так как 1. 4>0, 2. 4³ =64.

Следствие из определения арифметического корня.

(n√a)ⁿ = a.
n√(aⁿ) = a.

Например, (5√2)⁵ = 2.

Извлечение корня n-ой степени

Извлечением корня n-ой степени называется действие, с помощью которого отыскивается корень n-ой степени. Извлечение корня n-ой степени является обратным действием к возведению в n-ую степень.

Рассмотрим пример.

Решить уравнение x³ = -27.

Перепишем это уравнение в виде (-x)³=27.

Положим у=-х, тогда y³=27. Это уравнение имеет один положительный корень y= 3√27 = 3.

Отрицательных корней у этого уравнения нет, так как y³

Получаем, что уравнение у³ =27 имеет только один корень.

Возвращаясь к исходному уравнению, получаем, что оно имеет тоже только один корень x=-y=-3.

Ответ: х=-3.

Нужна помощь в учебе?

Предыдущая тема: Функция y=x^n: линейная функция, квадратичная, кубическая и y=1/x
Следующая тема:&nbsp&nbsp&nbspСвойства арифметического корня n-ой степени: 5 свойств с доказательством

Все неприличные комментарии будут удаляться.

www.nado5.ru

Корень n-й степени — это… Что такое Корень n-й степени?

Корень (морфология)
Корень (растение)

Смотреть что такое «Корень n-й степени» в других словарях:

КОРЕНЬ — муж. корешек, шечек, коренек ·умалит. корнишка презрительное, корнища увеличительное, подземная часть всякого растения. У деревьев различают становой и боковые корни, а при них корешки и мелкие мочки. вбирающие влагу. Корень бывает: луковичный,… … Толковый словарь Даля
Корень квадратный — Квадратный корень из (корень 2 й степени) это решение уравнения вида . Несмотря на то, что в первую очередь под и подразумеваются числа, в различных рассмотрениях они могут быть математическими объектами различной природы, в том числе такими как … Википедия
Корень (значения) — Корень: В Викисловаре есть статья «корень» Корень (в ботанике) вегетативный осевой подземный орган растения, обладающий сп … Википедия
КОРЕНЬ — (матем.), 1) К. степени п из числа а всякое число х (обозначаемое корень n ой степени из числа a, а наз. подкоренным выражением), п я степень к рого равна а (хn = а). Действие нахождения К. наз. извлечением К. 2) К. ур ния число, к рое после… … Естествознание. Энциклопедический словарь
КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь
Корень алгебраического уравнения — Корень многочлена над полем k элемент , который после подстановки его вместо x обращает уравнение в тождество. Свойства Если c является корнем многочлена p(x … Википедия
Корень уравнения — Корень многочлена над полем k элемент , который после подстановки его вместо x обращает уравнение в тождество. Свойства Если c является корнем многочлена p(x … Википедия
КОРЕНЬ — КОРЕНЬ, корня, мн. корни, корней, м. 1. Вросшая в землю часть растения, через к рую оно всасывает соки из почвы. Бурей выворотило деревья с корнями. Дуб глубоко пустил корни в землю. || Древесина или вещество этой части растения. Лакричный корень … Толковый словарь Ушакова
КОРЕНЬ — в математике ..1) корень степени n из числа a всякое число x (обозначаемое , a называется подкоренным выражением), n я степень которого равна a (). Действие нахождения корня называется извлечением корня2)] Корень уравнения число, которое после… … Большой Энциклопедический словарь
КОРЕНЬ (в математике) — КОРЕНЬ, в математике 1) корень степени n из числа a всякое число x (обозначаемое , a называется подкоренным выражением), n я степень которого равна a (). Действие нахождения корня называется извлечением корня. 2) Корень уравнения число, которое… … Энциклопедический словарь

dic.academic.ru

РубрикаПолезно знать