Компоненты уравнений – Презентация на тему: «1.Основные понятия 2.Компоненты арифметических действий и нахождение неизвестных компонентов — при сложении — при вычитании — при умножении

Срез на знания компонентов уравнения (начальные классы)

Тест на тему «Решение уравнений. Компоненты уравнения»

для учащихся 2-4 классов

1.Для того, чтобы найти неизвестное уменьшаемое, надо:

а) из суммы вычесть известное слагаемое
б) сложить разность и вычитаемое
в) из разности вычесть вычитаемое

2. Для того, чтобы найти неизвестное делимое, надо:

а) из суммы вычесть известное слагаемое

б) сложить разность и вычитаемое

в) частное умножить на делитель

3. Для того, чтобы найти неизвестное слагаемое, надо:

а) из суммы вычесть известное слагаемое

б) сложить разность и вычитаемое

в) из разности вычесть вычитаемое

4. Для того, чтобы найти неизвестный множитель, надо:

а) из суммы вычесть известное слагаемое

б) сложить разность и вычитаемое

в) произведение разделить на известный множитель

5. Решите уравнения

а) х — 20 = 26

б) у : 7 = 2

в) 68 – х = 60

г) 35 : х = 7

Тест на тему «Решение уравнений. Компоненты уравнения»

для учащихся 2-4 классов

1.Для того, чтобы найти неизвестное уменьшаемое, надо:

а) из суммы вычесть известное слагаемое
б) сложить разность и вычитаемое
в) из разности вычесть вычитаемое

2. Для того, чтобы найти неизвестное делимое, надо:

а) из суммы вычесть известное слагаемое

б) сложить разность и вычитаемое

в) частное умножить на делитель

3. Для того, чтобы найти неизвестное слагаемое, надо:

а) из суммы вычесть известное слагаемое

б) сложить разность и вычитаемое

в) из разности вычесть вычитаемое

4. Для того, чтобы найти неизвестный множитель, надо:

а) из суммы вычесть известное слагаемое

б) сложить разность и вычитаемое

в) произведение разделить на известный множитель

5. Решите уравнения

а) х — 20 = 26

б) у : 7 = 2

в) 68 – х = 60

г) 35 : х = 7

Рассуждаем так:

первая запись – это равенство, но в нем отсутствуют буквы латинского алфавита, значит, она не является уравнением;

вторая запись – это неравенство, поэтому не соответствует определению уравнения;

третья запись – это математическое равенство, которое содержит неизвестное число, обозначенное буквой латинского алфавита, значит, является уравнением;

четвертая запись не является равенством, значит, это не уравнение.

infourok.ru

Уравнение компонента — Справочник химика 21

    В общем случае полюсное уравнение компонента системы с сосредоточенными параметрами имеет следующий вид  [c.137]

    Полюсные уравнения компонентов ХТС для исследования гидродинамических процессов, связанные с измерением последовательной переменной — потока вещества Q (1) и параллельной переменной — давления Р 1), будут  

[c.137]

    Полюсные уравнения компонентов ХТС при исследовании тепловых процессов, включающие последовательную переменную — тепло- [c.138]

    Полюсные уравнения компонентов реактора в матричной форме будут  [c.142]

    Сигнальный граф тепловых процессов, построенный непосредственно по топологии структурного графа реактора (см. рис. 1У-22, б), изображен на рис. У-20, а. Сигнальный граф, показанный на рис. У-20, б, строят с учетом полюсных уравнений компонентов (1У,16) и соотношений, полученных из структурного графа Тз ( ) = Т о ( ) — Тм ( ), где Гд (з) — перепад температур. Исходя из топологии сигнального графа (см. рис. У-20, б) и применяя универсаль- 

[c.248]

    Как видно из приведенного выше уравнения, компоненты, для которых в данных условиях Х>1, преимущественно остаются в газе, а те компоненты, для которых 7Стемпература процесса, тем меньше может быть давление, необходимое для ожижения заданной части исходного газа. Четкость разделения компонентов также улучшается со снижением температуры процесса. Обычно для выделения газового бензина искусственный холод не применяется, и температура охлажденного газа определяется температурой охлаждающей технической воды чаще всего процесс ведут при 25—30 С. Давление выбирается в зависимости от конкретных условий процесса разделения, пределы применяемых давлений довольно широкие. 

[c.34]

    II балансовые уравнения компонентов раствора [c.293]

    Может показаться, что в правой части уравнения компонент 1 играет особую роль. Однако легко показать, что это не так и что величина ф не зависит от того, мольные доли каких веществ выбраны в качестве независимых переменных [7], т.е. если правую часть уравнения (11.18) обозначить через Ф1,то будем иметь [c.277]

    Техника эксперимента определяется в некоторой степени числом и природой фигурирующих в стехиометрическом уравнении компонентов. [c.195]

    В этих уравнениях компоненты скорости 17 , Ну, и а также напряжение сил давления р являются функциями только координат точек пространства, а от времени не зависят. 

[c.48]

    Время удерживания и коэффициенты емкости. Переведем вышеизложенное на язык уравнений. Компонент i распределяется между двумя фазами таким образом, что его содержание в подвижной фазе (т) составляет qi,m, а в неподвижной фазе (s)—qi,s. Молекулы растворенного вещества, находящиеся в подвижной фазе, перемещаются вдоль колонки с той же скоростью (и), что и подвижная фаза. Поскольку число таких молекул составляет лишь определенную долю от их общего числа, средняя скорость всех молекул сорбата описывается уравнением [c.10]

    Компонентами называются химически разнородные независимые составные части системы, минимум которых дает возможность выразить состав каждой фазы химическим уравнением. Компонентами в солевых системах принимаются вода И соли, не связанные между собой стехиометрическим уравнением если такое уравнение, устанавливающее связь между составными частями системы, имеется, тогда число компонентов уменьшается на единицу. [c.51]

    В этих уравнениях компоненты напряжений заменены соответствующими значениями градиентов скорости, приведенными в табл. 2-3. [c.228]

    Появление в уравнении компоненты скорости жидкости о обусловлено циркуляцией жидкости. Следовательно 

[c.257]

    Для каждого компонента получим следующие уравнения Компонент хц [c.243]

    Уравнение энергии для третьего случая и уравнение диффузии при х,- = О записываются аналогично. Входящие в оба уравнения компоненты скорости Уд. и Vy описываются одними и теми же функциями. Если граничные условия для температуры и концентрации подобны, то будут подобными и рещения двух уравнений. Это положение лежит в основе метода аналогии процессов тепло- и массообмена. [c.390]

    В этих уравнениях компоненты теплового поля Нг выражаются в виде [c.127]

    Растворитель может поступать на ступень п либо в состоянии насыщения оборотным рафинатом, либо недонасыщенным. В первом случае точка +1 лежит на кривой равновесия, во втором—между ней и точкой С5. Во втором случае в уравнении (2-133) изменится второе отношение отрезков в правой части, а с ним и количеств возвращаемого рафината поступающего в аппарат с мешалкойо При состоянии насыщения количество возвращаемого рафината-может увеличиться только в случае увеличения расхода растворителя. В Ьтом случае изменению подвергается отрезок из-за передвижения рабочего полюса При росте расхода растворителя и увеличении возврата рафината рабочий полюс передвигается в направлении точки Сз- Координата х у1. из уравнения (2-138) вычисляется по уравнению (2-106) и основанному на нем балансовому уравнению компонента А  

[c.161]

    Эти четыре уравнения дают замкнутое описание процессов переноса в растворах электролитов, и поэтому имеет смысл еще раз сказать о физическом содержании каждого из них. Согласно первому уравнению, компоненты в растворе могут двигаться за счет миграции, диффуз11и и конвекции. Второе уравнение просто отражает тот факт, что электрический ток обусловлен движением заряженных компонентов. Третье уравнение дает условие материального баланса, а четвертое — условие электронейтральности. Хотя некоторые детали описания могут изменяться, любая теория растворов электролитов должна рассматривать эти физические явления. [c.247]

    Исключая из данного уравнения компоненты, обусловливающие равновесие реакции автопротолиза, получим равновесие, называемое вторичной реакцией ионной самодиссоциации  

[c.62]

    Концентрации всех входящих в данное уравнение компонентов выражены в грамм-молях. Для перевода pH в [Н+] удобно пользоваться данными табл. 38. Величина константы К в зависимости от температуры данной воды (in situ) находится по табл. 39. [c.215]

---

chem21.info

Памятка для обучающегося «Правила нахождения компонентов при решении уравнений», 5 класс

ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ		ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ
Компоненты при сложении: I слагаемое, II слагаемое. Результат сложения: Сумма. I сл + II сл = Сум I сл = Сум – II сл II сл = Сум – I сл	Компоненты при вычитании: Уменьшаемое, вычитаемое. Результат вычитания: Разность. Ум – Выч = Разн Ум = Разн + Вычит Вычит = Ум – Разн	Компоненты при сложении: I слагаемое, II слагаемое. Результат сложения: Сумма. I сл + II сл = Сум I сл = Сум – II сл II сл = Сум – I сл	Компоненты при вычитании: Уменьшаемое, вычитаемое. Результат вычитания: Разность. Ум – Выч = Разн Ум = Разн + Вычит Вычит = Ум – Разн
Сложение показывает сумму всех слагаемых	Вычитание показывает на сколько уменьшаемое больше вычитаемого	Сложение показывает сумму всех слагаемых	Вычитание показывает на сколько уменьшаемое больше вычитаемого
Компоненты при умножении: I множитель, II множитель. Результат умножения: Произведение. I мн · II мн = Произвед I мн = Произвед : II мн II мн = Произвед : I мн	Компоненты при делении: Делимое, делитель Результат деления: Частное . Делим : делит = Частное Делим = Част · делит делит = Делим : Част	Компоненты при умножении: I множитель, II множитель. Результат умножения: Произведение. I мн · II мн = Произвед I мн = Произвед : II мн II мн = Произвед : I мн	Компоненты при делении: Делимое, делитель Результат деления: Частное . Делим : делит = Частное Делим = Част · делит делит = Делим : Част
Умножение показывает сумму нескольких одинаковых слагаемых	Деление показывает во сколько раз делимое больше делителя	Умножение показывает сумму нескольких одинаковых слагаемых	Деление показывает во сколько раз делимое больше делителя

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Уменьшаемое, вычитаемое.

Результат вычитания: Разность.

Ум – Выч = Разн

Ум = Разн + Вычит

Вычит = Ум – Разн

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Уменьшаемое, вычитаемое.

Результат вычитания: Разность.

Ум – Выч = Разн

Ум = Разн + Вычит

Вычит = Ум – Разн

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Компоненты при умножении:

I множитель, II множитель.

Результат умножения: Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Делимое, делитель

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Компоненты при умножении:

I множитель, II множитель.

Результат умножения: Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Делимое, делитель

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

infourok.ru

компоненты уравнения.docx — проверочная работа по математике 2 …

Допиши высказывания.
1. Что бы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
2. Что бы найти неизвестное вычитаемое нужно из уменьшаемого вычесть разность.
3. Что бы найти неизвестное уменьшаемое нужно к разности прибавить вычитаемое.
4. Что бы найти неизвестный множитель нужно произведение разделить на известный
множитель.
5. Что бы найти неизвестное делимое нужно частное умножить на делитель.
6. Что бы найти произведение нужно перемножить множители.
7. Что бы найти частное нужно делимое разделить на делитель.
Реши уравнения
Х * 36= 0
У : 18 = 1
Реши задачу.
На клумбе расцвело 9 ромашек, а колокольчиков на 1/3 меньше. Сколько расцвело
всего цветов?
Допиши высказывания.
1.
Что бы найти неизвестное уменьшаемое нужно
Что бы найти неизвестное слагаемое нужно ___________________________
___________________________________________________________________
Что бы найти неизвестное вычитаемое нужно
2.
__________________________________________________________________________
3.
__________________________________________________________________________
4.
__________________________________________________________________________
5.
__________________________________________________________________________
6.
__________________________________________________________________________
7.
__________________________________________________________________________
Что бы найти произведение нужно
Что бы найти частное нужно
Что бы найти неизвестный множитель нужно
Что бы найти неизвестное делимое нужно
Реши уравнения
Х * 36= 0
У : 18 = 1
Реши задачу.
На клумбе расцвело 9 ромашек, а колокольчиков на 1/3 меньше. Сколько расцвело
всего цветов?
Допиши высказывания.

znanio.ru

Конспект урока математики в 3-м классе по теме «Уравнение»

Разделы: Начальная школа

---

Тема: «Уравнение».

Тип урока: открытие новых знаний.

Основные цели:

• Сформировать представление об уравнении, как равенство с переменной.
• Ввести в речевую практику понятие корни уравнения.
• Вспомнить все изученные виды уравнений и правила их решения.
• Систематизировать изученные виды уравнений и показать их связь с количественным описанием реальных величин.
• Отрабатывать навыки решения уравнений на нахождение компонентов арифметических действий.
• Отрабатывать умения, комментировать решение уравнений, используя математический язык.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение.

Демонстрационный материал:

ХОД УРОКА

1. Самоопределение к учебной деятельности:

Цели:

• создать мотивацию к деятельности на уроке посредством создания математических образов.
• определить содержательные рамки урока: решения уравнений на нахождение компонентов арифметических действий.

Организация учебного процесса на этапе 1:

– Какую тему изучали на предыдущем уроке? (Равенства и неравенства)
– Что мы называем неравенством?
– Что мы называем равенством?
– Со всеми ли заданиями мы справились на прошлом уроке? (Да)
– А как вы думаете, всё ли (?) мы узнали о равенствах на прошлом уроке? (Да, нет)
– А хотите, проверим?!

2. Актуализация знаний и фиксация затруднения в деятельности

Цель: воспроизвести знания, умения и навыки, достаточные для построения нового способа действия.

– К нам с математической планеты прилетели гости. (На доске: «солнышко» и «домик»)      
– Внимательно посмотрите на наших гостей и составьте всевозможные равенства, используя их числа и математические знаки. (Дети выходят к доске и делают запись).

3 + 2 = 5                                 3 • 2 = 6
2 + 3 = 5                                 2 • 3 = 6
5 – 2 = 3                                 6 : 3 = 2
5 – 3 = 2                                 6 : 2 = 3

– А, как вы думаете, какие имена  дали нашим героям на математической планете?  (Целое и площадь.)
– Почему? (Круглое «солнышко» – целое, а лучики –  части, прямоугольный «домик» – площадь)
– Обозначьте графически, в каких примерах живут наши герои.
– Наши гости несли вам подарок в мешочке, но по дороге всё перепуталось. Давайте поможем навести порядок. В мешочке карточки с названиями компонентов действий, расставьте их на свои места.

Учитель достаёт карточки с названием компонентов в разном порядке и дети расставляют  их на свои места.

На доске

… + … = …                           … • … = …
… – … = …                           … : … = …

– Молодцы, с этим заданием вы справились! Наши гости остались довольны.
– «Солнышко» задаёт вопросы:

1. Как найти неизвестное слагаемое?
2. Как найти неизвестное вычитаемое?
3. Как найти неизвестное уменьшаемое?

– Теперь послушайте вопросы «домика».

• Как найти неизвестный множитель?
• Как найти неизвестное делимое?
• Как найти неизвестный делитель?

– Давайте подведём итог:

1. Какими компонентами может быть целое? (Суммой и уменьшаемым)
2. Какими компонентами могут быть части? (Слагаемыми, вычитаемым и разностью)
3. Какими компонентами может быть площадь? (Произведением и делимым)
4. Какими компонентами могут быть стороны? (Множителями, делителем и частным)

Они решили, что вы сможете выполнить и следующее задание.

Каждой группе (варианту) даётся  задание в течение 2-х – 3-х минут записать по одному уравнению в общем виде, используя для обозначения неизвестного члена уравнения букву х, а для обозначения известных членов буквы а и в, и сформулировать правило нахождения корня для своего уравнения.
Дети должны записать следующие уравнения и проговорить правила нахождения неизвестного компонента на математическом языке:

х + а = в                    х • а = в
а – х = в                     а : х = в
х – а = в                     х : а = в

3. Выявление причин затруднения и постановка цели деятельности.

Цели:

• выявить и зафиксировать место и причину затруднения;
• согласовать цель и тему урока.

– Смогли ли вы составить уравнения? (Да)
– Умеете ли вы находить неизвестные компоненты в данных уравнениях? (Умеем)
– А как вы думаете, что может быть корнем уравнения, если его нужно найти? (Корень – это ответ)
– Что же вызвало затруднение? (Проговорить правила нахождения неизвестного компонента на математическом языке.)
– Какова же цель нашего урока? (Научиться проговаривать правила нахождения неизвестного компонента на математическом языке – обозначается на доске)
– С чем же мы будем работать сегодня на уроке? (С уравнениями)
– Какая же тема урока? («Уравнения» – обозначается на доске)

4. Построение проекта выхода из затруднения

Цели:

• организовать построение детьми нового способа проговаривания, устраняющего причину затруднения;
• зафиксировать новый способ действий в речи и знаково.

– Давайте вспомним алгоритм решения уравнений на сложение и вычитание (к первому столбику)

• Находим и выделяем части и целое.
• Определяем, что неизвестно.
• Вспоминаем правило нахождения целого или части.
• Находим целое или часть.
• Записываем ответ.

(Дети проговаривают  алгоритм решения уравнений и  пошагово вывешивают на доске).

– А теперь вспомним алгоритм решения уравнений на умножение и деление (ко второму столбику)

• Находим и выделяем площадь и стороны.
• Определяем, что неизвестно.
• Вспоминаем правило нахождения площади или стороны.
• Находим площадь или сторону .
• Записываем ответ.

(Дети проговаривают  алгоритм решения уравнений и  пошагово вывешивают на доске).

– А можно ли объединить 2 алгоритма, используя математический язык?
– Давайте попробуем.
– Посмотрим на 1-й шаг каждого алгоритма.
– Можно ли заменить эти 2 предложения одним, используя математический язык?

Вспомнить компоненты действия данного уравнения. Убираются 1-е шаги алгоритмов и заменяются 1-м новым шагом.  Аналогично идёт работа со следующими  шагами.

На доске появляется новый алгоритм:

1. Вспомнить компоненты действия данного уравнения.
2. Определить неизвестный компонент.
3. Вспомнить  правило нахождения неизвестного компонента.
4. Применить правило и  найти неизвестный компонент.
5. Записать корень уравнения.

5. Первичное закрепление во внешней речи

Цель: cоздать условия для фиксации изученного способа действий во внешней речи.

Организация учебного процесса на этапе 5:

Стр.78 №1 (а, д  – 1-е уравнения)

Ученик у доски решает уравнение с комментированием по алгоритму.

Стр.78 №1 (I – б, г, II – в, е –1-е уравнения) – работа в парах с проговариванием друг другу во внешней речи.

6. Самостоятельная работа с самопроверкой по эталону

Цель: организовать самопроверку умения решать уравнения с применением нового алгоритма.

– Решите уравнения с пошаговой записью по алгоритму (задание по вариантам)

y + 439 = 811                         90 • k = 270

– Проверьте по эталону.

y + 439 = 811
1	Вспомнить компоненты действия данного уравнения	Слагаемое, слагаемое, сумма
2	Определить неизвестный компонент	Неизвестный компонент – слагаемое.
3	Вспомнить  правило нахождения неизвестного компонента	Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
4	Применить правило и  найти неизвестный компонент	811 – 439 = 372
5	Записать корень уравнения.	y = 372

 

90 • k = 270
1	Вспомнить компоненты действия данного уравнения	Множитель,  множитель, произведение
2	Определить неизвестный компонент	Неизвестный компонент – множитель
3	Вспомнить  правило нахождения неизвестного компонента	Чтобы найти неизвестный множитель надо произведение разделить на известный множитель
4	Применить правило и  найти неизвестный компонент	270 : 90 = 3
5	Записать корень уравнения.	k = 3

– Проверьте. Поставьте на полях «+», если вы верно справились с заданием.
– У кого были ошибки? (Ответы детей)
– На каком шаге были допущены ошибки? (Ответы детей)
– Понял ли ты, почему у тебя возникла ошибка? (Ответы детей)

7. Включение в систему знаний и повторение

Цели:

• Повторение компонентов действий.
• Организовать повторение записи предложения в виде выражения.

Организация учебного процесса на этапе 7:

Задание № 3 стр. 78

8. Рефлексия деятельности на уроке.

Цели:

• зафиксировать в речи новый способ действий, изученный на уроке;
• зафиксировать затруднения, которые остались, и способ их преодоления;
• оценить собственную деятельность на уроке.

Организация учебного процесса на этапе 8:

– Здорово! Вы сумели ответить  на все вопросы наших гостей.
– Чему же вы сами научились на уроке? (Научились владеть математическим языком при решении уравнений)
– Когда было трудно? Удалось ли справиться с трудностями? Как? (Ответы детей)
– Над чем еще надо поработать? Как вы будете это делать? (Ответы детей)
– Кто сегодня собой доволен? Почему?
– Как вы оцениваете свою работу на уроке? Оцените свою работу по 10-балльной лесенке (на доске изображена лестница с 10 ступеньками, на ступеньки  которой дети ставят свои магниты).

Домашнее задание

• Выучить правила на стр. 77.
• Составить одно уравнение на сложение или вычитание, а другое на умножение или деление. И решите их с пошаговой записью по алгоритму.

xn--i1abbnckbmcl9fb.xn--p1ai

Уравнение.

Равенство с неизвестным числом называют уравнением.

Например:х + 23 = 45; 65 -х = 13; 12 -дг = 48;45 :х= 3.

Решить уравнение — значит найти такое значение неизвестного числа, при котором равенство будет верным. [5,с.248]

Это число называют корнем уравнения.

Например:

х+ 23 = 45; х= 22, так как 22 + 23 = 45.

Таким образом, данное определение задает также способ проверки уравнения: подстановка найденного значения неизвестного числа в выражение, вычисление его значения и сравнение полученного результата с заданным числом (ответом).

Если значение неизвестного числа найдено верно, то получается верное равенство.

Способы решения уравнений.

Изучение простейших уравнений и способов их решений прочно вошло в систему начальной математической подготовки. Уравнения являются одним из средств моделирования изучаемых фрагментов реальности, и знакомство с ними является существенной частью ма­тематического образования. В то же время, знакомство младших школьников с уравнениями подготавливает их к изучению математики в основной школе.

В математике под уравнением принято понимать «аналитическую запись задачи о разыскании значений аргументов, при которых значения данных двух функций равны. Аргументы, от которых эти функции зависят, называются неизвестными, а значения неизвестных, при которых значения функций равны, — решениями — корнями уравнения»[6]. Это значит, что понятие уравнения, во-первых, связано с аналитическим выражением (в нашем случае с арифметическим), а во-вторых, — с понятием переменной, принимающей значения из определенного множества.

В начальной школе рассматриваются два способа решения уравнения.

Способ подбора

Подбирается подходящее значение неизвестного числа либо из заданных значений, либо из произвольного множества чисел.

Выбранное число должно при подстановке в выражение превращать его в верное равенство. Например:

Из чисел 7, 10, 5, 4, 1, 3 подбери для каждого уравнения такое значение х, при котором получится верное равенство: 9 + х=14 7-х=2 х-1 = 9 х+5 = б

Каждое из предложенных чисел проверяется подстановкой в выражение и сравнением полученного значения с ответом.

При большом количестве предложенных значений этот способ отнимает много времени и сил. При самостоятельном подборе значений выражений ребенок может не найти самостоятельно возможное значение неизвестного.

Способ использования взаимосвязи компонентов действий.

Используются правила взаимосвязи компонентов действий.

Например:

Реши уравнение: 9 + х=14

Неизвестно слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Значит, х = 14 — 9; х = 5.

Реши уравнение: 7 -х=2

Неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое нужно из уменьшаемого вычесть разность. Значит, х = 1 — 2; х = 5.

Реши уравнение: х-1 = 9

Неизвестно уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Значит, х = 9 + 1; х = 10.

Для решения уравнений с действиями умножения и деления используются правила зависимости компонентов умножения и деления.

Например:

Реши уравнение: 96:х=24

Неизвестен делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. Значит, х = 96 : 24; х = 4. Проверим решение: 24 • 4 = 96.

Реши уравнение: х:23 = 4

Неизвестно делимое. Чтобы найти неизвестное делимое, нужно делитель умножить на частное. Значит, х = 23 • 4; х = 92. Проверим решение: 92 : 23 = 4.

Реши уравнение: о:- 14 = 84

Неизвестен множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Значит,х= 84:14;х=6. Проверим решение: х • 14 = 84.

Использование данных правил дает более быстрый способ решения уравнений. Трудность заключается в том, что многие дети путают правила взаимосвязи компонентов действий и названия компонентов (необходимо хорошо знать 6 правил и названия 10 компонентов).

Для более трудных уравнений используется метод подбора, например:

35 + х + х + х= 35 — очевидно, что неизвестное может принимать только нулевое значение;

78-х-х = 76 — очевидно, что х = 1, поскольку 78 — 1 — 1 = 76.

Для уравнений со скобками вида (6 + х) — 5 = 38 используется правило взаимосвязи компонентов действий. Левую часть уравнения рассматривают сначала как разность, считая выражение в скобках единым неизвестным компонентом. Этот единый неизвестный компонент — уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое:

Таким образом уравнение приобретает привычный вид. В этом уравнении требуется найти неизвестное слагаемое: х = 43-6;х=37.

Проверим решение (подставим найденное значение неизвестного в первоначальное выражение): (6 + 37) — 5 = (6 — 5) + 37 = 1 + 37 = 38.

Ряд альтернативных учебников математики для начальных классов практикует знакомство детей с более сложными уравнениями (И.И. Аргинская, Л.Г. Петерсон), для решения которых правила взаимосвязи компонентов действий рекомендуется применять многократно.

Например:

Реши уравнение: (у-3)-5-875 = 210

Решение:

Рассмотрим левую часть уравнения и определим порядок действий.

1 2 3

(у- 3)- 5 -875 = 210

Вид выражения в левой части определяем по последнему действию: последнее действие — вычитание, значит, начинаем рассматривать выражение как разность.

Уменьшаемое (у — 3) • 5, вычитаемое 875, значение разности 210.

Неизвестное содержится в уменьшаемом. Найдем уменьшаемое (рассматриваем все это выражение как единое уменьшаемое): чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.

(у- 3)- 5 = 210 + 875;

(у — 3) • 5 = 1085: у

Снова определим порядок действий: (у — 3) ·5 = 1085.

По последнему действию считаем выражение в левой части произведением. Первый множитель (у — 3), второй множитель 5, значение произведения 1085. Неизвестное содержится в первом множителе. Найдем его (считаем все выражение у — 3 неизвестным). Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.

у — 3 = 1085 : 5;

у- 3 = 215.

Получили уравнение, в котором неизвестно уменьшаемое. Найдем его:

у = 215 + 3;

у = 218.

Проверим решение, подставив найденное значение неизвестного в первоначальное уравнение:

(218-3)-5-875 = 210.

Вычислив значение левой части, убеждаемся в том, что получено верное равенство. Значит, уравнение решено верно.

Анализ приведенного способа решения показывает, что это длительный трудоемкий процесс, требующий от ребенка четкого знания всех правил, высокого уровня анализа и умения воспринимать комплексную структуру переменного, получаемую при пошаговом решении, как единое целое (высокий уровень синтеза и абстрагирования).

Взрослый, знакомый с универсальным методом решения подобных уравнений, применяемым в старших классах (раскрытие скобок, перенос компонентов уравнения слева направо) хорошо видит несовершенство и излишнюю трудоемкость этого метода. В связи с этим рядом методистов справедливо высказываются сомнения в целесообразности активного внедрения уравнений такой сложной структуры в курс математики начальной школы. Этот способ решения является нерациональным с математической точки зрения и будет забыт и отброшен, как только учитель математики в 5—7 классах познакомит ребенка с общими приемами решения уравнений подобного вида.[5,с.252]

studfiles.net

Уравнения 5 класс Как найти компонент уравнения:

Описание презентации Уравнения 5 класс Как найти компонент уравнения: по слайдам

Уравнения 5 класс

Как найти компонент уравнения: Вычитаемое Слагаемое Делитель Уменьшаемое Делимое

Выберите выражение, которое является уравнением: 64 – (24 +12)= 28 13 + х = 34 15 > 7 + х 34 + 6 <

Выбери уравнение, в котором верно найден корень: 28 : х = 7 х = 4 2 • у = 9 у = 18 с – 7 = 8 с =

Помогите Маше и Мише «поймать» уравнение, корень которого равен 18. х + 37 = 64 х : 2 = 9 х – 38 =

Проверьте свою память! Сейчас Вы увидите числа, которые «исчезнут» через 15 секунд. Попробуйте их запомнить, а чисел, то у Вас хорошая память. Готовы к проверке?

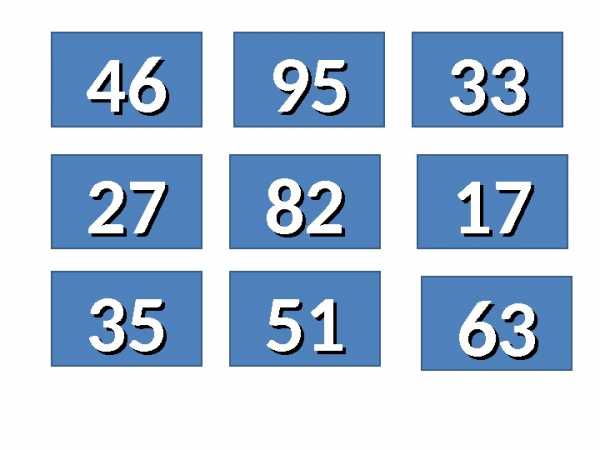
Запишите числа в тетрадь 40 секунд для записи «пошли» …

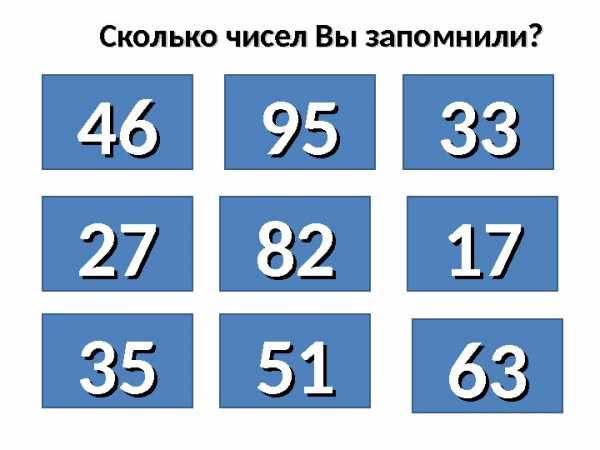4646 9595 3333 2727 8282 1717 3535 5151 6363 Сколько чисел Вы запомнили?

Помогите Маше перейти к Мише Какой компонент неизвестен в уравнении Х + 24 = 17 ? делитель уменьшаемое слагаемоеразность

Помогите Маше перейти к Мише частное. Какой компонент неизвестен в уравнении Х : 24 = 17 ? делимое делитель вычитаемое

Помогите Маше перейти к Мише Какой компонент неизвестен в уравнении 24 – Х = 17 ? уменьшаемое слагаемоевычитаемое

А сейчас порешаем!

Встретимся позже

present5.com