Как решать прогрессии геометрические – Формулы геометрической прогрессии, геометрические последовательности, бесконечные геометрические прогрессии

Геометрическая прогрессия | Онлайн калькулятор

Геометрическая прогрессия — это числовая последовательность, в которой все ее члены расположены в порядке, подчиняющемся определенной закономерности. Формула геометрической прогрессии определяет, что каждое следующее число будет получено умножением предыдущего на знаменатель прогрессии — постоянное число, не меняющее свое значение в пределах одной последовательности. b_n=b₁ q^(n-1)

В зависимости от знаменателя прогрессии, выписанные члены геометрической прогрессии могут давать различный вид ряда. Если знаменатель является числом положительным, больше 1 (k > 1), тогда он будет увеличивать значение каждого следующего числа. Такая прогрессия будет монотонно возрастать на протяжении всего ряда. Если знаменатель — положительный, но находится между 0 и 1 (0 , тогда он будет каждый раз уменьшать значение следующего члена, и такая прогрессия будет называться

бесконечно убывающая геометрическая прогрессия.

Если для все возрастающей последовательности, можно только найти сумму первых членов геометрической прогрессии, то сумма членов бесконечно убывающей прогрессии будет равна вполне конкретному числовому значению, которое может рассчитать калькулятор. Третий случай представлен отрицательным знаменателем (k , тогда прогрессия становится знакочередующейся, то есть первые члены геометрической прогрессии определяют порядок знаков для всей последовательности чисел. Как знаменатель геометрической прогрессии, так и первый член геометрической прогрессии по определению не могут быть равны нулю.

Существует всего несколько

формул геометрической прогрессии, из которых можно вывести все необходимые для решения конкретных задач:

• Формула первого члена геометрической прогрессии;

• Формула n члена геометрической прогрессии;

• Формула суммы первых членов геометрической прогрессии;

• Формула суммы бесконечно убывающей геометрической прогрессии;

• Формула знаменателя геометрической прогрессии.

Таким образом, если условиями задана геометрическая прогрессия с хотя бы двумя параметрами из всех выше представленных, для нее можно будет найти любую из всех прочих переменных.

allcalc.ru

9 класс. Алгебра. Прогрессии. — Геометрическая прогрессия.

Комментарии преподавателя

Посмотрев этот видеоурок, пользователи смогут получить представление о теме «Определение и свойства геометрической прогрессии, формула n-го члена». В ходе занятия учитель познакомит с понятием геометрической прогрессии, расскажет о ее свойствах. Кроме того, на уроке будет дана формула n-го члена и будет показано, как правильно применять ее на практике.

 

 

 

Тема: Гео­мет­ри­че­ская про­грес­сия

Урок: Опре­де­ле­ние и свой­ства гео­мет­ри­че­ской про­грес­сии, фор­му­ла n–го члена

На уроке да­ет­ся опре­де­ле­ние 

гео­мет­ри­че­ской про­грес­сии, вы­во­дит­ся фор­му­ла об­ще­го члена, ре­ша­ют­ся ти­по­вые за­да­чи.

Чис­ло­вую по­сле­до­ва­тель­ность, все члены ко­то­рой от­лич­ны от нуля и каж­дый член ко­то­рой, на­чи­ная со вто­ро­го, по­лу­ча­ет­ся из преды­ду­ще­го члена умно­же­ни­ем его на одно и то же число q, на­зы­ва­ют гео­мет­ри­че­ской про­грес­си­ей. При этом число q на­зы­ва­ют зна­ме­на­те­лем про­грес­сии.

Ма­те­ма­ти­че­ская за­пись.

гео­мет­ри­че­ская про­грес­сия, ее члены , при этом:

Иная за­пись:, т.е. .

Рас­смот­рим при­ме­ры гео­мет­ри­че­ских про­грес­сий:

 здесь каж­дый сле­ду­ю­щий член по­лу­ча­ет­ся из преды­ду­ще­го умно­же­ни­ем на 2; по­лу­чен­ная по­сле­до­ва­тель­ность при этом воз­рас­та­ет (

2.  здесь каж­дый сле­ду­ю­щий член по­лу­ча­ет­ся из преды­ду­ще­го умно­же­ни­ем на ; по­лу­чен­ная по­сле­до­ва­тель­ность при этом убы­ва­ет (

Те­перь вы­ве­дем фор­му­лу n–го члена гео­мет­ри­че­ской про­грес­сии.

Рас­смот­рим гео­мет­ри­че­скую про­грес­сию , при этом

.

Тогда,

. . . . . . . . . . .

n=1,2,3,…

До­ка­жем по­лу­чен­ную фор­му­лу ме­то­дом пол­ной ма­те­ма­ти­че­ской ин­дук­ции.

Дано:гео­мет­ри­че­ская про­грес­сия,

.

До­ка­зать:.

До­ка­за­тель­ство.

1. Про­ве­рим спра­вед­ли­вость фор­му­лы дляn =1: 

2. Пред­по­ло­жим, что фор­му­ла спра­вед­ли­ва для n=k: 

3. До­ка­жем, что из спра­вед­ли­во­сти фор­му­лы для n=k сле­ду­ет спра­вед­ли­вость фор­му­лы для n=k+1: 

Вывод:  фор­му­ла верна для всех 

Рас­смот­рим гео­мет­ри­че­скую про­грес­сию как функ­цию на­ту­раль­но­го ар­гу­мен­та и по­стро­им ее гра­фик.

Обо­зна­чим, тогда 

,  это по­ка­за­тель­ная функ­ция на­ту­раль­но­го ар­гу­мен­та.

Рас­смот­рим при­ме­ры.

1.  

.

Пе­рей­дя к функ­ции, имеем

Со­ста­вим таб­ли­цу зна­че­ний функ­ции.

n	1	2	3	4
	1	2	4	8

И по­стро­им ее гра­фик.

Рис. 1.

, по­это­му гра­фик – это толь­ко от­дель­ные точки, ко­то­рые лежат на по­ка­за­тель­ной кри­вой.

2.  ;

.

Пе­рей­дя к функ­ции, имеем

Со­ста­вим таб­ли­цу зна­че­ний функ­ции.

n	1	2	3	4
	1

И по­стро­им ее гра­фик.

Рис. 2

Снова гра­фик – это от­дель­ные точки, ле­жа­щие на по­ка­за­тель­ной кри­вой.

Из гра­фи­ков видно, что если гео­мет­ри­че­ская про­грес­сия воз­рас­та­ет, то воз­рас­та­ет очень быст­ро, а если убы­ва­ет, то убы­ва­ет тоже быст­ро (как по­ка­за­тель­ная функ­ция).

Далее рас­смот­рим ти­по­вые за­да­чи, для ре­ше­ния ко­то­рых по­на­до­бит­ся фор­му­ла об­ще­го члена гео­мет­ри­че­ской про­грес­сии:

1. Дано:гео­мет­ри­че­ская про­грес­сия, . Найти: . Ре­ше­ние:  Ответ: 

2. Дано:гео­мет­ри­че­ская про­грес­сия,. Про­ве­рить, яв­ля­ет­ся ли число 1536 чле­ном этой про­грес­сии, если да, найти его номер. Ре­ше­ние:  Ответ: 

3. Дано:гео­мет­ри­че­ская про­грес­сия, .  Найти:  Ре­ше­ние:  Ответ: 

4. Дано:гео­мет­ри­че­ская про­грес­сия, .  Найти:  Ре­ше­ние:  Ответ: 

Если из­вест­ны два члена гео­мет­ри­че­ской про­грес­сии то спра­вед­ли­ва фор­му­ла:

.

Дей­стви­тель­но,  Рас­смот­рим еще одну за­да­чу.

5. Дано:гео­мет­ри­че­ская про­грес­сия, .  Найти:  Ре­ше­ние:  Ответ: 

н­та.

Вы­ве­дем далее фор­му­лу суммы ко­неч­но­го числа чле­нов гео­мет­ри­че­ской про­грес­сии.

Дано: гео­мет­ри­че­ская про­грес­сия.

Найти:

Ре­ше­ние:.

Умно­жим обе части этого ра­вен­ства на q:

.

И вы­чтем из пер­во­го ра­вен­ства вто­рое:

,

 ,

.

В по­лу­чен­ной фор­му­ле , рас­смот­рим част­ный слу­чай

Гео­мет­ри­че­ская про­грес­сия  имеет nрав­ных чле­нов, по­это­му ее сумма

Итак, , при ;   при .

Далее рас­смот­рим  ти­по­вые за­да­чи, для ре­ше­ния ко­то­рых по­на­до­бит­ся фор­му­ла суммы чле­нов гео­мет­ри­че­ской про­грес­сии:

1. Дано:гео­мет­ри­че­ская про­грес­сия, . Найти:  Ре­ше­ние: . Ответ: 

2. Дано:гео­мет­ри­че­ская про­грес­сия, . Найти: . Ре­ше­ние:  Ответ: 

3.  «Ле­ген­да об изоб­ре­та­те­ле шах­мат». Дано:

www.kursoteka.ru

Арифметическая и геометрическая прогрессии. Решения

На Ваше рассмотрение представлены решения примеров повышенной сложности на арифметическую и геометрическую прогрессии. Методика вычислений является полезной для практических занятий как в школе, так и ВУЗах и соответствует школьной программе. Если приведенные примеры для Вас трудны прочтите для начала простые задачи на арифметическую и геометрическую прогрессию.

Пример 1. В геометрической прогрессии b₁₀* b₁₄* b₂₁=-0,125. Вычислить b₁₅.
Решение. Приведем методику которая упростит решение подобных примеров. Для начала найдем сумму индексов членов прогрессии.
10+14+21=45.
Сумма 45 нацело делится на 15 и получаем 3. Заданное произведение членов прогресии можно представить в виде
b₁₀* b₁₄* b₂₁=(b₁₅)^3
Это следует и со свойств геометрической прогреси.
Отсюда вычисляем искомый член прогрессии

Итак, 15 член прогрессии равен -0,5.

 

Пример 2. Сумма трех чисел, представляющих возрастающую арифметическую прогрессию равна 21. Если к ним, соответственно, добавить 2, 3, и 9 то образованные числа составят геометрическую прогрессию. Найти наибольшее из искомых членов проргресии.
Решение. Таким заданием можно проверить знание формул арифметической и геометрической прогрессии.
Обозначим члены возрастающей прогрессии через a-d, a, a+d.
Тогда их сумма равна 3a=21, откуда a=21/3=7.
Такое быстрое решение получили за счет удачного выбора формул членов прогресии. Таким образом средний член арифметической прогрессии известен.
Далее найдем неизвестные члены геометрической прогрессии
Первый – a-d+2=7-d+2=9-d
второй a+3=7+3=10.
третий a+d+9=7+d+9=16+d.
По свойству геометрической прогрессии о среднем геометрическом значении получим что квадрат среднего ее члена равен произведению равноудаленных, т.е.

Подставим члены геометрической прогрессии в формулу
(9-d)(16+d)=10^2=100.
Думаю Ви знаете что делать с подобным уравнением.
Раскроем скобки и сведем к квадратному уравнению относительно разницы арифметической прогрессии.


Находим дискриминант

и шаг арифметической прогрессии

Отсюда находим нужный член арифметической прогрессии
a+d=7+4=11.
Вот такие сложные задачи на прогрессию Вам могут встретиться в обучении.

 

Пример 3. Три числа которые составляют возрастающую арифметическую прогрессию дают в сумме 15. Если к первому и второму из них добавить по единице, а к третьему числу прибавить 4, то новые числа составят геометрическую прогрессию. Найти старшый член заданной прогресии.
Решение. Задача аналогична предыдущей. Вводим те же обозначения что и в предыдущем примере, тогда средний член арифметической прогрессии равен 15/3=5, а соседние – 5-d и 5+d.
По условию запишем члены геометрической прогрессии
(5-d+1)=6-d; 5+1=6; 5+d+4=9+d
и составим из них уравнение
(6-d)(9+d)=6*6=36.
Раскрываем скобки и сводим к квадратному уравнению


Вычисляем дискриминант

и разницу арифметической прогрессии
d=(-3+9)/2=3.
Больший из членов прогресии равен 8
a+d=5+3=8.

 

Пример 4. Три числа b₁, b₂, b₃ образуют возрастающую геометрическую прогрессию. Вычислить b₃ если b₁*b₂*b₃=64, b₁+b₂+b₃=14.
Решение. Опять имеем задание на составление уравнения. Обозначим члены геометрической прогрессии в нужном для нас виде
b/q;b;b*q.
Подставив в условие можно найти средний член геометрической прогрессии
b/q*b*b*q=b^3=64.
Отсюда средний член геометрической прогрессии равен корню кубическому из 64

С учетом найденного значения, запишем второе условие задания

b₁+b₂+b₃=14;

Умножым на знаменатель прогресии

и сведем к квадратному уравнению

Вычислим дискриминант уравнения

и знаменатель геометрической прогрессии

Второе значение отбрасываем, так как при нем геометрическая прогрессия становится убывающей, а по условию мы ищем возрастающую прогрессию.
Теперь без труда находим старший член геометрической прогрессии
b*q=4*2=8.

 

Пример 5. Три числа b₁, b₂, b₃ образуют убивающую геометрическую прогрессию. Вычислить b₃ если b₁*b₂*b₃=27, b₁+b₂+b₃= 13.
Решение. По свойству геометрической прогрессии имеем
b₂/q*b₂*b₂*q=2^3=27.
Отсюда второй член геометрической прогресии равен b[2]=3.
Из второго условия получим уравнение


Найдем дискриминант квадратного уравнения

и определим знаменатель прогрессии

Первое значение q=3 не удовлетворяет начальное условие (убивающая прогресия).
При q=1/3 третий член геометрической прогрессии равен
b[3]=b[2]*q=3/3=1.
Рекомендуем используйте приведенный алгоритм вычислений в подобных задачах.

 

Пример 6. Определить седьмой член возрастающей арифметической прогрессии если а₃+а₉=24, а₃*а₉=108.
Решение. Задача не сложная, поскольку имеем два условия и две неизвестные. Так что решение найти можно. Выразим из первого уравнения a[9] и подставим во второе


Последнее уравнение решаем через дискриминант


С первого условия
а₃+а₉=24
видим, что при а₃=18 прогрессия не будет возрастающей. Итак, остается а₃=6. Отсюда
a[9]=24-a[3]=24-6=18.
С другой стороны
a[9]=a[3]+6d
имеем условие для нахождения разницы прогрессии
6+6d=18; 6d=12; d=12/6=2.
По формуле находим седьмой член арифметической прогрессии
a[7]=a[3]+4d=6+4*2=14.
Вот и весь алгоритм подобных вычислений.

 

Пример 7. Определить восьмой член возрастающей арифметической прогрессии если а₂+а₇=18, а₂*а₇=56.
Решение. Подобнаяе по схеме вычислений задача уже рассматривалась. Выразим из первого уравнения a[2] и подставим во второе
a[2]=18-a[7]; (18-a[7]) a[7]=56.
Раскроеем скобки и сведем к квадратному уравнению

С помощью дискриминанта

вычислим неизвестный член прогрессии

С первого условия делаем вывод что только при a[7]=14 арифметическая прогрессия будет возрастающей.
Соответственно второй член прогресии равен
a[2]=18-a[7]=18-14=4.
По формуле
a[7]=a[2]+5d
определяем шаг прогрессии
14=4+5d; 10=5d; d=2.
Находим 8 член арифметической прогрессии
a[8]=a[7]+d=14+2=16.
Для самопроверки можете подставить найдены члены прогрессии в условие задания.

 

Пример 8. Вычислить сумму первых восьми членов нисходящей арифметической прогрессии если а₂+а₆=24, а₂*а₆=128.
Решение. Чтобы найти сумму прогрессии нам нужно знать первый и восьмой член прогрессии, или 1 член прогрессии и разность (шаг).
Для начала определим из двух уравнений хотя бы один член прогрессии
a[2]=24-a[6];
(24-a[6])*a[6]=128.
При раскрытии скобок получим квадратное уравнение

Как решать квадратные уравнения Вы уже знаете. Дискриминант принимает значение

Далее считаем 6 член арифметической прогрессии

При a[6]=8 арифметическая прогрессия является убывающей. Находим разницу прогрессии
a[2]=24-a[6]=24-8=16.
a[6]=a[2]+4d=16+4d=8;
4d=-8;d=-2.
Легко заметить что значение второго члена прогрессии всегда совпадает с корнем уравнения который отвергаем по условию задачи. Это своего рода подсказка правильности вычислений.
Находим первый и восьмой член прогрессии
a[1]=a[2]-d=16-(-2)=18;
a[8]=a[6]+2d=8+2*(-2)=4.
Найденные значения подставляем в формулу суммы арифметической прогрессии
S=(a[1]+a[8])*8/2=(18+4)*8/2=88.
Сумма восьми членов прогрессии равна 88.

Конечно это не все примеры, которые можно встретить в интернете среди возможных, однако и на их базе можно взять для себя несколько удачных приемов которые можно использовать на практике при решении упражнений на арифметическую и геометрическую прогрессии. Навыки приходят с практикой, поэтому ищите подобные задачи и учитесь решать!

Похожие материалы:

yukhym.com

Геометрическая прогрессия. Задачи на прогрессии и последовательности.

В этой статье рассмотрены задачи на геометрические прогрессии, и последовательности, которые нельзя отнести ни к арифметическим, ни  к геометрическим прогрессиям.

Сначала вспомним, что мы знаем о последовательностях.

Последовательность – это ряд чисел, который подчиняется определенному правилу. Если каждое последующее больше (или же меньше) предыдущего на определенное число, то это арифметическая прогрессия. Если числа отличаются во сколько-то раз, то такой ряд – геометрическая прогрессия. Если правило получения последующих членов ряда сложнее – то это просто последовательность.

Числа в геометрической прогрессии можно получить умножением (или делением) на одно и то же число, называемое знаменателем прогрессии. Члены геометрической прогрессии обозначают обычно буквой b с индексом, указывающим на номер элемента в ряду. А знаменатель обозначают буквой q. Тогда, зная первый член прогрессии и знаменатель, можно найти n-ный член:

Сумму нескольких членов прогрессии можно найти по формуле:

Или еще можно использовать такую:

Свойства:

Ну, к бою! Решаем задачи.

1. Гео­мет­ри­че­ская про­грес­сия  за­да­на усло­ви­я­ми:, . Най­ди­те .

Сначала определим знаменатель прогрессии:

Теперь можем определить и восьмой член: 

2. Последовательности заданы несколькими первыми членами. Какая из них – геометрическая прогрессия?

а) 1; 2; 3; 5;…              б) 1; 2; 4; 8;…                 в) 1; 3; 5; 7;…             г).

Нужно выбрать последовательность, в которой каждое последующее число больше или меньше предыдущего в определенное количество раз. Из всех представленных последовательностей только во второй каждое последующее число вдвое больше предыдущего. Именно она и является геометрической прогрессией. Такая закономерность более не наблюдается ни в одной из представленных последовательностей, поэтому ответ: б).

3. Дана гео­мет­ри­че­ская про­грес­сия, зна­ме­на­тель ко­то­рой равен 2, а . Най­ди­те сумму пер­вых шести её чле­нов.

Воспользуемся формулой суммы:

Ответ: 47,25

4. В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 40, а сумма вто­ро­го и тре­тье­го чле­нов равна 120. Най­ди­те пер­вые три члена этой про­грес­сии.

Дано следующее:

;  

Запишем условие, применяя формулу n-ного члена:

Во втором уравнении вынесем за скобку :

Оказывается, можно заменить выражение в скобках, воспользовавшись первым уравнением, и это позволит найти знаменатель прогрессии:

Тогда из первого уравнения , . Отсюда легко найти остальные члены: , .

Ответ: 10, 30, 90.

5. Биз­не­смен Руб­ли­ков по­лу­чил в 2000 году при­быль в раз­ме­ре 50000 руб­лей. Каж­дый сле­ду­ю­щий год его при­быль уве­ли­чи­ва­лась на 200% по срав­не­нию с преды­ду­щим годом. Сколь­ко руб­лей за­ра­бо­тал Руб­ли­ков за 2003 год?

С первого прочтения может быть не ясно сразу, что эта задача – на геометрическую прогрессию. Увидев слова “на 200%” некоторые могут ошибиться, подумав, что тут надо применять формулы арифметической прогрессии. Давайте разберемся, что же означает это условие задачи. Если бы прибыль бизнесмена выросла на 100 %, то это значило бы, что он получил столько, сколько в прошлом году, да еще столько же – то есть в два раза больше. Прибыль увеличилась на 200 % – значит, бизнесмен заработал столько же, сколько в прошлом году, да еще в 2 раза больше – то есть всего в три раза больше! А на следующий год – еще в три раза,  вот и вырисовывается геометрическая прогрессия со знаменателем 3. Первый ее член: . Всего бизнесмен трудился три года, поэтому искомое – :

– был Рубликов –  стал Миллиончиков!

Рассмотрим теперь задачи на последовательности.

6. По­сле­до­ва­тель­ность за­да­на фор­му­лой  . Какое из ука­зан­ных чисел яв­ля­ет­ся чле­ном этой по­сле­до­ва­тель­но­сти?

а)6                       б)16                 в)9              г)19

Чтобы выяснить, является ли какое-либо из чисел членом данной последовательности, нужно идти от обратного: подставить данное число в формулу и посмотреть, будут ли у полученного уравнения целые корни. Уравнение простое, решается устно. При вычитании 3 из 6, 16 и 9 квадрата целого числа не получится, а вот если вычесть 3 из 19 – получится 16, это и есть решение.

Ответ: 16

7. Последовательность задана формулой: . Сколько членов в этой последовательности больше 2?

Можно перефразировать задачу: сколько членов данной последовательности удовлетворяют неравенству ? Поскольку неравенство строгое, то число 2 ему не удовлетворяет, поэтому знаменатель должен быть меньше 6. Решаем неравенство:

Получили n=4.

Можно было и сразу решать неравенство: .

easy-physic.ru

Внеклассный урок — Геометрическая прогрессия

Геометрическая прогрессия

 

Геометрическая прогрессия – это такая последовательность отличных от нуля чисел, которая получается в результате умножения каждого последующего члена на одно и то же число, не равное нулю.

Пример геометрической прогрессии: 2, 6, 18, 54, 162.

Здесь каждый член после первого в 3 раза больше предыдущего. То есть каждый последующий член является результатом умножения предыдущего члена на 3:

2 · 3 = 6

6 · 3 = 18

18 · 3 = 54

54 · 3 = 162.

 

Знаменатель геометрической прогрессии.

Знаменатель геометрической прогрессии – это число, равное отношению второго и любого последующего члена к предыдущему члену прогрессии. Ее обычно обозначают буквой q.

В нашем примере при делении второго члена на первый, третьего на второй и т.д. мы получаем 3. Число 3 и является знаменателем данной геометрической прогрессии.

 

Свойства геометрической прогрессии:

1) Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних членов, стоящих перед ним и после него: bn2 = bn-1 · bn+1   2) Верно и обратное утверждение: если в последовательности чисел квадрат любого ее члена, начиная со второго, равен произведению двух соседних членов, стоящих перед ним и после него, то эта последовательность является геометрической прогрессией:

Пример:
Вернемся к нашей геометрической прогрессии 2, 6, 18, 54, 162. Возьмем четвертый член и возведем его в квадрат:

54² = 2916.

Теперь перемножим члены, стоящие слева и справа от числа 54:

18 · 162 = 2916.

Как видим, квадрат третьего члена равен произведению соседних второго и четвертого членов.

 

Как найти определенный член геометрической прогрессии.

Чтобы найти n-й член геометрической прогрессии, следует применить формулу: bn = b1· qn – 1

Пример 1: Возьмем некую геометрическую прогрессию, в которой первый член равен 2, а знаменатель геометрической прогрессии равен 1,5. Надо найти 4-й член этой прогрессии.

Дано:
b₁ = 2
q = 1,5
n = 4
————
b₄ — ?

Решение.
Применяем формулу b_n = b₁ · q^{n – 1}, вставляя в нее соответствующие значения:

b₄ = 2 · 1,5^{4 – 1} = 2 · 1,5³ = 2 · 3,375 = 6,75.

Ответ: Четвертый член заданной геометрической прогрессии – число 6,75.

 

Пример 2: Найдем пятый член геометрической прогрессии, если первый и третий члены равны соответственно 12 и 192.

Дано:
b₁ = 12
b₃ = 192
————
b₅ — ?

Решение.

1) Сначала нам надо найти знаменатель геометрической прогрессии, без которой решить задачу невозможно. В качестве первого шага с помощью нашей формулы выводим формулу для b₃:

b₃ = b₁ · q^{3 – 1} = b₁ · q²

Теперь мы можем найти знаменатель геометрической прогрессии:

           b₃       192
q² = —— = —— = 16
           b₁        12

q = √16 = 4 или –4.

2) Осталось найти значение b₅.

Если q = 4, то

b₅ = b₁q^5-1 = 12 · 4⁴ = 12 · 256 = 3072.

При q = –4 результат будет тот же. Таким образом, задача имеет одно решение.

Ответ: Пятый член заданной геометрической прогрессии – это число 3072.

 

Как найти сумму первых n членов геометрической прогрессии.

При q ≠ 1 сумму любого количества первых членов геометрической прогрессии можно найти с помощью одной из следующих формул:                                                                            bnq – b1                                                                   Sn = ————                                                                               q – 1                                                                             b1 (qn – 1)                                                                    Sn = —————                                                                                 q – 1 Если q = 1, то все члены прогрессии просто равны первому члену:                                                                               Sn = nb1

 

Пример: Найдем сумму первых пяти членов геометрической прогрессии (b_n), в которой первый член равен 2, а знаменатель геометрической прогрессии 3.

Дано:

b₁ = 2

q = 3

n = 5
————
S₅ – ?

Решение.

Применяем вторую формулу из двух приведенных выше:

          b₁ (q⁵ – 1)        2 (3⁵ – 1)             2 · (243 – 1)                  484
S₅ = ————— = ————— = ———————— = ————— = 242
              q – 1                3 – 1                        2                              2

Ответ: Сумма первых пяти членов заданной геометрической прогрессии равна 242.

 

Сумма бесконечной геометрической прогрессии.

Следует различать понятия «сумма бесконечной геометрической прогрессии» и «сумма n членов геометрической прогрессии». Второе понятие относится к любой геометрической прогрессии, а первое – только к такой, где знаменатель меньше 1 по модулю.

Сумма бесконечной геометрической прогрессии – это предельное число, к которому сходится последовательность прогрессии. Говоря иначе, какой бы длинной не была геометрическая прогрессия, сумма ее членов не больше какого-то определенного числа и практически равна этому числу. Оно и называется суммой геометрической прогрессии. Не любая геометрическая прогрессия имеет такую предельную сумму. Она может быть только у такой прогрессии, знаменатель которой – дробное число меньше 1.

 

Пример-пояснение:

Составим геометрическую прогрессию, в которой первый член – число 2, а знаметатель равен 1/2:

2, 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64 и т.д.

Сложим все полученные члены прогрессии:

2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = 255/64 ≈ 3,98 ≈ 4.

Можно продолжить прогрессию до 10, 100, миллиона членов, но во всех случаях сумма членов прогрессии будет практически равна 4. Число 4 и является суммой данной геометрической прогрессии.

Чтобы найти сумму бесконечной геометрической прогрессии, не надо складывать все ее члены. Для этого существует замечательная и довольно простая формула.

 

Сумма S геометрической прогрессии вычисляется по формуле:

b1                                                                        S = ————                                                                                  1 – q b1 – первый член геометрической прогрессии; q – знаменатель прогрессии; |q| < 1.

 

Решим наш пример с помощью этой формулы.

В нем b₁ = 2, q = 1/2. Итак:

               2                    2
S  =  ————  =  ———— = 4.
          1 – 1/2               1/2

Пример решен.

raal100.narod.ru

Геометрическая прогрессия решение задач онлайн калькулятор.

Основные понятия и определения.

Геометрической прогрессией  называется числовая последовательность следующего вида:

где каждый член , начиная со второго, равен произведению предыдущего  члена и числа   , так называемого знаменателя геометрической прогрессии, а первый член прогрессии имеет конкретное значение.

Для наглядности можно привести следующие примеры геометрической прогрессии:

а) Это геометрическая прогрессия, у которой

б)  Это геометрическая прогрессия, у которой

в)  Это геометрическая прогрессия, у которой

г)  Это геометрическая прогрессия, у которой

Можно заметить, что если и , то геометрическая прогрессия возрастающая. А если и , то геометрическая прогрессия убывающая.

Если отбросить все члены геометрической прогрессии, которые следуют за выбранным конкретным числом, то она станет конечной.

Для вычисления n-ого члена геометрической прогрессии  используется следующая формула:

Необходимо знать, что  квадрат каждого члена геометрической прогрессии (кроме первого и последнего) равен произведению предшествующего и последующего членов этой прогрессии (характеристическое свойство геометрической прогрессии):

Для вычисления суммы n членов конечной геометрической прогрессии используется формула:

Для вычисления суммы членов бесконечно убывающей геометрической прогрессии используется формула:

Пример 1: Составить формулу n-ого члена числовой последовательности

Легко заметить, что данная числовая последовательность является геометрической прогрессией, у которой

Составим формулу n-ого члена:

Ответ:

Пример 2: Составить формулу n-ого члена числовой последовательности

Легко заметить, что данная числовая последовательность является геометрической прогрессией, у которой

Составим формулу n-ого члена:

Ответ:

Пример 3: Составить формулу n-ого члена числовой последовательности

Легко заметить, что данная числовая последовательность является геометрической прогрессией, у которой

Составим формулу n-ого члена:

Ответ:

 

 

Пример 4: Дана геометрическая прогрессия

а) Известно, что . Найти .

б) Известно, что . Найти .

в) Известно, что . Найти .

г) Известно, что . Найти .

Во всех случаях в основе будет лежать формула для вычисления n-ого члена геометрической прогрессии:

а) Так как необходимо найти пятый член геометрической прогрессии, то мы имеем следующие условия: .

Воспользуемся вышеприведенной формулой:

б) Так как известно, что .

Найдем , используя вышеприведенную формулу:

в) Так как задан пятый член геометрической прогрессии, то мы имеем следующие условия: .

Найдем , используя вышеприведенную формулу:

г) Так как задан первый и восьмой член геометрической прогрессии, то мы имеем следующие условия: .

Найдем , используя вышеприведенную формулу:

 

Ответ: а) б) в)  г)

Пример 5: Между числами 2 и 18 вставьте три числа так, чтобы получилась геометрическая прогрессия.

 По условию задачи имеем:   Нужно найти . Составим формулу для пятого члена геометрической прогрессии, используя формулу вычисления n-ого члена:

Тогда, если, то имеем следующие члены геометрической прогрессии:

А если, то имеем следующие члены геометрической прогрессии:

Ответ: или

Пример 6: Фигура составляется из квадратиков так, как показано на рисунке. В каждом следующем ряду в 2 раза квадратов больше, чем в предыдущем. Сколько квадратов в 17 ряду?

 

Легко заметить, что данную задачу можно решить, опираясь на понятия геометрической прогрессии, у которой  так как в первом ряду фигуры четыре квадрата, а так как в каждом последующем ряду квадратов в 2 раза больше, чем в предыдущем.

Опираясь на полученные выводы, найдем :

Примечание: На примере данной задачи видно, что не целесообразно рисовать семнадцать рядов фигуры и считать количество квадратов в нем, как делают многие ученики, что ведет к большому числу ошибок. Гораздо разумнее увидеть, что задача сводится к нахождению n-ого члена геометрической прогрессии.

Ответ:

Пример 7: Разность между седьмым и пятым членами геометрической прогрессии равна 96, сумма пятого и шестого членов прогрессии равна 96. Найти пятнадцатый член этой прогрессии.

По условию задачи имеем:  Составим формулы для пятого, шестого и седьмого члена, используя формулу вычисления n-ого члена  геометрической прогрессии:

Подставим полученные формулы в записанное нами ранее условие задачи:

Составим систему уравнений и решим ее:

 

Подставив значение  во второе уравнение системы, получим , то есть .

Подставив значение  во второе уравнение системы, получим , то есть уравнение не имеет решений.

Таким образом, мы имеем геометрическую прогрессию, у которой .

Так как необходимо найти пятнадцатый член этой прогрессии, воспользуемся формулой вычисления n-ого члена  геометрической прогрессии:

 

Ответ:

Пример 8: Дана конечная геометрическая прогрессия

а) Известно, что . Найти сумму .

б) Известно, что. Найти .

Во всех случаях в основе будет лежать формула для вычисления суммы n членов конечной геометрической прогрессии:

а) Так как известно, что

Воспользуемся вышеприведенной формулой:

б) Так как известно, что.

Воспользуемся формулой вычисления n-ого члена  геометрической прогрессии:

Используем вышеприведенную формулу суммы:

Так как ранее мы получили, что , то имеем:

Ответ: а) б)

Пример 9: Дана бесконечно убывающая геометрическая прогрессия  Известно, что . Найти сумму .

В основе будет лежать формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии:

 

Ответ:

Пример 10: Найти сумму первых восьми членов геометрической прогрессии, у которой второй член равен 6, а четвертый равен 24.

Воспользуемся формулой вычисления n-ого члена  геометрической прогрессии и выразим второй и четвертый члены:

Так как по условию второй и четвертый члены геометрической прогрессии равны 6 и 24 соответственно, то составим систему уравнений:

Поделим второе уравнение системы на первое и получим:

Подставив значение  в первое уравнение системы, получим , то есть .

Подставив значение  в первое уравнение системы, получим , то есть .

В основе будет лежать формула для вычисления суммы n членов конечной геометрической прогрессии:

Если  и , то сумма первых восьми членов геометрической прогрессии будет вычислена следующим образом:

Если  и , то сумма первых восьми членов геометрической прогрессии будет вычислена следующим образом:

 

 

Ответ:  или

Пример 11: При каких значениях  числа ,  и  образуют конечную геометрическую прогрессию?

Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению:

Решим это уравнение:

При этом значении заданные выражения принимают соответственно значения . Это геометрическая прогрессия, у которой  

Ответ:

 

Автор статьи: Каташева Г.Г.

ktoreshit.ru

Прогрессия в геометрических задачах

Задачи по теме «Арифметическая и геометрическая прогрессии» в большинстве своем являются достаточно простыми. Для их решения используется всего лишь четыре формулы – это формулы нахождения n-ого члена прогрессии и формулы вычисления суммы n первых членов прогрессии. Однако сложность состоит в том, как и где увидеть в задаче прогрессию и правильно определить и записать необходимые формулы. Достаточно часто задачи на прогрессию встречаются и в геометрии, но суть их решения остается той же – записать нужную формулу и решить ее. Приведенные ниже примеры продемонстрируют вам это.

Пример 1.

Длины сторон AB, BC, AC треугольника ABC образуют в указанном порядке арифметическую прогрессию. Найти во сколько раз высота треугольника ABC, опущенная из вершины A на сторону BC, больше радиуса, вписанной в этот треугольник окружности.

Решение.

Рассмотрим треугольник ABC и проведем в нем высоту AH = h (рис. 1).

Зная, что стороны AB, BC, AC треугольника ABC образуют в указанном порядке арифметическую прогрессию, введем следующие обозначения. Пусть AB = a, тогда BC = a + d, а AC = a + 2d. Здесь d – это разность арифметической прогрессии. Теперь запишем формулы для вычисления площади треугольника.

Итак, во-первых, S_ABC можно вычислить с помощью высоты, проведенной из вершины A к стороне BC. Имеем:

S_ABC = 1/2 AH · BC = 1/2 · h · (a + d).

Во-вторых, площадь треугольника можно вычислить с помощью полупериметра и радиуса вписанной в этот треугольник окружности:

S_ABC = p · r = (AB + BC + CA)/2 · r = (a + a + d + a + 2d)/2 · r = (3a + 3d) · r = = 3(a + d)/2 · r.

Полученные для площади треугольника ABC выражения можно приравнять. Будем иметь:

½ · h · (a + d) = 3(a + d)/2 · r.

Левую и правую части полученного уравнения можно сократить на (a + d) ≠ 0.

1/2 h = 3/2 r. Выразим h:

h = 3 r.

Таким образом, мы получили, что высота треугольника в три раза больше радиуса вписанной в этот треугольник окружности.

Ответ: 3.

Пример 2.

В окружность радиусом √3 вписан правильный треугольник, в треугольник вписана окружность, в окружность снова вписан правильный треугольник и т.д. Найти сумму периметров всех треугольников.

Решение.

1) Так как радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной около этого треугольника окружности, то радиус окружности, описанной коло треугольника A₁A₂A₃ (R₁ = √3) в два раза больше радиуса окружности, описанной около треугольника B₁B₂B₃ (R₂ = R₁/2). Он же, в свою очередь, в два раза больше радиуса окружности, описанной около треугольника C₁C₂C₃ (R₃ = R₂/2 = R₁/4) и т. д. (R_n = R₁/2^{n — 1}) (рис. 2).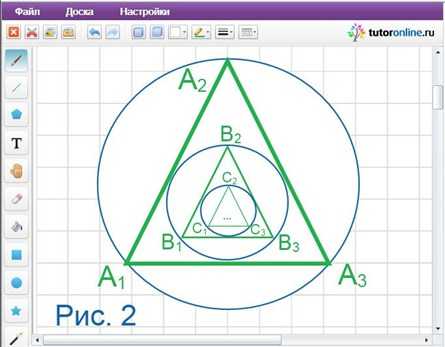

2) Выразим стороны правильных треугольников через радиусы описанных около них окружностей по формуле a₃ = R√3. Тогда имеем:

A₁A₂ = R₁√3;

B₁B₂ = R₂√3 = R₁√3/2;

C₁C₂ = R₃√3 = R₁√3/4 и т. д.

Периметры соответствующих треугольников равны:

P_A1A2A3 = 3R₁√3;

P_B1B2B3 = 3R₁√3/2;

P_C1C2C3 = 3R₁√3/4 и т. д.

Сумма периметров треугольников (3R₁√3 + 3R₁√3/2 + 3R₁√3/4 + …) представляет собой сумму бесконечно убывающей геометрической прогрессии со знаменателем q = 1/2 и первым членом a₁ = 3R₁√3 = 3 · √3 · √3 = 9.

С помощью формулы суммы бесконечно убывающей геометрической прогрессии S = a₁/(1 – q) находим, что

P_A1A2A3 + P_B1B2B3 + P_C1C2C3 + … = 9/(1 – 1/2) = 18.

Ответ: 18.

К большинству задач по геометрии, а уж тем более к тем из них, в которых необходимо побороться с прогрессией, многие ученики – пользователи нашего сайта – относятся в лучшем случае настороженно. Но когда с помощью наших онлайн репетиторов ученики вдруг начинают понимать ход решения задачи и видеть, какие правила и формулы можно и нужно применять в той или иной ситуации, их чувство самооценки растет и заставляет стремиться к новым свершениям.

Самое главное в решении задач – это научиться не просто, отрешенно вчитываться в текст, а быть настроенным на получение конечного результата. Только тогда решение любой задачи станет приятным и легким делом, не будет ставить в тупик, а будет давать пищу для воображения и ума.

Решение задач – это по-настоящему творческий процесс, и Вы почувствуете это, занимаясь с нами.  

 Остались вопросы? Не знаете, как решать задачи по геометрии?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru