Как перевести логарифм в число – Внеклассный урок — Логарифмы. Логарифм. Потенцирование. Логарифмирование.
Число в виде логарифма | Логарифмы
Как представить число в виде логарифма?
Используем определение логарифма.
Логарифм — это показатель степени, в которую надо возвести основание, чтобы получить число, стоящее под знаком логарифма.
Таким образом, чтобы представить некоторое число c в виде логарифма по основанию a, надо под знак логарифма поставить степень с тем же основанием, что и основание логарифма, а в показатель степени записать это число c:
Примеры.
В виде логарифма можно представить абсолютно любое число — положительное, отрицательное, целое, дробное, рациональное, иррациональное:
Чтобы в стрессовых условиях контрольной или экзамена не перепутать a и c, можно воспользоваться таким правилом для запоминания:
то, что внизу, идёт вниз, то, что вверху, идёт вверх.
Например, нужно представить число 2 в виде логарифма по основанию 3.
У нас есть два числа — 2 и 3. Эти числа — основание и показатель степени, которую мы запишем под знак логарифма. Остаётся определить, которое из этих чисел нужно записать вниз, в основание степени, а которое — вверх, в показатель.
Основание 3 в записи логарифма стоит внизу, значит, когда мы будем представлять двойку в виде логарифма по основанию 3, 3 также запишем вниз, в основание. 2 стоит выше тройки. И в записи степени двойку запишем выше тройки, то есть, в показатель степени:
www.logarifmy.ru
число в виде логарифма | математика-повторение
Под знаком логарифма могут находиться только положительные числа, причем, основание логарифма не равно единице.
Примеры.
I. Представить число 2 в виде логарифма по основанию: 1) 3; 2) 5; 3) 10.
Решение.
1) 2=log33²=log39;
2) 2=log55²=log525;
3) 2=lg10²=lg100.
II. Представить в виде десятичного логарифма числа: 1) -1; 2) -2; 3) -3.
Решение.
1) -1=lg10—1=lg0,1;
2) -2=lg10-2=lg0,01;
3) -3=lg10-3=lg0,001.
Решить уравнение:
1) lg (x-9)+lg (2x-1)=2.
Решение.
lg ((x-9)(2x-1))=lg102; представили сумму логарифмов в виде логарифма произведения и число 2 в правой части равенства записали в виде десятичного логарифма (логарифма с основанием 10).
lg (2x2-18x-x+9)=lg100; упростили выражения под знаками логарифмов.
2x2-19x+9=100; получили после потенцирования.
2x2-19x-91=0. Получили квадратное уравнение вида: ax2+bx+c=0.
a=2, b=-19, c=-91. Решим квадратное уравнение по общей формуле.
D=b2-4ac=(-19)2-4∙2∙(-91)=361+728=1089=332>0; два действительных корня:
Проверка. Значение х=-3,5 не удовлетворяет условию существования логарифма.
Проверяем данное равенство при х=13.
lg (13-9)+lg (2∙13-1)=2;
lg4+lg25=2;
lg (4∙25)=2;
lg100=2;
2=2.
Ответ: 13.
2) log3(x+1)+log3(x+3)=1.
Решение.
Сумму логарифмов заменим логарифмом произведения, единицу в правой части представим в виде логарифма с основанием 3:
log ((x+1)(x+3))=log33;
log (x2+x+3x+3)=log33. Потенцируем:
x2+4x+3=3;
x2+4x=0;
x (x+4)=0;
x=0 или x+4=0, отсюда x=-4.
Анализируем результаты:
х=-4 не подойдет, так как при этом значении под знаком логарифма окажутся отрицательные числа, что недопустимо.
Проверим значение х=0.
Проверка.
log3(0+1)+log3(0+3)=1;
log31+log33=1;
0+1=1;
1=1.
Ответ: 0.
www.mathematics-repetition.com
Логарифмы / math5school.ru
Формулы перехода от десятичного к натуральному логарифму и наоборот
Определение логарифма
Логарифмом положительного числа b по основанию а (a > 0, a ≠ 1) называется такой показатель степени c, в которую нужно возвести число а, чтобы получить число b.
Записывают: с = loga b, что означает a c= b.
Из определения логарифма следует справедливость равенства:
a loga b = b, (а > 0, b > 0, a ≠ 1),
называемого основным логарифмическим тождеством.
В записи loga b число
Из определения логарифмов вытекают следующие важные равенства:
loga 1 = 0,
loga а = 1.
Первое следует из того, что a 0 = 1, а второе – из того, что a 1 = а. Вообще имеет место равенство
loga a r = r.
Свойства логарифмов
Для положительных действительных чисел a (a ≠ 1), b, c справедливы следующие соотношения:
loga (b · c) = loga b + loga c
loga (b ⁄ c) = loga b – loga c
loga b p = p · loga b
loga q b = 1/q · loga b
loga q b p = p/q · loga b
loga pr b ps = loga r b s
loga b = logc b ⁄ logc a (c ≠ 1)
loga b = 1 ⁄ logb a (b ≠ 1)
loga
c loga b = b loga c
Замечание 1. Если а > 0, a ≠ 1, числа b и c отличны от 0 и имеют одинаковые знаки, то
loga (b · c) = loga |b| + loga |c|
loga (b ⁄ c) = loga |b| – loga |c| .
Замечание 2. Если p и q – чётные числа, а > 0, a ≠ 1 и b ≠ 0, то
loga pr b ps = loga r |b s|
loga q b p = p/q · loga |b| .
Для любых положительных, отличных от 1 чисел a и b верно:
loga b > 0 тогда и только тогда, когда a > 1 и b > 1 или 0 < a < 1 и 0 < b < 1;
loga b < 0 тогда и только тогда, когда
Десятичный логарифм
Десятичным логарифмом называется логарифм, основание которого равно 10.
Обозначаются символом lg:
log10 b = lg b.
Десятичные логарифмы до изобретения в 70-х годах прошлого века компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня.
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже – с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log, Log, Log10, причём следует иметь в виду, что первые два варианта могут относиться и к натуральному логарифму.
Таблица десятичных логарифмов целых чисел от 0 до 99
| Десятки | Единицы | |||||||||
| 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | – | 0 | 0,30103 | 0,47712 | 0,60206 | 0,69897 | 0,77815 | 0,84510 | 0,90309 | 0,95424 |
| 1 | 1 | 1,04139 | 1,07918 | 1,11394 | 1,14613 | 1,17609 | 1,20412 | 1,23045 | 1,25527 | 1,27875 |
| 2 | 1,30103 | 1,32222 | 1,34242 | 1,36173 | 1,38021 | 1,39794 | 1,41497 | 1,43136 | 1,44716 | 1,46240 |
| 3 | 1,47712 | 1,49136 | 1,50515 | 1,51851 | 1,53148 | 1,54407 | 1,55630 | 1,56820 | 1,57978 | 1,59106 |
| 4 | 1,60206 | 1,61278 | 1,62325 | 1,63347 | 1,64345 | 1,65321 | 1,66276 | 1,67210 | 1,68124 | 1,69020 |
| 5 | 1,69897 | 1,70757 | 1,71600 | 1,72428 | 1,73239 | 1,74036 | 1,74819 | 1,75587 | 1,76343 | 1,77085 |
| 6 | 1,77815 | 1,78533 | 1,79239 | 1,79934 | 1,80618 | 1,81291 | 1,81954 | 1,82607 | 1,83251 | 1,83885 |
| 7 | 1,84510 | 1,85126 | 1,85733 | 1,86332 | 1,86923 | 1,87506 | 1,88081 | 1,88649 | 1,89209 | 1,89763 |
| 8 | 1,90309 | 1,90849 | 1,91381 | 1,91908 | 1,92428 | 1,92942 | 1,93450 | 1,93952 | 1,94448 | 1,94939 |
| 9 | 1,95424 | 1,95904 | 1,96379 | 1,96848 | 1,97313 | 1,97772 | 1,98227 | 1,98677 | 1,99123 | 1,99564 |
Натуральный логарифм
Натуральным логарифмом называется логарифм, основание которого равно числу е, математической константе, являющейся иррациональным числом, к которому стремится последовательность
аn = (1 + 1/n)n при n → +∞.
Иногда число e называют числом Эйлера или числом Непера. Значение числа е с первыми пятнадцатью цифрами после запятой следующее:
е = 2,718281828459045… .
Натуральный логарифм обозначаются символом ln:
loge b = ln b.
Натуральные логарифмы являются самыми удобными при проведении различного рода операций, связанных с анализом функций.
Таблица натуральных логарифмов целых чисел от 0 до 99
| Десятки | Единицы | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | – | 0 | 0,69315 | 1,09861 | 1,38629 | 1,60944 | 1,79176 | 1,94591 | 2,07944 | 2,19722 |
| 1 | 2,30259 | 2,39790 | 2,48491 | 2,56495 | 2,63906 | 2,70805 | 2,77259 | 2,83321 | 2,89037 | 2,94444 |
| 2 | 2,99573 | 3,04452 | 3,09104 | 3,13549 | 3,17805 | 3,21888 | 3,25810 | 3,29584 | 3,33220 | 3,36730 |
| 3 | 3,40120 | 3,43399 | 3,46574 | 3,49651 | 3,52636 | 3,55535 | 3,58352 | 3,61092 | 3,63759 | 3,66356 |
| 4 | 3,68888 | 3,71357 | 3,73767 | 3,76120 | 3,78419 | 3,80666 | 3,82864 | 3,85015 | 3,87120 | 3,89182 |
| 5 | 3,91202 | 3,93183 | 3,95124 | 3,97029 | 3,98898 | 4,00733 | 4,02535 | 4,04305 | 4,06044 | 4,07754 |
| 6 | 4,09434 | 4,11087 | 4,12713 | 4,14313 | 4,15888 | 4,17439 | 4,18965 | 4,20469 | 4,21951 | 4,23411 |
| 7 | 4,24850 | 4,26268 | 4,27667 | 4,29046 | 4,30407 | 4,31749 | 4,33073 | 4,34381 | 4,35671 | 4,36945 |
| 8 | 4,38203 | 4,39445 | 4,40672 | 4,41884 | 4,43082 | 4,44265 | 4,45435 | 4,46591 | 4,47734 | 4,48864 |
| 9 | 4,49981 | 4,51086 | 4,52179 | 4,5326 | 4,54329 | 4,55388 | 4,56435 | 4,57471 | 4,58497 | 4,59512 |
Формулы перехода от десятичного к натуральному логарифму и наоборот
Так как lg е = 1 / ln 10 ≈ 0,4343, то lg b ≈ 0,4343 · ln b;
так как ln 10 = 1 / lg e ≈ 2,3026, то ln b ≈ 2,3026 · lg b.
math4school.ru
Логарифм корня | Логарифмы
Как преобразовать логарифм степени и логарифм корня?
Если под знаком логарифма стоит положительное выражение, показатель степени можно вынести за знак логарифма.
(x>0).
Например,
Если в показателе степени стоит сумма или разность, за знак логарифма выражение следует выносить, взяв его в скобки:
Если показатель степени под знаком логарифма — нечетное число, то основание степени должно быть положительным (так как при возведении в степень с нечётным показателем отрицательного числа результат — отрицательное число).
Таким образом,
Если выражение, стоящее под знаком логарифма, может принимать как положительные, так и отрицательные значения, то при вынесении за знак логарифма чётного показателя оставшееся основание степени нужно записать под знаком модуля.
Например,
Чтобы преобразовать логарифм корня, нужно от корня перейти к степени с дробным показателем, после чего воспользоваться предыдущим правилом.
Например,
Если выражение под корнем — степень с чётным показателем, после преобразования под знаком логарифма запишем его под знаком модуля:
www.logarifmy.ru
Как считать логарифм с калькулятором
Вычисление логарифмов в обучающем процессе зачастую заканчивается записью легкой формы логарифмического выражения. Впрочем на практике изредка нужно вычислить точное значение логарифма числа по заданному основанию. Причем точность логарифма изредка требуется достаточно высокая. Множество высчитываемых логарифмов являются иррациональными числами. Ранее числовое значение логарифма определялось по особым логарифмическим таблицам. Сегодня обнаружить логарифм числа дозволено с подмогой калькулятора, проведя ряд несложных действий.
Вам понадобится
- Инженерный калькулятор
Инструкция
1. В калькуляторе, как водится, присутствует функция вычисления естественного логарифма, то есть логарифма всякого числа по основанию е. Но исходя из свойств логарифма и правил проведения операций над ними, дозволено вычислить логарифм на калькуляторе по любому иному основанию. Для этого необходимо применить формулу перехода от основания е к необходимому вам новому основанию.
2. С учетом формулы перехода, исполните вычисление логарифма числа b по основанию а на калькуляторе, запоминая полученные промежуточные итоги в память устройства. Для этого вначале вычислите естественный логарифм числа а, которое является основанием вашего начального логарифма. Нажмите на калькуляторе клавишу [MC] для обнуления памяти калькулятора. После этого наберите число основания а и нажмите на функцию естественного логарифма [ln].
3. Сбережете полученное значение логарифма в память с подмогой кнопки [M+]. Дальше очистите окно итогов для дальнейших вычислений клавишей [C].
4. Вычислите настоящий логарифм числа b, заданного в вашем начальном логарифме. Для этого наберите на калькуляторе последовательность: вначале число b, потом [ln]. Получите логарифм заданного числа, но по основанию е.
5. Вычислите логарифм по заданному основанию а. Для этого надобно поделить, полученное последним, значение логарифма b на имеющееся в памяти промежуточное значение логарифма а. Нажмите ступенчато кнопки: [/] и [MR]. На экране высветиться первое вычисленное число. Произведите деление, нажав клавишу [=]. Калькулятор выдаст вам на экран значение, которое является логарифмом заданного числа a по основанию b.
Существует три вида инженерных калькуляторов: с обратной польской, арифметической и формульной записью. Бывают и такие калькуляторы, которые поддерживают переключения способов ввода выражений. Применение всего из них имеет свои особенности.

Инструкция
1. Определите, какой способ ввода поддерживает ваш калькулятор. Если на нем отсутствует клавиша со знаком равенства, но есть клавиша со стрелкой, направленной вверх, перед вами — машинка с обратной польской записью. Присутствие клавиши со знаком равенства говорит о том, что в приборе применяется арифметический способ ввода. Наконец, если индикатор калькулятора, помимо сегментных знакомест, имеет еще и матричные, то агрегат рассчитан на формульную запись. В последнем случае, взамен знака равенства на соответствующей клавише может быть нанесено слово «EXE» либо «Enter».
2. Дабы произвести расчет на калькуляторе с обратной польской записью, нужно сначала определить очередность выполнения действий. Делается это по общепризнанным математическим правилам.Действия с двумя операндами исполняйте дальнейшим образом. Введите 1-й операнд. Нажмите кнопку со стрелкой вверх, дабы перенести его на один регистр стека вверх. Введите 2-й операнд, и лишь позже этого нажмите на клавишу математического действия. На индикаторе отобразится итог вычисления.Для выполнения действия с одним операндом легко введите его, а после этого нажмите на соответствующую этому действию кнопку.
3. На калькуляторе с арифметической записью действия с двумя операндами исполняйте так же, как на обыкновенном калькуляторе. Действия же с одним операндом исполняйте так же, как на машинке с обратной польской записью.Если на клавиатуре присутствуют клавиши со скобками, надобность в определении очередности вычислений отсутствует. Следует, впрочем, не допускать превышения яруса вложенности скобок, указанного в инструкции. При отсутствии инструкции определить данный ярус дозволено опытным путем, нажав клавишу с открывающей скобкой несколько раз и подметив, позже которого по счету нажатия появилось сообщение об ошибке.
4. В калькулятор с формульной записью выражение вводят так же, как оно записывается на бумаге. Если поле ввода однострочное, формулы, содержащие дроби, преобразовывают в «одноэтажные» с подмогой скобок и знака деления. При необходимости, введенное выражение дозволено скорректировать, пользуясь клавишами с горизонтальными стрелками, а также кнопками «Insert», «Backspace» и «Delete» (на различных калькуляторах их наименования могут различаться). После этого нажимают клавишу «EXE» либо «Enter» и получают итог. Если данный итог требуется разместить в следующую формулу, пользуются клавишей «ANS».
5. Во многих калькуляторах некоторые из клавиш способны исполнять больше одной функции. Примитивное нажатие клавиши соответствует выполнению той операции, наименование которой указано прямо на ней. Другие операции обозначены рядом с кнопкой тем либо другим цветом. Дабы принудить калькулятор исполнить такую функцию, следует вначале нажать регистровую клавишу, имеющую тот же цвет (она может именоваться «F», «2ndF», «S»), а после этого — кнопку, рядом с которой указана надобная вам операция.
Видео по теме
Логарифмы применяются при решении тех уравнений в математике и прикладных науках, в которых неведомые величины присутствуют как показатели степени. Логарифм с основанием, равным константе «e» («число Эйлера», 2,718281828459045235360…), именуется «естественным» и записывается почаще каждого как ln(x). Он показывает степень, в которую следует построить константу e, дабы получить число, указанное в качестве довода естественного логарифма (x).
Инструкция
1. Используйте калькулятор для вычисления естественного логарифма. Это может быть, скажем, калькулятор из базового комплекта программ операционной системы Windows. Ссылка на его запуск упрятана достаточно велико в основное меню ОС — раскройте его щелчком по кнопке «Пуск», после этого откройте его раздел «Программы», перейдите в подраздел «Типовые», а после этого в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Дозволено взамен мыши и перемещений по меню применять клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.
2. Переключите интерфейс калькулятора в расширенный режим, дозволяющий осуществлять вычисления логарифмов. По умолчанию он открывается в «обыкновенном» виде, а вам необходим «инженерный» либо «ученый» (в зависимости от версии применяемой ОС). Раскройте в меню раздел «Вид» и выберите соответствующую строку.
3. Введите довод, естественный логарифм которого необходимо вычислить. Это дозволено сделать как с клавиатуры, так и щелкая мышкой соответствующие кнопки в интерфейсе калькулятора на экране.
4. Кликните кнопку с надписью ln — программа рассчитает логарифма по основанию e и покажет итог.
5. Воспользуйтесь каким-нибудь из онлайн-калькуляторов в качестве альтернативного варианта вычисления значения естественного логарифма. Скажем, тем, тот, что расположен по адресу http://calc.org.ua. Его интерфейс предельно примитивен — есть исключительное поле ввода, куда вам нужно впечатать значение числа, логарифм от которого нужно вычислить. Среди кнопок обнаружьте и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ожидания результата, следственно итог вычисления вы получите фактически мигом. Исключительная специфика, которую следует рассматривать — разделителем между дробной и целой частью вводимого числа тут неукоснительно должна быть точка, а не запятая.
На практике почаще каждого используются десятичные логарифмы, которые принято называть стандартными. Для их нахождения составлены особые таблицы, применяя которые дозволено обнаружить значение логарифма всякого правильного числа с той либо другой точностью, заранее приведя его к стандартному виду. Для решения большинства задач абсолютно довольны четырехзначные таблицы Брадиса с точностью до 0,0001, которые содержатся мантиссы десятичных логарифмов. Отзыв дозволено легко обнаружить по одному виду числа. Обращение с таблицами крайне примитивное.

Вам понадобится
- — формула перехода от одного основания логарифма к иному;
- — четырехзначные математические таблицы Брадиса.
Инструкция
1. Приведите логарифм к стандартному виду, если его основание не равно 10. Используйте формулу перехода от одного основания к иному.
2. Обнаружьте отзыв логарифма. Если число огромнее либо равно единице, то сосчитайте число цифр в целой части данного числа. Отнимите из этого числа единицу и получите значение колляции. Скажем, у логарифма числа 56,3 колляция равна 1. Если число является десятичной дробью, меньшей 1, то сосчитайте в ней число нулей до первой цифры, чудесной от нуля. Сделайте негативным подученное значение колляции. Скажем, у логарифма числа 0,0002 колляция равна -4.
3. Определите число для нахождения мантиссы как целое. Проигнорируйте в данном числе запятую, если она есть и отбросьте все нули, стоящие в конце числа. Расположение запятой в десятичном числе и последние нули никаким образом не влияют на величину мантиссы. Запишите образовавшееся целое число. Скажем, у логарифма числа 56,3 оно равно 563. В зависимости от того, сколько цифр содержится в этом числе, зависит алгорифм работы с четырехзначными таблицами. Существует три типа алгорифмов.
4. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения является трехзначным. Обнаружьте в четырехзначных математических таблицах Брадиса таблицу XIII «Мантиссы десятичных логарифмов». Перейдите на строчку, содержащую в первом столбце «N» эти две первые цифры числа, по которому ищется мантисса. Скажем, если имеем число 563, то ищите строчку, где в первом столбе стоит 56. После этого продвигайтесь по этой строчке вправо до ее пересечения со столбцом, номер которого совпадает с третьей цифрой начального числа. В нашем примере это столбец с номером 3. На пересечении обнаруженной строки и столбца находится значение мантиссы. Мантисса, обнаруженная по числу 563 равна 0,7505.
5. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения состоит из 2-х либо одной цифры. Припишите мысленно к этому числу такое число нулей, дабы оно стало трехзначным. Если число равно 56, то получается 560. Обнаружьте мантиссу по полученному трехзначному числу. Для этого исполните действия из шага 4. Мантисса по числу 560 равна 0,7482.
6. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения является четырехзначным. Обнаружьте мантиссу для числа, изображенного первыми тремя цифрами данного числа. Для этого исполните действия из шага 4. После этого передвигайтесь по горизонтальной строке от обнаруженной мантиссы в правую часть таблицы, расположенную за вертикальной толстой чертой и содержащей поправки на четвертую цифру. Обнаружьте в области поправок столбец с номером, совпадающим с четвертой цифрой числа. Прибавьте поправку, находящуюся на пересечении строки и столбца, к мантиссе, обнаруженной по трехзначному числу. Скажем, если число для нахождения мантиссы равно 5634, то мантисса по 563 равна 0,7505. Поправка по цифре 4 равна 3. Окончательный итог равен 0,7508.
7. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее содержит больше четырех цифр. Округлите число до четырех знаков так, дабы все цифры, начиная с пятой, были нулями. Отбросьте последние нули и обнаружьте мантиссу по четырехзначному числу. Для этого исполните действия из шага 7.
8. Обнаружьте логарифм числа как сумму колляции и мантиссы. В рассматриваемом примере логарифм числа 56,3 равен 1,7505.
Видео по теме
Логарифмом числа x по основанию a именуется такое число y, что a^y = x. От того что логарифмы облегчают дюже многие фактические вычисления, значимо уметь ими пользоваться.

Инструкция
1. Логарифм числа x по основанию a будем обозначать loga(x). Скажем, log2(8) — логарифм числа 8 по основанию 2. Он равен 3, так как 2^3 = 8.
2. Логарифм определен только для позитивных чисел. Негативные числа и нуль не имеют логарифмов вне зависимости от основания. При этом сам логарифм может быть любым числом.
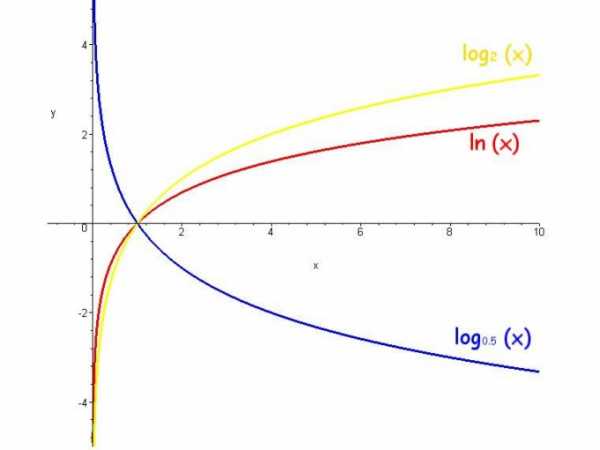
3. Основанием логарифма может служить всякое позитивное число, помимо единицы. Впрочем на практике почаще каждого применяются два основания. Логарифмы по основанию 10 именуются десятичными и обозначаются lg(x). Десятичные логарифмы почаще каждого встречаются в утилитарных вычислениях.
4. Второе знаменитое основание для логарифмов — иррациональное трансцендентное число e = 2,71828… Логарифм по основанию e именуется естественным и обозначается ln(x). Функции e^x и ln(x) владеют специальными свойствами, значимыми для дифференциального и интегрального исчисления, следственно настоящие логарифмы почаще применяются в математическом обзоре.
5. Логарифм произведения 2-х чисел равен сумме логарифмов этих чисел по тому же основанию: loga(x*y) = loga(x) + loga(y). Скажем, log2(256) = log2(32) + log2(8) = 8.Логарифм частного 2-х чисел равен разности их логарифмов: loga(x/y) = loga(x) — loga(y).
6. Дабы обнаружить логарифм числа, возведенного в степень, надобно логарифм самого числа умножить на показатель степени: loga(x^n) = n*loga(x). При этом показатель степени может быть любым числом — позитивным, негативным, нулем, целым либо дробным.От того что x^0 = 1 для всякого x, то loga(1) = 0 для всякого a.
7. Логарифм заменяет умножение сложением, возведение в степень умножением, а извлечение корня делением. Следственно в неимение вычислительной техники логарифмические таблицы приметно упрощают расчеты.Дабы обнаружить логарифм числа, не входящего в таблицу, его необходимо представить в виде произведения 2-х либо больше чисел, логарифмы которых есть в таблице, и обнаружить окончательный итог, сложив эти логарифмы.
8. Довольно легкой метод вычислить настоящий логарифм — воспользоваться разложением этой функции в степенной ряд:ln(1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*((x^n)/n).Данный ряд дает значения ln(1 + x) для -1 < x ?1. Иными словами, так дозволено вычислить естественные логарифмы чисел от 0 (но не включая 0) до 2. Настоящие логарифмы чисел за пределами этого ряда дозволено обнаружить путем суммирования обнаруженных, пользуясь тем, что логарифм произведения равен сумме логарифмов. В частности ln(2x) = ln(x) + ln (2).
9. Для фактических вычислений изредка бывает комфортно перейти от естественных логарифмов к десятичным. Всякий переход от одного основания логарифмов к иному совершается по формуле:logb(x) = loga(x)/loga(b).Таким образом, log10(x) = ln(x)/ln(10).
Знаменитый французский математик и звездочет XVIII-XIX столетий Пьер-Симон Лаплас утверждал, что изобретение логарифмов «продлило жизнь астрономам», ускорив процесс вычислений. И подлинно, взамен того, дабы умножать многозначные числа, довольно обнаружить по таблицам их логарифмы и сложить их.
Инструкция
1. Логарифм — один из элементов элементарной алгебры. Слово «логарифм» происходит от греческого «число, отношение» и обозначает степень, в которую нужно построить число, стоящее в основании, дабы получить итоговое число. Скажем, запись «2 в 3 степени равно 8» дозволено представить как log_2 8 = 3. Существуют вещественные и комплексные логарифмы.
2. Логарифм вещественного числа имеет место только при правильном основании, не равном 1, и для итогового числа огромнее нуля. Особенно используемыми основаниями логарифмов являются число е (экспонента), 10 и 2. При этом логарифмы называют, соответственно, естественными, десятичными и двоичными и записывают как ln, lg и lb.
3. Основное логарифмическое тождество a^log_a b = b. Простейшие правила логарифмов вещественных чисел: log_a a=1 и log_a 1=0. Основные формулы приведения: логарифм произведения — log_a (b*c) = log_a |b| + log_a |c|;логарифм частного — log_a (b/c) = log_a |b| — log_a |c|, где b и c — позитивные.
4. Логарифмической функцией именуется логарифм переменного числа. Область значений такой функции — бесконечность, ограничения — основание правильное и не равно 1, причем функция нарастает при основании огромнее 1 и убывает при основании от 0 до 1.
5. Логарифмическую функцию комплексного числа называют многозначной, так как для всякого комплексного числа существует логарифм. Это следует из определения комплексного числа, которое состоит из вещественной части и мнимой. И если для вещественной части логарифм определяется однозначно, то для мнимой неизменно имеется безмерное уйма решений. Для комплексных чисел применяются, в основном, настоящие логарифмы, так как такие логарифмические функции связаны с числом е (экспонентой) и используются в тригонометрии.
6. Логарифмы находят использование не только в математике, но и в иных областях науки, скажем: физике, химии, астрономии, сейсмологии, истории и даже теории музыки (звуков).
7. 8-значные таблицы логарифмической функции наравне с тригонометрическими впервой опубликовал шотландский математик Джон Непер в 1614 году. В России особенно вестимы таблицы Брадиса, изданные впервой в 1921 году. В реальное же время для подсчета логарифмических и других функций применяются калькуляторы, следственно применение печатных таблиц ушло в прошлое.
Видео по теме
Полезный совет
Число е — экспонента, ее значение равно 2,7182818281828…. Существует вестимая мнемоническая фраза для запоминания: «Экспоненту помнить метод есть легкой: два и семь десятых, двукратно Лев Толстой», где «Лев Толстой» = «1828» (год рождения писателя).
Термин «логарифм » случился от 2-х греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую нужно построить непрерывное значение (основание), дабы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом «e», то логарифм называют «естественным».

Вам понадобится
- Доступ в интернет, Microsoft Office Excel либо калькулятор.
Инструкция
1. Воспользуйтесь во множестве представленными в интернете онлайн-калькуляторами — это, вероятно, самый стремительный и примитивный метод вычисления естественного логарифм а. Поиском соответствующего обслуживания вам заниматься не придется, потому что многие поисковые системы и сами имеют встроенные калькуляторы, абсолютно пригодные для работы с логарифм ами. Скажем, перейдите на основную страницу самого огромного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций тут не понадобится, примитивно наберите в поле ввода запроса необходимое математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет абсолютно довольно, дабы Google отобразил верный результат с точностью до восьми знаков позже запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
2. Используйте соответствующую встроенную функцию, если надобность вычисления значения естественного логарифм а появляется при работе с данными в знаменитом табличном редакторе Microsoft Office Excel. Эта функция тут вызывается с применением общепризнанного обозначения такого логарифм а в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен итог вычисления, и введите знак равенства — так в этом табличном редакторе обязаны начинаться записи в ячейках, содержащих формулы. После этого наберите наименование функции (LN) и в скобках укажите числовое значение, логарифм которого требуется вычислить — скажем, =LN(457). Позже того, как вы нажмете Enter, в этой ячейке таблицы отобразится итог вычисления естественного логарифм а.
3. Откройте программу-калькулятор, которая устанавливается совместно с операционной системой, если оба приведенных выше метода вам не подходят. Обнаружить соответствующую ссылку в ОС Windows 7 дозволено, если раскрыть основное меню щелчком по кнопке «Пуск», а после этого ввести «каль» в поле «Обнаружить программы и файлы». Ссылка с наименованием «Калькулятор» будет первой строкой в итоге поиска. В иных версиях ОС ее нужно искать в подразделе «Типовые» раздела «Все программы» основного меню. Переключите калькулятор в больше функциональный режим, нажав сочетание клавиш Alt + 2. После этого введите значение, настоящий логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит итог.
Видео по теме
jprosto.ru
Внеклассный урок — Логарифмы. Логарифм. Потенцирование. Логарифмирование.
Логарифмы
Логарифм числа b по основанию а – это показатель степени, в которую нужно возвести число а, чтобы получить число b.
Формула | Примеры |
loga b = c (при a > 0, a ≠ 1, b > 0). Это означает, что ac = b. | log525 = 2 Читается так: логарифмом числа 25 по основанию 5 является 2.
log464 = 3 Логарифмом числа 64 по основанию 4 является 3. |

Говоря иначе, логарифмирование – это действие, обратное возведению в степень.
Логарифм по основанию 10 называют десятичным логарифмом.
Примеры десятичного логарифма:
log10 100
log10 5
log10 0,01
Десятичный логарифм обозначают символом lg. Таким образом:
вместо log10 100 следует писать lg 100;
вместо log10 5 пишем lg 5;
вместо log10 0,01 пишем lg 0,01.
Логарифмирование и потенцирование.
Логарифмирование – это нахождение логарифмов заданных чисел или выражений.
b
Пример: Найдем логарифм x = a2 · — .
c
Решение.
Последовательно воспользуемся сразу всеми тремя основными свойствами логарифмов, которые изложены выше (логарифм произведения, логарифм частного и логарифм степени):
b
lg x = lg (a2 · —) = lg a2 + lg b – lg c = 2lg a + lg b – lg c.
c
Потенцирование – это нахождение чисел или выражений по данному логарифму числа (выражения).
Потенцировать – значит освобождаться от значков логарифмов в процессе решения логарифмического выражения.
Например, надо решить уравнение log2 3x = log2 9.
Убираем значки логарифмов – то есть потенцируем:
3х = 9.
В результате получаем простое уравнение, которое решается за несколько секунд:
х = 9 : 3 = 3.
Но потенцирование не сводится к простому и произвольному убиранию значков логарифмов. Для этого в обоих частях уравнения как минимум должно быть одинаковое значение основания (в нашем случае это число 2). Подробнее о потенцировании и его правилах – в следующем разделе.
raal100.narod.ru
