Как найти среднее квадратическое отклонение пример – Показатели вариации признака (среднее линейное отклонение, дисперсия простая и взвешенная), среднее квадратическое отклонение.

Как найти среднеквадратическое отклонение

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом  (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

• Определите среднее (простое среднее арифметическое ряда значений).
• Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
• Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее   мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить

отклонение роста каждой из собак от среднего:

   

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

• Когда мы имеем дело с генеральной совокупностью при вычислении дисперсии, мы делим на  (как и было сделано в рассмотренном нами примере).
• Когда мы имеем дело с выборкой, при вычислении дисперсии делим на .

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки =  мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

.

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

.

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

.

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

.

Для второго примера получится:

.

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

yourtutor.info

Среднее квадратическое отклонение, Линейное отклонение

Среднее квадратическое отклонение

Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:

1. Для первичного ряда:

2. Для вариационного ряда:

Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:

Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.

Примеры нахождения cреднего квадратического отклонения: Пример 1, Пример 2

Для альтернативных признаков формула среднего квадратичного отклонения выглядит так:

где р — доля единиц в совокупности, обладающих определенным признаком;

q — доля единиц, не обладающих этим признаком.

Понятие среднего линейного отклонения

Среднее линейное отклонение определяется как средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средних арифметических.

1. Для первичного ряда:

2. Для вариационного ряда:

где сумма n — сумма частот вариационного ряда.

Пример нахождения cреднего линейного отклонения: Пример 1

Преимущество среднего абсолютного отклонения как меры рассеивания перед размахом вариации, очевидно, так как эта мера основана на учете всех возможных отклонений. Но этот показатель имеет существенные недостатки. Произвольные отбрасывания алгебраических знаков отклонений могут привести к тому, что математические свойства этого показателя являются далеко не элементарными. Это сильно затрудняет использование среднего абсолютного отклонения при решении задач, связанных с вероятностными расчетами.

Поэтому среднее линейное отклонение как мера вариации признака применяется в статистической практике редко, а именно тогда, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется оборот внешней торговли, состав работающих, ритмичность производства и т. д.

Среднее квадратическое

Среднее квадратическое применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.

Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.

Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

Средняя квадратичная взвешенная вычисляется по формуле:

где f — признак веса.

Средняя кубическая

Средняя кубическая применяется, например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:

Средняя кубическая взвешенная:

При расчете средних величин и дисперсии в интервальных рядах распределения истинные значения признака заменяются центральными значениями интервалов, которые отличны от средней арифметической значений, включенных в интервал. Это приводит к возникновению систематической погрешности при расчете дисперсии. В.Ф. Шеппард определил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала как в сторону повышения, так и в сторону понижения величины дисперсии.

Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по значительному количеству исходных данных (n > 500). Однако исходя из того, что в ряде случаев обе погрешности, действуя в разных направлениях компенсируют друг друга, можно иногда отказаться от введения поправок.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина.
В практике статистики часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для таких сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.

Для осуществления таких сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с разными средним арифметическим используется относительный показатель вариации — коэффициент вариации.

Структурные средние

Для характеристики центральной тенденции в статистических распределениях не редко рационально вместе со средней арифметической использовать некоторое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.

Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.

Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

univer-nn.ru

Дисперсия и среднее квадратичное отклонение. Примеры вычисления

Математическое ожидание не дает достаточно полной информации о случайной величине, поскольку одному и тому же значению математического ожидания может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.

Например. Законы распределения двух случайных величин и заданные таблицами:

Вычислить математическое ожидание и

Решение. Находим математическое ожидание по класической формуле

Получили, что для двух различных законов распределения математическое ожидание принимает одинаковое значения (0), при этом возможные значения случайных величин и различаются. Из приведенного примера видно, что в случае равенства математических ожиданий случайные величин и имеют тенденцию к колебаниям относительно и причем имеет больший размах рассеяния относительно сравнительно случайной величине относительно . Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.

Для определения дисперсии рассматривается отклонение случайной величины от своего математического ожидания

Математическое ожидание такого отклонения случайной величины всегда равна нулю. В этом легко убедиться из следующего соотношения

Таки образом, отклонение не может быть мерой рассеивания случайной величины.

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от своего математического ожидания

Для дискретной случайной величины дисперсия вычисляется по формуле

для непрерывной находят интегрированием

Если непрерывная величина заданная на интервале то дисперсия равна интегралу с постоянными пределами интегрирования

Дисперсия обладает следующими свойствами

1. Если случайная величина состоит из одной тотчки — постоянная величина, то дисперсия равна нулю

2. Дисперсия от произведения постоянной на случайную величину равна квадрату постоянной умноженной на дисперсию случайной величины

3. Если и — постоянные величины, то для дисперсии справедлива зависимость

Это следует из двух предыдущих свойств.

Дисперсию можно вычислить по упрощенной формуле:

которая в случае дискретной случайной величины имеет вид

для непрерывной определяется зависимостью

и для непрерывной на промежутке соотношением

Приведенные формулы очень удобны в вычислениях, и их, в отличие от предыдущих, используют в обучении

Также следует помнить, что дисперсия всегда принимает неотрицательные значения . Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.

Для сравнения удобно пользоваться числовыми характеристиками одинаковой размерности случайной величиной. Для этого вводят в рассмотрение среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»

—————————————-

Рассмотрим примеры для ознакомления с практической стороной определения этих величин.

Пример 1. Закон распределения дискретной случайной величины заданы таблицей:

Вычислить дисперсию и среднее квадратическое отклонение .

Решение. Согласно свойствами дисперсии получим:

—————————————-

Пример2. Есть четыре электрические лампочки, каждая из которых имеет дефект с вероятностью ( — вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины — число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение

Решение. Дискретная случайная величина — число лампочек, которые будут опробованы — приобретает такие возможных значений:

Вычислим соответствующие вероятности:

Последнюю вероятность можно трактовать следующим образом: четвертая лампочка будет испытана, когда третья перегорит, а четвертая — нет, или если и четвертая перегорит.

В табличной форме закон распределения иметь следующий вид:

Для нахождения среднего квадратического отклонения найдем сначала значение дисперсии. Для дискретной случайной величины она примет значение:

Среднее квадратичное отклонение находим добычей корня квадратного из дисперсии.

—————————————-

Пример 3. Закон распределения вероятностей дискретной случайной величины заданы в виде функции

Вычислить среднее квадратическое отклонение и дисперсию

Решение. С помощью функции распределения вероятностей формируем закон распределения в виде таблицы

На основе таблицы распределения вычисляем дисперсию

————————

Подобных примеров можно привести множество, основная их суть в правильном применении приведенных в начале статьи формул для вычисления дисперсии и математического ожидания. Применяйте их там где это необходимо и не допускайте ошибок при определении дисперсии.

yukhym.com

Геометрическая простая

Для расчетов средней геометрической простой используется формула:

где:

• —цепной коэффициент роста

• —число этих коэффициентов роста

• П — знак произведения

• —количество уровней ряда

• —значение начального уровня ряда

• —значение конечного уровня ряда

Геометрическая взвешенная

Для определения средней геометрической взвешенной применяется формула:

редние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической.

Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:

Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.

Квадратическая простая

Средняя квадратическая простая вычисляется по формуле:

Квадратическая взвешенная

Средняя квадратическая взвешенная равна:

22. Абсолютные показатели вариации включают:

размах вариации

среднее линейное отклонение

дисперсию

среднее квадратическое отклонение

Размах вариации (r)

Размах вариации — это разность между максимальным и минимальным значениями признака

Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.

Пример

Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет. Решение: размах вариации = 9 — 2 = 7 лет.

Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .

При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю , либо возводить значения отклонений в квадрат

Среднее линейное и квадратическое отклонение

Среднее линейное отклонение — этосредняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

Среднее линейное отклонение простое:

Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.

В нашем примере: лет;

Ответ: 2,4 года.

Среднее линейное отклонение взвешенное применяется для сгруппированных данных:

Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).

Среднее квадратическое отклонение

Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака отсредней арифметической:

Среднее квадратическое отклонение простое:

Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.

Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.

studfiles.net

Среднее квадратическое отклонение.

Определение.Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии.

 

Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.

 

Пример. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины Х.

Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96.

Таким образом, закон распределения может считаться биноминальным.

 

Пример. Найти дисперсию дискретной случайной величины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления этого события в каждом испытании равны и известно, что М(Х) = 0,9.

Т.к. случайная величина Х распределена по биноминальному закону, то

Пример. Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63.

По формуле дисперсии биноминального закона получаем:

 

Пример. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р₁=0,3; p₂=0,4; p₃=0,5; p₄=0,6. Найти математическое ожидание и дисперсию числа отказавших приборов.

Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.

Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем .

1) Не отказал ни один прибор.

2) Отказал один из приборов.

0,302.

3) Отказали два прибора.

4) Отказали три прибора.

5) Отказали все приборы.

Получаем закон распределения:

x
x2
p	0,084	0,302	0,38	0,198	0,036

Математическое ожидание:

Дисперсия:

 

Средним квадратичным отклонениемназывается квадратный корень из дисперсии.

 

МодойМ₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

 

Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным.

 

Медианой M_D случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

 

Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

 

Начальным моментомпорядка k случайной величины Х называется математическое ожидание величины Х^k.

 

Для дискретной случайной величины: .

Для непрерывной случайной величины: .

Начальный момент первого порядка равен математическому ожиданию.

 

Центральным моментомпорядка k случайной величины Х называется математическое ожидание величины

 

Для дискретной случайной величины: .

Для непрерывной случайной величины: .

Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.

Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии.

 

Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

 

Кроме рассмотренных величин используются также так называемые абсолютные моменты:

Абсолютный начальный момент: .

Абсолютный центральный момент: .

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.

 

Пример. Для рассмотренного выше примера определить математическое ожидание и дисперсию случайной величины Х.

 

 

Пример. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.

Т.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или непоявления события в другом опыте).

Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна

Таким образом, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз.

Для составления закона распределения надо найти вероятности каждого из этих событий.

1) Белый шар не появился вовсе: 2) Белый шар появился один раз:

3) Белый шар появиться два раза: .

4) Белый шар появиться три раза:

5) Белый шар появиться четыре раза:

6) Белый шар появился пять раз:

Получаем следующий закон распределения случайной величины Х.

х
х2
р(х)	0,0102	0,0768	0,2304	0,3456	0,2592	0,0778

 

 

При решении практических задач зачастую точно найти закон распределения случайной величины довольно сложно. Однако, все происходящие процессы, связанные со случайными величинами, можно разделить на несколько типов, каждому из которых можно поставить в соответствие какой – либо закон распределения.

Выше были рассмотрены некоторые типы распределений дискретной случайной величины такие как биноминальное распределение и распределение Пуассона.

Рассмотрим теперь некоторые типы законов распределения для непрерывной случайной величины.

 

 

Лекция № 4

Тема: Формы представления статистических данных.

План:

1. Выборка из генеральной совокупности.

2. Статистический ряд.

 

lektsia.com

18. Среднее квадратическое отклонение, методика расчета, значение.

Приближенный метод оценки колеблемости вариационного ряда — определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение (σ — сигма). Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю.

3. Возводят каждое отклонение в квадрат d².

4. Перемножают квадраты отклонений на соответствующие частоты d²*p.

5. Находят сумму произведений ( d²*p)

6. Вычисляют среднее квадратическое отклонение по формуле:

при n больше 30, или при n меньше либо равно 30, где n — число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

— 68,3% значений вариант находится в пределах М1

— 95,5% значений вариант находится в пределах М2

— 99,7% значений вариант находится в пределах М3

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение — именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.

studfiles.net

81. Среднее квадратическое отклонение, методика расчета, применение.

Приближенный метод оценки колеблемости вариационного ряда — определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение (σ — сигма). Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю.

3. Возводят каждое отклонение в квадрат d².

4. Перемножают квадраты отклонений на соответствующие частоты d²*p.

5. Находят сумму произведений ( d²*p)

6. Вычисляют среднее квадратическое отклонение по формуле:

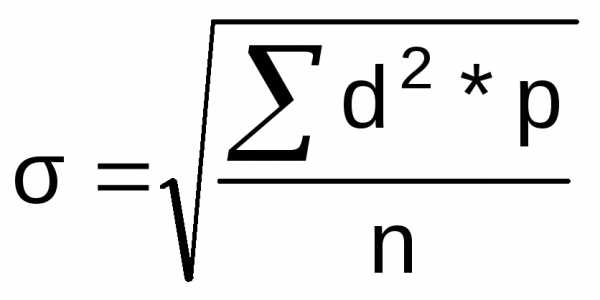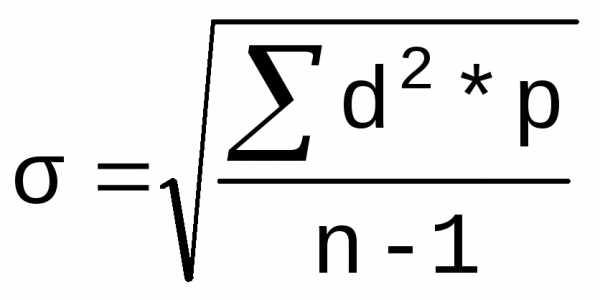при n больше 30, или при n меньше либо равно 30, где n — число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

— 68,3% значений вариант находится в пределах М1

— 95,5% значений вариант находится в пределах М2

— 99,7% значений вариант находится в пределах М3

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение — именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

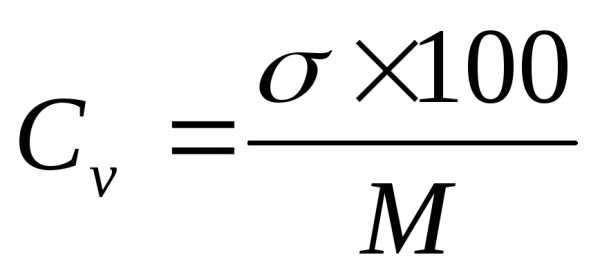
Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.

studfiles.net