Формулы корней тригонометрических уравнений таблица – Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия
Простейшими тригонометрическими уравнениями называют уравнения вида:
sin x = a , cos x = a ,
tg x = a , ctgx = a .
где a – произвольное число.
Решение уравнения sin x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения sin x = a представлено на рисунке 1

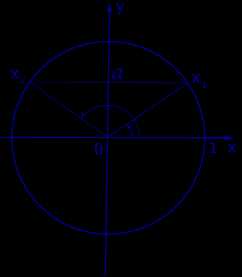
Рис. 1
Частные случаи решения уравнений sin x = a
Уравнение: sin x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: > |
Уравнение: sin x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: sin x = 1 Решение: |
Решение уравнения cos x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения cos x = a представлено на рисунке 2
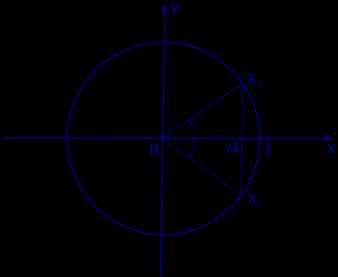
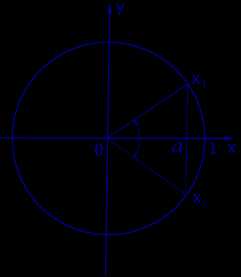
Рис. 2
Частные случаи решения уравнений cos x = a
Уравнение: cos x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 1 Решение: |
Решение уравнения tg x = a
| Обычная форма записи решения: | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.

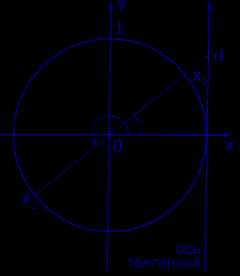
Рис. 3
Частные случаи решения уравнений tg x = a
Уравнение: Решение: |
Уравнение: tg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 0 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 1 Решение: |
Уравнение: Решение: |
Решение уравнения ctg x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
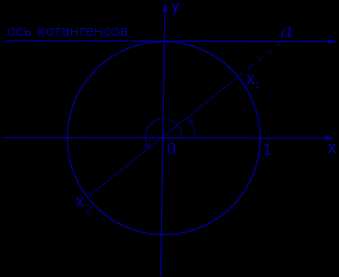
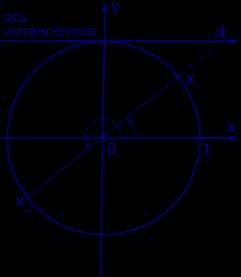
Рис. 4
Частные случаи решения уравнений ctg x = a
Уравнение: Решение: |
Уравнение: ctg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: ctg x = 0 Решение: |
Решение: |
Уравнение: ctg x = 1 Решение: |
Уравнение: Решение: |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Основные виды тригонометрических уравнений
Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.
\(\blacktriangleright\) Квадратные тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^2(x)+bf(x)+c=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos
x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к квадратному уравнению.
Часто при решении таких уравнений используются
основные тождества: \[\begin{array}{|ccc|}
\hline \sin^2 \alpha+\cos^2 \alpha =1&& \mathrm{tg}\, \alpha \cdot
\mathrm{ctg}\, \alpha
=1\\ &&\\
\mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos
\alpha}&&\mathrm{ctg}\, \alpha
=\dfrac{\cos \alpha}{\sin \alpha}\\&&\\
1+\mathrm{tg}^2\, \alpha =\dfrac1{\cos^2 \alpha} && 1+\mathrm{ctg}^2\, \alpha=\dfrac1{\sin^2 \alpha}\\&&\\
\hline
\end{array}\]
формулы двойного угла: \[\begin{array}{|lc|cr|}
\hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\
\sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\
& & & \cos{2\alpha}=1-2\sin^2 \alpha\\
\hline &&&\\
\mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\,
\alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha
= \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\
\hline
\end{array}\]
Пример 1. Решить уравнение \(6\cos^2x-13\sin x-13=0\)
С помощью формулы \(\cos^2\alpha=1-\sin^2\alpha\) уравнение сводится к виду:
\(6\sin^2x+13\sin x+7=0\). Сделаем замену \(t=\sin x\). Т.к. область значений синуса \(\sin x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:
\(6t^2+13t+7=0\). Корни данного уравнения \(t_1=-\dfrac76, \ t_2=-1\).
Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену:
\(\sin x=-1 \Rightarrow x=-\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).
Пример 2. Решить уравнение \(5\sin 2x=\cos 4x-3\)
С помощью формулы двойного угла для косинуса \(\cos
2\alpha=1-2\sin^2\alpha\) имеем:
\(\cos4x=1-2\sin^22x\). Сделаем эту подстановку и получим:
\(2\sin^22x+5\sin 2x+2=0\). Сделаем замену \(t=\sin 2x\). Т.к. область значений синуса \(\sin 2x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:
\(2t^2+5t+2=0\). Корни данного уравнения \(t_1=-2, \ t_2=-\dfrac12\).
Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену: \(\sin 2x=-\dfrac12 \Rightarrow x_1=-\dfrac{\pi}{12}+\pi n, \ x_2=-\dfrac{5\pi}{12}+\pi n, n\in\mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\, x+3\mathrm{ctg}\,x+4=0\)
Т.к. \(\mathrm{tg}\,x\cdot \mathrm{ctg}\,x=1\), то \(\mathrm{ctg}\,x=\dfrac1{\mathrm{tg}\,x}\). Сделаем замену \(\mathrm{tg}\,x=t\). Т.к. область значений тангенса \(\mathrm{tg}\,x\in\mathbb{R}\), то \(t\in\mathbb{R}\). Получим уравнение:
\(t+\dfrac3t+4=0 \Rightarrow \dfrac{t^2+4t+3}{t}=0\). Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Таким образом:
\(\begin{cases} t^2+4t+3=0\\t\ne 0 \end{cases} \Rightarrow \left[\begin{gathered} \begin{aligned} &t_1=-3\\&t_2=-1 \end{aligned}\end{gathered}\right.\)
Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=-3\\ &\mathrm{tg}\,x=-1 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=-\mathrm{arctg}\,3+\pi n\\ &x=-\dfrac{\pi}4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Кубические тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^3(x)+bf^2(x)+cf(x)+d=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos
x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к кубическому уравнению.
Часто при решении таких уравнений в дополнение к предыдущим формулам используются
формулы тройного угла: \[\begin{array}{|lc|cr|}
\hline &&&\\
\sin {3\alpha}=3\sin \alpha -4\sin^3\alpha &&&
\cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline
\end{array}\]
Пример 4. Решить уравнение \(11\cos 2x-3=3\sin 3x-11\sin x\)
При помощи формул \(\sin 3x=3\sin x-4\sin^3x\) и \(\cos2x=1-2\sin^2x\) можно свести уравнение к уравнению только с \(\sin x\):
\(12\sin^3x-9\sin x+11\sin x-3+11-22\sin^2 x=0\). Сделаем замену \(\sin x=t, \ t\in[-1;1]\):
\(6t^3-11t^2+t+4=0\). Подбором находим, что один из корней равен \(t_1=1\). Выполнив деление в столбик многочлена \(6t^3-11t^2+t+4\) на \(t-1\), получим:
\((t-1)(2t+1)(3t-4)=0 \Rightarrow\) корнями являются \(t_1=1, \ t_2=-\dfrac12, \ t_3=\dfrac43\).
Таким образом, корень \(t_3\) не подходит. Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\sin x=1\\&\sin x=-\dfrac12 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}2+2\pi n\\[1ex]&x=-\dfrac{\pi}6+2\pi n\\[1ex] &x=-\dfrac{5\pi}6+2\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Однородные тригонометрические уравнения второй степени: \[I. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=0}}, \quad a\ne 0,c\ne 0\]
Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin^2 x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).
Аналогично и \(\sin x=0\) не является решением такого уравнения.
Значит, данное уравнение можно делить на \(\cos^2 x\) или на \(\sin^2 x\). Разделим, например, на \(\cos^2 x\):
\(a \ \dfrac{\sin^2x}{\cos^2x}+b \ \dfrac{\sin x\cos x}{\cos^2x}+c \ \dfrac{\cos^2x}{\cos^2x}=0 \Leftrightarrow a\mathrm{tg}^2\,x+b\mathrm{tg}\,x+c=0\)
Таким образом, данное уравнение при помощи деления на \(\cos^2x\) и замены \(t=\mathrm{tg}\,x\) сводится к квадратному уравнению:
\(at^2+bt+c=0\), способ решения которого вам известен.
Уравнения вида \[I’. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=d}}, \quad a\ne0,c\ne 0\] с легкостью сводятся к уравнению вида \(I\) с помощью использования основного тригонометрического тождества: \[d=d\cdot 1=d\cdot (\sin^2x+\cos^2x)\]
Заметим, что благодаря формуле \(\sin2x=2\sin x\cos x\) однородное уравнение можно записать в виде
\(a\sin^2 x+b\sin 2x+c\cos^2x=0\)
Пример 5. Решить уравнение \(2\sin^2x+3\sin x\cos x=3\cos^2x+1\)
Подставим вместо \(1=\sin^2x+\cos^2x\) и получим:
\(\sin^2x+3\sin x\cos x-4\cos^2x=0\). Разделим данное уравнение на \(\cos^2x\):
\(\mathrm{tg}^2\,x+3\mathrm{tg}\,x-4=0\) и сделаем замену \(t=\mathrm{tg}\,x, \ t\in\mathbb{R}\). Уравнение примет вид:
\(t^2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=1\\&\mathrm{tg}\,x=-4 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}4+\pi n\\[1ex]&x=-\mathrm{arctg}\,4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=0}}, a\ne0, b\ne 0\]
Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).
Аналогично и \(\sin x=0\) не является решением такого уравнения.
Значит, данное уравнение можно делить на \(\cos x\) или на \(\sin x\). Разделим, например, на \(\cos x\):
\(a \ \dfrac{\sin x}{\cos x}+b \ \dfrac{\cos x}{\cos x}=0\), откуда имеем \(a\mathrm{tg}\, x+b=0 \Rightarrow \mathrm{tg}\, x=-\dfrac ba\)
Пример 6. Решить уравнение \(\sin x+\cos x=0\)
Разделим правую и левую части уравнения на \(\sin x\):
\(1+\mathrm{ctg}\, x=0 \Rightarrow \mathrm{ctg}\, x=-1 \Rightarrow x=-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\)
\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=c}}, a\ne0, b\ne 0, c\ne 0\]
Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:
1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества: \({\large{\sin x=2\sin{\dfrac x2}\cos{\dfrac x2}, \qquad \cos x=\cos^2 {\dfrac x2}-\sin^2 {\dfrac x2},\qquad c=c\cdot \Big(\sin^2 {\dfrac x2}+\cos^2 {\dfrac x2}\Big)}}\) данное уравнение сведется к уравнению \(I\):
Пример 7. Решить уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Распишем \(\sin 2x=2\sin x\cos x, \ \cos 2x=\cos^2x-\sin^2 x, \ -1=-\sin^2 x-\cos^2x\). Тогда уравнение примет вид:
\((1+\sqrt3)\sin^2x+2\sin x\cos x+(1-\sqrt3)\cos^2x=0\). Данное уравнение с помощью деления на \(\cos^2x\) и замены \(\mathrm{tg}\,x=t\) сводится к:
\((1+\sqrt3)t^2+2t+1-\sqrt3=0\). Корнями этого уравнения являются \(t_1=-1, \ t_2=\dfrac{\sqrt3-1}{\sqrt3+1}=2-\sqrt3\). Сделаем обратную замену:
\(\left[ \begin{gathered} \begin{aligned}&\mathrm{tg}\,x=-1\\ &\mathrm{tg}\,x=2-\sqrt3 \end{aligned}\end{gathered}\right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=-\dfrac{\pi}4+\pi n\\[1ex] &x=\mathrm{arctg}\,(2-\sqrt3)+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{\alpha}=\dfrac{2\mathrm{tg}\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2} &&& \cos{\alpha}=\dfrac{1-\mathrm{tg}^2\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2}\\&&&\\ \hline \end{array}\] уравнение сведется к квадратному уравнению относительно \(\mathrm{tg}\, \dfrac x2\)
Пример 8. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Сделаем подстановку \(\sin 2x=\dfrac{2\mathrm{tg}\,x}{1+\mathrm{tg}^2\,x}, \ \cos2x=\dfrac{1-\mathrm{tg}^2\,x}{1+\mathrm{tg}^2\,x}\) и замену \(\mathrm{tg}\,x=t\):
\(\dfrac{(\sqrt3+1)t^2+2t+1-\sqrt3}{1+t^2}=0 \Rightarrow (\sqrt3+1)t^2+2t+1-\sqrt3=0\) (т.к. \(1+t^2\geqslant 1\) при всех \(t\), то есть всегда \(\ne 0\))
Таким образом, мы получили то же уравнение, что и, решая первым способом.
3 СПОСОБ: при помощи формулы вспомогательного угла.
\[{\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac
a{\sqrt{a^2+b^2}}\]
Для использования данной формулы нам понадобятся формулы сложения углов: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha &&& \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &&&\\ \hline \end{array}\]
Пример 9. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на \(\sqrt{1^2+(-\sqrt3)^2}=2\):
\(\dfrac12\sin 2x-\dfrac{\sqrt3}2\cos 2x=-\dfrac12\)
Заметим, что числа \(\dfrac12\) и \(\dfrac{\sqrt3}2\) получились табличные. Можно, например, взять за \(\dfrac12=\cos \dfrac{\pi}3, \ \dfrac{\sqrt3}2=\sin \dfrac{\pi}3\). Тогда уравнение примет вид:
\(\sin 2x\cos \dfrac{\pi}3-\sin \dfrac{\pi}3\cos 2x=-\dfrac12 \Rightarrow \sin\left(2x-\dfrac{\pi}3\right)=-\dfrac12\)
Решениями данного уравнения являются:
\(\left[ \begin{gathered} \begin{aligned} &2x-\dfrac{\pi}3=-\dfrac{\pi}6+2\pi n\\[1.5ex] &2x-\dfrac{\pi}3=-\dfrac{5\pi}6+2\pi n \end{aligned} \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=\dfrac{\pi}{12}+\pi n\\[1.5ex] &x=-\dfrac{\pi}4+\pi n \end{aligned} \end{gathered} \right. \ \ n\in\mathbb{Z}\)
Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.
\(\blacktriangleright\) Если тригонометрическое уравнение можно свести к виду \[{\Large{a(\sin x\pm \cos x)+b\sin x\cos x+c=0}}, \text{где } a\ne 0, b\ne 0,\] то с помощью формулы \[{\large{(\sin x\pm\cos x)^2=1\pm2\sin x\cos x}} \ \ (*)\] данное уравнение можно свести к квадратному.
Для этого необходимо сделать замену \(t=\sin x\pm \cos x\), тогда \(\sin x\cos x=\pm \dfrac{t^2-1}2\).
Заметим, что формула \((*)\) есть не что иное, как формула сокращенного умножения \((A\pm B)^2=A^2\pm 2AB+B^2\) при подстановке в нее \(A=\sin x, B=\cos x\).
Пример 10. Решить уравнение \(3\sin 2x+3\cos 2x=16\sin x\cos^3x-8\sin x\cos x\).
Вынесем общий множитель за скобки в правой части: \(3\sin 2x+3\cos
2x=8\sin x\cos x(2\cos^2 x-1)\).
По формулам двойного угла \(2\sin x\cos x=\sin 2x, 2\cos^2x-1=\cos
2x\) имеем: \[3(\sin 2x+\cos 2x)=4\sin 2x\cos 2x\] Заметим, что полученное уравнение как раз записано в необходимом нам виде. Сделаем замену \(t=\sin 2x+\cos 2x\), тогда \(\sin 2x\cos
2x=\dfrac{t^2-1}2\). Тогда уравнение примет вид: \[3t=2t^2-2 \Rightarrow 2t^2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).
По формулам вспомогательного аргумента \(\sin2x+\cos
2x=\sqrt2\sin\left(2x+\dfrac{\pi}4\right)\), следовательно, сделав обратную замену: \[\left[ \begin{gathered} \begin{aligned}
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=2\\[1ex]
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac12 \end{aligned}
\end{gathered} \right. \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&\sin\left(2x+\dfrac{\pi}4\right)=\sqrt2\\[1ex]
&\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \end{aligned}
\end{gathered} \right.\] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от \(-1\) до \(1\). Значит: \(\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&2x+\dfrac{\pi}4=-\arcsin {\dfrac1{2\sqrt2}}+2\pi n\\[1ex]
&2x+\dfrac{\pi}4=\pi+\arcsin {\dfrac1{2\sqrt2}}+2\pi n
\end{aligned}
\end{gathered} \right. \Rightarrow \)
\(\Rightarrow \left[ \begin{gathered} \begin{aligned}
&x=-\dfrac12\arcsin {\dfrac1{2\sqrt2}}-\dfrac{\pi}8+\pi n\\[1ex]
&x=\dfrac{3\pi}8+\dfrac12\arcsin {\dfrac1{2\sqrt2}}+\pi n
\end{aligned}
\end{gathered} \right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Формулы сокращенного умножения в тригонометрическом варианте:
\(I\) Квадрат суммы или разности \((A\pm B)^2=A^2\pm 2AB+B^2\):
\((\sin x\pm \cos x)^2=\sin^2 x\pm 2\sin x\cos x+\cos^2x=(\sin^2 x+\cos^2 x)\pm 2\sin x\cos x=1\pm \sin 2x\)
\(II\) Разность квадратов \(A^2-B^2=(A-B)(A+B)\):
\((\cos x-\sin x)(\cos x+\sin x)=\cos^2x-\sin^2x=\cos 2x\)
\(\sin^2x-\cos^2x=-\cos2x\)
\(III\) Сумма или разность кубов \(A^3\pm B^3=(A\pm B)(A^2\mp AB+B^2)\):
\(\sin^3x\pm \cos^3x=(\sin x\pm \cos x)(\sin^2x\mp \sin x\cos x+\cos^2x)=(\sin x\pm \cos x)(1\mp \sin x\cos x)=\)
\(=(\sin x\pm \cos x)(1\mp \frac12\sin 2x)\)
\(IV\) Куб суммы или разности \((A\pm B)^3=A^3\pm B^3\pm 3AB(A\pm B)\):
\((\sin x\pm \cos x)^3=(\sin x\pm \cos x)(\sin x\pm \cos x)^2=(\sin x\pm \cos x)(1\pm \sin 2x)\) (по первой формуле)
shkolkovo.net
Отбор корней тригонометрических уравнений с заданными условиями
Разделы: Математика
Цели:
- Обобщение, углубление решений тригонометрических уравнений с отбором корней с заданными условиями, тригонометрических преобразований.
- Развитие логики, мышления, памяти, алгоритмизации.
- Воспитание самостоятельности, самокритичности и критичности, сознательности.
План урока.
- Орг момент
- Актуализация знаний учащихся.
- Исторические сведения
- Решения с комментариями. Обобщение методов решений
- Подведение итогов
- Домашнее задание
- Выставление
- Выводы
Оборудование: индивидуальные карточки, таблица ответов, таблица заданий, компьютер и интерактивная доска, портрет, доска, карточки с домашней работой.
ХОД УРОКА
I. До урока проверяется домашнее задание.
II. Оргмомент (объявляется тема урока, ставит учитель цели на урок и краткий план урока)
Запишем число и тему урока «Отбор корней
тригонометрических уравнений с заданными
условиями».
Итак, сегодня на уроке, мы вспомним формулы
тригонометрических преобразований, решение
простейших тригонометрических уравнений,
различные методы тригонометрических уравнений и
целью нашего урока является решать
тригонометрические уравнения с условиями. Но а
пока посчитаем устно
III. Актуализация знаний учащихся
Игра «Морской бой» (устный счет)
На каждой парте лист с заданиями:
Продолжение Приложение 1 слайды 2-4
Таблица ответов:
Правильный ответ помечается: о
Неверный ответ: х
Если учащийся набрал 4 правильных ответа – 5
Если же ошибается, то учащийся больше не
отвечает.
В это время более сильные учащиеся выполняют
задания по карточкам.
При решении тригонометрических уравнений
следует учесть, что не существует единого метода
их решения (как, например, для квадратных
уравнений). Такие уравнения решают с помощью
тождественных преобразований, сводящих к одному
или нескольким простейшим уравнениям. За этими
карточками спрятан портрет ученого математика.
Чтобы увидеть картину, вам необходимо найти
соответствие. Я называю формулу вы должны
указать номер, который соответствует данной
формуле.
1) cos(a + b)
2) sina+sinb
3) cosa – cosb
4) sin(a–b)
5) cos2a
6)
7) sin2a
8) cosx*cosy
9) cosa+cosb
10) tg 2a
11) sinx*cosy
12)
Исторические сведения.
Итак, это ученый Леонард Эйлер. (
Имя Эйлера дорого всему прогрессивному
человечеству, которое чтит в нём одного из
величайших геометров мира. В качестве члена
Петербургской и Берлинской Академий наук Эйлер
содействовал развитию математических наук в
обеих странах и распространению в них
физико-математических знаний.
Он был, прежде всего, математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность.
IV. Решение уравнения с комментариями. Обобщение
Тригонометрические уравнения обычно имеют
бесконечные серии решений, задаваемые с помощью
параметра, принимающего целые значения. И
сегодня на уроке мы решим тригонометрические
уравнения с выбором корней на заданные
условия.
Даны уравнения:
;
;
;
4sin2x + 2sinxcosx + 4cos2x = 3;2sin2x – 5cosx – 5 = 0
Найдите соответствия, указав стрелками.
| Уравнения, алгебраические относительно одной из тригонометрической функций. | Уравнения, решаемые понижением порядка. | Однородные тригонометрические уравнения I степени | Однородные тригонометрические уравнения II степени | Уравнения, сводящиеся к простейшим введением вспомогательного угла. |
Решите их, отбирая корни, учитывая условия.
1) Решите уравнение 2sin2x – 5cosx – 5 = 0, в ответе укажите значение 5(tgx0 + 4), где х0 – наименьший положительный корень.
Решение.
Ответ: 20
2) Решить уравнение . Найти сумму корней принадлежащих промежутку
Решение.
Корни, принадлежащие промежутку
Их сумма равна 0.
Ответ: 0
3) Решите уравнение , найдите модуль разности корней
принадлежащих промежутку
Решение.
Обе части уравнения разделю на
Корни уравнения, принадлежащие промежутку
Ответ:
4) Решите уравнение 4sin2x + 2sinxcosx+4cos2
Решение.
4sin2x + 2sinxcosx + 4cos2x = 3cos2x + 3sin2x,
sin2x + 2sinxcosx + cos2x = 0
Корень, принадлежащий промежутку
5)Решить уравнение , найдите отношение большего корня к меньшему принадлежащих промежутку
Ответ: 3.
V. Подведение итогов:
Домашнее задание: ДКР (2 варианта)
Выставление оценок: За устную работу, за карточки, за решение уравнений, за дополнение.
Учащиеся делают выводы. Обобщают методы решения тригонометрических уравнений.
Литература:
- Башмаков М.И. Алгебра и начала анализа: Учеб.для 10-11 кл. сред. Шк. – М.: Просвещение, 1991.
- Виленкин Н.Я. и др. Алгебра и математический анализ. 10 кл.: Учеб.пособие для шк. и кл. с углубл. изуч. математики – 12-е изд., М.: Мнемозина, 2011.
- Денищева Л.О., Корешкова Т.А. Алгебра и начала анализа 10-11 классы Тематические зачеты и тесты. М.: Мнемозина, 2005.
- Математика в школе 1991.
- Модркович А.Г. Алгебра и начала анализа. 10-11 кл. Задачник для общеобраз. учреждений (профильный уровень) – 8-е изд. – М.:Мнемозина, 2011.
- Модркович А.Г. Алгебра и начала анализа. 10-11 кл. Учеб для общеобраз. учреждений (профильный уровень). – 8-е изд. – М.: Мнемозина, 2011.
- Прудников В.Е. Русские педагоги-математики XVIII-XIX веков. Учпедгид. – М.: 1956.
- Сборник задач по математике для подготовки к вступительным экзаменам Уфимского Государственного нефтяного технического университета. Уфа – 2012.
19.01.2014
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Внеклассный урок — Простейшие тригонометрические уравнения: обобщения, таблицы значений x, примеры
Простейшие тригонометрические уравнения: обобщения, таблицы значений x, примеры
Уравнение sin x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения sin x = a:
x = (-1)n · arcsin α + πn где n – любое целое число (n ∈ Z). |
Частные случаи, когда уравнение sin x = а имеет более простое решение:
| |
|
|
|
|
|
|
Остальные значения x в уравнении sin x = а:
| | |
1 | π | 5π |
1 | π | 5π |
√2 | π | 3π |
√2 | π | 3π |
√3 | π | 2π |
√3 | π | 2π |
Уравнение cos x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения cos x = a:
x = ± arccos α + 2πk где k – любое целое число (k ∈ Z). |
Частные случаи, когда уравнение cos x = а имеет более простое решение:
| |
| π |
| |
| |
Остальные значения x в уравнении cos x = а:
|
| |
1 | π | π |
1 | 2π | 2π |
√2 | π | π |
√2 | 3π | 3π |
√3 | π | π |
√3 | 5π | 5π |
Уравнения tg x = a и ctg x = a.
Формула решения уравнения tg x = a:
x = arctg a + πk где a – любое действительное число (a ∈ R), k – любое целое число (k ∈ Z). |
Формула решения уравнения ctg x = a:
x = arcctg a + πk где a – любое действительное число (a ∈ R), k – любое целое число (k ∈ Z). |
Значения x в уравнениях tg x = а и ctg x = а:
|
| |
| | |
√3 | | π |
√3 | | π |
| | π |
| | π |
| √3 | π |
| √3 | π |
| | π |
Примеры.
1) Решим уравнение
√2
sin 3x = ——
2
Решение.
Для простоты заменим переменную 3x обобщенной переменной t. Итак:
3x = t .
Тогда наше уравнение принимает привычный вид:
√2
sin t = ——
2
Применяем формулу:
√2
t = (–1)n arcsin —— + πn
2
Находим значение арксинуса:
√2 π
arcsin —— = —
2 4
Подставляем это значение арксинуса:
π
t = (–1)n — + πn
4
Теперь вместо t вновь подставляем переменную 3x:
π
3x = (–1)n — + πn
4
Находим значение переменной, применяя правило деления дробей:
π π 1 πn π πn
x = (–1)n — : 3 + πn : 3 = (–1)n — ∙ — + —— = (–1)n —— + ——
4 4 3 3 12 3
Ответ:
π πn
x = (–1)n —— + ——
12 3
2) Решим уравнение
1
cos 2x = – —
2
Решение.
Напомним: решать пример будем по формуле
x = ± arccos a + 2πn.
Для простоты можем заменить 2x на t. Тогда наша формула примет вид t = ± arccos a + 2πn. Но в данном случае можем обойтись и без этого.
Итак, вычисляем значение арккосинуса:
1 2π
2x = ± arccos (– —) + 2πn = ± —— + 2πn
2 3
Находим значение x, применяя правило деления дробей:
2π 2π 1 2π π
x = ± —— : 2 + 2πn : 2 = ± —— ∙ — + πn = ± —— + πn = ± — + πn
3 3 2 6 3
Ответ:
π
x = ± — + πn
3
3) Решим уравнение
π √3
tg (4x – —) = ——
6 3
Решение.
Напомним: здесь мы применяем формулу
x = arctg a + πn.
Чтобы не запутаться при следующем шаге, заменим в формуле переменную x на переменную t:
t = arctg a + πn.
Далее отмечаем, что:
π
t = (4x – —).
6
Тогда наше уравнение принимает следующий вид:
π √3
4x – — = arctg —— + πn.
6 3
Находим значение арктангенса:
√3 π
arctg —— = —
3 6
Подставляем значение арктангенса в нашу формулу:
π π
4x – — = — + πn.
6 6
Находим значение 4x:
π π 2π π
4x = — + — + πn = —— + πn = — + πn
6 6 6 3
Осталось найти значение x, применяя правило деления дробей:
π π 1 πn π πn
x = — : 4 + πn : 4 = — ∙ — + —— = —— + ——
3 3 4 4 12 4
Ответ:
π πn
x = —— + ——, n ∈ Z
12 4
raal100.narod.ru
Формулы корней простейших тригонометрических уравнений
Documents войти Загрузить ×- Математика
Related documents

открытый урок в 9 классеx

otkryt_urok_algebry_v___klx

ЕРЕМЕЕВА МАРИНА ЛЕОНИДОВНА Учитель математики МБОУ «Гимназия №4» ЕМР

Урок-игра по алгебре и началам анализа в10 классе Тема «Тригонометрические уравнения»

Тема: Решение простейших тригонометрических уравнений

Шпора по МатАну 1

Тестовые задания по аттестации

Решения 3

План-конспект открытого занятия Тема занятия: «Наибольшее и наименьшее значения функции»

ИСПОЛЬЗОВАНИЕ РАЗНОУРОВНЕВЫХ ЗАДАНИЙ

Основное тригонометрическое тождество

Урок-зачет в 10 классе по теме «Тригонометрические уравнения

Тестовые задания по алгебре для 10

Шпар
studydoc.ru
Тригонометрические уравнения
Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.
В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.
Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.
Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.
Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:


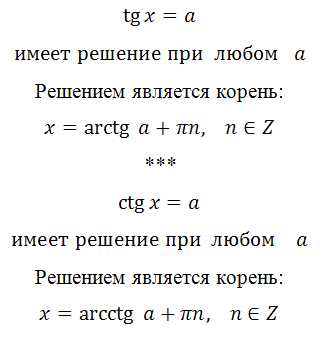
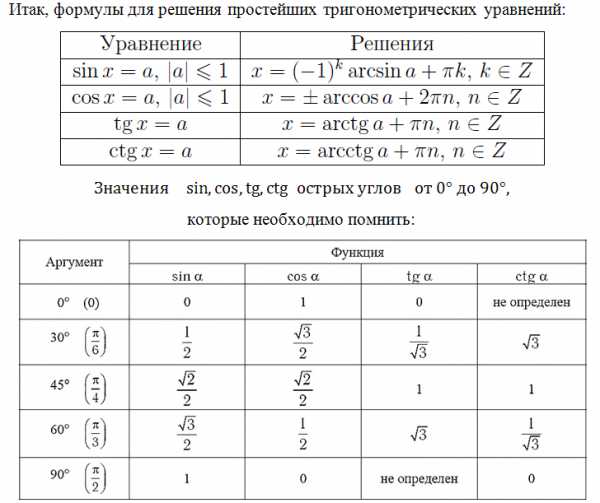
Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.
Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».
Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.
Итак, рассмотрим следующие задачи:
Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
Решением уравнения cos x = a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Значит
Выразим x:
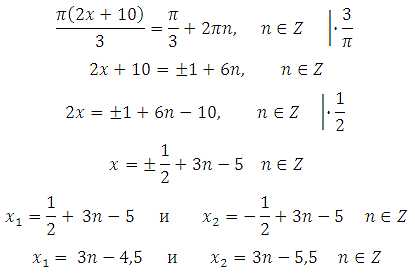
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.
Вычисляем:
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
Ответ: –1,5
Решите самостоятельно:
Посмотреть решение
Решите уравнение:
В ответе напишите наименьший положительный корень.
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90о до 90о синус которого равен a.
Значит
Выразим x (умножим обе части уравнения на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …
При n = 0 х = (– 1)0 + 4∙0 + 3 = 4
При n = 1 х = (– 1)1 + 4∙1 + 3 = 6
При n = 2 х = (– 1)2 + 4∙2 + 3 = 12
Проверим при n = –1 х = (–1)–1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
Ответ: 4
Решите самостоятельно:
Посмотреть решение
Решите уравнение:
В ответе напишите наименьший положительный корень.
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90о до 90о, тангенс которого равен a.
Значит
Выразим x (умножим обе части уравнения на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n = 1,2,3… Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Ответ: 0,25
Решите самостоятельно:
Посмотреть решение
Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.
Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для
то данные формулы вам помогут:
Спасибо за внимание, учитесь с удовольствием!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Формулы корней тригонометрических уравнений таблица
Центр окружности описанной около треугольника ABC лежит на стороне ab.Радиус окружности равен 8,5.Найдите bc, если ac=8. Для специалистов все). Загрузить jpg. Реклама. Попроси больше объяснений; Следить ? Отметить нарушение ? GsLife 06.11.2015. Войти чтобы добавить комментарий.
Узнать ещё
Знание — сила. Познавательная информация
Формулы тригонометрических уравнений
Для удобной работы все формулы для решения простейших тригонометрических уравнений, включая частные случаи, а также таблицы арксинусов, арккосинусов, арктангенсов и арккотангенсов собраны на одной странице.
При │a│>1 это уравнение решений не имеет.
При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:
При │a│>1 это уравнение решений не имеет.
При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:
Уравнение имеет бесконечное множество решений при любых значениях a.
Уравнение имеет бесконечное множество решений при любых значениях a.
21 комментарий на «Формулы тригонометрических уравнений»
Отличный сайт, спасибо, помог.
Спасибо за отличную оценку!
Я рада, что сайт Вам помог.
Пожалуйста!) Успехов Вам в учебе!
Сайт действительно хороший =)
Интересно, просто, ясно.
Спасибо Вам, Светлана Иванова!
Ариша, спасибо за теплый отзыв!
Опечатка в таблице арккотангенсов )
А так все отлично, хорошая статья
Опечатку исправила. Спасибо!
Не силен в этих науках и школу прогуливал всегда! Жалею теперь об этом! Но вот беда ума не могу приложить что может значить arccos0,932 что это? с чем его едят? И как его посчитать! Смотрю на выше написанное и не пойму как мне это применить! Помгите убогому!
Антон, разобраться в математике можно в любом возрасте, было бы желание. Но придется потрудиться (а где без этого?).
Arccos 0,932 — это такое число из промежутка [0;П], косинус которого равен 0,932.
Можно открыть таблицу Брадиса и найти угол, косинус которого равен этому числу: [0,932 approx cos ]Далее, если требуется ответ представить в радианах, градусы переводим в радианы. [pi = , Rightarrow = frac,][ = 21 cdot frac = frac.]Отсюда [arccos 0,932 approx frac.]
Если же arccos 0,932 появился в ходе решения тригонометрического уравнения — оставляйте его в таком виде.
Например:[cos x = 0,932][x = pm arccos 0,932 + 2pi n, n in Z.]Все, дальше ничего считать не надо (запись в таком виде — точное решение, а при нахождении арккосинуса ответ станет не точным, а приближенным. Поэтому его и не принято упрощать).
Светлана спасибо вам большое за помощь)Есть еще один вопросик я весь google перекопал. Какова единица измерения числа которое получается в результате вычисления cos или sin угла например sin47.376 градусов =0,735??какая единица измерения Arccos0,735=42.692. что это за величина и какая ее единица измерения? Голова дымит, а надо знать это, а то на работу не возьмут!
Косинус угла и синус угла — это просто число (в пределах от -1 до 1). Неважно, задан угол в градусах или в радианах.
Теперь — об арксинусах и арккосинусах. Если использовать таблицу Брадиса, arccos0,735 ищем как угол, косинус которого равен 0,735. [cos approx 0,735]То есть Ваши 42.692, насколько я понимаю, градусы. Но в градусах значения арккосинуса и арксинуса не оставляют. Нужно перевести в радианы. [ = 42 cdot frac = frac.]7П/30 радиан, радианы не пишут. Радианная мера позволяет от градусной меры угла перейти к числам, чтобы потом графики тригонометрических функций в декартовой системе координат строить можно было, например.
Спасибо вы целиком и полностью удовлетворили мой интерес!
Спасибо за шпору =), пошел сдавать
Ещё о таблицах. Точнее их отсутствии…
На калькуляторе мы получаем cos, затем arccos. Верно ли я понимаю, что значения arccos вычисляются в радианной мере, и после этого следует обязательно перевести в градусную меру? (Таблицы Брадиса, также как и любые другие, идут уже (!) с перерасчетом радианов в градусы. ) …но таблиц нет, к примеру. Некоторые on-line–научные калькуляторы имеют опцию переключения с градусов в радианы и/или наоборот; при этом по умолчанию может стоять опция (галочка) как радианной меры, так и градусной.
Вопрос: в каких случаях надобно переходить с радианов в градусы?
(функции MS Office Excel, например, предусматривают именно трёхстадийный процесс вычисления: cos, arccos, затем перевод радианов в градусы).
И ещё вопросик: Таблицы содержат значения синусов/косинусов только для острых углов в ПРЯМОУГОЛЬНОМ треугольнике?
Пример, имеется равносторонний треугольник (все стороны и углы равны), нам надо найти угол (мы его не знаем). Сторона (все три стороны равны) = 60 см. Т. е. поделив все [равные] стороны получим
Sin = cos = tg = ctg = sec = cosec = 1
Но по этому значению угол [каковой реально 60°] найти в таблицах невозможно. Спасибо!
Nick, прошу прощения, что затянула с ответом. Меня мучает совесть(
С калькулятором я практически не работаю, предпочитаю считать либо устно, либо письменно. Если нужно, пользуюсь таблицами Брадиса. Над нюансами вычислений с калькулятором не задумывалась.
Значения синуса и косинуса зависят только от угла, но не от вида треугольника. Мы вводим определение синуса в прямоугольном треугольнике как отношение противолежащего катета к гипотенузе, потом расширяем определение, называя синусом угла альфа ординату точки единичной окружности, полученной из точки (1;0) поворотом на угол альфа.
Синус угла в произвольном треугольнике можно найти посредством через теорему синусов, через площадь треугольника (из формулы S=1/2 ab sin α), или провести высоту и рассмотреть прямоугольный треугольник.
В таблице Брадиса значения тригонометрических функций даны только для острых углов. Для тупых углов значения находят с помошью формул приведения.
Объясните мне, пожалуйста, если п принадлежит Z, где п — , Z — .я не могу понять когда п четное, п — нечетное и что такое Z?
Тамара, семейство решений для общего случая уравнений sinx=a
Можно разбить на два семейства решений:
1) при n=2k (то есть для чётных)
2) при n=2m+1 (то есть для нечётных)
Z — множество целых чисел, то есть 0; ±1; ±2; ±3; …
Страница интересная, но я не нашла частные случаи для тангенса и котангенса. Помогите пожалуйста(очень нужно
Евгения, формул частных случаем для тангенса и котангенса нет. Иногда частными случаями называют уравнения вида tgx=1; tgx=-1; ctgx=1; ctgx=-1, но общая формула верна и для каждого из этих случаев.
Формулы корней тригонометрических уравнений таблица
Узнать ещё
Знание — сила. Познавательная информация
Формулы тригонометрических уравнений
Для удобной работы все формулы для решения простейших тригонометрических уравнений, включая частные случаи, а также таблицы арксинусов, арккосинусов, арктангенсов и арккотангенсов собраны на одной странице.
При │a│>1 это уравнение решений не имеет.
При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:
При │a│>1 это уравнение решений не имеет.
При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:
Уравнение имеет бесконечное множество решений при любых значениях a.
Уравнение имеет бесконечное множество решений при любых значениях a.
21 комментарий на «Формулы тригонометрических уравнений»
Отличный сайт, спасибо, помог.
Спасибо за отличную оценку!
Я рада, что сайт Вам помог.
Пожалуйста!) Успехов Вам в учебе!
Сайт действительно хороший =)
Интересно, просто, ясно.
Спасибо Вам, Светлана Иванова!
Ариша, спасибо за теплый отзыв!
Опечатка в таблице арккотангенсов )
А так все отлично, хорошая статья
Опечатку исправила. Спасибо!
Не силен в этих науках и школу прогуливал всегда! Жалею теперь об этом! Но вот беда ума не могу приложить что может значить arccos0,932 что это? с чем его едят? И как его посчитать! Смотрю на выше написанное и не пойму как мне это применить! Помгите убогому!
Антон, разобраться в математике можно в любом возрасте, было бы желание. Но придется потрудиться (а где без этого?).
Arccos 0,932 — это такое число из промежутка [0;П], косинус которого равен 0,932.
Можно открыть таблицу Брадиса и найти угол, косинус которого равен этому числу: [0,932 approx cos ]Далее, если требуется ответ представить в радианах, градусы переводим в радианы. [pi = , Rightarrow = frac,][ = 21 cdot frac = frac.]Отсюда [arccos 0,932 approx frac.]
Если же arccos 0,932 появился в ходе решения тригонометрического уравнения — оставляйте его в таком виде.
Например:[cos x = 0,932][x = pm arccos 0,932 + 2pi n, n in Z.]Все, дальше ничего считать не надо (запись в таком виде — точное решение, а при нахождении арккосинуса ответ станет не точным, а приближенным. Поэтому его и не принято упрощать).
Светлана спасибо вам большое за помощь)Есть еще один вопросик я весь google перекопал. Какова единица измерения числа которое получается в результате вычисления cos или sin угла например sin47.376 градусов =0,735??какая единица измерения Arccos0,735=42.692. что это за величина и какая ее единица измерения? Голова дымит, а надо знать это, а то на работу не возьмут!
Косинус угла и синус угла — это просто число (в пределах от -1 до 1). Неважно, задан угол в градусах или в радианах.
Теперь — об арксинусах и арккосинусах. Если использовать таблицу Брадиса, arccos0,735 ищем как угол, косинус которого равен 0,735. [cos approx 0,735]То есть Ваши 42.692, насколько я понимаю, градусы. Но в градусах значения арккосинуса и арксинуса не оставляют. Нужно перевести в радианы. [ = 42 cdot frac = frac.]7П/30 радиан, радианы не пишут. Радианная мера позволяет от градусной меры угла перейти к числам, чтобы потом графики тригонометрических функций в декартовой системе координат строить можно было, например.
Спасибо вы целиком и полностью удовлетворили мой интерес!
Спасибо за шпору =), пошел сдавать
Ещё о таблицах. Точнее их отсутствии…
На калькуляторе мы получаем cos, затем arccos. Верно ли я понимаю, что значения arccos вычисляются в радианной мере, и после этого следует обязательно перевести в градусную меру? (Таблицы Брадиса, также как и любые другие, идут уже (!) с перерасчетом радианов в градусы. ) …но таблиц нет, к примеру. Некоторые on-line–научные калькуляторы имеют опцию переключения с градусов в радианы и/или наоборот; при этом по умолчанию может стоять опция (галочка) как радианной меры, так и градусной.
Вопрос: в каких случаях надобно переходить с радианов в градусы?
(функции MS Office Excel, например, предусматривают именно трёхстадийный процесс вычисления: cos, arccos, затем перевод радианов в градусы).
И ещё вопросик: Таблицы содержат значения синусов/косинусов только для острых углов в ПРЯМОУГОЛЬНОМ треугольнике?
Пример, имеется равносторонний треугольник (все стороны и углы равны), нам надо найти угол (мы его не знаем). Сторона (все три стороны равны) = 60 см. Т. е. поделив все [равные] стороны получим
Sin = cos = tg = ctg = sec = cosec = 1
Но по этому значению угол [каковой реально 60°] найти в таблицах невозможно. Спасибо!
Nick, прошу прощения, что затянула с ответом. Меня мучает совесть(
С калькулятором я практически не работаю, предпочитаю считать либо устно, либо письменно. Если нужно, пользуюсь таблицами Брадиса. Над нюансами вычислений с калькулятором не задумывалась.
Значения синуса и косинуса зависят только от угла, но не от вида треугольника. Мы вводим определение синуса в прямоугольном треугольнике как отношение противолежащего катета к гипотенузе, потом расширяем определение, называя синусом угла альфа ординату точки единичной окружности, полученной из точки (1;0) поворотом на угол альфа.
Синус угла в произвольном треугольнике можно найти посредством через теорему синусов, через площадь треугольника (из формулы S=1/2 ab sin α), или провести высоту и рассмотреть прямоугольный треугольник.
В таблице Брадиса значения тригонометрических функций даны только для острых углов. Для тупых углов значения находят с помошью формул приведения.
Объясните мне, пожалуйста, если п принадлежит Z, где п — , Z — .я не могу понять когда п четное, п — нечетное и что такое Z?
Тамара, семейство решений для общего случая уравнений sinx=a
Можно разбить на два семейства решений:
1) при n=2k (то есть для чётных)
2) при n=2m+1 (то есть для нечётных)
Z — множество целых чисел, то есть 0; ±1; ±2; ±3; …
Страница интересная, но я не нашла частные случаи для тангенса и котангенса. Помогите пожалуйста(очень нужно
Евгения, формул частных случаем для тангенса и котангенса нет. Иногда частными случаями называют уравнения вида tgx=1; tgx=-1; ctgx=1; ctgx=-1, но общая формула верна и для каждого из этих случаев.
Формулы корней тригонометрических уравнений таблица
Тригонометрические уравнения — формулы, решения, примеры
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего; решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
Делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
Находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a, b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt `:
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a>=cos \varphi`, ` \frac b> =sin \varphi`, `\frac c>=C`, тогда:
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt `, получим:
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac =1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.

poiskvstavropole.ru
