Если в квадратном уравнении нет с – Квадратное уравнение, корни квадратного уравнения, решение квадратного уравнения.

Как решать неполные квадратные уравнения?

Научившись решать уравнения первой степени, безусловно, хочется работать с другими, в частности, с уравнениями второй степени, которые по-другому называются квадратными.

Квадратные уравнения — это уравнения типа ах ² + bx + c = 0, где переменной является х, числами будут — а, b, с, где а не равняется нулю.

Если в квадратном уравнении один или другой коэффициент (с или b) будет равняться нулю, то это уравнение будет относиться к неполному квадратному уравнению.

Как решить неполное квадратное уравнение, если ученики до сих пор умели решать только уравнения первой степени? Рассмотрим неполные квадратные уравнения разных видов и несложные способы их решения.

а) Если коэффициент с будет равен 0, а коэффициент b не будет равен нулю, то ах ² + bх + 0 = 0 сводится к уравнению вида ах ² + bх = 0.

Чтобы решить такое уравнение, нужно знать формулу решения неполного квадратного уравнения, которая заключается в том, чтобы левую часть его разложить на множители и позже использовать условие равенства произведения нулю.

Например, 5х ² — 20х = 0. Раскладываем левую часть уравнения на множители, при этом совершая обычную математическую операцию: вынос общего множителя за скобки

5х (х — 4) = 0

Используем условие, гласящее, что произведения равны нулю.

5 х = 0 или х — 4 = 0

х = 0/5 х = 4

х = 0

Ответом будет: первый корень — 0; второй корень — 4.

б) Если b = 0, а свободный член не равен нулю, то уравнение ах ² + 0х + с = 0 сводится к уравнению вида ах ² + с = 0. Решают уравнения двумя способами: а) раскладывая многочлен уравнения  в левой части на множители; б) используя свойства арифметического квадратного корня. Такое уравнение решается одним из методов, например:

4х ² — 25 = 0

4х ² = 25

х ² = 25/4

х = ± √ 25/4

 х = ± 5/2. Ответом будет: первый корень равен 5/2; второй корень равен — 5/2.

в) Если b будет равен 0 и с будет равен 0, то ах ² + 0 + 0 = 0 сводится к уравнению вида ах ² = 0. В таком уравнении x будет равен 0. 

Как видите, неполные квадратные уравнения могут иметь не более двух корней.

Научившись решать уравнения первой степени, безусловно, хочется работать с другими, в частности, с уравнениями второй степени, которые по-другому называются квадратными.

Квадратные уравнения — это уравнения типа ах ² + bx + c = 0, где переменной является х, числами будут — а, b, с, где а не равняется нулю.

Если в квадратном уравнении один или другой коэффициент (с или b) будет равняться нулю, то это уравнение будет относиться к неполному квадратному уравнению.

Как решить неполное квадратное уравнение, если ученики до сих пор умели решать только уравнения первой

elhow.ru

Вы не забыли, как решать неполное квадратное уравнение?

Как решать неполное квадратное уравнение? Известно, что оно является частным вариантом равенства ах²+вх+с = о, где а, в и с — вещественные коэффициенты при неизвестном х, и где а ≠ о, а в и с будут нулями — одновременно или порознь. Например, с = о, в ≠ о или наоборот. Мы почти вспомнили определение квадратного уравнения.

Уточним

Трехчлен второй степени равен нулю. Первый его коэффициент а ≠ о, в и с могут принимать любые значения. Значение переменной х тогда будет корнем уравнения, когда при подстановке обратит его в верное числовое равенство. Остановимся на вещественных корнях, хотя решениями уравнения могут быть и комплексные числа. Полным принято называть уравнение, в котором ни один из коэффициентов не равен о, а ≠ о, в ≠ о, с ≠ о.
Решим пример. 2х²-9х-5 = о, находим
D = 81+40 = 121,
D положительный, значит корни имеются, х₁ = (9+√121):4 = 5, а второй х₂ = (9-√121):4 = -о,5. Проверка поможет убедиться, что они верные.

Вот поэтапное решение квадратного уравнения

Через дискриминант можно решить любое уравнение, в левой части которого известный квадратный трехчлен при а ≠ о. В нашем примере. 2х²-9х-5 = 0 (ах²+вх+с = о)

• Находим сначала дискриминант D по известной формуле в²-4ас.
• Проверяем, каким будет значение D: у нас больше нуля, бывает равным нулю или меньше.
• Знаем, что если D › о, квадратное уравнение имеет всего 2 разных действительных корня, их обозначают х₁ обычно и х₂,
  вот как вычислили:
  х₁ = (-в+√D):(2а), а второй: х₂ = (-в-√D):(2а).
• D = o ― один корень, или, говорят, два равных:
  х₁ равно х₂ и равно -в:(2а).
• И наконец, D ‹ o означает, что уравнение не имеет никаких вещественных корней.

Рассмотрим, какие бывают неполные уравнения второй степени

1. ах²+вх = o. Свободный член, коэффициент с при х⁰, здесь равен нулю, в ≠ o.
   Как решать неполное квадратное уравнение такого вида? Выносим х за скобки. Вспоминаем, когда произведение двух множителей равно нулю.
   x(ax+b) = o, это может быть, когда х = о или когда ax+b = o.
   Решив 2-е линейное уравнение, имеем x = -в/а.
   В результате имеем корни х₁ = 0,_{по вычислениямx2 = -b/a.}
2. Теперь коэффициент при х равен о, а с не равен (≠) о.
   x²+с = о. Перенесем с в правую часть равенства, получим x² = -с. Это уравнение только тогда имеет вещественные корни, когда -с положительное число (с ‹ о),
   х₁ тогда равен √(-с), соответственно х₂ ― -√(-с). В противном случае уравнение совсем не имеет корней.
3. Последний вариант: b = c= o, то есть ах² = о. Естественно, такое простенькое уравнение имеет один корень, x = о.

Частные случаи

Как решать неполное квадратное уравнение рассмотрели, а теперь возмем любые виды.

• В полном квадратном уравнении второй коэффициент при х ― четное число.
  Пусть k = o,5b. Имеем формулы для вычисления дискриминанта и корней.
  D/4 = k²— ас, корни вычисляются так х_1,2 = (-k±√(D/4))/а при D › o.
  x = -k/a при D = o.
  Нет корней при D ‹ o.
• Бывают приведенные квадратные уравнения, когда коэффициент при х в квадрате равен 1, их принято записывать x² +рх+ q = o. На них распространяются все вышеприведенные формулы, вычисления же несколько проще.
  Пример, х²-4х-9 = 0. Вычисляем D: 2²+9, D = 13.
  х₁ = 2+√13, х₂ = 2-√13.
• Кроме того, к приведенным легко применяется теорема Виета. В ней говорится, что сумма корней уравнения равна –p, второму коэффициенту с минусом (имеется ввиду противоположный знак), а произведение этих же корней будет равно q, свободному члену. Проверьте, как легко можно было бы устно определить корни этого уравнения. Для неприведенных (при всех коэффициентах, не равных нулю) эта теорема применима так: сумма x₁+x₂ равна -в/а, произведение х₁·х₂ равно с/a.

Сумма свободного члена с и первого коэффициента а равна коэффициенту b. В этой ситуации уравнение имеет не менее чем один корень (легко доказывается), первый обязательно равен -1, а второй –с/а, если он существует. Как решать неполное квадратное уравнение, можно проверить самостоятельно. Проще простого. Коэффициенты могут находиться в некоторых соотношениях между собой

• x²+x = o, 7х²-7 = o.
• Сумма всех коэффициентов равна о.
  Корни у такого уравнения — 1 и с/а. Пример, 2х²-15х+13 = o.
  x₁ = 1, х₂ = 13/2.

Существует ряд других способов решения разных уравнениий второй степени. Вот, например, метод выделения из данного полинома полного квадрата. Графических способов несколько. Когда часто имеешь дело с такими примерами, научишься «щелкать» их, как семечки, ведь все способы приходят на ум автоматически.

fb.ru

Квадратные уравнения

Примеры:

\(3x^2-26x+5=0\)
\((4-x)(4x-3)=3\)
\(\frac{x^2}{2}\)\(+\) \(\frac{2x}{3}\)\(=\)\(\frac{x-2}{6}\)

В первом примере \(a=3\), \(b=-26\), \(c=5\). В двух других \(a\),\(b\) и \(c\) не выражены явно. Но если эти уравнения преобразовать к виду \(ax^2+bx+c=0\), они обязательно появятся.

Коэффициент \(a\) называют первым или старшим коэффициентом, \(b\) – вторым коэффициентом, \(c\) – свободным членом уравнения.

Левая часть уравнения, то есть выражение \(ax^2+bx+c\), является квадратным трехчленом.

Виды квадратных уравнений

Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.

Полное квадратное уравнение \(6x^2-x-2=0\) \(x^2-4x+3=0\) \(\frac{x^2}{2}-3x+1=0\)

Неполное квадратное уравнение \(5x^2=0\) \(x^2-25=0\) \(\frac{1}{2}x^2-x=0\)

Как решать квадратные уравнения

В данной статье мы рассмотрим вопрос решения полных квадратных уравнений. Про решение неполных — смотрите здесь.

Итак, стандартный алгоритм решения полного квадратного уравнения: 

1. Преобразовать уравнение к виду \(ax^2+bx+c=0\).

2. Выписать значения коэффициентов \(a\), \(b\) и \(c\).
   Пока не отработали решение квадратных уравнений до автоматизма, не пропускайте этот этап! Особенно обратите внимание, что знак перед членом берется в коэффициент. То есть, для уравнения \(2x^2-3x+5=0\), коэффициент \(b=-3\), а не \(3\).

3. Вычислить значение дискриминанта по формуле \(D=b^2-4ac\).

4. Вычислить корни уравнения по формулам \(x_1=\frac{-b + \sqrt{D}}{2a}\)   и   \(x_1=\frac{-b — \sqrt{D}}{2a}\).
   

Примеры:

Решите квадратное уравнение \(2x(1+x)=3(x+5)\)
Решение:

\(2x(1+x)=3(x+5)\)		Равносильными преобразованиями приведем уравнение к виду \(ax^2+bx+c=0\). Сначала раскрываем скобки.
\(2x+2x^2=3x+15\)		Теперь переносим все слагаемые влево, меняя знак…
\(2x+2x^2-3x-15=0\)		…и приводим подобные слагаемые.
\(2x^2-x-15=0\)		Уравнение приняло нужный нам вид. Выпишем коэффициенты.
\(a=2\),      \(b=-1\),     \(c=-15\)		Найдем дискриминант по формуле \(D=b^2-4ac\).
\(D=(-1)^2-4·2·(-15) =1+120=121\)		Найдем корни уравнения по формулам \(x_1=\frac{-b + \sqrt{D}}{2a}\) и \(x_2=\frac{-b — \sqrt{D}}{2a}\).
\(x_1=\frac{-(-1) + \sqrt{121}}{2·2}=\frac{1+11}{4}=3\) \(x_2=\frac{-(-1) — \sqrt{121}}{2·2}=\frac{1-11}{4}=-2,5\)		Записываем ответ:

Ответ: \(x_1=3\), \(x_2=-2,5\).

Решите квадратное уравнение \(x^2+9=6x\)
Решение:

\(x^2+9=6x\)		Тождественными преобразованиями приведем уравнение к виду \(ax^2+bx+c=0\).
\(x^2-6x+9=0\)		Выпишем коэффициенты.
\(a=1\),      \(b=-6\),   \(c=9\)		Найдем дискриминант по формуле \(D=b^2-4ac\).
\(D=(-6)^2-4·1·9=36-36=0\)		Найдем корни уравнения по формулам \(x_1=\frac{-b + \sqrt{D}}{2a}\) и \(x_1=\frac{-b — \sqrt{D}}{2a}\).
\(x_1=\frac{-(-6) + \sqrt{0}}{2·1}=\frac{6+0}{2}=3\) \(x_2=\frac{-(-6) — \sqrt{0}}{2·1}=\frac{6-0}{2}=3\)		В обоих корнях получилось одинаковое значение. Нет смысла писать его в ответ два раза.

Ответ: \(x=3\).

Решите квадратное уравнение \(3x^2+x+2=0\)
Решение:

\(3x^2+x+2=0\)		Уравнение сразу дано в виде \(ax^2+bx+c=0\), преобразования не нужны. Выписываем коэффициенты.
\(a=3\),    \(b=1\),   \(c=2\)		Найдем дискриминант по формуле \(D=b^2-4ac\).
\(D=1^2-4·3·2=1-24=-23\)		Найдем корни уравнения по формулам \(x_1=\frac{-b + \sqrt{D}}{2a}\) и \(x_1=\frac{-b — \sqrt{D}}{2a}\).
\(x_1=\frac{-1 + \sqrt{-23}}{2·3}\) \(x_2=\frac{-1- \sqrt{-23}}{2·3}\)		Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.

Ответ: нет корней.

Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут).

Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета. Это быстрее, но требует определенного навыка.

Пример. Решить уравнение \(x^2-7x+6=0\).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут \(6\), а в сумме \(7\). Простым подбором получаем, что эти числа: \(1\) и \(6\). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: \(x_1=1\), \(x_2=6\).

Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты \(b\) и \(c\).

Смотрите также:
Квадратные уравнения (шпаргалка)

Скачать статью

cos-cos.ru

Квадратное уравнение, корни квадратного уравнения, решение квадратного уравнения.

Квадратное уравнение – что это?

 

Квадратное уравнение – это уравнение, которое имеет вид:

\(ax^2+bx+c=0\)

 

Что такое a, b и с? Это коэффициенты. У каждого есть свои названия:

а – старший коэффициент;

b – средний коэффициент;

с – свободный член;

a, b, c – абсолютно любые числа. Но здесь важно: а ≠ 0.

 

Почему именно так? Давай поразмышляем: если предположить, что а все же будет равно 0, то наше уравнение уже не будет квадратным и превратится в линейное:

\(bx+c=0\)

А такие уравнения ты уже решать умеешь, поэтому мы вернемся обратно к квадратным уравнениям.

 

Как выглядит квадратное уравнение?

 

К слову, квадратное уравнение может выглядеть необязательно как стандартное: \(ax^2+bx+c=0\)

Оно может иметь и другой вид, например:

\(ac^2+bx=c\)

(здесь свободный член с находится по другую сторону знака равно) или \(ax^2=c\) (тут средний коэффициент b = 0, а с находится по другую сторону знака равно). Также коэффициенты могут быть отрицательными и т.д.

Однако следует помнить, что абсолютно любое квадратное уравнение можно привести к стандартному виду:

\(ax^2+bx+c=0\)

 

Как же решать квадратное уравнение?

 

Существует всего три результата решения квадратного уравнения:

1. Уравнение не имеет решения.
2. Уравнение имеет только один корень.
3. Уравнение имеет два корня.

 

Как определить, под какой из этих случаев подпадет наше квадратное уравнение? Для этого нам понадобится дискриминант: он нам поможет в решении квадратного уравнения. Дискриминантом (образован от латинского discrimino – «разбираю»)  мы обозначим следующее выражение:

\(D=b^2-4ac\),

где D – дискриминант, а a, b, c – коэффициенты квадратного уравнения.

 

Чем конкретно нам может помочь дискриминант?

1. Если D < 0 – то квадратное уравнение не имеет решений;
2. Если D = 0 – то уравнение будет иметь только один корень;
3. Если D > 0 – то уравнение имеет два решения.

То есть благодаря дискриминанту мы будем знать о результате и количестве решений квадратного уравнения.

Итак, мы посчитали, чему равен наш дискриминант, потом определили количество решений уравнения, что дальше? А дальше определяем корни квадратного уравнения по формулам.

1. В первом случае, когда D < 0, считать ничего не нужно, т.к. уравнение не имеет решений. Это значит, что корней квадратного уравнения на множестве действительных чисел нет.
2. Во втором варианте, когда D = 0, решение будет одно и единственный корень квадратного уравнения будет равен: \(x=\frac{-b}{2a}\)
3. Третий случай, при D > 0, наиболее сложный из всех трех возможных: в ответе должно получиться два корня квадратного уравнения.

\(x_1=\frac{-b+\sqrt D}{2a}\)– первый корень квадратного уравнения;

\(x_1=\frac{-b-\sqrt D}{2a}\)– второй корень квадратного уравнения.

 

Решение квадратных уравнений на самом деле не настолько сложное, как кажется на первый взгляд. Всего-то нужно запомнить несколько формул и алгоритм действий. Главное — не бояться вида квадратных уравнений, мы уверены: все у тебя получится! Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Как решать квадратное уравнение | Подготовка к ЕГЭ по математике

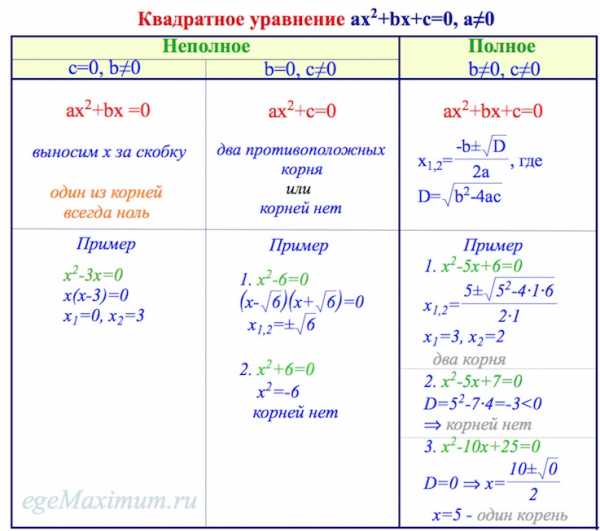
Надеюсь, вы внимательно изучили таблицу, приведенную выше. Если все еще есть вопросы, – давайте разбираться.

Во первых, почему рассматриваются только случаи при ? Просто потому, что при у нас уже будет не квадратное уравнение, а линейное.

Формулу дискриминанта знают практически все, но почему же тогда возникают все же сложности с решением уравнений?

Начнем с того, что иногда происходит путаница с коэффициентами , и . Ни в коем случае мы не считаем, что – это тот коэффициент, что стоит на первом месте! Но – тот, что при . Давайте договоримся, что будем приводить всякое квадратное уравнение к стандартному виду, ставя на первое место слагаемое, содержащее , на последнее – свободный от член (если таковой имеется). Например, уравнение будем переписывать так .

Далее, некоторых может сбить с толку минусовой коэффициент при старшем члене (то есть ). В этом случае советую домножать обе части уравнения на -1. Например, встречая уравнение , переписывать его в таком виде , и только потом высчитывать дискриминант, находить корни.

И, наконец, замечу, находятся и такие товарищи, которые, встречая, например, уравнение , спешат выносить за скобку, путая это уравнение с неполным. Нет, это обычное полное квадратное уравнение, которое после переноса влево примет вид , – решаем мы его через дискриминант.

Поэтому, давайте договоримся всякое уравнение приводить к такому виду, чтобы справа стоял только ноль и ничего больше.

Плавно перешли к неполным квадратным уравнениям. Если мы будем придерживаться последного совета, то мы не сможем спутать неполное уравнение с полным уж это точно. Справа будет два слагаемых (вырожденный случай – одно), а не три как у полного уравнения. Можно, конечно, и такие уравнения решать через дискриминант,но проще поступить иначе.

У нас в случае неполного уравнения будет всегда получаться либо уравнение с двумя , либо с одним . Что делать, в случае, если у нас оба слагаемых содержат (например, )? Ну, конечно, выносить его за скобку (), в этом случае будем всегда получать, что произведение двух множителей равно . Когда такое возможно? Конечно, когда один из множителей равен нулю (либо , либо ). В этом случае у нас всегда один из корней будет нулевым.

Во втором же случае, неполное уравнение будет содержать лишь одно слагаемое с (например, или ). Если свободный член отрицательный (как в первом случае, ), то мы всегда сможем разложить левую часть на множители по формуле

разность квадратов  ( для уравнения имеем , далее ). Если же свободный член положителен, то уравнение не имеет корней (действительно, в уравнении первое слагаемое должно бы быть равным -3, чтобы в сумме с 3 дать 0, но такое невозможно).

В общем, каждое отдельно взятое квадратное уравнение мы решам одним из трех способов, – выбор не велик.

Заметим, также, что в случае полного квадратного уравнения в зависимости от того, какой дискриминант мы получаем, – на выходе разное количество корней. Если , то будем иметь два корня, если , то имеем

один корень (или два совпавших), наконец, если , то корней нет.

Смотрите также статью «Что делать, если дискриминант громоздкий?»

egemaximum.ru

Квадратные уравнения (способы решения)

Разделы: Математика

---

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.

Определение

Уравнение вида ax² + bx + c = 0, где a, b, c — действительные числа, причем a ≠ 0, называют квадратным уравнением.

Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным .
Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент,

c — свободный член.

Корни уравнения ax2 + bx + c = 0 находят по формуле

Выражение D = b²— 4ac называют дискриминантом квадратного уравнения.

• если D < 0, то уравнение не имеет действительных корней;
• если D = 0, то уравнение имеет один действительный корень;
• если D > 0, то уравнение имеет два действительных корня.

В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.

Формулы

Полное квадратное уравнение

Неполные квадратные уравнения

Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.

Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.

Способы решения неполных квадратных уравнений:

1. c = 0, то уравнение примет вид
   ax² + bx = 0.
   x(ax + b) = 0 ,
   x = 0 или ax + b = 0, x = —b : a.
2. b = 0, то уравнение примет вид
   ax² + c = 0,
   x² = —c / a,
   x_{1, 2} = ±√(-c / a).
3. b = 0 и c = 0 , то уравнение примет вид
   ax² = 0,
   x = 0

Решение неполного квадратного уравнения

Квадратные уравнения с комплексными переменными

Сначала рассмотрим простейшее квадратное уравнение

z² = a, где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:

1. имеет один корень z = 0, если а = 0;
2. имеет два действительных корня z_{1, 2} = ±√a
3. Не имеет действительных корней, если a < 0

Решение квадратных уравнений с помощью графиков

Не используя формул квадратное уравнение можно решить графическим способом. Например x² + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x²; y = x + 1.

y = x², квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.

Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.

Решение задач с помощью квадратных уравнений

Процессы	Скорость км/ч	Время ч.	Расстояние км.
Вверх по реке	10 — x	35 / (10 — x)	35
Вверх по протоку	10 — x + 1	18 / (10 — x + 1)	18
V течения	x
V притока	x + 1

Зная, что скорость в стоячей воде равна 10 км/ч, составим уравнение.

ОДЗ: ∀ x ≠ 9, 10.

Практикум

т.к. D₁
Ответ: корней нет.
Ответ: x = 2,5.

Заключение

Ещё в древности люди пользовались ими не зная, что это – квадратные уравнения.

В наше время невозможно представить себе решение как простейших, так и сложных задач не только в математике, но и в других точных науках, без применения решения квадратных уравнений.

Надеюсь и вы открыли для себя что-нибудь новое

Презентация

20.06.2009

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Квадратное уравнение | Учитель математики.ру

Из этой статьи Вы узнаете:

1. Как узнать «в лицо» квадратное уравнение
2. Полные и неполные квадратные уравнения
3. Расположение членов квадратного уравнения
4. Как найти коэффициенты квадратного уравнения

Как по внешнему виду уравнения определить, будет ли ли это уравнение квадратным уравнением или не будет. А очень просто!

Как узнать «в лицо» квадратное уравнение

Во-первых,  в этом уравнении обязательно должен быть член с , то есть  в квадрате, например, .

Именно отсюда и пошло название — квадратное уравнение. По-другому их называют уравнениями второй степени, так как стоит во второй степени. В этом уравнении ещё могут быть (а могут и не быть) члены, содержащие в первой степени, например,  или члены, которые вообще безо всякого , то есть просто «чистые» числа без переменной, например, число .

Во-вторых, уравнение не должно иметь членов, содержащих в третьей степени или в четвёртой или в любой другой степени, большей, чем . Иными словами, самая большая степень переменной в квадратном уравнении равна . Например, уравнение  не является квадратным уравнением, так как здесь есть . А в квадратном уравнении не должно быть  в степени, большей, чем число .

В третьих,  уравнение обязательно должно быть целым. Иначе говоря, в уравнении нигде не должно быть деления на выражение с переменной, то есть с .

Например, уравнение   не является целым уравнением,  потому что в первом члене есть деление на выражение с переменной.  В знаменателе стоит ,  то есть делится на . Такое уравнение называется дробно-рациональным уравнением. Квадратным оно, конечно, не является, хотя здесь есть .

А вот если первый член этого уравнения записать как умножить на , то в результате получим уже целое уравнение . А будет ли оно квадратным? Да, будет! Потому что здесь есть и нет  в степени, большей чем 2.

Полные и неполные квадратные уравнения

Приведём примеры конкретных квадратных уравнений. Например, таких:
1) ;
2) ;
3) ;
4) .

Обратите внимание на некоторые особенности этих уравнений.

Во-первых, у них у всех есть . Причём, нет в степени, большей, чем .

Во-вторых, справа стоит число .

В третьих, в левой части уравнения все члены расположены в строго определённом порядке. На первом месте всегда стоит член с , на втором месте член с переменной , на третьем — число, не связанное с .

Если все члены уравнения перемешаны и стоят не на своих местах, то надо обязательно такое уравнение преобразовать. Далее поговорим об этом подробнее.

Первое уравнение имеет полный набор членов. У него есть и , и , и свободный член . Такие уравнения называются полные квадратные уравнения.
Итак, уравнение является полным квадратным уравнением.

А вот во втором уравнении нет свободного члена.
В третьем уравнении нет .
А в четвёртом нет и , и свободного члена .

Такие уравнения называются неполные квадратные уравнения.

Итак, уравнения


являются неполными квадратными уравнениями.

Каждое из четырёх уравнений, записанных выше, можно представить в виде такой общей формулы , где буквами  и обозначены какие-то конкретные числа. Эти числа называют коэффициентами квадратного уравнения.

Каждый коэффициент имеет специальное название:

это первый коэффициент или иначе старший коэффициент;
это второй коэффициент;
это свободный член.

Число не называют третий коэффициент. Для него существует специальное название «свободный член». Потому что он свободен от переменной !

Расположение членов квадратного уравнения

Для безошибочного решения квадратного уравнения очень важно правильно располагать все его составляющие.

Для этого надо чётко знать, что:

в правой части квадратного уравнения должно стоять число ;
в левой части на первом месте должно стоять слагаемое с ;
на втором месте слагаемое с переменной  ;
на третьем месте — свободный член (число без ).

Если квадратное уравнение записано в соответствии с этими правилами, то говорят, что это квадратное уравнение записано в стандартном виде.

А теперь посмотрим, как всё это выглядит на практике.

В соответствии с предложенными выше рекомендациями, преобразуем уравнение к стандартному виду.

Мы видим, что это уравнение напоминает квадратное уравнение. Здесь есть и член с ,  и член с , и свободный член. Надо только расставить их по своим местам. Сделаем это.

Во-первых, правая часть должна быть равна нулю. Значит, одночлен надо перенести влево с противоположным знаком. Напомню, что при переносе члена из одной части уравнения в другую часть знак этого члена меняется на противоположный. После переноса данное уравнение примет такой вид . Итак, правая часть уравнения стала равной нулю.

Во-вторых, в левой части уравнения на первом месте должно стоять слагаемое с , на втором месте слагаемое с переменной , на третьем — свободный член.

Выполним эти требования, пользуясь переместительным законом сложения. Знаки слагаемых при этом не меняем, так как мы не переносим слагаемые из одной части уравнения в другую. Эти слагаемые как были в левой части, так они в левой части и остались. Они просто меняются местами друг с другом. Уравнение станет таким . 

Как найти коэффициенты квадратного уравнения

Итак, после всех преобразований мы получили уравнение . Это уравнение уже записано в стандартном виде. Общий вид уравнения таков . Напомню — буквами  обозначены коэффициенты квадратного уравнения.

В уравнении коэффициенты чётко видны: , , .
это то число, которое стоит перед ,то есть число .
это то число, которое стоит перед , то есть число .
это свободный член, то есть число .

А вот с уравнением  не всё так просто! В левой части квадратного уравнения должно стоять три члена, а здесь их только два. Есть член с , есть член с , но нет свободного члена, который обозначается буквой . Это значит, что он просто равен нулю, то есть .

Если записать уравнение так, чтобы слева было три члена, то получим следующее . А теперь мы запросто можем выписать его коэффициенты, получим: , , .

В уравнении почти аналогичная ситуация. Только здесь не хватает члена с переменной .

Преобразуем данное уравнение так, чтобы все три члена были явно видны и стояли на своих местах. Получим (крестиком обозначен знак умножения).

А теперь легко выписать его коэффициенты ; ; .

А как же найти коэффициенты квадратного уравнения ? У него в левой части вообще только один член! Он содержит .

Здесь нет члена с , значит, коэффициент перед равен нулю. Нет и свободного члена , значит, он тоже равен нулю.

Пользуясь этой информацией, запишем данное уравнение так, чтобы явно были видны все три члена и они стояли бы на своих местах. Получим такое уравнение. А теперь выписываем коэффициенты ; ; .

Вот так хитренько устроены квадратные уравнения!

vebuchitel.ru