Действия над событиями теория вероятности – 1.Предмет теории вероятности. Виды событий. Действия над событиями.

Краткий конспект лекций по теории вероятностей Лекция1 Вероятность

35

В теории вероятностей рассматриваются такие явления или опыты, конкретный исход которых не определяется однозначно условиями опыта (случаен), но по результатам большого числа экспериментов в среднем может быть предсказан (свойство статистической устойчивости).

Элементарным событием (элементарным исходом)называется любое событие — исход опыта, которое нельзя представить в виде объединения других событий. Так как исход опыта случаен, то и любое элементарное событие случайно, далее будем говорить просто о событиях, не подчеркивая их случайность.

Пространством элементарных событий  (исходов) называется множество всех элементарных событий (исходов). {₁, …_{n …}}, если в результате опыта обязательно наступает какой-либо из элементарных исходов и только один (один исход исключает любой другой). Пространство элементарных событий может содержать конечное, счетное и даже бесконечное множество элементарных событий.

Случайным событием (событием) называется подмножество пространства элементарных событий. Любое множество – это совокупность элементов. Элементами события являются элементарные события, образующие это событие.

Пример. Бросается одна монета, она может упасть гербом (₁=Г) или решкой (₁=Р).=(Г,Р).

Пример. Бросаются две монеты = {(Г, Г), (Г,Р), (Р,Г), (Р,Р)}

Пример. Капля дождя падает на прямоугольную площадку.

= {(x,y),a<x<b,c<y<d}

Достоверное событие – событие, которое всегда происходит в результате данного опыта, оно содержит все элементарные события и обозначается.

Невозможное событие– событие, которое не может произойти в результате данного опыта, оно не содержит элементарных событий и обозначается.

Действия над событиями.

События определены как множества, поэтому действия над ними аналогичны действиям над множествами и хорошо иллюстрируются диаграммами Венна.

Пространство будем обозначать прямоугольником, элементарное событие – точкой прямоугольника, а каждое событие – подмножеством точек этого прямоугольника. Результат операции над событиями будем заштриховывать.

Пусть выбираются карты из колоды карт. Событие А – выбор червонной карты, событие В – выбор десятки

	Суммой двух событий А и В называется событие С = А + В (или С = АВ), состоящее из элементарных событий, принадлежащих либо А, либо В. Пример. С = А + В – выбор любой червонной карты или любой десятки
	Произведением двух событий А и В называется событие D = AB (или D = AB), состоящее из элементарных событий, принадлежащих и А и В. Пример. АВ– выбор десятки червей
	Разностью двух событий А и В называется событие А\В, состоящее из элементарных событий, принадлежащих А и не принадлежащих В. Пример. А\В –выбор любой червонной карты, кроме десятки

Классификация событий Событие, состоящее из всех элементарных событий, не содержащихся в а, обозначим и будем называть противоположным событием.

Пример. А –выбор червонной карты; –выбор любой карты другой масти.. = \А

Два события А и В будем называть совместными, если каждое из них содержит хотя бы одно общее элементарное событие, т.е если АВ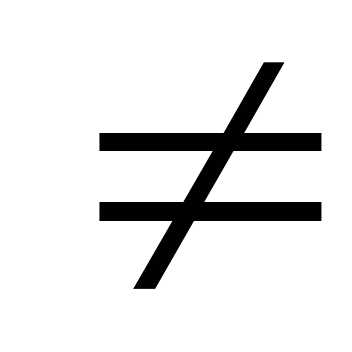Ø и несовместными, если АВ = Ø.

Пример. А – выбор червонной карты и В

– выбор десятки – совместные события, так как

АВ = выбор червонной десятки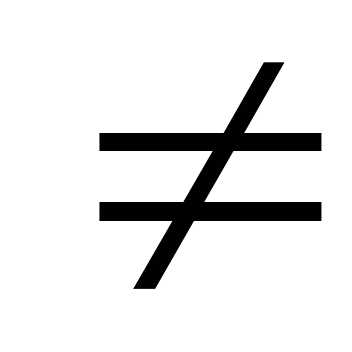Ø

Пример. А – выпадение четного числа очков А = {2, 4, 6}. В – выпадение нечетного числа очков В = {1, 3, 5}. Очевидно, что А и В несовместны.

studfiles.net

1.Случайные события и действия над ними. Виды случайных событий. Комбинации событий Пространство элементарных событий.

В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, напри-мер, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к по-ловине количества бросков; нельзя заранее предсказать результат одного выстрела из дан-ного орудия по данной цели, но при большом числе выстрелов частота попадания прибли-жается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет

теории вероятностей.

Основным интуитивным понятием классической теории вероятностей является

случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:

а) достоверное событие – событие, которое всегда происходит при проведении опыта;

б) невозможное событие – событие, которое в результате опыта произойти не может;

в) случайное событие – событие, которое может либо произойти, либо не произойти. Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным – выпадение 10 очков, а случайным – выпадение 3 очков.

Алгебра событий.

1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В.

Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.

Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событие А (исходов, благоприятных событию А), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событие А+В, является объединением множеств исходов, благоприятных событиям А или В (рис. 1).

2. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично

произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.

Геометрической иллюстрацией множества исходов опыта, благоприятных появлению произведения событий А и В, является пересечение областей, соответствующих исходам, благоприятным А и В.

3. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет.

Введем еще несколько категорий событий.

4. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются

несовместными.

Замечание 1. Если изобразить графически области исходов опыта, благоприятных несовместным событиям, то они не будут иметь общих точек.

Замечание 2. Из определения несовместных событий следует, что их произведение является невозможным событием.

5. Говорят, что события А₁, А₂,…,А_п образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы.

Замечание. В частности, если события, образующие полную группу, попарно несовмест-ны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями.

6. События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое.

studfiles.net

Лекция 20

Тема: Теория вероятностей.

Время: 2 ч.

Вопросы:

1. Основы теории вероятности.

2. Случайные события. Понятие. Классификация событий.

3. Операции над событиями.

4. Действия над случайными событиями.

5. Эмпирическая вероятность.

6. Классическое определение вероятности.

7. Сведения из комбинаторики.

1. Основы теории вероятностей.

Мы переходим к изучению совершенно новых математических объектов, связанных с понятием случайности. Случайность как явление реальной жизни хорошо нам знакома.

Например: Случайными бывают попутчики, встречи, звонки и т.д. Многое в нашей жизни случайно, т.е. не обусловлено четкими причинно-следственными связями.

Даже в бытовом уровне мы различаем два вида событий – детерминированные и случайные. В детерминированном событии мы точно знаем, что данная причина приведет к единственному и вполне определенному следствию. Мы нажимаем на кнопку, и лампа загорается: между действием и результатом существует четкая однозначная связь. Исход случайного события непредсказуем, он зависит от случайных факторов. Например, подбрасывание монеты или кубика. Нельзя узнать заранее, на какую сторону упадет монета, или какая грань выпадет на кубике.

Существуют также бытовые представления о вероятности. Например, оценивая шансы на выигрыш, мы неосознанно подсчитываем его вероятность.

Теория вероятностей зародилась как наука в XVII в. под влиянием интереса к такому несерьезному занятию, как азартные игры. Дальнейшее развитие теории вероятностей в XVIII в. Связано с именами таких математиков, как Якоб Бернулли (1654 — 1705), Даниил Бернулли (1700 — 1782), Абрахам Де Муавр (1667 — 1754) и Жорж Луи Бюффон (1707 — 1788). Значительный вклад в теорию вероятностей внесли русские математики П.Л.Чебышев (1821 — 1894) и его ученики А.М. Ляпунов (1857 — 1918), А.А.Марков (1856 — 1922).

2. Случайные события. Понятие. Классификация событий.

Мы уже дали некоторую начальную классификацию, разделив, события на детерминированные и случайные. Рассмотрим основные черты случайного события как математического объекта. Какие наблюдения можно сделать, например, при бросании монеты? Во-первых, исход этого эксперимента непредсказуем. Однако возможных исходов всего два: может выпасть либо «орел», либо «решка». Условия реального эксперимента при повторении неизбежно меняются (бросание монеты происходит всегда по-разному). При математическом определении случайного события мы считаем, что эксперимент можно повторить неограниченное число раз при одинаковых условиях. Это важные характеристики случайного события.

События, с неясным исходом, но и не случайные называют неопределенными.

Давайте, при бросании монеты будем наблюдать, за количеством выпадения «орлов». — относительная частота,n – количество испытаний, 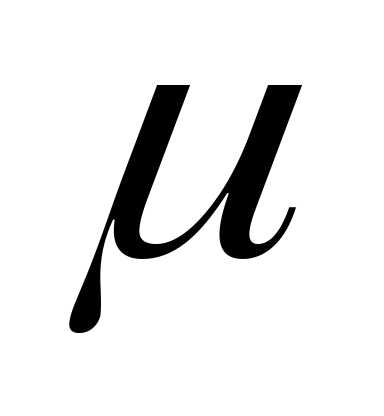— частота данного случайного события. При увеличении числа испытаний относительная частота события имеет тенденцию к стабилизации. Такое поведение характерно для любого случайного событий и носит названиестатистической устойчивости.

Итак, случайное событие характеризуется тремя особенностями:

• Неопределенностью исхода единичного эксперимента;

• Возможностью неограниченного повторения в одинаковых условиях;

• Стабилизацией относительной частоты.

Случайные события в теории вероятностей обычно обозначают прописными латинскими буквами А,В,С и т.д.

studfiles.net

3. Операции над событиями.

Суммой событий А и В (обозначается А+В) называют событие, состоящее в появлении хотя бы одного из двух событий А или В.

Аналогично определяется сумма большего числа событий

Пример 1: Появление чётной грани игральной кости есть сумма трёх событий: выпадение 2, выпадение 4, выпадение 6.

Произведением событий А и В (обозначается А·В) называют событие, состоящее в появлении обоих событий А и В.

Пример 2: Пусть событие А – при бросании двух монет появление герба на первой монете, событие В – появление герба на второй монете; тогда произведение А·В – это появление гербов на обеих монетах.

Произведение несовместных событий – событие невозможное. Сумма и произведение событий аналогичны объединению и пересечению множеств, соответственно.

  Вероятность суммы А+В несовместимых событий А и В равна сумме вероятностей событий А и В, т.е. Р(А+В)=Р(А)+Р(В)

8. Действия над случайными событиями.

Говорят, что событие В следует из события А, если событие В происходит всегда, когда произошло событие А.

События А и В равны, если из А следует В и из В следует А.

Суммой двух событий А и В называется событие А+В, состоящее в том, что произошло событие А или событие В.

Сложение событий удовлетворяет коммутативному и ассоциативному законам.

А + В = В + А

А + (В + С) = (А + В) + С

Из события А следует сумма этого события с любым событием В:

Пример 3: Стрельба по мишени. Пусть стрелок сделал 5 выстрелов по мишени.

Событие С = «стрелок попал не меньше трех раз» есть сумма трех событий:

С=

Событие D = «стрелок попал хотя бы один раз» произойдет, если стрелок попал один раз, или два раза, или три раза и т.д. Значит, D=A₁+A₂+A₃+A₄+A₅.

Произведением двух событий А и В называется событие АВ, состоящее в том, что событие А и событие В произошли одновременно. Умножение событий так же, как и сложение, коммутативно и ассоциативно.

А* В = В * А,

А*(В * С)=(А * В)*С

Из события АВ следуют событие А и событие В:

АВА, АВВ

Сложение и умножение событий удовлетворяют двум дистрибутивным законам.

А*(В + С) = А*В + А*С,

А + В*С = (А+В)*(А+С).

Пример 4: Одновременное бросание двух кубиков. Событие С состоит в том, что сумма чисел на обоих кубиках четна. Это может произойти, когда оба числа четные или оба нечетные. Пусть А₁ = «на первом кубике четное число», В₁= «на первом кубике нечетное число», А₂, В₂ – те же события для второго кубика. Тогда С = А₁А₂+В₁В₂.

Событие называетсяпротивоположным событию А, если оно состоит в том, что не произошло событие А. Например, выпадение «орла» при бросании монеты противоположно выпадению «решки».

Событие называется достоверным, если оно происходит всегда. Например, событие состоящее в том, что при бросании монеты выпадает «орел» или «решка», является достоверным.

Событие, не наступающее никогда, называется невозможным. Например, одновременное выпадение «орла» и «решки» невозможно.

События образуют полный набор, если они несовместны, а их сумма есть достоверное событие. Например, при бросании монеты полный набор состоит из двух событий: выпадение «орла» или «решки». Действительно, событие «выпал орел или решка» является достоверным.

studfiles.net

Предмет теории вероятностей. Случайные события, их классификация. Действия над событиями. Алгебра событий.

Стр 1 из 4Следующая ⇒

Предмет теории вероятностей. Случайные события, их классификация. Действия над событиями. Алгебра событий.

Теорвер – наука, изучающая закономерности, присущие случайным массовым событиям. Предметом теорвера явл. Метаматические модели случайных явлений.

Пусть проводится некоторый опыт, исход к. предсказать невозможно. Случайным событием назыв. Любой исход опыта, к. м/произойти, либо не произойти.

Классификация:
1)достоверные – если событие обязательно наступит в рез-те данного опыта
2)невозможные – если событие в рез-те данного опыта заведомо не произойдет
3)(?)несовместимые – 2 обытия: если наступление одного исключает наступление другого
4)совместные – иначе

5)события А1,…Аn – попарно несовместные, если любые 2 из них несовместны

6)несколько событий в данном опыте назыв. равновозможными, если ни одно из них не явл. Объективно более возможным, чем другое
Действия:
1) сумма 2х событий А и В назыв. Событие,состоящее в наступлении хотя бы одного из них.

(А+В ~ АUВ)

2) произведением 2х событий назыв. Событие,сотоящее в совместном наступлении событий А и В

(А )

3)разностью 2х событий А и В назыв. Событие, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В

(А\В)

4)Противоположным к событию А назыв. Событие , к. происходит тогда и только тогда, когда не происходит событие А

5)событие А влечет событие В (А ) / или А явл. Частным случаем события В – если из того, что происходит событие А следует, что происхдит событие В

2. Статистическое, классическое и геометрическое определения вероятности.

Классическое. Пусть проводится опыт с n исходами. Такие исходы назыв. Случайными/элементарными событиями, а опыт. Назыв. Классическим. Случай , к.приводит к наступлению события А назыв. Благоприятствующим событию А, т.е. А. Вероятностью события А или классической вероятностью назыв. Отношение числа m,т.е. числа благоприятствующих случаев события а к общему числу случаев n.
Р(А) = m/n
Геометрическое. В области ῼ случаным образом выбирается точка x. При этом попадание точки в область – это достоверное событие,а в область А (А ) – случайное событие. Пусть площад оласти А – S_A, а площадь всей области — S_ῼ. Тогда геометрическая вероятность наступления события:
Р(А) = S_A/ S_ῼ
Статистическое. Статистической вероятностью события А называется относительная частота появления этого события в произведённых испытаниях:

Р(А) = (А) = m/n, где Р(А)– вероятность появления события А; – относительная частота появления события А; m- число испытаний, в которых появилось событие А; n- общее число испытаний.

Схема выбора без возвращения и с возвращением. Перестановки. Размещения. Сочетания.

Пусть задано множ-во, состоящее из n эл-ов. Размещение из n элементов по m назыв.любое упорядоченное подмнож-во данного множ-ва, содержащее m эл-ов. Т.е. размещения – это выборки, состоящие из m эл-ов, к.отличаются друг от друга либо составом эл-ов, либо порядком их следования.
A_n^m = n!/(n-m)!
Перестановками из n эл-ов назыв. Размещения из n по n эл-ов./
Р_n = n!
Сочетаниями из n эл-ов по m назыв.любое подмножество исходного множж-ва, к.содержит m эл-ов. Порядок не важен, отличаются только составом эл-ов.

C_n^m = n!/((n-m)! * m!)
Если при выборе m эл-ов из n, эл-ы возвращаются и упорядочиваются, то говорят, что это размещение с повторением. Они отличаются друг от друга составом эл-ов, порядком и кол-вом повторений эл-ов.

= n^m – размещения с повторением
Сочетания с повторениями – это выборки, состоящие из m эл-ов, выбранные из исходного множ-ва, состоящего из n эл-ов, при этом эл-ы возвращаются и не упорядочиваются.

= C_n+m-1^m
Пусть множ-во состоит из n эл-ов и пусть в нем имеется k различных эл-ов. 1ый эл-т повторяется n1 раз, 2ой – n2,…,kый – nk раз; n1+n2+n3+… = n. Перестановки из n эл-ов данного множ-ва назыв. Перестановками с повторениями из n эл-ов. Число таких перестановок – P_n(n1, …, nk)
P_n(n1, …, nk) = n!/(n1!*n2!*…*nk!)

Теорема Чебышева

Определение сходимости по вер-ти. Пусть заданы СВ Х1,…,Хn, т.е. бесконечное кол-во СВ. Эти СВ сходятся по вер-ти к величине А (случайной или неслучайной), если Р(|Xn — A|< )->1 при n->

= 1; Xn A при n->

Теорема Бернулли
Если вер-ть наступления события А в одном испытании равна р, число наступления этого события при n независимых испытаниях равно n_A ,то для любого справедливо равенство

= 1, т.е. относительная частота P^*(A) = n_A/n наступления события А в n испытаниях сходится по вер-ти к вер-ти события А.

 

Основные понятия математической статистики Генеральная и выборочная совокупности, понятие вариационного ряда. Статистический ряд частот. Интервальный ряд. Гистограмма и полигон частот.

Мат. Статистика – раздел математики,в к.изучаются методы сбора, систематизации и обработки рез-тов наблюдений массовых случайных явлений для выявления сущ-вующих закономерностей.
Совокупность всех подлежащих изучению объектов или всех рез-тов наблюдений над каким-то объектом назыв.генральной совокупностью.

Выборочной совокупностью/выборкой назыв.совокупность объектов, отобранных случайным образом из генеральной совокупности.

Последовательность вариант, записанных по возрастанию, назыв.вариационным рядом.

Гистограмма частот – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных га оной прямой, основания которых одинаковы и равны ширине класса, а высота равна или частоте попадания в интервал или относительной частоте . Ширину интервала можно определить по формуле Стерджеса: (двоичный лог)
Полигон частот– ломаная линия, отрезки которой соединяют точки с координатами , .

Статистический ряд частот представляется в виде таблице, где сверху указаны варианты СВ xi, а снизу – их количество в выборке.

 

Предмет теории вероятностей. Случайные события, их классификация. Действия над событиями. Алгебра событий.

Теорвер – наука, изучающая закономерности, присущие случайным массовым событиям. Предметом теорвера явл. Метаматические модели случайных явлений.

Пусть проводится некоторый опыт, исход к. предсказать невозможно. Случайным событием назыв. Любой исход опыта, к. м/произойти, либо не произойти.

Классификация:
1)достоверные – если событие обязательно наступит в рез-те данного опыта
2)невозможные – если событие в рез-те данного опыта заведомо не произойдет
3)(?)несовместимые – 2 обытия: если наступление одного исключает наступление другого
4)совместные – иначе

5)события А1,…Аn – попарно несовместные, если любые 2 из них несовместны

6)несколько событий в данном опыте назыв. равновозможными, если ни одно из них не явл. Объективно более возможным, чем другое
Действия:
1) сумма 2х событий А и В назыв. Событие,состоящее в наступлении хотя бы одного из них.

(А+В ~ АUВ)

2) произведением 2х событий назыв. Событие,сотоящее в совместном наступлении событий А и В

(А )

3)разностью 2х событий А и В назыв. Событие, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В

(А\В)

4)Противоположным к событию А назыв. Событие , к. происходит тогда и только тогда, когда не происходит событие А

5)событие А влечет событие В (А ) / или А явл. Частным случаем события В – если из того, что происходит событие А следует, что происхдит событие В

2. Статистическое, классическое и геометрическое определения вероятности.

Классическое. Пусть проводится опыт с n исходами. Такие исходы назыв. Случайными/элементарными событиями, а опыт. Назыв. Классическим. Случай , к.приводит к наступлению события А назыв. Благоприятствующим событию А, т.е. А. Вероятностью события А или классической вероятностью назыв. Отношение числа m,т.е. числа благоприятствующих случаев события а к общему числу случаев n.
Р(А) = m/n
Геометрическое. В области ῼ случаным образом выбирается точка x. При этом попадание точки в область – это достоверное событие,а в область А (А ) – случайное событие. Пусть площад оласти А – S_A, а площадь всей области — S_ῼ. Тогда геометрическая вероятность наступления события:
Р(А) = S_A/ S_ῼ
Статистическое. Статистической вероятностью события А называется относительная частота появления этого события в произведённых испытаниях:

Р(А) = (А) = m/n, где Р(А)– вероятность появления события А; – относительная частота появления события А; m- число испытаний, в которых появилось событие А; n- общее число испытаний.

Рекомендуемые страницы:

lektsia.com

Операции над событиями. Правила сложения и умножения вероятностей

Вероятностью события А называют отношение числа m исходов испытаний, благоприятствующих наступлению события А, к общему числу n всех равновозможных несовместных исходов: Р(А)=m/n. Условной вероятностью события А (или вероятностью события А при условии, что наступило событие В), называется число РВ(А) = Р(АВ)/Р(В), где А и В – два случайных события одного и того же испытания. Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них. Сумма двух событий обозначается А+В. Правила сложения вероятностей: правило сложения вероятностей совместных событий А и В: Р(А+В) = Р(А)+Р(В)-Р(АВ), где Р(А) – вероятность события А, Р(В) – вероятность события В, Р(А+В) – вероятность появления хотя бы одного из двух событий, Р(АВ)- вероятность совместного появления двух событий. правило сложения вероятностей несовместных событий А и В: Р(А+В) = Р(А)+Р(В), где Р(А) – вероятность события А, Р(В) – вероятность события В. Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет. Произведение двух событий обозначается АВ. Правила умножения вероятностей: правило умножения вероятностей зависимых событий А и В: Р(АВ)= Р(А)*РА(В)= Р(В)*РВ(А), где РА(В) – условная вероятность наступления события В, если событие А уже наступило, РВ(А) – условная вероятность наступления события А, если событие В уже наступило; правило умножения вероятностей независимых событий А и В: Р(АВ) = Р(А)*Р(В), где Р(А) – вероятность события А, Р(В) – вероятность события В. Примеры решения задач по теме «Операции над событиями. Правила сложения и умножения вероятностей» Задача 1. В коробке имеется 250 лампочек, из них 100 по 90Вт, 50 — по 60Вт, 50 — по 25Вт и 50 – по 15Вт. Определить вероятность того, что мощность любой наугад взятой лампочки не превысит 60Вт. Решение. 1. Рассматриваем следующие события: А = {мощность лампочки равна 90Вт}, вероятность Р(А)=100/250=0,4; В = {мощность лампочки равна 60Вт}; С = {мощность лампочки равна 25Вт}; D = {мощность лампочки равна 15Вт}. 2. События А, В, С, D образуют полную систему, так как все они несовместны и одно из них обязательно наступит в данном опыте (выборе лампочки). Вероятность наступления одного из них есть достоверное событие, тогда Р(А)+Р(В)+Р(С)+Р(D)=1. 3. События {мощность лампочки не более 60Вт} (т.е. меньше или равна 60Вт), и {мощность лампочки более 60Вт} (в данном случае – 90Вт) являются противоположными. По свойству противоположных чисел Р(В)+Р(С)+Р(D)=1-Р(А). 4. Учитывая, что Р(В)+Р(С)+Р(D)=Р(В+С+D), получим Р(В+С+D)= 1-Р(А)=1-0,4=0,6. Задача 2. Вероятность поражения цели первым стрелком при одном выстреле равна 0,7, а вторым стрелком – 0,9. Найти вероятность того, что а) цель будет поражена только одним стрелком; б) цель будет поражена хотя бы одним стрелком. Решение. 1. Рассматриваем следующие события: А1 = {первый стрелок поражает цель}, Р(А1)=0,7 из условия задачи; А̄1 = {первый стрелок промахнулся}, при этом Р(А1)+Р(А̄1) = 1, поскольку А1 и А̄1 – противоположные события. Отсюда Р(А̄1)=1-0,7=0,3; А2 = {второй стрелок поражает цель}, Р(А2)=0,9 из условия задачи; А̄2 = {второй стрелок промахнулся}, при этом Р(А̄2)=1-0,9=0,1. 2. Событие А={цель поражена только одним стрелком} означает, что наступило одно из двух несовместных событий: либо А1А̄2, либо А̄1А2. По правилу сложения вероятностей Р(А)= Р(А1А̄2)+Р(А̄1А2). По правилу умножения вероятностей независимых событий: Р(А1А̄2)= Р(А1)*Р(А̄2)= 0,7*0,1=0,07; Р(А̄1А2)= Р(А̄1)*Р(А2)=0,3*0,9=0,27. Тогда Р(А)= Р(А1А̄2)+Р(А̄1А2)=0,07+0,27=0,34. 3. Событие B={цель поражена хотя бы одним стрелком} означает, что либо цель поразил первый стрелок, либо цель поразил второй стрелок, либо цель поразили оба стрелка. Событие B̄={цель не поражена ни одним стрелком} является противоположным событию В, а значит Р(В)=1-Р(B̄). Событие B̄ означает одновременное появление независимых событий Ā1 и Ā2, следовательно Р(B̄)=Р(Ā1Ā2)= Р(Ā1)*Р(Ā2)=0,3*0,1=0,3. Тогда Р(В)= 1-Р(B̄)=1-0,3=0,7. Задача 3. Экзаменационный билет состоит из трех вопросов. Вероятность того, что студент ответит на первый вопрос 0,7; на второй – 0,9; на третий – 0,6. Найти вероятность того, что студент, выбрав билет ответит: а) на все вопросы; г) по крайней мере на два вопроса. Решение. 1. Рассматриваем следующие события: А1 = {студент ответил на первый вопрос}, Р(А1)=0,7 из условия задачи; А̄1 = {студент не ответил на первый вопрос}, при этом Р(А1)+Р(А̄1) = 1, поскольку А1 и А̄1 – противоположные события. Отсюда Р(А̄1)=1-0,7=0,3; А2 = {студент ответил на второй вопрос}, Р(А2)=0,9 из условия задачи; А̄2 = {студент не ответил на второй вопрос}, при этом Р(А̄2)=1-0,9=0,1; А3 = {студент ответил на третий вопрос}, Р(А3)=0,6 из условия задачи; А̄3 = {студент не ответил на третий вопрос}, при этом Р(А̄3)=1-0,6=0,4. 2. Событие А = {студент ответил на все вопросы} означает одновременное появление независимых событий А1, А2 и А3, т.е. Р(А)= Р(А1А2А3).По правилу умножения вероятностей независимых событий: Р(А1А2А3)= Р(А1)*Р(А2)*Р(А3)= 0,7*0,9*0,6=0,378. Тогда Р(А)= Р(А1А2А3)=0,378. 3. Событие D = {студент ответил по крайней мере на два вопроса} означает, что дан ответ на любые два вопроса или на все три, т.е. наступило одно из четырех несовместных событий: либо A1A2Ā3, либо А1Ā2А3, либо А̄1А2А3, либо А1А2А3. По правилу сложения вероятностей несовместных событий: Р(D)= Р(A1A2Ā3)+ Р(А1Ā2А3)+Р(А̄1А2А3)+Р(А1А2А3). По правилу умножения вероятностей независимых событий: Р(A1A2Ā3)= Р(A1)*Р(A2)*Р(Ā3)= 0,7*0,9*0,4=0,252; Р(А1Ā2А3)= Р(А1)*Р(Ā2)*Р(А3)= 0,7*0,1*0,6=0,042; Р(А̄1А2А3)= Р(А̄1)*Р(А2)*Р(А3)= 0,3*0,9*0,6=0,162; Р(А1А2А3)= Р(А1)*Р(А2)*Р(А3)= 0,7*0,9*0,6=0,378. Тогда Р(D)= 0,252+0,042+0,162+0,378= 0,834. Другие статьи по данной теме: Список использованных источников Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004; Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006; Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007; Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.

www.ekonomika-st.ru

Понятие события, операции над событиями / Теория вероятности [Калинин В.М., Тихомиров С.Р. Лекции по теории вероятностей и математической статистике] / 3dstroyproekt.ru

Понятие события

Событие является первоначальным понятием в Т.В. Под событием понимается результат некоторого эксперимента. Т.В. интересуется только тем, произошло событие или нет.

События можно разделить на три класса.

1. Достоверное событие — всегда происходит в эксперименте — $\Omega $.
2. Невозможное событие — $\emptyset $- никогда не происходит.
3. Случайное событие — в одних и тех же условиях может происходить, а может не происходить, обозначается: $A=\left\{ { расшифровка }\right\} $

Например: эксперимент: подбрасываем монеты, результат эксперимента — случайное событие

$A=$ { монета упала гербом } ,

$B=$ { монета упала решкой } ,

$C=$ { монета упала ребром } .

В Т.В. событие и эксперимент не разделяют.

Опр Совокупность всех событий для данного эксперимента называется пространством элементарных событий. { Оно может быть конечным или бесконечным } .

Операции над событиями

Опр Произведением событий $A$ и $B$ называется событие С которое происходит тогда когда происходит и $A$ и $B$, обозначается: $C=A\cap B$.

Опр Произведением группы из n — событий — $A_1 \,,\,A_2 \ldots A_n $ есть событие $A$, обозначается $A=A_1 \cap A_2 \cap A_3 \ldots A_n $.

Опр Суммой событий $A$ и $B$ называется третье событие С которое происходит при наступлении хотя бы одного из событий $A$ или $B$, обозначается $C=A\cup B$.

Опр Суммой группы событий $A_1 \ldots A_n $ называется событие $C=A_1 \cup A_2 \cup \ldots \cup A_n $.

Опр Разностью событий $A$ и $B$ называется третье событие С которое происходит тогда когда $A$ происходит, а $B$ не происходит: $C=A / { \vphantom { A B } } B$.

Опр Событие $\overline A $ называется противоположным событию $A$, если оно происходит тогда, когда $A$ не происходит.

Опр Говорят, что событие $A$ влечет событие $B$, если при наступлении события $A$ обязательно происходит событие $B$, обозначается: $A\subset B$.

Опр События $A$ и $B$ называются равносильными или тождественными, если $A\subset B$ и $B\subset A$ т.е. при наступлении одного, второе обязательно происходит.

Опр События $A$ и $B$ называются несовместными, если они одновременно происходить не могут $A\cap B=\emptyset $.

Опр Группа событий называется полной, если хотя бы одно из событий происходит обязательно $A_1 \cup A_2 \cup A_3 \cup \ldots \cup A_n =\Omega $

Опр Полная группа событий называется полной группой попарно-несовместных событий, если любые два события этой группы одновременно произойти не могут.

Геометрическая интерпретация операций над событиями

Пусть событие $A$ — { выбрали случайные точки, они попали в круг } , $B$ — { точки попали в квадрат }

Свойства операций над событиями

1. $A\cap A=A$
2. $A\cap \overline A =\emptyset $
3. $A\cap \Omega =A$
4. $A\cap \emptyset =\emptyset $
5. $A\cap B=B\cap A$
6. $A\cap ( { B\cap C } )=( { A\cap B } )\cap C$
7. $A\cup A=A$
8. $A\cup \overline A =\Omega $
9. $A\cup \Omega =\Omega $
10. $A\cup \emptyset =A$
11. $A\cup B=B\cup A$
12. $A\cup ( { B\cup C } )=( { A\cup B } )\cup C$
13. $A\cap ( { B\cup C } )=( { A\cap B } )\cup ( { A\cap C } )$
14. $A\cup ( { B\cap C } )=( { A\cup B } )\cap ( { A\cup C } )$

Формулы Де Моргана.

1. $\overline { A\cup B } =\overline A \cap \overline B $
2. $\overline { A\cap B } =\overline A \cup \overline B $

3dstroyproekt.ru