Дано множество small m a b c найти его собственные подмножества – Найдите ВСЕ подмножества множества M= {a,b,c}. Как это делать, объясните пожалуйста!
Подмножество | Математика | FANDOM powered by Wikia
Подмно́жество в теории множеств — это понятие части множества.
Файл:Venn А subset В.svg- Множество $ A $ является подмножеством множества $ B $, если любой элемент, принадлежащий $ A $ также принадлежит $ B $. Пишут: $ A \subset B $ или $ A \subseteq B $. Таким образом,
- $ (A \subset B) \Leftrightarrow ( x \in A \Rightarrow x \in B ). $
- Множество $ B $ в таком случае называется надмно́жеством множества $ A $, и этот факт часто записывают: $ B \supset A $ или $ B \supseteq A. $
Собственное подмножество Править
Из определения прямо следует, что пустое множество обязано быть подмножеством любого множества. Также, очевидно, любое множество является своим подмножеством:
- $ \emptyset \subset B,\; B \subset B \quad \forall B. $
Если $ A \subset B $, и $ A \not= \emptyset,\; A \not= B, $ то $ A $ называется со́бственным или нетривиа́льным подмножеством.
- $ B \subset B. $=
- $ (A \subset B \; \and \; B \subset A) \Leftrightarrow (A = B). $
- $ (A \subset B \;\and \; B \subset C ) \Rightarrow ( A \subset C ). $
- Таким образом отношение подмножества является отношением частичного порядка на булеане $ 2^{M} $ — семействе всех подмножеств любого объемлющего множества $ M. $
- Для любых двух множеств $ A $ и $ B $ следующие утверждения эквивалентны:
- $ A \subset B. $
- $ A \cap B = A. $
- $ A \cup B = B. $
- $ B^{\complement} \subset A^{\complement}. $
- $ A = \{1,2,3,4,5\},\; B = \{1,2,3\},\; C = \{4,5,6,7\}. $
Тогда
- $ B \subset A,\; C \not\subset A. $
be-x-old:Падмноства
bn:উপসেট
ca:Subconjunt
cs:Podmnožinael:Υποσύνολοeo:Subaroet:Alamhulkfiu-vro:Alambhulkhe:תת קבוצה
hu:Részhalmaz
is:Hlutmenginl:Deelverzameling
no:Delmengde
pl:Podzbiórsimple:Subset
sk:Podmnožina
sl:Podmnožica
sv:Delmängd
uk:Підмножина
ru.math.wikia.com
С++ Подмножество с данной суммой элементов
void itmathrepetitor_ru()
{
setlocale(LC_ALL, «Russian»);
double *a, s, p;
int n, k, ires;
bool flag;
do
{
cout << «Введите кол-во элементов множества: «;
cin >> n;
}
while (n<1); // проверка на допустимое значение n
a=new double [n]; // выделяем память
for (int i=0; i<n; i++) // запрашиваем n чисел
{
cout << «Введите «<<(i+1)<<» элемент : «;
cin >> a[i];
flag=false; //www.itmathrepetitor.ru
for (int j=0; j<i; j++) // проверка на повтор
{
if (a[i]==a[j]) // нашли повтор
{
flag=true;
break;
}
}
if (flag) // если повтор был
{
cout<<«Такой элемент уже есть в множестве»<<endl;
i—;
}
}
cout<<«Введите сумму чисел: «;
cin>>s; //www.itmathrepetitor.ru
cout<<«Множество: «<<endl; // показ множества
for (int i=0; i<n; i++)
cout<<a[i]<<» «;
cout<<endl;
ires=-1;
k=powf(2,n); // количество подмножеств
for (int i=0; i<k; i++) // перебор подмножеств
{
p=0;
flag=false;
for (int j=0; j<n; j++) // перебираем числа из подмножества
if (i & (1<<j))
{
p+=a[j]; // накапливаем сумму
flag=true; // подмножество не пусто
}
if (p==s && flag) // если сумма совпала и подмножество не пусто
{
ires=i;
break; //www.itmathrepetitor.ru
}
}
if (ires==-1)
{
cout<<«Подмножество с данной суммой не существует»<<endl;
}
else
{
cout<<«Подмножество с данной суммой:»<<endl;
for (int j=0; j<n; j++)
if (ires & (1<<j))
{
cout<<a[j]<<» «;
}
cout<<endl; //www.itmathrepetitor.ru
}
delete [] a; // удаляем память
}
www.itmathrepetitor.ru
Praktichekie_zanyatiya
Дискретная математика: Математическая логика
Типовые задачи для проведения практических занятий
Занятие 1. Множества. Операции над множествами. Диаграммы Эйлера-Венна
1. Дано множество M={a, b, c, d, e}. Найти все его подмножества
2.. Дано множество M={a, b, c, d, e}. Найти все его собственные подмножества
3. Определить мощность булеана для M={a, b, c, d, e}.
4. Определить мощность декартова произведения для M и N, если /M/=10, а /N/=25.
5. Построить декартово произведение M={a, b, c,} и N={a, d, e}.
6. Нарисовать круги Эйлера-Венна для ,
7. Для заданных множеств I={1,2,3,4,5,6,7,8,9}, A={1,3,5,7,9}, B={1,2,3,8,9} и C={2,3,5,6,9} вычислить множества:
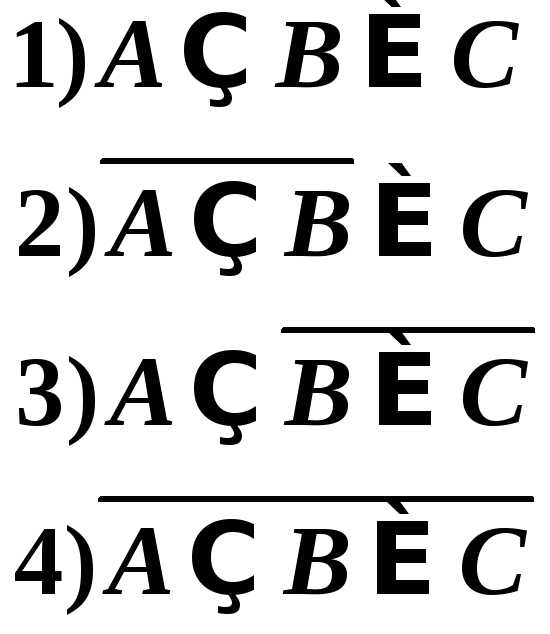
Занятие 2. Бинарные отношения. Исследование свойств бинарных отношений. Отношение эквивалентности. Отношение толерантности
1. Построить бинарное отношение R(M) и определить его свойства.
R={(a, b)/ res(b, a)=0}
2. Построить бинарное отношение R и определить его свойства. M= {1,2,..,10},
R= {(a, b)/ res(b, a)=1}
3. Построить бинарное отношение R(M) и определить его свойства. M= {1,2,..,10},
R= {(a, b)/
4. На множестве M1= {a, b, c, d, e, f} построить бинарное отношение толерантности R, при условии, что .
5. Определить свойства бинарного отношенияT, заданного на множестве M2= {a, b, c, d, e, f}
6. На множестве M1= {a, b, c, d, e, f} построить бинарное отношение эквивалентности
7. Определить свойства бинарного отношенияT, заданного на множестве M2= {a, b, c, d, e, f}
8. На множестве M1={a, b,c, d, e, f} построить бинарное отношение эквивалентности R, при условии, что .
9. Определить свойства бинарного отношенияT, заданного на множестве M2= {a, b
Занятие 3. Отношение упорядочивание. Экстремальные характеристики отношения упорядочивания. Проверочная работа № 1(20 мин)
1. На множестве M1= {a, b, c, d, e, f} построить бинарное отношение частичного порядка R, при условии, что
2. На множестве M1= {a, b, c, d, e,
3. Определить все экстремальные характеристики
для выделенного подмножества X= {a, b, c}
частично упорядоченного множества Y
4. Определить все экстремальные характеристики
для выделенного подмножества X = {a, b, c}
частично упорядоченного множества Y
5.Определить все экстремальные характеристики
частично упорядоченного множества Y.
Занятие 4. Алгебра логики. Формализация логических высказываний. Основные операции над высказываниями. Простейшие логические функции. Построение таблиц истинности логических функций. Формализация логических высказываний. Проверочная работа № 2 (20 мин.).
1. Даны три высказывания: А: «Идет дождь», В: «Ветрено», С: «Ясно».
Формализовать следующее сложное высказывание: «Неверно, что ясно бывает тогда и только тогда, когда дует ветер или идет дождь»
2. Даны три высказывания: А: «Идет дождь», В: «Ветрено», С: «Ясно».
Формализовать следующее сложное высказывание: «Ясная погода является необходимым условием для отсутствия дождя или отсутствия ветра»
3. Даны три высказывания: А: «Идет дождь», В: «Ветрено», С: «Ясно».
Формализовать следующее сложное высказывание: «Ясная погода является необходимым и достаточным условием для отсутствия дождя или отсутствия ветра»
4. Даны три высказывания: А: «Идет дождь»,
Формализовать следующее сложное высказывание: «Ясная погода является достаточным условием для отсутствия дождя или отсутствия ветра»
5. Построить таблицу истинности следующей функции:
6. Даны две функции, f1 и f2. Определить, являются ли они двойственными друг другу.
7. Даны две функции, F1 и F2. Определить, являются ли они эквивалентными друг другу.
F 1(a, b, c) = 1{000, 001,011,101,100.111}
F 2(a, b, c) = b → c
8. Даны две функции, f1 и f2. Определить, являются ли они двойственными друг другу.
Занятие 5. Построение совершенных ДНФ и совершенных КНФ аналитически и с помощью таблиц истинности. Минимизация по Квайну-МакКласски
1. Дана следующая логическая функция . Построить для нее
таблицу истинности
Совершенную ДНФ
Совершенную КНФ
2. Дана следующая логическая функция . Построить для нее
таблицу истинности
Совершенную ДНФ
Совершенную КНФ
3. Дана следующая логическая функция . Построить для нее
таблицу истинности
Совершенную ДНФ
Совершенную КНФ
4. Для функции , используя аналитический вывод, построить совершенную дизъюнктивную нормальную форму (Сов_ДНФ).
5. Для функции , используя аналитический вывод, построить совершенную дизъюнктивную нормальную форму (Сов_ДНФ).
6. Для функции , используя аналитический вывод, построить совершенную конъюнктивную нормальную форму (Сов_КНФ).
8. Построить минимальную ДНФ с помощью метода Квайна-МакКласки для функции f=1{0000, 0001, 0010, 0011,1100, 1101}
9. Построить минимальную ДНФ с помощью метода Квайна-МакКласки для функции f=1{0100, 0101, 0110, 0111,1000, 1001 }.
Занятие 6. Исследование систем булевых функций на полноту. Проверочная работа № 3 (20 мин.)
1.Построить монотонную функцию от трех переменных, принадлежащую классу К0
3.Дана функция F1=1{001, 010,100, 111}, заданная своей областью истинности. Определить, являются ли она линейной.
4. Построить самодвойственную функцию от трех переменных, принадлежащую классу К1.
5.Определит, является ли монотонной функция
6. Доопределить функцию f(a, b, c), q1 ={100}, q0={010, 110} таким образом, чтобы она стала полной.
7. Дана функция F1=1{001, 010,100, 111}, заданная своей областью истинности. Определить, являются ли она линейной.
Занятие 7. Операции над предикатами. Исчисление предикатов. Вывод формул в исчислении предикатов.
1.Определить
область истинности предиката,
если предикаты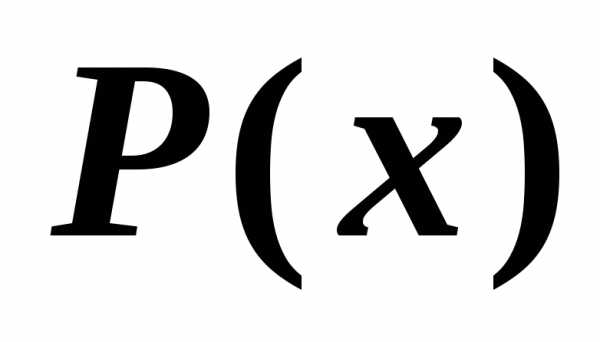
,
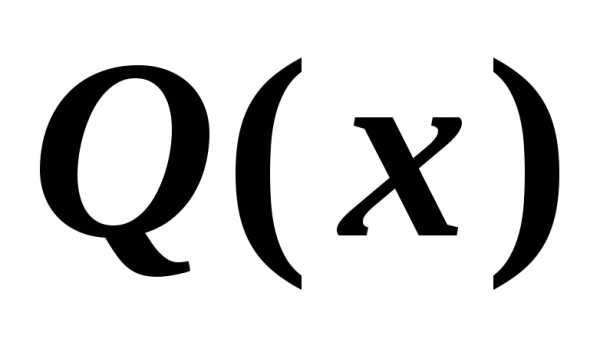и
заданы
на множестве натуральных чиселN:
:
«число Х делится на 5»
:
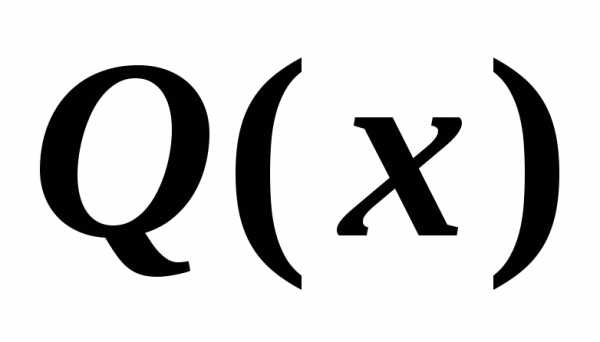«число Х делится на 3»
:
«число Х четное»
2.
Определить
область истинности предиката,
если предикаты
,
и
заданы
на множестве натуральных чиселN:
:
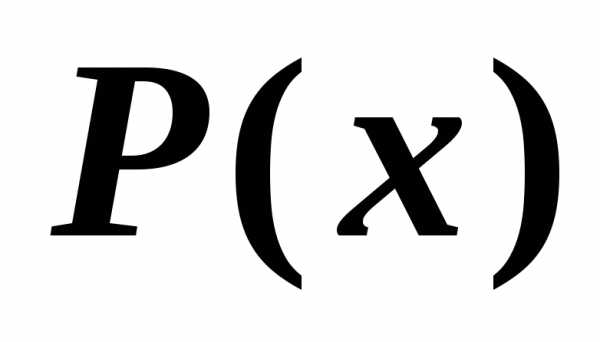«число Х делится на 5»
:
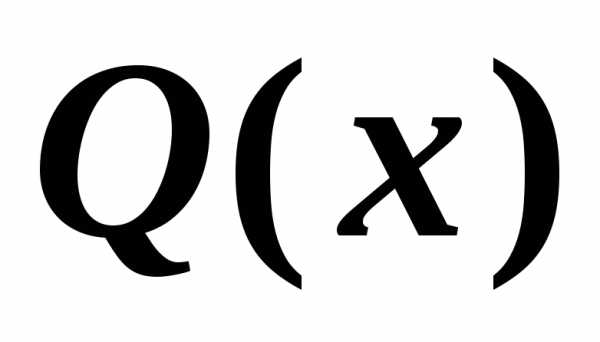«число Х делится на 2»
:
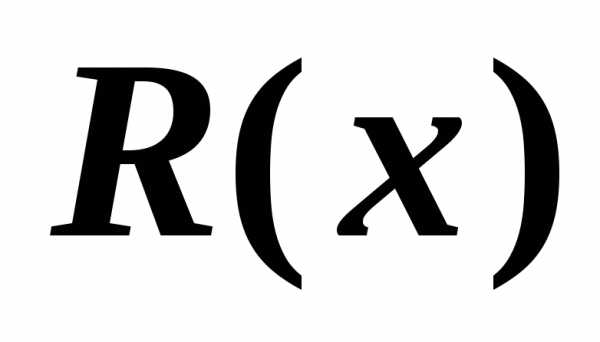«число Х нечетное»
3.
Определить
область истинности предиката,
если предикаты
,
и
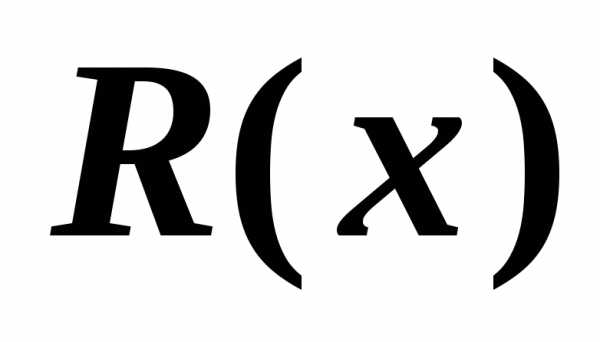заданы
на множестве натуральных чиселN:
:
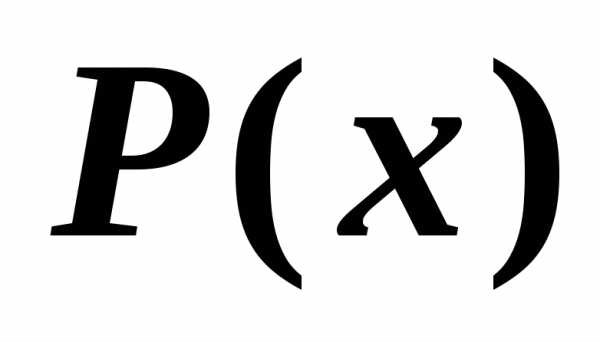«число Х делится на 7»
:
«число Х делится на 3»
:
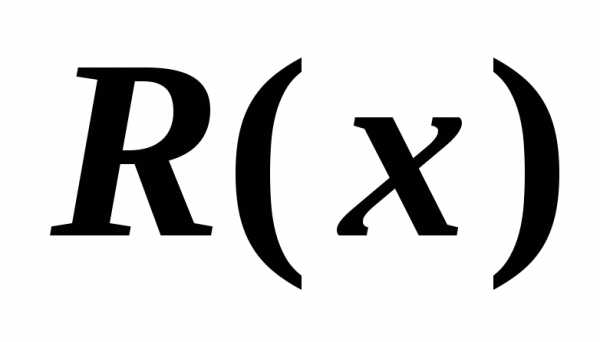«число Х нечетное»
4. Найти область
истинности предиката 
5. Изобразить на декартовой плоскости область истинности предиката
6. Изобразить на декартовой плоскости область истинности предиката
7. Даны следующие условия для Х и Y:
Записать их в виде формулы исчисления предикатов.
Занятие 8. Виды математических доказательств. Доказательство теоремы дедукции. Прямые и косвенные доказательства теорем в исчислении предикатов. Проверочная работа № 4 (20 мин.).
1.Даны формулы и. Проверить, являются ли они равносильными
2. Даны формулы и. Проверить, являются ли они равносильными
3. Даны формулы и. Проверить, являются ли они равносильными
4. Доказать общезначимость формулы
5. Доказать общезначимость формулы
ЛИТЕРАТУРА
Основная
Лихтарникова Л.М., Сукачева Т.Г. Математическая логика/Курс лекций. — СПб.: Издательство «Лань», 1998.-288с.
Горбатов В.А. Фундаментальные основы дискретной математики. — М.: Наука. Физматлит, 1999.-544с.
Новиков Ф.А. Дискретная математика для программистов. — СПб.: Питер, 2001. – 304с.
Капитонова Ю.В., Кривой С.Л., Летичесвский А.А., Луцкий Г.М. Лекции по дискретной математике. – СПб.: БХВ-Петербург, 2004. – 624 с.
Гусева А.И. Учимся информатике: задачи и методы их решения.- М.: ДИАЛОГ-МИФИ, 2003.
Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М., Физматлит, 1995. 247.
Дополнительная
Методические материалы на сайтах cyber.mephi.ru, porteai.mephi.ru/kaf/022, porteai.mephi.ru/kaf/064
9
studfiles.net