Cos 1 2x 1 решение – Тригонометрические уравнения, системы, неравенства — §1 Тригонометрические уравнения — ЗФТШ, МФТИ
cos x = 1/2 решение
Доброй ночи!
Уравнения вида, которое вы нам предоставили — очень часто вызывает различные затруднение у учеников и студентов тоже. Но это, на самом деле, не так страшно и не так сложно, как может показаться на первый взгляд. Прежде, чем разобраться с Вашей уравнением cos x = 1/2, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло, так как вид особо не изменился. Но чтоб решать такие уравнения, то надо использовать известное правило, которое выглядит таким образом:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
А уже, учитывая всё выше написанное, приведём решение нашего уравнения к нормальному виду и получим такое:
Ответ:
ru.solverbook.com
cos 2x = 1 решение
Доброй ночи!
Уравнения вида, которое вы предоставили, не такое трудное, как Вам могло показаться. Давайте попробуем решить Ваше уравнение cos 2х = 1. Но первым делом нам следует подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло, так как вид особо не изменился. Но чтоб решать такие уравнения, то надо использовать известное правило, которое выглядит так:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Но у нас будет не просто х, а двойной:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Чтоб найти х надо каждый член поделить на два и из этого получим следующее:
Ответ:
cos 2x = 1/2 решение
Доброй ночи!
Уравнения вида, которое вы предоставили, не такое трудное, как Вам могло показаться. Давайте попробуем решить Ваше уравнение cos 2х = 1/2. Но первым делом нам следует подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло, так как вид особо не изменился. Но чтоб решать такие уравнения, то надо использовать известное правило, которое выглядит так:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Но у нас будет не просто х, а двойной:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Чтоб найти х надо каждый член поделить на два и из этого получим следующее:
Ответ:
ru.solverbook.com
cos 2x = — 1/2 решение
Доброй ночи!
Уравнения вида, которое вы предоставили, не такое трудное, как Вам могло показаться. Давайте попробуем решить Ваше уравнение cos 2х = 1/2. Но первым делом нам следует подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Да, я понимаю, что это Вам особо не помогло, так как вид особо не изменился. Но чтоб решать такие уравнения, то надо использовать известное правило, которое выглядит так:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Но у нас будет не просто х, а двойной:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Чтоб найти х надо каждый член поделить на два и из этого получим следующее:
Ответ:
ru.solverbook.com
Репетитор по математике и физике » Решение тригонометрических уравнений

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравненияпринадлежащие промежутку
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем (на всякий случай, эта запись означает, что числа и принадлежат множеству целых чисел):
Другими словами, нам нужно подобрать такое число из промежутка косинус которого был бы равен Это число Используя это, получаем:
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
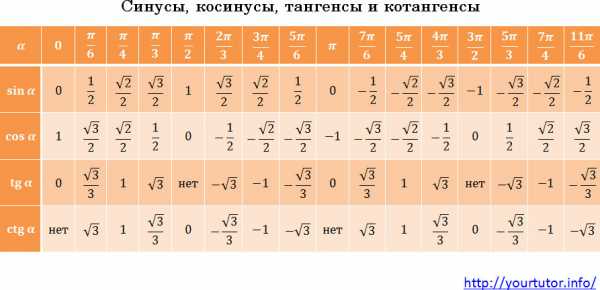
Таблица значений тригонометрических функций
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку Воспользуемся для этого методом двойных неравенств. Вы помните, что и — целые числа:
1)
2)
Задача для самостоятельного решения №1. Найдите корни уравнения принадлежащие промежутку
Показать ответОтвет:Решение линейных тригонометрических уравнений
Пример 2. Найдите корни уравнения
принадлежащие промежутку
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на , уравнение тогда примет вид:
Подберем такое число, синус которого равен а косинус равен Например, пусть это будет число . С учетом этого перепишем уравнение в виде:
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности и Это и есть ключ к решению. Имеем:
Осуществляем отбор решений, входящих в промежуток :
1)
2)
Задача для самостоятельного решения №2.
Решение тригонометрических уравнений методом замены переменной
Пример 3. Дано уравнениеа) Решите уравнение.
б) Укажите корни, принадлежащие отрезке
Решение. Сразу оговорим ограничения, накладываемые на переменную в этом уравнении: Откуда взялось это ограничение? Правильно, функция не существует при этих значениях Используем замену переменной: Тогда уравнение принимает вид:
Переходим к обратной замене:
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.
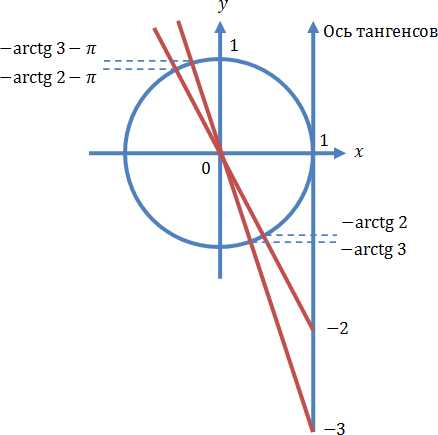
Отбор корней с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: Обратите внимание на один существенный момент. На рисунке точки и принадлежат оси тангенсов, а точки и — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
Ответ:
Задача для самостоятельного решения №3. Дано уравнение
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку
Показать ответОтвет:Решение тригонометрических уравнений методом разложения на множители
Пример 4. Дано уравнение
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку
Решение. Равносильными преобразования приводим уравнение к виду:
Осуществляем отбор решений с помощью единичной окружности.
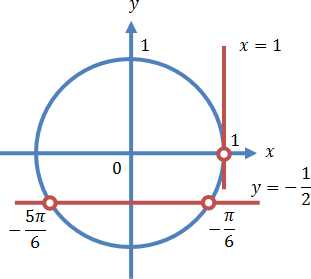
Отбор решений с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий:
Задача для самостоятельного решения №4. Дано уравнение
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку
Показать ответОтвет:Комбинированные уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.
Пример 5. Решите уравнение:
Решение. Данное уравнение эквивалентно следующей системе:
Обратите внимание! Писать, что нет никакой необходимости, поскольку по условию это выражение равно выражению
yourtutor.info
Решение тригонометрических уравнений. Как решить тригонометрическое уравнение.
Решение тригонометрических уравнений требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью «Основные тригонометрические формулы».
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.
Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения, для наглядности будем использовать уже знакомый тригонометрический круг.
sinх = а

cos x = a
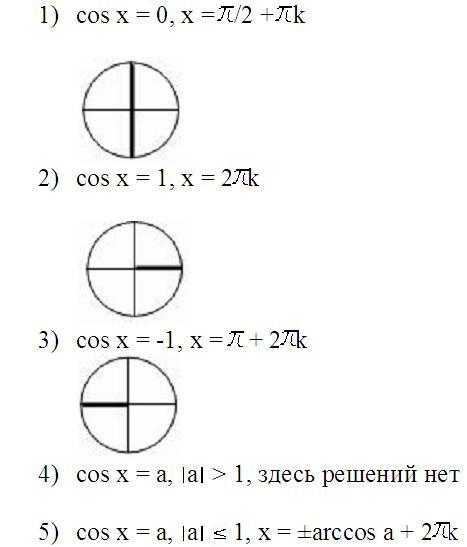
tg x = a
cot x = a
Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.
Метод замены переменной и подстановки
- cos(x + /6) = 1
x + /6 = 2 k
x1 = — /6 + 2 k
- cos(x + /6) = ?
x + /6 = ±arccos 1/2 + 2 k
x2 = ± /3 — /6+ 2 k
Решение тригонометрических уравнений через разложение на множители
- 2sin(x/2) = 0
Это простейшее тригонометрическое уравнение, решение которого
х/2 = k
x1 = 2 k
- cos(x/2) — sin(x/2) = 0
Это уравнение является однородным и решается третьим методом, который мы рассмотрим ниже.
Делим уравнение на cos(x/2) и получаем опять же простейшее тригонометрическое уравнение:
1 — tg(x/2) = 0
tg(x/2) = 1
x/2 = arctg 1 + k
x/2 = /4+ k
x2 = /2+ 2 k
Приведение к однородному уравнению
Решение уравнений, через переход к половинному углу
Введение вспомогательного угла
Преобразование произведения в сумму
Универсальная подстановка
- x (2k + 1) ,
тогда, воспользовавшись тригонометрическими формулами, получим:3[(2tg(x/2))/(1 + tg2 (x/2)] — 4[(1 – tg2 (x/2))/(1 + tg2 (x/2)] = 3
6tg(x/2) – 4 + 4tg2 (x/2) = 3 + 3tg2 (x/2)
tg2 (x/2) + 6tg(x/2) – 7 = 0
Делаем замену tg(x/2) на y и получаем квадратное уравнение:
y2 + 6y -7 = 0
корни которого y1 = -7, y2 = 1
Идем обратно и получаем два простейших уравнения:
1) tg(x/2) = -7
х1 = -2arctg 7 + 2 k
2) tg(x/2) = 1
x2 = /2 + 2k
- x = (2k + 1) ,
тогда 3sin[(2k +1) ] – 4cos[(2k + 1) ] = 4 3
Получаем – решение имеет только первое условие.
Пример.
Решить уравнение 2cos2 (x + /6) – 3sin( /3 – x) +1 = 0
Используя формулы приведения получим:
2cos2 (x + /6) – 3cos(x + /6) +1 = 0
Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:
2y2 – 3y + 1 + 0
Корни которого y1 = 1, y2 = 1/2
Теперь идем в обратном порядке
cos(x + /6) = y
Подставляем найденные значения y и получаем два варианта ответа:
Пример.
Как решить уравнение sin x + cos x = 1 ?
Перенесем все влево, чтобы справа остался 0:
sin x + cos x – 1 = 0
Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
sin x — 2 sin2 (x/2) = 0
Делаем разложение на множители:
2sin(x/2) * cos(x/2) — 2 sin2 (x/2) = 0
2sin(x/2) * [cos(x/2) — sin(x/2)] = 0
Получаем два уравнения
Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:
а) переносят все его члены в левую часть;
б) выносят все общие множители за скобки;
в) приравнивают все множители и скобки к 0;
г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
д) решают полученное уравнение относительно tg.
Пример.
Решить уравнение 3sin2x + 4 sin x • cos x + 5 cos2x = 2
Воспользуемся формулой sin2 x + cos2 x = 1 и избавимся от открытой двойки справа:
3sin2x + 4 sin x • cos x + 5 cos x = 2sin2x + 2cos2x
sin2x + 4 sin x • cos x + 3 cos2x = 0
Делим на cos x:
tg2x + 4 tg x + 3 = 0
Заменяем tg x на y и получаем квадратное уравнение:
y2 + 4y +3 = 0, корни которого y1=1, y2 = 3
Отсюда находим два решения исходного уравнения:
1) tg x = –1
x1 = /4+ k
2) tg x = –3
x2 = arctg 3 + k
Пример.
Решить уравнение 3sin x – 5cos x = 7
Переходим к x/2:
6sin(x/2) * cos(x/2) – 5cos2 (x/2) + 5sin2 (x/2) = 7sin2 (x/2) + 7cos2 (x/2)
Пререносим все влево:
2sin2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos2 (x/2) = 0
Делим на cos(x/2):
tg2 (x/2) – 3tg(x/2) + 6 = 0
Ну а дальше уже по отработанной схеме …
Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,
где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
Обе части уравнения разделим на :
Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:
cos * sin x + sin * cos x = С
или sin(x + ) = C
Решением этого простейшего тригонометрического уравнения будет
х = (-1) k * arcsin С — + k, где
Следует отметить, что обозначения cos и sin взаимозаменяемые.
Пример.
Решить уравнение sin 3x – cos 3x = 1
В этом уравнении коэффициенты:
а = , b = -1, поэтому делим обе части на = 2
(/2) * sin 3x – (1/2)cos 3x = 1/2
cos( /6) * sin 3x – sin( /6) * cos 3x =1/2
sin(3x – /6) = 1/2
Получаем ответ
x = (-1) k * /18 + /18 + k/3
Здесь мы будем просто использовать тригонометрические формулы
Пример.
Решить уравнение 2 sin x * sin 3x = cos 4x
Левую часть преобразуем в сумму:
cos 4x – cos 8x = cos 4x
Получаем простейшее уравнение:
cos 8x = 0
8x = /2 + k
x = /16 + k/8
Пример.
Решить тригонометрическое уравнение 3sin x – 4cos x = 3
Здесь возможны 2 случая:
Основные методы решения тригонометрических уравнений, мы рассмотрели. Если у вас остались какие либо вопросы о том, как решать тригонометрические уравнения, задавайте их в комментариях ниже.
Будем рады любым ваших вопросам.
Заметка: собираетесь выступать http://prezentacii.com портал готовых презентаций.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Тригонометрические уравнения, системы, неравенства — §1 Тригонометрические уравнения — ЗФТШ, МФТИ
Чтобы решить тригонометрическое уравнение надо путём тригонометрических преобразований свести его к простейшему тригонометрическому уравнению. Напомним формулы решений простейших тригонометрических уравнений.
1. `sinx=a`. Если `|a|>1`, решений нет. Если `|a|<=1`, то
`x=(-1)^n arcsin a+pi n, n in Z`.
Отметим, что последнюю формулу иногда удобнее расписать отдельно для чётных `(n=2k, k in Z)` и нечётных `(n=2k+1, k in Z)n`. А именно
x=arcsina+2πk,π-arcsina+2πk, k∈Z.x=\left[\begin{array}{l}\mathrm{arc}\sin a+2\pi k,\\\pi-\mathrm{arc}\sin a+2\pi k,\;k\in Z.\end{array}\right.
2. `cosx=a`. Если `|a|>1`, решений нет. Если `|a|<=1`, то
`x=+- arccosa+2pin, n in Z`.
3. `»tg»x=a`. При любом `a` `x=»arctg»a+pin, n in Z`.
4. `»ctg»x=a`. При любом `a` `x=»arctg»a+pin, n in Z`.
Отметим несколько частных случаев простейших тригонометрических уравнений, в которых ответ можно записать более просто, чем по общим формулам.
а) `sinx=1`. Тогда `x=pi/2+2pin,n in Z`.
б) `sinx=-1`. Тогда `x=-pi/2+2pin, n in Z`.
в) `cosx=0`. Тогда `x=pi/2+pin, n in Z`.
г) `cosx=-1`. Тогда `x=pi+2pin, n in Z`.
Рассмотрим несколько типовых способов решения тригонометрических уравнений.
I. Разложение на множители
Решить уравнение
`3sin2x-3cosx+2sinx-1=0`.
Используя формулу `sin2x=2sinxcosx`, преобразуем данное уравнение
`6sinxcosx-3cosx+2sinx-1=0`,
`3cosx(2sinx-1)+(2sinx-1)=0`,
`(2sinx-1)(3cosx+1)=0`.
Уравнение распадается на два:
1) `2sinx-1=0`, `sinx=1/2` и `x=(-1)^npi/6+pin,n in Z`.
2) `3cosx+1=0`, `cosx=-1/3` и `x=+- arccos(-1/3)+2pin,n in Z`.
`x=(-1)^npi/6+pin,n in Z`; `x=+-arccos(-1/3)+2pin,n in Z`.
Отметим, что в сериях решений 1) и 2) не было бы ошибкой использовать разные буквы (например, `n` и `m`), т. к. идёт перечисление решений.
Решить уравнение
`sin2x+cos(5x-pi/6)=0`.
Используя формулу приведения `sin2x=cos(pi/2-2x)`, преобразуем наше уравнение `cos(pi/2-2x)+cos(5x-pi/6)=0` или `2cos((3x+pi/3)/2)*cos((7x-(2pi)/3)/2)=0`.
Уравнение распадётся на два:
1) `cos((3x+pi/3)/2)=0`; `(3x+pi/3)/2=pi/2+pin,ninZ`;
`3x+pi/3=pi+2pin,ninZ`; `x=(2pi)/9+(2pin)/3,ninZ`.
2) `cos((7x-(2pi)/3)/2)=0`; `(7x-(2pi)/3)/2=pi/2+pin,ninZ`;
`7x-(2pi)/3=pi+2pin,ninZ`; `x=(5pi)/21+(2pin)/7,ninZ`.
`x=(2pi)/9+(2pin)/3,ninZ`; `x=(5pi)/21+(2pin)/7,ninZ`.
II. Сведение уравнения к алгебраическому от одного переменного
Решить уравнение `4sin^3x=3cos(x+(3pi)/2)`.
По формуле приведения `cos(x+(3pi)/2)=sinx`,
поэтому уравнение запишется: `4sin^3x=3sinx`.
`sinx(4sin^2x-3)=0`⇔sinx=0, x=πn,n∈Z.sinx=±32, x=±π3+πn,n∈Z.\Leftrightarrow\left[\begin{array}{l}\sin x=0,\;x=\pi n,n\in Z.\\\sin x=\pm\dfrac{\sqrt3}2,\;x=\pm\dfrac\pi3+\pi n,n\in Z.\end{array}\right.
Отметим, что в случае двух уравнений `sinx=+-(sqrt3)/2` мы записали не объединение стандартных формул `(-1)^n(+-pi/3)+pin,ninZ`, а более простую, которая получается, если изобразить решения этих уравнений на тригонометрическом круге (рис. 1). (Две верхние точки – решения уравнения `sinx=(sqrt3)/2`, а две нижние – решения уравнения `sinx=-(sqrt3)/2`).
`x=pin,ninz`; `x=+-pi/3+pin,n inZ`.
Решить уравнение `cos2x+sin^2x=0,5`.
Воспользуемся формулой `cos2x=1-2sin^2x`.
Получим: `1-sin^2x=0,5` или `sin^2x=1/2`, `sinx=+-1/sqrt2`.
`x=+-pi/4+pin,ninZ`. (1)
Это уравнение можно решить и пользуясь формулой `sin^2x+(1-cos2x)/2`. Тогда оно преобразуется к виду: `cos2x=0`, `2x=pi/2+pin,ninZ`, или
`x=pi/4+(pin)/2, ninZ`. (2)
Геометрически множества точек (1) и (2) совпадают (рис. 2). Так что решения тригонометрических уравнений могут быть записаны в разной форме.
III. Однородные уравнения
(хотя формально эти уравнения можно отнестик предыдущему типу)
Решить уравнение `5sin^2x-4sinx*cosx-cos^2x=0`.
Это однородное уравнение второго порядка. Так как `cosx!=0` (иначе из нашего уравнения следовало бы, что `sinx=0` что противоречит основному тригонометрическому тождеству `sin^2x+cos^2x=1`), то разделим наше уравнение на `cos^2x`. Получим уравнение `5″tg»^2x-4″tg»x-1=0`. Откуда `»tg»x=1` или `»tg»x=-1/5`. Следовательно, `x=pi/4+pin,ninZ`, или `x=-«arctg»1/5+pin,ninZ`.
`x=pi/4+pin,ninZ`; `x=-«arctg»1/5+pin,ninZ`.
Решить уравнение `2+3sinxcosx=7sin^2x`.
Воспользуемся основным тригонометрическим тождеством `1=sin^2x+cos^2x`. Преобразуем наше уравнение к однородному уравнению второго порядка: `2(sin^2x+cos^2x)+3sinxcosx=7sin^2x` или `5sin^2x-3sinxcosx-2cos^2x=0`. Здесь `cosx!=0` (в противном случае из последнего уравнения следовало бы, что `sinx!=0` что противоречит основному тригонометрическому тождеству). Делим последнее уравнение на `cos^2x`. Получаем уравнение `5″tg»^2x-3″tg»x-2=0`.
Откуда `»tg»x=1` или `»tg»x=-2/5`. И значит, `x=pi/4+pin,ninZ`, или `x=-«arctg»2/5+pin,ninZ`
`x=pi/4+pin,ninZ`, `x=-«arctg»2/5+pin,ninZ`
Наконец рассмотрим уравнение, сводящееся к однородному третьего порядка.
Решить уравнение `sin^3x+13cos^3x-cosx=0`.
Перепишем это уравнение так:
`sin^3x+13cos^3x-cosx(cos^2x+sin^2x)=0` или
`sin^3x+12cos^3x-cosxsin^2x=0`.
Это однородное уравнение третьего порядка. Деля его на `cos^3x` (`cosx!=0` для решений нашего уравнения), получим уравнение относительно `»tg»x`
`»tg»^3x-«tg»^2x+12=0`.
Делаем замену: `t=»tg»x`. Алгебраическое уравнение `t^3-t^2+12=0` имеет корень `t=-2` (находится подбором среди целых делителей числа `12`). Далее деля многочлен `t^3-t^2+12` на `(t+12)`, раскладываем левую часть алгебраического уравнения на множители
`(t+2)(t^2-3t+6)=0`.
Уравнение `t^2-3t+6=0` не имеет действительных корней, т. к. `D<0`. Итак, `»tg»x=-2` или `x=-«arctg»2+pin,ninZ`.
`x=-«arctg»2+pin,ninZ`.
IV. Использование формулы дополнительного угла
Напомним эту формулу `asin alpha +bcos alpha=sqrt(a^2+b^2)sin(alpha+varphi)`, где `varphi` определяется (неоднозначно) из равенств
`cosvarphi=a/(sqrt(a^2+b^2))`, `sinvarphi=b/(sqrt(a^2+b^2))(a^2+b^2!=0)`.
Например, `sinalpha+cos alpha=sqrt2sin(alpha+pi/4)`. Формулу дополнительного угла можно записать и в другом виде, например,
`asinalpha+bcosalpha=sqrt(a^2+b^2)cos(alpha+varphi)`, где
`cosvarphi=b/(sqrt(a^2+b^2))`, `sinvarphi=-a/(sqrt(a^2+b^2))`.
Решить уравнение `4sinx-3cosx=5`.
1-ый способ. По формуле дополнительного угла преобразуем уравнение:
`sqrt(16+9)sin(x+varphi)=5`, `sin(x+varphi)=1`, `cosvarphi=4/5`, `sinvarphi=-3/5`.
Можно взять `varphi=-arcsin 3/5`. Решением уравнения будет: `x+varphi=pi/2+2pin,ninZ`.
`x=arcsin 3/5+pi/2+2pin,ninZ`.
2-й способ. Воспользуемся формулами:
`sinx=2sin x/2 cos x/2`, `cosx=cos^2 x/2 -sin^2 x/2`, `1=sin^2 x/2+cos^2 x/2`.
Тогда уравнение `4sinx-3cosx=5` запишется в виде
`8sin x/2 cos x/2-3(cos^2 x/2-sin^2 x/2)=5(sin^2 x/2+cos^2 x/2)` или
`2sinx^2 x/2-8sin x/2cos x/2+8cos^2 x/2=0`.
Это однородное уравнение второго порядка, деля которое на `2cos^2 x/2`, получим уравнение `»tg»^2 x/2-4″tg» x/2+4=0` или `(«tg» x/2-2)^2=0`. Итак, `»tg» x/2=2`, значит `x/2=»arctg»2+pin,ninZ`, или `x=2″arctg»2+2pin,ninZ`.
`x=2″arctg»2+2pin,ninZ`.
Отметим, что формы ответа при решении способами 1 и 2 различны, хотя, конечно, это одно и то же множество точек.
Решить уравнение `sin2x-2(sinx+cosx)-1=0`.
Сделаем замену: `t=sinx+cosx`. Тогда
`t^2=sin^2x+2sinxcosx+cos^2x=1+sin2x`.
Откуда `sin2x=t^2-1`. Наше уравнение преобразуется в такое:
`t^2-2t-2=0`. `t_1=1+sqrt3`, `t_2=1-sqrt3`.
Так как `t=sinx+cosx=sqrt2sin(x+pi/4)<=sqrt2`, то `t_1=1+sqrt3>sqrt2` не даёт решений. Число `|1-sqrt3|<=sqrt2` и уравнение `sin(x+pi/4)=(1-sqrt3)/(sqrt2)` имеет решения:
`x+pi/4=(-1)^n arcsin (1-sqrt3)/(sqrt2) +pin,ninZ`.
`x=-pi/4+(-1)^n arcsin (1-sqrt3)/(sqrt2) +pin,ninZ`.
Отметим, что подобным образом решаются уравнения вида: `F(sin2x, sinx+-cosx)=0`. Замена `t=sinx+-cosx`.
Рассмотрим ещё одно часто встречающееся приложение формулы дополнительного угла.
Найти наибольшее и наименьшее значения выражения `f(x)=8sin^2x+3sin2x-11`.
Преобразуем выражение, используя формулу `2sinx^2x=1-cos2x`. Получаем:
`f(x)=(4-4cos2x)+3sin2x-11=3sin2x-4cos2x-7=`
`=5sin(2x+varphi)-7`.
Здесь можно взять `varphi=-arcsin 4/5`. Так как `-1<=sin(2x+varphi)<=1`, то `-5<=sin(2x+varphi)<=5` и `-12<=5sin(2x+varphi)-7<= -2`. При этом значение `f(x)=-12` принимается при `2x+varphi=-pi/2+2pin,ninZ`, а значение `f(x)=-2` принимается при `2x+varphi=pi/2+2pin,ninZ`.
`max_Rf(x)=-2`, `min_R f(x)=-12`.
Рассмотрим теперь более сложные тригонометрические уравнения, в которых надо делать отбор корней.
V. Рациональные тригонометрические уравнения
Решить уравнение `(cos2x+cosx+1)/(2sinx+sqrt3)=0`.
ОДЗ `sinx!=-sqrt3/2`.
Не будем решать это неравенство, а изобразим на тригонометрическом круге (рис. 3а) точки, не удовлетворяющие ОДЗ.
Решаем уравнение `cos2x+cosx+1=0`.
Преобразуем его: `(2cos^2x-1)+cosx+1=0`, `2cos^2x+cosx=0`,
`cosx(2cosx+1)=0 iff`cosx=0, x=π2+πn,n∈Z,cosx=-12, x=±2π3+2πn,n∈Z.\left[\begin{array}{l}\cos x=0,\;x=\dfrac\pi2+\pi n,n\in Z,\\\cos x=-\dfrac12,\;x=\pm\dfrac{2\pi}3+2\pi n,n\in Z.\end{array}\right.
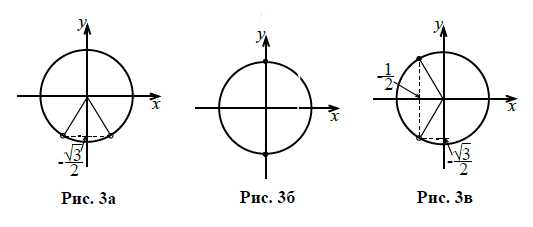
Изобразим решения уравнения `cosx=0` на тригонометрическом круге (рис. 3б). Они удовлетворяют ОДЗ.
Изобразим решения уравнения `cosx=-1/2` на тригонометрическом круге (рис. 3в). Мы видим, что точки `x=-(2pi)/3+2pin,ninZ`, не удовлетворяют ОДЗ, а точки `x=(2pi)/3+2pin,ninZ`, удовлетворяют ОДЗ. Таким образом,
`x=pi/2+pin,ninZ`, `x=(2pi)/3+2pin,ninZ`.
Решить уравнение `(sinx)/(sin3x)+(sin5x)/(sinx)=8cosxcos3x`.
ОДЗ sin3x≠0sinx≠0⇔x≠πm3,m∈Z.\left\{\begin{array}{l}\sin3x\neq0\\\sin x\neq0\end{array}\right.\Leftrightarrow x\neq\dfrac{\pi m}3,m\in Z.
Умножим уравнение на `sinx*sin3x`. Получим:
`sin^2x+sin3x*sin5x=8sinxcosx*sin3x*cos3x`.
Преобразуем это уравнение:
`(1-cos2x)/2+1/2(cos2x-cos8x)=2sin2x*sin6x`.
Ещё раз воспользуемся формулой
`sinalpha*sinbeta=1/2(cos(alpha-beta)-cos(alpha+beta))`
в правой части последнего уравнения и умножим его на `2`. Получим
`(1-cos2x)+(cos2x-cos8x)=2(cos4x-cos8x)` или `1+cos8x-2cos4x=0`.
Далее: `1+(2cos^24x-1)-2cos4x=0`, `2cos4x(cos4x-1)=0 iff` ⇔cos4x=1.cos4x=0.\Leftrightarrow\left[\begin{array}{l}\cos4x=1.\\\cos4x=0.\end{array}\right.
Если `cos4x=1`, то `4x=2pin,x=(pin)/2,ninZ`.
1. Изображаем точки
`x=(pin)/2,ninZ`, (3)
на тригонометрическом круге (рис. 4а). Геометрически их `4` штуки (для `n=0,1,2,3` – далее они повторяются).
2. Изображаем точки
`x=(pim)/3,m inZ` (4)
которые не удовлетворяют ОДЗ на тригонометрическом круге (4б). Их `6` штук (для `m=0,1,2,3,4,5` – далее они повторяются).
Видно, что совпадения точек в `(3)` и `(4)` будут при `x=pin,ninZ`. Эти значения надо исключить из решения, т. е. в ответ пойдут точки
`x=pi/2+pin,ninZ`.
С решениями уравнения
`cos4x=0`, `4x=pi/2+pin,ninZ`,
или `x=pi/8+(pin)/4,ninZ`, можно поступить аналогично, сделав отбор на тригонометрическом круге. Но когда точек–решений на тригонометрическом круге много, и много точек, не входящих в ОДЗ, то удобнее воспользоваться аналитическим способом отбора решений. В данном случае точек — решений на тригонометрическом круге в серии `x=pi/8+(pin)/4,ninZ`, будет `8` штук (различные при `n=0, 1, 2, 3, 4, 5, 6, 7` – далее они повторяются), а точек, не входящих в ОДЗ на тригонометрическом круге `6`. Посмотрим, есть ли совпадения, т. е. существуют ли целые `m` и `n` такие, что
`pi/8+(pin)/4=(pim)/3 iff 1/8+n/4=m/3 iff`
`iff 3+6n=8m iff 3=2(4m-3n)`.
Последнее равенство невозможно, т. к. слева стоит нечётное число, а справа чётное.
Отметим, что и для решений уравнения `cos4x=1` отбор можно было сделать аналитически. А именно смотрим, существуют ли целые `m` и `n` такие, что `(pin)/2=(pim)/3 iff 3n=2m`. Видим, что `n` делится на `2`. Тогда `n=2k` и `m=3k,kinZ`. Т. е. из решения уравнения `cos4x=1` надо исключить `x=(pin)/2`, где `n=2k`, т. е. оставить `x=(pin)/2` с `n=2k+1,kinZ`. Но при `n=2k+1` в серии `x=(pin)/2` останутся `x=pi/2(2k+1)=pi/2+pik,kinZ`, что и было нами получено на тригонометрическом круге.
`x=pi/2+pin,ninZ`; `x=pi/8+(pin)/4,ninZ`.
Иногда отбор решений предлагается сделать в условии задачи.
а) Решить уравнение `2/(«tg»^2x)-1/(«tg»x)-3=0`.
б) Указать корни, принадлежащие отрезку `[-(3pi)/2; -pi/2]`.
а) Сделаем замену `t=1/(«tg»x)`. Получим уравнение `2t^2-t-3=0`. Его решение `t_1=-1` и `t_2=3/2`.
1) `»tg»x=-1`. Следовательно, `x=-pi/4+pin,ninZ`.
2) `»tg»x=2/3`. Тогда `x=»arctg»2/3+pin,ninZ`.
б) Сделаем отбор корней, принадлежащих отрезку `[-(3pi)/2; -pi/2]`.
1) Решаем неравенство `-(3pi)/2<=-pi/4+pin<=-pi/2`. Оно равносильно неравенству `-5/4<=n<=-1/4`. Т. к. `ninZ`, то последнему неравенству удовлетворяет только `n=-1`. Итак, из серии решений `x=-pi/4+pin,ninZ`, только корень `x=-(5pi)/4 in [-(3pi)/2; -pi/2]`.
2) Аналогично решаем неравенство
`-(3pi)/2<=»arctg»2/3+pin<=-pi/2`. (5)
Т. к. `ninZ`, то в силу правого неравенства `n<0`. Число `n=-1` подходит, т. к. неравенство (5) в этом случае преобразуется в неравенство `-pi/2<=»arctg»2/3<=pi/2`, что верно, `n=-2` не удовлетворяет (5), т. к. в этом случае получим `pi/2<=»arctg»2/3`, что неверно. Аналогично не подходит `n< -2`. Итак, из серии решений `x=»arctg»2/3+pin,ninZ`, только корень `(«arctg»2/3-pi)in[-(3pi)/2; -pi/2]`.
а) `x=-pi/4+pin,ninZ`; `x=»arctg»2/3+pin,ninZ`.
б) `x=-(5pi)/4` и `x=»arctg»2/3-pi`.
Найти наименьший корень уравнения `»ctg»6x-«tg»5x=1/(cos5x)`,
принадлежащий отрезку `[(8pi)/17; (40pi)/17]`.
Преобразуем данное уравнение
`(cos6x)/(sin6x)-(sin5x)/(cos5x)=1/(cos5x)`,
`(cos6x*cos5x-sin6x*sin5x)/(sin6x*cos5x)=1/(cos5x)`,
`(cos11x)/(sin6x*cos5x)=1/(cos5x)`.
Последнее уравнение равносильно `cos11x=sin6x` при условии `sin6x*cos5x!=0`.
Решаем уравнение `cos11x-sin6x=0`. Преобразуем его:
`cos11x-cos(6x-pi/2)=0` или `-2sin((17x)/2-pi/4)sin((5x)/2+pi/4)=0`.
1) Если `sin((5x)/2+pi/4)=0` то `(5x)/2+pi/4=pin,ninZ`, откуда `5x=-pi/2+2pin,ninZ`.
Эти числа не являются корнями исходного уравнения, т. к. нарушается условие `cos5x!=0`.
2) Если `sin((17x)/2-pi/4)=0`, то `x=(pi(1+4n))/(34),ninZ`. Находим, при каких `ninZ`, эти числа лежат на отрезке `[(8pi)/17;(40pi)/17]`. Решаем неравенства
`(8pi)/(17)<=(pi(1+4n))/34<=(40pi)/17 iff 15/4<=n<=79/4`.
Значит, `4<=n<=19,ninZ`. Итак, на отрезок `[(8pi)/17;(40pi)/17]` попадают числа `(17pi)/34, 21/34 pi, 25/34 pi,…`. Первое из них не удовлетворяет условию `cos5x!=0` `(«т». «к». (17pi)/34=pi/2)` и, следовательно, не является решением уравнения. Число `(21pi)/34` удовлетворяет условию `sin6x*cos5x!=0`; значит, именно оно является минимальным корнем на данном отрезке.
VI. Тригонометрические уравнения с корнем квадратным
Решить уравнение `sqrt(cos2x-5sinx)=-2cosx`.
Это уравнение равносильно системе
cos2x-5sinx=4cos2x.cosx≤0.\left\{\begin{array}{l}\cos2x-5\sin x=4\cos^2x.\\\cos x\leq0.\end{array}\right.
Неравенство должно выполняться, т. к. правая часть уравнения равна корню квадратному, а он неотрицателен по определению. (Отметим, что в системе мы не пишем неравенство `cos2x-5sinx>=0`, т. е. подкоренное выражение неотрицательно, т. к. оно равно квадрату правой части). Решаем уравнение: `cos2x-5sinx=4cos^2x`. Преобразуем его:
`(1-2sin^2x)-5sinx=4(1-sin^2x)` или `2sin^2x-5sinx-3=0`.
Заменяя `sinx=t`, получим квадратное уравнение: `2t^2-5t-3=0`.
Откуда `t_1=3`, `t_2=-1/2`. Т. к. `|sinx|<=1`, то `t_1=3` не даёт решений.
Если же `sinx=-1/2`, то на тригонометрическом круге (рис. 5) имеем две точки. Но правая точка не подходит, т. к. должно быть `cosx<=0`. Итак,
Решить уравнение `sqrt(5-cos2x)=cosx-3sinx`.
Это уравнение эквивалентно системе
5-cos2x=cosx-3sinx2,cosx-3sinx≥0.\left\{\begin{array}{l}5-\cos2x=\left(\cos x-3\sin x\right)^2,\\\cos x-3\sin x\geq0.\end{array}\right.
Решаем уравнение. Преобразуем его к однородному.
`5(sin^2x+cos^2x)-(cos^2x-sin^2x)=cos^2x-6sinxcosx+9sin^2x`
или `3sin^2x-6sinxcosx-3cos^2x=0`.
Далее `2sinxcosx+(cos^2x-sin^2x)=0` или `sin2x+cos2x=0`.
Это однородное уравнение 1-го порядка. Оно эквивалентно уравнению `»tg»2x=-1`.
Отсюда `2x=-pi/4+pin,ninZ`, или `x=-pi/8+(pin)/2,ninZ`.
Изобразим решения на тригонометрическом круге (рис. 6). Это `4` точки (`n=0,1,2,3` — далее они повторяются).
Для этих точек надо проверить неравенство `cosx-3sinx>=0`. Ясно, что точка `x_1` удовлетворяет этому неравенству, т. к. `cosx_1>0` и `sinx_1<0`. Для точки `x_3`, диаметрально противоположной точке `x_1`, `sinx` и `cosx` меняют знак, меняет знак и выражение `(cosx-3sinx)`, и, следовательно, для `x_3` неравенство не выполняется. Точка `x_2` не удовлетворяет неравенству, т. к. `sinx_2>0`, `cosx_2>0`, но `sinx_2>cosx_2` в виду того, что `pi/4<x_2<pi/2`, так что выражение `cosx_2-3sinx_2<0`. Точка `x_4` диаметрально противоположна `x_2`. Следовательно,
`cosx_4-3sinx_4=-(cosx_2-3sinx_2)>0`,
и, значит, это решение. Учитывая, что решения имеют период `2pi`, получаем
`x=-pi/8+2pin,ninZ`; `x=11/8pi+2pin,ninZ`.
VII. Уравнения с модулем
Решить уравнение `sin3x+|sinx|=sin2x`.
Решение уравнения сводится к объединению решений двух систем.
1) sinx≥0,sin3x+sinx=sin2x.\left\{\begin{array}{l}\sin x\geq0,\\\sin3x+\sin x=\sin2x.\end{array}\right.
2) sinx<0,sin3x-sinx=sin2x.\left\{\begin{array}{l}\sin x<0,\\\sin3x-\sin x=\sin2x.\end{array}\right.
Решаем первую систему. Уравнение `sin3x+sinx=sin2x` преобразуем:
`2sin2xcosx=sin2x` или `sin2x(2cosx-1)=0`.
Значит,
sin2x=0,cosx=12.\left[\begin{array}{l}\sin2x=0,\\\cos x=\frac12.\end{array}\right.
Изображаем решения уравнения `sin2x=0` на тригонометрическом круге: `x=(pin)/2,ninZ`, (рис. 7). В силу неравенства `sinx>=0` не подходит нижняя точка, т. е. в решения системы входят
`x=pin,ninZ`, и `x=pi/2+2pin,ninZ`.
Аналогично, изображаем на тригонометрическом круге (рис. 8) решения уравнения `cosx=1/2`. Нижняя точка не удовлетворяет неравенству `sinx>=0`. Значит, остаются в качестве решений системы
`x=pi/3+2pin,ninZ`.
Итак, решениями первой системы являются
`x=pin`; `x=pi/2+2pin`; `x=pi/3+2pin,ninZ`.
Решаем вторую систему. Уравнение `sin3x-sinx=sin2x` преобразуем:
`2cos2x*sinx=2sinxcosx`.
Т. к. в этой системе `sinx!=0`, то можно сократить уравнение на `2sinx`. Оно запишется:
`cos2x=cosx` или `2cos^2x-cosx-1=0`.
Отсюда `cosx=1` или `cosx=-1/2`. На тригонометрическом круге этим уравнениям удовлетворяют соответственно точки (рис. 9 и рис. 10). Неравенству `sinx<0` удовлетворяет только одна из этих трёх точек, находящаяся в нижней полуплоскости, а именно
`x=pi/3+pi+2pin,ninZ`.
В ответе две серии решений
`x=pi/3+2pin,ninZ` и `x=pi/3+pi+2pin,ninZ`,
соответствующие двум диаметрально противоположным точкам тригонометрического круга, можно задать одной формулой:
`x=pi/3+pin,ninZ` (но это не обязательно).
`x=pin`; `x=pi/2+2pin`; `x=pi/3+pin,ninZ`.
zftsh.online
