Что такое модуль числа это – Показатель числа по модулю — это… Что такое Показатель числа по модулю?

Модуль числа. | tutomath

Модуль числа вводится новое понятие в математике. Разберем подробно, что такое модуль числа и как с ним работать?

Рассмотрим пример:

Мы вышли из дома в магазин. Прошли 300 м, математически это выражение можно записать как +300, смысл числа 300 от знака “+” не поменяется. Расстояние или модуль числа в математике это одно и тоже можно записать так: |300|=300. Знак модуля числа обозначается двумя вертикальными линиями.

А потом в обратном направлении прошли 200м. Математически обратный путь мы можем записать как -200. Но мы не говорим так “мы прошли минус двести метров”, хотя мы вернулись, потому что расстояние как величина остается положительной. Для этого в математике ввели понятие модуля. Записать расстояние или модуль числа -200 можно так: |-200|=200.

Свойства модуля.

Определение:
Модуль числа или абсолютная величина числа – это расстояние от отправной точки до точки назначения.

Модуль целого числа не равного нулю, всегда положительное число.

Записывается модуль так:

1. Модуль положительного числа равно самому числу.
|a|=a

2. Модуль отрицательного числа равно противоположному числу.
|-a|=a

3. Модуль нуля, равен нулю.
|0|=0

4. Модули противоположных чисел равны.
|a|=|-a|=a

Вопросы по теме:
Что такое модуль числа?
Ответ: модуль — это расстояние от отправной точки до точки назначения.

Если перед целым числом поставить знак “+” , что произойдет?
Ответ: число не поменяет свой смысл, например, 4=+4.

Если перед целым числом поставить знак “-” , что произойдет?
Ответ: число изменится на противоположное число, например, 4 и -4.

У каких чисел одинаковый модуль?
Ответ: у положительных чисел и нуля модуль будет тот же. Например, 15=|15|.

У каких чисел модуль – противоположное число?
Ответ: у отрицательных чисел, модуль будет равен противоположному числу. Например, |-6|=6.

Пример №1:
Найдите модуль чисел: а) 0 б) 5 в) -7?

Решение:
а) |0|=0
б) |5|=5

в)|-7|=7

Пример №2:
Существуют ли два различных числа, модули которых равны?

Решение:
|10|=10
|-10|=10

Модули противоположных чисел равны.

Пример №3:
Какие два противоположных числа, имеют модуль 9?

Решение:
|9|=9
|-9|=9

Ответ: 9 и -9.

Пример №4:
Выполните действия: а) |+5|+|-3| б) |-3|+|-8| в)|+4|-|+1|

Решение:
а) |+5|+|-3|=5+3=8
б) |-3|+|-8|=3+8=11
в)|+4|-|+1|=4-1=3

Пример №5:
Найдите: а) модуль числа 2 б) модуль числа 6 в) модуль числа 8 г) модуль числа 1 д) модуль числа 0.

Решение:

а) модуль числа 2 обозначается как |2| или |+2| это одно и тоже.
|2|=2

б) модуль числа 6 обозначается как |6| или |+6| это одно и тоже.
|6|=6

в) модуль числа 8 обозначается как |8| или |+8| это одно и тоже.
|8|=8

г) модуль числа 1 обозначается как |1| или |+1| это одно и тоже.
|1|=1

д) модуль числа 0 обозначается как |0|, |+0| или |-0| это одно и тоже.
|0|=0

tutomath.ru

Модуль числа

Модулем неотрицательного действительного числа a называют само это число:

|а| = а

Модулем отрицательного действительного числа х называют противоположное число:

|а| = — а

Короче это записывают так:

Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).

Модуль числа 5 равен 5, так как точка В(5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5

Расстояние точки М(-6) от начала отсчета О равно 6 единичным отрезкам. Число 6 называют модулем числа -6. Пишут: |-6| = 6

Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули:

|-а| = |а|

Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков:

|0| = 0

На практике используют различные свойства модулей:

|а| ? 0

|а·b| = |а| · |b|

|а|ⁿ = аⁿ , n є Z, a ? 0, n > 0

|а| = | — а|

|а + b|  ?  |а| + |b|

|а·q| = q·|а| , где q — положительное число

|а|² = а²

Значение |a — b|  равно расстоянию на числовой прямой между точками, изображающими числа a и b.

Пример 1.

, т.к. 

, т.к. 

Пример 2.

Упростить выражение  , если a

Решение.

Так как по условию а

Ответ: 

Пример 3.

Вычислить

Решение.

Имеем

Теперь раскроем знаки модулей.

Воспользуемся тем, что 1 0.

Но тогда |?3 — 2| = -(?3 — 2) = 2- ?3 ,

а |?3 — 1| = ?3 — 1

В итоге получаем

Ответ: 1

Здесь Вы нашли ответ на вопрос : что такое модуль числа , и какие его свойства.

mirurokov.ru

Модуль числа

Модуль числа a — это расстояние от начала координат до точки

А(a).

Чтобы понять это определение, подставим вместо переменной a любое число, например 3 и попробуем снова прочитать его:

Модуль числа 3 — это расстояние от начала координат до точки А(3).

Становится ясно, что модуль это ни что иное, как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3)

Расстояние от начала координат до точки А(3) равно 3 (трём единицам или трём шагам).

Модуль числа обозначает двумя вертикальными линиями, например:

Модуль числа 3 обозначается так: |3|

Модуль числа 4 обозначается так: |4|

Модуль числа 5 обозначается так: |5|

Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:

|3| = 3

Читается как: «Модуль числа три равен три»

---

Теперь попробуем найти модуль числа -3. Опять же возвращаемся к определению и подставляем в него число -3. Только вместо точки A используем новую точку B. Точку A мы уже использовали в первом примере.

Модулем числа —3 называют расстояние от начала координат до точки B(—3).

Расстояние от одного пункта до другого не может быть отрицательным. Поэтому и модуль любого отрицательного числа, будучи являясь расстоянием тоже не будет отрицательным. Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:

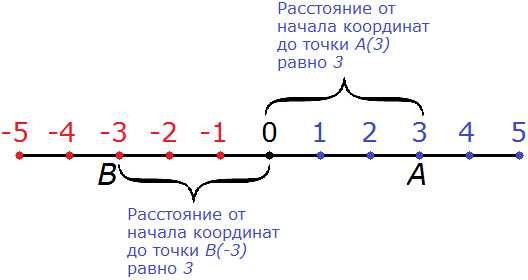
|-3| = 3

Читается как: «Модуль числа минус три равен три»

---

Модуль числа 0 равен 0, та как точка с координатой 0 совпадает  с началом координат, т.е. расстояние от начала координат до точки O(0) равно нулю:

|0| = 0

«Модуль нуля равен нулю»

---

Делаем выводы:

• Модуль числа не может быть отрицательным;
• Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу;
• Противоположные числа имеют равные модули.

Примеры:

| 1 | = 1

| -1| = 1

| 2 | = 2

| -2| = 2

| 0 | = 0

---

Противоположные числа

Числа, отличающиеся только знаками называют противоположными. Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числа −2 знак минуса, а у 2 знак плюса, но мы его не видим, потому что плюс, как мы говорили ранее, по традиции не пишут.

Еще примеры противоположных чисел:

−1 и 1

−3 и 3

−5 и 5

−9 и 9

Противоположные числа имеют равные модули. Например, найдём модули для −2 и 2

|−2| и |2|

2 = 2

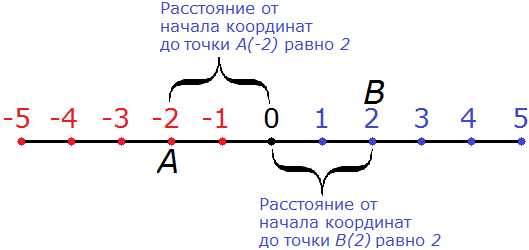
На рисунке видно, что расстояние от начала координат до точек A(−2) и B(2) одинаково равно двум шагам.

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Навигация по записям

spacemath.xyz

Определение модуля | Математика

1. Определение модуля:

Модулем числа а называется расстояние (в единичных отрезках) от начала координат до точки А с координатой а.

Пример.

Модуль числа 7 равен 7, так как точка D с координатой 7 удалена от начала отсчета на 7 единичных отрезков.

Модуль числа -6 равен 6, так как точка С с координатой 6 удалена от начала отсчета на 6 единичных отрезков. Пишут:

   

2. По определению модуля, модуль — это расстояние.

А так как расстояние не может быть отрицательным числом, то и модуль не может быть отрицательным числом.

3. Модуль положительного числа равен самому числу.

Например,

   

4. Модуль отрицательного числа равен противоположному числу.

Например,

   

5. Модуль нуля равен нулю:

   

6. Противоположные числа имеют равные модули:

   

Например,

   

Из определения модуля:

www.for6cl.uznateshe.ru

Модуль числа – что это такое: что значит абсолютная величина

В школе на уроке математики каждый год ученики разбирают новые темы. 6 класс обычно изучает модуль числа – это важное понятие в математике, работа с которым встречается далее в алгебре и высшей математики. Очень важно изначально правильно понять объяснение термина и разобраться в этой теме, чтобы успешно проходить прочие темы.

Содержание статьи

Величины в математике

Для начала следует понимать, что абсолютная величина – это параметр в статистике (измеряется количественно), который характеризует изучаемое явление по его объему. При этом явление должно осуществляться в определенных временных рамках и с определенным месторасположением. Различают значения:

• суммарные – подходят для группы единиц или полностью всей совокупности;
• индивидуальные – подходят только для работы с единицей некой совокупности.

Это интересно! Основы геометрии: что это такое биссектриса треугольника

Понятия широко используются в статистических измерениях, результатом которых являются показатели, характеризующие абсолютные размеры у каждой единицы некоего явления. Измеряются они в двух показателях: натуральном, т.е. физические единицы (шт., люди) и условно-натуральном. Модуль в математике является отображением данных показателей.

Модуль числа

Что такое модуль числа?

Важно! Данное определение «module» с латыни переводиться как «мера» и означает абсолютную величину любого натурального числа.

Но у данного понятия есть и геометрическое объяснение, поскольку модулю в геометрии равняется расстояние от начала системы координат до точки X, которое измеряется в привычных единицах измерения.

Для того, чтобы определить данный показатель у числа, следует не учитывать его знак (минус, плюс), но при этом следует помнить то, что он никогда не может быть отрицательным. Данное значение на бумаге выделяется графически в виде квадратных скобок — |a|. При этом, математическое определение такое:

|х| = х, если х больше или равен нулю и -х, если меньше нуля.

Английский ученый Р. Котес был тем человеком, кто впервые применил данное понятие в математических расчетах. А вот К. Вейерштрасс, математик из Германии, придумал и ввел в использование графический символ.

Это интересно! Как разложить на множители квадратный трехчлен: формула

В геометрии module можно рассмотреть на примере координатной прямой, на которое нанесены 2 произвольные точки. Предположим, одна — А имеет значение 5, а вторая В — 6. При подробном изучении чертежа станет ясно, что расстояние от А до В – 5 единиц от нуля, т.е. начала координат, а точка В размещена от начала координат на 6 единиц. Можно сделать вывод, что module точки, А = 5, а точки В = 6. Графически это можно обозначить так: | 5 | = 5. Т. е. расстояние от точки до начала координат является модулем данной точки.

Полезное видео: что такое модуль действительного числа?

Свойства

Как у любого математического понятия, у module есть свои математические свойства:

1. Он всегда положительный, поэтому модулем положительного значения будет оно само, например, модуль числа 6 и -6 равен 6. Математически это свойство можно записать как |a| = a, при a> 0;
2. Показатели противоположных чисел равны между собой. Это свойство понятнее в геометрическом изложении, поскольку на прямой данные числа располагаются в разных местах, но при этом от начала отсчета их отделяет равное количество единиц. Математически это записывается так: |а| = |-а|;
3. Модуль нуля равен нулю, при условии, что действительное число – это ноль. Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0;
4. Если требуется найти модуль двух умножающихся цифр, стоит понимать, что он будет равен полученному произведению. Другими словами, произведение величин А и В = АВ, при условии, что они положительные или же отрицательные, и тогда произведение равняется -АВ. Графически это можно записать как |А*В| = |А| * |В|.

Это интересно! Считаем правильно: как находить процент от суммы и числа

Успешное решение уравнений с модулем зависит от знания данных свойств, которое поможет любому правильно вычислять и работать с данным показателем.

Свойства модуля

Важно! Показатель не может быть отрицательным, поскольку он определяет расстояние, которое всегда положительное.

В уравнениях

В случае работы и решения математических неравенств, в которых присутствует module, всегда необходимо помнить, что для получения итогового правильного результата следует раскрыть скобки, т.е. открыть знак module. Зачастую, в этом и есть смысл уравнения.

При этом стоит помнить, что:

• если в квадратных скобках записано выражение, его необходимо решить: |А + 5| = А + 5, при А больше или равным нулю и 5-А, в случае А меньше нуля;
• квадратные скобки чаще всего должны раскрываться независимо от значений переменной, например, если в скобках заключено выражение в квадрате, поскольку при раскрытии в любом случае будет положительное число.

Это интересно! Уроки математики: умножение на ноль — главное правило

Очень легко решаются уравнения с module путем занесения значений в систему координат, поскольку тогда легко увидеть визуально значения и их показатели.

Полезное видео: модуль действительного числа и его свойства

Вывод

Принцип понимания такого математического понятия, как module, крайне важен, поскольку оно используется в высшей математике и прочих науках, поэтому необходимо уметь работать с ним.

Вконтакте

Facebook

Twitter

Google+

znaniya.guru

Модуль числа. Свойства абсолютной величины

Модуль числа – это расстояние от начальной точки до соответствующей точки на координатной прямой. Модуль числа так же называется абсолютной величиной числа.

Для обозначения модуля используются две вертикальные черты, в которые заключается число, абсолютная величина которого берётся.

Рассмотрим координатную прямую с точками A и B:

Точка A соответствует числу -5, которое находится в пяти единичных отрезках от начальной точки, то есть длина отрезка AO равна 5. Так как модуль равен расстоянию от начала координат до точки, то модуль числа -5 равен 5, это можно записать так:

|-5| = 5

Точка B соответствует числу 4,5, значит длина отрезка OB равна 4,5. Следовательно модуль числа 4,5 равен 4,5:

|4,5| = 4,5

Точка O соответствует числу 0 и является начальной точкой, следовательно модулем нуля будет нуль:

|0| = 0

Из данных примеров можно сделать вывод, что модуль числа – это положительное число или нуль.

Следует иметь ввиду, что чем дальше от нуля точка, изображающая данное число, тем больше модуль этого числа.

Свойства абсолютной величины числа

Модулем (или абсолютной величиной) положительного числа называют само это число.

Например, модулем числа +6 является число +6 (или просто 6), пишут:

|+6| = +6.

Модулем (или абсолютной величиной) отрицательного числа называют противоположное ему (положительное) число.

Например, модулем числа -6 является число +6, пишут:

|-6| = +6.

Модулем числа 0 является число 0.

|0| = 0.

Модули противоположных чисел равны: |a| = |-a|:

|+4| = |-4| = 4.

naobumium.info

Что такое модуль числа?

Что такое модуль числа?

это его абсолютная величина. /6/=6, /-6/=6. Всегда положительное число получается.

Тупо его значение. Без знака. Пишется вот так: |7| это модуль -7 и 7

Числа есть положительные и отрицательные. МОДУЛЬ числа — его АБСОЛЮТНАЯ величина. Тогда числа «а = 12345» и «в = -12345» равны по модулю. Это понятие будет необходимо в «векторном» исчислении.

Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число =(корень берётся со знаком плюс) . При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно М. числа z. М. допускает следующее геометрическое истолкование: комплексное число z = х + iy можно изобразить вектором, исходящим из начала прямоугольной системы координат и имеющим конец в точке с координатами (х, у) ; длина этого вектора и есть М. комплексного числа z. = 2) М. перехода от системы логарифмов при основании а к системе логарифмов при основании b есть число М = 1/logab; для получения логарифмов чисел х при основании b, если известны логарифмы этих чисел при основании а, надо последние умножить на М. перехода: logbx = М logax.

Кароче Маш! Надо было сразу идти ко мне! Модуль числа — это расстояние на координатной прямой от 0 до точки, которая соответствует этому числу. например _____.-5————-0_______________! -5=/5/ — это расстояние отмеченное прирывистой линией!

это отрицательные и положительные числа,

Модулем числа А называют расстояние от начала координат до точки А

Модулем неотрицательного действительного числа a называют само это число |а| = а.

Модуль числа-расстояние от тоски A(а) до начала отсчёта (до точки О (о)). Модуль числа обозначается |a| (Модуль числа А

это его абсолютная величина. /6/=6, /-6/=6. Всегда положительное число получается.

логично -6=6 6=6 сё

Модулем числа называют расстояние от начала координата до любой точки

Число (+5м) =(5)*(+1м) и (-5м) =(5):(-1м). В этом сложном числе модулем является величина, размер (5). Григорий.

Войдите, чтобы написать ответ

education.ques.ru