Четверти на окружности – [Билет 17] Радианная и градусная меры углов. Тригонометрическая окружность. Соответствия между действительными числами и точками на тригонометрической окружности.

Четверть числовой окружности

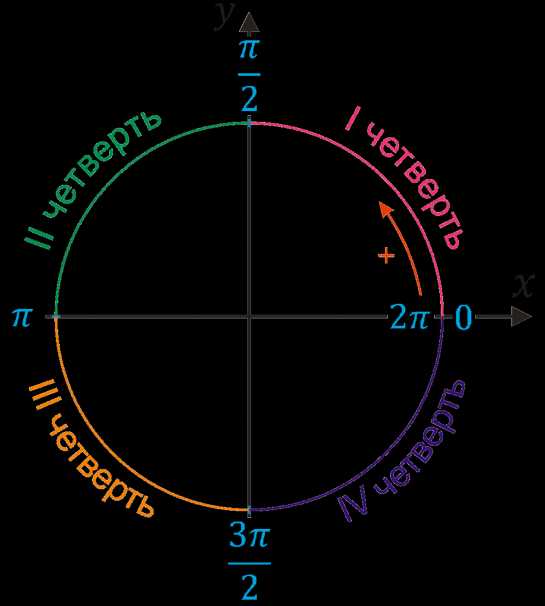
Если посмотреть на числовую окружность, то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

\((\)\(\frac{π}{2}\)\(;π)\)- вторая четверть		\((0;\)\(\frac{π}{2}\)\()\) — первая четверть
\((π;\)\(\frac{3π}{2}\)\()\) — третья четверть		\((\)\(\frac{3π}{2}\)\(;2π)\) — четвертая четверть

Почему так важно определять какой четверти принадлежит угол?

Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций.

Например, для любого угла из второй четверти — синус положителен, а косинус, тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.

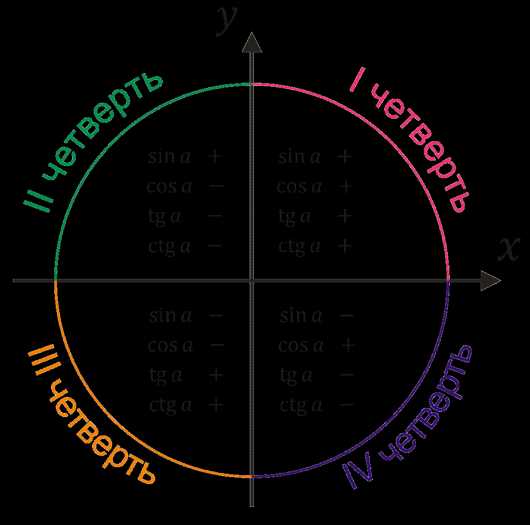
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.

Пример (ЕГЭ):

Найдите \(\sin⁡a\), если \(\cos⁡a=-0,6\) и \(π<a<\)\(\frac{3π}{2}\)		Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла?  Основное тригонометрическое тождество. Запишем его.
\(\sin^2⁡a+\cos^2⁡a=1\)		Подставим известное, и проведем вычисления.
\(\sin^2⁡a+(-0,6)^2=1\) \(\sin^2⁡a+0,36=1\) \(\sin^2⁡a=0,64\)
\(\sin⁡a=0,8\)   или   \(\sin⁡a=-0,8\)		У нас два ответа, и оба нам подходят. Но у угла не может быть два синуса! Один лишний! А какой? Вот тут нам и поможет знание о четвертях: обратите внимание, что у нас в условии есть двойное неравенство  \(π<a<\) \(\frac{3π}{2}\), то есть угол \(a\) такой, что больше \(π\), но меньше \(\frac{3π}{2}\). Значит он лежит в третьей четверти. А в третьей четверти синус отрицателен. Поэтому верный ответ: \(-0,8\).

Ответ: \(\sin⁡a=-0,8\).

Про непостоянство четвертей:

Важно понимать, что, например, первой четверти принадлежат не только углы от \(0\) до \(\frac{π}{2}\), но и углы от \(2π\) до \(\frac{5π}{2}\), и от \(4π\) до \(\frac{9π}{2}\), и от \(6π\) до \(\frac{13π}{2}\) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

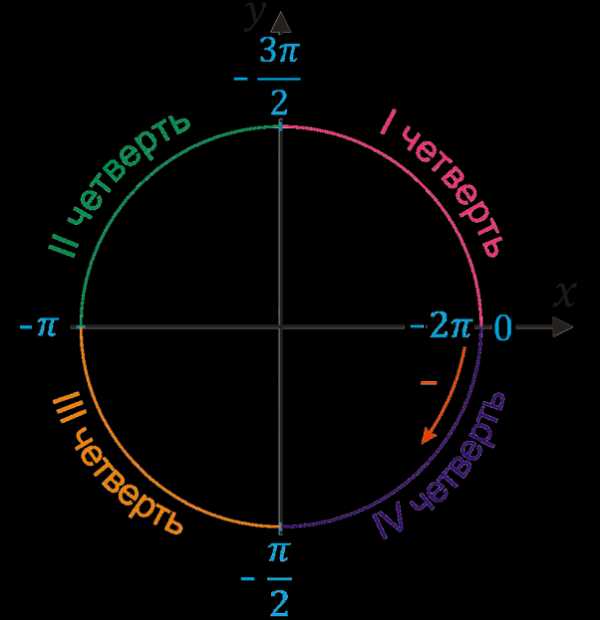
Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.

\((-π;-\)\(\frac{3π}{2}\)\()\)- вторая четверть		\((-\)\(\frac{3π}{2}\)\(;-2π)\) — первая четверть
\((-\)\(\frac{π}{2}\)\(;-π)\) — третья четверть		\((0;-\)\(\frac{π}{2}\)\()\) — четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
Как обозначать точки на числовой окружности

Скачать статью

cos-cos.ru

Числовая окружность, макеты числовой окружности — урок. Алгебра, 10 класс.

Единичная окружность — это окружность, радиус которой принимается за единицу измерения.

Длина единичной окружности \(l\) равна l=2π⋅R=2π⋅1=2π

Считаем, что R=1.

Если взять π≈3,14, то длина окружности \(l\) может быть выражена числом 2π≈2⋅3,14=6,28

 

Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры \(CA\) и \(DB\) (см. рис.)

 

 

Принято называть дугу \(AB\) — первой четвертью, дугу \(BC\) — второй четвертью, дугу \(CD\) — третьей четвертью, дугу \(DA\) — четвёртой четвертью, причём, это открытые дуги, т.е. дуги без их концов.  

 

Длина каждой четверти единичной окружности равна 14⋅2π=π2

 

Принято в обозначении дуги на первом месте писать букву, обозначающую начало дуги, а на втором месте писать букву, обозначающую конец дуги.

 

Для работы с числовой окружностью часто используются два макета числовой окружности.

Каждая из четырёх четвертей числовой окружности разделена на две равные части и около каждой из полученных восьми точек записано число, которому она соответствует.

 

 

 

Каждая из четырёх четвертей числовой окружности разделена на три равные части и около каждой из полученных двенадцати точек записано число, которому она соответствует.

 

 

Для числовой окружности верно следующее утверждение:

Если точка \(M\) числовой окружности соответствует числу \(t\), то она соответствует и числу вида t+2πk,k∈ℤ

 

На указанных двух макетах написаны числа, соответствующие точкам, при первом обходе числовой окружности в положительном направлении, т.е. на промежутке 0;2π

Таким образом,

единичная окружность с установленным соответствием между действительными числами и точками окружности называется числовой окружностью.

www.yaklass.ru

Тригонометрия: синус, косинус, тангенс, котангенс

История тригонометрии

Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.

Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.

В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.

Основные величины тригонометрии

Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.

В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.

Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:

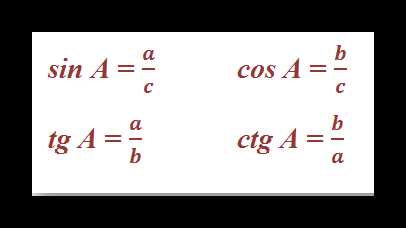
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:

Тригонометрический круг

Графически соотношение упомянутых величин можно представить следующим образом:

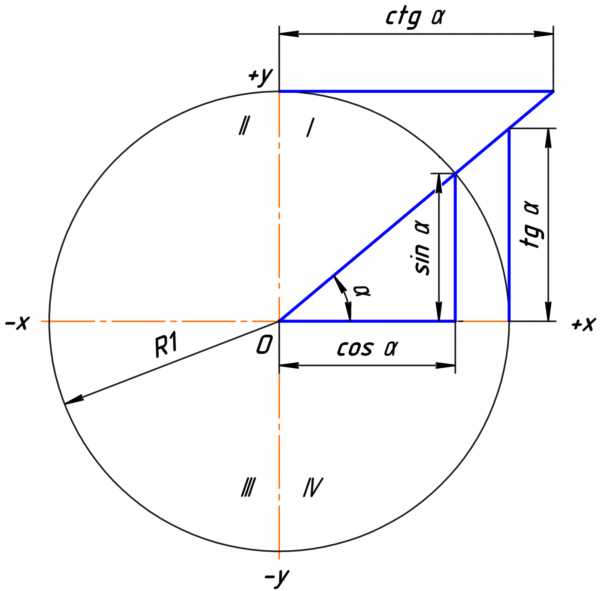
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.

Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.

Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.

Данные углы выбраны отнюдь не случайно. Обозначение π  в таблицах стоит для радиан. Рад  — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.

Углы в таблицах для тригонометрических функций соответствуют значениям радиан:

Итак, не трудно догадаться, что 2π – это полная окружность или 360°.

Свойства тригонометрических функций: синус и косинус

Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.

Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:

Синусоида	Косинусоида
y = sin x	y = cos x
ОДЗ [-1; 1]	ОДЗ [-1; 1]
sin x = 0, при x = πk, где k ϵ Z	cos x = 0, при x = π/2 + πk, где k ϵ Z
sin x = 1, при x = π/2 + 2πk, где k ϵ Z	cos x = 1, при x = 2πk, где k ϵ Z
sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z	cos x = — 1, при x = π + 2πk, где k ϵ Z
sin (-x) = — sin x, т. е. функция нечетная	cos (-x) = cos x, т. е. функция четная
функция периодическая, наименьший период — 2π	функция периодическая, наименьший период — 2π
sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk)	cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk)
возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk]	возрастает на промежутке [-π + 2πk, 2πk]
убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk]	убывает на промежутках [2πk, π + 2πk]
производная (sin x)’ = cos x	производная (cos x)’ = — sin x

Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.

Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:

Убедиться в верности формулы очень просто. Например, для x =  π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.

Свойства тангенсоиды и котангенсоиды

Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.

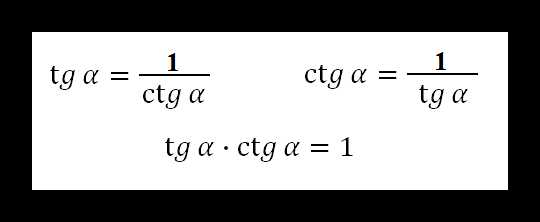
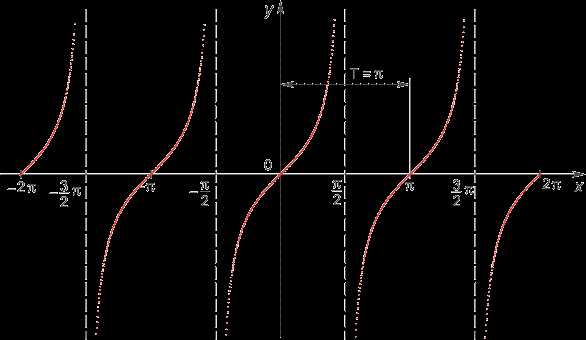
Основные свойства котангенсоиды:

1. Y = tg x.
2. В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
3. Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
4. Наименьший положительный период тангенсоиды равен π.
5. Tg (- x) = — tg x, т. е. функция нечетная.
6. Tg x = 0, при x = πk.
7. Функция является возрастающей.
8. Tg x › 0, при x ϵ (πk, π/2 + πk).
9. Tg x ‹ 0, при x ϵ ( — π/2 + πk, πk).
10. Производная (tg x)’ = 1/cos²⁡x .

Рассмотрим графическое изображение котангенсоиды ниже по тексту.

 

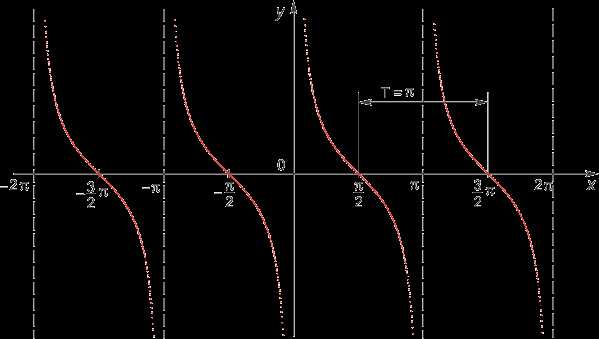
Основные свойства котангенсоиды:

1. Y = ctg x.
2. В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
3. Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
4. Наименьший положительный период котангенсоиды равен π.
5. Ctg (- x) = — ctg x, т. е. функция нечетная.
6. Ctg x = 0, при x = π/2 + πk.
7. Функция является убывающей.
8. Ctg x › 0, при x ϵ (πk, π/2 + πk).
9. Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
10. Производная (ctg x)’ = — 1/sin²⁡x Исправить

Похожие статьи

Рекомендуем почитать:

karate-ege.ru

Точки на числовой окружности

При изучении тригонометрии в школе каждый ученик сталкивается с весьма интересным понятием «числовая окружность». От умения школьного учителя объяснить, что это такое, и для чего она нужна, зависит, насколько хорошо ученик пойдём тригонометрию впоследствии. К сожалению, далеко не каждый учитель может доступно объяснить этот материал. В результате многие ученики путаются даже с тем, как отмечать точки на числовой окружности. Если вы дочитаете эту статью до конца, то научитесь делать это без проблем.

Итак, приступим. Нарисуем окружность, радиус которой равен 1. Самую «правую» точку этой окружности обозначим буквой O:

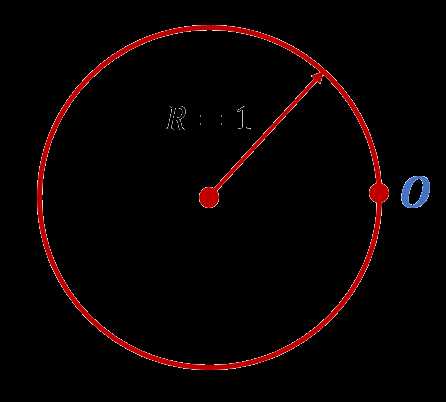
Поздравляю, вы только что нарисовали единичную окружность. Поскольку радиус этой окружности равен 1, то её длина равна .

Каждому действительному числу можно поставить в соответствие длину траектории вдоль числовой окружности от точки O. За положительное направление принимается направление движения против часовой стрелки. За отрицательное – по часовой стрелке:

Расположение точек на числовой окружности

Как мы уже отмечали, длина числовой окружности (единичной окружности) равна . Где тогда будет располагаться на этой окружности число ? Очевидно, от точки O против часовой стрелки нужно пройти половину длины окружности, и мы окажемся в нужной точке. Обозначим её буквой B:

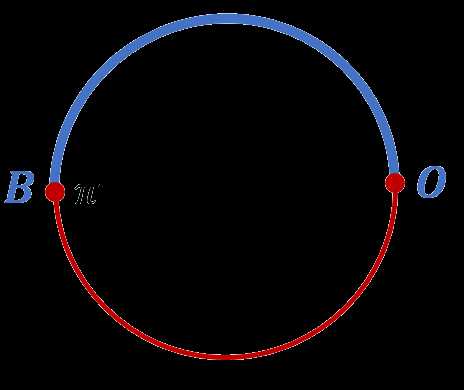
Обратите внимание, что в ту же точку можно было бы попасть, пройдя полуокружность в отрицательном направлении. Тогда бы мы отложили на единичной окружности число . То есть числам и соответствует одна и та же точка.

Причём этой же точке соответствуют также числа , , , и, вообще, бесконечное множество чисел, которые можно записать в виде , где , то есть принадлежит множеству целых чисел. Всё это потому, что из точки B можно совершить «кругосветное» путешествие в любую сторону (добавить или вычесть длину окружности ) и попасть в ту же самую точку. Получаем важный вывод, который нужно понять и запомнить.

Каждому числу соответствует единственная точка на числов

yourtutor.info

10 класс. Алгебра. Тригонометрические функции. Числовая окружность. — Числовая окружность. Числовая окружность на координатной плоскости.

Комментарии преподавателя

Для  любой функ­ции неза­ви­си­мый ар­гу­мент от­кла­ды­ва­ет­ся либо на чис­ло­вой пря­мой, либо на окруж­но­сти. Оха­рак­те­ри­зу­ем и чис­ло­вую пря­мую, и чис­ло­вую окруж­ность.

Пря­мая ста­но­вит­ся чис­ло­вой (ко­ор­ди­нат­ной) пря­мой, если от­ме­че­но на­ча­ло ко­ор­ди­нат, вы­бра­ны на­прав­ле­ние и мас­штаб (рис. 1).

Чис­ло­вая пря­мая уста­нав­ли­ва­ет вза­им­но-од­но­знач­ное со­от­вет­ствие между всеми точ­ка­ми пря­мой и всеми дей­стви­тель­ны­ми чис­ла­ми.

На­при­мер, берем число  от­кла­ды­ва­ем на ко­ор­ди­нат­ной оси, по­лу­ча­ем точку  Возь­мем число  от­кла­ды­ва­ем на оси, по­лу­ча­ем точку  (рис. 2).

И на­о­бо­рот, если мы взяли любую точку  на ко­ор­ди­нат­ной пря­мой, то най­дет­ся един­ствен­ное со­от­вет­ству­ю­щее ей дей­стви­тель­ное число (рис. 2).

К та­ко­му со­от­вет­ствию люди при­шли не сразу. Чтобы по­нять это, вспом­ним ос­нов­ные чис­ло­вые мно­же­ства.

Сна­ча­ла ввели мно­же­ство на­ту­раль­ных чисел 

Затем мно­же­ство целых чисел 

Мно­же­ство ра­ци­о­наль­ных чисел 

Пред­по­ла­га­лось, что этих мно­жеств будет до­ста­точ­но, и су­ще­ству­ет вза­им­но-од­но­знач­ное со­от­вет­ствие между всеми ра­ци­о­наль­ны­ми чис­ла­ми и точ­ка­ми пря­мой. Но ока­за­лось, что на чис­ло­вой пря­мой есть бес­чис­лен­ное мно­же­ство точек, ко­то­рые нель­зя опи­сать чис­ла­ми вида 

При­мер – ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка с ка­те­та­ми 1 и 1. Она равна  (рис. 3).

Най­дет­ся ли среди мно­же­ства ра­ци­о­наль­ных чисел число, в точ­но­сти рав­ное  Нет, не най­дет­ся. До­ка­жем этот факт.

До­ка­жем ме­то­дом от про­тив­но­го. Пред­по­ло­жим, что су­ще­ству­ет дробь, рав­ная т.е. 

Тогда  Воз­ве­дем обе части в квад­рат,   Оче­вид­но, что пра­вая часть ра­вен­ства де­лит­ся на 2, . Зна­чит и  Тогда  Но тогда и  А зна­чит,  Тогда по­лу­ча­ет­ся, что дробь  со­кра­ти­мая. Это про­ти­во­ре­чит усло­вию, зна­чит 

Число  ир­ра­ци­о­наль­ное. Мно­же­ство ра­ци­о­наль­ных и ир­ра­ци­о­наль­ных чисел об­ра­зу­ют мно­же­ство дей­стви­тель­ных чисел  Если мы возь­мем любую точку на пря­мой, ей будет со­от­вет­ство­вать ка­кое-ли­бо дей­стви­тель­ное число. И если мы возь­мем любое дей­стви­тель­ное число, ему будет со­от­вет­ство­вать един­ствен­ная точка на ко­ор­ди­нат­ной пря­мой.

Уточ­ним, что такое чис­ло­вая окруж­ность и ка­ко­вы вза­и­мо­от­но­ше­ния между мно­же­ством точек окруж­но­сти и мно­же­ством дей­стви­тель­ных чисел.

На­ча­ло от­сче­та – точка A. На­прав­ле­ние от­сче­та – про­тив ча­со­вой стрел­ки – по­ло­жи­тель­ное, по ча­со­вой стрел­ке – от­ри­ца­тель­ное.  Мас­штаб – длина окруж­но­сти  (рис. 4).

Вводя эти три по­ло­же­ния, мы имеем чис­ло­вую окруж­ность. Ука­жем, каким об­ра­зом каж­до­му числу  по­ста­вить в со­от­вет­ствие точку на окруж­но­сти и на­о­бо­рот.

Задав число  по­лу­ча­ем точку на окруж­но­сти  

 (рис. 4).

Каж­до­му дей­стви­тель­но­му числу со­от­вет­ству­ет точка на окруж­но­сти. А на­о­бо­рот?

Точка  со­от­вет­ству­ет числу . А если взять числа  Все эти числа своим об­ра­зом на окруж­но­сти имеют толь­ко одну точку 

На­при­мер,  со­от­вет­ству­ет точке B (рис. 4).

Возь­мем все числа  Все они со­от­вет­ству­ют точке B. Нет вза­им­но-од­но­знач­но­го со­от­вет­ствия между всеми дей­стви­тель­ны­ми чис­ла­ми и точ­ка­ми окруж­но­сти.

Если есть фик­си­ро­ван­ное число  то ему со­от­вет­ству­ет толь­ко одна точка окруж­но­сти

Если есть точка окруж­но­сти, то ей со­от­вет­ству­ет мно­же­ство чисел

В от­ли­чии от пря­мой, ко­ор­ди­нат­ная окруж­ность не об­ла­да­ет вза­им­но-од­но­знач­ным со­от­вет­стви­ем между точ­ка­ми и чис­ла­ми. Каж­до­му числу со­от­вет­ству­ет толь­ко одна точка, но каж­дой точке со­от­вет­ству­ет бес­чис­лен­ное мно­же­ство чисел, и мы можем их за­пи­сать.

Рас­смот­рим ос­нов­ные точки на окруж­но­сти.

За­да­но число  Найти, какой точке на окруж­но­сти оно со­от­вет­ству­ет.

Раз­де­лив дугу  по­по­лам, по­лу­ча­ем точку  (рис. 5).

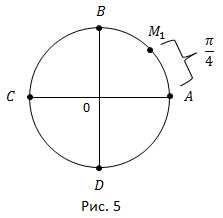
Об­рат­ная за­да­ча – дана точка  се­ре­ди­на дуги  Найти все дей­стви­тель­ные числа, ко­то­рые ей со­от­вет­ству­ют.

От­ме­тим на чис­ло­вой окруж­но­сти все дуги, крат­ные  (рис. 6).

Важны

www.kursoteka.ru

Тригонометрия. Единичная окружность

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (322,7 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

Цель: научить использовать единичную окружность при решении различных тригонометрических заданий.

В школьном курсе математики возможны различные варианты введения тригонометрических функций. Наиболее удобной и часто используемой является «числовая единичная окружность». Её применение в теме «Тригонометрия» весьма обширно.

Единичная окружность используется для:

– определения синуса, косинуса, тангенса и котангенса угла;
– нахождения значений тригонометрических функций для некоторых значений числового и углового аргумента;
– выведение основных формул тригонометрии;
– выведения формул приведения;
– нахождения области определения и области значений тригонометрических функций;
– определения периодичности тригонометрических функций;
– определения четности и нечетности тригонометрических функций;
– определения промежутков возрастания и убывания тригонометрических функций;
– определения промежутков знакопостоянства тригонометрических функций;
– радианного измерения углов;
– нахождения значений обратных тригонометрических функций;
– решение простейших тригонометрических уравнений;
– решение простейших неравенств и др.

Таким образом, активное осознанное владение учащимися данным видом наглядности дает неоспоримые преимущества для овладения разделом математики «Тригонометрия». 

Использование ИКТ на уроках преподавания математики позволяет облегчить овладение числовой единичной окружностью. Конечно, интерактивная доска имеет широчайший диапазон применения, однако не во всех  классах она есть. Если же говорить о применении  презентаций, то на просторах Интернета и их выбор велик, и каждый педагог может найти наиболее  приемлемый вариант для своих уроков.

В чем особенность представляемой мною презентации?

Данная презентация предполагает различные варианты использования и не является наглядностью к конкретному уроку в теме «Тригонометрия». Каждый слайд данной презентации  можно использовать обособлено, как на этапе объяснения материала, формирования навыков, так и для рефлексии. При создании данной презентации особое внимание уделялось «читаемости» её с дальнего расстояния, поскольку количество учеников со сниженным зрением постоянно растет. Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических  заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.

Данная презентация поможет педагогам познакомить учеников с единичной окружностью в 9 классе на уроках геометрии при изучении темы «Соотношения между сторонами и углами треугольника».  И, конечно, она поможет расширить и углубить навык работы с единичной окружностью при решении тригонометрических заданий у учащихся старшего звена обучения на уроках алгебры.

Слайды 3, 4 поясняют построение единичной окружности;  принцип определения местоположения точки на единичной окружности  в I и II координатных четвертях; переход от геометрических определений функций синус и косинус (в прямоугольном треугольнике)  к алгебраическим на единичной окружности.

Слайды 5-8  поясняют, как найти значения тригонометрических функций для основных углов I координатной четверти.

Слайды 9-11 поясняет знаки функций в координатных четвертях; определение промежутков знакопостоянства тригонометрических функций.

Слайд 12 используется для формирования  представлений о положительных и отрицательных значениях углов; знакомством с понятием периодичности тригонометрических функций.

Слайды 13, 14   используются при переходе на радианную меру угла.

Слайды 15-18  не анимированы и используются   при решении различных тригонометрических заданий, закрепления и проверки результатов усвоения материала.

Содержание:

1. Титульный лист.
2. Целеполагание.
3. Построение единичной окружности. Основные значения углов в градусной мере.
4. Определение синуса и косинуса угла на единичной окружности.
5. Табличные значения для синуса  в порядке возрастания.
6. Табличные значения для косинуса  в порядке возрастания.
7. Табличные значения для тангенса  в порядке возрастания.
8. Табличные значения для котангенса  в порядке возрастания.
9. Знаки функции sin α.
10. Знаки функции cos α.
11. Знаки функций tg α и ctg α.
12. Положительные и отрицательные значения углов на единичной окружности.
13. Радианная мера угла.
14. Положительные и отрицательные значения углов в радианах на единичной окружности.
15. Различные варианты единичной окружности для закрепления и проверки результатов усвоения материала.

12.04.2013

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Тригонометрический круг. Основные значения тригонометрических функций

 

Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы,  или вы совсем нетерпеливы,  – то вот он, тригонометрический круг:

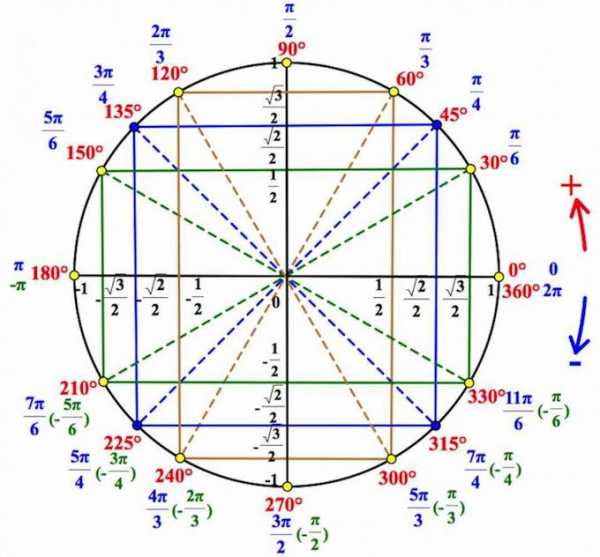
Мы же здесь будем все подробно разбирать шаг за шагом.

Тригонометрический круг – не роскошь, а необходимость

 

Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций,  столько формул…  А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…

Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.

Если вы постоянно смотрите в таблицу со значениями тригонометрических формул,  давайте избавляться от этой привычки!

Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!

К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, 300 градусов, или -45.

Никак?.. можно, конечно, подключить формулы приведения…  А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!

А при решении тригонометрических уравнений и неравенств   без тригонометрического круга  – вообще никуда.

Знакомство с тригонометрическим кругом

 

Давайте по порядку.

Сначала выпишем вот такой ряд чисел:

А теперь такой:

И, наконец, такой:

Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .

Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».

И зачем оно нам?

Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.

Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).

От луча  «0-Старт» откладываем в направлении стрелки (см. рис.) углы .

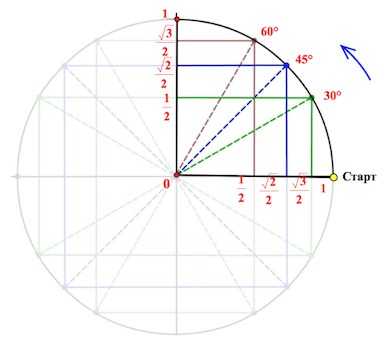Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.

Это почему же, спросите вы?

Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.

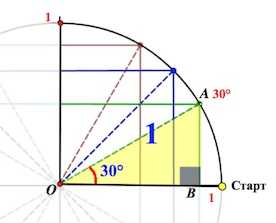
Треугольник АОВ – прямоугольный, в нем  . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).

Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора

Надеюсь, уже что-то становится понятно?

Наконец, что такое синус, косинус в прямоугольном треугольнике?

 

Так вот точка  В и будет соответствовать  значению , а точка М – значению

Аналогично с остальными значениями первой четверти.

Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось  (oy) – осью синусов.   Про тангенс и котангенс позже.

Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.

Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.

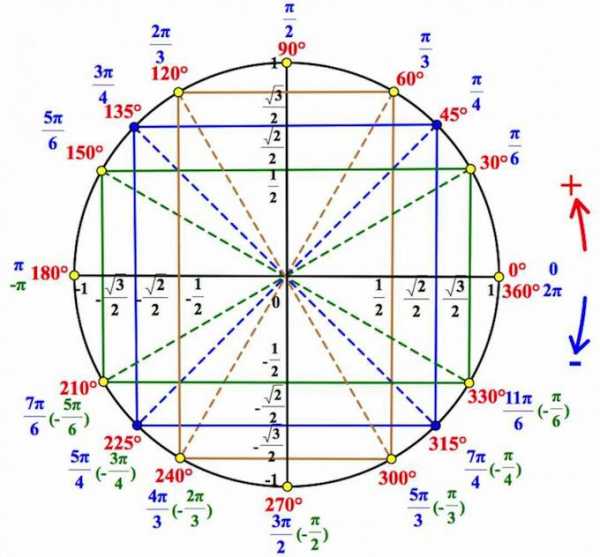
А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.

 

egemaximum.ru