Абсолютное значение числа это – абсолютное значение действительного числа — это… Что такое абсолютное значение действительного числа?
абсолютное значение числа — это… Что такое абсолютное значение числа?
- абсолютное значение числа
абсолютное значение числа
модуль числа
абсолютная величина числа
—
[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]абсолютное значение
Величина числа без учета его знака.
Так, числа +18 и -18 имеют одно и то же абсолютное значение: 18.
[http://www.morepc.ru/dict/]Тематики
- информационные технологии в целом
Синонимы
- модуль числа
- абсолютная величина числа
Справочник технического переводчика. – Интент. 2009-2013.
- абсолютное значение погрешности
- абсолютное измерение
Смотреть что такое «абсолютное значение числа» в других словарях:
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — на теле отображение тела Кв множество действительных чисел, удовлетворяющее условиям: А. з. часто обозначается вместо . А. з. наз. также нормой, мультипликативным нормированием. А. з. могут рассматриваться на любом кольце со значениями в линейно… … Математическая энциклопедия
Значение (значения) — Значение: Значение смысловое содержание слова, фразы или знака. Значение функции результат вычисления функции. Абсолютное значение модуль числа. Значение величины отношение измеренной физической величины к единице… … Википедия
Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
ГОСТ 31369-2008: Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава — Терминология ГОСТ 31369 2008: Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава оригинал документа: 2.1 высшая теплота сгорания (superior calorific value): Количество… … Словарь-справочник терминов нормативно-технической документации
МОЛЕКУЛЯРНЫЙ ВЕС — есть относительный вес молекулы вещества. Кроме возможности находиться в трех различных фазах (см. Аггрвгатное состояние) вещества обладают способностью распределяться одно в другом, образуя так наз. растворы. Согласно вант Гоффу (van t Hoff)… … Большая медицинская энциклопедия
Московский химический лицей № 1303 — Лицей № 1303 … Википедия
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
ВРЕМЯ — обозначает течение, длительность и последовательность событий. Оно есть условие существования конечных вещей и существ тварного мира. Согласно христ. учению, В. как творение Божие подчинено домостроительству спасения и своими границами имеет… … Православная энциклопедия
предел повторяемости — 3.7 предел повторяемости: Абсолютная разность результатов максимального и минимального значений из указанного числа измерений, выполненных в условиях повторяемости по ГОСТ Р ИСО 5725 1. Источник … Словарь-справочник терминов нормативно-технической документации
technical_translator_dictionary.academic.ru
Абсолютное значение — это… Что такое Абсолютное значение?
1) Нормирование — от глагола «Нормировать» в первом значении : НОРМИРОВАТЬ, нормирую, нормируешь, сов. и несов., что. Регулировать что-н., установить (устанавливать) законные пределы чему-н., ввести (вводить) в норму. Нормировать зарплату. Нормировать работу. (Толковаый словарь русского языка под редакцией Ушакова.)
2) Норми́рование(мат.) — отображение элементов поля F в некоторое упорядоченное поле P x→|x|, обладающее следующими свойствами:
1)|x|≥0 и |x|=0 только при x=0
2)|xy| ≤ |x||y|
3)|x+y| ≤ |x|+|y|
Если вместо 3) выполняется более сильное условие:
3a)|x+y| ≤ max(|x|,|y|), то нормирование называется неархимедовым.
Значение | x | (иногда обозначаемое ) называется нормой элемента
Примеры нормирований
- Нормирование, при котором |0|=0, |x|=1 для остальных x. Такое нормирование называется тривиальным.
- Обычная абсолютная величина в поле действительных чисел R или модуль в поле комплексных чисел C является нормированием.
- Пусть Q — поле рациональных чисел, а p — некоторое простое число. Любое рациональное число можно представить в виде дроби x=apn/b, где a и b не кратны p. Можно определить следующее нормирование |x|p=p-n
Свойства нормы
- |1|=|-1|=1
- | |x|-|y| |≤|x-y| (в этом случае абсолютная величина в упорядоченном поле P берётся от разности двух норм |x|-|y| элементов поля F)
- Действительнозначное нормирование является неархимедовым тогда и только тогда, когда существует положительное число A, такое, что для любой суммы единичных элементов поля F :
3b) |1+1+…+1|≤A
Пусть данное условие выполнено. Тогда для любых элементов x и y из поля F имеем:
|(x+y)n
Извлекая из обеих частей корень и переходя к пределу при n→∞ получаем условие 3a). Обратное утверждение очевидно.
Нормированное поле как метрическое пространство
Из свойств 1-3 немедленно следует, что определяя расстояние между двумя элементами действительнозначного нормированного поля F как норму разности |x-y| мы превращеем его в метрическое пространство, в случае неархимедовой нормы — в ультраметрическое пространство. Разные нормы определяют разные метрики. Если при этом они определяют одинаковую топологию в F, то такие нормы называются зависимыми.
Пополнение
Как и для любого метрического пространства можно ввести понятие полноты и доказать, что любое нормированное поле F изоморфно вкладывается в полное нормированное поле F*, то есть существует изоморфизм . Норма в F* продолжает норму в F, то есть для каждого x из F: , причём F плотно в F* относительно этой нормы. Любое такое поле F* определено однозначно с точностью до изоморфизма, сохраняющего нормы (изометрии) и тождественного на F; оно называется пополнением поля F.
Пример. Пополнением поля рациональных чисел Q с p-адической метрикой является поле p-адических чисел Qp.
Литература
- Ван дер Варден Б. Л. Алгебра — М: Наука. 1975.
- Зарисский О., Самюэль П. Коммутативная алгебра т.2 — М: ИЛ. 1963.
- Ленг С. Алгебра — М: Мир. 1967.
См. также
- Теорема Островского
- Аппроксимационная теорема
Wikimedia Foundation. 2010.
dic.academic.ru
§ 3. Абсолютная величина числа
Определение.Абсолютной величиной(илимодулем) действительного
числа (обозначается
(обозначается
Ясно, что всегда
 .
(3.1)
.
(3.1)
Свойства абсолютных величин:
1)
;
2);
3);
4)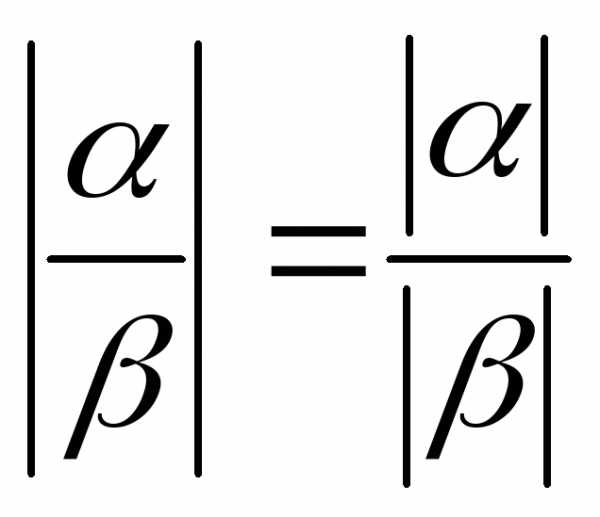 .
.
Доказательство.1) Если, тов силу (3.1). Если, то. Первое свойство доказано.
2) Имеем , отсюда. Второе свойство доказано.
3) , третье свойство доказано.
Четвертое свойство доказывается так же, как свойство 3).
Замечание. Свойство 1) распространяется на любое число слагаемых, свойство 3) – на любое число сомножителей.
Отметим также, что
,
т.е.худовлетворяет неравенству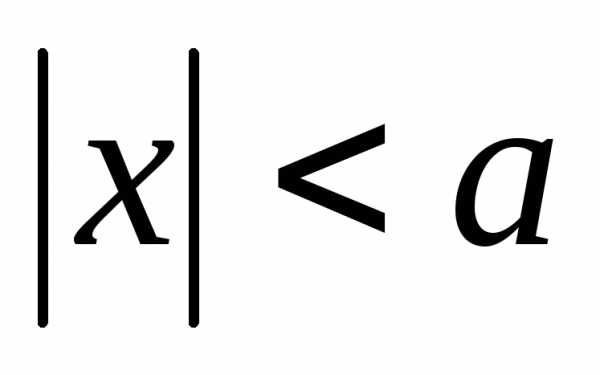 тогда и только тогда, когда принадлежит
интервалу
тогда и только тогда, когда принадлежит
интервалу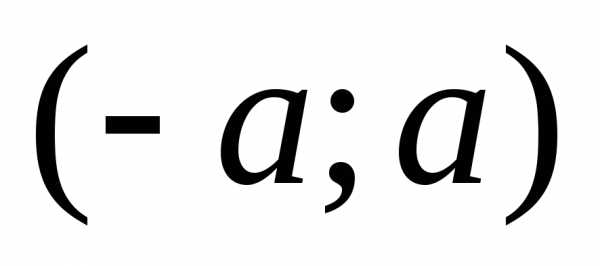 .
.
Геометрический смысл модуля действительного
числа состоит в том, что 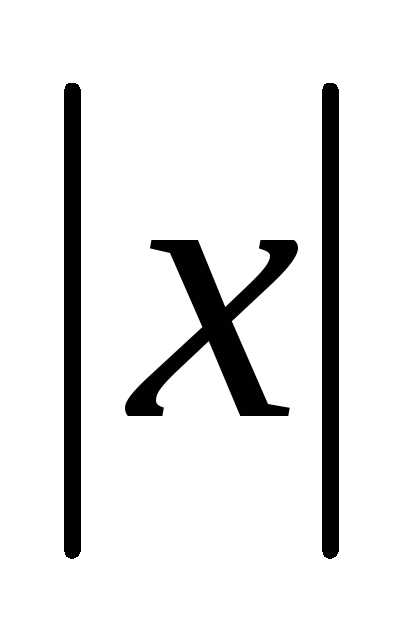 равен расстоянию от точкихна
числовой прямой до нуля.
равен расстоянию от точкихна
числовой прямой до нуля.
§ 4. Понятие числовой последовательности. Бесконечно большая и бесконечно малая последовательности, их свойства
Определение 1. Если каждому значениюn из множества
натуральных чиселставится в соответствие по определенному
закону некоторое действительное число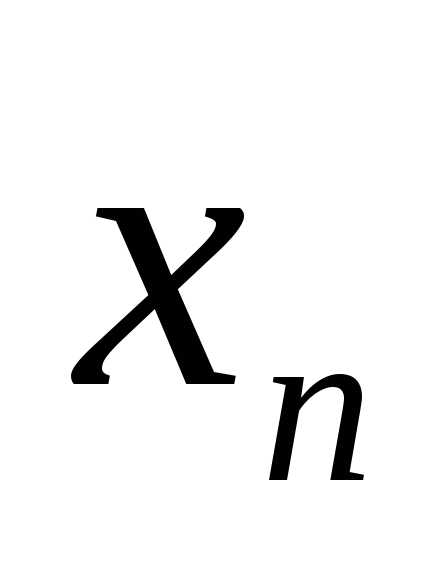 ,
то множество занумерованных действительных
чисел называетсячисловой
последовательностью .
,
то множество занумерованных действительных
чисел называетсячисловой
последовательностью .
– члены последовательности,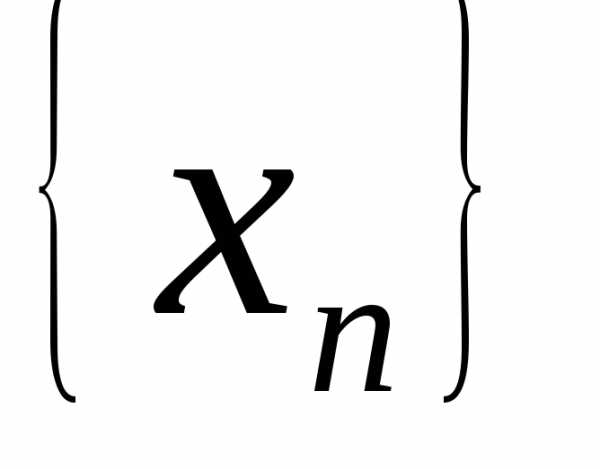 –
сокращенная запись последовательности.
Например,.
–
сокращенная запись последовательности.
Например,.
Определение 2. Пусть даны две
последовательности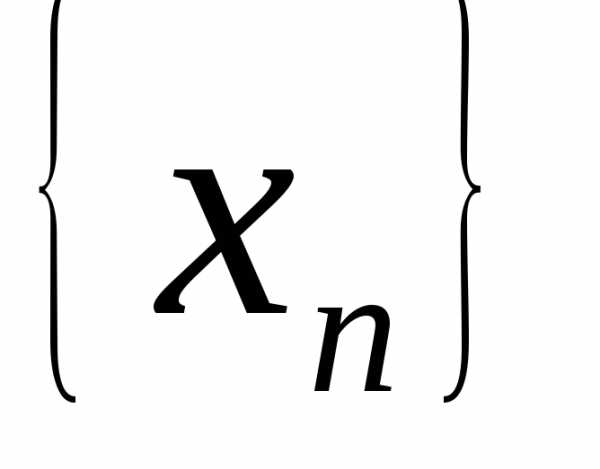 и
и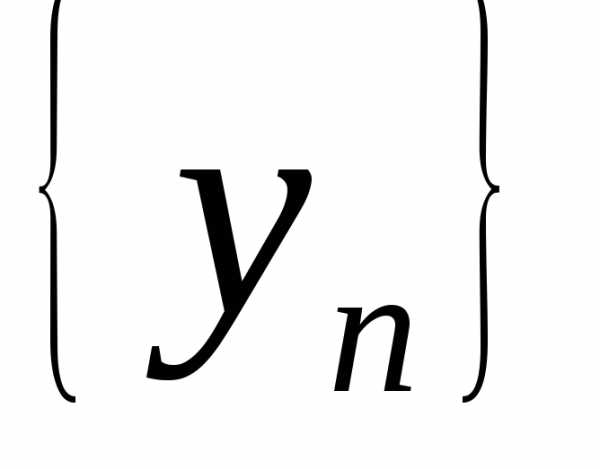 .
Последовательностиназываются соответственно суммой,
разностью, произведением и частным
последовательностей
.
Последовательностиназываются соответственно суммой,
разностью, произведением и частным
последовательностей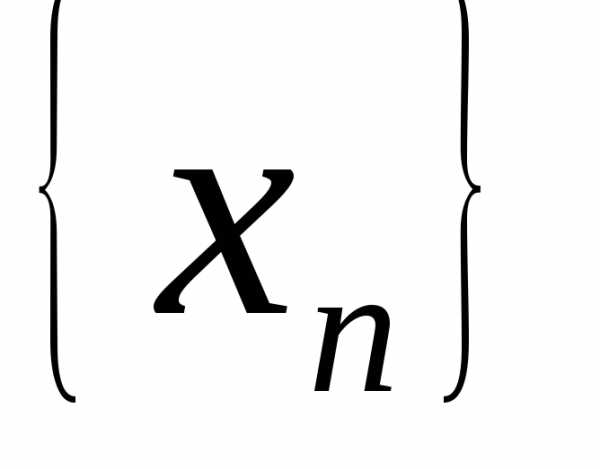 и
и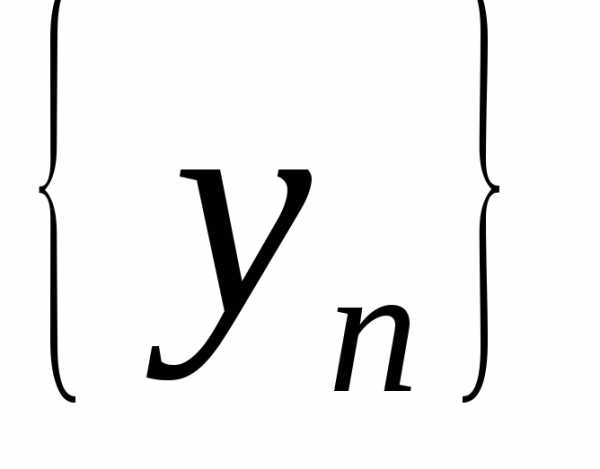 .
.
Определение 3. Последовательность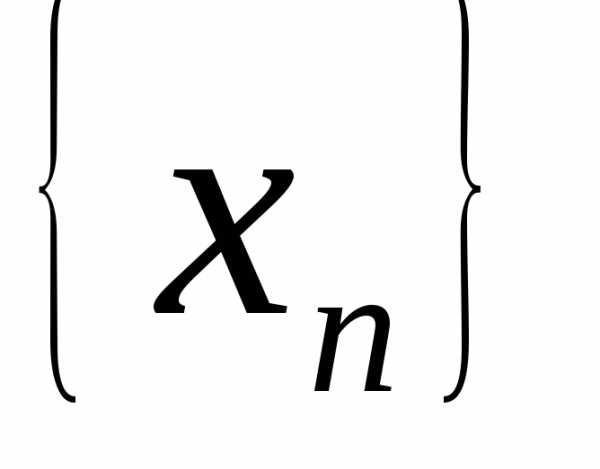 называетсяограниченной, если
множество ее членов ограничено, т.е.
существует число
называетсяограниченной, если
множество ее членов ограничено, т.е.
существует число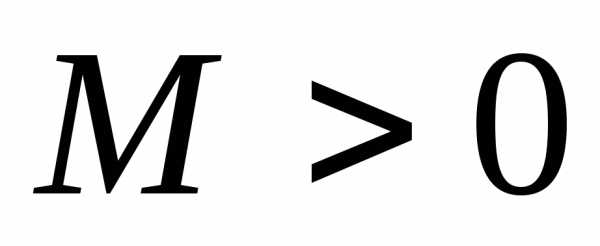 ,
такое, что.
Последовательность
,
такое, что.
Последовательность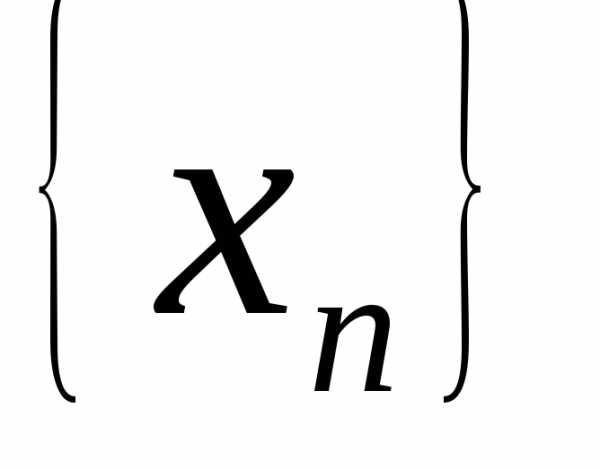 называетсяограниченной сверху (снизу), если существует
числоМ, такое, что.
называетсяограниченной сверху (снизу), если существует
числоМ, такое, что.
Если последовательность 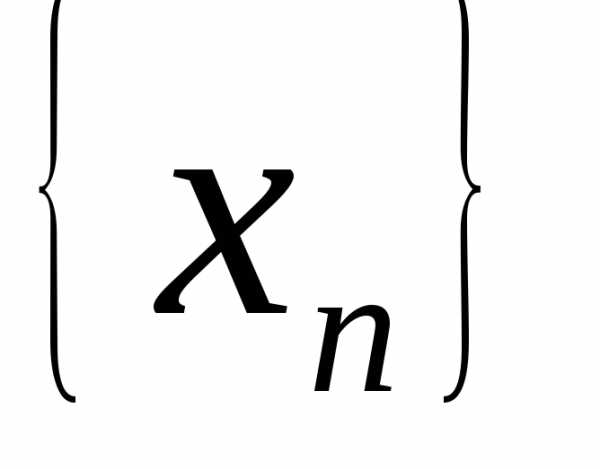 неограниченна, то для любого числа
неограниченна, то для любого числа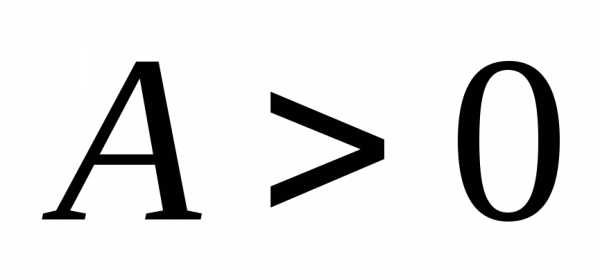 найдется номерnтакой, что
найдется номерnтакой, что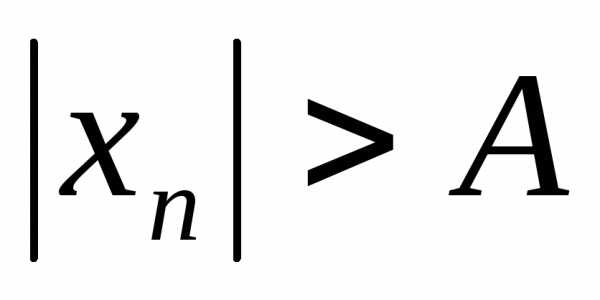 .
Ясно, что если последовательность
ограничена только снизу или только
сверху, то она неограниченна. Среди
неограниченных последовательностей
выберем бесконечно большие
последовательности.
.
Ясно, что если последовательность
ограничена только снизу или только
сверху, то она неограниченна. Среди
неограниченных последовательностей
выберем бесконечно большие
последовательности.
Определение 4. Последовательность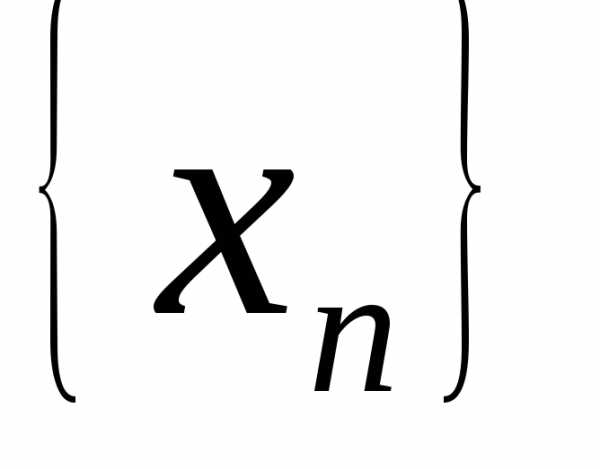 называетсябесконечно большой,
если для любого
называетсябесконечно большой,
если для любого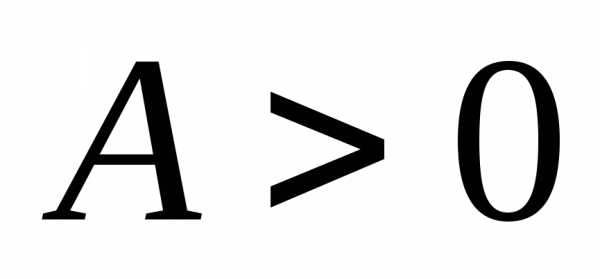 найдется номерN,
такой, что
найдется номерN,
такой, что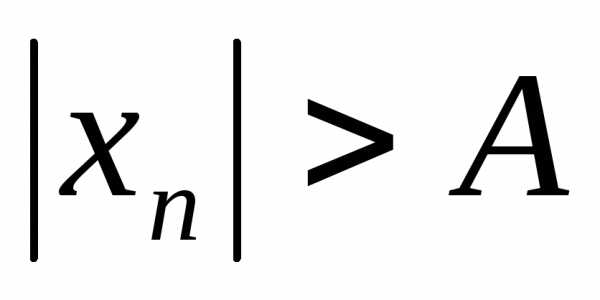 для всех
для всех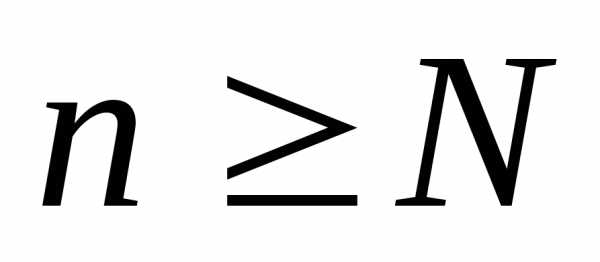 .
.
Всякая бесконечно большая последовательность неограниченна, но не всякая неограниченная последовательность бесконечно большая. Примером этого может служить последовательность .
Определение 5. Последовательность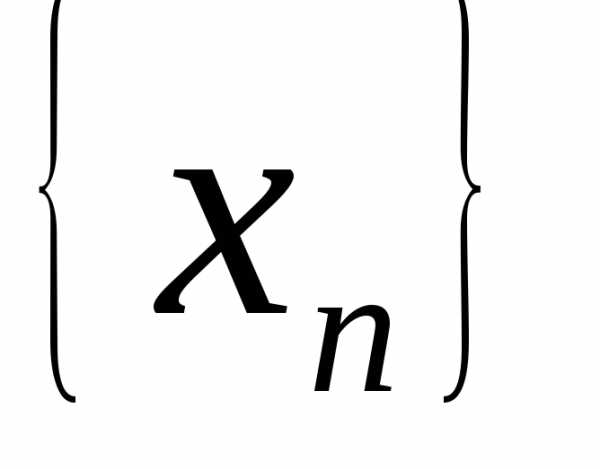 называетсябесконечно малой,
если для любого
называетсябесконечно малой,
если для любого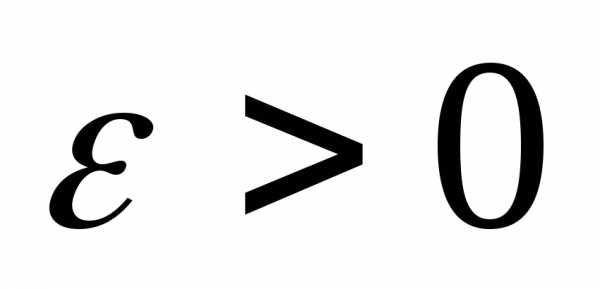 найдется номерN,
такой, что
найдется номерN,
такой, что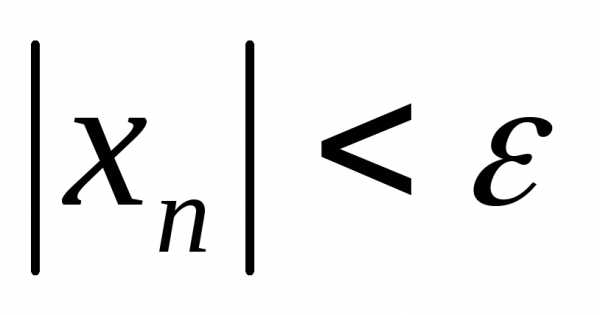 для всех
для всех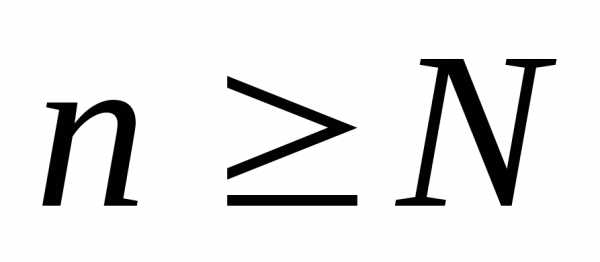 .
.
Установим основные свойства бесконечно малых последовательностей.
Теорема 1. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть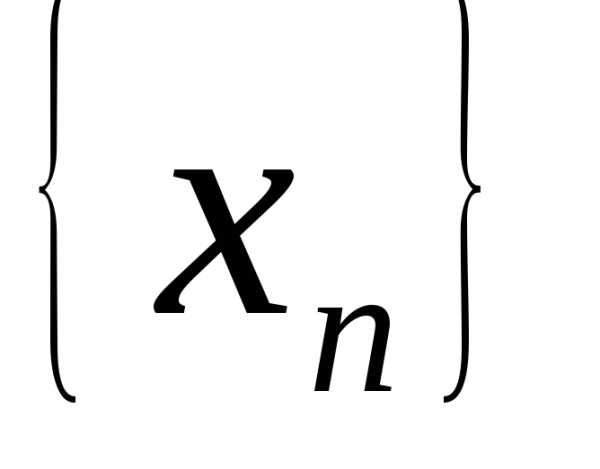 и– бесконечно малые последовательности.
Возьмем
и– бесконечно малые последовательности.
Возьмем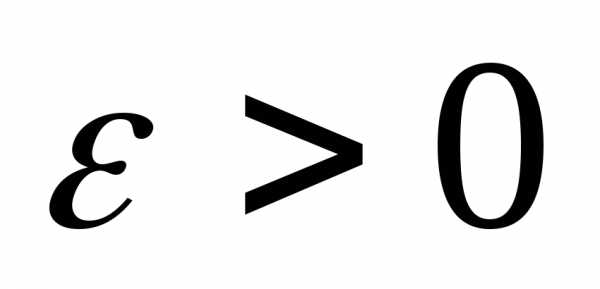 произвольно и положим
произвольно и положим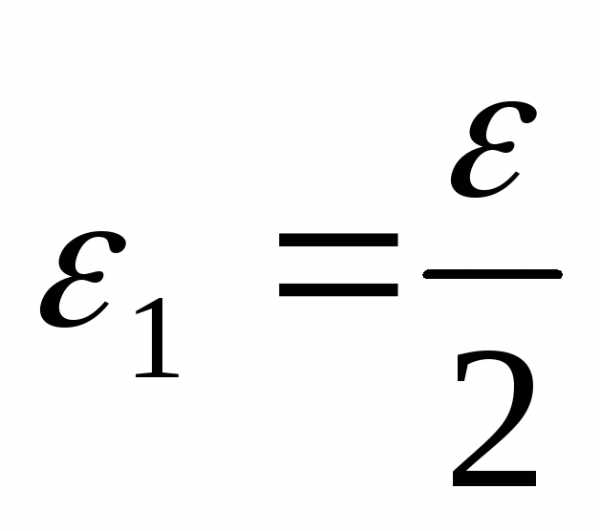 .
По определению 5 для
.
По определению 5 для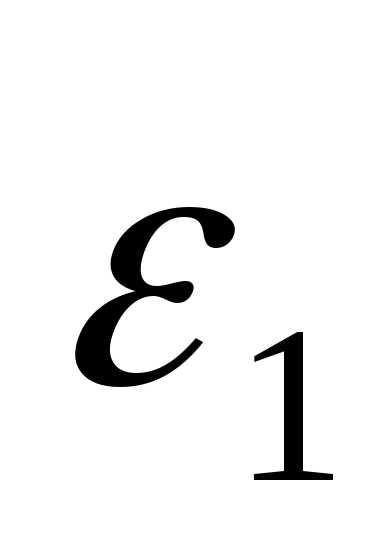 найдутся номера
найдутся номера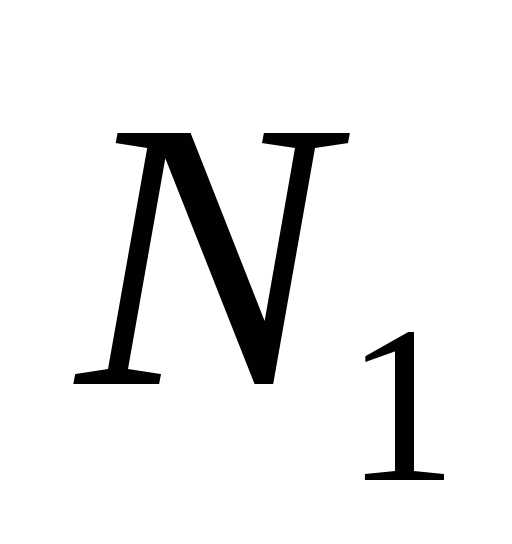 и
и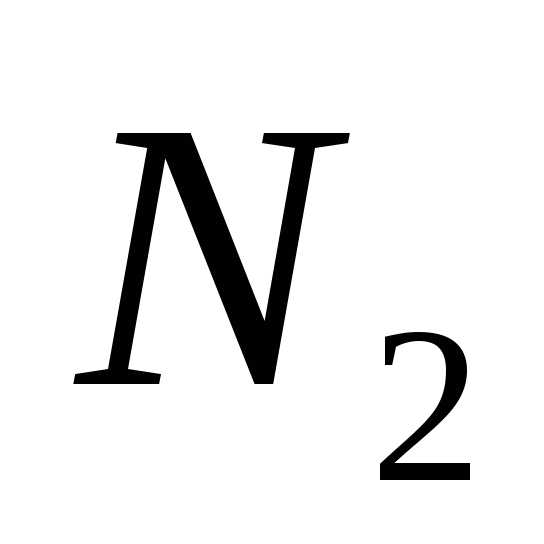 ,
такие, что
,
такие, что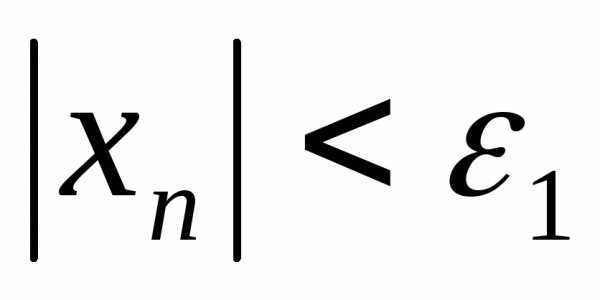 для всех
для всех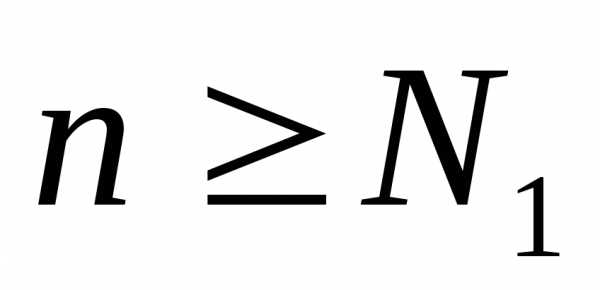 и
и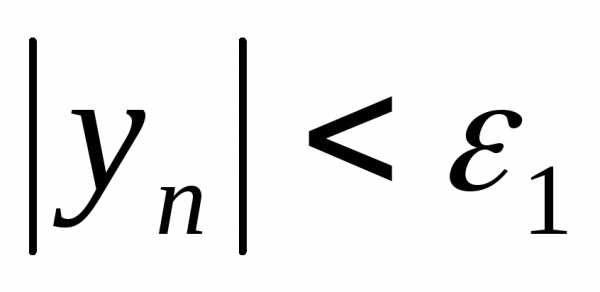 для всех
для всех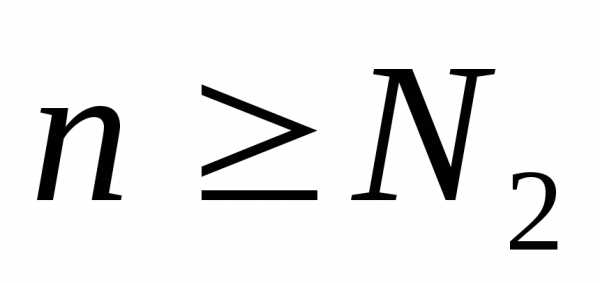 .
Положим.
Тогда для всех
.
Положим.
Тогда для всех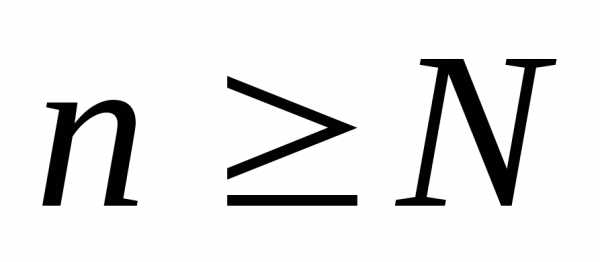 и по определению 5 последовательность
и по определению 5 последовательность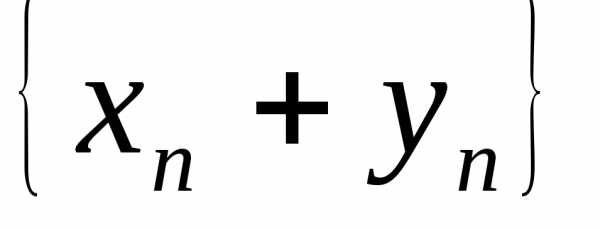 бесконечно
малая. Теорема доказана.
бесконечно
малая. Теорема доказана.
Аналогично доказываются
Теорема 2. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 3. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
(Можно поручить студентам доказать теоремы 2, 3 и следствие самостоятельно).
Теорема 4. Всякая бесконечно малая последовательность ограничена.
Доказательство. Пусть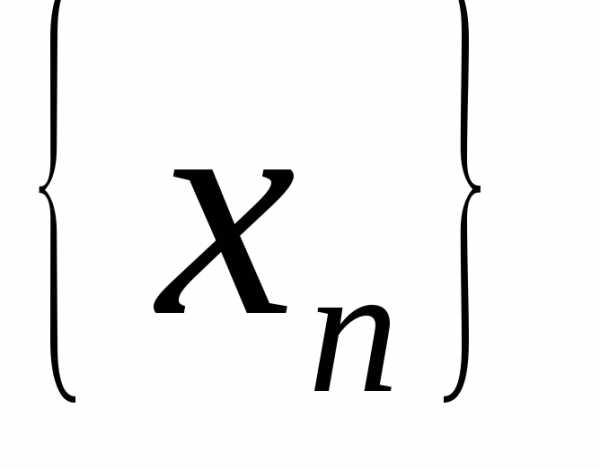 – бесконечно малая последовательность.
Положим
– бесконечно малая последовательность.
Положим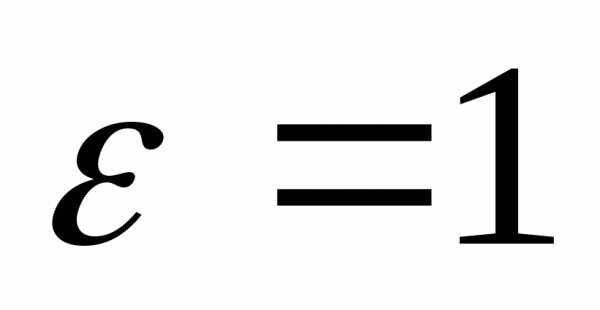 .
По определению 5 найдется номерN,
такой, что
.
По определению 5 найдется номерN,
такой, что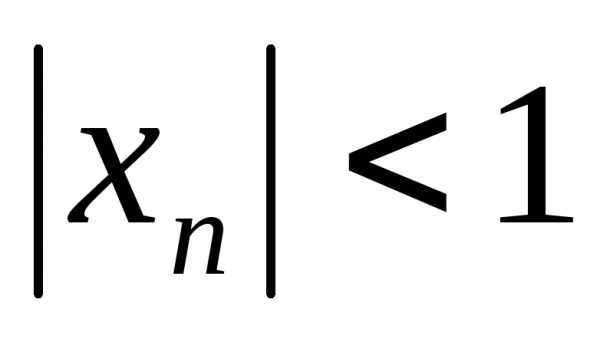 для всех
для всех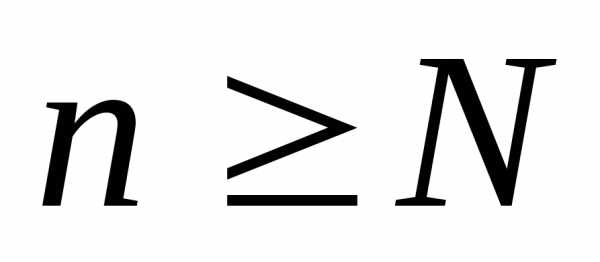 .
Обозначим.
Тогда
.
Обозначим.
Тогда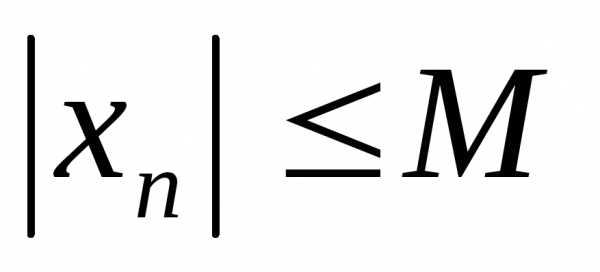 для всехn. Теорема
доказана.
для всехn. Теорема
доказана.
Следствие теорем 3и 4. Произведение двух (любого конечного числа) бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 5. Если все члены бесконечно
малой последовательности равны одному
и тому же числус, то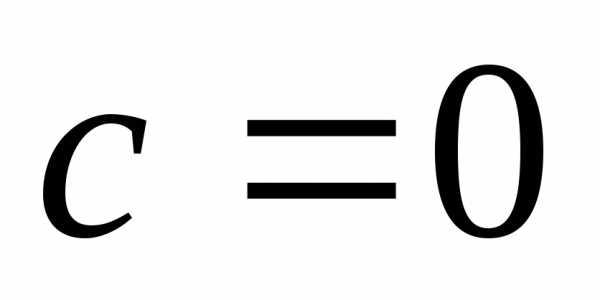 .
.
Доказательство. Предположим
противное, т.е. что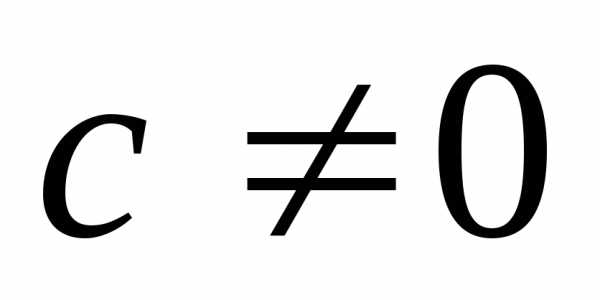 .
Возьмем
.
Возьмем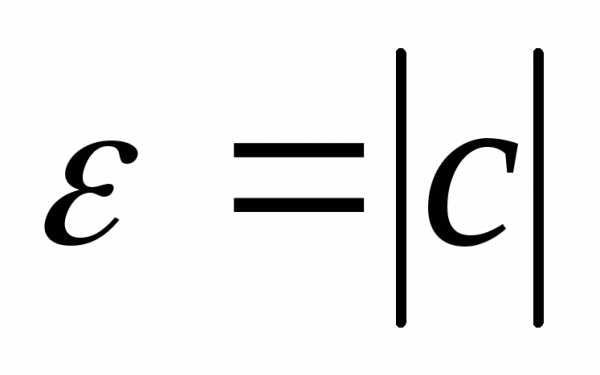 .
По определению 5 найдется номерN,
такой, что
.
По определению 5 найдется номерN,
такой, что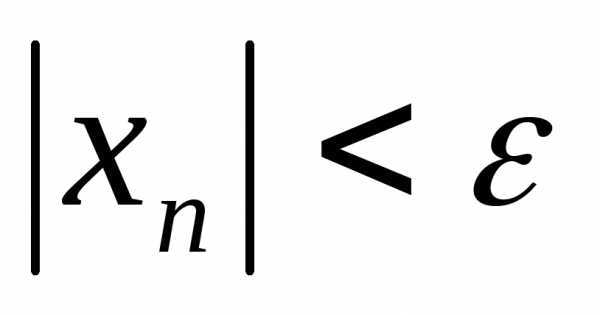 для всех
для всех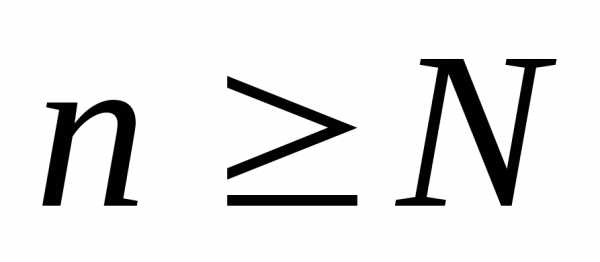 ,
т.е.
,
т.е.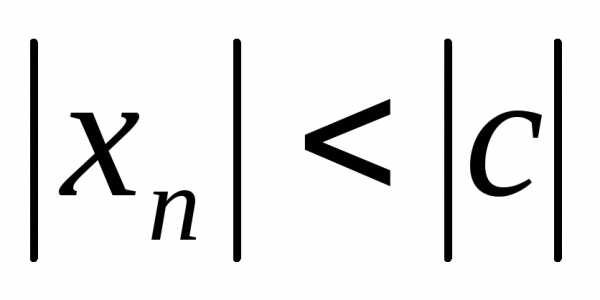 для всех
для всех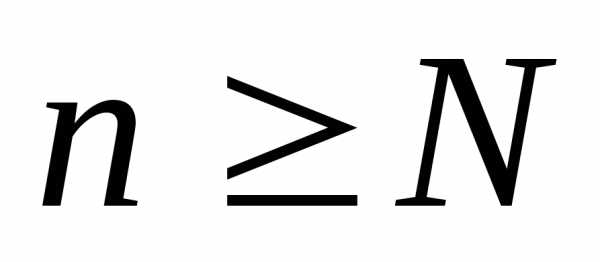 ,
а этого не может быть, так как
,
а этого не может быть, так как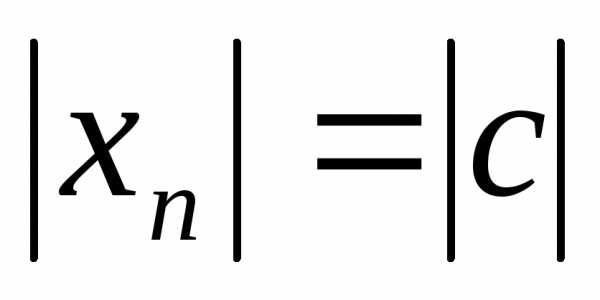 для всехn. Противоречие
доказывает утверждение теоремы.
для всехn. Противоречие
доказывает утверждение теоремы.
Теорема 6. Если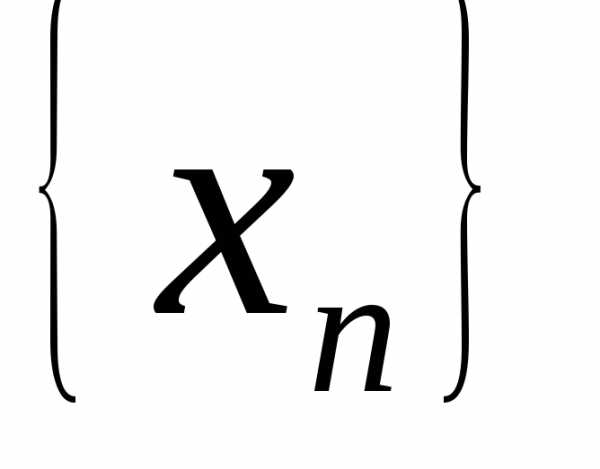 – бесконечно большая последовательность,
то
– бесконечно большая последовательность,
то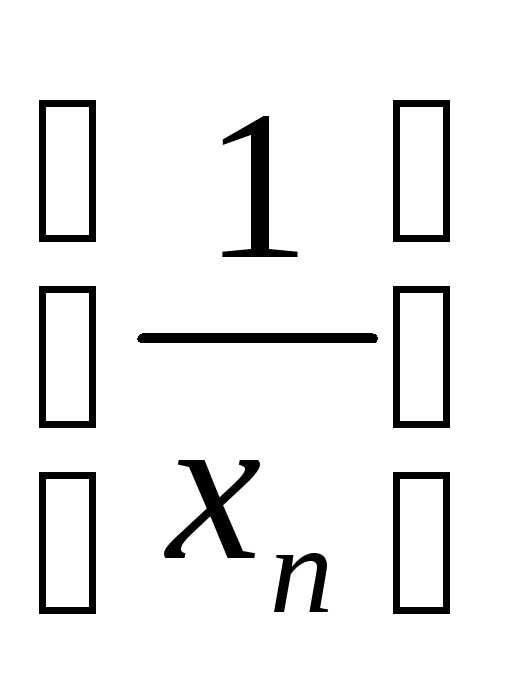 –
бесконечно малая последовательность.
–
бесконечно малая последовательность.
Доказательство. Возьмем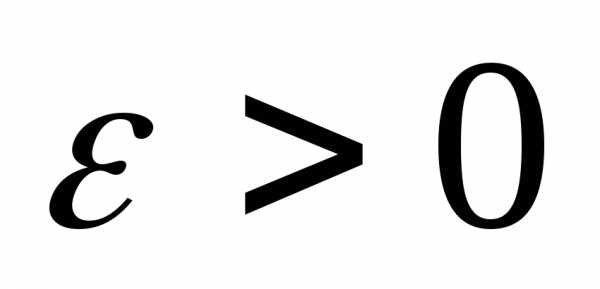 произвольно и положим
произвольно и положим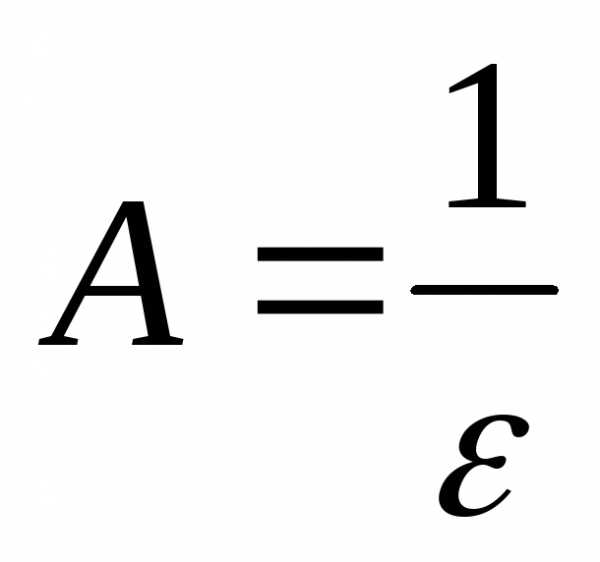 .
Тогда по определению 4 найдется номерN, такой, что
.
Тогда по определению 4 найдется номерN, такой, что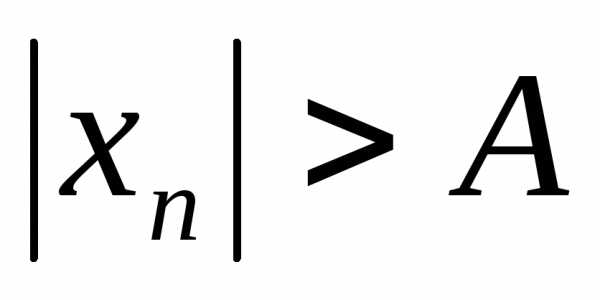 для всех значений
для всех значений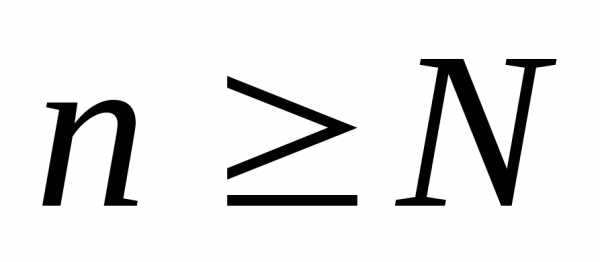 .
Отсюда
.
Отсюда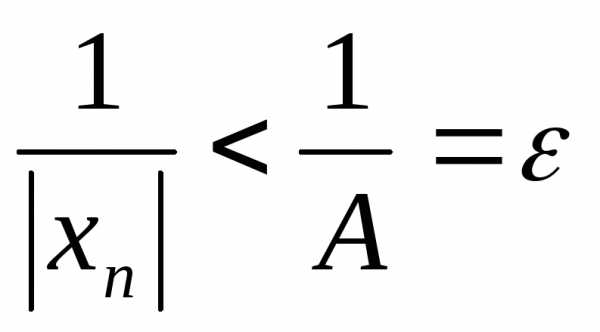 для всех
для всех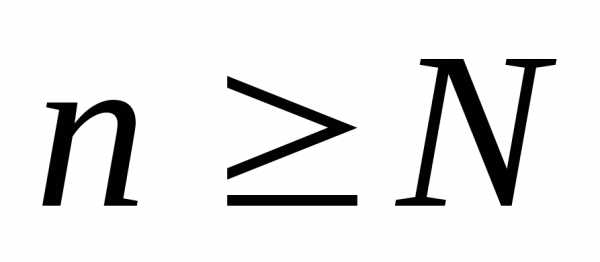 ,
т.е.
,
т.е.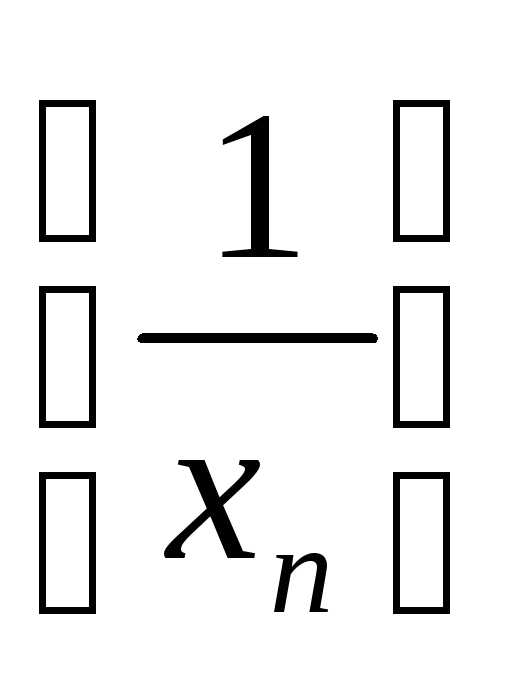 –
бесконечно малая последовательность
по определению 5. Теорема доказана.
–
бесконечно малая последовательность
по определению 5. Теорема доказана.
Теорема 7. Если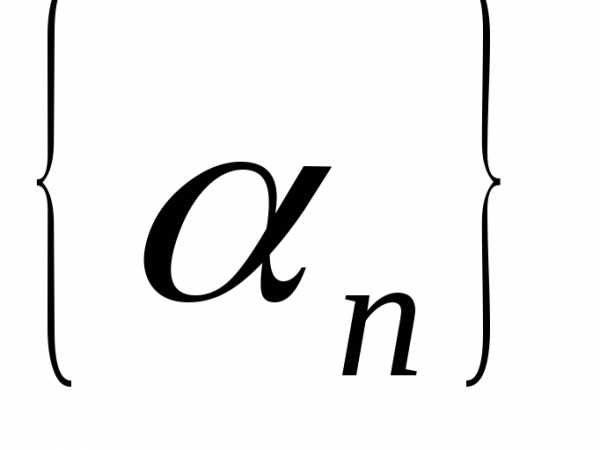 –
бесконечно малая последовательность
и все члены этой последовательности
отличны от нуля, то последовательность
–
бесконечно малая последовательность
и все члены этой последовательности
отличны от нуля, то последовательность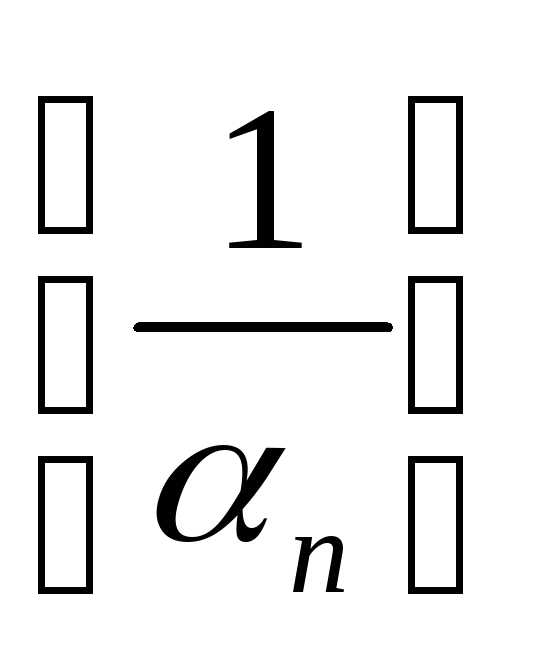 –
бесконечно большая (доказать
самостоятельно).
–
бесконечно большая (доказать
самостоятельно).
studfiles.net
Абсолютная величина — это… Что такое Абсолютная величина?
График вещественной функции Модуль и другие характеристики комплексного числаАбсолю́тная величина́ или мо́дуль числа — неотрицательное число, определение которого зависит от типа числа . Обозначается: .
В случае вещественного абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:
Обобщением этого понятия является модуль комплексного числа , также иногда называемый абсолютной величиной[1]. Он определяется по формуле:
Основные свойства
С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина означает расстояние между точками и и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.
Вещественные числа
Комплексные числа
Алгебраические свойства
Для любых имеют место следующие соотношения:
Как для вещественных, так и для комплексных имеют место соотношения:
История
Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.
В языках программирования
Поскольку эта функция вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа.
Обобщение
Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую . Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.
См. также
Примечания
dic.academic.ru
Абсолютная величина Википедия
График вещественной функции Модуль |z|{\displaystyle |z|} и другие характеристики комплексного числа z{\displaystyle z}Абсолю́тная величина́, или мо́дуль числа x{\displaystyle x} (в математике) — неотрицательное число, определение которого зависит от типа числа x{\displaystyle x}. Обозначается: |x|{\displaystyle |x|}.
В случае вещественного x{\displaystyle x} абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:
- |x|={ x,x⩾0−x, x<0{\displaystyle \ |x|={\begin{cases}\ \ x,&x\geqslant 0\\-x,&\ x<0\end{cases}}}
Обобщением этого понятия является модуль комплексного числа z=x+iy,{\displaystyle z=x+iy,} также иногда называемый абсолютной величиной[1]. Он определяется по формуле:
- |z|=|x+iy|=x2+y2{\displaystyle |z|=|x+iy|={\sqrt {x^{2}+y^{2}}}}
Основные свойства
С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина |x1−x2|{\displaystyle |x_{1}-x_{2}|} означает расстояние между точками x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.
Вещественные числа
- Область определения: (−∞;+∞){\displaystyle (-\infty ;+\infty )}.
- Область значений: [0;+∞){\displaystyle [0;+\infty )}.
- Функция чётная.
- Функция дифференцируема всюду, кроме нуля. В точке x=0{\displaystyle x=0} функция претерпевает излом.
Комплексные числа
Алгебраические свойства
Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие соотношения:
- |x|=x2=x⋅sgnx=max{x,−x}{\displaystyle \ |x|={\sqrt {x^{2}}}=x\cdot \operatorname {sgn} x={\rm {max}}\,\{x,\,-x\}} (см. Функция sgn(x)).
- a⩽|a|{\displaystyle a\leqslant |a|}
- −|a|⩽a{\displaystyle -|a|\leqslant a}.
- Квадрат модуля числа равен квадрату этого числа: |a|2=a2{\displaystyle |a|^{2}=a^{2}}
Как для вещественных, так и для комплексных a,b{\displaystyle a,b} имеют место соотношения:
История
Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.
В языках программирования
Поскольку эта функция вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа. В программе Wolfram Mathematica Abs[x].
Обобщение
Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую ‖x‖{\displaystyle \|x\|}. Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.
См. также
Примечания
wikiredia.ru
Абсолютное значение — число — Большая Энциклопедия Нефти и Газа, статья, страница 1
Абсолютное значение — число
Cтраница 1
Абсолютное значение числа, находящегося в регистре второго операнда, помещается на место первого. [1]
Разделим абсолютное значение чисел X и У с заменой операции вычитания делителя из делимого, или делителя из остатков операций сложения в модифицированном обратном оде, а операцию восстановления остатков — в модифицированном прямом коде. [2]
РОН передается абсолютное значение числа, а при загрузке отрицательной — число со знаком минус. Операции записи служат для передачи слов, символов ( байт), полуслов или совокупности слов из ОП в РОН. При этом состояние РОН не изменяется. Операции пересылки используются для перемещения полей переменной длины в ОП. При этом байты, составляющие поле, записываются в ячейки ОП, соответствующие другому полю. [3]
Интересно установить абсолютное значение чисел подобия и пределы их изменения в практических задачах техники. [4]
Нередко вместо абсолютных значений чисел циклов применяют относительные величины — частости. Это не меняет формы графиков и удобно при сопоставлении рядов различного объема. [5]
Разница в абсолютных значениях числа Ми, по нашим данным и расчетам Дайслера невелика, однако характер зависимости несколько иной. Это различие трудно объяснить, так как с методикой расчета Дайслера нам познакомиться не удалось. [6]
Команда LPR помещает абсолютное значение числа с фиксированной точкой, содержащегося в общем регистре второго операнда, в общий регистр первого операнда. Если исходное число отрицательное, то перед загрузкой оно преобразуется в положительное путем перехода к дополнительному коду. Если содержимое регистра второго операнда до выполнения команды LPR уже было положительным, то оно без изменений помещается в принимающий регистр. [7]
Так как логарифмируют абсолютные значения чисел, записанных в столбце 6, необходимо определить знак постоянной интегрирования С. По расположению графика относительно оси абсцисс судят о знаке С. Затем следует провести асимптоту к построенной логарифмической временной характеристике. Однако обычно проводят касательную к ней в некоторой точке, выбранной таким образом, чтобы наибольшая часть точек логарифмической характеристики возможно ближе прилегала к касательной. [9]
Что же касается большего абсолютного значения числа переноса К по сравнению с Na, то это обстоятельство отражает большую прочность связи Na — О. [10]
Если в кодировании положительных значений абсолютное значение числа тем больше, чем больше единиц в его записи, то для отрицательных значений нули и единицы как бы поменяются местами — и абсолютное значение числа тем больше, чем больше будет в записи нулей. [11]
Схема алгоритма определения максимального по абсолютному значению числа Лтах из набора трех заданных чисел А, А2, АЗ приведена на рис. 3.2. В алгоритме принята нумерация блоков по зонам. [12]
При работе с сильноосновными аниони-товыми мембранами абсолютные значения чисел переноса получаются больше, чем при работе со слабоосновными мембранами, но отношение чисел переноса гораздо выше на слабоосновных мембранах. В целях обогащения раствора мо-либдатом эффективнее применить, таким образом, сильноосновные мембраны, для наиболее полной сепарации более пригодны слабоосновные анионитовые мембраны. [14]
Это выражение является производящей функцией для абсолютных значений чисел Стирлинга первого рода ( — l) h ns ( n, k) ( разд. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Абсолютная величина | Математика | FANDOM powered by Wikia
Абсолютная величина или модуль, вещественного числа x есть расстояние от x до нуля.
Более точно: абсолютная величина x есть неотрицательное число, обозначаемое |x|, определяемое следующим образом: если x ≥ 0, то |x|=x; если x < 0, то |x| = −x. Для абсолютной величины имеют место следующие соотношения:
- |a| ≥ 0
- |a| = 0 тогда и только тогда, когда a = 0.
- |ab| = |a||b|
- $ |a^k| = |a|^k $ если $ a^k $ определено.
- неравенство треугольника
- |a+b| ≤ |a| + |b| или
- |a − b| ≥ ||a| − |b||
Альтернативные определенияПравить
- $ |x|={\rm max}\,\{x,\,-x \} $, то есть модуль числа $ \!x $ есть максимальное их двух чисел $ \!x $ и $ \!(-x) $,
- $ |x|=\sqrt{x^2} $.
Абсолютная величина комплексного числаПравить
Абсолютная величина или модуль комплексного числа z = x + iy (x и y — вещественные числа) — неотрицательное число (обозначаемое |z|), определяемое по формуле $ |z|=\sqrt{x^2+y^2} $.
Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля введен в 19 веке Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в 19 веке.
ca:Valor absolut cs:Absolutní hodnotaeo:Absoluta valoroet:Absoluutväärtus fa:قدر مطلق (ریاضی)gl:Valor absoluto he:ערך מוחלט hu:Abszolútérték-függvény is:Algildinl:Absolute waarde no:Absoluttverdi pl:Wartość bezwzględnask:Absolútna hodnota sl:Absolutna vrednost sr:Апсолутна вредност sv:Absolutbelopp th:ค่าสัมบูรณ์uk:Абсолютна величина vi:Giá trị tuyệt đối
ru.math.wikia.com
