2 синус х 1 – Sin x 1 2 — Помогите пожалуйста) ) sin x= (-1/2) Синус икс = (минус одна вторая). — 22 ответа
sin x = 1 / 2 чему равен х
Задание.
Найти значение х при .
Решение.
Найти значение аргумента функции синус, при котором он равен какому-либо значению, означает определить, при каких аргументах значение синуса будет именно таким, как указано в условии.
В данном случае нам нужно выяснить, при каких значениях значение синуса будет равным 1/2. Это можно сделать несколькими способами.
Например, использовать график функции синус, по которому определить при каких значениях х функция синус будет равна 1/2.
Другим способом является использование тригонометрического круга. Напомню, что значения синусов лежат на оси Оу.
Самым распространенным способом является обращение к таблице значений синуса, особенно если речь идет о таких стандартных для этой функции значениях, как 1/2.
Во всех случаях не стоит забывать об одном из важнейших свойств синуса — о его периоде.
Найдем в таблице значение 1/2 для синуса и посмотрим какие аргументы ему соответствуют. Интересующие нас аргументы равны Пи / 6 и 5Пи / 6.
Возьмем второе значение, и проделаем те же шаги, что и в предыдущем случае:
Полным решением исходного уравнения будет:
и
q может принимать значение любого целого числа.
Ответ. и , q — целое.
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .
Отметим на оси ординат точку с ординатой :
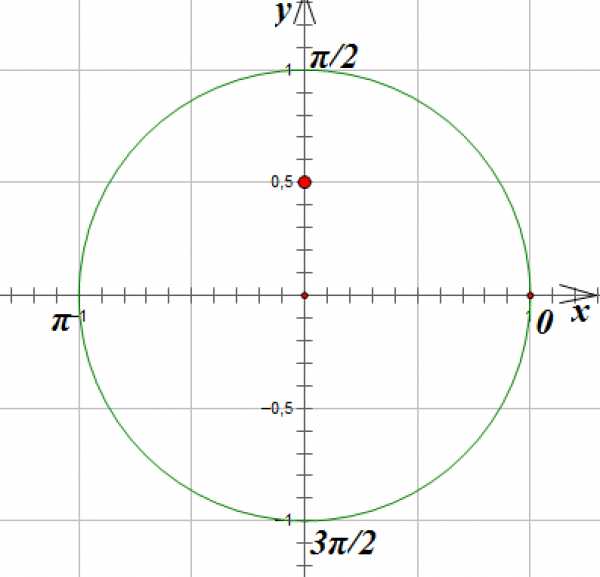
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату. Эти точки соответствуют углам поворота на и радиан:
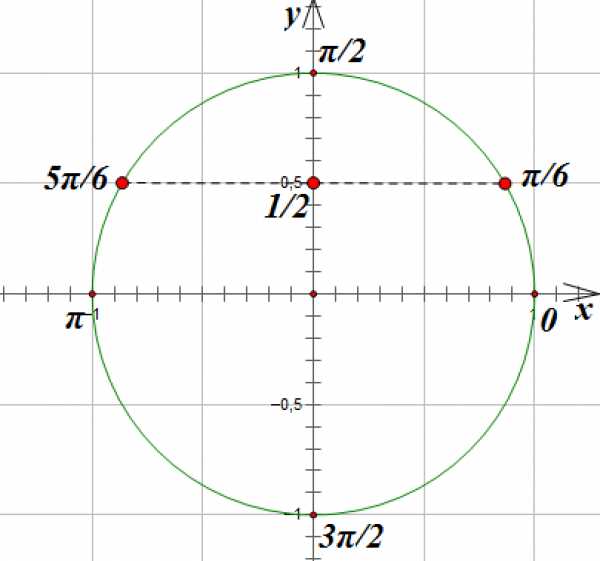
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем ( то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
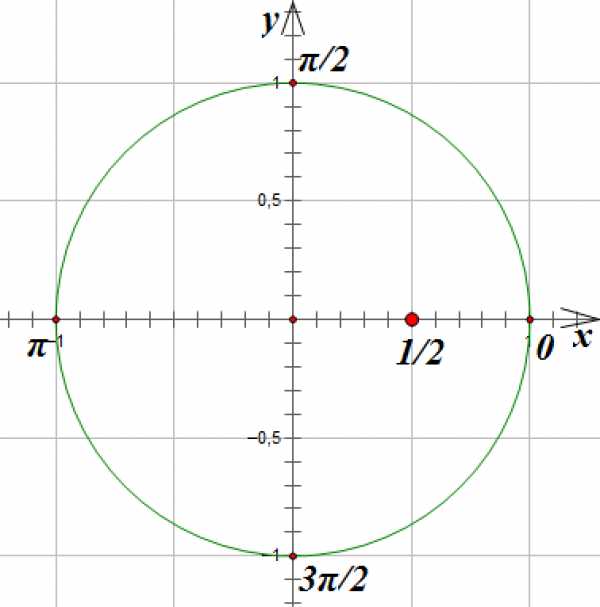
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
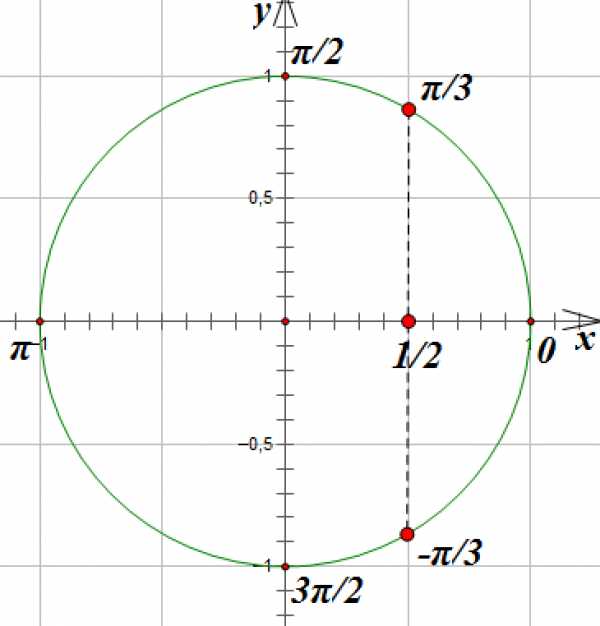
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
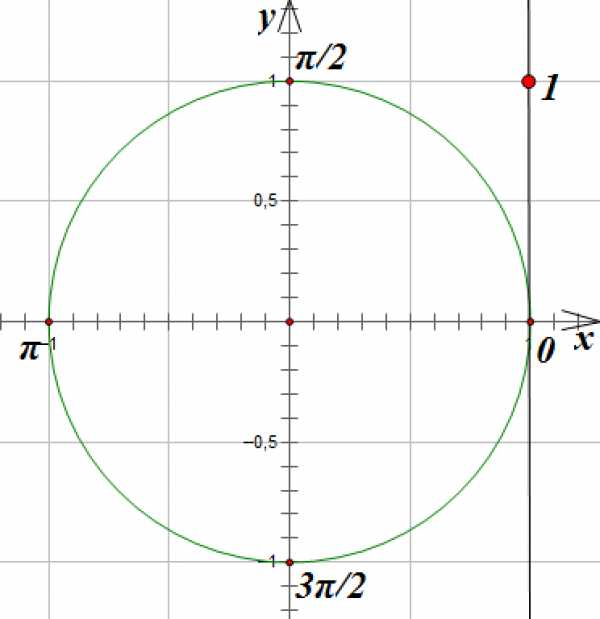
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
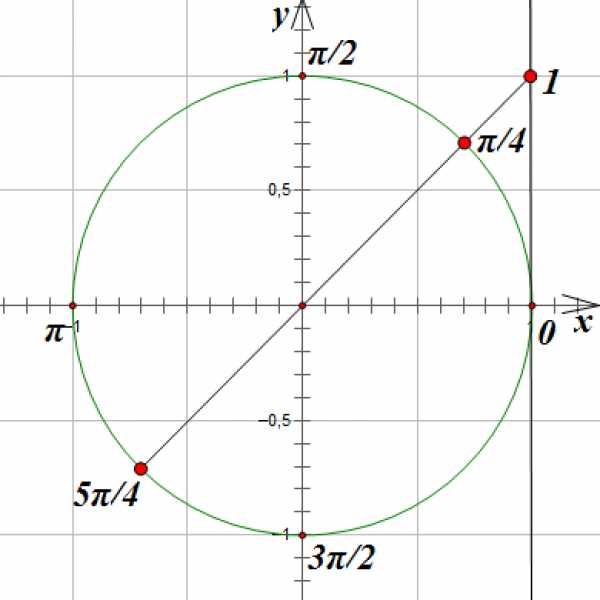
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
,
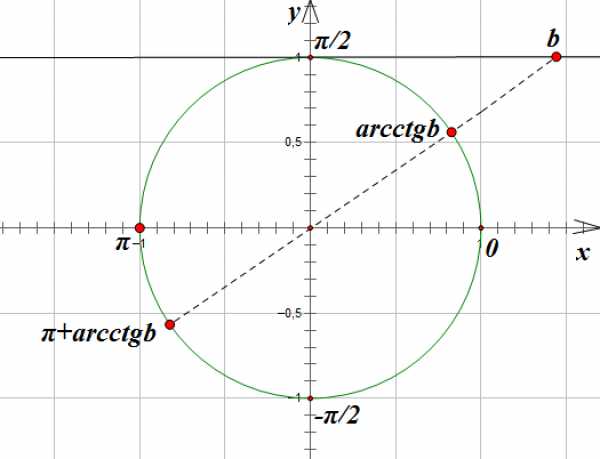
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
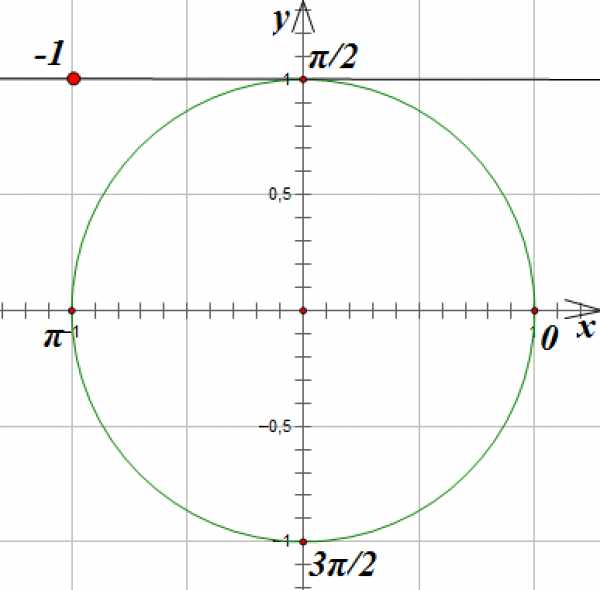
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
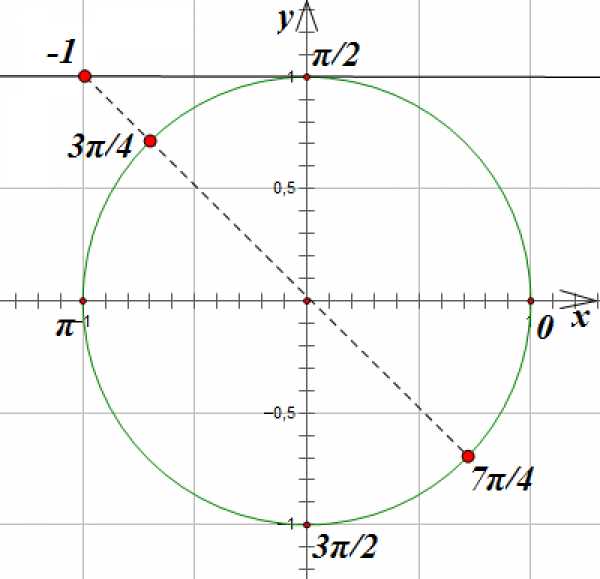
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
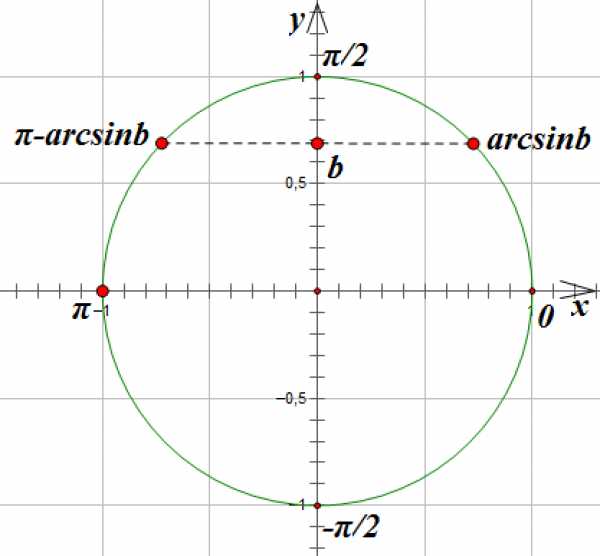
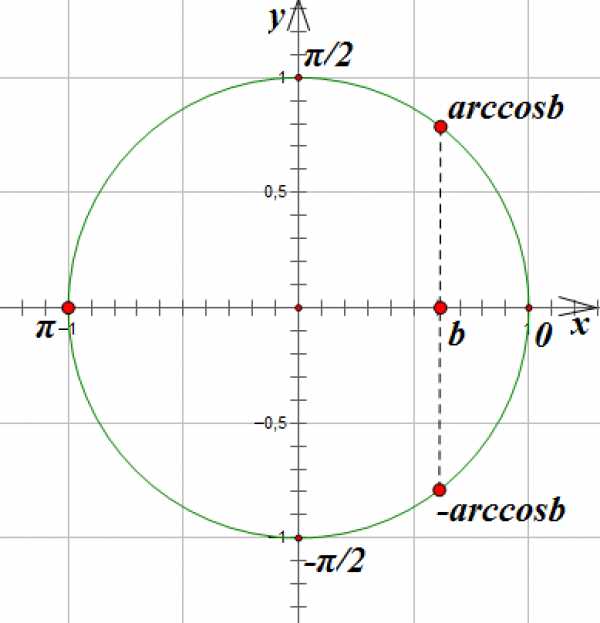
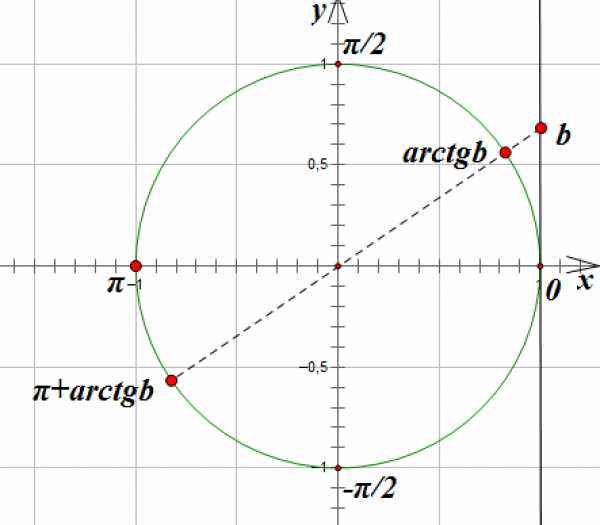
ОСОБЫЕ РЕШЕНИЯ:
1
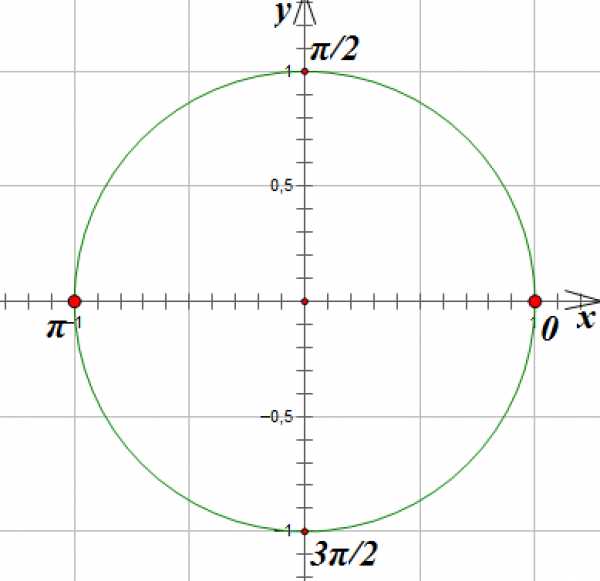
Отметим на окружности точки, ордината которых равна 0:
2.
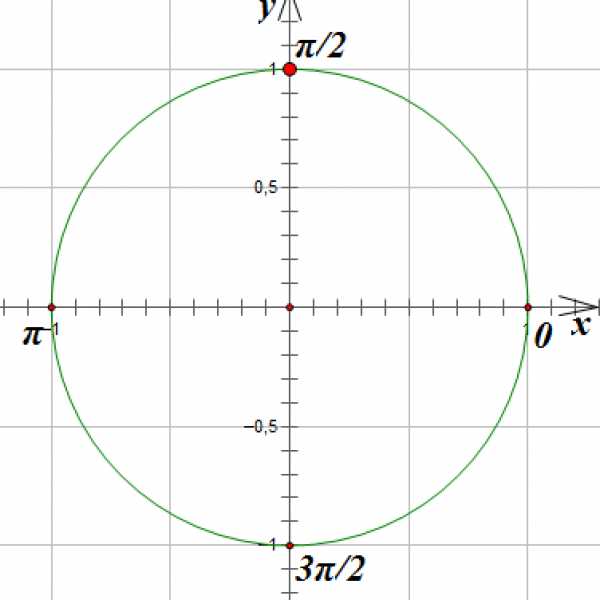
Отметим на окружности единственную точку, ордината которой равна 1:
3.
Отметим на окружности единственную точку, ордината которой равна -1:
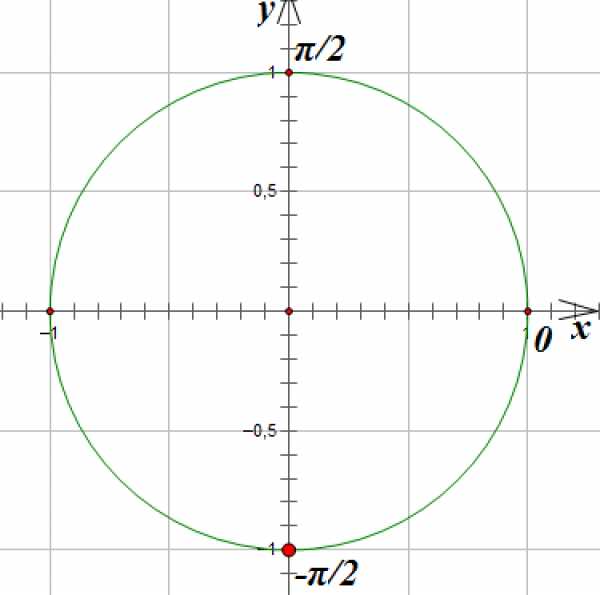
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
4.
Отметим на окружности точки, абсцисса которых равна 0:
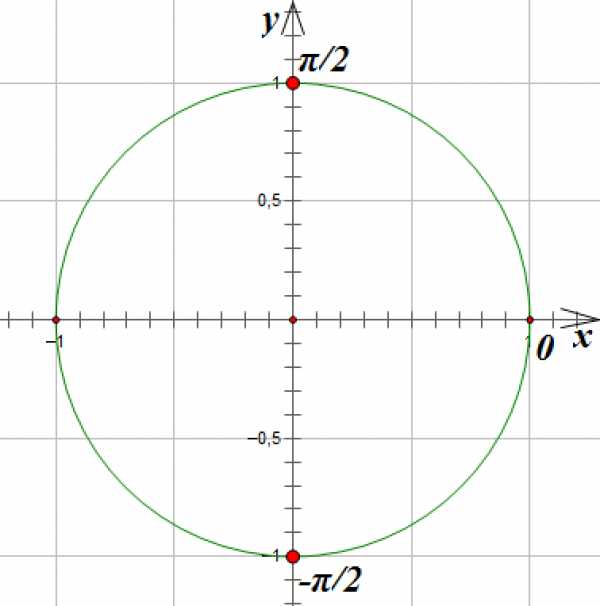
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
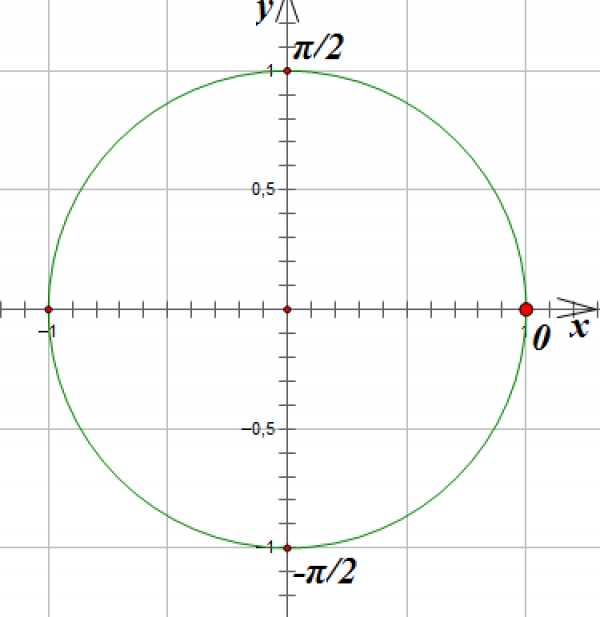
6.
Отметим на окружности единственную точку, абсцисса которой равна -1:
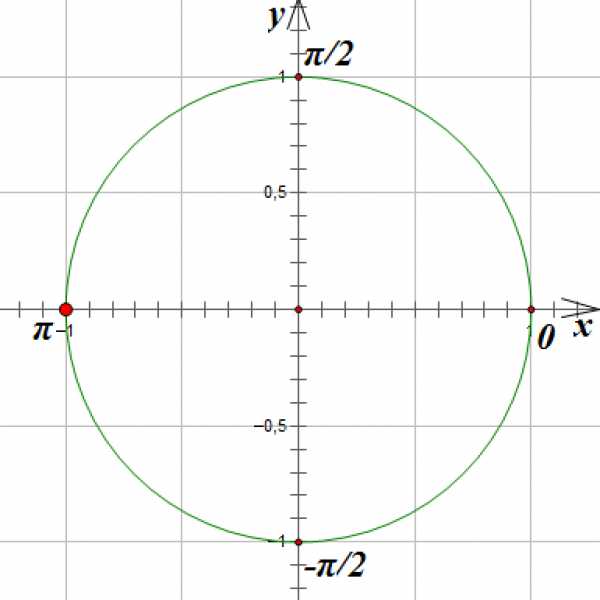
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
. Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и Задание 13»
ege-ok.ru
100 формул / Все формулы по тригонометрии
Основные тригонометрические тождества
Формулы, связывающие тригонометрические функции одного и того же аргумента:
\(sin^2x+cos^2x=1\)
\(tgx= \frac{sinx}{cosx}\)
\(ctgx= \frac{cosx}{sinx}\)
\(tgxctgx=1\)
\(tg^2x+1= \frac{1}{cos^2x}\)
\(ctg^2x+1= \frac{1}{sin^2x}\)
Формулы двойного аргумента (угла)
\(sin2x=2cosxsinx\)
\(sin2x= \frac{2tgx}{1+tg^2x}= \frac{2ctgx}{1+ctg^2x} = \frac{2}{tgx+ctgx}\)
\(cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x\)
\(cos2x= \frac{1-tg^2x}{1+tg^2x}= \frac{ctg^2x-1}{ctg^2x+1}= \frac{ctgx-tgx}{ctgx+tgx} \)
\(tg2x= \frac{2tgx}{1-tg^2x}= \frac{2ctgx}{ctg^2x-1}= \frac{2}{ctgx-tgx}\)
\(ctg2x= \frac{ctg^2x-1}{2ctgx}= \frac{ctgx-tgx}{2}\)<br><br>
Формулы тройного аргумента (угла)
\(sin3x=3sinx-4sin^3x\)
\(cos3x=4cos^3x-3cosx\)
\(tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}\)
\(ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}\)
Формулы половинного аргумента (угла)
\(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\)
\(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\)
\(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\)
\(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\)
\(tg \frac{x}{2}= \frac{1-cosx}{sinx}= \frac{sinx}{1+cosx}\)
\(ctg \frac{x}{2}= \frac{1+cosx}{sinx}= \frac{sinx}{1-cosx}\)
Формулы квадратов тригонометрических функций
\(sin^2x= \frac{1-cos2x}{2}\)
\(cos^2x= \frac{1+cos2x}{2}\)
\(tg^2x= \frac{1-cos2x}{1+cos2x}\)
\(ctg^2x= \frac{1+cos2x}{1-cos2x}\)
\(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\)
\(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\)
\(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\)
\(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\)
Формулы кубов тригонометрических функций
\(sin^3x= \frac{3sinx-sin3x}{4}\)
\(cos^3x= \frac{3cosx+cos3x}{4}\)
\(tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}\)
\(ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}\)
Формулы тригонометрических функций в четвертой степени
\(sin^4x= \frac{3-4cos2x+cos4x}{8}\)
\(cos^4x= \frac{3+4cos2x+cos4x}{8}\)
Формулы сложения аргументов
\(sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta\)
\(cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta \)
\(tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}\)
\(ctg(\alpha + \beta)= \frac{-1 + ctg \alpha ctg \beta }{ctg \alpha + ctg \beta}\)
\(sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta\)
\(cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta\)
\(tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}\)
\(ctg(\alpha — \beta)= \frac{-1 — ctg \alpha ctg \beta }{ctg \alpha — ctg \beta}\)
Формулы суммы тригонометрических функций
\(sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}\)
\(cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}\)
\(tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta} \)
\(ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{sin \alpha sin \beta}\)
\((sin\alpha + cos\alpha)^2= 1+sin2\alpha \)
Формулы разности тригонометрических функций
\(sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}\)
\(cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}\)
\(tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta} \)
\(ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}\)
\((sin\alpha — cos\alpha)^2= 1-sin2\alpha \)
Формулы произведения тригонометрических функций
\(sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}\)
\(sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}\)
\(cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}\)
\(tg\alpha \cdot tg\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} = \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta}\)
\(ctg\alpha \cdot ctg\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} = \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta}\)
\(tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}\)
100formul.ru
sin 2x = 1/2 решение
Доброй ночи!
Уравнения вида, которое вы предоставили, не такое трудное, как Вам могло показаться. Давайте попробуем решить Ваше уравнение sin 2х = 1/2. Но первым делом нам следует подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло, так как вид особо не изменился. Но чтоб решать такие уравнения, то надо использовать известное правило, которое выглядит так:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Но у нас будет не просто х, а двойной:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Чтоб найти х надо каждый член поделить на два и из этого получим следующее:
Ответ:
ru.solverbook.com
sin 2x = 1 решение
Добрый вечер!
Уравнения вида, которое вы предоставили, не такое трудное, как Вам могло показаться. Давайте попробуем решить Ваше уравнение sin 2х = 1. Но первым делом нам следует подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло, так как вид особо не изменился. Но чтоб решать такие уравнения, то надо использовать известное правило, которое выглядит так:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Но у нас будет не просто х, а двойной:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Чтоб найти х надо каждый член поделить на два и из этого получим следующее:
Ответ:
ru.solverbook.com
Уравнение sin x = a
Значения синуса заключены в промежутке [-1; 1], т.е. -1 ≤ sin α ≤ 1. Поэтому если |а| > 1, то уравнение sin x = a не имеет корней. Например, уравнение sin x = 2 корней не имеет.
Обратимся к некоторым задачам.
Задача 1.
Решить уравнение sin x = 1/2.
Решение.
Отметим, что sin x – это ордината точки единичной окружности, которая получена в результате поворота точки Р (1; 0) на угол х вокруг начала координат.
Ордината, равная ½, присутствует у двух точек окружности М1 и М2.
Так как 1/2 = sin π/6, то точка М1 получается из точки Р (1; 0) посредством поворота на угол х1 = π/6, а также на углы х = π/6 + 2πk, где k = +/-1, +/-2, …
Точка М2 получается из точки Р (1; 0) в результате поворота на угол х2 = 5π/6, а также на углы х = 5π/6 + 2πk, где k = +/-1, +/-2, …, т.е. на углы х = π – π/6 + 2πk, где k = +/-1, +/-2, ….
Итак, все корни уравнения sin х = 1/2 можно найти по формулам х = π/6 + 2πk, х = π – π/6 + 2πk, где k € Z.
Эти формулы могут объединиться в одну: х = (-1)n π/6 + πn, где n € Z (1).
Действительно, если n – четное число, т.е. n = 2k, то из формулы (1) получаем х = π/6 + 2πk, а если n – нечетное число, т.е. n = 2k + 1, то из формулы (1) получаем х = π – π/6 + 2πk.
Ответ. х = (-1)n π/6 + πn, где n € Z.
Задача 2.
Решить уравнение sin x = -1/2.
Решение.
Ординату -1/2 имеют две точки единичной окружности М1 и М2, где х1 = -π/6, х2 = -5π/6. Следовательно, все корни уравнения sin x = -1/2 можно найти по формулам х = -π/6 + 2πk, х = -5π/6 + 2πk, k € Z.
Эти формулы мы можем объединить в одну: х = (-1)n (-π/6) + πn, n € Z (2).
Действительно, если n = 2k, то по формуле (2) получаем х = -π/6 + 2πk, а если n = 2k – 1, то по формуле (2) находим х = -5π/6 + 2πk.
Ответ. х = (-1)n (-π/6) + πn, n € Z.
Таким образом, каждое из уравнений sin x = 1/2 и sin x = -1/2 имеет бесконечное множество корней.
На отрезке -π/2 ≤ х ≤ π/2 каждое из этих уравнений имеет только один корень:
х1 = π/6 – корень уравнения sin x = 1/2 и х1 = -π/6 – корень уравнения sin x = -1/2.
Число π/6 называют арксинусом числа 1/2 и записывают: arcsin 1/2 = π/6; число -π/6 называют арксинусом числа -1/2 и пишут: arcsin (-1/2) = -π/6.
Вообще уравнение sin x = а, где -1 ≤ а ≤ 1, на отрезке -π/2 ≤ х ≤ π/2 имеет лишь один корень. Если а ≥ 0, то корень заключен в промежутке [0; π/2]; если а < 0, то в промежутке [-π/2; 0). Этот корень называют арксинусом числа а и обозначают arcsin а.
Таким образом, арксинусом числа а € [–1; 1] называется такое число а € [–π/2; π/2], синус которого равен а.
аrcsin а = α, если sin α = а и -π/2 ≤ х ≤ π/2 (3).
Например, аrcsin √2/2 = π/4, так как sin π/4 = √2/2 и – π/2 ≤ π/4 ≤ π/2;
аrcsin (-√3/2) = -π/3, так как sin (-π/3) = -√3/2 и – π/2 ≤
– π/3 ≤ π/2.
Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что корни уравнения sin х = а, где |а| ≤ 1, выражаются формулой
х = (-1)n аrcsin а + πn, n € Z (4).
Также мы можем доказать, что для любого а € [-1; 1] справедлива формула аrcsin (-а) = -аrcsin а.
Из формулы (4) следует, что корни уравнения
sin х = а при а = 0, а = 1, а = -1 можно находить по более простым формулам:
sin х = 0 х = πn, n € Z (5)
sin х = 1 х = π/2 + 2πn, n € Z (6)
sin х = -1 х = -π/2 + 2πn, n € Z (7)
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
sin 2
Единичная окружность помогает понять, чему равны sin 1, sin 2, sin 3, sin 4, sin 5, sin 6.
Итак, речь идет об углах в радианах. 1 радиан — это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, 5 и 6 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу. Впрочем, если вспомнить, что п приближенно равно 3,14, задача существенно упростится.
Рисунок позволяет наглядно определять приблизительные значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их.
Поскольку синус — это ордината соответствующей точки на единичной окружности (как это легко запомнить — здес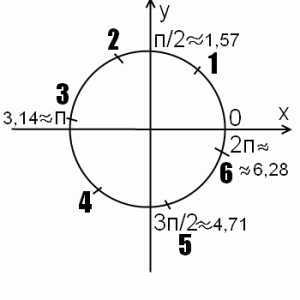
ь), то для нахождения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6 достаточно определить значение y в точках 1, 2, 3, 4, 5 и 6 радиан.
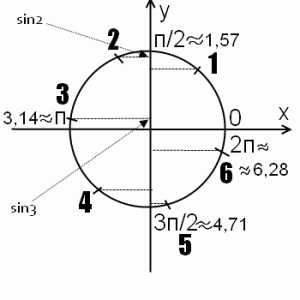Поскольку синус — это y, то вверху, над осью x, синус принимает положительные значения. Поэтому sin 1>0, sin 2>0, sin 3>0.
Соответственно внизу синус отрицателен: sin 4<0, sin 5<0, sin 6<o. Поэтому легко сравнить sin2 и sin4, например: sin2>sin4, ведь любое положительное число больше любого отрицательного.
Если требуется сравнить значения синуса одного знака, например, sin2 и sin3, то исходя из геометрических соображений, sin2>sin3.
Если нужно уточнить, чему равен 1 радиан, 2, 3, 4, 5 и 6 радиан в градусах, то приближенные значения таковы:
Приближенно чему равен синус 1, синус 2 и синус 3, можно узнать по таблицам Брадиса:
Используя геометрические соображения, можно найти и приблизительные значения углов, больших 6 радиан.
www.uznateshe.ru