12 натуральное число – CGI script error

12 (число) | Математика | FANDOM powered by Wikia

12 (двенадцать) — натуральное число между 11 и 13. Также обозначается словом дюжина. 12² = 144 в старину называлось гроссом, а 12³ = 1728 называлось массой.

Файл:Dodecahedron.jpg Файл:Rhombicdodecahedron.jpg

Геометрия Править

Химия, физика, астрономия Править

• Атомный номер магния
• Стандартная Модель физики элементарных частиц выделяет:
  • 12 лептонов, включая античастицы: $ e^-/e^+, \nu_e/\overline\nu_e, \mu^-/\mu^+, \nu_\mu/\overline\nu_\mu, \tau^-/\tau^+, \nu_\tau/\overline\nu_\tau $
  • 12 кварков, включая античастицы: $ u/\overline u, d/\overline d, s/\overline s, c/\overline c, b/\overline b, t/\overline t $
  • 12 бозонов: фотон, 3 тяжёлых бозона слабого взаимодействия ($ W^\pm, Z\,\! $), 8 глюонов
• Две двенадцатигранные формы кристаллов кубической кристаллографической системы: ромбододекаэдр и пентагондодекаэдр
• 1 моль определяется как количество атомов в 12 граммах изотопа углерода $ {}^{12}C $
• 1 атомная единица массы (а. е. м.) составляет 1/12 массы атома изотопа углерода $ {}^{12}C $
• Двенадцатый спутник Юпитера — Лиситея (Лизистея)
• Астероид 12 Виктория назван в честь древнеримской богини победы, но подразумевалась также и королева Великобритании Виктория.
• Шаровое скопление M12 в Змееносце.
• Звезда Тау Кита (Tau Ceti) распложена в 12 световых годах от Земли
• На Земле год состоит из 12 месяцев.

Биология, медицина, психология Править

История, мифология Править

Файл:Leonardo da Vinci (1452-1519) — The Last Supper (1495-1498).jpg
• У Иисуса Христа было 12 учеников, впоследствии все они, за исключением Иуды Искариота, стали апостолами. Вместо него 12 апостолом стал Матфий
• Было 12 столпов манихейской веры
• Храм Соломона делился на 12 частей
• 12 сыновей Иакова основали 12 колен Израилевых (Быт 49.28)
• В буддизме процесс перерождения живых существ, представлял собой «колесо», образуемое 12 ступенями
• Собор Двенадцати Апостолов — собор в Кремле (до 1681 церковь Апостола Филиппа)
• Когда Аллах послал Мусе откровение ударить по морю посохом, море расступилось, образовав 12 проходов
• Звезда Давида имеет 12 углов
• Двунадесятые праздники — 12 важнейших христианских праздников в православии
• В христианской традиции двенадцатая ночь после Рождества — праздник Богоявления: с 5 на 6 января по григорианскому календарю и с 18 на 19 января по юлианскому
• 12 — одно из пяти возможных количеств куполов в православном храме (1, 3, 5, 7, 12)
• еврейская девочка проходит обряд «Бат-Мицва» в возрасте двенадцати лет

Литература и искусствоПравить

Литература Править

Художественные фильмы Править

Телевидение Править

Музыка Править

Файл:Klaviatur.png

Живопись Править

Лингвистика и языки Править

Запись числа в других системах письма Править

Право, законодательство Править

Файл:Wall clock.jpg
• События
• События, праздники, дни рождения и смерти известных людей:

12 января | 12 февраля | 12 марта | 12 апреля | 12 мая | 12 июня | 12 июля | 12 августа | 12 сентября | 12 октября | 12 ноября | 12 декабря

Файл:Telephone-keypad.png
• В таблице символов ASCII и Юникод под номером 12 стоит управляющий символ FF (Шаблон:Lang — подача страницы) предписывающий принтеру перейти к началу следующей страницы
• 12 функциональных клавиш на клавиатуре компьютера (F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12)
• 12 кнопок на телефоне с кнопочным набором (1, 2, 3, 4, 5, 6, 7, 8, 9, 0, *, #)
• 12 вольт — наиболее распространённое номинальное бортовое напряжение на автомобиле, аккумуляторной батареи и напряжение питания многих слаботочных устройств.
• В самых мощных автомобильных двигателях 12 цилиндров
• Метровый диапазон телевизионного вещания разбит на 12 каналов.

Модели техники Править

Файл:Be-12P-200.jpg

Автотрассы Править

Единицы измерения Править

Денежные системы Править

В других областях Править

• 12 данов в дзюдо.
• 12 звёзд расположены по кругу на флаге Европейского Союза.
• В школах многих стран обучение длится 12 лет (обычно с 5 до 17 или с 6 до 18 лет).
• K-12 в США и Канаде — аббревиатура, обозначающая школьное образование.
• Болельщиков, поддерживающих футбольную команду, часто называют «12-м игроком»

Шаблон:Избранная статьяar:12 (عدد) ca:Dotze ceb:Douze co:12 (numeru) da:12 (tal)eo:Dek dueu:Hamabihe:12 (מספר) ht:12 (nonm) hu:12 (szám) ia:12 (numero) id:12 (angka)ku:Dazde la:Duodecim lmo:Nümar 12 lt:12 (skaičius) nah:Mahtlāctli omōme nap:Dùrece nl:12 (getal) nn:Talet 12 no:12 (tall) pl:12 (liczba)sl:12 (število) sv:12 (tal) th:12uk:12 (число) vi:12 (số) vls:12 (getal) yi:צוועלףzh-yue:12

ru.math.wikia.com

Натуральные числа. Ряд натуральных чисел. Математика 5 класс

История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.

Натуральные числа – это числа которые мы используем при счете предметов.

Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….

Нуль не относится к натуральным числам.

Все натуральные числа или назовем множество натуральных чисел обозначается символом N.

Таблица натуральных чисел.



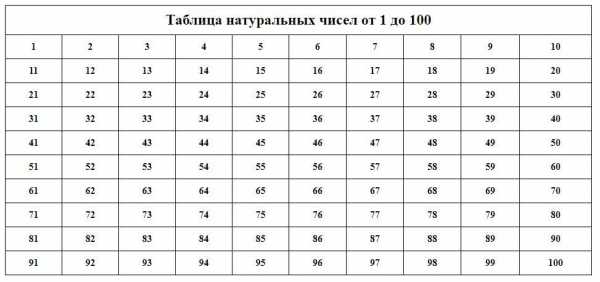
Натуральный ряд.

Натуральные числа, записанные подряд в порядке возрастания, образуют

натуральный ряд или ряд натуральных чисел.

Свойства натурального ряда:

• Наименьшее натуральное число – единица.
• У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
• Натуральный ряд не имеет наибольшего числа, он бесконечен.

Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5

Пример №2:
Нуль является натуральным числом?
Ответ: нет.

Пример №3:


Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.

Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.

Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.

Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5,  б)67,  в)9998.
Ответ: а)6,  б)68,  в)9999.

Пример №7:
Сколько чисел находится в натуральном ряду между числами:  а)1 и 5, б)14 и 19.


Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.

Пример №8:
Назовите предыдущее число  за числом  11.
Ответ: 10.

Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.

tutomath.ru

12 — двенадцать. натуральное четное число. регулярное число (число хемминга). в ряду натуральных чисел находится между числами 11 и 13. Все о числе двенадцать.

1. Главная
2. О числе 12

12 — двенадцать. Натуральное четное число. Регулярное число (Число Хемминга). В ряду натуральных чисел находится между числами 11 и 13.

Like если 12 твое любимое число!

Распространенные значения и факты

12 регион — Республика Марий Эл

Столица

Йошкар-Ола

Автомобильный код

12

Федеральный округ

Приволжский

Экономический район

Волго-Вятский

Дата образования

4 ноября 1920 г.

Территория

23, 2 тыс. кв. км 0,14 % от Рф 77 место в РФ

Население

Общая численность 728 тыс. чел. 0,50 % от Рф 66 место в РФ

Изображения числа 12

Склонение числа «12» по падежам

Падеж	Вспомогательное слово	Характеризующий вопрос	Склонение числа 12
Именительный	Есть	Кто? Что?	двенадцать
Родительный	Нет	Кого? Чего?	двенадцати
Дательный	Дать	Кому? Чему?	двенадцати
Винительный	Видеть	Кого? Что?	двенадцать
Творительный	Доволен	Кем? Чем?	двенадцатью
Предложный	Думать	О ком? О чём?	двенадцати

Перевод «двенадцать» на другие языки

Азербайджанский

on iki

Албанский

dymbëdhjetë

Английский

twelve

Арабский

اثنا عشر

Армянский

տասներկու

Белорусский

дванаццаць

Болгарский

дванадесет

Вьетнамский

mười hai

Голландский

twaalf

Греческий

δώδεκα

Грузинский

თორმეტი

Иврит

שנים עשר

Идиш

צוועלף

Ирландский

dhá cheann déag de

Исландский

tólf

Испанский

doce

Итальянский

dodici

Китайский

十二

Корейский

열두

Латынь

duodecim,

Латышский

divpadsmit

Литовский

dvylika

Монгольский

арван хоёр

Немецкий

zwölf

Норвежский

tolv

Персидский

دوازده

Польский

dwanaście

Португальский

doze

Румынский

doisprezece

Сербский

дванаест

Словацкий

dvanásť

Словенский

dvanajst

Тайский

สิบสอง

Турецкий

oniki

Украинский

дванадцять

Финский

kaksitoista

Французский

douze

Хорватский

dvanaest

Чешский

dvanáct

Шведский

tolv

Эсперанто

dekdu

Эстонский

kaksteist

Японский

12

Перевод «12» на другие языки и системы

Римскими цифрами

Римскими цифрами

XII

Сервис перевода арабских чисел в римские

Арабско-индийскими цифрами

Арабскими цифрами

١٢

Восточно-арабскими цифрами

۱۲

Деванагари

१२

Бенгальскими цифрами

১২

Гурмукхи

੧੨

Гуджарати

૧૨

Ория

୧୨

Тамильскими цифрами

௧௨

Телугу

౧౨

Каннада

೧೨

Малаялам

൧൨

Тайскими цифрами

๑๒

Лаосскими цифрами

໑໒

Тибетскими цифрами

༡༢

Бирманскими цифрами

၁၂

Кхемерскими цифрами

១២

Монгольскими цифрами

᠑᠒

В других системах счисления

12 в двоичной системе

1100

12 в троичной системе

110

12 в восьмеричной системе

14

12 в десятичной системе

12

12 в двенадцатеричной системе

10

12 в тринадцатеричной системе

C

12 в шестнадцатеричной системе

C

QR-код, MD5, SHA-1 числа 12

Адрес для вставки QR-кода числа 12, размер 500×500:

http://pro-chislo.ruhttp://pro-chislo.ru//data/moduleImages/QRCodes/12/1c2f3b313bc207fd525d3c465120abe0.png

MD2 от 12

d818fdda9b607de69729f9e602ed56ef

MD4 от 12

114c5a33b8d4127fbe492bd6583aeb4d

MD5 от 12

c20ad4d76fe97759aa27a0c99bff6710

SHA1 от 12

7b52009b64fd0a2a49e6d8a939753077792b0554

SHA256 от 12

6b51d431df5d7f141cbececcf79edf3dd861c3b4069f0b11661a3eefacbba918

SHA384 от 12

1e237288d39d815abc653befcab0eb70966558a5bbc10a24739c116ed2f615be31e81670f02af48fe3cf5112f0fa03e8

SHA512 от 12

5aadb45520dcd8726b2822a7a78bb53d794f557199d5d4abdedd2c55a4bd6ca73607605c558de3db80c8e86c3196484566163ed1327e82e8b6757d1932113cb8

GOST от 12

7b7218b78010faebef72a3445a95e354ee3767fbacc940f6bfce41a73bf3581a

Base64 от 12

MTI=

12й день в году

12й день в не високосном году — 12 января

День работников Прокуратуры России

12й день в високосном году — 12 января

Математические свойства числа 12

Простые множители

2 * 2 * 3

Делители

1, 2, 3, 4, 6, 12

Количество делителей

6

Сумма делителей

28

Простое число

Нет

Предыдущее простое

11

Следующее простое

13

12е простое число

37

Число Фибоначчи

Нет

Число Белла

Нет

Число Каталана

Нет

Факториал

Нет

Регулярное число (Число Хемминга)

Да

Совершенное число

Нет

Полигональное число

пятиугольник(3)

Квадрат

144

Квадратный корень

3.4641016151378

Натуральный логарифм (ln)

2.484906649788

Десятичный логарифм (lg)

1.0791812460476

Синус (sin)

-0.53657291800043

Косинус (cos)

0.84385395873249

Тангенс (tg)

0.63585992866158

Фильмы про 12

12 Рождественских желаний (12 Wishes of Christmas (2011)), 2011 год

В преддверии Рождества жизнь Лоры Линдси распадается на части, словно карточный домик. Когда ситуация достигает пика критичности, женщина, находясь в…

12 метров без головы (12 Meter ohne Kopf), 2009 год

В самом начале 15 века, на территории Восточной Фризии, когда страх перед морскими пиратами постепенно сходил на нет, бравый капитан…

12 раундов (12 Rounds), 2009 год

Полицейский из Нового Орлеана по имени Дэнни Фишер арестовывает одного из самых разыскиваемых и опасных преступников во всем мире –…

Все фильмы о числе 12 (6)

Комментарии о числе 12

pro-chislo.ru

как сложить все натуральные числа и получить -1/12?

Вопрос ученому: — Я слышал, что сумма всех натуральных чисел равна −1/12. Это какой-то фокус, или это правда?

Ответ пресс-службы МФТИ — Да, такой результат можно получить при помощи приема, называемого разложением функции в ряд.

Вопрос, заданный читателем, достаточно сложный, и потому мы отвечаем на него не обычным для рубрики «Вопрос ученому» текстом на несколько абзацев, а некоторым сильно упрощенным подобием математической статьи.

В научных статьях по математике, где требуется доказать некоторую сложную теорему, рассказ разбивается на несколько частей, и в них могут поочередно доказываться разные вспомогательные утверждения. Мы предполагаем, что читатели знакомы с курсом математики в пределах девяти классов, поэтому заранее просим прощения у тех, кому рассказ покажется слишком простым — выпускники могут сразу обратиться к http://en.wikipedia.org/wiki/Ramanujan_summation.

Сумма всего

Начнем с разговора о том, как можно сложить все натуральные числа. Натуральные числа — это числа, которые используются для счета цельных предметов — они все целые и неотрицательные. Именно натуральные числа учат дети в первую очередь: 1, 2, 3 и так далее. Сумма всех натуральных чисел будет выражением вида 1+2+3+… = и так до бесконечности.

Ряд натуральных чисел бесконечен, это легко доказать: ведь к сколь угодно большому числу всегда можно прибавить единицу. Или даже умножить это число само на себя, а то и вычислить его факториал — понятно, что получится еще большая величина, которая тоже будет натуральным числом.

Детально все операции с бесконечно большими величинами разбираются в курсе математического анализа, но сейчас для того, чтобы нас поняли еще не сдавшие данный курс, мы несколько упростим суть. Скажем, что бесконечность, к которой прибавили единицу, бесконечность, которую возвели в квадрат или факториал от бесконечности — это все тоже бесконечность. Можно считать, что бесконечность — это такой особый математический объект.

И по всем правилам математического анализа в рамках первого семестра сумма 1+2+3+…+бесконечность — тоже бесконечна. Это легко понять из предыдущего абзаца: если к бесконечности что-то прибавить, она все равно будет бесконечностью.

Однако в 1913 году блестящий индийский математик-самоучка Сриниваса Рамануджан Айенгор придумал способ сложить натуральные числа несколько иным образом. Несмотря на то, что Рамануджан не получал специального образования, его знания не были ограничены сегодняшним школьным курсом — математик знал про существование формулы Эйлера-Маклорена. Так как она играет важную роль в дальнейшем повествовании, о ней придется тоже рассказать подробнее.

Формула Эйлера-Маклорена

Для начала запишем эту формулу:

Как можно видеть, она достаточно сложна. Часть читателей может пропустить этот раздел целиком, часть может прочитать соответствующие учебники или хотя бы статью в Википедии, а для оставшихся мы дадим краткий комментарий. Ключевую роль в формуле играет произвольная функция f(x), которая может быть почти чем угодно, лишь бы у нее нашлось достаточное число производных. Для тех, кто не знаком с этим математическим понятием (и все же решился прочитать написанное тут!), скажем еще проще — график функции не должен быть линией, которая резко ломается в какой-либо точке.

Производная функции, если предельно упростить ее смысл, является величиной, которая показывает то, насколько быстро растет или убывает функция. С геометрической точки зрения производная есть тангенс угла наклона касательной к графику.

Слева в формуле стоит сумма вида «значение f(x) в точке m + значение f(x) в точке m+1 + значение f(x) в точке m+2 и так до точки m+n». При этом числа m и n — натуральные, это надо подчеркнуть особо.

Справа же мы видим несколько слагаемых, и они кажутся весьма громоздкими. Первое (заканчивается на dx) — это интеграл функции от точки m до точки n. Рискуя навлечь на себя гнев всей кафедры математики за примитивность подхода к интегралам, скажем, что это площадь под кривой f(x) на графике от m до n; интегралы очень широко используются в самых разных науках.

На графике «по горизонтальной оси — время, по вертикальной — скорость» интеграл, то есть площадь под кривой, будет равен пройденному пути. На графике «ежемесячные платежи по вертикали, по горизонтали время» интегралом будет сумма, пришедшая на счет за все время.

Второе слагаемое, обозначенное как B₁(f(n) + f(m)), — это так называемое число Бернулли.

Третье слагаемое — сумма от чисел Бернулли (B_2k), поделенных на факториал удвоенного значения числа k и умноженных на разность производных функции f(x) в точках n и m. Причем, что еще сильнее усложняет дело, тут не просто производная, а производная 2k-1 порядка. То есть все третье слагаемое выглядит так:

Число Бернулли B₂ («2» так как в формуле стоит 2k, и мы начинаем складывать с k=1) делим на факториал 2 (это пока просто двойка) и умножаем на разность производных первого порядка (2k-1 при k=1) функции f(x) в точках n и m

+

Число Бернулли B₄ («4» так как в формуле стоит 2k, а k теперь равно 2) делим на факториал 4 (1×2х3×4=24) и умножаем на разность производных третьего порядка (2k-1 при k=2) функции f(x) в точках n и m

+

Число Бернулли B₆ (см.выше) делим на факториал 6 (1×2х3×4х5×6=720) и умножаем на разность производных пятого порядка (2k-1 при k=3) функции f(x) в точках n и m

+

…

Суммирование продолжается вплоть до k=p. Числа k и p получаются некоторыми произвольными величинами, которые мы можем выбирать по-разному, вместе с m и n — натуральными числами, которыми ограничен рассматриваемый нами участок с функцией f(x). То есть в формуле целых четыре параметра, и это вкупе с произвольностью функции f(x) открывает большой простор для исследований.

Оставшееся скромное R, увы, тут не константа, а тоже довольно громоздкая конструкция, выражаемая через уже упомянутые выше числа Бернулли. Теперь самое время пояснить, что это такое, откуда взялось и почему вообще математики стали рассматривать столь сложные выражения.

Числа Бернулли и разложения в ряд

В математическом анализе есть такое ключевое понятие как разложение в ряд. Это значит, что можно взять какую-то функцию и написать ее не напрямую (например y = sin(x^2) + 1/ln(x) + 3x), а в виде бесконечной суммы множества однотипных слагаемых. Например, многие функции можно представить как сумму степенных функций, умноженных на некоторые коэффициенты — то есть сложной формы график сведется к комбинации линейной, квадратичной, кубической… и так далее — кривых.

В теории обработки электрических сигналов огромную роль играет так называемый ряд Фурье — любую кривую можно разложить в ряд из синусов и косинусов разного периода; такое разложение необходимо для преобразования сигнала с микрофона в последовательность нулей и единиц внутри, скажем, электронной схемы мобильного телефона. Разложения в ряд также позволяют рассматривать неэлементарные функции, а ряд важнейших физических уравнений при решении дает именно выражения в виде ряда, а не в виде какой-то конечной комбинации функций.

В XVII столетии математики стали вплотную заниматься теорией рядов. Несколько позже это позволило физикам эффективно рассчитывать процессы нагрева различных объектов и решать еще множество иных задач, которые мы здесь рассматривать не будем. Заметим лишь то, что в программе МФТИ, как и в математических курсах всех ведущих физических вузов, уравнениям с решениями в виде того или иного ряда посвящен как минимум один семестр.

Якоб Бернулли исследовал проблему суммирования натуральных чисел в одной и той же степени (1^6 + 2^6 + 3^6 + … например) и получил числа, при помощи которых можно разложить в упомянутый выше степенной ряд другие функции — например, tg(x). Хотя, казалось бы, тангенс не очень-то похож хоть на параболу, хоть на какую угодно степенную функцию!

Полиномы Бернулли позже нашли свое применение не только в уравнениях матфизики, но и в теории вероятностей. Это, в общем-то, предсказуемо (ведь ряд физических процессов — вроде броуновского движения или распада ядер — как раз и обусловлен разного рода случайностями), но все равно заслуживает отдельного упоминания.

-1/12

Громоздкая формула Эйлера-Маклорена использовалась математиками для разных целей. Так как в ней, с одной стороны, стоит сумма значений функций в определенных точках, а с другой — есть и интегралы, и разложения в ряд, при помощи этой формулы можно (в зависимости от того, что нам известно) как взять сложный интеграл, так и определить сумму ряда.

Сриниваса Рамануджан придумал этой формуле иное применение. Он ее немного модифицировал и получил такое выражение:

В качестве функции f(x) он рассмотрел просто x — пусть f(x) = x, это вполне правомерное допущение. Но для этой функции первая производная равна просто единице, а вторая и все последующие — нулю: если все аккуратно подставить в указанное выше выражение и определить соответствующие числа Бернулли, то как раз и получится −1/12.

Это, разумеется, было воспринято самим индийским математиком как нечто из ряда вон выходящее. Поскольку он был не просто самоучкой, а талантливым самоучкой, он не стал всем рассказывать про поправшее основы математики открытие, а вместо этого написал письмо Годфри Харди, признанному эксперту в области как теории чисел, так и математического анализа. Письмо, кстати, содержало приписку, что Харди, вероятно, захочет указать автору на ближайшую психиатрическую лечебницу: однако итогом, конечно, стала не лечебница, а совместная работа.

Парадокс

Суммируя все сказанное выше, получим следующее: сумма всех натуральных чисел получается равной −1/12 при использовании специальной формулы, которая позволяет разложить произвольную функцию в некоторый ряд с коэффициентами, называемыми числами Бернулли. Однако это не значит, что 1+2+3+4 оказывается больше, чем 1+2+3+… и так до бесконечности. В данном случае мы имеем дело с парадоксом, который обусловлен тем, что разложение в ряд — это своего рода приближение и упрощение.

Можно привести пример намного более простого и наглядного математического парадокса, связанного с выражением чего-то одного через что-то другое. Возьмем лист бумаги в клеточку и нарисуем ступенчатую линию с шириной и высотой ступеньки в одну клетку. Длина такой линии, очевидно, равна удвоенному числу клеток — а вот длина спрямляющей «лесенку» диагонали равна числу клеток, умноженному на корень из двух. Если сделать лесенку очень мелкой, она все равно будет той же длины и практически не отличимая от диагонали ломаная линия окажется в корень из двух раз больше той самой диагонали! Как видите, для парадоксальных примеров писать длинные сложные формулы вовсе не обязательно.

Формула Эйлера-Маклорена, если не вдаваться в дебри математического анализа, является таким же приближением, как и ломаная линия вместо прямой. Используя это приближение можно получить те самые −1/12, однако это далеко не всегда бывает уместно и оправдано. В ряде задач теоретической физики подобные выкладки применяются для расчетов, но это тот самый передний край исследований, где еще рано говорить о корректном отображении реальности математическими абстракциями, а расхождения разных вычислений друг с другом — вполне обычное дело.

Так, оценки плотности энергии вакуума на основе квантовой теории поля и на основе астрофизических наблюдений различаются более чем на 120 порядков. То есть в 10^120 степени раз. Это одна из нерешенных задач современной физики; тут явно просвечивает пробел в наших знаниях о Вселенной. Или же проблема — в отсутствии подходящих математических методов для описания окружающего мира. Физики-теоретики совместно с математиками пытаются найти такие способы описать физические процессы, при которых не будет возникать расходящихся (уходящих в бесконечность) рядов, но это далеко не самая простая задача.

mipt.ru

Сумма всех натуральных чисел действительно равна -1/12?

Не совсем так. Сумма всех натуральных чисел — расходящийся ряд. Расходящихся рядов существует бесконечно много, однако все они расходятся по-разному и существует соблазн (а иногда и потребность) как-то различать эти ряды между собой. Поэтому (а иногда и из спортивного интереса) математиками придуманы различные приёмы суммирования расходящихся рядов, так называемые методы регуляризации. Для чего нужны подобные фокусы? Слышали о перенормировках в квантовой электродинамике, о том, что вычисления дают бесконечные массы частиц, но особыми приёмами их можно преобразовать к конечному виду? Вот это, грубо говоря, из той же оперы. Равенство тут не означает эквивалентность на множестве рациональных чисел, поскольку расходящийся ряд (сумма всех натуральных чисел) не принадлежит ни множеству натуральных, ни множеству рациональных чисел, а является объектом совсем иного класса. Но по определённым (и весьма строгим) правилам этому объекту можно сопоставить число -1/12. Правила сопоставления очень похожи на правила суммирования рядов. Подробнее см. в Википедии <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/1_+_2_+_3_+_4_+_⋯» target=»_blank»>http://ru.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_%E2%8B%AF</a> <a rel=»nofollow» href=»http://en.wikipedia.org/wiki/1_+_2_+_3_+_4_+_…» target=»_blank»>http://en.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_%E2%80%A6</a> ДОПОЛНЕНИЕ. Или вот тут обсуждение почитайте <a rel=»nofollow» href=»http://www.linux.org.ru/forum/talks/7152512″ target=»_blank»>http://www.linux.org.ru/forum/talks/7152512</a>

Нет, конечно, это не так. «Сумма» всех натуральных чисел равна +бесконечности. Наверняка то «доказательство» написано так, что ошибка спрятана где-то внутри. Хотя, конечно, смотря что понимать под словом «сумма бесконечного ряда». Обычное определение — предел суммы конечного отрезка ряда. Здесь это, разумеется, бесконечность. Но возможны и другие, более «хитрые», понимания «суммы».

«На дурака не нужен нож Ему с три короба наврешь — и делай с ним что хошь! » «Приключения Буратино». Рекомендую к просмотру. Не ютуб!

натуральное число — это целое положительное число. При сложении его с другим целым положительным в результате никак отрицательное получится не может.

Умники, блин. Специальные методы суммирования, использующиеся в некоторых разделах математики, позволяют присвоить конечные значения расходящимся числовым рядам. В частности, один из таких способов предоставляет метод, основанный на регуляризации аналитического продолжения дзета-функции Римана и суммирование по методу Рамануджана, позволяют сопоставить данному ряду некое конечное значение: -1/12. Доказано больше 100 лет назад. <a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Натуральный_ряд» target=»_blank»>https://ru.wikipedia.org/wiki/Натуральный_ряд</a>

«Все нетривиальные нули дзетта-функции имеют вещественную часть равную одной второй».Эту гипотезу Риман вывел еще в 18 веке. Она не доказана и неопровергнута до сих пор. За ее доказательство или опровержение будет выплачено миллион долларов американским институтом Клея. Пока ее никто не получил.

touch.otvet.mail.ru

-1/12 это сумма всех натуральных чисел. Пятничная разминка мозга

Чему равна сумма целых натуральных чисел от 1 до бесконечности? Безусловно бесконечности, чему же еще. Однако видео по вот этой ссылке http://www.youtube.com/watch?v=E-d9mgo8FGk  доказывает, что сумма натуральных чисел равна -1/12. Минус одна/двенадцатая!

 



 

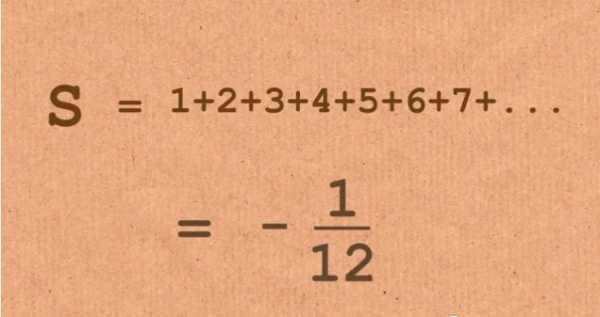
Сопровождающий текст на английском, но математика понятна и доступна ученику начальных классов без перевода. Только сложения, вычитания, никаких сложных действий.

Засада кроется в самом начале. Когда авторы рассматривают последовательность 1-1+1-1+1-….. они утверждают, что  там,  в бесконечности, в конце концов результат этой последовательности действий будет либо «один»  либо «ноль». Однако мы не знаем, где она там закончится, поэтому вывод — результат равен 1/2. Если принять это за основу все дальнейшее становится логичным и сумма всех натуральных чисел действительно равно -1/12.

Не могу притянуть математику, чтобы опровергнуть первый расчет 1/2. Если идти через лимиты, то не совсем понятно, какую функцию подставить. Интегральная оценка действительно должна дать в пределе 1/2. Оптическая — возьмем белый цвет и черный и будем быстро их переключать — тоже даст серый 1/2 🙂 Вероятностная тем более.

По хорошему если описать 1-1+1-1+1-… функцией, то значение функции при числе элементов равное бесконечности должно быть не определено.  Соответственно все остальные рассуждения дальше рушатся. Но может быть есть другие варианты? У кого как с математикой?

P.S.: Хорошо дети выросли. Старший подсказывает, что в  качестве функции можно рассмотреть (-1) в степени n, при n стремящейся к бесконечности. В конечном итоге если откинуть первые члены, можно оставить (-1) в степени бесконечность.  Если подогнать под предел,  получается ряд, который не сходится. А раз он не сходится, то и решения нет.  Дурят нашего брата.

vsobolev.com

11 — одиннадцать. натуральное нечетное число. 5е простое число. в ряду натуральных чисел находится между числами 10 и 12. Все о числе одиннадцать.

1. Главная
2. О числе 11

11 — одиннадцать. Натуральное нечетное число. 5е простое число. В ряду натуральных чисел находится между числами 10 и 12.

Like если 11 твое любимое число!

Распространенные значения и факты

11 регион — Республика Коми

Столица

Сыктывкар

Автомобильный код

11

Федеральный округ

Северо-Западный

Экономический район

Северный

Дата образования

5 декабря 1936 г.

Территория

415, 9 тыс. кв. км 2,44 % от РФ 11 место в РФ

Население

Общая численность 1 019 тыс, чел. 0,70 % от РФ 54 место в РФ

Изображения числа 11

Склонение числа «11» по падежам

Падеж	Вспомогательное слово	Характеризующий вопрос	Склонение числа 11
Именительный	Есть	Кто? Что?	одиннадцать
Родительный	Нет	Кого? Чего?	одиннадцати
Дательный	Дать	Кому? Чему?	одиннадцати
Винительный	Видеть	Кого? Что?	одиннадцать
Творительный	Доволен	Кем? Чем?	одиннадцатью
Предложный	Думать	О ком? О чём?	одиннадцати

Перевод «одиннадцать» на другие языки

Азербайджанский

on bir

Албанский

njëmbëdhjetë

Английский

eleven

Арабский

أحد عشر

Армянский

տասնմեկ

Белорусский

адзінаццаць

Болгарский

единадесет

Вьетнамский

mười một

Голландский

elf

Греческий

έντεκα

Грузинский

eleven

Иврит

אחד עשר

Идиш

עלף

Ирландский

aon cheann déag

Исландский

ellefu

Испанский

once

Итальянский

undici

Китайский

十一

Корейский

열한

Латынь

undecim

Латышский

vienpadsmit

Литовский

vienuolika

Монгольский

арван нэгэн

Немецкий

elf

Норвежский

elleve

Персидский

یازده

Польский

jedenaście

Португальский

onze

Румынский

unsprezece

Сербский

једанаест

Словацкий

jedenásť

Словенский

eleven

Тайский

สิบเอ็ด

Турецкий

on bir

Украинский

одинадцять

Финский

yksitoista

Французский

onze

Хорватский

jedanaest

Чешский

jedenáct

Шведский

elva

Эсперанто

dek unu

Эстонский

üksteist

Японский

11

Перевод «11» на другие языки и системы

Римскими цифрами

Римскими цифрами

XI

Сервис перевода арабских чисел в римские

Арабско-индийскими цифрами

Арабскими цифрами

١١

Восточно-арабскими цифрами

۱۱

Деванагари

११

Бенгальскими цифрами

১১

Гурмукхи

੧੧

Гуджарати

૧૧

Ория

୧୧

Тамильскими цифрами

௧௧

Телугу

౧౧

Каннада

೧೧

Малаялам

൧൧

Тайскими цифрами

๑๑

Лаосскими цифрами

໑໑

Тибетскими цифрами

༡༡

Бирманскими цифрами

၁၁

Кхемерскими цифрами

១១

Монгольскими цифрами

᠑᠑

В других системах счисления

11 в двоичной системе

1011

11 в троичной системе

102

11 в восьмеричной системе

13

11 в десятичной системе

11

11 в двенадцатеричной системе

B

11 в тринадцатеричной системе

B

11 в шестнадцатеричной системе

B

Известные люди умершие в 11 лет

• Хатико Пёс породы акита-ину, являющийся символом верности и преданности в Японии. Смерть наступила в 1935 году в 11 лет.
• Чуковская, Мария Корнеевна Младшая дочь Корнея Чуковского и героиня его стихов и рассказов для детей; туберкулёз. Смерть наступила в 1931 году в 11 лет.
• Скрябин, Юлиан Александрович Младший сын Александра Скрябина (от Татьяны Шлёцер), талантливый и подававший большие надежды пианист и композитор; трагически погиб. Смерть наступила в 1919 году в 11 лет.

QR-код, MD5, SHA-1 числа 11

Адрес для вставки QR-кода числа 11, размер 500×500:

http://pro-chislo.ruhttp://pro-chislo.ru//data/moduleImages/QRCodes/11/0cb3199ff7dd33c3ca0a953b328b8f0e.png

MD2 от 11

3f1bfe20bface460c8c64316b3b58c34

MD4 от 11

282fbfeb1d5ccb63947013be1dc02475

MD5 от 11

6512bd43d9caa6e02c990b0a82652dca

SHA1 от 11

17ba0791499db908433b80f37c5fbc89b870084b

SHA256 от 11

4fc82b26aecb47d2868c4efbe3581732a3e7cbcc6c2efb32062c08170a05eeb8

SHA384 от 11

9b20aa6472eef4fd186d231637b1c1d55a5a434cc9130d6afcaaf486253a20c23a4eaeea419594c17f46bc53c7cee12e

SHA512 от 11

74a49c698dbd3c12e36b0b287447d833f74f3937ff132ebff7054baa18623c35a705bb18b82e2ac0384b5127db97016e63609f712bc90e3506cfbea97599f46f

GOST от 11

6a015a0f86de26f49624ca463ced5dd911c7dfe148e1c40cee995d1c5bfa1228

Base64 от 11

MTE=

11й день в году

11й день в не високосном году — 11 января

День заповедников и национальных парков

День заповедников и национальных парков — официальный праздник, который отмечается в Российской Федерации по инициативе ряда экологических организаций. Эта дата отмечается в России ежегодно 11 января. Приказ о создании первого Баргузинского заповедника (Республика Бурятия) был подписан 29 декабря 1916 года (11 января по новому стилю).

Всемирный день «спасибо»

11й день в високосном году — 11 января

Математические свойства числа 11

Простые множители

11

Делители

1, 11

Количество делителей

2

Сумма делителей

12

Простое число

Да (5е простое число)

Предыдущее простое

7

Следующее простое

13

11е простое число

31

Число Фибоначчи

Нет

Число Белла

Нет

Число Каталана

Нет

Факториал

Нет

Регулярное число (Число Хемминга)

Нет

Совершенное число

Нет

Полигональное число

Нет

Квадрат

121

Квадратный корень

3.3166247903554

Натуральный логарифм (ln)

2.3978952727984

Десятичный логарифм (lg)

1.0413926851582

Синус (sin)

-0.9999902065507

Косинус (cos)

0.0044256979880508

Тангенс (tg)

5.9508464542

Фильмы про 11

11 жертв (Random 11), 2011 год

Со времени череды страшных и загадочных убийств, совершённых в Токио, прошло уже десять лет. Мицуко Уэнджи — детектив, посвящающий всё…

11-11-11 (11-11-11), 2011 год

Красивая дата 11 ноября (11.11.2011 г.) омрачена происходящими за несколько дней до неё жуткими событиями. По всему миру прокатывается волна…

11 заповедей (11 commandements, Les), 2004 год

Весь земной шар постигла огромная беда. Люди перестали смеяться. В каждом уголке – лишь уныние и мрак. Но бог Смеха…

Все фильмы о числе 11 (6)

Комментарии о числе 11

pro-chislo.ru