10 в 5 степени равно – , 1 10,
Сколько будет 10 в минус пятой степени?? И вообще расскажите пожалуйста, что значит минусовая степень…
Это значит 1 разделить на 10 в пятой степени
Это значит РАЗДЕЛИТЬ на число в такой положительной степени. Только-то И 10^-5=1/100000=0.00001
минусовая степень. Вот вам формула 10^-n = 1/10^n. То есть, 2 во второй степени — это 4, а 2 в минус второй степени — это одна четвёртая. Следовательно, 10 в минус пятой степени это это 1 статысечная.. . Вроде бы (:
10^-5 =0,00001= одна стотысячная = 1/100 000= 1/ 10^5
1*10 в пятой степени означает, что запятую надо передвинуть на 5 позиций вправо, получится 100000. 1*10 в минус пятой — на 5 позиций влево: 0,00001.
Что такое отрицательная степень. Можно объяснить так. С положительносй степенью все понятно. Надо основание перемножить столько раз, чему равен показатель степени a^n = a*a*a*…*a и так n раз Отсюда видно важное свойство. Если показатель уменьшать на 1, то результат будет меньше в «a» раз Людям захотелось ввести отрицательную степень. Это понятие вроде бы бессмысленное. Понятие ввели так, чтобы сохранить это важное свойство. Поэтому a^1 = a a^0 в «a» раз меньше, то есть a/a = 1 a^(-1) еще в «a» раз меньше, то есть 1/a a^(-2) еще в «a» раз меньше, то есть 1/a^2 и тд a^(-n) = 1/a^n 10^-5 = 1/10^5
a^1 = a a^0 в «a» раз меньше, то есть a/a = 1 a^(-1) еще в «a» раз меньше, то есть 1/a a^(-2) еще в «a» раз меньше, то есть 1/a^2 и тд a^(-n) = 1/a^n 10^-5 = 1/10^5
a^1 = a a^0 в «a» раз меньше, то есть a/a = 1 a^(-1) еще в «a» раз меньше, то есть 1/a a^(-2) еще в «a» раз меньше, то есть 1/a^2 и тд a^(-n) = 1/a^n 10^-5 = 1/10^5
touch.otvet.mail.ru
Сколько будет 10 в минус 2, 3, 4, 5, 6, 7, 8, 9 степени?
Сколько будет 10 в минус 2, 3, 4, 5, 6, 7, 8, 9 степени?
Если число имеет отрицательную степень, то число степени показывает нам насколько чисел после запятой мы должны отойти. Вот указанные значения:
0,01 — десять минус второй степени
0,001 — десять минус третьей степени
В минусовой степени число 10, это уже будет не целое число, а десятичное и количество знаков после запятой соответствует значению срепени.
Вторая орицательная срепень — 0,01
Третья отрицательная степень — 0,001
Четвертая отричарельная степень — 0,0001
Пятая отрицательная степень — 0,00001
Шестая отрицательная степень — 0, 000001
Седьмая отрицательная степень — 0,0000001
Восьмая отрицарельная степень — 0,00000001
Девятая отрицательная степень — 0, 000000001
Итак, 10 в минус второй степени будет 0,01;
10 в минус третьей степени будет 0,001;
10 в минус четвертой степени будет 0,0001;
10 в минус пятой степени будет 0,00001;
10 в минус шестой степени будет 0,000001;
10 в минус седьмой степени будет 0,0000001;
10 в минус восьмой степени будет 0,00000001;
10 в минус девятой степени будет 0,000000001.
Для определения степени числа 10 нам для начала нужно разобраться с понятием степени.Например вместо записи шести одинаковх множителей 4 4 4 4 4 4 пишут 4 (6)-где цифра 6 находится в верхнем правом углу.В нашем случае ответы будут следующими.
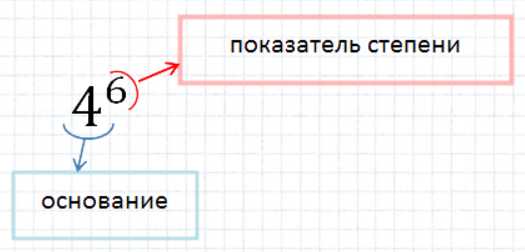
Минус перед показателем степени означает, что число равно единица деленная на заданное число в заданной степени без минуса. Т.е. в общем виде число А в степени минус n равно 1/А^n (единица деленная на А в степени n). Следовательно, 10 в минус 2; 3; 4 и т.д.степени равно 1/10^2 = 1/100 = 0,01; 1/10^3 = 1/1000 = 0,001; 1/10^4 = 1/10000 = 0,0001 и т.д. Т.е. 10^ -n = 1/10^n
С каждым последующим числом в минусовой степени единицы все дальше отодвигается от запятой и нуля. То есть 10 в минус первой степени — это одна десятая. А минус второй — это уже одна сотая. Потом идет одна тысячная, десяти-, стотысячная, миллионная и т. д.
Такую степень придумали, чтобы можно было записывать целыми числами значения, которые значительно ниже 1.
Интересующее вас число десять в минус второй, третьей, четвертой, пятой, шестой, седьмой, восьмой и девятой степенях имеет следующие значения:
-2 степень будет 0,01
-3 степень будет 0,001
-4 степень будет 0,0001
-5 степень будет 0,00001
-6 степень будет 0, 000001
-7 степень будет 0,0000001
-8 степень будет 0,00000001
-9 степень будет 0, 000000001
Число в минусовой степени наверняка у многих вызывает затруднения и сразу же в голое возникает куча закономерных вопросов, о том как же рассчитать и получить это число без минусовой степени. А на самом-то деле всего-то нужно единцу разделить на данное число в положительной степени, вот и получаем:
Как верно было сказано, 10 в минусовой степени представляет собой единицу, которую следует разделить на 10 в искомой степени (в нашем случае во 2, 3, 4… и так до 9).
Для наглядности прошу обратить внимание на следующий пример:
Здесь четко видно, что существует возможность мгновенно ответить на вопрос: сколько будет 10 в любой минусовой степени — для этого нужно просто сдвигать десятичную точку: так, 10 в минус 1 степени — один ноль перед единицей, в минус 3 — три нуля перед единицей, в минус 9 — 9 и так далее…
Кстати, глядя на эту табличку, сразу понятно, сколько будет 10, например, в нулевой степени.
Из школьного курса математики мы знаем, что число десять в минусовой степени будет равняться: 0,01 (минус 2), 0,001 (-3), 0,0001(-4), 0,00001 (-5), 0,000001 (-6), 0,0000001 (- 7-й), 0,00000001 (-8) и 0,000000001 ( в минус 9 степени). Это и будет правильными ответами на ваш вопрос из школьного учебника.
info-4all.ru
Почему число в степени 0 равно 1? — Науколандия
Существует правило, что любое число, кроме нуля, возведенное в нулевую степень, будет равно единице:
20 = 1; 1.50 = 1; 100000 = 1
Однако почему это так?
Когда число возводится в степень с натуральным показателем, то имеется в виду, что оно умножается само на себя столько раз, каков показатель степени:
43 = 4 × 4 × 4; 26 = 2 × 2 × 2 × 2 × 2 × 2
Когда же показатель степени равен 1, то при возведении имеется всего лишь один множитель (если тут вообще можно говорить о множителях), и поэтому результат возведения равен основанию степени:
Но как в таком случае быть с нулевым показателем? Что на что умножается?
Попробуем пойти иным путем. Известно, что если у двух степеней одинаковые основания, но разные показатели, то основание можно оставить тем же самым, а показатели либо сложить друг с другом (если степени перемножаются), либо вычесть показатель делителя из показателя делимого (если степени делятся):
32 × 31 = 32+1 = 33 = 3 × 3 × 3 = 27
45 ÷ 43 = 45–3 = 42 = 4 × 4 = 16
А теперь рассмотрим такой пример:
82 ÷ 82 = 82–2 = 80 = ?
Что если мы не будем пользоваться свойством степеней с одинаковым основанием и произведем вычисления по порядку их следования:
Вот мы и получили заветную единицу. Таким образом нулевой показатель степени как бы говорит о том, что число не умножается само на себя, а делится само на себя.
И отсюда становится понятно, почему выражение 00 не имеет смысла. Ведь нельзя делить на 0.
Можно рассуждать по-другому. Если имеется, например, умножение степеней 52 × 50 = 52+0 = 52, то отсюда следует, что 52 было умножено на 1. Следовательно, 50 = 1.
