Задать множество перечислением элементов: Задайте перечислением элементов множество. A=(x I x e N,x<8)
| |||||||||||||||
| |||||||||||||||
Множества и операции над ними
1. Множества и операции над ними
Множество и его элементыПустое множество
Способы задания множеств
Подмножества данного множества
Операции над множествами
2. Понятия теории множеств
Множество- совокупностьобъектов, обладающих
определенным свойством,
объединенных в единое целое.
Например:
Множество цифр:
0;1;2;3;4;5;6;7;8;9
Множество букв русского алфавита
Предметы, из которых состоит
множество, называются его
ЭЛЕМЕНТАМИ
Например:
1). Цифра 6 – элемент множества цифр.
2). Буква Л – элемент множества букв
русского алфавита
Для обозначения множеств используют большие
буквы латинского алфавита или фигурные скобки,
внутри которых записывают элементы
множества(при этом порядок элементов не имеет
значения).
Например:
1). А— множество цифр: А={0;1;2;3;4;5;6;7;8;9}.
2). W— множество букв русского алфавита:
Ц;Ч;Ш;Щ; Ь;Ы;Ъ;Э;Ю;Я }
Для обозначения элементов множества
используют малые буквы латинского
алфавита
Например:
1). f = 6 – элемент множества цифр
2). а = Р – элемент множества букв русского
алфавита
Принадлежность предмета данному множеству
обозначается
Непринадлежность – символом
Например:
1). f = 6 ; 6 є А, где А— множество цифр.
2). К є W, где W— множество букв русского
алфавита
Множество может быть:
1). Конечное :
Например: А— множество цифр
2). Бесконечное:
Например: N – множество натуральных чисел
3). Пустое:
ø- множество, в котором нет ни одного элемента
õ 25
2
Если множество В состоит из некоторых элементов
множества А
(и только из них),
то множество В называется ПОДМНОЖЕСТВОМ
На диаграмме Эйлера-Венна
множества А
утверждение «множество А
является подмножеством
множество В» изображают так
 Например:
1).
В= {5;9;0 }, А= { 0;1;2;3;4;5;6;7;8;9 }, то À
(читается В содержится в А)
Подмножеством
данного множества
А является и само
множество А
Пустое множество, по
определению, считают
подмножеством
всякого множества
W= {А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;Ц;Ч;Ш;Щ;Ь;Ы;Ъ;Э;Ю;Я },
C W
(читается С содержится в W)
8. Способы задания множеств
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВПеречислением элементов множества;
с помощью некоторого свойства,
объединяющего элементы;
описанием получения множества.
Например:
1). К = {х : -5 ≤ х ≤ 6 }-описанием характеристического
свойства элементов
2). Т = {х : 0 ≤ х ≤ 9, х є N } –описанием
характеристического свойства элементов
3). Множество учеников данного класса определяется
их списком в классном журнале — перечислением
элементов
4). Множество цифр: А = {0,1,2,3,4,5,6,7,8,9} перечислением элементов
9.
Множества называются РАВНЫМИ, если они состоят из одних и тех же элементов Равенство множеств А и В записывают в виде А=ВОтношение «=» называется отношением равенства
Например:
1). Равными являются все пустые множества
2). Множество корней уравнения
х²=49; L= {-7; 7 },
Множество корней уравнения | х |=7; M= {-7; 7 },
=> L=М
10. Решение задач
1.Задайте перечислением элементов множества:а) А—множество гласных букв русского алфавита.
Решение
А = {а, е, ё, и, о, у, ы, э, ю, я }
б) В—множество корней уравнения х³-4х=0.
Решение
х (х²-4)=0
х=0 или х= ±2
В={-2; 0; 2 }
в) С—множество простых четных чисел.
Решение
С={2}
11. 3. Какие из следующих множеств являются пустыми?
множество решений уравнений х²-4=0множество решений уравнений х+1 = х+1
множество кругов, у которых диаметр меньше радиуса
5. Даны множества:
а) множество А всех трапеций.
б) множество В всех прямоугольников.
в) множество С всех четырехугольников.
г) множество D всех квадратов.
д) множество H всех параллелограммов.
е ) множество F всех многоугольников.
Запишите с помощью знака
эти множества в таком порядке,
чтобы каждое предыдущее множество являлось подмножеством
последующего.
D
Решение
B
H
A
C
F
13. Операции над множествами
Суммой, или объединением произвольногоназывается множество, состоящее из тех и только
тех элементов, которые принадлежат хотя бы
одному из множеств А,В.
Объединение множеств обозначается
На диаграмме Эйлера-Венна объединение двух
множеств выглядит так
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.
14. ОБЪЕДИНЕНИЕ МНОЖЕСТВ А и В
Например:L= { 5;7;9;3;1},
W= { 1;0;8;2;4;5;6 } =>
С =А U B
КUM
LUW={0;1;2;3;4;5;6;7;8;9}
Пересечением любого конечного или
бесконечного множества множеств называется
множество, состоящее из тех и только тех
элементов, которые принадлежат множествам
А и В одновременно.
Пересечение множеств обозначается
На диаграмме Эйлера-Венна пересечение двух
множеств выглядит так
Пример:
{1,2,3} {2,3,4} = {2,3}
16. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ А и В
Например:L= { 5;7;9;3;1},
W= { 1;0;8;2;4;5;6 }
=> К = L ∩ W= { 1;5 }
С= А ∩ В
К∩М=ø
Разностью между множеством В и
множеством А называется множество
всех элементов из В , не являющихся
элементами из А .
Разность двух множеств обозначается
На диаграмме Эйлера-Венна разность
двух множеств выглядит так
18. РАЗНОСТЬ МНОЖЕСТВ А и В
Решение задач:1. Дано: M = { a;b;c;d } , N = { b;d } .
Найти: а) M \ N; б) N \ M; в) (M \ N) U (N \ M)
2. Найти разность множеств К = {1;2;3;7;8;9;) } и М = {2;0;8 }.
19. Дополнением множества А называется множество, состоящее из всех элементов, не принадлежащих множеству А (но принадлежащих
À..
A
U
À
A
À
À
U R, A 0;1 À ;0 1;
20.
Задача. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколькоучащихся в классе?
Решение:
Пусть А- множество учащихся изучающих
английский язык, Ф — множество учащихся
изучающих французский язык, О множество учащихся изучающих
английский и французский язык.
25-18=7(уч.) – изучают только английский;
27-18=9(уч.)– изучают только французский;
3)18+(7+9)=34(уч.)
Ответ: в классе 34 ученика.
Определение множества:
Примеры множеств:
Составьте множества из соответствующих элементов:
1.Множество может быть задано перечислением всех его элементов или списком. В этом случае элементы множества записывают внутри фигурных скобок, например: или A={студент А., рабочий Л., школьник М.}. •Мы говорим, что число 5 натуральное, т.е. утверждаем, что число 5 принадлежит множеству натуральных чисел.
Пример: Множество действительных корней уравнения x2 +1=0.Пример: Множество людей, проживающих на Солнце. •Число элементов конечного множества называют мощностью этого множества и обозначают символом Card A или |A|. •В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества. Его принято называть универсальным (универсумом) и
•Наглядно отношения между множествами изображают при помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или диаграммами Эйлера – Венна).
Если мощность множества n, то у этого множества 2n подмножеств. Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Симметрической разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (А\В) È (В\А).
• Множество детей является подмножеством всего населения. Пример 1: На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и |
Множества принято обозначать заглавными латинскими буквами. Объекты, которые образуют множество, называют элементами множества и для обозначения элементов используют, как правило, малые буквы латинского алфавита. 
..,xn}
— множество некоторых элементов x1,x2,…,xn
Эта зависимость между множествами
называется включением. Для любого множества А
имеют место включения: ÆÌ А и А
Ì А
. 
Например, если А={1,2,3,4}, B={3,1,4,2
Из 1000 абитуриентов задачу по алгебре решили 800,
по планиметрии — 700, а по стереометрии — 600 
Ни одной задачи не
решилиМножества и операции над ними. Решение задач с помощью кругов Эйлера
Современный математический язык более краток и заменяет разговорный язык специальными буквенными и символьными выражениями. Понятия и обозначения языка теории множеств составляет фундамент современного математического языка. Всякий объект, входящий во множество, называют его элементом. Например, если множество – дни недели, то понедельник элемент этого множества.
Блок 1. Множества и операции над ними.
Презентация. (Слайд 2) Вопросы к слайду 2:
- Перечислите элементы множеств:
а) арабских цифр; (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
б) натуральных чисел; (1; 2; 3; 4;…)
в) целых чисел (…-2; -1; 0; 1; 2;…).
- Как называется множество цветов, стоящих в вазе? (букет).
- Перечислите элементы множества планет солнечной системы. (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун).
- Как называется множество фруктовых деревьев и кустарников растущих у дома? (сад).
- Приведите примеры множеств, элементами которого являются геометрические фигуры.
- Какие названия применяют для обозначения множеств животных? (млекопитающие, земноводные, хладнокровные и т.п.).
- Перечислите элементы множества видов спорта (футбол, теннис, волейбол и т. п.).
- Какие названия применяют для обозначения множеств кораблей? (флотилия, эскадра).
Задайте сами множество описанием.
(Слайд 3) Множества обычно обозначают большими буквами латинского алфавита: А, В, С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных разделах математики, что для них ввели специальные обозначения:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел.
(Слайд 4) Чтобы не забыть, что перечисляемые элементы объединены вместе в некоторое множество, такое перечисление производят внутри фигурных скобок {,}.
Например, цифры десятичной системы счисления задаются множеством
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Если множество состоит из чисел, то при их перечислении иногда удобнее использовать не запятую, а знак препинания “ ; ” – точку с запятой. Так как “перечислительную” запятую можно спутать с “десятичной” запятой.
Элементы множества можно перечислять в произвольном порядке. От изменения порядка перечисления элементов само множество не меняется. Например, множество гласных букв русского алфавита задается {А, Е, Ё, И, О, У, Ы, Э, Ю, Я} или {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Эти множества состоят из одних и тех же
элементов, их называют равными, а для записи
равенства двух множеств употребляют знак “ = ”.
{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Чтобы задать конечное множество, можно просто перечислить все его элементы.
Например, запись А = {2; 3; 5; 7; 11; 13} означает, что множество А состоит из первых шести простых чисел.
Однако задавать множество путем перечисления его элементов удобно только в том случае, когда их число невелико. Если число элементов множества достаточно велико или множество бесконечно, то явное перечисление элементов такого множества невозможно.
Способы задания, описания множеств весьма
разнообразны. Например, множество всех квадратов
натуральных чисел можно записать {1; 4; 9; 16; 25; …}, а
множество всех чисел, которые больше 5 и меньше 12
записать {х | 5< х <12} или (5; 12). В примерах
использован оборот “ … и так далее” и символ “ |
” внутри фигурных скобок заменяющий комбинацию
слов “ … таких, что …”.
(Множество всех х таких,
что 5< х <12).
Описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один объект, отвечающий этому описанию. Предположим, о множестве С сказано, что оно состоит из чисел, делящихся на 6, но не делящихся на 3. Таких чисел просто нет. В подобных случаях множество называют пустым и обозначают символом O, в фигурные скобки его не ставят, так как никакого перечисления элементов пустого множества не происходит.
(Слайд 5) Задание 1. [3]
1) Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {– 2, – 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}; г) А = {0,1; 0,01; 0,001; 0,0001; …}; д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества: М = {5,4,6}, Р = {4,5,6}, Т = {5,6,7},
S = {4, 6}.
Какое из утверждений неверно?
а) М = Р. б) Р S. в) М Т. г) Р = Т.
(Слайд 6) Словесные обороты, как “элемент х принадлежит множеству А” или “х – элемент множества А”, достаточно длинны и не всегда удобны в записи решений конкретных задач.
В математике эти выражения кратко записывают так: х А, где – знак принадлежности.
Например, 5N, лучше читать не буквально, а в “литературном переводе”, “5 – число натуральное”. Наряду со знаком принадлежит используют и его “отрицание” – знак (знак не принадлежит). Запись 0 N означает, что нуль не натуральное число.
(Слайд 7) Задание 2. [3; 1]
1. Запишите на символическом языке следующее утверждение:
а) число 10 – натуральное; б) число – 7 не является натуральным; в) число – 100 является целым; г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5 N; б) -5 Z; в) 2,(45) Q?
3.
Верно ли, что:
а) 0,7 {х | х2 – 1 < 0}; б) – 7 {х | х2 + 16х ? – 64}?
(Слайд 8) Возьмем множество А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}. Каждый элемент множества А принадлежит также и множеству В. В таких случаях говорят, что множество А является подмножеством множества В, и пишут: А В.
Знак “” называют знаком включения.
Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью так называемых кругов Эйлера (Леонард Эйлер российский ученый — математик, механик, физик и астроном.). Множество изображается в виде некоторого круга, а его элементы изображаются точками этого круга (рис 1).
Рис. 1
Пустое множество считают
подмножеством любого множества. А В. Будем считать, что все элементы
рассматриваемых множеств взяты из некоторого
одного и того же “универсального” множества К.
Это множество будем изображать квадратом, а
рассматриваемые множества А, В, С, … –
подмножества множества К – кругами (или другими
полученными из них фигурами, которые выделим
штриховкой).
(Слайд 9) Задание 3. [3; 1]
1. Даны множества: А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.
Поставьте вместо … знак включения ( или ) так, чтобы получилось верное утверждение: а) А… D; б) А…В; в) С…А; г) С…В.
2. Даны три множества А = {1, 2, 3,…, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16,…,36}.
Верно ли, что: а) А В; б) В С; в) С А; г) С В?
(Слайд 10) Из данных множеств с помощью специальных операций можно образовывать новые множества:
1) Пересечением множества А и В
называют множество, состоящие из всех общих
11элементов множеств А и В, т.
е. из всех элементов,
которые принадлежат и множеству А, и множеству В
(рис. 2). Пересечение множеств А и В обозначают так:
АВ. Это определение
можно записать и так: АВ
= {х | х А и х В}. Иными словами,
пересечение двух множеств – это их общая часть.
Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АВ = {3; 9}. Если А = {10; 20; …90; 100}
и В = {6; 12; 18;…}, то АВ = {30;
60; 90}. Можно рассматривать пересечение не только
двух, но трех, четырех и т. д. множеств.
Пересечение множеств В, С и D обозначают так: ВСD.
Рис. 2
(Слайд 11) Задание 4. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АВ; б) АС; в) СВ.
2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}.
Найдите АВ.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АВ) С.
(Слайд 12)
2) Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В (рис. 3). Объединение множеств А и В обозначают так: АUВ.
Рис. 3
Это определение можно записать и так: АUВ = {х | х А или х В}. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АUВ = {1; 3; 5; 7; 9; 11; 12}. Можно рассматривать объединение не только двух, но трех, четырех и т.д. множеств. Объединение множеств В, С и D обозначают так: ВUСUD.
(Слайд 13) Задание 5. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АUВ; б) АUС; в) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АUВ)UС.
3. Даны три числовых промежутка: А = (7,7; 11), В = [; ], С = (; 13].
Найдите (АUВ)UС.
Продолжение статьи
Приложение
Презентация
Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Тема урока: Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Цель урока: изучить понятия множество, подмножество, элементы множества, пустое множество и операций над множествами: пересечение, объединение; проводить несложные систематизации; приводить примеры различных множеств и подмножеств, правильно проводить логические рассуждения.Воспитание аккуратности при работе в тетради, самостоятельности, грамотной математической речи.
Развитие мышления учащихся (в ходе выполнения заданий актуализации и на протяжении всего урока). внимания учащихся (выполнение заданий на нахождение соответствия). Развитие памяти учащихся
СТРУКТУРА УРОКА
1.Организационный момент
2.Устный счет
3. Изучение нового материала
4.Закрепление
5.Подведение итогов
6.Рефлексия
7.Домашнее задание
Ход урока
1.Организационный момент
Вступительное слово учителя
2. Устный счет
1) 52 + 32 2)67 – 25 3) 51:10 4) 47 -3 : 2
3. Изучение нового материала
Часть 1
Эпиграф:
Множество возникает путем объединения
отдельных предметов в единое целое.
Оно есть множественность мыслимая как единое.
Ф. Хаусдорф
Множество представляет собой объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам.
Обозначают А,В,Р,…
Например:
множество зверей,
множество учеников;
множество столов;
множество стульев;
Предметы, составляющие данное множество, называются его элементами.
Обозначают .
Если множество А состоит из элементов a , c , k , то записывают это так: А = { a , c , k }.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий — из элементов: сложение, вычитание, умножение, деление.
Множества, состоящие из чисел, называют числовыми множествами.
N – множество натуральных чисел,
Z – множество целых чисел.
Виды множеств
Подмножество
Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством множества А.
Пустое множество, по определению, считают подмножеством всякого множества.Обозначают Ø
Если два множества состоят из одних и тех же элементов, то они называются равными.
Например, А = { a , c , k , m , n } и В = { m , n , a , c , k }, А = В.
Множество является заданным, т.е. известным, если ясно, какие у него элементы. Поэтому, чтобы задать множество, можно просто перечислить все его элементы.
Круги́ Э́йлера[— геометрическая схема, с помощью которой можно изобразить отношения междуподмножествами, для наглядного представления. Изобретены Леонардом Эйлером.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов.
Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Практическая работа
Задание1
Перечислите множество фруктов
Перечислите множество овощей
Перечислите множество школьных предметов учеников 6 класса
Задание 2
Начертите три круга изображающие круги Эйлера. В самом маленьком круге напишите, те знания и умения которые вы приобрели в дошкольном возрасте (множества А), во втором круге – чем пополнились ваши знания в начальной школе (множества В) и в самом большом круге чему вы научились в 5-6 классах (множество С). В каком отношении находятся эти множества? (ответ А подмножества множества В и в – подмножества множества С)
1.Дано множество {11; 34; 60; 16; 90}. Принадлежит ли этому множеству число, которое получится при сложении 60 и 30, при вычитании 9 из 17, при делении 72 на 8, при вычитании И из 48, при умножении 20 на 3? [да; нет; нет; да; да].
2.По какому признаку составлено множество {зима, весна, лето, осень}, {11. 13, 15, 17, 19}? [времена года, [нечетные числа большие 10 и меньшие 20].
3.По какому признаку составлено множество {6,3,5,2,4}? [Множество чисел, больших 1 и меньших 7. Является ли это мно жество подмножеством натуральных чисел? [Да].
4.Назовите множество дней одной недели; множество месяцев одного года. Является ли множество дней одной недели подмно жеством множества дней одного месяца? [Да].
5.Даны следующие множества:
А — множество учеников данной школы;
В — множество учеников пятых классов данной школы;
С — множество учащихся всех школ данного города;
Д — множество учащихся пятых классов, посещающих кружковые занятия по математике;
Е — множество всех учащихся школ России.
[ Д ВАСЕ].
Перечислить буквы, обозначающие множества, так, чтобы каждая буква (кроме последней) обозначала подмножество следующего множества.
6.Даны множества:
А — множество натуральных чисел;
В — множество четных чисел;
С — множество нечетных чисел;
Д — множество чисел, делящихся на 5;
Е — множество чисел, делящихся на 10.
[ВА, СА, ДА, ЕА, ДС, ЕВ, ДЕ].
Указать, какие из данных множеств являются подмножествами других данных множеств.
7.Назовите множество натуральных чисел, расположенных между числами 21 и 22.
[Ø]
(Объяснение учителя).
Часть 2.Решим ЗАДАЧУ № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22.
6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
Введем обозначения:
В — множество всех учащихся;
М — множество учащихся (кружковцев), увлекающихся мате матикой;
JI — множество учащихся (кружковцев), увлекающихся лите ратурой;
И — множество учащихся (кружковцев), увлекающихся историей.
Из условия задачи следует, что все условия пересекаются.
Для составления схемы воспользуемся «кругами Эйлера».
Пересечение множеств М, JI и Д содержит 6 элементов (МЛИ|=6 это следует из условия задачи).
Пересечение множеств М и Л содержит 32 элемента (|MЛ|=32), но 6 элементов принадлежат множеству И (смотри рисунок).
Можно определить, сколько человек записать в кружки по мате матике и литературе (32-6=26 человек).
Пересечение множеств М и И содержит 11 элемента (|МИ|=11), но 6 элементов принадлежат множеству JI; следовательно в кружки по математике и истории записалось 11-6=5 человек.
ЛИ содержит 8 человек (|ЛИ|=8), но 6 элементов принадлежат множеству М, значит в кружки по литературе и истории записалось 8-6=2 человека.
Теперь легко определить сколько учащихся посещают только один кружок:
по математике — 51-(6+26+5)= 14 человек;
по литературе — 40-(6+26+2)=6 человек;
по истории — 22-(6+5+2)=9 человек;
всего записалось — 14+6+9+26+5+6+2=68 человек;
не записалось — 70-68=2 человека.
Решим ЗАДАЧУ № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием — 25, ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15, баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Введем обозначения:
Л — множество лыжников;
Б — множество баскетболистов;
П — множество пловцов.
По условию задачи все три множества пересекаются. Число эле ментов пересечения трёх множеств обозначим через X.
Пересечение множеств Б и П (БП) содержит 15 человек (|БП| = 15), но X человек принадлежат множеству Л. Можно определить, сколько человек занимаются баскетболом и плава нием: 15-Х (чел.).
Пересечение множеств JI и П (ЛП) содержит 18 человек (|ЛП|=18), но X человек принадлежат множеству Б. Можно определить, сколько человек занимаются лыжами и плаванием: 18-Х (чел.
).
Пересечение множеств Б и JI (БЛ) содержит 16 человек (|БЛ|= 16), но X человек принадлежат множеству П. Можно определить, сколько человек занимаются баскетболом и лыжами: 16-Х (чел.).
Теперь легко определить, сколько учащихся занимаются только баскетболом:
26-(16-Х+Х+15-Х)=26-(31 -X).
Сколько учащихся занимаются только плаванием:
25-(18-Х+Х+15-Х)=25-(33-Х).
Сколько учащихся занимаются только лыжами:
27-(16-Х+Х+18-Х)=27-(34-Х).
По условию задачи известно, что в классе 40 человек и один чело век освобожден от занятий по физкультуре. Следовательно, можно составить уравнение:
25-(33-Х)+27-(34-Х)+26-(31 -Х)+15-X+l 8-Х+16-Х+Х+1 =40.
Отсюда, Х= 10, т. е. 10 человек одновременно занимаются баскет болом, плаванием и лыжами.
26-(31-10)=5 (чел.) занимаются только баскетболом.
3 (чел.) занимаются только лыжами.
25-(33-10)=2 (чел.) занимаются только плаванием.
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал.
Сколько учащихся не выписывают ни журнала, ни газеты?
32-15=17 (чел.) — выписывают только газету.
21-15=6 (чел.) — выписывают только журнал.
40—(15+17+6)=2 (чел.).
Ответ: 2 человека не выписывают ни газеты, ни журнала.
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
35-10=25 (чел.) — посещают кружки.
Пусть X чел. посещают и биологический, и математический кружки, тогда 20-Х (чел.) — посещают математический кружок, а 11 -X (чел.) — посещают биологический кружок.
Известно, что всего в кружках занимаются 25 человек. Следо вательно, можно составить уравнение:
20-Х+11-Х+Х=25
Х=6
Ответ: 6 биологов увлекаются математикой.
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
Пусть X чел. владеют тремя языками, тогда (85-Х) чел. Владе ют только английским языком,(80-Х) чел. — только испанским, (75-Х) чел. — только немецким. По условию задачи известно, что среди 100 человек нет таких, которые знают только два иностранных языка, но все владеют по крайней мере одним иностранным языком. Следовательно, можно составить уравнение:
85-Х+Х+80-Х+75-Х=100
Х=70.
Ответ: 70 человек знают три иностранных языка.
Часть 3. Отношения между множествами. Операции над множествами. Разбиение множества на классы.
Между двумя множествами существует несколько видов отношений. Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В =∅ .
Например, А = { a , c , k }, В = { d , e , m , n }, общих элементов у этих множеств нет, поэтому множества не пересекаются.
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠∅ . Например, множества А = { a , c , k } и В = { c , k , m , n } пересекаются, т. к. у них есть общие элементы c , k .
Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В⊂ А)
Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.
а) б) в) г) д)
Определение.
Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А∩ В. Таким образом, по определению, А ∩ В = { х | х ∈ А и х ∈ В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∩ В = { a , c }.
Если изобразить множества А и В при помощи кругов Эйлера-Венна, то пересечением данных множеств является заштрихованная область (рис. 3).
Для пересечения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∩ В = В ∩ А.
2) Сочетательное или ассоциативное свойство:(А ∩ В) ∩ С = А ∩ (В ∩ С).
3) А ∩ ∅ = ∅ (пустое множество является поглощающим элементом).
4) А ∩ U = А (универсальное множество является нейтральным элементом).
5) Если В ⊂А, то А∩В = В
Определение. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А∪ В. Таким образом, по определению, А ∪ В = { х | х ∈А или х∈В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∪ В = { a , c , k , m , n , b , d , e }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то объединением данных множеств является заштрихованная область
Для объединения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∪ В = В ∪ А.
2) Сочетательное или ассоциативное свойство:(А ∪ В)∪ С = А ∪ (В ∪ С).
3) А ∪ ∅= А (пустое множество является нейтральным элементом).
4) А ∪ U = U (универсальное множество является поглощающим элементом).
5) Если В ⊂А, то А∪В = В
Операции объединения и пересечения множеств связаны законами дистрибутивности или иначе распределительными свойствами:
(А ∪ В) ∩С = (А∩С) ∪ (В∩С) и (А∩В) ∪ С = (А ∪ С) ∩(В ∪ С).
П р и м е р 1. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.
Р е ш е н и е. Запишем множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств войдут все элементы множества А и несовпадающие с ними элементы из множества В: А ∪ В = { м, а, т, е, и, к, с, р, о, я }.
П р и м е р 2 . В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки.
Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?
Р е ш е н и е. Через А обозначим множество школьников, изучающих английский язык, через В – множество школьников, изучающих немецкий язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18 школьников, поставим это число в пересечение множеств А и В. Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит, только английский язык изучают 7 человек, укажем это число на диаграмме. Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9 человек. Поместим и это число на диаграмму. Теперь известно количество элементов в каждой части множеств, изображенных на диаграмме. Чтобы ответить на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 = 34. Ответ: 34 человека в классе изучают иностранные языки.
Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. Таким образом, по определению разности А \ В = { х | х ∈ А и х ∉В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А \ В = { k , m , n }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством множества А. В этом случае разность множеств А и В называют дополнением подмножества В до множества А и обозначают В’А. Дополнение можно изобразить как показано на рис. 5. Если В – подмножество универсального множества U, то дополнение подмножества В до U обозначают В’.
Например, если В – множество однозначных натуральных чисел, то В’– множество неоднозначных натуральных чисел, если С – множество равнобедренных треугольников, то С’ – множество треугольников, у которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству обладают рядом свойств.
1) (А \ В) \ С = (А \ С) \ В.
2) (А∪В) \ С = (А \ С) ∪ (В \ С).
3) (А \ В) ∩ С = (А ∩С) \ (В ∩ С).
4) (А ∪ В)’ = А’ ∩ В’.
5) (А ∩ В)’ = А’ ∪В’.
Четвертое свойство формулируется так: дополнение к объединению двух множеств равно пересечению дополнений к этим множествам. Пятое свойство формулируется аналогично.
П р и м е р 1. А – множество натуральных чисел, кратных 3, В – множество натуральных чисел, кратных 5. Задать описанием характеристического свойства множество А \ В и назвать три числа, принадлежащих этому множеству.
Р е ш е н и е. По определению разность данных множеств состоит из натуральных чисел, кратных 3 и не кратных 5. Поэтому разности множеств А и В принадлежат числа 9, 24, 33.
Задания для самостоятельной работы по теме :
Приведите примеры множеств А, В, С, если отношения между ними таковы:
2.
Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?
3. Даны множества А = { a , b , c , d , e , f , k } и В = { a , c , e , k , m , p }. Найдите А ∪ В , А ∩ В , А \ В , В \ А .
4. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.
5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие).
На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.
6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø б)А U В=А
7. Пусть Х= { x N/ 1 x 15}. Задайте с помощью перечисления следующие его подмножества:
А – подмножество всех четных чисел;
В – подмножество всех нечетных чисел;
С – подмножество всех чисел, кратных 3;
D – подмножество всех чисел, являющихся квадратами;
E – подмножество всех простых чисел.
В каких отношениях они находятся?
6. Рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.
Раздаточный материал
ЗАДАЧа № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
ЗАДАЧа № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием — 25, ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15, баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками.
Сколько человек знают три иностранных языка?
Перепишите набор, перечислив его элементы, используя соответствующие обозначения набора
Дэвид К.
спросил • 29.07.19Дж={ х | x является целым числом и -4≤x<-1}
Патрик Б. ответил • 29.07.19
Репетитор/учитель математики и информатики
Набор в форме реестра:
{-4,-3,-2}
Все еще ищете помощи? Получите правильный ответ, быстро.
ИЛИ
Найдите онлайн-репетитора сейчас Выберите эксперта и встретьтесь онлайн.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ – — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° − ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ е ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А А Â Ã Ä Å Æ Ç Э Э Ê Ë Я Я Я Я Ð С Ò О Ô Õ О Ø О Ш Ù Ú Û О Ý Ÿ Þ а а â г ä å æ ç э э э ë я я я я ð с ò о ô х о ø œ ш ù ú û ü ý þ ÿ А В Г Δ Е Ζ Η Θ я Κ Λ М N Ξ О Π Р Σ Т Υ Φ Χ Ψ Ом α β γ дельта ε ζ η θ я κ λ мю ν ξ о π р ς о т υ ф х ψ ю ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊
Перепишите множество L, перечислив его элементы.
Обязательно используйте соответствующее обозначение набора . Виктория С.
спросил • 28.01.19л= {у | y является целым числом и -4 <=y <-2
Тим Т. ответил • 13.04.20
Математика: K-12 класс для Advanced Calc, Ring Theory, Cryptography
Все еще ищете помощи? Получите правильный ответ, быстро.
ИЛИ
Найдите онлайн-репетитора сейчас Выберите эксперта и встретьтесь онлайн.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ – — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° − ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ е ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А А Â Ã Ä Å Æ Ç Э Э Ê Ë Я Я Я Я Ð С Ò О Ô Õ О Ø О Ш Ù Ú Û О Ý Ÿ Þ а а â г ä å æ ç э э э ë я я я я ð с ò о ô х о ø œ ш ù ú û ü ý þ ÿ А В Г Δ Е Ζ Η Θ я Κ Λ М N Ξ О Π Р Σ Т Υ Φ Χ Ψ Ом α β γ дельта ε ζ η θ я κ λ мю ν ξ о π р ς о т υ ф х ψ ю ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊
Перепишите это множество F, перечислив его элементы.
Обязательно используйте соответствующую нотацию множества. Ф = { | y является целым числом и 1 Дэвид Т.
спросил • 25.11.18Марк М. ответил • 25.11.18
Учитель математики — высококвалифицированный специалист NCLB
2 — единственное целое число от 1 до 3
{ 2 }
Все еще ищете помощи? Получите правильный ответ, быстро.
ИЛИ
Найдите онлайн-репетитора сейчас Выберите эксперта и встретьтесь онлайн.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ – — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° − ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ е ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А А Â Ã Ä Å Æ Ç Э Э Ê Ë Я Я Я Я Ð С Ò О Ô Õ О Ø О Ш Ù Ú Û О Ý Ÿ Þ а а â г ä å æ ç э э э ë я я я я ð с ò о ô х о ø œ ш ù ú û ü ý þ ÿ А В Г Δ Е Ζ Η Θ я Κ Λ М N Ξ О Π Р Σ Т Υ Φ Χ Ψ Ом α β γ дельта ε ζ η θ я κ λ мю ν ξ о π р ς о т υ ф х ψ ю ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊
4.
1: Введение в наборыНабор представляет собой набор объектов. Объекты в наборе называются его элементами или элементами . Элементами набора могут быть любые типы объектов, включая наборы! Члены набора даже не обязательно должны быть одного типа. Например, набор может состоять из чисел и имен, хотя у него может и не быть значимого применения.
Мы обычно используем заглавные буквы, такие как \(A\), \(B\), \(C\), \(S\) и \(T\) для обозначения множеств, и обозначаем их общие элементы соответствующими им строчные буквы \(a\), \(b\), \(c\), \(s\) и \(t\) соответственно.Чтобы указать, что \(b\) является элементом множества \(B\), мы принимаем обозначение \(b\in B\), что означает «\(b\) принадлежит \(B\)» или «\(b\) является элементом \(B\)». Мы также пишем \(B\mathbb{N}i b\) и говорим: «\(B\) содержит \(b\) (как элемент)».
Мы обозначаем эти обозначения для некоторых специальных наборов чисел: \[\begin{array}{ccl} \mathbb{R} &=& \mbox{множество действительных чисел}, \\ \mathbb{Q} &=& \mbox{множество рациональных чисел}, \\ \mathbb{Z} &=& \mbox{множество целых чисел}, \\ \mathbb{N} &=& \mbox{множество натуральных чисел (целые положительные числа )}.
\end{array} \nonumber\] Все это бесконечные множества, потому что все они содержат бесконечно много элементов. Напротив, конечные множества содержат конечное число элементов.
Мы можем использовать метод реестра для описания множества, если оно состоит только из небольшого числа элементов. Перечислим все его элементы явно, как в \[A = \mbox{множество натуральных чисел, не превосходящих 7} = \{1,2,3,4,5,6,7\}. \nonnumber\] Для наборов с большим количеством элементов покажите первые несколько записей, чтобы отобразить шаблон, и используйте многоточие, чтобы указать «и так далее.Например, \[\{1,2,3,\ldots,20\} \nonumber\] представляет собой набор первых 20 положительных целых чисел. Повторяющийся шаблон может быть расширен до бесконечности, как в \[\begin{array}{ccl} \mathbb{N} &=& \{1,2,3,\ldots\} \\ \mathbb{Z} &=& \{\ldots,-2,-1,0,1,2,\ldots\} \end{array} \nonumber\] Целые числа бывают трех видов: положительные, отрицательные и беззнаковое целое число ноль.
Что касается четности, целое число может быть либо четным, либо нечетным. Целое число четно тогда и только тогда, когда оно делится на два.Следовательно, множество четных целых чисел можно описать как \(\{\ldots,-4,-2,0,2,4,\ldots\}\).
Мы можем использовать нотацию построения набора для описания набора. Например, набор натуральных чисел определяется как \[\mathbb{N} = \{x\in\mathbb{Z} \mid x>0 \}. \nonnumber\] Здесь вертикальная черта \(\mid\) читается как «такой, что» или «для которого». Следовательно, правая часть уравнения произносится как «множество \(x\), принадлежащих множеству целых чисел, таких что \(x>0\)», или просто «множество целых чисел \(x\ ) такое, что \(x>0\).2\) где \(x\in\mathbb{Z}\). Он представляет собой набор квадратов: \(\{0,1,4,9,16,25,\ldots\}\).
Пример \(\PageIndex{2}\label{например:setintro-02}\)
Множество \[\{ 2n \mid n\in\mathbb{Z} \} \nonumber\] описывает множество четных чисел. Мы также можем записать набор как \(2\mathbb{Z}\).
практическое упражнение \(\PageIndex{3}\label{he:setintro-03}\)
Описать множество \(\{2n+1 \mid n\in\mathbb{Z}\}\) с помощью ростерного метода.
практическое упражнение \(\PageIndex{4}\label{he:setintro-04}\)
Используйте метод списка для описания множества \(\{3n \mid n\in\mathbb{Z}\}\).
Интервал — это набор действительных чисел, все из которых лежат между двумя действительными числами. Должны ли конечные точки быть включены или исключены, зависит от того, является ли интервал открытым , закрытым или полуоткрытым . Мы принимаем следующие обозначения интервалов для их описания: \[\displaylines{ (a,b) = \{x\in\mathbb{R} \mid a < x < b \}, \cr [a, b] = \{x\in\mathbb{R} \mid a\leq x\leq b \}, \cr [a,b) = \{x\in\mathbb{R} \mid a\leq x < b \}, \cr (a,b] = \{x\in\mathbb{R} \mid a < x\leq b \}.\cr} \nonumber\] Подразумевается, что \(a\) должно быть меньше или равно \(b\).
Следовательно, обозначение \((5,3)\) не имеет особого смысла. Как насчет \([3,3]\)? Является ли это законным обозначением?
Интервал содержит не только целые числа, но и все числа между двумя конечными точками. Под числами мы подразумеваем целые числа и десятичные числа. Например, \((1,5) \neq \{2,3,4\}\), поскольку интервал \((1,5)\) также включает десятичные числа, такие как \(1,276\), \(\ sqrt{2}\) и \(\pi\).
Мы можем использовать \(\pm\infty\) в записи интервала: \[\begin{array}{rcl} (a,\infty) &=& \{ x\in\mathbb{R} \mid a< x \}, \\ (-\infty,a) &=& \{ x\in\mathbb{R} \mid x, а не числа. Бессмысленно говорить \(x\leq\infty\) или \(-\infty\leq x\). По той же причине мы можем писать \([a,\infty)\) и \((-\infty,a]\), но , а не \([a,\infty]\) или \([- \infty,а]\).
Пример \(\PageIndex{3}\label{например:setintro-03}\)
Запишите интервалы \((2,3)\), \([2,3]\) и \((2,3]\) в описательной форме.
2 \leq 1\} \nonumber\] в интервальной форме.2 \leq 5 \}. \end{array} \nonumber\] Один состоит только из целых чисел, а другой содержит вещественные числа. Таким образом, \(S=\{-2,-1,0,1,2\}\) и \(T=\big[-\sqrt{5},\sqrt{5}\,\big]\ ).
практическое упражнение \(\PageIndex{5}\label{he:setintro-05}\)
Какое из следующих множеств \[\{x\in\mathbb{Z} \mid 1 практическое упражнение \(\PageIndex{6}\label{he:setintro-06}\) Объясните, почему \([2,7\,] \neq\{2,3,4,5,6,7\}\).+\). практическое упражнение \(\PageIndex{8}\label{he:setintro-08}\) Как обозначается множество отрицательных целых чисел? Некоторые математики также принимают следующие обозначения: \[\begin{aligned} bS &=& \{ bx \mid x\in S \}, \\ a+bS &=& \{ a+bx \mid x\in S \}. \end{aligned} \nonumber\] Соответственно, мы можем записать множество четных целых чисел как \(2\mathbb{Z}\), а множество нечетных целых чисел можно представить как \(1+2\mathbb{Z }\). Пустой набор — это набор, не содержащий ни одного элемента.2 < 0\} \nonumber\] являются примерами пустых множеств. Второй пример иллюстрирует типичное применение пустого множества. Он предоставляет удобный способ объявить, что проблема не имеет решения: мы говорим, что множество решений — это пустое множество. Мы обозначаем пустое множество с помощью обозначений \(\emptyset\) или \(\{\,\}\). Например, можете ли вы объяснить, почему \((3,3)=\emptyset\)? практическое упражнение \(\PageIndex{9}\label{he:setintro-09}\) Что означает обозначение \([7,7\,]\)? Как бы вы описали множества \((7,7)\), \((7,7\,]\) и \([7,7)\)? Пример \(\PageIndex{7}\label{например:setintro-07}\) Определите, какие из этих утверждений верны.2+3)\geq0\} &=& \emptyset. \end{выровнено} \nonumber\] Ответы: правда, правда, ложь и ложь соответственно. Пример \(\PageIndex{8}\label{например:setintro-08}\) Когда мы пишем \(3,4,5,\ldots,n\), мы имеем в виду список целых чисел от 3 до \(n\) включительно. Два множества \(A\) и \(B\) называются равными , если они содержат один и тот же набор элементов. Более строго мы определяем \[A = B \Leftrightarrow \forall x \, (x \in A \Leftrightarrow x \in B). \nonumber\] Поскольку элементы множества сами по себе могут быть множествами, соблюдайте осторожность и используйте правильные обозначения при сравнении содержимого двух множеств. Пример \(\PageIndex{9}\label{например:setintro-09}\) Объясните, почему \(\big\{0,\{1\}\big\} \neq \{0,1\}\). Множество \(\big\{0,\{1\}\big\}\) состоит из двух элементов: целого числа \(0\) и множества \(\{1\}\). Набор \(\{0,1\}\) также состоит из двух элементов, оба из которых являются целыми числами; а именно 0 и 1. Следующая аналогия может оказаться полезной. Представьте, что набор представляет собой коробку. Когда вы откроете первую коробку, вы найдете два предмета. Одним из них является число 0; другой — еще один ящик, содержащий число 1. Второй ящик также содержит два элемента, оба из которых являются числами. То, что вы найдете в этих двух коробках, не одно и то же. Следовательно, множества, которые они представляют, различны. практическое упражнение \(\PageIndex{10}\label{he:setintro-10}\) Назовите различия между наборами \(\big\{0,\{1\}\big\}\) и \(\big\{\{0\},\{1\}\big\}\) . Пример \(\PageIndex{10}\label{например:setintro-10}\) Правда или ложь: \(\mathbb{Z}=\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\}\big\ }\)? Набор слева равен \(\mathbb{Z}\), а \[\mathbb{Z} = \{\ldots,-3,-2,-1,0,1,2,3,\ldots \}. Следовательно, они не равны. Обратите внимание, что \[\mathbb{Z} \neq \big\{\{\ldots,-3,-2,-1\}, \{0\}, \{1,2,3,\ldots\}\ big\} \nonumber\] либо потому, что набор справа — это набор из трех наборов, а набор слева — это набор целых чисел.Один состоит из трех элементов; другой имеет бесконечно много элементов. Чтобы уменьшить путаницу, вместо набора наборов мы могли бы сказать набор наборов или семейство наборов . Например, \[\big\{\{1,3,5,\ldots,\}, \{2,4,6,\ldots\,\}\big\} \nonumber\] — это семейство из двух множества, одним из которых является множество положительных нечетных целых чисел; другой — набор положительных четных целых чисел. Определение Набор называется конечным , если он имеет конечное число элементов.Количество элементов в конечном множестве \(A\) называется его мощностью и обозначается через \(|A|\). Следовательно, \(|A|\) всегда неотрицательно. Если \(A\) бесконечное множество, некоторые авторы пишут \(|A|=\infty\). Пример \(\PageIndex{11}\label{например:setintro-11}\) Хотя это тривиально, что \(|\{1,4,7,8\}| = 4\) и \(|\{0,1\}| = 2\), может быть неочевидно, что \ [\big|\big\{0,\{1\}\big\}\big| = 2, \nonumber\] и \[\big|\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\,\}\ большой\}| = 3.2-x-12<0\}|\) Помните, что ваши ответы не должны быть отрицательными. практическое упражнение \(\PageIndex{12}\label{he:setintro-12}\) Объясните, почему неправильно говорить \(|\emptyset|=\emptyset\). На самом деле бессмысленно говорить \(|\emptyset|=\emptyset\). Мы завершаем этот раздел важным замечанием о множествах.Из определения равенства множеств следует, что мы не считаем повторяющиеся элементы отдельными элементами. Например, предположим, что в небольшом студенческом клубе три офицера: и пусть \(A\) представляет собой множество его должностных лиц, а \(B\) — множество должностей в его исполнительном совете, тогда \(|A|=2\) и \(|B|= 3\), потому что \[A = \{ \mbox{Мэри}, \mbox{Джон} \}, \nonumber\] и \[B = \{ \mbox{кресло}, \mbox{заместитель председателя}, \ mbox{секретарь}\}.\номер\] Пример \(\PageIndex{12}\label{например:setintro-12}\) Найдите ошибки в следующем операторе: \[|\{-2,2\}| = \{\,|-2|,|2|\} = \{2\} = 2, \номер\] и исправьте их. Этот оператор содержит несколько ошибок. Первая ошибка заключается в предположении, что мы можем распределить символы «абсолютного значения» \(|\quad|\) по содержимому множества: \[|\{-2,2\}| \neq \{\,|-2|,|2|\}. \nonnumber\] В конце концов, две вертикальные черты в данном случае не означают абсолютное значение.Вместо этого это означает мощность множества \(\{-2,2\}\). Следовательно, \(|\{-2,2\}|=2\). Второе равенство \(\{\,|-2|,|2|\} = \{2\}\) верно. После принятия абсолютных значений обе записи становятся равными 2. Однако мы не пишем \(\{|-2|,|2|\} = \{2,2\}\), потому что набор не должен содержать повторений. Поэтому правильно говорить \(\{\,|-2|,|2|\} = \{2\}\). Последнее равенство \(\{2\}=2\) неверно. Мы не можем сравнивать множество с числом. Представьте себе набор \(\{2\}\) как коробку, содержащую только один объект, и этот объект имеет номер 2.Напротив, 2 справа оставлен на открытом воздухе без какой-либо защиты. Весь оператор содержит несколько ошибок; некоторые из них являются синтаксическими ошибками, а некоторые — концептуальными. Тем не менее, у нас есть \(|\{-2,2\}|=2\). Хотя окончательный ответ правильный, аргумент, используемый для его получения, не является таковым. В некоторых ситуациях мы хотим считать повторяющиеся элементы отдельными элементами, например \(S=\{1,2,2,2,3,3,4,4\}\).Такой набор мы называем мультимножеством вместо обычного набора. В этом случае \(|S|=8\). Упражнение \(\PageIndex{2}\label{ex:setintro-02}\) Используйте метод реестра для описания этих наборов: Упражнение \(\PageIndex{3}\label{ex:setintro-03}\) Запишите каждое из следующих множеств в виде \(\{n\in\mathbb{Z} \mid p(n)\}\) с логическим утверждением \(p(n)\), описывающим свойство \( н\). Упражнение \(\PageIndex{4}\label{ex:setintro-04}\) Повторите предыдущую задачу, но запишите множества в виде \(\{ f(n) \mid n\in S\}\), где \(f(n)\) — формула, описывающая структуру элементов, а \(S\) — соответствующий набор чисел. Упражнение \(\PageIndex{12}\label{ex:setintro-12}\) Приведите примеры множеств \(A\), \(B\) и \(C\) таких, что: Упражнение \(\PageIndex{13}\label{ex:setintro-13}\) Определите, являются ли следующие утверждения правильными или неправильными синтаксически .—\). В математике мы имеем дело с различными наборами чисел, символов и даже уравнений. Мы даем этим типам коллекций особое название в математике; мы называем их комплектов . Мы можем захотеть описать эти наборы, чтобы понять их свойства или обсудить их отношения друг с другом. Вы встретите как большие, так и маленькие наборы; поэтому вам следует научиться тому, как описывать эти наборы . Прежде чем мы приступим к описанию множеств, важно научиться определять и записывать множество. В этой статье мы узнаем: Помните, что в конце этой статьи мы предоставили пробный тест и ключ к ответу.Не забудьте проверить свое понимание. Начнем с определения набора. Набор — это набор четко определенных объектов. Мы называем эти объекты элементами или элементами множества. Как и в обычном языке, мы обычно говорим о наборах столовых приборов или наборах стульев и т. д. В математике мы также можем говорить о наборах чисел, наборах уравнений или наборах переменных. Например, множество натуральных чисел содержит все натуральные числа.Следовательно, каждое натуральное число является элементом или членом этого множества. Мы обычно применяем понятие множества в качестве предварительного условия для понимания некоторых разделов математики, таких как алгебра, математический анализ и теория вероятностей. Написать набор по математике довольно просто. Мы просто: Например, числа 5,6 и 7 являются членами множества {5,6,7} По соглашению мы должны использовать заглавную букву для обозначения множества и строчные буквы для обозначения элементов множества. Также мы всегда должны ставить знак равенства после заглавной буквы непосредственно перед записью элементов множества. Допустим, мы хотим записать множество A с элементами a, b и c. Итак, мы запишем его следующим образом: A={a,b,c} Мы также можем записать множество B, которое имеет элементы 1,2,3, 4 и 5, следующим образом: Мы также можем писать наборы внутри набора.Например, устанавливает D и E ниже. Мы используем символ ∈, чтобы показать, что объект является членом множества. Символ читается как «является элементом» или «является членом» 1 является элементом множества B выше, поэтому мы пишем 1 ∈ B. не член множества. Символ читается как «не является элементом» или «не является членом».’ 7 не является элементом множества B выше, поэтому мы пишем 7 ∉ B. В некоторых случаях в математике мы будем встречать очень большие множества или даже бесконечные множества. Это делает невозможным перечисление всех элементов множества. В таких случаях мы: Мы можем поставить знак многоточия между перечисленными элементами, чтобы показать, что между перечисленными элементами есть другие элементы, или после перечисленных элементов, чтобы показать другие элементы после тех, которые мы перечислили. Запишем множество A всех нечетных чисел от 30 до 70 как: A = {31,33,35,…,67,69} Запишем также множество N всех натуральных чисел как: N ={1,2,3,4,…} Мы учитываем эти свойства при записи множеств. Это исключает двусмысленность. Например, «множество всех низкорослых людей» определено неправильно, но «множество всех людей ростом менее 5».5 футов хорошо определены. Элементы в наборе не должны повторяться. Например, мы должны записать набор {1,3,5,3,7,9,7} как {1,3,5,7,9}. Теперь мы можем без труда научиться описывать множества. Когда мы указываем элементы набора, мы просто описываем набор.Наиболее распространенными методами, используемыми для описания наборов, являются: Давайте углубимся в детали. При использовании этого метода мы описываем множество словами, используя словесное высказывание. Мы должны убедиться, что выражение правильно определено. Примеры наборов, написанных методом словесного описания: Этот метод также называется методом табуляции. При использовании этого метода мы перечисляем элементы набора в строке между фигурными скобками. Мы называем этот метод нотацией реестра, поскольку реестр представляет собой список элементов в наборе. Этот метод также известен как метод перечисления , потому что мы обычно перечисляем элементы один за другим. Нотация реестра — это простой метод описания наборов, но неудобный при описании больших наборов. Представьте, что вы используете метод реестра для описания набора всех натуральных чисел, меньших 100! Примеры наборов, записанных с использованием нотации реестра: Теперь давайте преобразуем наборы выше из метода словесного описания в нотацию реестра. При использовании этого метода мы: Мы должны гарантировать, что свойство, которое мы используем для описания элементов набора, должно быть общим для всех элементов этого набора.Это помогает нам четко сказать, какие объекты принадлежат набору, а какие нет. Мы можем описать множество K, используя нотацию конструктора множеств, как показано ниже. К={ х | x имеет свойство M} или Мы читаем это как ‘множество K — множество всех элементов x, так, что x обладает свойством M.’ Вертикальная черта (|) или двоеточие (:) могут использоваться взаимозаменяемо для замены фразы «такой, что» или «для чего» при описании наборов.Мы используем либо вертикальную черту, либо двоеточие, чтобы отделить переменную, которую мы установили, от свойства, которое мы используем для описания элементов набора. Нотация построителя наборов более подходит, чем нотация реестра, поскольку ее можно использовать для описания как больших, так и малых наборов. Давайте воспользуемся нотацией построителя множеств для описания множества T всех целых чисел больше 5. Мы описываем множество T, как показано ниже: T={ y | y — целое число, y>5 } Преобразуем приведенные выше примеры в нотацию построителя наборов. Примеры наборов, записанных с использованием нотации конструктора наборов A={ x| x — цвет американского флага } Мы также можем использовать нотацию построителя множеств для описания интервалов действительных чисел, как показано в таблице ниже. В таблице ниже показаны некоторые наборы чисел, с которыми вы можете столкнуться в процессе изучения математики. До сих пор нам было так весело описывать множества.Теперь пришло время попробовать ответить на несколько вопросов. Доказательство: Нам нужно показать, что для любого элемента \(x\) если \(x\in \emptyset\), то \(x\in S\). Поскольку в пустом множестве нет элементов, посылка этого вывода всегда ложна. Мы знаем, что \(\mathrm{F}\rightarrow p\) всегда верно, поэтому теорема верна.∎ Доказательство: Нам нужно показать, что для любого элемента \(x\) если \(x\in S\), то \(x\in S\).
По определению, если мы выбираем элемент \(S\) (для посылки), то он находится в \(S\) (для заключения).∎ Доказательство: [Бессодержательные доказательства скучны, поэтому я не буду делать еще одно. Стратегия доказательства: Поскольку мы опровергаем универсальное утверждение, все, что нам нужно сделать, это найти контрпример.Эта теорема , а не означает, что мы не можем найти два множества, для которых \(A\times B = B\times A\), просто не всегда верно. Доказательство: Предположим, \(A=\{a\}\) и \(B=\{b\}\). Потом,
\[A\times B = \{(a,b)\}\,,\\B\times A = \{(b,a)\}\,.\]
Поскольку \((a,b)\ne (b,a)\), мы видим, что \(A\times B \ne B\times A\).∎ Вернуться на первую страницу заметок курса.Авторское право © 2013, Грег Бейкер. В современной математике практически все основано на очень важном понятии набор . Набор — это просто набор элементов или членов. Например, у вас может быть набор друзей: Ф
знак равно
{Абдул, Гретхен, Хьюберт, Джабари, Ксиомара} или набор чисел: Д
знак равно
{
−
3. Существует два метода представления множества: (i) Реестр или табличная форма (ii) Форма построения набора. Реестр или табличная форма: В форме реестра перечислены все элементы набора, элементы разделены запятыми и заключены в фигурные скобки { }. Например: Z
знак равно
в
набор
из
все
целые числа
знак равно
{
…
,
−
3
,
−
2
,
−
1
,
0
,
1
,
2
,
3
,
…
} Форма конструктора сетов: В форме построителя набора все элементы набора должны обладать одним свойством, чтобы стать членом этого набора. Например: Z
знак равно
{
Икс
:
Икс
является
ан
целое число
} Ты можешь читать
Z
знак равно
{
Икс
:
Икс
является
ан
целое число
}
как «Набор
Z
равняется всем значениям
Икс
такой, что
Икс
является целым числом.» М
знак равно
{
Икс
|
Икс
>
3
} (Это последнее обозначение означает «все действительные числа
Икс
такой, что
Икс
больше, чем
3
«Так, например,
3. Вы также можете иметь набор, который вообще не имеет элементов.Это специальное множество называется пустым множеством, и мы пишем его специальным символом
∅
. Если
Икс
является элементом множества
А
, мы пишем
Икс
е
А
, и если
Икс
не является элементом
А
мы пишем
Икс
∉
А
. Итак, используя наборы, определенные выше, −
862
е
Z
, поскольку
−
862
является целым числом, и 2.9
∉
М
, поскольку
2,9
не больше, чем
3
. Смотрите также
подмножества
и
операции над множествами
.
Подразумевается, что \(n\geq3\). Следовательно, множество \[\{3,4,5,\ldots,n\} \nonumber\] пусто, когда \(n=2\).
Вы открываете коробку, чтобы посмотреть на ее содержимое. Сам блок можно сравнить с фигурными скобками \(\{\) и \(\}\). Он содержит именно то, что мы называем элементами множества, которое он представляет.Содержимое двух наборов \(\big\{0,\{1\}\big\}\) и \(\{0,1\}\) показано в полях, показанных на рисунке \(\PageIndex{ 1}\).
\nonumber\] Это бесконечное множество. Набор справа состоит всего из трех элементов:
Объяснять. Каким должно быть значение \(|\emptyset|\)? стул: Мэри, заместитель председателя: Джон, секретарь: Джон; 
Ясно, что \(\{2\} \neq 2\). Резюме и обзор
2+18=0\}\).
2\in\mathbb{Q}\) Описание наборов – методы и примеры
Что такое множество в математике?
Как записать множество в математике?
D={p,q,{p,q,r}}
E={1,2,{3,5},6}
Набор D содержит набор {p,q,r}, а набор E содержит набор {3,5}.
Принадлежность к множеству
Наборы A и N иллюстрируют это. Свойства множеств
Порядок записи элементов в набор не имеет значения. Например, набор {1,2,3,4} можно записать как {4,3,2,1} или {2,4,3,1}. Все эти наборы одинаковы.
Как описать набор?
Метод словесного описания
Реестровое обозначение или метод составления списков
Мы всегда должны разделять элементы запятыми.
Этот способ удобен при описании небольших множеств. Ограничения нотации реестра
A={белый,красный,синий}
B={1,2,3,4,5,6,7,8,9}
C={2,4,6,8,….}
D= {-11,-12,-13,-14} Нотация построителя набора
K={ x : x имеет свойство M}, где x — переменная множества
Преимущество нотации построителя наборов
Мы выбираем y в качестве переменной нашего множества и идентифицируем подходящее свойство, описывающее множество.В этом случае y должно быть целым числом больше 5.
B={ y : y — натуральное число меньше 10}
C={ x : x — четное число}
D={ м | m — целое число от -10 до -15 }
Интервал Описание [a,b] { x | a≤ x ≤b} (замкнутый интервал) (a,b] { x | a< x ≤b} (полуоткрытый интервал) a,b,b ) { x | a≤ x (a,b) { x | < x Различные методы описания наборов
5 6 6 набор-строитель набора 76 Обозначение реестра
набор всех нечетных положительных чисел, меньших или равных 5 {x:x — нечетное число и 0 {1,2,3,4,5} Описание наборов of Numbers in Mathematics
Набор Набор 7 Описание Natural Numbers N N = {1,2,3, …}
n = {x | x — натуральное число} Целые числа W W={0,1,2,3,…}
W={x| x — целое число} Целые числа Z Z={…,-3,-2,-1,0,1,2,3,…}
Z={x| x целое число} Рациональные числа Q Q={x| x — рациональное число}
Q={x| x можно записать в виде p/q, где q≠0} Действительные числа R R={x| x действительное число} Комплексные числа C C={x: x комплексное число}
C={x+yi| a,b∈R и i — воображаемая единица }
М ={ х | x ∈R,0< x <1}
N={1,3,5,7,9} Ключ ответа
Предыдущий урок | Главная страница | Следующий урок комплектов
комплектов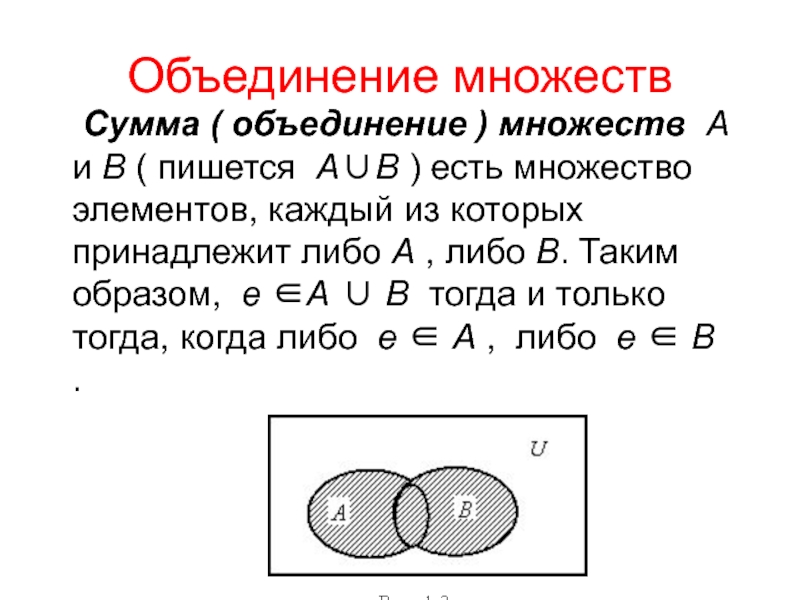
55\,.\]
например множество рациональных чисел, множество простых чисел, множество студентов на сегодняшней лекции.
{+}}\) и т. д.для наборов целых чисел/рациональных чисел больше нуля.
]
\конец{выравнивание}\]
\] комплектов
4
,
12
,
9999
}
1
есть в наборе
М
, но
2
не является. Вертикальная полоса | означает «такой, что».)