Всемирного тяготения: Закон всемирного тяготения Ньютона • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Закон всемирного тяготения Ньютона • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Между всеми телами во Вселенной действует сила взаимного притяжения.
На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в поместье своих родителей и вдруг увидел луну в дневном небе. И тут же на его глазах с ветки оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое время работал над законами движения (см. Законы механики Ньютона), он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.
Чтобы в полной мере оценить весь блеск этого прозрения, давайте ненадолго вернемся к его предыстории.

Прозрение же Ньютона как раз и заключалось в том, что он объединил эти два типа гравитации в своем сознании. С этого исторического момента искусственное и ложное разделение Земли и остальной Вселенной прекратило свое существование.
Результаты ньютоновских расчетов теперь называют законом всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы двух тел, а D — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:
F = GMm/D2
где G — гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет приблизительно 6,67 × 10–11.
 В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.
В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.Второй момент заключается в том, что сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. Прямо сейчас на вас действует сила земного притяжения, рассчитываемая по вышеприведенной формуле, и вы ее реально ощущаете как свой вес. Если вы что-нибудь уроните, оно под действием всё той же силы равноускоренно устремится к земле. Галилею первому удалось экспериментально измерить приблизительную величину ускорения свободного падения (см. Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой
Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой
Для Галилея g было просто экспериментально измеряемой константой. По Ньютону же ускорение свободного падения можно вычислить, подставив в формулу закона всемирного тяготения массу Земли M и радиус Земли D, помня при этом, что, согласно второму закону механики Ньютона, сила, действующая на тело, равняется его массе, умноженной на ускорение. Тем самым то, что для Галилея было просто предметом измерения, для Ньютона становится предметом математических расчетов или прогнозов.
Наконец, закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения.
Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением

Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим
Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться.
Я допускаю, что кого-то из историков от моей версии хватит удар, но на самом деле меня этот вопрос мало беспокоит. Как бы то ни было, яблоко Ньютона остается красивой притчей и блестящей метафорой, описывающей непредсказуемость и таинство творческого познания природы человеком. А является ли этот рассказ исторически достоверным — это уже вопрос вторичный.
См. также:
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ. | ||
Открыт Ньютоном в 1667 году на основе анализа движения планет (з-ны Кеплера) и, в частности, Луны. В этом же направлении работали Р.Гук (оспаривал приоритет) и Р.Боскович. |
| |
Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними. | ||
Закон справедлив для:
Гравитационное взаимодействие существенно при больших массах. | Примеры: Притяжение электрона к протону в атоме водорода » 2×10-11 Н.
Тяготение между Землей и Луной» 2×1020 Н.
Тяготение между Солнцем и Землей » 3,5×1022 Н. | |
Применение:
| ||
Внимание!:
| ||
Анализ закона:
|
| |
В Международной системе единиц (СИ) G=6,67.10-11. | G=6,67.10-11 | |
Впервые прямые измерения гравитационной постоянной провел Г. Кавендиш с помощью крутильных весов в 1798 г. | ||
Пусть m1=m2=1 кг, R=1 м, тогда: G=F (численно). Физический смысл гравитационной постоянной: гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга. | ||
То, что гравитационная постоянная G очень мала показывает, что интенсивность гравитационного взаимодействия мала. |
| |
СИЛА ТЯЖЕСТИ | ||
Сила тяжести — это сила притяжения тел к Земле (к планете). |
| |
— из закона Всемирного тяготения. (где M — масса планеты, m — масса тела, R — расстояние до центра планеты). — сила тяжести из второго закона Ньютона (где m — масса тела, g — ускорение силы тяжести). | ||
— ускорение силы тяжести не зависит от массы тела (опыты Галилея). | g0=9,81 м/с2 — на поверхности Земли | |
Если обозначить R0 радиус планеты, а h — расстояние до тела от поверхности планеты, то: | ||
Ускорение силы тяжести зависит:
| ||
Закон Всемирного Тяготения, гравитация, притяжение, сила, ускорение свободного падения. Направление силы, Ньютон
Тестирование онлайн
Основные понятия и определения.
Закон всемирного тяготение, ускорение свободного падения.
— По какому закону вы собираетесь меня повесить?
— А мы вешаем всех по одному закону — закону Всемирного Тяготения.
Закон всемирного тяготения
Явление гравитации — это закон всемирного тяготения. Два тела действуют друг на друга с силой, которая обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их масс.
Математически мы можем выразить этот великий закон формулой
Тяготение действует на огромных расстояниях во Вселенной. Но Ньютон утверждал, что взаимно притягиваются все предметы. А правда ли, что любые два предмета притягивают друг друга? Только представьте, известно, что Земля притягивает вас, сидящих на стуле. Но задумывались ли о том, что компьютер и мышка притягивают друг друга? Или карандаш и ручка, лежащие на столе? В этом случае в формулу подставляем массу ручки, массу карандаша, делим на квадрат расстояния между ними, с учетом гравитационной постоянной, получаем силу их взаимного притяжения. Но, она выйдет на столько маленькой (из-за маленьких масс ручки и карандаша), что мы не ощущаем ее наличие. Другое дело, когда речь идет о Земле и стуле, или Солнце и Земле. Массы значительные, а значит действие силы мы уже можем оценить.
Вспомним об ускорении свободного падения. Это и есть действие закона притяжения. Под действием силы тело изменяет скорость тем медленнее, чем больше масса. В результате, все тела падают на Землю с одинаковым ускорением.
В результате, все тела падают на Землю с одинаковым ускорением.
Чем вызвана эта невидимая уникальная сила? На сегодняшний день известно и доказано существование гравитационного поля. Узнать больше о природе гравитационного поля можно в дополнительном материале темы.
Задумайтесь, что такое тяготение? Откуда оно? Что оно собой представляет? Ведь не может быть так, что планета смотрит на Солнце, видит, насколько оно удалено, подсчитывает обратный квадрат расстояния в соответствии с этим законом?
Направление силы притяжения
Есть два тела, пусть тело А и В. Тело А притягивает тело В. Сила, с которой тело А воздействует, начинается на теле B и направлена в сторону тела А. То есть как бы «берет» тело B и тянет к себе. Тело В «проделывает» то же самое с телом А.
Каждое тело притягивается Землей. Земля «берет» тело и тянет к своему центру. Поэтому эта сила всегда будет направлена вертикально вниз, и приложена она с центра тяжести тела, называют ее силой тяжести.
Главное запомнить
1) Закон и формулу;
2) Направление силы тяжести
Некоторые методы геологической разведки, предсказание приливов и в последнее время расчет движения искусственных спутников и межпланетных станций. Заблаговременное вычисление положения планет.
Можем ли мы сами поставить такой опыт, а не гадать, притягиваются ли планеты, предметы?
Такой прямой опыт сделал Кавендиш (Генри Кавендиш (1731-1810) — английский физик и химик) при помощи прибора, который показан на рисунке. Идея состояла в том, чтобы подвесить на очень тонкой кварцевой нити стержень с двумя шарами и затем поднести к ним сбоку два больших свинцовых шара. Притяжение шаров слегка перекрутит нить — слегка, потому что силы притяжения между обычными предметами очень слабы. При помощи такого прибора Кавендишу удалось непосредственно измерить силу, расстояние и величину обеих масс и, таким образом, определить постоянную тяготения G.
Уникальное открытие постоянной тяготения G, которая характеризует гравитационное поле в пространстве, позволила определить массу Земли, Солнца и других небесных тел. Поэтому Кавендиш назвал свой опыт «взвешиванием Земли».
Поэтому Кавендиш назвал свой опыт «взвешиванием Земли».
Интересно, что у различных законов физики есть некоторые общие черты. Обратимся к законам электричества (сила Кулона). Электрические силы также обратно пропорциональны квадрату расстояния, но уже между зарядами , и невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество как два разных проявления одной и той же сущности.
Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Как можно говорить, что одно действует сильнее другого? Ведь все зависит от того, какова масса и каков заряд. Рассуждая о том, насколько сильно действует тяготение, вы не вправе говорить: «Возьмем массу такой-то величины», потому что вы выбираете ее сами. Но если мы возьмем то, что предлагает нам сама Природа (ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами, с нашими мерами), тогда мы сможем сравнивать. Мы возьмем элементарную заряженную частицу, такую, например, как электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Но если мы возьмем то, что предлагает нам сама Природа (ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами, с нашими мерами), тогда мы сможем сравнивать. Мы возьмем элементарную заряженную частицу, такую, например, как электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Вопрос: каково отношение силы тяготения к электрической силе? Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Это вызывает глубочайшее недоумение. Откуда могло взяться такое огромное число?
Люди ищут этот огромный коэффициент в других явлениях природы. Они перебирают всякие большие числа, а если вам нужно большое число, почему не взять, скажем, отношение диаметра Вселенной к диаметру протона — как ни удивительно, это тоже число с 42 нулями. И вот говорят: может быть, этот коэффициент и равен отношению диаметра протона к диаметру Вселенной? Это интересная мысль, но, поскольку Вселенная постепенно расширяется, должна меняться и постоянная тяготения. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.
И вот говорят: может быть, этот коэффициент и равен отношению диаметра протона к диаметру Вселенной? Это интересная мысль, но, поскольку Вселенная постепенно расширяется, должна меняться и постоянная тяготения. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.
Эйнштейну пришлось видоизменить законы тяготения в соответствии с принципами относительности. Первый из этих принципов гласит, что расстояние х нельзя преодолеть мгновенно, тогда как по теории Ньютона силы действуют мгновенно. Эйнштейну пришлось изменить законы Ньютона. Эти изменения, уточнения очень малы. Одно из них состоит вот в чем: поскольку свет имеет энергию, энергия эквивалентна массе, а все массы притягиваются, — свет тоже притягивается и, значит, проходя мимо Солнца, должен отклоняться. Так оно и происходит на самом деле. Сила тяготения тоже слегка изменена в теории Эйнштейна. Но этого очень незначительного изменения в законе тяготения как раз достаточно, чтобы объяснить некоторые кажущиеся неправильности в движении Меркурия.
Но этого очень незначительного изменения в законе тяготения как раз достаточно, чтобы объяснить некоторые кажущиеся неправильности в движении Меркурия.
Физические явления в микромире подчиняются иным законам, нежели явления в мире больших масштабов. Встает вопрос: как проявляется тяготение в мире малых масштабов? На него ответит квантовая теория гравитации. Но квантовой теории гравитации еще нет. Люди пока не очень преуспели в создании теории тяготения, полностью согласованной с квантовомеханическими принципами и с принципом неопределенности.
ВСЕМИРНОГО ТЯГОТЕНИЯ ЗАКОН • Большая российская энциклопедия
В книжной версии
Том 6. Москва, 2006, стр. 46
Скопировать библиографическую ссылку:
Авторы: Е. 2$ раз в продольном направлении, т. е. ведёт себя точно так же, как и электрич. сила притяжения между двумя разноимёнными электрически заряженными телами, движущимися с теми же скоростями. Это находится в соответствии с Пуанкаре принципом относительности. В случае сильных гравитационных полей, создаваемых массивными звёздами, появляется более сложная зависимость силы притяжения от расстояния.
2$ раз в продольном направлении, т. е. ведёт себя точно так же, как и электрич. сила притяжения между двумя разноимёнными электрически заряженными телами, движущимися с теми же скоростями. Это находится в соответствии с Пуанкаре принципом относительности. В случае сильных гравитационных полей, создаваемых массивными звёздами, появляется более сложная зависимость силы притяжения от расстояния.
Закон всемирного тяготения Ньютона
Чувствуете, как вас тянет к другим людям? На самом деле это и правда происходит, согласно закону всемирного тяготения Ньютона.
Признайтесь, вы тоже не до конца поняли, что такое закон всемирного тяготения Ньютона, когда учились в школе? Это неудивительно: человечество, за исключением нескольких астрономов и физиков, даже не подозревало о нем до 1687 года, да и потом еще лет 200 ученые трудились над строгим обоснованием гениальной теории Ньютона. Так что нет ничего стыдного даже для взрослого человека в том, чтобы освежить свои знания о неведомой силе, которая притягивает все тела во Вселенной, определяет траектории движения планет Солнечной системы, создает приливы и отливы и запускает течение рек на Земле, а однажды подсказала ученым сам факт существования планеты Нептун.
Так что нет ничего стыдного даже для взрослого человека в том, чтобы освежить свои знания о неведомой силе, которая притягивает все тела во Вселенной, определяет траектории движения планет Солнечной системы, создает приливы и отливы и запускает течение рек на Земле, а однажды подсказала ученым сам факт существования планеты Нептун.
По легенде, теория гравитации родилась в голове Ньютона благодаря упавшему на него яблоку, и это не пустой миф. Близкие знакомые ученого оставили свидетельства о разговоре с ним и о самом «яблочном инциденте», который, по-видимому, случился в 1666 году, когда молодой Исаак пережидал эпидемию бубонной чумы в поместье своей матери. Находясь в самоизоляции, 23-летний юноша размышлял о том, почему яблоко падает перпендикулярно к земной поверхности, а не вбок или вверх, и пришел к выводу о том, что яблоко притягивает Землю так же, как Земля притягивает яблоко.
Пока чума косила англичан, погубив пятую часть населения Лондона, научная мысль Ньютона шагала за пределы нашей планеты и он спрашивал себя: как далеко простирается эта незримая сила (гравитация) и не она ли удерживает Луну вблизи Земли, не давая ей улететь? История с падением яблока стала популярна благодаря Вольтеру, описавшему инцидент со слов племянницы Ньютона, и биографу Уильяму Стьюкли, который изложил ее в книге «Воспоминания о жизни Ньютона», выпущенной в 1752 году.
На формулировку закона всемирного тяготения у гениального британского ученого ушло два десятка лет: впервые он оповестил мир о нем в 1687 году — в своем фундаментальном труде «Математические начала натуральной философии». Так наконец удалось дать объяснение траектории движения планет вокруг Солнца, обосновать открытия немецкого астронома Кеплера, сформулированные в начале XVII века, ответив на главный вопрос: почему планеты движутся не по кругу, а по эллиптической орбите? Закон всемирного тяготения Ньютона и сама идея гравитации помогли объяснить феномены, о которых эмпирическим путем уже догадывались самые наблюдательные ученые. Большинство же людей верили в божий промысел, считали Землю центром Вселенной и даже не подозревали о том, что на яблоко и Луну влияют одни и те же физические законы.
Притяженья больше нет?Если все тела во Вселенной притягиваются, то почему мы чувствуем притяжение только к Земле, а не к холодильнику или друг к другу? Все дело в массе и расстоянии: до тех пор, пока масса предмета мала, а расстояние велико, мы не чувствуем никакого притяжения. И лишь когда речь идет о такой махине, как Земля, мы сполна ощущаем силу тяжести — одну из самых заметных проявлений силы всемирного тяготения.
И лишь когда речь идет о такой махине, как Земля, мы сполна ощущаем силу тяжести — одну из самых заметных проявлений силы всемирного тяготения.
Закон всемирного тяготения гласит: два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними
Для подсчета используется формула: F = G ∙ (m1 ∙ m2) / R², где m — масса, R — расстояние между телами, G — гравитационная постоянная, значение которой было определено экспериментально. Эта постоянная G очень мала (6,67 ∙ 10–11 м³ / (кг ∙ с²)) — именно поэтому сила, с которой притягиваются тела небольшой массы, нами совершенно не ощущается.
Был ли Ньютон первооткрывателем?С момента публикации «Начал» многим ученым не нравилось, что Ньютон не объяснил физическую природу гравитации, не назвал ее источник, не привел доказательства. Некоторые ученые считали, что ученый промышляет плагиатом: мысль о том, что движение планет объясняется действием силы, которая притягивает каждую планету к Солнцу, уже высказывалась ранее, в том числе английским физиком Робертом Гуком — он даже сформулировал, что эта сила убывает обратно пропорционально квадрату расстояния от Солнца. Свою теорию Гук изложил в том самом 1666 году, когда на Исаака упало яблоко, а в 1679 году посылал Ньютону письмо, где предлагал сотрудничать по решению этой задачи, но получил отказ и заверения о том, что эта тема давно не занимает адресата. В дальнейшем Гук требовал указывать его имя как первого автора закона тяготения и открыто обвинял Ньютона в плагиате. Ученые конфликтовали до конца жизни Гука, а спор о том, кто был первым, продолжался даже в XX веке.
Свою теорию Гук изложил в том самом 1666 году, когда на Исаака упало яблоко, а в 1679 году посылал Ньютону письмо, где предлагал сотрудничать по решению этой задачи, но получил отказ и заверения о том, что эта тема давно не занимает адресата. В дальнейшем Гук требовал указывать его имя как первого автора закона тяготения и открыто обвинял Ньютона в плагиате. Ученые конфликтовали до конца жизни Гука, а спор о том, кто был первым, продолжался даже в XX веке.
«К сожалению, нам неизвестны детали того логического пути, которым Ньютон пришел к закону всемирного тяготения», — писали американские ученые в книге «Физика» в 1960 году.
«Если связать в одно все предположения и мысли Гука о движении планет и тяготении, высказанные им в течение почти 20 лет, то мы встретим почти все главные выводы «Начал» Ньютона, только высказанные в неуверенной и мало доказательной форме. Не решая задачи, Гук нашел ее ответ», — писал советский ученый Сергей Вавилов. Ньютон был блестящим математиком и смог решить поставленную Гуком задачу.
Лишь после того, как ньютоновская теория стала основой небесной механики в XVIII веке, физики приняли ее более благосклонно. Закон всемирного тяготения Ньютона стал подарком для астрономов, так как математически объяснил почти все, что происходит во Вселенной. Но, пожалуй, главным вкладом Ньютона в астрономию стало открытие в 1846 году Нептуна — самой дальней от Земли планеты и первой, обнаруженной путем математических расчетов.
Этому знаменательному событию предшествовало открытие Урана в 1781 году английским астрономом Уильямом Гершелем. Наблюдавшие за ее движением астрономы многие годы народились в затруднении: реальная орбита Урана не совпадала с вычисленной. Это недоразумение заставляло думать о том, что за Ураном прячется еще одна планета, которая влияет на нее своим притяжением. Французский математик Урбен Леверье провел расчеты с помощью ньютоновой механики и указал астрономам, где именно нужно искать восьмую планету. 2}}\ — ускорение свободного падения на высоте hh от поверхности Земли.
2}}\ — ускорение свободного падения на высоте hh от поверхности Земли.
Силой тяжести называют силу, с которой тело притягивается к планете:
\[\boxed{F = mg} — \mathrm{сила}\ \mathrm{тяжести}\]
Рассмотрим твёрдое тело, расположенное на горизонтальной неподвижной опоре: под действием силы тяжести тело деформируется. Если тело находится на опоре, то на нижний слой действуют все верхние слои, и, как следствие, этот слой деформируется наибольшим образом. На предпоследний слой действует меньшее количество слоёв, и он деформируется меньше. Таким образом, тело, бывшее прямоугольным, примет вид трапеции. Нижний слой приблизился при такой деформации к центру тела, а значит, возникла сила упругости, направленная в сторону, противоположную направлению смещения частиц при деформации. Сила упругости, возникшая внутри данного тела, направлена перпендикулярно опоре. Эту силу, созданную деформированным телом и приложенную к опоре, называют весом тела. Опора под действием веса деформируется. Противоположная весу сила упругости действует на данное тело со стороны деформированной опоры и тоже направлена перпендикулярно опоре, но называется силой реакции опоры NN (от слова normal — перпендикуляр).
Противоположная весу сила упругости действует на данное тело со стороны деформированной опоры и тоже направлена перпендикулярно опоре, но называется силой реакции опоры NN (от слова normal — перпендикуляр).
| Рис. 9 |
На рисунке 9 тело не касается опоры для того, чтобы показать, что вес приложен к опоре, а сила реакции опоры к телу. В действительности площадь реального соприкосновения твёрдых тел невелика. Большей частью между телами находится тонкий слой воздуха.
Вполне очевидно, что если опоры нет, то и веса тело иметь не будет. Такое случится в том случае, если тело движется под действием только одной силы – силы тяготения.
Невесомостью называют состояние тела, когда оно движется под действием только силы тяготения.
Так же легко понять, что если на тело действует две силы (сила тяжести и сила реакции опоры), то эти силы не обязательно равны друг другу. Одна из них может быть больше другой.
Одна из них может быть больше другой.
Рассмотрим движение тела, помещённого в лифт. Пусть сам лифт движется с ускорением a→\vec a. Такое ускорение будет в двух случаях: 1) лифт поднимается равно ускорено, 2) лифт опускается равнозамедленно. Второй закон Ньютона для данного тела примет вид:
| Рис. 10 |
N→+mg→=ma→.\vec N + m \vec g = m \vec a.
При рассмотрении данного движения из лабораторной неподвижной системы отсчёта OyOy увидим, что в проекции на вертикальную ось OyOy второй закон запишется следующим образом:
N-mg=ma,N — mg = ma,
откуда
N=ma+mg=m(g+a).N = ma + mg = m(g+a).
Но по третьему закону Ньютона знаем, что сила реакции опоры и вес тела равны и противоположны, следовательно:
N=P,N = P,
тогда: P=m(g+a) -\boxed{P = m(g+a)}\ — вес тела, движущегося с ускорением, направленным вверх (рис. 10). 2}{R})}\ — вес тела, движущегося с ускорением, направленным вверх (вогнутая дорога).
2}{R})}\ — вес тела, движущегося с ускорением, направленным вверх (вогнутая дорога).
Важное дополнение:
Для рассматриваемой силы, называемой весом, важно понимать и уметь правильно изображать точку приложения этой силы.
На рисунке 11а показан лифт, у которого нет ускорения. Тогда сила тяжести равна силе реакции опоры . А по третьему закону Ньютона, сила реакции опоры равна весу тела. Точка приложения силы тяжести расположена в геометрическом центре тела, если тело однородно и правильной формы. Точка приложения силы реакции опоры должна быть изображена внутри тела вблизи с нижней поверхностью тела на линии действия силы тяжести. Последнее свойство на рисунке не выдержано для удобства изображения (иначе силы на рисунке будут накладываться друг на друга). Точка приложения веса тела находится внутри опоры (пола лифта) вблизи поверхности на линии действия силы реакции опоры.
Рис. 2} = \frac 18 F = 10\ \text{Н}.\] 2} = \frac 18 F = 10\ \text{Н}.\]Сила притяжения шаров станет меньше на 10 Н10\ \text{Н}, следовательно, станет равной 70 Н70\ \text{Н}. Для проверки закона всемирного тяготения измерили рекордно слабое гравитационное поле — НаукаТАСС, 10 марта. Ученые провели самую точную проверку закона всемирного тяготения Ньютона. Для этого они измерили рекордно слабое гравитационное поле, которое образовали две микроскопических золотых сферы массой в 90 мг и радиусом в 1 мм. Описание эксперимента опубликовал научный журнал Nature. На эту тему «Ранее подобные измерения проводили для объектов массой в килограмм и более, а мы сделали это со сферами массой в 90 мг. Это открывает дорогу для еще более точных измерений – например, для тел, сопоставимых по массе с самыми крупными элементарными частицами», –пишут исследователи. Физиков давно интересует, работает ли классический закон всемирного тяготения на микроскопических масштабах. Проверить это сложно, поскольку хотя гравитация действует на очень большие расстояния, но при этом ее тяжело измерить. Однако подобные эксперименты очень важны для физиков, так как благодаря им можно проверить, существуют ли скрытые измерения пространства и какими свойствами обладают темная материя и энергия. Большой шаг в эту сторону сделали физики под руководством профессора Венского университета Маркуса Аспельмейера. Они создали установку, с помощью которой можно с максимальной точностью определить, с какой силой притягивают друг друга сферы из золота диаметром всего в миллиметр и массой в 90 миллиграмм. Установка выглядит как сделанное из сверхтонкой проволоки маленькое коромысло. К его середине прикреплено зеркало, а также нить, на которой вся конструкция может вращаться вокруг своей оси. К концам коромысла прикрепляются объекты, гравитационные свойства которых физики пытаются изучить. На эту тему Зеркало постоянно подсвечивает луч лазера, отражение которого улавливает фотодетектор. С помощью этой установки Аспельмейер и его коллеги проследили, как по мере удаления и сближения шариков друг с другом их притягивала еще одна золотая сфера, которую ученые поместили на небольшом расстоянии от одного из шариков. Результаты измерений физики использовали для вычисления гравитационной постоянной G, значение которой определено не максимально точно. Из-за того, что гравитационные взаимодействия между сферами очень малы (они не превышают 0,09 пиконьютонов), ученые повторяли эксперимент более 350 раз, чтобы исключить влияние всех источников помех. В итоге авторы эксперимента получили относительно точное значение G, которое расходится с общепринятыми оценками примерно на 9%. Ученые надеются, что дальнейшие измерения с еще более легкими объектами помогут проверить, было ли это расхождение простой погрешностью измерений или же оно существует на самом деле. Закон всемирного тяготения НьютонаКак обсуждалось ранее в Уроке 3, Исаак Ньютон сравнил ускорение Луны с ускорением объектов на Земле. Полагая, что за каждую из них ответственны гравитационные силы, Ньютон смог сделать важный вывод о зависимости силы тяжести от расстояния. Это сравнение привело его к выводу, что сила гравитационного притяжения между Землей и другими объектами обратно пропорциональна расстоянию, отделяющему центр Земли от центра объекта.Но расстояние — не единственная переменная, влияющая на величину гравитационной силы. Рассмотрим знаменитое уравнение Ньютона . F net = m • a Ньютон знал, что сила, вызывающая ускорение яблока (гравитация), должна зависеть от массы яблока. Но закон всемирного тяготения Ньютона распространяет гравитацию за пределы Земли. Закон всемирного тяготения Ньютона говорит о универсальности гравитации.Место Ньютона в Зале славы гравитации связано не с его открытием гравитации, а с его открытием универсальности гравитации. ВСЕ объектов притягивают друг друга силой гравитационного притяжения. Гравитация универсальна. Эта сила гравитационного притяжения напрямую зависит от масс обоих объектов и обратно пропорциональна квадрату расстояния, разделяющего их центры. Поскольку гравитационная сила прямо пропорциональна массе обоих взаимодействующих объектов, более массивные объекты будут притягивать друг друга с большей силой гравитации.Таким образом, когда масса любого объекта увеличивается, сила гравитационного притяжения между ними также увеличивается. Если масса одного из предметов увеличивается вдвое, то сила тяжести между ними увеличивается вдвое. Если масса одного из предметов увеличивается втрое, то сила тяжести между ними увеличивается втрое. Если масса обоих объектов увеличивается вдвое, то сила тяжести между ними увеличивается в четыре раза; и так далее. Поскольку сила тяжести обратно пропорциональна квадрату расстояния разделения между двумя взаимодействующими объектами, большее расстояние разделения приведет к более слабым силам гравитации.Так как два объекта отделены друг от друга, сила гравитационного притяжения между ними также уменьшается. Пропорциональности, выраженные универсальным законом всемирного тяготения Ньютона, графически представлены на следующем рисунке. Обратите внимание, как сила тяжести прямо пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния разделения. Еще один способ представления пропорциональностей — это выражение отношений в форме уравнения с использованием константы пропорциональности.Это уравнение показано ниже. Константа пропорциональности (G) в приведенном выше уравнении известна как универсальная гравитационная постоянная . Блоки на G могут показаться довольно странными; тем не менее они разумны.Когда единицы на G подставляются в приведенное выше уравнение и умножаются на м 1 • м 2 единиц и делятся на d 2 единиц, результатом будет Ньютоны — единица силы. Использование уравнения тяготения Ньютона для решения задачЗнание значения G позволяет нам вычислить силу гравитационного притяжения между любыми двумя объектами известной массы и известного расстояния разделения.В качестве первого примера рассмотрим следующую проблему.
Решение задачи заключается в подстановке известных значений G (6.673 x 10 -11 Н м 2 / кг 2 ), м 1 (5,98 x 10 24 кг), м 2 (70 кг) и d (6,38 x 10 6 м) в универсальное уравнение гравитации и решение для F grav . Решение следующее:
Решение задачи заключается в подстановке известных значений G (6,673 x 10 -11 Н · м 2 / кг 2 ), м 1 (5,98 x 10 24 кг), м 2 (70 кг) и d (6. Можно сделать два общих концептуальных комментария к результатам двух приведенных выше расчетов. Во-первых, обратите внимание на то, что сила тяжести, действующая на ученика (также известная как вес ученика), меньше на самолете на высоте 40000 футов, чем на уровне моря. Это иллюстрирует обратную зависимость между разделительным расстоянием и силой тяжести (или, в данном случае, весом ученика).На большей высоте ученик весит меньше. Однако простое изменение на 40 000 футов от центра Земли практически незначительно. Это изменение высоты изменило вес ученика на 2 Н, что намного меньше 1% от первоначального веса. Расстояние в 40000 футов (от поверхности земли до высотного самолета) не так уж и далеко по сравнению с расстоянием 6,38 x 10 6 м (что эквивалентно почти 20000000 футов от центра Земли до поверхность земли).Это изменение расстояния похоже на капля в ведре по сравнению с большим радиусом Земли. Второй концептуальный комментарий к приведенным выше примерным расчетам заключается в том, что использование универсального уравнения гравитации Ньютона для вычисления силы тяжести (или веса) дает тот же результат, что и при его вычислении с использованием уравнения, представленного в Блоке 2: F grav = m • g = (70 кг) • (9.8 м / с 2 ) = 686 НОба уравнения дают один и тот же результат, потому что (как мы изучим позже в Уроке 3) значение g эквивалентно отношению (G • M земля ) / (R земля ) 2 . Универсальность гравитации Гравитационные взаимодействия существуют не просто между Землей и другими объектами; и не просто между Солнцем и другими планетами.Гравитационные взаимодействия существуют между всеми объектами с интенсивностью, которая прямо пропорциональна произведению их масс.
Сегодня закон всемирного тяготения Ньютона является широко принятой теорией. Он направляет усилия ученых при изучении планетных орбит. Зная, что все объекты оказывают гравитационное влияние друг на друга, небольшие возмущения в эллиптическом движении планеты можно легко объяснить.По мере того, как планета Юпитер приближается к планете Сатурн по своей орбите, она имеет тенденцию отклоняться от своего плавного пути; это отклонение, или возмущение , легко объяснить, если учесть влияние гравитационного притяжения между Сатурном и Юпитером. Сравнение Ньютоном ускорения яблока с ускорением луны привело к удивительно простому выводу о природе гравитации, которая пронизывает всю Вселенную. Все объекты притягивают друг друга с силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна расстоянию между ними.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Gravitation Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Gravitation Interactive позволяет учащемуся интерактивно исследовать закон обратных квадратов гравитации. Проверьте свое понимание Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Gravitation Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Gravitation Interactive позволяет учащемуся интерактивно исследовать закон обратных квадратов гравитации. Проверьте свое понимание 1. Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц.Если расстояние между двумя объектами удвоится, какова новая сила притяжения между двумя объектами? 2. Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если расстояние между двумя объектами уменьшится вдвое, то какова новая сила притяжения между двумя объектами? 3.Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если бы масса обоих объектов увеличилась вдвое, и если бы расстояние между объектами осталось прежним, то какой была бы новая сила притяжения между двумя объектами? 4. 5.Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если бы масса обоих объектов была утроена, и если бы расстояние между объектами было удвоено, то какой была бы новая сила притяжения между двумя объектами? 6. Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если бы масса объекта 1 была удвоена, и если бы расстояние между объектами было утроено, то какой была бы новая сила притяжения между двумя объектами? 7.Считается, что с возрастом звезда претерпевает множество изменений. Один из последних этапов жизни звезды — это гравитационный коллапс в черную дыру. 8. Недавно завершив свой первый курс физики, Дон Велл разработала новый бизнес-план на основе темы «Физика для лучшей жизни » ее учителя.Доун узнала, что объекты весят разное количество на разном расстоянии от центра Земли. Ее план включает покупку золота на вес на одной высоте, а затем продажу его на другой высоте по той же цене за вес. Следует ли Dawn покупать на большой высоте и продавать на низкой или наоборот? 9. Фред очень беспокоится о своем весе, но редко что-то с ним делает. Узнав о законе всемирного тяготения Ньютона на уроке физики, он начинает беспокоиться о возможном влиянии изменения массы Земли на его вес.Во время (редкого) свободного времени за обеденным столом он говорит: «Как бы изменился мой вес, если бы масса Земли увеличилась на 10%?» Как бы вы ответили Фреду? 10.
Закон всемирного тяготения НьютонаЗакон всемирного тяготенияОбъекты с массой ощущают силу притяжения, которая пропорциональна их массе и обратно пропорциональна квадрату расстояния. Цели обученияВыразите закон всемирного тяготения в математической форме Основные выводыКлючевые моменты
Ключевые термины
В то время как яблоко могло и не поразить сэра Исаака Ньютона в голову, как предполагает миф, падение одного из них действительно вдохновило Ньютона на одно из величайших открытий в механике: Закон всемирного тяготения . Размышляя о том, почему яблоко никогда не падает вбок, вверх или в любом другом направлении, кроме перпендикулярного земле, Ньютон понял, что сама Земля должна быть ответственна за движение яблока вниз. Теоретически предполагая, что эта сила должна быть пропорциональна массам двух задействованных объектов, и используя предыдущую интуицию о соотношении обратных квадратов силы между Землей и Луной, Ньютон смог сформулировать общий физический закон с помощью индукции. Закон всемирного тяготения гласит, что каждая точечная масса притягивает любую другую точечную массу во Вселенной силой, направленной по прямой линии между центрами масс обеих точек, и эта сила пропорциональна массам объектов и обратно пропорциональна их разделению. Эта сила притяжения всегда направлена внутрь, от одной точки к другой.Закон распространяется на все объекты большой или малой массы. Два больших объекта можно рассматривать как точечные массы, если расстояние между ними очень велико по сравнению с их размерами или если они сферически симметричны. Для этих случаев масса каждого объекта может быть представлена как точечная масса, расположенная в его центре масс. Хотя Ньютон смог сформулировать свой Закон всемирного тяготения и проверить его экспериментально, он мог только вычислить относительную гравитационную силу по сравнению с другой силой.2 [/ латекс]. Из-за величины [латекса] \ text {G} [/ latex] гравитационная сила очень мала, если не задействованы большие массы. Силы на двух массах : Все массы притягиваются друг к другу. Сила пропорциональна массам и обратно пропорциональна квадрату расстояния. Гравитационное притяжение сферических тел: однородная сфераТеорема о оболочке утверждает, что сферически-симметричный объект влияет на другие объекты, как если бы вся его масса была сосредоточена в его центре. Цели обученияСформулируйте теорему о оболочке для сферически-симметричных объектов Основные выводыКлючевые моменты
|





 Поэтому погрешности в подобных измерениях могут возникать даже из-за самых слабых помех.
Поэтому погрешности в подобных измерениях могут возникать даже из-за самых слабых помех. Благодаря этому на то, в каком направлении будет отражаться луч света, влияют даже малейшие сдвиги в положении сфер и прикрепленного к ним «коромысла».
Благодаря этому на то, в каком направлении будет отражаться луч света, влияют даже малейшие сдвиги в положении сфер и прикрепленного к ним «коромысла». Кроме того, эти опыты дадут физикам шанс вплотную приблизиться к тому пределу масс, где теоретически должны действовать квантовые гравитационные эффекты. Благодаря этому можно будет проверить теории, которые допускают их существование.
Кроме того, эти опыты дадут физикам шанс вплотную приблизиться к тому пределу масс, где теоретически должны действовать квантовые гравитационные эффекты. Благодаря этому можно будет проверить теории, которые допускают их существование. А поскольку сила, вызывающая ускорение яблока вниз, также вызывает ускорение земли вверх (третий закон Ньютона), эта сила также должна зависеть от массы Земли.Таким образом, для Ньютона сила тяжести, действующая между Землей и любым другим объектом, прямо пропорциональна массе Земли, прямо пропорциональна массе объекта и обратно пропорциональна квадрату расстояния, разделяющего центры объектов. земля и объект.
А поскольку сила, вызывающая ускорение яблока вниз, также вызывает ускорение земли вверх (третий закон Ньютона), эта сила также должна зависеть от массы Земли.Таким образом, для Ньютона сила тяжести, действующая между Землей и любым другим объектом, прямо пропорциональна массе Земли, прямо пропорциональна массе объекта и обратно пропорциональна квадрату расстояния, разделяющего центры объектов. земля и объект. Вывод Ньютона о величине гравитационных сил символически резюмируется как
Вывод Ньютона о величине гравитационных сил символически резюмируется как Если расстояние между двумя объектами увеличивается вдвое (увеличивается в 2 раза), то сила гравитационного притяжения уменьшается в 4 раза (2 во второй степени). Если расстояние между любыми двумя объектами увеличивается в три раза (увеличивается в 3 раза), то сила гравитационного притяжения уменьшается в 9 раз (3 во второй степени).
Если расстояние между двумя объектами увеличивается вдвое (увеличивается в 2 раза), то сила гравитационного притяжения уменьшается в 4 раза (2 во второй степени). Если расстояние между любыми двумя объектами увеличивается в три раза (увеличивается в 3 раза), то сила гравитационного притяжения уменьшается в 9 раз (3 во второй степени). Точное значение G было экспериментально определено Генри Кавендишем через столетие после смерти Ньютона. (Этот эксперимент будет обсуждаться позже в Уроке 3.) Значение G составляет
Точное значение G было экспериментально определено Генри Кавендишем через столетие после смерти Ньютона. (Этот эксперимент будет обсуждаться позже в Уроке 3.) Значение G составляет .
. 39 x 10 6 м) в универсальное уравнение гравитации и решение для F grav . Решение следующее:
39 x 10 6 м) в универсальное уравнение гравитации и решение для F grav . Решение следующее: Как показано на диаграмме ниже, расстояние разделения становится гораздо более важным при значительном изменении.
Как показано на диаграмме ниже, расстояние разделения становится гораздо более важным при значительном изменении. Итак, когда вы сидите на своем месте в классе физики, вас притягивает гравитационное влечение к партнеру по лаборатории, к столу, за которым вы работаете, и даже к своей книге по физике. Революционная идея Ньютона заключалась в том, что гравитация универсальна — ВСЕ объекты притягиваются пропорционально произведению их масс. Гравитация универсальна. Конечно, большинство гравитационных сил настолько минимальны, чтобы их можно было заметить.Гравитационные силы распознаются только тогда, когда массы объектов становятся большими. Чтобы проиллюстрировать это, используйте универсальное уравнение тяготения Ньютона для вычисления силы тяжести между следующими знакомыми объектами. Нажмите кнопки, чтобы проверить ответы.
Итак, когда вы сидите на своем месте в классе физики, вас притягивает гравитационное влечение к партнеру по лаборатории, к столу, за которым вы работаете, и даже к своей книге по физике. Революционная идея Ньютона заключалась в том, что гравитация универсальна — ВСЕ объекты притягиваются пропорционально произведению их масс. Гравитация универсальна. Конечно, большинство гравитационных сил настолько минимальны, чтобы их можно было заметить.Гравитационные силы распознаются только тогда, когда массы объектов становятся большими. Чтобы проиллюстрировать это, используйте универсальное уравнение тяготения Ньютона для вычисления силы тяжести между следующими знакомыми объектами. Нажмите кнопки, чтобы проверить ответы. )
) 
 901 x 10 27 кг
901 x 10 27 кг
 Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если бы масса обоих объектов была удвоена, и если бы расстояние между объектами было удвоено, то какой была бы новая сила притяжения между двумя объектами?
Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если бы масса обоих объектов была удвоена, и если бы расстояние между объектами было удвоено, то какой была бы новая сила притяжения между двумя объектами? Что будет с орбитой планет солнечной системы, если наша звезда (Солнце превратится в черную дыру)? (И, конечно, это предполагает, что планеты не подвержены влиянию предыдущих стадий развития Солнца.)
Что будет с орбитой планет солнечной системы, если наша звезда (Солнце превратится в черную дыру)? (И, конечно, это предполагает, что планеты не подвержены влиянию предыдущих стадий развития Солнца.)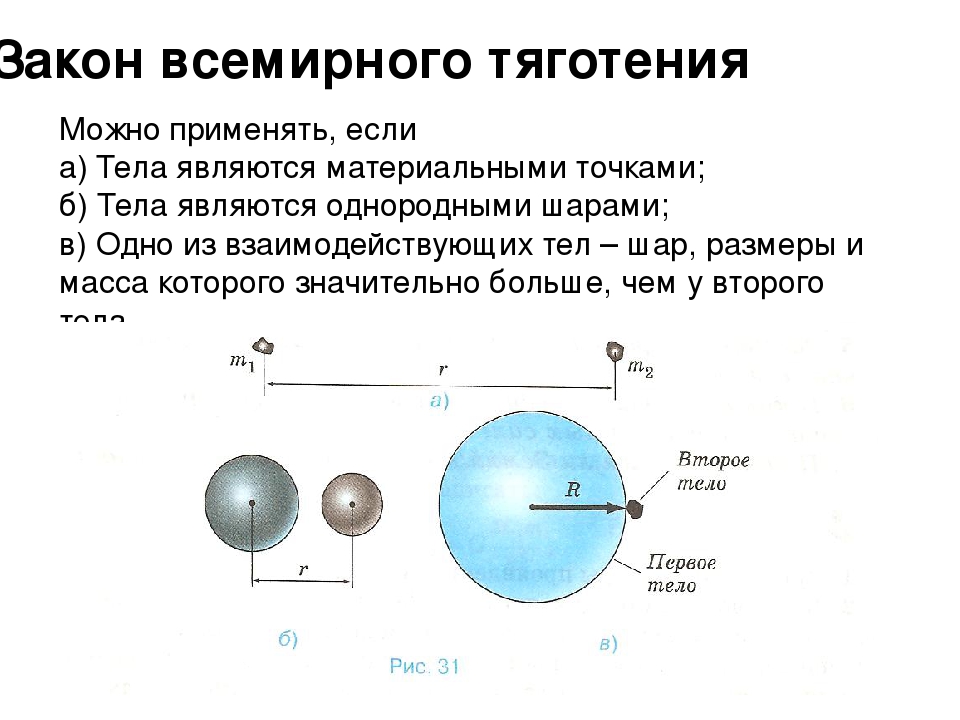 При сравнении данных о массе и размере планет Земля и Юпитер было замечено, что Юпитер примерно в 300 раз массивнее Земли. Можно быстро заключить, что объект на поверхности Юпитера и будет весить в 300 раз больше, чем на поверхности Земли.Например, можно было ожидать, что человек, который весит 500 Н на Земле, будет весить 150000 Н на поверхности Юпитера. Но это не так. Фактически, человек массой 500 N на Земле весит около 1500 N на поверхности Юпитера. Объясните, как это может быть.
При сравнении данных о массе и размере планет Земля и Юпитер было замечено, что Юпитер примерно в 300 раз массивнее Земли. Можно быстро заключить, что объект на поверхности Юпитера и будет весить в 300 раз больше, чем на поверхности Земли.Например, можно было ожидать, что человек, который весит 500 Н на Земле, будет весить 150000 Н на поверхности Юпитера. Но это не так. Фактически, человек массой 500 N на Земле весит около 1500 N на поверхности Юпитера. Объясните, как это может быть. 2} [/ latex] где [latex] \ text {G} [/ latex] — гравитационная постоянная.
2} [/ latex] где [latex] \ text {G} [/ latex] — гравитационная постоянная.