Все производные формулы: Полная таблица производных элементарных функций
Полная таблица производных элементарных функций
Самый частый вопрос, который возникает у старшеклассников на уроках алгебры, звучит примерно так: «А нам это в жизни пригодится?». Отвечаем: пригодится! Математика тесно связана с физикой, которая описывает окружающий нас мир. И формулы из таблицы производных основных элементарных функций тоже имеют практический смысл.
Что такое производная и зачем она нужна
Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:
Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю. |
Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.
Процесс нахождения производной называется дифференцированием.
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.
у = 10
у′ = 0
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.
у = 10 + 3х
Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1, а также по правилам вычисления производных (c*f(x))’=cf'(x) и (f(x)+g(x))’=f'(x)+g'(x).
у = 10 + 3х
у′ = 0 + 3
у′ = 3
Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.
Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.
Быстрее освоить производные поможет обучение на курсах по математике в онлайн-школе Skysmart.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Производные основных элементарных функций
Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Поэтому приведем стандартную таблицу производных.
Функция f (x) | Производная f’ (х) |
|---|---|
С (т. е. константа, любое число) | 0 |
х | 1 |
xn | nxn-1 |
√x | 1/(2√x) |
sin x | |
cos x | -sin x |
tg x | 1/cos2(х) |
ctg x | -1/sin2x |
ex | ex |
ax | ax * ln a |
1/x | |
logax | 1/(x * ln a) |
Элементарные функции можно складывать, умножать друг на друга, находить их разность или частное — словом, выполнять любые математические операции.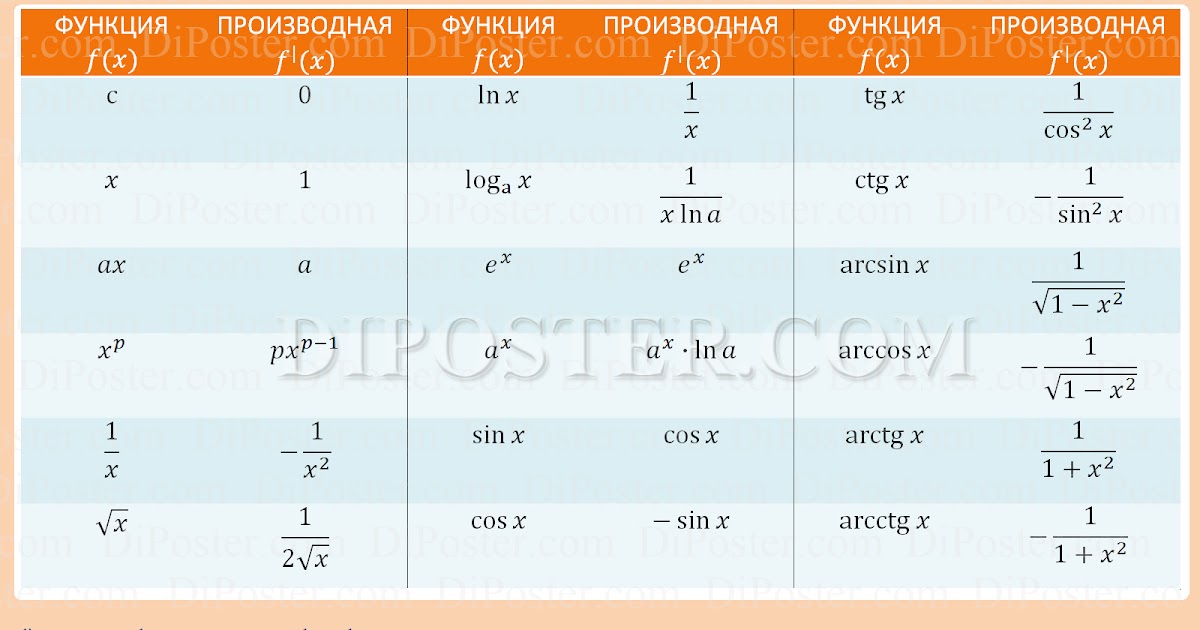
Общие правила дифференцирования
Для решения задач на дифференцирование нужно запомнить (или записать в шпаргалку) пять несложных формул:
(c ⋅ f)′ = c ⋅ f′
(u + v)′ = u′ + v′
(u — v)′ = u′ — v′
(u ⋅ v)′ = u′v + v′u
(u/v)’ = (u’v — v’u)/v2
В данном случае u, v, f — это функции, а c — константа (любое число).
С константой все просто — ее можно смело выносить за знак производной. Специально запоминать придется лишь формулы, где требуется разделить одну функцию на другую или перемножить их и найти производную от результата.
Например: требуется найти производную функции y = (5 ⋅ x3).
y′ = (5 ⋅ x3)′
Вспомним, что константу, а в данном случае это 5, можно вынести за знак производной:
y′ = (5 ⋅ x3)’ = 5 ⋅ (x3)′ = 5 ⋅ 3 ⋅ х3-1 = 15х2
Попробуйте самостоятельно решить эти примеры.
Правила дифференцирования сложных функций
Конечно, далеко не все функции выглядят так, как в вышеуказанной таблице. Как быть с дифференцированием, например, вот таких функций: y = (3 + 2x2)4?
Сложной функцией называют такое выражение, в котором одна функция словно вложена в другую. Производную сложной функции f(y) можно найти по следующей формуле: |
Пример 1
Найдем производную функции y(x) = (3 + 2x2)4.
Заменим 3 + 2x2 на u и тогда получим y = u4.
Согласно приведенному выше правилу дифференцирования сложных функций у нас получится:
y = y′u ⋅ u′x = 4u3 ⋅ u’x
А теперь выполним обратную замену и подставим исходное выражение:
4u3 ⋅ u′x = 4 (3 + 2x2)3 ⋅ (3 + 2x2)′ = 16 (3 + 2x2)3 ⋅ х
Пример 2
Найдем производную для функции y = (x3 + 4) cos x.
Для дифференцирования этой функции воспользуемся формулой (UV)′ = U′V + V′U.
y′ = (x3 + 4)′ ⋅ cos x + (x3 + 4) ⋅ cos x′ = 3x2 ⋅ cos x + (x3 + 4) ⋅ (-sin x) = 3x2 ⋅ cos x – (x3 + 4) ⋅ sin x
Ответы на задания
Шпаргалки по математике родителей
Все формулы по математике под рукой
формулы, значение, как писать функции
Производная функции – одно из фундаментальных понятий в математике, без понимания которого становится невозможным решение большинства математических и физических задач. Что же это такое?
Что же это такое?
Производная функции — краткое описание, суть
Если совсем просто, то:
Производная – это скорость изменения функции в данной точке.
Выражаясь математическим языком, это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Формула:
Она понимается в двух смыслах: геометрическом и физическом.
Геометрический смысл: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл: производная пути по времени равна скорости прямолинейного движения. Таким образом, значение скорости в определённый момент времени t0 определяется по формуле:
Вычисление производной называется дифференцированием. Обратный процесс – интегрированием.
youtube.com/embed/OO2RUE6_YD0″>Основные правила нахождения производных
Дифференцирование строится на следующих правилах.
Правило №1: производная от произведения числа на функцию равна
(c * f (x))’ = c * f’ (x),
где с – любое число.
Правило №2: производная от суммы функций равна
(f (x) + g (x))’ = f ‘ (x) + g’ (x).
Правило №3: производная от разности функций равна
(f (x) – g (x))’ = f ‘ (x) – g’ (x).
Правило №4: производная от произведения двух функций равна
(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x).
Правило №5: производная от дроби равна
Существует и так называемая сложная функция (композиция функции) вида f (g(x)). В данном случае f (x) считается внешней функцией, g (x) – внутренней.
Правило дифференцирования сложной функции
Производная сложной функции вычисляется по формуле:
[ f (g (x))]’ = f ‘ (g (x)) g’ (x).
Задача: продифференцировать (x+2)¹⁰. Обозначим её как u=x+2.
Решение: так как (x¹⁰)’=10x⁹,
то ((x+2) ¹⁰)’=(u¹⁰)’=10u⁹⋅u’=10(x+2) ⁹⋅1=10(x+2) ⁹.
Ответ: 10(x+2) ⁹.
Логарифмическая производная
Логарифмическая производная — это производная от натурального логарифма функции.
Вычисляется по формуле:
Часто применяется для упрощения дифференцирования некоторых функций.
Пример поиска производной
Пусть y = y(x).
Для удобства прологарифмируем данную функцию:
ln y = ln y(x).
Теперь вычислим производную по правилу дифференцирования сложной функции:
Из этого следует, что
Тогда ответ:
Производная обратной функции
Теорема: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равная обратной величине производной данной функции.
Общая формула:
Формулы и пример решения
Производные обратных тригонометрических функций:
Задача: продифференцировать y=x²-7lnx.
Решение: находим по формуле
отсюда
Производная функции, заданной параметрически
Пусть функция задана параметрическим уравнением:
Тогда производная равна:
Формулировка, решение примеров
Задача: продифференцировать функцию.
Решение: (при записи производной всегда необходимо писать t в нижнем индексе)
Подставляем в формулу:
Ответ:
В ответе составляется система, в которой кроме полученной производной необходимо писать х = t – 4.
Производная неявной функции
Если функция у = у(х) задана уравнением F (x; y(x)) = 0 то говорят, что она задана неявно.
Теоретическое обоснование
Для нахождения производной неявной функции нужно:
- Продифференцировать обе части уравнения по независимой переменной х предполагая, что у – это дифференцируемая по х функция.
- Решить полученное уравнение относительно производной у’ (х).
Решение в примерах
Задача: решить функцию , заданную неявно:
Решение:
1) перенесём 3у -1 в левую часть и дифференцируем обе части равенства
Получим
Считая, что у – это функция от х, находим производную как от сложной функции:
Тогда
Для заданной функции имеем:
2) Решаем полученное уравнение относительно у’:
Ответ:
Полная таблица производных
Приводим табличную форму, которая существенно облегчает вычисления:
Формул из этого списка достаточно для дифференцирования любой элементарной функции.
Решение элементарных производных, примеры
Задача№1: найти производную функции
Решение: данная функция является сложной, поэтому
Ответ:
Задача №2: найти производную функции
Решение:
Ответ:
Изучение производных и интегралов занимает большое количество времени. ФениксХэлп может помочь вам в решении контрольных и самостоятельных работ по этой теме и многим другим.
Производная формула — Что такое Производная формула? Примеры
Производная помогает нам узнать изменение отношения между двумя переменными. Рассмотрим независимую переменную «х» и зависимую переменную «у». Изменение значения зависимой переменной по отношению к изменению значения выражения независимой переменной можно найти с помощью формулы производной. Математически формула производной полезна для определения наклона линии, наклона кривой и определения изменения одного измерения по отношению к другому измерению. В этом разделе мы узнаем больше о формуле производной и решим несколько примеров. 9{n — 1}\)
В этом разделе мы узнаем больше о формуле производной и решим несколько примеров. 9{n — 1}\)
Правила формулы производных
Существуют некоторые основные формулы производных, т.е. набор формул производных, которые используются на разных уровнях и аспектах. На изображении ниже есть правила.
Вывод формулы производной
Пусть f(x) — функция, область определения которой содержит открытый интервал относительно некоторой точки \(x_0\). Тогда функция f(x) называется дифференцируемой в точке \((x)_{0}\), а производная f(x) в точке \((x)_{0}\) представляется по формуле как:
f'(x)= lim Δx→0 Δy/Δx
⇒ f'(x)= lim Δx→0 [f(\((x)_{0}\)+Δx)− f(\((x)_{0}\))]/∆x
Производная функции y = f(x) может быть обозначена как f′(x) или y′(x).
Кроме того, нотация Лейбница популярна для записи производной функции y = f(x) в виде df(x)/dx, т.е. dy/dx
Список формул производных
Ниже перечислены еще несколько важных используемых формул производных в различных областях математики, таких как исчисление, тригонометрия и т. д. Для дифференцирования тригонометрических функций используются различные формулы производных, перечисленные здесь. Все производные формулы выводятся из дифференцирования первого начала.
д. Для дифференцирования тригонометрических функций используются различные формулы производных, перечисленные здесь. Все производные формулы выводятся из дифференцирования первого начала.
Производные формулы элементарных функций
- \(\dfrac{d}{dx}\).x n = n. х н-1
- \(\dfrac{d}{dx}.k\) = 0, где k — константа
- \(\dfrac{d}{dx}\).e x = e x
- \(\dfrac{d}{dx}\).a x = a x . log\(_e\) .a , где a > 0, a ≠ 1
- \(\dfrac{d}{dx}\).logx = 1/x, x > 0
- \(\dfrac{d}{dx}\). лог\(_а\) е = 1/х лог\(_а\) е
- \(\dfrac{d}{dx}\).√x =1/(2 √x)
Формулы производных тригонометрических функций
- \(\dfrac{d}{dx}\).sin x= cos x
- \(\dfrac{d}{dx}\).cosx= -sin x
- \(\dfrac{d}{dx}\).tan x = sec 2 x , x ≠ (2n+1) π/2 , n ∈ I
- \(\dfrac{d}{dx}\). cot x = — cosec 2 x, x ≠ nπ, n ∈ I
- \(\dfrac{d}{dx}\).
 sec x = sec x tan x, x ≠ (2n+1) π/2 , n ∈ I
sec x = sec x tan x, x ≠ (2n+1) π/2 , n ∈ I - \(\dfrac{d}{dx}\).cosec x = — cosec x cot x, x ≠ nπ, n ∈ I
Производные формулы гиперболических функций
- \(\dfrac{d}{dx}\). sinx = кошх
- \(\dfrac{d}{dx}\). кошх = грех хх
- \(\dfrac{d}{dx}\). тангенс hx = сек ч 2 x
- \(\dfrac{d}{dx}\). кроватка hx = -cosec h 2 x
- \(\dfrac{d}{dx}\). сек hx = -sech hx tan hx
- \(\dfrac{d}{dx}\). cosec hx = -cosec hx cot hx 92}}\)
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронируйте бесплатный пробный урок
Примеры с использованием формулы производной
Пример 1. Найдите производную x 7 с помощью формулы производной.
Решение:
Используя формулу производной, \(\dfrac{d}{dx}. {n — 1} \) 9{n — 1} \)
{n — 1} \) 9{n — 1} \)
Каковы основные правила формулы производной?
Основные правила производных формул:
- Постоянное правило
- Постоянное множественное правило
- Силовое правило
- Правило суммы
- Правило различия
- Правило продукта (формула дифференциации УФ)
- Цепное правило
- Частное правило
Какая производная от f(x) = 25 ?
Поскольку функция f(x) постоянна, согласно формуле производной ее производная будет равна нулю, т.е. f’(x) = 0
Как использовать формулу производной?
Формулы производных получаются с использованием определения f'(x) = \(\lim _{h \rightarrow 0}\dfrac{f(x+h)-f(x)}{h}\). Это вытекает из дифференциации первого принципа. Например, если f(x) = sin x, то f(x+ ∆x) = sin(x+ ∆x)
f(x+ ∆x) -f(x) = sin(x+ ∆x) — sin x = 2 sin ∆x/2 .cos(x+ x/2)
Теперь \(\dfrac{f(x+ ∆x) -f(x)}{∆x}\) = \(\dfrac{sin\dfrac{∆x}{2}}{\dfrac{∆x}{ 2}}\) cos(x+x/2)
⇒\(\lim _{∆x\стрелка вправо 0}\dfrac{f(x+∆x)-f(x)}{∆x}\) = cos x
Таким образом, производная от sin x = cos x.
Исчисление I. Формулы дифференцирования
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-3: Формулы дифференцирования
В первом разделе этой главы мы увидели определение производной и вычислили пару производных, используя это определение. Как мы видели в этих примерах, вычисление пределов требовало большого объема работы, а функции, с которыми мы работали, были не очень сложными.
Как мы видели в этих примерах, вычисление пределов требовало большого объема работы, а функции, с которыми мы работали, были не очень сложными.
Для более сложных функций использование определения производной было бы почти невыполнимой задачей. К счастью для нас, нам не придется слишком часто использовать это определение. Нам придется использовать его время от времени, однако у нас есть большой набор формул и свойств, которые мы можем использовать, чтобы значительно упростить нашу жизнь и позволят нам избежать использования определения, когда это возможно. 9\prime} = f’\left( x \right) \pm g’\left( x \right)\hspace{0.25in} \mbox{OR} \hspace{0.25in}\frac{d}{{dx} }\left( {f\left( x \right) \pm g\left( x \right)} \right) = \frac{{df}}{{dx}} \pm \frac{{dg}}{ {дх}}\)
Другими словами, чтобы дифференцировать сумму или разность, все, что нам нужно сделать, это дифференцировать отдельные термины, а затем сложить их вместе с соответствующими знаками. Обратите внимание, что это свойство не ограничивается двумя функциями.
Другими словами, мы можем «вынести» мультипликативную константу из производной, если нам нужно. Доказательство этого свойства см. в разделе «Доказательство различных производных формул» главы «Дополнительно».
Обратите внимание, что мы не включили здесь формулы для производных произведений или частных двух функций. Производная произведения или частное двух функций не есть произведение или частное производных отдельных частей. Мы рассмотрим их в следующем разделе.
Далее давайте кратко рассмотрим пару основных «вычислительных» формул, которые позволят нам фактически вычислить некоторые производные.
Формулы
- Если \(f\left( x \right) = c\), то \(\displaystyle f’\left( x \right) = 0\hspace{0.25in} \mbox{OR} \hspace {0,25 дюйма}\frac{d}{{dx}}\left( c \right) = 0\)
Производная константы равна нулю.
 Доказательство этой формулы см. в разделе «Доказательство различных производных формул» в главе «Дополнительно». 9{n — 1}}\), \(n\) — любое число.
Доказательство этой формулы см. в разделе «Доказательство различных производных формул» в главе «Дополнительно». 9{n — 1}}\), \(n\) — любое число.Эту формулу иногда называют степенным правилом . Все, что мы здесь делаем, это ставим исходный показатель степени вперед, умножаем и затем вычитаем единицу из исходного показателя степени.
Также обратите внимание, что для использования этой формулы \(n\) должно быть числом, оно не может быть переменной. Также обратите внимание, что основание, \(x\), должно быть переменной, а не числом. В некоторых последующих разделах будет заманчиво злоупотреблять степенным правилом, когда мы запускаем некоторые функции, где показатель степени не является числом и/или основание не является переменной.
Доказательство этой формулы см. в разделе «Доказательство различных производных формул» в главе «Дополнительно». На самом деле в этом разделе есть три разных доказательства.
 { — \,\,\frac{1}{2}}} + 9{\ кв. 2 — 1}} \]
{ — \,\,\frac{1}{2}}} + 9{\ кв. 2 — 1}} \]Ответ немного запутан, и мы не будем уменьшать показатели степени до десятичных дробей. Тем не менее, эта проблема не так уж сложна, она просто выглядит так на первый взгляд.
Существует общее правило, касающееся деривативов этого класса, и вам необходимо выработать привычку его использовать. Когда вы видите радикалы, вы всегда должны сначала преобразовать радикал в дробную экспоненту, а затем максимально упростить экспоненту. Соблюдение этого правила избавит вас от многих проблем в будущем. 92}} \right)\) Показать решение
В этой функции мы не можем просто дифференцировать первое слагаемое, дифференцировать второе слагаемое, а затем снова умножать их. Это просто не сработает. Мы подробно обсудим это в следующем разделе, поэтому, если вы не уверены, что верите в это, подождите немного, и мы скоро рассмотрим это, а также покажем вам пример того, почему это не сработает.
Тем не менее, эту производную можно сделать.
 3}}} + 4\) увеличивается, уменьшается или не изменяется в \(х = — 2\)?
94}}}\]
3}}} + 4\) увеличивается, уменьшается или не изменяется в \(х = — 2\)?
94}}}\]Обратите внимание, что мы переписали последний член производной обратно в виде дроби. Это не то, что мы делали до сих пор, и это делается здесь только для того, чтобы помочь с оценкой на следующем этапе. Часто проще проводить оценку с положительными показателями.
Итак, вычислив производную, получим
\[f’\left( { — 2} \right) = 6\left( 4 \right) — \frac{{900}}{{16}} = — \frac{{129}}{4} = — 32.25\]
Итак, при \(x = — 2\) производная отрицательна, поэтому функция убывает при \(x = — 2\).
Пример 4 Найдите уравнение касательной к \(f\left( x \right) = 4x — 8\sqrt x \) в точке \(x = 16\).
Показать решение
Мы знаем, что уравнение касательной задается как,
\[y = f\left( a \right) + f’\left( a \right)\left( {x — a} \right)\] 9{\ гидроразрыва {1} {2}}}}} \]
Опять же, обратите внимание, что мы убрали отрицательную экспоненту в производной исключительно ради оценки.
 Все, что нам нужно сделать, это вычислить функцию и производную в рассматриваемой точке \(x = 16\).
Все, что нам нужно сделать, это вычислить функцию и производную в рассматриваемой точке \(x = 16\).\[f\влево( {16} \вправо) = 64 — 8\влево( 4 \вправо) = 32\hspace{0,25 дюйма}\hspace{0,25 дюйма}f’\влево( 16 \вправо) = 4 — \ дробь{4}{4} = 3\]
Тогда касательная будет равна 92} + 60т — 10\]
Определите, когда объект движется вправо и когда объект движется влево.
Показать решение
Единственный способ узнать наверняка, в каком направлении движется объект, — это иметь скорость на руках. Напомним, что если скорость положительна, объект движется вправо, а если скорость отрицательна, то объект движется влево.
Нам нужна производная, чтобы получить скорость объекта. Производная и, следовательно, скорость равна 92} — 7t + 10} \вправо) = 6\влево( {t — 2} \вправо)\влево( {t — 5} \вправо)\]
Причина факторинга дериватива станет очевидной в ближайшее время.

Теперь нам нужно определить, где производная положительная, а где отрицательная. Есть несколько способов сделать это. Мы предпочитаем следующий метод.
Поскольку многочлены непрерывны, мы знаем из теоремы о промежуточном значении, что если многочлен когда-либо меняет знак, то он должен сначала пройти через нуль. Итак, если бы мы знали, где производная равна нулю, мы знали бы только точки, в которых производная равна 9.0306 может изменить знак.
Из факторизованной формы производной видно, что производная будет равна нулю при \(t = 2\) и \(t = 5\). Нанесем эти точки на числовую прямую.
Теперь мы можем видеть, что эти две точки делят числовую прямую на три отдельных участка. В каждой из этих областей мы знаем , что производная будет того же знака. Напомним, что производная может менять знак только в двух точках, которые используются для деления числовой строки на области.
Следовательно, все, что нам нужно сделать, это проверить производную в контрольной точке в каждой области, и производная в этой области будет иметь тот же знак, что и контрольная точка.


 sec x = sec x tan x, x ≠ (2n+1) π/2 , n ∈ I
sec x = sec x tan x, x ≠ (2n+1) π/2 , n ∈ I Доказательство этой формулы см. в разделе «Доказательство различных производных формул» в главе «Дополнительно». 9{n — 1}}\), \(n\) — любое число.
Доказательство этой формулы см. в разделе «Доказательство различных производных формул» в главе «Дополнительно». 9{n — 1}}\), \(n\) — любое число.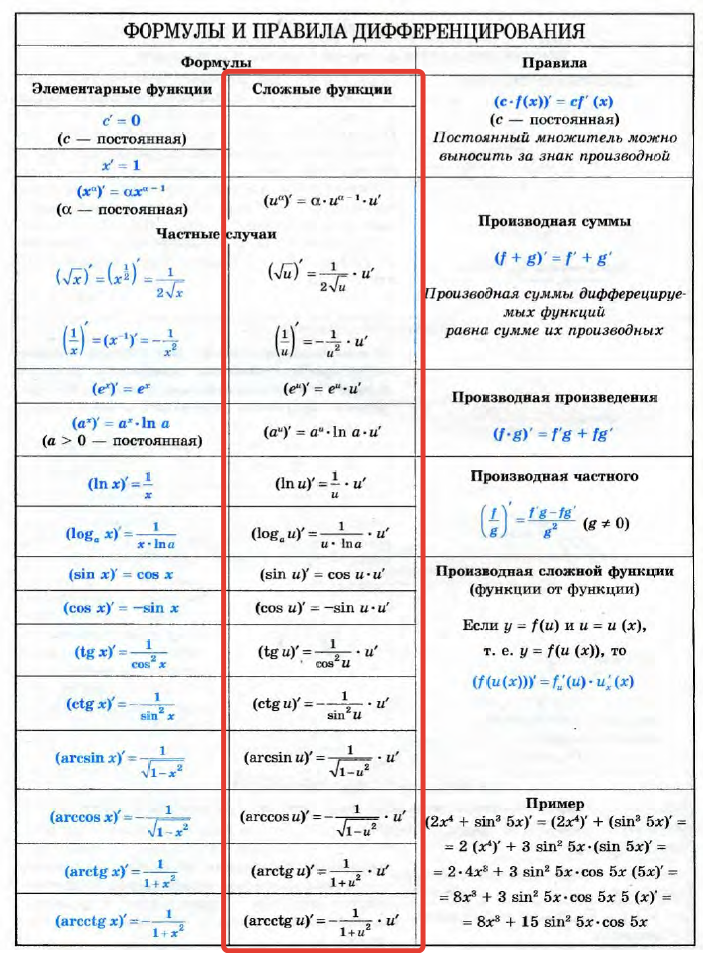 { — \,\,\frac{1}{2}}} + 9{\ кв. 2 — 1}} \]
{ — \,\,\frac{1}{2}}} + 9{\ кв. 2 — 1}} \] 3}}} + 4\) увеличивается, уменьшается или не изменяется в \(х = — 2\)?
94}}}\]
3}}} + 4\) увеличивается, уменьшается или не изменяется в \(х = — 2\)?
94}}}\] Все, что нам нужно сделать, это вычислить функцию и производную в рассматриваемой точке \(x = 16\).
Все, что нам нужно сделать, это вычислить функцию и производную в рассматриваемой точке \(x = 16\).
