Возведение в куб суммы: Куб суммы, формулы и вычисления онлайн

Возведение в квадрат и куб суммы и разности двух выражений. Разложение на множители с помощью формул квадрата суммы и

88. Возведение в квадрат и куб суммы и разности двух выражений. Разложение на множители с помощью формул квадрата суммы и квадрата разности.

Мы уже знаем, как умножить многочлен на многочлен. Но для некоторых случаев есть формулы, которые помогут существенно ускорить расчеты. Это формулы сокращенного умножения. Сегодня мы познакомимся с четырьмя из них.

Возведем в квадрат сумму (a+b):

(a+b)² = (a+b)(a+b)

Применим правило умножения многочлена на многочлен:

(a+b)(a+b) = a*a+a*b+b*a+b*b = a²+ab+ab+b² = a²+2ab+b²

Мы получили формулу:

(a+b)² = a²+2ab+b²

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Аналогично выведем формулу для квадрата разности:

(a-b)² = (a-b)(a-b) = a*a-a*b-b*a+b*b = a²-ab-ab+b² = a²-2ab+b²

(a-b)² = a²-2ab+b²

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Теперь, используя эти формулы, выведем формулы для куба суммы и куба разности двух выражений:

(a+b)³ = (a+b)(a+b)² = (a+b)(a²+2ab+b²) = a*a²+a*2ab+a*b²+b*a²+b*2ab+b*b² = a³+2a

2b+ab²+a²b+2ab²+b³ = a³+3a²b+3ab²+b³

(a+b)^{3= a3+3a2b+3ab2+b3}

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб третьего выражения.

Это правило не так-то легко запомнить? Достаточно выучить формулу! Правило – это всего лишь ее словесное описание.

Аналогично найдем формулу куба разности:

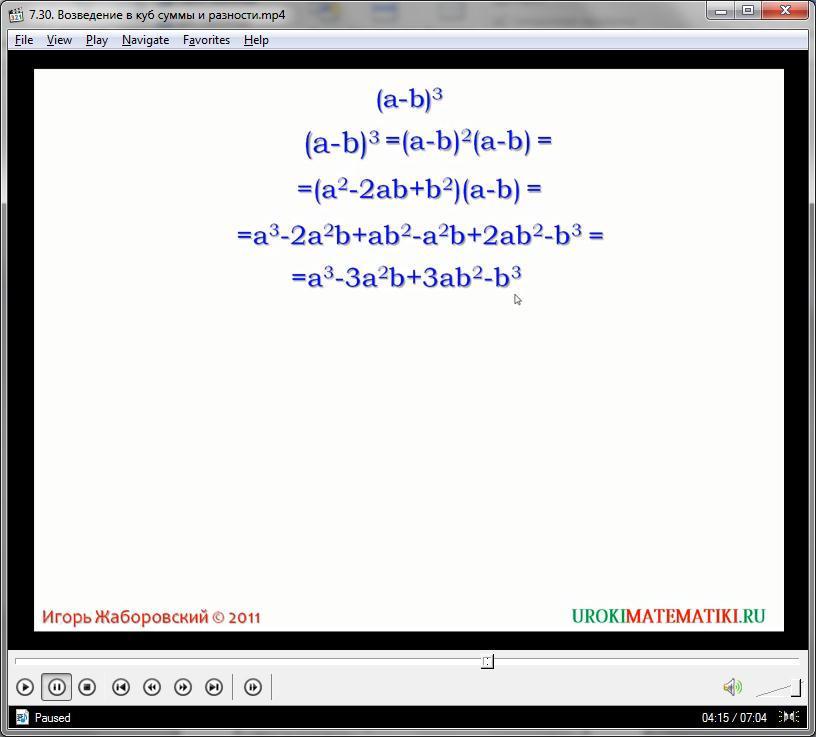
(a-b)³ = (a-b)(a-b)² = (a-b)(a²-2ab+b²) = a*a²-a*2ab+a*b²-b*a²+b*2ab-b*b² = a³-2a²b+ab²-a²b+2ab²-b³ = a³-3a²b+3ab²-b³

(a-b)³ = a³-3a²b+3ab²-b³

Если в формуле для куба суммы все одночлены соединены знаками «+», что понятно – минусу просто неоткуда взяться, то в формуле для куба разности знаки между одночленами чередуются: «-» «+» «-».

Формулы сокращенного умножения используются также при разложении на множители.

Пример 1. Разложим на множители многочлен 81a²-18ab+b².

Можно ли слагаемое 81а² представить в виде квадрата одночлена? 81 – это квадрат числа 9. Тогда 81а² = 9²а² = (9а)². Причем -18аb = -2*9a*b.

«Свернем» многочлен, используя формулу квадрата суммы:

81a²-18ab+b^{2= (9а)2-2*9a*b+b2= (9а-b)2= (9а-b)(9а-b).}

Урок 31. куб суммы. куб разности — Алгебра — 7 класс

Алгебра

7 класс

Урок № 31

Куб суммы. Куб разности

Перечень вопросов, рассматриваемых в теме:

• Формулы сокращённого умножения.
• Куб суммы. Куб разности.
• Разложение многочлена на множители.
• Тождественные преобразования.
• Вычисление значения числовых выражений.

Тезаурус:

Формулы сокращённого умножения.

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

(a + b)(a – b) = a² – b²

a³ + b³ = (a + b)(a² – ab + b²)

a³ – b³ = (a – b)(a² + ab + b²)

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a – b)³ = a³ – 3a²b + 3ab² – b³

Применение:

• упрощение умножения многочленов;
• разложение многочлена на множители;
• вычисление значения числового выражения;
• тождественные преобразования.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Куб суммы.

Рассмотрим произведение:

(a + b)³ = (a + b)²(a + b) = (a

2 + 2ab + b²)(a + b).

Применив правило умножения многочленов, и приведя подобные члены, получим:

a³ + 2a²b + b²a + a²b + 2ab² + b ³= a³ + 3a²b + 3ab² + b³.

Итак, доказано равенство, которое называют «куб суммы»: (a + b)³ = a³ + 3a²b + 3ab² + b³

Читается так: «куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, плюс куб второго числа».

Куб разности.

Аналогично докажем формулу «куб разности».

Рассмотрим произведение:

(a – b)³ = (a – b)²(a – b) =(a² – 2ab + b²)(a – b)

Применив правило умножения многочленов, получим:

a³ – 2a²b + b²a ^{– a2b + 2ab2 – b3 = a3 – 3a2b + 3ab2 – b3}

Доказано равенство, которое называют «куб разности»:

(a – b)³ = a³ – 3a²b + 3ab² – b

3

Читается так: «куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, минус куб второго числа».

Формулы суммы и разности кубов часто используют для упрощения выражений.

Разбор решения заданий тренировочного модуля.

Задача 1.

Найдите куб двучлена:

(a + 3)³ = a³ + 3a² · 3 + 3a · 3² + 3³ = a³ + 9a² + 27a + 27.

(10 – a)³ =10³ – 3 · 10² a + 3 · 10 · a² – a

3 = 1000 – 300a + 30a² – a³.

Задача 2.

Упростите: x³ + 3x(x + 4) – (x + 2)³

x³ + 3x² + 12x – (x³ + 6x² + 12x + 8) =

x³ + 3x² + 12x – x³ – 6x² – 12x – 8 =

= -3x² – 8.

Ответ: -3x² – 8.

Задача 3.

Решите уравнение:

x³ + 9x² – (x + 3)³ = 0

x³ + 9x² – (x³ + 9x² + 27x + 27) = 0

x³ + 9x² – x³ – 9x² – 27x – 27 = 0

-27x = 27

Ответ: х = -1.

Презентация для объяснения нового материала по теме «Куб суммы и куб разности»

библиотека
материалов

Содержание слайдов

Номер слайда 1

Возведение в куб суммы и разности двух выражений

Номер слайда 2

П 32(a + b)³ = (a + b)²(a + b)== a³ + 2a²b + ab²+ a²b+ 2ab² +b³= Куб суммы. Куб суммы … равен кубу первого … плюс утроенное произведение квадрата первого на второе…плюс утроенное произведение первого на квадрат второго плюс куб второго…(a + b)³ = a³ +3a²b +3ab² +b³= (a² + 2ab +b²)( a+ b)== a³ + 3a²b + 3ab²+b³

Номер слайда 3

П 32(a — b)³ = (a — b)²(a — b)== a³ — a²b — 2a²b +2ab²+ ab² — b³= Куб разности. Куб разности … равен кубу первого … минус утроенное произведение квадрата первого на второе…плюс утроенное произведение первого на квадрат второго … минус куб второго…(a — b)³ = a³ -3a²b +3ab² — b³= (a² — 2ab +b²)( a- b)== a³ — 3a²b + 3ab²- b³

Номер слайда 4

Пример 5(2х + 3)³ ==8х³ + 36х²+54х + 27. (2х)³ +3·(2х)²·3 + 3·2х·3² +3³ =Пример 6(3х – 5)³ =(3х)³ -3·(3х)²·5 + 3·3х·5² — 5³ ==27х³ — 135х² + 225х — 125.

Возведение скобки в куб

Станем опять сначала на точку зрения арифметики и рассмотрим возведение в куб суммы и разности двух чисел. Получим:

Словами эти равенства читаются так:

1) Куб суммы двух чисел равняется кубу первого числа, плюс произведение тройки на квадрат первого числа и на второе число, плюс произведение тройки на первое число и на квадрат второго числа, плюс куб второго числа.

2) Куб разности двух числе равен кубу первого числа, минус произведение тройки на квадрат первого числа и на второе, плюс произведение тройки на первое число и на квадрат второго, минус куб второго числа.

Теперь мы можем сразу написать, что, например,

Здесь сначала написан куб первого числа, т. е. (2a 3 b) 3 , а это = 8a 9 b 3 , затем «минус произведение 2 на квадрат первого числа и на второе», т. е. –3 ∙ (2a³b)² ∙ (3a)= –3 ∙ 4a 6 b 2 ∙ 3a = – 36a 7 b 2 , затем «плюс произведение тройки на первое число и на квадрат второго», т. е. +3 ∙ (2a³b) ∙ (3a)² = +3 ∙ 2a₃b ∙ 9a 2 = 54a 5 b, наконец, «минус куб второго числа», т. е. –(3a) 3 = –27a 3 .

Мы можем наши равенства переписать в виде:

и читаем их так:

Куб двучлена равен кубу первого члена, плюс произведение числа (+3) на квадрат первого члена и на второй, плюс произведение числа (+3) на первый член и на квадрат второго, плюс куб второго члена.

Например: (–3a 4 – ab) 3 = (–3a 4 ) 3 + (+3) (–3a 4 ) 2 (–ab) + (–3a 4 ) (–ab) 2 + (–ab) 3 = –27a 12 – 27a 9 b – 3a 5 b 2 – a 3 b 3 и т. п.

Если потребуется возвести в куб трехчлен, то можно или сводить дело к умножению

[Например: (x² – 2x – 1)³ = (x² – 2x – 1)(x² – 2x – 1)(x² – 2x – 1) = …]

или, приняв временно два члена (лучше первые два) за одно число, свести дело к возведению в куб двучлена:

Куб суммы двух выражений равен сумме кубов этих выражений, сложенной с утроенным произведением квадрата первого выражения на второе и утроенным произведением квадрата второго выражения на первое.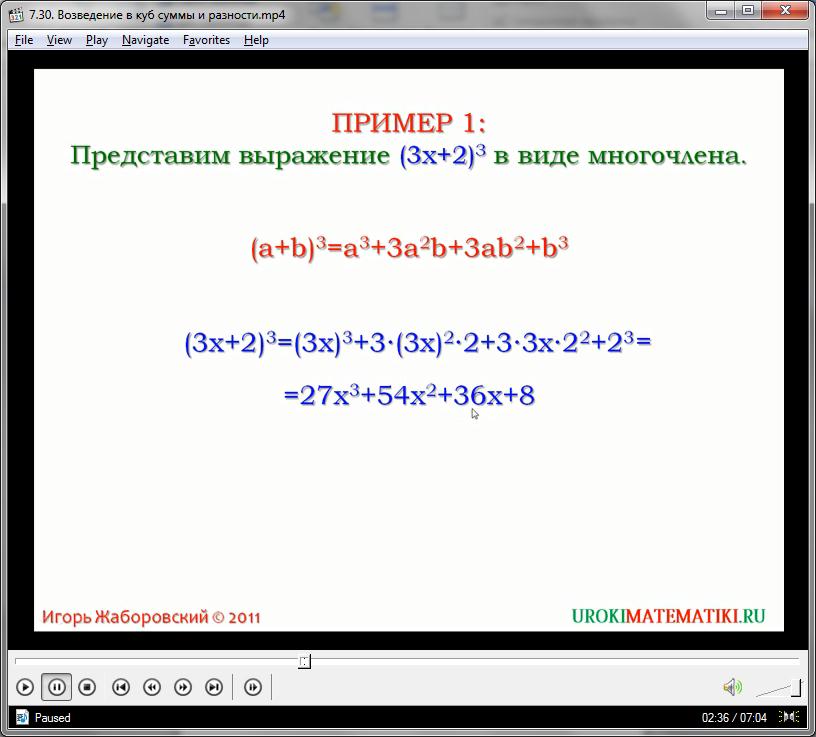

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Здесь (a + b) 3 — куб суммы, a 3 + b 3 — сумма кубов, 3a 2 b — утроенное произведение квадрата первого выражения на второе, 3ab 2 — утроенное произведение квадрата второго выражения на первое.

Вывести эту формулу можно путем умножения многочленов:

(a + b) 3 = (a + b) 2 (a + b) = (a 2 + 2ab + b 2 )(a + b) = a 3 + a 2 b + 2a 2 b + 2ab 2 + ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Куб разности двух выражений равен разности кубов этих выражений минус утроенное произведение квадрата первого выражения на второе и плюс утроенное произведение квадрата второго выражения на первое.

(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3 .

Вывести эту формулу можно путем умножения многочленов:

(a – b) 3 = (a – b) 2 (a – b) = (a 2 – 2ab + b 2 )(a – b) = a 3 – a 2 b – 2a 2 b + 2ab 2 + ab 2 – b 3 = a 3 – 3a 2 b + 3ab 2 – b 3 .

Обратите внимание, что минус там, где b в нечетной степени.

При любых значениях a и b верно равенство

( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . (1)

( a + b ) 3 = ( a + b ) ( a 2 + 2 a b + b 2 ) =

= a 3 + 2 a 2 b + a b 2 + a 2 b + 2 a b 2 + b 3 =

= a 3 + 3 a 2 b + 3 a b 2 + b 3

Так как равенство (1) верно при любых значениях a и b,
то оно является тождеством. Это тождество называется
формулой куба суммы. Если в эту формулу вместо a и b
подставить какие-нибудь выражения, например 5 y 3 и 2 z ,
то опять получится тождество.

( 5 y 3 + 2 z ) 3 = 125 y 9 + 150 y 6 z + 60 y 3 z 2 + 8 z 3 . (2)

Поэтому формула куба суммы читается так:

куб суммы двух выражений равен кубу первого выражения
плюс утроенное произведение квадрата первого выражения и второго,
плюс утроенное произведение первого выражения на квадрат второго,
плюс куб второго выражения.

При любых значениях a и b верно равенство

( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 . (3)

( a − b ) 3 = ( a − b ) ( a 2 − 2 a b + b 2 ) =

= a 3 − 2 a 2 b + a b 2 − a 2 b + 2 a b 2 − b 3 =

= a 3 − 3 a 2 b + 3 a b 2 − b 3

Так как равенство (3) верно при любых значениях a и b,
то оно является тождеством. Это тождество называется
формулой куба разности. Если в эту формулу вместо a и b
подставить какие-нибудь выражения, например 5 y 3 и 2 z ,
то опять получится тождество.

( 5 y 3 − 2 z ) 3 = 125 y 9 − 150 y 6 z + 60 y 3 z 2 − 8 z 3 . (4)

Поэтому формула куба разности читается так:

куб разности двух выражений равен кубу первого выражения
минус утроенное произведение квадрата первого выражения и второго,
плюс утроенное произведение первого выражения и квадрата второго,
минус куб второго выражения.

Как раскрыть скобки куб суммы пример. Возведение многочленов в квадрат

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Ключевые слова:

квадрат суммы, квадрат разности, куб суммы, куб разности, разность квадратов, сумма кубов, разность кубов

Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй величины. (a+b) 2 =a 2 +2ab+b 2

• Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй.величины (a-b) 2 =a 2 -2ab+b 2
• Произведение суммы двух величин на их разность равно разности их квадратов . (a+b)(a-b)=a 2 -b 2
• К уб суммы двух величин равен кубу первой величины плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй.

  (a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

• К уб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй.

  (a-b) 3 =a 3 -3a 2 b+3ab 2 -b 3

• Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов . (a+b)(a 2 -ab+b 2)=a 3 +b 3
• Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.

  (a — b)(a 2 +ab+b 2)=a 3 — b 3

Очень часто приведение многочлена к стандартному виду можно осуществить путём применения формул сокращённого умножения. Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Формулы сокращённого умножения нужно знать наизусть:

Пример . Докажем формулу a 3 +b 3 = (a + b )(a 2 – ab + b 2).

Имеем: (a + b )(a 2 – ab + b 2) = a 3 – a 2 b + ab 2 + ba 2 – ab 2 – b 3

Приводя подобные слагаемые, мы видим, что

(a + b )(a 2 – ab + b 2) = a 3 +b 3 , что и доказывает нужную формулу.

Аналогично доказывается, что (a — b )(a 2 + ab + b 2) = a 3 – b 3

Мало просто знать наизусть формулы сокращенного умножения. Надо еще научиться видеть в конкретном алгебраическом выражении эту формулу.

Например:

49m 2 – 42mn + 9n 2 = (7m – 3n) 2

Или другой пример, посложнее:

Тут 3x 2 можно представить как ( √ 3x) 2

Полезно еще и знать, как возводить двучлен в степень большую, чем 3. Формула, позволяющая выписывать разложение алгебраической суммы двух слагаемых произвольной степени, впервые была предложена Ньютоном в 1664–1665 г. и получила название бинома Ньютона. Коэффициенты формулы называются биномиальными коэффициентами. Если n – положительное целое число, то коэффициенты обращаются в нуль при любом k > n, поэтому разложение содержит лишь конечное число членов. Во всех остальных случаях разложение представляет собой бесконечный (биномиальный) ряд. (Условия сходимости биномиального ряда впервые были установлены в начале 19 в. Н.Абелем.) Такие частные случаи, как

(a+b) 2 =a 2 +2ab+b 2 и (a+b) 3 =a 3 +3a 2 b+3ab 2 + b 3

были известны задолго до Ньютона. Если n – положительное целое число, то биномиальный коэффициент при a n-k b k в формуле бинома есть число комбинаций из n по k , обозначаемое C k n . При небольших значениях n коэффициенты можно найти из треугольника Паскаля :

в котором каждое из чисел за исключением единиц равно сумме двух соседних чисел, стоящих строкой выше. Для данного n соответствующая (n-я) строка треугольника Паскаля дает по порядку коэффициенты биномиального разложения n-й степени, в чем нетрудно убедиться при n = 2 и n = 3.

Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.

Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.

Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу. 7.

Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты

Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад

Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7 ).

Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

правила применения формул сокращенного умножения

При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения . Всего таких формул семь. Их все необходимо знать наизусть.

Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

a 2 — b 2 = (a — b)(a + b)

Квадрат суммы

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(a + b) 2 = a 2 + 2ab + b 2

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел , не используя калькулятор или умножение в столбик. Поясним на примере:

Найти 112 2 .

Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2
112 = 100 + 1

Запишем сумму чисел в скобки и поставим над скобками квадрат.
112 2 = (100 + 12) 2

Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.

(8a + с) 2 = 64a 2 + 16ac + c 2

Предостережение!!!

(a + b) 2 не равно a 2 + b 2

Квадрат разности

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

(a — b) 2 = a 2 — 2ab + b 2

Также стоит запомнить весьма полезное преобразование:

(a — b) 2 = (b — a) 2
Формула выше доказывается простым раскрытием скобок:

(a — b) 2 = a 2 — 2ab + b 2 = b 2 — 2ab + a 2 = (b — a) 2

Куб суммы

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Запомнить эту «страшную» на вид формулу довольно просто.

Выучите, что в начале идёт a 3 .

Два многочлена посередине имеют коэффициенты 3.

В спомним, что любое число в нулевой степени есть 1. (a 0 = 1, b 0 = 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b. В этом можно убедиться:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Предостережение!!!

(a + b) 3 не равно a 3 + b 3

Куб разности

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a 3 стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.

(a — b) 3 = + a 3 — 3a 2 b + 3ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3

Сумма кубов ( Не путать с кубом суммы!)

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a 3 + b 3 = (a + b)(a 2 — ab + b 2)

Сумма кубов — это произведение двух скобок.

Первая скобка — сумма двух чисел.

Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:

A 2 — ab + b 2
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.

Разность кубов (Не путать с кубом разности!!!)

Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

a 3 — b 3 = (a — b)(a 2 + ab + b 2)

Будьте внимательны при записи знаков. Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

Трудно запоминаются формулы сокращенного умножения? Делу легко помочь. Нужно просто запомнить, как изображается такая простая вещь, как треугольник Паскаля. Тогда вы вспомните эти формулы всегда и везде, вернее, не вспомните, а восстановите.

Что же такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена вида в многочлен.

Разложим, например, :

В этой записи легко запоминается, что вначале стоит куб первого, а в конце — куб второго числа. А вот что посередине — запоминается сложно. И даже то, что в каждом следующем слагаемом степень одного множителя все время уменьшается, а второго — увеличивается — несложно заметить и запомнить, труднее дело обстоит с запоминанием коэффициентов и знаков (плюс там или минус?).

Итак, сначала коэффициенты. Не надо их запоминать! На полях тетрадки быстренько рисуем треугольник Паскаля, и вот они — коэффициенты, уже перед нами. Рисовать начинаем с трех единичек, одна сверху, две ниже, правее и левее — ага, уже треугольник получается:

Первая строка, с одной единичкой — нулевая. Потом идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно по краям снова приписать единички, а в центре записать число, полученное сложением двух чисел, стоящих над ним:

Записываем третью строку: опять по краям единицы, и опять, чтобы получить следующее число в новой строке, сложим числа, стоящие над ним в предыдущей:

Как вы уже догадались, мы получаем в каждой строке коэффициенты из разложения двучлена в многочлен:

Ну а знаки запомнить еще проще: первый — такой же, как в раскладываемом двучлене (раскладываем сумму — значит, плюс, разность — значит, минус), а дальше знаки чередуются!

Вот такая это полезная штука — треугольник Паскаля. Пользуйтесь!

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Что значит куб разности чисел. Возведение многочленов в квадрат

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения . Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).

Первая формула сокращенного умножения называется разность квадратов . Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.

а 2 — b 2 = (а — b)(a + b)

Разберем для наглядности:

22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)

Вторая формула о сумме квадратов . Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.

(а + b) 2 = a 2 +2ab + b 2

Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.

Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

Третья формула это квадрат разности . Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.

(а +b) 2 = а 2 — 2аb + b 2

где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2

Четвертая формула сокращенного умножения называется куб суммы . Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.

(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3

Пятая, как вы уже поняли называется куб разности . Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.

(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3

Шестая называется — сумма кубов . Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.

а 3 + b 3 = (а+b)(а 2 -аb+b 2)

По другому можно сказать сумму кубов можно назвать произведение в двух скобках.

Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.

а 3 — b 3 = (а-b)(а 2 +аb+b 2)

И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.

Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!

Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм . Там все очень подробно написано и показано. Будет интересно!

Рассмотрим теперь возведение в квадрат двучлена и, применяясь к арифметической точке зрения, будем говорить о квадрате суммы, т. е. (a + b)² и о квадрате разности двух чисел, т. е. (a – b)².

Так как (a + b)² = (a + b) ∙ (a + b),

то найдем: (a + b) ∙ (a + b) = a² + ab + ab + b² = a² + 2ab + b², т. е.

(a + b)² = a² + 2ab + b²

Этот результат полезно запомнить и в виде вышеописанного равенства и словами: квадрат суммы двух чисел равен квадрату первого числа плюс произведение двойки на первое число и на второе число, плюс квадрат второго числа.

Зная этот результат, мы можем сразу написать, напр.:

(x + y)² = x² + 2xy + y²
(3ab + 1)² = 9a² b² + 6ab + 1

(x n + 4x)² = x 2n + 8x n+1 + 16x 2

Разберем второй из этих примеров. Нам требуется возвести в квадрат сумму двух чисел: первое число есть 3ab, второе 1. Должно получиться: 1) квадрат первого числа, т. е. (3ab)², что равно 9a²b²; 2) произведение двойки на первое число и на второе, т. е. 2 ∙ 3ab ∙ 1 = 6ab; 3) квадрат 2-го числа, т. е. 1² = 1 – все эти три члена должно сложить между собою.

Совершенно также получим формулу для возведения в квадрат разности двух чисел, т. е. для (a – b)²:

(a – b)² = (a – b) (a – b) = a² – ab – ab + b² = a² – 2ab + b².

(a – b)² = a² – 2ab + b² ,

т. е. квадрат разности двух чисел равен квадрату первого числа, минус произведение двойки на первое число и на второе, плюс квадрат второго числа .

Зная этот результат, мы можем сразу выполнять возведение в квадрат двучленов, представляющих с точки зрения арифметики разность двух чисел.

(m – n)² = m² – 2mn + n²
(5ab 3 – 3a 2 b) 2 = 25a 2 b 6 – 30a 3 b 4 + 9a 4 b 2

(a n-1 – a) 2 = a 2n-2 – 2a n + a 2 и т. п.

Поясним 2-ой пример. Здесь мы имеем в скобках разность двух чисел: первое число 5ab 3 и второе число 3a 2 b. В результате должно получиться: 1) квадрат первого числа, т. е. (5ab 3) 2 = 25a 2 b 6 , 2) произведение двойки на 1-ое и на 2-ое число, т. е. 2 ∙ 5ab 3 ∙ 3a 2 b = 30a 3 b 4 и 3) квадрат второго числа, т. е. (3a 2 b) 2 = 9a 4 b 2 ; первый и третий члены надо взять с плюсом, а 2-ой с минусом, получим 25a 2 b 6 – 30a 3 b 4 + 9a 4 b 2 . В пояснение 4-го примера заметим лишь, что 1) (a n-1)2 = a 2n-2 … надо показателя степени умножить на 2 и 2) произведение двойки на 1-ое число и на 2-ое = 2 ∙ a n-1 ∙ a = 2a n .

Если встать на точку зрения алгебры, то оба равенства: 1) (a + b)² = a² + 2ab + b² и 2) (a – b)² = a² – 2ab + b² выражают одно и тоже, а именно: квадрат двучлена равен квадрату первого члена, плюс произведение числа (+2) на первый член и на второй, плюс квадрат второго члена. Это ясно, потому что наши равенства можно переписать в виде:

1) (a + b)² = (+a)² + (+2) ∙ (+a) (+b) + (+b)²
2) (a – b)² = (+a)² + (+2) ∙ (+a) (–b) + (–b)²

В некоторых случаях так именно и удобно толковать полученные равенства:

(–4a – 3b)² = (–4a)² + (+2) (–4a) (–3b) + (–3b)²

Здесь возводится в квадрат двучлен, первый член которого = –4a и второй = –3b. Далее мы получим (–4a)² = 16a², (+2) (–4a) (–3b) = +24ab, (–3b)² = 9b² и окончательно:

(–4a – 3b)² = 6a² + 24ab + 9b²

Возможно было бы также получить и запомнить формулу для возведения в квадрат трехчлена, четырехчлена и вообще любого многочлена. Однако, мы этого делать не будем, ибо применять эти формулы приходится редко, а если понадобится какой-либо многочлен (кроме двучлена) возвести в квадрат, то станем сводить дело к умножению. Например:

31. Применим полученные 3 равенства, а именно:

(a + b) (a – b) = a² – b²
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²

к арифметике.

Пусть надо 41 ∙ 39. Тогда мы можем это представить в виде (40 + 1) (40 – 1) и свести дело к первому равенству – получим 40² – 1 или 1600 – 1 = 1599. Благодаря этому, легко выполнять в уме умножения вроде 21 ∙ 19; 22 ∙ 18; 31 ∙ 29; 32 ∙ 28; 71 ∙ 69 и т. д.

Пусть надо 41 ∙ 41; это все равно, что 41² или (40 + 1)² = 1600 + 80 + 1 = 1681. Также 35 ∙ 35 = 35² = (30 + 5)² = 900 + 300 + 25 = 1225. 3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Сумма и разница кубиков

Сумма или разница двух кубиков может быть разложена на произведение биномиальный умножить на трехчлен.

Это, Икс 3 + у 3 знак равно ( Икс + у ) ( Икс 2 — Икс у + у 2 ) и Икс 3 — у 3 знак равно ( Икс — у ) ( Икс 2 + Икс у + у 2 ) .

Мнемоника знаков факторизации — слово «SOAP», буквы означают «Тот же знак», что и в середине исходного выражения, «Противоположный знак» и «Всегда положительный».

Это, Икс 3 ± у 3 знак равно ( Икс [ Такой же подписать ] у ) ( Икс 2 [ Противоположный подписать ] Икс у [ Всегда Положительный ] у 2 )

Пример 1:

Фактор 27 п 3 + q 3 .

Попробуйте записать каждый из терминов в виде куба выражения.

27 п 3 + q 3 знак равно ( 3 п ) 3 + ( q ) 3

Для перезаписи используйте факторизацию суммы кубов.

27 п 3 + q 3 знак равно ( 3 п ) 3 + ( q ) 3 знак равно ( 3 п + q ) ( ( 3 п ) 2 — 3 п q + q 2 ) знак равно ( 3 п + q ) ( 9 п 2 — 3 п q + q 2 )

Пример 2:

Фактор 40 ты 3 — 625 v 3 .

Вынести за скобки GCF из двух условий.

40 ты 3 — 625 v 3 знак равно 5 ( 8 ты 3 — 125 v 3 )

Попробуйте записать каждый член бинома в виде куба выражения.

8 ты 3 — 125 v 3 знак равно ( 2 ты ) 3 — ( 5 v ) 3

Для перезаписи используйте факторизацию разности кубов.

5 ( 8 ты 3 — 125 v 3 ) знак равно 5 ( ( 2 ты ) 3 — ( 5 v ) 3 ) знак равно 5 [ ( 2 ты — 5 v ) ( ( 2 ты ) 2 + 10 ты v + ( 5 v ) 2 ) ] знак равно 5 ( 2 ты — 5 v ) ( 4 ты 2 + 10 ты v + 25 v 2 )

Формула суммы кубиков

— Примеры

Формула для нахождения сложения двух многочленов a ³ + b ³ известна как формула суммы кубов. Давайте узнаем больше о формуле суммы кубов на нескольких решенных примерах. Эта формула факторизации очень удобна при решении алгебраических выражений различных типов. Запомнить эту формулу также легко, и это можно сделать за считанные минуты. Это очень похоже на формулу разницы в кубиках.

Что такое формула суммы кубов?

В этом разделе давайте пойдем дальше и поймем, что именно означает, когда некоторые имеют в виду сумму кубиков. Формула суммы кубиков имеет следующий вид:

a ³ + b ³ = (a + b) (a ² — ab + b ² )

где,

• a — первая переменная
• b — вторая переменная

Доказательство формулы суммы кубов

Чтобы доказать или проверить эту формулу суммы кубов, то есть a ³ + b ³ = (a + b) (a ² — ab + b ² ), нам нужно доказать, что здесь LHS = RHS.
Член LHS = a ³ + b ³
При решении члена RHS получаем,
= (a + b) (a ² — ab + b ² )
Умножая a и b отдельно на (a ² + ab + b ² ), мы получаем
= a (a ² — ab + b ² ) + b (a ² — ab + b ² )
= a ³ — a ² b + ab ² + a ² b — ab ² + b ³
= a ³ — a ² b + a ² b + ab ² — ab ² + b ³
= A ³ — 0 + 0 + b ³
= A ³ + b ³
Следовательно, доказано, что LHS = RHS

Отличное обучение в старшей школе по простым подсказкам

Занимаясь заучиванием наизусть, вы, вероятно, забудете концепции. С Cuemath вы будете учиться наглядно и будете удивлены результатами.

Забронируйте бесплатную пробную версию Класс

Примеры формулы суммы кубов

Пример 1: Используйте формулу суммы кубов, чтобы найти множитель 216x ³ + 64.

Найти: множитель 216x ³ + 64, используя формулу суммы кубов.

216x ³ + 64 = (6x) ³ + 4 ³

Используя формулу суммы кубов,

a ³ + b ³ = (a + b) (a ² — ab + b ² )

Ставить значения,

(6x) ³ + 4 ³ = (6x + 4) ((6x) ² — 6x × 4 + 4 ² )

(6x) ³ + 4 ³ = (6x + 4) (36x ² — 24x +16)

(6x) ³ + 4 ³ = 8 (3x + 2) (9x ² — 6x + 4)

Ответ: Коэффициент 216x ³ + 64 равен 2 (3x + 2) (9x ² — 6x + 4).

Пример 2: Найдите множитель 8x ³ + 125y ³ .

Найти: множитель 8x ³ + 125y ³ , используя формулу суммы кубов.

8x ³ + 125y ³ = (2x) ³ + (5y) ³

Используя формулу суммы кубов,

a ³ + b ³ = (a + b) (a ² — ab + b ² )

Ставить значения,

(2x) ³ + (5y) ³ = (2x + 5y) ((2x) ² — (2x) (5y) + (5y) ² )

(2x) ³ + (5y) ³ = (2x + 5y) (4x ² — 10xy + 25y ² )

Ответ: Коэффициент 8x ³ + 125y ³ равен (2x + 5y) (4x ² — 10xy + 25y ² ).

Пример 3: Упростить 19 ³ + 20 ³ , используя формулу суммы кубов.

Решение: Найти 19 ³ + 20 ³

Предположим, что a = 19 и b = 20
Используя формулу суммы кубов a ³ + b ³ = (a + b) (a ² — ab + b ² )
Мы заменим их в формуле a ³ + b ³
a ³ + b ³ = (a + b) (a ² — ab + b ² )
19 ³ +20 ³ = (19 + 20) (19 ² — (19) (20) +20 ² )
= (39) (361-380 + 400)
= (39) (381)
= 14 859
Ответ: 19 ³ + 20 ³ = 14859.

FAQ по формуле суммы кубов

Что такое формула разложения суммы кубов?

a ³ + b ³ формула известна как формула суммы кубов, она читается как куб плюс b куб. Его расширение выражается как ³ + b ³ = (a + b) (a ² — ab + b ² ).

Что такое формула суммы кубов в алгебре?

Формула суммы кубов — одно из важных алгебраических тождеств.Он представлен как ³ + b ³ и читается как куб плюс b куб. Формула суммы кубов (a ³ + b ³ ) выражается как ³ + b ³ = (a + b) (a ² — ab + b ² ).

Как упростить числа с помощью формулы суммы кубов?

Давайте разберемся с использованием формулы суммы кубов, то есть формулы ³ + b ³ , с помощью следующего примера.
Пример: Найдите значение 100 ³ + 2 ³ , используя формулу суммы кубов.
Чтобы найти: 100 ³ + 2 ³
Предположим, что a = 100 и b = 2.
Мы подставим их в формулу формулы суммы кубов, то есть a ³ + b ³
a ³ + b ³ = (a + b) (a ² — ab + b ² )
100 ³ +2 ³ = (100 + 2) (100 ² — (100) (2) +2 ² )
= (102) (10000-200 + 4)
= (102) (9804)
= 1000008
Ответ: 100 ³ + 2 ³ = 1000008.3 как сила или нет.

Запишите формулу суммы кубов a ³ + b ³ = (a + b) (a ² — ab + b ² )

подставляет значения a и b в формулу суммы кубов (a ³ + b ³ ) и упрощает.

Факторизация суммы кубов: формула и примеры — видео и стенограмма урока

Является ли выражение суммой кубиков?

Выражение должно соответствовать двум критериям, чтобы его можно было разложить на сумму кубов. Во-первых, каждый член должен быть кубом. Другими словами, каждый член должен быть результатом трехкратного умножения одного и того же выражения на себя. Вот несколько примеров:

• x 3 — это куб, потому что он является результатом трехкратного умножения x на себя
  ( x * x * x ).
• 27 — это куб, потому что он является результатом умножения 3 на себя трижды
  (3 * 3 * 3).

Кроме того, вы можете найти куб, содержащий как числа, так и переменные.Например, 64 z 9 является кубом, потому что существует выражение (4 z 3), которое при трехкратном умножении на себя (4 z 3) (4 z 3) (4 z 3) будет равно 64 z 9.

Обратите внимание, что каждая часть каждого члена должна быть кубом; 7 x 6 и 8 y 2 не являются кубами, потому что 7 не является кубом (хотя x 6 является), а y 2 не является кубом (хотя 8 является).

Во-вторых, каждый член должен иметь один и тот же знак, обычно оба положительные. Обратите внимание, что если оба знака отрицательные, вы можете вынести из обоих членов коэффициент -1, чтобы каждый из них был положительным. Если оба термина имеют противоположные знаки, вы можете попробовать разложить выражение на множители как разность квадратов или разность кубов. Теперь давайте посмотрим, как использовать формулу суммы кубов для разложения проблемы.

Факторинг суммы кубов

Для вычисления суммы кубов вы будете использовать уже упомянутую формулу:

a 3 + b 3 = ( a + b ) ( a 2 — ab + b 2)

Обратите внимание на то, что a и b представляют отдельные выражения, построенные в кубе.Каждая из них может быть переменной ( x ), числом (3) или их комбинацией (4 y 2). Во-первых, вы должны определить, что такое a и b . По сути, вы спрашиваете, что мне нужно в кубе, чтобы получить первый член, и что мне нужно в кубе, чтобы получить второй член? После того, как вы это сделаете, вы вставите выражения, которые вы нашли для a и b , в формулу и упростите их, чтобы завершить разложение. Посмотрим на несколько примеров.

Примеры

Можно ли разложить следующие выражения на сумму кубов? Если да, то коэффициент.

Пример 1:
y 5 + 27

Это выражение нельзя разложить на множители как сумму кубов, потому что первый член ( y 5) не является кубом. Другими словами, нет ничего, что можно умножить само на себя три раза, чтобы получить y 5. Следовательно, выражение не может быть разложено на множители.

Пример 2:
x 3 + 64

Это выражение можно разложить на сумму кубов, поскольку оба члена имеют одинаковый знак (+) и каждое выражение представляет собой куб.

x можно преобразовать в куб, чтобы получить x 3
4 можно преобразовать в куб, чтобы получить 64.

Таким образом, вставив a = x и b = 4 в формулу суммы кубов, получим:

( x + 4) (x2 — ( x ) (4) + 42)

Упрощение ( x ) (4) до 4 x и от 42 до 16 дает окончательный ответ
( x + 4) ( x 2-4 x + 16).

Пример 3:
8 x 3 + 27 y 6

Оба члена имеют одинаковый знак, но является ли каждый член кубом? да.

(2 x ) (2 x ) (2 x ) = 8 x 3 и

(3 y 2) (3 y 2) (3y2) = 27 y 6

Таким образом, a = 2 x и b = 3 y 2. Подстановка их в формулу дает следующую факторизацию:

(2 x ) 3 + (3 y 2) 3
= (2 x + 3 y 2) [(2 x ) 2 — (2 x ) (3 y 2) + (3 y 2) 2]
= (2 x + 3 y 2) (4 x 2-6 xy 2 + 9 y 4

Пример 4:
-2 x 3 — 54

Первое, уведомление что, хотя все термины имеют одинаковый знак (-), они не являются положительными, как в предыдущих примерах.Однако это не проблема, поскольку мы извлекаем множитель отрицательного числа, чтобы сделать каждый член положительным.

Кроме того, обратите внимание, что -2 и -54 не являются кубами. Однако у них общий коэффициент 2 или, в данном случае, технически -2. Сначала вы множите -2 из обоих членов, чтобы получить:

-2 ( x 3 + 27)

Затем вы можете перейти к множителю x 3 + 27 как сумме кубов, где a = x и b = 3. Таким образом, имеем:

-2 ( x + 3) ( x 2 — ( x ) (3) + 32)
= -2 ( x + 3) ( x 2-3 ​​ x + 9)

Резюме урока

Сумма кубов — это двухчленное выражение, в котором оба члена являются кубами и каждый член имеет одинаковый знак.Факторизуется по следующей формуле:

a 3 + b 3 = ( a + b ) ( a 2 — ab + b 2)

Для того, чтобы разложите выражение на множители как сумму кубов, сначала необходимо проверить, соответствует ли оно критериям:

• Выражение должно содержать два члена, каждый с одинаковым знаком.
• Каждый член должен быть кубом.

Помните, что иногда вам может потребоваться сначала выделить общий множитель, прежде чем вы сможете определить, являются ли члены кубами. Если эти критерии соблюдены, вы можете разложить сумму кубиков на множители по формуле. Наконец, убедитесь, что вы упростили свой ответ после ввода значений в формулу.

mathschallenge.net

Часто задаваемые вопросы

Есть ли формула для сложения последовательности кубиков?

Изучая первые пять сумм, можно сделать замечательное открытие:

1 ³ = 1
1 ³ +2 ³ = 9
1 ³ +2 ³ +3 ³ = 36
1 ³ +2 ³ +3 ³ +4 ³ = 100
1 ³ +2 ³ +3 ³ +4 ³ +5 ³ = 225

Кажется, что сумма всегда квадратная, но что еще более примечательно, это сумма первых n кубиков, 1 ³ +2 ³ +… + n ³ = ( n ( n +1) / 2) ² , который является квадратом числа треугольника n ^th .

Например, 1 ³ +2 ³ + … + 10 ³ = (10 × 11/2) ² = 55 ² = 3025.

Используя аналогичный метод, использованный для доказательства этой формулы для суммы квадратов, мы докажем этот результат дедуктивно; есть надежда, что это даст некоторое представление о том, как дальше может быть найден ряд сил.

Доказательство

	r 4 — ( r -1) 4	=	n 4 — ( n -1) 4 + ( n -1) 4 — ( n -2) 4 + … + 3 4 — 2 4 + 2 4 –1 4 + 1 4 –0 4
		=	n 4

Но r ⁴ — ( r –1) ⁴ = r ⁴ — ( r ⁴ –4 r ³ +6 r ² –4 r +1) = 4 r ³ –6 r ² +4 r –1.

∴ ∑ 4 r 3 –6 r 2 +4 r –1	=	4∑ r 3 — 6∑ r 2 + 4∑ r — ∑1
	=	4∑ r 3 -6 n ( n +1) (2 n +1) / 6 + 4 n ( n +1) / 2- n
	=	4∑ r 3 — n ( n +1) (2 n +1) + 2 n ( n +1) — n
	=	№ 4 .

∴ 4∑ r 3	=	n 4 + n ( n +1) (2 n +1) — 2 n ( n +1) + n
	=	n ( n 3 + ( n +1) (2 n +1) — 2 ( n +1) + 1
	=	n ( n 3 + 2 n 2 +3 n +1 — 2 n –2 + 1)
	=	n ( n 3 +2 n 2 + n )
	=	n 2 ( n 2 +2 n +1)
	=	n 2 ( n +1) 2
∴ ∑ r 3	=	n 2 ( n +1) 2 /4
	=	( n ( n +1) / 2) 2

Другими словами, сумма первых n кубиков является квадратом суммы первых n натуральных чисел. 3} называется разницей двух кубов, потому что вычитаются два кубических члена.

Итак, вот формулы, которые резюмируют, как разложить на множители сумму и разность двух кубов. Внимательно изучите их.

---

Случай 1: Сумма двух кубов

Наблюдения:

• Для случая «суммы» биномиальный множитель в правой части уравнения имеет средний знак, который равен положительным .

• Помимо случая «сумма», средний знак трехчленного множителя всегда будет находиться напротив среднего знака данной задачи.Следовательно, это отрицательное значение .

---

Случай 2: Различие двух кубов

Наблюдения:

• Для случая «разницы» биномиальный коэффициент в правой части уравнения имеет средний знак, равный минус .

• Помимо случая «разницы», средний знак трехчленного множителя всегда будет противоположен среднему знаку данной задачи. Следовательно, это положительное значение .4} г.

  Иногда может показаться, что проблема не решается суммой или разностью двух кубов. Если вы видите что-то подобное, попробуйте убрать общие факторы. Для чисел наибольший общий делитель равен 3, а для переменных наибольший общий множитель — «xy». Следовательно, общим общим фактором будет их произведение, которое равно \ left (3 \ right) \ left ({xy} \ right) = 3xy.

  После разложения вы увидите, что у нас есть простая задача о разнице двух кубов.{{2}} — {6} {x} — {1} $$$.

  Разница кубиков — Math Central

  Привет, Билл.

  Разница в кубах — это, конечно, идеальный куб минус идеальный куб.

  Я полагаю, у вашего ученика уже есть формула

  a ³ — b ³ = (a — b) (a ² + ab + b ² )

  Мы можем доказать это, используя полиномиальное деление.

  Сначала мы смотрим на корни a ³ — b ³ и сразу же видим, что если a = b, то a ³ — b ³ = 0, поэтому (a-b) является множителем.

  Затем перепишите его: a ³ — b ³ = a ³ + 0a ² b + 0ab ² — b ³ и используйте синтетическое (или длинное) деление, чтобы найти другой множитель. Я буду использовать длинное деление:

  Вы можете сделать что-то очень похожее для суммы кубиков.

  Однако есть и геометрический способ увидеть это тоже, по крайней мере, когда a и b положительны, а a> b:

  Например, скажем, a = 4 и b = 2.Вот 4 ³ -2 ³ :

  а здесь 3 ³ -2 ³ :

  Давайте сначала разберем 3 ³ — 2 ³ . Красный объект разбивается на другие цвета:

  Итак, красный объект состоит из оранжевой части, которая имеет размер 3 ² , плюс желтой части, которая имеет размер 3×2, и золотой части, которая составляет 2 ² . Таким образом, исходный 3 ³ — 1 ³ равен компонентам 3 ² + 3×2 + 2 ² .Теперь, поскольку (3-2) = 1, мы можем умножить на это и ничего не менять, поэтому мы показали

  3 ³ -2 ³ = (3-2) (3 ² + 3×2 + 2 ² )

  А как насчет того, чтобы попробовать что-нибудь посложнее, например 5 ³ — 2 ³ ?

  У нас такая же разбивка, но всего 3 копии! Это имеет смысл, потому что (5-2) = 3.

  Итак, мы показали, что

  5 ³ -2 ³ = (5-2) (5 ² + 5×2 + 2 ² )

  , как и предсказывала формула, и наше деление в столбик доказано алгебраически.

  Если вы внимательно посмотрите на последнюю диаграмму, вы можете рассматривать ее как ³ — b ³ и показать, что количество копий всегда (a-b), тем самым доказывая общий случай.