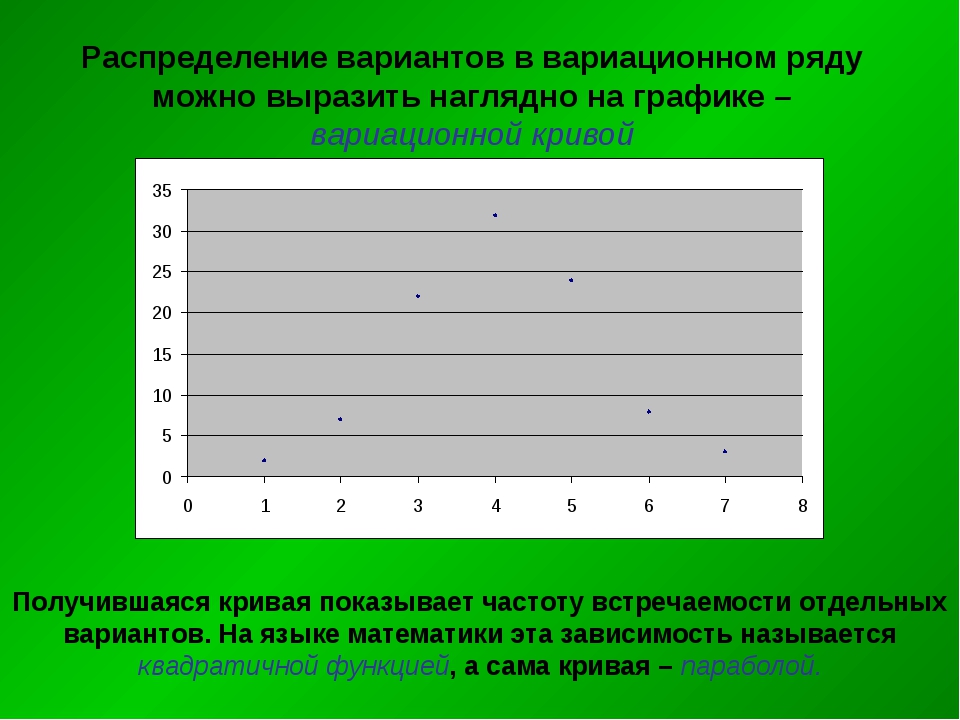
Вариационный ряд распределения это: Вариационные ряды — доступная и полная информация
Дискретный вариационный ряд и его характеристики
п.1. Классификация рядов распределения
Статистический ряд распределения – это количественное распределение единиц совокупности на однородные группы по некоторому варьирующему признаку.
В зависимости от природы признака различают атрибутивные и вариационные ряды.
Атрибутивный ряд распределения построен на качественном признаке.
Вариационный ряд распределения построен на количественном признаке.
Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т.п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.
По упорядоченности вариационные ряды делятся на упорядоченные (ранжированные) и неупорядоченные. Упорядочить ряд можно по возрастанию или убыванию исследуемого признака.
По характеру непрерывности признака вариационные ряды делятся на дискретные и интервальные.
Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.
Варианты – это отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариант.
Например:
Распределение учеников по оценкам за контрольную работу| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
В данном ряду признак – это оценка, варианты признака \(x_i\) – это множество {2;3;4;5}, частоты \(f_i\) – это количество учеников, получивших каждую из оценок.
п.2. Дискретный вариационный ряд, полигон частот и кумулята
Дискретный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся прерывно и принимающему конечное множество значений.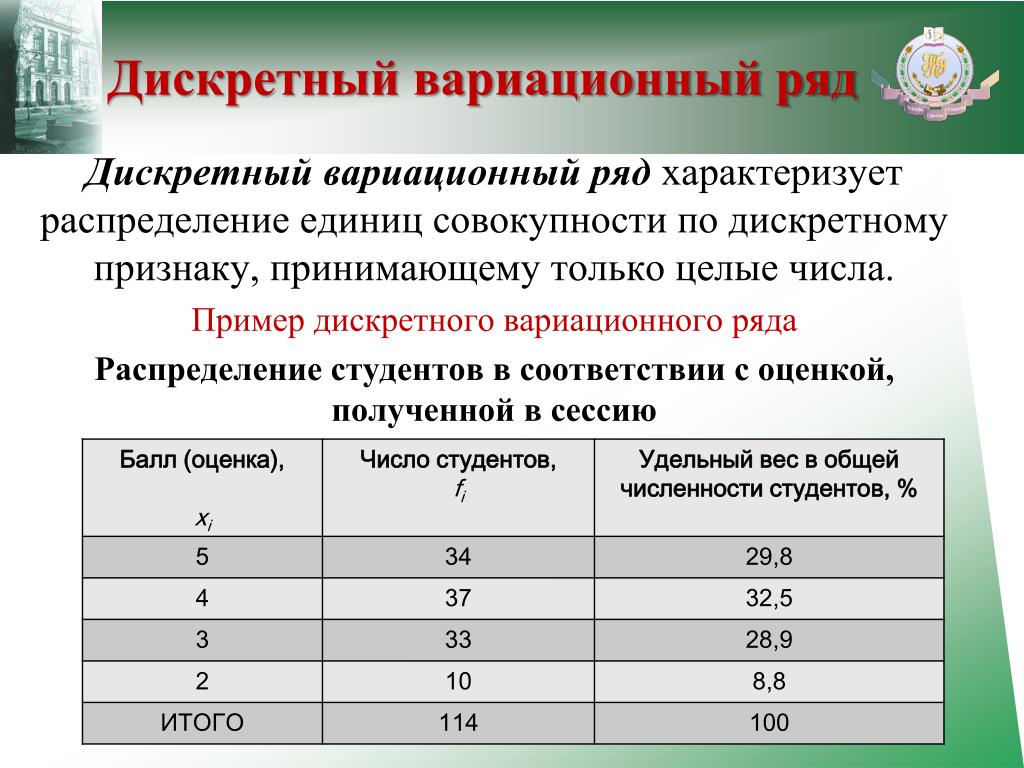 k f_i\)
k f_i\)
Полигон частот – это ломаная, которая соединяет точки \((x_i,f_i)\).
Например:
| Для распределения учеников по оценкам из нашего примера получаем такой полигон: |
Относительная частота варианты \(x_i\) — это отношение частоты \(f_i\) к общему количеству исходов: $$ w_i=\frac{f_i}{N},\ \ i=\overline{1,k} $$ Относительная частота \(w_i\) является эмпирической оценкой вероятности варианты \(x_i\) в исследуемом ряду.
Полигон относительных частот – это ломаная, которая соединяет точки \((x_i,w_i)\).
Полигон относительных частот является эмпирическим законом распределения исследуемого признака.
Накопленные относительные частоты – это суммы: $$ S_1=w_1,\ \ S_i=S_{i-1}+w_i,\ \ i=\overline{2,k} $$ Кумулята – это ломаная, которая соединяет точки \((x_i,S_i)\).

Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | |
| \(w_i\) | 0,0909 | 0,4545 | 0,3030 | 0,1515 | 1 |
| \(S_i\) | 0,0909 | 0,4545 | 0,8485 | 1 | — |
Полигон относительных частот (эмпирический закон распределения)
Кумулята (красная ломаная) и эмпирическая функция распределения (ступенчатая синяя кривая).
Эмпирическая функция распределения: $$ F(x)= \begin{cases} 0,\ x\leq 2\\ 0,0909,\ 2\lt x\leq 3\\ 0,5455,\ 3\lt x\leq 4\\ 0,8485,\ 4\lt x\leq 5\\ 1,\ x\gt 5 \end{cases} $$
п.
 k x_iw_i $$
k x_iw_i $$Мода дискретного вариационного ряда – это варианта с максимальной частотой: $$ M_o=x*,\ \ f(x*)=\underset{i=\overline{1,k}}{max}f_i $$ Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
На полигоне частот мода – это абсцисса самой высокой точки.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.Алгоритм:
1. Отсортировать ряд по возрастанию.
2а. Если общее количество измерений N нечётное, найти \(m=\lceil\frac N2\rceil\) и округлить в сторону увеличения. \(M_e=x_m\) — искомая медиана.
2б. Если общее количество измерений N чётное, найти \(m=\frac N2\) и вычислить медиану как среднее \(M_e=\frac{x_m+x_{m+1}}{2}\).
На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
1) Найдем выборочную среднюю для распределения учеников по оценкам:
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(x_if_i\) | 6 | 45 | 40 | 25 | 116 |
$$ X_{cp}=\frac{6+45+40+25}{33}=\frac{116}{33}\approx 3,5 $$ Средняя оценка за контрольную – 3,5.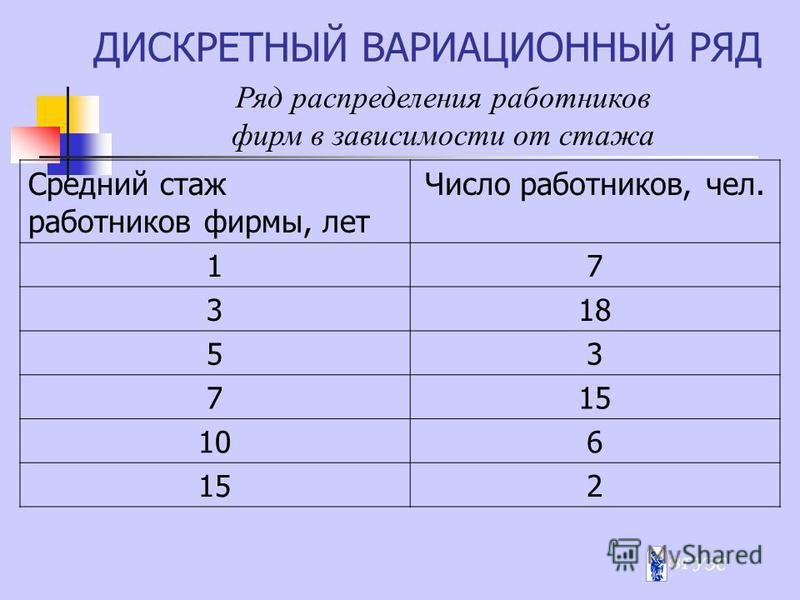
2) Найдем моду. Максимальная частота – 15 человек – у троечников. Значит: \(M_o=3\).
Находим: \(m=\lceil\frac N2\rceil=17\)
Смотрим на ряд слева направо. Сначала у нас идет 3 двоечника, затем 15 троечников.
Вместе их 18, и 17-й человек в ряду — троечник. Группа троечников является медианной: \(M_e=3\).
Также, медиану можно найти по графику кумуляты. (3;0,5455) – это первая слева точка, в которой ордината больше 0,5. Значит, медиана равна абсциссе этой точки, т.е. \(M_e=3\).
п.4. Степень асимметрии вариационного ряда
В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».

Мода, медиана и выборочная средняя совпадут, если вариационный ряд является симметричным: $$ X_{cp}=M_o=M_e $$ Если вершина распределения сдвинута влево и правая часть ветви длиннее левой (длинный правый хвост), такая асимметрия называется правосторонней. При правосторонней асимметрии: $$ M_o\lt M_e\lt X_{cp} $$ Если вершина распределения сдвинута вправо и левая часть ветви длиннее правой (длинный левый хвост), такая асимметрия называется левосторонней. При левосторонней асимметрии: $$ M_o\gt M_e\gt X_{cp} $$ Для умеренно асимметричных рядов (по Пирсону) модуль разности между модой и средней не более 3 раз превышает модуль разности между медианой и средней: $$ \frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}\geq 3 $$
Например:
Для распределения учеников по оценкам мы получили \(X_{cp}=3,5;\ M_o=3;\ M_e=3\).
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом \(\frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=\frac{0,5}{0,5}=1\lt 3\), т.
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.8. Примеры
Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
| Число постоянных заказчиков | 0 | 1 | 2 | 3 | 4 | 5 |
| Число фрилансеров | 22 | 35 | 27 | 11 | 3 | 1 |
Исследуйте полученный вариационный ряд.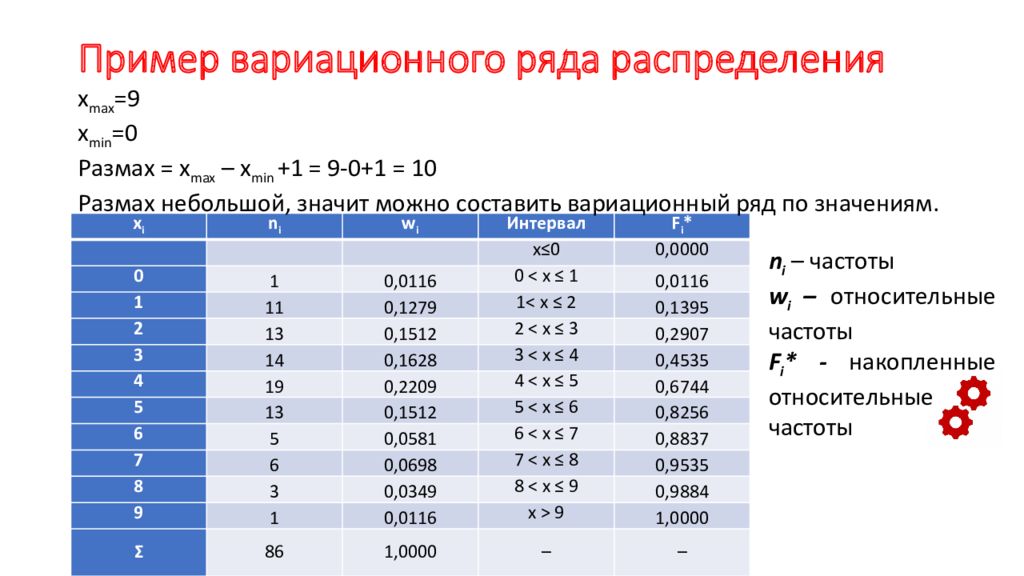 2}\approx 1,109 $$ Коэффициент вариации: $$ V=\frac{s}{X_{cp}}\cdot 100\text{%}=\frac{1,109}{1,39}\cdot 100\text{%}\approx 79,8\text{%}\gt 33\text{%} $$ Представленная выборка неоднородна. Полученное значение средней \(X_{cp}=1,39\) не может быть распространено на генеральную совокупность всех фрилансеров.
2}\approx 1,109 $$ Коэффициент вариации: $$ V=\frac{s}{X_{cp}}\cdot 100\text{%}=\frac{1,109}{1,39}\cdot 100\text{%}\approx 79,8\text{%}\gt 33\text{%} $$ Представленная выборка неоднородна. Полученное значение средней \(X_{cp}=1,39\) не может быть распространено на генеральную совокупность всех фрилансеров.
1. Статистические ряды распределения. Теория статистики: конспект лекций
Читайте также
15. Статистические таблицы
15. Статистические таблицы Статистическая таблица – таблица, которая дает количественную характеристику статистической совокупности и представляет собой форму наглядного изложения полученных в результате статистической сводки и группировки числовых (цифровых)
19. Статистические карты
19. Статистические карты
Статистические карты представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризую–щих уровень или степень распространения того или иного явления на определенной территории.
38. Ряды агрегатных индексов с постоянными и переменными весами
38. Ряды агрегатных индексов с постоянными и переменными весами При изучении динамики экономических явл* ний строятся и исчисляются индексы за ряд последов тельных периодов. Они образуют ряды либо бази ных, либо цепных индексов. В ряду базисных индексе сравнение
6. Статистические термины
6. Статистические термины Статистическая информация, получаемая в результате наблюдения, необходима для предоставления органам государственного управления, для обеспечения информацией руководителей предприятий, компаний и т. д., для информирования общественности об
44. Статистические методы
44. Статистические методы
Особенно широко используются статистические методы при изучении финансовых инвестиций. В основе изучения финансовых инвестиций лежит построение уравнения эквивалентности, так называемого баланса финансовой операции. Содержание данного
В основе изучения финансовых инвестиций лежит построение уравнения эквивалентности, так называемого баланса финансовой операции. Содержание данного
45. Статистические модели
45. Статистические модели Для эффективной работы на фондовом рынке необходимо знать, как доходность конкретного наименования акций (или портфеля акций конкретного инвестора) связана со средней рыночной доходностью всей совокупности акций, т. е. с рыночным индексом. Для
3. Статистические таблицы
3. Статистические таблицы После того как данные статистического наблюдения собраны и даже сгруппированы, их трудно воспринимать и анализировать без определенной, наглядной систематизации. Результаты статистических сводок и группировок получают оформление в виде
4. Ряды агрегатных индексов с постоянными и переменными весами
4. Ряды агрегатных индексов с постоянными и переменными весами
При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексов сравнение
Ряды агрегатных индексов с постоянными и переменными весами
При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексов сравнение
18. Статистические ряды распределения и их графическое изображение
18. Статистические ряды распределения и их графическое изображение Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.Различают атрибутивные и вариационные ряды
19. Статистические таблицы
19. Статистические таблицы
В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях.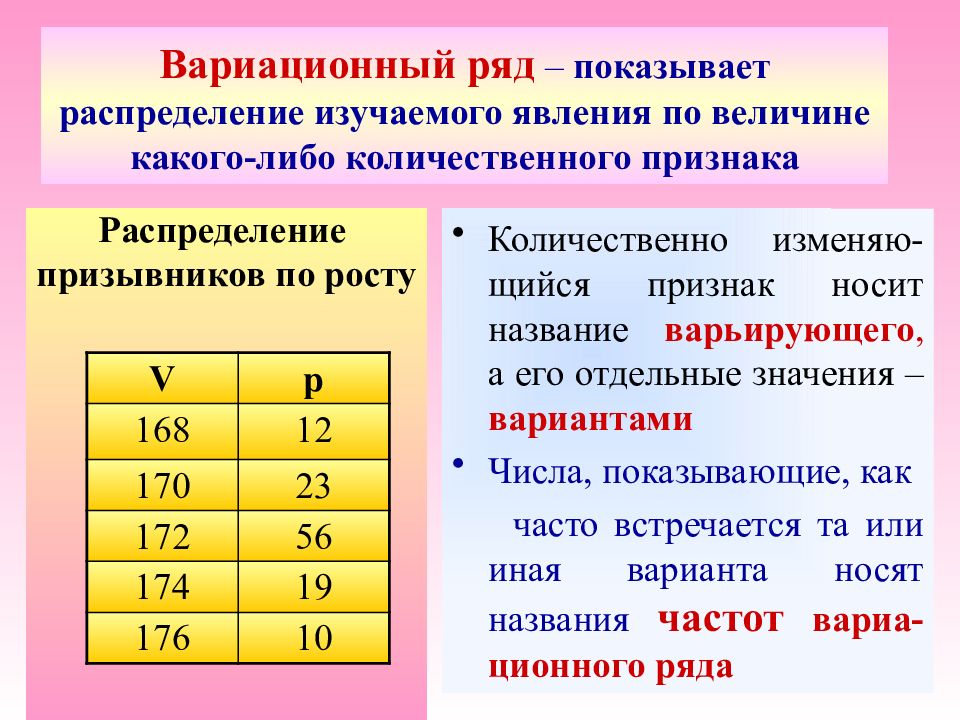 Статистическая таблица
Статистическая таблица
Статистические методы
Статистические методы Подсчет в толпе. Метод, честно говоря, наивный, но очень популярный. Организатор ресторанного бизнеса берет блокнот и карандаш, становится у двери похожего заведения в равноценном районе и считает, сколько человек проходит мимо в единицу времени.
1. Статистические ряды распределения
1. Статистические ряды распределения В результате обработки и систематизации первичных данных статистического наблюдения получают группировки, называемые рядами распределения.Статистические ряды распределения представляют собой упорядоченное расположение единиц
3. Статистические таблицы
3. Статистические таблицы
В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения. Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
ЛЕКЦИЯ № 10. Ряды динамики и их изучение в коммерческой деятельности
ЛЕКЦИЯ № 10. Ряды динамики и их изучение в коммерческой деятельности 1. Основные понятия о рядах динамики Все процессы и явления, протекающие в общественной жизни человека, являются предметом изучения статистической науки они находятся в постоянном движении и
Глава 6 АНГЛО-АМЕРИКАНЦЫ СМЫКАЮТ РЯДЫ
Глава 6 АНГЛО-АМЕРИКАНЦЫ СМЫКАЮТ РЯДЫ Генуэзская конференция16 апреля 1922 года на генуэзской вилле «Альберта» немецкая делегация, присутствовавшая на послевоенной международной конференции по экономике, взорвала бомбу, ударная волна от которой докатилась до другого
Международные статистические данные
Международные статистические данные
Интернет существенно упростил сбор данных в мировом масштабе. В большинстве развитых и многих развивающихся странах обеспечен интернет-доступ к статистической информации. В свободном доступе размещают свои данные и международные
В большинстве развитых и многих развивающихся странах обеспечен интернет-доступ к статистической информации. В свободном доступе размещают свои данные и международные
| Главная > Учебные материалы > Математика: Вариационные ряды | ||||
|
1.Вариационный ряд. 2.Числовые характеристики вариационного ряда.
|
||||
| 24 25 26 27 28 29 30 31 32 | ||||
1. Вариационный ряд. Вариационный ряд.
Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара. |
||||
Таб.1 По данным таблицы построим полигон распределения частот (рис.1) |
Рис.1 |
|||
|
В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). |
||||
Таб. 2 По данным таблицы построим гистограмму распределения частот (рис.2) |
Рис.2 |
|||
|
Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. |
||||
2.Числовые характеристики вариационного ряда. |
||||
|
Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости. |
||||
|
Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической. |
||||
|
Дисперсией s2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической. |
||||
|
Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии. |
||||
|
Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака. |
||||
Пример. |
||||
В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины. |
||||
|
Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен. |
||||
Как видно из таблицы сумма произведений xini = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда. |
||||
По данным таблицы построим гистограмму распределения частот.
|
||||
Построим и эмпирическую функцию распределения случайной величины (кумуляту). |
||||
|
Далее найдем моду и медиану случайной величины Х. Наиболее вероятное значение случайной величины Х (мода) равно Mo = 34,117. Т.е. Pmax (34,1) = 0,1975. Медиана — Ме = 34,3 (как видно из графика). Теперь рассчитаем начальный и центральный моменты k — го порядка и сведем эти данные в таблицу.
|
||||
Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:
|
||||
| 24 25 26 27 28 29 30 31 32 | ||||
ВАРИАЦИОННЫЙ РЯД — это.
 .. Что такое ВАРИАЦИОННЫЙ РЯД?
.. Что такое ВАРИАЦИОННЫЙ РЯД?- ВАРИАЦИОННЫЙ РЯД
- ВАРИАЦИОННЫЙ ряд — последовательность значений наблюденной величины, расположенных в порядке возрастания. Напр., вариационный ряд значений 1, — 3, 0, 5, 3, 4 имеет вид -3, 0, 1, 3, 4, 5.
Большой Энциклопедический словарь. 2000.
- ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- ВАРИАЦИЯ
Смотреть что такое «ВАРИАЦИОННЫЙ РЯД» в других словарях:
ВАРИАЦИОННЫЙ РЯД — англ. variation distribution; нем. Variationreihe. Совокупность к. л. величин, расположенных в порядке их возрастания; полностью определяется указанием различных значений, входящих в него величин и числа членов ряда. см. СТАТИСТИКА. Antinazi.… … Энциклопедия социологии
Вариационный ряд — совокупность значений варьирующего признака (РД 52.
 24.564 96)… Источник: МЕТОДИЧЕСКИЕ УКАЗАНИЯ . ОХРАНА ПРИРОДЫ. ГИДРОСФЕРА. ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ ПОДСИСТЕМЫ МОНИТОРИНГА АНТРОПОГЕННОГО ЭВТРОФИРОВАНИЯ ПРЕСНОВОДНЫХ ЭКОСИСТЕМ. РД… … Официальная терминология
24.564 96)… Источник: МЕТОДИЧЕСКИЕ УКАЗАНИЯ . ОХРАНА ПРИРОДЫ. ГИДРОСФЕРА. ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ ПОДСИСТЕМЫ МОНИТОРИНГА АНТРОПОГЕННОГО ЭВТРОФИРОВАНИЯ ПРЕСНОВОДНЫХ ЭКОСИСТЕМ. РД… … Официальная терминологиявариационный ряд — упорядоченная выборка — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы упорядоченная выборка EN set of variate values … Справочник технического переводчика
вариационный ряд — последовательность значений наблюдаемой величины, расположенных в порядке возрастания. Например, вариационный ряд значений 1, –3, 0, 5, 3, 4 имеет вид –3, 0, 1, 3, 4, 5. * * * ВАРИАЦИОННЫЙ РЯД ВАРИАЦИОННЫЙ РЯД, последовательность значений… … Энциклопедический словарь
ВАРИАЦИОННЫЙ РЯД — Упорядоченное изображение реально существующего распределения особей в группе по величине признака. Вариационный ряд это двойной ряд чисел, состоящий из обозначения классов и соответствующих частот.
 Показывает, как изменяется признак от… … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных
Показывает, как изменяется признак от… … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животныхвариационный ряд — variacinė eilutė statusas T sritis augalininkystė apibrėžtis Bet kurio kiekybinio požymio didėjimo ar mažėjimo tvarka išdėstyti variantai. atitikmenys: angl. variational series rus. вариационный ряд … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas
вариационный ряд — 3.3 вариационный ряд: Совокупность значений варьирующего признака [8]. Величина интервала (интервальная разность) разность между верхними и нижними границами интервала [8]. Источник: Р 52.24.661 2004: Оценка риска антропогенного воздейс … Словарь-справочник терминов нормативно-технической документации
Вариационный ряд — последовательность каких либо чисел, расположенная в порядке возрастания их величин. Например, В. р. чисел 1, 3, 8, 2 имеет вид 3, 1, 2, 8.
 Промежуток между крайними членами В. р. называют интервалом варьирования, а длину этого интервала… … Большая советская энциклопедия
Промежуток между крайними членами В. р. называют интервалом варьирования, а длину этого интервала… … Большая советская энциклопедияВАРИАЦИОННЫЙ РЯД — расположение значений случайной выборки с функцией распределения в порядке их возрастания: В. р. служит для построения эмпирич. функции распределения где число членов ряда, меньших х. Важными характеристиками В. р. являются его крайние члены и… … Математическая энциклопедия
ВАРИАЦИОННЫЙ РЯД — последовательность значений наблюдаемой величины, расположенных в порядке возрастания. Напр., В. р. значений 1, 3, 0, 5, 3, 4 имеет вид 3, 0, 1, 3, 4, 5 … Естествознание. Энциклопедический словарь
Вариационный ряд — Викизнание… Это Вам НЕ Википедия!
Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины
равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число называется рангом порядковой статистики
Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения , то совместная плотность распределения элементов вариационного ряда имеет вид
Если элементы вариационного ряда независимы и имеют общую плотность распределения , то совместная плотность распределения элементов вариационного ряда имеет вид
Пример 1[править]
Приведем оценки 45 студентов по курсу статистика в порядке сдачи экзамена:
5 3 3 4 2 4 4 3 5 4 4 5 5 4 4
3 3 3 2 5 5 4 4 4 3 4 3 4 5 4
4 4 4 3 3 4 3 4 3 2 3 2 3 3 3
При таком представлении информации трудно делать какие-либо выводы об успеваемости. Произведем группировку данным путем подсчета количества различных оценок.
оценки 2 3 4 5
количество 4 16 18 7
Как видим, вместо 45 чисел осталось 8, при этом повысилась информативность таблицы, более 50% студентов сдали предмет на хорошо и отлично. Данный пример показывает, что эти данные лучше сгруппировать, то есть разделить их на однородные группы по некоторому признаку. Благодаря группировке данные приобретают систематизированный вид. Если данные систематизированы по времени, то моделью группировки будет временный ряд. Если же по любому другому признаку — то ряд распределения. А для количественных признаков — вариационный ряд.
Если же по любому другому признаку — то ряд распределения. А для количественных признаков — вариационный ряд.
Пусть Х — одномерный количественный признак и в результате n его измерений наблюдалось n его значений x(1),x(2)…..x(n), среди которых могут быть одинаковые. Эти значения называют вариантами. Пусть среди имеющихся n вариант имеется k различных . Причем x1 встречается m1 раз, xk — mk раз. Понятно, что .
Вариационный ряд обычно записывается в одном из видов: в таблице с частотами mi, через относительные частоты Wi=mi/n. В зависимости от типа признака различают дискретные и интервальные вариационные ряды. В зависимости от объема исходных данных и области допустимых значений одномерного количественного признак, частотные распределения также подразделяются на дискретные и интервальные. Если различных вариант очень много (более 10-15), то эти варианты группируют, выбирая определенное число интервалов группировки и получая таким образом интервальное частотное распределение. Алгоритм группировки массива данных состоит из следующих шагов:
Алгоритм группировки массива данных состоит из следующих шагов:
- 1) находят минимальную и максимальную варианты
- 2) весь диапазон значений признака [Xmin,Xmax] разбивают на к интервалов одинаковой длины .
Число К обычно берется в пределах 10-15. Редки случаи, когда требуется более 25 и менее 8 группировок. Существуют формулы для определения “оптимального” значения К и построения таким образом оптимального распределения частот. Формула Старджеса . Для больших n эта формула дает оценку снизу для К.
- 3) находят граничные точки каждого из интервалов и т.д.
- 4) подсчитываем число вариант Mi, попавших в интервал , причем варианты, попавшие на границы интервалов, относят только к одному из интервалов, результат заносят в таблицу .
Пример 2[править]
Приведем вариационный ряд почасовой оплаты 303 рабочих промышленности
Xi 2.49 2.50 2.51 2.52 2.53 2.54 2.55 2.56 2.57 2.58 2.59 2.6 2.61
Mi 1 4 1 1 0 3 2 0 3 2 1 8 1
2. 62 3 2.72 9 2.82 11 2.92 6 3.02 2 3.12 0 3.22 1 3.32 1
62 3 2.72 9 2.82 11 2.92 6 3.02 2 3.12 0 3.22 1 3.32 1
2.63 0 2.73 3 2.83 3 2.93 2 3.03 0 3.13 0 3.23 0 3.33 0
2.64 5 2.74 10 2.84 4 2.94 4 3.04 3 3.14 2 3.24 0 3.34 2
2.65 7 2.75 11 2.85 7 2.95 8 3.05 4 3.15 4 3.25 3 3.35 2
2.66 3 2.76 4 2.86 5 2.96 5 3.06 2 3.16 2 3.26 1 3.36 0
2.67 2 2.77 2 2.87 3 2.97 2 3.07 0 3.17 0 3.27 0 3.37 1
2.68 3 2.78 9 2.88 8 2.98 3 3.08 2 3.18 2 3.28 0
2.69 2 2.79 5 2.89 4 2.99 1 3.09 0 3.19 1 3.29 0
2.70 14 2.8 22 2.90 16 3.0 9 3.10 7 3.20 4 3.30 4
2.71 4 2.81 3 2.91 3 3.01 1 3.11 0 3.21 0 3.31 0
Построим для данного ряда интервальное частотное распределение.
- 1) X min = 2,49 Xmax=3,37
- 2)
Для удобства вычислений возьмем К=10. и т.д.
Для наглядного представления дискретных частотных распределений могут применяться вертикальные линии. Каждый из примеров можно рассматривать либо как выборку, либо как генеральную совокупность.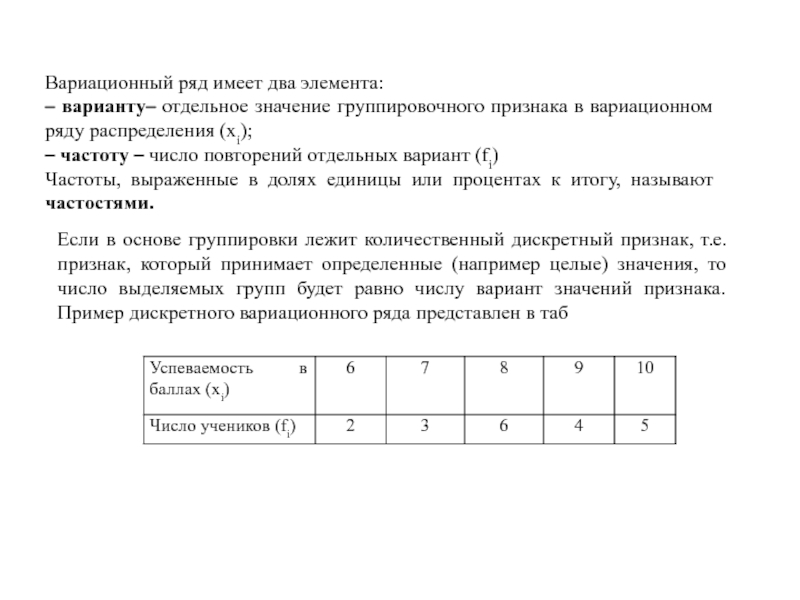 Обычно данные собирают и анализируют для практических результатов.
пример.
Обычно данные собирают и анализируют для практических результатов.
пример.
Абсолютное частотное распределение прибыли 100 крупных межнациональных компаний, базирующихся в США за 1988 г.
Класс компании, размер прибыли, млн.$ Число компаний в классе
-1500-0 3 |||
0-500 41 |||| |||| |||| |||| |||| |||| |||| |||| |||| |||| |
500 — 1000 32 |||| |||| |||| |||| |||| |||| |||| ||||
1000 — 1500 9 |||| |||| |
1500 — 2000 6 |||| ||
2000 — 2500 6 |||| ||
2500 — 5500 3 |||
Меры изменчивости: диапазон, межквартильный размах, дисперсия и стандартное отклонение
Мера изменчивости — это сводная статистика, которая представляет величину дисперсии в наборе данных. Насколько разнятся ценности? В то время как мера центральной тенденции описывает типичное значение, меры изменчивости определяют, насколько далеко точки данных имеют тенденцию падать от центра. Мы говорим о вариативности в контексте распределения ценностей. Низкая дисперсия указывает на то, что точки данных обычно плотно сгруппированы вокруг центра.Высокая дисперсия означает, что они имеют тенденцию падать дальше.
Низкая дисперсия указывает на то, что точки данных обычно плотно сгруппированы вокруг центра.Высокая дисперсия означает, что они имеют тенденцию падать дальше.
В статистике изменчивость, дисперсия и разброс являются синонимами, обозначающими ширину распределения. Подобно тому, как существует множество показателей центральной тенденции, существует несколько показателей изменчивости. Из этого сообщения в блоге вы узнаете, почему так важно понимать изменчивость ваших данных. Затем я исследую наиболее распространенные меры изменчивости — диапазон, межквартильный размах, дисперсию и стандартное отклонение. Я помогу вам определить, какой из них лучше всего подходит для ваших данных.
Два графика ниже графически показывают разницу для распределений с одинаковым средним значением, но с большей или меньшей дисперсией. Панель слева показывает распределение, которое плотно сгруппировано вокруг среднего, тогда как распределение на правой панели более разбросано.
Связанное сообщение : Меры центральной тенденции: среднее, медиана и мода
Почему важно понимать изменчивость
Давайте сделаем шаг назад и сначала разберемся, почему так важно понимать изменчивость. Аналитики часто используют среднее значение, чтобы резюмировать центр населения или процесса. Хотя среднее значение имеет значение, люди часто еще больше реагируют на изменчивость. Когда распределение имеет меньшую изменчивость, значения в наборе данных более согласованы. Однако, когда изменчивость выше, точки данных более различаются, и экстремальные значения становятся более вероятными. Следовательно, понимание изменчивости помогает понять вероятность необычных событий.
Аналитики часто используют среднее значение, чтобы резюмировать центр населения или процесса. Хотя среднее значение имеет значение, люди часто еще больше реагируют на изменчивость. Когда распределение имеет меньшую изменчивость, значения в наборе данных более согласованы. Однако, когда изменчивость выше, точки данных более различаются, и экстремальные значения становятся более вероятными. Следовательно, понимание изменчивости помогает понять вероятность необычных событий.
В некоторых ситуациях экстремальные значения могут вызвать проблемы! Вы видели прогноз погоды, в котором метеоролог показывает сильную жару и засуху в одном районе и наводнение в другом? Было бы неплохо их усреднить вместе! Часто мы чувствуем дискомфорт в крайности сильнее, чем в среднем.Понимание этой изменчивости вокруг среднего дает важную информацию.
Изменчивость везде. Время, которое вы добираетесь до работы, каждый день немного меняется. Когда вы заказываете любимое блюдо в ресторане несколько раз, оно не всегда одно и то же. Детали, сходящие с конвейера, могут казаться идентичными, но имеют несколько разную длину и ширину.
Детали, сходящие с конвейера, могут казаться идентичными, но имеют несколько разную длину и ширину.
Это все примеры реальной изменчивости. Некоторая степень вариации неизбежна. Однако излишняя непоследовательность может вызвать проблемы.Если ваша утренняя поездка на работу займет намного больше времени, чем среднее время в пути, вы опоздаете на работу. Если блюдо в ресторане сильно отличается от обычного, оно может вам совсем не понравиться. И, если изготовленная деталь слишком сильно не соответствует спецификации, она не будет работать должным образом.
Некоторые вариации неизбежны, но проблемы возникают в крайних случаях. Распределения с большей изменчивостью производят наблюдения с необычно большими и малыми значениями чаще, чем распределения с меньшей изменчивостью.
Вариабельность также может помочь вам оценить неоднородность образца.
Пример различной степени изменчивости
Давайте взглянем на два гипотетических ресторана с пиццей. Оба они заявляют, что среднее время доставки составляет 20 минут.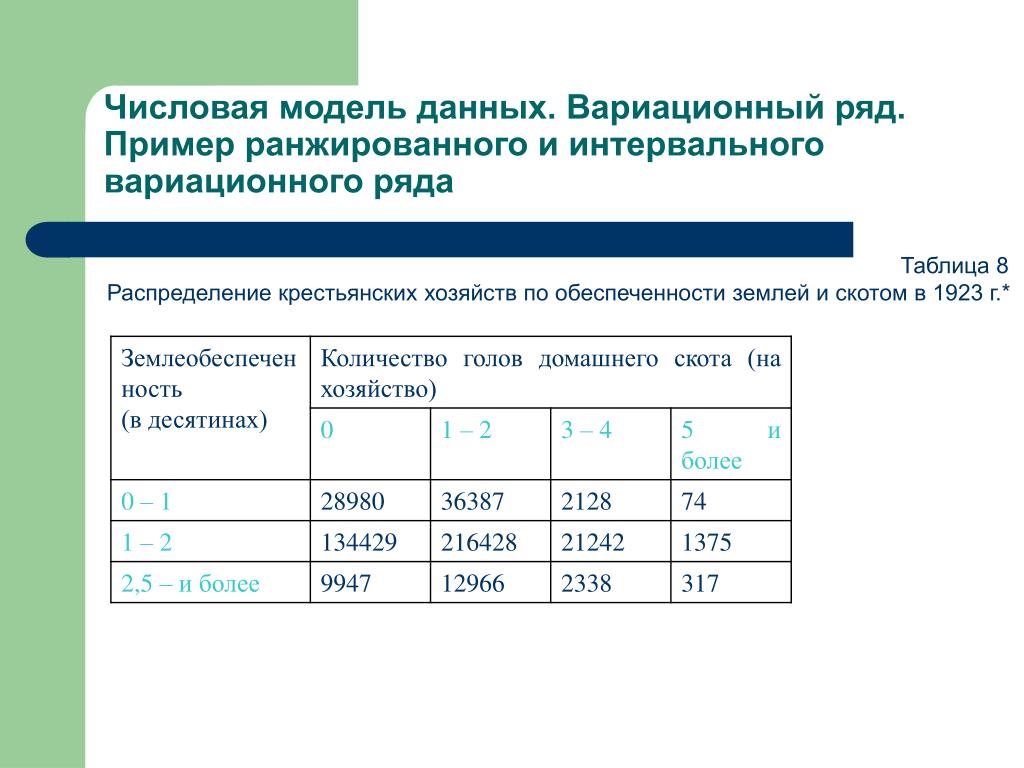 Когда мы голодны, они оба звучат одинаково хорошо! Однако эта эквивалентность может быть обманчива! Чтобы определить ресторан, из которого следует заказывать, когда вы голодны, нам необходимо проанализировать их разнообразие.
Когда мы голодны, они оба звучат одинаково хорошо! Однако эта эквивалентность может быть обманчива! Чтобы определить ресторан, из которого следует заказывать, когда вы голодны, нам необходимо проанализировать их разнообразие.
Предположим, мы изучаем их сроки доставки, рассчитываем вариабельность для каждого места и определяем, что их вариативность различна.Мы вычислили стандартные отклонения для обоих ресторанов — к этому показателю мы вернемся позже в этом посте. Насколько значительна эта разница в том, чтобы быстро доставить пиццу клиентам?
На графиках ниже показано распределение сроков доставки и дан ответ. Ресторан с более переменным временем доставки имеет более широкую кривую распределения. Я использовал одинаковые шкалы на обоих графиках, чтобы вы могли визуально сравнить два распределения.
На этих графиках мы считаем неприемлемым 30-минутное или более длительное ожидание.Мы ведь голодны! Заштрихованная область на каждой диаграмме представляет собой долю времени доставки, превышающую 30 минут. Почти 16% доставок для ресторана с высокой вариативностью превышают 30 минут. С другой стороны, только 2% доставок занимают слишком много времени из-за ресторана с низкой вариабельностью. У них обоих в среднем время доставки 20 минут, но я знаю, где разместить заказ, когда проголодаюсь!
Почти 16% доставок для ресторана с высокой вариативностью превышают 30 минут. С другой стороны, только 2% доставок занимают слишком много времени из-за ресторана с низкой вариабельностью. У них обоих в среднем время доставки 20 минут, но я знаю, где разместить заказ, когда проголодаюсь!
Как показывает этот пример, центральная тенденция не дает полной информации.Нам также необходимо понимать изменчивость в середине распределения, чтобы получить полную картину. Теперь перейдем к различным способам измерения изменчивости!
Диапазон
Начнем с диапазона, потому что это наиболее простой для вычисления и понятный способ измерения изменчивости. Диапазон набора данных — это разница между наибольшим и наименьшим значениями в этом наборе данных. Например, в двух наборах данных ниже набор данных 1 имеет диапазон от 20 до 38 = 18, а набор данных 2 имеет диапазон от 11 до 52 = 41.Набор данных 2 имеет более широкий диапазон и, следовательно, большую изменчивость, чем набор данных 1.
Хотя диапазон легко понять, он основан только на двух самых крайних значениях в наборе данных, что делает его очень чувствительным к выбросам. Если одно из этих чисел необычно высокое или низкое, оно влияет на весь диапазон, даже если оно нетипично.
Кроме того, размер набора данных влияет на диапазон. Как правило, вы с меньшей вероятностью будете наблюдать экстремальные значения. Однако по мере увеличения размера выборки у вас появляется больше возможностей для получения этих экстремальных значений.Следовательно, когда вы собираете случайные выборки из одной и той же совокупности, диапазон имеет тенденцию увеличиваться по мере увеличения размера выборки. Следовательно, используйте диапазон для сравнения изменчивости только тогда, когда размеры выборки аналогичны.
Подробнее читайте в моем посте «Диапазон в статистике».
Межквартильный размах (IQR). . . и другие процентили
Межквартильный размах — это средняя половина данных. Чтобы визуализировать это, подумайте о среднем значении, которое разделяет набор данных пополам. Точно так же вы можете разделить данные на кварталы. Статистики называют эти кварталы квартилями и обозначают их от низкого до высокого как Q1, Q2 и Q3. Самый низкий квартиль (Q1) содержит четверть набора данных с наименьшими значениями. Верхний квартиль (Q4) содержит четверть набора данных с самыми высокими значениями. Межквартильный размах — это средняя половина данных, которая находится между верхним и нижним квартилями. Другими словами, межквартильный диапазон включает 50% точек данных, которые попадают между Q1 и Q3.IQR — это красная область на графике ниже.
Точно так же вы можете разделить данные на кварталы. Статистики называют эти кварталы квартилями и обозначают их от низкого до высокого как Q1, Q2 и Q3. Самый низкий квартиль (Q1) содержит четверть набора данных с наименьшими значениями. Верхний квартиль (Q4) содержит четверть набора данных с самыми высокими значениями. Межквартильный размах — это средняя половина данных, которая находится между верхним и нижним квартилями. Другими словами, межквартильный диапазон включает 50% точек данных, которые попадают между Q1 и Q3.IQR — это красная область на графике ниже.
Межквартильный размах — надежная мера изменчивости, так же как и медиана — надежная мера центральной тенденции. Выбросы не оказывают существенного влияния ни на один из показателей, потому что они не зависят от каждого значения. Кроме того, межквартильный размах отлично подходит для асимметричных распределений, как и медиана. Как вы узнаете, при нормальном распределении стандартное отклонение показывает процент наблюдений, которые отклоняются от среднего значения на определенное расстояние. Однако это не работает для искаженных распределений, и IQR — отличная альтернатива.
Однако это не работает для искаженных распределений, и IQR — отличная альтернатива.
Я разделил приведенный ниже набор данных на квартили. Межквартильный диапазон (IQR) простирается от нижней границы Q2 до верхней границы Q3. Для этого набора данных диапазон составляет 21–39.
Связанное сообщение : Межквартильный размах: определение и использование и что такое надежная статистика?
Использование других процентилей
Когда у вас асимметричное распределение, я считаю, что отчет о медиане с межквартильным размахом является особенно хорошей комбинацией.Межквартильный диапазон эквивалентен области между 75-м и 25-м процентилями (75–25 = 50% данных). Вы также можете использовать другие процентили для определения разброса различных пропорций. Например, диапазон между 97,5-м процентилем и 2,5-м процентилем покрывает 95% данных. Чем шире эти диапазоны, тем выше вариабельность вашего набора данных.
Соответствующее сообщение : Процентили: интерпретация и расчеты
Разница
Дисперсия — это средний квадрат разницы значений от среднего. В отличие от предыдущих мер вариабельности, дисперсия включает все значения в расчет путем сравнения каждого значения со средним. Чтобы вычислить эту статистику, вы вычисляете набор квадратов разностей между точками данных и средним значением, суммируете их, а затем делите на количество наблюдений. Следовательно, это средний квадрат разницы.
В отличие от предыдущих мер вариабельности, дисперсия включает все значения в расчет путем сравнения каждого значения со средним. Чтобы вычислить эту статистику, вы вычисляете набор квадратов разностей между точками данных и средним значением, суммируете их, а затем делите на количество наблюдений. Следовательно, это средний квадрат разницы.
Существуют две формулы для дисперсии в зависимости от того, рассчитываете ли вы дисперсию для всей генеральной совокупности или используете выборку для оценки дисперсии генеральной совокупности.Уравнения приведены ниже, а затем я прорабатываю пример в таблице, чтобы помочь воплотить его в жизнь.
Дисперсия совокупности
Формула дисперсии генеральной совокупности следующая:
В уравнении σ 2 — это параметр генеральной совокупности для дисперсии, μ — параметр для среднего значения генеральной совокупности, а N — количество точек данных, которые должны включать всю совокупность.
Вариант выборки
Чтобы использовать выборку для оценки дисперсии генеральной совокупности, используйте следующую формулу.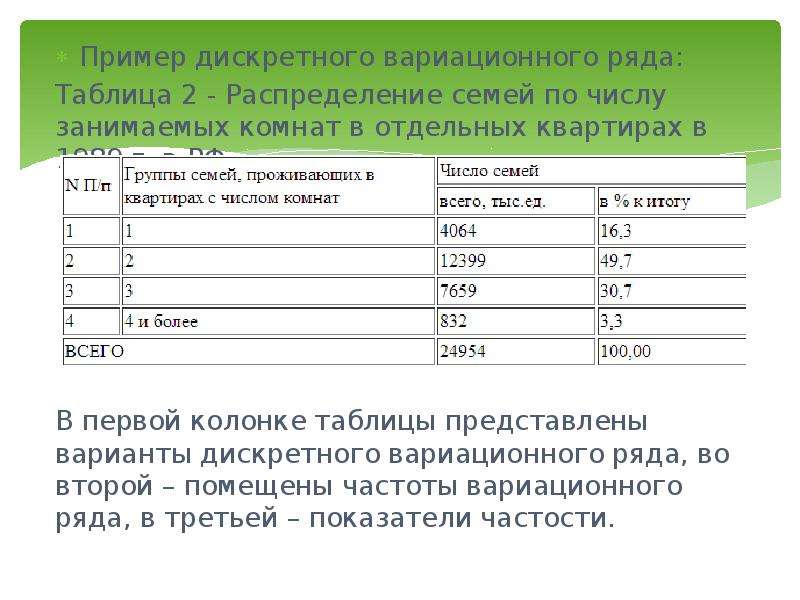 Использование предыдущего уравнения с выборочными данными ведет к недооценке изменчивости. Поскольку обычно невозможно измерить всю генеральную совокупность, статистики гораздо чаще используют уравнение для выборочной дисперсии.
Использование предыдущего уравнения с выборочными данными ведет к недооценке изменчивости. Поскольку обычно невозможно измерить всю генеральную совокупность, статистики гораздо чаще используют уравнение для выборочной дисперсии.
В уравнении s 2 — это дисперсия выборки, а M — выборочное среднее. N-1 в знаменателе исправляет тенденцию выборки недооценивать дисперсию генеральной совокупности.
Пример расчета выборочной дисперсии
Я проработаю пример, используя формулу для выборки набора данных с 17 наблюдениями в таблице ниже.Цифры в скобках представляют номер соответствующего столбца таблицы. Процедура включает в себя взятие каждого наблюдения (1), вычитание выборочного среднего (2) для вычисления разницы (3) и возведение этой разницы в квадрат (4). Затем я суммирую квадраты разностей внизу таблицы. Наконец, я беру сумму и делю ее на 16, потому что я использую уравнение выборки дисперсии с 17 наблюдениями (17 — 1 = 16). Разница для этого набора данных составляет 201.
Поскольку в расчетах используются квадраты разностей, дисперсия выражается в квадратах, а не в исходных единицах данных.Хотя более высокие значения дисперсии указывают на большую изменчивость, для конкретных значений нет интуитивной интерпретации. Несмотря на это ограничение, различные статистические тесты используют дисперсию в своих расчетах. Для примера прочтите мой пост о F-тесте и ANOVA.
Хотя интерпретировать саму дисперсию сложно, стандартное отклонение решает эту проблему!
Подробнее читайте в моем посте про дисперсию.
Стандартное отклонение
Стандартное отклонение — это стандартная или типичная разница между каждой точкой данных и средним значением.Когда значения в наборе данных сгруппированы ближе друг к другу, вы получаете меньшее стандартное отклонение. С другой стороны, чем больше разброс значений, тем больше стандартное отклонение, потому что стандартное расстояние больше.
Удобно, что стандартное отклонение использует исходные единицы данных, что упрощает интерпретацию.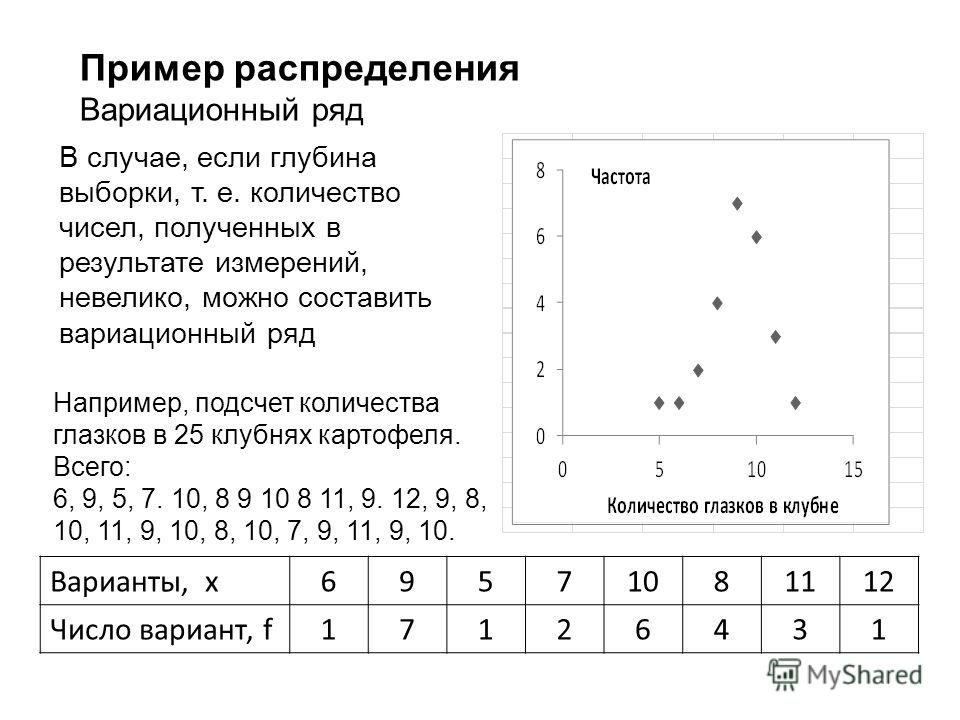 Следовательно, стандартное отклонение — наиболее широко используемый показатель изменчивости. Например, в примере доставки пиццы стандартное отклонение 5 указывает, что типичное время доставки составляет плюс или минус 5 минут от среднего.Часто указывается вместе со средним значением: 20 минут (стандартное отклонение 5).
Следовательно, стандартное отклонение — наиболее широко используемый показатель изменчивости. Например, в примере доставки пиццы стандартное отклонение 5 указывает, что типичное время доставки составляет плюс или минус 5 минут от среднего.Часто указывается вместе со средним значением: 20 минут (стандартное отклонение 5).
Стандартное отклонение — это просто квадратный корень из дисперсии. Напомним, что дисперсия выражена в квадрате. Следовательно, квадратный корень возвращает значение в натуральных единицах. Символ стандартного отклонения как параметра генеральной совокупности — σ, тогда как s представляет его как выборочную оценку. Чтобы вычислить стандартное отклонение, вычислите дисперсию, как показано выше, а затем извлеките из нее квадратный корень. Вуаля! У вас стандартное отклонение!
В разделе отклонений мы вычислили отклонение 201 в таблице.
Следовательно, стандартное отклонение для этого набора данных составляет 14,177.
Стандартное отклонение аналогично среднему абсолютному отклонению. Оба используют исходные единицы данных и сравнивают значения данных, чтобы оценить изменчивость. Однако есть отличия. Чтобы узнать больше, прочитайте мой пост о среднем абсолютном отклонении (MAD).
Оба используют исходные единицы данных и сравнивают значения данных, чтобы оценить изменчивость. Однако есть отличия. Чтобы узнать больше, прочитайте мой пост о среднем абсолютном отклонении (MAD).
Люди часто путают стандартное отклонение со стандартной ошибкой среднего. Обе меры оценивают изменчивость, но имеют совершенно разные цели.Чтобы узнать больше, прочитайте мой пост Стандартная ошибка среднего.
Связанное сообщение : Использование стандартного отклонения
Эмпирическое правило стандартного отклонения нормального распределения
Когда у вас есть нормально распределенные данные или примерно так, стандартное отклонение становится особенно ценным. Вы можете использовать его для определения доли значений, попадающих в заданное число стандартных отклонений от среднего. Например, при нормальном распределении 68% значений будут находиться в пределах +/- 1 стандартного отклонения от среднего.Это свойство является частью эмпирического правила. Это правило описывает процент данных, которые попадают в определенные числа стандартных отклонений от среднего для колоколообразных кривых.
Это правило описывает процент данных, которые попадают в определенные числа стандартных отклонений от среднего для колоколообразных кривых.
| Среднее +/- стандартное отклонение | Процент содержащихся данных |
| 1 | 68% |
| 2 | 95% |
| 3 | 99,7% |
Давайте еще раз посмотрим на пример доставки пиццы, где среднее время доставки составляет 20 минут, а стандартное отклонение — 5 минут.Используя эмпирическое правило, мы можем использовать среднее значение и стандартное отклонение, чтобы определить, что 68% времени доставки приходится на 15-25 минут (20 +/- 5), а 95% — между 10-30 минутами (20 + / — 2 * 5).
Похожие сообщения : Нормальное распределение и эмпирическое правило
Что лучше: размах, межквартильный размах или стандартное отклонение?
Во-первых, вы, вероятно, заметили, что я не включил дисперсию в качестве одного из вариантов в заголовке выше. Это потому, что дисперсия выражена в квадратах и не обеспечивает интуитивной интерпретации. Итак, я вычеркнул это из списка. Давайте рассмотрим три других показателя изменчивости.
Это потому, что дисперсия выражена в квадратах и не обеспечивает интуитивной интерпретации. Итак, я вычеркнул это из списка. Давайте рассмотрим три других показателя изменчивости.
Когда вы сравниваете образцы одинакового размера, рассмотрите возможность использования диапазона в качестве меры изменчивости. Это достаточно интуитивная статистика. Просто имейте в виду, что один выброс может сбить диапазон. Диапазон особенно подходит для небольших выборок, когда у вас недостаточно данных для надежного расчета других показателей, и вероятность получения выброса также ниже.
Когда у вас асимметричное распределение, медиана является лучшим измерителем центральной тенденции, и имеет смысл связать ее либо с межквартильным диапазоном, либо с другими диапазонами на основе процентилей, потому что вся эта статистика делит набор данных на группы с определенными пропорциями.
Для нормально распределенных данных или даже данных, которые не сильно искажены, лучше всего использовать проверенную комбинацию, сообщающую среднее значение и стандартное отклонение. Эта комбинация является наиболее распространенной.Вы по-прежнему можете дополнить этот подход диапазонами базового процентиля по мере необходимости.
Эта комбинация является наиболее распространенной.Вы по-прежнему можете дополнить этот подход диапазонами базового процентиля по мере необходимости.
За исключением отклонений, статистика в этом посте представляет собой абсолютные меры изменчивости, поскольку они используют единицы измерения исходной переменной. Прочтите мой пост о коэффициенте вариации, чтобы узнать об относительной мере вариабельности , равной , которая может быть полезной при некоторых обстоятельствах.
Аналитики часто используют меры изменчивости для описания своих наборов данных. Узнайте, как анализировать описательную статистику в Excel.
Если вы изучаете статистику и вам нравится подход, который я использую в своем блоге, ознакомьтесь с моей электронной книгой Introduction to Statistics!
Выучить больше! СвязанныеМеры вариации: определение, виды и примеры
Описательная статистика> Меры вариации
Вариант — это способ показать , как данные распределены, или распределены . В статистике используются несколько показателей вариации.
В статистике используются несколько показателей вариации.
Различные меры отклонения
Диапазон
Диапазон — одна из основных мер вариации. Это разница между наименьшим элементом данных в наборе и наибольшим. Например, диапазон 73, 79, 84, 87, 88, 91 и 94 равен 21, потому что 94-73 равен 21.
Квартили
квартили делят ваши данные на четверти: самые низкие 25%, следующие самые низкие 25%, вторые по величине 25% и самые высокие 25%.
Набор чисел (-2, -1,0,1,2), разделенных на четыре квартиля.
Межквартильный размах
Межквартильный размах — один из самых популярных показателей вариации, используемых в статистике. Это мера того, как данные распределяются вокруг среднего значения. Основная формула:
IQR = Q 3 — Q 1
Подробнее см. Межквартильный размах в статистике: что это такое и как его найти.
Разница
Дисперсия сообщает вам, насколько далеко разброс набор данных, но это абстрактное число, которое на самом деле полезно только для расчета стандартного отклонения.
В этом видео показано, как найти и то, и другое:
Не можете посмотреть видео? Кликните сюда.
Сумма квадратов
Сумма квадратов — это довольно продвинутая методика, которая измеряет, как данные изменяются вокруг центрального числа, например среднего. Он широко используется в регрессионном анализе, чтобы вычислить, насколько хорошо точки данных соответствуют линии наилучшего соответствия. Для получения дополнительной информации о том, как это вычислить, см .: Сумма квадратов.
Эмпирическое правило
Сколько данных находится на определенном расстоянии от среднего? Если у вас нормальное распределение, эмпирическое правило может вам это сказать.Например:
- Около 68% результатов будут находиться между +1 и -1 стандартными отклонениями от среднего.

- Около 95% будет находиться в диапазоне от +2 до -2 стандартных отклонений.
Если у вас есть другое (ненормальное) распределение, вы все равно можете вычислить эти проценты, используя теорему Чебышева.
————————————————— ————————-Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Вариация: нормальное распределение, диапазон и стандартное отклонение
1.18: Вариация: нормальное распределение, диапазон и стандартное отклонение
В области психологии существует несколько способов организовать измерения черты, черты или характеристики ( i. е. , переменные). Качественные данные, такие как этническая принадлежность, могут быть сведены в таблицу для подсчета частот, чтобы предоставить информацию о доле, а также о разнообразии групп в выборке или популяции. С другой стороны, исследователи могут выполнять более широкий набор вычислений на количественных данных. Например, среднее значение, мода и медиана являются основными показателями тенденции для определения типичного значения переменной в заданном наборе числовых данных. Точно так же существует несколько подходов к оценке расстояния оценок друг от друга, называемых вариабельностью или вариацией , включая диапазон, дисперсию и стандартное отклонение.
е. , переменные). Качественные данные, такие как этническая принадлежность, могут быть сведены в таблицу для подсчета частот, чтобы предоставить информацию о доле, а также о разнообразии групп в выборке или популяции. С другой стороны, исследователи могут выполнять более широкий набор вычислений на количественных данных. Например, среднее значение, мода и медиана являются основными показателями тенденции для определения типичного значения переменной в заданном наборе числовых данных. Точно так же существует несколько подходов к оценке расстояния оценок друг от друга, называемых вариабельностью или вариацией , включая диапазон, дисперсию и стандартное отклонение.
Диапазон
Диапазон вычисляет расстояние или разницу между только высшим и наименьшим значениями переменной, но не предоставляет подробных сведений о промежуточных оценках. Высокое значение означает более широкий разброс оценок, но выбросы могут привести к неправильной интерпретации. По этим причинам диапазон считается менее точным методом измерения вариации.
По этим причинам диапазон считается менее точным методом измерения вариации.
Отклонение
Исследователи обычно используют дисперсию для оценки среднего расстояния всех оценок в выборке или генеральной совокупности вокруг среднего.Во-первых, среднее значение определяется путем деления суммы всех исходных оценок конкретной переменной на общее количество оценок в выборке. Вычитание среднего из каждой из исходных оценок дает набор оценок отклонения, который будет состоять как из положительных, так и из отрицательных целых чисел, в зависимости от того, являются ли оценки выше или ниже среднего. Попытки вычислить среднее значение оценок отклонения будет недостаточно, потому что положительные целые числа аннулируют отрицательные целые числа, приводящие к нулевой сумме.Возведение в квадрат отклонений преобразует отрицательные оценки отклонения в положительные, при этом обеспечивая разумную оценку расстояния между средним значением и каждой точкой данных. Суммирование квадратов отклонений образует сумму квадратов (SS).
SS делится либо на общее количество точек данных (N), либо на степени свободы (N-1), если дисперсия вычисляется для выборки или оценивается для совокупности баллов, соответственно. Разделение суммы квадратов отклонений дает совокупную оценку общего расстояния между оценками и средним значением.
Стандартное отклонение
Квадратный корень из дисперсии — это стандартное отклонение. Этот арифметический шаг служит для уравновешивания квадратов отклонений на предыдущем шаге формулы дисперсии. Стандартное отклонение не только описывает общий разброс оценок в генеральной совокупности или наборе выборки, но также используется для оценки расстояния между конкретной оценкой и средним значением. Если оценки соответствуют нормальной кривой, расположение оценки относительно центра кривой может соотноситься с вероятностью ее появления (вероятностью).
Последствия изменения
Уменьшение диапазона оценок в выборке или генеральной совокупности соответствует уменьшению дисперсии. Например, данные, полученные от женщин, демонстрируют низкий разброс таких характеристик, как речевые способности, математические способности и рост, по сравнению с данными мужчин. В этих случаях понимание источников различий среди мужчин, таких как экологические или биологические факторы, так же важно, как и распознавание межгрупповых различий.
Например, данные, полученные от женщин, демонстрируют низкий разброс таких характеристик, как речевые способности, математические способности и рост, по сравнению с данными мужчин. В этих случаях понимание источников различий среди мужчин, таких как экологические или биологические факторы, так же важно, как и распознавание межгрупповых различий.
Меры распространения | Как и когда использовать меры распространения
Показатели распространения | Как и когда использовать меры распространения | Статистика ЛаэрдВведение
Мера разброса, иногда также называемая мерой дисперсии, используется для описания изменчивости в выборке или генеральной совокупности.Обычно он используется в сочетании с показателем центральной тенденции, например средним или медианным, для обеспечения общего описания набора данных.
Почему важно измерять разброс данных?
Существует множество причин, по которым мера разброса значений данных важна, но одна из основных причин касается ее взаимосвязи с мерами центральной тенденции. Мера разброса дает нам представление о том, насколько хорошо среднее, например, представляет данные.Если разброс значений в наборе данных велик, среднее значение не так репрезентативно для данных, как если бы разброс данных был небольшим. Это потому, что большой разброс указывает на то, что между индивидуальными оценками, вероятно, есть большие различия. Кроме того, в исследованиях часто считается положительным, если в каждой группе данных мало вариаций, поскольку это указывает на сходство.
Мера разброса дает нам представление о том, насколько хорошо среднее, например, представляет данные.Если разброс значений в наборе данных велик, среднее значение не так репрезентативно для данных, как если бы разброс данных был небольшим. Это потому, что большой разброс указывает на то, что между индивидуальными оценками, вероятно, есть большие различия. Кроме того, в исследованиях часто считается положительным, если в каждой группе данных мало вариаций, поскольку это указывает на сходство.
Мы будем рассматривать диапазон, квартили, дисперсию, абсолютное отклонение и стандартное отклонение.
Диапазон
Диапазон — это разница между наивысшим и наименьшим баллами в наборе данных и является самой простой мерой разброса. Таким образом, мы рассчитываем диапазон как:
Диапазон = максимальное значение — минимальное значение
Например, рассмотрим следующий набор данных:
| 23 | 56 | 45 | 65 | 59 | 55 | 62 | 54 | 85 | 25 |
Максимальное значение — 85, минимальное — 23. В результате получается диапазон 62, что составляет 85 минус 23. Хотя использование диапазона в качестве меры разброса ограничено, оно устанавливает границы оценок. Это может быть полезно, если вы измеряете переменную, имеющую критически низкий или высокий порог (или оба), которые не следует пересекать. Диапазон мгновенно сообщит вам, превышало ли хотя бы одно значение эти критические пороги. Кроме того, диапазон можно использовать для обнаружения любых ошибок при вводе данных. Например, если вы записали возраст школьников в своем исследовании, а ваш диапазон составляет от 7 до 123 лет, вы знаете, что совершили ошибку!
В результате получается диапазон 62, что составляет 85 минус 23. Хотя использование диапазона в качестве меры разброса ограничено, оно устанавливает границы оценок. Это может быть полезно, если вы измеряете переменную, имеющую критически низкий или высокий порог (или оба), которые не следует пересекать. Диапазон мгновенно сообщит вам, превышало ли хотя бы одно значение эти критические пороги. Кроме того, диапазон можно использовать для обнаружения любых ошибок при вводе данных. Например, если вы записали возраст школьников в своем исследовании, а ваш диапазон составляет от 7 до 123 лет, вы знаете, что совершили ошибку!
Квартили и межквартильный размах
Квартили говорят нам о разбросе набора данных, разбивая набор данных на кварталы, точно так же, как медиана разбивает его пополам.Например, рассмотрим оценки 100 учащихся ниже, которые были отсортированы от наименьшего до наивысшего балла, и квартили, выделенные красным.
| Заказать | Оценка | Заказать | Оценка | Заказать | Оценка | Заказать | Оценка | Заказать | Оценка |
| 1-й | 35 | 21-я | 42 | 41-я | 53 | 61-й | 64 | 81-я | 74 |
| 2-й | 37 | 22-я | 42 | 42-я | 53 | 62-я | 64 | 82-я | 74 |
| 3-й | 37 | 23-й | 44 | 43-й | 54 | 63-й | 65 | 83-й | 74 |
| 4-я | 38 | 24-я | 44 | 44-я | 55 | 64-й | 66 | 84-я | 75 |
| 5-я | 39 | 25-я | 45 | 45 | 55 | 65-я | 67 | 85-я | 75 |
| 6-й | 39 | 26-я | 45 | 46-я | 56 | 66-я | 67 | 86-я | 76 |
| 7-я | 39 | 27-я | 45 | 47-я | 57 | 67-я | 67 | 87-я | 77 |
| 8-й | 39 | 28-я | 45 | 48-я | 57 | 68-я | 67 | 88-я | 77 |
| 9-я | 39 | 29-я | 47 | 49-я | 58 | 69-я | 68 | 89-я | 79 |
| 10-я | 40 | 30-й | 48 | 50-я | 58 | 70-я | 69 | 90 | 80 |
| 11-я | 40 | 31-я | 49 | 51-я | 59 | 71-я | 69 | 91-я | 81 |
| 12-я | 40 | 32-я | 49 | 52-я | 60 | 72-я | 69 | 92-я | 81 |
| 13-я | 40 | 33-й | 49 | 53-й | 61 | 73-й | 70 | 93-й | 81 |
| 14-й | 40 | 34-я | 49 | 54-я | 62 | 74-я | 70 | 94-я | 81 |
| 15 | 40 | 35-я | 51 | 55-я | 62 | 75-я | 71 | 95-я | 81 |
| 16-я | 41 | 36-я | 51 | 56-я | 62 | 76-я | 71 | 96-я | 81 |
| 17-я | 41 | 37-я | 51 | 57-я | 63 | 77-я | 71 | 97-я | 83 |
| 18 | 42 | 38-я | 51 | 58-я | 63 | 78-я | 72 | 98-я | 84 |
| 19-й | 42 | 39-й | 52 | 59-я | 64 | 79-я | 74 | 99-я | 84 |
| 20-й | 42 | 40-я | 52 | 60-я | 64 | 80-е | 74 | 100-я | 85 |
Первый квартиль (Q1) находится между 25-м и 26-м оценками учащегося, второй квартиль (Q2) между 50-м и 51-м оценками учащегося, а третий квартиль (Q3) между 75-м и 76-м. оценки студента.Отсюда:
оценки студента.Отсюда:
Первый квартиль (Q1) = (45 + 45) ÷ 2 = 45
Второй квартиль (Q2) = (58 + 59) ÷ 2 = 58,5
Третий квартиль (Q3) = (71 + 71) ÷ 2 = 71
В приведенном выше примере у нас четное количество баллов (100 студентов, а не нечетное число, например 99 студентов). Это означает, что при вычислении квартилей мы берем сумму двух оценок по каждому квартилю, а затем их половину (отсюда Q1 = (45 + 45) ÷ 2 = 45).Однако, если бы у нас было нечетное количество баллов (скажем, 99 студентов), нам нужно было бы взять только один балл для каждого квартиля (то есть 25-го, 50-го и 75-го баллов). Вы должны понимать, что второй квартиль также является медианой.
Квартили — полезная мера разброса, поскольку на них гораздо меньше влияют выбросы или искаженный набор данных, чем на эквивалентные меры среднего и стандартного отклонения. По этой причине квартили часто указываются вместе с медианой как лучший выбор для измерения разброса и центральной тенденции, соответственно, при работе с асимметричными данными и / или данными с выбросами. Обычный способ выражения квартилей — это межквартильный размах. Межквартильный диапазон описывает разницу между третьим квартилем (Q3) и первым квартилем (Q1), рассказывая нам о диапазоне средней половины баллов в распределении. Следовательно, для наших 100 студентов:
Обычный способ выражения квартилей — это межквартильный размах. Межквартильный диапазон описывает разницу между третьим квартилем (Q3) и первым квартилем (Q1), рассказывая нам о диапазоне средней половины баллов в распределении. Следовательно, для наших 100 студентов:
Межквартильный размах = Q3 — Q1
= 71–45
= 26
Однако следует отметить, что в журналах и других публикациях вы обычно видите межквартильный диапазон, указанный как 45–71, а не рассчитанный диапазон.
Небольшое отклонение от этого — это полумежквартильный размах, который составляет половину межквартильного размаха = ½ (Q3 — Q1). Следовательно, для наших 100 студентов это будет 26 ÷ 2 = 13.
Главная О нас Связаться с нами Положения и условия Конфиденциальность и файлы cookie © Lund Research Ltd, 2018Основная статистика для исследования данных: Меры вариации
Что такое меры вариации? Меры вариации описывают ширину распределения. Они определяют, насколько разбросаны значения в наборе данных.Их также называют мерами дисперсии / распространения.
Они определяют, насколько разбросаны значения в наборе данных.Их также называют мерами дисперсии / распространения.
В этой статье мы рассмотрим 4 меры вариации.
- Диапазон
- Межквартильный размах (IQR)
- Дисперсия
- Стандартное отклонение
Мы также увидим примеры того, как вычислять эти меры вариации и когда их использовать. Но прежде чем мы начнем, давайте разберемся, зачем нам нужны меры вариации в дополнение к мерам центра при изучении данных для визуализации.
Зачем нужны меры вариации?Единая статистика — мода, медиана или среднее значение могут не быть моделью, которая точно представляет весь набор данных. Каждый раз, когда мы используем одно число для представления данных, мы теряем ощущение изменчивости данных.
Средние значения рассказывают всю историю?
Среднее значение — хороший показатель для сравнения показателей «группы» с течением времени. Один из способов думать о среднем — это как снимок из фильма.Он не рассказывает всей истории, он просто дает снимок кадра. Средние значения игнорируют влияние неизбежных изменений данных.
Один из способов думать о среднем — это как снимок из фильма.Он не рассказывает всей истории, он просто дает снимок кадра. Средние значения игнорируют влияние неизбежных изменений данных.
Вот пример двух выборок с одинаковым средним значением и разными стандартными отклонениями. Красное население имеет среднее значение 100 и стандартное отклонение 10; синяя популяция имеет среднее значение 100 и стандартное отклонение 50.
Какие недостатки у усредненных?
- Средние значения не говорят всей картины
- Средние значения подвержены выбросам.Выбросы искажают средние значения и тянут их в своем направлении. Средние значения заставляют нас полагать, что точки данных сгруппированы вокруг точки выше или ниже, чем то, где они на самом деле сгруппированы.
- Средние значения не учитывают сегменты данных.
Понимание мер вариации«… многие люди склонны думать о« среднем »как о« типичном »; Проблема с этим предположением во многих наборах данных — конечно, в тех, которые касаются людей — в том, что существует множество исключений из «типичных».
в сторонуdatascience.comМожно даже возразить, что не существует такого понятия, как «типичный».Например, статистикой, которую часто неправильно используют, является средний уровень разводов в Соединенных Штатах, который часто называют «около 50%». Если кто-то исследует вопрос, он обнаружит, что средний уровень разводов широко варьируется в зависимости от таких факторов, как возраст, уровень образования, профессия, раса, география, религиозные убеждения и т. Д. Таким образом, каждый по-разному классифицируется по этим факторам, что приводит к множеству различный средний уровень разводов в зависимости от того, какие факторы описывают измеряемые факторы.”
Диапазон
Диапазон — это простейшая мера вариации. Диапазон набора данных — это разница между самым высоким и самым низким значением в наборе данных.
Диапазон также больше всего подвержен выбросам, поскольку он использует только крайние значения.
Межквартильный размах (IQR)
Межквартильный размах или IQR описывает средние 50% значений в порядке от наименьшего к наибольшему значению.
Для расчета IQR мы находим медианное значение нижней и верхней половины данных. Это квартиль 1 и квартиль 3. IQR — это разница между квартилем 3 и квартилем 1.
IQR считается хорошим показателем вариации в искаженных наборах данных, поскольку он устойчив к выбросам.
Разница
Дисперсия — это средний квадрат разницы значений от среднего.
Чтобы вычислить дисперсию, мы возводим в квадрат разницу между каждым значением данных и средним значением.Мы делим сумму этих квадратов на количество элементов в наборе данных.
Поскольку дисперсия — это величина, возведенная в квадрат, нет интуитивного способа сравнить дисперсию непосредственно со значениями данных или средним значением.
Стандартное отклонение
Стандартное отклонение — это мера того, насколько значения данных отклоняются от среднего. Чем больше стандартное отклонение, тем больше вариация.
Чем больше стандартное отклонение, тем больше вариация.
Стандартное отклонение рассчитывается как квадратный корень из дисперсии.
Стандартное отклонение использует исходные единицы данных, что упрощает интерпретацию.Следовательно, стандартное отклонение является наиболее часто используемой мерой вариации.
Вычислить диапазон, IQR, стандартное отклонение и дисперсию: примерРассмотрим небольшой набор данных о росте 10 человек. Вот как мы можем рассчитать диапазон, дисперсию, стандартное отклонение и межквартильный размах.
Расчет диапазона, дисперсии и стандартного отклонения Расчет межквартильного размахаВот видеоурок, чтобы узнать больше о вычислении межквартильного размаха.
Когда использовать диапазон, IQR, стандартное отклонение и дисперсию?- Диапазон использует только экстремальные значения набора данных и, следовательно, очень чувствителен к выбросам.
 Рекомендуется использовать диапазон только для очень маленьких распределений без выбросов.
Рекомендуется использовать диапазон только для очень маленьких распределений без выбросов. - IQR подходит для искаженных распределений. Это потому, что IQR устойчив к выбросам в данных. Для описания данных они обычно используются в паре с медианой.
- Стандартное отклонение — хороший показатель изменчивости для нормальных распределений или распределений, которые не сильно искажены. В сочетании со значением означает, что это хороший способ описания данных.
- Отклонение мало используется, поскольку оно представлено в квадратах и не является интуитивно понятной мерой.
Центральная тенденция и изменчивость — Социология 3112 — Кафедра социологии
Цели обучения
- Поймите и вычислите три способа определения центра распределения
- Понять и рассчитать четыре способа дисперсии или изменчивости в распределении можно определить
- Поймите, как перекос и уровень измерения могут помочь определить, какие меры центральная тенденция и изменчивость наиболее подходят для данного распределения
Ключевые термины
Меры центральной тенденции: категорий или баллов, которые описывают, что является «средним» или «типичным» для данного распределения. К ним относятся мода, медиана и среднее значение.
К ним относятся мода, медиана и среднее значение.
Процентиль: балл, ниже которого падает определенный процент данного распределения.
Положительно искаженное распределение: распределение с горсткой чрезвычайно больших значений.
Распределение с отрицательным перекосом: распределение с очень низкими значениями.
Меры изменчивости: числа, которые описывают разнообразие или дисперсию в распределении данного
Переменная.
Коробчатая диаграмма: графическое представление диапазона, межквартильного размаха и медианы данного
Переменная.
Режим
Режим — это категория с наибольшей частотой (или процентом). Это не
частота сама. Другими словами, если кто-то спросит у вас режим раздачи
как показано ниже, ответ будет кокосовым, а НЕ 22. Возможно иметь больше, чем
один режим в раздаче. Такие распределения считаются бимодальными (если есть
два режима) или мультимодальный (если режимов больше двух). Распределения без
чистый режим называется однородным. Режим не особо полезен, но есть
единственная мера центральной тенденции, которую мы можем использовать с номинальными переменными. Ты найдешь
почему это единственная подходящая мера для номинальных переменных, поскольку мы узнаем о
медиана и среднее значение далее.
Возможно иметь больше, чем
один режим в раздаче. Такие распределения считаются бимодальными (если есть
два режима) или мультимодальный (если режимов больше двух). Распределения без
чистый режим называется однородным. Режим не особо полезен, но есть
единственная мера центральной тенденции, которую мы можем использовать с номинальными переменными. Ты найдешь
почему это единственная подходящая мера для номинальных переменных, поскольку мы узнаем о
медиана и среднее значение далее.
Любимые вкусы мороженого:
Кокос = 22
Шоколад = 15
Ваниль = 7
Клубника = 9
Медиана
Медиана — это самое среднее число. Другими словами, это число делит
распределение ровно пополам, так что половина случаев выше медианы, и
половина ниже. Он также известен как 50-й процентиль, и его можно вычислить для
порядковые и интервальные / отношения переменные. Концептуально найти медиану довольно просто.
и влечет за собой только упорядочение всех ваших наблюдений от наименьшего к наибольшему
а затем найти то число, которое попадает в середину. Обратите внимание, что нахождение медианы
требует сначала упорядочить все наблюдения от наименьшего к наибольшему. Вот почему
медиана не является подходящей мерой центральной тенденции для номинальных переменных,
поскольку номинальные переменные не имеют внутреннего порядка.(На практике определение медианы может
проявите больше активности, особенно если у вас много наблюдений — см.
ваш учебник для объяснения того, как найти медиану в таких ситуациях).
Он также известен как 50-й процентиль, и его можно вычислить для
порядковые и интервальные / отношения переменные. Концептуально найти медиану довольно просто.
и влечет за собой только упорядочение всех ваших наблюдений от наименьшего к наибольшему
а затем найти то число, которое попадает в середину. Обратите внимание, что нахождение медианы
требует сначала упорядочить все наблюдения от наименьшего к наибольшему. Вот почему
медиана не является подходящей мерой центральной тенденции для номинальных переменных,
поскольку номинальные переменные не имеют внутреннего порядка.(На практике определение медианы может
проявите больше активности, особенно если у вас много наблюдений — см.
ваш учебник для объяснения того, как найти медиану в таких ситуациях).
Некоторые из вас, вероятно, уже задаются вопросом: «Что будет, если у вас четное число
случаев? Тогда не будет среднего числа, верно? »Это очень проницательное наблюдение,
и я рад, что вы спросили. Если в вашем наборе данных четное количество наблюдений, медиана будет
среднее из двух крайних чисел. Например, для чисел 18, 14, 12,
8, 6 и 4 медиана равна 10 (12 + 8 = 20; 20/2 = 10).
Если в вашем наборе данных четное количество наблюдений, медиана будет
среднее из двух крайних чисел. Например, для чисел 18, 14, 12,
8, 6 и 4 медиана равна 10 (12 + 8 = 20; 20/2 = 10).
Одним из преимуществ медианы является то, что она нечувствительна к выбросам. Выброс — это наблюдение, которое находится на ненормальном расстоянии от других значений в выборке. Наблюдения которые значительно больше или меньше других в выборке, могут повлиять на некоторые статистических показателей таким образом, чтобы они вводили в заблуждение, но медиана невосприимчив к ним.Другими словами, не имеет значения, будет ли наибольшее число 20 или 20,000; он по-прежнему считается только одним числом. Учтите следующее:
Распределение 1: 1, 3, 5, 7, 20
Распределение 2: 1, 3, 5, 7, 20,000
Эти два распределения имеют идентичные медианы, хотя в распределении 2 очень
большой выброс, который в конечном итоге приведет к значительному искажению среднего значения, поскольку мы
увидеть через мгновение.
Среднее
Среднее — это то, что люди обычно называют «средним». Это высшая мера центральной тенденции, я имею в виду, что он доступен для использования только с интервалом / соотношением переменные. Среднее значение учитывает ценность каждого наблюдения и, таким образом, обеспечивает самая информативная из всех мер центральной тенденции. Однако в отличие от медианы среднее значение чувствительно к выбросам.Другими словами, один чрезвычайно высокий (или низкий) значение в вашем наборе данных может значительно повысить (или понизить) среднее значение. Среднее, часто отображается как переменная x или y с линией над ней (произносится как «x-bar» или «y-bar»), представляет собой сумму всех баллов, деленную на общее количество баллов. В статистических обозначение, мы бы записали его следующим образом:
В этом уравнении — среднее значение, X — значение каждого случая, а N — общее
количество дел. Сигма (Σ) просто говорит нам сложить все оценки вместе.
Тот факт, что вычисление среднего требует сложения и деления, является самой причиной
его нельзя использовать ни с номинальными, ни с порядковыми переменными. Мы не можем рассчитать среднее
для расы (белый + белый + черный / 3 =?) больше, чем мы можем рассчитать среднее значение за год
в школе (первокурсник + первокурсник + старший / 3 =?)
Сигма (Σ) просто говорит нам сложить все оценки вместе.
Тот факт, что вычисление среднего требует сложения и деления, является самой причиной
его нельзя использовать ни с номинальными, ни с порядковыми переменными. Мы не можем рассчитать среднее
для расы (белый + белый + черный / 3 =?) больше, чем мы можем рассчитать среднее значение за год
в школе (первокурсник + первокурсник + старший / 3 =?)
Процентили
Процентиль — это число, ниже которого попадает определенный процент распределения.Например, если вы набрали 90-й процентиль по тесту, 90 процентов учащихся
кто прошел тест набрал меньше вас. Если вы набрали 72-й процентиль в тесте,
72 процента студентов, сдавших тест, набрали меньше баллов, чем вы. Если забил в 5-м
процентиль теста, возможно, этот предмет не для вас. Как вы помните, медиана падает
на 50-м процентиле. Пятьдесят процентов наблюдений попадают под него.
Как вы помните, медиана падает
на 50-м процентиле. Пятьдесят процентов наблюдений попадают под него.
Симметричные и асимметричные распределения
Симметричное распределение — это распределение, в котором среднее значение, медиана и мода являются
такой же. С другой стороны, асимметричное распределение — это распределение с экстремальными значениями.
с одной или другой стороны, которые отталкивают медианное значение от среднего в одном направлении
или другой. Если среднее значение больше медианы, говорят, что распределение
быть смещенным в положительную сторону.Другими словами, существует очень большое значение, которое «тянет»
среднее значение к верхнему концу распределения. Если среднее значение меньше, чем
медиана, распределение считается отрицательно смещенным. Другими словами, есть
чрезвычайно малое значение, которое «подтягивает» среднее значение к нижней границе распределения.
Распределение доходов обычно имеет положительный перекос из-за небольшого количества
люди, которые зарабатывают безбожные деньги.Рассмотрим (по общему признанию датированный) случай
Футболисты Высшей лиги как крайний пример. Средняя годовая зарплата для MLS
игрок в 2010 году составлял около 138000 долларов, но средняя годовая зарплата составляла всего около
53000 долларов. Среднее значение было почти в три раза больше медианы, благодаря немалому
часть зарплаты Дэвида Бекхэма в 12 миллионов долларов.
Другими словами, есть
чрезвычайно малое значение, которое «подтягивает» среднее значение к нижней границе распределения.
Распределение доходов обычно имеет положительный перекос из-за небольшого количества
люди, которые зарабатывают безбожные деньги.Рассмотрим (по общему признанию датированный) случай
Футболисты Высшей лиги как крайний пример. Средняя годовая зарплата для MLS
игрок в 2010 году составлял около 138000 долларов, но средняя годовая зарплата составляла всего около
53000 долларов. Среднее значение было почти в три раза больше медианы, благодаря немалому
часть зарплаты Дэвида Бекхэма в 12 миллионов долларов.
При попытке решить, какую меру центральной тенденции использовать, вы должны учитывать
как уровень измерения, так и перекос.Это не так для номинальных и порядковых
переменные. Если переменная номинальная, очевидно, что мода является единственной мерой центрального
склонность к использованию. Если переменная порядковая, лучше всего подходит медиана.
потому что он предоставляет больше информации об образце, чем режим. Но если
переменная — интервал / соотношение, вам нужно определить, является ли распределение симметричным
или перекошенный.Если распределение симметрично, среднее значение является лучшим показателем центрального
тенденция. Если распределение искажено в положительную или отрицательную сторону, медиана
точнее. В качестве примера того, почему среднее значение может быть не лучшим измерителем центрального
тенденцию к неравномерному распределению, рассмотрим следующий отрывок из книги Чарльза Уилана
Обнаженная статистика: снимая страх с данных (2013):
Если переменная номинальная, очевидно, что мода является единственной мерой центрального
склонность к использованию. Если переменная порядковая, лучше всего подходит медиана.
потому что он предоставляет больше информации об образце, чем режим. Но если
переменная — интервал / соотношение, вам нужно определить, является ли распределение симметричным
или перекошенный.Если распределение симметрично, среднее значение является лучшим показателем центрального
тенденция. Если распределение искажено в положительную или отрицательную сторону, медиана
точнее. В качестве примера того, почему среднее значение может быть не лучшим измерителем центрального
тенденцию к неравномерному распределению, рассмотрим следующий отрывок из книги Чарльза Уилана
Обнаженная статистика: снимая страх с данных (2013):
«Среднее или среднее значение имеет некоторые проблемы, а именно то, что оно склонно к
искажение «выбросами», то есть наблюдениями, находящимися дальше от центра. Чтобы понять эту концепцию, представьте, что десять парней сидят на барных стульях.
в питейном заведении среднего класса в Сиэтле; каждый из этих парней зарабатывает 35000 долларов
в год, что составляет средний годовой доход группы 35 000 долларов. Билл Гейтс идет
в бар с говорящим попугаем, сидящим на его плече. (У попугая нет ничего
это связано с примером, но это как бы приправляет вещи.) Предположим ради
Например, Билл Гейтс имеет годовой доход в 1 миллиард долларов. Когда Билл сидит
опустившись на одиннадцатый барный стул, средний годовой доход посетителей бара повысится до
около 91 миллиона долларов. Очевидно, что никто из первых десяти пьющих не стал богаче (хотя
было бы разумно ожидать, что Билл Гейтс купит один или два раунда). Если бы я описал
завсегдатаи этого бара имеют средний годовой доход в размере 91 миллиона долларов, говорится в сообщении.
Чтобы понять эту концепцию, представьте, что десять парней сидят на барных стульях.
в питейном заведении среднего класса в Сиэтле; каждый из этих парней зарабатывает 35000 долларов
в год, что составляет средний годовой доход группы 35 000 долларов. Билл Гейтс идет
в бар с говорящим попугаем, сидящим на его плече. (У попугая нет ничего
это связано с примером, но это как бы приправляет вещи.) Предположим ради
Например, Билл Гейтс имеет годовой доход в 1 миллиард долларов. Когда Билл сидит
опустившись на одиннадцатый барный стул, средний годовой доход посетителей бара повысится до
около 91 миллиона долларов. Очевидно, что никто из первых десяти пьющих не стал богаче (хотя
было бы разумно ожидать, что Билл Гейтс купит один или два раунда). Если бы я описал
завсегдатаи этого бара имеют средний годовой доход в размере 91 миллиона долларов, говорится в сообщении. будет как статистически правильным, так и сильно вводящим в заблуждение [Примечание: медиана будет
остается неизменным].Это не бар, где тусуются мультимиллионеры; это бар, где
группа парней с относительно низкими доходами случайно сидит рядом с Биллом Гейтсом
и его говорящий попугай «.
будет как статистически правильным, так и сильно вводящим в заблуждение [Примечание: медиана будет
остается неизменным].Это не бар, где тусуются мультимиллионеры; это бар, где
группа парней с относительно низкими доходами случайно сидит рядом с Биллом Гейтсом
и его говорящий попугай «.
Меры изменчивости
Помимо определения показателей центральной тенденции, нам может потребоваться подвести итоги степень изменчивости нашего распределения.Другими словами, нам нужно определить, имеют ли наблюдения тенденцию группироваться или они имеют тенденцию к распространению вне. Рассмотрим следующий пример:
Пример 1: {0, 0, 0, 0, 25}
Пример 2: {5, 5, 5, 5, 5}
Обе эти выборки имеют идентичные средства (5) и одинаковое количество наблюдений. (n = 5), но степень вариации между двумя образцами значительно различается.Образец 2 не имеет вариабельности (все оценки одинаковы), тогда как Образец 1 имеет
относительно больше (один случай существенно отличается от других четырех). В этом курсе
мы рассмотрим четыре показателя изменчивости: диапазон, межквартильный
диапазон (IQR), дисперсия и стандартное отклонение.
(n = 5), но степень вариации между двумя образцами значительно различается.Образец 2 не имеет вариабельности (все оценки одинаковы), тогда как Образец 1 имеет
относительно больше (один случай существенно отличается от других четырех). В этом курсе
мы рассмотрим четыре показателя изменчивости: диапазон, межквартильный
диапазон (IQR), дисперсия и стандартное отклонение.
Диапазон
Диапазон — это разница между наивысшим и наименьшим баллами в наборе данных и это простейшая мера разброса.Мы вычисляем диапазон, вычитая наименьшее значение от наибольшего значения. В качестве примера рассмотрим следующий набор данных:
23 | 56 | 45 | 65 | 69 | 55 | 62 | 54 | 85 | 25 |
Максимальное значение — 85, минимальное — 23. Это дает нам диапазон 62 (85
— 23 = 62). Хотя использование диапазона в качестве меры изменчивости мало что нам говорит,
это действительно дает нам некоторую информацию о том, насколько далеко друг от друга самые низкие и самые высокие оценки
являются.
Это дает нам диапазон 62 (85
— 23 = 62). Хотя использование диапазона в качестве меры изменчивости мало что нам говорит,
это действительно дает нам некоторую информацию о том, насколько далеко друг от друга самые низкие и самые высокие оценки
являются.
Квартили и межквартильный размах
«Квартиль» — это еще одно слово, которое специалисты по статистике используют, чтобы почувствовать себя значимыми. В основном это означает «четверть» или «четверть».»Футбольный матч состоит из четырех квартилей, как и Twix королевского размера. Найти квартили распределения так же просто, как взломать это до четвертых. Каждая четвертая содержит 25 процентов от общего количества наблюдений.
Квартили делят упорядоченный набор данных на четыре равные части. Ценности, разделяющие
каждая часть называется первым, вторым и третьим квартилями; и они обозначены
на Q1, Q2 и Q3 соответственно.
Ценности, разделяющие
каждая часть называется первым, вторым и третьим квартилями; и они обозначены
на Q1, Q2 и Q3 соответственно.
Q1 — это «среднее» значение в первой половине упорядоченного по рангу набора данных.
Q2 — медианное значение набора данных
Q3 — «среднее» значение второй половины упорядоченного набора данных
Q4 технически будет самым большим значением в наборе данных, но мы игнорируем это при расчете
IQR (мы уже имели дело с ним, когда рассчитывали диапазон).
Таким образом, межквартильный размах равен Q3 минус Q1 (или 75-й процентиль минус
25-й процентиль, если вы предпочитаете так думать).В качестве примера рассмотрим
следующие числа: 1, 3, 4, 5, 5, 6, 7, 11. Q1 — среднее значение в первом
половина набора данных.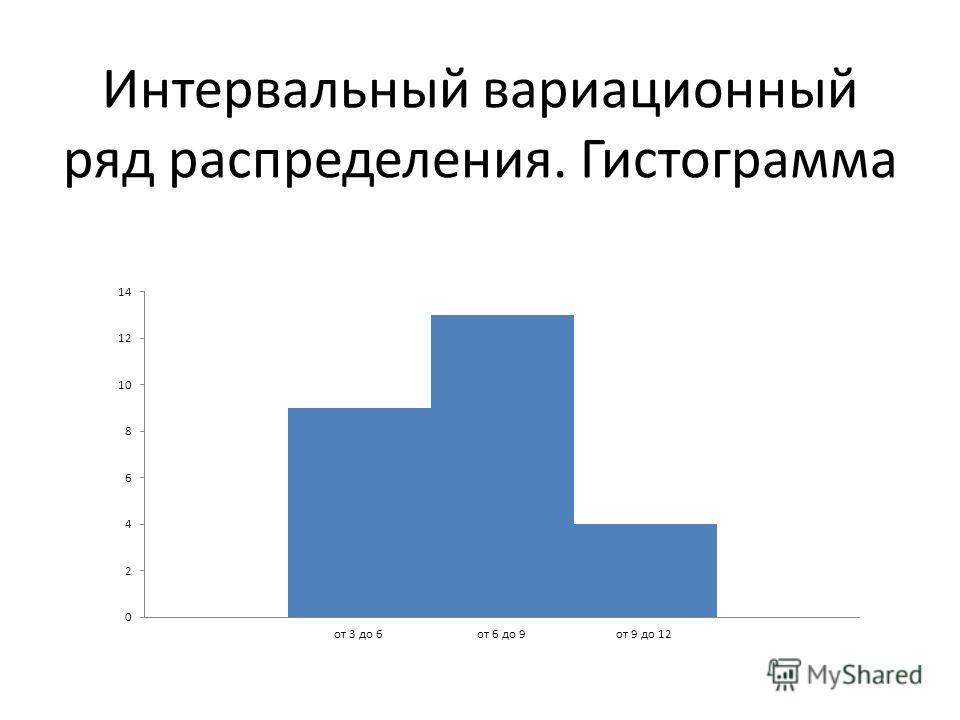 Поскольку в первой половине есть четное количество точек данных
в наборе данных среднее значение является средним из двух средних значений; это,
Q1 = (3 + 4) / 2 или Q1 = 3,5. Q3 — среднее значение во второй половине данных.
набор. Опять же, поскольку вторая половина набора данных имеет четное количество наблюдений,
среднее значение — это среднее из двух средних значений; то есть Q3 = (6 + 7) / 2
или Q3 = 6.5. Межквартильный размах составляет Q3 минус Q1, поэтому IQR = 6,5 — 3,5 = 3.
Поскольку в первой половине есть четное количество точек данных
в наборе данных среднее значение является средним из двух средних значений; это,
Q1 = (3 + 4) / 2 или Q1 = 3,5. Q3 — среднее значение во второй половине данных.
набор. Опять же, поскольку вторая половина набора данных имеет четное количество наблюдений,
среднее значение — это среднее из двух средних значений; то есть Q3 = (6 + 7) / 2
или Q3 = 6.5. Межквартильный размах составляет Q3 минус Q1, поэтому IQR = 6,5 — 3,5 = 3.
Коробчатые участки
Ящичковая диаграмма (также известная как диаграмма ящиков и усов) разбивает набор данных на квартили.
Тело коробчатой диаграммы состоит из «коробки» (отсюда и название), которая идет от
от первого квартиля (Q1) до третьего квартиля (Q3). Внутри рамки горизонтальная линия
Рисуется в Q2, который обозначает медианное значение набора данных.Две вертикальные линии, известные
как усы, простираются сверху и снизу коробки. Нижний ус идет от
Q1 до наименьшего значения в наборе данных, а верхний ус идет от Q3 до
наибольшее значение. Ниже приведен пример прямоугольного графика с положительным перекосом с различными
компоненты помечены.
Внутри рамки горизонтальная линия
Рисуется в Q2, который обозначает медианное значение набора данных.Две вертикальные линии, известные
как усы, простираются сверху и снизу коробки. Нижний ус идет от
Q1 до наименьшего значения в наборе данных, а верхний ус идет от Q3 до
наибольшее значение. Ниже приведен пример прямоугольного графика с положительным перекосом с различными
компоненты помечены.
Выбросы — это экстремальные значения, которые по той или иной причине исключаются. из набора данных.Если набор данных включает один или несколько выбросов, они отображаются на графике. отдельно точками на графике. На диаграмме выше есть несколько выбросов внизу.
Как интерпретировать коробчатую диаграмму
Горизонтальная линия, проходящая через центр прямоугольника, указывает, где медиана
падает. Кроме того, коробчатые диаграммы отображают две общие меры изменчивости или разброса.
в наборе данных: диапазон и IQR.Если вас интересует распространение всех
данных, он представлен на диаграмме вертикальным расстоянием между наименьшими
значение и наибольшее значение, включая любые выбросы. Средняя половина набора данных
попадает в межквартильный диапазон. На прямоугольной диаграмме представлен межквартильный размах.
по ширине коробки (Q3 минус Q1).
Кроме того, коробчатые диаграммы отображают две общие меры изменчивости или разброса.
в наборе данных: диапазон и IQR.Если вас интересует распространение всех
данных, он представлен на диаграмме вертикальным расстоянием между наименьшими
значение и наибольшее значение, включая любые выбросы. Средняя половина набора данных
попадает в межквартильный диапазон. На прямоугольной диаграмме представлен межквартильный размах.
по ширине коробки (Q3 минус Q1).
Разница
Дисперсия — это мера изменчивости, которая показывает, насколько далеко каждое наблюдение падает от среднего значения распределения.В этом примере мы будем использовать следующие пять чисел, которые представляют собой мои ежемесячные покупки комиксов за последние пять месяцев:
2, 3, 5, 6, 9
Формула расчета дисперсии обычно записывается так:
Это уравнение выглядит устрашающе, но оно не так уж и плохо, если разбить его на
его составные части. S2x — это обозначение, используемое для обозначения дисперсии выборки.
Эта гигантская сигма (Σ) является знаком суммы; это просто означает, что мы собираемся добавлять вещи
вместе. X представляет каждое из наших наблюдений, а x с линией над ним.
(часто называемый «x-bar») представляет собой среднее значение нашего распределения. Заглавная буква «N» на
внизу — общее количество наблюдений. По сути, эта формула говорит
нам вычесть среднее значение из каждого из наших наблюдений, возвести разницу в квадрат, добавить
их все вместе и разделить на N-1.Давайте сделаем пример, используя приведенные выше числа.
S2x — это обозначение, используемое для обозначения дисперсии выборки.
Эта гигантская сигма (Σ) является знаком суммы; это просто означает, что мы собираемся добавлять вещи
вместе. X представляет каждое из наших наблюдений, а x с линией над ним.
(часто называемый «x-bar») представляет собой среднее значение нашего распределения. Заглавная буква «N» на
внизу — общее количество наблюдений. По сути, эта формула говорит
нам вычесть среднее значение из каждого из наших наблюдений, возвести разницу в квадрат, добавить
их все вместе и разделить на N-1.Давайте сделаем пример, используя приведенные выше числа.
1. Первым шагом в вычислении дисперсии является определение среднего значения распределения. В этом случае среднее значение равно 5 (2 + 3 + 5 + 6 + 9 = 25; 25/5 = 5).
2.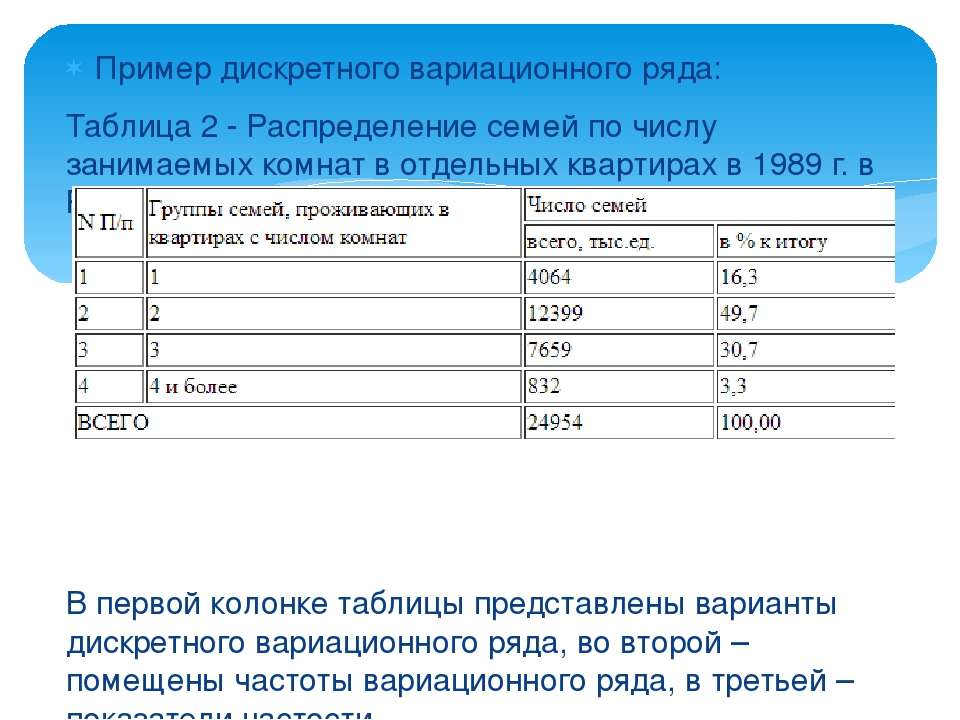 Второй шаг — вычесть среднее значение (5) из каждого наблюдения:
Второй шаг — вычесть среднее значение (5) из каждого наблюдения:
2-5 = -3
3-5 = -2
5-5 = 0
6-5 = 1
9-5 = 4
Обратите внимание: мы можем проверить нашу работу после этого шага, сложив все наши ценности вместе.Если они в сумме равны нулю, мы знаем, что находимся на правильном пути. Если они что-то складывают помимо нуля, нам, вероятно, следует еще раз проверить нашу математику (-3 + -2 + 0 + 1 + 4 = 0, мы золотые).
3. В-третьих, мы возводим в квадрат каждый из этих ответов, чтобы избавиться от отрицательных чисел:
(-3) 2 = 9
(-2) 2 = 4
(0) 2 = 0
(1) 2 = 1
(4) 2 = 16
4.В-четвертых, складываем их все вместе:
9 + 4 + 0 + 1 + 16 = 30
5. Наконец, делим на N-1 (общее количество наблюдений равно 5, поэтому 5-1 = 4)
30/4 = 7,5
После всех этих довольно утомительных вычислений остается одно число, которое
быстро и лаконично резюмирует количество изменчивости в нашем распределении. В
чем больше число, тем больше вариативность в нашем распределении.Пожалуйста, обрати внимание:
отклонение никогда не может быть отрицательным. Если вы получите дисперсию меньше, чем
ноль, вы сделали что-то не так.
В
чем больше число, тем больше вариативность в нашем распределении.Пожалуйста, обрати внимание:
отклонение никогда не может быть отрицательным. Если вы получите дисперсию меньше, чем
ноль, вы сделали что-то не так.
Стандартное отклонение
Однако есть одно ограничение на использование дисперсии в качестве единственной меры изменчивости.
Когда мы возводим числа в квадрат, чтобы избавиться от негативов (шаг 3), мы также случайно
квадрат нашей единицы измерения.Другими словами, если мы говорим о милях, мы
случайно превратили нашу единицу измерения в квадратные мили. Если бы мы говорили
насчет комиксов, мы случайно превратили нашу единицу измерения в комиксы
в квадрате (что, разумеется, не всегда имеет смысл). Чтобы
Решив эту проблему, мы вычисляем стандартное отклонение.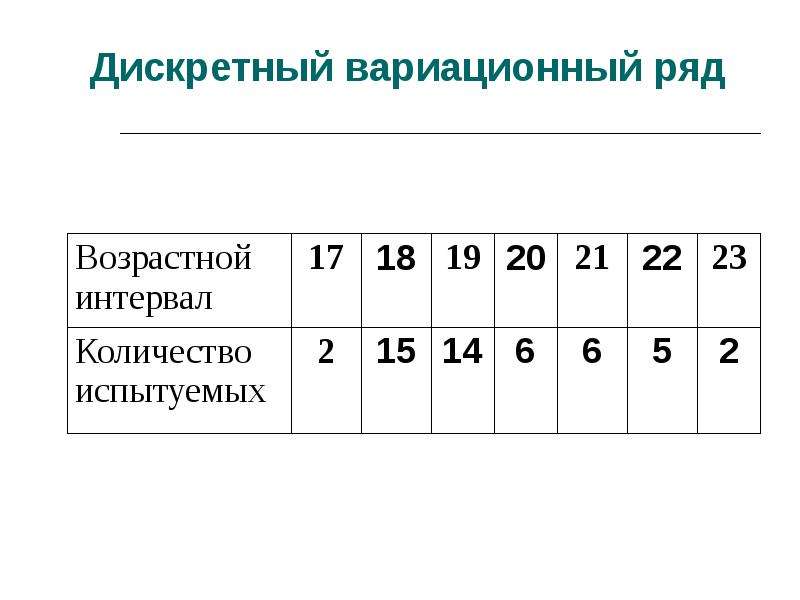 Формула стандарта
отклонение выглядит так:
Формула стандарта
отклонение выглядит так:
Другими словами, вычислить стандартное отклонение так же просто, как взять квадрат корень дисперсии, обращая квадрат, который мы сделали при вычислении дисперсии.В нашем примере стандартное отклонение равно квадратному корню из 7,5 или 2,74. Интерпретация не меняется; большое стандартное отклонение указывает на большее изменчивость, тогда как небольшое стандартное отклонение указывает на относительно небольшой количество изменчивости. Как и в случае с дисперсией, стандартное отклонение составляет всегда позитивный.
Помните: ключевое различие между дисперсией и стандартным отклонением — это
единица измерения.Мы вычисляем стандартное отклонение, чтобы положить нашу переменную
обратно в исходную метрику. «Мили в квадрате» снова равняются милям, а
«Комиксы в квадрате» снова превратились в комиксы.
«Мили в квадрате» снова равняются милям, а
«Комиксы в квадрате» снова превратились в комиксы.
Основные моменты
- Меры центральной тенденции говорят нам, что общего или типичного в нашей переменной.
- Три показателя центральной тенденции — это мода, медиана и среднее значение.
- Режим используется почти исключительно с данными номинального уровня, так как это единственная мера центральной тенденции, доступной для таких переменных. Медиана используется с порядковым номером данные или когда переменная уровня интервала / отношения искажена (вспомните пример Билла Гейтса). Среднее значение можно использовать только с данными уровня интервала / отношения.
- Меры изменчивости — это числа, которые описывают, насколько вариативность или разнообразие
есть в раздаче.

- Четыре меры изменчивости — это диапазон (разница между большим и наименьших наблюдений), межквартильный размах (разница между 75-м и 25-й процентиль) дисперсия и стандартное отклонение.
- Дисперсия и стандартное отклонение — два тесно связанных показателя изменчивости. для переменных уровня интервала / отношения, которые увеличиваются или уменьшаются в зависимости от того, насколько близко наблюдения сгруппированы вокруг среднего.
- Меры центральной тенденции и изменчивости в SPSS
Чтобы программа SPSS рассчитала для вас меры центральной тенденции и изменчивости, щелкните
«Анализировать», «Описательная статистика», затем «Частоты». Меры центральной тенденции
и изменчивость также можно рассчитать, нажав на «Описательные» или «Исследовать»
но «Частоты» дает вам больше контроля и предлагает наиболее полезные варианты выбора. от.Открывшееся диалоговое окно должно быть вам хорошо знакомо. Как ты это сделал
при расчете частотных таблиц переместите переменные, для которых вы хотите
вычислить меры центральной тенденции и изменчивости в правой части
коробка. Вы можете снять флажок «Отображать частотные таблицы», если не хотите
видеть любые таблицы и предпочел бы видеть только статистику. Затем нажмите кнопку
справа помечено как «Статистика.»В открывшемся диалоговом окне вы можете выбрать как
сколько угодно статистических данных (Примечание: SPSS использует термин «Дисперсия», а не
«Изменчивость», но эти два слова синонимичны). Также имейте в виду, что SPSS
рассчитает статистику для любой переменной независимо от уровня измерения. Это
будет, например, вычислять среднее значение для расы или пола, даже если это не имеет смысла
как бы то ни было.
от.Открывшееся диалоговое окно должно быть вам хорошо знакомо. Как ты это сделал
при расчете частотных таблиц переместите переменные, для которых вы хотите
вычислить меры центральной тенденции и изменчивости в правой части
коробка. Вы можете снять флажок «Отображать частотные таблицы», если не хотите
видеть любые таблицы и предпочел бы видеть только статистику. Затем нажмите кнопку
справа помечено как «Статистика.»В открывшемся диалоговом окне вы можете выбрать как
сколько угодно статистических данных (Примечание: SPSS использует термин «Дисперсия», а не
«Изменчивость», но эти два слова синонимичны). Также имейте в виду, что SPSS
рассчитает статистику для любой переменной независимо от уровня измерения. Это
будет, например, вычислять среднее значение для расы или пола, даже если это не имеет смысла
как бы то ни было.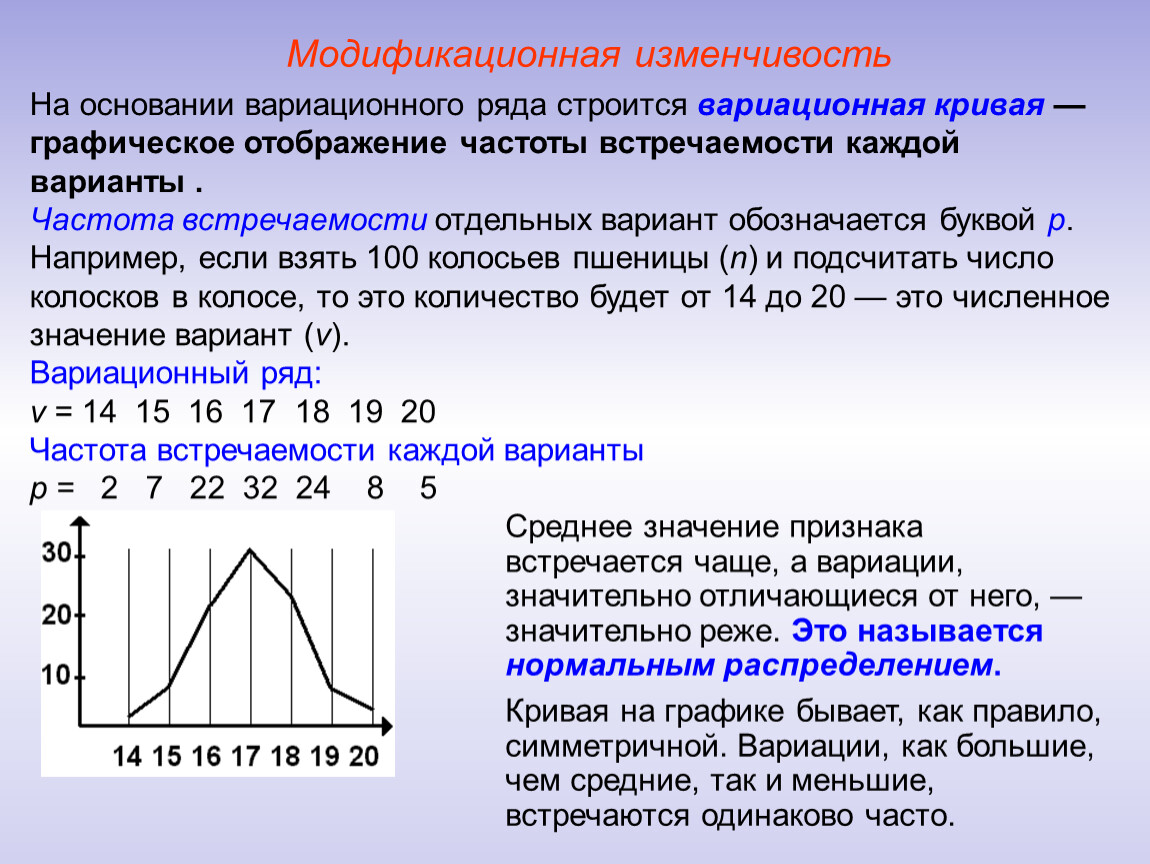 Самец + самец + самка / 3 = 0,66? Совершенно нелогично. Это один из многих
обстоятельства, в которых вам придется быть умнее, чем пакет анализа данных
ты используешь. То, что SPSS позволяет вам что-то делать, не обязательно означает
это хорошая идея.
Самец + самец + самка / 3 = 0,66? Совершенно нелогично. Это один из многих
обстоятельства, в которых вам придется быть умнее, чем пакет анализа данных
ты используешь. То, что SPSS позволяет вам что-то делать, не обязательно означает
это хорошая идея.
При расчете показателей изменчивости иногда полезно включить рамку
участок. Для этого нажмите «Графики», затем «Устаревшие диалоги» и выберите «Коробчатая диаграмма».» В виде
в случае с графиками, которые вы создали в предыдущей главе, у вас будет несколько
варианты выбора. Вообще говоря, вам понадобится одна коробчатая диаграмма для каждого
переменной, поэтому выберите «Сводные данные по отдельным переменным». Переместите переменные, которые вы
хотите, чтобы в пустом поле справа отображались блочные диаграммы, и нажмите OK. Если вы захотите отредактировать коробчатые графики, вы можете сделать это почти так же, как вы это делали.
графики в главе 2.Вот видео-пошаговое руководство:
Если вы захотите отредактировать коробчатые графики, вы можете сделать это почти так же, как вы это делали.
графики в главе 2.Вот видео-пошаговое руководство:
Упражнения
- Выберите три переменные из любого из трех наборов данных (одну номинальную, одну порядковую и один интервал / соотношение) и рассчитайте все соответствующие меры центральной тенденции для каждый.
- Используя ADD Health Dataset, NIS Dataset и World Values Survey, рассчитайте
стандартное отклонение, дисперсия и диапазон для переменной «ВОЗРАСТ» в каждом.Какой опрос
имеет наибольшую вариативность в возрасте? В каком опросе меньше всего различий по возрасту? (Примечание:
для этого вам потребуется открыть набор данных, вычислить меры изменчивости и
затем откройте следующий набор данных.
 Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент).
Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент). - Выберите любую переменную отношения интервалов и используйте ее для создания прямоугольной диаграммы.Теперь интерпретируйте коробчатый сюжет. Каков приблизительный диапазон, IQR и медиана этой переменной?
Статистика: меры вариации
Статистика: показатели вариацииДиапазон
Диапазон — это простейшая мера вариации, которую можно найти. Это просто наивысшее значение за вычетом наименьшее значение.
ДИАПАЗОН = МАКСИМАЛЬНЫЙ - МИНИМАЛЬНЫЙ
Поскольку диапазон использует только самые большие и самые маленькие значения, на него сильно влияют экстремальные значения, то есть — она не устойчива к изменениям.
Разница
«Среднее отклонение»
Диапазон включает только самые маленькие и самые большие числа, и было бы желательно иметь
статистика, включающая все значения данных.
Первая попытка, которую можно сделать, — это то, что они могут назвать средним отклонением от среднее значение и определите его как:
Проблема в том, что это суммирование всегда равно нулю. Таким образом, среднее отклонение всегда будет равно нулю. Поэтому среднее отклонение никогда не используется.
Разница в численности населения
Итак, чтобы оно не равнялось нулю, отклонение от среднего возводится в квадрат и называется «квадратом отклонение от среднего ». Это« среднеквадратичное отклонение от среднего »называется дисперсией.
Несмещенная оценка дисперсии совокупности
Можно было бы ожидать, что дисперсия выборки будет просто дисперсией генеральной совокупности с генеральной совокупностью.
среднее значение заменено выборочным средним. Однако одно из основных применений статистики — оценка
соответствующий параметр.Проблема с этой формулой состоит в том, что расчетное значение не совпадает с
параметр. Чтобы противодействовать этому, сумма квадратов отклонений делится на единицу меньше. чем размер выборки.
чем размер выборки.
Стандартное отклонение
Возникла проблема с отклонениями. Напомним, что отклонения были возведены в квадрат. Это означает, что единицы также были возведены в квадрат. Чтобы вернуть единицы измерения к исходным значениям данных, квадрат root надо брать.
Стандартное отклонение выборки не является объективной оценкой стандартного отклонения генеральной совокупности.
На калькуляторе нет ключа отклонения. У него есть ключ стандартного отклонения. Ты чтобы найти дисперсию, придется возвести в квадрат стандартное отклонение.
Сумма квадратов (ярлыки)
Сумма квадратов отклонений от среднего дается сокращенным обозначением и несколькими альтернативные формулы.
Небольшое алгебраическое упрощение возвращает:
Что не так с первой формулой, спросите вы? Рассмотрим следующий пример — последняя строка итоги по столбцам
- Всего значений данных: 23
- Разделите на количество значений, чтобы получить среднее значение: 23/5 = 4.
 2 = 0,16
2 = 0,1623 0,00 (Всегда) 5,2 Как вы думаете, неплохо. Но это может стать очень плохим, если среднее значение выборки не окажется «красивое» рациональное число. Подумайте о среднем значении 19/7 = 2,714285714285 … вычитания становятся неприятными, и когда вы их возводите в квадрат, они действительно плохи. Еще одна проблема с Первая формула состоит в том, что она требует, чтобы вы знали среднее значение заранее. Для калькулятора это было бы означают, что вам нужно сохранить все введенные числа.TI-82 делает это, но большинство в научных калькуляторах нет.
Теперь рассмотрим формулу быстрого доступа. Единственное, что вам нужно найти, — это сумма значения и сумма квадратов значений. Здесь нет вычитания, десятичных знаков или дробей. до конца. Последняя строка, как и раньше, содержит суммы столбцов.
- Запишите каждое число в первом столбце и квадрат каждого числа во втором столбце.

- Итого по первой колонке: 23
- Итого второй столбец: 111
- Вычислите сумму квадратов: 111 — 23 * 23/5 = 111 — 105.2
4 16 5 25 3 9 6 36 5 25 23 111 Теорема Чебышева
Доля значений, попадающих в пределы k стандартных отклонений среднего, будет не менее , где k — число больше 1.
«В пределах k стандартных отклонений» интерпретируется как интервал: до.
Теорема Чебышева верна для любого набора выборок, независимо от распределения.
Эмпирическое правило
Эмпирическое правило справедливо только для колоколообразных (нормальных) распределений. Следующие утверждения верны.
- Примерно 68% значений данных находятся в пределах одного стандартного отклонения от среднего.
- Примерно 95% значений данных находятся в пределах двух стандартных отклонений от среднего.
- Примерно 99,7% значений данных находятся в пределах трех стандартных отклонений от среднего.
К эмпирическому правилу мы вернемся позже в главе, посвященной нормальным вероятностям.
Использование TI-82, чтобы найти эти значения
Вы можете использовать TI-82, чтобы найти меры центральной тенденции и меры вариации. используя возможности калькулятора по работе со списками.
Содержание .
- Запишите каждое число в первом столбце и квадрат каждого числа во втором столбце.

 Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.
Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.
Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.



 24.564 96)… Источник: МЕТОДИЧЕСКИЕ УКАЗАНИЯ . ОХРАНА ПРИРОДЫ. ГИДРОСФЕРА. ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ ПОДСИСТЕМЫ МОНИТОРИНГА АНТРОПОГЕННОГО ЭВТРОФИРОВАНИЯ ПРЕСНОВОДНЫХ ЭКОСИСТЕМ. РД… … Официальная терминология
24.564 96)… Источник: МЕТОДИЧЕСКИЕ УКАЗАНИЯ . ОХРАНА ПРИРОДЫ. ГИДРОСФЕРА. ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ ПОДСИСТЕМЫ МОНИТОРИНГА АНТРОПОГЕННОГО ЭВТРОФИРОВАНИЯ ПРЕСНОВОДНЫХ ЭКОСИСТЕМ. РД… … Официальная терминология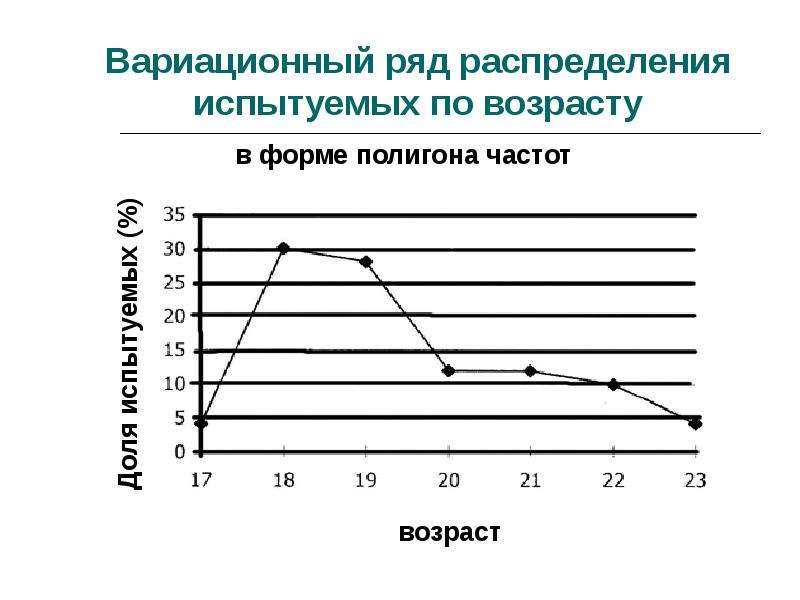 Показывает, как изменяется признак от… … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных
Показывает, как изменяется признак от… … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных Промежуток между крайними членами В. р. называют интервалом варьирования, а длину этого интервала… … Большая советская энциклопедия
Промежуток между крайними членами В. р. называют интервалом варьирования, а длину этого интервала… … Большая советская энциклопедия
 Можно даже возразить, что не существует такого понятия, как «типичный».Например, статистикой, которую часто неправильно используют, является средний уровень разводов в Соединенных Штатах, который часто называют «около 50%». Если кто-то исследует вопрос, он обнаружит, что средний уровень разводов широко варьируется в зависимости от таких факторов, как возраст, уровень образования, профессия, раса, география, религиозные убеждения и т. Д. Таким образом, каждый по-разному классифицируется по этим факторам, что приводит к множеству различный средний уровень разводов в зависимости от того, какие факторы описывают измеряемые факторы.”
Можно даже возразить, что не существует такого понятия, как «типичный».Например, статистикой, которую часто неправильно используют, является средний уровень разводов в Соединенных Штатах, который часто называют «около 50%». Если кто-то исследует вопрос, он обнаружит, что средний уровень разводов широко варьируется в зависимости от таких факторов, как возраст, уровень образования, профессия, раса, география, религиозные убеждения и т. Д. Таким образом, каждый по-разному классифицируется по этим факторам, что приводит к множеству различный средний уровень разводов в зависимости от того, какие факторы описывают измеряемые факторы.” Рекомендуется использовать диапазон только для очень маленьких распределений без выбросов.
Рекомендуется использовать диапазон только для очень маленьких распределений без выбросов.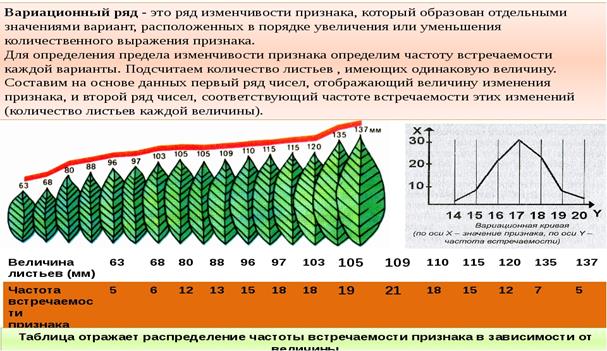
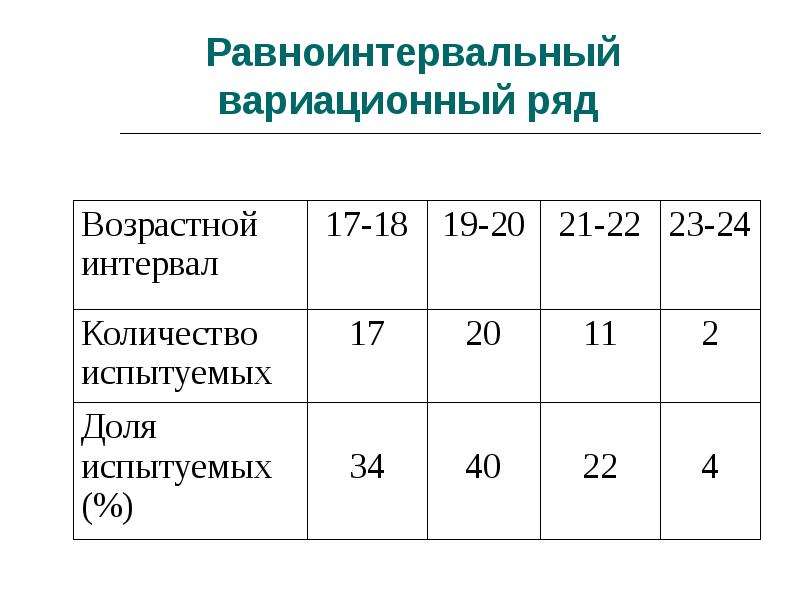 Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент).
Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент). 2 = 0,16
2 = 0,16