Вариационный ряд это распределения: Вариационные ряды — доступная и полная информация
1. Статистические ряды распределения. Теория статистики: конспект лекций
Читайте также
15. Статистические таблицы
15. Статистические таблицы Статистическая таблица – таблица, которая дает количественную характеристику статистической совокупности и представляет собой форму наглядного изложения полученных в результате статистической сводки и группировки числовых (цифровых)
19. Статистические карты
19. Статистические карты Статистические карты представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризую–щих уровень или степень распространения того или иного явления на определенной территории.
38.
 Ряды агрегатных индексов с постоянными и переменными весами
Ряды агрегатных индексов с постоянными и переменными весами
38. Ряды агрегатных индексов с постоянными и переменными весами При изучении динамики экономических явл* ний строятся и исчисляются индексы за ряд последов тельных периодов. Они образуют ряды либо бази ных, либо цепных индексов. В ряду базисных индексе сравнение
6. Статистические термины
6. Статистические термины Статистическая информация, получаемая в результате наблюдения, необходима для предоставления органам государственного управления, для обеспечения информацией руководителей предприятий, компаний и т. д., для информирования общественности об
44. Статистические методы
 В основе изучения финансовых инвестиций лежит построение уравнения эквивалентности, так называемого баланса финансовой операции. Содержание данного
В основе изучения финансовых инвестиций лежит построение уравнения эквивалентности, так называемого баланса финансовой операции. Содержание данного
45. Статистические модели
45. Статистические модели Для эффективной работы на фондовом рынке необходимо знать, как доходность конкретного наименования акций (или портфеля акций конкретного инвестора) связана со средней рыночной доходностью всей совокупности акций, т. е. с рыночным индексом. Для
3. Статистические таблицы
3. Статистические таблицы После того как данные статистического наблюдения собраны и даже сгруппированы, их трудно воспринимать и анализировать без определенной, наглядной систематизации. Результаты статистических сводок и группировок получают оформление в виде
4.
 Ряды агрегатных индексов с постоянными и переменными весами
Ряды агрегатных индексов с постоянными и переменными весами
4. Ряды агрегатных индексов с постоянными и переменными весами При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексов сравнение
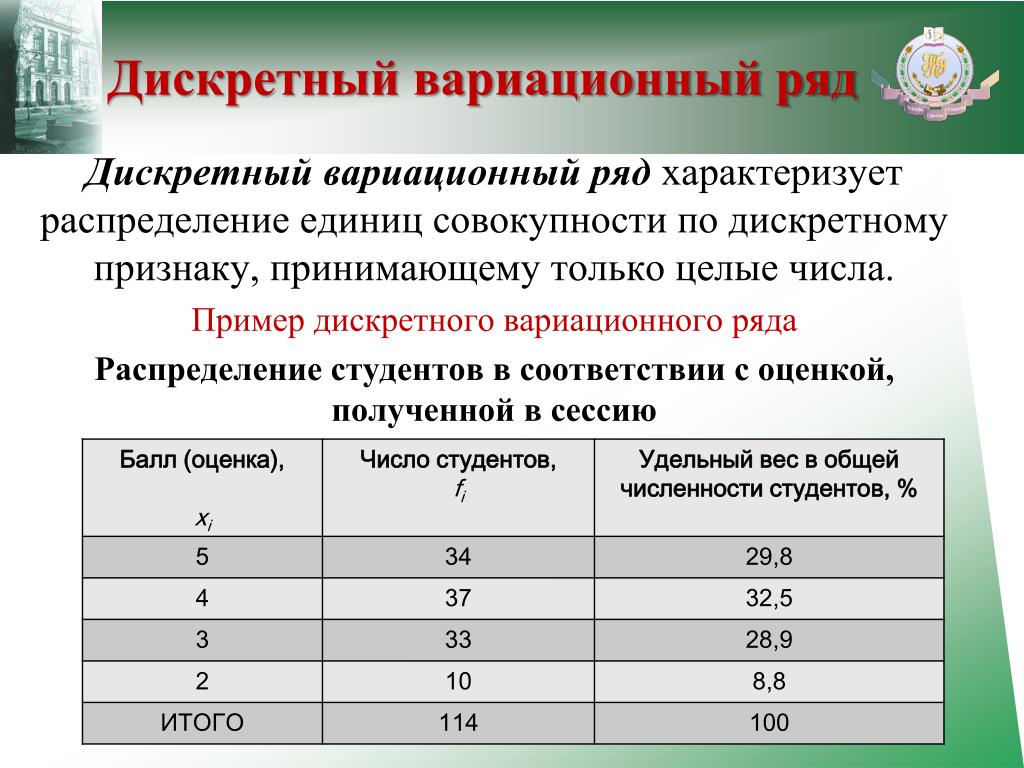
18. Статистические ряды распределения и их графическое изображение
18. Статистические ряды распределения и их графическое изображение Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.Различают атрибутивные и вариационные ряды
19. Статистические таблицы
 Статистические таблицы
В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
Статистические таблицы
В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
Статистические методы
Статистические методы Подсчет в толпе. Метод, честно говоря, наивный, но очень популярный. Организатор ресторанного бизнеса берет блокнот и карандаш, становится у двери похожего заведения в равноценном районе и считает, сколько человек проходит мимо в единицу времени.
1. Статистические ряды распределения
1. Статистические ряды распределения
В результате обработки и систематизации первичных данных статистического наблюдения получают группировки, называемые рядами распределения. Статистические ряды распределения представляют собой упорядоченное расположение единиц
Статистические ряды распределения представляют собой упорядоченное расположение единиц
3. Статистические таблицы
3. Статистические таблицы В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
ЛЕКЦИЯ № 10. Ряды динамики и их изучение в коммерческой деятельности
ЛЕКЦИЯ № 10. Ряды динамики и их изучение в коммерческой деятельности 1. Основные понятия о рядах динамики Все процессы и явления, протекающие в общественной жизни человека, являются предметом изучения статистической науки они находятся в постоянном движении и
Глава 6 АНГЛО-АМЕРИКАНЦЫ СМЫКАЮТ РЯДЫ
Международные статистические данные
Международные статистические данные
Интернет существенно упростил сбор данных в мировом масштабе.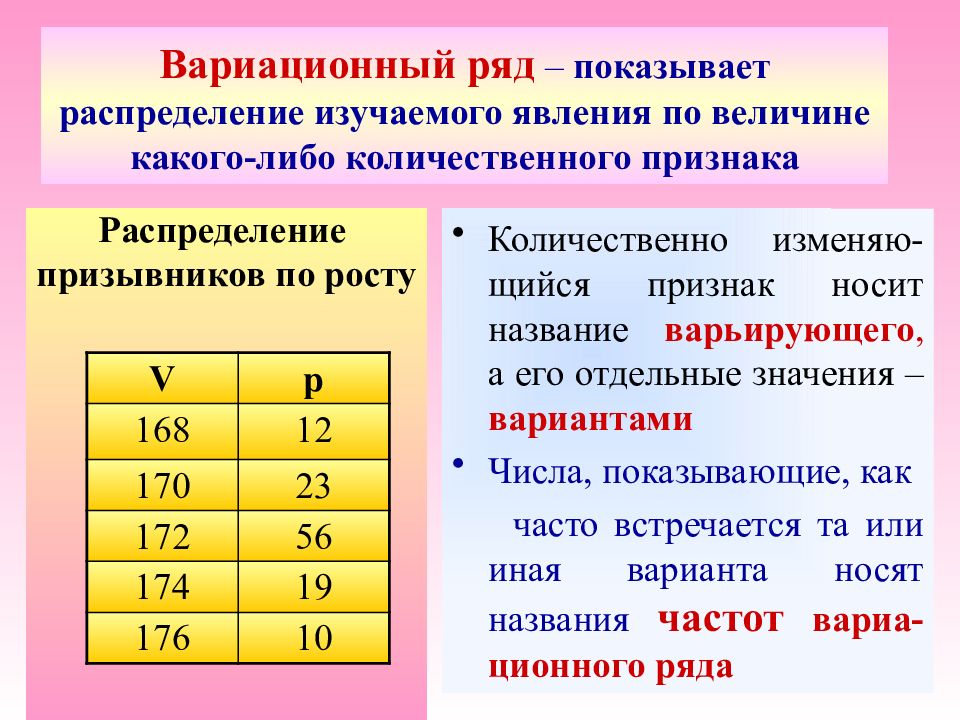
Атрибутивные и вариационные ряды распределения. Ранжирование данных.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Распределение может быть по признакам, не имеющим количественной меры (атрибутивным), и по признакам, в которых изменяется их количественная мера (вариационные ряды).
Атрибутивные ряды распределения. Примерами таких распределений являются распределение населения на городское и сельское, мужское и женское, товарооборота на продовольственные и непродовольственные товары, занятого населения по отраслям и профессиям.
Вариационные ряды. Примерами служат распределение рабочих по размеру среднемесячной заработной платы, предприятий по объемам производства или численности работающих.
В вариационном ряду различают два элемента: варианты и частоты. Вариантами называются отдельные значения группировочного признака, которые он принимает в вариационном ряду. Частотами называют числа, показывающие, как часто встречаются те или иные варианты.
Вариационные ряды по способу построения бывают интервальными и дискретными. Интервальные вариационные ряды – ряды, в которых значения вариант даны в виде интервалов (например, численность населения по возрастам).
Характер вариационного ряда (интервальный или дискретный) определяется характером вариации. Вариация может быть непрерывной и прерывной (дискретной).
Примерами непрерывной вариации служат урожайность сельскохозяйственных культур, заработная плата, объемы производства.Примерами дискретной вариации могут служить число членов семьи, тарифный разряд рабочего, число комнат в квартире, число рабочих на предприятии.
Если дискретная вариация проявляется в широких пределах (например, численность рабочих на предприятии), то строятся интервальные вариационные ряды.
Ранжированный ряд — это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
НОУ ИНТУИТ | Лекция | Сводка и группировка статистических данных
Аннотация: После того как статистическая информация получена в виде данных статистических анкет, отчетности и других документов, возникает задача ее систематизации и упорядочивания, поскольку из разрозненных сведений первичных документов, содержащих информацию только по одной единице наблюдения, нельзя сделать правильного вывода обо всей совокупности в целом. Для этого полученную информацию сводят воедино, группируют, подводят итоги по группам и совокупности в целом. Таким образом, наступает следующий этап статистического исследования — сводка и группировка статистических материалов.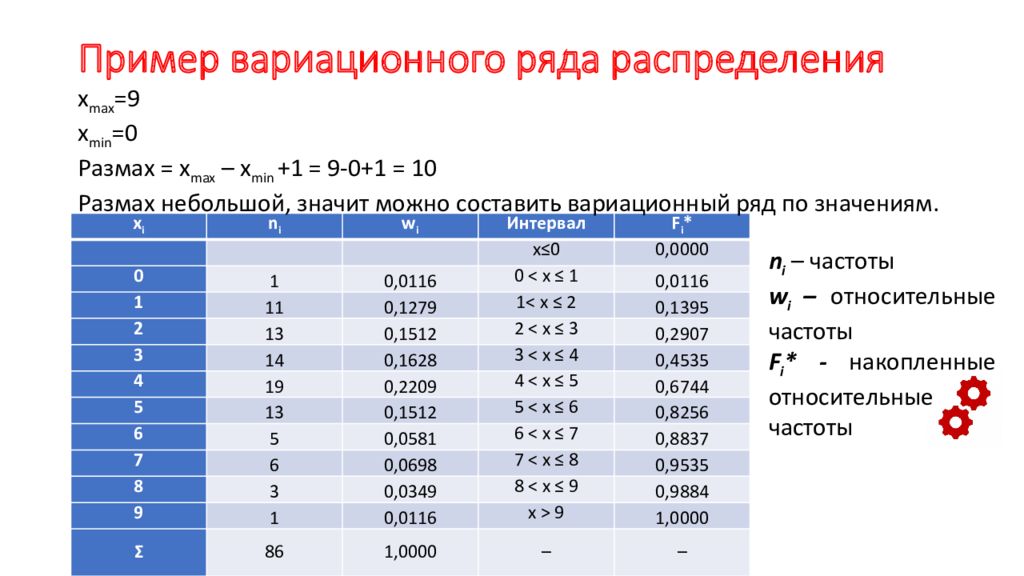
3.1. Задачи и виды статистической сводки
Статистическая сводка — это первичная обработка данных статистического наблюдения с целью их систематизации. Она предполагает сведение полученной статистической информации о единицах наблюдения в массив данных, упорядоченных по значению какого-либо признака.
По глубине обработки материала различают простую и сложную сводку.
Простая сводка предполагает сведение полученных данных в статистические таблицы, подведение общих итогов по совокупности в целом.
Сложная сводка осуществляется с применением метода группировок по определенной программе, предусматривающей следующие этапы:
- выбор группировочных признаков;
- определение порядка формирования групп; intuit.ru/2010/edi»>разработка системы показателей для характеристики групп и статистической совокупности в целом;
- разработка макетов статистических таблиц для представления результатов сводки;
- распределение единиц наблюдения на группы по изучаемым признакам;
- подведение групповых и общих итогов;
- оформление результатов сводки в виде статистических таблиц.
По технике выполнения различают ручную сводку и сводку с использованием компьютерных технологий.
По форме обработки статистической информации, собранной в процессе наблюдения, сводка может быть децентрализованной и централизованной. В первом случае данные сначала сводятся по территориям, а затем в центральной организации проводится обработка уже систематизированных данных. Во втором случае вся работа по первичной обработке собранной информации осуществляется в центральной организации.
Во втором случае вся работа по первичной обработке собранной информации осуществляется в центральной организации.
Результатом проведения статистической сводки является получение обобщающих статистических таблиц, которые содержат итоговые данные по показателям, характеризующим единицы наблюдения. Этими итоговыми данными могут быть суммарные значения показателей, рассчитанные как для всей совокупности в целом, так и для отдельных групп единиц, если проводилась разбивка на группы; средние значения, относительные показатели.
| Главная > Учебные материалы > Математика: Вариационные ряды | ||||
|
1.  Вариационный ряд. Вариационный ряд.2.Числовые характеристики вариационного ряда.
|
||||
| 24 25 26 27 28 29 30 31 32 | ||||
1.Вариационный ряд. Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. |
||||
Таб.1 По данным таблицы построим полигон распределения частот (рис.1) |
Рис.1 |
|||
|
В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. |
||||
Таб. 2 По данным таблицы построим гистограмму распределения частот (рис.2) |
Рис.2 |
|||
|
Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. |
||||
2.Числовые характеристики вариационного ряда. |
||||
|
Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости. |
||||
|
Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической. |
||||
|
Дисперсией s2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической. |
||||
|
Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии. |
||||
|
Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака. |
||||
Пример. |
||||
В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины. |
||||
|
Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен. |
||||
Как видно из таблицы сумма произведений xini = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда. |
||||
По данным таблицы построим гистограмму распределения частот.
|
||||
Построим и эмпирическую функцию распределения случайной величины (кумуляту). |
||||
|
Далее найдем моду и медиану случайной величины Х. Наиболее вероятное значение случайной величины Х (мода) равно Mo = 34,117. Т.е. Pmax (34,1) = 0,1975. Медиана — Ме = 34,3 (как видно из графика). Теперь рассчитаем начальный и центральный моменты k — го порядка и сведем эти данные в таблицу.
|
||||
Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:
|
||||
| 24 25 26 27 28 29 30 31 32 | ||||
Вариационный ряд — Викизнание.
 .. Это Вам НЕ Википедия!
.. Это Вам НЕ Википедия!Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины
равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число называется рангом порядковой статистики
Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения , то совместная плотность распределения элементов вариационного ряда имеет вид
Пример 1[править]
Приведем оценки 45 студентов по курсу статистика в порядке сдачи экзамена:
5 3 3 4 2 4 4 3 5 4 4 5 5 4 4
3 3 3 2 5 5 4 4 4 3 4 3 4 5 4
4 4 4 3 3 4 3 4 3 2 3 2 3 3 3
При таком представлении информации трудно делать какие-либо выводы об успеваемости. Произведем группировку данным путем подсчета количества различных оценок.
оценки 2 3 4 5
количество 4 16 18 7
Как видим, вместо 45 чисел осталось 8, при этом повысилась информативность таблицы, более 50% студентов сдали предмет на хорошо и отлично. Данный пример показывает, что эти данные лучше сгруппировать, то есть разделить их на однородные группы по некоторому признаку. Благодаря группировке данные приобретают систематизированный вид. Если данные систематизированы по времени, то моделью группировки будет временный ряд. Если же по любому другому признаку — то ряд распределения. А для количественных признаков — вариационный ряд.
Пусть Х — одномерный количественный признак и в результате n его измерений наблюдалось n его значений x(1),x(2)…..x(n), среди которых могут быть одинаковые. Эти значения называют вариантами. Пусть среди имеющихся n вариант имеется k различных . Причем x1 встречается m1 раз, xk — mk раз. Понятно, что .
Вариационный ряд обычно записывается в одном из видов: в таблице с частотами mi, через относительные частоты Wi=mi/n. В зависимости от типа признака различают дискретные и интервальные вариационные ряды. В зависимости от объема исходных данных и области допустимых значений одномерного количественного признак, частотные распределения также подразделяются на дискретные и интервальные. Если различных вариант очень много (более 10-15), то эти варианты группируют, выбирая определенное число интервалов группировки и получая таким образом интервальное частотное распределение. Алгоритм группировки массива данных состоит из следующих шагов:
В зависимости от типа признака различают дискретные и интервальные вариационные ряды. В зависимости от объема исходных данных и области допустимых значений одномерного количественного признак, частотные распределения также подразделяются на дискретные и интервальные. Если различных вариант очень много (более 10-15), то эти варианты группируют, выбирая определенное число интервалов группировки и получая таким образом интервальное частотное распределение. Алгоритм группировки массива данных состоит из следующих шагов:
- 1) находят минимальную и максимальную варианты
- 2) весь диапазон значений признака [Xmin,Xmax] разбивают на к интервалов одинаковой длины .
Число К обычно берется в пределах 10-15. Редки случаи, когда требуется более 25 и менее 8 группировок. Существуют формулы для определения “оптимального” значения К и построения таким образом оптимального распределения частот. Формула Старджеса . Для больших n эта формула дает оценку снизу для К.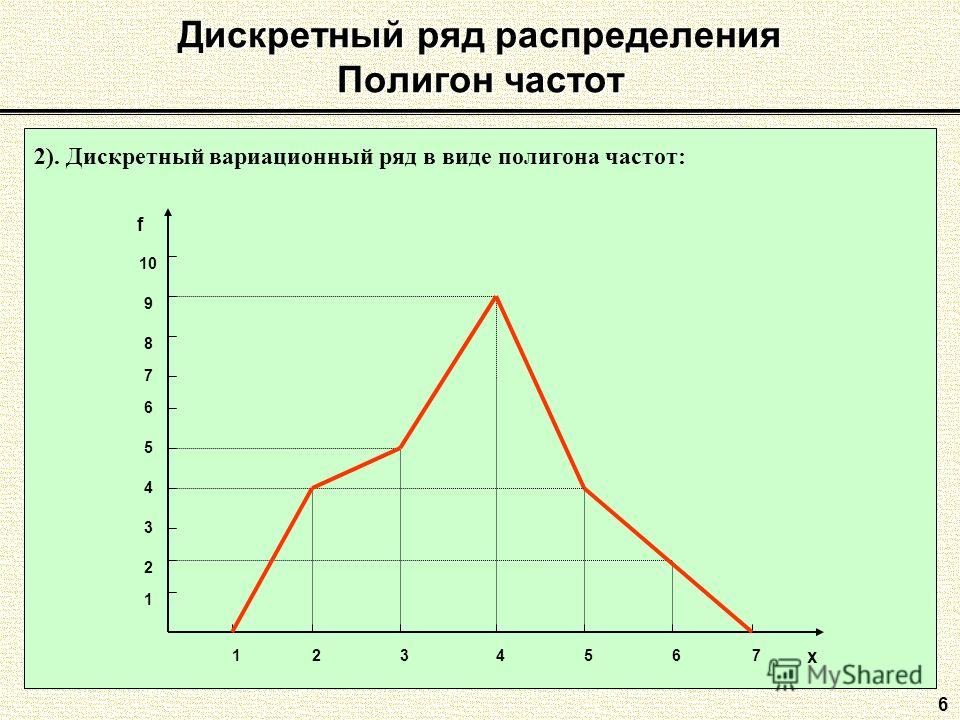
- 3) находят граничные точки каждого из интервалов и т.д.
- 4) подсчитываем число вариант Mi, попавших в интервал , причем варианты, попавшие на границы интервалов, относят только к одному из интервалов, результат заносят в таблицу .
Пример 2[править]
Приведем вариационный ряд почасовой оплаты 303 рабочих промышленности
Xi 2.49 2.50 2.51 2.52 2.53 2.54 2.55 2.56 2.57 2.58 2.59 2.6 2.61
Mi 1 4 1 1 0 3 2 0 3 2 1 8 1
2.62 3 2.72 9 2.82 11 2.92 6 3.02 2 3.12 0 3.22 1 3.32 1
2.63 0 2.73 3 2.83 3 2.93 2 3.03 0 3.13 0 3.23 0 3.33 0
2.64 5 2.74 10 2.84 4 2.94 4 3.04 3 3.14 2 3.24 0 3.34 2
2.65 7 2.75 11 2.85 7 2.95 8 3.05 4 3.15 4 3.25 3 3.35 2
2.66 3 2.76 4 2.86 5 2.96 5 3.06 2 3.16 2 3.26 1 3.36 0
2.67 2 2.77 2 2.87 3 2.97 2 3.07 0 3.17 0 3.27 0 3.37 1
2.68 3 2.78 9 2.88 8 2.98 3 3.08 2 3.18 2 3.28 0
2.69 2 2.79 5 2.89 4 2.99 1 3.09 0 3.19 1 3.29 0
2.70 14 2.8 22 2. 90 16 3.0 9 3.10 7 3.20 4 3.30 4
90 16 3.0 9 3.10 7 3.20 4 3.30 4
2.71 4 2.81 3 2.91 3 3.01 1 3.11 0 3.21 0 3.31 0
Построим для данного ряда интервальное частотное распределение.
- 1) X min = 2,49 Xmax=3,37
- 2)
Для удобства вычислений возьмем К=10. и т.д.
Для наглядного представления дискретных частотных распределений могут применяться вертикальные линии. Каждый из примеров можно рассматривать либо как выборку, либо как генеральную совокупность. Обычно данные собирают и анализируют для практических результатов. пример.
Абсолютное частотное распределение прибыли 100 крупных межнациональных компаний, базирующихся в США за 1988 г.
Класс компании, размер прибыли, млн.$ Число компаний в классе
-1500-0 3 |||
0-500 41 |||| |||| |||| |||| |||| |||| |||| |||| |||| |||| |
500 — 1000 32 |||| |||| |||| |||| |||| |||| |||| ||||
1000 — 1500 9 |||| |||| |
1500 — 2000 6 |||| ||
2000 — 2500 6 |||| ||
2500 — 5500 3 |||
Вариация, Коэффициент вариации, Размах вариации, Вариационный ряд
Понятие вариации
Вариация определяет различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период (момент времени). Причиной вариации бывают разные условия существования разных единиц совокупности. Например, даже близнецы в процессе жизни приобретают различия в росте, весе, а также в таких признаках, как уровень образования, доход, количество детей и т.д.
Причиной вариации бывают разные условия существования разных единиц совокупности. Например, даже близнецы в процессе жизни приобретают различия в росте, весе, а также в таких признаках, как уровень образования, доход, количество детей и т.д.
Вариация возникает в результате того, что сами значения признака складываются под суммарным влиянием разнообразных условий, которые разным образом сочетаются в каждом отдельном случае. Таким образом, величина любого варианта объективна.
Вариация характерна всем без исключения явлениям природы и общества, кроме законодательно закрепленных нормативных значений отдельных социальных признаков. Исследования вариации в статистике имеют огромное значение, помогают познать сущность изучаемого явления. Нахождение вариации, выяснение ее причин, выявление влияния отдельных факторов дают важную информацию для внедрения научно обоснованных управленческих решений.
Средняя величина дает обобщенную характеристику признака совокупности, но она не раскрывает её строения. Среднее значение не показывает, как располагаются вокруг нее варианты осредненного признака, распределены ли они вблизи средней или отклоняются от нее. Средняя в двух совокупностях может быть одинаковой, но в одном варианте все индивидуальные значения отличаются от нее незначительно, а в другом — эти отличия велики, т.е. в первом случае вариация признака мала, а во втором — велика, это имеет очень важное значение для характеристики значимости средней величины.
Среднее значение не показывает, как располагаются вокруг нее варианты осредненного признака, распределены ли они вблизи средней или отклоняются от нее. Средняя в двух совокупностях может быть одинаковой, но в одном варианте все индивидуальные значения отличаются от нее незначительно, а в другом — эти отличия велики, т.е. в первом случае вариация признака мала, а во втором — велика, это имеет очень важное значение для характеристики значимости средней величины.
Для того, чтобы руководитель организации, управляющий, научный работник могли изучать вариацию и управлять ей, статистикой разработаны специальные методы исследования вариации (система показателей). С их помощью вариация находится, характеризуются ее свойства. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение, коэффициент вариации.
Вариационный ряд и его формы
Вариационный ряд — это упорядоченное распределение единиц совокупности чаще по возрастающим (реже убывающим) значениям признака и подсчет числа единиц с тем или иным значением признака. Когда численность единиц совокупности большая, ранжированный ряд становится громоздким, его построение занимает длительное время. В такой ситуации вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.
Когда численность единиц совокупности большая, ранжированный ряд становится громоздким, его построение занимает длительное время. В такой ситуации вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.
Существуют следующие формы вариационного ряда:
- Ранжированный ряд представляет собой, перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
- Дискретный вариационный ряд — это таблица, состоящая из двух строк или граф: конкретных значений варьирующего признака х и числа единиц совокупности с данным значение f — признака частот. Он строится тогда, когда признак принимает наибольшее число значений.
- Интервальный ряд.
Размах вариации
Размах вариации определяется как абсолютная величина разности между максимальными и минимальными значениями (вариантами) признака:
Размах вариации показывает только крайние отклонения признака и не отражает отдельных отклонений всех вариантов в ряду. Он характеризует пределы изменения варьирующего признака и зависим от колебаний двух крайних вариантов и абсолютно не связан с частотами в вариационном ряду, т. е. с характером распределения, что придает этой величине, случайный характер. Для анализа вариации нужен показатель, который отражает все колебания вариационного признака и даёт общую характеристику. Простейший показатель такого вида — среднее линейное отклонение.
Он характеризует пределы изменения варьирующего признака и зависим от колебаний двух крайних вариантов и абсолютно не связан с частотами в вариационном ряду, т. е. с характером распределения, что придает этой величине, случайный характер. Для анализа вариации нужен показатель, который отражает все колебания вариационного признака и даёт общую характеристику. Простейший показатель такого вида — среднее линейное отклонение.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Страница не найдена |
Страница не найдена | 404. Страница не найдена
Страница не найдена
Архив за месяц
ПнВтСрЧтПтСбВс
12
24252627282930
31
12
12
1
3031
12
15161718192021
25262728293031
123
45678910
12
17181920212223
31
2728293031
1
1234
567891011
12
891011121314
11121314151617
28293031
1234
12
12345
6789101112
567891011
12131415161718
19202122232425
3456789
17181920212223
24252627282930
12345
13141516171819
20212223242526
2728293031
15161718192021
22232425262728
2930
Архивы
Июн
Июл
Авг
Сен
Окт
Ноя
Дек
Метки
Настройки
для слабовидящих
Меры вариации: определение, виды и примеры
Описательная статистика> Меры вариации
Вариант — это способ показать , как данные распределены, или распределены .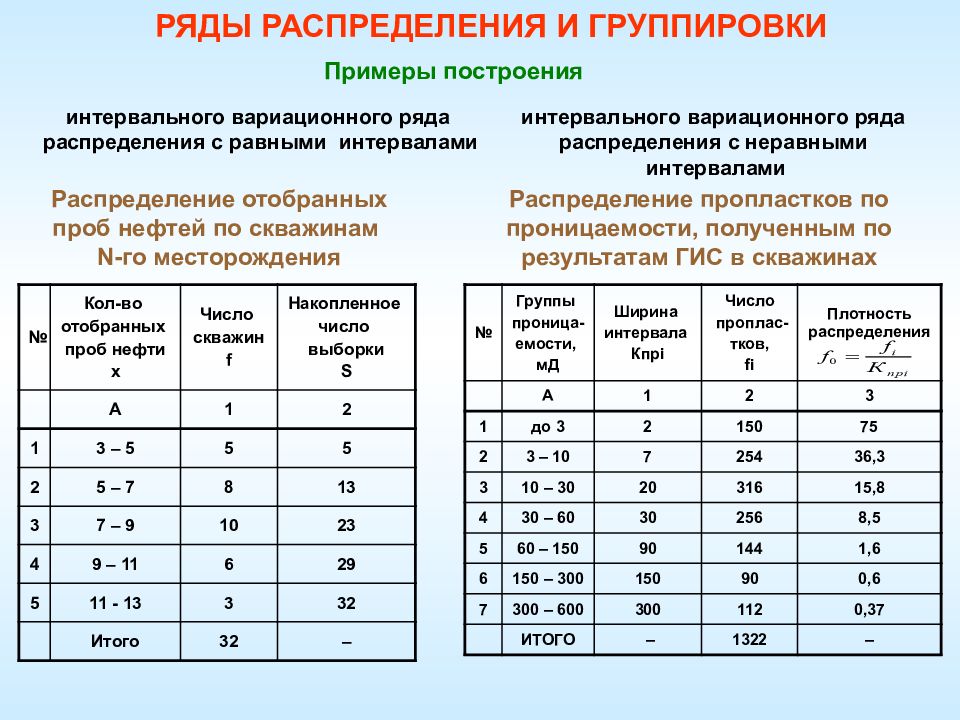 В статистике используется несколько мер вариации.
В статистике используется несколько мер вариации.
Различные меры отклонения
Диапазон
Диапазон — одна из самых основных мер вариации. Это разница между наименьшим элементом данных в наборе и наибольшим.Например, диапазон 73, 79, 84, 87, 88, 91 и 94 равен 21, потому что 94–73 это 21.
Квартили
квартили делят ваши данные на кварталы: самые низкие 25%, следующие самые низкие 25%, вторые по величине 25% и самые высокие 25%.
Набор чисел (-2, -1,0,1,2), разделенных на четыре квартиля.
Межквартильный размах
Межквартильный размах — один из самых популярных показателей вариации, используемых в статистике. Это мера того, как данные распределяются вокруг среднего значения.Основная формула:
IQR = Q 3 — Q 1
Подробнее см. Межквартильный размах в статистике: что это такое и как его найти.
Разница
Дисперсия сообщает вам, насколько далеко разброс набор данных, но это абстрактное число, которое на самом деле полезно только для расчета стандартного отклонения. В этом коротком видео показано, как найти и то, и другое:
В этом коротком видео показано, как найти и то, и другое:
Сумма квадратов
Сумма квадратов — это довольно продвинутая методика, которая измеряет, как данные изменяются вокруг центрального числа, например среднего.Он широко используется в регрессионном анализе, чтобы вычислить, насколько хорошо точки данных соответствуют линии наилучшего соответствия. Подробнее о том, как это вычислить, см. Сумма квадратов.
Эмпирическое правило
Сколько данных находится на определенном расстоянии от среднего? Если у вас нормальное распределение, эмпирическое правило может вам это сказать. Например:
- Около 68% результатов будут находиться в диапазоне от +1 до -1 стандартного отклонения от среднего.
- Около 95% будет находиться в диапазоне от +2 до -2 стандартных отклонений.
Если у вас есть другое (ненормальное) распределение, вы все равно можете вычислить эти проценты, используя теорему Чебышева.
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Типы вариаций в архиве данных временных рядов
Традиционные методы анализа временных рядов связаны с разложением ряда на тренд , — сезонным изменением и другими нерегулярными колебаниями . Хотя этот подход не всегда лучший, но все же полезен (Kendall and Stuart, 1996).
Компоненты, из которых состоит временной ряд, называются компонентом данных временного ряда.Ниже описаны четыре основных компонента данных временных рядов.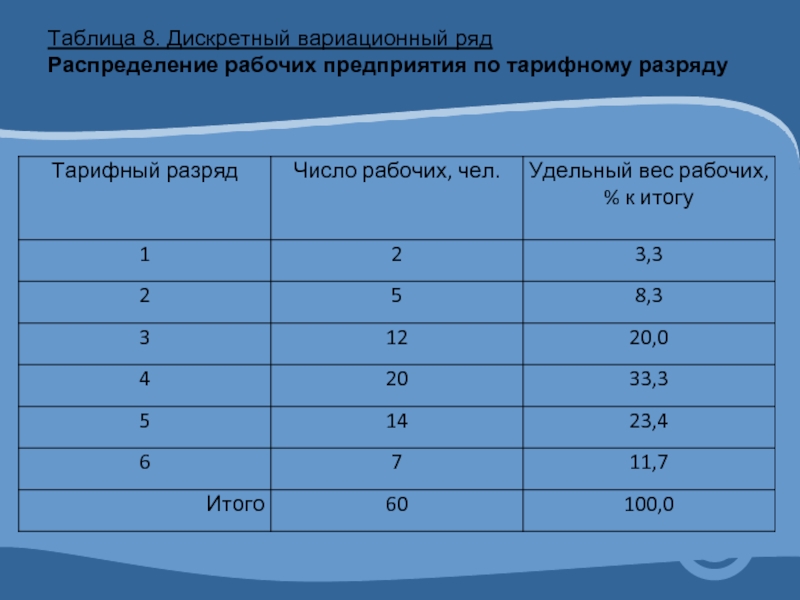
Различные источники отклонений:
- Сезонный эффект (сезонные колебания или сезонные колебания)
Многие из временных рядов данных демонстрируют сезонное изменение , которое представляет собой годовой период, например, продажи и показания температуры. Этот тип вариации легко понять, и его можно легко измерить или удалить из данных, чтобы получить десезонизированные данные.Сезонные колебания — это любые регулярные колебания (колебания) с периодом менее одного года, например, стоимость различных видов фруктов и овощей, одежда, показатели безработицы, среднесуточное количество осадков, увеличение продаж чая зимой, увеличение продаж. мороженого летом и т. д., во всех случаях наблюдаются сезонные колебания. Изменения, которые повторяются в течение определенного периода, также называются сезонными вариациями , например, движение на дорогах в утренние и вечерние часы, распродажи на фестивалях, таких как EID, и т. Д., увеличение количества пассажиров в выходные и т. д. Сезонные колебания вызваны климатом, социальными обычаями, религиозной деятельностью и т.д.
Д., увеличение количества пассажиров в выходные и т. д. Сезонные колебания вызваны климатом, социальными обычаями, религиозной деятельностью и т.д. - Другие циклические изменения (циклические изменения или циклические колебания)
Временной ряд показывает Изменения в фиксированный период из-за какой-либо другой физической причины, например, суточных колебаний температуры. Циклическое изменение — это несезонный компонент, который изменяется в узнаваемом цикле.Иногда ряды демонстрируют колебания, которые не имеют фиксированного периода, но в некоторой степени предсказуемы. Например, на экономические данные влияют бизнес-циклы с периодом от 5 до 7 лет. В еженедельных или ежемесячных данных циклический компонент может описывать любые регулярные изменения (колебания) данных временных рядов. Циклическое изменение носит периодический характер и повторяется как деловой цикл, который состоит из четырех фаз (i) пик (ii) рецессия (iii) минимума / депрессии (iv) расширения .
- Тренд (вековой тренд или долгосрочная вариация)
Это долгосрочное изменение. Здесь мы принимаем во внимание количество доступных наблюдений и делаем субъективную оценку того, что является долгосрочным. Чтобы понять значение долгосрочной перспективы, пусть, например, климатические переменные иногда демонстрируют циклические изменения в течение очень длительного периода времени, например, 50 лет. Если бы у кого-то были данные за 20 лет, это долгосрочное колебание могло бы показаться тенденцией, но если бы были доступны данные за несколько сотен лет, то были бы видны долгосрочные колебания.Эти движения носят систематический характер, при этом движения широкие, устойчивые, демонстрируя медленный подъем или спад в одном и том же направлении. Тренд может быть линейным или нелинейным (криволинейным). Некоторые примеры вековых тенденций: рост цен, рост загрязнения, увеличение потребности в пшенице, повышение уровня грамотности, снижение смертности из-за достижений науки. Получение средних значений за определенный период — простой способ обнаружить тенденцию в сезонных данных. Изменение средних значений со временем свидетельствует о наличии тренда в данном ряду, хотя существуют более формальные тесты для обнаружения тренда во временных рядах .
Получение средних значений за определенный период — простой способ обнаружить тенденцию в сезонных данных. Изменение средних значений со временем свидетельствует о наличии тренда в данном ряду, хотя существуют более формальные тесты для обнаружения тренда во временных рядах . - Другие нерегулярные колебания (нерегулярные колебания)
Когда тренд и циклических вариаций удаляются из набора данных временного ряда, остается остаток , который может быть или не быть случайным. Различные методы анализа рядов этого типа исследуют, чтобы увидеть, «можно ли объяснить нерегулярные вариации с помощью моделей вероятности, таких как скользящего среднего или авторегрессионных моделей , то есть мы можем увидеть, остались ли какие-либо циклические вариации в остатках.Эти колебания, возникающие из-за внезапных причин, называются остаточными колебаниями (нерегулярные колебания или случайные или беспорядочные колебания) и непредсказуемы, например, рост цен на сталь из-за забастовки на заводе, несчастный случай из-за отказа поломки, наводнение, земля быстрая, война и т. д.
д.
Нравится:
Нравится Загрузка …
Изменчивость в статистике
Статистики используют сводные меры для описания степени изменчивости или распространить в наборе данных.Наиболее распространенные меры изменчивости — это диапазон, межквартильный размах (IQR), дисперсия и стандартное отклонение.
Примечание: Ваш браузер не поддерживает видео в формате HTML5. Если вы просматриваете эту веб-страницу в другом браузере (например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеоматериал об этом уроке.
Диапазон
Диапазон — это разница между наибольшими и наименьшие значения в набор значений.
Например, рассмотрите следующие числа: 1, 3, 4, 5, 5, 6, 7, 11.
Для этого набора чисел диапазон будет 11 — 1 или 10.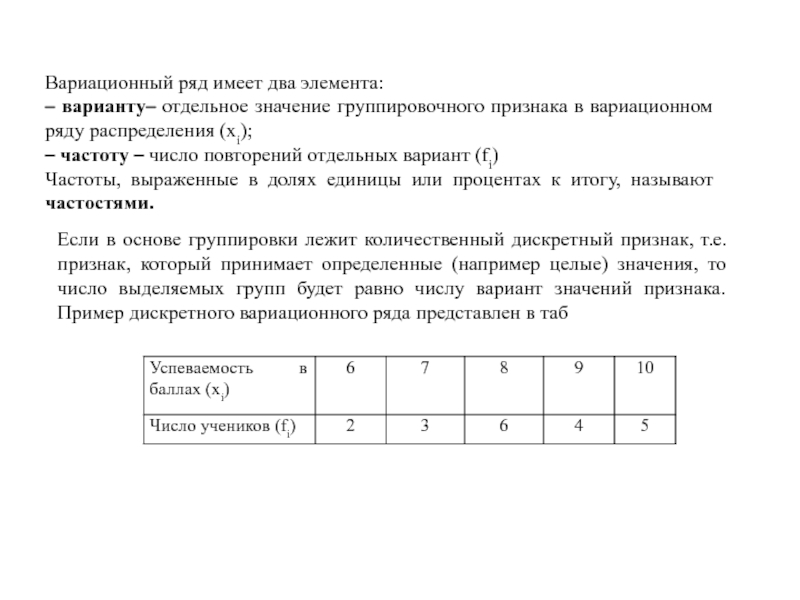
Межквартильный размах (IQR)
Межквартильный размах (IQR) является мерой изменчивости, на основе разделения набора данных на квартили.
Квартили делят упорядоченный набор данных на четыре равные части. Ценности, которые деление каждой части называется первым, вторым и третьим квартилями; и обозначаются Q1, Q2 и Q3 соответственно.
- Q1 — это «среднее» значение в первой половине ранжированной набор данных.
- Q2 — это медиана значение в наборе.
- Q3 — это «среднее» значение в секундах половине ранжированной набор данных.
Межквартильный размах равен Q3 минус Q1. Например, рассмотрим следующие числа: 1, 2, 3, 4, 5, 6, 7, 8.
Q2 — это медиана всего набора данных — среднее значение.В этом примере у нас есть четное количество
точки данных, поэтому медиана равна среднему из двух средних значений. Таким образом, Q2 =
(4 + 5) / 2 или Q2 = 4.5. Q1 — среднее значение в первой половине набора данных. Поскольку есть
четное количество точек данных в первой половине набора данных, среднее значение
среднее из двух средних значений; это,
Q1 = (2 + 3) / 2 или Q1 = 2,5. Q3 — среднее значение во втором тайме.
набора данных. Опять же, поскольку вторая половина набора данных имеет четный
количество наблюдений, среднее значение — среднее из двух
средние значения; то есть Q3 = (6 + 7) / 2 или Q3 = 6.5. Межквартильный
диапазон равен Q3 минус Q1, поэтому IQR = 6,5 — 2,5 = 4.
Таким образом, Q2 =
(4 + 5) / 2 или Q2 = 4.5. Q1 — среднее значение в первой половине набора данных. Поскольку есть
четное количество точек данных в первой половине набора данных, среднее значение
среднее из двух средних значений; это,
Q1 = (2 + 3) / 2 или Q1 = 2,5. Q3 — среднее значение во втором тайме.
набора данных. Опять же, поскольку вторая половина набора данных имеет четный
количество наблюдений, среднее значение — среднее из двух
средние значения; то есть Q3 = (6 + 7) / 2 или Q3 = 6.5. Межквартильный
диапазон равен Q3 минус Q1, поэтому IQR = 6,5 — 2,5 = 4.
Обратите внимание, что этот процесс разделил набор данных на четыре части равного размера. Первая часть состоит из 1 и 2; вторая часть, 3 и 4; третья часть, 5 и 6; и четвертая часть, 7 и 8.
Альтернативное определение IQR
В некоторых текстах межквартильный размах определяется иначе.Он определяется как разница между наибольшее и наименьшее значения в середине 50% набора данные.
Чтобы вычислить межквартильный размах с использованием этого определения, сначала удалите наблюдения из нижнего квартиля. Затем удалите наблюдения от верхнего квартиля. Затем, исходя из оставшихся наблюдений, вычислить разницу между наибольшим и наименьшим значениями.
Например, рассмотрите следующие числа: 1, 2, 3, 4, 5, 6, 7, 8.После удаления наблюдений из нижнего и верхнего квартилей, у нас осталось: 3, 4, 5, 6. Межквартильный размах (IQR) будет быть 6 — 3 = 3.
Разница
в Население, дисперсия — средний квадрат отклонение от среднего значения генеральной совокупности, определяемое по следующей формуле:
σ 2 = Σ (X i — μ) 2 / N
где σ 2 — дисперсия генеральной совокупности, μ — среднее значение генеральной совокупности, X i — i -й элемент от популяции, N — количество элементов в популяции.
Наблюдения с простая случайная выборка может использоваться для оценки дисперсии генеральной совокупности. Для этого дисперсия выборки определяется по несколько иной формуле: и использует несколько иное обозначение:
с 2 = Σ (x i — х) 2 / (п — 1)
, где с 2 — выборочная дисперсия, x — среднее значение выборки, x i — это i -й элемент из выборки, а n — количество элементов в выборке.Используя эту формулу, образец дисперсию можно рассматривать как объективную оценку истинной совокупности дисперсия. Следовательно, если вам нужно оценить неизвестную дисперсию совокупности, Эта формула основана на данных простой случайной выборки.
Стандартное отклонение
Стандартное отклонение — это квадратный корень из дисперсия. Таким образом, стандартное отклонение генеральной совокупности составляет:
.σ = sqrt [σ 2 ] = sqrt [Σ (X i — μ) 2 / N]
где σ — стандартное отклонение генеральной совокупности, μ — среднее значение генеральной совокупности, X i — i -й элемент от популяции, N — количество элементов в популяции.
Статистики часто используют простые случайные выборки для оценки стандартного отклонения генеральной совокупности на основе данных выборки. Учитывая простую случайную выборку, наилучшая оценка стандартного отклонения генеральной совокупности это:
s = sqrt [s 2 ] = sqrt [Σ (x i — x) 2 / (n — 1)]
, где с — стандартное отклонение выборки, x — среднее значение выборки, x i — это i -й элемент из выборки, а n — количество элементов в выборке.
Влияние смены единиц измерения
Иногда исследователи меняют единицы измерения (минуты на часы, футы на метры и т. Д.). Вот как влияет на показатели изменчивости, когда мы меняем единицы измерения.
- Если вы добавите константу к каждому значению, расстояние между значениями изменится. не изменить. В результате все меры изменчивости (диапазон, межквартильный размах, стандартное отклонение и дисперсия) остаются одно и тоже.
- С другой стороны, предположим, что вы умножаете каждое значение на константу.Этот имеет эффект умножения диапазона, межквартильного диапазона (IQR), и стандартное отклонение на эту константу. Он имеет еще больший влияние на дисперсию. Он умножает дисперсию на квадрат константы.
Проверьте свое понимание
Проблема 1
Популяция состоит из четырех наблюдений: {1, 3, 5, 7}. Какая разница?
(А) 2
(В) 4
(К) 5
(Г) 6
(E) Ничего из вышеперечисленного
Решение
Правильный ответ (С).Во-первых, нам нужно вычислить среднее значение генеральной совокупности.
μ = ΣX / N = (1 + 3 + 5 + 7) / 4 = 4
Затем мы подставляем все известные значения в формулу для дисперсии население, как показано ниже:
σ 2 = Σ (X i — μ) 2 / N
σ 2 = [(1 — 4) 2 + (3-4) 2 + (5-4) 2 + (7-4) 2 ] / 4
σ 2 = [(-3) 2 +
(-1) 2 + (1) 2 + (3) 2 ] / 4
σ 2 = [9 + 1 + 1 + 9] / 4
= 20/4 = 5
Примечание: Иногда учащиеся не уверены в том, что знаменатель в формуле для дисперсии должно быть N или (n — 1).Мы используем N для вычисления дисперсия населения, основанная на данных населения ; и мы используем (n — 1) для оценки дисперсии населения, на основе данных выборки . В этой задаче мы вычисляем дисперсия населения на основе данных о населении, поэтому в этом решении в знаменателе используется N.
Проблема 2
Простая случайная выборка состоит из четырех наблюдений: {1, 3, 5, 7}.На основе этого образца наблюдения, какова наилучшая оценка стандартное отклонение населения?
(А) 2
(В) 2,58
(К) 6
(г) 6,67
(E) Ничего из вышеперечисленного
Решение
Правильный ответ (B). Во-первых, нам нужно вычислить выборочное среднее.
х = Σx / п = (1 + 3 + 5 + 7) / 4 = 4
Затем мы подставляем все известные значения в формулу для стандартного отклонения образец, как показано ниже:
с = sqrt [Σ (x i — x) 2 / (n — 1)]
с = sqrt {[(1 — 4) 2 + (3-4) 2 + (5–4) 2 + (7–4) 2 ] / (4–1)}
с = sqrt {[(-3) 2 + (-1) 2 +
(1) 2 + (3) 2 ] / 3}
с = sqrt {[9 + 1 + 1 + 9] / 3} = sqrt (20/3) = sqrt (6.67) = 2,58
Примечание: Эта задача попросила нас оценить стандартное отклонение населения, на основе данных выборки . Для этого мы использовали (n — 1) в знаменатель формулы стандартного отклонения. Если бы проблема попросила нас вычислить стандартное отклонение совокупности на основе данных совокупности , мы бы использовали N в знаменателе.
Описание дистрибутивов | Статистическое мышление: имитационный подход к моделированию неопределенности
Одним из важных шагов в любом статистическом анализе является обобщение данных.Рекомендуется изучить как графическое, так и числовое обобщение ваших данных. Эти резюме часто являются частью доказательств, которые исследователи используют для подтверждения любых выводов, сделанных на основе данных. Они также позволяют исследователям обнаруживать структуру, которая в противном случае могла бы быть упущена из виду в фактически собранных необработанных данных. Наконец, как графические, так и числовые сводки данных часто указывают на другие анализы, которые могут быть выполнены с данными.
После того, как для исследования собраны необработанные данные, бывает сложно извлечь из них какой-либо смысл.Например, Google нередко сталкивается с миллионами дел. Как может Google — или любой исследователь в этом отношении — перейти от всех этих необработанных данных к чему-то, что может помочь им ответить на их исследовательские вопросы?
Вместо того, чтобы рассматривать все эти случаи по отдельности, исследователи изучают данные коллективно, часто путем их построения. Это то, что подразумевается под графическим обзором данных; это буквально картина распределения.
Существует множество различных типов графиков, которые были созданы для графического обобщения данных.Каждый из них может предоставить несколько иное представление данных. Образно говоря, вы можете представить каждый из этих типов сюжета как отдельную фотографию одного и того же человека. Некоторые могут быть цветными, другие — черно-белыми. Некоторые могут быть сняты с разных точек зрения, ракурсов или расстояний. Хотя все фотографии «суммируют» одного и того же человека, вы можете заметить характеристики этого человека на некоторых фотографиях, которые не видны на других. Однако многие фотографии показывают то же самое.
Форма
Точечный график, предоставляемый TinkerPlots ™, очень полезен.Это позволяет нам очень легко резюмировать форму распределения. Форма используется для описания симметрии распределения. Как и следовало ожидать, симметричные распределения имеют одинаковую форму по обе стороны от центра. (Другой способ думать об этом заключается в том, что если вы сложите распределение в центре, свернутая половина распределения будет довольно хорошо совмещена с другой половиной.) Например, «колоколообразная» («приблизительно нормальная») распределения симметричны.
Когда распределение является асимметричным, оно называется перекошенным распределением .Распределение, показанное на рисунке 1, является асимметричным распределением. В этом распределении, похоже, есть более длинный хвост в правой части распределения. Поскольку хвост находится в правой части распределения, статистики сказали бы, что он «наклонен вправо» или «положительно наклонен». Аналогичным образом, распределение, которое направлено влево, «смещено влево» или «смещено отрицательно».
Рисунок 1: Это распределение смещено вправо или положительно.
Расположение
Помимо общей формы распределения, также полезно резюмировать местоположение распределения.Расположение распределения обеспечивает обобщение так называемого «типичного» значения для данных. «Типичное» значение можно оценить по графику распределения. Вы также можете использовать более формально рассчитанные итоги местоположения, такие как среднее значение, медиана или мода. Эти значения легко вычислить с помощью TinkerPlots ™.
При просмотре графика распределения аналитики данных часто принимают во внимание количество мод или «горбов», которые видны на графике распределения. Здесь концепция режима немного отличается (хотя и связана) с концепцией режима, которую вы, возможно, изучали на предыдущих курсах по математике или статистике.Режим распределения дает общее представление о часто встречающихся значениях или измерениях. Это может быть одно число, но много раз — нет. Например, первый горб распределения, показанный на рисунке ниже, предполагает, что значения около девяти очень распространены. Однако фактическое значение девяти может отображаться в данных только один или два раза.
Рисунок 2: Бимодальное распределение, показывающее два режима. Один режим около 9, а другой около 12.
Распределение может быть унимодальным (один режим), бимодальным (два режима), мультимодальным (много режимов) или однородным (без режимов).Показанное выше распределение является бимодальным — обратите внимание, что есть два горба. Равномерные распределения имеют примерно одинаковую частоту для всех возможных значений (они выглядят по существу плоскими) и, следовательно, не имеют мод.
Вариант
Третьей характеристикой распределения, которую следует резюмировать, является вариация. Обобщение вариации дает представление о том, насколько изменчивы данные. Одним из методов численного обобщения изменчивости данных является количественная оценка того, насколько близки наблюдения относительно «типичного» значения в среднем.Близки ли наблюдения по большей части к «типичному» значению? Далеко от «типичного» значения? Как близко?
Оказывается, форма распределения также помогает описать вариации данных. Например, колоколообразные распределения имеют большинство наблюдений, близких к «типичному» значению, а более экстремальные наблюдения отображаются как ниже, так и выше «типичного» значения (вариация одинакова по обе стороны от «типичного» значения. ). В то время как у асимметричных распределений есть много наблюдений рядом с «типичным» значением, но экстремальные значения отклоняются от этого значения только в одном направлении (данные по одной стороне от «типичного» значения больше, чем по другой).
Рисунок 3: Большинство наблюдений в этом распределении сгруппированы между 0 и 2. Есть некоторые наблюдения больше 2 (до 10), хотя они редки.
Одна вещь, которая влияет на вариацию, и которую следует описать, — это то, есть ли наблюдения, которые отличаются от других наблюдений. Часто эти наблюдения имеют очень большие или маленькие значения по сравнению с другими наблюдениями. Эти наблюдения называются потенциальных выбросов или крайних случаев .Например, в показанном ранее положительно искаженном распределении наблюдение со значением около 10, вероятно, будет рассматриваться как потенциальный выброс.
Собираем все вместе
Rotten Tomatoes — это веб-сайт, на котором собраны отзывы кинокритиков о фильмах. Веб-сайт отмечает каждый отзыв как положительный или отрицательный, а затем присваивает фильму оценку на основе процента положительных отзывов. Помимо оценок критиков, каждому фильму также присваивается оценка, основанная на отзывах широкой публики с использованием той же методологии (обзоры сведены в таблицу, так что оценка представляет собой процент положительных отзывов широкой публики).График, показанный ниже, показывает точечный график распределения оценок широкой публики за 134 фильма, выпущенные в 2009 году.
Рис. 4. Оценки 134 фильмов, выпущенных в 2009 году, на основе отзывов широкой публики. Оценки представляют собой процент положительных отзывов для каждого фильма.
Письменное описание распределения может выглядеть следующим образом:
Распределение оценок для этой выборки из 134 фильмов довольно симметрично. Средний балл для этих фильмов составляет около 60, что указывает на то, что типичный фильм, выпущенный в 2009 году, получил положительные отзывы около 60% публики.Распределение также указывает на то, что оценки фильмов различаются. Большинство фильмов в выборке имеют рейтинг от 35 до 85, что свидетельствует о больших расхождениях во мнении публики о качестве этих фильмов.
Обратите внимание, что описание включает в себя описание формы, расположения и вариации распределения. Он также включает контекст данных, в данном случае музыку к фильму. Это помогает читателю интерпретировать описание.
Коэффициент вариации
Значение и определение коэффициента вариации
Коэффициент вариации (CV) относится к статистической мере распределения точек данных в ряду данных вокруг среднего значения.Он представляет собой отношение стандартного отклонения к среднему значению. Коэффициент вариации — полезная статистика при сравнении степени вариации от одного ряда данных к другому, хотя средние значения значительно отличаются друг от друга.
Согласно Investopedia, CV позволяет определить предполагаемую волатильность по сравнению с суммой дохода, ожидаемой от инвестиций. Проще говоря, более низкое отношение стандартного отклонения к средней доходности указывает на лучшее соотношение риска и доходности.
Формула для коэффициента вариации
Рассчитанный как отношение стандартного отклонения к среднему, коэффициент вариации вычисляется по следующей формуле:
Коэффициент вариации = стандартное отклонение / ожидаемая доходность
Расчет коэффициента вариации
Основные этапы вычисления коэффициента вариации:
1. Вычислите среднее значение выборки, используя формулу μ = ‘x i / n, где n указывает количество точек данных x i в выборке, а общая сумма по всем значениям i.2] / 3 = 1,667.
3. Определите стандартное отклонение выборки, вычислив квадратный корень из результата, полученного на шаге 2. Затем разделите его на среднее значение выборки. Полученный таким образом результат — коэффициент вариации.
Чтобы продолжить вышеупомянутый пример, √ (1,667) /3,5 = 0,3689.
Приложения
Коэффициент вариации является общим в прикладных областях вероятности, таких как теория восстановления, теория массового обслуживания и теория надежности.В этих полях экспоненциальное распределение обычно более важно, чем нормальное распределение. Стандартное отклонение экспоненциального распределения эквивалентно его среднему значению, поэтому коэффициент вариации равен 1. Распределения с коэффициентом вариации меньше 1 считаются низко-дисперсионными, тогда как те, у которых CV больше 1 считаются высокой дисперсией.
Центральная тенденция и изменчивость — Социология 3112 — Кафедра социологии
Цели обучения
- Поймите и вычислите три способа определения центра распределения
- Понять и вычислить четыре способа дисперсии или изменчивости в распределении можно определить
- Поймите, как перекос и уровень измерения могут помочь определить, какие меры центральная тенденция и изменчивость наиболее подходят для данного распределения
Ключевые термины
Меры центральной тенденции: категорий или оценок, которые описывают, что является «средним» или «типичным» для данного распределения.К ним относятся мода, медиана и среднее значение.
Процентиль: балл, ниже которого падает определенный процент данного распределения.
Распределение с положительным перекосом: распределение с небольшим количеством чрезвычайно больших значений.
Распределение с отрицательным перекосом: распределение с очень низкими значениями.
Меры изменчивости: чисел, которые описывают разнообразие или дисперсию в распределении данного
Переменная.
Блок-диаграмма: графическое представление диапазона, межквартильного размаха и медианы данного
Переменная.
Режим
Режим — это категория с наибольшей частотой (или в процентах). Это не частота сама. Другими словами, если кто-то спросит у вас режим раздачи как показано ниже, ответом будет кокос, а НЕ 22.Возможно иметь больше, чем один режим в раздаче. Такие распределения считаются бимодальными (если есть два режима) или мультимодальный (если режимов больше двух). Распределения без чистый режим называется однородным. Режим не особо полезен, но есть единственная мера центральной тенденции, которую мы можем использовать с номинальными переменными. Ты найдешь почему это единственная подходящая мера для номинальных переменных, поскольку мы узнаем о медиана и среднее значение далее.
Любимые вкусы мороженого:
Кокос = 22
Шоколад = 15
Ваниль = 7
Клубника = 9
Медиана
Медиана — это самое среднее число. Другими словами, это число делит распределение ровно пополам, так что половина случаев выше медианы, и половина ниже.Он также известен как 50-й процентиль, и его можно вычислить для порядковые и интервальные / относительные переменные. Концептуально найти медиану довольно просто. и влечет за собой только упорядочение всех ваших наблюдений от наименьшего к наибольшему а затем найти то число, которое попадает в середину. Обратите внимание, что нахождение медианы требует сначала упорядочить все наблюдения от наименьшего к наибольшему. Вот почему медиана не является подходящей мерой центральной тенденции для номинальных переменных, поскольку номинальные переменные не имеют внутреннего порядка.(На практике определение медианы может проявите больше активности, особенно если у вас много наблюдений — см. ваш учебник для объяснения того, как найти медиану в таких ситуациях).
Некоторые из вас, вероятно, уже задаются вопросом: «Что будет, если у вас четное число? случаев? Тогда не будет среднего числа, верно? »Это очень проницательное наблюдение, и я рад, что вы спросили.Если в вашем наборе данных четное количество наблюдений, медиана будет среднее из двух крайних чисел. Например, для чисел 18, 14, 12, 8, 6 и 4 медиана равна 10 (12 + 8 = 20; 20/2 = 10).
Одним из преимуществ медианы является то, что она не чувствительна к выбросам. Выброс — это наблюдение, которое находится на ненормальном расстоянии от других значений в выборке. Наблюдения которые значительно больше или меньше других в выборке, могут повлиять на некоторые статистических показателей таким образом, чтобы они вводили в заблуждение, но медиана невосприимчив к ним.Другими словами, не имеет значения, будет ли наибольшее число 20 или 20,000; он по-прежнему считается только одним числом. Учтите следующее:
Распределение 1: 1, 3, 5, 7, 20
Распределение 2: 1, 3, 5, 7, 20,000
Эти два распределения имеют идентичные медианы, хотя в распределении 2 очень большой выброс, который в конечном итоге приведет к значительному искажению среднего значения, поскольку мы увидеть через мгновение.
Среднее
Среднее — это то, что люди обычно называют «средним». Это высшая мера центральной тенденции, я имею в виду, что он доступен для использования только с интервалом / соотношением переменные. Среднее значение учитывает ценность каждого наблюдения и, таким образом, обеспечивает самая информативная из всех мер центральной тенденции. Однако в отличие от медианы среднее значение чувствительно к выбросам.Другими словами, один чрезвычайно высокий (или низкий) значение в вашем наборе данных может значительно повысить (или понизить) среднее значение. Среднее, часто отображается как переменная x или y с линией над ней (произносится как «x-bar» или «y-bar»), представляет собой сумму всех баллов, деленную на общее количество баллов. В статистических обозначение, мы бы записали его следующим образом:
В этом уравнении — среднее значение, X — значение каждого случая, а N — общее количество дел.Сигма (Σ) просто говорит нам сложить все оценки вместе. Тот факт, что вычисление среднего требует сложения и деления, является самой причиной его нельзя использовать ни с номинальными, ни с порядковыми переменными. Мы не можем вычислить среднее для расы (белый + белый + черный / 3 =?) больше, чем мы можем рассчитать среднее значение за год в школе (первокурсник + первокурсник + старший / 3 =?)
Процентили
Процентиль — это число, ниже которого попадает определенный процент распределения.Например, если вы набрали 90-й процентиль по тесту, 90 процентов учащихся кто прошел тест набрал меньше вас. Если вы набрали 72-й процентиль в тесте, 72 процента студентов, сдавших тест, набрали меньше очков. Если забил в 5-м процентиль теста, возможно, этот предмет не для вас. Как вы помните, медиана падает на 50-м процентиле. Пятьдесят процентов наблюдений попадают под него.
Симметричные и асимметричные распределения
Симметричное распределение — это распределение, в котором среднее значение, медиана и мода являются одно и тоже. С другой стороны, асимметричное распределение — это распределение с экстремальными значениями. с одной или другой стороны, которые отталкивают медианное значение от среднего в одном направлении или другой. Если среднее значение больше медианы, говорят, что распределение быть смещенным в положительную сторону.Другими словами, существует очень большое значение, которое «тянет» среднее значение к верхнему концу распределения. Если среднее значение меньше, чем медиана, распределение считается отрицательно смещенным. Другими словами, есть чрезвычайно малое значение, которое «подтягивает» среднее значение к нижней границе распределения. Распределение доходов обычно имеет положительный перекос из-за небольшого количества люди, которые зарабатывают безбожные деньги.Рассмотрим (по общему признанию датированный) случай Футболисты Высшей лиги как крайний пример. Средняя годовая зарплата для MLS игрок в 2010 году составлял около 138000 долларов, но средняя годовая зарплата составляла всего около 53000 долларов. Среднее значение было почти в три раза больше медианы, благодаря немалому часть зарплаты Дэвида Бекхэма в 12 миллионов долларов.
При попытке решить, какую меру центральной тенденции использовать, вы должны учитывать как уровень измерения, так и перекос.Это не так для номинальных и порядковых переменные. Если переменная номинальная, очевидно, что мода является единственной мерой центральной склонность к использованию. Если переменная порядковая, лучше всего подходит медиана. потому что он предоставляет больше информации об образце, чем режим. Но если переменная — интервал / соотношение, вам нужно определить, является ли распределение симметричным или перекошенный.Если распределение симметрично, среднее значение является лучшим показателем центрального тенденция. Если распределение искажено в положительную или отрицательную сторону, медиана точнее. В качестве примера того, почему среднее значение может быть не лучшим измерителем центрального тенденцию к неравномерному распределению, рассмотрим следующий отрывок из книги Чарльза Уилана Обнаженная статистика: снимая страх с данных (2013):
«Среднее или среднее значение имеет некоторые проблемы, а именно то, что оно склонно к искажение «выбросами», то есть наблюдениями, находящимися дальше от центра.Чтобы понять эту концепцию, представьте, что десять парней сидят на барных стульях. в питейном заведении среднего класса в Сиэтле; каждый из этих парней зарабатывает 35000 долларов в год, что составляет средний годовой доход для группы 35 000 долларов. Билл Гейтс идет в бар с говорящим попугаем, сидящим на его плече. (У попугая нет ничего это связано с примером, но это как бы приправляет вещи.) Предположим ради Например, годовой доход Билла Гейтса составляет 1 миллиард долларов. Когда Билл сидит на одиннадцатом барном стуле средний годовой доход посетителей бара возрастает до около 91 миллиона долларов. Очевидно, что никто из первых десяти пьющих не стал богаче (хотя было бы разумно ожидать, что Билл Гейтс купит один или два раунда). Если бы я описал завсегдатаи этого бара имеют средний годовой доход в размере 91 миллиона долларов, говорится в сообщении. будет как статистически правильным, так и сильно вводящим в заблуждение [Примечание: медиана будет оставаться без изменений].Это не бар, где тусуются мультимиллионеры; это бар, где группа парней с относительно низкими доходами сидит рядом с Биллом Гейтсом и его говорящий попугай «.
Меры изменчивости
Помимо определения показателей центральной тенденции, нам может потребоваться подвести итоги степень изменчивости нашего распределения.Другими словами, нам нужно определить, имеют ли наблюдения тенденцию группироваться вместе или они имеют тенденцию к распространению вне. Рассмотрим следующий пример:
Пример 1: {0, 0, 0, 0, 25}
Пример 2: {5, 5, 5, 5, 5}
Обе эти выборки имеют идентичные средства (5) и одинаковое количество наблюдений. (n = 5), но степень вариации между двумя образцами значительно различается.Образец 2 не имеет вариабельности (все оценки одинаковы), тогда как Образец 1 имеет относительно больше (один случай существенно отличается от других четырех). В этом курсе мы рассмотрим четыре показателя изменчивости: диапазон, межквартильный диапазон (IQR), дисперсия и стандартное отклонение.
Диапазон
Диапазон — это разница между наивысшим и наименьшим баллами в наборе данных и это простейшая мера распространения.Мы вычисляем диапазон, вычитая наименьшее значение от наибольшего значения. В качестве примера рассмотрим следующий набор данных:
23 | 56 | 45 | 65 | 69 | 55 | 62 | 54 | 85 | 25 |
Максимальное значение — 85, минимальное — 23.Это дает нам диапазон 62 (85 — 23 = 62). Хотя использование диапазона в качестве меры изменчивости мало что говорит нам, он дает нам некоторую информацию о том, насколько далеко друг от друга самые низкие и самые высокие оценки находятся.
Квартили и межквартильный размах
«Квартиль» — это еще одно слово, которое специалисты по статистике используют, чтобы почувствовать себя значимыми. Это в основном означает «четверть» или «четверть».»Футбольный матч состоит из четырех квартилей, как и Twix королевского размера. Найти квартили распределения так же просто, как сломать это до четвертых. Каждая четвертая содержит 25 процентов от общего количества наблюдений.
Квартили делят упорядоченный набор данных на четыре равные части. Ценности, разделяющие каждая часть называется первым, вторым и третьим квартилями; и они обозначаются на Q1, Q2 и Q3 соответственно.
Q1 — это «среднее» значение в первой половине упорядоченного по рангу набора данных.
Q2 — это медианное значение набора данных
Q3 — это «среднее» значение второй половины ранжированного набора данных
Q4 технически будет самым большим значением в наборе данных, но мы игнорируем это при расчете
IQR (мы уже имели дело с ним, когда рассчитывали диапазон).
Таким образом, межквартильный размах равен Q3 минус Q1 (или 75 процентиль минус 25-й процентиль, если вы предпочитаете так думать).В качестве примера рассмотрим следующие числа: 1, 3, 4, 5, 5, 6, 7, 11. Q1 — среднее значение в первом половина набора данных. Поскольку в первой половине есть четное количество точек данных в наборе данных среднее значение является средним из двух средних значений; это, Q1 = (3 + 4) / 2 или Q1 = 3,5. Q3 — среднее значение во второй половине данных. набор. Опять же, поскольку вторая половина набора данных имеет четное количество наблюдений, среднее значение — это среднее из двух средних значений; то есть Q3 = (6 + 7) / 2 или Q3 = 6.5. Межквартильный размах составляет Q3 минус Q1, поэтому IQR = 6,5 — 3,5 = 3.
Коробчатые участки
Ящичковая диаграмма (также известная как диаграмма ящиков и усов) разбивает набор данных на квартили. Тело коробчатой диаграммы состоит из «коробки» (отсюда и название), которая идет от от первого квартиля (Q1) до третьего квартиля (Q3). Внутри рамки горизонтальная линия отображается в точке Q2, которая обозначает медиану набора данных.Две вертикальные линии, известные как усы, простираются сверху и снизу коробки. Нижний ус идет от Q1 до наименьшего значения в наборе данных, а верхний ус идет от Q3 до наибольшее значение. Ниже приведен пример прямоугольного графика с положительным перекосом с различными компоненты помечены.
Выбросы — это экстремальные значения, которые по той или иной причине исключаются. из набора данных.Если набор данных включает один или несколько выбросов, они отображаются на графике. отдельно точками на графике. На диаграмме выше есть несколько выбросов внизу.
Как интерпретировать коробчатую диаграмму
Горизонтальная линия, проходящая через центр прямоугольника, указывает, где медиана падает. Кроме того, коробчатые диаграммы отображают две общие меры изменчивости или разброса. в наборе данных: диапазон и IQR.Если вас интересует распространение всех данных, он представлен на диаграмме вертикальным расстоянием между наименьшими значение и наибольшее значение, включая любые выбросы. Средняя половина набора данных попадает в межквартильный диапазон. На прямоугольной диаграмме представлен межквартильный размах. по ширине коробки (Q3 минус Q1).
Разница
Дисперсия — это мера изменчивости, которая показывает, насколько далеко каждое наблюдение падает от среднего значения распределения.В этом примере мы будем использовать следующие пять цифр, которые представляют собой мои ежемесячные покупки комиксов за последние пять месяцев:
2, 3, 5, 6, 9
Формула расчета дисперсии обычно записывается так:
Это уравнение выглядит устрашающе, но оно не так уж и плохо, если разбить его на его составные части.S2x — это обозначение, используемое для обозначения дисперсии выборки. Эта гигантская сигма (Σ) является знаком суммы; это просто означает, что мы собираемся добавлять вещи все вместе. X представляет каждое из наших наблюдений, а x с линией над ним. (часто называемый «x-bar») представляет собой среднее значение нашего распределения. Заглавная буква «N» на внизу — общее количество наблюдений. По сути, эта формула говорит нам вычесть среднее значение из каждого из наших наблюдений, возвести разницу в квадрат, добавить их все вместе и разделить на N-1.Давайте сделаем пример, используя приведенные выше числа.
1. Первым шагом в вычислении дисперсии является определение среднего значения распределения. В этом случае среднее значение равно 5 (2 + 3 + 5 + 6 + 9 = 25; 25/5 = 5).
2. Второй шаг — вычесть среднее значение (5) из каждого наблюдения:
2-5 = -3
3-5 = -2
5-5 = 0
6-5 = 1
9-5 = 4
Обратите внимание: мы можем проверить нашу работу после этого шага, сложив все наши ценности вместе.Если они в сумме равны нулю, мы знаем, что находимся на правильном пути. Если они что-то складывают помимо нуля, нам, вероятно, следует еще раз проверить нашу математику (-3 + -2 + 0 + 1 + 4 = 0, мы золотые).
3. В-третьих, мы возводим в квадрат каждый из этих ответов, чтобы избавиться от отрицательных чисел:
(-3) 2 = 9
(-2) 2 = 4
(0) 2 = 0
(1) 2 = 1
(4) 2 = 16
4.В-четвертых, складываем их все вместе:
9 + 4 + 0 + 1 + 16 = 30
5. Наконец, делим на N-1 (общее количество наблюдений равно 5, поэтому 5-1 = 4)
30/4 = 7,5
После всех этих довольно утомительных вычислений остается одно число, которое быстро и лаконично резюмирует количество изменчивости в нашем распределении. В чем больше число, тем больше вариативность в нашем распределении.Пожалуйста, обрати внимание: отклонение никогда не может быть отрицательным. Если вы получите дисперсию меньше, чем ноль, вы сделали что-то не так.
Стандартное отклонение
Однако есть одно ограничение на использование дисперсии в качестве единственной меры изменчивости. Когда мы возводим числа в квадрат, чтобы избавиться от негативов (шаг 3), мы также случайно квадрат нашей единицы измерения.Другими словами, если мы говорим о милях, мы случайно превратили нашу единицу измерения в квадратные мили. Если бы мы говорили насчет комиксов, мы случайно превратили нашу единицу измерения в комиксы в квадрате (что, разумеется, не всегда имеет смысл). Чтобы Решив эту проблему, мы вычисляем стандартное отклонение. Формула стандарта отклонение выглядит так:
Другими словами, вычислить стандартное отклонение так же просто, как взять квадрат корень дисперсии, обращая квадрат, который мы сделали при вычислении дисперсии.В нашем примере стандартное отклонение равно квадратному корню из 7,5 или 2,74. Интерпретация не меняется; большое стандартное отклонение указывает на большее изменчивость, тогда как небольшое стандартное отклонение указывает на относительно небольшой количество изменчивости. Как и в случае с дисперсией, стандартное отклонение составляет всегда позитивный.
Помните: ключевое различие между дисперсией и стандартным отклонением — это единица измерения.Мы вычисляем стандартное отклонение, чтобы положить нашу переменную обратно в исходную метрику. «Мили в квадрате» снова равняются милям, а «Комиксы в квадрате» снова стали комиксами.
Основные моменты
- Меры центральной тенденции говорят нам, что общего или типичного в нашей переменной.
- Три показателя центральной тенденции — это мода, медиана и среднее значение.
- Режим используется почти исключительно с данными номинального уровня, так как это единственная мера центральной тенденции, доступной для таких переменных. Медиана используется с порядковым номером данные или когда переменная уровня интервала / отношения искажена (вспомните пример Билла Гейтса). Среднее значение можно использовать только с данными уровня интервала / отношения.
- Меры изменчивости — это числа, которые описывают, насколько вариативность или разнообразие есть в раздаче.
- Четыре меры изменчивости — это диапазон (разница между большим и наименьших наблюдений), межквартильный размах (разница между 75-м и 25 процентили) дисперсия и стандартное отклонение.
- Дисперсия и стандартное отклонение — два тесно связанных показателя изменчивости. для переменных уровня интервала / отношения, которые увеличиваются или уменьшаются в зависимости от того, насколько близко наблюдения сгруппированы вокруг среднего.
- Меры центральной тенденции и изменчивости в SPSS
Чтобы SPSS рассчитал для вас меры центральной тенденции и изменчивости, щелкните «Анализировать», «Описательная статистика», затем «Частоты». Меры центральной тенденции и изменчивость также можно рассчитать, нажав на «Описательные» или «Исследовать». но «Частоты» дает вам больше контроля и предлагает наиболее полезные варианты выбора. из.Открывшееся диалоговое окно должно быть вам хорошо знакомо. Как ты это сделал при расчете частотных таблиц переместите переменные, для которых вы хотите вычислить меры центральной тенденции и изменчивости в правой части коробка. Вы можете снять флажок «Отображать частотные таблицы», если не хотите видеть любые таблицы и предпочел бы видеть только статистику. Затем нажмите кнопку справа помечено как «Статистика.»В открывшемся диалоговом окне вы можете выбрать как сколько угодно статистических данных (Примечание: SPSS использует термин «Дисперсия», а не «Изменчивость», но эти два слова синонимичны). Также имейте в виду, что SPSS рассчитает статистику для любой переменной независимо от уровня измерения. Это например, вычислит среднее значение для расы или пола, даже если это не имеет смысла как бы то ни было.Самец + самец + самка / 3 = 0,66? Совершенно нелогично. Это один из многих обстоятельства, в которых вам придется быть умнее, чем пакет анализа данных ты используешь. То, что SPSS позволяет вам что-то делать, не обязательно означает это хорошая идея.
При расчете показателей изменчивости иногда полезно включить рамку участок. Для этого нажмите «Графики», затем «Устаревшие диалоги» и выберите «Коробчатая диаграмма».» В виде в случае с графиками, которые вы создали в предыдущей главе, у вас будет несколько варианты выбора. Вообще говоря, вам понадобится одна коробчатая диаграмма для каждого переменной, поэтому выберите «Сводные данные по отдельным переменным». Переместите переменные, которые вы хотите, чтобы в пустом поле справа отображались блочные диаграммы, и нажмите OK. Если вы захотите отредактировать коробчатые графики, вы можете сделать это почти так же, как вы это делали. графики в главе 2.Вот видео-пошаговое руководство:
Упражнения
- Выберите три переменные из любого из трех наборов данных (одну номинальную, одну порядковую и один интервал / соотношение) и рассчитайте все соответствующие меры центральной тенденции для каждый.
- Используя ADD Health Dataset, NIS Dataset и World Values Survey, рассчитайте стандартное отклонение, дисперсия и диапазон для переменной «ВОЗРАСТ» в каждом.Какой опрос имеет наибольшую вариативность в возрасте? В каком опросе меньше всего различий по возрасту? (Примечание: для этого вам потребуется открыть набор данных, вычислить меры изменчивости и затем откройте следующий набор данных. Результаты каждого из них останутся в вашем окне «Вывод». независимо от того, какой набор данных у вас открыт в данный момент).
- Выберите любую переменную отношения интервалов и используйте ее для создания прямоугольной диаграммы.Теперь интерпретируйте коробчатый сюжет. Каков приблизительный диапазон, IQR и медиана этой переменной?
Расчет диапазона, IQR, дисперсии, стандартного отклонения
Вариабельность описывает, насколько далеко друг от друга находятся точки данных и от центра распределения. Помимо показателей центральной тенденции, показатели изменчивости дают вам описательную статистику, которая обобщает ваши данные.
Вариабельность также называется разбросом, разбросом или дисперсией.Чаще всего измеряется следующим образом:
Почему изменчивость имеет значение?
В то время как центральная тенденция, или среднее значение, говорит вам, где находится большинство ваших точек, изменчивость суммирует, насколько далеко они друг от друга. Это важно, потому что это говорит вам, имеют ли точки тенденцию быть сгруппированными вокруг центра или более широко разбросанными.
Низкая изменчивость идеальна, потому что это означает, что вы можете лучше предсказать информацию о популяции на основе данных выборки. Высокая вариабельность означает, что значения менее согласованы, поэтому делать прогнозы труднее.
Наборы данных могут иметь одну и ту же центральную тенденцию, но разные уровни изменчивости, или наоборот. Если вы знаете только центральную тенденцию или изменчивость, вы ничего не можете сказать о другом аспекте. Оба они вместе дают вам полное представление о ваших данных.
Пример: изменчивость в нормальном распределении Вы исследуете количество времени, которое ежедневно проводят за телефоном разные группы людей.Используя простые случайные выборки, вы собираете данные из 3 групп:
- Образец А: старшеклассники,
- Образец Б: студенты колледжа,
- Образец C: взрослые сотрудники, занятые полный рабочий день.
У всех трех ваших образцов среднее время использования телефона — 195 минут или 3 часа 15 минут. Это значение по оси X, где находятся вершины кривых.
Хотя данные соответствуют нормальному распределению, каждая выборка имеет разный разброс. Образец A имеет наибольшую вариабельность, а образец C — наименьшую вариабельность.
Диапазон
Диапазон показывает разброс ваших данных от наименьшего до наибольшего значения в распределении.Это самый простой способ измерить изменчивость.
Чтобы найти диапазон, просто вычтите наименьшее значение из наибольшего значения в наборе данных.
Пример диапазона У вас есть 8 точек данных из образца A.| Данные (минуты) | 72 | 110 | 134 | 190 | 238 | 287 | 305 | 324 |
|---|
Наивысшее значение ( H ) — 324 , а наименьшее ( L ) — 72 .
R = H — L
R = 324 — 72 = 252
Диапазон ваших данных: 252 минуты .
Поскольку используются только 2 числа, диапазон зависит от выбросов и не дает никакой информации о распределении значений. Лучше всего использовать его в сочетании с другими мерами.
Что может сделать корректура для вашей статьи?
РедакторыScribbr не только исправляют грамматические и орфографические ошибки, но и укрепляют ваше письмо, убеждаясь в том, что в вашей статье нет нечетких слов, лишних слов и неуклюжих фраз.
См. Пример редактирования
Межквартильный размах
Межквартильный размах дает вам разброс середины вашего распределения.
Для любого распределения, упорядоченного от меньшего к большему, межквартильный диапазон содержит половину значений. В то время как первый квартиль (Q1) содержит первые 25% значений, четвертый квартиль (Q4) содержит последние 25% значений.
Межквартильный размах — это третий квартиль (Q3) минус первый квартиль (Q1). Это дает нам диапазон средней половины набора данных.
Пример межквартильного размаха Чтобы найти межквартильный размах ваших 8 точек данных, вы сначала находите значения в Q1 и Q3.Умножьте количество значений в наборе данных (8) на 0,25 для 25-го процентиля (Q1) и на 0,75 для 75-го процентиля (Q3).
Позиция Q1: 0,25 x 8 = 2
Q3 Позиция: 0.75 х 8 = 6
Q1 — это значение во второй позиции, то есть 110 . Q3 — это значение на 6-й позиции, которое составляет 287 .
IQR = Q3 — Q1
IQR = 287 — 110 = 177
Межквартильный диапазон ваших данных 177 минут .
Как и диапазон, межквартильный диапазон использует при вычислении только 2 значения. Но на IQR меньше влияют выбросы: 2 значения взяты из средней половины набора данных, поэтому они вряд ли будут крайними значениями.
IQR дает последовательную меру изменчивости как для искаженного, так и для нормального распределения.
Пятизначная сводка
Каждая раздача может быть организована с помощью сводки из пяти номеров :
- Наименьшее значение
- Q1: 25-й процентиль
- Q2: медиана
- Q3: 75-й процентиль
- Наивысшее значение (Q4)
Эти пятизначные сводки можно легко визуализировать с помощью диаграмм в виде ящиков и усов.
Пример графика в виде прямоугольников и усов Для каждого из наших образцов горизонтальные линии в прямоугольнике показывают Q1, медианное значение и Q3, в то время как усы в конце показывают самые высокие и самые низкие значения.Стандартное отклонение
Стандартное отклонение — это средняя величина изменчивости в вашем наборе данных.
Он сообщает вам, в среднем, насколько далеко каждая оценка отличается от среднего значения. Чем больше стандартное отклонение, тем более изменчивым является набор данных.
Есть шесть шагов для определения стандартного отклонения вручную:
- Перечислите каждую оценку и найдите их среднее значение.
- Вычтите среднее значение из каждой оценки, чтобы получить отклонение от среднего.
- Возведите в квадрат каждое из этих отклонений.
- Сложите все квадраты отклонений.
- Разделите сумму квадратов отклонений на n — 1 (для выборки) или N (для генеральной совокупности).
- Найдите квадратный корень из найденного числа.
| Шаг 1: Данные (минуты) | Шаг 2: Отклонение от среднего значения | Шаги 3 + 4: Квадратное отклонение |
|---|---|---|
| 72 | 72 — 207.5 = -135,5 | 18360,25 |
| 110 | 110–207,5 = -97,5 | 9506,25 |
| 134 | 134 — 207,5 = -73,5 | 5402,25 |
| 190 | 190 — 207,5 = -17,5 | 306,25 |
| 238 | 238 — 207,5 = 30,5 | 930,25 |
| 287 | 287 — 207,5 = 79,5 | 6320,25 |
| 305 | 305 — 207.5 = 97,5 | 9506,25 |
| 324 | 324 — 207,5 = 116,5 | 13572,25 |
| Среднее значение = 207,5 | Сумма = 0 | Сумма квадратов = 63904 |
n — 1 = 7
63904/7 = 9129,14
Пример стандартного отклоненияс = √9129.14 = 95,54
Стандартное отклонение ваших данных — 95,54 . Это означает, что в среднем каждая оценка отклоняется от среднего на 95,54 балла.
Формула стандартного отклонения для совокупностей
Если у вас есть данные по генеральной совокупности, используйте формулу стандартного отклонения генеральной совокупности:
| Формула | Пояснение |
|---|---|
|
Формула стандартного отклонения для образцов
Если у вас есть данные из выборки, используйте формулу стандартного отклонения выборки:
| Формула | Пояснение |
|---|---|
|
Зачем использовать
n — 1 для стандартного отклонения выборки?Выборки используются для статистических выводов о популяции, из которой они произошли.
Если у вас есть данные о населении, вы можете получить точное значение стандартного отклонения населения. Поскольку вы собираете данные от каждого члена популяции, стандартное отклонение отражает точную величину изменчивости в вашем распределении, генеральной совокупности.
Но когда вы используете данные выборки, стандартное отклонение вашей выборки всегда используется как оценка стандартного отклонения генеральной совокупности. Использование n в этой формуле дает вам тенденциозную оценку, которая постоянно недооценивает изменчивость.
Уменьшение выборки n до n — 1 делает стандартное отклонение искусственно большим, давая вам консервативную оценку изменчивости.
Хотя это не беспристрастная оценка, это менее смещенная оценка стандартного отклонения: лучше переоценить, чем недооценить изменчивость в выборках.
Разница между смещенными и консервативными оценками стандартного отклонения становится намного меньше, когда у вас большой размер выборки.
Разница
Дисперсия — это среднее квадратов отклонений от среднего. Отклонение от среднего — это то, насколько далеко результат от среднего.
Дисперсия — это квадрат стандартного отклонения. Это означает, что единицы отклонения намного больше, чем у типичного значения набора данных.
Хотя интуитивно интерпретировать число дисперсии сложнее, важно рассчитать дисперсию для сравнения различных наборов данных в статистических тестах, таких как ANOVA.
Дисперсия отражает степень разброса набора данных. Чем больше разброс данных, тем больше отклонение от среднего.
Пример дисперсии Чтобы получить дисперсию, возведите стандартное отклонение в квадрат.с = 95,5
с 2 = 95,5 x 95,5 = 9129,14
Разница ваших данных — 9129,14.
Чтобы найти отклонение вручную, выполните все шаги для стандартного отклонения, кроме последнего шага.
Формула дисперсии для популяций
| Формула | Пояснение |
|---|---|
|
Формула отклонения для образцов
| Формула | Пояснение |
|---|---|
|
Смещенная и несмещенная оценки дисперсии
Беспристрастная оценка в статистике — это оценка, которая не дает постоянно ни высоких, ни низких значений — у нее нет систематической ошибки.
Как и для стандартного отклонения, существуют разные формулы для дисперсии генеральной совокупности и выборки. Но хотя объективной оценки стандартного отклонения нет, есть оценка дисперсии выборки.
Если в формуле дисперсии выборки используется выборка n , дисперсия выборки будет смещена в сторону меньших чисел, чем ожидалось. Уменьшение выборки n до n — 1 искусственно увеличивает дисперсию.
В этом случае смещение не только снижается, но и полностью устраняется.Формула выборочной дисперсии дает совершенно объективные оценки дисперсии.
Так почему же стандартное отклонение выборки не является также объективной оценкой?
Это потому, что стандартное отклонение выборки происходит от нахождения квадратного корня из дисперсии выборки. Поскольку извлечение квадратного корня не является линейной операцией, такой как сложение или вычитание, несмещенность формулы дисперсии выборки не переносится на формулу стандартного отклонения выборки.
Каков наилучший показатель изменчивости?
Наилучший показатель изменчивости зависит от вашего уровня измерения и распределения.
Уровень измерения
Для данных, измеренных на порядковом уровне, размах и межквартильный размах являются единственными подходящими показателями изменчивости.
Для более сложных интервалов и уровней отношения также применимы стандартное отклонение и дисперсия.
Распределение
Для нормального распределения можно использовать все меры. Стандартное отклонение и дисперсия предпочтительнее, потому что они учитывают весь ваш набор данных, но это также означает, что на них легко влияют выбросы.
Для асимметричных распределений или наборов данных с выбросами лучше всего подходит межквартильный размах. На него меньше всего влияют экстремальные значения, поскольку он фокусируется на разбросе в середине набора данных.

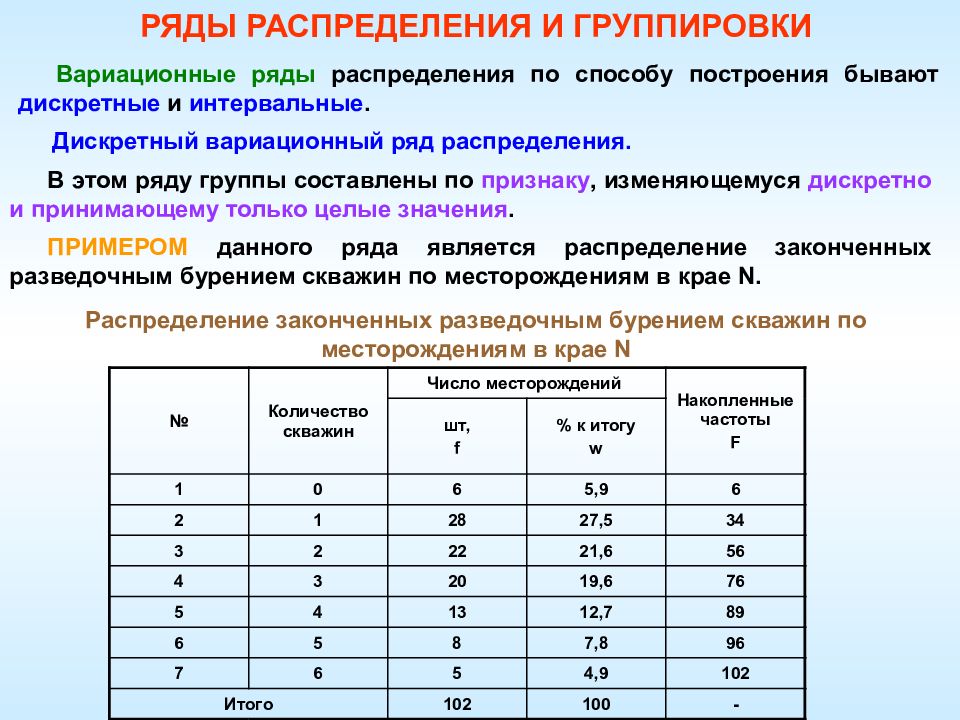 От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.
От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.
Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.
Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.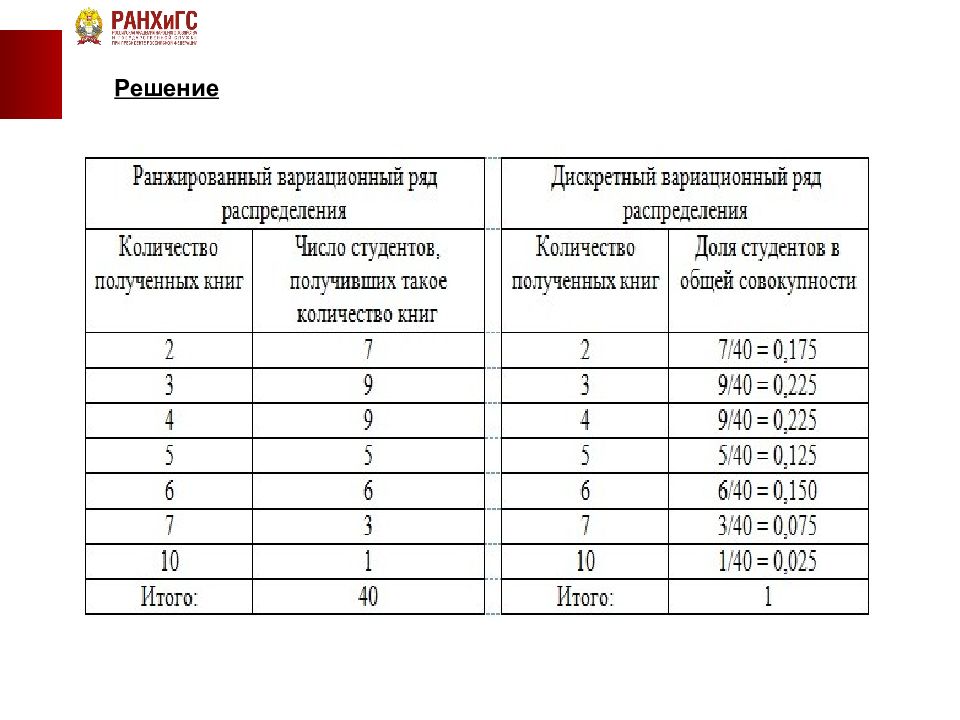


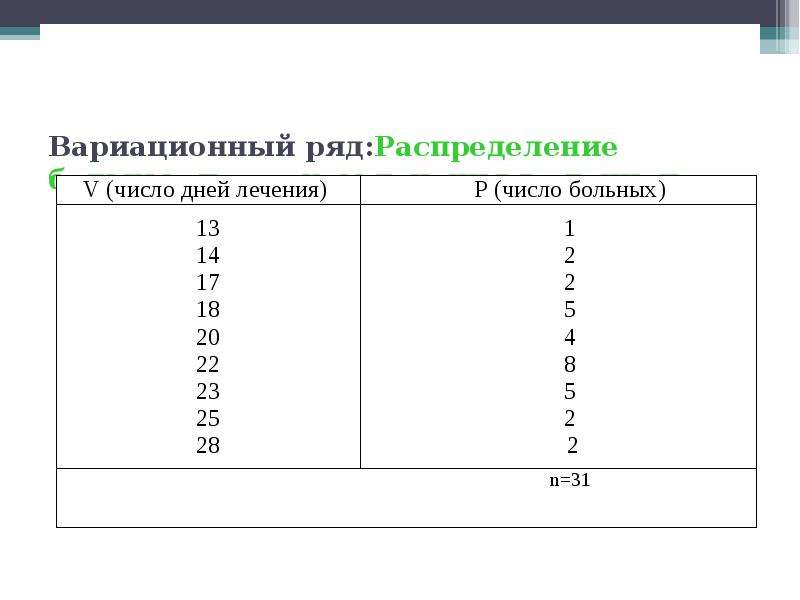 Д., увеличение количества пассажиров в выходные и т. д. Сезонные колебания вызваны климатом, социальными обычаями, религиозной деятельностью и т.д.
Д., увеличение количества пассажиров в выходные и т. д. Сезонные колебания вызваны климатом, социальными обычаями, религиозной деятельностью и т.д.
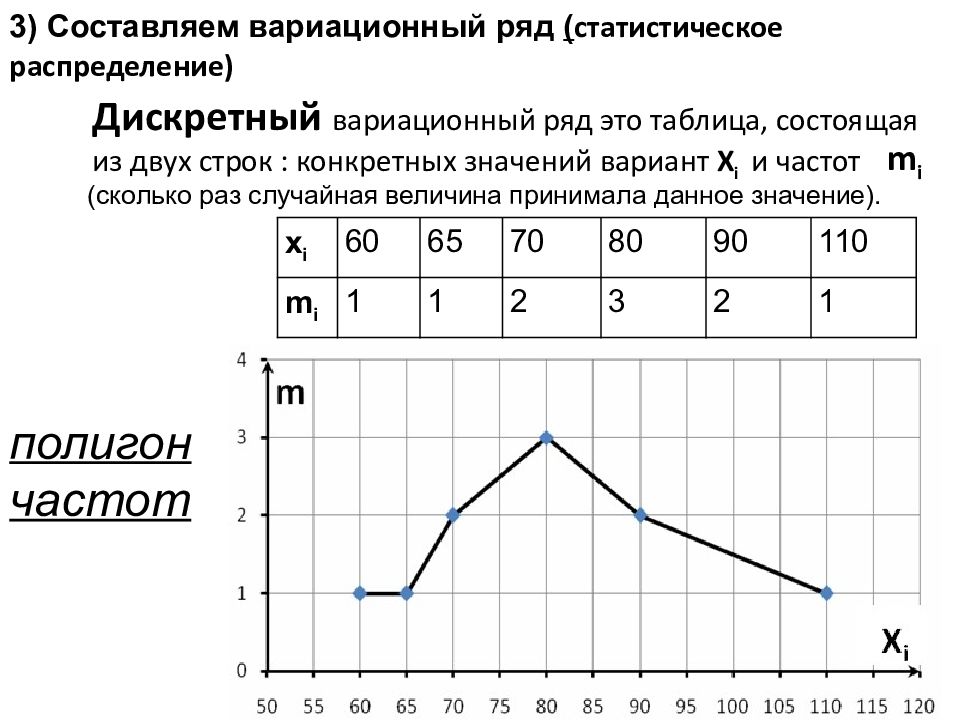 Получение средних значений за определенный период — простой способ обнаружить тенденцию в сезонных данных. Изменение средних значений со временем свидетельствует о наличии тренда в данном ряду, хотя существуют более формальные тесты для обнаружения тренда во временных рядах .
Получение средних значений за определенный период — простой способ обнаружить тенденцию в сезонных данных. Изменение средних значений со временем свидетельствует о наличии тренда в данном ряду, хотя существуют более формальные тесты для обнаружения тренда во временных рядах . д.
д.