Уравнение квадрата: Формула квадрата?

Как решать квадратные уравнения? Формулы и Примеры

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

• x² — 2x + 6 = 0
• x² — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x² ), а значит уравнение называется приведенным.

• 2x² − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Запоминаем!

У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.

Пример 1. Превратим неприведенное уравнение: 8x² + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x

2 + 2,5x — 1,125 = 0.

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax² + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax² + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:
Если b = 0, то квадратное уравнение принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0. Если c = 0, то квадратное уравнение выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2 + bx = 0. Если b = 0 и c = 0, то квадратное уравнение выглядит так ax2 = 0. Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax² + c = 0, при b = 0;
• ax² + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax

² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0

2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x² = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x² = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6x² = 0

   x²

   = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax

² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax

2 + c = 0:

• перенесем c в правую часть: ax² = — c,
• разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x

2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению х2= -c/a, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8x² + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8x² = — 5

2. Разделим обе части на 8:

   x² = — 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x² + 5 = 0 не имеет корней.

Как решить уравнение ax

² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5x² + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = 0,125,
   х = 0,125/0,5

4. Разделить:

   х = 0,25

5. Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2).

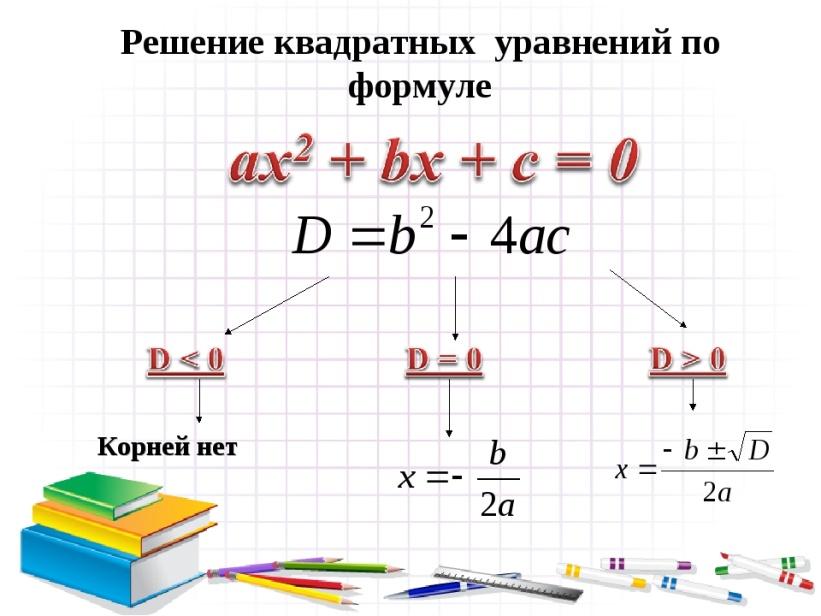
Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b² − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

, .

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b²−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x² + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 28² — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x² = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6x² = 0 | *(-1)

   6x² — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6x² = 54

   х² = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x²— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x²— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x²— 10 = 39

   x²= 39 + 10

   x²= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x²— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)² — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b² — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax² + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)²— 4ac = 4n² — 4ac = 4(n²— ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n² -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n²— ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n²— ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Формула Виета

---

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x² + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

 

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x² + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x² − 6x + 8 = 0.

Как решаем:

1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

   Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

   Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

3. Значит числа 4 и 2 — корни уравнения x² − 6x + 8 = 0. p>

    

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x² — 4 x — 6 = 0, чем 1100x² — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x² — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x²— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x² — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов.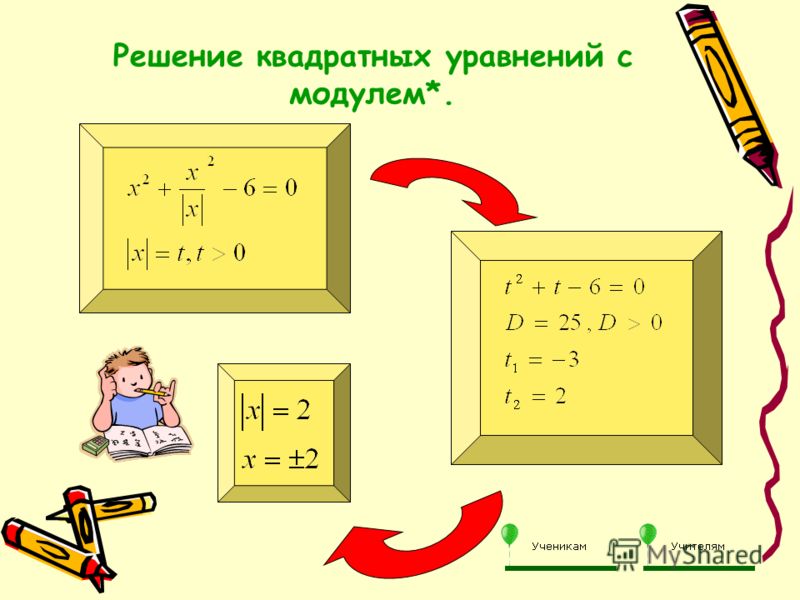 Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x² + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x²— 3x + 7 = 0 перейти к решению 2x² + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x²— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Квадрат. Формулы и свойства квадрата

Навигация по странице: Определение квадрата Основные свойства квадрата Диагональ квадрата Периметр квадрата Площадь квадрата Окружность описанная вокруг квадрата Окружность вписанная в квадрат

Определение.

Квадрат — это четырехугольник у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.

Рис. 1		Рис.2

Основные свойства квадрата

Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.

1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:

AB = BC = CD = AD

2. Противоположные стороны квадрата параллельны:

AB||CD,   BC||AD

3. Все четыре угла квадрата прямые:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Сумма углов квадрата равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

5. Диагонали квадрата имеют одинаковой длины:

AC = BD

6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры

7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:

AC┴BD		AO = BO = CO = DO =	d
			2

8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности

9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:

ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°

10. Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:

ΔAOB = ΔBOC = ΔCOD = ΔDOA

Диагональ квадрата

Определение.

Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата.

Диагональ любого квадрата всегда больше его стороны в√2 раз.

Формулы определения длины диагонали квадрата

1. Формула диагонали квадрата через сторону квадрата:

d = a·√2

2. Формула диагонали квадрата через площадь квадрата:

d = √2S

3. Формула диагонали квадрата через периметр квадрата:

d =	P
	2√2

4. Формула диагонали квадрата через радиус описанной окружности:

d = 2R

5. Формула диагонали квадрата через диаметр описанной окружности:

d = D_о

6. Формула диагонали квадрата через радиус вписанной окружности:

d = 2r√2

7. Формула диагонали квадрата через диаметр вписанной окружности:

d = D_в√2

8. Формула диагонали квадрата через длину отрезка l:

d = l	2√10
	5

Периметр квадрата

Определение.

Периметром квадрата называется сумма длин всех сторон квадрата.

Формулы определения длины периметра квадрата

1. Формула периметра квадрата через сторону квадрата:

P = 4a

2. Формула периметра квадрата через площадь квадрата:

P = 4√S

3. Формула периметра квадрата через диагональ квадрата:

P = 2d√2

4. Формула периметра квадрата через радиус описанной окружности:

P = 4R√2

5. Формула периметра квадрата через диаметр описанной окружности:

P = 2D_о√2

6. Формула периметра квадрата через радиус вписанной окружности:

P = 8r

7. Формула периметра квадрата через диаметр вписанной окружности:

P = 4D_в

8. Формула периметра квадрата через длину отрезка l:

P = l	8
	√5

Площадь квадрата

Определение.

Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.

Площадь квадрата больше площади любого четырехугольника с таким же периметром.

Формулы определения площади квадрата

1. Формула площади квадрата через сторону квадрата:

S = a²

2. Формула площади квадрата через периметр квадрата:

S =	P2
	16

3. Формула площади квадрата через диагональ квадрата:

S =	d2
	2

4. Формула площади квадрата через радиус описанной окружности:

S = 2R²

5. Формула площади квадрата через диаметр описанной окружности:

S =	Do2
	2

6. Формула площади квадрата через радиус вписанной окружности:

S = 4r²

7. Формула площади квадрата через диаметр вписанной окружности:

S = D_в²

8. Формула площади квадрата через длину отрезка l:

S = l 2	16
	√5

Окружность описанная вокруг квадрата

Определение.

Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.

Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз.

Радиус окружности описанной вокруг квадрата равен половине диагонали.

Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.

Формулы определения радиуса окружности описанной вокруг квадрата

1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:

R = a	√2
	2

2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:

R =	P
	4√2

3. Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:

R =	√2S
	2

4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:

R =	d
	2

5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:

R =	Dо
	2

6. Формула радиуса круга описанного вокруг квадрата через радиус вписанной окружности:

R = r √2

7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:

R = Dв	√2
	2

8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:

R = l	√10
	5

Окружность вписанная в квадрата

Определение.

Кругом вписанным в квадрат называется круг, который примыкает к серединам сторон квадрата и имеет центр на пересечении диагоналей квадрата.

Радиус вписанной окружности равен половине стороны квадрата.

Площадь круга вписанного в квадрат меньше площади квадрата в 4/π раза.

Формулы определения радиуса круга вписанного в квадрат

1. Формула радиуса круга вписанного в квадрат через сторону квадрата:

r =	a
	2

2. Формула радиуса круга вписанного в квадрат через диагональ квадрата:

r =	d
	2√2

3. Формула радиуса круга вписанного в квадрат через периметр квадрата:

r =	P
	8

4. Формула радиуса круга вписанного в квадрат через площадь квадрата:

r =	√S
	2

5. Формула радиуса круга вписанного в квадрат через радиус описанной окружности:

r =	R
	√2

6. Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности:

r =	Dо
	2√2

7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности:

r =	Dв
	2

8. Формула радиуса круга вписанного в квадрат через длину отрезка l:

r =	l
	√5

Все таблицы и формулы

Квадратные уравнения

Пример квадратного уравнения :

Функция создает красивые кривые, подобные этой:

Имя

Название Quadratic происходит от «quad», что означает квадрат, потому что переменная возводится в квадрат (например, x ² ).

Его также называют «уравнением степени 2» (из-за «2» на x )

Стандартная форма

Стандартная форма квадратного уравнения выглядит следующим образом:

• a , b и c — известные значения. и не могут быть 0.

• « x » — это переменная или неизвестная (мы пока этого не знаем).

 

Вот несколько примеров:

2x 2 + 5х + 3 = 0		В этом a=2 , b=5 и c=3
х 2 — 3х = 0		Это немного сложнее: Где ? Итак, a=1 , так как мы обычно не пишем «1x 2 » б = −3 А где c ? Ну c=0 , так что не показано.
5x — 3 = 0		Ой! Это , а не квадратное уравнение: оно отсутствует x 2 (другими словами a=0 , что означает, что оно не может быть квадратным)

 

Поиграй с этим

Поиграйте с «Проводником квадратных уравнений», чтобы увидеть:

• график функции и
• решений (называемых «корнями»).

 

Скрытые квадратные уравнения!

Как мы видели ранее, Стандартная форма квадратного уравнения равна

.

топор ² + Ьх + с = 0

Но иногда квадратное уравнение выглядит не так!

Например:

Замаскированный		В стандартной форме	а, б и в
x 2 = 3x − 1	Переместить все термины в левую часть	x 2 − 3x + 1 = 0	а=1, б=-3, с=1
2(ш 2 — 2ш) = 5	Разверните (раскройте скобки), и переместите 5 влево	2w 2 − 4w − 5 = 0	а=2, б=-4, с=-5
z(z−1) = 3	Разверните и переместите 3 влево	z 2 — z — 3 = 0	а=1, б=-1, с=-3

 

Как их решить?

« решений » квадратного уравнения, где равно нулю .

Их еще называют « корни «, или иногда « нули »

 

Обычно есть 2 решения (как показано на этом графике).

 

И есть несколько способов найти решения:

Мы можем разложить квадратное уравнение на множители (найти, на что умножить, чтобы получить квадратное уравнение)

Или мы можем достроить квадрат

Или мы можем использовать специальную квадратичную формулу :

Просто подставьте значения a, b и c и выполните вычисления.

Рассмотрим этот метод более подробно.

О квадратичной формуле

Плюс/Минус

Во-первых, что это за плюс/минус, который выглядит как ± ?

± означает, что есть ДВА ответа:

х = −b + √(b ² − 4ac) 2a

х = −b − √(b ² − 4ac) 2a

Вот пример с двумя ответами:

Но не всегда так получается!

• Представьте, что кривая «просто касается» оси x.
• Или представьте, что кривая такая высокая он даже не пересекает ось X!

Тут нам поможет «Дискриминант»…

Дискриминант

Видите ли вы b ² − 4ac в приведенной выше формуле? Он называется Дискриминант , потому что он может «различать» возможные типы ответов:

• когда b ² − 4ac положителен, мы получаем два действительных решения
• когда он равен нулю, мы получаем только ОДНО действительное решение (оба ответа одинаковы)
• при отрицательном результате получаем пару Комплексных решений

Комплексные решения? Давайте поговорим о них после того, как увидим, как пользоваться формулой.

 

Использование квадратичной формулы

Просто подставьте значения a, b и c в квадратную формулу и выполните вычисления.

Пример: решить 5x

² + 6x + 1 = 0

Коэффициенты: a = 5, b = 6, c = 1

Квадратичная формула:x = −b ± √(b ² − 4ac) 2a

Поставьте a, b и c: x = −6 ± √(6 ² − 4×5×1) 2×5

Решить:x = −6 ± √(36−20) 10

х = −6 ± √(16) 10

х = −6 ± 4 10

x = −0,2 или −1

Ответ: x = −0,2 или x = −1

и мы увидим их на этом графике.

Чек -0,2 :		5×( −0,2 ) 2 + 6×( −0,2 ) + 1 = 5×(0,04) + 6×(−0,2) + 1 = 0,2 − 1,2 + 1 = 0
Чек -1 :		5×( −1 ) 2 + 6×( −1 ) + 1 = 5×(1) + 6×(−1) + 1 = 5 − 6 + 1 = 0

 

Вспоминая формулу

Добрый читатель предложил спеть ее под «Pop Goes the Weasel»:

♫	«х равно минус b		♫	«Вокруг тутового куста
	плюс или минус квадратный корень			Обезьяна погналась за лаской
	b-квадрат минус четыре a c			Обезьяна думала, что все это забава
	ВСЕ более двух дюймов			Поп! идет ласка»

Попробуйте спеть ее несколько раз, и она застрянет у вас в голове!

Или вы можете вспомнить эту историю:

х = −b ± √(b ² − 4ac) 2а

«Отрицательный мальчик думал «да» или «нет» о том, чтобы пойти на вечеринку,
на вечеринке он разговаривал с квадратным мальчиком, но не с 4 классными цыпочками.
Все было кончено в 2 часа ночи. »

Комплексные решения?

Когда Дискриминант (значение b ² − 4ac ) отрицателен, мы получаем пару Комплексных решений… что это значит?

Это означает, что наш ответ будет включать воображаемые числа. Ух ты!

Пример: решить 5x

² + 2x + 1 = 0

Коэффициенты равны : a=5, b=2, c=1 4ac = 2 ² − 4×5×1
              = −16

Используйте квадратичную формулу : x = -2 ± √(-16) 10

√(−16) = 4 i
(где i — мнимое число √−1)

Итак:x = −2 ± 4 i Ответ: x = −0,2 ± 0,4 Вот почему мы остановились на комплексных числах.

В каком-то смысле это проще: нам не нужно больше вычислять, мы оставляем его равным −0,2 ± 0,4 и .

Пример: Решить x

² − 4x + 6,25 = 0

Коэффициенты равны : a=1, b=-4, c=6,25

Обратите внимание, что дискриминант 9 0:10090 отрицателен − 4ac = (−4) ² − 4×1×6,25
              = −9

Используйте квадратичную формулу :

√(−9) = 3 i
(где i — мнимое число √−1)

SO: x = 4 ± 3 I 2

Ответ: x = 2 ± 1,5 I

. График не переходит на X-AXIS. Вот почему мы остановились на комплексных числах.

НО перевернутое зеркальное отражение нашего уравнения действительно пересекает ось x в точке 2 ± 1,5 (примечание: отсутствует i ).

Просто интересный факт для вас!

 

Резюме

• Квадратное уравнение в стандартной форме: ax ² + bx + c = 0
• Квадратные уравнения можно разложить на множители
• Квадратичная формула: х = −b ± √(b ² − 4ac) 2а
• Когда дискриминант ( b ² −4ac ) равен:
  • положительный, есть 2 реальных решения
  • ноль, есть одно действительное решение
  • отрицательный, есть 2 комплексных решения

 

360, 361, 1201, 1202, 2333, 2334, 3894, 3895, 2335, 2336

Завершение квадрата

» Завершение Квадрата » вот где мы. ..

… возьмем квадратное уравнение следующим образом:		и превратите его в это:
топор 2 + Ьх + с = 0		а(х+ d ) 2 + е = 0

Для тех из вас, кто торопится, могу сказать, что: d = b 2a

и: e = c − b ² 4a

Но если у вас есть время, позвольте мне показать вам, как « Заполнить Квадрат » самостоятельно.

Завершение квадрата

Допустим, у нас есть простое выражение вида x ² + bx. Наличие x дважды в одном и том же выражении может усложнить жизнь. Что мы можем сделать?

Что ж, немного вдохновившись геометрией, мы можем преобразовать его вот так:

Как видите x ² + bx можно переставить почти в квадрат. ..

… и мы можем заполнить квадрат с (б/2) ²

В алгебре это выглядит так:

x 2 + шт.	+ (б/2) 2	=	(х+b/2) 2
	«Заполните Квадрат »

Итак, сложив (b/2) ² , мы можем завершить квадрат.

Результат (x+b/2) ² имеет x только один раз , что проще в использовании.

Сохранение равновесия

Теперь… мы не можем просто прибавить (b/2) ² без вычитания ! В противном случае меняется все значение.

Итак, давайте посмотрим, как это сделать правильно на примере:

Начните с:
	(в данном случае «b» равно 6)
Заполните квадрат:
	Также вычесть новый термин
Упростите это, и все готово.

Результат:

x ² + 6x + 7   =   (x+3) ² − 2

И теперь x появляется только один раз, и наша работа выполнена!

Быстрый подход

Вот быстрый способ получить ответ. Вам может понравиться этот метод.

Сначала подумайте о желаемом результате: (x+d) ² + e

После расширения (x+d) ² получаем: x ² + 2dx + d ² + e

Теперь посмотрим, сможем ли мы преобразовать наш пример в эту форму, чтобы обнаружить d и e

Пример: попытаться вписать x

² + 6x + 7 в x ² + 2dx + d ² + e

Теперь мы можем «форсировать» ответ:

• Мы должны знать, что
  • вверх как 2dx, поэтому d должно быть 3
  • Далее мы видим, что 7 должно стать d ² + e = 9 + e, поэтому e должно быть −2

  И мы получаем тот же результат (x+3) ² − 2, что и выше!

   

  Теперь давайте рассмотрим полезное приложение: решение квадратных уравнений. ..

  Решение общих квадратных уравнений путем заполнения квадрата

  Мы можем дополнить квадрат до решить квадратное уравнение (найти где оно равно нулю).

  Но общее квадратное уравнение может иметь коэффициент а перед х ² :

  топор ² + Ьх + с = 0

  Но с этим легко справиться… просто сначала разделите все уравнение на «а», а затем продолжайте:

  х ² + (б/а)х + с/а = 0

  шагов

  Теперь мы можем решить квадратное уравнение за 5 шагов:

  • Шаг 1 Разделить все слагаемые на a (коэффициент х ² ).
  • Шаг 2 Переместите числовое выражение ( c/a ) в правую часть уравнения.
  • Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же значение в правую часть уравнения.

  Теперь у нас есть что-то похожее на (x + p) ² = q, которое можно довольно легко решить:

  • Шаг 4 Извлеките квадратный корень из обеих частей уравнения.
  • Шаг 5 Вычтите число, оставшееся в левой части уравнения, чтобы найти x .

  Примеры

  Хорошо, несколько примеров помогут!

  Пример 1: Решить x

  ² + 4x + 1 = 0

  Шаг 1 можно пропустить в этом примере, поскольку коэффициент x ² равен 1

  Шаг 2 9Шаг 3 правая часть уравнения.

  (б/2) ² = (4/2) ² = 2 ² = 4

  х ² + 4х + 4 = -1 + 4

  = 3

  Шаг 4 Извлеките квадратный корень из обеих частей уравнения:

  x + 2 = ±√3 = ±1,73 (до 2 знаков после запятой)

  Шаг 5 Вычтите 2 с обеих сторон:

  x = ±1,73 – 2 = -3,73 или -0,27

  А вот еще интересная и полезная штука. В конце шага 3 у нас было уравнение: (х + 2) 2 = 3 Это дает нам вершину (точка поворота) x 2 + 4x + 1: (-2, -3)

   

  Шаг 1 правая часть уравнения:

  x ² – 0,8x = 0,4

  Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте это, добавив то же число в правую часть уравнения:

  (b/2) ² = (0,8/2) ² = 0,4 ² = 0,16

  x ² — 0,8x + 0,16 = 0,4 + 0,16

  (x — 0,4) ^{2 20 + 0,16}

  (x — 0,4) ^2. = 0,56

  Шаг 4 Извлеките квадратный корень из обеих частей уравнения:

  x – 0,4 = ±√0,56 = ±0,748 (до 3 десятичных знаков)

  Шаг 5 Вычтите (-0,4) из обоих сторон (другими словами, добавьте 0,4):

  x = ±0,748 + 0,4 = -0,348 или 1,148

  Почему «Завершить квадрат»?

  Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу, чтобы решить квадратное уравнение?

  Ну, одна причина указана выше, где новая форма не только показывает нам вершину, но и упрощает решение.

  Бывают также случаи, когда форма ax ² + bx + c может быть частью более крупного вопроса , и перестановка ее в виде a(x+ d ) ² +

  2 e 9 дает 90 решение проще, потому что x появляется только один раз.

  Например, «x» может быть функцией (например, cos(z) ), и ее изменение может открыть путь к лучшему решению.

  Также завершение квадрата является первым шагом в выводе квадратичной формулы

  Думайте об этом как о еще одном инструменте в вашем наборе математических инструментов.

   

  364, 1205, 365, 2331, 2332, 3213, 3896, 3211, 3212, 1206

   

  Сноска: значения «d» и «e»

  Как я получил значения d и e из верхней части страницы?

  Начните с
  Разделить уравнение на a
  Положите c/a на другую сторону
  Добавить (b/2a) 2 на обе стороны
  «Заполните квадрат»
  Теперь верни все обратно. РубрикаРазное Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт