Умножить матрицу а на матрицу в: Онлайн калькулятор. Умножение матриц.
определение, свойства и примеры решения задач
Задание. Вычислить $AB$ и $BA$, если $ A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right) $ , $ B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right) $
Решение. Так как $ A=A_{3 \times 2} $ , а $ B=B_{2 \times 2} $ , то произведение возможно и результатом операции умножения будет матрица $ C=C_{3 \times 2} $ , а это матрица вида $ C=\left( \begin{array}{ll}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right) $ .
Вычислим элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{32}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $ C=A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $ .
Выполним произведения в более компактном виде:
$ C=A B=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right)_{3 \times 2} \cdot \left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)_{2 \times 2}= $
$ =\left( \begin{array}{ccc}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $
Найдем теперь произведение $ D=B A=B_{2 \times 2} \cdot A_{3 \times 2} $. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $ A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $ .
Действия с матрицами
Матрицы и действия с ними, определителиСложение матриц
Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц \(A=\{A_{ik}\}\) и \(B=\{B_{ik}\}\), матрица \(A+B\), определяется следующим образом: \((A+B)_{ik}=A_{ik}+B_{ik}\), \(1 \leq i \leq m, 1 \leq k \leq n\). Иными словами: складываются элементы матриц \(A\) и \(B\), стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.
Пример. Пусть
\[
A=\left(
\begin{array}{ccc}
1 &4 & -1 \\
3 & -6 & 7
\end{array}
\right) ,
\]
\[
B=\left(
\begin{array}{ccc}
2 &1 & 0 \\
1 & 3 & 4
\end{array}
\right) ,
\]
тогда
\[
A+B=\left(
\begin{array}{ccc}
3 & 5 & -1 \\
4 & -3 & 11
\end{array}
\right) . \]
\]
Умножение матрицы на число
Пусть \(A=\{a_{ik}\}\) — матрица типа \((m,n)\), \(\lambda\) — произвольное число. Тогда матрица \(\{\lambda a_{ik}\}\) называется произведением числа \(\lambda \) на матрицу \(A\) и обозначается \(\lambda \cdot A\).
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 7 & 5 & 2 \\ 3 & -6 & 7 \end{array} \right) , \] тогда \[ 5A=\left( \begin{array}{ccc} 5 &20 & -5 \\ 35 & 25 & 10 \\ 15 & -30 & 35 \end{array} \right) . \]
Замечание.
Как и в обычной, в матричной арифметике знак умножения иногда не указывают, так что выражения \(c\cdot A\) и \(cA\) равноправны.
Пусть \[ A=\left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right), B=\left( \begin{array}{cc} 1 & -2 \\ 3 & 4 \end{array} \right). \]
Вычислить \(3A-2B\).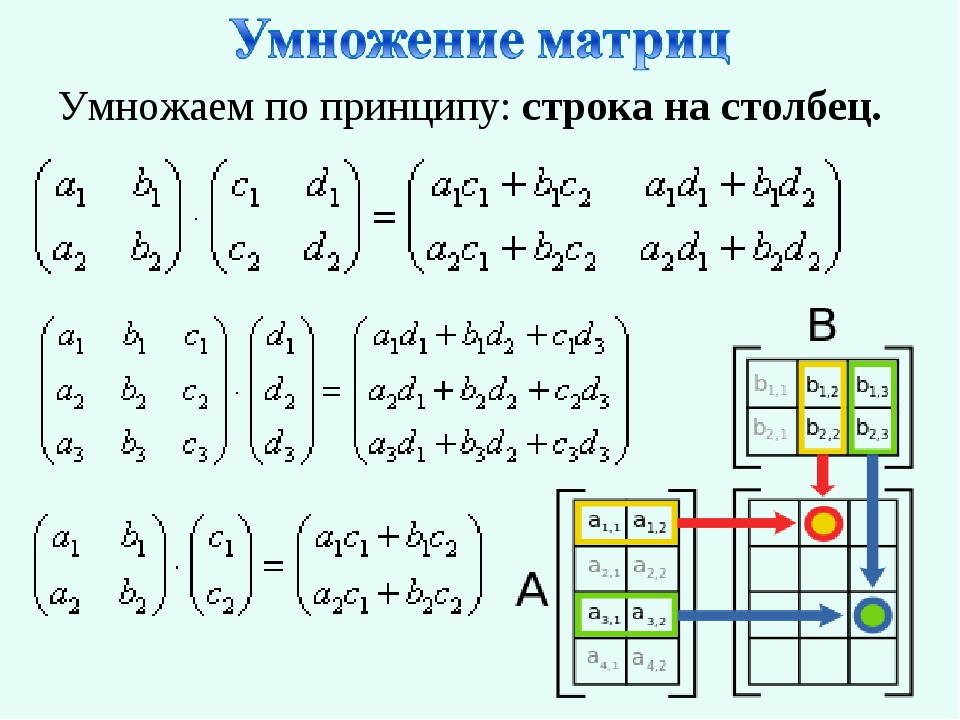 T\) (это выражение занимает меньше места).
T\) (это выражение занимает меньше места).
Элементарные свойства операций с матрицами
Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.
1. Для любых матриц \(A,B,C\) одного типа \((A+B)+C=A+(B+C)\)(ассоциативность сложения).
2. Для любых матриц \(A,B\) одного типа \(A+B=B+A\) (коммутативность сложения).
3. Пусть \((m,n)\)-матрица \(O\) состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа \((m,n)\), \(A+O=A\), \(0\cdot A=O\) для любой матрицы \(A\) того же типа.
4. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1+c_2)A=c_1A+c_2A\).
5. Для любых матриц \(A,B\) одного типа и любого числа \(c\) верно \(c(A+B)=cA+cB\).
6. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1c_2)A=c_1(c_2A)\).
7. Для любой матрицы \(A\) верно \(1\cdot A=A\).
8. Для любых матриц \(A,B\) одного типа \((A+B)^T=A^T+B^T\). na_{im}b_{mk}.
\]
Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!
na_{im}b_{mk}.
\]
Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , B=\left( \begin{array}{cc} 2 &1 \\ 1 & 3 \\ -3 &5 \end{array} \right) . \]
В данном случае матрица \(A\) имеет тип (2,3), матрица \(B\) имеет тип (3,2), так что типы матриц согласнованы и в результате умножения \(A\) на \(B\) получим матрицу типа \((2,2)\). Получаем:
\[
AB=\left (
\begin{array}{cc}
1\cdot 2 +4 \cdot 1+(-1)\cdot (-3) & 1\cdot 1 +4 \cdot 3+(-1)\cdot 5\\
3\cdot 2 +(-6) \cdot 1+7\cdot (-3) &3\cdot 1 +(-6) \cdot 3+7\cdot 5
\end{array}
\right )=
\left( \begin{array}{cc} 9 & 8\\ -21 & 20
\end{array} \right). T\).
T\).
6. Для квадратных матриц \(A,B\) одного типа \(det(AB)=detA \cdot detB\).
7. Рассмотрим квадратную матрицу порядка \(n\), \(E=diag\{1,1,1,…,1\}\). Такая матрица играет выделенную роль в умножении матриц: для любых матриц \(A,B\) имеем \(EA=A\), \(BE=B\). Матрица \(E\) называется единичной матрицей порядка \(n\). Согласно описанным выше результатам, \(detE=1\).
1. Умножить матрицы:
а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]
б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). \]
2. Вычислить
\[
\left( \begin{array}{cc} 3 & 2 \\ -4 & -2 \end{array} \right)^5. {-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right).
\]
{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right).
\]
Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.
Найти обратную матрицу для матрицы
1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]
2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]
3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]
Матричные уравнения
Матричными уравнениями называются уравнения вида
\[ AX=G, \quad \quad(12)\]
\[ XB=G, \quad \quad(13)\]
\[ AXB=G, \quad \quad(14)\]
где матрицы \(A,B,G\) заданы и требуется построить матрицу \(X\). {-1}.
\]
{-1}.
\]
1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]
2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]
3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]
4. Найти решение матричного уравнения (13), если
\[
B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) ,
G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) .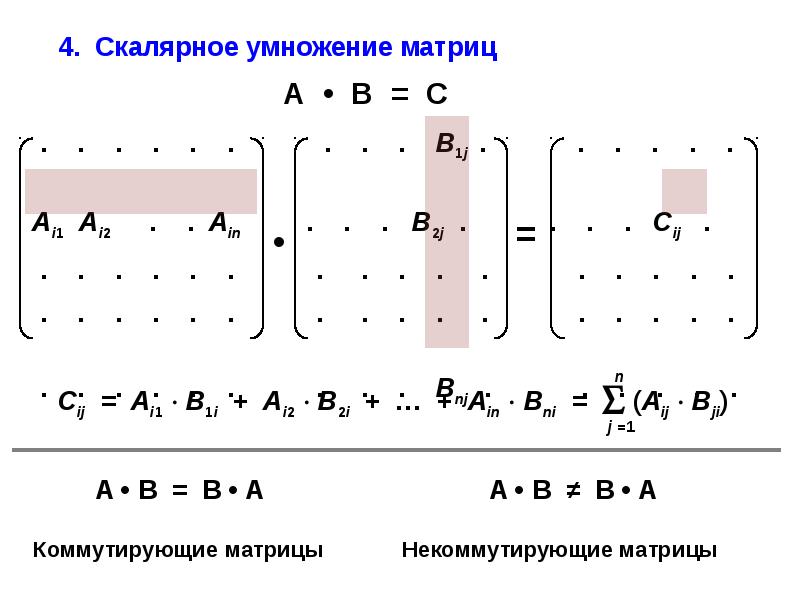 \]
\]
5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]
6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]
5
55. Умножение матриц.
Рассмотрим правило умножения двух квадратных матриц второго и третьего порядков. Пусть даны две матрицы
Произведением матрицы А на матрицу В называется матрица С= А В, элементы которой составляются следующим образом:
Как видим, элемент матрицы-произведения,
находящийся на пересечении i-й строки и
k-го столбца,
представляет собой сумму парных произведений
элементов i-й строки первой
матрицы на элементы k-го столбца второй матрицы.
Например, элемент, стоящий во второй строке и первом столбце матрицы произведения АВ, равен сумме парных произведений элементов второй строки матрицы А на элементы первого столбца матрицы В.
Это правило сохраняется для умножения квадратных матриц третьего и более высокого порядка, а также для умножения прямоугольных матриц, в которых число столбцов матрицы-множимого равно числу строк матрицы-множителя.
Пример1
Пример2
Пример3.
Видим , что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько имеет их матрица-множимое, и столько столбцов, сколько имеет матрица-множитель. Рассмотрим еще пример:
С другой стороны, как установлено выше,
Следовательно, произведение двух матриц, вообще говоря, не подчиняется переместительному закону:
АВ
ВА.
Можно проверить, что умножение матриц подчиняется сочетательному закону:
А(ВС) = (АВ)С.
Отметим любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль-матрице.
Пример 4. Если
то
При умножении матриц второго порядка особое значение имеет квадратная матрица
При умножении любой квадратной матрицы
второго порядка на матрицу Е снова
получается матрица А.
Действительно,
Аналогично EA =A.
Матрица Е называется единичной матрицей. Единичная матрица n-го порядка имеет вид
Если в матрице (1), обозначаемой буквой А, сделать все строки столбцами с тем же номером, то получим матрицу
называемую транспонированной к матрице А.
Понятие о матрице | Сложение матриц | Вычитание матриц и умножение матриц на число |
Умножение матриц | Контакты первого и второго порядков в эпидемиологии | Матрицы и сети |
Главная
Транспонирование матриц. Умножение матриц.
К оглавлению
I. Транспонирование матриц
Транспонирование
матриц – переход от матрицы А
к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Пример 1. Составить транспонированную матрицу, полученную из А:
Решение: Поменяем местами строки и столбцы, сохраняя порядок:
Примеры для самостоятельного решения:
Составить из исходной матрицы транспонированную матрицу:
II. Умножение матриц
Пример 1. Рассмотрим для начала простейший пример, когда необходимо найти произведение двух матриц А и В размером 2´2, если
Решение:
Элементы матрицы С находятся по следующему алгоритму:
Элемент матрицы С, стоящий на первой строке, в первом столбце находится как сумма произведений первой строки матрицы А на первый столбец матрицы В.
Элемент матрицы С,
стоящий на первой строке, во втором столбце находится как сумма произведений первой строки матрицы А на второй столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, в первом столбце находится как сумма произведений второй строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, во втором столбце находится как сумма произведений второй строки матрицы
Таким образом, мы получили
То есть мы получили, что
Пример 2. Найдем результат произведения двух матриц
Решение:
то есть мы должны получить матрицу размера 3´3.
Пример 3. В предыдущем примере мы рассмотрели случай умножения
матрицы А на матрицу В, а в данном примере рассмотрим
случай произведения матрицы В
на А.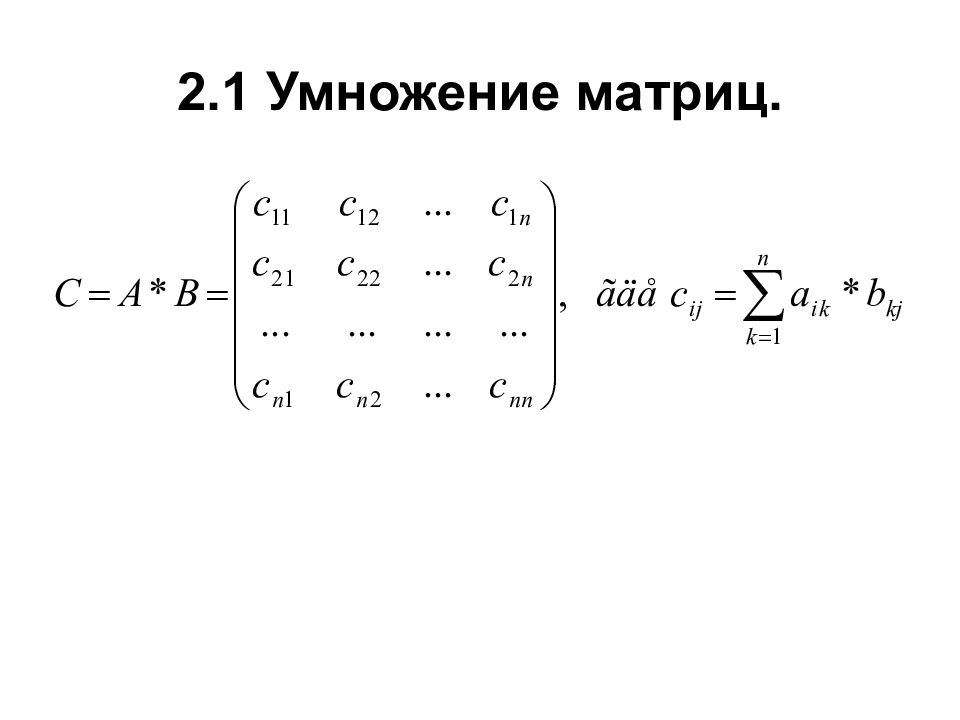
Решение:
Пример 4. Найти произведение двух матриц:
Решение: В первом случае найдем произведение:
Во втором случае найдем произведение:
Пример 5. Вычислить значение многочлена от матрицы
Решение. В многочлен подставим вместо х матрицу А, вместо числа 3 используем матрицу 3Е, где Е – единичная матрица 2-го порядка
Теперь получим окончательный результат
III. Примеры для самостоятельного решения
I. Найти произведение матриц:
II. Найти значение многочлена от матрицы А
К оглавлению
Умножение матрицы на число в excel.
 Функции для работы с матрицами в Excel
Функции для работы с матрицами в ExcelВ разделе на вопрос Как создать матрицу в Excel???? заданный автором Masha Kalganova лучший ответ это Что конкретно нужно сделать?
Документ эксель — безразмерная (всеразмерная) матрица, каждый элемент которой может быть числом, текстом или любым другим значением. Да хоть формулой.
Если напечатать 3 циферки в ряд, под ними еще 3 в ряд, под ними еще 3 в ряд, получим квадратную матрицу 3х3.
Вопрос в чем?
Умножение матрицы на число в Excel
Формулы написать?
В верхней левой клетке новой матрицы
=левая верхняя клетка старой матрицы * клетка с числом (ткнуть мышкой) , нажать F4 дабы стало $x$y, где x,y — координаты клетки. Это зафиксирует клетку при копировании. Далее жмем Enter и копируем содержимое клетки в 2 соседние клетки в ряд. Далее копируем эти 3 клетки в следующие 3 ряда и получаем тот же результат, что у меня на картинке. То есть умножение матрицы на число.
Блин, математику не знают, а в интернете лазают!
Решение систем линейных алгебраических уравнений в Excel
Методы решения систем линейных алгебраических уравнений хорошо описаны
в учебнике «Основы вычислительной математики. Демидович Б.П., Марон И.А. 1966″.
Скачать — 11Мб
Демидович Б.П., Марон И.А. 1966″.
Скачать — 11Мб
1. Метод обратной матрицы (решение в Excel)
Если дано уравнение:
A*X = B, где A — квадратная матрица, X,B — вектора;
причем B — известный вектор (т е столбец чисел), X — неизвестный вектор,
то решение X можно записать в виде:
X = A -1 *B, где A -1 — обратная от А матрица.
В MS Excel обратная матрица вычисляется функцией МОБР(), а перемножаются матрицы
(или матрица на вектор) — функцией МУМНОЖ().
Имеются «тонкости» использования этих матричных действий в Excel. Так, чтобы вычислить обратную матрицу от матрицы А, нужно:
1. Мышкой выделить квадратную область клеток, где будет размещена
обратная матрица.
2. Начать вписывать формулу =МОБР(3. Выделить мышкой матрицу А. При этом правее скобки впишется
соответствующий диапазон клеток.
4. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter
5. Должна вычислиться обратная матрица и заполнить предназначенную
для неё область
Чтобы умножить матрицу на вектор:
1. Мышкой выделить область клеток, где будет размещён результат
умножения
2. Начать вписывать формулу =МУМНОЖ(3. Выделить мышкой матрицу — первый сомножитель. При этом правее скобки впишется
соответствующий диапазон клеток.
4. С клавиатуры ввести разделитель; (точка с запятой)
5. Выделить мышкой вектор- второй сомножитель. При этом правее скобки впишется
соответствующий диапазон клеток.
6. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter
7. Должно вычислиться произведение и заполнить предназначенную
для него область
Есть и другой спососб, при котором используется кнопка построителя функции Excel.
Пример СЛАУ 4-го порядка
Мышкой выделить область клеток, где будет размещён результат
умножения
2. Начать вписывать формулу =МУМНОЖ(3. Выделить мышкой матрицу — первый сомножитель. При этом правее скобки впишется
соответствующий диапазон клеток.
4. С клавиатуры ввести разделитель; (точка с запятой)
5. Выделить мышкой вектор- второй сомножитель. При этом правее скобки впишется
соответствующий диапазон клеток.
6. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter
7. Должно вычислиться произведение и заполнить предназначенную
для него область
Есть и другой спососб, при котором используется кнопка построителя функции Excel.
Пример СЛАУ 4-го порядка
Скачать документ Excel, в котором этот пример решён различными методами.
2. Метод Гаусса
Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. А чтобы решить реальную СЛАУ, лучше применить в Excel метод обратной матрицы или воспользоваться специальными программами, например, этойКраткое описание.

3. Метод Якоби (метод простых итераций)
Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.
(1)’ = (1) + 0,43*(2) — 0,18*(3) – 0,96*(4)
(2)’ = (2) + 0,28*(1) – 1,73*(3) + 0,12*(4)
(3)’ = (3) – 0,27*(1) — 0,75*(2) + 0,08*(4)
(4)’ = (4) + 0,04*(1) – 6,50*(2) + 8,04*(3)
Примечание: подбор коэффицентов выполнен на листе «Анализ».
Решаются системы уравнений, цель которых — обратить внедиагональные
элементы в нуль. Коэффиценты — это округлённые результаты решения
таких систем уравнений. Конечно, это не дело.
В результате получаю систему уравнений:
Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую:
Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид:
А вектор В2:
Способ 1
Рассмотрим матрицу А размерностью 3х4 . Умножим эту матрицу на число k . При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k .
Умножим эту матрицу на число k . При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k .
Введем элементы матрицы в диапазон В3:Е5 , а число k — в ячейку Н4 . В диапазоне К3: N 5 вычислим матрицу В , полученную при умножении матрицы А на число k : В=А* k . Для этого введем формулу =B3*$H$4 в ячейку K 3 , где В3 — элемент а 11 матрицы А .
Примечание: адрес ячейки H 4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 В .
Таким образом, мы умножили матрицу А в Excel и получим матрицу В .
Для деления матрицы А на число k в ячейку K 3 введем формулу =B3/$H$4 В .
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k Ctrl+ Shift+ Enter
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/h5, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В , т.е. с ij = а ij + b ij .
Рассмотрим матрицы А и В размерностью 3х4 . Вычислим сумму этих матриц. Для этого в ячейку N 3 введем формулу =B3+h4 , где B3 и h4 — первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H 3 ), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N 3 вниз и вправо на весь диапазон матрицы С .
Для вычитания матрицы В из матрицы А (С=А — В ) в ячейку N 3 введем формулу =B3 — h4 и скопируем её на весь диапазон матрицы С .
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А , нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В . После ввода формулы нажимаем сочетание клавиш Ctrl+ Shift+ Enter , чтобы значениями заполнился весь диапазон.
После ввода формулы нажимаем сочетание клавиш Ctrl+ Shift+ Enter , чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В .
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2 . При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ() . Для этого выделим диапазон L 3: M 5 — в нём будут располагаться элементы матрицы С , полученной в результате умножения. На вкладке Формулы выберем Вставить функцию .
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК .
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В . Для этого напротив массива1 щёлкнем по красной стрелке.
Для этого напротив массива1 щёлкнем по красной стрелке.
А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В , и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С . После ввода значений нажимаем на клавиатуре сочетание клавиш Shift + Ctrl ОК .
ВАЖНО. Если просто нажать ОК С .
Мы получим результат умножения матриц А и В .
Мы можем изменить значения ячеек матриц А и В , значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4 , с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3 .
Выделим диапазон Н3: J 6 , в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК .
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5 А Shift + Ctrl и щелкаем левой кнопкой мыши по кнопке ОК .
ВАЖНО. Если просто нажать ОК , то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А , если А А -1 =А -1 А=Е , где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3 , найдем для неё обратную матрицу с помощью функции =МОБР() .
Для этого выделим диапазон G 3: I 5 , который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию .
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК .
В диалоговом окне Аргументы функции указываем диапазон массива В3: D 5 , содержащего элементы матрицы А . Нажимаем на клавиатуре сочетание клавиш Shift + Ctrl и щелкаем левой кнопкой мыши по кнопке ОК .
ВАЖНО. Если просто нажать ОК , то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3 , вычислим для неё определитель с помощью функции =МОПРЕД() .
Для этого выделим ячейку Н4 , в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию .
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК .
В диалоговом окне Аргументы функции указываем диапазон массива В3: D 5 , содержащего элементы матрицы А . Нажимаем ОК .
Нажмите для увеличения
Мы вычислили определитель матрицы А .
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del , то программа выдаст предупреждение: Нельзя изменять часть массива .
Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del , то программа выдаст предупреждение: Нельзя изменять часть массива .
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.
РХТУ им. Д.B. Менделеева Кафедра ИКМ Методическое пособие по изучению Excel
Операции с матрицами в Excel
Как и над числами, над матрицами можно
проводить ряд операций, причем в случае
с матрицами некоторые из операций
являются специфическими.
Транспонирование .
Транспонированной называется матрица (A T), в которой столбцы исходной матрицы (А) заменяются строками с соответствующими номерами.
Пример . Пусть в диапазон ячеек А1:Е2 введена матрица размера 2×5. Необходимо получить транспонированную матрицу.
Выделить указателем мыши при нажатой левой кнопке блок ячеек, где будет находиться транспонированная матрица. В нашем примере блок размера 5 x2 в диапазоне А4:В8.
Стандартная вставка функции.
Мастер функций в рабочем полеКатегория выбратьСсылки и массивы , а в рабочем полеФункция – имя функции ТРАСП (рис.1)
рис.1
Появившееся диалоговое окно ТРАСП
мышью отодвинуть в сторону от исходной
матрицы и ввести диапазон исходной
матрицы А1:Е2 в рабочее поле Массив (указателем мыши при нажатой левой
кнопке). После чего, не нажимая кнопку
ОК, нажать сочетание клавишCTRL+SHIFT+ENTER(рис. 2)
2)
Если транспонированная матрица не появилась в заданном диапазоне А4:В8, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.
В результате в диапазоне А4:В8 появится транспонированная матрица.
Рис.2
Вычисление определителя матрицы
Пусть в диапазон А1:С3 введена матрица. Необходимо вычислить определитель матрицы
Табличный курсор поставить в ячейку, в которой требуется получить значение определителя, например. В А4.
Нажать на панели инструментов Стандартная кнопкуВставка функции
В появившемся диалоговом окне Мастер функций в рабочем полеКатегории выбратьМатематические, а в рабочем полеФункция – имя функции МОПРЕД. После этого нажать на кнопку ОК.
Появившееся диалоговое окно МОПРЕД
мышью отодвинуть в сторону от исходной
матрицы и ввести диапазон исходной
матрицы А1:С3 в рабочее поле Массив (указателем мыши при нажатой левой
кнопке). После чего нажать кнопку ОК.
После чего нажать кнопку ОК.
В ячейке А4 появится значение определителя матрицы.
Нахождение обратной матрицы
Пусть в диапазон А1:С3 введена матрица. Необходимо в диапазоне А5:С7 получить обратную матрицу.
Выделить блок ячеек под обратную матрицу (в нашем примере А5:С7)
Нажать на панели инструментов Стандартная кнопкуВставка функции
В появившемся диалоговом окне Мастер функций в рабочем полеКатегории выбратьМатематические, а в рабочем полеФункция – имя функции МОБР. После этого нажать на кнопку ОК.
Появившееся диалоговое окно МОБР мышью отодвинуть в сторону от исходной матрицы и ввести диапазон исходной матрицы А1:С3 в рабочее поле Массив (указателем мыши при нажатой левой кнопке). После чего, не нажимая кнопку ОК, нажать сочетание клавишCTRL+SHIFT+ENTER
Если обратная матрица не появилась в
заданном диапазоне А1:С3, то надо щелкнуть
указателем мыши в строке формул и
повторить нажатие клавиш CTRL+SHIFT+ENTER.
В результате в диапазоне А1:С3 появится обратная матрица.
Сложение и вычитание матриц, умножение и деление матрицы на число
Пример. Пусть матрица А введена в диапазон А1:С2, а матрица В – в диапазон А4:С5. Необходимо найти матрицу С, являющуюся их суммой, в диапазоне Е1:G2.
Табличный курсор установить в левый верхний угол результирующей матрицы – ячейку Е1.
Ввести формулу для вычисления первого элемента результирующей матрицы =А1+А4 (предварительно установить английскую раскладку клавиатуры)
Скопируйте введенную формулу в остальные ячейки результирующей матрицы.
В результате в ячейках E1:G2 появится матрица, равная сумме исходных матриц.
Подобным образом вычисляется разность матриц, только в формуле вместо знака +, ставится знак -.
Если необходимо умножить (разделить) матрицу А на число k, то формула будет иметь вид =А1*k.
Рис.3
Умножение матриц
Произведение двух матриц определено,
если число столбцов первой матрицы
произведения равно числу строк второй
матрицы произведения.
Пример . Пусть матрица введена в диапазонA1:D3, а матрица В – в диапазон А4:В7. Необходимо найти произведение этих матриц С=Аx В.
Выделить блок ячеек указателем мыши при нажатой левой кнопке под результирующую матрицу. Если матрица А имеет размерность 3 x 4, а матрица В имеет размерность 4 x 3, то результирующая матрица С имеет размерность 3 x 3. Поэтому следует внимательно следить, чтобы размерность матрицы С в точности соответствовала определению произведения двух матриц. Пусть матрица С будет размещаться в диапазонеF1:G3.
Нажать на панели инструментов Стандартная кнопкуВставка функции
В появившемся диалоговом окне Мастер функций в рабочем полеКатегории выбратьМатематические, а в рабочем полеФункция – имя функции МУМНОЖ. После этого нажать на кнопку ОК.
Появившееся диалоговое окно МУМНОЖ
мышью отодвинуть в сторону от исходной
матрицы и ввести диапазон первой матрицы
А1:D3 в рабочее полеМассив1 (указателем мыши при нажатой левой
кнопке), а диапазон матрицы В – А4:В7
ввести в рабочее полеМассив2 . После
чего, не нажимая кнопку ОК, нажать
сочетание клавишCTRL+SHIFT+ENTER(рис.3)
После
чего, не нажимая кнопку ОК, нажать
сочетание клавишCTRL+SHIFT+ENTER(рис.3)
Рис.4
Если произведение матриц не появилось в заданном диапазоне А1:С3, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.
В результате в диапазоне F1:G3 появится обратная матрица.
Вычислим определитель (детерминант) матрицы с помощью функции МОПРЕД() или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).
Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.
Для вычисления определителя в MS EXCEL есть специальная функция МОПРЕД() . В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см. файл примера ).
Массив может быть задан не только как интервал ячеек, например A7:B8 , но и как , например =МОПРЕД({5;4:3;2})
. Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Для матриц порядка 2 можно определитель можно вычислить без использования функции МОПРЕД() . Например, для вышеуказанной матрицы выражение =A7*B8-B7*A8 вернет тот же результат.
Для матрицы порядка 3, например размещенной в диапазоне A16:C18 , выражение усложняется =A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18) (разложение по строке).
В файле примера для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.
Свойства определителя
Теперь о некоторых свойствах определителя (см. файл примера ):
- Определитель равен определителю исходной матрицы
- Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
- Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
- Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет равен определителю исходной матрицы, умноженному на
k
- Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
- det(А)=1/det(А -1), где А -1 — матрице А (А — квадратная невырожденная матрица).

Вычисление определителя матрицы по определению (до 6 порядка включительно)
СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОПРЕД() .
Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции МОПРЕД() ) придется вспомнить определение:
Определителем квадратной матрицы порядка n
х n
является сумма, содержащая n!
слагаемых (=ФАКТР(n)
). Каждое слагаемое представляет собой произведение n
элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А
. Перед k-ым
слагаемым появляется коэффициент (-1)
, если элементы матрицы А
в произведении упорядочены по номеру строки, а количество инверсий в k-ой
перестановке множества номеров столбцов нечетно.
где (α 1 ,α 2 ,…,α n ) — перестановка чисел от 1 до n , N(α 1 ,α 2 ,…,α n ) — число , суммирование идёт по всем возможным перестановкам порядка n .
Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.
Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:
- а21*а12*а33
- а21*а32*а13
- а11*а32*а23
- а11*а22*а33
- а31*а22*а13
- а31*а12*а23
а21, а12 и т.д. — это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.
Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т. к. определители матрицы и ее равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго — 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).
к. определители матрицы и ее равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго — 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).
Теперь понятно, почему среди слагаемых нет а11*а22*а13, т.к. согласно определения (в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А ), а в нашем слагаемом нет элемента из строки 3.
Примечание : Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 1, 2), (3, 2, 1). См. статью
Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т. к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).
к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).
СОВЕТ : Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье .
Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.
Примечание : Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье
Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.
Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.
Сложив все слагаемые: (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.
В файле примера на листе 4+, и зменяя порядок матрицы с помощью , можно вычислить определитель матрицы до 6 порядка включительно.
Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования МОПРЕД() не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).
Вконтакте
Одноклассники
Google+
Умножение матрицы на число — Энциклопедия по машиностроению XXL
В алгебре матриц определяются следующие действия над матрицами а) сложение матриц б) умножение матрицы на число в) умножение матриц. Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.
[c.41]
Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.
[c.41]Умножение матрицы на число. Если к—вещественное или комплексное число, то произведение ХА матрицы А на число к определяется формулой [c.95]
Умножение матрицы на число I (которое можно записать справа, так и слева матрицы) эквивалентно умножению на I кв дого элемента этой матрицы если [c.40]
При умножении матрицы на некоторое число необходимо умножить на это число все элементы матрицы, т. е. [c.144]
Умножение (деление) матрицы на число. Для этого необходимо каждый элемент матрицы умножить (разделить) на это число. [c.181]
Определение 4. Произведением матрицы Л размера тХп на число а называется матрица С тех же размеров, элементы которой получаются из соответствующих элементов матрицы Л умножением их на число а, т. е.
[c.41]
е.
[c.41]
Л]- -[В] умножение тензора на число Тв=%ТА, гле матрица [В]—%[А умножение тензора на тензор (скаляр-ное) Тс=Гл7 в, где матрица [С]=[А][В]. [c.61]
Еще большее число показателей требует для своего расчета применение умножения матриц на векторы. Вектор — это матрица с одной строкой или одним столбцом. Данная операция, таким образом, есть частный случай умножения матриц. Ее результатом является вектор. Примером такой операции является вычисление потребностей в материалах. [c.53]
В табл. 7.1 приведена скорость выполнения операции умножения матрицы на вектор. В первой колонке представлены выражения для числа тактовых циклов, необходимых для завершения одной операции умножения. Умножение матрицы тХп на вектор /гХ1 требует 2тп операций сложения и умножения. Если предположить, что биты данных проходят в системе с частотой 10 МГц (величина 0,1 мкс/бит является достаточно обоснованной для существующих электронных устройств), то можно вычислить скорость выполнения операций. Представлены два случая. Первый из них соответствует п = т = 32, при /=16 (I эквивалентно точности вычислений), а второй случай относится к п = т=128, / = 32. В табл. 7.2 представлены аналогичные данные для умножителей, выполняющих умножение матрицы на матрицу с точностью I цифр. В третьем столбце показаны результаты для /=16, п = т = к = 32, а четвертый столбец соответствует / = 32, п = т = к= 28. Во всех случаях результаты даны для операций с фиксированной запятой, выполняемых в одну секунду. Ни один цифровой процессор (оптический или элект-
[c.207]
Представлены два случая. Первый из них соответствует п = т = 32, при /=16 (I эквивалентно точности вычислений), а второй случай относится к п = т=128, / = 32. В табл. 7.2 представлены аналогичные данные для умножителей, выполняющих умножение матрицы на матрицу с точностью I цифр. В третьем столбце показаны результаты для /=16, п = т = к = 32, а четвертый столбец соответствует / = 32, п = т = к= 28. Во всех случаях результаты даны для операций с фиксированной запятой, выполняемых в одну секунду. Ни один цифровой процессор (оптический или элект-
[c.207]
В символьных вычислениях центральное место занимает операция вычисления внутреннего произведения, эквивалентная умножению составляющих элементов на вектор (векторное умножение), на матрицу (умножение матрицы на матрицу) или на корреляционную функцию. В предыдущих разделах была установлена общность процедур вычисления внутреннего произведения для большого числа алгоритмов из области цифровых вычислений. В одном типичном представлении символьных вычислений отношения знаний выражаются в терминах логического сопоставления с образцом, процедура которого определяется поиском соглашения по предпосылке-условию (с левой стороны) соотношения если [А], тогда [В] (см. разд. 10.3.5). Здесь [А] является подпространством Л -мерного векторного пространства
[c.354]
разд. 10.3.5). Здесь [А] является подпространством Л -мерного векторного пространства
[c.354]
Умножение матрицы на скаляр р равносильно умножению всех ее элементов на это число Ьу = р ау 1 = 1,2,] =1,2,…,11. [c.156]
Умножение матрицы [Aij] на скаляр X дает матрицу [КАц. Произведение двух матриц [Aij] и определено только в том случае, если число столб- [c.18]
Суммой двух матриц А и В одинакового порядка (тХп) называется матрица того же порядка, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц. Перемножать можно только матрицы, у которых число столбцов в первой матрице совпадает с числом строк во второй. Каждый элемент матрицы — произведения С=ВА — определяется по правилу умножения строки на столбец, которое для квадратных матриц приводит к формуле [c.46]
Мы уже говорили, что, записывая уравнение (4.19) в виде г = кг, мы просто пользуемся символическим обозначением для указания определенной операции А, совершаемой над координатной системой (или над вектором). Но, расширяя наше понятие о матрицах, можно сделать так, что эта запись будет указывать на действительное умножение на умножение матриц. Матрицы, рассматривавшиеся нами до сих пор, были квадратными, т. е. число их строк равнялось числу столбцов. Однако можно рассматривать также матрицы, состоящие всего лишь из одного столбца, такие, как
[c.119]
Но, расширяя наше понятие о матрицах, можно сделать так, что эта запись будет указывать на действительное умножение на умножение матриц. Матрицы, рассматривавшиеся нами до сих пор, были квадратными, т. е. число их строк равнялось числу столбцов. Однако можно рассматривать также матрицы, состоящие всего лишь из одного столбца, такие, как
[c.119]
Любую матрицу при помощи элементарных преобразований строк и столбцов, заключающихся в перестановке строк (столбцов), умножении строки (столбца) на число и сложении строк (столбцов) между собой, можно привести к каноническому виду. Ранг канонической матрицы равен числу единиц на ее главной диагонали. [c.16]
Ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимаются замена строк столбцами, а столбцов соответствующими строками перестановка строк матрицы вычеркивание строки, все элементы которой равны нулю умножение какой-либо строки на число, отличное от нуля прибавление к элементам одной строки соответствующих элементов другой строки. [c.53]
[c.53]
Г. Умножение матриц. Рассмотрим (т X Р) Матрицу а и (/ X ) Матрицу Ъ—число столбцов а равно числу строк Ъ. Такие матрицы, взятые в указанной последовательности а, Ь, называются конформными. Действие умножения определено для конформных матриц. Произведением их с — аЬ называется (т X )»Матрица, элемент /-Й строки и /г-го столбца которой ра ен сумме произведений элементов /-й строки матрицы а на элементы /г-го столбца матрицы Ь [c.762]
Матрицы, имеющие одинаковое число строк и столбцов, можно складывать (или вычитать) поэлементно. Умножение матрицы [Л,/] на скаляр X дает матрицу [М,у]. Произведение двух матриц определено только в том случае, когда число столбцов в первом множителе Л равно числу строк во втором множителе Произведением (М X Р)-матрицы на (Р X Л )-матрицу будет (М х Ы)-матрица. Умножение матриц обычно обозначается простым написанием их символов один за другим, например [c.32]
Гамильтониан (2. 8), (2.9) зависит от 21 параметра. Существует три типа простейших преобразований, которые изменяют (в частности, исключают) параметры в гамильтониане без изменения уравнений движения. К первому типу относятся групповые преобразования 30(3) х 30(3). С их помощью в представлении (2.9) матрицы А и С могут быть одновременно приведены к диагональному виду. Добавление к гамильтониану произвольной линейной комбинации функций Казимира Рг,Р2, которые являются однородными квадратичными функциями, позволяет исключить еще два параметра. Умножение гамильтониана на произвольную константу Н аН с заменой времени t 1, также позволяет уменьшить число параметров на единицу. Таким образом, квадратичное семейство гамильтонианов (2.8) либо (2.9)) определяется двенадцатью параметрами.
[c.181]
8), (2.9) зависит от 21 параметра. Существует три типа простейших преобразований, которые изменяют (в частности, исключают) параметры в гамильтониане без изменения уравнений движения. К первому типу относятся групповые преобразования 30(3) х 30(3). С их помощью в представлении (2.9) матрицы А и С могут быть одновременно приведены к диагональному виду. Добавление к гамильтониану произвольной линейной комбинации функций Казимира Рг,Р2, которые являются однородными квадратичными функциями, позволяет исключить еще два параметра. Умножение гамильтониана на произвольную константу Н аН с заменой времени t 1, также позволяет уменьшить число параметров на единицу. Таким образом, квадратичное семейство гамильтонианов (2.8) либо (2.9)) определяется двенадцатью параметрами.
[c.181]
Второй способ состоит в умножении соответствующего диагонального элемента матрицы на некоторое большое число, скажем 10 , перед модификацией соответствующего коэффициента нагрузки. В рассматриваемом случае мы бы получили
[c. 486]
486]
Матрица рассеяния 5(Л) не зависит от Л и также сводится к умножению на число (б). [c.109]
Таком образом, для выполнения алгоритма (55) требуются два прямых и одно обратное преобразование Ф/рье, а также прямое умножение матрицы на матрицу. Если в качестве дижретного преобразования Фурье использовать алгоритм БПФ, число опера дай сложения составит 2N og2 , а число операций умножения -. [c.63]
Однако этот критерий, строго говоря, не имеет смысла. Путем почленного умножения уравнений на числа, большие единицы, определитель системы линейных алгебраических уравнений можно сделать сколь угодно большим. Обусловленность системы при этом не изменится. В теории матриц вводятся числа обусловленности, инвариантные относительно подобных преобразований. К таким числам относятся числа Тюринга и Тодда. [c.181]
SUBROUTINE SKM (А, S, М, N) — программа умножения матрицы на скаляр. А — исходная и результирующая матрица S — скалярная величина М, N — целые числа, определяющие размер матрицы.
[c.251]
А — исходная и результирующая матрица S — скалярная величина М, N — целые числа, определяющие размер матрицы.
[c.251]
Рассмотрение данного примера было вызвано необходимостью обеспечить высокую скорость при выполнении операции внутреннего произведения в линейной алгебре (например, для умножения матрицы на вектор или матрицы на матрицу), в противном случае эти операции становятся бессысленными. Операции внутреннего произведения включают умножение двух чисел и сложение результата с третьим числом. Например, 2-разрядный умножитель-сумматор умножает два 2-раз-рядных числа М ц Ы, прибавляет результат к 5-разрядному входному числу X и выводит результаты в виде 5-разрядного числа У. В синхронизированном режиме работы выходной сигнал У мог бы подаваться по цепи обратной связи на вход X для того, чтобы достичь эффекта многократного накопления результата (если имеется возможность накопления до трех произведений и при этом не возникает переполнение). [c.155]
Одна из целей цифровых оптических вычислений состоит в достижении большей гибкости системы, чем у их аналоговых предшественников. Особенность оптических компьютеров состоит в том, что они скорее выполняют не монолитные операции, а ряд простых операций, которые можно объединить для выполнения широкого круга задач. Однако в данном случае это не так плохо, поскольку при построении оптических процессоров, осуществляющих функции регистра, их возможности поднимутся на качественно новый уровень. С этой точки зрения матричное умножение (под которым подразумевают либо умножение матрицы на вектор, либо матрицы на матрицу), возможно, является наиболее полезной операцией среднего уровня из числа тех, которые только можно придумать. Многие сложные проблемы, например калмановское фильтрование,
[c.183]
Особенность оптических компьютеров состоит в том, что они скорее выполняют не монолитные операции, а ряд простых операций, которые можно объединить для выполнения широкого круга задач. Однако в данном случае это не так плохо, поскольку при построении оптических процессоров, осуществляющих функции регистра, их возможности поднимутся на качественно новый уровень. С этой точки зрения матричное умножение (под которым подразумевают либо умножение матрицы на вектор, либо матрицы на матрицу), возможно, является наиболее полезной операцией среднего уровня из числа тех, которые только можно придумать. Многие сложные проблемы, например калмановское фильтрование,
[c.183]
Разновидности основной архитектуры. Сообщалось и о других способах преобразования схем вычисления свертки в схемы умножителей матрицы на матрицу. В [16] для получения промежуточного произведения при вычислении внутреннего произведения двух векторов используется основная схема вычисления свертки с интегрированием по времени. Все промежуточные произведения вычисляются параллельно на независимых друг от друга умножителях и суммируются с помощью цилиндрической линзы. Таким образом, для перемножения двух векторов, состоящих из п элементов, с точностью в I знаков требуется п входов для каждого вектора, 21—1 фотодетекторных элементов и 21—1 тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет п1 Ь—1) . Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы тХп и вектора пХ все т умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов тп), а элементы вектора Ь сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий т 21—1) циклов при этом i используется т(21—1) детекторов выходного сигнала.
Все промежуточные произведения вычисляются параллельно на независимых друг от друга умножителях и суммируются с помощью цилиндрической линзы. Таким образом, для перемножения двух векторов, состоящих из п элементов, с точностью в I знаков требуется п входов для каждого вектора, 21—1 фотодетекторных элементов и 21—1 тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет п1 Ь—1) . Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы тХп и вектора пХ все т умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов тп), а элементы вектора Ь сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий т 21—1) циклов при этом i используется т(21—1) детекторов выходного сигнала. Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов Ь при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также тп входов для одной матрицы и п входов для другой, а также т 21—1) детекторов выходного сигнала. Затраты времени на вычисления составляют k + m—1) 21—1) тактовых циклов.
[c.200]
Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов Ь при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также тп входов для одной матрицы и п входов для другой, а также т 21—1) детекторов выходного сигнала. Затраты времени на вычисления составляют k + m—1) 21—1) тактовых циклов.
[c.200]
Правильный результат получают уже в смешанном формате, путем умножения исходной матрицы на дополненный вектор. Эта процедура может быть выполнена с помощью любого из обсуждавшихся выше вариантов умножения матрицы на матрицу. Ценой этого будет служить увеличение объема памяти, необходимое для записи вектора, и задача класса умножение матрицы на вектор оказывается отданной в уплату за задачу класса матрица — матрица. В целом же кажется более выгодным использовать оптические методы для выполнения суммирования вдоль противодиагоналей. В число возможных оптических способов решения такой задачи входит сегментация цилиндрических линз, сегментация голографических линз или применение матриц оптических волокон, соединяющих соответствующие элементы с детекторами, на которых происходит суммирование. [c.203]
[c.203]
В работе [20] предлолсхемы построения процессоров внешнего произведения. В первом случае используется перекрестное включение одномерных входных модуляторов (рис. 7.14). Для умножения матрицы на вектор в один из модуляторов вводят целый столбец матрицы, а элементы вектора размещаются в другом модуляторе. Матричный модулятор должен обладать т1 разрядами, а модулятор для ввода вектора должен иметь I разрядов. Когда оба модулятора загружены, то от источника света подается импульс света и перекрестное произведение записывается на матрице пг1х1 интегрирующих по времени детекторов. Если суммирование осуществляется оптически, необходимо только т(21—1) детекторов. Каждое промежуточное произведение может быть накоплено на детекторе за время загрузки входного сигнала в модулятор, которое полагаем равным т1. Полное число тактовых импульсов для операции умножения матрицы на вектор составляет пт1. Для умножения матрицы на матрицу требуется кт 21—1) детекторов, при этом необходимое число тактовых циклов составляет лишь пт1 (если т>к).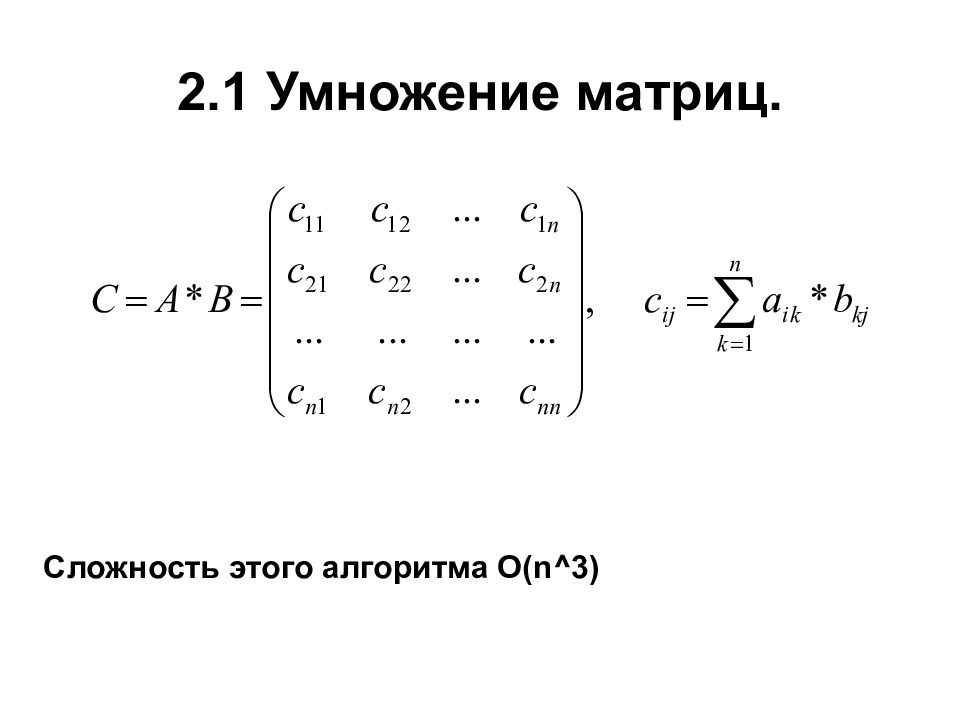 [c.203]
[c.203]
Все процессоры характеризуются тем, что чем больше объем задачи, тем быстрее они работают. Например, умножители матрицы на вектор (за одним исключением) работают со скоростью в десятки мегаопераций в секунду, характерной для небольших по объему задач. Процессоры умножения матрицы на матрицу работают со скоростями порядка гигаопераций в секунду, что характерно для задач большего масштаба. Очевиден выигрыш в быстродействии, получаемый для параллельной обработки. Более неопределенной характеристикой является абсолютная величина быстродействия. Представленные здесь цифры являются лишь оценками, но они действительно отражают общие свойства оптических вычислений. За небольшим числом исключений имеется очень небольшая разница (менее чем на порядок по величине) между разными видами оптических процессоров, используемых для решения заданной задачи. Возможности оптических процессоров, как представляется, достаточно жестко ограничены определенными скоростями. При сравнении с возможностями электронных процессоров скорости вряд ли произведут на читателя глубокое впечатление. На момент написания книги на промышленно освоенных электронных устройств удается достичь скоростей около 50 мегаопераций в секунду. Разрабатываемые в настоящее время умножители матрицы на вектор не позволят превзойти эту величину. Умножители матрицы на матрицу демонстрируют существенно более высокие возможности.
[c.208]
На момент написания книги на промышленно освоенных электронных устройств удается достичь скоростей около 50 мегаопераций в секунду. Разрабатываемые в настоящее время умножители матрицы на вектор не позволят превзойти эту величину. Умножители матрицы на матрицу демонстрируют существенно более высокие возможности.
[c.208]
Матрица S обладает рядом универсальных свойств, вытекаюших из симметрии задачи и закона сохранения энергии. Отметим одно из них. Известно, что при умножении столбца или строки матрицы на число q ее детерминант увеличивается в q раз. Умножая первый и третий столбец мат- [c.96]
Поэтому математической моделью излучающей системы может служить соотношение (2.24) или (2.27), т. е. систему излучателей можно описывать матрицей как [/)], так и [/)] . Размерности матриц [ )] и [/)] одинаковы, и для хранения их в ЭВМ требуются одинаковые объемы памяти. В модели (2.24) нахождение коэффициентов мод токов [/] связано с решением системы линейных алгебраических уравнений, а в модели (2.27) эти коэффициенты находятся путем умножения матрицы на вектор, что требует существенно меньшего числа операций. Матрицы [В] и имеют порядок MNxMN), т. е. с ростом числа излучателей и числа учитываемых мод он быстро увеличивается.
[c.62]
В модели (2.24) нахождение коэффициентов мод токов [/] связано с решением системы линейных алгебраических уравнений, а в модели (2.27) эти коэффициенты находятся путем умножения матрицы на вектор, что требует существенно меньшего числа операций. Матрицы [В] и имеют порядок MNxMN), т. е. с ростом числа излучателей и числа учитываемых мод он быстро увеличивается.
[c.62]
В АР с большим числом излучателей матрица [ )] содержит много элементов с малой абсолютной величиной, которые соответствуют излучателям, далеко отстоящим друг от друга. Поскольку в итерационных методах умножение матрицы на вектор является единственной операцией с матрицей, то это позволяет легко исключить операции с элементами матрицы [О], имеющими малое значение. Сохраняя в матрице [1>] только те элементы, которые соответствуют учету взаимодействия не более чем с Ь ближайшими излучателями, можно существенно уменьшить затраты машинного времени (8, 9 в табл. 3.1). Например, расчет токов АР из 21X21 полуволновых вибраторов над экраном ( =с у=0,6Я,) методом сопряженных градиентов с учетом взаимодействия
[c. 110]
110]
Умножение двух матриц возможно, если число столбцов первой равно числу строк второй матрицы. Произведением матрицы А = = [aij] размера тХР на матрицу В = [Ьр,] размера рХп является матрица С = [с,/,] размера тХп, в которой каждый элемент iu определяется по правилу умножения строки на столбец элементы /-Н строки первой матрицы умножаются на соответствуюн не элементы kio столбца второй матрицы и полученные произведения складываются [c.104]
В случае, когда элементами матрицы являются матрицы-блоки, умножение выполняется по тем же правилам, как если бы элементами матриц были числа, т. е. строки первой матрицы-сомно-жителя умножаются на столбцы второй матрицы-сомножителя (см., например, Г а н т м а х е р Ф. Р., Теория матриц, 5), [c.184]
Умножение на скаляр а тензора Т ь любого ранга вследствие инва-риашносга первого можно выполнять в любом множестве координат. Для этого необходамо каждую компоненту матрицы тензора в выбранной множестве координат умножить на число, характеризующее скал ф. Ранг тензора, получаемого в результате такого умножения, равен рангу тензора, участвующему в этом действии
[c.242]
Ранг тензора, получаемого в результате такого умножения, равен рангу тензора, участвующему в этом действии
[c.242]
Произведением матрицы [A]—[aik]m,n на число а называется матрица a,[A]=[aaik]m.n, полученная умножением всех элементов матрицы [Л] на число сг. пример [c.37]
Быстродействие оптических матричных умножителей было уже описано в табл. 7.1 и 7.2. При вычислении отношения Псалтиса числа в табл. 7.1 и 7.2 имеют коэффициент запаса 2, поскольку были учтены операции умножения и сложения. Для умножителей матриц на векторы соотношение Псалтиса показано в табл. 7.3. Умножители матрицы на матрицы показаны в табл. 7.4. Вычисления проведены для тех же случаев, что и в табл. 7.1 и 7.2. Второй столбец табл. 7.3 предполагает значение / = 16, п=т = 32, в то время как для третьего столбца /=32, п = т= 28. В табл. 7.4 второй столбец соответствует значениям /=16, n = m = = 32, а третий столбец относится к / = 32, п=т = k=l28.
[c. 210]
210]
Полученный результат справедлив при любом выборе ортонор-мированной системы функций Если система // выбрана произвольно, то для построения матрицы гамильтониана потребуется большое число функций //, и соответствующее представление группы симметрии будет иметь очень высокую размерность. Если, с другой стороны, взять в качестве функций /г собственные состояния гамильтониана, то действие на них гамильтониана сведется к умножению их на некоторое число (собственное значение энергии), и матрица гамильтониана окажется диагональной. Любое преобразование симметрии должно поэтому переводить либо в себя, либо в вырожденное состояние. Размерность представления, порожденного данной функцией / , не может превышать степень вырождения состояния. Таким образом, между размерностью представления группы и степенью вырождения состояния, породившего это представление, существует тесная связь. В частности, если под действием неприводимого представления все состояния некоторой совокупности преобразуются друг через друга, то это означает, что и под действием операции симметрии эти состояния будут преобразовываться друг через друга, т. е. мы не можем найти никакой линейной комбинации (никакого унитарного преобразования), представляющей исключение. Из симметрии гамильтониана поэтому следует, что эти состояния должны быть вырожденными. Мы пришли тем самым, правда с помощью интуитивных соображений, к одному из важных результатов теории групп. Если группа симметрии гамильтониана имеет многомерные неприводимые представления, это означает, что собственные состояния гамильтониана должны быть вырожденными.
[c.38]
е. мы не можем найти никакой линейной комбинации (никакого унитарного преобразования), представляющей исключение. Из симметрии гамильтониана поэтому следует, что эти состояния должны быть вырожденными. Мы пришли тем самым, правда с помощью интуитивных соображений, к одному из важных результатов теории групп. Если группа симметрии гамильтониана имеет многомерные неприводимые представления, это означает, что собственные состояния гамильтониана должны быть вырожденными.
[c.38]
Линейная алгебра на Python. [Урок 3]. Действия над матрицами
Тема третьего урока: действия над матрицами. В рамках нее будут рассмотрены следующие вопросы: умножение матрицы на число, сложение и умножение матриц.
Действия над матрицамиУмножение матрицы на числоПри умножении матрицы на число, все элементы матрицы умножаются на это число:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6') >>> C = 3 * A >>> print(C) [[ 3 6 9] [12 15 18]]
Рассмотрим свойства операции умножения матрицы на число.
Свойство 1. Произведение единицы и любой заданной матрицы равно заданной матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> L = 1 * A
>>> R = A
>>> print(L)
[[1 2]
[3 4]]
>>> print(R)
[[1 2]
[3 4]]
Свойство 2. Произведение нуля и любой матрицы равно нулевой матрице, размерность которой равна исходной матрицы:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = 0 * A
>>> R = Z
>>> print(L)
[[0 0]
[0 0]]
>>> print(R)
[[0 0]
[0 0]]
Свойство 3. Произведение матрицы на сумму чисел равно сумме произведений матрицы на каждое из этих чисел:
Произведение матрицы на сумму чисел равно сумме произведений матрицы на каждое из этих чисел:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3
>>> L = (p + q) * A
>>> R = p * A + q * A
>>> print(L)
[[ 5 10]
[15 20]]
>>> print(R)
[[ 5 10]
[15 20]]
Свойство 4. Произведение матрицы на произведение двух чисел равно произведению второго числа и заданной матрицы, умноженному на первое число:
➣ Численный пример
➤Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3
>>> L = (p * q) * A
>>> R = p * (q * A)
>>> print(L)
[[ 6 12]
[18 24]]
>>> print(R)
[[ 6 12]
[18 24]]
Свойство 5. Произведение суммы матриц на число равно сумме произведений этих матриц на заданное число:
Произведение суммы матриц на число равно сумме произведений этих матриц на заданное число:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> k = 3
>>> L = k * (A + B)
>>> R = k * A + k * B
>>> print(L)
[[18 24]
[30 36]]
>>> print(R)
[[18 24]
[30 36]]Сложение матриц
Складывать можно только матрицы одинаковой размерности — то есть матрицы, у которых совпадает количество столбцов и строк.
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 6 3; 8 2 7')
>>> B = np.matrix('8 1 5; 6 9 12')
>>> C = A + B
>>> print(C)
[[ 9 7 8]
[14 11 19]]
Рассмотрим свойства сложения матриц.
Свойство 1. Коммутативность сложения. От перестановки матриц их сумма не изменяется:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = A + B
>>> R = B + A
>>> print(L)
[[ 6 8]
[10 12]]
>>> print(R)
[[ 6 8]
[10 12]]
Свойство 2. Ассоциативность сложения. Результат сложения трех и более матриц не зависит от порядка, в котором эта операция будет выполняться:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('1 7; 9 3')
>>> L = A + (B + C)
>>> R = (A + B) + C
>>> print(L)
[[ 7 15]
[19 15]]
>>> print(R)
[[ 7 15]
[19 15]]
Свойство 3. Для любой матрицы существует противоположная ей , такая, что их сумма является нулевой матрицей :
Для любой матрицы существует противоположная ей , такая, что их сумма является нулевой матрицей :
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = A + (-1)*A
>>> print(L)
[[0 0]
[0 0]]
>>> print(Z)
[[0 0]
[0 0]]Умножение матриц
Умножение матриц это уже более сложная операция, по сравнению с рассмотренными выше. Умножать можно только матрицы, отвечающие следующему требованию: количество столбцов первой матрицы должно быть равно числу строк второй матрицы.
Для простоты запоминания этого правила можно использовать диаграмму умножения, представленную на рисунке 1.
Рисунок 1 — Диаграмма матричного умножения
Рассмотрим умножение матриц на примере.
➣ Численный пример
Каждый элемент cij новой матрицы является суммой произведений элементов i-ой строки первой матрицы и j-го столбца второй матрицы. Математически это записывается так:
Математически это записывается так:
➤Пример на Python
Решим задачу умножения матриц на языке Python. Для этого будем использовать функцию dot() из библиотеки Numpy:
>>> A = np.matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8; 9 1; 2 3')
>>> C = A.dot(B)
>>> print(C)
[[31 19]
[85 55]]
Ниже представлены свойства произведения матриц. Примеры свойств будут показаны для квадратной матрицы.
Свойство 1. Ассоциативность умножения. Результат умножения матриц не зависит от порядка, в котором будет выполняться эта операция:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')
>>> L = A. dot(B.dot(C))
>>> R = (A.dot(B)).dot(C)
>>> print(L)
[[192 252]
[436 572]]
>>> print(R)
[[192 252]
[436 572]]
dot(B.dot(C))
>>> R = (A.dot(B)).dot(C)
>>> print(L)
[[192 252]
[436 572]]
>>> print(R)
[[192 252]
[436 572]]
Свойство 2. Дистрибутивность умножения. Произведение матрицы на сумму матриц равно сумме произведений матриц:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')
>>> L = A.dot(B + C)
>>> R = A.dot(B) + A.dot(C)
>>> print(L)
[[35 42]
[77 94]]
>>> print(R)
[[35 42]
[77 94]]
Свойство 3. Умножение матриц в общем виде не коммутативно. Это означает, что для матриц не выполняется правило независимости произведения от перестановки множителей:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4') >>> B = np.matrix('5 6; 7 8') >>> L = A.dot(B) >>> R = B.dot(A) >>> print(L) [[19 22] [43 50]] >>> print(R) [[23 34] [31 46]]
Свойство 4. Произведение заданной матрицы на единичную равно исходной матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> E = np.matrix('1 0; 0 1')
>>> L = E.dot(A)
>>> R = A.dot(E)
>>> print(L)
[[1 2]
[3 4]]
>>> print(R)
[[1 2]
[3 4]]
>>> print(A)
[[1 2]
[3 4]]
Свойство 5. Произведение заданной матрицы на нулевую матрицу равно нулевой матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4') >>> Z = np.matrix('0 0; 0 0') >>> L = Z.dot(A) >>> R = A.dot(Z) >>> print(L) [[0 0] [0 0]] >>> print(R) [[0 0] [0 0]] >>> print(Z) [[0 0] [0 0]]
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Как перемножить две матрицы вместе
Умножение матриц
Существует ровно два способа умножения матриц. Первый способ — умножить матрицу на скаляр. Это известно как скалярное умножение. Второй способ — умножить матрицу на другую матрицу. Это известно как умножение матриц.
Второй способ — умножить матрицу на другую матрицу. Это известно как умножение матриц.
на самом деле является очень простой операцией с матрицами. Чтобы умножить скаляр на матрицу, мы просто берем скаляр и умножаем его на каждую запись в матрице.Сделаем пример.
Вопрос 1 : Рассчитать 2A2A2A, если
Уравнение 1: Пример скалярного умножения 1, часть 1Вопрос заключается в том, чтобы выяснить, что такое 2A2A2A. Другими словами, мы находим
Уравнение 1: Пример скалярного умножения 1, часть 2Обратите внимание: если мы умножим на 2 каждую запись в матрице, мы получим следующее:
Уравнение 1: Пример скалярного умножения 1, часть 3Очень просто! Сделаем еще один.
Вопрос 2 : Рассчитать 0A0A0A, если
Уравнение 2: Пример скалярного умножения 2 балла.1Опять пытаемся найти 0A0A0A. Это значит, что мы будем искать ответ на
. Уравнение 2: Пример скалярного умножения 2, часть 2 Матрица будет странной формы, но концепция останется прежней.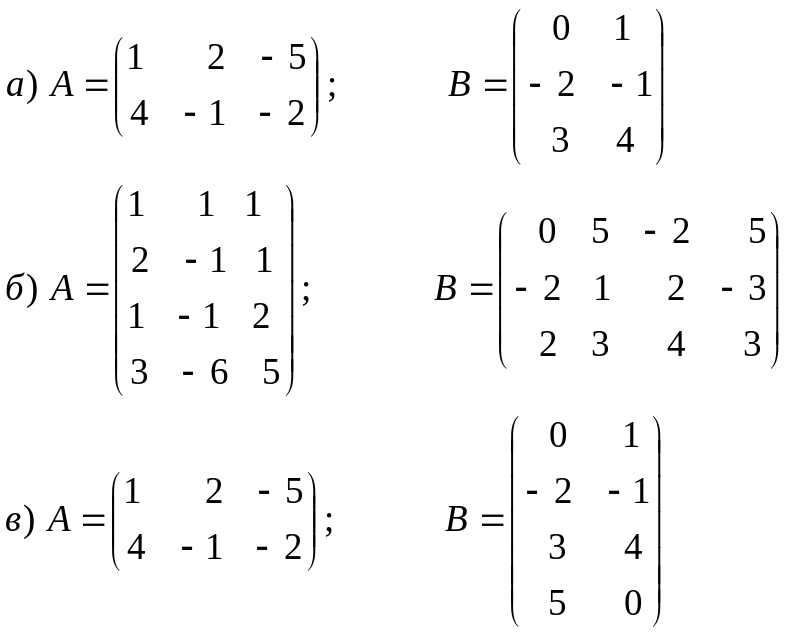 Мы по-прежнему будем умножать скаляр 0 на каждую запись в матрице. Это дает нам:
Мы по-прежнему будем умножать скаляр 0 на каждую запись в матрице. Это дает нам:
Обратите внимание, что все элементы в матрице равны 0. Это известно как нулевая матрица, равная 3 x 2.
Теперь, когда мы хорошо знакомы со скалярным умножением, почему бы нам не перейти к матричному умножению?
Как умножать матрицыЧтобы умножить матрицу на другую матрицу, нам сначала нужно узнать, что такое скалярное произведение.
Что такое скалярный продукт?
Скалярное произведение (также известное как умножение векторов) — это способ вычисления произведения двух векторов. Например, пусть два вектора будут:
Уравнение 3: Пример скалярного произведения, часть 1Как мне перемножить эти два вектора? Просто умножьте соответствующие записи и сложите продукты вместе. Другими словами,
Уравнение 3: Пример скалярного произведения, часть 2 Таким образом, мы получаем одно значение путем перемножения векторов. Однако обратите внимание, что два вектора имеют одинаковое количество записей.Что, если один из векторов имеет другое количество элементов, чем другой? Например, пусть
Однако обратите внимание, что два вектора имеют одинаковое количество записей.Что, если один из векторов имеет другое количество элементов, чем другой? Например, пусть
Если бы я перемножил соответствующие записи и сложил их вместе, то получил бы:
Уравнение 4: Пример отказа скалярного произведения, часть 2Здесь возникла проблема. Первые три записи имеют соответствующие записи для умножения, а последняя запись — нет. Итак, что мы делаем здесь? Ответ: здесь мы ничего не можем сделать. Это просто означает, что мы не можем вычислить скалярное произведение этих двух векторов.
Итак, в заключение, мы не можем найти скалярное произведение двух векторов с разным количеством элементов. Они должны иметь одинаковое количество записей.
Матричное умножение 2 x 2
Так какой смысл было изучать скалярное произведение? Что ж, мы будем использовать скалярное произведение, когда будем перемножать две матрицы. При умножении матрицы на другую матрицу мы хотим рассматривать строки и столбцы как вектор. Точнее говоря, мы хотим рассматривать каждую строку первой матрицы как векторы, а каждый столбец второй матрицы — как векторы.Сделаем пример.
При умножении матрицы на другую матрицу мы хотим рассматривать строки и столбцы как вектор. Точнее говоря, мы хотим рассматривать каждую строку первой матрицы как векторы, а каждый столбец второй матрицы — как векторы.Сделаем пример.
Вопрос 3 : Найдите A∙BA \пуля BA∙B, если
Уравнение 5: Пример умножения матриц 2 x 2, часть 1Умножение двух матриц даст нам:
Уравнение 5: Пример умножения матриц 2 x 2, часть 2Теперь строки и столбцы, на которые мы фокусируемся, равны
. Уравнение 5: Пример умножения матриц 2 x 2, часть 3, где r1r_{1}r1 – первая строка, r2r_{2}r2 – вторая строка, а c1,c2c_{1}, c_{2}c1,c2 – первый и второй столбцы.Теперь мы собираемся рассматривать каждую строку и столбец, которые мы видим здесь, как вектор.
Обратите внимание, что умножение матрицы 2 x 2 на другую матрицу 2 x 2 дает матрицу 2 x 2. Другими словами, в полученной матрице должно быть 4 элемента.
Уравнение 5: Пример умножения матриц 2 x 2, часть 4 Как именно получить первую запись? Обратите внимание, что первая запись расположена в первой строке и первом столбце. Поэтому мы просто берем скалярное произведение r1r_{1}r1 и c1c_{1}c1. Таким образом, первая запись будет
Поэтому мы просто берем скалярное произведение r1r_{1}r1 и c1c_{1}c1. Таким образом, первая запись будет
Готово! Это то, что мы получаем, когда мы умножаем матрицы 2 x 2. В общем случае формула умножения матриц для матриц 2 x 2 равна
. Формула 1: Формула умножения матриц 2 x 2Умножение матриц 3×3
Теперь процесс умножения матриц 3 x 3 очень похож на процесс умножения матриц 2 x 2.Опять же, почему бы нам не сделать пример умножения матриц?
Вопрос 4 :Найти A∙BA \ пулю BA∙B если
Уравнение 6: Пример умножения матриц 3 x 3, часть 1Во-первых, обратите внимание, что их умножение должно дать нам еще одну матрицу 3 x 3. Другими словами,
Уравнение 6: Пример умножения матриц 3 x 3, часть 2 Теперь давайте пометим все наши строки в первой матрице и столбцы во второй матрице. {st}1-м столбце, поэтому мы берем скалярное произведение r1r_{1}r1 и c1c_{1}c1.{nd}2-й столбец. Таким образом, мы берем скалярное произведение r1r_{1}r1 и c2c_{2}c2. Это дает нам:
{st}1-м столбце, поэтому мы берем скалярное произведение r1r_{1}r1 и c1c_{1}c1.{nd}2-й столбец. Таким образом, мы берем скалярное произведение r1r_{1}r1 и c2c_{2}c2. Это дает нам:
Если мы будем продолжать находить все записи и выполнять скалярное произведение, соответствующее строкам и столбцам, мы получим окончательный результат.
Уравнение 6: Пример умножения матриц 3 x 3, часть 6Готово! Обратите внимание, что чем больше матрицы, тем более утомительным становится умножение матриц. Это потому, что нам приходится иметь дело со все большим количеством чисел! В общем случае формула умножения матриц для матриц 3 x 3 равна
. Формула 2: Формула умножения матриц 3 x 3 Как умножать матрицы разных размеров? До сих пор мы перемножали матрицы одинаковых размеров.Кроме того, мы знаем, что умножение двух матриц одинаковой размерности дает матрицу одинаковой размерности. Но что произойдет, если мы умножим матрицу разных размеров? Как узнать размеры вычисляемой матрицы? Во-первых, нам нужно увидеть, что умножение матриц дает вам определенную матрицу.
Определена ли матрица?
В некоторых случаях невозможно перемножить две матрицы. В этих случаях мы называем матрицу undefined .Как мы можем сказать, что они не определены?
Произведение двух матриц определяется только в том случае, если количество столбцов в первой матрице равно количеству строк второй матрицы .
Попробуем использовать это определение в этом примере.
Вопрос 5 : Пусть
Уравнение 7: Пример заданной матрицы, часть 1Определен ли A∙BA \пуля BA∙B?
Во-первых, обратите внимание, что первая матрица имеет 3 столбца . Кроме того, вторая матрица имеет 3 строки .Так как они оба равны 3, то я знаю, что определено A∙BA \bullet BA∙B.
Теперь, когда мы знаем, что оно определено, как нам узнать размеры A∙BA \пули BA∙B?
Свойство измерения
Чтобы найти размеры A∙BA\пули BA∙B, нам нужно сначала посмотреть размеры и отдельно.
Уравнение 7: Пример заданной матрицы, часть 2Теперь мы собираемся расположить размеры матриц рядом следующим образом:
Уравнение 7: Пример заданной матрицы pt.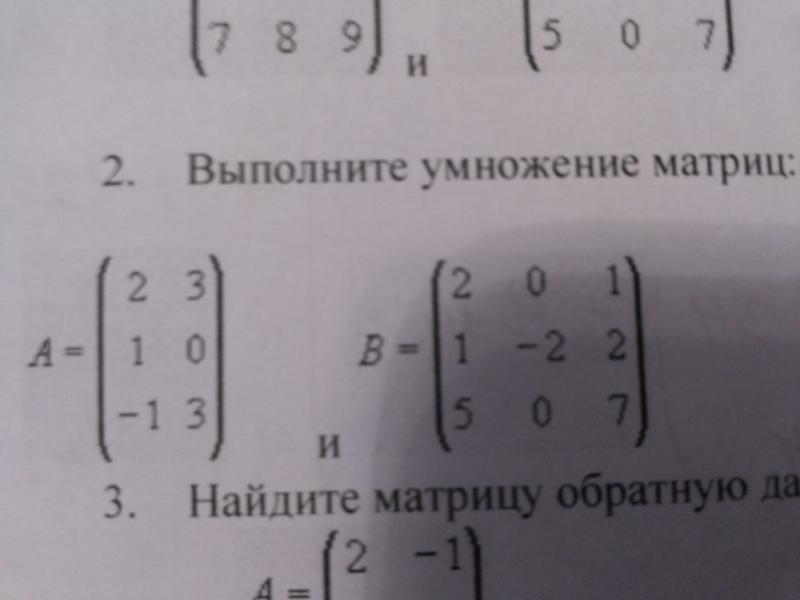 3
3Сейчас мы собираемся взять первое число и последнее число и объединить их, чтобы получить размеры A∙BA \ пули BA∙B. Обратите внимание, что первое число — 2 , а последнее — 4 . Таким образом, размеры A∙BA \пули BA∙B будут:
Уравнение 7: Пример заданной матрицы, часть 4Теперь, когда мы знаем размеры матрицы, мы можем просто вычислить каждую запись, используя скалярные произведения. Это даст нам:
Уравнение 7: Пример заданной матрицы pt.5Теперь, когда мы очень хорошо знаем, как умножать матрицы, почему бы не взглянуть на некоторые правила умножения матриц?
Свойства умножения матрицИтак, какие свойства на самом деле имеет умножение матриц? Во-первых, давайте формально все определим.
Пусть X,Y,ZX, Y, ZX,Y,Z — матрицы, InI_{n}In — единичная матрица, OnO_{n}On — нулевая матрица. Если все пять из этих матриц имеют одинаковые размеры, то мы будем иметь следующие свойства умножения матрицы на матрицу:
Формула 3: свойства умножения матриц Ассоциативное свойство утверждает, что порядок умножения не имеет значения. Другими словами, вычисление X∙YX \bullet YX∙Y и затем умножение на ZZZ даст вам тот же результат, что и вычисление Y∙ZY \bullet ZY∙Z с последующим умножением на XXX. Сделаем пример.
Другими словами, вычисление X∙YX \bullet YX∙Y и затем умножение на ZZZ даст вам тот же результат, что и вычисление Y∙ZY \bullet ZY∙Z с последующим умножением на XXX. Сделаем пример.
Вопрос 6 : Покажите, что свойство ассоциативности работает с этими матрицами:
Уравнение 8: Пример ассоциативного свойства, часть 1Глядя на левую часть уравнения в ассоциативном свойстве, мы видим, что (XY)Z(XY)Z(XY)Z дает:
Уравнение 8: Пример ассоциативного свойства pt.2Теперь, глядя на правую часть уравнения в ассоциативном свойстве, мы видим, что X(YZ)X(YZ)X(YZ) дает:
Уравнение 8: Пример ассоциативного свойства, часть 3Посмотрите, как левая и правая части уравнения равны. Следовательно, мы знаем, что свойство ассоциативности действительно работает! Опять же, это означает, что порядок умножения матриц не имеет значения!
Теперь следующим свойством является распространяемое свойство . В дистрибутивном свойстве указано, что:
Формула 4: Распределительная собственность Мы видим, что нам разрешено использовать технику фольги и для матриц. Чтобы показать, что это свойство работает, давайте рассмотрим пример.
Чтобы показать, что это свойство работает, давайте рассмотрим пример.
Вопрос 7 : Покажите, что свойство распределения работает для следующих матриц:
Уравнение 9: Пример распределительной собственности, часть 1Обратите внимание, что левая часть уравнения равна X(Y+Z)X(Y+Z)X(Y+Z). Отсюда вычисления, которые дают нам:
Уравнение 9: Пример распределительной собственности, часть 2Теперь давайте проверим, дает ли нам то же самое правая часть уравнения. Обратите внимание, что правая часть уравнения равна XY+XZXY + XZXY+XZ.Вычисление дает нам:
Уравнение 9: Пример распределительной собственности, часть 3Обратите внимание, что левая часть уравнения точно такая же, как и правая часть уравнения. Таким образом, мы можем подтвердить, что свойство дистрибутива действительно работает.
Является ли умножение матриц коммутативным?
Мы знаем, что умножение матриц удовлетворяет как ассоциативным, так и дистрибутивным свойствам, однако о коммутативности мы вообще не говорили. Означает ли это, что умножение матриц ему не удовлетворяет? На самом деле это не так, и мы можем проверить это на примере.
Означает ли это, что умножение матриц ему не удовлетворяет? На самом деле это не так, и мы можем проверить это на примере.
Вопрос 8 : Если умножение матриц коммутативно, то должно быть верно следующее:
Уравнение 10: нарушение коммутативного свойства, часть 1Показать, что XYeqYXXY эквивалентно YXXYeqYX, если
Уравнение 10: нарушение коммутативного свойства, часть 2Сначала мы вычисляем левую часть уравнения. Вычисление XYXYXY дает нам:
Уравнение 10: нарушение коммутативного свойства, часть 3Теперь вычислив правую часть уравнения, мы имеем:
Уравнение 10: нарушение коммутативного свойства pt.4Как видите,
Уравнение 10: нарушение коммутативного свойства, часть 5Потому что у нас есть
Уравнение 10: нарушение коммутативного свойства, часть 6Эти две матрицы совершенно разные.
Теперь осталось еще несколько свойств умножения матриц. Однако эти свойства относятся к нулевой и единичной матрицам.
Умножение матриц для нулевой матрицы
Свойство матричного умножения для нулевой матрицы утверждает следующее:
Формула 5: умножение матриц на нулевую матрицу, где ООО — нулевая матрица.
Это означает, что если вы умножите нулевую матрицу на другую ненулевую матрицу, то вы получите нулевую матрицу. Давайте проверим, так ли это на примере.
Вопрос 9 : Покажите, что уравнение OX=OOX = OOX=O и XO=OXO = OXO=O выполняется, если:
Уравнение 11: Умножение матриц для примера нулевой матрицы, часть 1Давайте сначала посмотрим на уравнение
Уравнение 11: Умножение матриц для примера нулевой матрицы, часть 2Обратите внимание, что вычисление OXOXOX дает нам:
Уравнение 11: Умножение матриц для примера с нулевой матрицей, часть.3Мы видим, что OX=OOX = OOX=O, так что уравнение выполняется. Точно так же, если мы посчитаем XOXOXO, мы получим:
Уравнение 11: Умножение матриц для примера нулевой матрицы, часть 4Мы видим, что уравнение XO=OXO = OXO=O выполняется, так что мы закончили.
Умножение матриц для матрицы идентичности
А как насчет свойства умножения матриц для единичных матриц? Ну, в свойстве указано следующее:
Формула 6: умножение матриц для матрицы идентичности, где InI_{n}In — единичная матрица размера n×nn \times nn×n.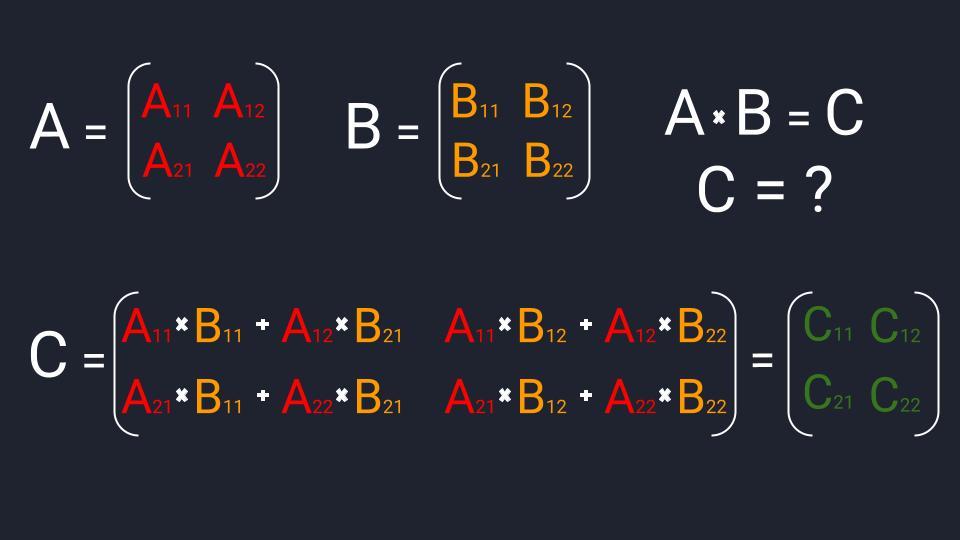 Опять же, мы можем видеть, что следующие уравнения выполняются на примере.
Опять же, мы можем видеть, что следующие уравнения выполняются на примере.
Вопрос 10 : Покажите, что уравнения XI2=XX I_{2} = XXI2=X и I2X=XI_{2} X = XI2X=X выполняются со следующими матрицами
Уравнение 12: Умножение матриц для примера единичной матрицы, часть 1Итак, для уравнения XI2=XX I_{2} = XXI2=X имеем:
Уравнение 12: Умножение матриц для примера единичной матрицы, часть 2Итак, уравнение верно. Подобно уравнению I2X=XI_{2}X = XI2X=X, мы имеем:
Уравнение 12: Умножение матриц для примера единичной матрицы, часть.3Опять же, уравнение верно. Итак, мы закончили с вопросом, и оба уравнения верны. На этом заканчиваются все свойства матричного умножения. Теперь, если вы хотите посмотреть на реальное применение умножения матриц, я рекомендую вам прочитать эту статью.
https://www.mathsisfun.com/алгебра/matrix-multipliing.html
Умножение матриц — 2×2, 3×3
Умножение матриц или умножение матриц — одна из операций, которые можно выполнять над матрицами в линейной алгебре. Умножение матрицы A на матрицу B возможно, когда обе заданные матрицы A и B совместимы. Умножение матриц — это бинарная операция, которая дает матрицу из двух заданных матриц.
Умножение матрицы A на матрицу B возможно, когда обе заданные матрицы A и B совместимы. Умножение матриц — это бинарная операция, которая дает матрицу из двух заданных матриц.
Умножение матриц было впервые введено в 1812 году французским математиком Жаком Филиппом Мари Бине для представления линейных карт с использованием матриц. Давайте разберемся с правилом умножения матриц в следующих разделах.
Что такое умножение матриц?
Умножение матриц — это двоичная операция, результатом которой также является матрица при умножении двух матриц.В линейной алгебре умножение матриц возможно только тогда, когда матрицы совместимы. В общем случае умножение матриц, в отличие от арифметического, не является коммутативным, а это означает, что умножение матриц A и B, заданных как AB, не может быть равно BA, т. е. AB ≠ BA. Поэтому порядок умножения для умножения матриц важен.
Предположим, у нас есть две матрицы A и B, произведение матрицы A на матрицу B можно представить как (AB). Это означает, что результирующая матрица для умножения любой матрицы m × n «A» на матрицу «B» размера n × p может быть представлена как матрица «C» порядка m × p.Давайте разберемся с этой концепцией подробно в следующем разделе.
Это означает, что результирующая матрица для умножения любой матрицы m × n «A» на матрицу «B» размера n × p может быть представлена как матрица «C» порядка m × p.Давайте разберемся с этой концепцией подробно в следующем разделе.
Две матрицы A и B называются совместимыми, если количество столбцов в A равно количеству строк в B. Это означает, что если A — матрица порядка m×n, а B — матрица порядка n×p , то можно сказать, что матрицы A и B совместимы.
Правила умножения матриц
Как мы изучили, две матрицы можно перемножать только тогда, когда они совместимы, а это означает, что для существования умножения матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице, в приведенном выше случае ‘н’.Если A — матрица порядка m×n, а B — матрица порядка n×p, то порядок произведения матриц равен m×p.
Примеры:
а) Умножение матрицы 4 × 3 на матрицу 3 × 4 верно и дает матрицу порядка 4 × 4
б) матрицы 7×1 и 1×2 совместимы; произведение дает матрицу 7 × 2.
c) Умножение матрицы 4 × 3 на матрицу 2 × 3 НЕВОЗМОЖНО.
Как умножать матрицы?
Общий процесс умножения матриц мы можем понять по методике: «Первые строки умножаются на столбцы (элемент за элементом), а затем строки заполняются. Перемножение матриц можно выполнить с помощью следующих шагов:
- Убедитесь, что количество столбцов в матрице 1 st равно количеству строк в матрице 2 nd (совместимость матриц).
- Умножьте элементы строки i th первой матрицы на элементы столбца j th второй матрицы и сложите произведения. Это будет элемент, который находится в строке i th и столбце j th результирующей матрицы.
- Разместите добавленные товары на соответствующие позиции.
Давайте лучше разберем эти шаги для умножения матриц на примере.
Пример: Умножьте приведенные ниже матрицы, чтобы найти их произведение \( \begin{pmatrix}
1 и 2 \
3 и 4 \ 5 и 1 \
\end{pmatrix} \text{and}\begin{pmatrix}
2\\
4\
\end{pmatrix}
\).
Решение: Данные матрицы имеют порядок 3×2 и 2×1 . Таким образом, t заданные матрицы совместимы, мы можем выполнить умножение матриц, и матрица произведения будет иметь порядок 3×1.
\(\begin{pmatrix}
1 и 2 \
3 и 4 \ 5 и 1 \
\end{pmatrix}.\begin{pmatrix}
2\\
4\
\end{pmatrix}\\\\
= \begin{pmatrix}
(1\times2)+(2\times4) \\
(3\times2)+(4\times4) \\ (5\times2)+(1\times4) \\
\end{pmatrix} \\\\ = \begin{pmatrix}
2+8 \\
6+16\10+4\
\end{pmatrix}
\\\\
= \begin{pmatrix}
10\
22\14\
\end{pmatrix}\)
Следовательно, матрица произведения равна \(\begin{pmatrix}
10\
22\14\
\end{pmatrix}
\)
В результирующей матрице мы видим, что первый элемент первой строки получается путем умножения элементов первой строки первой матрицы на соответствующие элементы первого столбца второй матрицы и последующего сложения.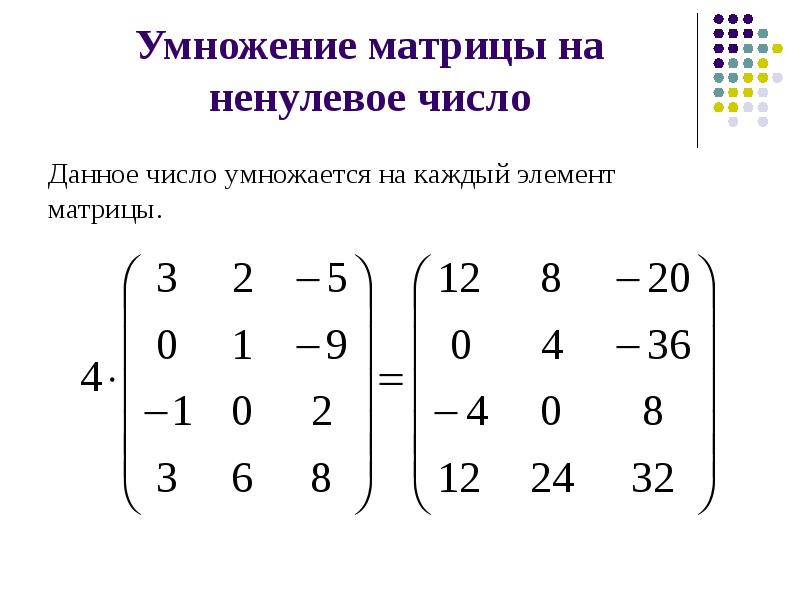 т. е. в общем случае найти элемент в строке i th и столбце j th в матрице произведения,
т. е. в общем случае найти элемент в строке i th и столбце j th в матрице произведения,
- Возьмем элементы i -й -й строки первой матрицы.
- Возьмем элементы j -го -го столбца второй матрицы.
- Умножьте соответствующие элементы.
- Добавить все продукты.
Формула умножения матриц 2×2
Процесс одинаков для матрицы любого порядка.Умножаем элементы каждой строки первой матрицы на элементы каждого столбца второй матрицы (поэлементно), как показано на рисунке. Наконец, мы добавляем продукты. Результатом произведения двух матриц 2×2 снова является матрица 2×2.
Формула умножения матриц 3×3
Умножение матриц 3×3 можно выполнить с помощью формулы умножения матриц, так как любые две матрицы 3×3 совместимы. Процесс точно такой же для матрицы любого порядка.Результатом произведения двух матриц 3×3 снова является матрица 3×3.
Здесь матрицы имеют одинаковые размеры, поэтому результирующая матрица также имеет одинаковую размерность 3×3.
Пример:
\(\ влево(\begin{массив}{ррр}
1&2&-1\
3 & 2 & 0 \
-4 и 0 и 2
\end{массив}\right)\) \(\left(\begin{массив}{rrr}
3 и 4 и 2 \
0&1&0\
-2 и 0 и 1
\конец{массив}\справа)\)
= \(\left(\begin{массив}{rrr}
1(3)+2(0)+(-1)(-2) и 1(4)+2(1)+(-1)0 и 1(2)+2(0)+(-1)( 1)\
3(3)+2(0)+(0)(-2) и 3(4)+2(1)+(0)0 и 3(2)+2(0)+(0)(1) \ \
-4(3)+0(0)+(2)(-2) и -4(4)+0(1)+(2)0 и -4(2)+0(0)+(2)( 1)\
\конец{массив}\справа)\)
= \(\left(\begin{массив}{rrr}
5 и 6 и 1 \
9 и 14 и 6 \
-16&-16&-6\
\конец{массив}\справа)\)
Свойства умножения матриц
Существуют определенные свойства операции умножения матриц в линейной алгебре в математике.Эти свойства приведены ниже,
- Некоммутативный: Умножение матриц является некоммутативным, т.
 е. для умножения двух матриц A и B AB ≠ BA.
е. для умножения двух матриц A и B AB ≠ BA. - Дистрибутивность: Свойство дистрибутивности можно применять при перемножении матриц, т. е. A(B + C) = AB + BC, учитывая, что A, B и C совместимы.
- Произведение со скаляром: Если произведение матриц A и B, AB определено, то c(AB) = (cA)B = A(Bc), так что c является скаляром.
- Транспонирование: Транспонирование произведения матриц A и B может быть задано как (AB) T = B T A T , где T обозначает транспонирование.
- Комплексное сопряжение: Если A и B комплексные записи, то (AB) * = B * A *
- Ассоциативность: Умножение матриц является ассоциативным. Для трех матриц A, B и C, произведения (AB)C и A(BC) определены, тогда (AB)C = A(BC).
Нестандартное мышление:
- Используя приведенные ниже матрицы, проверьте, является ли умножение матриц коммутативным или нет.

\( \begin{pmatrix}
1&0\\
2 и 4 \
\end{pmatrix} \text{and}\begin{pmatrix}
6 и 8\\
4 и 3 \
\end{pmatrix}
\) - Является ли умножение матриц ассоциативным?
Важные примечания по умножению матриц:
- Для умножения матриц данные матрицы должны быть совместимы.
- Порядок матрицы произведения можно получить по следующему правилу:
Если A — матрица порядка m×n, а B — матрица порядка n×p, то порядок матрицы произведения равен m×p. - Умножение матриц указывает на умножение строк на столбцы.
☛ Похожие темы:
Часто задаваемые вопросы по умножению матриц
Что такое умножение матриц в линейной алгебре?
Умножение матриц — одна из бинарных операций, которые можно применять к матрицам в линейной алгебре.Чтобы умножить две матрицы A и B, количество столбцов в матрице A должно быть равно количеству строк в матрице B. ⇒AB существует.
⇒AB существует.
Как умножать матрицы 3×3?
матрицы 3×3 в математике могут быть умножены путем умножения строк первой матрицы на столбцы второй матрицы для получения соответствующих элементов матрицы произведения.
Что такое формула умножения матриц?
Формула умножения матриц используется для выполнения умножения матриц в целом.Например, для матриц 3×3 формула выглядит следующим образом:
Можно ли перемножать матрицы порядка 2×3 и 2×2?
Нет, мы не можем умножать матрицы 2×3 и 2×2, потому что для умножая матрицы, две матрицы должны быть совместимы. Поскольку количество столбцов в первой матрице (3) не равно количеству строк во второй матрице (2), мы не можем выполнить умножение матриц для этого случая.
Какова цель умножения матриц?
Умножение матриц важно для облегчения вычислений в линейной алгебре и используется для представления линейных карт.Это важный инструмент во многих областях математики, а также в прикладной математике, статистике, физике, экономике и технике.
Чему равно произведение матриц порядков 2×1 и 2×2?
Нет, их нельзя перемножить, так как эти матрицы несовместимы. Количество столбцов первой матрицы не равно количеству строк второй матрицы.
Когда мы можем найти произведение матриц?
Умножение матриц возможно, только если матрицы совместимы i.е., умножение матриц допустимо только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы.
Всегда ли умножение матриц коммутативно?
Умножение матриц, в отличие от арифметического умножения, не является коммутативным. Это означает, что порядок умножения матриц имеет значение.
Всегда ли определено умножение матриц?
Умножение матриц возможно только в том случае, если матрицы совместимы.Чтобы умножение матриц существовало, количество столбцов в первой матрице должно быть равно количеству строк во второй матрице
Умножение матриц
Вы можете умножить только два
матрицы
если их
Габаритные размеры
являются
совместимый
, что означает, что количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Если А знак равно [ а я Дж ] является м × н матрица и Б знак равно [ б я Дж ] является н × п матрица, продукт А Б является м × п матрица.
А Б знак равно [ с я Дж ] , где с я Дж знак равно а я 1 б 1 Дж + а я 2 б 2 Дж + … + а я н б н Дж .
(Запись в
я
й
ряд и
Дж
й
столбец обозначается двойным нижним индексом
а
я
Дж
,
б
я
Дж
, и
с
я
Дж
.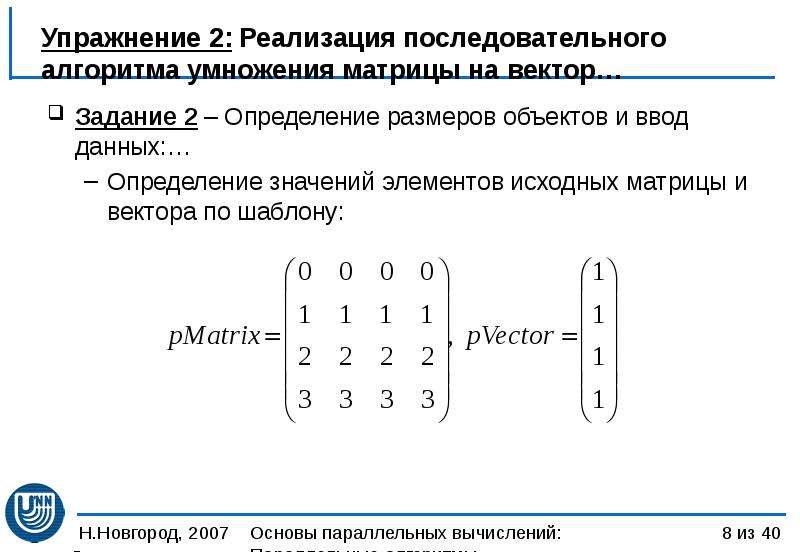 Например, запись
а
23
это запись во второй строке и третьем столбце.)
Например, запись
а
23
это запись во второй строке и третьем столбце.)
Определение матричного умножения указывает на умножение строк за столбцами, где элементы в я й ряд А умножаются на соответствующие записи в Дж й столбец из Б а затем добавить результаты.
Умножение матриц НЕ является коммутативным. Если ни А ни Б является единичной матрицей, А Б ≠ Б А .
Умножение строки на столбец
Мы начнем с того, что покажем вам, как умножить 1 × н матрица н × 1 матрица. Первый — это всего лишь одна строка, а второй — один столбец. По вышеприведенному правилу продукт является 1 × 1 матрица; другими словами, одно число.
Во-первых, давайте назовем записи в строке
р
1
,
р
2
,
. ..
,
р
н
, а записи в столбце
с
1
,
с
2
,
…
,
с
н
. Тогда произведение строки и столбца равно
1
×
1
матрица
..
,
р
н
, а записи в столбце
с
1
,
с
2
,
…
,
с
н
. Тогда произведение строки и столбца равно
1
×
1
матрица
[ р 1 с 1 + р 2 с 2 + … + р н с н ] .
Пример:
Найдите продукт.
[ 1 4 0 ] ⋅ [ 2 − 1 5 ]
Мы должны умножить
1
×
3
матрица
1
×
3
матрица. Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.
Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.
Продукт:
[ ( 1 ) ( 2 ) + ( 4 ) ( − 1 ) + ( 0 ) ( 5 ) ] знак равно [ 2 + ( − 4 ) + 0 ] знак равно [ − 2 ]
Умножение больших матриц
Теперь, когда вы знаете, как умножать строку на столбец, умножать большие матрицы несложно. Для вступления в
я
й
ряд и
Дж
й
столбец матрицы продуктов, умножьте каждую запись в
я
й
строку первой матрицы соответствующей записью в
Дж
й
столбец второй матрицы и сложения результатов.
Для вступления в
я
й
ряд и
Дж
й
столбец матрицы продуктов, умножьте каждую запись в
я
й
строку первой матрицы соответствующей записью в
Дж
й
столбец второй матрицы и сложения результатов.
Возьмем следующую задачу на умножение 2 × 3 матрица с 3 × 2 матрица, чтобы получить 2 × 2 матрица как произведение.Элементы матрицы произведения называются е я Дж когда они в я й ряд и Дж й столбец.
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 − 1 0 2 − 1 ] знак равно [ е 11 е 12 е 21 е 22 ]
Получить
е
11
, умножить ряд
1
первой матрицы по столбцу
1
второй.
е 11 знак равно [ 1 0 1 ] ⋅ [ 3 − 1 2 ] знак равно 1 ( 3 ) + 0 ( − 1 ) + 1 ( 2 ) знак равно 5
Получить е 12 , умножить ряд 1 первой матрицы по столбцу 2 второй.
е 12 знак равно [ 1 0 1 ] ⋅ [ 5 0 − 1 ] знак равно 1 ( 5 ) + 0 ( 0 ) + 1 ( − 1 ) знак равно 4
Получить
е
21
, умножить ряд
2
первой матрицы по столбцу
1
второй.
е 21 знак равно [ 0 1 2 ] ⋅ [ 3 − 1 2 ] знак равно 0 ( 3 ) + 1 ( − 1 ) + 2 ( 2 ) знак равно 3
Получить е 22 , умножить ряд 2 первой матрицы по столбцу 2 второй.
е 22 знак равно [ 0 1 2 ] ⋅ [ 5 0 1 ] знак равно 0 ( 5 ) + 1 ( 0 ) + 2 ( − 1 ) знак равно − 2
Записав матрицу произведения, получим:
[ е 11 е 12 е 21 е 22 ] знак равно [ 5 4 3 − 2 ]
Поэтому мы показали:
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 − 1 0 2 − 1 ] знак равно [ 5 4 3 − 2 ]
Матрица
Умножение определено (стр. Как и при сложении матриц, размеры матриц имеют значение, когда мы умножаем.Для умножения матриц для работы столбцы второй матрицы должны иметь одинаковые номера элементов, как и строки первой матрицы.
Если, используя вышеуказанные матрицы, Б имел бы только две строки, его столбцы были бы слишком короткими для умножения
против рядов А .Затем « AB »
не существовало бы; продукт был бы «неопределенным».
Аналогично, если B имел, скажем, четыре ряда или, если A имел две или четыре колонки, затем AB не существовало бы, потому что A и В не было бы нужных размеров. Другими словами, для AB существовать (то есть, чтобы сам процесс умножения матриц был способный функционировать разумно), A должно иметь то же количество столбцов, что и B имеет ряды; глядя на матрицы, строки A должны быть той же длины, что и столбцы B . Вы можете использовать этот факт для быстро проверить, определено ли данное умножение. Напишите продукт по размерам матрицы. В случае вышеуказанной проблемы A 23 года а В равно 32, так АВ есть (23)(32). Средние значения совпадают: …так что умножение определено. Кстати, вы помните, что AB , матрица продукта, была 22. Вы также можете увидеть это на размерах: Используя это, вы можете видеть, что ВА должна быть отличная матрица от AB , потому что: Продукт ВА определено (то есть мы можем сделать умножение), но произведение, когда
матрицы перемножаются в таком порядке, будет 33,
не 22.
Умножение работает так же, как и в предыдущей задаче, проходя по рядам и вниз столбцы.Я не буду пытаться снова рисовать свои руки, но вы можете видеть вычисления в следующих цветах: Авторское право Элизабет Стапель 2003-2011 Все права защищены Тогда ответ: Умножение матриц
Вероятно, впервые Коммутативный
Собственность когда-либо
была проблема. Помните, когда они сделали большое дело, еще в средней школе
или ранее, примерно как « аб. << Предыдущая Топ | 1 | 2 | 3 | Возвращение к индексу Далее >>
|
|
Операции с матрицами
Что касается линейной алгебры, то двумя наиболее важными операциями с векторами являются сложение векторов [сложение двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр).Аналогичные операции определены для матриц.
Добавление матрицы . Если А и В матрицы одинакового размера , то их можно сложить. (Это похоже на ограничение на добавление векторов, а именно, могут быть добавлены только векторы из одного и того же пространства R n ; например, вы не можете добавить 2-вектор к 3-вектору.) Если = [ A IJ ] и B = [ B IJ ] Оба M x N Matrices, затем их сумма, C = A + B , также является матрицей m x n , и ее элементы задаются формулой
Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B .
Пример 1 : Рассмотрим следующие матрицы:
Какие два можно добавить? Какова их сумма?
Поскольку можно добавлять только матрицы одинакового размера, определяется только сумма F + H ( G нельзя добавлять ни к F , ни к H ). Сумма F и H равна
Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (когда оно определено) также коммутативно; то есть для любых матриц A и B одинакового размера A + B всегда будет равно B + A .
Пример 2 : Если любую матрицу A добавить к нулевой матрице того же размера, то результат явно равен A :
Это матричный аналог утверждения a + 0 = 0 + a = a , которое выражает тот факт, что число 0 является аддитивной единицей в множестве действительных чисел.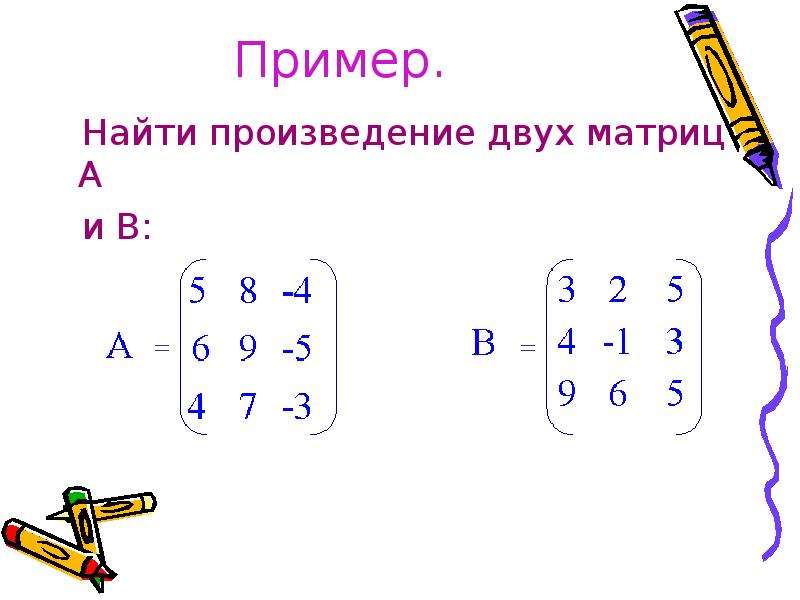
Пример 3 : Найдите матрицу B такую, что A + B = C , где
Если
, тогда матричное уравнение A + B = C становится
Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, это последнее уравнение подразумевает
Следовательно,
Этот пример мотивирует определение матрицы вычитанием : если A и B являются матрицами одинакового размера, то элементы A − B находятся путем простого вычитания элементов B из соответствующие записи A .Поскольку уравнение A + B = C эквивалентно B = C − A , использование матричного вычитания выше даст тот же результат:
Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то
Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то
То есть матрица кА получается умножением каждой записи А на к .
Пример 4 : Если
, то скалярное число 2 A получается путем умножения каждой записи A на 2:
Пример 5 : Если A и B являются матрицами одинакового размера, то A − B = A + (− B ), где B кратно 8000s − , (−1) В . Если
, затем
Это определение вычитания матриц согласуется с определением, показанным в примере 8.
Пример 6 : Если
, затем
Умножение матриц . Безусловно, наиболее важной операцией с матрицами является умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя n ‐векторами. Записав r в виде матрицы строк 1 x n и c в виде матрицы столбцов n x 1, скалярное произведение r и c равно
Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя n ‐векторами. Записав r в виде матрицы строк 1 x n и c в виде матрицы столбцов n x 1, скалярное произведение r и c равно
Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей.Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом произведении: сначала идет вектор-строка, затем — вектор-столбец.
Теперь последний шаг: как перемножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно совпадать с количеством строк B ; если это условие не выполняется, то продукт AB не определен. Этот критерий следует из установленного выше ограничения для умножения матрицы строк r на матрицу столбцов c , а именно, что количество элементов в r должно совпадать с числом элементов в c . Если A равно m x n и B равно n x p , то произведение AB определено, и размер матрицы произведения м х 8 АВ 908 будет р . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размерность продукта:
Если A равно m x n и B равно n x p , то произведение AB определено, и размер матрицы произведения м х 8 АВ 908 будет р . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размерность продукта:
мышление M x N Matrix A , состоящий из векторов ROW R R 1 , R 2 , …, R M от R N и N x Matrix x P Matrix B Как состоит из разных векторов C C 1 , C 2 , …, C P от R п ,
и
Правило для вычисления записей матрицы продукта ab R R I · C J 23 J = ( AB ) IJ , то есть
Пример 7 : Даны две матрицы
определить, какой матричный продукт, AB или BA , определен и оценить его.
Поскольку A имеет размер 2 x 3, а B имеет размер 3 x 4, произведение AB в указанном порядке определено, а размер матрицы произведения AB будет равен 2 x 4. Произведение BA определяется как , а не как , поскольку первый фактор ( B ) имеет 4 столбца, а второй фактор ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы, чтобы можно было определить их произведение.
Скалярное произведение строки 1 в A и столбца 1 в B дает запись (1, 1) в AB . С 90 005
запись (1, 1) в AB равна 1:
Скалярное произведение строки 1 в A и столбца 2 в B дает запись (1, 2) в AB ,
и скалярное произведение строки 1 в A и столбца 3 в B дает запись (1, 3) в AB :
Первая строка произведения завершается скалярным произведением строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB :
Теперь для второй строки AB : Скалярное произведение строки 2 в A и столбца 1 в B дает (2, 1) запись в AB ,
и скалярное произведение строки 2 в A и столбца 2 в B дает запись (2, 2) в AB :
Наконец, скалярное произведение строки 2 в A со столбцами 3 и 4 в B дает (соответственно) (2, 3) и (2, 4) записи в AB :
Следовательно,
Пример 8 : Если
и
вычислить запись (3, 5) произведения CD .
Во-первых, обратите внимание, что, поскольку C равно 4 x 5, а D равно 5 x 6, произведение CD действительно определено, и его размер равен 4 x 6. Однако нет необходимости вычислять все двадцать четыре записи CD , если требуется только одна конкретная запись. Запись (3, 5) числа CD представляет собой скалярное произведение строки 3 числа C и столбца 5 числа D :
.Пример 9 : Если
убедиться, что
но
В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; на самом деле, они даже не одного размера!
Предыдущий пример иллюстрирует, пожалуй, самое важное различие между умножением скаляров и умножением матриц.Для действительных чисел a и b всегда выполняется уравнение ab = ba , т. е. умножение действительных чисел коммутативно; порядок, в котором записаны факторы, не имеет значения. Однако утверждение о том, что умножение матриц коммутативно, совершенно неверно. Для матриц А и В , приведенных в Примере 9, были определены оба продукта АВ и ВА , но они определенно не были идентичными. На самом деле матрица АВ была 2 х 2, а матрица ВА была 3 х 3.Вот еще одна иллюстрация некоммутативности умножения матриц: Рассмотрим матрицы
Однако утверждение о том, что умножение матриц коммутативно, совершенно неверно. Для матриц А и В , приведенных в Примере 9, были определены оба продукта АВ и ВА , но они определенно не были идентичными. На самом деле матрица АВ была 2 х 2, а матрица ВА была 3 х 3.Вот еще одна иллюстрация некоммутативности умножения матриц: Рассмотрим матрицы
Поскольку C имеет размер 3 x 2, а D имеет размер 2 x 2, продукт CD определен, его размер равен 3 x 2, а
Произведение DC , однако, не определено, поскольку количество столбцов D (которое равно 2) не равно количеству строк C (которое равно 3). Следовательно, CD ≠ DC , поскольку DC даже не существует.
Из-за чувствительности к порядку записи коэффициентов обычно не говорят просто: «Умножьте матрицы на и B на ». Обычно важно указать, какая матрица стоит первой, а какая второй в продукте. По этой причине выражение «Умножить A справа на B » означает, что получится произведение AB , а «Умножить A слева на B » означает образование произведения BA . .
По этой причине выражение «Умножить A справа на B » означает, что получится произведение AB , а «Умножить A слева на B » означает образование произведения BA . .
Пример 10 : Если
и x — это вектор (−2, 3), покажите, как A можно умножить справа на x , и вычислите произведение.
Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Таким образом, если 90 265 x 90 266 записывается как матрица 2 x 1 90 807 столбцов 90 808 90 005
, то можно вычислить произведение A x , и результатом будет другая матрица столбцов 2 x 1:
Пример 11 : Рассмотрим матрицы
Если A справа умножить на B , получится
, но если A умножить слева на B , получится
Обратите внимание, что оба продукта определены и имеют одинаковый размер, но они не равны.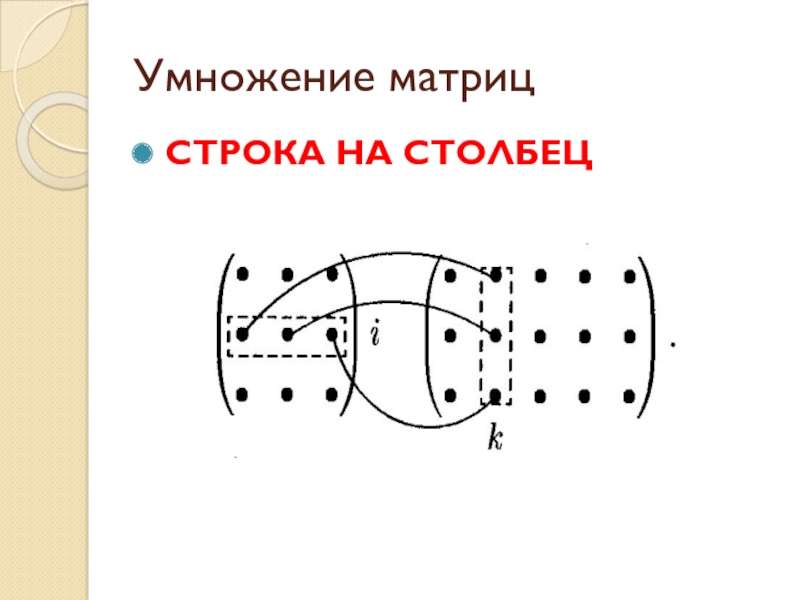
Пример 12 : Если A и B являются квадратными матрицами такими, что AB = BA , то говорят, что A и B коммутируют . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют.
Пусть
— две произвольные диагональные матрицы 2 x 2. Затем
и
с A 11 B 11 = B 11 11 и 11 и A 22 22 B 22 = B 22 A 22 , AB действительно равно BA , что и требовалось.
Хотя умножение матриц обычно не коммутативно, оно иногда коммутативно; например, если
, затем
Несмотря на подобные примеры, следует отметить, что в общем случае умножение матриц не является коммутативным .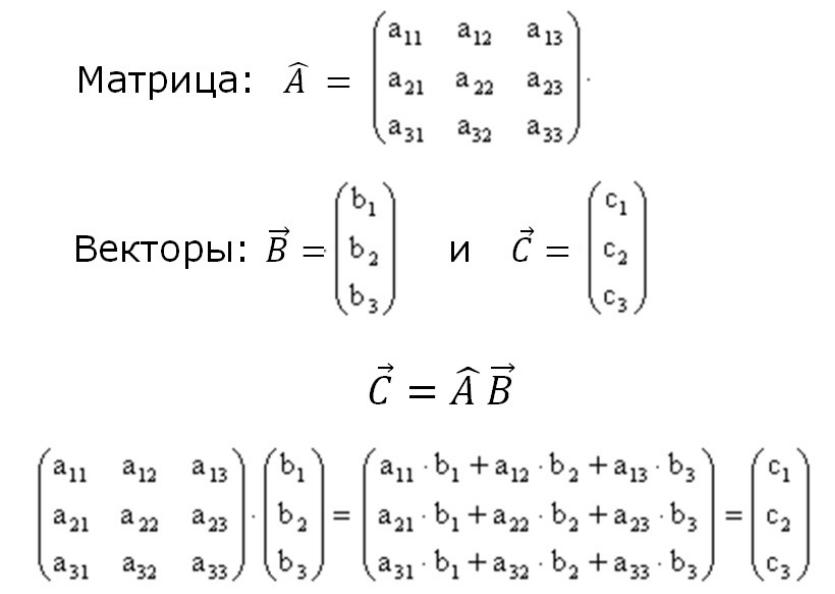
Существует еще одно различие между умножением скаляров и умножением матриц. Если a и b — действительные числа, то уравнение ab = 0 подразумевает, что a = 0 или b = 0.То есть произведение действительных чисел может равняться 0 только в том случае, если хотя бы один из множителей сам равен 0. Однако аналогичное утверждение для матриц неверно. Например, если
, затем
Обратите внимание, что хотя ни G , ни H не являются нулевой матрицей, продукт GH является таковым.
Еще одно различие между умножением скаляров и умножением матриц заключается в отсутствии общего закона сокращения для умножения матриц.Если a, b и c являются действительными числами, где a ≠ 0, то, исключая множитель a , уравнение ab = ac подразумевает b = c . Для матричного умножения такого закона не существует; то есть утверждение AB = AC означает, что , а не подразумевает B = C , даже если A не равно нулю. Например, если
Например, если
потом оба
и
Таким образом, хотя AB = AC и A не является нулевой матрицей, B не равно C .
Пример 13 : Хотя умножение матриц не всегда коммутативно, оно равно всегда ассоциативно . То есть, если A, B и C являются любыми тремя матрицами, для которых определено произведение (AB)C , то произведение A(BC) также определено, и
То есть, пока порядок факторов неизменен, то, как они сгруппированы , не имеет значения.
Проверить закон ассоциативности для матриц
Первый с
продукт (AB)C это
Сейчас, с
продукт A(BC)
Следовательно, (AB)C = A(BC) , как и ожидалось.Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны для устранения какой-либо неоднозначности, потому что двусмысленности нет.
Пример 14 : Для матриц
проверьте уравнение ( AB ) T = B T A T .
Первый,
подразумевает
Сейчас, с
B T A T действительно равно ( AB ) T .На самом деле уравнение
справедливо для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если произведение AB определено, то транспонирование произведения равно произведению транспонирования в обратном порядке .
Матрицы тождества . Нулевая матрица 0 m x n играет роль аддитивного тождества в наборе m x n матриц точно так же, как число 0 играет роль в множестве действительных чисел (вспомним пример 7).То есть, если A является матрицей m x n и 0 = 0 m x n , то
Это матричный аналог утверждения, что для любого действительного числа a ,
Имея на руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как
Есть ли матрица, играющая эту роль ? Рассмотрим матрицы
и убедитесь, что
и
Таким образом, AI = IA = A . В самом деле, можно легко показать, что для этой матрицы I оба произведения AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно,
В самом деле, можно легко показать, что для этой матрицы I оба произведения AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно,
— это мультипликативная идентичность в наборе матриц 2 x 2. Аналогично, матрица
— это мультипликативная идентичность в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I 3 — это матрица [δ ij ] 3 x 3 .) В общем случае матрица I n — диагональная матрица nxn , в которой каждый диагональный элемент равен 1, — называется единичной матрицей порядка n и служит мультипликативным тождеством в множестве всех Матрицы nxn .
Существует ли мультипликативная идентичность в наборе всех m x n матриц, если m ≠ n ? Для любой матрицы A в м мкн MXN ( R ), матрица I M M M — это Left Identity ( I M A = A ), а I N — это правильный идентификатор ( AI n = A ). Таким образом, в отличие от набора n x n матриц, набор неквадратных m x n матриц не обладает кв. двусторонней тождественностью, потому что I m ≠ I n n , если
Таким образом, в отличие от набора n x n матриц, набор неквадратных m x n матриц не обладает кв. двусторонней тождественностью, потому что I m ≠ I n n , если
Пример 15 : Если A является квадратной матрицей, то A 2 обозначает произведение AA, A 3 обозначает произведение AAA и так далее. Если А это матрица
показывают, что A 3 = − A .
Расчет
показывает, что A 2 = − I . Умножение обеих частей этого уравнения на A дает A 3 = − A , что и требовалось. [Техническое примечание: можно показать, что в определенном смысле набор матриц вида
, где a и b — действительные числа, структурно идентично набору комплексных чисел , a + bi . Поскольку матрица A в данном примере имеет такой вид (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i , а аналог матрицы матричное уравнение A 2 = − I , полученное выше, равно i 2 = −1, уравнение, определяющее мнимую единицу, i .]
Поскольку матрица A в данном примере имеет такой вид (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i , а аналог матрицы матричное уравнение A 2 = − I , полученное выше, равно i 2 = −1, уравнение, определяющее мнимую единицу, i .]
Пример 16 : Найти недиагональную матрицу, коммутирующую с
Задача состоит в том, чтобы задать недиагональную матрицу B такую, что AB = BA .Как и A , матрица B должна быть 2 x 2. Один из способов получить такую матрицу B состоит в том, чтобы сформировать A 2 , поскольку если B = A 2 ,
(Это уравнение доказывает, что A 2 будет коммутировать с A для любой квадратной матрицы A ; коммутировать с A . )
)
В данном случае
, который не является диагональным. Эта матрица B действительно коммутирует с A , что подтверждается вычислениями
и
Пример 17 : Если
докажи что
для каждого положительного целого числа n .
Несколько предварительных вычислений показывают, что данная формула верна:
Однако, чтобы установить, что формула верна для всех натуральных чисел n , необходимо привести общее доказательство.Это будет сделано здесь с использованием принципа математической индукции , который звучит следующим образом. Пусть P(n) обозначает предложение относительно натурального числа n . Если можно показать, что
и
, то оператор P(n) действителен для всех положительных целых чисел n . В данном случае оператор P(n) является утверждением
.Поскольку A 1 = A , утверждение P (1) безусловно верно, поскольку
Теперь, если предположить, что P(n) верно, то есть предположить, что
теперь необходимо установить справедливость утверждения P ( n + 1), которое равно
Но это утверждение действительно верно, потому что
По принципу математической индукции доказательство завершено.
Обратная матрица . Пусть a — заданное действительное число. Поскольку 1 является мультипликативной единицей в множестве действительных чисел, если существует число b такое, что
, затем b называется обратным или мультипликативным обратным и обозначается как −1 (или 1/ ). Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет данной матрицей n x n .Поскольку I = I n является мультипликативным тождеством в наборе n x n матриц, если существует матрица B такая, что
, то B называется (мультипликативным) , обратным числа A , и обозначается как A −1 (читается « A , обратное»).
Пример 18 : Если
, затем
с
и
Еще одно различие между умножением скаляров и умножением матриц обеспечивается существованием инверсий.Хотя каждое ненулевое действительное число имеет обратное, существуют ненулевые матрицы, у которых нет обратного .
Пример 19 : Показать, что ненулевая матрица
не имеет обратного.
Если бы у этой матрицы была обратная, то
для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка произведения также должна быть нулевой строкой:
(Когда звездочка * появляется в качестве записи в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку запись (2, 2) произведения не может равняться 1, произведение не может равняться единичной матрице. Поэтому невозможно построить матрицу, которая может служить обратной для A .
Если матрица имеет обратную, говорят, что она обратима . Матрица в примере 23 обратима, а матрица в примере 24 — нет. Позже вы изучите различные критерии для определения того, является ли данная квадратная матрица обратимой.
Пример 20 : Пример 18 показал, что
Учитывая, что
проверьте уравнение ( AB ) −1 = B −1 A −1 .
Сначала вычислите AB :
Далее вычислить B −1 A −1 :
Теперь, поскольку произведение AB и B −1 A −1 равно I ,
B −1 A −1 действительно является инверсией AB . На самом деле уравнение
верно для любых обратимых квадратных матриц того же размера.Это говорит о том, что если A и B — обратимые матрицы одного размера, то их произведение AB также обратимо, и обратное произведение равно произведению обратных в обратном порядке . (Сравните это уравнение с уравнением, включающим транспонирование в примере 14 выше.) Этот результат можно доказать в общем случае, применив ассоциативный закон для матричного умножения. С
и
следует, что ( AB ) -1 = B -1 A -1 , как и требовалось.
Пример 21 : обратная матрица
это
Покажите, что обратное число B T равно ( B −1 ) T .
Форма B T и ( B −1 ) T и умножить:
Этот расчет показывает, что ( B −1 ) T является обратным к B T .[Строго говоря, это показывает только то, что ( B −1 ) T есть прямое обратное B T , то есть когда оно умножает B справа, продукт является личностью. Также правда, что ( B -1 ) T 3) T B T = I , что означает ( B -1 ) T — это Left Extry из Б Т .Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратную, нет различия между левой и правой обратной матрицей.] Таким образом,
уравнение, которое на самом деле верно для любой обратимой квадратной матрицы B . Это уравнение говорит о том, что если матрица обратима, то обратима и ее транспонирование, а инверсия транспонирования — это транспонирование инверсии.
Пример 22 : Используйте распределительное свойство для умножения матриц, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: Если матрица 2 x 7 удовлетворяет 9080 уравнение D 2 − D − 6 I = 0 , какое выражение для D −1 ?
По приведенному выше распределительному свойству D 2 − D = D 2 − DI = D(D − I) .Поэтому из уравнения D 2 − D − 6 I = 0 следует D(D − I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
.
, что подразумевает
В качестве иллюстрации этого результата матрица
удовлетворяет уравнению D 2 − D − 6 I = 0 , как вы можете убедиться.С 90 005
и
матрица 1/6 ( DI ) действительно равна D -1 , как заявлено.
Пример 23 : Уравнение ( A + B ) 2 = A 2 + 2 AB + B 2 — это личность, если A и B являются действительными числами. Показать, однако, что ( A + B ) 2 = A 2 + 2 AB + B 2 — не Идентичность, если A и B являются матрицами 2 x 2.[Примечание: распределительные законы для матричного умножения: A ( B ± C ) = AB ± AC , приведенные в примере 22, и сопутствующий закон ( A ± B ) 08 С = АС ± до н.э. .]
Дистрибутивные законы для матричного умножения подразумевают
Поскольку умножение матриц не является коммутативным, BA обычно не будет равно AB , поэтому сумма BA + AB не может быть записана как 2 AB .В общем случае ( А + В ) 2 ≠ А 2 + 2 АВ + В 2 . [Любые матрицы A и B , которые не коммутируют (например, матрицы в приведенном выше примере 16), дадут конкретный контрпример к утверждению ( A + B ) 2 = A 2 + 2 AB + B 2 , что также установило бы, что это не личность.]
Пример 24 : Предположим, что B является обратимым. Если A коммутирует с B , покажите, что A также будет коммутировать с B −1 .
Доказательство . Сказать « A коммутирует с B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность:
Пример 25 : Число 0 имеет только один квадратный корень: 0.Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A такие, что A 2 = 0 .
Точно так же, как число a называется квадратным корнем из b , если a 2 = b , матрица A называется квадратным корнем из B , если А 2 = Б . Пусть
— произвольная матрица 2 x 2.Возведение его в квадрат и установка результата равным 0 дает
Элементы (1, 2) в последнем уравнении подразумевают b ( a + d ) = 0, что выполняется, если (Случай 1) b = 0 или (Случай 2) d = − и .
Случай 1. Если b = 0, диагональные записи подразумевают a = 0 и d = 0, а записи (2, 1) подразумевают, что c произвольно. Таким образом, для любого значения c каждая матрица формы
— это квадратный корень из 0 2×2 .
Случай 2. Если d = − a , то обе недиагональные записи будут равны 0, а диагональные записи будут равны a 2 + bc . Таким образом, если b и c выбраны так, что bc = − a 2 , A 2 будет равно 0 .
Аналогичная цепочка рассуждений, начинающаяся с (2, 1) записей, приводит либо к a = c = d = 0 (и b произвольно), либо к тому же выводу, что и раньше: пока b и c выбраны так, что bc = − a 2 , матрица A 2 будет равна 0 .
Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет обладать тем свойством, что ее квадрат равен нулевой матрице 2 на 2:
Поскольку существует бесконечно много значений a, b и c , таких что bc = − a 2 , нулевая матрица 0 2×2 имеет бесконечно много квадратных корней. Например, выбор a = 4, b = 2 и c = −8 дает ненулевую матрицу
.
, квадрат которого равен
Умножение матриц
Цели
- Понимать композиции преобразований.
- Понимать взаимосвязь между матричными произведениями и композициями матричных преобразований.
- Освойте основы алгебры с использованием матриц.
- Рецепт: умножение матриц (два способа).
- Фото: композиция трансформаций.
- Словарное слово: состав .
В этом разделе мы изучаем композиции преобразований. Как мы увидим, композиция — это способ объединения трансформаций в цепочку.Композиция матричных преобразований соответствует понятию , умножающего двух матриц вместе. Мы также обсуждаем сложение и скалярное умножение преобразований и матриц.
Композиция в линейной алгебре означает то же самое, что и в исчислении. Вот определение.
Определение
Пусть T:Rn→Rm и U:Rp→Rn — преобразования. Их композиция есть преобразование T◦U:Rp→Rm, определяемое
(Т◦U)(х)=Т(U(х)).
Составление двух преобразований означает объединение их в цепочку: T◦U — это преобразование, которое сначала применяет U, а затем применяет T (обратите внимание на порядок операций). Точнее, чтобы оценить T◦U на входном векторе x, сначала вы оцениваете U(x), затем берете этот выходной вектор U и используете его как входной вектор T: то есть (T◦U)(x )=Т(U(x)). Конечно, это имеет смысл только тогда, когда выходные данные U являются действительными входными данными T, то есть когда диапазон U содержится в домене T.
RpxRnU(x)RmT◦U(x)UTT◦UВот изображение композиции T◦U как «машины», которая сначала запускает U, затем получает его выходные данные и передает их в T; аналогичная картина есть в этом подразделе в Разделе 3.1.
T◦UUTRpxRmT◦U(x)U(x)RnДомен и домен композиции
- Для определения T◦U кодовый домен U должен совпадать с доменом T.
- Домен T◦U является доменом U.
- Кодовый домен T◦U является кодовым доменом T.
Напомним из этого определения в разделе 3.1, что преобразование тождества — это преобразование IdRn:Rn→Rn, определенное как IdRn(x)=x для каждого вектора x.
Окончательное свойство называется ассоциативностью .Разворачивая обе стороны, он говорит:
S◦(T◦U)(x)=S(T◦U(x))=S(T(U(x)))=S◦T(U(x))=(S◦T)◦U (Икс).
Другими словами, и S◦(T◦U), и (S◦T)◦U являются преобразованиями, определяемыми применением сначала U, затем T, затем S.
Композиция преобразований , а не коммутативна вообще. То есть, вообще говоря, T◦UB=U◦T, даже когда определены обе композиции.
В этом подразделе мы вводим кажущуюся несвязанной операцию над матрицами, а именно матричное умножение.Как мы увидим в следующем подразделе, умножение матриц в точности соответствует композиции соответствующих линейных преобразований. Сначала нам понадобится терминология.
Обозначение
Пусть A — матрица размера m × n. Обычно мы будем писать aij для записи в i-й строке и j-м столбце. Он называется i,j записью матрицы.
a11···a1j···a1n………ai1···aij···ain………am1···amj···amnEIIIGFJJJHjthcolumnithrowОпределение (умножение матриц)
Пусть A — матрица размера m×n, а B — матрица размера n×p.Обозначим столбцы матрицы B через v1,v2,…,vp:
.B=C|||v1v2···vp|||D.
Произведение AB представляет собой матрицу m×p со столбцами Av1, Av2,…, Avp:
AB=C|||Av1Av2···Avp|||D.
Другими словами, умножение матриц определяется столбец за столбцом или «распределяется по столбцам B».
Для определения векторов Av1,Av2,…,Avp количество строк B должно быть равно количеству столбцов A.
Размеры матриц в матричном произведении
- Чтобы AB был определен, количество строк B должно равняться количеству столбцов A.
- Произведение матрицы m×n и матрицы n×p является матрицей m×p.
Если B имеет только один столбец, то AB также имеет один столбец. Матрица с одним столбцом — это то же самое, что и вектор, поэтому определение произведения матриц обобщает определение произведения матриц на вектор из этого определения в разделе 2.3.
Если А — квадратная матрица, то мы можем умножить ее саму на себя; мы определяем его степени как
А2=ААА3=АААи т.д.
Правило строки-столбца для умножения матриц
Напомним из этого определения в Разделе 2.3 видно, что произведение вектора-строки на вектор-столбец равно скаляру
.Aa1a2···anBEIIGx1x2…xnFJJH=a1x1+a2x2+···+anxn.
Следующая процедура нахождения матричного произведения гораздо лучше приспособлена для ручных вычислений; предыдущее определение больше подходит для доказательства теорем, таких как эта теорема ниже.
Рецепт: Правило строки-столбца для умножения матриц
Пусть A — матрица размера m×n, пусть B — матрица размера n×p, и пусть C=AB. Тогда ij-я запись C — это i-я строка A, умноженная на j-й столбец B:
cij=ai1b1j+ai2b2j+···+ainbnj.
Вот схема:
a11···a1k···a1n………ai1···aik···ain………am1···amk···amnEIIIGFJJJHithrowb11···b1j· ··b1p………bk1···bkj···bkp………bn1···bnj···bnpEIIIIGFJJJJHjthcolumn=c11···c1j···c1p. ……..ci1···cij···cip………cm1···cmj···cmpEIIIGFJJJHijentryПравило строки-столбца для умножения матрицы на вектор в разделе 2.3 гласит, что если A имеет строки r1,r2,…,rm и x является вектором, то
Ax=EIIG—r1——r2—…—rm—FJJHx=EIIGr1xr2x…rmxFJJH.
Определение умножения матриц равно
.AC|||c1c2···cp|||D=C|||Ac1Ac2···Acp|||D.
Отсюда следует, что
EIIG—r1——r2—…—rm—FJJHC|||c1c2···cp|||D=EIIGr1c1r1c2···r1cpr2c1r2c2···r2cp………rmc1rmc2··· rmcpFJJH.
Хотя умножение матриц удовлетворяет многим ожидаемым свойствам (см. конец раздела), нужно быть осторожным при выполнении матричных арифметических действий, так как есть несколько свойств, которые в общем случае не выполняются.
Меры предосторожности при умножении матриц
Хотя умножение матриц вообще не является коммутативным, существуют примеры матриц A и B с AB=BA.Например, это всегда работает, когда A является нулевой матрицей или когда A=B. Читателю предлагается найти другие примеры.
Цель этого подраздела — показать, что умножение матриц соответствует композиции преобразований, т. е. стандартная матрица для T◦U является произведением стандартных матриц для T и для U. Трудно поверить, что наша сложная Формула умножения матриц на самом деле означает что-то интуитивное, например, «связывание двух преобразований вместе»!
Теорема
Пусть T:Rn→Rm и U:Rp→Rn — линейные преобразования, а A и B — их стандартные матрицы соответственно, так что A — матрица размера m×n, а B — матрица размера n×p.Тогда T◦U:Rp→Rm — линейное преобразование, а его стандартная матрица — произведение AB.
Доказательство
Сначала проверим линейность T◦U. Пусть u,v — векторы в Rp. Затем
T◦U(u+v)=T(U(u+v))=T(U(u)+U(v))=T(U(u))+T(U(v))=T ◦U(u)+T◦U(v).
Если c скаляр, то
T◦U(cv)=T(U(cv))=T(cU(v))=cT(U(v))=cT◦U(v).
Поскольку T◦U удовлетворяет двум определяющим свойствам в разделе 3.3, это линейное преобразование.
Теперь, когда мы знаем, что T◦U является линейным, имеет смысл вычислить его стандартную матрицу.Пусть C — стандартная матрица T◦U, поэтому T(x)=Ax, U(x)=Bx и T◦U(x)=Cx. По этой теореме в разделе 3.3 первый столбец C — это Ce1, а первый столбец B — Be1. У нас есть
T◦U(e1)=T(U(e1))=T(Be1)=A(Be1).
По определению, первый столбец произведения AB является произведением A на первый столбец B, то есть Be1, поэтому
Ce1=T◦U(e1)=A(Be1)=(AB)e1.
Отсюда следует, что C имеет тот же первый столбец, что и AB. Тот же аргумент, примененный к i-му стандартному вектору координат ei, показывает, что C и AB имеют один и тот же i-й столбец; поскольку у них одинаковые столбцы, это одна и та же матрица.
Теорема оправдывает наш выбор определения произведения матриц. Это единственная причина, по которой матричные произведения определяются таким образом. Перефразируя:
Продукты и композиции
Матрица композиции двух линейных преобразований есть произведение матриц преобразований.
Напомним из этого определения в разделе 3.3, что единичная матрица — это матрица n × n, столбцы которой являются стандартными векторами координат в Rn.Единичная матрица является стандартной матрицей преобразования идентичности: то есть x=IdRn(x)=Inx для всех векторов x в Rn. Для любого линейного преобразования T:Rn→Rm имеем
ИКм◦T=T
, и по тому же признаку мы имеем для любой m × n матрицы A мы имеем
ИмА=А.
Аналогично имеем T◦IRn=T и AIn=A.
В этом подразделе мы опишем еще две операции, которые можно выполнять над преобразованиями: сложение и скалярное умножение. Затем мы переводим эти операции на язык матриц.Это аналогично тому, что мы сделали для композиции линейных преобразований, но гораздо менее тонко.
Определение
- Пусть T,U:Rn→Rm — два преобразования. Их 90 807 сумма 90 808 есть преобразование T+U:Rn→Rm, определяемое формулой
(Т+У)(х)=Т(х)+У(х).
Обратите внимание, что добавление преобразований определяется только в том случае, если оба преобразования имеют один и тот же домен и кодовый домен. - Пусть T:Rn→Rm — преобразование, а c — скаляр. Скалярное произведение числа c на T представляет собой преобразование cT:Rn→Rm, определяемое формулой
(сТ)(х)=с·Т(х).
Чтобы подчеркнуть, сумма двух преобразований T,U:Rn→Rm представляет собой еще одно преобразование, называемое T+U; его значение на входном векторе x является суммой выходов T и U. Точно так же произведение T на скаляр c является другим преобразованием, называемым cT; его значением на входном векторе x является вектор c·T(x).
В одном из приведенных выше свойств мы использовали 0 для обозначения преобразования Rn→Rm, которое равно нулю для каждого входного вектора: 0(x)=0 для всех x. Это называется нулевым преобразованием .
Приведем теперь аналогичные операции для матриц.
Определение
Факт
Пусть T,U:Rn→Rm — линейные преобразования со стандартными матрицами A, B соответственно, и пусть c — скаляр.
- Стандартной матрицей для T+U является A+B.
- Стандартной матрицей для cT является cA.
Ввиду вышеизложенного следующие свойства являются следствием соответствующих свойств преобразований. Они также легко проверяются непосредственно из определений.
В одном из приведенных выше свойств мы использовали 0 для обозначения матрицы размера m×n, все элементы которой равны нулю. Это стандартная матрица нулевого преобразования, и она называется нулевой матрицей .
Мы также можем комбинировать сложение и скалярное умножение матриц с умножением матриц. Поскольку умножение матриц соответствует композиции преобразований (теорема), следующие свойства являются следствием соответствующих свойств преобразований.
Большинство приведенных выше свойств легко проверить непосредственно из определений. Однако свойство ассоциативности (AB)C=A(BC) таковым не является (попробуйте!). Гораздо проще доказать, связав умножение матриц с композицией преобразований и используя тот очевидный факт, что композиция преобразований ассоциативна.
Как быстро и правильно умножать матрицы за шесть простых шагов
Допустим, нам даны две матрицы A и B, где
, и нас попросили найти продукт AB.Чтобы увидеть, имеет ли смысл AB, запишите размеры матриц в тех позициях, в которых вы хотите их умножить. В этом случае мы пишем
Чтобы убедиться, что продукт имеет смысл, просто проверьте, совпадают ли два числа внутри. Если да, то товар можно брать, если не согласны, то товар не имеет смысла. Например, хотя продукт AB имеет смысл, продукт BA — нет. Действительно, внутренние числа
не совпадают.
Опять же, мы можем использовать технику записи размеров по порядку.Возьмем те же A и B сверху. Записываем
Внешние номера по порядку обозначают размеры изделия. Читая внешние числа слева направо, мы получаем 1 × 3, что соответствует размерности
.или продукт AB. Мы вычислим это сами через минуту! Напомним,
• Запишите размеры двух матриц A и B.
• Проверьте, совпадают ли внутренние числа.
• Если они согласны, прочтите размеры ответа с внешних чисел
Особый случай — умножение вектора-строки на матрицу
В нашем примере мы напишем
.Убедитесь, что вы записываете их в порядке их появления!
Умножьте первую строку B на первую запись A, вторую строку на вторую запись и так далее.
что равно
Сложите строки, полученные на шаге 3, чтобы получить ответ
Общий случай — две матрицы
Допустим, мы хотим умножить новую матрицу A’ на ту же матрицу B, где
Делаем шаги 0 и 1, видим
произведение имеет смысл, и результат должен быть 3 X 3. Мы найдем вывод построчно.
В нашем примере мы напишем
.Чтобы найти первую строку нашего ответа 3×3, вычислите произведение, первую строку A’ умножить на B.
, это проблема, которую мы только что решили. Итак, первая строка нашего ответа —
.Чтобы найти вторую строку нашего ответа 3×3, вычислите, что я оставлю читателю, чтобы убедиться, что это
Наконец, третья строка нашего ответа 3×3 , поэтому мы умножаем
и затем добавить
Мы нашли три строки нашей матрицы решений и делаем вывод
Обычный способ формулировки этой точки зрения состоит в том, что при умножении AB A действует на B посредством операций со строками.Мы рассматриваем B как набор векторов-строк, и строки A заставляют нас брать линейные комбинации векторов-строк в B, чтобы сформировать строки решения. Существует эквивалентная перспектива операций со столбцами. У каждого есть свое место. Следите за дальнейшим сообщением о том, как каждая из этих точек зрения вступает в игру при решении матричного уравнения Ax = b.


 matrix('1 2 3; 4 5 6')
>>> C = 3 * A
>>> print(C)
[[ 3 6 9]
[12 15 18]]
matrix('1 2 3; 4 5 6')
>>> C = 3 * A
>>> print(C)
[[ 3 6 9]
[12 15 18]] dot(B.dot(C))
>>> R = (A.dot(B)).dot(C)
>>> print(L)
[[192 252]
[436 572]]
>>> print(R)
[[192 252]
[436 572]]
dot(B.dot(C))
>>> R = (A.dot(B)).dot(C)
>>> print(L)
[[192 252]
[436 572]]
>>> print(R)
[[192 252]
[436 572]] matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = A.dot(B)
>>> R = B.dot(A)
>>> print(L)
[[19 22]
[43 50]]
>>> print(R)
[[23 34]
[31 46]]
matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = A.dot(B)
>>> R = B.dot(A)
>>> print(L)
[[19 22]
[43 50]]
>>> print(R)
[[23 34]
[31 46]] matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = Z.dot(A)
>>> R = A.dot(Z)
>>> print(L)
[[0 0]
[0 0]]
>>> print(R)
[[0 0]
[0 0]]
>>> print(Z)
[[0 0]
[0 0]]
matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = Z.dot(A)
>>> R = A.dot(Z)
>>> print(L)
[[0 0]
[0 0]]
>>> print(R)
[[0 0]
[0 0]]
>>> print(Z)
[[0 0]
[0 0]] е. для умножения двух матриц A и B AB ≠ BA.
е. для умножения двух матриц A и B AB ≠ BA.
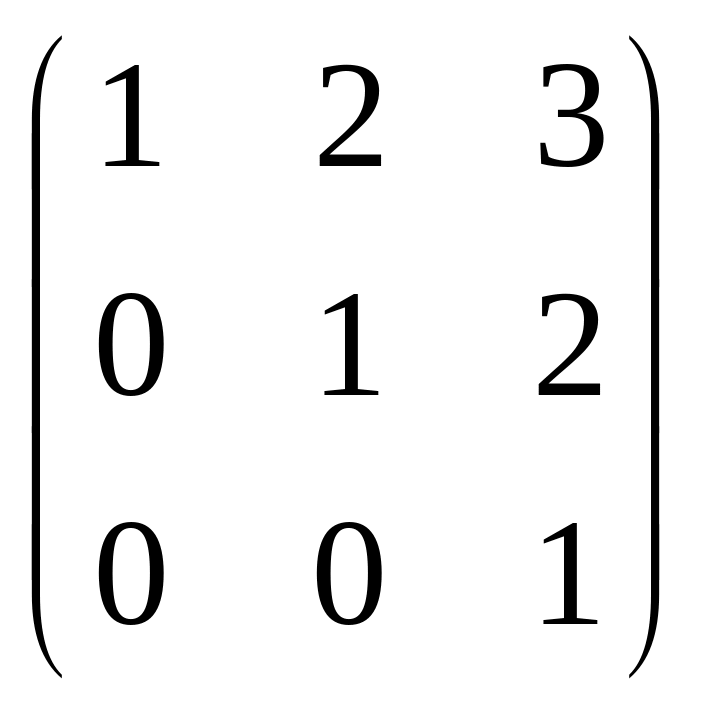 2 из 3)
2 из 3) 
 В частности, умножение матриц не является «коммутативным»;
вы не можете изменить порядок факторов и ожидать, что в конечном итоге
такой же результат. (Вы должны ожидать увидеть «концептуальный» вопрос
относящийся к этому факту на вашем следующем тесте.)
В частности, умножение матриц не является «коммутативным»;
вы не можете изменить порядок факторов и ожидать, что в конечном итоге
такой же результат. (Вы должны ожидать увидеть «концептуальный» вопрос
относящийся к этому факту на вашем следующем тесте.) = ба «или» 56
= 65″? Это «правило»
вероятно, казался довольно глупым в то время, потому что вы уже знали, что
порядок не имеет значения в умножении.Знакомство с этими правилами
тогда было, вероятно, бессмысленно, так как заказ не имел значения за все, что вы тогда умножали. Ну а теперь Закон Коммутативности
имеет значение, потому что порядок имеет значение для умножения матриц.
Всегда помните, что для матриц AB почти наверняка не равно BA .
= ба «или» 56
= 65″? Это «правило»
вероятно, казался довольно глупым в то время, потому что вы уже знали, что
порядок не имеет значения в умножении.Знакомство с этими правилами
тогда было, вероятно, бессмысленно, так как заказ не имел значения за все, что вы тогда умножали. Ну а теперь Закон Коммутативности
имеет значение, потому что порядок имеет значение для умножения матриц.
Всегда помните, что для матриц AB почти наверняка не равно BA . Доступный
от
Доступный
от