Умножение матрицы на единичную матрицу: Умножение на единичную матрицу

Содержание

Умножение на единичную матрицу

На основании правила умножения матриц получаем:

АЕ =	а₁₁	а₁₂^.	1	0	=	а₁₁	а₁₂
АЕ =	а₂₁	а₂₂	0	1	=	а₂₁	а₂₂

EA=	1	0 ^.	а₁₁	а₁₂	=	а₁₁	а₁₂
EA=	0	1	а₂₁	а₂₂	=	а₂₁	а₂₂,

т.е. АЕ = ЕА = А (11)

Произведение квадратной матрицы любого порядка на соответствующую единичную матрицу равняется первоначальной матрице. Таким образом, при умножении матриц единичная матрица играет роль единицы, поэтому и называется единичной.

Понятие обратной матрицы

Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умноженной на А (как справа, так и слева), даёт единичную матрицу. Обозначив обратную матрицу через А^-1, запишем

А^-1А = АА^-1 = Е (12)

Если обратная матрица А^-1 существует, то матрица А называется обратимой

. Операция вычисления обратной матрицы называется обращением матрицы. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной.

Нахождение матрицы, обратной данной

Пусть дана невырожденная матрица

а₁₁

а₁₂

а₁₃

А=

а₂₁

а₂₂

а₂₃

а₃₁

а₃₂

а₃₃

а₁₁

а₁₂

D_А =

а₂₁

а₂₂

а₂₃

≠ 0

а₃₁

а₃₂

а₃₃

Обратной матрицей А^-1 будет матрица

A₁₁/D_А

A₂₁/D_А

A₃₁/D_А

A^-1 =

A₁₂/D_А

A₂₂/D_А

A₃₂/D_А

( 13 )

A₁₃/D_А

A₂₃/D_А

A₃₃/D_А

где А_ij – алгебраическое дополнение элемента а_ij определителя D_A.

Убедиться в этом можно, умножая матрицу А на матрицу А^-1. Например, элементы с₁₁ и с₂₃ определяются так:

···

c₂₃=a₂₁···=

== 0

В итоге

а₁₁

а₁₂

₁₃

A₁₁/D_А

A₂₁/D_А

A₃₁/D_А

С=AA^-1=

а₂₁

а₂₂

а₂₃

12/D_А

A₂₂/D_А

A₃₂/D_А

а₃₁

а₃₂

а₃₃

A₁₃/D_А

A₂₃/D_А

A₃₃/D_А

Матрица

A₁₁

A₂₁

A₃₁

A₁₂

A₂₂

A₃₂

( 14 )

A₁₃

A₂₃

A₃₃

называется матрицей, присоединённой к А. (Используется также обозначение ). Обратная матрица А^-1 через присоединённую выражается так:

=	1		( 15 )
	D_A

Обратную матрицу будем находить по следующей схеме:

1. Находим определитель матрицы А.

2. Находим алгебраическое дополнение всех элементов а_ij матрицы и записываем новую матрицу.

3. Меняем местами строки и столбцы полученной матрицы (транспонируем матрицу).

4. Умножаем полученную матрицу на 1/D_A.

Пример 6. (Лена Иванова, КШ-061).

Дана матрица

Найти обратную матрицу.

1. Вычисляем определитель матрицы А:

	2	5	7		2	5	7
D_A =	6	3	4	=	0	-12	-17	=	(492 — 493) = -1
	5	-2	-3		0	-29/2	-41/2

Так как D_A ≠ 0, то матрица А является невырожденной, и, значит, можно найти матрицу А^-1.

2. Находим алгебраические дополнения элементов этого определителя:

A₁₁=	3	4	= -1,	A₂₁= —	5	7	= 1,	A₃₁=	5	7	= -1,
	-2	-3			-2	-3			3	4

A₁₂= —	6	4	= 38,	A₂₂=	2	7	= -41,	A₃₂= —	2	7	= 34,
	5	-3			5	-3			6	4

A₁₃=	6	3	= -27,	A₂₃=-	2	5	= 29,	A₃₃=	2	5	= -24.
	5	-2			5	-2			6	3

Следовательно,

	-1	1	-1		1	-1	1
A^-1 = -1	38	-41	34	=	-38	41	-34
	-27	29	-24		27	-29	24

Лекция 4.

определение, свойства и примеры решения задач

Задание. Вычислить $AB$ и $BA$, если $ A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right) $ , $ B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right) $

Решение. Так как $ A=A_{3 \times 2} $ , а $ B=B_{2 \times 2} $ , то произведение возможно и результатом операции умножения будет матрица $ C=C_{3 \times 2} $ , а это матрица вида $ C=\left( \begin{array}{ll}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right) $ .

Вычислим элементы матрицы $C$ :

$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $

$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $

$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $

$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $

$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $

$ c_{32}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $

Итак, $ C=A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $ .

Выполним произведения в более компактном виде:

$ C=A B=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right)_{3 \times 2} \cdot \left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)_{2 \times 2}= $

$ =\left( \begin{array}{ccc}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $

Найдем теперь произведение $ D=B A=B_{2 \times 2} \cdot A_{3 \times 2} $. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. $ A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .

как найти произведение двух или трех разных размеров, условия и формулы

Мы помним, что матрицы – это таблицы взаимосвязанных элементов, которые позволяют упростить математические вычисления и систематизировать определённую информацию. Их можно складывать, вычитать, умножать между собой. В этой статье подробнее остановимся на последнем алгоритме – матричном произведении.

Умножение матриц — определение

Матричное умножение – это одна из основных операций, которая проводится исключительно с согласованными матрицами.

При произведении матриц A и B получается новая матрица C. В математическом виде формула будет выглядеть так:

Но для начала разберёмся, что такое согласованные матрицы.

Согласованные матрицы

Согласованными матрицами называют матрицы вида A = [m ☓ n] и B = [n ☓ k], где количество столбцов А равно количеству строк В.

Индексы показывают координаты равных элементов.

Для того, чтобы умножить А и В, нужно взять строку в первой матрице и столбец во второй, перемножить одинаковые элементы и сложить полученные произведения.

Основные свойства матричного произведения

Размеры, то есть количество строк (m) и столбцов (n), влияют на особенности матричного произведения. Следовательно, для двух главных видов – квадратных и прямоугольных – действуют разные свойства произведения. Однако умножение любого вида всегда некоммуникативное. Это означает, что матрицы нельзя менять местами (АВ ≠ ВА).

Умножение квадратных матриц

Для квадратных матриц существует единичная матрица Е. В ней элементы по главной диагонали равны единице, а оставшиеся – нулю. Произведение любой квадратной матрицы на неё не влияет на результат.

В математическом виде это выглядит так: ЕА = АЕ = А

Также существует обратная матрица А (-1), при умножении на которую исходная A = [m ☓ n] даёт в результате единичную матрицу E.

Следовательно, формула такова: АА(-1) = Е

Умножение прямоугольных матриц

Существуют четыре основных свойства умножения:

Сочетательное свойство, или ассоциативность: (AB)C = A(BC)
Распределительное свойство, или дистрибутивность: А(В+С) = АВ + АС / (А+В)С = АС + ВС
Умножение на единичную матрицу: ЕА = А
Умножение на нулевую матрицу: 0А = 0

Напомним, что у нулевой матрицы все элементы равны нулю.

Произведение трех матриц

Произведение АВС можно получить двумя альтернативными способами:

Найти АВ и умножить на С
Найти ВС и умножить на А

(АВ) С = А (ВС)

Данное свойство называется ассоциативностью матричного умножения и действует на все виды согласованных матриц. Сами они не переставляются, меняется только порядок их умножения.

Умножение матрицы на число

Для умножения на число необходимо умножить каждый матричный элемент на это число:

Дроби вносить не нужно, поскольку они могут затруднить дальнейшие операции.

Умножение матрицы на вектор

Здесь работает правило «строка на столбец».

При умножении на вектор-столбец важно, чтобы количество столбцов в матрице совпадало с количеством строк в векторе-столбце. Результатом произведения будет вектор-столбец.

При умножении на вектор-строку матрица должна быть только вектором-столбцом. Важно, чтобы количество строк в векторе-столбце совпадало с количеством столбцов в векторе-строке. Результатом произведения будет квадратная матрица.

Примеры задач на умножение матриц

Задача №1: выполнить умножение и найти С, если A = [m ☓ n] и B = [n ☓ k] равны.

Решение:

c₁₁ = a₁₁·b₁₁ + a₁₂·b₂₁ = 4·3 + 2·(-3) = 12 — 6 = 6

c₁₂ = a₁₁·b₁₂ + a₁₂·b₂₂ = 4·1 + 2·4 = 4 + 8 = 12

c₂₁ = a₂₁·b₁₁ + a₂₂·b₂₁ = 9·3 + 0·(-3) = 27 + 0 = 27

c₂₂ = a₂₁·b₁₂ + a₂₂·b₂₂ = 9·1 + 0·4 = 9 + 0 = 9

Ответ:

Задача №2: вычислить С, если А = [m ☓ n] и вектор-столбец В равны.

Решение:

c11 = a11·b11 + a12·b21 = 2·1 + (-1)·2 + 3·(-1) = -3

c21 = a11·b12 + a12·b22 = 4⋅1 + 2⋅2 + 0⋅2 = 8

c31 = a21·b11 + a22·b21 = −1⋅1 + 1⋅2 + 1⋅(−1) = 0

Ответ:

Изучение матричных операций очень увлекательное, но сложное занятие. Если у вас нет времени на учёбу, ФениксХэлп может помочь в решении контрольных и самостоятельных работ, написании статей и диссертаций.

Действия с матрицами

Матрицы и действия с ними, определители

Сложение матриц

Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц $A=\{A_{ik}\}$ и $B=\{B_{ik}\}$, матрица $A+B$, определяется следующим образом: $(A+B)_{ik}=A_{ik}+B_{ik}$, $1 \leq i \leq m, 1 \leq k \leq n$. Иными словами: складываются элементы матриц $A$ и $B$, стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , \] \[ B=\left( \begin{array}{ccc} 2 &1 & 0 \\ 1 & 3 & 4 \end{array} \right) , \] тогда \[ A+B=\left( \begin{array}{ccc} 3 & 5 & -1 \\ 4 & -3 & 11 \end{array} \right) . \]

Умножение матрицы на число

Пусть $A=\{a_{ik}\}$ — матрица типа $(m,n)$, $\lambda$ — произвольное число. Тогда матрица $\{\lambda a_{ik}\}$ называется произведением числа $\lambda $ на матрицу $A$ и обозначается $\lambda \cdot A$.

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 7 & 5 & 2 \\ 3 & -6 & 7 \end{array} \right) , \] тогда \[ 5A=\left( \begin{array}{ccc} 5 &20 & -5 \\ 35 & 25 & 10 \\ 15 & -30 & 35 \end{array} \right) . \]

Замечание.

Как и в обычной, в матричной арифметике знак умножения иногда не указывают, так что выражения $c\cdot A$ и $cA$ равноправны.

Пусть \[ A=\left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right), B=\left( \begin{array}{cc} 1 & -2 \\ 3 & 4 \end{array} \right). \]

Вычислить $3A-2B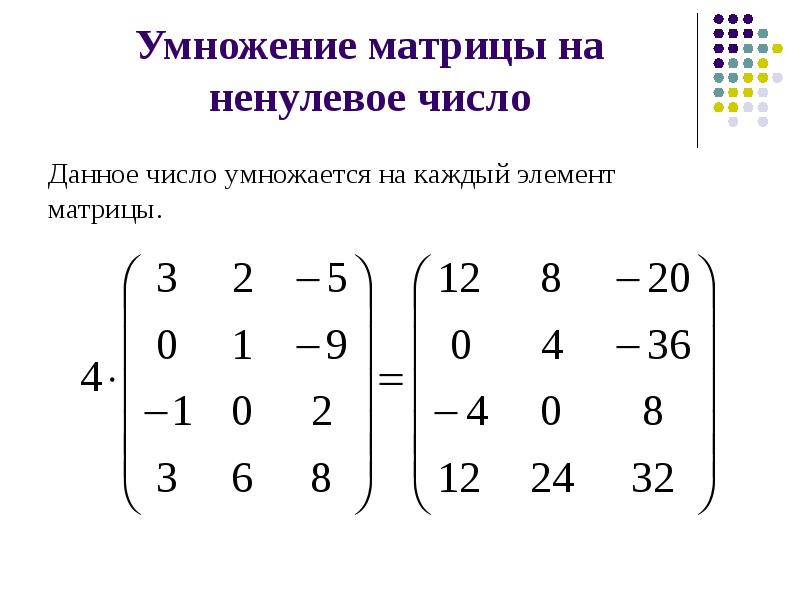$. T\) (это выражение занимает меньше места).

Элементарные свойства операций с матрицами

Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.

1. Для любых матриц $A,B,C$ одного типа $(A+B)+C=A+(B+C)$(ассоциативность сложения).

2. Для любых матриц $A,B$ одного типа $A+B=B+A$ (коммутативность сложения).

3. Пусть $(m,n)$-матрица $O$ состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа $(m,n)$, $A+O=A$, $0\cdot A=O$ для любой матрицы $A$ того же типа.

4. Для любых чисел $c_1,c_2$ и любой матрицы $A$ верно $(c_1+c_2)A=c_1A+c_2A$.

5. Для любых матриц $A,B$ одного типа и любого числа $c$ верно $c(A+B)=cA+cB$.

6. Для любых чисел $c_1,c_2$ и любой матрицы $A$ верно $(c_1c_2)A=c_1(c_2A)$.

7. Для любой матрицы $A$ верно $1\cdot A=A$.

8. Для любых матриц $A,B$ одного типа $(A+B)^T=A^T+B^T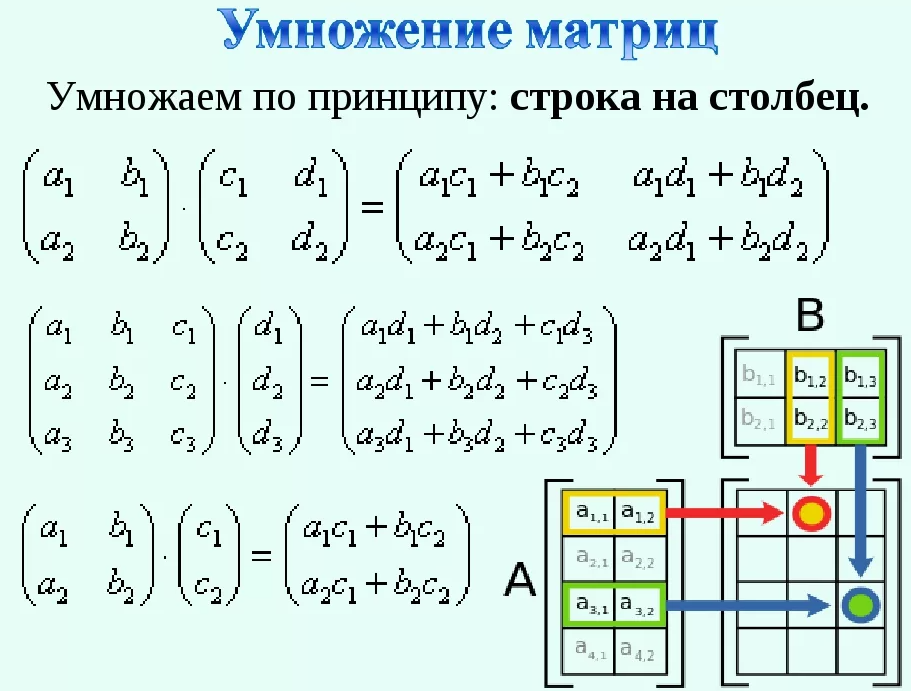$. na_{im}b_{mk}. \] Таким образом следует вычислить все $mp$ элементов матрицы $C$. Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы $A$ и $B$, их типы должны быть согласованы!

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , B=\left( \begin{array}{cc} 2 &1 \\ 1 & 3 \\ -3 &5 \end{array} \right) . \]

В данном случае матрица $A$ имеет тип (2,3), матрица $B$ имеет тип (3,2), так что типы матриц согласнованы и в результате умножения $A$ на $B$ получим матрицу типа $(2,2)$. Получаем: \[ AB=\left ( \begin{array}{cc} 1\cdot 2 +4 \cdot 1+(-1)\cdot (-3) & 1\cdot 1 +4 \cdot 3+(-1)\cdot 5\\ 3\cdot 2 +(-6) \cdot 1+7\cdot (-3) &3\cdot 1 +(-6) \cdot 3+7\cdot 5 \end{array} \right )= \left( \begin{array}{cc} 9 & 8\\ -21 & 20 \end{array} \right). T\).

6. Для квадратных матриц $A,B$ одного типа $det(AB)=detA \cdot detB$.

7. Рассмотрим квадратную матрицу порядка $n$, $E=diag\{1,1,1,…,1\}$. Такая матрица играет выделенную роль в умножении матриц: для любых матриц $A,B$ имеем $EA=A$, $BE=B$. Матрица $E$ называется единичной матрицей порядка $n$. Согласно описанным выше результатам, $detE=1$.

1. Умножить матрицы:

а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]

б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). \]

2. Вычислить \[ \left( \begin{array}{cc} 3 & 2 \\ -4 & -2 \end{array} \right)^5.{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right). \]

Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.

Найти обратную матрицу для матрицы

1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]

2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]

3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]

Матричные уравнения

Матричными уравнениями называются уравнения вида \[ AX=G, \quad \quad(12)\] \[ XB=G, \quad \quad(13)\] \[ AXB=G, \quad \quad(14)\] где матрицы $A,B,G$ заданы и требуется построить матрицу $X$.{-1}. \]

1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]

2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]

3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]

4. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) , G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) . \]

5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]

6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]

Линейная алгебра

Линейная алгебра

Две матрицы A и B называются равными ,если они имеют

один и тот же порядок и если элементы стоящие на соответствующих местах равны.

К линейным операциям относятся :

Умножение матрицы на число

Для того чтобы умножить матрицу на число нужно каждый элемент

матрицы умножить на это число:

Сложение матриц.
Складывать можно только матрицы одинаковых размеров:
Свойства линейных операций
Если матрица в качестве элементов имеет нули , то такая матрица называется нулевой.
Произведение матриц .

Пример:
.==
.=
.
Если для матриц А и В выполняется равенство А* В=В*А ,то
матрицы называются перестановочными.
Если для матриц А , В , С имеет смысл операция произведения,
то выполняются равенства
A(B*C)=(A*B)*C
A(B+C)=AB+AC
(B+C)A=BA+CA
Транспонирование матриц

Рассмотрим матрицы
A^T называется транспонированной по отношению к A
Если A_T получена из матрицы А заменой строк на столбцы то
назавают главной диагональю
Очевидно:
Если А является квадратной матрицей(n*n), то элементы матрицы
Если для квадратной матрицы выполняется условие
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.
Понятие обратной матрицы.
Обратные матрицы существуют только для квадратных матриц. Квадратная матрица ,у которой на главной диагонали стоят
единицы, а вне главной диагонали — нули, называется единичной матрицей.
Например, единичная матрица второго порядка:
Теорема.
Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
Определение обратной матрицы:
Матрица В называется обратной для матрицы А , если А и В перестановочны и А*В=В*А=Е
Обозначение обратной матрицы:
Теорема.
Если матрица А имеет обратную ,то ее определитель отличен от
нуля.
Доказательство.
Так как А имеет обратную матрицу, то
Воспользуемся теоремой о том ,что определитель произведения
равен произведению определителей.
что и требовалось доказать.
Нахождение обратной матрицы методом Крамера
Теорема.
Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.
Доказательство.
Пусть матрица А такова, что её определитель отличен от нуля.
Докажем, что существует матрица В, такая что:
*=

Отсюда, в частности, следует:
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля , то эту систему можно решить методом Крамера причем решение (3) — единственно.
Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.
Алгоритм нахождения обратной матрицы методом Крамера.
Первоначально находим определитель матрицы А и если он
равен нулю , то обратной матрицы не существует.
Если определитель отличен от нуля , то находим союзную
матрицу
состоящую из алгебраических дополнений элементов матрицы А.
Элементарные преобразования матриц.
Эквивалентные матрицы.
К элементарным преобразованиям относятся:
умножение любой строки матрицы на число , отличное от нуля;

пример
=
к любой строке можно добавить любую другую строку , умноженую на любое число;
перестановка двух строк.
Матрицы, полученные с помощью элементарных преобразований
называются эквивалентными
А~ В , В~ С , А~ С
Вычисление обратной матрицы с помощью элементарных преобразований.
Расмотрим квадратную матрицу А и предположим , что
тогда используя элементарные преобразования эту матрицу
можно привести к единичной матрице .Таким образом единичная
матрица эквивалентна любой невырожденой матрице того же
порядка.
Теорема
Если элементарные преобразования:
переводят невырожденую матрицу А в единичную , то
те же самые преобразования, взятые в том же порядке, переводят
единичную матрицу в обратную для A.
Доказательство:
отсюда

назад | оглавление | вперёд

Error
Jump to… Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейЗадачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
learnopengl. Урок 1.7 — Трансформации / Хабр
Теперь мы знаем как создавать объекты, раскрашивать их и накладывать на них текстуры, но они все еще довольно скучны, поскольку являются статическими объектами. Мы можем попробовать заставить их двигаться изменяя координаты вершин для каждого кадра, но это довольно муторно и требует процессорных вычислений. Есть гораздо более удобный способ для совершения трансформаций над объектом — это применение матриц. Но это не значит, что мы сейчас будем разговаривать про кунг фу и искусственный цифровой мир.

Матрицы — это очень мощные математические конструкции, которые поначалу пугают, но стоит к ним привыкнуть и они сразу станут крайне полезными. Во время обсуждения матриц требуется также немного углубиться в математику. Также для более склонных к математике читателей я оставлю ссылки на дополнительные ресурсы по этой теме.
Как бы то ни было, для полного понимания трансформаций мы, во первых, должны разобраться с векторами. Основная задача этой главы — дать вам основные математические знания, которые нам понадобятся позже.

Вектора
В самом простом определении, вектора — это не более чем направления. У вектора может быть направление и магнитуда (также иногда называется модулем или длиной). Вы можете представлять себе вектора в качестве направлений на карте сокровищ: “Сделайте 10 шагов налево, теперь 3 шага на север и теперь 5 шагов направо”. В данном примере “налево” — это направление, а “10 шагов” — это длина вектора. Направления на этой карте сокровищ составляются из 3 векторов. Вектора могут иметь любую размерность, но чаще всего используются двухкомпонентные и четырехкомпонентные вектора. Если вектор двухкомпонентный, то он описывает направление на плоскости (или на 2D графике), если вектор трехкомпонентный, то он описывает направление в трехмерном мире.
Ниже вы можете видеть 3 вектора, каждый из которых представлен в виде (x, y) в качестве стрелок на 2D графике. Поскольку более интуитивно представлять вектора в 2D (чем в 3D), то вы можете думать о 2D векторах, как о 3D векторах, но с нулевой z координатой. До тех пор, пока вектор описывает направление — позиция вектора не меняет его значения. На графике можно увидеть, что вектора v и w одинаковы, хотя из позиции отличаются:
Когда математики описывают вектора, они предпочитают использовать символы нижнего регистра с небольшой черточкой сверху. Пример:
Поскольку вектора зачастую описывают направление — то иногда их тяжело представить в виде позиции. Обычно мы визуализируем вектор следующим образом: мы устанавливаем центр в (0, 0, 0), а затем указываем направление, описанное точкой. Таким образом получается позиционный вектор (также мы можем взять за центр другую точку, а потом сказать “Этот вектор указывает на точку в пространстве из этой точки”). Позиционный вектор (3, 5) будет указывать на точку (3, 5) на графе с основанием (0, 0). С помощью векторов мы можем описывать как направления так и позиции в двухмерном и трехмерном пространствах.
Также мы можем производить над векторами некоторые математические действия.

Скалярные векторные операции
Скаляр — это одно число (или однокомпонентный вектор, если вы хотите продолжать работать с векторами). Во время сложения/вычитания/умножения или деления вектора на скаляр мы просто складываем/вычитаем/умножаем или делим каждый элемент вектора на этот скаляр. Пример:
Где вместо сложения может быть вычитание, умножение или деление.

Обратный вектор
Обращение (отрицание) вектора — это получение вектора, чье направление противоположно исходному. Обратный вектор для вектора, указывающего на северо-восток, будет вектор, указывающий на юго-запад. Для обращения вектора мы просто умножаем вектор на -1. Пример:

Сложение и вычитание
Сложение двух векторов производится покомпонентно. Пример:
Визуально сумма векторов v=(4,2) и k=(1,2) выглядит так:
Также как и с обычным сложением и вычитанием, вычитание векторов — это тоже сложение, но с обратным вторым вектором:
Вычитание векторов друг из друга порождают вектор, который является разницей в позициях операндов:

Длина
Для получения длины (модуля) вектора мы используем теорему Пифагора, которые вы, возможно, помните со школы.2. Пример расчета длины:
Вычисленное значение: 4.47
Также существует специальный вид векторов, называемый единичными векторами. Особенность таких векторов в том, что их длина всегда равна 1. Мы можем преобразовать любой вектор в единичный делением этого вектора на его длину:
Такой вектор называется нормализованным. Единичные векторы обозначаются с небольшой крышей над буквой. С ними, также, проще работать, поскольку нам приходится заботиться только о направлении такого вектора.

Умножение вектора на вектор
Умножение двух векторов выполняется довольно странно. Нормальное умножение не применимо, поскольку оно не имеет визуального смысла, но у нас есть 2 специфических подхода, из которых можно выбирать во время умножения: первый — скалярное произведение, которое изображается как точка, а второе — векторное произведение, которое изображается как крест.

Скалярное произведение
Скалярное произведение двух векторов эквивалентно скалярному произведению длин этих векторов, умноженное на косинус угла между ними. Если это предложение сбило вас с толку, то посмотрите на формулу:
Где угол между векторами описан как тета. Почему это может быть интересно? Что же, представим если вектора v и k являются единичными векторами. Соответственно формула сокращается до:
Теперь скалярное произведение определяет только угол между двумя векторами. Вы возможно помните, что функция cos становится 0, с углом в 90 градусов ну и 1 с углом 0. Это позволяет легко проверять ортогональны ли вектора или параллельны друг другу (ортогональность означает, что вектора прямоугольны). Если хотите узнать больше про sin или cosine, то рекомендую видео Khan Academy про базовую тригонометрию.

Вы также можете вычислить угол между двумя неединичными векторами, но для этого вам придется разделить результат на длины этих векторов, чтобы остаться только с cos.
Так как же считать скалярное произведение? Скалярное произведение — это умножение компонентов векторов и последующее сложение результатов.-1) в данном случае — это 143.1 градуса. Таким образом мы эффективно вычислили угол между этими двумя векторами. Скалярное произведение очень полезно во время работы со светом.

Векторное произведение
Векторное произведение возможно только в трехмерном пространстве и принимает на вход два непараллельных вектора, а возвращает вектор, который ортогонален входным. Если входные вектора ортогональны друг другу, то векторное произведение создаст 3 ортогональных вектора. Далее вы узнаете, почему это может быть полезно. Следующее изображение показывает как это выглядит трехмерном пространстве:
В отличии от других операций, векторное произведение не очень интуитивно без углубления в линейную алгебру, так что лучше просто запомнить формулу. Ниже представлено векторное произведение между двумя ортогональными векторами A и B.
Как вы можете видеть, в этой формуле не очень много смысла. В любом случае после всех этих шагов вы получите вектор, который будет ортогонален входным.

Матрицы
Теперь, после того как мы обсудили почти все на счет векторов, настало время углубиться в матрицы. Матрица, обычно, это четырехугольних из набора чисел, символов и/или выражений. Вот пример матрицы 2х3:
Доступ к элементам матрицы осуществляется с помощью (i,j), где i — это строка, а j — это столбец. Вот почему матрица выше называется 2х3 (3 столбца и 2 строки). Такая система — обратна той, что используется в 2D графах (x, y). Для получения значения 4 из матрицы выше, мы должны указать индекс (2, 1) (вторая строка, первый столбец).
Матрицы, по факту, ничего более чем четырехугольные массивы математических выражений. Они также обладают очень приятным набором математических свойств и, также как и вектора, имеют несколько операций — сложение, вычитание и умножение.

Сложение и вычитание
Сложение матрицы со скаляром выполняется следующим образом:
Скаляр просто прибавляется во всем элементам матрицы. Тоже самое происходит и при вычитании:
Сложение и вычитание между двумя матрицами выполняется поэлементно. Таким образом операции сложения и вычитания могут быть применены только к матрицам одинакового размера. Пример:
Тоже самое, только с вычитанием:

Умножение матрицы на скаляр
Также как сложение и вычитание, умножение матрицы на скаляр производится умножением каждого элемента матрицы на скаляр. Пример:

Умножение матриц
Умножение матриц не очень сложное, но и не такое простое. Умножение имеет несколько ограничений:

Вы можете умножать только матрицы, где число столбцов первой совпадает с числом строк второй матрицы.

Умножение матриц не коммутативно. A * B != B * A.

Вот пример умножения двух матриц 2х2:
Сейчас, возможно вы пытаетесь понять, что же тут вообще происходит? Умножение матриц — это комбинация из нормального умножения и сложения с использованием строк левой матрицы со столбцами правой матрицы. Следующее изображение должно внести немного ясности:
В начале мы берем верхнюю строку левой матрицы и левый столбец правой матрицы. Выбранные нами строка и столбец определяет то, какой элемент результирующей матрицы мы собираемся рассчитать. Если бы мы взяли первую строку левой матрицы, то мы собираемся работать с верхней строкой результирующей матрицы, затем мы выбираем столбец в правой матрице, он определяет то, с каким столбцом результирующей матрицы мы работаем. Для вычисления нижнего-правого элемента мы должны выбрать нижнюю строку левой матрицы и правый столбец правой матрицы.
Для вычисления результирующего значения мы перемножаем элементы строки и столбца с помощью обычного умножения. Результаты умножения затем складываются и мы получаем результат. Вот оттуда и идет первое ограничение.
В результате получается матрица размером (n, m), где n — количество строк в левой матрице, а m — количество столбцов в правой матрице.
Если у вас возникла проблема — то не волнуйтесь. Просто продолжайте вычислять руками и возвращайтесь к этому уроку, когда возникают сложности. Вскоре умножение матриц будет на автомате.
Давайте закроем вопрос умножения матриц одним большим примером. Для представления алгоритма использованы цвета. Для тренировки попробуйте сами посчитать результат, а затем сравнить с результатом в примере.
Как вы можете видеть умножение матриц довольно муторный процесс с большим количеством мест, где можно ошибиться. И эти проблемы лишь растут при увеличении размеров. Если вы все еще жаждите больше математических свойств матриц я крайне рекомендую видео Khan Academy.

Умножение матрицы на вектор
Мы уже использовали вектора в прошлых уроках. Мы использовали их, чтобы представлять позиции, цвета и текстурные координаты. Теперь давайте немного углубимся в кроличью нору и расскажем, что вектор — это на самом деле просто Nx1 матрица, где N — это количество компонентов вектора. Если вы чуть подумаете об этом — это имеет смысл. Вектора, прямо как матрицы — массив чисел, но только с 1 колонкой. И как же нам поможет эта информация? Что же, если у нас есть матрица MxN мы сможем ее умножить на Nx1 вектор, так как количество столбцов матрицы равно количеству строк вектора.
Но зачем нам вообще уметь умножать матрицу на вектор? Довольно много различных 3D/2D трансформаций можно выполнить, умножая матрицу на вектор, получая измененный вектор. Если вы все еще не уверены в том, что полностью понимаете текст выше, то вот немного примеров:

Единичная матрица
В OpenGL обычно работают с матрицами трансформации размерами 4х4 по той причине, что большинство векторов имеет 4 компонента. Самая простая матрица трансформации которую можно обсудить — это единичная матрица. Единичная матрица — это NxN матрица, заполненная нулями, но с 1 по диагонали. Как мы можете заметить эта матрица совершенно не изменяет вектор:
Вектор выглядит нетронутым. Это становится очевидно из правил умножения: первый результирующий элемент — это каждый элемент первой строки матрицы, умноженные на каждый элемент вектора. Поскольку каждый элемент строки равен 0, кроме первого — то мы получаем 1 * 1 + 0 * 2 + 0 * 3 + 0 * 4 = 1. Тоже самое применяется и к остальным 3 элементам вектора.
Вы можете спросить, зачем вообще может понадобится матрица трансформации, которая ничего не трансформирует? Единичная матрица зачастую является отправной точкой для генерации других матриц трансформации и если мы углубимся в линейную алгебру, это также очень удобная матрица для доказательства теорем и решения линейных уравнений.

Матрица масштабирования
Когда мы масштабируем вектор — мы увеличиваем длину стрелки на величину масштабирования, сохраняя направление. Пока мы работаем в 2 или 3 размерностях мы можем определить масштабирование вектором из 2 или 3 величин, каждая из которых масштабирует одну из осей (x, y или z).
Давайте попробуем масштабировать вектор v = (3,2). Мы будем масштабировать вектор по оси x на 0.5, что сделает его в 2 раза уже; и масштабируем вектор по оси y на 2, что увеличит высоту в 2 раза. Давайте посмотрим как будет выглядеть если мы масштабируем вектор на (0.5, 2). Запишем результат в виде s.
Помните, что OpenGL зачастую работает в 3D пространстве, соответственно для 2D можно оставить Z координату, равную 1. Операция масштабирования, которую мы только что выполнили, является неоднородной, поскольку величина масштабирования для каждой оси различается. Если бы величина масштабирования была бы одинаковой — то такое преобразование называется однородным.
Давайте построим матрицу трансформации которая выполнит для нас масштабирование. Мы уже увидели на единичной матрице, что диагональный элемент будет умножен на соответствующий элемент вектора. Что если мы заменим единицы в единичной матрице на тройки? В таком случае мы умножим все элементы вектора на это значение. Соответственно если мы представим величины масштабирования как (S1, S2, S3) то мы сможем определить матрицу масштабирования для любого вектора (x, y, z):
Заметьте, что 4 элемент вектора равняется 1. Этот компонент обозначается как w и будет потом использован для других задач.

Матрица сдвига
Сдвиг — это процесс добавления одного вектора к другому для получения нового вектора с другой позицией, то-есть сдвиг вектора на основании вектора сдвига. Мы уже обсуждали сложение векторов, поэтому для вас это не будет чем-то новым.
Также как и с матрицей масштабирования в матрице 4х4 есть несколько позиций для выполнения требуемых операций, для сдвига — это верхние 3 элемента четвертой колонки. Если мы представим вектор сдвига как (Tx, Ty, Tz) — то мы можем определить матрицу сдвига следующим образом:
Это работает, потому что все значения вектора умножаются на w компонент вектора и складываются с начальным значениями. Это было бы невозможно при использовании матриц 3х3.

Гомогенные координаты
Компонента вектора w также называется гомогенной координатой. Для получения 3D вектора из гомогенной координаты мы делим x, y и z координаты на w. Обычно этого не замечают, так как w большую часть времени равна 1.0. Использование гомогенных координат имеет несколько преимуществ: они позволяют нам выполнять сдвиги на 3D векторах (без w компоненты это было бы невозможно) и в следующей главе мы используем значение w для создания 3D визуализаций.
Также когда гомогенная координата равна 0 — то вектор считается вектором направления, так как вектор с компонентой w равной 0 не может быть сдвинут.
С матрицей сдвига мы можем двигать объекты по всем 3 направлениям (x, y, z), что делает эту матрицу крайне полезной для наших задач.

Матрица вращения
Последние пару трансформаций были довольно просты для понимания и представления в 2D или 3D пространстве, но вращения немного более заковыристые. Если вы хотите узнать как же именно эти матрицы формируются — то я рекомендую видео Khan Academy про линейную алгебру.
Для начала давайте определим что вообще такое — вращение вектора. Вращение в 2D и 3D определяется углом. Угол может выражаться в углах или в радианах, в которых полный оборот — это 360 градусов или 2Pi соответственно. Я предпочитаю работать с градусами, поскольку они более логичны для меня.

Большинство вращательных функций требует угол в радианах, но благо преобразование из одной системы в другую выполнить довольно пр
Что такое единичная матрица?
Идентификационная матрица
Узнав о нулевой матрице, пришло время изучить другой тип матрицы, содержащий постоянный определенный набор значений, каждый раз, пора нам изучить единичные матрицы.
Что такое единичная матрица?
Единичная матрица — это заданная квадратная матрица любого порядка, которая содержит на своей главной диагонали элементы со значением, равным единице, в то время как остальные элементы матрицы равны нулю.
Чтобы по частям объяснить это определение, давайте начнем с напоминания, что квадратная матрица относится к матрице, содержащей одинаковое количество строк и столбцов.Порядок матрицы определяется ее размерами, а ее главная диагональ относится к массиву элементов внутри матрицы, которые образуют наклонную линию от верхнего левого угла к нижнему правому углу. Учитывая характеристики единичной матрицы, мы также можем заключить, что этот тип матриц также является диагональными матрицами.
Диагональная матрица — это матрица, в которой все элементы ее элементов равны нулю, за исключением элементов, находящихся на ее главной диагонали. В этом случае все ненулевые элементы матрицы будут иметь значение, равное единице, и это одна из причин, по которой единичную матрицу иногда также называют единичной матрицей.
В случае обозначения матричной линейной алгебры единичная матрица служит объектом, эквивалентным единице в числовой алгебре (другая причина, почему она называется единичной матрицей). Другими словами, единичная матрица эквивалентна единице, но в данном случае это алгебраический объект с размерами и организацией массива, который можно использовать в операциях с другими массивами упорядоченных чисел (другими матрицами).
В следующем разделе мы рассмотрим свойства единичной матрицы, и определение единичной матрицы будет иметь гораздо больший смысл, особенно в случае умножения матриц, включая единичную матрицу (см. Свойство номер 3).Математически единичная матрица представлена как:
Уравнение 1: Общее выражение единичной матрицы Не путайте с идентичностью матрицы, обратите внимание, что единичная матрица имеет столько же главных диагональных элементов, сколько ее порядок (обозначается субиндексом n в члене, находящемся в левой части уравнения). Примеры матриц идентичности разных размеров можно увидеть в следующем уравнении: Уравнение 2: Примеры матриц идентичности разных размеров Помните, что порядок матрицы относится к количеству содержащихся в ней строк и столбцов, которые также называются ее размерами mxn.Обратите внимание: поскольку единичная матрица является квадратной матрицей, она содержит одинаковое количество строк и столбцов, поэтому ее порядок можно обозначать просто как nxn или как однозначный субиндекс, как показано в уравнениях 1 и 2, которые мы называем » n «(учитывая, что размеры m и n, полученные из типичной записи матриц, равны для квадратных матриц, только одна из этих букв необходима в качестве субиндекса для описания порядка таких матриц).
Итак, в уравнении 2 мы легко можем видеть, что I2 относится к единичной матрице с двумя строками и двумя столбцами, которая в то же время имеет только два элемента на своей главной диагонали; обозначение I3 соответствует единичной матрице порядка 3 или матрице, содержащей три строки и три столбца и 3 элемента на своей главной диагонали; и система обозначений продолжается таким же образом для любого субиндекса n.
Свойства матрицы идентичности
Идентификационная матрица всегда является квадратной матрицей:
Как видно из уравнений 1 и 2, порядок единичной матрицы всегда равен n, что относится к размерам nxn (то есть всегда одинаковое количество строк и столбцов в матрица).
Единичная матрица способна перемножать любую матрицу любого порядка (размерности), если она соответствует следующим правилам:
Если при умножении единичная матрица является первым множителем, то единичная матрица должна иметь размеры с таким количеством столбцов, какое количество строк в умножаемой матрице.Уравнение 3: Умножение единичной матрицы на неединичную матрицу
Если единичная матрица является вторым множителем при умножении, единичная матрица должна иметь такое же количество строк, что и матрица, которая умножает ее, имеет столбец. Уравнение 4: Умножение неединичной матрицы на единичную матрицу Эти два правила исходят из условий умножения матриц.
В результате первых двух правил, если единичная матрица умножает квадратную матрицу тех же размеров, результатом также будет квадратная матрица, которая будет такой же, как неединичная матрица умножения, независимо от порядок, в котором матрицы перемножаются друг на друга.
Следуя двум уравнениям из второго свойства, объясненного выше, из всех свойств единичной матрицы, главное из них можно четко наблюдать в уравнениях 3 и 4: всякий раз, когда единичная матрица умножает другую матрицу, умножение может быть решено (следуя правилам для умножения матриц) результат равен задействованной неединичной матрице. Математически говоря: Уравнение 5: Умножение единичной матрицы на другую матрицу Если задуматься, это эквивалент умножения обычного действительного числа на единицу (на единицу).Любое число, умноженное на единицу, дает такое же исходное число. То же самое касается матрицы, умноженной на единичную матрицу, результатом всегда является одна и та же исходная неединичная (неединичная) матрица, и, таким образом, как объяснялось ранее, единичная матрица получает псевдоним «единичная матрица».
Умножение матрицы на обратную приведет к единичной матрице того же порядка, что и умножаемые матрицы. Математически говоря: Уравнение 6: Умножение матрицы на обратную ей Матрицы, участвующие в таком умножении, называются мультипликативными обратными друг другу.Мы оставим объяснение об обратных матрицах для последующих уроков, начиная с темы об обратных матрицах 2×2. На данный момент просто важно, чтобы вы знали, что это одно из свойств единичной матрицы, которое мы можем использовать для решения матричных уравнений.
Определитель единичной матрицы In всегда равен 1, а ее след равен n. Хотя мы до сих пор не видели, что такое определитель, на данный момент важно знать, что причина, по которой определитель любой единичной матрицы равен единице, заключается в том, что диагональ этих матриц содержит только единицы, а остальные элементы внутри них матрицы нули.Мы представим концепцию определителя в следующем уроке, который называется определителем матрицы 2×2, где определитель единичной матрицы будет объяснен более подробно.
С другой стороны, этот след гораздо проще объяснить. К настоящему времени вы должны знать, что след матрицы относится к сложению элементов, найденных на ее главной диагонали. Поскольку единичная матрица имеет диагональные элементы, все равные единице, при добавлении их всех для получения трассировки у вас всегда будет столько элементов, сколько соответствует порядку единичной матрицы, то есть n.В качестве примера возьмем следующую единичную матрицу: Уравнение 7: Пример единичной матрицы порядка 3×3 Уравнение 7 показывает единичную матрицу 3×3, таким образом, n = 3 для этой матрицы. Таким образом, след представляет собой сложение элементов его диагонали, то есть трех элементов значения 1, сложенных друг с другом, и, таким образом, след равен 3. Следовательно, след единичной матрицы равен n .
Последнее свойство мы начнем с вопроса: обратима ли единичная матрица? Ответ положительный.Мы объясним больше по этой теме в нашем уроке об обратимой матрице 2×2, а пока просто помните: инверсия единичной матрицы сама по себе. Уравнение 8: единичная матрица как обратная мультипликативная сама себе. Мы можем доказать, что матрица, обратная единице, — это сама матрица, умножив их вместе. Помните из нашего четвертого свойства, что умножение матрицы на ее инверсию дает единичную матрицу, и поэтому мы вычислили соответствующее умножение для этого случая (показанного в уравнении 8) и доказали, что инверсия единичной матрицы 2×2 есть сама.
Примеры задач с идентификационной матрицей
Используя свойства, изученные в предыдущем разделе, и определение единичной матрицы, данное в начале этого урока, решите следующие примеры задач:
Пример 1
Учитывая матрицы ниже: Уравнение 9: матрицы A и B Выполните следующие матричные операции:
I3⋅AI_ {3} \ cdot AI3 ⋅A
В этом случае у нас есть пример третьего свойства единичной матрицы: умножение с использованием единичной матрицы и любой другой матрицы, если определенная по правилам умножения матриц, результатом будет неединичная матрица (в данном случае матрица A).Итак, это умножение происходит следующим образом: Уравнение 10: Умножение матриц с использованием единичной матрицы
2A + 4I32A + 4I_ {3} 2A + 4I3
Для этой матричной операции мы вычисляем два случая скалярного умножения, второй из которых включает единичную матрицу 3×3. Решение такой операции идет как: Уравнение 11: сложение двух умножений скалярных матриц
−4B + 2I2-4B + 2I_ {2} −4B + 2I2
Еще раз, эта операция состоит в использовании единичной матрицы для сложения двух скалярных умножений, где второе умножение включает единичную матрицу 2×2.Решаем их так, как показано ниже: Уравнение 12: сложение двух умножений скалярных матриц
I2⋅BI_ {2} \ cdot BI2 ⋅B
По третьему свойству мы знаем, что результатом этого умножения является матрица B: Уравнение 13: Умножение единичной матрицы 2×2 на другую матрицу того же порядка
0⋅I40 \ cdot I_ {4} 0⋅I4
В этом случае у нас есть скалярное умножение единичной матрицы на ноль, таким образом, результатом должна быть нулевая матрица, как показано ниже: Уравнение 14: Скалярное умножение единичной матрицы, дающее нулевую матрицу
Пример 2
Покажите, являются ли следующие матрицы мультипликативно инверсными друг другу:
Имея матрицы X и Y, как показано ниже: Уравнение 15: матрицы X и Y Произведем матричное умножение X ⋅ \ cdot⋅ Y: Уравнение 16: Умножение матриц X и Y Учитывая, что результатом является единичная матрица, мы заключаем, что X и Y являются мультипликативными обратными друг другу.
Имея матрицы A и B, как показано ниже: Уравнение 17: матрицы A и B Произведем матричное умножение A ⋅ \ cdot⋅ B: Уравнение 18: Умножение матриц A и B Таким образом, A и B мультипликативно инвертируют друг друга.
Имея матрицы C и D, как показано ниже: Уравнение 19: матрицы C и D Произведем матричное умножение C ⋅ \ cdot⋅ D: Уравнение 20: Умножение матриц C и D Хотя матрица, полученная в результате вышеописанной операции, очень похожа, она не является единичной матрицей.Следовательно, эта операция показывает, что C и D НЕ являются мультипликативными обратными друг другу.
Имея матрицы E и F, как показано ниже: Уравнение 21: матрицы E и F Произведем матричное умножение E ⋅ \ cdot⋅ F: Уравнение 22: Умножение матриц E и F Следовательно, E и F мультипликативно инвертируют друг друга.
Итак, мы завершаем этот урок, когда узнали, что такое единичная матрица и ее свойства. В последующих уроках имейте в виду, что для простоты мы могли бы называть единичную матрицу единичной матрицей.
Прежде чем мы уйдем, позвольте нам порекомендовать вам следующую небольшую ссылку, кратко определяющую единичную матрицу, и эту статью, которая связывает темы умножения матриц и единичной матрицы, говоря о коммутативном свойстве умножения любой квадратной матрицы на матрицу. единичная матрица того же порядка (точно так же, как описано в третьем свойстве во втором разделе этого урока) и как это не применяется к другим умножениям матриц.
Итак, на сегодня все, до встречи на следующем уроке!
Идентификационная матрица и ее свойства
Единичная матрица — это квадратная матрица, которая имеет единицы по главной диагонали и нули для всех остальных элементов.Эта матрица часто записывается просто как \ (I \) и отличается тем, что действует как 1 при умножении матриц. В этом уроке мы рассмотрим это свойство и некоторые другие важные идеи, связанные с тождественными матрицами.
реклама
Единичная матрица всегда является квадратной матрицей
Хотя мы говорим «единичная матрица», мы часто говорим об «единичной матрице». Для любого целого числа \ (n \) существует соответствующая единичная матрица \ (n \ times n \).Эти матрицы называются квадратными, поскольку количество строк и столбцов всегда одинаковое.
Во избежание путаницы часто используется нижний индекс. Таким образом, на рисунке выше идентичность \ (2 \ times 2 \) может быть обозначена как \ (I_2 \), а идентичность \ (3 \ times 3 \) может быть указана как \ (I_3 \).
Умножение любой матрицы на единицу дает саму матрицу
При работе с матричным умножением размер матрицы важен, поскольку умножение не всегда определяется.Следовательно, для матрицы \ (m \ times n \) \ (A \) мы говорим:
Это показывает, что до тех пор, пока учитывается размер матрицы, умножение на единицу похоже на умножение на 1 с числами. Например, рассмотрим следующую матрицу.
Это матрица \ (2 \ times 4 \), поскольку в ней 2 строки и 4 столбца. Вы можете проверить, что \ (I_2 A = A \):
и \ (A I_4 = A \):
С другими квадратными матрицами все намного проще.Рассмотрим пример ниже, где \ (B \) — матрица \ (2 \ times 2 \). Здесь мы можем использовать тождество \ (2 \ times 2 \) как для правого, так и для левого умножения.
Произведение двух обратных матриц всегда тождество
Одна из концепций, интенсивно изучаемых в математике, — это концепция обратимых матриц, то есть тех матриц, которые имеют обратную. По определению, когда вы перемножаете две матрицы, обратные друг другу, вы получите единичную матрицу.Рассмотрим следующие матрицы:
Для этих матриц \ (AB = BA = I \), где \ (I \) — единичная матрица \ (2 \ times 2 \).
Следовательно, \ (A \) и \ (B \) — обратные матрицы. Вы можете изучить эту идею подробнее здесь: обратные матрицы.
Сводка
Единичная матрица — это фундаментальная идея при работе с матрицами — независимо от того, работаете ли вы с простым умножением, обращением или даже решением матричных уравнений. Изучая такие темы, убедитесь, что у вас есть фундаментальные представления об этой матрице.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанные
Матрица идентичности — Концепция
При вычислении матрицы важно понимать единичную матрицу .Мы можем думать об единичной матрице как о мультипликативной единице квадратных матриц или как об единице квадратных матриц. Любая квадратная матрица, умноженная на единичную матрицу равных размеров слева или справа, не меняется. Единичная матрица часто используется в доказательствах и при вычислении обратной матрицы.
Мы говорим о квадратных матрицах, и одна действительно важная квадратная матрица — это единичная матрица, о которой мы поговорим чуть позже.Во-первых, давайте взглянем на матрицу a, b и i, я сначала хочу умножить на i, чтобы перебрать 1 умножить на 1, чтобы 1 плюс 0, было 1, 0-1 это -1, 3 + 0 это 3 и 0+ 0 равно 0, поэтому обратите внимание: 1, -1,3,0 1, -1,3,0 Я получаю ту же матрицу, полученную из этого продукта, на самом деле это просто матрица a.
А теперь позвольте мне умножить i на b, так вот i и вот b, я получаю 2 + 0 2, здесь 3 + 0 3, я получаю 0-1 -1, и я получаю 0 + 4 4 и снова 2,3 -1 , 4 точно так же, это матрица b, поэтому мы замечаем, что когда мы умножаем на эту специальную матрицу i, мы получаем матрицу, с которой мы начали, так что 8 раз i будет просто a, i умножить b будет просто b, i называется единичной матрицей.Это единичная матрица порядка 2, поэтому единичная матрица — это матрица, в которой по диагонали стоят единицы, а во всем остальном — нули. У других других порядков квадратных матриц они тоже есть. Вот единичная матрица порядка 3, вот единичная матрица порядка 4, и, как вы видели раньше, если я умножу матрицу 3 на 3 на эту матрицу, она останется неизменной, так что это вроде как умножение единицы действительных чисел, которое это число 1, которое вы умножаете 5 на 1, вы получаете 5, поэтому при умножении число остается неизменным.
Единичная матрица действительно важна в алгебре матриц, как вы увидите в следующем выпуске.
6.2 — Операции с матрицами
6.2 — Операции с матрицами
Равенство
Две матрицы равны тогда и только тогда, когда
Порядок матриц одинаковый
Соответствующие элементы матриц одинаковые
Дополнение
Порядок матриц должен быть таким же
Сложите соответствующие элементы вместе
Матрица сложения коммутативная
Матрица сложения ассоциативна
Вычитание
Порядок матриц должен быть таким же
Вычесть соответствующие элементы
Вычитание матрицы не коммутативно (как и вычитание действительных чисел)
Матричное вычитание не ассоциативное (как и вычитание действительных чисел)
Скалярное умножение
Скаляр — это число, а не матрица.
Матрица может быть любого порядка
Умножить все элементы в матрице на скаляр
Скалярное умножение коммутативно
Скалярное умножение ассоциативно
Нулевая матрица
Матрица любого заказа
Состоит из всех нулей
Обозначается заглавной буквой O
Аддитивный идентификатор для матриц
Любая матрица плюс нулевая матрица является исходной матрицей
Умножение матриц
A _{m × n} × B _{n × p} = C _{m × p}
Количество столбцов в первой матрице должно быть равно количество строк во второй матрице.То есть внутренние размеры должны быть одинаковыми.
Порядок произведения — это количество строк в первой матрице на количество столбцов в вторая матрица. То есть габариты изделия — это габариты внешние.
Поскольку количество столбцов в первой матрице равно количеству строк во второй матрицу, вы можете объединить записи.
Каждый элемент в строке i из первой матрицы объединяется в пару с элементом в столбце j из вторая матрица.
Элемент в строке i , столбце j продукта формируется путем умножения этих парных элементов. и суммируя их.
Каждый элемент в продукте представляет собой сумму произведений элементов из строка i первой матрицы и столбец j второй матрицы.
Будет n продуктов, которые суммируются для каждого элемента в продукте.
См. Полный пример умножения матриц.
Умножение матриц некоммутативно
Умножение действительных чисел.
Внутренние размеры могут не совпадать при изменении порядка матриц.
Не просто перемножайте соответствующие элементы вместе
Поскольку порядок (размеры) матриц не обязательно должны быть одинаковыми, может не быть соответствующие элементы умножаются вместе.
Умножьте строки первого столбца на столбцы второго и сложите.
Нет матричного деления
Нет определенного процесса для деления матрицы на другую матрицу.
Матрица может быть разделена скаляром.
Идентификационная матрица
Квадратная матрица
Единицы по главной диагонали
Нули везде
Обозначается I. Если указан нижний индекс, это порядок единичной матрицы.
I — мультипликативное тождество для матриц
Любая матрица, умноженная на единичную матрицу, является исходной матрицей.
Умножение на единичную матрицу коммутативно, хотя порядок изменить
Идентификационная матрица размера 2
Идентификационная матрица размера 3
I ₃ = 1 0 0
0 1 0
0 0 1
Свойства матриц
Имущество Пример
Коммутативность сложения А + В = В + А
Ассоциативность сложения А + (В + С) = (А + В) + С
Ассоциативность скалярного умножения (кд) А = с (дА)
Скалярная идентичность 1А = А (1) = А
Распределительные c (A + B) = cA + cB
Распределительные (с + г) А = сА + дА
Аддитивный идентификатор А + О = О + А = А
Ассоциативность умножения А (ВС) = (АВ) С
Распределительный левый A (B + C) = AB + AC
Распределитель правый (А + В) С = АС + ВС
Скалярная ассоциативность / коммутативность c (AB) = (cA) B = A (cB) = (AB) c
Мультипликативная идентичность IA = AI = A
Свойства действительных чисел, не являющиеся свойствами матриц
Коммутативность умножения
Вы не можете изменить порядок задачи умножения и ожидать получить то же самое продукт.AB ≠ BA
Вы должны быть осторожны при разложении общих множителей, чтобы убедиться, что они одно и тоже боковая сторона. AX + BX = (A + B) X и XA + XB = X (A + B), но AX + XB не учитывается.
Свойство нулевого продукта
Тот факт, что произведение двух матриц является нулевой матрицей, не означает, что одна из им была нулевая матрица.
Мультипликативное свойство равенства
Если A = B, то AC = BC. Это свойство все еще верно, но обратное не обязательно верно.То, что AC = BC, не означает, что A = B.
Поскольку умножение матриц не коммутативно, вы должны быть осторожны, чтобы умножение до или после умножения с обеих сторон уравнения. То есть, если A = B, тогда AC = BC или CA = CB, но AC ≠ CB.
Нет матричного деления
Надо умножить на обратную матрицу
Оценка функции с помощью матрицы
Рассмотрим функцию f (x) = x ² — 4x + 3 и матрицу A
Первоначальная попытка оценить f (A) будет заключаться в замене каждого x с помощью A, чтобы получить f (A) = A ² — 4A + 3.Есть одно небольшое проблема, однако. Константа 3 равна не матрица, и вы не можете добавить матрицы и скаляры вместе. Итак, умножаем константа матрицей идентичности.
f (A) = A ² — 4A + 3I.
Оцените каждый член функции, а затем сложите их.
A ² = 1 2 * 1 2 = 7 10
3 4 3 4 15 22
-4 А = -4 1 2 = -4 -8
3 4 -12 -16
3I = 3 1 0 = 3 0
0 1 0 3
f (А) = 7 10 + -4 -8 + 3 0 = 6 2
15 22 -12 -16 0 3 3 9
Факторинговые выражения
Показаны некоторые примеры факторинга.Упрощайте и решайте как обычно, но помните эта матрица умножение не коммутативно и нет матричного деления.
2X + 3X = 5X
AX + BX = (A + B) X
ХА + ХВ = Х (А + В)
AX + 5X = (A + 5I) X
AX + XB не учитывает
Решение уравнений
Систему линейных уравнений можно записать как AX = B, где A — коэффициент матрица, X — вектор-столбец, содержащий переменные, а B — правая боковая сторона. В следующем разделе мы узнаем, как решить это уравнение.
Если существует более одной системы линейных уравнений с одним и тем же коэффициентом матрица, то вы можете расширить матрицу B, чтобы она содержала более одного столбца. Ставить каждую правую часть в свой столбец.
Умножение матриц
Умножение матриц включает суммирование произведения. Это уместно там, где вы нужно умножайте вещи вместе, а затем Добавлять. Например, умножение количества единиц на стоимость единицы будет дать общую Стоимость.
Единицы по продукту найдены путем выполнения модульного анализа на матрицы.Этикетки для продукта — это этикетки строк первого матрица и метки столбцов вторая матрица.
4. Умножение матриц
Важно: Мы можем умножать матрицы только в том случае, если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Пример 1
a) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно, и это дает матрицу 2 × 4 в качестве ответа.
b) Допускается умножение матрицы 7 × 1 на матрицу 1 × 2; это дает матрицу 7 × 2
c) НЕЛЬЗЯ умножить матрицу 4 × 3 на матрицу 2 × 3.
Как умножить 2 матрицы
Сначала мы используем буквы, чтобы увидеть, что происходит. Позже мы увидим пример чисел.
В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]`
Ответом будет матрица 2 × 2.
Умножаем и складываем элементы следующим образом. Мы обрабатываем по 1-й строке первой матрицы, поэлементно умножая на 1-й столбец второй матрицы.Складываем получившихся продуктов . Наш ответ находится в позиции a ₁₁ (вверху слева) матрицы ответов.
Мы делаем аналогичный процесс для 1-й строки первой матрицы и 2-го столбца второй матрицы. Результат помещается в позицию a ₁₂.
Теперь займемся второй строкой первой матрицы и первым столбцом второй матрицы. Результат помещается в позицию a ₂₁.
Наконец, мы делаем вторую строку первой матрицы и второй столбец второй матрицы. Результат помещается в позицию a ₂₂.
Итак, результат умножения наших двух матриц будет следующим:
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]` `= [(au + bw + cy, av + bx + cz), (du + ew + fy, dv + ex + fz)] `
Теперь давайте посмотрим на числовой пример.
Пользователи телефона
ПРИМЕЧАНИЕ: Если вы разговариваете по телефону, вы можете прокрутить любую матрицу шириной на этой странице вправо или влево, чтобы увидеть все выражение.
Пример 2
Умножить:
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
Ответ
Это 2 × 3 умножить на 3 × 2, что даст нам 2 × 2 отвечать.
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((0xx3 + -1xx1 + 2xx6,0xx-1 + -1xx2 + 2xx1), (4xx3 + 11xx1 + 2xx6,4xx -1 + 11xx2 + 2xx1))`
`= ((0-1 + 12,0-2 + 2), (12 + 11 + 12, -4 + 22 + 2))`
`= ((11,0), (35,20))`
Наш ответ — матрица 2 × 2.
Умножение матриц 2 × 2
Процесс одинаков для матрицы любого размера. Мы умножаем на строк первой матрицы и на столбцов второй матрицы поэлементно. Затем мы добавляем продукты:
`((a, b), (c, d)) ((e, f), (g, h))` `= ((ae + bg, af + bh), (ce + dg, cf + dh )) `
В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.
Пример 3
Умножить:
`((8,9), (5, -1)) ((- 2,3), (4,0))`
Ответ
`((8,9), (5, -1)) ((- 2,3), (4,0))`
`= ((8 xx -2 + 9xx4,8xx3 + 9xx0), (5xx-2 + -1xx4,5xx3 + -1xx0))`
`= ((-16 + 36,24 + 0), (- 10+ -4,15 + 0))`
`= ((20,24), (- 14,15))`
Матрицы и системы одновременных линейных уравнений
Теперь мы видим, как написать систему линейных уравнений, используя умножение матриц.
Пример 4
Система уравнений
−3 x + y = 1
6 x -3 y = −4
можно записать как:
`((-3,1), (6, -3)) ((x), (y)) = ((1), (- 4))`
Матрицы
идеально подходят для компьютерного решения задач, потому что компьютеры легко образуют массивы . Мы можем опустить алгебраические символы. Компьютеру требуются только первая и последняя матрицы для решения системы, как мы увидим в разделе «Матрицы и линейные уравнения».
Примечание 1 — Обозначение
Care с записью и умножением матриц .
Следующие выражения имеют различных значений:
AB — это матричное умножение
A × B — это перекрестное произведение , которое возвращает вектор
A * B используется в компьютерной нотации, но не на бумаге
A • B точечное произведение , которое возвращает скаляр .
[Дополнительную информацию о векторных и скалярных величинах см. В главе «Вектор».]
Примечание 2 — Коммутативность умножения матриц
Имеет ли `AB = BA`?
Посмотрим, правда ли это на примере.
Пример 5
Если
`A = ((0, -1,2), (4,11,2))`
и
`B = ((3, -1), (1,2), (6,1))`
найдите AB, и BA.
Ответ
Мы выполнили AB выше, и ответ был:
`AB = ((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((11,0), (35,20))`
Теперь BA — это (3 × 2) (2 × 3), что даст 3 × 3:
`BA = ((3, -1), (1,2), (6,1)) ((0, -1,2), (4,11,2))`
`= ((0-4, -3-11,6-2), (0 + 8, -1 + 22,2 + 4), (0 + 4, -6 + 11,12 + 2))`
`= ((-4, -14,4), (8,21,6), (4,5,14))`
Итак, в этом случае AB НЕ равно BA.
Фактически, для большинства матриц нельзя изменить порядок умножения и получить тот же результат.
В общем случае при умножении матриц закон коммутативности не выполняется, т.е. AB ≠ BA . Есть два распространенных исключения:
.
Идентификационная матрица: IA = AI = A .?
, инверсия матрицы: A ^-1 A = AA ^-1 = I.
В следующем разделе мы узнаем, как найти обратную матрицу.
Пример 6 — Умножение на идентификационную матрицу
Учитывая, что
`A = ((- 3,1,6), (3, -1,0), (4,2,5))`
найдите AI .
Ответ
`AI = ((-3,1,6), (3, -1,0), (4,2,5)) ((1,0,0), (0,1,0), (0 , 0,1)) `
`= ((- 3 + 0 + 0,0 + 1 + 0,0 + 0 + 6), (3 + 0 + 0,0 + -1 + 0,0 + 0 + 0), (4 + 0 + 0,0 + 2 + 0,0 + 0 + 5)) `
`= ((- 3,1,6), (3, -1,0), (4,2,5))`
`= A`
Мы видим, что умножение на единичную матрицу не меняет значения исходной матрицы.
То есть
AI = A
Упражнения
1. Если возможно, найдите BA и AB .
`A = ((- 2,1,7), (3, -1,0), (0,2, -1))`
`B = (4 \ \ -1 \ \ \ 5)`
Ответ
`BA = (4 \ \ -1 \ \ \ 5) ((- 2,1,7), (3, -1,0), (0,2, -1))`
`= (-8 + (- 3) +0 \ \ \ 4 + 1 + 10 \ \ \ 28 + 0 + (- 5))`
`= (- 11 \ \ 15 \ \ 23)`
AB невозможно.(3 × 3) × (1 × 3).
2. Определите, если B = A ^-1, учитывая:
`A = ((3, -4), (5, -7))`
`B = ((7,4), (5,3))`
Ответ
Если B = A ^-1, то AB = I.
`AB = ((3, -4), (5, -7)) ((7,4), (5,3))`
`= ((21-20,12-12), (35-35,20-21))`
`= ((1,0), (0, -1))`
`! = I`
Таким образом, B НЕ является обратной величиной A.2 + 0)) `
`= ((1,0), (0,1))`
`= I`
4. Оцените следующее умножение матриц, которое используется для управления движением роботизированного механизма.
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
Ответ
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
`= ((2 (0,5) -4 (0,866) +0), (2 (0,866) +4 (0,5) +0), (0 + 0 + 0))`
`= ((- 2,464), (3,732), (0))`
Интерпретация этого заключается в том, что рука робота движется из позиция (2, 4, 0) в позицию (-2.46, 3.73, 0). То есть это перемещается в плоскости x-y , но его высота остается на уровне z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят, на сколько градусов нужно переместиться.
Интерактивное умножение матриц
Идентификационная матрица
Марко Табога, доктор философии
Единичная матрица — это квадратная матрица, все диагональные элементы которой равны единица, а недиагональные элементы которой равны нулю.
Матрицы идентичности играют ключевую роль в линейной алгебре.В частности, их роль в матричном умножении похожа на роль, которую играет число 1 в умножении действительных числа:
Определение
Ниже приводится формальное определение.
Таким образом, записи, индекс строки которых и индекс столбца совпадают (т.е. элементы, расположенные на главной диагонали) равны . Все остальные записи равны .
Когда , есть только одна запись, а также
Примеры
Ниже приведены некоторые примеры матриц идентичности.
Пример В единичная матрица является
Пример В единичная матрица является
Пример В единичная матрица является
Произведения с тождественной матрицей
Ключевым свойством является то, что матрица остается неизменной, когда ее умножают на единичная матрица. {- 1} [A] = [I] [/ latex].
Цели обучения
Попрактикуйтесь в нахождении обратной матрицы и опишите ее свойства
Ключевые выводы
Ключевые моменты
Определение обратной матрицы требует коммутативности — умножение должно работать одинаково в любом порядке.
Чтобы быть обратимой, матрица должна быть квадратной, потому что единичная матрица также должна быть квадратной.
Чтобы определить обратную матрицу [latex] \ begin {pmatrix} 3 & 4 \\ 5 & 6 \ end {pmatrix} [/ latex], установите [latex] \ begin {pmatrix} 3 & 4 \\ 5 & 6 \ end {pmatrix} \ begin {pmatrix} a & b \\ c & d \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \\ 0 & 1 \ end {pmatrix} [/ latex].Затем решите для [латекс] a [/ латекс], [латекс] b [/ латекс], [латекс] c [/ латекс] и [латекс] d [/ латекс].
Ключевые термины
сингулярная матрица : матрица, не имеющая обратной.
матрица : прямоугольное расположение чисел или членов, имеющее различное применение, например преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.
обратная матрица : квадратная матрица [латекс] [A] [/ latex] с связанной матрицей [latex] [B] [/ latex], такая что [latex] [A] [/ latex] умножается на [latex] [B] [/ latex] и [latex] [B] [/ latex], умноженные на [latex] [A] [/ latex], оба равны единичной матрице.
единичная матрица : Диагональная матрица, все диагональные элементы которой равны [latex] 1 [/ latex], а остальные равны [latex] 0 [/ latex].
Убедившись, что число [latex] 1 [/ latex] играет особую роль в умножении, [latex] 1x = x [/ latex], число, обратное числу, определяется как число, которое умножается на это число, чтобы получить [ латекс] 1 [/ латекс]. Матрица [latex] B [/ latex] является инверсией матрицы [latex] A [/ latex], если при умножении [латекс] A \ cdot B [/ latex] или [latex] B \ cdot A [/ латекс] дает единичную матрицу.{-1} [A] = [I] [/ latex]
Где [latex] [I] [/ latex] — это единичная матрица.
Обратите внимание, что, как и в определении единичной матрицы, это определение требует коммутативности — умножение должно работать одинаково в любом порядке.
Отметим также, что только квадратные матрицы могут иметь инверсию. Определение обратной матрицы основано на единичной матрице [latex] [I] [/ latex], и уже было установлено, что только квадратные матрицы имеют связанную единичную матрицу.
Метод нахождения обратной матрицы исходит непосредственно из определения вместе с небольшой алгеброй.
Поиск обратной матрицы
Пример: Найдите обратное выражение: [latex] \ begin {pmatrix} 3 & 4 \\ 5 & 6 \ end {pmatrix} [/ latex]
Во-первых, пусть верно следующее:
[латекс] \ displaystyle \ begin {pmatrix} 3 & 4 \\ 5 & 6 \ end {pmatrix} \ begin {pmatrix} a & b \\ c & d \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \\ 0 & 1 \ end {pmatrix} [/ latex]
Это ключевой шаг.Он устанавливает [latex] \ begin {pmatrix} a & b \\ c & d \ end {pmatrix} [/ latex] как искомую обратную, утверждая, что она заполняет определение обратной матрицы. При умножении этой загадочной матрицы на нашу исходную матрицу получается [латекс] [I] [/ латекс]. При решении для четырех переменных [латекс] a [/ латекс], [латекс] b [/ латекс], [латекс] c [/ латекс] и [латекс] d [/ латекс], обратная матрица будет быть найденным.
Далее производим умножение:
[латекс] \ displaystyle \ begin {pmatrix} 3a + 4c & 3b + 4d \\ 5a + 6c & 5b + 6d \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \\ 0 & 1 \ end {pmatrix } [/ латекс]
Чтобы две матрицы были равны, каждый элемент слева должен быть равен соответствующему элементу справа.Итак, чтобы эти две матрицы были равны друг другу:
[латекс] \ displaystyle 3a + 4c = 1 [/ латекс]
[латекс] \ displaystyle 3b + 4d = 0 [/ латекс]
[латекс] \ displaystyle 5a + 6c = 0 [/ латекс]
[латекс] \ displaystyle 5b + 6d = 1 [/ латекс]
Решите первые два уравнения для [latex] a [/ latex] и [latex] c [/ latex] и два вторых уравнения для [latex] b [/ latex] и [latex] d [/ latex], используя либо исключение или замена.
Результаты:
[латекс] \ displaystyle a = -3 [/ latex]
[латекс] \ displaystyle b = 2 [/ латекс]
[латекс] \ displaystyle c = 2 \ frac12 [/ латекс]
[латекс] \ displaystyle d = -1 \ frac 12 [/ латекс]
Решив для четырех переменных, результат обратный [латекс] \ begin {pmatrix} -3 & 2 \\ 2 \ frac 12 & -1 \ frac 12 \ end {pmatrix} [/ latex].
Если была найдена обратная, то для быстрой проверки ее правильности нужно умножить ее на исходную матрицу и посмотреть, дает ли матрица идентификации:
[латекс] \ displaystyle \ begin {pmatrix} -3 & 2 \\ 2 \ frac 12 & -1 \ frac 12 \ end {pmatrix} \ begin {pmatrix} 3 & 4 \\ 5 & 6 \ end {pmatrix} [/ латекс]
После умножения получается:
[латекс] \ displaystyle \ begin {pmatrix} (-3) (3) + (2) (5) & (-3) (4) + (2) (6) \\ (2 \ frac 12) (3 ) _ + (- 1 \ frac 12) (5) & (2 \ frac 12) (4) + (- 1 \ frac 12) (6) \ end {pmatrix} [/ latex]
Упрощение задачи дает:
[латекс] \ displaystyle \ begin {pmatrix} -9 + 10 & -12 + 12 \\ 7 \ frac 12-7 \ frac 12 & 10-9 \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \ \ 0 & 1 \ end {pmatrix} [/ латекс]
Следовательно, работает обратное.Но ждать!
Обратите внимание, чтобы полностью проверить это, нужно попробовать умножение в обоих порядках, потому что, как правило, изменение порядка умножения матриц меняет ответ. Определение обратной матрицы указывает, что она должна работать в обоих направлениях.
[латекс] \ displaystyle \ begin {pmatrix} 3 & 4 \\ 5 & 6 \ end {pmatrix} \ begin {pmatrix} -3 & 2 \\ 2 \ frac 12 & -1 \ frac 12 \ end {pmatrix} [/ латекс]
После умножения получаем:
[латекс] \ displaystyle \ begin {pmatrix} (3) (- 3) + (4) (2 \ frac 12) & (3) (2) + (4) (- 1 \ frac 12) \\ (5 ) (- 3) _ + (6) (2 \ frac 12) & (5) (2) + (6) (- 1 \ frac 12) \ end {pmatrix} [/ latex]
Упрощение задачи дает:
[латекс] \ displaystyle \ begin {pmatrix} -9 + 10 & 6-6 \\ -15 + 15 & 10-9 \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \\ 0 & 1 \ end {pmatrix} [/ латекс]
Итак, обратная матрица работает в обоих направлениях.
В некоторых случаях матрица, обратная квадратной, не существует. Это называется особой матрицей.
Решение систем уравнений с использованием обратных матриц
Система уравнений может быть легко решена с использованием концепции обратной матрицы и матричного умножения.
Цели обучения
Практика использования обратных матриц для решения системы линейных уравнений
Ключевые выводы
Ключевые моменты
Использование матриц для решения систем уравнений может значительно снизить нагрузку на вас.Например, рассмотрим следующие три уравнения: [латекс] x + 2y-z = 11 [/ latex], [latex] 2x-y + 3z = 7 [/ latex] и [latex] 7x-3y-2z = 2 [ /латекс].
Чтобы решить эти уравнения с использованием матриц, мы сначала определяем [латекс] 3 \ умножить на 3 [/ латекс] матрицу [латекс] [A] [/ латекс], которая является коэффициентами всех переменных в левой части равного знаки: [латекс] [A] = \ begin {bmatrix} 1 & 2 & -1 \\ 2 & -1 & 3 \\ 7 & -3 & -2 \ end {bmatrix} [/ latex] Затем определите [латекс] 3 \ times 1 [/ latex] matrix [latex] [B] [/ latex], которые представляют собой числа справа от знаков равенства: [latex] [B] = \ begin {bmatrix} 11 \\ 7 \\ 2 \ end {bmatrix }.[/ латекс]
Чтобы определить значения переменных, мы просто умножаем обратное [латекс] [A] [/ латекс] на [латекс] [B] [/ латекс]. Проще всего это сделать с помощью калькулятора. Калькулятор отвечает матрицей [латекс] 3 \ умножить на 1 [/ латекс], которая включает решение системы как: [латекс] x = 3 [/ латекс], [латекс] y = 5 [/ латекс] и [латекс] z = 2 [/ латекс].
Ключевые термины
обратная матрица : для матрицы [латекс] [A] [/ latex], если существует такая матрица [latex] [B] [/ latex], что [latex] [A] [/ latex] умножается на [ latex] [B] [/ latex] и [latex] [B] [/ latex], умноженные на [latex] [A] [/ latex], оба равны единичной матрице, тогда [latex] [B] [/ latex] равно инверсия [латекс] [A] [/ латекс].
линейное уравнение : полиномиальное уравнение первой степени (например, [латекс] x = 2y-7 [/ latex]).
Систему уравнений можно легко решить, используя концепции обратной матрицы и матричного умножения. В главе, посвященной системным уравнениям, мы видели, как решить два уравнения с двумя неизвестными. Но предположим, что у нас есть три уравнения с тремя неизвестными? Или четыре, или пять? Такие ситуации встречаются чаще, чем вы думаете в реальном мире.И даже если вам разрешено пользоваться калькулятором, совсем не очевидно, как решить такую задачу в разумные сроки.
Пример 1: Решите следующую систему линейных уравнений:
[латекс] \ displaystyle x + 2y-z = 11 \ 2x-y + 3z = 7 \ 7x-3y-2z = 2 [/ latex]
Шаг 1. Создайте матрицу [latex] A [/ latex], которая состоит из коэффициентов всех переменных из каждого уравнения из левой части знака равенства:
[латекс] \ displaystyle [A] = \ begin {bmatrix} 1 & 2 & -1 \\ 2 & -1 & 3 \\ 7 & -3 & -2 \ end {bmatrix} [/ latex]
Шаг 2. Увеличьте матрицу [latex] B [/ latex], которая состоит из констант, стоящих справа от знака равенства:
[латекс] \ displaystyle [B] = \ begin {bmatrix} 11 \\ 7 \\ 2 \ end {bmatrix} [/ latex]
Теперь, чтобы определить значения [latex] x [/ latex], [latex] y [/ latex] и [latex] z [/ latex], мы просто умножаем обратное значение [latex] [A] [/ латекс] раз [латекс] [B] [/ латекс].{-1}] [B] [/ latex], то есть обратная матрица [latex] [A] [/ latex], умноженная на матрицу [latex] [B] [/ latex].

Имущество	Пример
Коммутативность сложения	А + В = В + А
Ассоциативность сложения	А + (В + С) = (А + В) + С
Ассоциативность скалярного умножения	(кд) А = с (дА)
Скалярная идентичность	1А = А (1) = А
Распределительные	c (A + B) = cA + cB
Распределительные	(с + г) А = сА + дА
Аддитивный идентификатор	А + О = О + А = А
Ассоциативность умножения	А (ВС) = (АВ) С
Распределительный левый	A (B + C) = AB + AC
Распределитель правый	(А + В) С = АС + ВС
Скалярная ассоциативность / коммутативность	c (AB) = (cA) B = A (cB) = (AB) c
Мультипликативная идентичность	IA = AI = A

РубрикаРазное