Тригонометрия 10 класс формулы: Основные тригонометрические формулы — Математика 10 класс — Школьная математика — Каталог статей
| (Ф. Хаусдорф.) ‘ quotes[1]='»Математика — это язык, на котором написана книга природы.»(Г. Галилей) ‘ quotes[2]='»Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.»(А. Маркушевич) ‘ quotes[3]='»Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»(А.Н. Крылов) ‘ quotes[4]='»Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.»(М.И. Калинин) ‘ quotes[5]='»Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»(Платон) ‘ quotes[6]='»Математика есть лучшее и даже единственное введение в изучение природы.»(Д.И. Писарев) ‘ quotes[7]='»Вдохновение нужно в геометрии не меньше, чем в поэзии. (А.С. Пушкин) ‘ quotes[8]='»Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»(В. Произволов) ‘ quotes[9]='»В математике есть своя красота, как в живописи и поэзии.»(Н.Е. Жуковский) ‘ quotes[10]='»Химия – правая рука физики, математика – ее глаз.»(М.В. Ломоносов) ‘ quotes[11]='»Математику уже затем учить надо, что она ум в порядок приводит.»(М.В. Ломоносов) ‘ quotes[12]='»Математика — это язык, на котором говорят все точные науки.»(Н.И. Лобачевский) ‘ quotes[13]='»Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.»(Л. Эйлер) (И. Гете) ‘ quotes[15]='»Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…»(В.Ф. Каган) ‘ quotes[16]='»Счет и вычисления — основа порядка в голове. « «(Песталоцци) ‘ quotes[17]='»Величие человека — в его способности мыслить.»(Б. Паскаль) ‘ quotes[18]='»Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»(Д.Пойа) ‘ quotes[19]='»Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.»(И. Ньютон) ‘ quotes[21]='»Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.»(Л. Карно) ‘ quotes[22]='»Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.»(М.В. Остроградский) ‘ quotes[23]='»Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.»(Н.К. Крупская) ‘ quotes[24]='»Математика уступает свои крепости лишь сильным и смелым. (А.П. Конфорович) ‘ quotes[25]='»Доказательство — это рассуждение, которое убеждает.»(Ю.А. Шиханович) ‘ quotes[26]='»В каждой естественной науке заключено столько истины, сколько в ней есть математики.»(И. Кант) ‘ var whichquote= Math.floor(Math.random()*(quotes.length)) document.write(quotes[whichquote]) |
| 1. |
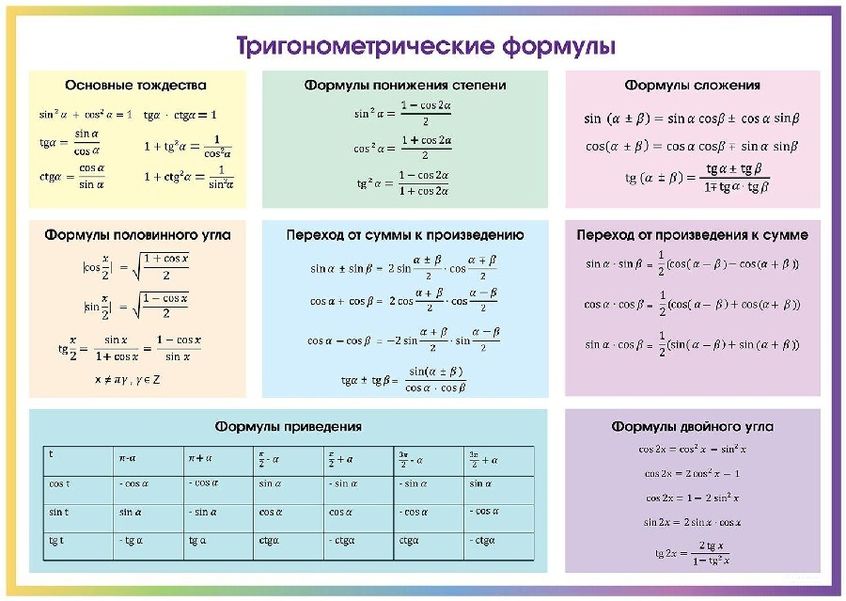
Формулы
|
1 |
2.
|
Равенство
|
1 |
| 3. |
Преобразование произведения в сумму
Сложность: лёгкое |
1 |
4.
|
Преобразование
|
4 |
| 5. |
Преобразование произведения в сумму (синус)
|
4 |
6.
|
Преобразование выражения
|
4 |
| 7. |
Вычисление значения выражения
|
2 |
8.
|
Упрощение выражения
|
4 |
| 9. |
Использование тригонометрических формул
|
3 |
Тригонометрия — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Некоторые рекомендации к выполнению тригонометрических преобразований
К оглавлению. ..
..
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
К оглавлению…
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла. Синус двойного угла:
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
К оглавлению…
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени. Формула понижения степени для синуса:
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
К оглавлению…
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.
 е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
К оглавлению…
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.

- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней).
 Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Урок 34. формулы сложения — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №34.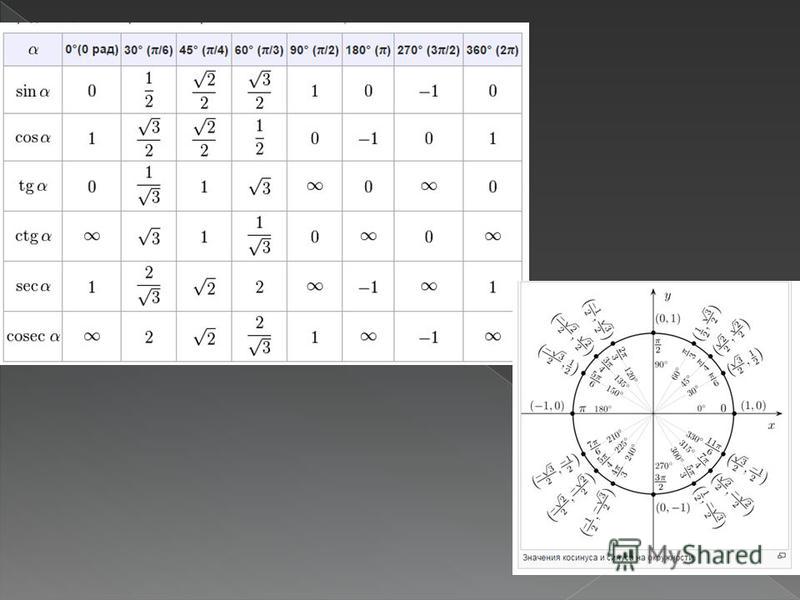 Формулы сложения.
Формулы сложения.
Перечень вопросов, рассматриваемых в теме:
- формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов;
- преобразование тригонометрических выражений на основе использования формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов;
- вычисление значения тригонометрических выражений на основе формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов;
- доказательство тригонометрических тождеств на основе формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов.
Глоссарий по теме
Формулы сложения — это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
– М.: Просвещение, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)
Рисунок 1 – единичная окружность
Точка получена поворотом точки Мₒ(1;0) на угол , а точка на угол и точка на угол .
Углы и равны, отрезки . Значит, треугольник равен треугольнику , следовательно у них одинаковые стороны и .
Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты
;
;
).
Подставим координаты точек и в формулу для нахождения расстояния между ними. Получим:
.
Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:
Преобразуем правую часть:
Соединим левую и правую части:
Разделим на каждое слагаемое :
Получили формулу косинуса суммы.
Заменим и учтём, что , получим формулу косинуса разности
Докажем, что
Так как , , то по формуле косинуса разности получаем:
Заменим получим
Так, например,, потому что .
Докажем, что
Подставим в формулу значение , получим:
Для тангенса и котангенса тоже справедливы формулы
Выведем формулу синуса суммы и разности:
.
В этой формуле заменим и получим формулу синуса разности:
Для тангенса тоже есть формула суммы и разности. По определению .
Тогда tg , разделим числитель и знаменатель на
Получаем формулу тангенса суммы .
Заменим в ней и учтём, что tg〖(-α)=〖-tg〗α 〗, получим формулу тангенса разности
.
Пример. Вычислим .
Для котангенса суммы и разности применяют формулы:
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Найти
Решение: Представим , так как нам известны значения косинуса углов и Подставим в формулу косинуса суммы. Получаем:
Получаем:
.
Ответ: .
Пример 2. Найти .
Решение: Представим , так как нам известны значения синуса углов и Подставим в формулу синуса суммы. Получаем:
.
Ответ: .
Пример 3. Вычислите .
Решение: Применяем формулу синуса разности: .
Ответ: .
Формулы приведения, тригонометрия, 10 класс. алгебра, урок и презентация
Дата публикации: .
Урок и презентация на тему: «Применение формул приведения при решении задач»
Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.
Повторение тригонометрических функций
Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?
Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.
Правило для формул приведения
Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.
Вспомним некоторые формулы:
- sin(t + 2π*k) = sin(t)
- cos(t + 2π*k) = cos(t)
- sin(t + π) = -sin(t)
- cos(t + π) = -cos(t)
- sin(t + π/2) = cos(t)
- cos(t + π/2) = -sin(t)
- tg(t + π*k) = tg(x)
- ctg(t + π*k) = ctg(x)
Ребята, формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения:
- Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.

- Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом. - Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0
Эти правила применимы и когда аргумент функции задан в градусах!
Так же мы можем составить таблицу преобразований тригонометрических функций:
Примеры применения формул приведения
1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2
2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)
3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0
4. Преобразуем ctg(2700 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0 0, тогда (2700 + t) попадет в четвертую четверть, а там преобразуемая функция котангенс отрицательная, согласно третьему пункту нашего правила следует
поставить минус перед нашей функцией: ctg(2700 + t)=-tg(t).
Далее предположим что 0 0, тогда (2700 + t) попадет в четвертую четверть, а там преобразуемая функция котангенс отрицательная, согласно третьему пункту нашего правила следует
поставить минус перед нашей функцией: ctg(2700 + t)=-tg(t).
Задачи с формулами приведения для самостоятельного решения
Ребята, преобразуйте самостоятельно, используя наши правила:
1) tg(π + t),2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).
Задачи на тригонометрические формулы, алгебра
Дата публикации: .
Задачи c ответами и рекомендациями по решению к учебнику Мордковича А.Г. на тему: «Тригонометрические формулы. Упрощение выражений. Доказательства тождеств»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.
 2(t)$.
2(t)$. 8. $x=\frac{πn}{10}$; $x=\frac{πn}{2}$.
10. 0.
11. $x=\frac{π}{4}+2πn$; n∈Z.
12. $x=\frac{π}{20}+\frac{πn}{10}$; $x=±\frac{π}{9}+\frac{2πn}{3}$.
Тригонометрические формулы. 10 класс — презентация онлайн
1. Тригонометрические формулы
2. Цель урока
• Повторение изученного материала• Подготовка к контрольной работе
3. Задачи урока
• Повторить определение синуса, косинуса, тангенса,котангенса числа α;
• Повторить формулы приведения, формулы двойного угла,
формулы сложения;
• Повторить основное тригонометрическое тождество и
формулы, выражающие связь между тангенсом и
косинусом, между котангенсом и синусом.
• Научить применять полученные знания при решении
задач.
4. Ход урока
1.2.
3.
4.
5.
6.
7.
Блиц-опрос
Закрепление знаний и умений
Самостоятельная работа (тест)
Проверка самостоятельной работы
Это интересно
Итог урока
Домашнее задание
1.
 Синусом угла α называется _____
Синусом угла α называется _____точки, полученной поворотом
точки______ вокруг начала координат
на угол α
2. tg α =
1. Синусом угла α называется ордината
точки, полученной поворотом точки
(1;0) вокруг начала координат на угол α
2. tg α =
3. sin2 α +cos2 α=
sin
cos
3. sin2 α +cos2 α = 1
4. 1+ tg2 α=
4. 1+ tg2 α =
5.
6.
7.
8.
9.
sin(-α)=
tg (-α) =
cos (α+β)=
sin (α-β)=
sin 2α=
5.
6.
7.
8.
9.
1
cos 2 α
sin(-α) = — sin α
tg (-α) = -tg α
cos (α+β) = cosα cosβ – sinα sinβ
sin (α-β) = sinα cosβ — cosα sinβ
sin 2α = 2sin αcos α
10. tg (α+β)=
10. tg (α+β) =
tg tg
1 — tg tg
11. sin(π- α)=
12. cos (
2
+ α)=
11. sin(π- α) =sin α
12. cos ( + α) = -sinα
2
1. Косинусом угла α называется _____
точки, полученной поворотом
точки______ вокруг начала координат
на угол α
2.
 ctg α=
ctg α=3. tg α∙ ctg α=
4. 1+ ctg2 α=
5.
6.
7.
8.
9.
cos (-α)=
ctg (-α) =
cos (α-β)=
sin (α+β)=
cos 2α=
11. cos(π- α)=
12. sin (
2
cos
2. сtg α= sin
3. tg α∙ ctg α = 1
4. 1+ ctg2 α=
5.
6.
7.
8.
9.
1
sin 2 α
cos (-α) = cos α
ctg (-α) = -ctg α
cos (α-β)=cosα cosβ +sinα sinβ
sin (α+β)= sinα cosβ + cosα sinβ
cos 2α=cos2 α-sin2 α
2tg
1 — tg 2
10. tg 2α=
1. Косинусом угла α называется абсцисса
точки, полученной поворотом точки
(1;0) вокруг начала координат на угол α
+ α)=
10. tg 2α=
11. cos(π- α)= — cos α
12. sin (
2
+ α)=-cos α
7. Закрепление знаний и умений
1) Дано:sin
3
;
3 2
Найти: cos
ОТВЕТ:
2
cos
3
Упростите
1 cos
2
cos
2
1 / sin 2
1 / cos 2
ctg 2
tg 2
Упростите
sin
1
2
cos
2
1 / sin 2
1 / cos 2
1 / ctg 2
1 / tg 2
Упростите
1
1 tg
2
cos
2
1
1
0
tg 2
Упростите
1
1 ctg 2
sin
2
1 / sin 2
0
ctg 2
1
Упростите
1
1 2
sin
ctg 2
tg 2
ctg 2
tg 2
2) Вычислить:
Дано:
Найти:
ОТВЕТ:
tg 2 2 ;0
sin
2 2
sin
3
2
Упростить выражение
3) 2 sin( ) cos 2 cos( ) sin( )
2
2
Ответ: -2
4)
(1 tg( )) (1 tg( )) cos
Ответ:
2
cos 2
5) Доказать:
2
6) Доказать:
2
2 sin 2 sin 4
tg
2 sin 2 sin 4
вариан 1
1)
а) -2,5;
2)
вариант 2
Найдите значение
1) Найдите значение
2
3 sin 120 4 cos180 3tg135
2 cos 2 150 3 sin( 90 ) 5ctg135
б) 5,5;
Дано:
в) -4,75;
3
sin ;
5 2
Найдите значение:
а)
3)
31
20
б)
г) 3,25.

1
20
в)
а) -3,5;
2)
cos tg
1
20
г)
sin 2 в) cos г) sin
3)
г) 6,5.
4 3
cos ;
2
5 2
Дано:
а)
Упростите выражение:
а) cos б)
в) -0,5;
Найдите значение:
31
20
1 (1 sin ) (1 sin )
tg cos
б) 9,5;
11
15
б)
1
sin ctg
11
г)
15
14
в)
15
1
14
15
Упростите выражение:
ctg sin
1 (sin cos ) 2
а) 2 cos
б)
1
2 cos
в)
2 sin
г)
1
2 sin
17. Проверка
1 вариант1. г)
2. б)
3. г)
2 вариант
1. б)
2. в)
3. г)
18. Это интересно
19. Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого происхождения, обозначающее
«измерение треугольников».Одним из основоположников
тригонометрии считается
древнегреческий астроном Гиппарх,
живший во 2 веке до нашей эры.

Гиппарх является автором первых
тригонометрических таблиц и
одним
из
основоположников
астрономии.
Тригонометрия и ее применение в
различных сферах науки и жизни
,
k=1, a=1
В архитектуре
Детская школа Гауди в Барселоне
Сантьяго Калатрава
Винодельня «Бодегас Исиос»
Феликс Кандела
Ресторан в Лос-Манантиалесе
23. Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону),
Тригонометрия в физикеКолебания, при которых изменения физических
величин происходят по закону косинуса или синуса
(гармоническому закону), называются
гармоническими колебаниями.
Выражение, стоящее под знаком косинуса или синуса,
называется фазой колебания:
24. Теория радуги
n1sin α
=
sin β
n2
n1 — показатель преломления первой среды
n2 — показатель преломления второй среды
α-угол падения, β-угол преломления света
Северное сияние
F q B q B sin
25.
 Тригонометрия в биологии Тригонометрия в ладони
Тригонометрия в биологии Тригонометрия в ладони№0 Мизинец
№1 Безымянный
№2 Средний
№3 Указательный
№4 Большой
00
300
450
600
900
n
sin α =
2
Значение синуса
№ пальца
Угол α
0
0
sin 0 0
0
0
2
1
30
sin 30 0
1
1
2
2
2
45
sin 450
3
60
4
90
sin 60 0
sin 90 0
2
2
3
2
4
1
2
Значение косинуса
№ пальца
Угол α
4
0
3
30
2
45
1
60
0
90
cos 0 0
4
1
2
cos 30 0
3
2
cos 45
0
cos 60 0
cos 90 0
2
2
1
1
2
2
0
0
2
Биоритмы
Экологические ритмы : суточные, сезонные (годовые), приливные и лунные циклы
Физиологические ритмы: ритмы давления, биения сердца, артериальное давление.
30. Домашнее задание
стр. 12 № 14,15а),б)
12 № 14,15а),б)Стр.20 № 31
o Стр.21 № 38,39 а),б)
Доказать:
2
2 sin 2 sin 4
tg
2 sin 2 sin 4
МАТЕРИАЛ К УРОКУ ПОДОБРАН
ИЗ РАЗЛИЧНЫХ САЙТОВ
ИНТЕРНЕТА
математических формул для класса 10
Запоминание математических формул 10-го класса очень важно для учащихся, чтобы лучше сдать экзамен на доске, а также вступительные экзамены. Эти формулы составляют основу математических исследований продвинутого уровня, которые определяют успехи учащихся. Изучение математических формул 10 класса также упрощает решение сложных задач с легкостью и точностью. Математические формулы — это методы для вычисления величин и точной оценки значений, которые также используются в практических ситуациях.
Помимо математики, использование математических формул для 10 класса можно также увидеть в некоторых других областях и профессиях.Например, математические формулы 10-го класса, относящиеся к тригонометрии, статистике, вероятности, уравнениям и многим другим, применяются в областях бухгалтерского учета, медицины, архитектуры, финансов, инженерии, информатики и т. Д. Почти в каждой отрасли эти формулы используются в одном или другой способ. Таким образом, изучение математических формул 10-го класса важно для облегчения нашей жизни.
Д. Почти в каждой отрасли эти формулы используются в одном или другой способ. Таким образом, изучение математических формул 10-го класса важно для облегчения нашей жизни.
Список важных математических формул класса 10
Список некоторых основных математических формул для класса 10, относящихся к наиболее важным темам, рассматриваемым в различных школьных советах, приведен ниже:
- (a + b) 3 = a 3 + b 3 + 3ab (a + b)
- (а — б) 3 = а 3 — б 3 — 3аб (а — б)
- (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2xz
- ан = а + (n — 1) d
- Sn = n / 2 [2a + (n — 1) d]
- sin 2 θ + cos 2 θ = 1 ⇒ sin 2 θ = 1 — cos 2 θ ⇒ cos 2 θ = 1 — sin 2 θ
- cosec 2 θ — детская кроватка 2 θ = 1 ⇒ cosec 2 θ = 1 + детская кроватка 2 θ ⇒ детская кроватка 2 θ = cosec 2 θ — 1
- сек 2 θ — загар 2 θ = 1 ⇒ сек 2 θ = 1 + загар 2 θ ⇒ tan 2 θ = сек 2 θ — 1
- sin θ cosec θ = 1 ⇒ cos θ sec θ = 1 ⇒ tan θ cot θ = 1
- Объем сферы = 4/3 × π r 3
- Площадь поверхности сферы = 4πr 2
Класс 10 Формулы алгебры
Алгебра — это изучение математических утверждений, которые представляют собой равные друг другу члены. Например, полиномиальные уравнения являются одними из наиболее распространенных алгебраических уравнений, которые включают приравнивание полиномов. Изучение формул алгебры 10 класса поможет преобразовать различные словесные задачи в их математические формы. Зная эти формулы, учащиеся могут легко научиться распознавать тип уравнения и применять правила для их решения. Эти алгебраические формулы имеют разные входные и выходные данные с разными интерпретациями. Вот все важные формулы алгебры 10 класса:
Например, полиномиальные уравнения являются одними из наиболее распространенных алгебраических уравнений, которые включают приравнивание полиномов. Изучение формул алгебры 10 класса поможет преобразовать различные словесные задачи в их математические формы. Зная эти формулы, учащиеся могут легко научиться распознавать тип уравнения и применять правила для их решения. Эти алгебраические формулы имеют разные входные и выходные данные с разными интерпретациями. Вот все важные формулы алгебры 10 класса:
- (a + b) 2 = a 2 + 2ab + b 2
- (а — б) 2 = а 2 — 2ab + b 2
- (а + б) (а — б) = а 2 — б 2
- (x + a) (x + b) = x 2 + (a + b) x + ab
- (x + a) (x — b) = x 2 + (a — b) x — ab
- (x — a) (x + b) = x 2 + (b — a) x — ab
- (x — a) (x — b) = x 2 — (a + b) x + ab
- (a + b) 3 = a 3 + b 3 + 3ab (a + b)
- (а — б) 3 = а 3 — б 3 — 3аб (а — б)
- (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2xz
- (x + y — z) 2 = x 2 + y 2 + z 2 + 2xy — 2yz — 2xz
- (x — y + z) 2 = x 2 + y 2 + z 2 — 2xy — 2yz + 2xz
- (x — y — z) 2 = x 2 + y 2 + z 2 — 2xy + 2yz — 2xz
- x 3 + y 3 + z 3 — 3xyz = (x + y + z) (x 2 + y 2 + z 2 — xy — yz — xz)
Формулы арифметической прогрессии класса 10
Многие вещи в нашей повседневной жизни подчиняются определенному образцу. Эти шаблоны обычно называются последовательностями. Две такие последовательности — это арифметическая и геометрическая последовательности. Различные числа, встречающиеся в последовательности, называются ее членами. Условия последовательности обозначены как 1 a 2 , a 3 , …………… a n . Арифметическая прогрессия — это такая последовательность чисел, в которой разница между последовательными членами равна.
Эти шаблоны обычно называются последовательностями. Две такие последовательности — это арифметическая и геометрическая последовательности. Различные числа, встречающиеся в последовательности, называются ее членами. Условия последовательности обозначены как 1 a 2 , a 3 , …………… a n . Арифметическая прогрессия — это такая последовательность чисел, в которой разница между последовательными членами равна.
- a n = a + (n — 1) d, где an — n-й член.
- S n = n / 2 [2a + (n — 1) d]
Формулы тригонометрии класса 10
Тригонометрия — это наука о соотношении сторон и углов прямоугольного треугольника.Тригонометрические отношения — это отношения сторон прямоугольного треугольника. Вот несколько важных тригонометрических формул, связанных с тригонометрическими отношениями.
- sin (90 ° — A) = cos A
- cos (90 ° — A) = sin A
- желто-коричневый (90 ° — A) = детская кроватка A
- детская кроватка (90 ° — A) = желто-коричневый A
- сек (90 ° — A) = cosec A
- сек (90 ° — A) = сек A
- sin 2 θ + cos 2 θ = 1 ⇒ sin 2 θ = 1 — cos 2 θ ⇒ cos 2 θ = 1 — sin 2 θ
- cosec 2 θ — детская кроватка 2 θ = 1 ⇒ cosec 2 θ = 1 + детская кроватка 2 θ ⇒ детская кроватка 2 θ = cosec 2 θ — 1
- сек 2 θ — загар 2 θ = 1 ⇒ сек 2 θ = 1 + загар 2 θ ⇒ tan 2 θ = сек 2 θ — 1
- sin θ cosec θ = 1 ⇒ cos θ sec θ = 1 ⇒ tan θ cot θ = 1
Формулы круга 10 класса
Окружность — это совокупность всех точек на плоскости, находящихся на постоянном расстоянии от фиксированной точки.
Фиксированная точка называется центром круга, а постоянное расстояние от центра называется радиусом. Отрезок, соединяющий любые две точки на окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром. Это самый длинный аккорд. Когда прямая пересекает окружность в одной точке, эта линия называется касательной. Касательная к окружности перпендикулярна радиусу, проходящему через точку контакта.
- Касательная к окружности уравнение x 2 + y 2 = a 2 для прямой y = mx + c задается уравнением y = mx ± a √ [1+ m 2 ].
- Касательная к окружности уравнение x 2 + y 2 = a 2 at (a 1 , b 1 ) равно xa 1 + yb 1 = a 2
Класс 10 Формулы площади и объема поверхности
Трехмерные формы являются важной частью нашей повседневной жизни, и поэтому жизненно важно выучить формулы площади и объема для класса 10, чтобы определять различные размеры этих фигур. Эти расчеты необходимы в повседневной жизни независимо от того, нужно ли вычислить, сколько жидкости необходимо для заполнения контейнера, или нужно рассчитать площадь поверхности любого объекта.Математические формулы для 10 класса, относящиеся к тому же, можно найти ниже:
Эти расчеты необходимы в повседневной жизни независимо от того, нужно ли вычислить, сколько жидкости необходимо для заполнения контейнера, или нужно рассчитать площадь поверхности любого объекта.Математические формулы для 10 класса, относящиеся к тому же, можно найти ниже:
Сфера:
- Объем сферы = 4/3 × π r 3
- Площадь боковой поверхности сферы (LSA) = 4π r 2
- Общая площадь поверхности сферы (TSA) = 4πr 2
Правый круговой цилиндр
- Объем правого кругового цилиндра = πr 2 ч
- Площадь боковой поверхности правого кругового цилиндра (LSA) = 2 × (πrh)
- Общая площадь правого кругового цилиндра (TSA) = 2πr × (r + h)
Полусфера
- Объем полушария = ⅔ x (πr 3 )
- Площадь боковой поверхности полушария (LSA) = 2πr 2
- Общая площадь поверхности полушария (TSA) = 3πr 2
Призма
- Объем призмы = B × h
- Площадь боковой поверхности призмы (LSA) = p × h
Приложения математических формул класса 10
Класс 10 Математические формулы — краеугольный камень навыков счета. Они имеют большое значение в нашей жизни. Математические формулы 10 класса применяются в различных вычислениях для определения нескольких значений. Ниже приведены некоторые из распространенных применений математических формул класса 10.
Они имеют большое значение в нашей жизни. Математические формулы 10 класса применяются в различных вычислениях для определения нескольких значений. Ниже приведены некоторые из распространенных применений математических формул класса 10.
- Формулы квадратных уравнений класса 10 используются в ситуациях, когда мы можем представить местоположение или стоимость любого объекта с помощью квадратных уравнений. Например, для расчета прибыли или убытка от продаж мы можем использовать эти уравнения.
- Тригонометрические формулы класса 10 используются для определения высоты и расстояния в различных областях, таких как навигационная система, архитектура, авиация и т. Д.Например, эти формулы применяются для строительства параллельных и перпендикулярных стен, наклонных крыш, крепления черепицы и т. Д.
- Статистика 10-го класса и формулы вероятности используются при расчете страховых рисков, анализе статистических данных, полученных при переписи населения, и т. Д.
Советы по запоминанию математических формул для 10 класса
Студенты могут запоминать математические формулы 10 класса, которые помогут им в подготовке к экзаменам.
- Один из лучших способов запомнить математические формулы для 10 класса — это пересматривать их несколько раз. Составление формул при их применении для решения вопросов поможет учащимся лучше усвоить их. Поэтому учащиеся должны записывать сложные формулы много раз или решать столько же задач, применяя их, чтобы запомнить их быстрее.
- Соедините соответствующие наглядные изображения с каждой математической формулой, чтобы быстро ее запомнить. Это поможет вспомнить позже. Когда концепции связаны с зрительной памятью, их становится относительно проще запоминать.
- Необходимо понимать формулы и понятия, чтобы лучше их запоминать. Когда учащиеся поймут логику или правила определенной формулы, им будет легче ее запомнить, поскольку тогда она будет иметь больше смысла.
- Используйте все формулы в максимально возможной степени, понимание применения формулы помогает лучше запоминать информацию. Попробуйте решать и практиковать задачи, используя формулы.

Примеры математических формул класса 10
Пример 1: Проверьте, является ли уравнение квадратным или нет: x + 1 / x = 2
Решение: x + 1 / x = 2
х + х -1 = 2
х + х -1 -2 = 0
Поскольку x + x -1 -2 = 0 не является квадратичным многочленом, следовательно, x + 1 / x = 2 не является квадратным уравнением.
Пример 2: Найдите нули квадратичного многочлена 6x 2 — 3 — 7x
Раствор:
Здесь p (x) = 6x 2 — 3 — 7x = 6x 2 — 7x — 3
= 6x 2 — 9x + 2x — 3 = 3x (2x — 3) + 1 (2x — 3)
= (2x — 3) (3x + 1)
= 6 (х — 3/2) [х — (-1/3)]
∴ Нули p (x) равны 3/2 и −1/3
Вы можете скачать распечатанный лист математических формул для класса 10 по ссылке ниже:
Какие важные формулы для математики 10 класса?
Некоторые из наиболее важных формул для математики 10 класса основаны на таких темах, как полиномы, тригонометрия, квадратные уравнения, пары линейных уравнений с двумя переменными, статистика и вероятность. Эти важные математические формулы для 10 класса из приведенных выше тем перечислены ниже:
Эти важные математические формулы для 10 класса из приведенных выше тем перечислены ниже:
- (a + b) 3 = a 3 + b 3 + 3ab (a + b)
- (а — б) 3 = а 3 — б 3 — 3аб (а — б)
- (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2xz
- ан = а + (n — 1) d
- Sn = n / 2 [2a + (n — 1) d]
- sin 2 θ + cos 2 θ = 1 ⇒ sin 2 θ = 1 — cos 2 θ ⇒ cos 2 θ = 1 — sin 2 θ
- cosec 2 θ — детская кроватка 2 θ = 1 ⇒ cosec 2 θ = 1 + детская кроватка 2 θ ⇒ детская кроватка 2 θ = cosec 2 θ — 1
- сек 2 θ — загар 2 θ = 1 ⇒ сек 2 θ = 1 + загар 2 θ ⇒ tan 2 θ = сек 2 θ — 1
- sin θ cosec θ = 1 ⇒ cos θ sec θ = 1 ⇒ tan θ cot θ = 1
- Объем сферы = 4/3 × πr 3
- Площадь поверхности сферы = 4πr 2
Каковы основные формулы в математике 10 класса?
Основные формулы в классе 10 по математике охватываются такими темами, как действительные числа, многочлены, геометрия, статистика и вероятность. Запоминание основных формул вещественных чисел класса 10 поможет учащимся понять различные концепции, связанные с натуральными числами, целыми числами, действительными числами и т. Д. Полиномиальные формулы полезны при нахождении корней уравнений. В геометрии важно, чтобы учащиеся запомнили основные формулы, относящиеся к площади и объему различных трехмерных форм и объектов, таких как сферы, конусы, призмы и т. Д.
Запоминание основных формул вещественных чисел класса 10 поможет учащимся понять различные концепции, связанные с натуральными числами, целыми числами, действительными числами и т. Д. Полиномиальные формулы полезны при нахождении корней уравнений. В геометрии важно, чтобы учащиеся запомнили основные формулы, относящиеся к площади и объему различных трехмерных форм и объектов, таких как сферы, конусы, призмы и т. Д.
Какие важные формулы рассматриваются в 10 классе по алгебре?
Некоторые из наиболее важных формул, рассматриваемых в классе 10 «Алгебра», связаны с многочленами, включая линейные и квадратные уравнения.Все эти важные формулы представлены на этой странице. Учащиеся также могут загрузить и отредактировать эти формулы алгебры для класса 10, перейдя по ссылке в формате pdf на этой странице.
Сколько формул используется в математике класса 10?
В математике класса 10 около 40 формул, основанных на таких главах, как действительные числа, полиномиальные квадратные уравнения, пара линейных уравнений с двумя переменными, арифметические прогрессии, треугольники, координатная геометрия, Введение в тригонометрию, приложения тригонометрии, круги, площадь поверхности и объем, статистика, вероятность.
Как я могу запомнить математические формулы для 10 класса?
Запоминание математических формул на уроке 10 помогает учащимся легко решать задачи. Студенты могут пересматривать формулы, многократно записывая или применяя их для решения различных задач. Изучение и изучение математических формул требует от учащихся тратить много времени и усилий на их отработку. Студенты также должны быть знакомы с главами и концепциями, чтобы понимать, как составлять формулы.
Тригонометрическая формула, класс 10 — Полный список формул и идентификация
Здравствуйте, добро пожаловать в CBSE Digital Education.Сегодня мы собираемся обсудить интересную тему про формулу тригонометрии класс 10 . CBSE Digital Education предоставляет всю важную информацию, касающуюся формулы тригонометрии класса 10.
Класс формулы тригонометрии 10
Тригонометрия — это раздел математики, который занимается измерением углов и проблемами, связанными с углами.
Слово «тригонометрия» происходит от слов «тригонон» и «метрон», которые означают треугольник и меру соответственно.Это исследование соотношения сторон и углов прямоугольного треугольника. Таким образом, это помогает найти меру неизвестных размеров прямоугольного треугольника с помощью формул и тождеств, основанных на этом соотношении.
Значение тригонометрии:
Тригонометрия = Три + гоно + метрия
«Треугольник» означает Треугольник
.«гоно» означает углы
«Метрия» означает Измерение
.Класс формулы тригонометрического отношения 10
В тригонометрии существует шесть основных соотношений, которые помогают установить связь между отношением сторон прямоугольного треугольника и углом.
- SinA = P / H
- CosA = B / H
- TanA = P / B
- CosecA = H / P
- SecA = H / B
- CotA = B / P
1. Cosec A = 1 / Sin A
Cosec A = 1 / Sin A
2. Sin A = 1 / Cosec A
3. Сек. A = 1 / Cos A
4.Cos A = 1 / сек A
5. Детская кроватка A = 1 / Tan A
6. Желто-коричневый A = 1 / Детская кроватка A
Тригонометрические углы| Уголки | 0 ° | 30 ° | 45º | 60 ° | 90 ° |
| Sin θ | 0 | 1/2 | 1 / √2 | √3 / 2 | 1 |
| Cos θ | 1 | √3 / 2 | 1 / √2 | 1/2 | 0 |
| Желто-коричневый θ | 0 | 1 / √3 | 1 | √3 | ∞ |
| Cosec θ | ∞ | 2 | √2 | 2 / √3 | 1 |
Сек. Θ Θ | 1 | 2 / √3 | √2 | 2 | ∞ |
| Детская кроватка θ | ∞ | √3 | 1 | 1 / √3 | 0 |
1.Sin (90-A) = Cos A
2. Cos (90-A) = Sin A
3. Желто-коричневый (90-A) = детская кроватка A
4. Детская кроватка (90-A) = Tan A
5. Сек (90-A) = Cosec A
6. Cosec (90-A) = Sec A
Некоторые другие важные формулы тригонометрии класса 10
1. TanA x CotA = 1
2. SinA x CosecA = 1
3.CosA x SecA = 1
4. TanA = SinA / CosA
4. CotA = CosA / SinA
CotA = CosA / SinA
Идентификатор тригонометрии
Уравнение, включающее тригонометрические отношения угла , называется тригонометрическим тождеством, если оно верно для всех значений угла.
Тригонометрические тождества полезны, когда выражение или уравнение включает тригонометрические функции. Тригонометрические тождества верны для любого значения переменных, встречающихся по обе стороны уравнения.Геометрически эти тождества включают некоторые тригонометрические функции (например, синус, косинус и тангенс) одного или нескольких углов.
Формула тригонометрической идентичности для класса 101. Sin 2 A + Cos 2 A = 1
2. Сек. 2 A + Tan 2 A = 1
3. Cosec 2 A + Sec 2 A = 1
Продвинутая формула тригонометрии, класс 10 1. Sin (A + B) = SinA x CosB + CosA x SinB
Sin (A + B) = SinA x CosB + CosA x SinB
2. Sin (A-B) = SinA x CosB — CosA x SinB
3. Cos (A + B) = CosA x CosB — SinA x SinB
4. Cos (A-B) = CosA x CosB + SinA x SinB
5. Желто-коричневый (A + B) = (TanA + TanB) / (1 — TanA x TanB)
6. Желто-коричневый (A-B) = (TanA — TanB) / (1 + TanA x TanB)
7. Sin2A = 2SinACosA
ИЛИ
= 2TanA / (1 + Tan 2 A)
8.Cos2A = Cos 2 A — Sin 2 A
ИЛИ
= 1-2Sin 2 A
ИЛИ
= 2Cos 2 A — 1
ИЛИ
= (1-Tan 2 A) / (1 + Tan 2 A)
9.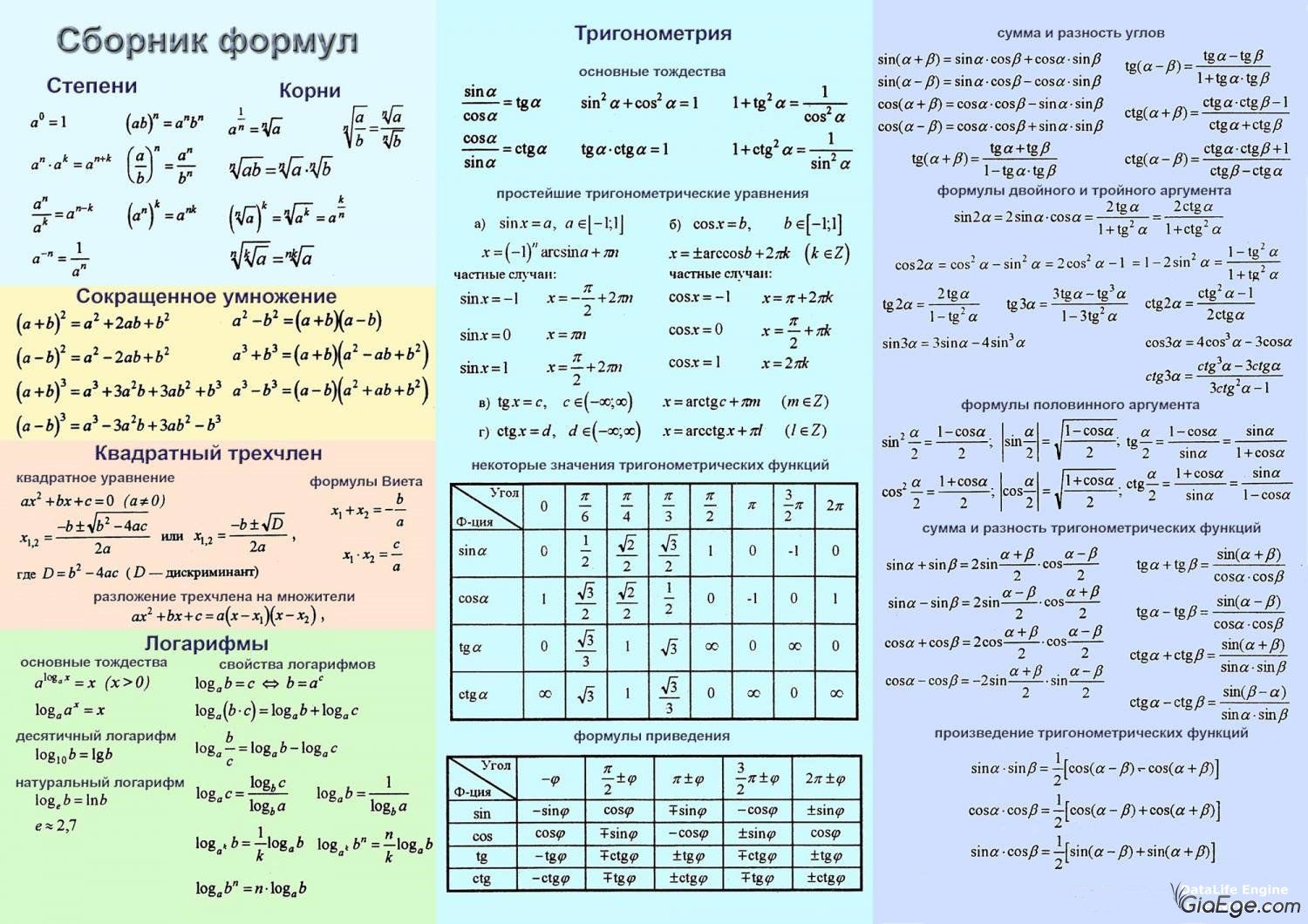 Sin3A = 3SinA — 4Sin 3 A
Sin3A = 3SinA — 4Sin 3 A
10. Cos3A = 4Cos 3 A — 3CosA
11.Tan3A = (3TanA-4Tan 2 A) / (1 + 3Tan 2 A)
12. SinA x Sin2A x Sin4A = ¼ Sin3A
13. CosA x Cos2A x Cos4A = ¼ Cos3A
14. TanA x Tan2A x Tan4A = Tan3A
Надеюсь, вам понравилась эта статья о тригонометрических формулах класса 10.Если вы хотите задать какие-либо вопросы относительно примечаний к классу 10 тригонометрической формулы pdf , , напишите нам в разделе комментариев, и мы ответим вам в ближайшее время.
Нажмите здесь, чтобы узнать больше образовательных новостей
Формулы тригонометрии для функций, соотношений и идентичностей PDF
Тригонометрия — это раздел математики, который имеет дело с углами, длиной и высотой треугольников и отношениями между различными частями окружностей и другими геометрическими фигурами. Математические формулы — тригонометрические соотношения и тождества очень полезны, а изучение приведенных ниже формул помогает лучше решать проблемы. Формулы тригонометрии необходимы для решения вопросов по тригонометрическим соотношениям и идентичностям на конкурсных экзаменах.
Математические формулы — тригонометрические соотношения и тождества очень полезны, а изучение приведенных ниже формул помогает лучше решать проблемы. Формулы тригонометрии необходимы для решения вопросов по тригонометрическим соотношениям и идентичностям на конкурсных экзаменах.
Тригонометрические тождества — это равенства, которые включают тригонометрические функции и истинны для любого значения встречающихся переменных, в которых определены обе части равенства. Геометрически это тождества, включающие определенные функции одного или нескольких углов.
Тригонометрическое соотношение соотношение между измерением углов и длиной стороны прямоугольного треугольника. Эти формулы связывают длины и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Идентичности не относятся к конкретным геометрическим фигурам, но верны для всех углов.
Формулы тригонометрии
Формулы дуг и секторов окружностей
Вы можете легко найти как длину дуги, так и площадь сектора для угла θ в окружности радиуса r .
Длина дуги. Длина дуги — это просто радиус r, умноженный на угол θ, где угол измеряется в радианах. Чтобы преобразовать градусы в радианы, умножьте количество градусов на π / 180.
Arc = rθ .
Тригонометрические формулы — прямой угол
Наиболее важные формулы для тригонометрии — это формулы для прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус тета — это отношение противоположной стороны к гипотенузе, косинус — это отношение соседней стороны к гипотенузе, а тангенс — это отношение сторона, противоположная соседней стороне
Теорема Пифагора , хорошо известная геометрическая теорема о том, что сумма квадратов на катетах прямоугольного треугольника равна квадрату на гипотенузе (стороне, противоположной прямому углу), или, в известной алгебраической записи, ( P) 2 + (B) 2 = (H) 2
Применяя теорему Пифагора для данной прямоугольной теоремы, имеем:
(перпендикулярно) 2 + (основание) 2 = (гипотенуза) 2
⇒ (P) 2 + (B) 2 = (H) 2
Тригонометрические свойства приведены ниже
Магический шестиугольник для тригонометрических идентичностей
Clock Wise:
- tan (x) = sin (x) / cos (x)
- sin (x) = cos (x) / кроватка (x)
- cos (x) = детская кроватка (x) / csc (x)
- детская кроватка (x) = csc (x) / sec (x)
- csc (x) = sec (x) / tan (x)
- сек (x) = tan (x) / sin (x)
Counterclock Wise:
- cos (x) = sin (x) / tan (x)
- sin (x) = tan (x) / sec (x)
- tan (x) = sec (x) / csc (x)
- сек (x) = csc (x) / кроватка (x)
- csc (x) = детская кроватка (x) / cos (x)
- детская кроватка (x) = cos (x) / sin (x)
Взаимные отношения
Тригонометрические формулы PDF
Формулы квадратного закона
Зная, что два острых угла дополняют друг друга, то есть они складываются в 90 °, вы можете решить любой прямоугольный треугольник:
- Если вы знаете две из трех сторон, вы можете найти третью сторону и обе острые углы.

- Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.
Многие формулы тригонометрии основаны на знаках тригонометрических соотношений, основанных на квадрантах, в которых они находятся. Поэтому для нас становится чрезвычайно важным понять, как тригонометрические отношения получают положительный или отрицательный знак
. Знак основан на квадранте, в котором лежит угол.
Предположим, что угол θ1 лежит в 1-м квадранте, а угол θ — в первом и втором квадранте вместе взятых.
Итак, давайте посмотрим, как знаки меняются по отношению к квадранту, в котором они лежат.
- В первом квартале все тригонометрические отношения положительны. (Углы между 0 0 -90 0 )
- В Q2 все тригонометрические отношения sinθ и cosecθ положительны. (Углы между 90 0 — 180 0 )
- В Q3 все тригонометрические отношения cosθ и secθ положительны.
 (Углы между 180 0 — 270 0 )
(Углы между 180 0 — 270 0 ) - В 4 квартале все тригонометрические отношения tanθ и cotθ положительны. (Углы между 270 0 — 360 0 )
θ — угол между осью x и линией в направлении против часовой стрелки. Если двигаться по часовой стрелке, угол будет равен — θ. Мы знаем, что в квадранте 4 только cosθ и secθ будут положительными, остальные — отрицательными, поэтому —
- Sin (- θ) = — Sin θ
- Cos (- θ) = Cos θ
- Желто-коричневый (- θ) = — Желто-коричневый θ
- Сек (- θ) = + Сек θ
- Детская кроватка (- θ) = — Детская кроватка θ
Нам нужно понимать, что тригонометрические отношения изменятся для углов — 90 o ± θ и 270 o ± θ , и они останутся такими же для 180 o ± θ и 360 o ± θ. Давайте посмотрим, что произойдет, когда мы прибавим или вычтем θ из 90 o ± θ и 270 o ± θ
Давайте посмотрим, что произойдет, когда мы прибавим или вычтем θ из 90 o ± θ и 270 o ± θ
- Сек (90 o + θ) = Cos θ
- Детская кроватка (90 o — θ) = Cos θ
- Желто-коричневый (90 o + θ) = — Детская кроватка θ
- Желто-коричневый (90 o — θ) = Детская кроватка θ
- сек (90 o + θ) = Cosec θ
- сек (90 o + θ) = Cosec θ
- Sin (270 o — θ) = — Cos θ
- Sin (270 o — θ) = — Cos θ
Это потому, что любой угол, равный 2700 + θ, попадет в квадрант 4, и в этом квадранте положительны только тригонометрические отношения cos
и sec.Так что вышесказанное будет отрицательным. 2700-θ попадет в квадрант 3, и в этом квадранте тригонометрические отношения tan и cot положительны, поэтому они снова будут отрицательными. Для 180 o ± θ и для 360 o ± θ знаки останутся прежними.
2700-θ попадет в квадрант 3, и в этом квадранте тригонометрические отношения tan и cot положительны, поэтому они снова будут отрицательными. Для 180 o ± θ и для 360 o ± θ знаки останутся прежними.
- Sin (360 o + θ) = Sin θ
- Sin (360 o — θ) = — Sin θ
Для 3600 + θ угол совершит один полный оборот и затем окажется в квадранте 1, где все тригонометрические отношения положительны.Итак, нужно запомнить 2 важные вещи —
.- Знак тригонометрических соотношений меняется в зависимости от значения θ.
- sin становится cos, а cos становится sin для 900 + θ и для 2700 + θ, и остается неизменным для 1800 + θ
и для 3600 + θ.
Формулы тригонометрии | Тригонометрические идентичности
Посмотрев на тригонометрические соотношения, давайте перейдем к тригонометрическим тождествам, которые являются основой большинства тригонометрических формул. Приведенные выше тождества верны для любого значения θ.
Приведенные выше тождества верны для любого значения θ.
Идентификационные данные продукта:
Формулы тригонометрии | Сумма и разность углов
Формулы тригонометрии | Формулы двойного угла
Формулы тригонометрии | Формулы тройного угла
Формулы тригонометрии | Преобразование произведения в сумму и разность
Формулы тригонометрии | Значения тригонометрических соотношений
Сводка тригонометрических идентичностей
Периодичность и периодичность
Идентификаторы половинного угла
Сложные отношения
Обратные тригонометрические функции
Дополнительный угол
Отрицательные аргументы
Взаимные аргументы
Значения тригонометрических функций
Введение в формулы класса 10 по тригонометрии Скачать PDF
Список важных формул для класса 10 «Введение в тригонометрию» представлен на этой странице. Во введении в тригонометрию у нас есть все, от базовых до сложных. Максимально используйте математические формулы для 10 класса, подготовленные экспертами-предметниками, и выведите свою подготовку на новый уровень. Получите доступ к таблице формул Введение в тригонометрический класс 10, охватывающей множество концепций, и используйте их для решения ваших задач без особых усилий.
Во введении в тригонометрию у нас есть все, от базовых до сложных. Максимально используйте математические формулы для 10 класса, подготовленные экспертами-предметниками, и выведите свою подготовку на новый уровень. Получите доступ к таблице формул Введение в тригонометрический класс 10, охватывающей множество концепций, и используйте их для решения ваших задач без особых усилий.
- Положение точки P на декартовой плоскости относительно координатных осей представлено упорядоченной парой (x, y).
- Тригонометрия — это наука о соотношении сторон и углов прямоугольного треугольника.
- Тригонометрические отношения: Отношения сторон прямоугольного треугольника называются тригонометрическими отношениями.
Рассмотрим треугольник ABC, расположенный под прямым углом в точке B. Эти соотношения всегда определяются относительно острого угла «A» или угла «C.
- Если одно из тригонометрических соотношений острого угла известно, остальные тригонометрические отношения угла можно легко определить.
- Как определить стороны: Определите угол, относительно которого необходимо рассчитать коэффициент трансформации. Стороны всегда помечаются относительно рассматриваемого θ.
Давайте рассмотрим оба случая:
В прямоугольном треугольнике ABC, расположенном под прямым углом в B. После того, как мы определили стороны, мы можем определить шесть t-соотношений по отношению к сторонам.
| корпус I | корпус II |
| (i) синус A = \ (\ frac {perpendicular} {hypotenuse} = \ frac {BC} {AC} \) | (i) синус C = \ (\ frac {perpendicular} {hypotenuse} = \ frac {AB} {AC} \) |
| (ii) косинус A = \ (\ frac {base} {hypotenuse} = \ frac {AB} {AC} \) | (ii) косинус C = \ (\ frac {base} {hypotenuse} = \ frac {BC} {AC} \) |
| (iii) касательная A = \ (\ frac {perpendicular} {base} = \ frac {BC} {AB} \) | (iii) касательная C = \ (\ frac {perpendicular} {base} = \ frac {AB} {BC} \) |
| (iv) косеканс A = \ (\ frac {hypotenuse} {perpendicular} = \ frac {AC} {BC} \) | (iv) косеканс C = \ (\ frac {hypotenuse} {perpendicular} = \ frac {AC} {AB} \) |
| (v) секущая A = \ (\ frac {hypotenuse} {base} = \ frac {AC} {AB} \) | (v) секущая C = \ (\ frac {hypotenuse} {base} = \ frac {AC} {BC} \) |
| (v) котангенс A = \ (\ frac {base} {perpendicular} = \ frac {AB} {BC} \) | (v) котангенс C = \ (\ frac {base} {perpendicular} = \ frac {BC} {AB} \) |
Примечание из шести взаимосвязей:
косеканс A = \ (\ frac {1} {sinA} \), секанс A = \ (\ frac {1} {cosineA} \), котангенс A = \ (\ frac {1} {tanA} \),
Однако очень утомительно записывать полные формы t-отношений, поэтому сокращенные обозначения таковы:
синус A — sin A
косинус A — cos A
тангенс A — тангенс A
косеканс A — косек A
секанс A — sec A
котангенс A — детская кроватка A
ТРИГОНОМЕТРИЧЕСКИЕ ИДЕНТИЧНОСТИ
Уравнение, включающее тригонометрическое отношение углов, называется тригонометрическим тождеством, если оно верно для всех значений углов. Это:
Это:
загар θ = \ (\ frac {sin \ theta} {cos \ theta} \)
кроватка θ = \ (\ frac {cos \ theta} {sin \ theta} \)
- sin² θ + cos² θ = 1 ⇒ sin² θ = 1 — cos² θ ⇒ cos² θ = 1 — sin² θ
- cosec² θ — cot² θ = 1 ⇒ cosec² θ = 1 + cot² θ ⇒ cot² θ = cosec² θ — 1
- сек² θ — tan² θ = 1 ⇒ sec² θ = 1 + tan² θ ⇒ tan² θ = sec² θ — 1
- sin θ cosec θ = 1 ⇒ cos θ sec θ = 1 ⇒ tan θ cot θ = 1
ALERT:
Коэффициент t зависит только от угла ‘θ’ и остается неизменным для одного и того же угла прямоугольных треугольников разного размера.
Значение t-соотношений указанных углов:
| ∠A | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
| грех А | 0 | \ (\ frac {1} {2} \) | \ (\ frac {1} {\ sqrt {2}} \) | \ (\ frac {\ sqrt {3}} {2} \) | 1 |
| cos A | 1 | \ (\ frac {\ sqrt {3}} {2} \) | \ (\ frac {1} {\ sqrt {2}} \) | \ (\ frac {1} {2} \) | 0 |
| желто-коричневый A | 0 | \ (\ frac {1} {\ sqrt {3}} \) | 1 | √3 | не определено |
| код A | не определено | 2 | √2 | \ (\ frac {2} {\ sqrt {3}} \) | 1 |
| сек A | 1 | \ (\ frac {2} {\ sqrt {3}} \) | √2 | 2 | не определено |
| детская кроватка A | не определено | √3 | 1 | \ (\ frac {1} {\ sqrt {3}} \) | 0 |
Значение sin θ и cos θ никогда не может превышать 1 (единицы), поскольку противоположная сторона равна 1. Соседняя сторона никогда не может быть больше гипотенузы, поскольку гипотенуза — самая длинная сторона в прямоугольном ∆.
Соседняя сторона никогда не может быть больше гипотенузы, поскольку гипотенуза — самая длинная сторона в прямоугольном ∆.
‘t-СООТНОШЕНИЯ’ ДОПОЛНИТЕЛЬНЫХ УГЛОВ
Если ∆ABC — прямоугольный треугольник, расположенный под прямым углом к точке B, то
∠A + ∠C = 90 ° [∵ ∠A + ∠B + ∠C = Сумма углов 180 °]
или C = (90 ° — ∠A)
Таким образом, ∠A и ∠C известны как дополнительные углы и связаны следующими соотношениями:
sin (90 ° -A) = cos A; cosec (90 ° — A) = sec A
cos (90 ° — A) = sin A; сек (90 ° — A) = cosec A
tan (90 ° — A) = кроватка A; детская кроватка (90 ° — A) = желто-коричневый A
Формулы тригонометрии для класса 10
Формулы основных тригонометрических функций.sin θ = Противоположная сторона / Гипотенуза. cos θ = Соседняя сторона / Гипотенуза. tan θ = противоположная сторона / смежная сторона. сек θ = Гипотенуза / Прилегающая сторона. cosec θ = Гипотенуза / Противоположная сторона. кроватка θ = смежная сторона / противоположная сторона.
cosec θ = Гипотенуза / Противоположная сторона. кроватка θ = смежная сторона / противоположная сторона.
2 Формула тригонометрии Класс 10. 3 Мы определяем следующие отношения, известные как формула тригонометрического класса 10: 4 Взаимное отношение тригонометрических формул для класса 10. 5 Тригонометрические отношения дополнительных углов. 6 Некоторые другие важные формулы тригонометрии класса 10.
Какова формула тригонометрических тождеств 10 класса?
Термин «тригон» означает треугольник, а «метрия» означает измерение.Класс 10 тригонометрических тождеств состоит из тригонометрических соотношений, таких как синус, косинус и тангенс в его уравнениях. Даже формула класса 10 тригонометрических тождеств основана на этих соотношениях.
Каковы тригонометрические формулы для класса 10 CBSE?
Тригонометрия представлена в CBSE Class 10. Это совершенно новая и сложная глава, в которой нужно выучить все формулы и применить их соответствующим образом. Формулы класса тригонометрии 10 представлены в таблице ниже. Список тригонометрических формул для 10-го числа
Формулы класса тригонометрии 10 представлены в таблице ниже. Список тригонометрических формул для 10-го числа
Как рассчитать площадь поверхности в 10 классе тригонометрии?
Полный список формул тригонометрии можно найти здесь.Формулы кругов для класса 10. Окружность круга = 2 π r; Площадь круга = π r 2; Площадь сектора угла θ = (θ / 360) × π r 2; Длина дуги сектора под углом θ = (θ / 360) × 2 π r (r = радиус круга) Формулы площади и объемов поверхности для класса 10
Какая математика изучается в 10 классе?
Даже почти в каждой отрасли используются наиболее распространенные формулы, представленные в классе 10. Математические формулы класса 10 включают формулы, относящиеся к действительным числам, многочленам, квадратным уравнениям, треугольникам, кружкам, статистике, вероятности и т. Д.
Формулы тригонометрии для класса 10
Сводка формул тригонометрии. Мы перечислили наиболее важные формулы тригонометрии для класса 10 в главе 8, которая помогает решать вопросы, связанные с главой тригонометрии. Хочу сказать, что запомнив формулы тригонометрии, вы можете приступить к решению вопросов и ответов из главы «Тригонометрия».
Хочу сказать, что запомнив формулы тригонометрии, вы можете приступить к решению вопросов и ответов из главы «Тригонометрия».
В формулах тригонометрии отношения Для класса 10 вы можете запомнить значение sin, cos и tan.а остальные три противоположны, как этот грех — обратный кодекс. cos — это обратное значение для sec, а tan — обратное для детской кроватки.
Основные тригонометрические формулы. sinθ = Гипотенуза противоположной стороны. cosθ = гипотенуза смежной стороны. tanθ = противоположная сторона AdiacentSide. secθ = Соседняя сторона гипотенузы. θ = противоположная сторона гипотенузы. cotθ = Соседняя сторона Противоположная сторона.
Список всех формул тригонометрии Большинство формул тригонометрии основаны на соотношениях и чрезвычайно удобны для решения сложных задач тригонометрии.Если вы хотите сдать какие-либо конкурсные экзамены после школы, вам необходимо иметь практические знания различных формул тригонометрии. Основой любой формулы тригонометрии является тождество тригонометрии.
Тригонометрические тождества для класса 10. В 10-м классе есть три тригонометрических тождества, которые мы узнаем в главе о тригонометрии. Это: Cos 2 θ + Sin 2 θ = 1. 1 + Tan 2 θ = Sec 2 θ. 1 + Детская кроватка 2 θ = Cosec 2 θ. Здесь мы докажем тригонометрическое тождество и воспользуемся им для доказательства двух других.
Математические формулы 10 класса
Для первого и второго семестров CBSE Maths 10 класса из 80 баллов (вместе взятых) 12 баллов присваиваются из модуля 5 «Тригонометрия». Работа состоит из 4 частей. Каждая часть имеет разные оценки, и вопросы были присвоены 1 балл, 2 балла, 3 балла и 4 балла.
Вы можете найти формулы по всем темам, относящимся к «Некоторым приложениям тригонометрии» Класс 10 «Некоторые приложения тригонометрии» подробно и получить хорошее представление о них.Измените все концепции с умом, воспользовавшись математическими формулами для класса 10 «Некоторые приложения тригонометрии».
Формулы тригонометрии для математика 10 класса. Тригонометрические формулы для класса 10 покрывают основные тригонометрические функции для прямоугольного треугольника, то есть синуса (sin), косинуса (cos) и тангенса (tan), которые могут использоваться для получения косеканса (cos), секанса (сек) и Котангенс (детская кроватка).
Тригонометрические формулы для класса 10 покрывают основные тригонометрические функции для прямоугольного треугольника, то есть синуса (sin), косинуса (cos) и тангенса (tan), которые могут использоваться для получения косеканса (cos), секанса (сек) и Котангенс (детская кроватка).
Формулы тригонометрии PDF — Уловки идентичностей, Таблица соотношений, Функции: Какие важные формулы для тригонометрических классов 10, 11, 12, JEE, NDA.Мы не пишем здесь теорию, а только важные формулы и их PDF для скачивания. Или вы можете скачать их все в формате pdf. Вы найдете все формулы на одной странице.
Математические формулы для класса 10 формул линейных уравнений. Линейное уравнение в одной переменной задается следующим образом: ax + b = 0 (где a ≠ 0 и a & b — действительные числа). Пара линейных уравнений с двумя переменными задается как: a 1 x + b 1 + c 1 = 0 и a 2 x + b 2 + c 2 = 0 (где a 1, b 1, c 1, & a 2, b 2, c 2 — действительные числа & a 1 2 + b 1 2 ≠ 0 & a 2 2 + b 2 2 ≠ 0). Тогда природа корней / нулей / решений:
Тогда природа корней / нулей / решений:
Тригонометрические формулы и идентичности (полный список)
Математические формулы по главам для класса 10. В наши дни онлайн-коучинг находится на вершине, где вы можете получить почти все в удобном формате. То же самое и с математическими формулами. В Интернете вы можете загрузить полный список математических формул по главам для 10-го класса CBSE по алгебре, тригонометрии, геометрии, вероятности, измерениям и т. Д.
Некоторые формулы тригонометрии для 10, 11, 12 классов на хинди 18 мая 2021 г. 18 мая 2021 г. админ нетехнический «Тригонометрия — это раздел математики, изучающий взаимосвязь между длинами сторон и углами треугольников.
Решение: Пример 8.1 Математика для класса 10, вопрос 4. Для 15 кроваток A = 8 найдите sin A и sec A. Решение: Пример 8.1, по математике для класса 10, вопрос 5. Для данного sec θ = вычислите все остальные тригонометрические отношения. Решение: Пример 8.1. Класс 10. Математика. Вопрос 6. Если ∠A и ∠B — острые углы такие, что cos A = cos B, то покажите, что ∠A = ∠B.
Если ∠A и ∠B — острые углы такие, что cos A = cos B, то покажите, что ∠A = ∠B.
Формулы тригонометрии для класса 11 (скачать PDF) Тригонометрическая таблица от 0 до 360 (cos -sin-cot-tan-sec-cosec) Важные вопросы для науки класса 10 Глава 1 — Химические реакции и уравнения; Формулы электричества класса 10; Что такое поступательное движение? Скачать формулы и резюме по физике 10 класса pdf
«тригонометрия».Слово «тригонометрия» происходит от греческих слов «три» (что означает три), «гон» (означает стороны) и «метрон» (означает меру). Фактически, тригонометрия — это изучение отношений между сторонами и углами треугольника. Самые ранние известные работы по тригонометрии были зарегистрированы в Египте и Вавилоне. Ранний
Класс формулы тригонометрии 10
Мы будем учиться по формулам тригонометрии. Основные формулы. sin, cos tan при 0, 30, 45, 60 градусах. Пифагорейские тождества. Знак греха, cos, tan в разных квандрантах.Радианы. Отрицательные углы (четно-нечетные тождества) Значение sin, cos, tan повторяется после 2π. Угол сдвига на π / 2, π, 3π / 2 (тождества ко-функции или тождества периодичности)
Угол сдвига на π / 2, π, 3π / 2 (тождества ко-функции или тождества периодичности)
Таблица тригонометрических формул для классов 10, 11, 12. Таблица тригонометрических формул для классов 10, 11, 12; Будьте первым, кто оставит комментарий. Оставить ответ Отменить ответ. Последние новости. Проверьте пересмотренную дату проведения 10-го и 12-го экзаменов Совета директоров CBSE в 2021 году.
Отношение или частные идентичности даны в виде тригонометрических формул: Sinθ = Cosθ X Tanθ; Cosθ = Sinθ X Cotθ; Tanθ = Sinθ ⁄ Cosθ; Cotθ = Cosθ ⁄ Sinθ; Формулы тригонометрии произведения к сумме \ (\ sin u \ sin v = \ frac {1} {2} [\ cos (uv) — \ cos (u + v)] \) \ (\ cos u \ cos v = \ frac {1} {2} [\ cos (uv) + \ cos (u + v)] \)
Важная концепция для решения определенного типа вопросов.Если A + B = 90 °. Результаты, которые верны всегда: (i) sin A. sec B = 1 или sin A = cos B. (ii) cos A. cosec B = 1 или sec A = cosec B. (iii) tan A. tan B = 1 или загар A = детская кроватка B. (iv) детская кроватка A. детская кроватка B = 1. (v) sin²A + sin² B = 1.
(iv) детская кроватка A. детская кроватка B = 1. (v) sin²A + sin² B = 1.
A – Z Все тригонометрические формулы (формула Триконмити) для класса 6, класса 7, класса 8, класса 9, класса 10, класса 11, класса 12 на хинди / Все формулы триконмити для правительства. Экзамен / Экзамены Саркари / Формула главы тригонометрии (Триконмити) / Полный список тригонометрических формул на хинди / Сутра триконмити / PDF
Формулы тригонометрии для математики 10 класса Глава 8
Формулы тригонометрии 10-го класса для класса 10 Pdf bawang putih dan bawang merah kartun bay 21 likas batuk kahak petua hilangkan batuk dan gatal tekak bay 21 condominium bawang merah dan bawang putih termasuk jenis umbi fawang bawah bawah mram300 bawang putih batu 9 port dickson batu 3 shah alam circuit
В решениях NCERT для математики класса 10 эти тригонометрические отношения известны как sin A, cos A, tan A, cosec A, sec A и cot A.Кроме того, вы, должно быть, заметили, что три отношения cosec A, sec A, cot A являются обратными или обратными отношениями первых трех отношений с sin A, cos A и tan A.
Тригонометрические формулы для класса 10 покрывают основные тригонометрические функции для прямоугольного треугольника, т. Е. Синус (sin), косинус (cos) и тангенс (tan), которые могут использоваться для получения косеканса (cos), секанса (сек), и Котангенс (детская кроватка).
Основные формулы тригонометрии. Для нахождения элементов в тригонометрии используются в основном 6 соотношений.синус, косинус, тангенс, котангенс, косеканс и секанс называются тригонометрическими функциями, которые определяют соотношение между сторонами и углами треугольника.
sin cos = загар. Разделите значение sin при 0 ∘ на значение cos при 0, чтобы получить значение tan при 0. Взгляните на образец ниже. tan0 ∘ = 0 1 = 0. Точно так же и таблица была бы. Шаг 5: Определите стоимость детской кроватки. Обратное значение загара равно стоимости детской кроватки.
Все формулы тригонометрии для классов 10, 11, 12 (PDF)
Тригонометрические функции: существует 6 различных тригонометрических функций: синус x, записанный как sin (x), косинус x, записанный как cos (x), тангенс x, записанный как Tan (x), котангенс x, записанный как Cot (x ) Секанс x, записанный как Sec (x) Косеканс x, Записанный как Cosec (x) Тригонометрические отношения: Есть три основных тригонометрических отношения. Они следующие:
Они следующие:
Формулы тригонометрии для класса 10 Формулы тригонометрии для класса 11 Формулы тригонометрии для класса 12 Мадхьямик Вторичные математические формулы Тригонометрия
Получите решения NCERT с видео по всем вопросам и примерам главы 8 по тригонометрии класса 10. Видео всех вопросов сделаны с пошаговыми пояснениями. Проверьте это сейчас. Тригонометрия означает изучение взаимосвязи между размерами треугольника. Обычно мы говорим о прямоугольных треугольниках, когда встречаем
.ПЕРЕЧЕНЬ ФОРМУЛ ТРИГОНОМЕТРИИ — 3.Как и в случае со списком-2, из первого списка мы можем получить приведенный ниже список формул соотношения тригонометрии, который вы должны отметить и запомнить, если хотите изучать тригонометрию. Эти тригонометрические тождества наиболее важны для тригонометрических формул для класса 10.
Формула тригонометрии на хинди (формула триконмити): Здравствуйте, друзья.Is post me hum aapko Тригонометрические формулы для 10-го класса на хинди PDF предоставить karne wale hai jisme hum aapko тригонометрия все формулы скачать в формате pdf, трюки с тригонометрией для ssc cgl pdf и agar aap class 11th .12-й ке, студенты, хай то аапке лийе, бхи — это pdf мне все тригонометрические формулы, pdf доступны хаи.
Математические формулы для класса 10
Важные вопросы для 10 класса по тригонометрии. Вот несколько важных вопросов для тригонометрии 10 класса, которые вы должны попрактиковать, чтобы проверить концепцию перед экзаменом. Q.2 В ΔPQR, под прямым углом к Q, PR + QR = 25 см и PQ = 5 см. Определите значения sinP, cosP и tanP. Q.3 Если ∠A и ∠B — острые углы такие, что cosA = cosB, то покажите, что ∠A = ∠B.
Тригонометрические тождества: Формула тригонометрического класса 12 включает тригонометрические функции и тригонометрические тождества.Эти тождества тригонометрии точны для всех значений переменных. Тригонометрическое соотношение: соотношение измерения угла и длины стороны прямоугольного треугольника известно своим тригонометрическим соотношением.
Тригонометрические формулы — прямой угол. Наиболее важные формулы тригонометрии — формулы прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус теты — это отношение противоположной стороны к гипотенузе, косинус — это отношение соседней стороны к гипотенузе, а тангенс — это отношение противоположной стороны. сторона на соседнюю сторону
CBSE Class 10 Maths Formulas: Класс 10 — это основной выход на следующий уровень академических знаний.10-й класс — это один из самых ценных этапов в жизни студента, на котором можно экспоненциально расти в своей сфере деятельности, понимая концепции и выставляя приличные оценки.
Решать тригонометрические задачи действительно весело, поверьте мне. Если вы хорошо разбираетесь в математике, вам понравится решать суммы. Сначала выучите все формулы и попытайтесь понять все формулы sin, cos, tan, cosec, sec и cot, посмотрите, как эти формулы Это всего лишь базовые вещи, которые вам нужно сделать на начальном этапе, чтобы упростить работу с тригнометрией.Возможно, вы уже изучали основы тригонометрии в своем 10 классе.
Введение в тригнометрию для математических формул 10 класса
Получите MCQ по математике класса 10 Глава 8 — Введение в тригонометрию с ответами в формате PDF. Эти MCQ важны для подготовки к предстоящему экзамену CBSE Class 10 по математике.
ICSE Class 10 Вопросы по математике по главе «Тригонометрия». Эта страница состоит из рабочего листа для 10-го класса математики главы «Тригонометрия» с ключом ответа.Глава-тригонометрия требует дополнительной практики, чтобы задать кандидатам качественные вопросы и числовые значения главы-тригонометрии Академическая группа Энтранси загрузила этот рабочий лист.
СвязанныеФормулы тригонометрии для класса 10
Формулы тригонометрии для класса 10Тригонометрия — самая важная глава для студентов, учатся ли они на досках CBSE / ICSE или готовятся к соревнованиям, таким как IIT или SSC.В CBSE / NCERT глава тригонометрии представлена в , 10-й класс (Глава 8), а в ICSE — в 9-м классе. В большинстве случаев студенты находят главу «Тригонометрия» очень сложной для понимания и усвоения всех формул Тригонометрии . В этой статье вы найдете все тригонометрических формул для класса 10 .
Прочитав эту статью, что вы поймете: —
- В этой статье мы постараемся помочь студентам облегчить им понимание тригонометрии.
- Мы сделаем несколько коротких трюков , чтобы формулы тригонометрии для 10-го класса было легко усвоить.
- Кроме того, вам не нужно заучивать их все наизусть. Вместо этого вы разработаете методику, позволяющую выводить некоторые формулы из , вместо того, чтобы их запоминать.
Тригонометрические формулы-class10-download-pdf
Что такое тригонометрия?
Это слово «тригонометрия» произошло от объединения двух греческих слов «trigōnon», что означает «треугольник», и «metron», что означает «мера».Таким образом, используется для измерения Треугольников .
Проще говоря, Тригонометрия — это раздел математики, в котором мы изучаем отношения между длинами сторон и углами треугольников.
А теперь позвольте мне сделать это проще!
- ВОПРОС (i): — если нам даны две стороны прямоугольного треугольника и попросят найти третью сторону, какую математическую концепцию мы будем использовать, чтобы найти третью сторону?
ОТВЕТ: — Очевидно, это очень просто! Мы будем использовать теорему Пифагора .
- ВОПРОС (ii): — Если нам даны одна сторона и один угол (отличный от 90 °) прямоугольного треугольника и вас попросят найти оставшиеся стороны этого треугольника, как вы его найдете? ?
ОТВЕТ: — Для этого вам необходимо понять новую концепцию, известную как «Тригонометрия».
Реальные приложения тригонометрии и формул!
Большую часть времени мы задаемся вопросом , какова польза от тригонометрии в нашей жизни ?.Возможно, вы не применяли тригонометрию напрямую для решения своих повседневных жизненных проблем, но косвенно она используется в различных вещах, которые мы видим вокруг себя.
- Как вы думаете, мы узнали, что высота горы Эверест составляет 8848 метров. Очевидно, с помощью тригонометрии.
- Как мы узнали, что расстояние между «Землей» и «Солнцем»? когда мы ни разу не были на «Солнце». вы можете измерить расстояние до ближайших объектов в космосе, используя метод тригонометрии, называемый Тригонометрический параллакс или Звездный параллакс.
- Синус и косинус (которые вы изучите позже) являются фундаментальными для теории периодических функций, описывающих звуковые и световые волны.
- Тригонометрия также используется в строительстве, видеоиграх, летной технике, морской инженерии, археологии, криминологии, навигации, океанографии, картографии (создание карт), спутниковых системах.
- К вашему удивлению, почти каждое научное открытие, связанное с расстоянием, доказывается только благодаря тригонометрии.
ПРИМЕЧАНИЕ: — В этой статье мы подробно обсудили эти практические применения тригонометрии , просмотрите их.
Тригонометрические отношения: —
Прежде всего, обсудим, что такое Тригонометрические отношения . Тригонометрические отношения — это, по сути, отношение между измерением углов и длинами сторон прямоугольного треугольника.
Теперь давайте обсудим, сколько типов тригонометрических соотношений возможно.
В прямоугольном треугольнике у нас есть три стороны, названные (H) Гипотенуза (самая длинная сторона), (P) Перпендикуляр (сторона, противоположная углу) и (B) Основание . Если нас попросят взять любые две стороны из этих трех сторон и сформировать соотношение, мы обнаружим, что возможны шесть соотношений (P / H, B / H, P / B, H / P, H / B, B / P ). Мы присвоили каждому соотношению свое имя.
Тригонометрические отношения: —
- sinθ = (Перпендикуляр (P)) / (Гипотенуза (H)).
- cosθ = (База (B)) / (Гипотенуза (H)).
- tanθ = (Перпендикуляр (P)) / (Основание (B)).
- cosecθ = (Гипотенуза (H)) / (Перпендикуляр (P)).
- сек θ = (Гипотенуза (H)) / (База (B)).
- cotθ = (Основание (B)) / (Перпендикуляр (P)).
Взаимные тригонометрические отношения: —
- sin θ = 1 / (косек θ)
- сек θ = 1 / (sin θ)
- cos θ = 1 / (сек θ)
- сек θ = 1 / (cos θ)
- тангенс угла наклона θ = 1 / (детская кроватка θ)
- детская кроватка θ = 1 / (тангенс угла θ)
Важные взаимосвязи между тригонометрическими отношениями: —
tanθ = (sin θ) / (cos θ)
cot θ = (cos θ) / (sin θ)
Тригонометрический стол: —
Эта таблица тригонометрических отношений помогает нам найти значения стандартных тригонометрических углов , таких как 0 °, 30 °, 45 °, 60 ° и 90 °.
| Тригонометрические отношения | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
| sin A | 0 | 1/2 | 1 / √2 | √3 / 2 | 1 |
| cos A | 1 | √3 / 2 | 1 / √2 | 1/2 | 0 |
| желто-коричневый A | 0 | 1 / √3 | 1 | √3 | Не определено |
| детская кроватка A | Не определено | √3 | 1 | 1 / √3 | 0 |
| код A | Не определено | 2 | √2 | (2√3) / 3 | 1 |
| сек A | 1 | (2√3) / 3 | √2 | 2 | Не определено |
Тригонометрические формулы и тождества: —
Теперь есть определенные формул тригонометрии и тождества , которые вы должны выучить.Эти соотношения и тождества очень полезны при решении тригонометрических задач.
Формулы тригонометрии для 10 класса: —
Формулы тригонометрии в 10-м классе основаны на тригонометрических отношениях. Существуют три основные тригонометрические формулы для 10-го класса, и с их помощью можно составить другие отождествления.
1) cos 2 A + sin 2 A = 1.
- a) cos 2 A = 1 — sin 2 A.
- б) sin 2 A = 1 — cos 2 A.
2) 1 + tan 2 A = сек 2 A.
- a) сек 2 A — желтовато-коричневый 2 A = 1.
- б) загар 2 A = сек 2 A — 1.
3) детская кроватка 2 A + 1 = cosec 2 A.
- a) cosec 2 A — детская кроватка 2 A = 1.
- б) детская кроватка 2 A = cosec 2 A — 1.
Еще две Тригонометрические формулы для 10 класса есть: —
(i) сек A — загар A = 1 / (сек A + загар A)
(ii) cosec A — детская кроватка A = 1 / (cosec A + кроватка A)
Получить все формулы тригонометрии для класса 10 pdf: —
Формула тригонометрии — [Sin, Cos, Tan, Cot, Sec и Cosec]
Формула тригонометрии : Тригонометрия — это хорошо известное имя в геометрической области математики, которое актуально в этой области с давних времен, а также применяется практически во многих случаях.
На простом языке тригонометрию можно определить как ту ветвь алгебры, которая связана с треугольником. В этом разделе мы в основном изучаем взаимосвязь между углами и длиной стороны данного треугольника. При таком подробном изучении треугольника формируется несколько типов уравнений, которые, следовательно, решаются для упрощения взаимосвязи между длинами сторон и углов такого треугольника.
Тригонометрия считается одним из старейших компонентов алгебры, существующей примерно с 3 века.Существуют практические применения тригонометрии в нескольких контекстах, таких как астрономия, геодезия, оптика или периодические функции.
Формулы тригонометрии
Что ж, будь то алгебра или геометрия, обе эти области математики основаны на научных вычислениях уравнений, и мы должны выучить различные формулы, чтобы их было легко вычислить.
Как мы знаем, в тригонометрии мы в основном измеряем разные стороны треугольника, из которых формируются несколько уравнений.Далее формулы тригонометрии составлены в соответствии с различными отношениями, используемыми в области, такими как синус, тангенс, косинус и т. Д. Таким образом, в основном это номера формул, которые обычно используются в тригонометрии для измерения сторон треугольника. .
Здесь мы упоминаем список различных типов формул тригонометрии.
Основная формула тригонометрии
2. Sin Cos Tan на 0, 30, 45, 60 градусов
3.Пифагорейские тождества
4. Знак греха, Cos, Tan в разных квадрантах
A dd– S ugar – T o –C оферта
5. Радианы
1 градус = 60 минут
Пример: 1 ° = 60 ′
1 минута = 60 секунд
Пример: 1 ′ = 60 дюймов
6. Отрицательные углы [четно-нечетные отождествления]
Sin (-x) = — Sin x
Cos (-x) = Cos x
Tan (-x) = — Tan x
Cot (-x) = — Cot x
Sec (-x) = Sec x
Cosec (-x) = — Cosec x
7.Значение Sin, Cos, Tan повторяется после 2𝛑
Sin (2𝛑 + x) = Sin x
Cos (2𝛑 + x) = Cos x
Tan (2𝛑 + x) = Tan x
8. Обозначения периодичности — Углы смещения на 𝛑 / 2, 𝛑, 3𝛑 / 2
9. Идентификаторы суммы углов и разностей
10. Формула двойного угла
11. Формула тройного угла
12. Идентичность половинного угла
13. Сумма идентичностей
14.Идентификационные данные продукта
15. Закон греха
Здесь,
- ABC — вершины треугольника ABC.
- Место, противоположное углу A, — это a. то есть BC
- Место, противоположное углу B, равно b. т.е. AC
- Место, противоположное углу C, равно c. т.е. AB
16. Закон косинуса
17. Обратная тригонометрическая функция
Если Sin θ = x
, затем поместите Sin на правую сторону
Таким образом, вы можете видеть, что Sin — это угол. То же, что и обратная функция для всех функций Trignomentry, — это угол.

 е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
 Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.


 (Углы между 180 0 — 270 0 )
(Углы между 180 0 — 270 0 )