Теория вероятности действия над событиями: Действия над событиями. Соотношения между событиями

Действия над событиями. Соотношения между событиями

содержание учебника

Суммой, или объединением, двух событий называется событие, состоящее в появлении хотя бы одного из них. Сумма двух событий А и В обозначается через А +В или . Аналогично определяется и обозначается сумма n событий — событие, состоящее в появлении хотя бы одного из них. Сумму n событий  обозначают так:

или

Проuзведением, или пересечением, двух событий называется событие, состоящее в одновременном их появлении. Произведение двух со­бытий А и В обозначается через АВ или . Аналогично определяется и обозначается произведение в случае большего числа событий. Произведение n событий обозначают:

или .

Понятия суммы и про изведения событий распространяются и на бесконечные последовательности событий. В этих случаях, например, применяют соответственно обозначения:

и 

Если событие А обязательно произойдет при появлении некоторого другого события В, то говорят, что событие В представляет собой

частный случай события А, и пишут , или (говорят также, что В влечет А).
Если и , т.е. события А и В в данном опыте могут появиться или не появиться вместе, то их называют равносильными, или эквивалентными, и пишут А = В.
Операции объединения и пересечения событий обладают некоторыми свойствами, аналогичными свойствам сложения и умножения чисел.
Эти операции коммутативны:

и .      (1.6.1)

Ассоциативны:

      (1.6.2)

и       (1.6.3)

И дистрибутивны:

      (1.6.4)

Указанные свойства следуют из определения действий объединения
и пересечения событий. Не все законы сложения и умножения чисел справедливы для объединения и пересечения событий. Например, для любого события А выполняются равенства

и .      (1.6.5)

Если U — достоверное, V — невозможное собьпие, А — любое событие, — событие, противоположное А, то выполняются равенства:

или .      (1.6.6)

или .      (1.6.7)

или .      (1.6.8)

или .      (1.6.9)

или .       (1.6.10)

или .      (1.6.11)

Из свойств операций пересечения и объединения следует, что для любых событий А и В имеем , т.е. или . (1.6.12) Формула (1.6.12) дает разложение любого события А на сумму двух непересекающихся (несовместных) событий.

Если , то и формула (1.6.12) принимает вид , или . (1.6.13)
Разностью событий А и В называется событие С, которое означает, что наступает событие А и не происходит событие В. Разность событий А и В обозначается так: А-В, или А\В.

Пример 1. Подбрасывается игральный кубик. Обозначим события: А — «выпадение шести очков», В — «выпадение трех очков», С — «выпадение четного числа очков», D — «выпадение числа очков, кратного трем». Каковы соотношения между этими событиями?

Решение.

Если выпало шесть очков, то тем самым выпало и четное число очков, т.е. событие

А влечет событие С: . Рассуждая аналогично, получаем , , А + В = D, CD = А.

Пример 2. Опыт — подбрасывание игрального кубика. События:  (k = 1, 2, 3, 4, 5, 6) — «выпадение k очков», А — «выпадение четного числа очков», В — «выпадение нечетного числа очков», С — «выпадение числа очков, кратного трем», D — «выпадение числа очков, большего трех».
Выразить события А, В, С и D через события .

Решение.

Событие А наступает тогда и только тогда, когда наступает  , или , или . Это означает, что . Рассуждая аналогичным образом, получаем:

В = А₁ + А₃ + А₅,  С = А₃ + А₆, D =А₄ + А₅ + А₆.

Пример 3. Пусть — произвольные события. Что означают события , , , , ?

Решение.

В соответствии с определением — произведение трех событий А, В, С, которые происходят одновременно, причем — событие, противоположное событию А. Следовательно, означает, что событие А не произошло, а события В и С произошли. Рассуждая аналогично, заключаем, что: — ни одно из трех данных событий не произошло,

— хотя бы одно из трех событий не произошло; — произошло ровно одно из трех событий; — произошло не более одного из трех событий.

Пример 4.  Опыт состоит в том, что стрелок производит 3 выстрела по мишени. Событие A_k — «попадание в мишень при k-ом выстреле» (k = 1, 2, 3). Выразить через A₁, А₂, А_з следующие события: А — «хотя бы одно попадание», В — «три попадания»; С — «три промаха»; D — «хотя бы один промах»; Е — «не меньше двух попаданий»; F — «не более одного попадания»; G — «попадание после первого выстрела».

Решение. Событие А наступает тогда и только тогда, когда наступает A₁, или А₂, или A_3. Это означает, что А = А₁ + А₂ + А₃. Три попадания будет тогда и только тогда, когда попадание наступит при каждом выстреле, т.е. события A₁, А₂, А₃ осуществляются все вместе: В =А₁

• А₂ • А₃. Три промаха будет тогда и только тогда, когда промах явится результатом каждого выстрела, т.е. события , ,  осуществляются все вместе: . Рассуждая аналогично, заключаем, что: , ,  ,  .

Пример 5.  Опыт — извлечение детали из ящика, в котором находятся изделия трех сортов. Обозначения событий: А — «извлечена деталь первого сорта», В — «извлечена деталь второго сорта», С — «извлечена деталь третьего сорта». Что представляют собой следующие события: А+В; ; АС; АВ+С?

Решение. А + В — это событие, которое происходит при наступлении хотя бы одного из событий А и В.

Следовательно, А + В в данном случае — деталь первого или второго сорта. Поскольку А + С — деталь первого или третьего сорта, то противоположное этому событие — деталь второго сорта. АС — невозможное c0бытие, поскольку деталь одновременно не может быть и первого и третьего сорта. АВ + С как сумма невозможного события и события С равно С, т.е. АВ + С — деталь третьего сорта.

Пример 6.  Доказать, что .

Решение. Для доказательства этого равенства достаточно показать, что  и . Если наступило событие , то это означает, что произошло событие, противоположное А + В, т.е. наступили  и одновременно: . С другой стороны, если произошло событие , то это означает, что произошло и , и , т.е. не наступило ни одно из событий А и В: . Итак, поскольку и , то по определению

.

Пример 7.  Доказать, что (A+C)(B+C)=AB+C.

Решение. Принимая во внимание равенства (1.6.1), (1.6.4), (1.6.5), (1.6.10), (1.6.11), получаем (А+С)(В+С) = А(В+С)+ С(В+С) = АВ + АС + СВ+ СС =АВ+(А+В)С+С =АВ+(А+B)C+CU =АВ+(А+В+U)С = АВ + UC = АВ + С.
(Здесь U — достоверное событие).

Задачи

1. Опыт состоит в подбрасывании трех монет. Монеты занумерованы и события означают выпадение герба соответственно на первой, второй и третьей монетах. Выразите через следующие события: А — «выпадение одного герба и двух цифр»; В — «выпадение не более одного герба»; С — «число выпавших гербов меньше числа выпавших цифр»; D — «выпадение хотя бы двух гербов»; Е — «на первой монете выпал герб, а на остальных — цифры»; F — «на первой монете выпала цифра и хотя бы на одной из остальных выпал герб».
2. Через произвольные события А, В, С найти выражения для следующих событий: а) произошло только событие А; б) произошло А и В, но С не произошло; в) произошли все три события; г) произошло, по крайней мере, одно из этих событий; д) произошло, по крайней мере, два события; е) произошло одно и только одно событие; ж) произошло два и только два события; з) ни одно событие не произошло; и) произошло не более двух событий.
3. Упростите выражение
4. Докажите, что и
5. Упростите выражение .
6. Докажите, что
7. Докажите, что и 

Ответы

1. ; ; ; ; ;   2. а) ; б) ; в) ABC; г) A+B+C; д) AB+AC+BC; е) ; ж) (AB+AC+BC)-ABC; з) ; и)   3. AB+BC+AC     5. U

Вопросы

1. Что называют суммой, или объединением, двух событий?
2. Как обозначают сумму двух событий?
3. Приведите примеры суммы двух событий.
4. Что называют суммой, или объединением, нескольких. событий?
5. Что называют произведением, или пересечением, двух событий?
6. Как обозначают произведение двух событий?
7. Что называют произведением нескольких событий?
8. Приведите примеры произведения трех событий.
9. Что называют разностью двух событий?
10. Приведите примеры разности двух событий.

содержание учебника

 

4.3. Действия над событиями

В этом разделе приводятся основные правила операций над событиями с использованием для наглядности их графического изображения в виде диаграмм.

Вначале введем понятие “поле событий” как совокупности всех случайных событий данного испытания, для которых определены вероятности. На рис. 4.1 поле событий изображено в виде заштрихованного прямоугольника.

1. Сумма (объединение) событий (рис. 4.2) представляет собой сложное событие, состоящее в появлении хотя бы одного из событий А и В. Объединение событий обозначается как , или.

2. Произведением (пересечением) событий А и В называется их совместное появление (рис. 4.3). Обозначается произведение событий как , или.

3. Достоверным событием называется событие, которое обязательно происходит в результате данного испытания (рис. 4.4). Оно обозначается обычно как Е.

4. Невозможное событие – событие, которое не может произойти в результате данного испытания. Принятое обозначение – .

5. Несовместными называются события, которые в результате данного испытания не могут произойти вместе (рис. 4.5). Примеры несовместных событий: попадание и промах при выстреле, выпадение двух и трех очков при бросании игральной кости. Рис. 4.5 наглядно показывает, что для несовместных событий .

6. Противоположным к А событием называется событие, состоящее в непоявлении события А (рис. 4.6). Обозначается противоположное событие символом . Примеры противоположных событий: промах и попадание при выстреле, выпадение герба или цифры при одном подбрасывании монеты.

                      

                    Рис. 4.1. Поле событий                                               Рис. 4.2. Сумма событий

                      

             Рис. 4.3. Произведение событий                                    Рис. 4.4. Достоверное событие

                      

            Рис. 4.5. Несовместные события                               Рис. 4.6. Противоположные события

4.4. Исчисление вероятностей

4.4.1.Примеры непосредственного определения вероятностей

Рассмотрим несколько примеров на вычисление вероятностей по формуле (4. 1).

Пример 4.1

Испытание состоит в подбрасывании игральной кости, на каждой из граней которой проставлено число очков (от 1 до 6). Какова вероятность того, что: 1) выпадает 2 очка? 2) выпадает нечетное число очков?

Решение 1: В данном испытании имеется 6 равновозможных случаев (выпадение 1, 2, 3, 4, 5, 6 очков), так как нет оснований предполагать, что появление какого-то определенного числа очков более вероятно (если, конечно, кость симметрична). Поэтому вероятность выпадения любого числа очков, в том числе и 2, при одном подбрасывании равна .

Событию А, заключающемуся в появлении нечетного числа очков, благоприятствуют три случая (выпадение 1, 3 и 5), поэтому по формуле (4.1) получаем

Решение 2: В данном испытании имеется 2 равновозможных исхода (выпадение четного числа очков (т.е. 2, 4, 6) и нечетного), так как кость симметрична, то очевидно, что эти исходы равновозможные.

Событию А, заключающемуся в появлении нечетного числа очков, благоприятствуют 1 случай из двух, поэтому по формуле (4.1) получаем 

Отметим, что построенную таким образом пространство элементарных событий непригодно для расчета вероятности того, что выпадает 2 очка, так как этому событию не благоприятствует не один из введенных нами элементарных исходов.

Пример 4.2

В урне 5 белых и 10 черных шаров, не отличающихся по размеру. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым?

Решение. В этом примере имеется 15 равновозможных (шары не отличаются по размеру) исходов опыта, причем ожидаемому событию (появлению белого шара) благоприятствуют 5 из них, поэтому искомая вероятность составит .

теория вероятностей | Определение, примеры и факты

образец места для пары игральных костей

Просмотреть все материалы

Ключевые люди:

Карл Фридрих Гаусс Пьер де Ферма Андрей Николаевич Колмогоров Симеон-Дени Пуассон Авраам де Муавр

Похожие темы:

Теорема Байеса Центральная предельная теорема стохастический процесс равнодушие вероятность

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

теория вероятностей , раздел математики, занимающийся анализом случайных явлений. Исход случайного события не может быть определен до того, как оно произойдет, но может быть любым из нескольких возможных исходов. Считается, что фактический результат определяется случайностью.

Слово вероятность имеет несколько значений в обычном разговоре. Два из них особенно важны для развития и приложений математической теории вероятностей. Одним из них является интерпретация вероятностей как относительных частот, примером чего могут служить простые игры с монетами, картами, костями и колесами рулетки. Отличительной особенностью азартных игр является то, что исход данного испытания нельзя предсказать с уверенностью, хотя совокупные результаты большого числа испытаний обнаруживают некоторую закономерность. Например, утверждение о том, что вероятность выпадения «орла» при подбрасывании монеты равна половине, согласно интерпретации относительной частоты, подразумевает, что при большом количестве подбрасываний относительная частота, с которой действительно выпадает «орел», будет приблизительно равна одной. -половина, хотя это не подразумевает исход любого данного броска. Есть много подобных примеров, связанных с группами людей, молекулами газа, генами и так далее. Актуарные заявления об ожидаемой продолжительности жизни для лиц определенного возраста описывают коллективный опыт большого числа людей, но не претендуют на то, чтобы сказать, что произойдет с каждым конкретным человеком. Точно так же прогнозы о вероятности возникновения генетического заболевания у ребенка родителей с известным генетическим составом являются утверждениями об относительной частоте встречаемости в большом количестве случаев, но не являются прогнозами относительно данного человека.

Эта статья содержит описание важных математических понятий теории вероятностей, проиллюстрированное некоторыми приложениями, которые стимулировали их развитие. Для более полной исторической обработки см. вероятность и статистику. Поскольку приложения неизбежно включают в себя упрощение предположений, фокусирующихся на одних особенностях проблемы за счет других, полезно начать с простых экспериментов, таких как подбрасывание монеты или бросание игральной кости, а затем посмотреть, как соотносятся эти, казалось бы, несерьезные исследования. к важным научным вопросам.

Эксперименты, выборочное пространство, события и равновероятные вероятности

Применение простых вероятностных экспериментов

Фундаментальным компонентом теории вероятностей является эксперимент, который может быть повторен, по крайней мере гипотетически, в практически идентичных условиях и который может привести к различным исходы различных испытаний. Набор всех возможных результатов эксперимента называется «выборочным пространством». Эксперимент с однократным подбрасыванием монеты приводит к выборке пространства с двумя возможными исходами: «орел» и «решка». Бросание двух игральных костей имеет выборочное пространство с 36 возможными исходами, каждый из которых может быть отождествлен с упорядоченной парой ( i , j ), где i и j принимают одно из значений 1, 2, 3, 4, 5, 6 и обозначают грани, отображаемые на отдельных костях. Важно думать о костях как об идентифицируемых (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1). «Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма граней, выпавших на двух костях, равна шести» состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1).

Викторина по Британике

Дайте определение: математические термины

Вот ваша миссия, если вы решите ее принять: Дайте определение следующим математическим терминам до того, как истечет время.

Третий пример — вытащить n шаров из урны с шарами разных цветов. Общим результатом этого эксперимента является n -кортеж, где i -я запись определяет цвет шара, полученного при i -м розыгрыше ( i = 1, 2,…, и ). Несмотря на простоту этого эксперимента, его глубокое понимание дает теоретическую основу для проведения опросов общественного мнения и выборочных опросов. Например, лица в популяции, поддерживающие определенного кандидата на выборах, могут быть идентифицированы шарами определенного цвета, те, кто поддерживает другого кандидата, могут быть идентифицированы другим цветом и так далее. Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение должно узнать об электоральных предпочтениях населения на основе выборки, взятой из этого населения.

Другим применением простых моделей урн является использование клинических испытаний, предназначенных для определения того, является ли новое лечение болезни, новое лекарство или новая хирургическая процедура лучше стандартного лечения. В простом случае, когда лечение можно рассматривать как успех или неудачу, цель клинического испытания состоит в том, чтобы выяснить, приводит ли новое лечение к успеху чаще, чем стандартное лечение. Больных этим заболеванием можно определить по шарикам в урне. Красные шарики — это те пациенты, которые вылечились новым лечением, а черные шарики — те, кто не вылечился. Обычно есть контрольная группа, которая получает стандартное лечение. Они представлены второй урной с, возможно, другой долей красных шаров. Цель опыта по извлечению из каждой урны некоторого количества шаров состоит в том, чтобы на основе выборки выяснить, в какой урне больше красных шаров. Вариант этой идеи можно использовать для проверки эффективности новой вакцины. Возможно, самым крупным и известным примером было испытание вакцины Солка от полиомиелита, проведенное в 1954. Она была организована Службой общественного здравоохранения США и охватила почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здравоохранения в промышленно развитых частях мира. Строго говоря, эти приложения представляют собой задачи статистики, основу для которых дает теория вероятностей.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

В отличие от экспериментов, описанных выше, многие эксперименты имеют бесконечно много возможных результатов. Например, можно подбрасывать монету до тех пор, пока впервые не выпадет «орел». Количество возможных бросков равно 9.0029 n = 1, 2,…. Другой пример — крутить спиннер. Для идеализированного счетчика, состоящего из отрезка прямой линии, не имеющего ширины и повернутого в его центре, набор возможных исходов представляет собой набор всех углов, которые конечная позиция счетчика образует с некоторым фиксированным направлением, что эквивалентно всем действительным числам в [0 , 2π). Многие измерения в естественных и социальных науках, такие как объем, напряжение, температура, время реакции, предельный доход и т. д., производятся на непрерывных шкалах и, по крайней мере, теоретически включают бесконечное множество возможных значений. Если повторные измерения на разных субъектах или в разное время на одном и том же субъекте могут привести к разным результатам, теория вероятностей является возможным инструментом для изучения этой изменчивости.

Из-за их сравнительной простоты сначала обсуждаются эксперименты с конечными выборками. На заре развития теории вероятностей математики рассматривали только те эксперименты, для которых казалось разумным, исходя из соображений симметрии, предположить, что все результаты эксперимента «одинаково вероятны». Тогда в большом числе испытаний все исходы должны встречаться примерно с одинаковой частотой. Вероятность события определяется как отношение числа случаев, благоприятных для события, т. е. числа исходов в подмножестве выборочного пространства, определяющего событие, к общему числу случаев. Таким образом, 36 возможных исходов при бросании двух игральных костей предполагаются равновероятными, а вероятность выпадения «шестёрки» равна числу благоприятных случаев, 5, делённому на 36, или 5/36.

Теперь предположим, что монета подбрасывается n раз, и рассмотрим вероятность того, что орел не выпадет за n подбрасываний. Результатом эксперимента является n -кортеж, k -й вход которого идентифицирует результат k -го броска. Поскольку есть два возможных исхода для каждого броска, количество элементов в пространстве выборки равно 2 ⁿ . Из них только один исход соответствует отсутствию орла, поэтому требуемая вероятность равна 1/2 ⁿ .

Немногим сложнее определить вероятность «не более одного орла». Помимо единственного случая, когда орёл не выпадает, существует n случаев, в которых выпадает ровно один орёл, потому что он может выпасть при первом, втором,… или n -м подбрасывании. Следовательно, имеется n + 1 случаев, благоприятных для получения не более одной головы, и желаемая вероятность равна ( n + 1)/2 ⁿ .

Элементарная теория вероятностей | Знания о здоровье

Статистика: элементарная теория вероятностей

Вероятность дает вероятность того, что определенное событие произойдет. Он определяется как положительное число от 0 (событие невозможно) до 1 (событие обязательно). Таким образом, чем выше вероятность данного события, тем более вероятно, что оно произойдет. Если А является определенным событием, то вероятность наступления А выражается как Р(А). Вероятность может быть выражена несколькими способами. А частотный подход заключается в наблюдении ряда конкретных событий из общего числа событий. Таким образом, мы можем сказать, что вероятность рождения мальчика равна 0,52, потому что из большого числа одноплодных рождений мы наблюдаем 52% мальчиков. Подход, основанный на модели , заключается в том, что модель или механизм определяет событие; таким образом, вероятность выпадения «1» на беспристрастном кубике равна 1/6, поскольку существует 6 возможностей, каждая из которых равновероятна, и все они складываются в единицу. Подход, основанный на мнении , заключается в том, что мы используем наш прошлый опыт, чтобы предсказать будущее событие, поэтому мы можем дать вероятность того, что наша любимая футбольная команда выиграет следующий матч, или будет ли завтра дождь.

Имея два события A и B, мы часто хотим определить вероятность того или иного события или обоих событий.

 

Правило сложения

Правило сложения используется для определения вероятности возникновения хотя бы одного из двух (или более) событий. В общем, вероятность события A или B определяется как:

          P(A или B) = P(A) + P(B) – P(A и B)

Если A и B являются взаимоисключающими , это означает, что они не могут встречаться вместе, то есть P(A и B)=0. Следовательно, для взаимоисключающих событий вероятность возникновения А или В определяется выражением:

          P(A или B) = P(A) + P(B)

Пример: если событие A состоит в том, что человек имеет группу крови O, а событие B состоит в том, что у него группа крови B, то эти события взаимно исключительным, поскольку человек может быть либо одним, либо другим. Следовательно, вероятность того, что данное лицо относится либо к группе О, либо к группе В, равна Р(А)+Р(В).

 

Правило умножения

Правило умножения определяет вероятность того, что два (или более) события произойдут одновременно. В общем, вероятность того, что произойдут события A и B, определяется как:

          P(A и B) = P(A) x P(B | A) = P(B) x P(A | B)

Обозначение P(B | A) представляет собой вероятность того, что событие B произойдет при условии, что событие A произошло, когда читается символ ‘|’, является ‘данной’. Это пример условной вероятности , при условии, что событие А произошло. Например, вероятность вытянуть туза червей из хорошо перетасованной колоды составляет 1/51. Вероятность туза червей при условии, что карта красная, составляет 1/26.

Пример: если событие A — человек заболел невропатией, а событие B — диабет, то P(A|B) — это вероятность развития невропатии при условии, что он диабетик.

Если A и B являются независимыми событиями , то вероятность события B не зависит от вероятности события A (и наоборот). Другими словами, P(B | A) = P(B). Следовательно, для независимых событий вероятность того, что произойдут события A и B, определяется как:

          P(A и B) = P(A) x P(B)

Пример. Если событие A состоит в том, что человек имеет группу крови O, а событие B – в том, что он диабетик, то вероятность того, что у кого-то есть группа крови O а быть диабетиком — это P(A)xP(B), предполагая, что диабет не связан с группой крови человека.

Обратите внимание, что если A и B исключают друг друга, то P(A|B)=0

 

Теорема Байеса

Из приведенного выше правила умножения мы видим, что:

          P(A) x P(B | A) = P(B) x P(A | B)

Это приводит к так называемой теореме Байеса:

 

\({\ rm{P}}\left( {\rm{B|A}}} \right) = {\rm{\;}}\frac{{{\rm{P}}\left( {\rm{ A|B}}} \right){\rm{P}}\left( {\rm{B}} \right)}}{{{\rm{P}}\left({\rm{A}} \right)}}\)

 

 

Таким образом, вероятность B при A равна вероятности A при B, умноженной на вероятность B, деленную на вероятность A.

Эта формула не подходит, если P(A)=0, то есть если A является событием, которое не может произойти.

Ниже приведен пример использования теоремы Байеса.

 

Чувствительность и специфичность

Результаты многих диагностических тестов представлены в виде непрерывной переменной (то есть такой, которая может принимать любое значение в заданном диапазоне), например, диастолического артериального давления или уровня гемоглобина. Однако для простоты обсуждения мы сначала предположим, что они были разделены на положительные и отрицательные результаты. Например, положительный диагностический результат «гипертонии» — это диастолическое артериальное давление выше 9.0 мм рт.ст.; тогда как для «анемии» требуется уровень гемоглобина менее 12 г/дл.

Для каждой диагностической процедуры (которая может включать лабораторное исследование взятого образца) необходимо задать ряд фундаментальных вопросов. Во-первых, если болезнь присутствует, какова вероятность того, что результат теста будет положительным? Это приводит к понятию чувствительности теста. Во-вторых, если заболевание отсутствует, какова вероятность того, что результат теста будет отрицательным? Этот вопрос относится к специфике теста. Ответить на эти вопросы можно только в том случае, если известен «истинный» диагноз. В случае органического заболевания это можно определить с помощью биопсии или, например, дорогостоящей и рискованной процедуры, такой как ангиография при заболеваниях сердца. В других ситуациях это может быть мнение «эксперта». Такие тесты обеспечивают так называемый «золотой стандарт».

Пример

Рассмотреть результаты анализа N-концевого промозгового натрийуретического пептида (NT-proBNP) для диагностики сердечной недостаточности при обследовании общей популяции у лиц старше 45 лет и у пациентов с существующий диагноз сердечной недостаточности, полученный Hobbs, Davis, Roalfe, et al (BMJ 2002) и обобщенный в таблице 1. Сердечная недостаточность была идентифицирована, когда NT-proBNP > 36 пмоль/л.

Таблица 1: Результаты анализа NT-proBNP в общей популяции старше 45 лет и у лиц с ранее диагностированной сердечной недостаточностью (согласно Hobbs, David, Roalfe et al. , BMJ 2002)

 

 

 

 

 

 

Положительный результат теста на сердечную недостаточность мы обозначаем как Т+, а положительный результат теста на сердечную недостаточность обозначается Т+, а положительный результат теста на сердечную недостаточность. Распространенность сердечной недостаточности у этих субъектов составляет 103/410=0,251, или примерно 25%. Таким образом, вероятность наличия заболевания у субъекта, выбранного случайным образом из объединенной группы, оценивается как 0,251. Мы можем записать это как P(D+)=0,251.

Чувствительность теста – это доля больных, у которых также положительный результат теста. Таким образом, чувствительность определяется выражением e/(e+f)=35/103=0,340 или 34%. Теперь чувствительность представляет собой вероятность положительного результата теста (событие T+) при наличии заболевания (событие D+) и может быть записана как P(T+|D+), где ‘|’ читается как «дано».

Специфичностью теста является доля здоровых людей, дающих отрицательный результат теста. Таким образом, специфичность составляет h/(g+h)=300/307=0,977 или 98%. Теперь специфичность — это вероятность отрицательного результата теста (событие Т-) при отсутствии заболевания (событие D-) и может быть записана как P(T-|D-).

Поскольку чувствительность зависит от наличия заболевания, а специфичность – от его отсутствия, теоретически они не зависят от распространенности заболевания. Например, если мы удвоим количество пациентов с истинной сердечной недостаточностью со 103 до 206 в таблице 1, так что теперь распространенность составит 103/(410+103)=20%, то мы можем ожидать, что в два раза больше пациентов будут давать положительный результат теста. Таким образом, 2×35=70 будет иметь положительный результат. В этом случае чувствительность будет 70/206=0,34, что не изменилось по сравнению с предыдущим значением. Аналогичный результат получается для специфичности.

Чувствительность и специфичность являются полезными статистическими данными, поскольку они дают согласованные результаты для диагностического теста в различных группах пациентов с различной распространенностью заболевания. Это важный момент; чувствительность и специфичность являются характеристиками теста, а не популяции, к которой применяется тест. Однако на практике, если заболевание встречается очень редко, точность, с которой можно оценить чувствительность, может быть ограниченной. Это связано с тем, что количество субъектов с заболеванием может быть небольшим, и в этом случае доля правильно диагностированных лиц будет иметь значительную неопределенность.

Два других широко используемых термина: частота ложноотрицательных результатов (или вероятность ложноотрицательных результатов), определяемая как f/(e+f)=1-чувствительность, и частота ложноположительных результатов (или вероятность ложноположительных результатов). ) или g/(g+h)=1-специфичность.

Эти концепции суммированы в таблице 2.

Таблица 2: Сводка определений чувствительности и специфичности

Это важно для консистенции, чтобы поставить в соответствии с диагнозом на правдивую диагностику на на посту вверху, а результат теста внизу.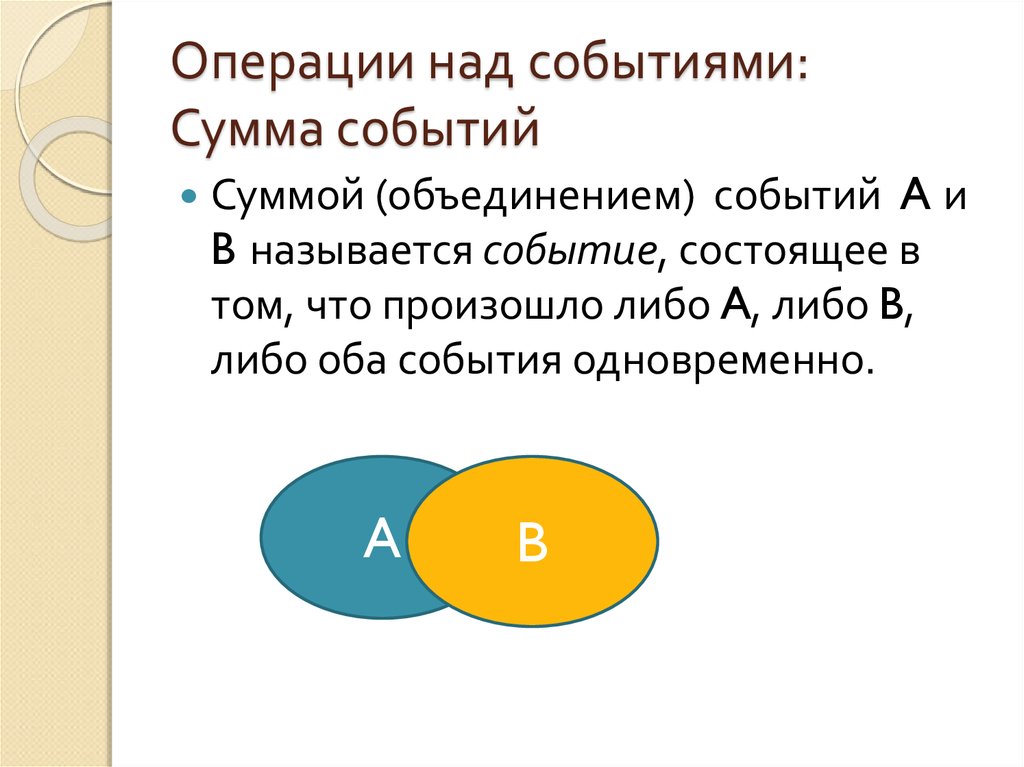 Поскольку чувствительность = 1–P (ложноотрицательный) и специфичность = 1–P (ложноположительный), возможно, полезная мнемоника для напоминания об этом состоит в том, что «чувствительность» и «отрицательный» содержат «n» в них, а «специфичность» и «положительный». в них есть буква «р».

 

Прогностическая ценность теста

Предположим, к врачу обращается пациент с болью в груди, указывающей на стенокардию, и что доступны результаты исследования, описанного в таблице 3.

Таблица 3: Результаты теста на толерантность к упражнениям у пациентов с подозрением на заболевание коронарной артерии

Распространенность коронарной болезни ARTe . Таким образом, врач считает, что у пациента ишемическая болезнь сердца с вероятностью 0,70. Что касается пари, можно было бы поставить шансы примерно 7:3 на то, что у пациента действительно ишемическая болезнь сердца. Теперь пациент проходит тест с физической нагрузкой, и результат положительный. Как это меняет шансы? Сначала необходимо рассчитать вероятность наличия у пациента заболевания при положительном результате теста. Из таблицы 3 930 мужчин с положительным тестом, из них 815 с ишемической болезнью сердца. Таким образом, оценка 0,70 для пациента корректируется в сторону увеличения до вероятности заболевания при положительном результате теста 815/930=0,88.

Это дает прогностическое значение положительного теста (положительное прогностическое значение):

        P(D+|T+) = 0,88.

Прогностическая ценность отрицательного теста (отрицательная прогностическая ценность):

        P(D-|T-) = 327/535 = 0,61.

На эти значения влияет распространенность заболевания. Например, если количество больных в таблице 3 удвоится, то прогностическая ценность положительного теста станет 1630/(1630+115)=0,9.3 и прогностическая ценность отрицательного теста 327/(327+416)=0,44.

 

Роль теоремы Байеса

Предположим, что событие A происходит при положительном результате нагрузочного теста, а событие B происходит при положительном результате ангиографии. Таким образом, вероятность наличия как положительного теста с физической нагрузкой, так и заболевания коронарной артерии равна P(T+ и D+). Из таблицы 3 вероятность выбрать одного мужчину с положительным тестом на физическую нагрузку и с ишемической болезнью сердца из группы 1465 мужчин составляет 815/1465=0,56.

Однако из правила умножения:

          P(T+ и D+) = P(T+|D+)P(D+)

P(T+|D+)=0,80 – чувствительность теста, а P(D+)= 0,70 — распространенность коронарной болезни, поэтому P(T+ и D+)=0,80×0,70=0,56, как и раньше.

Теорема Байеса позволяет связать прогностическую ценность положительного теста с чувствительностью теста, а прогностическую ценность отрицательного теста связать со специфичностью теста. Теорема Байеса позволяет сочетать предварительные оценки шансов диагноза с возможными результатами теста для получения так называемой «апостериорной» оценки диагноза. Он отражает процедуру вынесения клинического суждения.

В терминах теоремы Байеса диагностический процесс резюмируется следующим образом: } \right) = {\ rm {\;}} \ frac {{{\ rm {P}} ({\ rm {T}} + | {\ rm {D}} + ) {\ rm {P}} \left( {{\rm{D}} + } \right)}}{{{\rm{P}}\left( {{\rm{T}} + } \right)}}\)

 

Вероятность P(D+) — это априорная вероятность, а P(D+|T+) — апостериорная вероятность.

Теорему Байеса полезно обобщить, если мы выражаем ее в терминах вероятности события, а не вероятности. Формально, если вероятность события равна p , то коэффициенты определяются как p / (1- p ). Вероятность того, что у человека есть ишемическая болезнь сердца, до тестирования по таблице равна 0,70, поэтому шансы равны 0,70/(1-0,70)=2,33 (что также можно записать как 2,33:1).

 

Отношение правдоподобия

С точки зрения шансов мы можем обобщить теорему Байеса, используя так называемое положительное отношение правдоподобия (LR+), определяемое как:

 

\({\rm{LR}} + = {\ rm {\;}} \ frac {{{\ rm {P}} ({\ rm {T}} + | {\ rm {D}} + )}} {{{\ rm {P}} ({\rm{T}} + |D — )}} = \frac{{{\rm{Чувствительность}}}}{{1 — {\rm{Специфичность}}}}\)

 

Таким образом, отношение правдоподобия положительного теста представляет собой вероятность получения положительного результата, когда у субъекта есть заболевание, к вероятности положительного результата теста при условии, что у субъекта , а не есть заболевание.

Можно показать, что теорему Байеса можно обобщить следующим образом:

          Вероятность заболевания после теста = Вероятность заболевания до теста x отношение правдоподобия , поэтому вероятность заболевания после теста составляет 3,08×2,33=7,2. Это можно проверить по рассчитанной ранее посттестовой вероятности 0,88, так что посттестовые шансы составляют 0,88/(1–0,88)=7,3. (Это отличается от 7.2 из-за ошибок округления в расчетах.)

Пример

Этот пример иллюстрирует теорему Байеса на практике путем вычисления положительного прогностического значения для данных таблицы 3.

Мы используем формулу влево ( {{\ rm {D}} + {\ rm {| T}} + } \ right) = {\ rm {\;}} \ frac {{{\ rm {P}} ({\ rm {T }} + |{\rm{D}} + ){\rm{P}}\left( {{\rm{D}} + } \right)}}{{{\rm{P}}\left( {{\rm{T}} + } \right)}}\)

 

Из таблицы: P(T+)=930/1465=0,63, P(D+)=0,70 и P(T+|D+)= 0,80, таким образом:

Положительное прогностическое значение = (0,8 x 0,7)/0,63 = 0,89

. .. это то, что мы рассчитали ранее (за исключением небольшой ошибки округления).

Пример

Распространенность заболевания составляет 1 на 1000, и существует тест, который может выявить его с чувствительностью 100% и специфичностью 95%. Какова вероятность того, что у человека есть заболевание при положительном результате теста?

Многие люди, не задумываясь, могут предположить, что ответ будет 0,95, специфичность.

Используя теорему Байеса, однако: \frac{{{\rm{Чувствительность\;}} \times {\rm{Распространенность}}}}{{{\rm{Вероятность\;положительного\;результата}}}}\)

 

Для расчета вероятности положительного результата рассмотрим 1000 человек, из которых один человек болен. Тест обязательно обнаружит этого человека. Однако он также даст положительный результат у 5% из 999 человек без заболевания. Таким образом, общее количество срабатываний равно 1+(0,05×999)=50,95 и вероятность положительного результата 50,95/1000=0,05095.

Таким образом:

\({\rm{P}}\left( {{\rm{D}} + {\rm{|T}} + } \right) = {\rm{\;}}\ frac{{1{\rm{\;}} \times 0,001}}{{0,05095}} = 0,02\)

 

Полезность теста будет зависеть от распространенности заболевания в популяции, к которой он относится. было применено. В общем, полезный тест — это тот, который значительно изменяет предтестовую вероятность. Если заболевание очень редкое или очень распространенное, то вероятности заболевания при отрицательном или положительном тесте относительно близки, и поэтому тест имеет сомнительную ценность.

 

Независимость и взаимоисключающие события

В таблице 3, если бы результаты теста на толерантность к физической нагрузке были совершенно не связаны с наличием у пациента ишемической болезни сердца, то есть они были бы независимыми, мы могли бы ожидать:

          P(D+ и T+ )= P(T+) x P(D+).

Если мы оценим P(D+ и T+) как 815/1465=0,56, P(D+)=1023/1465=0,70 и P(T+)=930/1465=0,63, то разница:

          P(D+ и Т+) – P(D+)P(T+)=0,56–(0,70×0,63)=0,12

.…является грубой мерой того, являются ли эти события независимыми. В этом случае размер разницы предполагает, что они не являются независимыми. Очевидно, что вопрос о том, являются ли события независимыми, является важным и относится к статистическому выводу.

В общем, перед клиницистом стоит не простой вопрос «есть ли у больного заболевание сердца?», а целый набор различных диагнозов. Обычно эти диагнозы можно считать взаимоисключающими; то есть, если у пациента есть одно заболевание, у него нет ни одного из альтернативных дифференциальных диагнозов. Однако, особенно у пожилых людей, у пациента может быть ряд заболеваний, которые все имеют сходные симптомы.

Иногда учащиеся путают независимые события и взаимоисключающие события, но из вышеизложенного видно, что взаимоисключающие события не могут быть независимыми. Понятия независимости и взаимоисключающих событий используются для обобщения теоремы Байеса и ведут к анализу решений в медицине.

 

Ссылки

•        Статистические примечания BMJ http://bmj.bmjjournals.com/cgi/content/full/329/7458/168
•        Кэмпбелл М.Дж., Мачин Д. и Уолтерс С.Дж. Медицинская статистика: подход, основанный на здравом смысле 4-е изд.