Теория множеств чисел: Введение в теорию множеств / Хабр
Теория множеств | Понятия и категории
ТЕОРИЯ МНОЖЕСТВ — математическая теория о свойствах множеств, главным образом бесконечных, абстрагирующаяся от свойств элементов, составляющих эти множества. Различают «наивную» и аксиоматические Т. м. Само понятие множества относится к числу неопределяемых первоначальных математических понятий и может бьггь пояснено лишь на примерах. Так, можно говорить о множестве деревьев в лесу или о множестве бросаний симметричной монеты. Для задания множества достаточно указать характеристическое свойство элементов данного множества, которым обладают все элементы этого множества, и только они. В случае, если характеристическим свойством, которым мы хотим определить некое множество, не обладает ни один элемент, в Т.м. говорят о пустом множестве. Если каждый элемент множества X является элементом множества Y, то множество X называется подмножеством множества Y.
«Наивная» Т.м. была создана Г.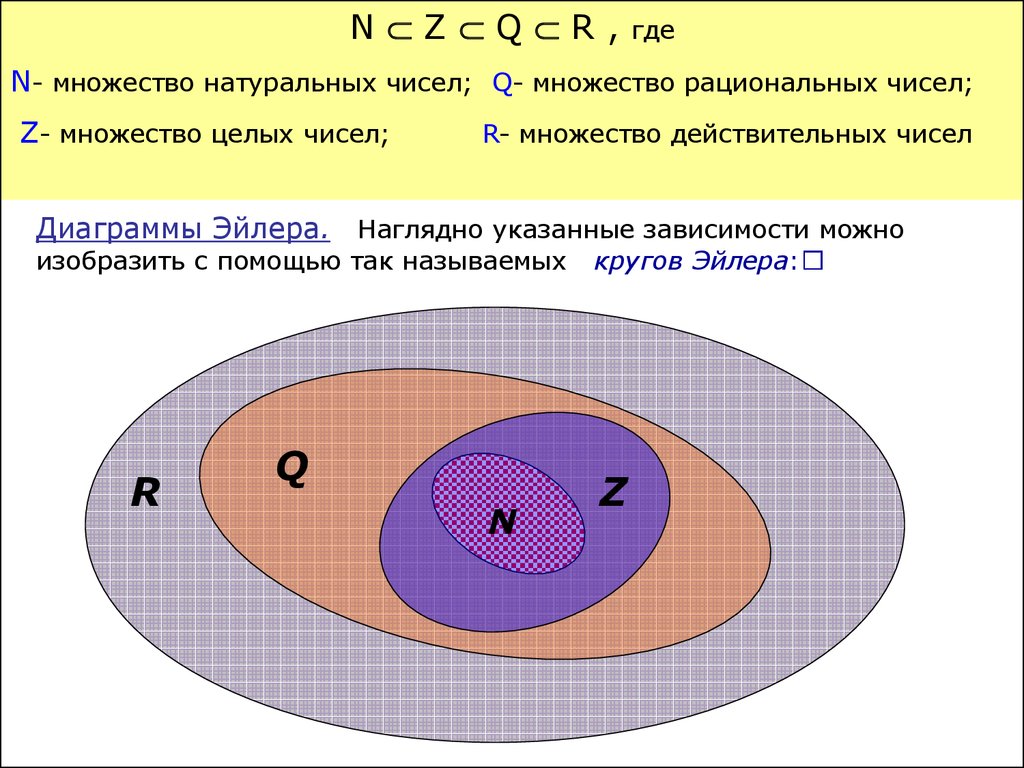

Первым шагом, который сделал Кантор в создании своей теории, было определение понятия мощности, или кардинального числа данного множества. Два множества называются эквивалентными или равномощными, если существует взаимно-однозначное соответствие, сопоставляющее каждому элементу одного множества некоторый (единственный) элемент другого множества. Все эквивалентные множества обладают тем общим свойством, которое можно выделить с помощью абстракции отождествления и которое Кантор назвал мощностью, или кардинальным числом множества. Почти четверть века Кантор посвятил систематическому изучению бесконечных множеств с точки зрения установления соответствия между ними. Так, он доказал, что множества целых, рациональных и алгебраических множеств равномощны множеству натуральных чисел, которое обычно называют счетным. Он также установил, что мощность всех подмножеств натуральных чисел несчетна и равна мощности всех действительных чисел. Способ, с помощью которого Кантору удалось доказать существование несчетных множеств, носит название диагонального метода, который является одним из наиболее сильных и известных методов Т.
Однако, как вскоре оказалось, «наивная» Т. м. не могла служить фундаментом классической математики вследствие обнаруженных парадоксов (см. Парадоксы в математике). Один из таких парадоксов обнаружил сам Кантор в 1895 г. Наиболее радикальную позицию по отношению к Т.м. заняли интуиционисты во главе с Брауэром (см. Интуиционизм), которые призывали вообще отказаться от концепции актуальной бесконечности. Сторонники Т.м., напротив, пошли по пути аксиоматизации этой науки, предложив ограничить употребление понятия множества в математике рамками определенных аксиоматических систем, с помощью которых удается избежать образования слишком обширных множеств, использование которых ведет к парадоксам. В настоящее время существует большое количество аксиоматических Т.м., по своему содержанию не многим отличающихся от наиболее признанной системы аксиом Цермело-Френкеля (ZF).
м. не могла служить фундаментом классической математики вследствие обнаруженных парадоксов (см. Парадоксы в математике). Один из таких парадоксов обнаружил сам Кантор в 1895 г. Наиболее радикальную позицию по отношению к Т.м. заняли интуиционисты во главе с Брауэром (см. Интуиционизм), которые призывали вообще отказаться от концепции актуальной бесконечности. Сторонники Т.м., напротив, пошли по пути аксиоматизации этой науки, предложив ограничить употребление понятия множества в математике рамками определенных аксиоматических систем, с помощью которых удается избежать образования слишком обширных множеств, использование которых ведет к парадоксам. В настоящее время существует большое количество аксиоматических Т.м., по своему содержанию не многим отличающихся от наиболее признанной системы аксиом Цермело-Френкеля (ZF).
Литература:
Кантор Г. Труды по теории множеств. М., 1985;
Френкель А., Бар-Хиллел И. Основания теории множеств. М., 1966;
Коэн П. Дж. Теория множеств и континуум-гипотеза. М., 1974.
Дж. Теория множеств и континуум-гипотеза. М., 1974.
Словарь философских терминов. Научная редакция профессора В.Г. Кузнецова. М., ИНФРА-М, 2007, с. 584-585.
Часть 1 элементы теории множеств и математической логики лекция 1 множества и операции над ними
Математика. Курс лекций для студентов специальности Психология
Часть 1. Элементы теории множеств и математической логики
Множества и операции над ними
1. Понятие множества
2. Способы задания множества
3. Отношения между множествами
3. Операции над множествами
1. Понятие множества
Понятия «множество», «элемент
множества», «элемент принадлежит
множеству» относятся к первичным,
неопределяемым понятиям современной
математики, они не определяются через
другие понятия.
Под множеством понимается всякая совокупность объектов (предметов, понятий), рассматриваемая как единое целое; при этом объекты этой совокупности называют элементами множества.
Примеры.
Множество студентов в данной аудитории.
Множество окружностей, имеющих центр в данной точке.
Множество всех букв русского алфавита.
Основатель теории множеств — Георг Кантор (1845-1918, нем. математик) писал: «Множество есть многое, мыслимое как единое, целое». Множества обозначаются большими буквами , элементы множества — малыми буквами .
Если объект является элементом множества (принадлежит ), то это обозначается . Если не является элементом множества (не принадлежит ), то пишут .
Пример. Рассмотрим множество
,
составленное из чисел 1 и 3. Числа 1 и 3
принадлежат множеству
,
что записывается как
,
.
Поэтому числа 1 и 3 являются элементами
множества
.
Числа 2, не принадлежат множеству
,
что записывается как
,
.
Рассмотрим множество
,
составленное из чисел 1 и 3. Числа 1 и 3
принадлежат множеству
,
что записывается как
,
.
Поэтому числа 1 и 3 являются элементами
множества
.
Числа 2, не принадлежат множеству
,
что записывается как
,
.
Элементами множества могут быть предметы различной природы (буквы, числа, люди, слова, точки, уравнения и т.д.). Именно этим объясняется общность теоретико-множественных понятий и их применимость к самым разным областям – математике, лингвистике, экономике, психологии, биологии и т.д.
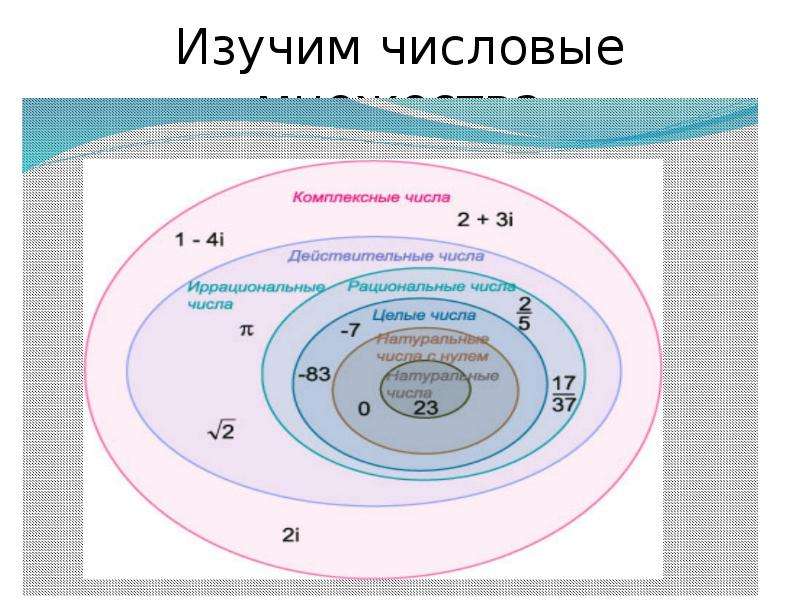
Множества, элементами которых являются числа, называются числовыми множествами.
Множество, которое не содержит ни одного элемента, называется пустым множеством и обозначается символом .
Примеры
Множество точек пересечения параллельных прямых – пустое множество.

Множество решений системы уравнений — пустое множество.
Понятие «множество» – как математическое, так и философское. Действительно, уже с рождения человек не только пополняет список объектов и явлений, но и начинает классифицировать их по определенным свойствам, объединяя тем самым объекты в некоторые совокупности, множества. Понятие множества используется для построения и других понятий, используемых не только в математике, но и в гуманитарных науках — например, в психологии – понятия отношения, понятия функции.
2. Способы задания множества
Множества могут быть заданы несколькими способами.
- Задание множества перечислением его элементов.
Названия всех элементов множества (в произвольном порядке) записывают в строку, отделяют запятыми и заключают в фигурные скобки.

Примеры
Множество из четырех букв записывается .
Множество, состоящее из одного элемента , обозначается как . Необходимо различать символы: — предмет, но — множество, состоящее из одного элемента (одноэлементное множество).
Перечислением можно задать только множество, содержащее конечное число элементов. Множества натуральных чисел, целых чисел, множество рациональных чисел, действительных чисел перечислением задать нельзя, так как они бесконечные множества.
Примеры
Множество точек плоскости, равноудаленных от двух точек.
Множество решений уравнения .
Множество может быть задано указанием характеристического свойства его элементов
,
то есть такого свойства, которым
обладают все элементы данного множества,
и только они:
. Здесь означает, что элемент является элементом известного множества
.
Запись означает, что элемент обладает свойством
.Свойство формулируется словами, символами или
выражается с помощью уравнения или
неравенства.
Здесь означает, что элемент является элементом известного множества
.
Запись означает, что элемент обладает свойством
.Свойство формулируется словами, символами или
выражается с помощью уравнения или
неравенства.
Замечание. Характеристических свойств, которыми обладают элементы множества, может быть несколько, тогда при перечислении они отделяются запятой или соединяются логическим союзом «и».
Примеры
Множество целых чисел, которые больше –3, но меньше 4, с помощью характеристического свойства записывается так: . Элементами множества являются только целые числа, которые больше (–3) и меньше 4, то есть числа . Множество содержит конечное число элементов и поэтому может быть задано также перечислением элементов: .
Число 2,5 принадлежит множеству .
Множество решений системы неравенств можно записать в виде .
 Здесь
— множество действительных чисел.
Неравенство
— первое характеристическое свойство;
неравенство
— второе характеристическое свойство,
которым обладают действительные числа
множества
.
Решая систему неравенств, получим:
.
Таким образом, множество
— бесконечное числовое множество,
состоящее из действительных чисел,
заключенных между числами 2 и 4, включая
число 2. На числовой оси множество
задает отрезок
,
замкнутый снизу и открытый сверху.
Здесь
— множество действительных чисел.
Неравенство
— первое характеристическое свойство;
неравенство
— второе характеристическое свойство,
которым обладают действительные числа
множества
.
Решая систему неравенств, получим:
.
Таким образом, множество
— бесконечное числовое множество,
состоящее из действительных чисел,
заключенных между числами 2 и 4, включая
число 2. На числовой оси множество
задает отрезок
,
замкнутый снизу и открытый сверху.
2 4
Рисунок 1.1
3. Отношения между множествами
Включение множеств
Рассмотрим множество натуральных чисел, не превосходящих 5, и множество положительных делителей числа 4. Сравнивая эти множества, замечаем, что все элементы множества являются также и элементами множества .
Отношения между множествами
наглядно изображаются с помощью множеств
точек, ограниченных замкнутыми кривыми,
— так называемых диаграмм Эйлера-Венна.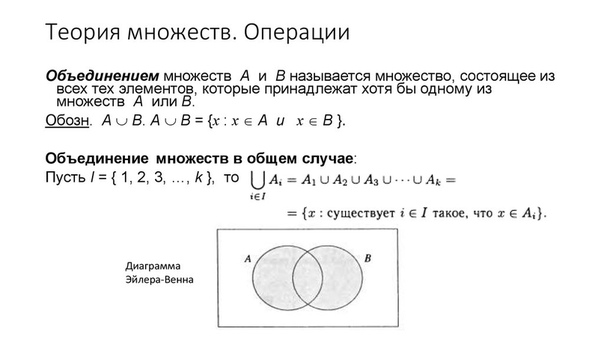 Например, на рисунке 2 приведена диаграмма
для отношения включения, когда
.
Например, на рисунке 2 приведена диаграмма
для отношения включения, когда
.
A
B
Рисунок 1.2
Примеры
Всякое натуральное число является элементом множества целых чисел, то есть . Всякое целое число является элементом множества рациональных чисел, то есть , а каждое рациональное число является элементом множества действительных чисел, то есть .
Любой правильный треугольник является элементом множества всех треугольников.
Множество параллелограммов является подмножеством множества четырехугольников.
Открытый отрезок является частью замкнутого отрезка , то есть .
Из определения отношения включения следуют его свойства.
Для отношения включения возможен
случай, когда существует хотя бы один
элемент множества
,
не принадлежащий множеству
. Тогда говорят, что множество является собственным подмножеством множества
,
и обозначают отношение строгого
включения как
.
Тогда говорят, что множество является собственным подмножеством множества
,
и обозначают отношение строгого
включения как
.
Пример. Элемент множества не принадлежит множеству , поэтому множество является собственным подмножеством множества , то есть , или .
Все подмножества любого множества , кроме пустого множества и самого множества , являются его собственными подмножествами, а остальные подмножества – несобственными.
Поставим задачу найти число всех подмножеств множества.
Если — пустое множество Ø, тогда само множество является единственным его подмножеством. Значит, число подмножеств пустого множества равно единице.
Одноэлементное множество имеет два подмножества – само множество и пустое множество. Значит, число подмножеств одноэлементного множества равно двум.

Если — двухэлементное множество , тогда его подмножествами являются само множество , пустое множество Ø, два одноэлементных множества и — всего 4 подмножеств. Значит, число подмножеств двухэлементного множества равно 4, или .
Пусть — трехэлементное множество , тогда его подмножествами являются: пустое множество ; три одноэлементных подмножества , , ; три двухэлементных подмножества , , и само множество — всего 8 подмножеств. Значит, число всех подмножеств трехэлементного множества равно — в два раза больше числа подмножеств двухэлементного множества.
Можно показать, что если конечное множество состоит из элементов, то число всех его подмножеств равно . Для бесконечного множества множество всех его подмножеств тоже бесконечно.
Равенство множеств
Множества и называются равными, если они состоят из одних и тех же элементов, то есть если любой элемент одного из множеств принадлежит другому множеству.

Примеры
1. , . Множества и состоят из одних и тех же элементов, поэтому они равные: .
2. Множество решений уравнения есть множество чисел 2 и 3, то есть . Множество простых чисел, меньших 5, также состоит из чисел 2 и 3, то есть . Значит, множества состоят из одних и тех же элементов и являются равными:.
Равенство множеств равносильно одновременной истинности утверждений: 1) для любых элементов и справедливо: если , то ; 2) если , то . На этом основывается доказательство равенства двух множеств.
4. Операции над множествами
Пересечение множеств
А В
Рисунок 1.3
Примеры
1. Даны числовые множества
,
. Найдем их пересечение:
.
Найдем их пересечение:
.
2. Множество — числовой промежуток — отрезок, открытый слева, множество — бесконечный числовой промежуток, замкнутый слева . Поскольку нет чисел, которые принадлежат одновременно множествам и , то пересечение данных числовых промежутков есть пустое множество: .
-1 0 3
Рисунок 1.4
3. Пусть — множество прямоугольников, — множество ромбов. Так как каждый четырехугольник, который одновременно является и прямоугольником, и ромбом, есть квадрат, то пересечение — это множество квадратов.
А В
Прямоугольники Квадраты Ромбы
Рисунок 1.5
Свойства операции пересечения множеств
1. пересечение множества с пустым множеством есть пустое множество 2. — пересечение множества с самим собой есть само множество | 3. — операция пересечения множеств коммутативна 4. — Операция пересечения множеств ассоциативна |
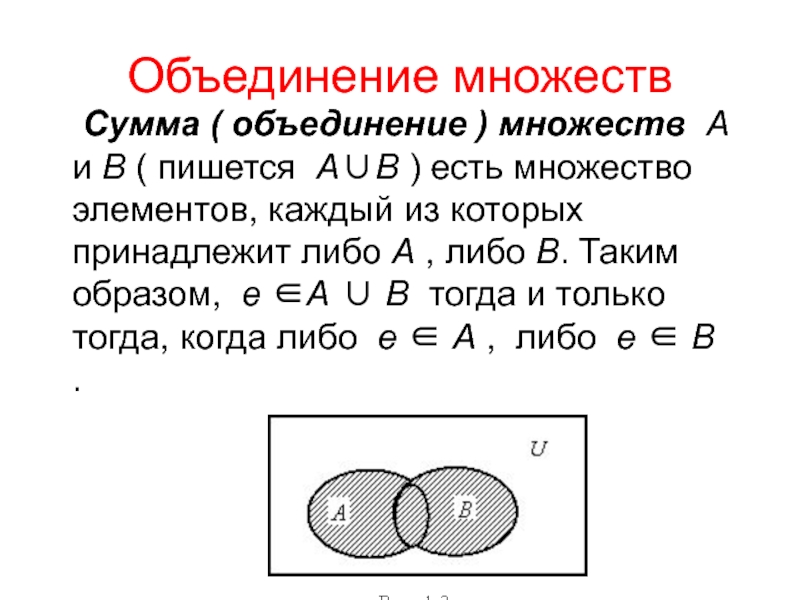
Объединение множеств
.
А В
Рисунок 1.6
Объединение множеств содержит все элементы множества и все элементы множества .
Примеры
Пусть , . При нахождении объединения множеств будем иметь в виду, что каждое объединение двух множеств содержит все элементы первого и второго множества, записанные по одному разу и в произвольном порядке:
.
Если , и — множества абитуриентов, получивших на экзаменах по математике, биологии, русскому языку «отлично», то пересечение — это абитуриенты, набравшие в сумме 15 баллов.
Свойства операция объединения множеств
1. , 2. , 3. — коммутативность (переместительный закон) 4. — ассоциативность (распределительный закон) | 5. — дистрибутивность пересечения, 6. — дистрибутивность объединения |
Нетрудно заметить, что объединение и пересечение множеств обладают свойствами, аналогичными свойствам суммы и произведения чисел.
Для любых конечных множеств и справедливо соотношение
,
где и — число элементов множеств А и В.
Вычитание множеств
Рисунок 1.7
Примеры
1. Пусть — множество равнобедренных треугольников, — множество прямоугольных треугольников. Тогда разность состоит из равнобедренных непрямоугольных треугольников.
2. Найдем разности множеств , :
; . Как видно, .
Свойства операции вычитания множеств
1. .
2. .
3. тогда и только тогда, когда .
Дополнение множества
Часто множества , … являются подмножествами некоторого более широкого множества , принимаемого за универсальное.
Примеры
1. Если — множество параллелограммов, — множество трапеций, — множество ромбов, — множество прямоугольников, — множество квадратов, то универсальным
множеством служит множество всех четырехугольников.
Если — множество параллелограммов, — множество трапеций, — множество ромбов, — множество прямоугольников, — множество квадратов, то универсальным
множеством служит множество всех четырехугольников.
2. Если — множество треугольников, — множество четырехугольников и так далее, то в качестве универсального множества можно выбрать множество всех многоугольников.
Рисунок 1.8
Пример. Пусть — множество всех прямоугольников, — множество квадратов. Тогда дополнение множества квадратов до множества всех прямоугольников есть — множество разносторонних прямоугольников.
Свойства операции дополненияДля любых множеств и , принадлежащих универсальному множеству , справедливы следующие свойства.
1. 2. ; 3. ; 4. ; 5. ; | 6. Дополнение объединения множеств равно пересечению дополнений этих множеств ; 7. Дополнение пересечения множеств равно объединению дополнений этих множеств . |
Что такое теория множеств?
Теория множеств составляет большую часть основы современной математики, и была формализована в конце 1800-х годов. Теория множеств описывает некоторые очень фундаментальные и интуитивные идеи о том, как вещи, называемые «элементами» или «членами», объединяются в группы. Несмотря на кажущуюся простоту идей, теория множеств довольно строгая. Стремясь устранить произвольность в своих теориях, математики с годами внушительно усовершенствовали теорию множеств.
В теории множеств множество — это любая четко определенная группа элементов или членов. Наборы обычно обозначаются заглавными буквами, выделенными курсивом, такими как A или B. Если два набора содержат одинаковые элементы, они могут быть показаны как эквивалентные со знаком равенства.
Наборы обычно обозначаются заглавными буквами, выделенными курсивом, такими как A или B. Если два набора содержат одинаковые элементы, они могут быть показаны как эквивалентные со знаком равенства.
Содержимое набора можно описать простым английским языком: A = все наземные млекопитающие. Содержимое также может быть указано в скобках: A = {медведи, коровы, свиньи и т. Д.} Для больших наборов можно использовать многоточие, где структура набора очевидна. Например, A = {2, 4, 6, 8 … 1000}. Один тип набора имеет нулевые члены, набор, известный как пустой набор . Он символизируется нулем с диагональной линией, восходящей слева направо. Хотя это кажется на первый взгляд тривиальным, математически оно оказывается весьма важным.
Некоторые наборы содержат другие наборы, поэтому они помечены как надмножества . Содержащиеся множества являются подмножествами . В теории множеств это отношение упоминается как «включение» или «сдерживание», символизируемое обозначением, которое выглядит как буква U, повернутая на 90 градусов вправо. Графически это можно представить в виде круга, содержащегося в другом, более крупном круге.
Графически это можно представить в виде круга, содержащегося в другом, более крупном круге.
Некоторые общие множества в теории множеств включают N, множество всех натуральных чисел; Z — множество всех целых чисел; Q — множество всех рациональных чисел; R — множество всех действительных чисел; и C, множество всех комплексных чисел.
Когда два набора перекрываются, но ни один из них не полностью встроен в другой, все это называется объединением наборов . Это представлено символом, похожим на букву U, но немного шире. В обозначениях набора A U B означает «набор элементов, которые являются членами либо A, либо B ». Переверните этот символ вверх дном, и вы получите пересечение A и B , которое относится ко всем элементам, которые являются членами обоих наборов. В теории множеств множества также можно «вычитать» друг из друга, что приводит к дополнениям. Например, B — A эквивалентно набору элементов, которые являются членами B, но не A.
Исходя из вышеизложенного, большая часть математики получена. Почти все математические системы содержат свойства, которые могут быть описаны в терминах теории множеств.
ДРУГИЕ ЯЗЫКИ
Теория множеств в математике и континуум проблема
Если у вас два множества, в каждом из которых бесконечное число элементов, то как ответить на вопрос, какое из множеств «больше»? Здесь приходит на помощь идея соответствия. Когда тысяча зрителей входит в кинотеатр, то каждый легко находит место, соответствующее купленному им билету, так как места в кинотеатре занумерованы. Задачу выяснения соответствия решает и контролер в электропоезде. Если вы подадите ему два десятка билетов и скажете, что эти билеты «на всех», он, пожалуй, не справится со своей работой. Но стоит каждому взять в руки свой билет, как безбилетник тут же обнаружится. Хотя математики имеют дело с числами, а не с железнодорожными «зайцами», эта идея сослужила им большую службу. Два множества, говорят математики, могут различаться количеством входящих в них элементов, то есть мощностью. Множество, состоящее из тысячи кресел, и множество, состоящее из тысячи зрителей, имеют одинаковую мощность.
Два множества, говорят математики, могут различаться количеством входящих в них элементов, то есть мощностью. Множество, состоящее из тысячи кресел, и множество, состоящее из тысячи зрителей, имеют одинаковую мощность.
Представьте себе теперь зрительный зал, в котором бесконечное число мест. Все эти места занумерованы подряд, и у каждого зрителя в руках билет, на котором указан номер его места. На четных местах сидят женщины, а на нечетных — мужчины. В перерыве мужчины вышли в фойе, а женщины решили поговорить и сели потеснее. Та женщина, которая сидела на месте с номером 2, пересела на место с номером 1, женщина с четвертого места перебралась на второе, с шестого — на третье, с сотого — на пятидесятое, с тысячного — на пятисотое и т. д. Когда мужчины вернулись в зрительный зал, то, к своему крайнему удивлению, обнаружили, что в зале нет ни одного свободного места.
Вы скажете — парадокс: зрителей стало в два раза меньше и в то же время осталось столько же. Но что значит для бесконечного множества «в два раза меньше»? Уменьшим его в сто, в миллион раз, оно все же останется бесконечным.
Если вы привыкли работать с числовой осью, вы знаете, что целые числа можно нанести на нее, оставив между ними одинаковые промежутки. Числовая ось бесконечна, и все целые положительные числа на ней уместятся. Однако промежуток между каждыми двумя соседними числами можно разделить пополам, и мы получим новые точки. Затем каждый новый промежуток можно делить еще и еще пополам, Этот процесс будет длиться без конца. Можно делить не пополам, а на три, на пять, на семь, одиннадцать частей, и каждый раз будем получать точки, которых не было раньше. Казалось бы, после такой процедуры вся числовая ось будет сплошь испещрена. Но даже если мы нанесем на нее все рациональные числа (то есть все числа, которые выражаются дробями), мы получим множество такой же мощности, как множество натуральных чисел 1, 2, 3, 4…
Иными словами, рациональных чисел столько же, сколько и натуральных. Чтобы убедиться в этом, достаточно разместить все рациональные числа по своим местам. Каждое рациональное число можно записать в виде отношения двух целых чисел: p/q. В первое кресло мы поместим число, у которого p + q = 2. Такое число одно, а именно единица: 1 — 1/1. Чисел, у которых р + q = будет два: 1/2 и 2=2/1. Первое из них мы поместим в кресло с номером 2, второе — в кресло с номером 3, следующие места займут числа, для которых рq = р + q = 5 и так далее.
В первое кресло мы поместим число, у которого p + q = 2. Такое число одно, а именно единица: 1 — 1/1. Чисел, у которых р + q = будет два: 1/2 и 2=2/1. Первое из них мы поместим в кресло с номером 2, второе — в кресло с номером 3, следующие места займут числа, для которых рq = р + q = 5 и так далее.
При этом из двух чисел с одинаковой суммой числителя и знаменателя мы сначала обеспечим местом то, у которого меньший числитель. В результате все положительные рациональные числа можно будет разместить в зале, где имеется мест не больше, чем натуральных чисел. Больше того, многие места окажутся свободными. Например, среди чисел, для которых р + q = 4, только два числа 1/3 и 3 будут новыми; число же 2/2= 1 уже получило свое место раньше.
Мы доказали сейчас важную теорему о том, что множество рациональных чисел, как говорят математики, «счетно», то есть имеет такую же мощность, как множество натуральных чисел. На первый взгляд может показаться, что любое бесконечное множество счетно. Однако это не так, что было установлено математиком Кантором. Оказалось, что множество всех вещественных чисел несчетно; другими словами, все вещественные числа нельзя занумеровать. Математики вслед за Кантором говорят, что множество всех вещественных чисел имеет мощность континуума. С помощью идеи соответствия нетрудно доказать, что ту же мощность континуума имеет и множество точек на отрезке и множество точек на плоскости. Кантор развил свою теорию дальше. Он построил множества, имеющие большую мощность, чем континуальные множества.
Однако это не так, что было установлено математиком Кантором. Оказалось, что множество всех вещественных чисел несчетно; другими словами, все вещественные числа нельзя занумеровать. Математики вслед за Кантором говорят, что множество всех вещественных чисел имеет мощность континуума. С помощью идеи соответствия нетрудно доказать, что ту же мощность континуума имеет и множество точек на отрезке и множество точек на плоскости. Кантор развил свою теорию дальше. Он построил множества, имеющие большую мощность, чем континуальные множества.
Однако вопрос о том, существуют ли множества, мощность которых заключена строго между мощностью множества натуральных чисел и мощностью множества всех точек отрезку оставался открытым.
Много десятилетий математики безуспешно пытались доказать гипотезу, что множества континуальной мощности представляют собой ступеньку, непосредственно следующую за счетными множествами. Этот вопрос так волновал математиков, что континуум-гипотеза была названа Д. Гильбертом первой среди поставленных им в 1903 году фундаментальных проблем математики.
Гильбертом первой среди поставленных им в 1903 году фундаментальных проблем математики.
В тридцатых годах известный математик Гёдель подверг континуум-гипотезу испытанию с помощью новейших средств математической логики. Он обнаружил, что эта гипотеза не может быть выведена на основе аксиом арифметики и теории множеств. Надежды математиков найти множества промежуточной мощности возродились. Однако многочисленные конструкции; предлагавшиеся на протяжении последних тридцати лет, неизменно оказывались ошибочными.
И вот проблемой занялся американский математик Поль Коэн. Изучая работы Геделя, Коэн понял, что только математическая логика может дать ответ на проблему континуума. Если континуум-гипотеза не может быть доказана на основе аксиом арифметики и теории множеств, то, может быть, ее удастся опровергнуть? Трудно математическое счастье! Сотни, иногда тысячи часов напряженных размышлений проходят, прежде чем ученый приходит (если приходит!) к намеченной цели. Коэну, как он сам говорит, «повезло». Меньше года работы над континуум-проблемой, и он обнаружил поразительнейший по своему характеру факт: континуум-гипотеза не может быть ни доказана, ни опровергнута.
Меньше года работы над континуум-проблемой, и он обнаружил поразительнейший по своему характеру факт: континуум-гипотеза не может быть ни доказана, ни опровергнута.
Она является самостоятельной аксиомой, не зависящей от остальных. Иными словами, можно строить теорию множеств, в которой континуум-гипотеза имеет место, а можно обойтись без нее, приняв противоположное предложение, — только это уже будет «другая» теория множеств.
По своему характеру результат Коэна можно сравнить с открытием математической теории игр (в основе которой лежит, например современная торговля на фондовом и валютном рынке, больше об этом можно узнать на сайте https://www.forexindikator.net/maximarkets-loxotron-i-moshenniki) и геометрии Лобачевского. Помните, там тоже устанавливалась независимость аксиомы параллельности (или V постулата Евклида) от остальных аксиом геометрии. Если из полного списка аксиом геометрии, указанного Д. Гильбертом, выбросить на время аксиому параллельности, то мы получим «более бедный» список аксиом, из которых, однако, можно вывести ряд теорем. Это будут, например, те теоремы, которые доказываются в школьном курсе геометрии до аксиомы параллельности. Свыше 2000 лет математики пытались вывести аксиому параллельности (или эквивалентный ей V постулат Евклида) из остальных аксиом, то есть доказать ее как теорему. Ведь именно так обстояло дело с континуум-гипотезой, которую безуспешно пытались вывести из аксиом арифметики и теории множеств?!
Это будут, например, те теоремы, которые доказываются в школьном курсе геометрии до аксиомы параллельности. Свыше 2000 лет математики пытались вывести аксиому параллельности (или эквивалентный ей V постулат Евклида) из остальных аксиом, то есть доказать ее как теорему. Ведь именно так обстояло дело с континуум-гипотезой, которую безуспешно пытались вывести из аксиом арифметики и теории множеств?!
После открытия Лобачевского и последовавших за ним работ Бельтрами, Кэли, Клейна, Гильберта стало ясно, что евклидову аксиому параллельности нельзя ни доказать, ни опровергнуть на основании остальных аксиом геометрии. Добавив аксиому параллельности к остальным аксиомам, мы получаем стройную, непротиворечивую теорию — евклидову геометрию, с которой знаком каждый старшеклассник. Но, добавив вместо евклидовой аксиомы параллельности противоположное предложение (через точку, лежащую вне прямой, проходят в плоскости не менее двух прямых, не пересекающихся с данной), мы получаем не менее стройную и также непротиворечивую теорию. Только это будет уже другая геометрия — геометрия Лобачевского.
Только это будет уже другая геометрия — геометрия Лобачевского.
В одной геометрии наряду с остальными аксиомами выполняется и аксиома параллельности, в другой геометрии по-прежнему справедливы все остальные аксиомы, но евклидова аксиома параллельности места не имеет. Это и означает, что аксиому параллельности невозможно ни доказать, ни опровергнуть, исходя из остальных аксиом геометрии. И, как установил Коэн, в таком же положении находится континуум-гипотеза по отношению к остальным аксиомам арифметики и теории множеств.
В науке часто бывает так: долгое время какая-то проблема остается незыблемой, не поддаваясь настойчивым атакам ученых. И вдруг одновременно ее решение находят совсем не связанные друг с другом люди, причем приходят к нему разными путями. Так произошло и с континуум-гипотезой.
Автор: В. Болтянский.
Теория множеств
Стар
План реферата.
Оглавление
1 часть Элементы и множества
Понятия
множества и элемента  Но как бы то ни было, выделение объектов
и из совокупностей – единственный (или
даже единственно возможный) способ организации
нашего мышления, поэтому неудивительно,
что он лежит в основе главного инструмента
описания точного знания – математики.
Но как бы то ни было, выделение объектов
и из совокупностей – единственный (или
даже единственно возможный) способ организации
нашего мышления, поэтому неудивительно,
что он лежит в основе главного инструмента
описания точного знания – математики.
Можно
сказать, что множество- это любая определенная совокупность
объектов. Объекты, из которых составлено
множество, называются его элементами. Элементы
множества различны и отличны друг от
друга. Примерами множеств могут быть:
множество людей, животных, растений на
нашей планете, а также множество N натуральных
чисел: 1,2,3,4…, множество Р простых чисел:2,3,5,7,11…,
множество Z целых чисел:…, -2,-1,0,1,2,…,
множество R вещественных чисел и т.д. Множество,
не содержащее элементов, называется пустым.
Обозначение Пустое множество является подмножеством
любого множества. Мощность пустого множества
равна нулю. Понятие пустого множества
(подобно понятию «нуль») возникает из
потребности, чтобы результат всякой операции
над множествами был также множеством.
Обычно в конкретных
Если объект х является элементом множества M, то говорят, что х принадлежит М. Обозначение : В противном случае говорят, что х не принадлежит М. Обозначение: Элементы множества сами могут являться множествами. Например, множество групп студентов состоит из элементов (групп), которые, в свою очередь, состоят из студентов.
Рисунок 1 Множества.
Рассмотрим все на примере:
Пусть даны два множества А и В, тогда
Следующее понятие
— подмножество в теории  Если С является подмножеством
В, то В называется надмножеством.
Если С является подмножеством
В, то В называется надмножеством.
2 часть Количество элементов в множестве.
Мощность множества – это обобщение понятия количества ( числа элементов множества ), которое имеет смысл для всех множеств, включая бесконечные.
Существует большие, есть меньшие бесконечные множества, среди них счётное множество является самым маленьким.
В теории множеств
счётное множество есть
Счётное множество
является «наименьшим»
Свойства счетного множества:
- Любое подмножество счётного множества конечно или счётно;
- Объединение конечного или счётного числа счётных множеств счётно;
- Прямое произведение конечного числа счётных множеств счётно;
- Множество всех конечных подмножеств счётного множества счётно;
- Множество всех подмножеств счётного множества счётно;
Несчётное множество
– такое бесконечное множество,
которое не является счётным. Таким
образом, любое множество является
либо конечным, либо счётным, либо несчётным. Множество
рациональных чисел и множество алгебраических
чисел счётны, однако множество вещественных
чисел континуально и, следовательно,
несчётно. Два множества называются равномощными,
если между ними существует биекция. Существование
биекции между множествами есть отношение
эквивалентности, а мощность множества
– это соответствующий ему класс эквивалентности.
Таким
образом, любое множество является
либо конечным, либо счётным, либо несчётным. Множество
рациональных чисел и множество алгебраических
чисел счётны, однако множество вещественных
чисел континуально и, следовательно,
несчётно. Два множества называются равномощными,
если между ними существует биекция. Существование
биекции между множествами есть отношение
эквивалентности, а мощность множества
– это соответствующий ему класс эквивалентности.
3 часть – операции над множествами.
В результате операций из исходных множеств получаются новые.
1 свойство – Сравнение множеств.множество элемент аксиоматический принность
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент B:
.
Если и , то A называется собственным подмножеством В. Заметим, что . По определению .
Два множества называются равными, если они являются подмножествами друг друга:
Теорема о сравнении
множеств. Для любых множеств A и B существует одна
и только одна из следующих возможностей: |A| = |B|, |A| < |B|, |A| > |B|.
Для любых множеств A и B существует одна
и только одна из следующих возможностей: |A| = |B|, |A| < |B|, |A| > |B|.
1 операция – объединение.
2 операция – пересечение.
3 операция – разность.
4 операция – симметрическая разность
5 операция – дополнение.
Операция дополнения
подразумевает некоторый
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Объединением двух множеств A È B (рис. 2.2.1) – называется третье множество, каждый элемент которого принадлежит хотя бы одному из множеств A и B
Пересечением множеств А∩В (рис 2.2.2), является множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам.
Разностью множеств A \ B = A – B – называется такое множество,
каждый элемент которого принадлежит
множеству A, но не принадлежит множеству
B.
Симметрическая разность A D B
Дополнение к множеству A называется множество всех элементов, не входящих в множество A
4 часть свойства операций над множествами.
Пусть задан универсум U. Тогда
Пусть задан универсум U. Тогда для всех A,B,C Ì U выполняются следующие свойства (табл. 2.3.1):
Свойства операций над множествами
Для объединения ( È ) | Для пересечения ( Ç ) |
Идемпотентность | |
A È A = A | A Ç A =A |
Коммутативность | |
A È B = B È A | A Ç B = B Ç A |
Ассоциативность | |
A È (B È C) = (A È B) È C | A Ç (B Ç C) = (A Ç B) Ç C |
Дистрибутивность | |
A È (B Ç C) = (A È B) Ç (A È C) | A Ç (B È C) = (A Ç B) È (A Ç C) |
Поглощение | |
(A Ç B) È A = A | (A È B) Ç A = A |
Свойства нуля | |
A È Æ = A | A Ç Æ = Æ |
Свойства единицы | |
A È U = U | A Ç U = U |
Инволютивность | |
= A | |
Законы де Моргана | |
Свойства дополнения | |
Выражение для разности | |
Выражение для симметрической разности | |
В справедливости перечисленных
свойств можно убедиться  Например, нарисовать диаграммы
Эйлера для левой и правой частей
равенства и убедиться, что они совпадают,
или же провести формальное рассуждение
для каждого равенства.
Например, нарисовать диаграммы
Эйлера для левой и правой частей
равенства и убедиться, что они совпадают,
или же провести формальное рассуждение
для каждого равенства.
Рассмотрим для примера первое равенство: A È A = А. Возьмем произвольный элемент х, принадлежащий левой части равенства, х Î A È A. По определению операции объединения È имеем хÎ A È хÎ A. В любом случае хÎ A. Взяв произвольный элемент из множества в левой части равенства, обнаружили, что он принадлежит множеству в правой части. Отсюда по определению включения множеств получаем, что A È A Ì А. Пусть теперь хÎ A. Тогда, очевидно, верно хÎ A È хÎ A. Отсюда по определению операции объединения имеем х Î A È A. Таким образом, А Ì A È A. Следовательно, по определению равенства множеств, A È A = А. Аналогичные рассуждения нетрудно провести и для остальных равенств.
4 часть Представление множеств в ЭВМ
Термин «представление»
(еще употребляют термин «реализация»)
применительно к  Задать представление
какого-либо объекта (в данном случае
множества) — значит описать в
терминах используемой системы программирования структуру
данных, используемую для хранения информации
о представляемом объекте, и алгоритмы
над выбранными структурами данных, которые
реализуют присущие данному объекту операции.
В данной работе предполагается, что в
используемой системе программирования
доступны такие общеупотребительные структуры
данных, как массивы, структуры (или записи)
и указатели. Таким образом, применительно
к множествам определение представления
подразумевает описание способа хранения
информации о принадлежности элементов
множеству и описание алгоритмов для вычисления
объединения, пересечения и других введенных
операций.
Задать представление
какого-либо объекта (в данном случае
множества) — значит описать в
терминах используемой системы программирования структуру
данных, используемую для хранения информации
о представляемом объекте, и алгоритмы
над выбранными структурами данных, которые
реализуют присущие данному объекту операции.
В данной работе предполагается, что в
используемой системе программирования
доступны такие общеупотребительные структуры
данных, как массивы, структуры (или записи)
и указатели. Таким образом, применительно
к множествам определение представления
подразумевает описание способа хранения
информации о принадлежности элементов
множеству и описание алгоритмов для вычисления
объединения, пересечения и других введенных
операций.
Следует подчеркнуть, что,
как правило, один и тот же объект
может быть представлен многими
разными способами, причем нельзя указать
способ, который является наилучшим для
всех возможных случаев. В одних случаях
выгодно использовать одно представление,
а в других — другое. Выбор представления
зависит от целого ряда факторов: особенностей
представляемого объекта, состава и относительной
частоты использования операций в конкретной
задаче и т. д. Умение выбрать наиболее
подходящее для данного случая представление
является основой искусства практического
программирования. Хороший программист
отличается тем, что он знает много разных
способов представления и умело выбирает
наиболее подходящий.
Выбор представления
зависит от целого ряда факторов: особенностей
представляемого объекта, состава и относительной
частоты использования операций в конкретной
задаче и т. д. Умение выбрать наиболее
подходящее для данного случая представление
является основой искусства практического
программирования. Хороший программист
отличается тем, что он знает много разных
способов представления и умело выбирает
наиболее подходящий.
Заключение.
Реферат выполнялся по теме: «Теория множеств». Здесь рассмотрены вопросы:
- Множества: элементы и множества, способы задания множеств, количество элементов в множестве;
- Операции над множествами: сравнение множеств, основные операции над множествами, свойства операций над множествами;
- Представление множеств в ЭВМ:
На основании найденной информа
После проделанной работы можно сделать следующий вывод:
Понятия «множества» и «элементы множеств» составляет основной словарь математической логики. Именно эти понятия закладывают основу, которая необходима для дальнейших построений.
Список использованной литературы
- Дискретная математика для программистов / Ф.А.Новиков. – СПб.: Питер, 2002. – 304 с.
- Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. – М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002. – 280 с. – (Серия «Высшее образование»)
Теория множеств > Базовая теория множеств (Стэнфордская философская энциклопедия)
Теория базовых наборов
Наборы — это четко определенные коллекции, полностью
характеризуется своими элементами. Таким образом, два множества равны тогда и только тогда, когда
если они имеют точно такие же элементы. Основное отношение в множестве
Теория есть теория элементальности или членства. Мы пишем \(a\in A\) в
указать, что объект \(a\) является элементом , или
элемент множества \(A\). Мы также говорим, что \(a\) принадлежит
до \(А\).Таким образом, множество \(А\) равно множеству \(В\) тогда и только тогда, когда для
каждое \(а\), \(а\в А\) тогда и только тогда, когда \(а\в В\). В частности, есть
только один набор без каких-либо элементов. Это множество называется, естественно,
пустой набор и представлен символом
\({\varничего}\).
Мы пишем \(a\in A\) в
указать, что объект \(a\) является элементом , или
элемент множества \(A\). Мы также говорим, что \(a\) принадлежит
до \(А\).Таким образом, множество \(А\) равно множеству \(В\) тогда и только тогда, когда для
каждое \(а\), \(а\в А\) тогда и только тогда, когда \(а\в В\). В частности, есть
только один набор без каких-либо элементов. Это множество называется, естественно,
пустой набор и представлен символом
\({\varничего}\).
Мы говорим, что \(A\) есть подмножество множества \(B\), записанное как \(A\subseteq B\), если каждый элемент \(A\) является элементом \(B\). Таким образом, \(A=B\), если и только если \(A\subseteq B\) и \(B\subseteq A\). Заметь \({\varnothing}\subseteq A\), для каждого набора \(A\).
Имея наборы \(A\) и \(B\), можно выполнить некоторые основные операции с из них получаются следующие наборы:
Множество \(A\cup B\), называемое объединением \(A\) и \(B\), чьи элементами являются элементы \(A\) и элементы \(B\).

Множество \(A\cap B\), называемое пересечением точек \(A\) и \(B\), элементами которого являются элементы, общие для \(A\) и \(B\).
Множество \(A-B\), называемое разностью между \(A\) и \(B\), чье элементами являются те элементы \(A\), которые не являются членами \(В\).
Проверка того, что эти операции удовлетворяют следующим свойства:
Имея объект \(a\), мы можем сформировать множество, в котором \(a\) является единственным элемент. Это множество обозначается через \(\{ a \}\). В более общем плане, учитывая \(a,b,c,\ldots\), мы можем сформировать множество, имеющее \(a,b,c,\ldots\) в качестве элементы, которые мы обозначаем через \(\{ a,b,c, \ldots\}\). Конечно можем на самом деле запишите все элементы множества, когда их не слишком много. многие из них. В случае бесконечных множеств это явно не так. возможно.
Если \(a=b\), то \(\{ a,b\}=\{ a\}\). Кроме того, для любых \(a\) и \(b\)
пара \(\{ a,b\}\) совпадает с парой \(\{ b,a\}\). Итак, если мы хотим
принять во внимание порядок, в котором два элемента пары
Учитывая, нам нужно найти другой способ представления пары. Таким образом, мы
определить упорядоченную пару \((a,b)\) как набор \(\{ \{ a\},\{
а, б\}\}\). Легко проверить, что две упорядоченные пары \((a,b)\) и
\((c,d)\) равны тогда и только тогда, когда \(a=c\) и \(b=d\). Заказ сейчас
важно, ибо если \(a\ne b\), то \((a,b)\ne (b,a)\).
Итак, если мы хотим
принять во внимание порядок, в котором два элемента пары
Учитывая, нам нужно найти другой способ представления пары. Таким образом, мы
определить упорядоченную пару \((a,b)\) как набор \(\{ \{ a\},\{
а, б\}\}\). Легко проверить, что две упорядоченные пары \((a,b)\) и
\((c,d)\) равны тогда и только тогда, когда \(a=c\) и \(b=d\). Заказ сейчас
важно, ибо если \(a\ne b\), то \((a,b)\ne (b,a)\).
Декартово произведение \(A\times B\) двух множеств, \(A\) и \(B\), определяется как множество всех упорядоченных пар \((a,b)\) таких, что \(а\в А\) и \(б\в В\).
Определив упорядоченные пары, теперь можно определить упорядоченных пар. тройки \((a,b,c)\) как \((a,(b,c))\), или вообще упорядоченных \(n\)-кортежи \((a_1,\ldots ,a_n)\) как \((a_1, (a_2,\ldots ,a_n))\).
Декартово произведение \(A_1 \times \ldots \times A_n\) множеств
\(A_1,\ldots , A_n\) — множество всех \(n\)-кортежей \((a_1,\ldots ,a_n)\)
такое, что \(a_i \in A_i\) для каждого \(1\leq i\leq n\). н\).
н\).
Бинарное отношение \(R\) на множестве \(A\) называется рефлексивным , если \((a,a)\in R\) для каждого \(a\in A\). Он называется симметричным , если \((b,a)\in R\) всякий раз, когда \((a,b)\in R\). И это называется транзитивным , если \((a,c)\in R\) всякий раз, когда \((a,b)\in R\) и \((b,c)\в R\). Отношение, которое является рефлексивным, симметричным и транзитивным называется отношением эквивалентности . Отношение тождества на любое множество \(A\) является парадигматическим примером эквивалентности связь.Другим примером является отношение на множестве всех конечных множества натуральных чисел, состоящие из всех пар \((a,b)\) таких, что \(a\) и \(b\) имеют одинаковое количество элементов.
Если \(R\) является отношением эквивалентности на множестве \(A\) и \((a,b)\in R\),
тогда мы говорим, что \(a\) и \(b\) \(R\)-эквивалентны . Для
каждый \(a\in A\), классов эквивалентности \(a\), обычно обозначаемый
через \([a]_R\), это множество всех элементов \(A\), которые являются \(R\)-эквивалентными
к \(а\). Множество всех классов \(R\)-эквивалентности называется
частное множество и обозначается \(A/R\). Можно легко
проверьте, что \(A/R\) является разделом раздела \(A\), то есть ни один элемент
из \(A/R\) пусто, любые два элемента из \(A/R\) не пересекаются, и каждый
\(a\in A\) принадлежит (ровно) одному элементу \(A/R\), а именно классу
\([а]_Р\).
Множество всех классов \(R\)-эквивалентности называется
частное множество и обозначается \(A/R\). Можно легко
проверьте, что \(A/R\) является разделом раздела \(A\), то есть ни один элемент
из \(A/R\) пусто, любые два элемента из \(A/R\) не пересекаются, и каждый
\(a\in A\) принадлежит (ровно) одному элементу \(A/R\), а именно классу
\([а]_Р\).
Если \(R\) является бинарным отношением, то вместо него обычно пишут \(aRb\) из \((a,b)\in R\).
Бинарное отношение \(R\) на множестве \(A\) называется антисимметричным если \(a=b\), когда \(aRb\) и \(bRa\).Отношение \(R\) на множестве \(A\), т.е.
рефлексивной, антисимметричной и транзитивной, называется
(рефлексивный) частичный заказ . Если удалить из \(R\) все пары
\((a,a)\), для каждого \(a\in A\), мы получаем строгих частичных
заказ. Отношение \(\subseteq\) на любом множестве множеств является примером
частичный заказ. Частичный порядок на заданном множестве \(A\) обычно
представленный символом \(\leq\), и соответствующий строгий частичный
упорядочение по \(<\). Частичный порядок \(\leq\) на множестве \(A\) с
дополнительное свойство, состоящее в том, что либо \(a\leq b\), либо \(b\leq a\) для всех
элементы \(a\) и \(b\) из \(A\), называется общим порядком , или линейный порядок .2\) также является линейным порядком на
\(В\). Если \(\leq\) — линейный порядок на множестве \(A\), то говорят, что \(a\in
A\) является \(\leq\)-наименьшим элементом \(A\), если нет \(b\in A\) различных
из \(a\) такое, что \(b\leq a\). Число \(0\) является наименьшим элементом
\(\mathbb{N}\), но \(\mathbb{Z}\) не имеет наименьшего элемента.
Частичный порядок \(\leq\) на множестве \(A\) с
дополнительное свойство, состоящее в том, что либо \(a\leq b\), либо \(b\leq a\) для всех
элементы \(a\) и \(b\) из \(A\), называется общим порядком , или линейный порядок .2\) также является линейным порядком на
\(В\). Если \(\leq\) — линейный порядок на множестве \(A\), то говорят, что \(a\in
A\) является \(\leq\)-наименьшим элементом \(A\), если нет \(b\in A\) различных
из \(a\) такое, что \(b\leq a\). Число \(0\) является наименьшим элементом
\(\mathbb{N}\), но \(\mathbb{Z}\) не имеет наименьшего элемента.
Линейный порядок \(\leq\) на множестве \(A\) является хорошим порядком , если
каждое непустое подмножество \(A\) имеет \(\leq\)-наименьший
элемент. Эквивалентно, если нет бесконечного строго убывающего
последовательность \[\ldots < a_2< a_1< a_0\] элементов \(A\).Таким образом,
обычный порядок \(\mathbb{N}\) является правильным порядком. Но обычное
порядок на \(\mathbb{Z}\) не такой, потому что в нем нет наименьшего элемента.
Функции
A (\(1\)-арная) функция на множестве \(A\) является бинарным отношением \(F\) на \(A\) такие, что для каждого \(a\in A\) существует ровно одна пара \((а,б)\в F\). Элемент \(b\) называется значением из \(F\) на \(a\) и обозначается через \(F(a)\). А множество \(A\) называется домен из \(F\).п\к Б\), для некоторого \(B\).
Функция \(F:A\to B\) является однозначной , если для всех элементов
\(a\) и \(b\) из \(A\), если \(a\ne b\), то \(F(a)\ne F(b)\). А также
равно на , если для любого \(b\in B\) существует некоторое \(a\in A\) такое
что \(F(a)=b\). Наконец, \(F\) является биективным , если оно взаимно однозначно.
и на. Таким образом, биекция \(F:A\to B\) устанавливает взаимно-однозначное
соответствие между элементами \(A\) и элементами \(B\), а \(A\)
является биективным с \(B\), если существует такой
биекция.Функция тождества на множестве \(A\), обозначаемая как
\(Id:A\to A\) и состоит из всех пар \((a,a)\), где \(a\in
A\) тривиально является биекцией.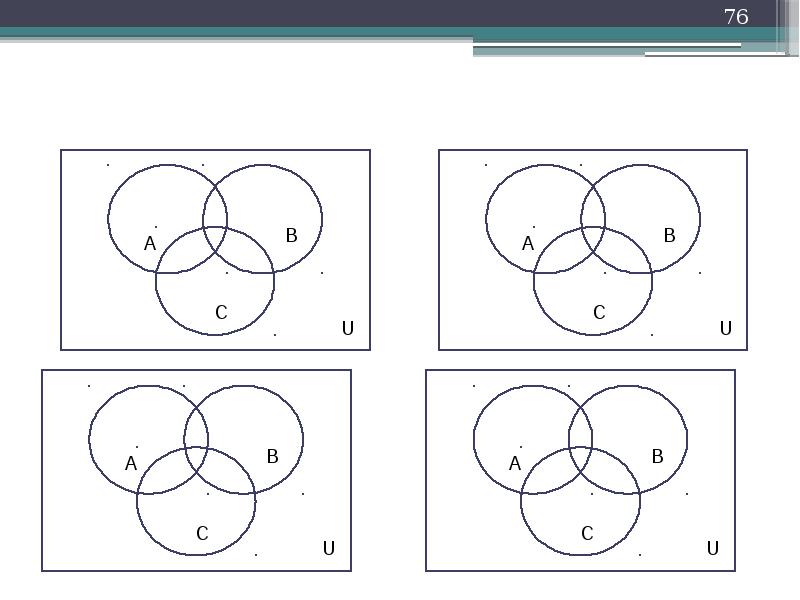
Учитывая функции \(F:A\to B\) и \(G:B\to C\), композиция \(F\) и \(G\) , записанные \(G\circ F\), есть функция \(G\circ F:A\to C\), элементами которого являются все пары \((a,G(F(a)))\), где \(a\in A\). Если \(F\) и \(G\) биекции, то и \(G\circ F\).
Наборы и формулы
Формальный язык теории множеств является языком первого порядка язык, единственным нелогическим символом которого является символ бинарного отношения \(\в\).
Дана любая формула \(\varphi(x,y_1,\ldots ,y_n)\) языка теории множеств и множеств \(A,B_1,\ldots ,B_n\), можно сформировать множество всех те элементы \(A\), которые удовлетворяют формуле \(\varphi(x,B_1,\ldots ,В_п)\). Это множество обозначается \(\{ a\in A: \varphi(a,B_1,\ldots ,В_п)\}\). Ниже приведены некоторые примеры
\({\varnothing}=\{ a\in A: a\ne a\}\)
\(А=\{а\в А: а=а\}\)
\(A-B=\{ a\in A: a\not \in B\}\).
\(A\cap B=\{ a\in A: a\in B\}\).

И если \(B\) и \(C\) являются подмножествами \(A\), то
Учитывая подмножество \(C\subseteq A\times B\), проекция \(C\) (по первой координате) есть множество
\(\{ a\in A: \существует b\in B ((a,b)\in C)\}\).
Однако это не тот случай, когда при любой формуле \(\varphi(x,y_1,\ldots,y_n)\) и множеств \(B_1,\ldots,B_n\), можно сформировать множество всех тех множеств, которые удовлетворяют формуле \(\varphi(x,B_1,\ldots,B_n)\).Пусть \(\varphi(x)\) будет формулой \(х\не \в х\). Если бы \(A\) было множеством всех множеств, удовлетворяющих формулы, то \(А\в А\) тогда и только тогда, когда \(А\не \в А\). Противоречие! Это противоречие известно как парадокс Рассела , после Бертран Рассел, открывший его в 1901 г. (см. парадокс Рассела).
Порядковый номер
Первое порядковое число — \({\varnothing}\). Учитывая порядковый номер
\(\alpha\), следующий больший порядковый номер, называемый
(немедленно) преемник \(\alpha\), это набор \(\alpha \cup \{
\альфа\}\). Таким образом, преемником \(\alpha\) является просто набор \(\alpha\)
вместе с еще одним элементом, а именно \(\alpha\)
сам. конечных порядковых номеров получены путем
начиная с \({\varnothing}\) и многократно беря преемника.
Таким образом, преемником \(\alpha\) является просто набор \(\alpha\)
вместе с еще одним элементом, а именно \(\alpha\)
сам. конечных порядковых номеров получены путем
начиная с \({\varnothing}\) и многократно беря преемника.
В теории множеств натуральных чисел определяются как конечные ординалы. Таким образом,
\(0= {\varnothing}\)
\(1= {\varnothing}\cup \{ {\varnothing}\}=\{ {\varnothing}\}\)
\(2= \{ {\varnothing}\} \cup \{\{{\varnothing}\}\}=\{ {\varnothing}, \{ {\varnothing}\}\}\)
\(3= \{ {\varnothing}, \{ {\varnothing}\}\}\cup \{ \{ {\varnothing}, \{ {\varnothing}\}\}\} =\{ {\varnothing}, \{ {\varnothing}\}, \{ {\varnothing}, \{ {\varnothing}\}\}\}\)
\(\вдоц\)
Обратите внимание, что \(1=\{ 0\}\), \(2=\{ 0,1\}\), \(3=\{ 0,1,2\}\) и в
вообще имеем \(n=\{ 0,1,2,\ldots ,n-1\}\).Итак, каждое натуральное число
\(n\) — это просто набор своих предшественников.
Множество \(A\) является конечным , если существует однозначное соответствие между некоторым натуральным числом \(n\) и элементами \(A\), т. е. биекция \(F:n\to A\), и в этом случае мы говорим, что \(A\) имеет \(n\) элементов. Множество бесконечно , если оно не конечно.
Множество всех конечных ординалов обозначается греческой буквой омега.
(\(\омега\)). Таким образом, \(\omega\) — это просто набор \(\mathbb{N}\) натуральных
числа.\(\omega\) также является порядковым номером, первым бесконечным
порядковый. Обратите внимание, что \(\omega\) не является преемником какого-либо порядкового номера, и
поэтому он называется предельным порядковым номером . Когда у нас есть \(\omega\), мы можем
продолжайте генерировать больше порядковых номеров, взяв его преемника \(\omega \cup
\{ \omega \}\), затем его преемник \((\omega \cup \{\omega\}) \cup
\{\omega \cup \{\omega \}\}\) и так далее. Все порядковые числительные больше
чем \(0\) производятся таким образом, а именно, либо путем взятия
преемник последнего произведенного порядкового номера, или, если такого последнего нет
порядковый номер, взяв набор всех произведенных до сих пор ординалов, как в
случай \(\omega\), который дает новый предельный порядковый номер. Обратите внимание, однако,
что нельзя взять множество всех порядковых номеров, ибо тогда это
множество было бы новым предельным ординалом, что невозможно, так как мы
уже все были.
Обратите внимание, однако,
что нельзя взять множество всех порядковых номеров, ибо тогда это
множество было бы новым предельным ординалом, что невозможно, так как мы
уже все были.
Как и в случае с конечными ординалами, каждый бесконечный ординал — это просто набор его предшественники. Одним из следствий этого является то, что отношение \(\in\) является строгим порядком на любом множестве ординалов. Таким образом, для любых ординалов \(\alpha\) и \(\beta\) мы определяем \(\alpha <\beta\) тогда и только тогда, когда \(\альфа\в\бета\). Тогда соответствующий рефлексивный порядок равен определяется как \(\alpha \leq \beta\) тогда и только тогда, когда \(\alpha <\beta\) или \(\альфа=\бета\).Заметим теперь, что \(\alpha \subseteq \beta\), если и только если \(\alpha \leq \beta\).
Счетные и несчетные множества
Если \(A\) конечное множество, то существует биекция \(F:n\to A\) между
натуральные числа \(n\) и \(A\). Любая такая биекция дает
a , считая элементов \(A\), а именно \(F(0)\) есть
первый элемент \(A\), \(F(1)\) — второй и так далее. Каждое бесконечное подмножество счетного множества также счетно: для
предположим, что \(F:\omega \to A\) является биекцией, а \(B\subseteq A\) является
бесконечный. Тогда множество \(\{ n\in \omega: F(n)\in B\}\) является бесконечным
подмножество \(\omega\), следовательно, счетно, и поэтому существует биекция
\(G:\omega \to \{n\in \omega : F(n)\in B\}\).Тогда состав
функция \(F\circ G:\omega \to B\) является биекцией. Объединение счетного множества и конечного множества также
исчисляемый. Более того, объединение двух счетных множеств также счетно: поскольку
мы уже показали, что объединение счетного множества и конечного
множество также счетно, достаточно убедиться, что объединение двух
непересекающиеся счетные множества также счетны.Итак, предположим, что \(A\) и \(B\) равны
счетные множества и \(F:\omega \to A\) и \(G:\omega \to B\)
биекций, то функция \(H:\omega \to A\cup B\), состоящая из всех
пар \((2n,F(n))\), плюс все пары \((2n+1, G(n))\) — биекция. Таким образом, множество \(\mathbb{Z}\), являющееся объединением двух счетных множеств,
а именно \[\mathbb{N}\cup \{-1,-2,-3,-4,\ldots \}\] также
исчисляемый. Декартово произведение двух бесконечных счетных множеств также
исчисляемый. Так как любое рациональное число задается парой целых чисел, т.е.
частное \(\frac{m}{n}\), где \(m,n\in \mathbb{Z}\) и \(n\ne 0\),
множество \(\mathbb{Q}\) рациональных чисел также счетно. Однако Георг Кантор обнаружил, что множество \(\mathbb{R}\) вещественных
числа не исчисляются. Предположим, что, стремясь к противоречию,
что \(F:\omega \to \mathbb{R}\) является биекцией. Пусть \(a_0=F(0)\). выберите
наименьшее \(k\) такое, что \(a_0 Существование несчетных множеств следует из гораздо более общего
факт, также обнаруженный Кантором.А именно, для любого множества \(A\) множество
все его подмножества, называемые степенным набором множества \(A\), и обозначаемые
\(\mathcal{P}(A)\), не является биективным с \(A\): предположим, что \(F:A\to
\mathcal{P}(A)\) является биекцией. Тогда подмножество \(\{ a\in A: a\not \in
F(a)\}\) множества \(A\) есть значение \(F(a)\) некоторого \(a\in A\). Но тогда \(a\in
F(a)\) тогда и только тогда, когда \(a\not \in F(a)\). Следовательно, если \(А\) — любое бесконечное
множество, то \(\mathcal{P}(A)\) несчетно. Существуют также неисчисляемые ординалы.множество всех конечных и
исчисляемые ординалы также являются порядковыми номерами, называемыми \(\omega_1\), и
первый неисчисляемый порядковый номер. Точно так же множество всех ординалов, которые
биективный с некоторым порядковым номером, меньшим или равным \(\omega_1\), также
порядковое число, называемое \(\omega_2\), и не биецируется с \(\omega_1\),
и так далее. Мощность , или размер, конечного множества \(A\) есть
единственное натуральное число \(n\), такое что существует биекция \(F:n\to
А\). В случае бесконечных множеств их мощность определяется не
натуральным числом, а бесконечным порядковым номером. Однако, в отличие от
конечные множества, бесконечное множество \(A\) биективно со многими различными
порядковые номера. Например, множество \(\mathbb{N}\) биективно с
\(\omega\), но и с его преемником \(\omega \cup \{\omega\}\): by
присваивая \(0\) \(\omega\) и \(n+1\) \(n\), для всех \(n\in \omega\), мы
получить биекцию между \(\omega \cup \{\omega \}\) и \(\omega\).Но
поскольку ординалы хорошо упорядочены, мы можем определить мощность
бесконечное множество как наименьший ординал, биективный с ним. В частности, мощность порядкового числа \(\alpha\) равна
наименьший порядковый номер \(\каппа\), который биецируется с ним. Заметь
\(\kappa\) не биективен ни с каким меньшим порядковым номером, иначе
будет \(\альфа\). Бесконечные кардиналы представлены буквой алеф
(\(\алеф\)) еврейского алфавита. Таким образом, наименьший бесконечный
кардинал — \(\omega =\aleph_0\), следующий — \(\omega_1=\aleph_1\),
который является первым несчетным кардиналом, затем следует
\(\omega_2=\aleph_2\) и т. д. Мощность любого множества \(A\), обозначаемого \(|A|\), является единственным
кардинальное число, биективное с \(A\).Мы уже видели, что
\(|\mathbb{R}|\) несчетно, следовательно, больше, чем \(\aleph_0\), но
неизвестно, какое это кардинальное число. Гипотеза о том, что
\(|\mathbb{R}|=\aleph_1\), сформулированная Кантором в 1878 г. Теория множеств — это раздел математики, посвященный изучению наборов объектов, их свойств и взаимосвязей между ними.В следующем списке представлены некоторые из наиболее примечательных символов теории множеств, а также их использование и значение. Для удобства чтения эти символы разделены по функциям на таблицы . Предпочитаете версию в формате PDF? Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX. В теории множеств константы часто представляют собой односимвольные символы, используемые для обозначения ключевых математических наборов . В следующей таблице представлены наиболее заметные из них, а также их соответствующее значение и примеры. Для других ключевых наборов чисел см. ключевые математические наборы в алгебре . Как и в других областях математики, в теории множеств часто используется определенный список из символов переменных для обозначения различных объектов и величин. В теории множеств разделители — это символы, используемые для обозначения разделения между независимыми математическими объектами, и часто встречаются в контексте определения множеств . В следующей таблице описаны наиболее распространенные из них, а также их соответствующее использование и значение. позволяют ссылаться на новые наборы через уже существующие наборы — существуют. В следующей таблице представлены наиболее примечательные из них, а также их соответствующий пример и значение. Следующие диаграммы, известные как диаграммы Венна , обеспечивают визуализацию пяти наборов ключей, упомянутых выше (где $A$ и $B$ представлены левым и правым кружками соответственно). В теории множеств реляционные символы часто используются для описания отношений между наборами или отношений между набором и его элементом. В следующей таблице представлены наиболее примечательные из этих символов, а также их соответствующее значение и пример. В теории множеств понятие мощности обеспечивает способ количественной оценки и сравнения размеров различных множеств.В следующей таблице описаны некоторые из наиболее заметных символов, связанных с кардинальностью, а также использование и значение каждого символа. (для освежения на греческих и еврейских символах, см. Греческие, ивритские и латинские символы . Основной список символов см. в разделе Математические символы.Списки символов, классифицированных по типу и по теме , см. на соответствующих страницах ниже. Предпочитаете версию в формате PDF? Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX. Я написал большую часть статьи в Википедии о фондах.
математики (сент.2012 — до этого,
другие авторы сосредоточились на более профессиональном и техническом
статья Математическая
вместо этого логика; Статья «Основы математики»
более вводный, исторический и философский) и улучшенный
тот, что о полноте
теорема. Этот список домашних страниц теоретиков множеств был вдохновлен теорией вычислимости, поддерживаемой Питером Чолаком при поддержке Теда Сламана.Он дополняется изящным списком Анджея Рослановского и сайтом ASL Херба Эндертона со ссылками на членов ASL. Примечание: Институциональные ссылки указывают на факультеты и/или институты. – А – – Б – – С – – Д – – ЭФ – – Г – – Н – – ИЖ – – К – – Л – – М – – НЕТ – – ПК – – Р – – Сб – – Си – – ТУВВ – – XYZ – Набор — это набор предметов, не больше и не меньше. Звучит просто, но теория множеств является одним из основных строительных блоков высшей математики, поэтому она помогает хорошо понять основы. На этой странице изложены принципы создания наборов и элементы внутри них.Это также объясняет операции с множествами. К сожалению, как и некоторые другие разделы математики, теория множеств имеет свой собственный язык, который необходимо понимать. Вот несколько полезных терминов и определений: Набор представляет собой набор объектов, имеющих нечто общее. Набором могут быть, например, простые числа, птицы, прилетевшие в ваш сад, или люди, которым вы отправляли рождественские открытки за последние пять лет. элемента набора — это его элементы, такие как простые числа, птицы или люди, как в приведенных выше примерах. Их также называют членами набора. Символ ∈ означает «является элементом». Например, вы можете написать 2 ∈ A, что будет означать, что 2 является элементом множества A. Вы также можете написать ∉ , что означает «не является элементом множества». Вы можете показать, что что-то есть в наборе, двумя простыми способами: ВНИМАНИЕ! Если вы собираетесь использовать многоточие (множественное число многоточий), убедитесь, что содержимое вашего набора недвусмысленно. Например, если бы в вашем наборе было каждое третье число от 1 до 50, было бы недостаточно написать {1…50}, потому что это также может быть каждое число от 1 до 50. Множества обычно обозначаются заглавными буквами, чтобы отличить их от переменных алгебры , которые обычно пишутся строчными буквами. могут содержать материальных или нематериальных элемента при условии, что вы определяете их четко и недвусмысленно. Мощность множества — это количество элементов, содержащихся в множестве. Наборы, содержащие одинаковые элементы, называются равными . Вы также можете сказать, что они эквивалентны или идентичны . Наборы все же могут быть идентичными, даже если один содержит один и тот же элемент дважды: равенство заключается в наличии одних и тех же составляющих, не в количествах или порядке .Так, например, все следующие множества равны: A = дни недели без выходных B = {понедельник, вторник, среда, четверг, пятница} C = {понедельник, понедельник, вторник, среда, четверг, вторник, пятница} Множество A, все элементы которого содержатся в другом, большем множестве B с большим количеством элементов, называется подмножеством множества B. Пустой набор вообще не содержит элементов.Пишется {} или Ø . Поскольку все пустые множества одинаковы, существует только одно (другими словами, все они равны). Это также подмножество любого другого множества во всем мире! Универсальный набор или U — это все. Однако он специфичен для конкретной проблемы, а не является «всем в целом мире». Это означает, что вы можете, например, определить универсальный набор как «все числа от 1 до 100» или «все числа от 1 до 10», в зависимости от вашей задачи. Точно так же, как числа можно складывать, вычитать, умножать и делить, существуют четыре основные операции над множествами: Объединение, Пересечение, Относительное дополнение и Дополнение Мы можем посмотреть на каждый из них, используя три набора: Союз похож на сложение. Помните! Если один и тот же номер появляется в обоих наборах, вам нужно включить его в общий набор только один раз. Объединение любого множества с самим собой есть оно само, A ∪ A = A. Объединение любого множества с пустым также само по себе, A ∪ ∅ = A Пересечение двух наборов — это элементы, которые у них есть общие. Символ пересечения ∩ . Использование трех вышеуказанных наборов: А ∩ В = {1, 2, 4, 7} ∩ {2, 5, 6, 8} = {2} А ∩ С = {1, 2, 4, 7} ∩ {5, 10, 15, 20} = {}. Другими словами, общих элементов нет, поэтому пересечение — это пустое множество. Если объединение похоже на сложение, то относительное дополнение немного похоже на вычитание. Вы начинаете с первого набора и убираете все элементы из второго набора. ВНИМАНИЕ! Вы НЕ получите все элементы, которые есть только в одном или другом! Обратное дополнение — это ТОЛЬКО те элементы первого набора , которые НЕ входят во второй набор. А – В = {1, 2, 4, 7} – {2, 5, 6, 8} = {1, 4, 7} Б – А = {2, 5, 6, 8} – {1, 2, 4, 7} = {5, 6, 8} В каждом случае единственное число, которое есть в обоих, это 2, так что это единственное число, которое удалено из первого набора. Дополнением к набору является все, чего в нем нет. Здесь пригодится универсальный набор, потому что дополнением является U (универсальный набор) — набор, с которым вы работаете. Символ дополнения — ‘, поэтому вы должны написать A’ или B’ для вышеприведенных наборов. Дополнение и обратное дополнение Как дополнение, так и обратное дополнение очень похожи на вычитание, НО могут показаться не очень полезными в повседневной жизни. Однако они чрезвычайно полезны для высшей математики, так что терпите их. Полезно понимать основы, чтобы потом при необходимости вернуться к ним. Чтобы понять место теории множеств в основаниях на данный момент, полезно обсудить образ, который представляет этот и вне его практики.Похоже, что теория множеств имеет совершенно разный образ для тех, кто ее практикует, и для тех, кто ее наблюдает. Наблюдателями этого предмета являются другие логики, математики и философы, а также довольно частые случайные наблюдатели, очарованные сказанными и невысказанными обещаниями предмета. Какой еще предмет обещает множество версий бесконечности, основу всей математики, а затем какие-то неразрешимые проблемы? Давайте рассмотрим эти концепции немного серьезнее, чтобы задать вопрос, который мы хотим задать в первую очередь: какова реальная роль теории множеств в основаниях математики сегодня? Мы также предлагаем читателю задуматься о том, что следует понимать под «основами математики». Для стороннего наблюдателя теория множеств представляется предметом, аксиомизированным ZFC. Неофициальные свидетельства работающих математиков свидетельствуют о том, что эта система аксиом считается более чем достаточной для того, что нужно математике. В то время как аксиома выбора или континуум-гипотеза все еще могут время от времени вызывать споры, математики в большинстве областей, кажется, с радостью принимают «достаточность» ZFC и с несколько меньшей уверенностью также ее «необходимость».Возможно, стоит упомянуть, что среди непрактиков также есть сторонники ZFC2, аксиоматизации ZFC в полной логике второго порядка. Некоторые философы, например Шапиро (1999), интересуются этой системой, поскольку она предлагает определенную категоричность. Именно Цермело (1930) доказал, что единственными моделями этой системы являются модели \(V_\kappa\) для сильно недостижимого кардинала \(\kappa\). Этот результат интересен с разных точек зрения, но не очень актуален для вопросов независимости в теории множеств, поскольку, например, ZFC2 решает континуальную проблему не больше, чем ZFC. Во всяком случае, с аксиоматизацией первого или второго порядка или даже без какой-либо аксиоматизации, теория множеств считается важной в основаниях математики, потому что многие классические понятия аксиоматизированы теорией и могут быть найдены в кумулятивная иерархия наборов.Напомним также, что Гильберт считал, что всю математику можно сформулировать в (наивной) теории множеств, которая, несомненно, забивает в основаниях место теории множеств. Расширения ZFC с помощью аксиом со строго более высокой степенью непротиворечивости Сноска 1 редко рассматриваются за пределами самого предмета, хотя мы должны упомянуть недавнюю философскую работу Вентури (2016), в которой приводится довод в пользу принятия принудительных аксиом (более подробное обсуждение см. ниже). и Джамоня 2013 для опроса).Не следует забывать работу Пенелопы Мэдди, которая посвятила большую часть своей работы объяснению методов, используемых теоретиками множеств для согласования аксиом, особенно тех, которые выходят за рамки ZFC, или работы Питера Кёлльнера. Не вдаваясь в дополнительные примеры, которые формируют внешнее представление о теории множеств, пожалуй, наиболее важным моментом, который следует здесь отметить, является то, что внешний взгляд на теорию множеств часто принимает как должное то, что теоретики множеств верят в единую вселенную теории множеств, поскольку так же, как математики верят в одну математику, и что теоретики множеств ищут правильные аксиомы для описания этой вселенной.Таким образом, с этой точки зрения тот факт, что, например, CH независим от ZFC, означает, что «правильная» аксиоматизация теории множеств расширила бы ZFC до чего-то, что разрешило бы CH. И этот посторонний не совсем неправ, сам Гёдель считал, что его теоремы о неполноте лишь показывают, что система ZFC слишком слаба, чтобы отвечать на эти вопросы, и поэтому следует искать новые аксиомы, которые, однажды добавленные к ZFC, ответили бы на них. Хотя инсайдер также принимает аксиомы ZFC, то есть их «необходимость», теоретику множеств ясно, что ZFC недостаточно. Существует универсальное убеждение в непротиворечивости больших кардинальных аксиом, и ZFC рассматривается просто как минимум того, что следует рассматривать как разумную систему. Большие кардиналы нужны не только для теории множеств, но и для некоторых, казалось бы, невинных утверждений о теории чисел.Например, Харви Фридман (2014) разработал теорию булевых отношений, которая демонстрирует необходимость больших кардиналов для получения определенных утверждений, считающихся «конкретными». Фридман и другие рассматривают это как очевидную причину для работающего математика принимать большие кардиналы. Отходя от больших кардиналов и их широкого признания, мы также утверждаем, что в теории множеств нет веры в единую вселенную аксиом. К философским воззрениям, которые можно читать или, чаще, читать между строк, в работах по теории множеств сегодня относятся следующие: «Учитывая неполноту, лучше сконцентрироваться на том, что можно сделать в ZFC, и понять, что не изучая независимость» (принято Сахароном Шелахом, некоторыми из его школы и некоторыми другими). Позиция Багариа очень характерна для современного теоретика множеств. Мы не чувствуем, что знаем достаточно, чтобы принять чью-либо сторону. Более того, некоторые из нас не верят, что когда-либо будет принята чья-то сторона. Какой бы разновидностью теории множеств мы ни занимались, у всех работающих в настоящее время теоретиков множеств есть одна общая черта.Мы принимаем, что существует много вселенных аксиом ZFC, которые все имеют разные свойства и удовлетворяют различным дополнительным утверждениям или аксиомам. Ни один из них не является окончательным. Этот явно плюралистический взгляд, безусловно, является единственно разумным на данный момент, учитывая тот факт, что математические данные не поддерживают выбор какой-либо из этих вселенных над любыми другими. Поэтому современные теоретики рабочих множеств не только не видят себя создателями уникального онтологического основания математики, но и не верят в такое уникальное основание и не претендуют на него даже для своего предмета.Меня спросили, означает ли это, что практикующие теоретики множеств больше не ищут абсолютную истину в форме одной вселенной или модели теории множеств. Я думаю, что дело в этом. Лучше всего это выражено в представлении о мультивселенной, сформулированном Хэмкинсом (2012). Если классическая позиция, которую Хэмкинс называет Вселенной, утверждает, что существует уникальный фоновый теоретико-множественный контекст или вселенная, в которой происходит вся наша математическая деятельность, то Мультиверсия представляет собой в точности плюралистическую противоположность, утверждая, что существует не одна вселенная, а множество, и только понимая их множество, мы понимаем действительную природу теории множеств.Multiverse View принимает любую вселенную, совместимую с ZFC. Теория множеств очень важна для понимания данных и баз данных. Хотя вы могли бы жить без него и по-прежнему оставаться хорошим разработчиком SQL, его понимание, безусловно, очень поможет. Итак, давайте углубимся в дело. Думаю, ты помнишь эти уроки из старшей школы. Для меня это была одна из самых скучных частей моего
образования, потому что многие вещи звучали так очевидно, и у вас просто были новые обозначения и операторы для работы с множествами —
опять довольно очевидный.Хотя большинство людей не будут использовать эти знания позже в своей жизни, это не относится к
те, кто занимается базами данных. Наборы могут содержать что угодно. Начнем с самого простого из возможных наборов, а именно с пустого набора — S =
{} . Как видите, пустой набор не содержит никаких данных. Мы ничего не знаем об этом наборе с тех пор, как
это не определено — нет типов данных или значений данных. У нас может быть набора чисел S = {1, 2, 3} или T = {1, 1, 2, 3,
1001} или U = {3, 1, 2} .Это намного интереснее, потому что у нас есть значения
определены, и мы также можем сказать, что все эти наборы содержат числовые данные. Примечание. Два набора равны, если они содержат один и тот же элемент, независимо от того, как они упорядочены. В нашем примере наборы S =
{1, 2, 3} и U = {3, 1, 2} совпадают. Наборы также могут содержать строки, например. A = {«Джек», «Джилл», «Джон»} , B = {«Загреб»,
«Белград», «Нью-Йорк», «Берлин», «Москва»} . Примечание: В теории множеств множество может содержать что угодно, и элементы множества даже не обязательно должны быть одинаковыми.
тип. Это тоже набор: C = {1, «Валет», 3.14, 14.02.2020} . Он содержит 4 отдельные сведения, а в
в этом случае они имеют разные типы данных. Нас больше интересуют наборы, содержащие структуры/записи/кортежи. Давайте посмотрим на один такой пример страна = {(1, Германия, Германия, DEU), (2, Сербия, Сербия, SRB), (3, Хорватия, Хорватия, HRV), (4, Соединенные Штаты Америки, Соединенные Штаты Америки, США), (5, Польша, Польша, POL), (6, Испания, Испания, ESP), (7, Россия, Россия, RUS)} .У нас есть список из 7 структур, содержащих данные по 7 разным странам. Этот
мы уже встречались, и эти данные на самом деле являются содержимым таблицы страны из
наша модель. Давайте вспомним модель, которую мы используем в этой серии статей. Если мы говорим с точки зрения теории множеств, вы можете рассматривать каждый стол как один набор.То же самое означает
результаты запроса. Технически результатом каждого запроса является новая таблица, и вы будете обращаться с ней так же, как с
обычная таблица – этот результат запроса также является набором; вы можете писать новые запросы, используя этот запрос в виде таблицы и т. д. В SQL Server у нас есть 3 важных оператора: UNION (ALL), INTERSECT и EXCEPT. Они возвращают результат связанных операторов из теории множеств (на картинке ниже). Самый простой способ объяснить это: Мы не будем анализировать ситуации, когда множества не имеют общих элементов (СОЕДИНЕНИЕ Б = все элементы из А и В, А
INTERSECT B = {}, A EXCEPT B = A, B EXCEPT A = B) и где множество A = множество B (A UNION B = A = B, A INTRSECT B = A = B,
A, КРОМЕ B = B, ЗА ИСКЛЮЧЕНИЕМ A = {}). До сих пор мы много говорили о теории множеств, а теперь пришло время немного попрактиковаться. Мы запишем несколько запросов
который покажет, как работают операторы UNION (ALL), INTERSECT и EXCEPT. — список всех клиентов с ровно 3 звонками выберите клиента.* от клиента от Customer , где ID IN ( SELECT CULLING.ID от клиента Внутренний присоединяйся к Customer.id = Call.customer_id Group по Customer.id , имеющих счет (*) = 3 ); — список всех клиентов из Берлина выберите клиента.* от клиента внутреннее соединение города по адресу customer.city_id = city.id где city.city_name = ‘Берлин’; Вы должны заметить несколько вещей: Теперь мы будем использовать два доступных оператора UNION. Любой из этих операторов (UNION (ALL), INTERSECT, EXCEPT) используется в
так, как вы просто помещаете его между запросами. 1 2 3 4 5 6 7 8 7 8 9 10 11 12 11 13 12 13 14 15 16 17 18 19 20 21 22 23 240004 23 25 26 25 27 26 27 28 293 30 29 30 31 32 33 34 35 36 37 38 39 — СОЮЗ — список всех клиентов с ровно 3 звонками выберите клиента.* от клиента от Customer , где ID IN ( SELECT CULLING.ID от клиента Внутренний присоединяйся к Customer.id = Call.customer_id Group по Customer.id , имеющих счет (*) = 3 ) ) Union — Список всех клиентов из Berlin Выберите клиента. * от клиента Внутреннее присоединиться к Customer.city_id = City.id , где город.city_name = ‘Берлин’; — Union All — Список всех клиентов с ровно 3 звонка Выбрать клиента. * от клиента Откуда ID в ( Выбор CULLING.ID от клиента Внутреннее Присоединение По Customer.id = call.customer_id Group по Customer.id , имеющийся счет (*) = 3 ) Union All — Список всех клиентов из Berlin Выберите Клиент.* от клиента внутреннее соединение города по адресу customer.city_id = city.id , где city.city_name = ‘Берлин’; Для этих двух возвращаемых наборов результатов вы должны заметить следующее: INTERSECT должен возвращать элементы/строки, которые присутствуют в обоих наборах. 1 2 3 4 5 6 7 8 7 8 9 10 11 12 11 13 12 13 14 15 16 17 18 19 — INTERSECT — список всех клиентов с ровно 3 звонками выберите клиента.* от клиента где идентификатор в ( выберите клиента.ID от клиента Внутреннее Присоединяйтесь к Customer.id = call.customer_id Group по Customer.id имея счет (*) = 3 ) Intersert — список всех клиенты из Берлина выберите клиента.* от клиента внутреннее соединение города по адресу customer.city_id = city.id , где city.city_name = ‘Берлин’; Все прошло, как и ожидалось, и вы можете видеть, что в результате была возвращена строка «Пекарня». Таким образом, все
конечные множества счетны. Бесконечное множество \(A\) есть
называется счетным , если существует биекция \(F:\omega \to A\)
между множеством натуральных чисел и \(A\).Набор \(\mathbb{N}\) из
натуральные числа (тривиально) счетны. Если \(A\) бесконечное подмножество
\(\omega\), то \(A\) также счетно: ибо пусть \(F:\omega \to A\) будет
такой, что \(F(n)\) является наименьшим элементом \(A\), не входящим в множество
\(\{ F(m)\in A: m
Таким образом, все
конечные множества счетны. Бесконечное множество \(A\) есть
называется счетным , если существует биекция \(F:\omega \to A\)
между множеством натуральных чисел и \(A\).Набор \(\mathbb{N}\) из
натуральные числа (тривиально) счетны. Если \(A\) бесконечное подмножество
\(\omega\), то \(A\) также счетно: ибо пусть \(F:\omega \to A\) будет
такой, что \(F(n)\) является наименьшим элементом \(A\), не входящим в множество
\(\{ F(m)\in A: m Для заданных множеств \(A\) и \(B\), которые без потери
общности, мы можем предположить, что они не пересекаются, и при заданных биекциях
\(F:\omega \to A\) и \(G:n\to B\), для некоторого \(n<\omega\) пусть \(H:\omega
\to A\cup B\) — биекция, заданная формулой: \(H(m)=G(m)\), для каждого
\(m
Для заданных множеств \(A\) и \(B\), которые без потери
общности, мы можем предположить, что они не пересекаются, и при заданных биекциях
\(F:\omega \to A\) и \(G:n\to B\), для некоторого \(n<\omega\) пусть \(H:\omega
\to A\cup B\) — биекция, заданная формулой: \(H(m)=G(m)\), для каждого
\(m Предположим, что \(F:\omega \to A\) и \(G:\omega \to B\) равны
биекции.m(2n+1)-1)=(F(m),G(n))\) также является биекцией.
Предположим, что \(F:\omega \to A\) и \(G:\omega \to B\) равны
биекции.m(2n+1)-1)=(F(m),G(n))\) также является биекцией.
Кардиналы
 Порядковые числа, которые не биективны с
любые меньшие порядковые числа называются количественными числами . Таким образом, все
натуральные числа являются количественными, как и \(\omega\), \(\omega_1\),
\(\omega_2\) и так далее.В общем, для любого кардинала \(\каппа\)
множество всех ординалов, которые биективны с некоторым ординалом \(\leq
\каппа\) тоже кардинал; это наименьший кардинал больше, чем
\(\каппа\).
Порядковые числа, которые не биективны с
любые меньшие порядковые числа называются количественными числами . Таким образом, все
натуральные числа являются количественными, как и \(\omega\), \(\omega_1\),
\(\omega_2\) и так далее.В общем, для любого кардинала \(\каппа\)
множество всех ординалов, которые биективны с некоторым ординалом \(\leq
\каппа\) тоже кардинал; это наименьший кардинал больше, чем
\(\каппа\). , является
Знаменитая гипотеза континуума .
, является
Знаменитая гипотеза континуума . Дополнительная литература
Полный список символов теории множеств
 Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации). Константы
Иерархия ключевых наборов чисел Название символа Объяснение Пример $ \ Varnothing $, $ \ Epdyset $, $ \ {\} $ Пустой набор $ | \ Varnothing | = 0 $ $ \ mathbb {n} $ набор натуральные номера $ 1 \ in \ mathbb {n} $ $ \ mathbb {z} $ набор из целых чисел Если $m, n \in \mathbb{Z}$, то $m+n, mn \in \mathbb{Z}$. 
$\mathbb{Q}$ Набор из рациональных чисел $\pi \notin \mathbb{Q}$ $\mathbb{R} 2 2 действительных числа $e \in \mathbb{R}$ $\mathbb{C}$ Набор из комплексных чисел $\mathbb{N} \subseteq \mathbb{Z} \subsete mathbb{Q} \subseteq \mathbb{R} \subseteq \mathbb{C}$ $\mathbb{U}, U$ Универсальный набор Когда $U = \mathbb{R}$ , $\overline{\mathbb{Q}} = \mathbb{R} \setminus \mathbb{Q}$. Переменные
 В следующей таблице описаны наиболее распространенные из них, а также их соответствующий пример и значение.
В следующей таблице описаны наиболее распространенные из них, а также их соответствующий пример и значение. Имя символа Используется для Пример $ A, B, C $ Наборы $ A \ SubseTQ B \ CUP C $ $ A, $ A, b, c$ Элементы множества Если $a \in A$ и $b \in B$, то $a, b \in A \cup B$. $\alpha, \beta, \gamma$ Порядковые номера Если $P(\beta)$ для всех $\beta < \alpha$ подразумевает $P(\alpha)$ для всех $\alpha$, то $P$, вообще говоря, выполняется по трансфинитной индукции. $\lambda$ Предельные ординалы $\lambda$ является предельным ординалом, если он не является ни $0$, ни последующим порядковым номером. $\kappa$ Кардинальные числа Для каждого конечного кардинального числа $\kappa$ его преемником является просто $\kappa + 1$. 
Разделители
Имя символа Объяснение Пример $ \ {\} $ Индикатор на Наборы $ \ {5, E, \ Pi, 1 \} $ $( )$ Индикатор для кортежей $(1, 2.2$
$\mathrm{for \ some \ } x \in \mathbb{Z} \} $ Операторы
 n A_i$, $\, \displaystyle \bigcup_{i \in I} A_i$
n A_i$, $\, \displaystyle \bigcup_{i \in I} A_i$ Обобщенное объединение множеств $A_i$ $\displaystyle \bigcup_{i=\{3, 5 , 8\}} [-i, i] = [-8, 8]$ $A \sqcup B$ Непересекающееся объединение множеств $A$ и $B$ Если $A = \{ 2, 5 \}$ и $B = \{ 1 ,2 \}$, то $A \sqcup B = \{ (2, a) , (5, а),$ $(1,b), (2,b) \}.n$
$\{ (a_i, i) \mid a_i \in A_i \}$ $A \setminus B$, $AB$ Разность наборов
($A$ минус $B$) $\{ 5, 6 ,8\} \setminus \{6, 9\} =$
$\{5, 8\}$ $A \, \треугольник \, B$, $A \ominus B$ Симметричная разность множеств $A$ и $B$ $A \, \треугольник \, B =$
$(A \setminus B) \cup (B \setminus A)$ $A \times B$ Декартово произведение
($A$ умножить на $B$) В общем, $A \times B \ne B \times A$. 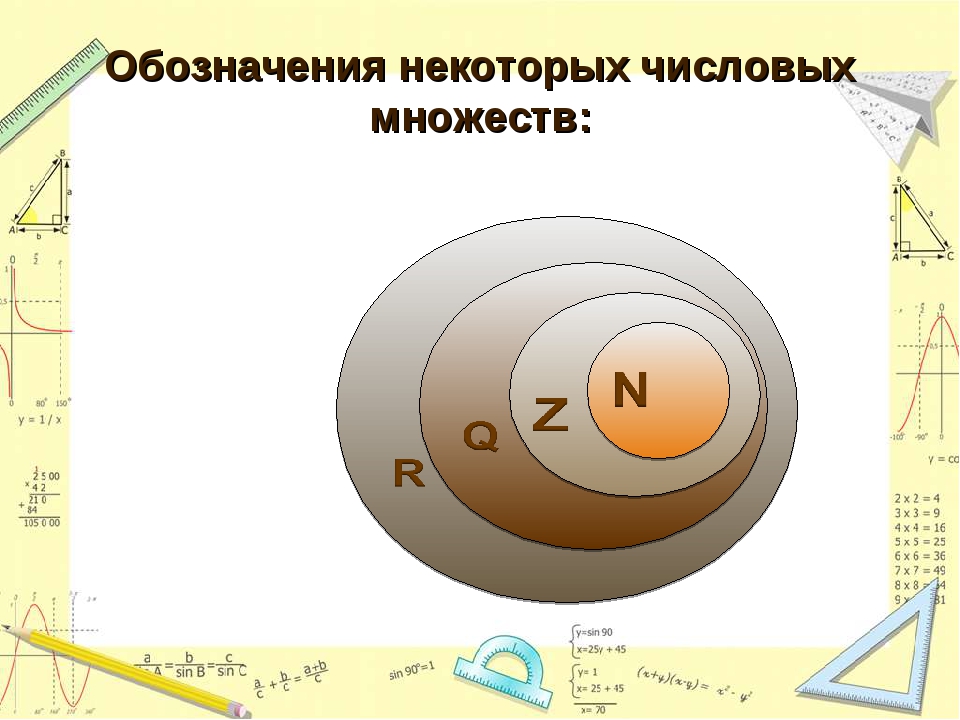 {|А|}$.
{|А|}$. Реляционные символы
Название символа Объяснение Пример $ x \ in $ Комплект
(Элемент $ x $ в комплекте $ a $) $ i \ in \mathbb{C}$ $x \notin A$ Непринадлежность набора
(элемент $x$ не входит в набор $A$) $\pi \notin \mathbb{Q} $ $A \ni x$ Включение множества
(множество $A$ включает элемент $x$) $A \ni x \iff x \in A$ $A \ not\ni x$ Множество невключений
(множество $A$ не включает элемент $x$) $\{a\} \not\ni \{a\}$ $ A = B$ Эквивалентность множеств
(Множества $A$ и $B$ равны) $\varnothing = \{ \}$ $A \subseteq B$ 3 Отношение подмножества
($A$ является подмножеством $B$) $\mathbb{N} \subseteq \mathbb{Q}$ $A \subset B$ Правильное отношение подмножества
($A$ является правильным подмножеством $B$) $A \subset B \iff$
$A \subseteq B \\mathrm{and}\ A \ne B$ $A \not\subseteq B$ Отношение, не являющееся подмножеством
($A$ есть не является подмножеством $B$) Если $A \not\subseteq B$, то существует $x \in A$ такое, что $x \notin B$. 
$A \supseteq B$ Отношение надмножества
($A$ является надмножеством $B$) $\{5, 8, 1\} \supseteq \{1, 8\} $ $A \supset B$ Собственное надмножество
($A$ является правильным надмножеством $B$) $A \supset B \iff \\ B \subset A$ $A \not\supseteq B$ Отношение без надмножества
($A$ не является надмножеством $B$) $\mathbb{N} \not\supseteq \mathbb{R}$ Символы, связанные с мощностью
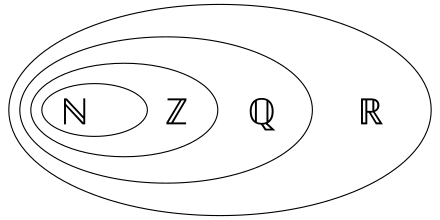 + = \aleph_{\alpha +1}$
+ = \aleph_{\alpha +1}$ Дополнительные ресурсы
Теория множеств и основы математики
Теория множеств и основы математики
О
(цель и автор) — Основы физики —
Другие темы и ссылки
Другие языки : FR —
ЭС —
ИТ —
Россия −
ТР —
LT
1.Первый
основы математики (подробности) — все в 1 файле (36 бумажных страниц)
— версия в формате pdf на 24 страницах (17+7 — обновлено в ноябре путем автоматического преобразования из html).
2. Теория множеств — все в одном
файл (40 бумажных страниц), pdf (37 страниц не обновляются).
Изменение обозначений было сделано вне стандартов (см. почему): из их определения
в 2.6 обозначение прямых образов множеств графом R изменено с R ∗ на R ⋆ , а для прообразов изменено
с р * до р ⋆ .
3. Алгебра 1 (все в одном файле: 32 бумажных страницы), с последними обновлениями
4. Арифметика и основы первого порядка (все в одном файле: 30 бумажных страниц)
5. Фундаменты второго порядка
Больше философских заметок (использует Часть 1
с философским
аспекты + рекурсия):
6. Основы геометрии (черновик)
7. Алгебра 2 (черновик)
Галуа
соединения (11 страниц в формате pdf).Строго он использует только части 1 (без дополнений) и 2.
Его положение
был перемещен с 3 по педагогическим причинам (более высокая сложность
уровне, в то время как более поздние тексты более непосредственно
интересно). Начало перенесено на 2.11.
Начало перенесено на 2.11.
Монотонные соединения Галуа (присоединения)
Верхняя и нижняя границы, инфимум и супремум
Комплектные решетки
Теорема о неподвижной точке
Транспорт закрытия
Предзаказ создан отношением
Конечные множества
Сгенерированные отношения эквивалентности и многое другое
Основанные отношения
Указатель специальных слов, словосочетаний и обозначений со ссылками Черновики дополнительных текстов, которые будут доработаны позже
Различные тексты готовы, но не классифицированы
Добавление в Википедию
домашних страниц по теории множеств | Джин А.
 Ларсон
Ларсон
Замечания, исправления, дополнения присылать к джал по уфл дот эду .
Выберите первую букву фамилии:
[A] [B] [C] [D] [EF] [G] [H] [IJ] [K] [L] [M] [NO] [PQ] [R] [Sa] [Si] [TUVW] [XYZ]
— Университет Сан-Паулу
 — Университет Джеймса Мэдисона
— Университет Джеймса Мэдисона Майкл — Детройтский университет Милосердия
Майкл — Детройтский университет Милосердия — Уэслианский университет
— Уэслианский университет (умер 20 октября 2010 г.)
(умер 20 октября 2010 г.) Т. — Кембриджский университет — Обладатель медали Филдса
Т. — Кембриджский университет — Обладатель медали Филдса — Калифорнийский университет в Беркли
— Калифорнийский университет в Беркли в Праге и Йехе в Пенсильванском государственном институте математики, AS CR, Прага
в Праге и Йехе в Пенсильванском государственном институте математики, AS CR, Прага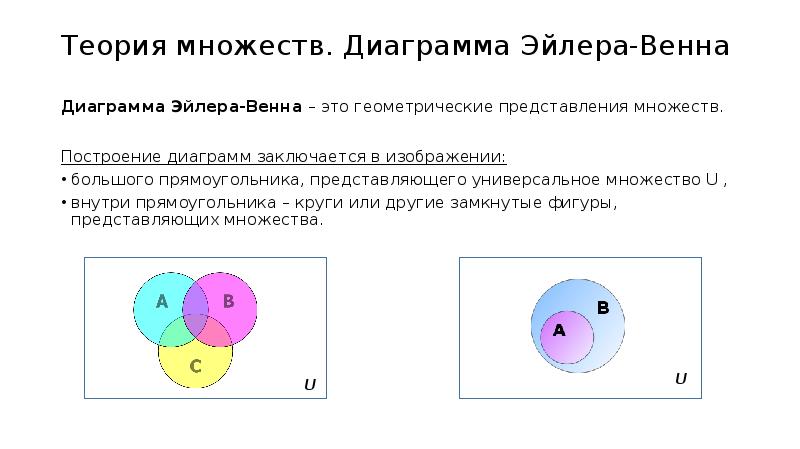 uni-wuppertal.de, [email protected]
uni-wuppertal.de, [email protected]
 — Университет Флориды
— Университет Флориды , Эндре, — Венгерский математический институт
, Эндре, — Венгерский математический институт
(переезд в Калифорнийский университет в Лос-Анджелесе в 2015 г.) fr, [email protected], [email protected]
fr, [email protected], [email protected] — Университет Флориды
— Университет Флориды

Саргсян Григор — Университет Рутгерса
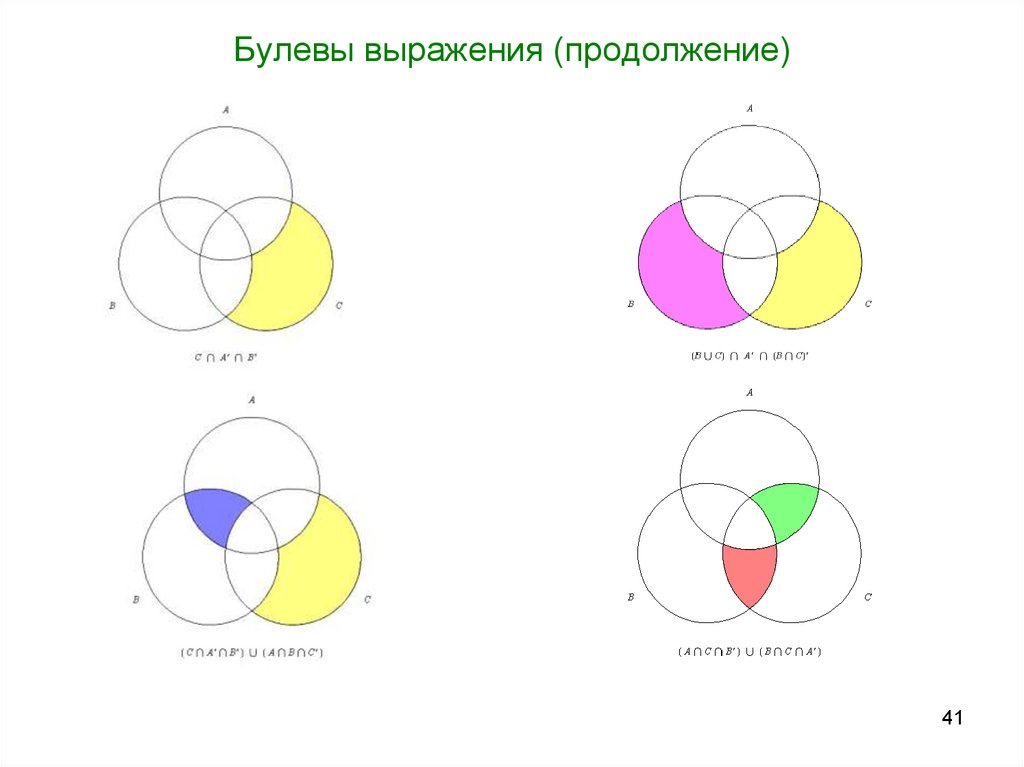 —
—
 К. — Университет Лидса
К. — Университет Лидса — Амхерстский колледж
— Амхерстский колледж — Университет Торонто
— Университет Торонто
Проблемы детерминированности, большие кардиналы и сильные аксиомы бесконечности
За дополнительной информацией обращайтесь в J.Ларсон в джал в ufl точка edu ; 
последнее изменение 6 декабря 2013 г. Простая теория множеств | SkillsYouNeed

Язык множеств: некоторые определения


 Символ ⊂ означает «является подмножеством». В этом случае A ⊂ B..
Символ ⊂ означает «является подмножеством». В этом случае A ⊂ B.. Работа с наборами
Союз
 Объединением двух множеств являются их объединенные элементы, то есть все элементы, входящие в либо множество.Символ союза ∪ .
Объединением двух множеств являются их объединенные элементы, то есть все элементы, входящие в либо множество.Символ союза ∪ . А ∪ В = {1, 2, 4, 7} ∪ {2, 5, 6, 8} = {1, 2, 4, 5, 6, 7, 8}
Перекресток
Относительное дополнение
 Обозначается знаком минус, −.
Обозначается знаком минус, −. Дополнение

В заключение…
Наборы Теория множеств и ее место в основаниях математики: новый взгляд на старый вопрос
 Должно ли оно быть онтологическим или эпистемическим? Мы дадим ответ в § 5.
Должно ли оно быть онтологическим или эпистемическим? Мы дадим ответ в § 5. (Это так, потому что по результатам Леви и Соловея (1967) можно изменить универсум теории множеств и изменить значения континуальной функции, сохраняя при этом тот же кардинал \(\каппа\) недоступным.) Учитывая, что существует В важном вопросе независимости нет никакого выигрыша в важном вопросе независимости, сами теоретики множеств не любят ZFC2, потому что он убирает большой кусок предмета, основанного на обоснованности, полноте (и, следовательно, компактности) логики первого порядка. А именно, взятые вместе, эти свойства говорят, что для любого множества \(\Sigma\) предложений логики первого порядка \(\models \Sigma\) тогда и только тогда, когда \(\vdash \Sigma\), то есть все предложения в \(\Sigma\) истинны в каждой модели тогда и только тогда, когда нет доказательства противоречия от \(\Sigma\).Поэтому, чтобы доказать непротиворечивость теории T , например \(\hbox {ZFC} + \lnot \hbox {CH}\), достаточно найти для нее модель. Довольно обширное обсуждение этих вопросов можно найти у Кунена (2011).
(Это так, потому что по результатам Леви и Соловея (1967) можно изменить универсум теории множеств и изменить значения континуальной функции, сохраняя при этом тот же кардинал \(\каппа\) недоступным.) Учитывая, что существует В важном вопросе независимости нет никакого выигрыша в важном вопросе независимости, сами теоретики множеств не любят ZFC2, потому что он убирает большой кусок предмета, основанного на обоснованности, полноте (и, следовательно, компактности) логики первого порядка. А именно, взятые вместе, эти свойства говорят, что для любого множества \(\Sigma\) предложений логики первого порядка \(\models \Sigma\) тогда и только тогда, когда \(\vdash \Sigma\), то есть все предложения в \(\Sigma\) истинны в каждой модели тогда и только тогда, когда нет доказательства противоречия от \(\Sigma\).Поэтому, чтобы доказать непротиворечивость теории T , например \(\hbox {ZFC} + \lnot \hbox {CH}\), достаточно найти для нее модель. Довольно обширное обсуждение этих вопросов можно найти у Кунена (2011).
 Но все эти философы настолько хорошо разбираются в теории множеств, что для целей этой статьи и гораздо шире, они определенно считаются инсайдерами теории множеств, а не аутсайдерами.
Но все эти философы настолько хорошо разбираются в теории множеств, что для целей этой статьи и гораздо шире, они определенно считаются инсайдерами теории множеств, а не аутсайдерами. Поиск новых аксиом известен как Программа Гёделя . Сноска 2 .Однако поиск новых аксиом не подразумевает веры в единую вселенную.
Поиск новых аксиом известен как Программа Гёделя . Сноска 2 .Однако поиск новых аксиом не подразумевает веры в единую вселенную. То есть, даже если бы «правильные» аксиомы были бы найдены, нет оснований надеяться, что они будут категоричными.Более того, довольно далеко отойдя от фундаментальных вопросов, как бы теоретики множеств ни понимали привилегированное положение предмета в отношении его способности формулировать математику, многие вообще считают, что предмет оснований не стоит заниматься и интересует гораздо больше. в математике бесконечности. Большинство придерживается мнения, что, безусловно, поиск уникальных совершенных оснований математики прекращен после теорем Гёделя (1930) о неполноте. Поскольку даже проблема континуума независима, большинство теоретиков множеств уже давно сместили акцент предмета на что-то другое, кроме аксиом, даже если сам Гёдель этого не сделал.
То есть, даже если бы «правильные» аксиомы были бы найдены, нет оснований надеяться, что они будут категоричными.Более того, довольно далеко отойдя от фундаментальных вопросов, как бы теоретики множеств ни понимали привилегированное положение предмета в отношении его способности формулировать математику, многие вообще считают, что предмет оснований не стоит заниматься и интересует гораздо больше. в математике бесконечности. Большинство придерживается мнения, что, безусловно, поиск уникальных совершенных оснований математики прекращен после теорем Гёделя (1930) о неполноте. Поскольку даже проблема континуума независима, большинство теоретиков множеств уже давно сместили акцент предмета на что-то другое, кроме аксиом, даже если сам Гёдель этого не сделал. Более настойчивым в решении проблемы континуума является точка зрения калифорнийской школы, продолжающей программу Гёделя, наиболее заметно представленную в настоящее время Хью Вудином.Они действительно верят, что мы должны найти новые аксиомы для завершения ZFC, по крайней мере, до решения проблемы континуума. Конечно, одна из таких аксиом состоит в том, что все множества конструируемы («\(V=L\)»). Однако среди практиков мало энтузиазма принять ее в качестве аксиомы, поскольку она дает очень ограничительный взгляд на теоретико-множественную вселенную, исключая, например, понятие измеримых кардиналов и, следовательно, большинство больших кардиналов, которые считается основой современной теории множеств, как обсуждалось выше.Другой набор утверждений составляют так называемые форсирующие аксиомы, такие как MA, PFA и другие. Теоретико-множественный универсум, в котором выполняется такое утверждение, насыщается при определенных форсирующих конструкциях. Это означает, что сама вселенная уже содержит некоторые объекты, которые в других вселенных пришлось бы добавлять принудительно.
Более настойчивым в решении проблемы континуума является точка зрения калифорнийской школы, продолжающей программу Гёделя, наиболее заметно представленную в настоящее время Хью Вудином.Они действительно верят, что мы должны найти новые аксиомы для завершения ZFC, по крайней мере, до решения проблемы континуума. Конечно, одна из таких аксиом состоит в том, что все множества конструируемы («\(V=L\)»). Однако среди практиков мало энтузиазма принять ее в качестве аксиомы, поскольку она дает очень ограничительный взгляд на теоретико-множественную вселенную, исключая, например, понятие измеримых кардиналов и, следовательно, большинство больших кардиналов, которые считается основой современной теории множеств, как обсуждалось выше.Другой набор утверждений составляют так называемые форсирующие аксиомы, такие как MA, PFA и другие. Теоретико-множественный универсум, в котором выполняется такое утверждение, насыщается при определенных форсирующих конструкциях. Это означает, что сама вселенная уже содержит некоторые объекты, которые в других вселенных пришлось бы добавлять принудительно. По мнению большинства людей, это не делает естественной аксиомой добавление к ZFC. Некоторые из принудительных аксиом, такие как PFA, действительно устанавливают значение континуума (чтобы быть \(\ алеф _ {2} \)), поэтому некоторые теоретики множеств считают, что такое утверждение может быть реальной аксиомой.Если назвать некоторые имена, то, возможно, Менахем Магидор в определенной степени придерживается такого мнения, высказанного в частных беседах, но письменных свидетельств этому нет. Но на самом деле, чтобы увидеть, насколько теоретики множеств не придерживаются ни одной из этих аксиом, взгляните на статью Джоан Багариа по теории множеств для [1]. В нем говорится: «Таким образом, центральной темой теории множеств является поиск и классификация новых аксиом. В настоящее время они делятся на два основных типа: аксиомы больших кардиналов и аксиомы принуждения».Затем математические свойства этих аксиом объясняются в двух отдельных разделах. Это конец. Нет никакого философского вывода или выбора относительно того, что и являются ли какие-либо из этих утверждений действительно аксиомами.
По мнению большинства людей, это не делает естественной аксиомой добавление к ZFC. Некоторые из принудительных аксиом, такие как PFA, действительно устанавливают значение континуума (чтобы быть \(\ алеф _ {2} \)), поэтому некоторые теоретики множеств считают, что такое утверждение может быть реальной аксиомой.Если назвать некоторые имена, то, возможно, Менахем Магидор в определенной степени придерживается такого мнения, высказанного в частных беседах, но письменных свидетельств этому нет. Но на самом деле, чтобы увидеть, насколько теоретики множеств не придерживаются ни одной из этих аксиом, взгляните на статью Джоан Багариа по теории множеств для [1]. В нем говорится: «Таким образом, центральной темой теории множеств является поиск и классификация новых аксиом. В настоящее время они делятся на два основных типа: аксиомы больших кардиналов и аксиомы принуждения».Затем математические свойства этих аксиом объясняются в двух отдельных разделах. Это конец. Нет никакого философского вывода или выбора относительно того, что и являются ли какие-либо из этих утверждений действительно аксиомами. Автор не принимает чью-либо сторону.
Автор не принимает чью-либо сторону. Изучение SQL: теория множеств
Теория множеств — математика и логика
Что такое множества в теории множеств?
Модель
Теория множеств и диаграммы Венна
Теория множеств и SQL
#1 Сначала мы протестируем два отдельных запроса и проанализируем набор результатов, который они возвращают
#2 СОЕДИНЕНИЕ и СОЕДИНЕНИЕ ВСЕ
#3 ПЕРЕСЕЧЕНИЕ


 Здесь
— множество действительных чисел.
Неравенство
— первое характеристическое свойство;
неравенство
— второе характеристическое свойство,
которым обладают действительные числа
множества
.
Решая систему неравенств, получим:
.
Таким образом, множество
— бесконечное числовое множество,
состоящее из действительных чисел,
заключенных между числами 2 и 4, включая
число 2. На числовой оси множество
задает отрезок
,
замкнутый снизу и открытый сверху.
Здесь
— множество действительных чисел.
Неравенство
— первое характеристическое свойство;
неравенство
— второе характеристическое свойство,
которым обладают действительные числа
множества
.
Решая систему неравенств, получим:
.
Таким образом, множество
— бесконечное числовое множество,
состоящее из действительных чисел,
заключенных между числами 2 и 4, включая
число 2. На числовой оси множество
задает отрезок
,
замкнутый снизу и открытый сверху.

 —
— ;
;