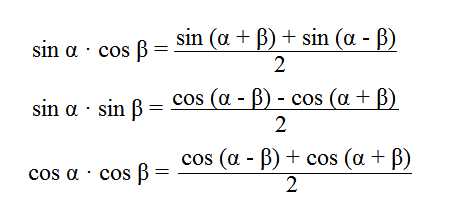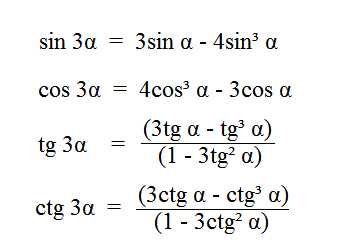Таблица формула тригонометрии – Тригонометрические формулы
Тригонометрическая таблица
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
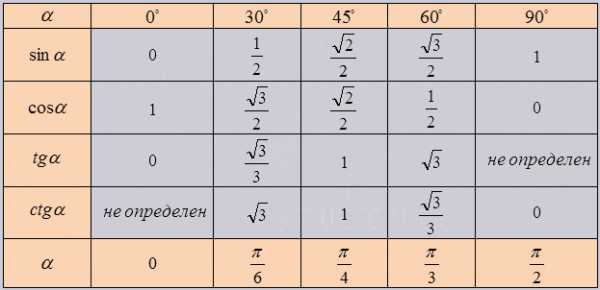
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 00=0, cos 00 = 1. tg 00 = 0, котангенс от 00 будет неопределенным
sin 900 = 1, cos 900 =0, ctg900 = 0,тангенс от 900 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 300 = 1/2, cos 300 = √3/2, tg 300 = √3/3, ctg 300
sin 450 = √2/2, cos 450 = √2/2, tg 450= 1, ctg 450 = 1
sin 600 = √3/2, cos 600 = 1/2, tg 600 =√3 , ctg 600 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
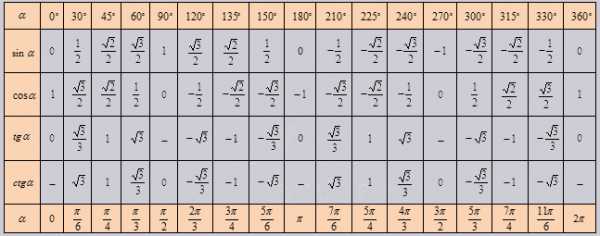
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600
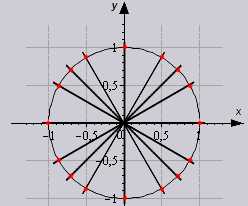
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
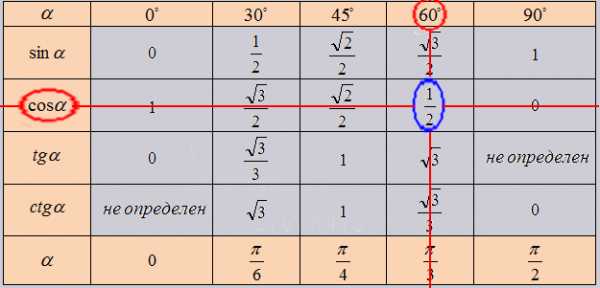
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020
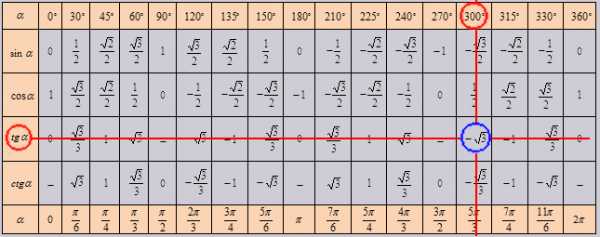
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
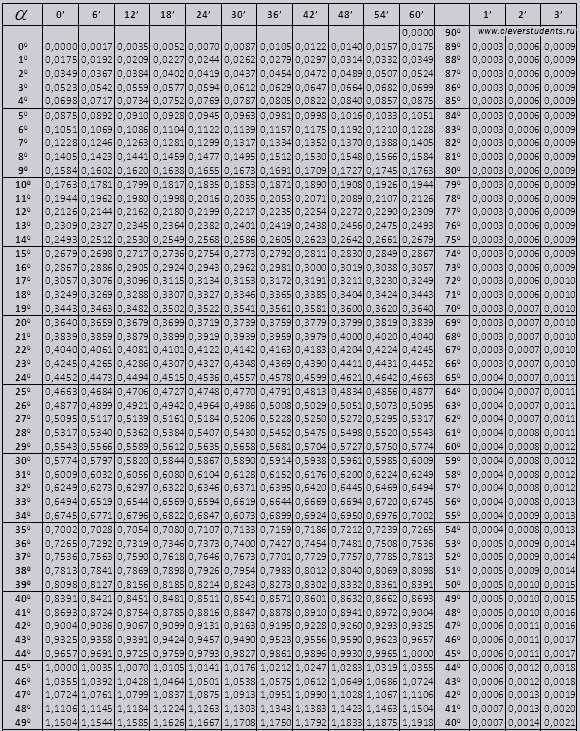
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
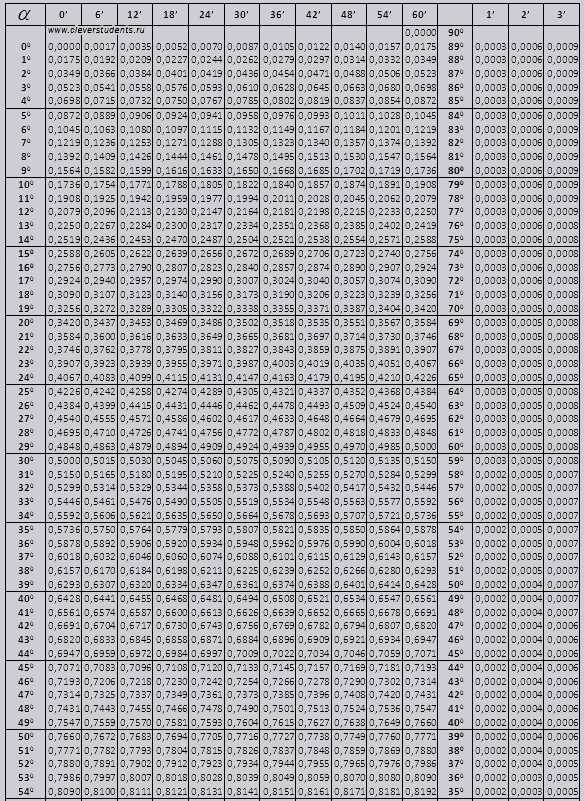

tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.
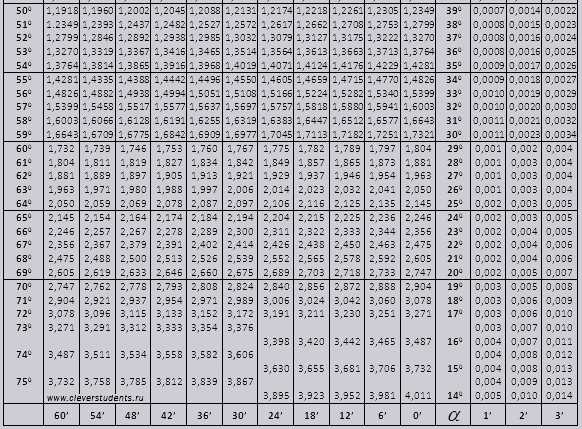
tg до 900 и ctg малых углов.


Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0.9397
Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78
а ctg 200 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Заметка: Стеновые отбойники — отбойная доска для защиты стен. Перейдите по ссылке настенные отбойники бескаркасные (http://www.spi-polymer.ru/otboyniki/) и узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Тригонометрические формулы — шпаргалка
Здесь можно найти тригонометрические формулы в удобном виде. А тригонометрические формулы приведения можно посмотреть на другой странице.
Основные тригонометрические тождества
— математические выражения для тригонометрических функций, выполняемые при каждом значении аргумента.
- sin² α + cos² α = 1
- tg α · ctg α = 1
- tg α = sin α ÷ cos α
- ctg α = cos α ÷ sin α
- 1 + tg² α = 1 ÷ cos² α
- 1 + ctg² α = 1 ÷ sin² α
Формулы сложения
- sin (α + β) = sin α · cos β + sin β · cos α
- sin (α — β) = sin α · cos β — sin β · cos α
- cos (α + β) = cos α · cos β — sin α · sin β
- cos (α — β) = cos α · cos β + sin α · sin β
- tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
- tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
- ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
- ctg (α — β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
https://uchim.org/matematika/trigonometricheskie-formuly — uchim.org
Формулы двойного угла
- cos 2α = cos² α — sin² α
- cos 2α = 2cos² α — 1
- cos 2α = 1 — 2sin² α
- sin 2α = 2sin α · cos α
- tg 2α = (2tg α) ÷ (1 — tg² α)
- ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Формулы тройного угла
- sin 3α = 3sin α — 4sin³ α
- cos 3α = 4cos³ α — 3cos α
- tg 3α = (3tg α — tg³ α) ÷ (1 — 3tg² α)
- ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)
Формулы понижения степени
- sin² α = (1 — cos 2α) ÷ 2
- sin³ α = (3sin α — sin 3α) ÷ 4
- cos² α = (1 + cos 2α) ÷ 2
- cos³ α = (3cos α + cos 3α) ÷ 4
- sin² α · cos² α = (1 — cos 4α) ÷ 8
- sin³ α · cos³ α = (3sin 2α — sin 6α) ÷ 32
Переход от произведения к сумме
- sin α · cos β = ½ (sin (α + β) + sin (α — β))
- sin α · sin β = ½ (cos (α — β) — cos (α + β))
- cos α · cos β = ½ (cos (α — β) + cos (α + β))
Мы перечислили довольно много тригонометрических формул, но если чего-то не хватает, пишите.
Всё для учебы » Математика в школе » Тригонометрические формулы — шпаргалка
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/trigonometricheskie-formuly
uchim.org
Основные формулы тригонометрии
Основное тригонометрическое тождество, синус суммы и разности, косинус суммы и разности. Основные формулы тригонометрии.
Тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций. Их всего четыре:
- Синус \( \displaystyle sin\left( x \right) \)
- Косинус \( \displaystyle cos\left( x \right) \)
- Тангенс \( \displaystyle tg\left( x \right) \)
Существует два способа решения тригонометрических уравнений:
Первый способ — с использованием формул.
| \( \displaystyle A \) | \( \displaystyle a \) | \( \displaystyle -1 \) | \( \displaystyle 0 \) | \( \displaystyle 1 \) |
| \( \displaystyle \sin x=A \) | \( \displaystyle {{\left( -1 \right)}^{n}}\arcsin \alpha +\pi n \) | \( \displaystyle -\dfrac{\pi }{2}+2\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{2}+2\pi n \) |
| \( \displaystyle \cos x=A \) | \( \displaystyle \pm \arccos \alpha +2\pi n \) | \( \displaystyle \pi +2\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle 2\pi n \) |
| \( \displaystyle tgx=A \) | \( \displaystyle arctg\alpha +\pi n \) | \( \displaystyle -\dfrac{\pi }{4}+\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
| \( \displaystyle ctgx=A \) | \( \displaystyle arcctg\alpha +\pi n \) | \( \displaystyle \dfrac{3\pi }{4}+\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
Второй способ — через тригонометрическую окружность.
Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее.

Основные формулы Тригонометрии:
Основное тригонометрическое тождество (нужно его помнить, даже если тебя разбудили среди ночи и спросили!)
\[ \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1 \]
Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса)
\[ \displaystyle tg\ \alpha =\dfrac{sin\ \alpha }{cos\ \alpha } \]
Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса)
\[ \displaystyle ctg\ \alpha =\dfrac{cos\ \alpha }{sin\ \alpha }=\dfrac{1}{tg\ \alpha } \]
Синус суммы и разности:
\[ \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \]
Косинус суммы и разности:
\[ \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \]
Тангенс суммы и разности:
\[ \displaystyle tg\left( \alpha \pm \beta \right)=\dfrac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta } \]
Формулы понижения степени:
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
\[ \displaystyle si{{n}^{2}}\alpha =\dfrac{1-cos2\alpha }{2} \]
\[ \displaystyle co{{s}^{2}}\alpha =\dfrac{1+cos2\alpha }{2} \]
\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]
\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]
\[ \displaystyle t{{g}^{2}}\alpha =\dfrac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \dfrac{\pi }{2}+\pi n,n\in Z \]
\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]
\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]
Из данных формул можно в частности вывести формулы тройного угла:
\[ \displaystyle sin3\alpha =3sin\alpha -4si{{n}^{3}}\alpha \]
\[ \displaystyle cos3a=4co{{s}^{3}}a-3cosa \]
\[ \displaystyle tg3\alpha =\dfrac{3tg\alpha -t{{g}^{3}}\alpha }{1-3t{{g}^{2}}\alpha } \]
\[ \displaystyle ctg3\alpha =\dfrac{3ctg\alpha -ct{{g}^{3}}\alpha }{1-3ct{{g}^{2}}\alpha } \]
Формулы преобразования суммы функций
Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.
\[ \displaystyle sin\alpha \pm sin\beta =2sin\dfrac{\alpha \pm \beta }{2}cos\dfrac{\alpha \mp \beta }{2} \]
\[ \displaystyle cos\alpha +cos\beta =2cos\dfrac{\alpha +\beta }{2}cos\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle cos\alpha -cos\beta =-2sin\dfrac{\alpha +\beta }{2}sin\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle tg\alpha \pm tg\beta =\dfrac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta } \]
\[ \displaystyle ctg\alpha \pm ctg\beta =\dfrac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta } \]
Формулы преобразования произведений функций
\[ \displaystyle sin\alpha sin\beta =\dfrac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2} \]
\[ \displaystyle sin\alpha cos\beta =\dfrac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2} \]
\[ \displaystyle cos\alpha cos\beta =\dfrac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2} \]
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Тригонометрия в таблицах
Таблицы по тригонометрии
Основные тригонометрические тождества:
Тригонометрические функции суммы и разности двух аргументов:
Представление суммы одноименных тригонометрических функций в виде произведения:
Преобразование произведения тригонометрических функций в сумму:
Формулы двойных аргументов:
Выражение тригонометрических функций через тангенс половинного аргумента:
Формулы приведения («формулы лошади»): a - острый угол!!!
Вопросы лошадке:
1) функция меняется?
2) какой был знак и какой поставить в ответ?
Решение тригонометрических уравнений:
cos x=1 <=>
cos x=0 <=>
cos x= — 1 <=>
Формулы тройных аргументов:
Кроме того, необходимо знать:
Соотношения между тригонометрическими функциями одного и того же аргумента:
urok.1sept.ru
| Главная > Учебные материалы > Математика: Тригонометрические формулы | ||||
     
|
||||
|
1.Знаки тригонометрических функций.
|
||||
| 1 2 3 4 5 6 7 8 | ||||
Знаки тригонометрических функций по четвертям в тригонометрическом круге |
||||
Значения тригонометрических функций для некоторых углов |
||||
Основные тригонометрические тождества |
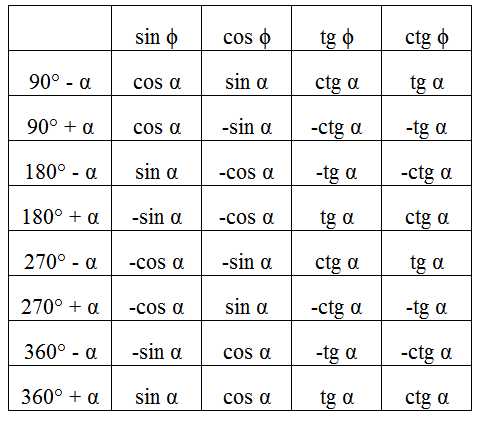
Формулы приведения |
|||
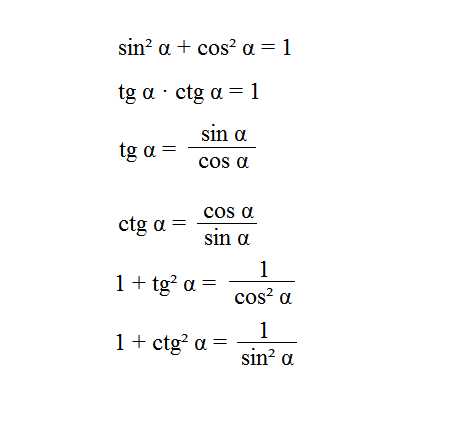 |
 |
|||
Формулы преобразования суммы |
Формулы сложения |
|||
 |
 |
|||
Формулы половинного аргумента |
Формулы понижения степени |
|||
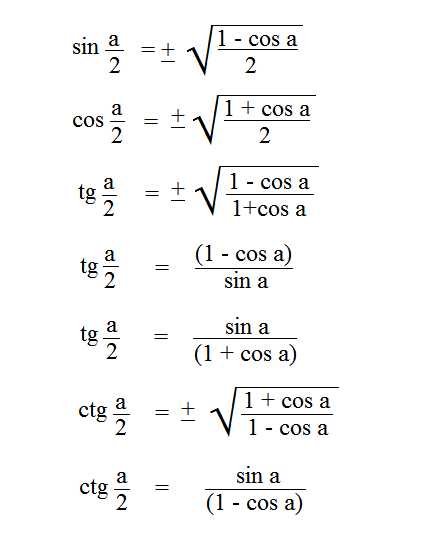 |
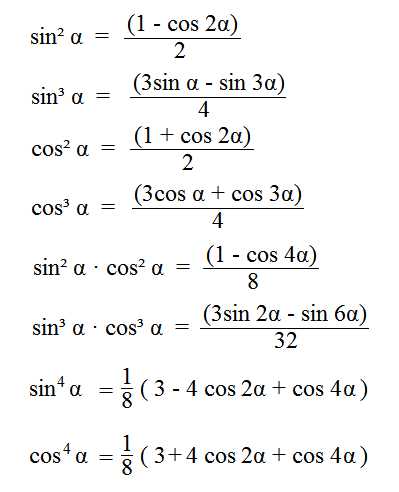 |
|||
 |
||||
Формулы двойного угла |
Переход от произведения к сумме |
|||
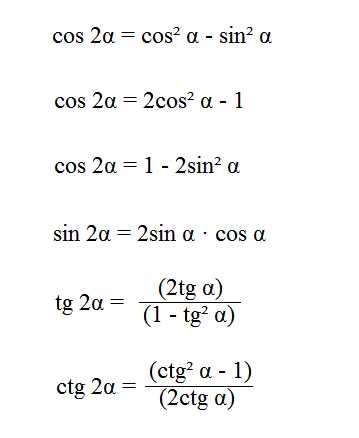 |
Формулы тройного угла
|
|||
| 1 2 3 4 5 6 7 8 | ||||
www.mathtask.ru
Формулы тригонометрии
Взаимосвязь основных тригонометрических функций, каких как косинус и синус, тангенс и котангенс — называется
Мы разберем самые основные из тригонометрических формул. С помощью которых можно решить большинство тригонометрических заданий. Для большего удобства объединим их по значению, по таблицам.
Начнем с тригонометрических тождеств.
Основы в тригонометрических тождествах определяют взаимосвязь косинуса и синуса, тангенса и котангенса в одном угле. И выходят из их определения и единичной окружности. Дают возможность выделить через любую функцию другую.
Далее рассмотрим тригонометрические формулы приведения.

Они вытекают из свойств синусов, косинусов, котангенсов и тангенсов. Тем самым выражают такие свойства функции как: периодичность, симметричность и сдвиг к рассматриваемому углу. так же дают возможность работать с углами в радиусе до 90 градусов и произвольные углы.
Формулы на сложение.
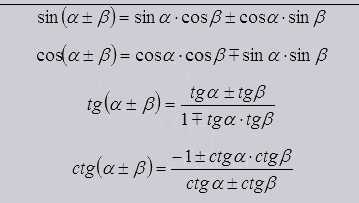
Формула для двойных, тройных и других углов.
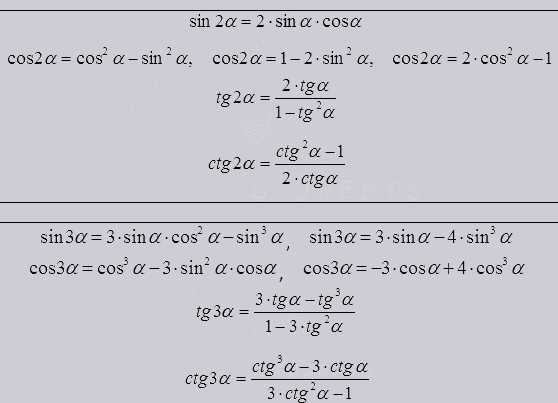
Из них видно что тригонометрическая функция двойного, тройного или какого то ни было угла выводится из т.ф. одинарных углов.
Так же как и одинарные, двойные, тройные и т.д. существуют и половинные углы
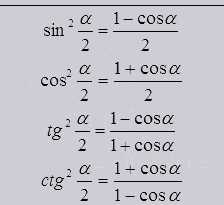
Из формул половинного угла видно, что он выходит из косинуса угла целого.
Так же существуют методы понижения степени выглядят они как:
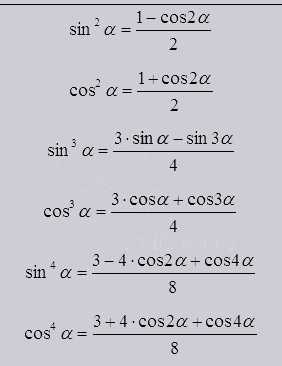

С помощью их использования возможно понизить функцию до первой степени. Взаимодействуя с натуральными степенями функций переводить до синусов и косинусов только кратных углов, в первую степень.
Сумма и разность в тригонометрической функции.

Помогают упростить тригонометрическое выражение, и разложить на множители синусы и косинусы.
Произведение синуса, косинуса, и одно на другое.
Метод универсальной тригонометрической подстановки.

Такая подстановка удобна тем, что функции получаются без корней.
Заметка: Актуальные предложения, участие в тендерах на строительство бесплатное! Перейдите по ссылке строительно монтажные тендеры (http://www.b2bsearch.ru/tenders/stroy) узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Тригонометрические формулы
Синус, косинус, тангенс
Рассмотрим три основные тригонометрические функции: синус, косинус и тангенс. Каждую из функций можно представить в виде отношения сторон прямоугольного треугольника.
Функция синуса:
Функция косинуса:
Функция косинуса:
Разделим на :
Запишем наше первое тождество:
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:
Преобразуем формулу:

После замены отношения сторон на функции синуса и косинуса получили тождество:
calcs.su