Свойства логарифмов примеры: Основные свойства логарифмов
8 $\log _{a} b=\frac{1}{\log _{b} a}$
9 $\log _{a} b=\frac{\log _{c} b}{\log _{c} a}$ — переход к новому основанию.
Примеры решения задач
Пример
Задание. Вычислить $\log _{a} \sqrt{a b}$, если $\log _{a} b=7$
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
$\log _{a} \sqrt{a b}=\frac{1}{2} \log _{a}(a b)=\frac{1}{2}\left(\log _{a} a+\log _{a} b\right)=\frac{1}{2}(1+7)=4$
Ответ. $\log _{a} \sqrt{a b}=4$
Больше примеров решенийЧитать дальше: основное логарифмическое тождество.
Слишком сложно?
Формулы и свойства логарифмов не по зубам? Тебе ответит эксперт через 10 минут!
Что такое логарифм простыми словами
Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
- Что такое логарифм и как его посчитать
- Зачем логарифмам специальные обозначения
- Основные свойства логарифмов — все формулы в одном месте
- 10 примеров логарифмов с решением
Логарифм имеет следующий вид:
где a – это основание логарифма,
b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.
Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Приведем пример:
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:
Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.
Еще примеры:
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифмДесятичный логарифм обозначается lg и имеет основание 10, т.е.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Например, вычислим lg100
Натуральный логарифмНатуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единицаЭто следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a0 = 1:
loga 1 = 0 – логарифмический ноль.
В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выраженияСначала преобразуем логарифм
Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:
Сумма логарифмов. Разница логарифмовЛогарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифмаВынесение показателя степени из логарифма:
Переход к новому основаниюКогда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.
Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:
Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:
1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:
Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:
7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:
4 + 3 = 7
10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log216. Поэтому сначала найдем значение log216, а затем подставим полученный результат в log4:
Надеюсь, теперь вы разобрались, что такое логарифм.
Урок 24. логарифмы. свойства логарифмов — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок № 24. Логарифм. Свойства логарифмов.
Перечень вопросов, рассматриваемых в теме
1. Определение логарифма.
2. Основное логарифмическое тождество.
3. Свойства логарифмов.
Глоссарий по теме
Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .
Логарифмирование – это действие нахождения логарифма числа.
Основное логарифмическое тождество:
Свойства логарифмов. При , справедливы равенства:
— логарифм произведения: ;
— логарифм частного: ;
— логарифм степени: .
Основная литература:
Колягин Ю.
Открытые электронные ресурсы:
http://fipi.ru/
Теоретический материал для самостоятельного изучения
При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение имеет корень 5, т. к. значит , В уравнении число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.
Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.
Дадим определение логарифма.
Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .
Т. е. логарифм числа по основанию , есть некоторое число такое, что .
Пример 1.
, т. к. выполнены все условия определения:
1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) .
Пример 2.
, т. к. выполнены все условия определения:
1) ; 2) 2 > 0, 2 ≠ 1; 3) .
Это действие называется логарифмированием.
Логарифмирование
Существует краткая запись определения логарифма:
так называемое основное логарифмическое тождество. Его используют при вычислениях.
Пример 3.
(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)
Пример 4.
(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)
Решим несколько задач с использованием определения логарифма.
Задача 1. Вычислить .
Решение. Пусть тогда по определению логарифма Приведем левую и правую части к одному основанию.
Задача 2. Вычислить .
Решение. Для вычисления воспользуемся свойствами степеней: 1) , 2) и основным логарифмическим тождеством: .
.
Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.
1. Логарифм произведения.
Логарифм произведения чисел по основанию равен сумме логарифма по основанию и логарифма по основанию .
Пример 5.
2. Логарифм частного.
Логарифм частного чисел по основанию равен разности логарифма по основанию и логарифма по основанию .
Пример 6.
3. Логарифм степени.
Логарифм числа по основанию равен произведению показателя и логарифма по основанию .
Пример 7.
Важно! Свойства выполняются при ,
Примеры и разбор решения заданий тренировочного модуля
№ 1. Вычислите: .
Решение:
Чтобы выполнить это задание нам понадобятся следующие определения и свойства:
- ;
- .
Представим в виде степени с рациональным показателем: . Далее воспользуемся свойством нахождения логарифма степени: . Вспоминаем таблицу квадратов: , значит , . Ответ: .
№ 2. Вычислите
Решение:
Чтобы выполнить это задание нам понадобятся следующие определения и свойства:
- ;
- ;
- ;
- .
.
Логарифмы и их свойства: определение и алгоритм решения
Рассмотрим уравнение ax = b, при a > 0 и a не равном единице. Это уравнение не имеет решений при b меньшем либо равным нулю. И имеет единственное решение при b > 0. Данное решение называют логарифмом b по основанию a b и обозначают следующим образом:
loga(b)
Логарифмом числа b по основанию f называется показатель степени, в которую необходимо возвести число а, чтобы получилось число b.
a(loga(b)) = b.
Данная формула называется основным логарифмическим тождеством. Она верна для любого положительного не равного единице a, и любого положительного b.
Примеры логарифмов
Рассмотрим несколько примеров:
1. Найти значение log2(32). 32 можно представить как 25. То есть для того, чтобы нам получить число 32, необходимо двойку возвести в пятую степень. Следовательно, log2(32) = 5.
2. Найти логарифм числа 1/9 по основанию √3. Так как (√3)4 = 1/9, получаем, что log√3(1/9) = -4.
3. Найти х такое, что будет верно неравенство: log8(x) = 1/3. Применим основное логарифмическое тождество:
x = 8(log8(x)) = 8(1/8) = 2.
Свойства логарифмов
У логарифмов есть несколько свойств, которые прямо следуют из свойств показательной функции. Основные свойства логарифмов:
1. loga(1) = 0;
2. loga(a) = 1;
3. loga(x*y) = loga(x) + loga(x) — логарифм произведения равен сумме логарифмов;
4. logx(x/y) = loga(x) — loga(y) — логарифм частного равен разности логарифмов;
5. loga(xp) = p* loga
Приведенные выше свойства будут справедливы для любого положительного числа а, не равного единице, любых положительны x и y, и любого действительного p.
Для логарифмов существует формула перехода к новому основанию:
loga(x) = (logb(x))/(logb(a)).
Данная формула будет иметь смысл лишь в том случае, когда обе её части будут иметь смысл. То есть должны выполняться следующие условия:
x > 0, a > 0,b > 0, a не равно единице, b не равно единице.
Логарифмы основанием которых является число 10, называются десятичными логарифмами. Логарифмы, основанием которых является число e, называются натуральными логарифмами.
Нужна помощь в учебе?
Предыдущая тема: Решение показательных уравнений и неравенств: алгоритм решения и примеры
Следующая тема:   Логарифмическая функция: основные свойства и графики
свойства, формулы, основание, виды для школьников и студентов
Формулы и свойства логарифмов
Для любых a>0, a≠1 и b>0, x>0, y>0 выполняются следующие свойства логарифмов.
Именно это свойство логарифмов позволяет вычислять точные значения в отличае от других методов вычисления.
Неточность других методов вычисления основывается на неверной корреляции остаточного члена логарифмического равенства.
Наряду с этим каждое из свойств является индивидуальным, равно как каждый из его членов. Всё это позволяет сделать вывод, что благодаря формулам, выведенным математиком, вычисления становятся простыми в рамках неравенств.
Основное логарифмическое тождество
Основание a, возведенное в степень логарифма с основанием a, будет равно b.
alogab=b
Логарифм единицы
Логарифмический ноль. Какое бы ни было основание логарифма, если в аргументе стоит 1, то логарифм всегда равен 0.
Вычисления такого логарифма применяются в балистике при расчете траектории движения объекта, находящегося в непосредственной близости от Земли. Это обусловлено наиболее точным значением ускорением свободного падения, равным 9,81. А при удалении от поверности Земли это значение изменяется, уменьшается пропорционально расстоянию удаления от поверхности.
loga1=0
Логарифм числа, равного основанию
Логарифмическая единица. Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.
logaa=1
Логарифм числа, обратного основанию
Если аргумент логарифма имеет значение обратное основанию, то значение логарифма будет равно -1.
loga1a=-1
Логарифм произведения двух положительных чисел
Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2-х логарифмов, у которых будут одинаковые основания.
logax·y=logax+logay
Логарифм частного
Логарифм частного. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.
logaxy=logax-logay
loga1y=-logay
Логарифм степени положительного числа
Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.
logaxn=nlogax
Логарифм корня числа
Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.
logaxn=logaxn
Основание логарифма в степени
loganx=logaxn, при n≠0
Формула перехода к новому основанию
logax=logbxlogbalogax=1logxa
Производная логарифма
Производная логарифмической функции по основанию равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.
При расчёте производной логарифма необходимо учитывать ложный коэффициент производной, при котором нарастает его гиперболическая составляющая. Это и есть главное условие корректного нахождения производной логарифма. В то же время, нельзя упускать второстепенные составляющие при расчёте. К ним относятся расчеты с применением общей суммы логарифмов, а также пропорциональная составляющая двух вычисляемых логарифмов. Такой подход можно применить не только для вычисления производной натурального логарифма, но и при расчете производной десятичного логарифма при возведении в степень x по основанию a.
logax′=1xlna
примеры решения перехода к новому основанию натурального логарифма и таблица или шпаргалка для этого в 10 классе
Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения. Ранее мы уже познакомились с понятием логарифма. А также рассмотрели основные свойства и примеры решения.
Ранее мы уже познакомились с понятием логарифма. А также рассмотрели основные свойства и примеры решения.
Формулы логарифмов сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства.
Формулы логарифмов. Логарифмы примеры решения
Теперь на основе этих формул(свойств), покажем примеры решения логарифмов.
Примеры решения логарифмов на основании формул
Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения logab = x, что равносильно ax = b, поэтому logaax = x.
Логарифмы, примеры:
log28 = 3, т.к. 23 = 8
log749 = 2, т.к. 72 = 49
log51/5 = -1, т.к. 5-1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
lg100 = 2
log10100 = 2, т.к. 102 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
Основное логарифмическое тождество
a logab = b
Пример.
82log83 = (82log83)2 = 32 = 9
Логарифм произведения равен сумме логарифмов loga (bc) = logab + logac
Пример.
log38,1 + log310 = log3 (8,1*10) = log381 = 4
Логарифм частного равен разности логарифмов
loga (b/c) = logab — logac
Пример.
9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа logab m = mlogab
Показатель степени основания логарифма loganb =1/n*logab
loganb m = m/n*logab,
если m = n, получим loganb n = logab
Пример.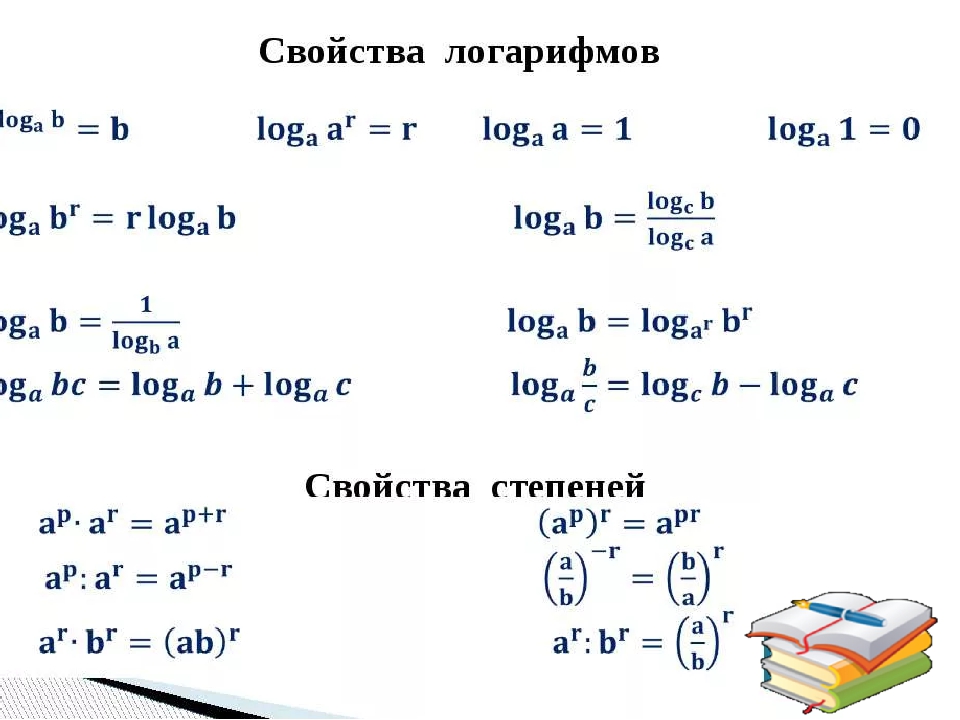
log49 = log223 2 = log23
Переход к новому основанию
logab = logcb/logca,
если c = b, получим logbb = 1
тогда logab = 1/logba
Пример.
log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям.
Источник: https://reshit.ru/formuly-logarifmov-logarifmy-primery-resheniya
Логарифм: что это? Все формулы. Простейшие уравнения и неравенства
Сейчас речь пойдет о трех страшных буквах: l o g.Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).
Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.
А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.
Тогда, если дело касается логарифма:
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?
На самом деле в этом и заключается основная формула (определение логарифма):
Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.
У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).
Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?
Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).
А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).
Как мы не можем существовать без еды, воды, интернета… Так и логарифм не представляет свое существование без ОДЗ.
Всегда, когда существует логарифм, должно быть:
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.
А теперь разберем теорию на практике:
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).
Два нужно четыре раза умножить само на себя, чтобы получить 16.
Ответ: 4.
Источник: https://ik-study.ru/ege_math/logharifmy
Логарифмы: правила, основные свойства и формулы :
Логарифмы и правила действий с ними достаточно емкие и простые. Следовательно, разобраться в данной теме вам не составит труда. После того как вы узнаете все правила натуральных логарифмов, любая задача решится самостоятельно.
Первое знакомство с этой темой может показаться скучным и бессмысленным, но именно при помощи логарифмов решились многие проблемы математиков XVI века. «О чем это?» — подумали вы.
Прочтите статью до конца и узнаете, что этот раздел «царицы наук» может быть интересен не только математикам, ученым точных наук, но и простым ученикам средних школ.
Определение логарифма
Начнем с определения логарифма. Как гласят многие учебники: логарифмом числа b по основанию a (logab) является некое число с, для которого выполняется такое равенство: b=ac.
То есть, говоря простыми словами, логарифм — определенная степень, в которую возводим основание, чтобы получить данное число. Но важно помнить, что логарифм вида logab имеет смысл только при: a>0; a — число, отличное от 1; b>0, следовательно, делаем вывод, что логарифм можно найти только у положительных чисел.
Классификация логарифмов по основанию
Логарифмы могут быть с любым положительным числом в основании. Но также существует два вида: натуральный и десятичный логарифмы:
- Натуральный логарифм — логарифм с основанием е (е — число Эйлера, численно приблизительно равняется 2,7, иррациональное число, которое ввели для показательной функции y = ex), обозначается как ln a = logea;
- Десятичный логарифм — логарифм с основанием 10, то есть log10a = lg a.
Основные правила логарифмов
Для начала нужно познакомиться с основным логарифмическим тождеством: alogab=b, далее следуют два таких основных правила:
- loga1 = 0 — так как любое число в нулевой степени равно 1;
- logaa = 1.
Благодаря открытию логарифма для нас не составит труда решить абсолютно любое показательно уравнение, ответ которого нельзя выразить натуральным числом, а только иррациональным. Например: 5х = 9, х = log59 (так как натурального х для данного уравнения не существует).
Действия с логарифмами:
- loga(x · y) = logax+ logay — чтобы найти логарифм произведения, нужно сложить логарифмы сомножителей.
 Обратите внимание на то, что основания логарифмов одинаковы. Если записать это в обратном порядке, то получим правило сложения логарифмов.
Обратите внимание на то, что основания логарифмов одинаковы. Если записать это в обратном порядке, то получим правило сложения логарифмов. - loga xy = logax — logay — чтобы найти логарифм частного, нужно найти разность логарифмов делимого и делителя. Обратите внимание: основания у логарифмов одинаковы. При записи в обратном порядке получаем правило вычитания логарифмов.
- logakxp = (p/k)*logax — таким образом, если в аргументе и основании логарифма стоят степени, то их можно выносить за знак логарифма.
- logax = logac xc — частный случай предыдущего правила, когда показатели степеней равны, их можно сократить.
- logax = (logbx)(logba) — так называемый модуль перехода, процедура приведения логарифма к другому основанию.
- logax = 1/logxa — частный случай перехода, смена мест основания и данного числа. Все выражение, образно говоря, переворачивается, и логарифм с новым основанием оказывается в знаменателе.
История возникновения логарифмов
В XVI веке возникла необходимость проведения многих приближенных вычислений для решения практических задач, главным образом, в астрономии (например, определение положения судна по Солнцу или звездам).
Эта потребность быстро росла и значительную трудность создавало умножение и деление многозначных чисел. И ученый-математик Непер при тригонометрических расчетах решил заменить трудоемкое умножение на обыкновенное сложение, сопоставив для этого некоторые прогрессии.
Тогда деление, аналогично, заменяется на процедуру попроще и надежнее — вычитание, а дабы извлечь корень n-ой степени, нужно разделить логарифм подкоренного выражения на n. Решение такой нелегкой задачи в математике явно отображало цели Непера в науке.
Вот как он писал об этом в начале своей книги «Рабдология»:
Я всегда старался, насколько позволяли мои силы и способности, освободить людей от трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики.
Название логарифма предложил сам Непер, он был получен путем совмещения греческих слов, которые в сочетании означали “число отношений”.
Основание логарифма ввел Спейдел. Его заимствовал Эйлер из теории о степенях и перенес в теорию логарифмов. Понятие логарифмирования стало известным благодаря Коппе в XIX веке. А использование натуральных и десятичных логарифмов, а также их обозначения появились благодаря Коши.
В 1614 году Джон Непер издал на латыни сочинение «Описание удивительной таблица логарифмов». Там было изложено краткое описание логарифмов, правил и их свойств. Так термин «логарифм» утвердился в точных науках.
Операцию логарифмирования и первое упоминание о ней появилось благодаря Валлису и Иоганну Бернулли, а окончательно установлена она была Эйлером в XVIII веке.
Именно заслуга Эйлера в распространении логарифмической функции вида y = logax на комплексную область. В первой половине XVIII века вышла его книга «Введение в анализ бесконечных», где были современные определения показательной и логарифмической функций.
Логарифмическая функция
Функция вида y = logах (имеет смысл, только если: а > 0, а ≠ 1).
Логарифмическая функция определяется множеством всех положительных чисел, так как запись logах существует только при условии — х > 0;.
Данная функция может принимать абсолютно все значения из множества R (действительных чисел). Так как у всякого действительного числа b есть положительное x, чтобы выполнялось равенство logaх = b, то есть, это уравнение имеет корень — х = аb (следует из того, что logaab= b).
Функция возрастает на промежутке a>0, а убывает на промежутке 01.
Следует помнить, что любые графики логарифмической функции у = logах имеют одну стационарную точку (1;0), так как logа 1 = 0. Это хорошо видно на иллюстрации графика ниже.
Это хорошо видно на иллюстрации графика ниже.
Как видим на изображениях, функция не имеет четности или нечетности, не имеет наибольших или наименьших значений, не ограничена сверху или снизу.
Логарифмическая функция y = logаx и показательная функция y = aх, где (а>0, а≠1), взаимно обратные. Это можно видеть на изображении их графиков.
Решение задач с логарифмами
Обычно решение задачи, содержащей логарифмы, основано на преобразовании их в стандартный вид или же направлено на упрощение выражений под знаком логарифма. Или же стоит переводить обычные натуральные числа в логарифмы с нужным основанием, проводить дальнейшие операции по упрощению выражения.
Есть некие тонкости, которые не стоит забывать:
- При решении неравенств, когда обе части стоят под логарифмами по правилу с одним основанием, не спешите «отбрасывать» знак логарифма. Помните о промежутках монотонности логарифмической функции. Так как, если основание больше 1 (случай, когда функция возрастает) — знак неравенства останется без изменений, но когда основание больше 0 и меньше 1 (случай, когда функция убывает) — знак неравенства изменится на противоположный;
- Не забывайте определения логарифма: logах = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. ОДЗ (область допустимых значений) существует практически для всех сложных функций.
При решении логарифмических уравнений рекомендуется пользоваться равносильными преобразованиями. Также, необходимо быть внимательным и учитывать возможные преобразования, которые способны привести к потере некоторых корней.
Это банальные, но масштабные ошибки, с которыми столкнулись многие на пути поиска верного ответа для задания. Правил решения логарифмов не так уж и много, поэтому эта тема проще, чем другие и последующие, но в ней стоит хорошо разобраться.
Вывод
Данная тема с первого взгляда может показаться сложной и громоздкой, но, исследуя ее глубже и глубже, начинаешь понимать, что тема просто заканчивается, а сложностей так ничего и не вызвало. Мы рассмотрели все свойства, правила и даже ошибки, касающиеся темы логарифмов. Успехов в обучении!
Мы рассмотрели все свойства, правила и даже ошибки, касающиеся темы логарифмов. Успехов в обучении!
Источник: https://www.syl.ru/article/407401/logarifmyi-pravila-osnovnyie-svoystva-i-formulyi
Свойства логарифмов
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что ac = b: log a b=c⇔ a c =b (a>0,a≠1,b>0)
Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Основное логарифмическое тождество
a log a b =b (a>0,a≠1) (2)
Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Два очевидных следствия определения логарифма
log a a=1 (a>0,a≠1) (3) log a 1=0 (a>0,a≠1) (4)
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.
Логарифм произведения и логарифм частного
log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) (5)
log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) (6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
Действительно, выражение log a (f(x)g(x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.
Преобразуя данное выражение в сумму log a f(x)+ log a g(x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Степень можно выносить за знак логарифма
log a b p =p log a b (a>0,a≠1,b>0) (7)
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
log a (f (x) 2 =2 log a f(x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Формула перехода к новому основанию
log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)
Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .
Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)
Несколько простых примеров с логарифмами
Пример 1. Вычислите: lg2 + lg50. Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5. Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b =b (a>0,a≠1) |
| log a a=1 (a>0,a≠1) |
| log a 1=0 (a>0,a≠1) |
| log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) |
| log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) |
| log a b p =p log a b (a>0,a≠1,b>0) |
| log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) |
| log a b= 1 log b a (a>0,a≠1,b>0,b≠1) |
Источник: http://www.repetitor2000.ru/svoistva_logarifmov_01.html
Вычисление логарифмов: способы, примеры, решения
Вычисление логарифмов по определению
В простейших случаях возможно достаточно быстро и легко выполнить нахождение логарифма по определению. Давайте подробно рассмотрим, как происходит этот процесс.
Его суть состоит в представлении числа b в виде ac, откуда по определению логарифма число c является значением логарифма. То есть, нахождению логарифма по определению отвечает следующая цепочка равенств: logab=logaac=c.
Итак, вычисление логарифма по определению сводится к нахождению такого числа c, что ac=b, а само число c есть искомое значение логарифма.
Учитывая информацию предыдущих абзацев, когда число под знаком логарифма задано некоторой степенью основания логарифма, то можно сразу указать, чему равен логарифм – он равен показателю степени. Покажем решения примеров.
Найдите log22−3, а также вычислите натуральный логарифм числа e5,3.
Определение логарифма позволяет нам сразу сказать, что log22−3=−3. Действительно, число под знаком логарифма равно основанию 2 в −3 степени.
Аналогично находим второй логарифм: lne5,3=5,3.
log22−3=−3 и lne5,3=5,3.
Если же число b под знаком логарифма не задано как степень основания логарифма, то нужно внимательно посмотреть, нельзя ли прийти к представлению числа b в виде ac. Часто такое представление бывает достаточно очевидно, особенно когда число под знаком логарифма равно основанию в степени 1, или 2, или 3, …
Вычислите логарифмы log525, и .
log525=2, и .
Когда под знаком логарифма находится достаточно большое натуральное число, то его не помешает разложить на простые множители. Это часто помогает представить такое число в виде некоторой степени основания логарифма, а значит, вычислить этот логарифм по определению.
В заключение этого пункта отметим, что мы не ставили целью рассмотреть все способы представления числа под знаком логарифма в виде некоторой степени основания. Наша цель заключалась в том, чтобы дать самые часто используемые варианты действий, приводящие к результату при вычислении логарифмов по определению.
Как решать «вложенные» логарифмические уравнения
Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого логарифма. Оба уравнения мы будем решать с помощью канонической формы.Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого. Оба уравнения мы будем решать с помощью канонической формы. Напомню, если у нас есть простейшее логарифмическое уравнение вида logaf(x) = b, то для решения такого уравнения мы выполняем следующие шаги. В первую очередь, нам нужно заменить число b:
b = logaab
Заметьте: ab— это аргумент. Точно так же в исходном уравнении аргументом является функция f(x). Затем мы переписываем уравнение и получаем вот такую конструкцию:
logaf(x) = logaab
Уже затем мы можем выполнить третий шаг — избавится от знака логарифма и просто записать:
f(x) = ab
В результате мы получим новое уравнение. При этом никаких ограничений на функцию f(x) не накладывается. Например, на ее месте также может стоять логарифмическая функция. И тогда мы вновь получим логарифмическое уравнение, которое снова сведем к простейшему и решим через каноническую форму.
При этом никаких ограничений на функцию f(x) не накладывается. Например, на ее месте также может стоять логарифмическая функция. И тогда мы вновь получим логарифмическое уравнение, которое снова сведем к простейшему и решим через каноническую форму.
Впрочем, хватит лирики. Давайте решим настоящую задачу. Итак, задача № 1:
log2 (1 + 3 log2x) = 2
Как видим, перед нами простейшее логарифмическое уравнение. В роли f(x) выступает конструкция 1 + 3 log2x, а в роли числа b выступает число 2 (в роли aтакже выступает двойка). Давайте перепишем эту двойку следующим образом:
2 = log2 22
Важно понимать, что первые две двойки пришли к нам из основания логарифма, т. е. если бы в исходном уравнении стояла 5, то мы бы получили, что 2 = log5 52. В общем, основание зависит исключительно от логарифма, который изначально дан в задаче. И в нашем случае это число 2.
Итак, переписываем наше логарифмическое уравнение с учетом того, что двойка, которая стоит справа, на самом деле тоже является логарифмом. Получим:
log2 (1 + 3 log2x) = log2 4
Переходим к последнему шагу нашей схемы — избавляемся от канонической формы. Можно сказать, просто зачеркиваем знаки log. Однако с точки зрения математики «зачеркнуть log» невозможно — правильнее сказать, что мы просто просто приравниваем аргументы:
1 + 3 log2x = 4
Отсюда легко находится 3 log2x:
3 log2x = 3
log2x = 1
Мы вновь получили простейшее логарифмическое уравнение, давайте снова приведем его к канонической форме. Для этого нам необходимо провести следующие изменения:
1 = log2 21 = log2 2
Почему в основании именно двойка? Потому что в нашем каноническом уравнении слева стоит логарифм именно по основанию 2. Переписываем задачу с учетом этого факта:
log2x = log2 2
Снова избавляемся от знака логарифма, т. е. просто приравниваем аргументы. Мы вправе это сделать, потому что основания одинаковые, и больше никаких дополнительных действий ни справа, ни слева не выполнялось:
е. просто приравниваем аргументы. Мы вправе это сделать, потому что основания одинаковые, и больше никаких дополнительных действий ни справа, ни слева не выполнялось:
х = 2
Вот и все! Задача решена. Мы нашли решение логарифмического уравнения.
Обратите внимание! Хотя переменная х и стоит в аргументе (т. е. возникают требования к области определения), мы никаких дополнительных требований предъявлять не будем.
Как я уже говорил выше, данная проверка является избыточной, если переменная встречается лишь в одном аргументе лишь одного логарифма. В нашем случае х действительно стоит лишь в аргументе и лишь под одним знаком log. Следовательно, никаких дополнительных проверок выполнять не требуется.
Тем не менее, если вы не доверяете данному методу, то легко можете убедиться, что х = 2 действительно является корнем. Достаточно подставить это число в исходное уравнение.
Давайте перейдем ко второму уравнению, оно чуть интересней:
log2 (log1/2 (2x− 1) + log2 4) = 1
Если обозначить выражение внутри большого логарифма функцией f(x), получим простейшее логарифмическое уравнение, с которого мы начинали сегодняшний видеоурок. Следовательно, можно применить каноническую форму, для чего придется представить единицу в виде log2 21 = log2 2.
Переписываем наше большое уравнение:
log2 (log1/2 (2x − 1) + log2 4) = log2 2
Изваляемся от знака логарифма, приравнивая аргументы. Мы вправе это сделать, потому что и слева, и справа основания одинаковые. Кроме того, заметим, что log2 4 = 2:
log1/2 (2x− 1) + 2 = 2
log1/2 (2x− 1) = 0
Перед нами снова простейшее логарифмическое уравнение вида logaf(x) = b. Переходим к канонической форме, т. е. представляем ноль в виде log1/2 (1/2)0 = log1/2 1.
Переписываем наше уравнение и избавляемся от знака log, приравнивая аргументы:
log1/2 (2x− 1) = log1/2 1
2x − 1 = 1
2х = 2
х = 1
Опять же мы сразу получили ответ. Никаких дополнительных проверок не требуется, потому что в исходном уравнении лишь один логарифм содержит функцию в аргументе.
Никаких дополнительных проверок не требуется, потому что в исходном уравнении лишь один логарифм содержит функцию в аргументе.
Следовательно, никаких дополнительных проверок выполнять не требуется. Мы можем смело утверждать, что х = 1 является единственным корнем данного уравнения.
А вот если бы во втором логарифме вместо четверки стояла бы какая-то функция от х (либо 2х стояло бы не в аргументе, а в основании) — вот тогда потребовалось бы проверять область определения. Иначе велик шанс нарваться на лишние корни.
Откуда возникают такие лишние корни? Этот момент нужно очень четко понимать. Взгляните на исходные уравнения: везде функция х стоит под знаком логарифма. Следовательно, поскольку мы записали log2x, то автоматически выставляем требование х > 0. Иначе данная запись просто не имеет смысла.
Однако по мере решения логарифмического уравнения мы избавляемся от всех знаков log и получаем простенькие конструкции. Здесь уже никаких ограничений не выставляется, потому что линейная функция определена при любом значении х.
Именно эта проблема, когда итоговая функция определена везде и всегда, а исходная — отнюдь не везде и не всегда, и является причиной, по которой в решении логарифмических уравнениях очень часто возникают лишние корни.
Но повторю еще раз: такое происходить лишь в ситуации, когда функция стоит либо в нескольких логарифмах, либо в основании одного из них. В тех задачах, которые мы рассматриваем сегодня, проблем с расширением области определения в принципе не существует.
Тонкости и хитрости решения
Сегодня мы переходим к более сложным задачам и будем решать логарифмическое уравнение, в основании которого стоит не число, а функция.
И пусть даже эта функция линейна — в схему решения придется внести небольшие изменения, смысл которых сводится к дополнительным требованиям, накладываемым на область определения логарифма.
Логарифмические уравнения. Методы решения
На самом деле существует целая масса подходов: это и разложение на множители, и потенцирование, и замена, и работа с основаниями…
Но все методы решения логарифмических уравнения роднит одно: их цель свести логарифмические уравнения к простейшему виду::
Если уравнение сведено к такому, что слева и справа от знака «равно» стоят логарифмы с одним основанием, то логарифмы мы «зачеркиваем» и решаем оставшееся уравнение. |
Однако, тут есть один подводный камень: поскольку логарифм определен только тогда, когда
то после нахождения корней логарифмического уравнения, мы обязаны сделать проверку!!! Я не поленюсь и повторю еще раз:
В ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЯХ МЫ ВСЕГДА ДЕЛАЕМ ПРОВЕРКУ ПОЛУЧЕННЫХ КОРНЕЙ!!
Те учащиеся, которые игнорируют это требование, как правило допускают глупейшие и непростительные ошибки!
Согласись, обидно решить правильно уравнение, а потом не сделать самую малость: проверку, и записать лишние корни, и записать из-за этого неправильный ответ!
Формулы логарифмов. Логарифмы примеры решения
Теперь на основе этих формул(свойств), покажем примеры решения логарифмов.
Примеры решения логарифмов на основании формул
Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения logab = x, что равносильно ax = b, поэтому logaax = x.
Логарифмы, примеры:
log28 = 3, т.к. 23 = 8
log749 = 2, т.к. 72 = 49
log51/5 = -1, т.к. 5-1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
lg100 = 2
log10100 = 2, т.к. 102 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
Основное логарифмическое тождество
a logab = b
Пример.
82log83 = (82log83)2 = 32 = 9
Логарифм произведения равен сумме логарифмов loga (bc) = logab + logac
Пример.
log38,1 + log310 = log3 (8,1*10) = log381 = 4
Логарифм частного равен разности логарифмов
loga (b/c) = logab — logac
Пример.
9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа logab m = mlogab
Показатель степени основания логарифма loganb =1/n*logab
loganb m = m/n*logab,
если m = n, получим loganb n = logab
Пример.
log49 = log223 2 = log23
Переход к новому основанию
logab = logcb/logca,
если c = b, получим logbb = 1
тогда logab = 1/logba
Пример.
log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям.
Область допустимых значений (ОДЗ) логарифма
Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться .
Почему так?
Начнем с простого: допустим, что . Тогда, например, число не существует, так как в какую бы степень мы не возводили , всегда получается . Более того, не существует ни для какого . Но при этом может равняться чему угодно (по той же причине – в любой степени равно ). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае : в любой положительной степени – это , а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что ).
При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть ), а вот не существует.
Например, (то есть ), а вот не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:
Решим уравнение .
Вспомним определение: логарифм – это степень, в которую надо возвести основание , чтобы получить аргумент . И по условию, эта степень равна : .
Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна , а произведение . Легко подобрать, это числа и .
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
– верно.
– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
Тогда, получив корни и , сразу отбросим корень , и напишем правильный ответ.
Использование свойств логарифмов при вычислении
Мощным инструментом вычисления логарифмов является использование свойств логарифмов.
Некоторые свойства логарифмов позволяют сразу указать значение логарифмов. К таким свойствам относятся свойство логарифма единицы и свойство логарифма числа, равного основанию: log11=logaa0=0 и logaa=logaa1=1. То есть, когда под знаком логарифма находится число 1 или число a, равное основанию логарифма, то в этих случаях логарифмы равны 0 и 1 соответственно.
Чему равны логарифмы и lg10?
Так как , то из определения логарифма следует .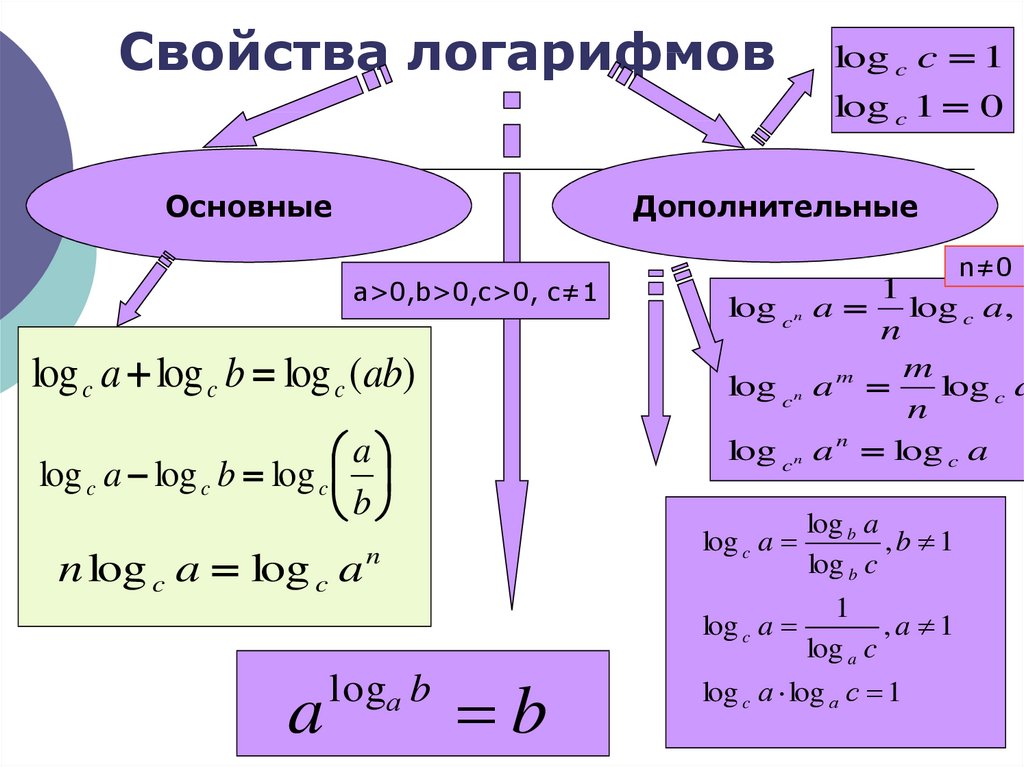
Во втором примере число 10 под знаком логарифма совпадает с его основанием, поэтому десятичный логарифм десяти равен единице, то есть, lg10=lg101=1.
и lg10=1.
Отметим, что вычисление логарифмов по определению (которое мы разобрали в предыдущем пункте) подразумевает использование равенства logaap=p, которое является одним из свойств логарифмов.
На практике, когда число под знаком логарифма и основание логарифма легко представляются в виде степени некоторого числа, очень удобно использовать формулу , которая соответствует одному из свойств логарифмов. Рассмотрим пример нахождения логарифма, иллюстрирующий использование этой формулы.
Вычислите логарифм .
.
Не упомянутые выше свойства логарифмов также используются при вычислении, но об этом поговорим в следующих пунктах.
Зачем в жизни нужны логарифмы?
Я уже говорил, что математики СУПЕРленивые люди? Это правда.
Вот представь себе, им лень умножать и они придумали логарифмы, которые позволяют заменить умножение сложением!
Им еще больше лень возводить в степень и они используют логарифмы, чтобы заменить возведение в степень умножением или делением!
То есть они используют логарифмы, чтобы быстро проделывать громоздкие вычисления.
Круто, да?
Пример Найдите корень уравнения.
Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:
То есть внесем число 3 справа под знак логарифма.
или
Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим
Делаем проверку:
Получаем:
Ответ:
Степень можно выносить за знак логарифма
log a b p =p log a b (a>0,a≠1,b>0) (7)
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
log a (f (x) 2 =2 log a f(x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Формула перехода к новому основанию
log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)
Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .
Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)
Несколько простых примеров с логарифмами
Пример 1. Вычислите: lg2 + lg50. Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5. Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b =b (a>0,a≠1) |
| log a a=1 (a>0,a≠1) |
| log a 1=0 (a>0,a≠1) |
| log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) |
| log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) |
| log a b p =p log a b (a>0,a≠1,b>0) |
| log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) |
| log a b= 1 log b a (a>0,a≠1,b>0,b≠1) |
Сложные задачи
Этот урок будет довольно длинным. В нем мы разберем два довольно серьезных логарифмических уравнения, при решении которых многие ученики допускают ошибки. За свою практику работы репетитором по математике я постоянно сталкивался с двумя видами ошибок:
В нем мы разберем два довольно серьезных логарифмических уравнения, при решении которых многие ученики допускают ошибки. За свою практику работы репетитором по математике я постоянно сталкивался с двумя видами ошибок:
- Возникновение лишних корней из-за расширения области определения логарифмов. Чтобы не допускать такие обидные ошибки, просто внимательно следите за каждым преобразованием;
- Потери корней из-за того, что ученик забыл рассмотреть некоторые «тонкие» случаи — именно на таких ситуациях мы сегодня и сосредоточимся.
Это последний урок, посвященный логарифмическим уравнениям. Он будет длинным, мы разберем сложные логарифмические уравнения. Устраивайтесь поудобней, заварите себе чай, и мы начинаем.
Первое уравнение выглядит вполне стандартно:
logx + 1 (x − 0,5) = logx − 0,5 (x + 1)
Сразу заметим, что оба логарифма являются перевернутыми копиями друг друга. Вспоминаем замечательную формулу:
logab = 1/logba
Однако у этой формулы есть ряд ограничений, которые возникают в том случае, если вместо чисел а и b стоят функции от переменной х:
b > 0
1 ≠ a > 0
Эти требования накладываются на основание логарифма. С другой стороны, в дроби от нас требуется 1 ≠ a > 0, поскольку не только переменная a стоит в аргументе логарифма ( следовательно, a > 0), но и сам логарифм находится в знаменателе дроби. Но logb 1 = 0, а знаменатель должен быть отличным от нуля, поэтому a ≠ 1.
Итак, ограничения на переменную a сохраняется. Но что происходит с переменной b? С одной стороны, из основания следует b> 0, с другой — переменная b≠ 1, потому что основание логарифма должно быть отлично от 1. Итого из правой части формулы следует, что 1 ≠ b > 0.
Но вот беда: второе требование (b ≠ 1) отсутствует в первом неравенстве, посвященном левому логарифму. Другими словами, при выполнении данного преобразования мы должны отдельно проверить, что аргумент bотличен от единицы!
Вот давайте и проверим. Применим нашу формулу:
Применим нашу формулу:
А теперь, прежде чем идти дальше, выпишем все требования области определения, накладываемые на исходную задачу:
1 ≠ х − 0,5 > 0; 1 ≠ х + 1 > 0
Вот мы и получили, что уже из исходного логарифмического уравнения следует, что и а, и b должны быть больше 0 и не равны 1. Значит, мы спокойно можем переворачивать логарифмическое уравнение:
Предлагаю ввести новую переменную:
logx + 1 (x − 0,5) = t
В этом случае наша конструкция перепишется следующим образом:
(t2− 1)/t = 0
Заметим, что в числителе у нас стоит разность квадратов. Раскрываем разность квадратов по формуле сокращенного умножения:
(t − 1)(t + 1)/t = 0
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Но в числителе стоит произведение, поэтому приравниваем к нулю каждый множитель:
t1 = 1;
t2 = −1;
t ≠ 0.
Как видим, оба значения переменной tнас устраивают. Однако на этом решение не заканчивается, ведь нам требуется найти не t, а значение x. Возвращаемся к логарифму и получаем:
logx + 1 (x − 0,5) = 1;
logx + 1 (x − 0,5) = −1.
Давайте приведем каждое из этих уравнений к канонической форме:
logx + 1 (x − 0,5) = logx + 1 (x + 1)1
logx + 1 (x − 0,5) = logx + 1 (x + 1)−1
Избавляемся от знака логарифма в первом случае и приравниваем аргументы:
х − 0,5 = х + 1;
х − х = 1 + 0,5;
0 = 1,5.
Такое уравнение не имеет корней, следовательно, первое логарифмическое уравнение также не имеет корней. А вот со вторым уравнением все намного интересней:
(х − 0,5)/1 = 1/(х + 1)
Решаем пропорцию — получим:
(х − 0,5)(х + 1) = 1
Напоминаю, что при решении логарифмических уравнений гораздо удобней приводить все десятичные дроби обычные, поэтому давайте перепишем наше уравнение следующим образом:
(х − 1/2)(х + 1) = 1;
x2 + x− 1/2x− 1/2 − 1 = 0;
x2 + 1/2x− 3/2 = 0.
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
(х + 3/2) (х − 1) = 0;
x1 = −1,5;
x2 = 1.
Получили два корня — они являются кандидатами на решение исходного логарифмического уравнения. Для того чтобы понять, какие корни действительно пойдут в ответ, давайте вернемся к исходной задаче. Сейчас мы проверим каждый из наших корней на предмет соответствия области определения:
1,5 ≠ х > 0,5; 0 ≠ х > −1.
Эти требования равносильны двойному неравенству:
1 ≠ х > 0,5
Отсюда сразу видим, что корень х = −1,5 нас не устраивает, а вот х = 1 вполне устраивает. Поэтому х = 1 — окончательное решение логарифмического уравнения.
Переходим ко второй задаче:
logx 25 + log125x 5 = log25x 625
На первый взгляд может показаться, что у всех логарифмов разные основания и разные аргументы. Что делать с такими конструкциями? В первую очередь заметим, что числа 25, 5 и 625 — это степени 5:
25 = 52>;>4
А теперь воспользуемся замечательным свойством логарифма. Дело в том, что можно выносить степени из аргумента в виде множителей:
logabn = n ∙ logab
На данное преобразование также накладываются ограничения в том случае, когда на месте bстоит функция. Но у нас b— это просто число, и никаких дополнительных ограничений не возникает. Перепишем наше уравнение:
2 ∙ logx 5 + log125x 5 = 4 ∙ log25x 5
Получили уравнение с тремя слагаемыми, содержащими знак log. Причем аргументы всех трех логарифмов равны.
Самое время перевернуть логарифмы, чтобы привести их к одному основанию — 5. Поскольку в роли переменной b выступает константа, никаких изменений области определения не возникает. Просто переписываем:
Как и предполагалось, в знаменателе «вылезли» одни и те же логарифмы. Предлагаю выполнить замену переменной:
log5x = t
В этом случае наше уравнение будет переписано следующим образом:
Выпишем числитель и раскроем скобки:
2 (t + 3) (t + 2) + t (t + 2) − 4t (t + 3) = 2 (t2 + 5t + 6) + t2 + 2t − 4t2 − 12t = 2t2 + 10t + 12 + t2 + 2t − 4t2 − 12t = −t2 + 12
Возвращаемся к нашей дроби. Числитель должен быть равен нулю:
А знаменатель — отличен от нуля:
t ≠ 0; t ≠ −3; t ≠ −2
Последние требования выполняются автоматически, поскольку все они «завязаны» на целые числа, а все ответы — иррациональные.
Итак, дробно-рациональное уравнение решено, значения переменной t найдены. Возвращаемся к решению логарифмического уравнения и вспоминаем, что такое t:
Приводим это уравнение к канонической форме, получим число с иррациональной степенью. Пусть это вас не смущает — даже такие аргументы можно приравнять:
У нас получилось два корня. Точнее, два кандидата в ответы — проверим их на соответствие области определения. Поскольку в основании логарифма стоит переменная х, потребуем следующее:
1 ≠ х > 0;
С тем же успехом утверждаем, что х ≠ 1/125, иначе основание второго логарифма обратится в единицу. Наконец, х ≠ 1/25 для третьего логарифма.
Итого мы получили четыре ограничения:
1 ≠ х > 0; х ≠ 1/125; х ≠ 1/25
А теперь вопрос: удовлетворяют ли наши корни указанным требованиям? Конечно удовлетворяют! Потому что 5 в любой степени будет больше нуля, и требование х > 0 выполняется автоматически.
С другой стороны, 1 = 50, 1/25 = 5−2, 1/125 = 5−3, а это значит, что данные ограничения для наших корней (у которых, напомню, в показателе стоит иррациональное число) также выполнены, и оба ответа являются решениями задачи.
Итак, мы получили окончательный ответ. Ключевых моментов в данной задаче два:
- Будьте внимательны при перевороте логарифма, когда аргумент и основание меняются местами. Подобные преобразования накладывают лишние ограничения на область определения.
- Не бойтесь преобразовывать логарифмы: их можно не только переворачивать, но и раскрывать по формуле суммы и вообще менять по любым формулам, которые вы изучали при решении логарифмических выражений. Однако при этом всегда помните: некоторые преобразования расширяют область определения, а некоторые — сужают.
Логарифм: что это? Все формулы. Простейшие уравнения и неравенства
Сейчас речь пойдет о трех страшных буквах: l o g.Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).
Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.
А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.
Тогда, если дело касается логарифма:
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?
На самом деле в этом и заключается основная формула (определение логарифма):
Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.
У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).
Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?
Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).
А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).
Как мы не можем существовать без еды, воды, интернета… Так и логарифм не представляет свое существование без ОДЗ.
Всегда, когда существует логарифм, должно быть:
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.
А теперь разберем теорию на практике:
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).
Два нужно четыре раза умножить само на себя, чтобы получить 16.
Ответ: 4.
Нахождение логарифмов через другие известные логарифмы
Информация этого пункта продолжает тему использования свойств логарифмов при их вычислении. Но здесь основное отличие состоит в том, что свойства логарифмов используются для того, чтобы выразить исходный логарифм через другой логарифм, значение которого известно. Приведем пример для пояснения. Допустим, мы знаем, что log23≈1,584963, тогда мы можем найти, например, log26, выполнив небольшое преобразование с помощью свойств логарифма: log26=log2(2·3)=log22+log23≈
В приведенном примере нам было достаточно использовать свойство логарифма произведения. Однако намного чаще приходится применять более широкий арсенал свойств логарифмов, чтобы вычислить исходный логарифм через заданные.
Вычислите логарифм 27 по основанию 60, если известно, что log602=a и log605=b.
Итак, нам нужно найти log6027. Несложно заметить, что 27=33, и исходный логарифм в силу свойства логарифма степени можно переписать как 3·log603.
Теперь посмотрим, как log603 выразить через известные логарифмы. Свойство логарифма числа, равного основанию, позволяет записать равенство log6060=1. С другой стороны log6060=log60(22·3·5)=
Наконец, вычисляем исходный логарифм: log6027=3·log603=
log6027=3·(1−2·a−b)=3−6·a−3·b.
Отдельно стоит сказать о значении формулы перехода к новому основанию логарифма вида . Она позволяет от логарифмов с любыми основаниями переходить к логарифмам с конкретным основанием, значения которых известны или есть возможность их отыскать. Обычно от исходного логарифма по формуле перехода переходят к логарифмам по одному из оснований 2, e или 10, так как по этим основаниям существуют таблицы логарифмов, позволяющие с определенной степенью точности вычислять их значения. В следующем пункте мы покажем, как это делается.
Источники
- http://www.cleverstudents.ru/logarithms/computation_of_logarithms.html
- https://www.berdov.com/docs/logarithm/reshenie-logarifmicheskih-uravneniy/
- https://youclever.org/book/logarifmicheskie-uravneniya-1
- https://rgiufa.ru/matematika-fizika-himiya/kakie-sushhestvuyut-formuly-logarifmov.html
- https://youclever.org/book/logarifmy-1
- https://repetitor-mathematics.ru/kak-reshat-logarifmicheskie-uravneniya-podrobnyiy-razbor/
Свойства логарифма — объяснение и примеры
Прежде чем перейти к свойствам логарифмов, давайте кратко обсудим связь между логарифмами и показателями . Логарифм числа определяется как степень или индекс, до которого необходимо возвести данное основание, чтобы получить число.
Учитывая это, x = M; где a и M больше нуля и a 1, то мы можем символически представить это в логарифмической форме как;
log a M = x
Примеры:
- 2 -3 = 1 / 8 ⇔ log 2 ( 1 / 8 ) = -3
- 10 -2 = 0.01 ⇔ log 10 01 = -2
- 2 6 = 64 ⇔ log 2 64 = 6
- 3 2 = 9 log 3 9 = 2
- 5 4 = 625 ⇔ журнал 5 625 = 4
- 7 0 = 1 ⇔ журнал 7 1 = 0
- 3 — 4 = 1/3 4 = 1/81 ⇔ журнал 3 1/81 = -4
- 10 -2 = 1/100 = 0,01 ⇔ лог 10 01 = -2
Логарифмические свойства
Логарифмические свойства и правила полезны, потому что они позволяют нам расширять, сжимать или решать логарифмические уравнения.Это по этим причинам.
В большинстве случаев вам предлагается запомнить правила при решении логарифмических задач, но как эти правила выводятся.
В этой статье мы рассмотрим свойства и правила логарифмов, полученных с помощью законов экспонент.
Свойство произведения логарифмов
Правило произведения гласит, что умножение двух или более логарифмов с общим основанием равно сложению отдельных логарифмов i.е.
log a (MN) = log a M + log a N
Доказательство
- Пусть x = log a M и y = log a
- Конвертировать каждое из эти уравнения к экспоненциальной форме.
⇒ a x = M
⇒ a y = N
- Умножьте экспоненциальные члены (M & N):
a x * a y = MN
- Поскольку основание обычное, поэтому сложите экспоненты:
a x + y = MN
- Взятие журнала с основанием «a» с обеих сторон.
журнал a (a x + y ) = log a (MN)
- Применение правила логарифма степени.
log a M n ⇒ n log a M
(x + y) log a a = log a (MN)
(x + y) = log a (MN)
- Теперь подставим значения x и y в уравнение, которое мы получили выше.
log a M + log a N = log a (MN)
Следовательно, доказано
log a (MN) = log a M + log a N
Примеры:
- log50 + log 2 = log100 = 2
- log 2 (4 x 8) = log 2 (2 2 x 2 3 ) = 5
Частное свойство логарифмов
Это правило гласит, что отношение двух логарифмов с одинаковым основанием равно разности логарифмов i.е.
журнал a (M / N) = журнал a M — журнал a N
Доказательство
- Пусть x = log a M и y = log a
- Преобразовать каждое из этих уравнений к экспоненциальной форме.
⇒ a x = M
⇒ a y = N
- Разделите экспоненциальные члены (M и N):
a x / a y = M / N
- Поскольку основание обычное, вычтите экспоненты:
a x — y = M / N
- Взятие бревна с основанием «a» с обеих сторон.
log a (a x — y ) = log a (M / N)
- Применение логарифмического правила степени с обеих сторон.
log a M n ⇒ n log a M
(x — y) log a a = log a (M / N)
(x — y) = log a (M / N)
- Теперь подставим значения x и y в уравнение, которое мы получили выше.
log a M — log a N = log a (M / N)
Следовательно, доказано
log a (M / N) = log a M — log a N
Степенное свойство логарифмов
В соответствии со степенным свойством логарифма логарифм числа «M» с показателем «n» равен произведению показателя степени с логарифмом числа ( без экспоненты) i.е.
log a M n = n log a M
Доказательство
x = log a M
- Перепишите в виде экспоненциального уравнения.
a x = M
- Возьмите степень n в обеих частях уравнения.
(a x ) n = M n
⇒ a xn = M n
- Зарегистрируйте обе части уравнения с основанием a.
log a a xn = log a M n
- log a a xn = log a M n ⇒ xn log a a = log a M n ⇒ xn = log a M n
- Теперь подставьте значения x и y в уравнение, которое мы получили выше, и упростите.
Мы знаем,
x = log a M
Итак,
xn = log a M n ⇒ n log a M = log a M n
Следовательно , доказано
log a M n = n log a M
Примеры:
log100 3 = 3 log100 = 3 x 2 = 6
Изменение базового свойства логарифмов
Согласно изменение базового свойства логарифма, мы можем переписать данный логарифм как отношение двух логарифмов с любым новым основанием.Он задается как:
log a M = log b M / log b N
или
log a M = log b M × log N b
Доказательство. можно сделать, используя свойство один к одному и правило мощности для логарифмов.
Доказательство
- Выразите каждый логарифм в экспоненциальной форме, разрешив;
Пусть,
x = log N M
- Преобразует его в экспоненциальную форму,
M = N x
- Применить свойство один к одному.
log b N x = log b M
x log b N = log b M
x = log b M / log b N
- Подстановка значение x.
log a M = log b M / log b N
или мы можем записать это как,
log a M = log b M × log a b
Значит, доказано.
Другие свойства логарифмов включают:
- Логарифм от 1 до любого конечного ненулевого основания равен нулю.
Доказательство:
log a 1 = 0⟹ a 0 = 1
- Логарифм любого положительного числа с тем же основанием равен 1.
Доказательство:
log a a = 1 ⟹ a 1 = a
Пример:
log 5 15 = log 15 / log 5
Практические вопросы1. Выразите следующие логарифмы в виде одного выражения
a. журнал 5 (x + 2) + журнал 5 (x — 2)
б.2log x — журнал (x -1)
c. 3log 2 (x) + log 2 (y — 2) — 2log a (z)
d. 4 log b (x + 2) — 3log b (x — 5)
e. 2log a (y) + 0,5log a (x + 4)
f. 2ln 8 + 5ln x
2. Разверните следующие логарифмы
a. журнал 2 (4xy 5 )
б. журнал (xy / z)
c. журнал 5 (ab) 1/2
d. журнал 4 (2x) 2
e.log 6 (ab) 4
3. Решите x в log (x — 2) — log (2x — 3) = log 2
4. Запишите эквивалентный логарифм log 2 x 8 .
5. Решите относительно x в каждом из следующих логарифмических уравнений
a. журнал 2 x = 3
б. журнал x 8 = 3
c. журнал 3 x = 1
d. журнал 3 [1 / (x + 1)] = 2
эл. журнал 4 [(x + 1) / (2x — 1)] = 0
f.журнал (1 / x + 1) = 2
г. log x 0,0001 = 4
6. Упростите журнал a a y
7. Запишите журнал b (2x + 1) = 3 в экспоненциальной форме.
8. Решите следующие логарифмы без калькулятора:
a. журнал 9 3
б. журнал 10000
c. ln e 7
d. ln 1
e. ln e -3
Предыдущий урок | Главная страница | Следующий урокСвойства логарифмов
Свойства логарифмовСодержание: Эта страница соответствует § 4.3 (с. 341) текста.
Предлагаемые задачи из текста:
с. 345 № 3, 7, 9, 11, 13, 25, 27, 33, 35, 45, 49, 53, 91
Изменение базы
Свойства логарифмов
Изменение базы
В то время как большинство научных калькуляторов имеют кнопки только для десятичного и натурального логарифмов, другие логарифмы могут быть вычислены с помощью следующей формулы замены основания.
Формула смены базы
Пример 1 .
Журнал вычислений 5 3. Формула замены базы позволяет нам вычислить это выражение, используя любое другое логарифм, поэтому мы решим эту проблему двумя способами, используя сначала натуральный логарифм, а затем десятичный.
Натуральный логарифм:
десятичный логарифм:
Упражнение 1 :
Из логарифмического тождества 1 следует, что log 2 8 = 3.
(a) Используйте калькулятор и формулу замены основания с натуральным логарифмом, чтобы убедиться, что логарифм 2 8 = 3.
(b) Используйте калькулятор и формулу замены основания с десятичным логарифмом, чтобы убедиться, что журнал 2 8 = 3.
Ответ
Упражнение 2 :
Из логарифмического тождества 2 следует, что. Убедитесь в этом, оценив log 4 7, а затем возведя 4 в эту степень.
Ответ
Вернуться к содержанию
Свойства логарифмов
| 1. log a (uv) = log a u + log a v | 1. ln (uv) = ln u + ln v |
| 2. log a (u / v) = log a u — log a v | 2. ln (u / v) = ln u — ln v |
| 3.журнал a u n = n журнал a u | 3. ln u n = n ln u |
Свойства слева относятся к любому основанию a.
Свойства справа являются повторением общих свойств натурального логарифма.
Многие логарифмические выражения можно переписать, развернуть или сжать, используя три указанных выше свойства. Расширение — это разбиение сложного выражения на более простые компоненты.Конденсация — обратное этому процесс.
Пример 2 .
Раскрытие выражения.
переписать с использованием экспоненциальной записи недвижимость 3 недвижимость 1
Пример 3 .
Раскрытие выражения.
недвижимость 2 недвижимость 1 недвижимость 3
Пример 4 .
Уплотнение выражения.
недвижимость 3 недвижимость 1 недвижимость 2
Распространенные ошибки
- Логарифмы разбивают произведения на суммы по свойству 1, но логарифм суммы нельзя переписать в .Для Например, мы ничего не можем сделать с выражением ln (x 2 + 1).
- log u — log v равен log (u / v) по свойству 2, не равен log u / log v.
Упражнение 3 :
(a) Разверните выражение. Ответ
(b) Уплотните выражение 3 log x + 2 log y — (1/2) log z. Ответ
Вернуться к содержанию
Свойства логарифмов | Колледж алгебры
Результаты обучения
- Перепишите логарифмическое выражение, используя правило степени, правило произведения или правило частного.
- Расширьте логарифмические выражения, используя комбинацию правил логарифмирования.
- Уплотните логарифмические выражения, используя правила логарифмирования.
Свойства логарифмов
Напомним, что логарифмическая и экспоненциальная функции «отменяют» друг друга. Это означает, что логарифмы имеют те же свойства, что и показатели. {a + b} [/ латекс].У нас есть аналогичное свойство для логарифмов, называемое правилом произведения для логарифмов , которое гласит, что логарифм произведения равен сумме логарифмов. Поскольку журналы являются показателями степени, и мы умножаем их как основания, мы можем складывать экспоненты. Мы будем использовать обратное свойство для вывода правила произведения ниже.
Для любого действительного числа x и положительных действительных чисел M , N и b , где [latex] b \ ne 1 [/ latex], мы покажем
[латекс] {\ mathrm {log}} _ {b} \ left (MN \ right) \ text {=} {\ mathrm {log}} _ {b} \ left (M \ right) + {\ mathrm { log}} _ {b} \ left (N \ right) [/ latex].{m + n} \ right) \ hfill & \ text {Применить правило произведения для показателей степени}. \ hfill \\ \ hfill & = m + n \ hfill & \ text {Применить обратное свойство журналов}. \ hfill \ \ \ hfill & = {\ mathrm {log}} _ {b} \ left (M \ right) + {\ mathrm {log}} _ {b} \ left (N \ right) \ hfill & \ text {Заменить на } m \ text {и} n. \ hfill \ end {array} [/ latex]
Обратите внимание, что повторное применение правила произведения для логарифмов позволяет упростить логарифм произведения любого количества факторов. Например, рассмотрим [латекс] \ mathrm {log} _ {b} (wxyz) [/ latex].Используя правило продукта для логарифмов, мы можем переписать этот логарифм продукта как сумму логарифмов его множителей:
[латекс] \ mathrm {log} _ {b} (wxyz) = \ mathrm {log} _ {b} w + \ mathrm {log} _ {b} x + \ mathrm {log} _ {b} y + \ mathrm { log} _ {b} z [/ латекс]
Общее примечание: правило произведения логарифмов
Правило произведения для логарифмов можно использовать для упрощения логарифма произведения, переписав его как сумму отдельных логарифмов.
[латекс] {\ mathrm {log}} _ {b} \ left (MN \ right) = {\ mathrm {log}} _ {b} \ left (M \ right) + {\ mathrm {log}} _ {b} \ left (N \ right) \ text {for} b> 0 [/ latex]
Пример: использование правила произведения для логарифмов
Разверните [латекс] {\ mathrm {log}} _ {3} \ left (30x \ left (3x + 4 \ right) \ right) [/ latex].
Показать решениеНачнем с написания уравнения равных сумм логарифмов каждого множителя.
[латекс] {\ mathrm {log}} _ {3} \ left (30x \ left (3x + 4 \ right) \ right) = {\ mathrm {log}} _ {3} \ left (30x \ right) + {\ mathrm {log}} _ {3} \ left (3x + 4 \ right) = {\ mathrm {log}} _ {3} \ left (30 \ right) + {\ mathrm {log}} _ { 3} \ left (x \ right) + {\ mathrm {log}} _ {3} \ left (3x + 4 \ right) [/ latex]
Последнее расширение выглядит так. Обратите внимание, как коэффициент [латекс] 30x [/ latex] можно разложить до суммы двух логарифмов:
[латекс] {\ mathrm {log}} _ {3} \ left (30 \ right) + {\ mathrm {log}} _ {3} \ left (x \ right) + {\ mathrm {log}} _ {3} \ left (3x + 4 \ right) [/ латекс]
Попробуйте
Разверните [латекс] {\ mathrm {log}} _ {b} \ left (8k \ right) [/ latex].{a-b} [/ латекс]. Правило частного для логарифмов говорит, что логарифм частного равен разности логарифмов. Как и в случае с правилом произведения, мы можем использовать обратное свойство для получения правила частного.
Для любого действительного числа x и положительных действительных чисел M , N и b , где [latex] b \ ne 1 [/ latex], мы покажем
[латекс] {\ mathrm {log}} _ {b} \ left (\ frac {M} {N} \ right) \ text {=} {\ mathrm {log}} _ {b} \ left (M \ справа) — {\ mathrm {log}} _ {b} \ left (N \ right) [/ latex].{2} + 6x} {3x + 9} \ right) & = \ mathrm {log} \ left (\ frac {2x \ left (x + 3 \ right)} {3 \ left (x + 3 \ right)} \ right) \ hfill & \ text {Разложите числитель и знаменатель на множители}. \ hfill \\ & \ text {} = \ mathrm {log} \ left (\ frac {2x} {3} \ right) \ hfill & \ text {Отменить общие множители}. \ Hfill \ end {array} [/ latex]
Затем мы применяем правило частного, вычитая логарифм знаменателя из логарифма числителя. Затем применяем правило продукта.
[латекс] \ begin {array} {lll} \ mathrm {log} \ left (\ frac {2x} {3} \ right) & = \ mathrm {log} \ left (2x \ right) — \ mathrm {log } \ left (3 \ right) \ hfill \\ \ text {} & = \ mathrm {log} \ left (2 \ right) + \ mathrm {log} \ left (x \ right) — \ mathrm {log} \ слева (3 \ справа) \ hfill \ end {array} [/ latex]
Общее примечание: Правило частного для логарифмов
Правило частного для логарифмов можно использовать для упрощения логарифма или частного, переписав его как разность отдельных логарифмов.
[латекс] {\ mathrm {log}} _ {b} \ left (\ frac {M} {N} \ right) = {\ mathrm {log}} _ {b} M — {\ mathrm {log}} _ {b} N [/ латекс]
Как сделать: учитывая логарифм частного, используйте правило частного логарифмов, чтобы записать эквивалентную разницу логарифмов
- Выразите аргумент в наименьших числах, разложив числитель и знаменатель на множители и отбросив общие термины.
- Запишите эквивалентное выражение, вычтя логарифм знаменателя из логарифма числителя.
- Убедитесь, что каждый член полностью раскрыт. Если нет, примените правило произведения для логарифмов, чтобы полностью раскрыть логарифм.
Пример: использование правила частного для логарифмов
Разверните [латекс] {\ mathrm {log}} _ {2} \ left (\ frac {15x \ left (x — 1 \ right)} {\ left (3x + 4 \ right) \ left (2-x \ right)} \ right) [/ латекс].
Показать решениеСначала отметим, что частное факторизуется в наименьших значениях, поэтому мы применяем правило частного.
[латекс] {\ mathrm {log}} _ {2} \ left (\ frac {15x \ left (x — 1 \ right)} {\ left (3x + 4 \ right) \ left (2-x \ right) )} \ right) = {\ mathrm {log}} _ {2} \ left (15x \ left (x — 1 \ right) \ right) — {\ mathrm {log}} _ {2} \ left (\ left (3x + 4 \ right) \ left (2-x \ right) \ right) [/ латекс]
Обратите внимание, что полученные члены являются логарифмами произведений.Для полного расширения мы применяем правило продукта.
[латекс] \ begin {array} {l} {\ mathrm {log}} _ {2} \ left (15x \ left (x — 1 \ right) \ right) — {\ mathrm {log}} _ {2 } \ left (\ left (3x + 4 \ right) \ left (2-x \ right) \ right) \\\ text {} = \ left [{\ mathrm {log}} _ {2} \ left (15 \ right) + {\ mathrm {log}} _ {2} \ left (x \ right) + {\ mathrm {log}} _ {2} \ left (x — 1 \ right) \ right] — \ left [ {\ mathrm {log}} _ {2} \ left (3x + 4 \ right) + {\ mathrm {log}} _ {2} \ left (2-x \ right) \ right] \ hfill \\ \ text {} = {\ mathrm {log}} _ {2} \ left (15 \ right) + {\ mathrm {log}} _ {2} \ left (x \ right) + {\ mathrm {log}} _ { 2} \ left (x — 1 \ right) — {\ mathrm {log}} _ {2} \ left (3x + 4 \ right) — {\ mathrm {log}} _ {2} \ left (2-x \ right) \ hfill \ end {array} [/ latex]
Анализ решения
В этом и последующих примерах есть исключения. {2} + 21x} {7x \ left (x — 1 \ right) \ left (x — 2 \ right)} \ right) [/ латекс].{2} \ right) \ hfill & = {\ mathrm {log}} _ {b} \ left (x \ cdot x \ right) \ hfill \\ \ hfill & = {\ mathrm {log}} _ {b} x + {\ mathrm {log}} _ {b} x \ hfill \\ \ hfill & = 2 {\ mathrm {log}} _ {b} x \ hfill \ end {array} [/ latex]
Обратите внимание, что мы использовали правило произведения для логарифмов , чтобы найти решение для приведенного выше примера. Таким образом, мы получили правило мощности для логарифмов , которое гласит, что логарифм степени равен экспоненте, умноженной на логарифм основания. Имейте в виду, что хотя входные данные логарифма не могут быть записаны как степень, мы можем изменить его на степень.{2}} \ right) [/ латекс].
Показать решение[латекс] -2 \ mathrm {ln} \ left (x \ right) [/ latex]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Правила логарифма— ChiliMath
В этом уроке вам будут представлены общие правила логарифмов, также известные как «правила журнала». Эти семь (7) логарифмов полезны при расширении логарифмов, сжатии логарифмов и решении логарифмических уравнений.Кроме того, поскольку логарифмическая функция, обратная логарифмической функции, является экспоненциальной функцией, я бы также рекомендовал вам изучить правила экспоненты. Поверьте, они всегда идут рука об руку.
Если вас когда-нибудь интересовало, почему работают правила логарифма, ознакомьтесь с моим уроком о доказательствах или обоснованиях свойств логарифмов.
Правила логарифмов
Описание правил логарифмирования
Правило 1: Правило продукта
Логарифм произведения — это сумма логарифмов факторов.
Правило 2: Правило доли
Логарифм отношения двух величин — это логарифм числителя минус логарифм знаменателя.
Правило 3: Правило силы
Логарифм экспоненциального числа — это показатель степени, умноженный на логарифм основания.
Правило 4: нулевое правило
Логарифм 1 такой, что b> 0, но b ≠ 1 равняется нулю.
Правило 5: Правило идентификации
Логарифм аргумента (в скобках), в котором аргумент совпадает с основанием, равен 1.Поскольку аргумент равен основанию, b должно быть больше 0, но не может быть равно 1.
Правило 6: Логарифм правила экспоненты (логарифм от основания до правила мощности)
Логарифм экспоненциального числа, основание которого совпадает с основанием журнала, равен экспоненте.
Правило 7. Показатель степени логарифмического правила (основание для правила логарифмической мощности)
Возведение логарифма числа к основанию равняется числу.
Примеры применения правил журнала
Пример 1: Оцените приведенное ниже выражение с помощью правил журнала.
{\ log _2} 8 + {\ log _2} 4
Выразите 8 и 4 как экспоненциальные числа с основанием 2. Затем примените правило мощности, а затем правило идентичности. После этого вы добавляете полученные значения, чтобы получить окончательный ответ.
Итак, ответ \ color {blue} 5.
Пример 2: Вычислите приведенное ниже выражение с помощью правил журнала.
{\ log _3} 162 — {\ log _3} 2
Мы не можем выразить 162 как экспоненциальное число с основанием 3. Похоже, что мы застряли, поскольку не существует правил, которые можно было бы применить напрямую.
Однако можно применять правила логарифма в обратном порядке! Обратите внимание, что логарифмическое выражение может быть выражено в виде одного или одного логарифмического числа с помощью обратного правила Quotient Rule. Звучит как план.
Мы сделали это! Применяя правила в обратном порядке, мы сгенерировали одно легко решаемое логарифмическое выражение. Окончательный ответ здесь \ color {blue} 4.
Пример 3: Вычислите выражение ниже.
Похоже, так много вещей происходит одновременно.Сначала проверьте, можно ли упростить каждое из логарифмических чисел. Если нет, подумайте о некоторых логарифмических правилах, которые, очевидно, применимы.
Наблюдением мы видим, что здесь задействованы две основы: 5 и 4. Так почему бы не объединить выражения, имеющие одну и ту же основу? Давайте упростим их отдельно.
Для журнала с основанием 5 сначала примените правило мощности, а затем правило коэффициента. Для журнала с базой 4 немедленно примените Правило продукта. Затем получите окончательный ответ, сложив два найденных значения.5}} \ вправо)
В скобках указано произведение множителей. Примените правило продукта, чтобы разбить их как сумму отдельных выражений журнала. Убедитесь, что вы стараетесь изо всех сил сводить числовые выражения к точным значениям, когда это возможно. Используйте Правило 5 (Правило идентификации) как можно чаще, потому что оно может упростить процесс упрощения.
Верно! Последняя строка в подробном решении, как показано выше, является окончательным ответом. Хотя надо признать, что они выглядят несколько «недоделанными».Пока мы знаем, что правильно применяем правила, это не должно нас беспокоить.
Пример 5 : развернуть логарифмическое выражение.
Подход состоит в том, чтобы сначала применить правило частного как разность двух логарифмических выражений, поскольку они представлены в дробной форме. Затем используйте правило произведения, чтобы разделить произведение факторов как сумму логарифмических выражений.
Пример 6 : развернуть логарифмическое выражение.
Значит, у этого есть радикальное выражение в знаменателе.{{1 \ over 2}}}. Как и в случае с проблемой №5, примените правило Quotient Rule для журналов, а затем используйте правило продукта.
Пример 7 : развернуть логарифмическое выражение.
Подобная проблема может вызвать у вас сомнения, действительно ли вы пришли к правильному ответу, потому что окончательный ответ все еще может выглядеть «незаконченным». Однако, если вы правильно применяете правила журнала на каждом этапе, беспокоиться не о чем.
Вы могли заметить, что нам нужно сначала применить правило частного, потому что выражение имеет дробную форму.
Возможно, вас заинтересует:
Уплотняющие логарифмы
Расширяющиеся логарифмы
Объяснение логарифма
Решение логарифмических уравнений
Доказательства логарифмических свойств
Свойства логарифма
Логарифмы и их обратные свойства
Напомним определение логарифма по основанию b : дано b> 0, где b ≠ 1,
y = logb x тогда и только тогда, когда x = на
Используйте это определение для преобразования логарифмов в экспоненциальную форму.Поступая так, мы можем получить несколько свойств:
logb 1 = 0, потому что b0 = 1 logb b = 1, потому что b1 = blogb (1b) = — 1, потому что b − 1 = 1b
Пример 1
Оценить:
- журнал 1
- ln e
- журнал 5 (15)
Решение:
Если основание не записано, предполагается, что оно равно 10.Это десятичный логарифм
.журнал 1 = журнал10 1 = 0
Натуральный логарифм по определению имеет основание e ,
ln e = loge = 1
Поскольку 5−1 = 15, получаем
журнал5 (15) = — 1
Кроме того, рассмотрим основание дробной части вида 1 / b, где b> 1.
log1 / b b = −1, поскольку (1b) −1 = 1−1b − 1 = b1 = b
Пример 2
Оценить:
- лог1 / 4 4
- журнал2/3 (32)
Решение:
- log1 / 4 4 = −1, поскольку (14) −1 = 4
- log2 / 3 (32) = — 1, поскольку (23) −1 = 32
Для экспоненциальной функции, определяемой формулой f (x) = bx, где b> 0 и b 1, обратным ей является логарифм по основанию b , f − 1 (x) = logb x.И поскольку f (f − 1 (x)) = x и f − 1 (f (x)) = x, у нас есть следующие обратные свойства логарифма При b> 0 мы имеем logb bx = x и blogb x = x, когда х> 0 .:
f − 1 (f (x)) = logb bx = xandf (f − 1 (x)) = blogb x = x, x> 0
Поскольку f − 1 (x) = logb x имеет область, состоящую из положительных значений (0, ∞), свойство blogb x = x ограничено значениями, где x> 0.
Пример 3
Оценить:
- лог5 625
- 5log5 3
- элн 5
Решение:
Примените обратные свойства логарифма.
- log5 625 = log5 54 = 4
- 5log5 3 = 3
- eln 5 = 5
Таким образом, когда b> 0 и b ≠ 1, мы имеем следующие свойства:
логб 1 = 0 | logb b = 1 |
log1 / b b = -1 | логб (1b) = — 1 |
logb bx = x | блогb x = x, x> 0 |
Попробуй! Оценить: журнал 0.00001
Ответ: −5
Произведение, частное и степенные свойства логарифмов
В этом разделе описаны три очень важных свойства логарифма. Эти свойства позволят нам расширить нашу способность решать гораздо больше уравнений. Начнем с того, что присвоим значения u и v следующим логарифмам, а затем запишем их в экспоненциальной форме:
logb x = u ⇒ bu = xlogb y = v ⇒ bv = y
Подставляем x = bu и y = bv в логарифм произведения logb (xy) и логарифм частного logb (xy).Затем упростите, используя правила экспонент и обратные свойства логарифма.
Логарифм произведения | Логарифм частного |
|---|---|
logb (xy) = logb (bubv) = logb bu + v = u + v = logb x + logb y | logb (xy) = logb (bubv) = logb bu − v = u − v = logb x − logb y |
Это дает нам два важных свойства: свойство произведения logarithmslogb (xy) = logb x + logb y; логарифм продукта равен сумме логарифма факторов.,
logb (xy) = logb x + logb y
и факторное свойство logarithmslogb (xy) = logb x − logb y; логарифм частного равен разности логарифма числителя и логарифма знаменателя.,
logb (xy) = logb x − logb y
На словах логарифм продукта равен сумме логарифма факторов. Точно так же логарифм частного равен разности логарифма числителя и логарифма знаменателя.
Пример 4
Запишите как сумму: log2 (8x).
Решение:
Примените свойство произведения логарифмов, а затем упростите.
log2 (8x) = log2 8 + log2 x = log2 23 + log2 x = 3 + log2 x
Ответ: 3 + log2 x
Пример 5
Запишите как разность: log (x10).
Решение:
Примените частное свойство логарифмов, а затем упростите.
журнал (x10) = журнал x − журнал 10 = журнал x − 1
Ответ: log x − 1
Затем мы начинаем с logb x = u и переписываем его в экспоненциальной форме. После возведения обеих сторон в степень n преобразовать обратно в логарифмическую форму, а затем обратно подставить.
logb x = u ⇒ bu = x (bu) n = (x) nlogb xn = nu ⇐ bnu = xnlogb xn = nlogb x
Это приводит нас к свойству мощности logarithmslogb xn = nlogb x; логарифм величины, возведенный в степень, равен этой степени, умноженной на логарифм количества.,
logb xn = nlogb x
Проще говоря, логарифм величины в степени равен этой степени, умноженной на логарифм величины.
Пример 6
Напишите как продукт:
- журнал2 x4
- log5 (х).
Решение:
Примените свойство логарифмов мощности.
log2 x4 = 4log2 x
Напомним, что квадратный корень можно выразить с помощью рациональных показателей x = x1 / 2.Сделайте эту замену, а затем примените степенное свойство логарифмов.
log5 (x) = log5 x1 / 2 = 12log5 x
Таким образом,
Свойство логарифмов продукта | logb (xy) = logb x + logb y |
Частное свойство логарифмов | logb (xy) = logb x − logb y |
Силовые свойства логарифмов | logb xn = nlogb x |
Мы можем использовать эти свойства для раскрытия логарифмов, включающих произведения, частные и степени, используя суммы, разности и коэффициенты.Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
Внимание! Важно отметить следующее:
журнал (xy) ≠ журнал x⋅log y и журнал (xy) ≠ журнал xlog y
Пример 7
Полностью развернуть: ln (2×3).
Решение:
Напомним, что натуральный логарифм является основанием логарифма e , ln x = loge x.Следовательно, применяются все свойства логарифма.
ln (2×3) = ln 2 + ln x3 Правило произведения для логарифмов = ln 2 + 3ln x Правило степени для логарифмов
Ответ: ln 2 + 3ln x
Пример 8
Полностью развернуть: журнал 10xy23.
Решение:
Начните с переписывания корня куба, используя рациональную экспоненту 13, а затем примените свойства логарифма.
журнал 10xy23 = журнал (10xy2) 1/3 = 13log (10xy2) = 13 (журнал 10 + журнал x + журнал y2) = 13 (1 + журнал x + 2log y) = 13 + 13log x + 23log y
Ответ: 13 + 13log x + 23log y
Пример 9
Полностью развернуть: log2 ((x + 1) 25y).
Решение:
Применяя свойство продукта к знаменателю, позаботьтесь о распределении отрицательного значения, полученного в результате применения свойства частного.
log2 ((x + 1) 25y) = log2 (x + 1) 2 − log2 (5y) = log2 (x + 1) 2− (log2 5 + log2 y) Распределить. = Log2 (x + 1) 2− log2 5 − log2 y = 2 log2 (x + 1) −log2 5 − log2 y
.Ответ: 2log2 (x + 1) −log2 5 − log2 y
Осторожно : Нет правила, позволяющего расширить логарифм суммы или разницы.Другими словами,
журнал (x ± y) ≠ журнал x ± log y
Попробуй! Полностью развернуть: ln (5y4x).
Ответ: ln 5 + 4ln y − 12ln x
Пример 10
Учитывая, что log2 x = a, log2 y = b и log2 z = c, запишите следующее в терминах a , b и c :
а. log2 (8x2y)
г.log2 (2x4z)
Решение:
Начните с расширения с использованием сумм и коэффициентов, а затем замените a и b на соответствующий логарифм.
log2 (8x2y) = log2 8 + log2 x2 + log2 y = log2 8 + 2log2 x + log2 y = 3 + 2a + b
Разверните и замените a , b и c , где это необходимо.
log2 (2x4z) = log2 (2×4) −log2 z1 / 2 = log2 2 + log2 x4 − log2 z1 / 2 = log2 2 + 4log2 x − 12log2 z = 1 + 4a − 12b
Далее мы упростим логарифмические выражения. Как мы увидим, важно иметь возможность объединить выражение, содержащее логарифмы, в единый логарифм с коэффициентом 1. Это будет одним из первых шагов при решении логарифмических уравнений.
Пример 11
Запишите как один логарифм с коэффициентом 1: 3log3 x − log3 y + 2log3 5.
Решение:
Начните с переписывания всех логарифмических членов с коэффициентом 1. Используйте для этого правило степени. Затем используйте правила произведения и частного для дальнейшего упрощения.
3log3x − log3y + 2log35 = {log3x3 − log3y} + log352 свойство частного = {log3 (x3y) + log325} свойство продукта = log3 (x3y⋅25) = log3 (25x3y)Ответ: log3 (25x3y)
Пример 12
Запишем одним логарифмом с коэффициентом 1: 12ln x − 3ln y − ln z.
Решение:
Начнем с записи коэффициентов логарифмов в виде степеней их аргумента, после чего мы дважды применим правило частного, работая слева направо.
12ln x − 3ln y − ln z = ln x1 / 2 − ln y3 − ln z = ln (x1 / 2y3) −ln z = ln (x1 / 2y3 ÷ z) = ln (x1 / 2y3⋅1z) = ln (x1 / 2y3z) или = ln (xy3z)
Ответ: ln (xy3z)
Попробуй! Запишите как один логарифм с коэффициентом 1: 3log (x + y) −6log z + 2log 5.
Ответ: log (25 (x + y) 3z6)
Основные выводы
- Для любого основания b> 0 и b ≠ 1 мы можем сказать, что logb 1 = 0, logb b = 1, log1 / b b = −1 и что logb (1b) = — 1.
- Обратные свойства логарифма: logb bx = x и blogb x = x, где x> 0.
- Свойство продукта логарифма позволяет нам записать произведение в виде суммы: logb (xy) = logb x + logb y.
- Факторное свойство логарифма позволяет нам записать частное как разность: logb (xy) = logb x − logb y.
- Степенное свойство логарифма позволяет нам записывать показатели в виде коэффициентов: logb xn = nlogb x.
- Поскольку натуральный логарифм является основанием — e логарифм, ln x = loge x, к нему применяются все свойства логарифма.
- Мы можем использовать свойства логарифма для расширения логарифмических выражений, используя суммы, разности и коэффициенты.Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
- Мы можем использовать свойства логарифма, чтобы объединить выражения, содержащие логарифмы, в единый логарифм с коэффициентом 1. Это важный навык, который необходимо изучить в этой главе.
Тематические упражнения
ln (1e)
log1 / 2 (12)
Часть A: Логарифмы и их обратные свойства
Оценить:
Найдите a :
log2 (xy2)
log5 (25x)
log3 (x3yz2)
журнал (xy3z2)
log5 (1x2yz)
log4 (116x2z3)
log3 (x2y3z)
журнал (2 (x + y) 3z2)
журнал (100×3 (y + 10) 3)
log7 (х (у + z) 35)
log5 (x3yz23)
журнал (x2y3z25)
log3 (27x2y3z)
log3 (xy3z)
log3 (9x2yz3)
log3 (x3yz2)
log2 5 + 2log2 x + log2 y
log3 4 + 3log3 x + 12log3 y
3log2 x − 2log2 y + 12log2 z
4log x − log y − log 2
log3 x − 2log3 y + 5log3 z
7log x − log y − 2log z
2ln x − 3ln y − ln z
23log3 x − 12 (log3 y + log3 z)
15 (log7 x + 2log7 y) −2log7 (z + 1)
−ln 2 + 2ln (x + y) −ln z
−3ln (x − y) −ln z + ln 5
13 (ln x + 2ln y) — (3ln 2 + ln z)
4log 2 + 23log x − 4log (y + z)
log2 3−2log2 x + 12log2 y − 4log2 z
2log5 4 − log5 x − 3log5 y + 23log5 z
журнал (x + 1) + журнал (x − 1)
журнал2 (x + 2) + журнал2 (x + 1)
ln (x2 + 2x + 1) −ln (x + 1)
ln (x2−9) −ln (x + 3)
log5 (x3-8) −log5 (x − 2)
log3 (x3 + 1) −log3 (x + 1)
журнал x + журнал (x + 5) −log (x2−25)
журнал (2x + 1) + журнал (x − 3) −log (2×2−5x − 3)
Часть B: Произведение, частное и степенные свойства логарифмов
Полностью развернуть.
Учитывая log3 x = a, log3 y = b и log3 z = c, запишите следующие логарифмы в терминах a , b и c .
Дано logb 2 = 0.43, logb 3 = 0,68 и logb 7 = 1,21, рассчитайте следующее. (Подсказка: разверните, используя суммы, разности и частные множителей 2, 3 и 7.)
Разверните, используя свойства логарифма, а затем округлите с помощью калькулятора до ближайшей десятой.
Записать в виде единственного логарифма с коэффициентом 1.
Выразите как единственный логарифм и упростите.
Ответы
3log3 x − log3 y − 2log3 z
−2log5 x − log5 y − log5 z
log7 2 + 12log7 x + 12log7 y
2log3 x + 13log3 y − log3 z
2 + 3log x − 3log (y + 10)
3log5 x − 13log5 y − 23log5 z
лн (6.2) −15≈ − 13,2
log2 (x3zy2)
ln (xzy6)
журнал (x7yz2)
log3 (x23yz)
log2 (2xy)
log2 (xy23)
ln ((x + y) 22z)
ln (xy238z)
log2 (3yx2z4)
журнал (xx − 5)
СВОЙСТВ ЛОГАРИФМОВ
СВОЙСТВА ЛОГАРИФМОВСвойство 1: , потому что.
- Пример 1: В уравнении
, база равна 14, а показатель степени равен
0. Помните, что логарифм — это показатель степени, а соответствующий
логарифмическое уравнение
где 0 — показатель степени.
Пример 2: В уравнении , база а показатель степени равен 0. Помните, что логарифм — это показатель степени, а соответствующий логарифмическое уравнение .
Пример 3: Используйте экспоненциальное уравнение написать логарифмический уравнение.База x больше 0, а показатель степени равен 0. Соответствующее логарифмическое уравнение имеет вид .
Свойство 2: , потому что.
- Пример 4: В уравнении
, основание 3, показатель степени 1,
и ответ — 3. Помните, что логарифм — это показатель степени,
и соответствующее логарифмическое уравнение
.
Пример 5: В уравнении , база 87, показатель степени 1, и ответ — 87.Помните, что логарифм — это показатель степени, и соответствующее логарифмическое уравнение .
Пример 6: Используйте экспоненциальное уравнение написать логарифмический уравнение. Если основание p больше 0, то .
Свойство 3: , потому что.
Пример 7: Поскольку вы знаете, что , вы можете написать логарифмический уравнение с основанием 3 как .
Пример 8: Поскольку вы знаете, что , вы можете написать логарифмический уравнение с основанием 13 как .
Пример 9: Используйте экспоненциальное уравнение написать логарифмический уравнение с основанием 4. Вы можете преобразовать экспоненциальное уравнение
к логарифмическому уравнению . Поскольку 16 можно записать как
, уравнение можно написать .
Вышеупомянутые правила одинаковы для всех положительных баз. Большинство Общие базы — это база 10 и база и . Логарифмы с с основанием 10 называются десятичный логарифм , а логарифмы с Основание e — это натуральный логарифм .На вашем калькуляторе база 10 логарифм отмечается log , а логарифм по основанию e отмечается по пер .
Бесконечное количество баз и всего несколько кнопок на вашем калькуляторе. Вы можете преобразовать логарифм с основанием это не 10 или e с эквивалентным логарифмом с основанием 10 или е. Если вас интересует обсуждение того, как изменить оснований логарифма, нажмите Изменение База.
Для обсуждения взаимосвязи графиков логарифмической функции и экспоненциальные функции, нажимайте на графики.
[Возврат меню к экспоненциальной функции]
[Алгебра] [Тригонометрия] [Сложный Переменные] Домашняя страница S.O.S MATHematicsВам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор: Нэнси МаркусАвторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час
Работа с экспонентами и логарифмами
Что такое экспонента?
Показатель числа означает , сколько раз В этом примере: 2 3 = 2 × 2 × 2 = 8 (2 используется 3 раза при умножении, чтобы получить 8) |
Что такое логарифм?
Логарифм идет в обратном направлении.
Возникает вопрос «какой показатель произвел это?»:
И отвечает на него так:
В этом примере:
- Экспонента принимает 2 и 3 и дает 8 (2, использованные 3 раза в умножении, дает 8)
- Логарифм берет 2 и 8 и дает 3 (2 дает 8 при трехкратном умножении)
Логарифм показывает , сколько одного числа нужно умножить, чтобы получить другое число
Таким образом, логарифм фактически дает вам показатель степени в качестве ответа :
(Также посмотрите, как связаны экспоненты, корни и логарифмы.)Работаем вместе
Показатели и логарифмы хорошо работают вместе, потому что они «отменяют» друг друга (пока основание «а» одинаково):
Это «обратные функции»
Выполнение одного, затем другого вернет вас к тому, с чего вы начали:
Выполнение a x , затем log a вернет вам x снова: Выполнение log a , затем a x вернет вам x снова:Жаль, что они пишутся так иначе … это заставляет вещи выглядеть странно. Так что можно подумать о x как о «вверх» и записать a (x) как о «вниз»:
поднимаясь вверх, затем вниз, снова возвращает вас обратно: вниз (вверх (x)) = x
идет вниз, затем вверх, снова возвращает вас обратно: вверх (вниз (x)) = x
Во всяком случае, важно то, что:
Логарифмическая функция «отменяется» экспоненциальной функцией.
(и наоборот)
Как в этом примере:
Пример, что такое
x в журнале 3 (x) = 5Начать с: log 3 (x) = 5
Мы хотим «отменить» журнал 3 , чтобы получить «x =»
Используйте экспоненциальную функцию (с обеих сторон): И мы это знаем, так что: x = 3 5Ответ: x = 243
А также:
Пример: вычислить y в
y = log 4 (1/4)Начать с: y = log 4 (1/4)
Используйте экспоненциальную функцию с обеих сторон:Упростить: 4 y = 1/4
Теперь простой трюк: 1/4 = 4 −1
Итак: 4 y = 4 −1
Итак: y = −1
Свойства логарифмов
Одна из сильных сторон логарифмов заключается в том, что они могут превращать умножение в сложение .
журнал a (m × n) = журнал a m + журнал a n
«логарифм умножения — это сумма журналов»
Почему это правда? См. Сноску.
Используя это свойство и законы экспонент, мы получаем следующие полезные свойства:
| журнал a (м × n) = журнал a м + журнал a n | логарифм умножения — это сумма бревен |
| бревно a (м / п) = бревно a м — бревно a n | лог деления разница бревен |
| журнал a (1 / n) = −log a n | это просто следует из предыдущего правила «деления», потому что log a (1) = 0 |
| бревно a (м r ) = r (бревно a м) | логарифм m с показателем r равен r, умноженному на логарифм m |
Помните: основание «а» всегда одинаково!
История: Логарифмы были очень полезны до изобретения калькуляторов… например, вместо умножения двух больших чисел, используя логарифмы, вы можете превратить это в сложение (намного проще!)
И в помощь были книги, полные таблиц логарифма.
Давайте повеселимся, используя свойства:
Пример: Упростить
журнал a ((x 2 +1) 4 √x)Начать с: log a ((x 2 +1) 4 √x)
Используйте log a (mn) = log a m + log a n : log a ((x 2 +1) 4 ) + log a (√x)
Используйте log a (m r ) = r (log a m) : 4 log a (x 2 +1) + log a (√x)
Также √x = x ½ : 4 log a (x 2 +1) + log a (x ½ )
Используйте log a (m r ) = r (log a m) снова : 4 log a (x 2 +1) + ½ log a (x)
Это насколько мы можем упростить… мы ничего не можем сделать с логом a (x 2 +1).
Ответ: 4 журнала a (x 2 +1) + ½ журнала a (x)
Примечание: нет правила для обработки журнала a (m + n) или журнала a (m − n)
Мы также можем применить правила логарифмирования «в обратном порядке» для объединения логарифмов:
Пример: превратите это в один логарифм:
log a (5) + log a (x) — log a (2)Начать с: log a (5) + log a (x) — log a (2)
Используйте log a (mn) = log a m + log a n : log a (5x) — log a (2)
Используйте бревно a (м / п) = бревно a м — бревно a n : бревно a (5x / 2)
Ответ: журнал a (5x / 2)
Натуральный логарифм и натуральные экспоненциальные функции
Когда основание равно e («Число Эйлера» = 2.718281828459 …) получаем:
- Натуральный логарифм log e (x) , который чаще записывается как ln (x)
- Естественная экспоненциальная функция e x
И та же идея, что одно может «отменить» другое, все еще верна:
ln (e x ) = x
e (ln x) = x
А вот их графики:
Натуральный логарифм | Естественная экспоненциальная функция | |
| График f (x) = ln (x) | График f (x) = e x | |
Проходит через (1,0) и (e, 1) | Проходит через (0,1) и (1, e) |
Это такая же кривая с перевернутыми осями x и y .
Это еще одна вещь, чтобы показать вам, что они являются обратными функциями.
На калькуляторе натуральный логарифм — это кнопка «ln». |
Всегда старайтесь использовать натуральные логарифмы и натуральную экспоненциальную функцию, когда это возможно.
Десятичный логарифм
Если база равна 10 , вы получите:
- Общий логарифм log 10 (x) , который иногда записывается как log (x)
Инженеры любят его использовать, но в математике он мало используется.
На калькуляторе десятичный логарифм — это кнопка «журнал». Это удобно, потому что показывает, насколько «большое» число в десятичной системе (сколько раз вам нужно использовать 10 при умножении). |
Пример: расчет журнала
10 100Ну, 10 × 10 = 100, поэтому, когда 10 используется 2 раз при умножении, вы получаете 100:
журнал 10 100 = 2
Аналогично log 10 1000 = 3, log 10 10 000 = 4 и т. Д.
Пример: расчет журнала
10 369Хорошо, лучше всего использовать кнопку «журнал» моего калькулятора:
журнал 10 369 = 2,567 …
Замена базы
Что, если мы хотим изменить основание логарифма?
Легко! Просто используйте эту формулу:
«x поднимается, a понижается»
Или другой способ думать об этом: log b a — это как «коэффициент преобразования» (та же формула, что и выше):
Итак, теперь мы можем преобразовать любую базу в любую другую.
Еще одно полезное свойство:
Видите, как меняются местами «x» и «a»?
Пример: вычислить 1 / лог
8 21 / лог 8 2 = лог 2 8
И 2 × 2 × 2 = 8, поэтому, когда 2 используется 3 раз при умножении, вы получаете 8:
1 / лог 8 2 = лог 2 8 = 3
Но мы чаще используем натуральный логарифм, поэтому стоит помнить об этом:
Пример: расчет журнала
4 22В моем калькуляторе нет кнопки « журнал 4 »… … но у него есть кнопка « ln «, поэтому мы можем использовать это: |
журнал 4 22 = ln 22 / ln 4
= 3,09 … / 1,39 …
= 2,23 (до 2 знаков после запятой)
Что означает этот ответ? Это означает, что 4 с показателем 2,23 равняется 22. Итак, мы можем проверить этот ответ:
Чек: 4 2,23 = 22,01 (достаточно близко!)
Вот еще один пример:
Пример: расчет журнала
5 125журнал 5 125 = ln 125 / ln 5
= 4.83 … / 1,61 …
= 3 (точно)
Я знаю, что 5 × 5 × 5 = 125, (5 используется 3 раз, чтобы получить 125), поэтому я ожидал ответа 3 , и это сработало!
Использование в реальном мире
Вот несколько примеров использования логарифмов в реальном мире:
Землетрясения
Магнитуда землетрясения в логарифмической шкале.
В знаменитой «шкале Рихтера» используется эта формула:
M = журнал 10 A + B
Где A — амплитуда (в мм), измеренная сейсмографом
, а B — поправочный коэффициент расстояния
В настоящее время есть более сложные формулы, но они все еще используют логарифмическую шкалу.
Звук
Громкость измеряется в децибелах (сокращенно дБ):
Громкость в дБ = 10 log 10 (p × 10 12 )
где p — звуковое давление.
Кислый или щелочной
Кислотность (или щелочность) измеряется в pH:
pH = −log 10 [H + ]
, где H + — молярная концентрация растворенных ионов водорода.
Примечание: в химии [] означает молярную концентрацию (моль на литр).
Другие примеры
Пример: решить 2 журнала
8 x = журнал 8 16Начать с: 2 журнала 8 x = журнал 8 16
Введите «2» в журнал: журнал 8 x 2 = журнал 8 16
Убрать бревна (они же основания): x 2 = 16
Решите: x = −4 или +4
Но … но … но … у вас не может быть журнала с отрицательным числом!
Таким образом, случай −4 не определен.
Ответ: 4
Проверка: воспользуйтесь калькулятором, чтобы убедиться, что это правильный ответ … также попробуйте случай «−4».
Пример: Решить e
−w = e 2w + 6Начнем с: e −w = e 2w + 6
Применить ln с обеих сторон: ln (e −w ) = ln (e 2w + 6 )
и ln (e w ) = w : −w = 2w + 6
Упростить: −3w = 6
Решить: w = 6 / −3 = −2
Ответ: w = −2
Чек: e — (- 2) = e 2 и e 2 (−2) +6 = e 2
Сноска: Почему
журнал (m × n) = log (m) + log (n) ?Чтобы увидеть , почему , мы будем использовать и:
| Сначала превратите m и n в «показатели логарифмов»: | |
Затем используйте один из законов экспонент Наконец отмените экспоненты. |
Это одна из тех умных вещей, которые мы делаем в математике, которую можно описать как «мы не можем сделать это здесь, поэтому давайте пройдемся по там , затем сделаем это, затем вернемся»
.
 Обратите внимание на то, что основания логарифмов одинаковы. Если записать это в обратном порядке, то получим правило сложения логарифмов.
Обратите внимание на то, что основания логарифмов одинаковы. Если записать это в обратном порядке, то получим правило сложения логарифмов.