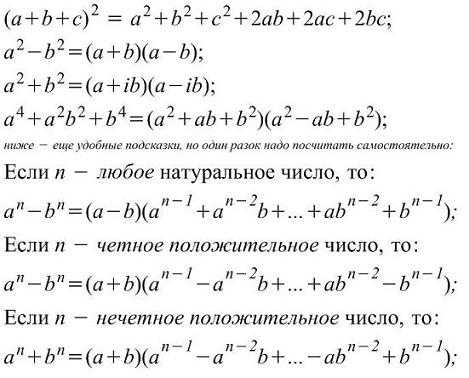Сумма n степеней – Бином Ньютона. Целая положительная степень n суммы. (a + b)n=. Родственные формулы.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Бином Ньютона. Целая положительная степень n суммы. (a + b)n=. Родственные формулы.
| |||||
dpva.ru
Разложение на множители суммы и разности степеней
Для любого натурального числа верно равенство
Доказательство. Чтобы убедиться в справедливости этого равенства, раскроем скобки и приведём подобные члены. Получим
При раскрытии скобок вслед за произведением каждого слагаемого на мы записывали его произведение на После приведения подобных слагаемых в сумме останутся только первое и последнее слагаемое, то есть
Если — нечётное число (), то после замены на в формуле разности степеней получим тождество
umath.ru
Помогите решить / разобраться (М)
Вот ещё занятный способ найти сумму степеней.Пусть есть какая-то функция ; введём оператор , который по такой функции выдаёт её разность . Обозначим через оператор , выдающий по функции её производную .
Представим в виде ряда Тейлора:
, где последнее выражение есть символическая запись предыдущего.
Отсюда получаем .
Итак , поэтому оператор суммирования .
Обозначим теперь . Хорошее свойство этой функции: , или же .
Поэтому , где — постоянная суммирования, которая определится условием .
Для функции известно разложение в ряд Тейлора по : , где — числа Бернулли, причём .
Поэтому .
и все более старшие производные зануляются, а даёт константу и поэтому её отбрасываем, так как константу суммирования всё равно надо подбирать отдельно. Получаем:
.
Мы получили известную формулу Бернулли: .
Таким же образом несложно показать, что если считать , а не , то получится такая же формула, только слева — сумма до : .
Символически это можно записать и так: где символически превращается в .
———————-
Наконец укажу практически удобный способ вычисления степенных сумм, который подходит, если вы не помните на память всякие штуки вроде чисел Бернулли. Он основывается на формуле, которую привёл Sonic86: , или , где — постоянная, которую можно определить, задав желаемое значение суммы при , а .
Мы таким образом легко просуммируем ; а хотим суммировать . Но несложно показать, что любой многочлен может быть представлен также в виде , а каогда мы его так представим — сможем просуммировать.
Вычислим например . Представим в нужном виде:
.
Поэтому , откуда , или .
dxdy.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница
|
dpva.ru
Формулы сумм ряда натуральных чисел в целочисленной степени
Сумма натурального ряда
Это известная формула, открытая еще Гауссом в шестилетнем возрасте.
Сумма натурального ряда где каждый элемент возведен во вторую степень
Сумма натурального ряда где каждый элемент возведен в третью степень
Сумма натурального ряда где каждый элемент возведен в четвертую степень
Сумма натурального ряда где каждый элемент возведен в пятую степень
Сумма натурального ряда где каждый элемент возведен в шестую степень
Сумма натурального ряда где каждый элемент возведен в седьмую степень
Сумма натурального ряда где каждый элемент возведен в восьмую степень
Сумма натурального ряда где каждый элемент возведен в девятую степень
Сумма натурального ряда где каждый элемент возведен в десятую степень
Сумма натурального ряда где каждый элемент возведен в одинадцатую степень
Сумма натурального ряда где каждый элемент возведен в двенадцатую степень
- ФРС. Фундаментальное решение системы уравнений >>
abakbot.ru
Сумма пятой степени | Формулы с примерами
1. 25 + 35 = (2 + 3) • (23 • 3 + 22 • 32 — 2 • 33 + 34) =
5 • (16 — 8 • 3 + 4 • 9
5 • (16 — 24 + 36 — 54 + 81) =
5 • 55 = 275 ;
a = 25 ;
b = 35 ;
2. 75 + 55 = (7 + 5) • (74 — 73 • 5 + 72 • 52 — 7 • 53 + 54) =
12 • (2 401 — 343 • 5 + 49 • 25 — 7 • 125 + 625) =
12 • (2 401 — 1 715 + 1 225 — 875 + 625) =
a = 75 ;
b = 55 ;
3. 35 + 35 = (3 + 5) • (34 — 33 • 5 + 32 • 52 — 3 • 53 + 54) =
8 • (81 — 27 • 5 + 9 • 25 — 3 • 125 + 625) =
8 • (81 — 135 + 225 — 375 + 625) =
8 • 421 = 3 368 ;
b = 55 ;
formula-xyz.ru
Сумма седьмой степени | Формулы с примерами
1. 17 + 37 = (1 + 3) • (16 — 15 • 3 + 14 • 32 — 13 • 33 + 12 • 34 — 1 • 35 + 36
4 • (1 — 3 + 9 — 27 + 81 — 243 + 729) =
4 • 547 = 2 188 ;
a = 17 ;
b = 37 ;
2. 27 + 37 = (2 + 3) • (26 — 25 • 3 + 24 • 32 — 23 • 33 + 24 • 34 — 2 • 35 + 36) =
5 • (64 — 32 • 3 + 16 • 9 — 8 • 27 + 4 • 81 — 2 • 243 + 729) =
5 • (64 — 96 + 144 — 216 + 324 — 486 + 729) =
5 • 463 = 2 315 ;
a = 27 ;
b = 37 ;
3. 37 + 57 = (3 + 5) • (36 — 35 • 5 + 34 • 52 — 33 • 53 + 32 • 54 — 3 • 55 + 56) =
8 • (729 — 125 • 5 + 81 • 25 — 27 • 125 + 9 • 625 — 3 • 3 125 + 15 625) =
8 • (729 — 625 + 2 025 — 3 375 + 5 625 — 9 375 + 15 625) =
80 312 ;
a = 37 ;
b = 57 ;
formula-xyz.ru