Сумма двух матриц: Сложение матриц / Сумма матриц онлайн

Понятно, что операция вычитания матриц в MS EXCEL реализуется аналогично (см. файл примера ).

Умножение матриц на число

Операция умножения матрицы на число определена для матриц любого порядка.

Произведение матрицы А и числа k — это матрица, элементы которой получаются умножением всех элементов исходной матрицы А на число k.

В MS EXCEL это реализовано с помощью формулы =A21*$D$21 (предполагается, что матрица находится в диапазоне

Сложение матриц — Энциклопедия по экономике

Вычитание матриц также сводится к вычитанию соответствующих элементов матриц. Как и в случае сложения матрицы должны быть согласованы для действия вычитания, т. е. должны иметь одинаковый размер.  [c.379]

Предложение. Операция сложения матриц удовлетворяет следующим свойствам  [c. 489]

С перечисленными выше операциями связаны некоторые законы матричной алгебры. Так, сложение матриц ассоциативно, если матрицы согласованы для сложения. Операция умножения матриц также ассоциативна, если только матрицы согласованы для умножения. Сложение матриц коммутативно в том случае, если матрицы согласованы для сложения. Операции с матрицами удовлетворяют требованиям дистрибутивного закона А(В + Q =AB +A в том случае, если матрицы В и С согласованы для сложения, а матрицы А и В согласованы для умножения. В общем случае умножение матриц не коммутативно. В трех случаях умножение матриц коммутативно — при умножении матрицы на нулевую матрицу, при умножении матрицы на диагональную матрицу, при умножении матрицы на скалярную величину.  [c.10]

Из правил сложения матриц и умножения матрицы на скаля — следует А — В = [al — btj].  [c.76]

След матрицы 80 Сложение матриц 75 Случайная переменная 20 Смешанные оценки 219 Собственные векторы 105  [c.441]

Умножение матрицы на число и сложение матриц  [c. 53]

Свойства умножения матрицы на число и сложения матриц(Л,5, С»—матрицы, k, I—числа)  [c.53]

Операции сложения и умножения блочных матриц проводятся по правилам соответствующих операций над матрицами, если заменить их элементы блоками  [c.275]

Таким образом, модель B G представляет собой матрицу 2×2, на которой области бизнеса изображаются окружностями с центрами на пересечении координат, образуемых соответствующими темпами роста рынка и величинами относительной доли фирмы на соответствующем рынке (рис. 7-2). Каждая нанесенная на матрицу окружность отражает только одну область бизнеса, характерную для исследуемой фирмы. Величина окружности пропорциональна общему размеру всего рынка или, иными словами, учитывается не только размер бизнеса у конкретной фирмы, а вообще его размер как отрасли в масштабах всей экономики. Чаще всего этот размер определяется простым сложением бизнеса фирмы и соответствующего бизнеса ее конкурентов. Иногда на каждой окружности (бизнес-области) выделяется сегмент, характеризующий относительную долю бизнес-области фирмы на данном рынке, хотя для получения стратегических выводов в данной модели это необязательно. Размеры рынка, как и бизнес-области, чаще всего оцениваются по объемам продаж, а иногда и по стоимости активов.  [c.174]

Основными матричными операциями являются умножение матрицы на число, сложение и перемножение двух матриц.  [c.54]

Матрицы сложение и умножение  [c.23]

МАТРИЦЫ СЛОЖЕНИЕ И УМНОЖЕНИЕ  [c.23]

Пусть число вершин в S равно п. Определим последовательность матриц Гт = у /0 (т = 1. …. п + 2) с помощью следующего рекуррентного соотношения Гт (-1 =. = Tm-Qm (операции сложения при умножении матриц — булевы), где Qm = qTf ,  [c.35]

Матрицы складываются друг с другом посредством сложения каждого элемента из одной матрицы с соответствующим элементом другой матрицы. Вычитание матриц достигается вычитанием каждого элемента второй матрицы из соответствующего элемента первой. В обобщенном виде это записывается так  [c.303]

Далее исходная матрица должна быть преобразована в единичную через сложение, вычитание, умножение или деление каждой строки. Когда матрица слева превратится в единичную, матрица, полученная справа, будет представлять собой обратную к исходной матрице. Это показано ниже.  [c.305]

Назовем эту таблицу для краткости таблицей выигрышей и обозначим ее буквой S, что понадобится нам при дальнейшем изложении. В математике таблицы чисел называются матрицами и над ними определены операции сложения, вычитания, умножения и транспонирования. Нам понадобятся только операции вычитания (сложения) и транспонирования матриц.  [c.15]

Сложение и вычитание матриц  [c.377]

Аддитивность А + В = В + А, т. е. матрицы согласованные для сложения можно складывать в любом порядке.  [c.378]

Коммутативность А + (В + С) = (А + В) + С, т. е., как и в обычной алгебре, можно вначале сложить матрицы В и С, а затем прибавить к ним А, или же вначале сложить А и В, а к ним прибавить С. Результат же сложения будет один и тот же.  [c.378]

Отметим, что матрицы S и S всегда согласованы для вычитания (сложения), поскольку при.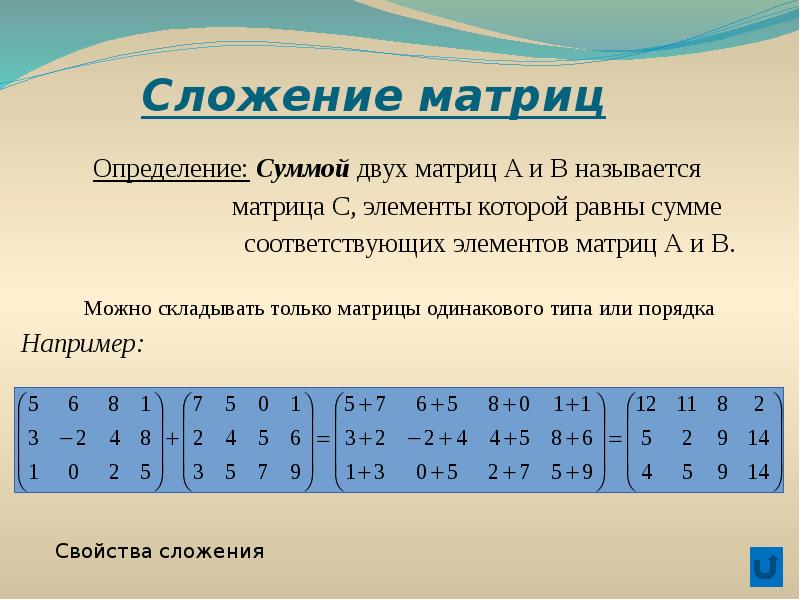 транспонировании размер квадратной матрицы не изменяется.  [c.379]

Под матрицей в математике принято понимать прямоугольную таблицу чисел, состоящую из т строк и я столбцов. Если число строк и столбцов в матрице одинаковое (т = п), матрица называется квадратной. Действия с матрицами (сложение, вычитание, умножение) производятся по разработанным математикой методам матричного исчисления.  [c.506]

Суммируются объемы продажи прибылей по СЗХ, находящимся в одной фазе жизненного цикла, и результаты фиксируются в верхних ячейках клеток ( экстраполяция ) в обоих блоках матрицы — краткосрочном и долгосрочном. Производится сложение по горизонтали, и полученные суммы вписываются в последние ячейки клеток каждой строки (прогнозируемые объемы продаж и прибылей по всем СЗХ в краткосрочной и долгосрочной перспективе).  [c.267]

Графоаналитический метод трудно записать в виде программы для ЭВМ в силу трудности формализации пожелания «зачеркнуть нули минимальным количеством прямых». Поэтому если размерность задачи большая и требуется процесс оптимизации автоматизировать, чаще всего применяют метод Мака. Он также основан на идее выбора в каждой строке минимального элемента. Чтобы распределить элементы по строкам и столбцам, здесь также используется идея сложения или вычитания одного и того же значения со всеми элементами строк или столбцов. По-прежнему будем рассматривать уже сбалансированную задачу, пользуясь понятиями «невыбранного» — Ml и «выбранного» — М2 подмножеств столбцов платежной матрицы.  [c.165]

Более сложная и содержательная платежная матрица может быть получена, если несколько модифицировать предложенную игру. Допустим, что оба участника имеют право загадывать числа от 1 до 4, что составляет их соответствующие стратегии. В случае, если результат сложения задуманных чисел будет четным, то второй игрок выплачивает первому получившуюся сумму, а если нечетным, то первый — второму. Запишем платежную матрицу для такой игры  [c.188]

Определение операций с матрицами (сложение, умножение и т. п.) следует из определения операций с линейными операторами.  [c.489]

В настоящее время в зарубежной литературе разработан алгоритм решения целочисленной задачи, но алгоритм этот очень сложен и при больших матрицах не решается на существующих ЭВМ. Подобные задачи решаются приближенным методом.  [c.252]

Оператор сложения (клавиша + ) А + В или А + х. А, В — матрицы (или векторы) одной размерности х — скаляр. Если складываются  [c.176]

Сложение двух матриц. Если А и В — две матрицы одного порядка, [c.75]

V. А (В + С) = АВ + АС и (В + С) А = ВА + СА, т. е. имеет место дистрибутивный закон умножения матриц относительно сложения. Элемент i/ матрицы А (В + С) равен  [c.78]

Основные операции сложения и умножения применимы также и к матрицам, подвергшимся разбиению, если процесс разбиения осуществлен подходящим образом. Например, если разбиение матрицы В порядка 3×4 имеет вид  [c.94]

М. м., с помощью к-рых моделируются последоват. звенья нар. х-ва, на основе использования правил сложения матриц образуют единый взаимосвязанный комплекс, наз. системой М. м. Так, М. м. экономики отрасли создаётся путём объединения М. м. предприятий с помощью т. п. вариантных матриц, отражающих разные технологич. варианты произ-ва продукции и услуг на разных предприятиях. Эти вариантные матрицы имеют самостоят, значение для межзаводского и межотраслевого анализа, организации нормативного х-ва отрасли. Вычитание и деление матриц обеспечивают процесс развёрстки плана отрасли по предприятиям, а представление их в виде систем линейных уравнении — применение методов математич. программирования д >я оптимального отраслевого планирования. Межотраслевые балансы экономики республики и нар. х-ва и целом могут строиться на основе объединения отраслевых матриц.  [c.421]

Определение. Суммой двух матриц А = ( iij) и В = (bij) размерностей m х п называется матрица А + В = С = (е -) размерности т х п с элементами ij = a + bij, т. е. при сложении матриц складываются соответствующие элементы.  [c.489]

I. А + В= В + А, т.е. для сложения имеет место комму тати ный закон. Матрицы А и В должны быть, конечно, одного и того я порядка. Этот закон выводится непосредственно из определени действия сложения матриц.  [c.77]

III, (А + В) 4- С = А + (В + С), т. е. для сложения матриц име ет место ассоциативный закон. Справедливость этого закона следуе из того, что сложение матриц выполняется поэлементно, а для элемек тов (чисел) не существенно, в каком порядке их складывать.  [c.77]

Расчет полных затрат весьма сложен, требует значительной вычислительной работы. Есть два основных споооЫреше-нж этой задачи, первый — подсчет кос венных затрат и их суммирование с прямыми, второй—непосредственное получение К,п,з. из матрицы коэффициентов прямых затрат с помощью операции, называемой обращением матрицы, В последнем случае решение системы уравнений МОБ приводит к матрице (таблице) коэффициентов полных затрат  [c.158]

Сложение, умножение и транспортирование матриц, основные свойства этих операций. Определение линейного оператора, его простейшие свойства. Изоморфные векторные пространства. Изоморфы евклидовых пространств. Матрица линейного оператора, ее преобразование при смене базиса. Подобные матрицы.  [c.11]

C#: Класс «Матрица» (сложение, вычитание, умножение матриц)

 Данный класс позволяет производить некоторые операции над матрицами:

1. Сложение матрицы А с матрицой Б
2. Вычитание матрицы Б из матрицы А
3. Умножение матрицы А на матрицу Б
4. Умножение матрица А на число
5.  Проверка матрицы А на единичность
6. Выполнение нексольких операций над матрицами одновременно, образуя матрицу D 

Так же он содержит операторы перегрузки и скрытые поля для соблудения инкапсуляции.

 Язык программирования С#

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace ConsoleApplication1
{
    class Matrix
    {
        // Скрытые поля
        private int n;
        private int[,] mass;

        // Создаем конструкторы матрицы
        public Matrix() { }
        public int N
        {
            get { return n; }
            set { if(value>0) n = value; }
        }

        // Задаем аксессоры для работы с полями вне класса Matrix
        public Matrix(int n)
        {
            this. n = n;
            mass = new int[this.n, this.n];
        }
        public int this [int i, int j]
        {
            get
            {
                return mass[i, j];
            }
            set
            {
                mass[i, j] = value;
            }
        }

        // Ввод матрицы с клавиатуры
        public void WriteMat()
        {
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    Console.WriteLine("Введите элемент матрицы {0}:{1}", i+1, j+1);
                    mass[i, j] = Convert. ToInt32(Console.ReadLine());
                }
            }
        }

        // Вывод матрицы с клавиатуры
        public void ReadMat()
        {
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    Console.Write(mass[i, j] + "\t");
                }
                Console.WriteLine();
            }
        }

        // Проверка матрицы А на единичность
        public void oneMat(Matrix a){
            int count = 0;
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    if (a[i, j] == 1 && i == j)
                    {
                        count++;
                    }
                }

            }
            if (count == a. N)
            {
                Console.WriteLine("Единичная");
            }
            else Console.WriteLine("Не единичная");
        }

        // Умножение матрицы А на число
        public static Matrix umnch(Matrix a, int ch)
        {
            Matrix resMass = new Matrix(a.N);
            for (int i = 0; i < a.N; i++)
            {
                for (int j = 0; j < a.N; j++)
                {
                    resMass[i, j] = a[i, j] * ch;
                }
            }
            return resMass;
        }

        // Умножение матрицы А на матрицу Б
        public static Matrix umn(Matrix a, Matrix b)
        {
            Matrix resMass = new Matrix(a. N);
            for (int i = 0; i < a.N; i++)
                for (int j = 0; j < b.N; j++)
                    for (int k = 0; k < b.N; k++)
                        resMass[i, j] += a[i, k]*b[k, j];

            return resMass;
        }

        // перегрузка оператора умножения
        public static Matrix operator *(Matrix a, Matrix b)
        {
            return Matrix.umn(a, b);
        }

        public static Matrix operator *(Matrix a, int b)
        {
            return Matrix.umnch(a, b);
        }

        // Метод вычитания матрицы Б из матрицы А
        public static Matrix razn(Matrix a, Matrix b)
        {
            Matrix resMass = new Matrix(a.N);
            for (int i = 0; i < a.N; i++)
            {
                for (int j = 0; j < b.N; j++)
                {
                    resMass[i, j] = a[i, j] - b[i, j];
                }
            }
            return resMass;
        }

        // Перегрузка оператора вычитания
        public static Matrix operator -(Matrix a, Matrix b)
        {
            return Matrix.razn(a, b);
        }
        public static Matrix Sum(Matrix a, Matrix b)
        {
            Matrix resMass = new Matrix(a.N);
            for (int i = 0; i < a.N; i++ )
            {
                for(int j = 0; j < b.N; j++)
                {
                    resMass[i, j] = a[i, j] + b[i, j];
                }
            }
            return resMass;
        }
        // Перегрузка сложения
        public static Matrix operator +(Matrix a, Matrix b)
        {
            return Matrix.Sum(a, b);
        }
        // Деструктор Matrix
        ~Matrix()
        {
            Console.WriteLine("Очистка");
        }

    }
    class MainProgram{

        static void Main(string[] args)
        {
            Console.WriteLine ("Введите размерность матрицы: ");
            int nn = Convert.ToInt32 (Console.ReadLine ());
            // Инициализация
            Matrix mass1 = new Matrix(nn);
            Matrix mass2 = new Matrix(nn);
            Matrix mass3 = new Matrix(nn);
            Matrix mass4 = new Matrix(nn);
            Matrix mass5 = new Matrix(nn);
            Matrix mass6 = new Matrix(nn);
            Matrix mass7 = new Matrix(nn);
            Matrix mass8 = new Matrix(nn);
            Console.WriteLine("ввод Матрица А: ");
            mass1.WriteMat();
            Console.WriteLine("Ввод Матрица B: ");
            mass2.WriteMat();

            Console.WriteLine("Матрица А: ");
            mass1.ReadMat();
            Console.WriteLine();
            Console.WriteLine("Матрица В: ");
            Console.WriteLine();
            mass2.ReadMat();

            Console.WriteLine ("Сложение матриц А и Б: ");
            mass4 = (mass1 + mass2);
            mass4.ReadMat ();

            Console.WriteLine ("Вычитание матриц А и Б: ");
            mass6 = (mass1 - mass2);
            mass6.ReadMat ();

            Console.WriteLine ("Умножение матриц А и Б: ");
            mass8 = (mass1 * mass2);
            mass8.ReadMat ();

            Console.WriteLine ("Умножение матрицы А на число 2: ");
            mass5 = (mass1 * 2);
            mass5.ReadMat ();

            Console.WriteLine ("Матрица D по формуле  D=3AB+(A-B)A: ");
            mass7 = ( (mass1 * 3) * mass2 + (mass1-mass2) * mass1);
            mass7.ReadMat ();

            Console.ReadKey();
        }
    }
}

Лабораторная работа № 8. Excel. Операции с матрицами. Сложение двух матриц.

Складывать матрицы можно только при условии, что они имеют одинаковый размер.

Чтобы сложить две матрицы, нужно сложить все их соответствующие элементы.

1. В ячейку B12 записать формулу =B4+B8.

2. Скопировать содержимое ячейки в диапазон ячеек B12:B14.

Результат на Рис. 11.

Рис. 11 Результат сложения.

Умножение матрицы на скаляр.

Чтобы умножить матрицу на скаляр, нужно умножить на скаляр каждый элемент матрицы.

1. Введем в ячейки электронной таблицы скаляр, представляющий собой константу и матрицу B4:C6, которую нужно умножить на него.

2. В ячейку B9 введем формулу =$B$3*B4.

3. Копируем формулы из ячейки B9 в диапазон B9:C11.

4. Результат отображается в ячейках B9:С11.

Рис. 12 Умножение матрицы на скаляр.

Перемножение матриц.

Две матрицы можно перемножить при условии, что количество столбцов первой матрицы равно количеству строк второй матрицы. («Внутренние» размеры матрицы должны совпадать, размеры результирующей матрицы состоят из «внешних» размеров).

1. Ввести матрицу 3х2 (произвольные числа) в ячейки A4:B6.

2. В ячейки A9:A10 ввести матрицу 2х1 (произвольные числа).

3. Выделить ячейки C4:C6.

4. В строке функций набрать формулу =МУМНОЖ(A4:B6;A9:A10).

5. Нажать сочетание клавиш CTRL+SHIFT+ENTER.

Рис. 13 Умножение матриц.

Транспонирование матриц.

Чтобы транспонировать любую матрицу, нужно поменять ее строки и столбцы. В Excel это можно сделать двумя способами. Рассмотрим оба метода.

С помощью команды меню «Специальная вставка»

1. Введите исходную матрицу.

2. Выделите ячейки, в которых содержатся эта матрица.

3. Скопируйте их содержимое в буфер обмена.

4. Установите указатель мыши на ячейку, в которой будет содержаться верхнее левое значение транспонированной матрицы.

5. Дайте команду Правка ► Специальная вставка.

6. Отобразится диалоговое окно Специальная вставка.

Рис. 14 Окно «Специальная вставка»

7. На панели Вставить установите переключатель в положение значение и установите флажок транспонировать, расположенный в нижней части диалогового окна.

8. Нажмите OK.

С помощью функции массива.

1. Введите исходную матрицу.

2. Укажите, куда нужно поместить результат (выделите диапазон ячеек).

3. В окне формул введите функцию =ТРАНСП(матрица).

4. Укажите с помощью мышки диапазон, в котором содержится матрица.

5. Завершите функцию нажатием клавиш CTRL+SHIFT+ENTER.

Задание.

Транспонируйте обоими способами приведенные ниже матрицы.

Обращение матриц.

Операция обращения матриц применима только к квадратным матрицам. Однако не для каждой матрицы существует обратная к ней матрица. Чтобы матрицу можно было обратить, она должна быть несингулярной. (детерминант матрицы должен быть отличен от 0).

Детерминант матрицы – это скалярная величина, которая вычисляется на основе всех матричных элементов и часто используется при решении систем уравнений.

Для вычисления детерминанта в Excel используется функция массива =МОПРЕД(матрица). Если он отличен от 0, то матрицу можно обратить.

1. Введите матрицу, которую нужно обратить.

2. Вычислите ее детерминант. Если он не равен 0 – продолжите процесс обращения, иначе измените исходные данные.

3. Укажите место для размещения обратной матрицы и ее правильный размер — он совпадает с размером исходной матрицы.

4. Начните вводить функцию массива =МОБР(матрица) и укажите с помощью мыши ячейки, в которых содержится обращаемая матрица.

5. Нажмите сочетание клавиш CTRL+SHIFT+ENTER.

Сложение матриц. Умножение матрицы на действительное (комплексное) число

ОПЕРАЦИИ НАД МАТРИЦАМИ

Сложение матриц. Умножение матрицы на действительное (комплексное) число

Рассмотрим множество M_mn всех матриц размерности mn с действительными (комплексными) элементами.

Определение 8. Суммой двух матриц одинаковой размерности называется матрица, каждый элемент которой равен сумме соответствующих элементов данных матриц.

Если а_рк и в_рк – соответствующие элементы матриц А и В соответственно и С = А + В, то с_рк = а_рк + в_рк .

Очевидно, сложение матриц обладает следующими свойствами:

• Сумма любых двух матриц одинаковой размерности определена и однозначна.

• А + В = В + А для любых матриц А и В из M_mn.

• (А + В) + С = А + (В + С) для любых А, В, С из M_mn .

• Матрица, все элементы которой равны нулю, играет роль нуля при сложении и называется нулевой матрицей. Её обозначают О (А + О = А ).

• Если обозначить А матрицу, все элементы которой противоположны соответствующим элементам матрицы А, то А + (А) = О, т.е. матрица (А) противоположна матрице А. Итак, каждая матрица имеет противоположную.

Определение 9. Произведением матрицы А на действительное (или комплексное) число  называется матрица В, все элементы которой равны соответствующим элементам матрицы А, умноженным на .

Если а_рк – элемент матрицы А, то в матрице В элемент в_рк =а_рк .

Умножение матрицы на число обладает следующими свойствами:

• Произведение любой матрицы на любое число определено и однозначно.

• 1А = А для любой матрицы А из M_mn .

• 0А = О для любой матрицы А из M_mn .

• ()А = (А) для любой матрицы А из M_mn и любых чисел  и .

• ( + )А = А + А для любой матрицы А из M_mn и любых чисел  и .

• (А + В) = А + В для любых матриц А и В из M_mn и любого числа .

• Если А  квадратная матрица n-го порядка, то А = ⁿА .

Простые и двойные суммы

Введём некоторые общематематические понятия и обозначения.

Определение 10. Сумма вида а₁ + а₂ + … +а_n называется простой суммой и обозначается . Следовательно, = а₁ + а₂ + … +а_n.

Свойства простых сумм:

1⁰. , 2⁰. .

Определение 10. Сумма вида

называется двойной суммой и обозначается .

Свойства двойных сумм:

1⁰. = ; 2⁰. = .

Умножение матриц

Пусть А – матрица размерности mn и В – матрица размерности n к. Произведением матрицы А на матрицу В называется матрица С, элементы которой получаются следующим образом: каждый элемент р-ой строки матрицы А умножается на соответствующий элемент q-го столбца матрицы В, полученные произведения складываются и результат ставится в пересечение р-ой строки и q-го столбца матрицы С, т.е. с_рq = (11).

Размерность матрицы С равна m к.

Пример 1.

= .

Пример 2. Произведение матриц не определено.

Но даже если АВ и ВА определены, то они не обязаны быть равны.

Пример 3. АВ = ,

АВ = .

В этом примере АВ и ВА определены, но АВ  ВА . Следовательно, для умножения матриц коммутативный закон не имеет места. Можно проверить:

1⁰. Если (АВ)С и А(ВС) определены, то (АВ)С = А(ВС).

2⁰. Если (А + В)С определено, то (А + В)С = АС + ВС.

3⁰. Если АВ определено, то (А)В =(АВ).

Умножение квадратных матриц одного порядка.

Произведение любых двух квадратных матриц одного порядка всегда определено. При умножении двух квадратных матриц n-го порядка получится матрица того же порядка.

Теорема 7. Определитель произведения квадратных матриц одного порядка равен произведению определителей сомножителей.

Доказательство. Пусть А = , В = . Составим

Тогда в (n +1)-м столбце на первых n местах будут стоять элементы первого столбца матрицы АВ, а на остальных местах – нули.

Если А  0, то матрица А называется невырожденной, если же А = 0, то матрица А вырожденная. Из теоремы 7 следует, что произведение двух невырожденных квадратных матриц одного порядка есть невырожденная матрица того же порядка, если же одна из матриц вырожденная, то их произведение – тоже вырожденная матрица.

Квадратная матрица Е = называется единичной матрицей. Легко проверить, что ЕА = АЕ для любой квадратной матрицы А, имеющей тот же порядок, что и Е. Очевидно, Е = 1.

Определение 11. Матрица В называется правой обратной для матрицы А, если ВА= Е и левой обратной для А, если АВ = Е.

Возникает вопрос, всякая ли квадратная матрица имеет левую или правую обратную матрицу. Если В – левая или правая обратная матрица, то (по теореме 7) ВА = АВ = 1, т.е. матрица А не может быть вырожденной.

Пусть А квадратная невырожденная матрица, найдём алгебраические дополнения для всех её элементов. Составим новую матрицу А^{ следующим образом: алгебраические дополнения элементов к-ой строки матрицы А поставим в к-ый столбец матрицы А, т.е. А = . Матрица А называется присоединённой для матрицы А. По правилу умножения матриц и свойствам определителя получаем, что}

АА^= А^А = = АЕ.

Так как А  0, то матрица В = существует и АВ = ВА = Е, т.е. матрица В является и левой и правой обратной матрицей для матрицы А. Эта матрица называется обратной матрицей для А и обозначается А^-1. Итак, получили

Теорема 8. Для всякой квадратной невырожденной матрицы существует обратная матрица. Обратная матрица перестановочна с данной матрицей и вычисляется по формуле

А^-1= (13)

Пример 4. Найдите обратную матрицу, если А = .

Решение. Найдём А = 10 + 12 + 0 – 0 + 4 + 12 = 36.

Составим присоединённую матрицу, для этого вычислим алгебраические дополнения. А₁₁ = = 14, А₁₂ = =  6, А₁₃ = = 3, А₂₁ == 8, А₂₂ = = 2, А₂₃ = = 1, А₃₁ = = 28, А₃₂ = = 16, А₃₃ = = 11. Используя теорему 8, получим А^-1 = .

Решение матричных уравнений

Рассмотрим простейшие матричные уравнения вида АХ = В (14) и ХА = В (15).

Возможны два случая: 1) матрица А квадратная невырожденная; 2) матрица А  либо вырожденная, либо прямоугольная.

1) Если А – квадратная и А  0, то уравнения (14) и (15) имеют единственное решение каждое: Х = А^-1В и Х = ВА^{-1соответственно, если эти произведения определены. И не имеют решения, если они не определены.}

2) А – квадратная матрица, но А = 0, либо А  прямоугольная матрица. Если матрица А имеет размерность mn, а матрица В – размерность рк, то, при m  р уравнение (14) не имеет решения, а при n  к не имеет решения уравнение (15). Если же m = р , то в уравнении (14) матрица Х должна иметь к столбцов, а в уравнении (15) она должна иметь р строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений.

Пример 5. Найдите матрицу Х, если АХ = В, где А = , В = .

Из примера 5 следует, что матрица А имеет обратную, поэтому Х = А^-1В. Используя найденную в примере 5 матрицу А^-1, получим Х =  = = .

Пример 6. Найдите матрицу Х, если ХА = В, где А = , В =. Так как А = 0, то для А обратной матрицы нет. По правилам умножения матриц, в матрице В столько строк, сколько их в матрице Х, и столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х должно быть два столбца и три строки. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х = . Тогда ХА = . Полученная матрица равна матрице В тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений. Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.

Матрицы сложения и вычитания

А матрица могут быть добавлены (или вычтены из) другой матрицы только в том случае, если две матрицы имеют одинаковые Габаритные размеры .

Чтобы добавить две матрицы, просто добавьте соответствующие записи и поместите эту сумму в соответствующую позицию в матрице, которая получится.

Пример 1:

Добавьте матрицы.

[ 1 5 — 4 3 ] + [ 2 — 1 4 — 1 ]

Сначала обратите внимание, что оба слагаемых 2 × 2 матрицы, чтобы мы могли их добавлять.

[ 1 5 — 4 3 ] + [ 2 — 1 4 — 1 ] знак равно [ 1 + 2 5 + ( — 1 ) — 4 + 4 3 + ( — 1 ) ]

знак равно [ 3 4 0 2 ]

Вычитание с помощью матриц так же просто.

Пример 2:

Вычесть.

[ 4 5 6 2 3 4 ] — [ 2 4 6 1 2 3 ]

Вычтите соответствующие записи.

[ 4 5 6 2 3 4 ] — [ 2 4 6 1 2 3 ] знак равно [ 4 — 2 5 — 4 6 — 6 2 — 1 3 — 2 4 — 3 ]

знак равно [ 2 1 0 1 1 1 ]

Нахождение суммы и разности двух матриц

Чтобы решить задачу, подобную описанной для футбольных команд, мы можем использовать матрицу , которая представляет собой прямоугольный массив чисел.Строка в матрице — это набор чисел, выровненных по горизонтали. Столбец в матрице — это набор чисел, выровненных по вертикали. Каждое число представляет собой запись , иногда называемую элементом матрицы. Матрицы (множественное число) заключаются в [] или () и обычно называются заглавными буквами. Например, три матрицы с именами [latex] A, B, \ text {} [/ latex] и [latex] C [/ latex] показаны ниже.

[латекс] A = \ left [\ begin {array} {cc} 1 & 2 \\ 3 & 4 \ end {array} \ right], B = \ left [\ begin {array} {ccc} 1 & 2 & 7 \\ 0 & -5 & 6 \\ 7 & 8 & 2 \ end {array} \ right], C = \ left [\ begin {array} {c} -1 \\ 0 \\ 3 \ end {array} \ begin {array} { c} 3 \\ 2 \\ 1 \ end {array} \ right] [/ latex]

Описание матриц

Матрицу часто называют ее размером или размерами: [latex] \ text {} m \ text {} \ times \ text {} n \ text {} [/ latex] с указанием [latex] m [/ latex] строк и [латексные] п [/ латексные] столбцы.Записи матрицы определяются сначала по строкам, а затем по столбцам. Например, чтобы найти запись в матрице [latex] A [/ latex], идентифицированную как [latex] {a} _ {ij}, \ text {} [/ latex], мы ищем запись в строке [latex] i, \ text {} [/ latex] столбец [латекс] j [/ latex]. В матрице [latex] A \ text {,} \ hspace {0.17em} [/ latex], показанной ниже, запись в строке 2, столбце 3 — [latex] {a} _ {23} [/ latex].

[латекс] A = \ left [\ begin {array} {ccc} {a} _ {11} & {a} _ {12} & {a} _ {13} \\ {a} _ {21} & {a} _ {22} & {a} _ {23} \\ {a} _ {31} & {a} _ {32} & {a} _ {33} \ end {array} \ right] [/ латекс]

Квадратная матрица — это матрица с размерами [latex] \ text {} n \ text {} \ times \ text {} n, \ text {} [/ latex], что означает, что в ней столько же строк, сколько и столбцов. .Матрица [latex] 3 \ times 3 [/ latex] выше является примером квадратной матрицы.

Матрица строк — это матрица, состоящая из одной строки с размерами [латекс] 1 \ text {} \ times \ text {} n [/ latex].

[латекс] \ left [\ begin {array} {ccc} {a} _ {11} & {a} _ {12} & {a} _ {13} \ end {array} \ right] [/ latex]

Матрица столбцов — это матрица, состоящая из одного столбца с размерами [латекс] m \ text {} \ times \ text {} 1 [/ latex].

[латекс] \ left [\ begin {array} {c} {a} _ {11} \\ {a} _ {21} \\ {a} _ {31} \ end {array} \ right] [/ латекс]

Матрица может использоваться для представления системы уравнений.В этих случаях числа представляют собой коэффициенты переменных в системе. Матрицы часто упрощают решение систем уравнений, потому что они не перегружены переменными. Мы рассмотрим эту идею дальше в следующем разделе, но сначала рассмотрим основные операции с матрицей .

A Общее примечание: матрицы

Матрица — это прямоугольный массив чисел, который обычно обозначается заглавной буквой: [latex] A, B, C, \ text {} [/ latex] и так далее.Каждая запись в матрице называется [latex] {a} _ {ij} [/ latex], так что [latex] i [/ latex] представляет строку, а [latex] j [/ latex] представляет столбец. Матрицы часто называют их размерами: [латекс] m \ times n [/ latex], обозначающий строки [latex] m [/ latex] и столбцы [latex] n [/ latex].

Пример 1: Нахождение размеров данной матрицы и поиск записей

Данная матрица [латекс] A: [/ латекс]

1. Какие размеры матрицы [латекс] А? [/ Латекс]
2. Какие записи есть у [latex] {a} _ {31} [/ latex] и [latex] {a} _ {22}? [/ Latex]

   [латекс] A = \ left [\ begin {array} {rrrr} \ hfill 2 & \ hfill & \ hfill 1 & \ hfill 0 \\ \ hfill 2 & \ hfill & \ hfill 4 & \ hfill 7 \\ \ hfill 3 & \ hfill & \ hfill 1 & \ hfill -2 \ end {array} \ right] [/ latex]

Решение

1. Размеры: [latex] \ text {} 3 \ text {} \ times \ text {} 3 \ text {} [/ latex], потому что есть три строки и три столбца.
2. Запись [latex] {a} _ {31} [/ latex] — это номер в строке 3, столбец 1, который равен 3. Запись [latex] {a} _ {22} [/ latex] — это номер в строка 2, столбец 2, то есть 4. Помните, сначала идет строка, затем столбец.

Сложение и вычитание матриц

Мы используем матрицы для перечисления данных или представления систем. Поскольку записи являются числами, мы можем выполнять операции с матрицами. Мы складываем или вычитаем матрицы, добавляя или вычитая соответствующие записи.

Для этого записи должны соответствовать.Следовательно, сложение и вычитание матриц возможно только тогда, когда матрицы имеют одинаковые размеры . Мы можем добавить или вычесть матрицу [latex] \ text {} 3 \ text {} \ times \ text {} 3 \ text {} [/ latex] и другую матрицу [latex] \ text {} 3 \ text {} \ times \ text {} 3 \ text {} [/ latex] матрица, но мы не можем добавить или вычесть матрицу [latex] \ text {} 2 \ text {} \ times \ text {} 3 \ text {} [/ latex] и матрица [latex] \ text {} 3 \ text {} \ times \ text {} 3 \ text {} [/ latex], потому что некоторые записи в одной матрице не будут иметь соответствующей записи в другой матрице.

Общее примечание: сложение и вычитание матриц

Для заданных матриц [латекс] A [/ латекс] и [латекс] B [/ латекс] одинаковых размеров, сложение и вычитание [латекса] A [/ латекса] и [латекса] B [/ латекса] даст матрицу [латекс ] C [/ латекс] или матрица [латекс] D [/ латекс] такой же размерности.

[латекс] A + B = C \ text {такой, что} {a} _ {ij} + {b} _ {ij} = {c} _ {ij} [/ latex]

[латекс] A-B = D \ text {такой, что} {a} _ {ij} — {b} _ {ij} = {d} _ {ij} [/ latex]

Матричное сложение коммутативно.

[латекс] A + B = B + A [/ латекс]

Тоже ассоциативный.

[латекс] \ влево (A + B \ вправо) + C = A + \ влево (B + C \ вправо) [/ латекс]

Пример 2: Нахождение суммы матриц

Найдите сумму [латекса] A [/ latex] и [латекса] B, \ text {} [/ latex] с учетом

[латекс] A = \ left [\ begin {array} {cc} a & b \\ c & d \ end {array} \ right] \ text {and} B = \ left [\ begin {array} {cc} e & f \\ g & h \ end {array} \ right] [/ latex]

Решение

Добавьте соответствующие записи.

[латекс] \ begin {массив} {l} A + B = \ left [\ begin {array} {cc} a & b \\ c & d \ end {array} \ right] + \ left [\ begin {array} {cc} e & f \\ g & h \ end {array} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {ccc} a + e & & b + f \\ c + g & & d + h \ end {array} \ right] \ hfill \ end {array} [/ latex]

Пример 3: Добавление матрицы

Найдите сумму [латекса] A [/ латекса] и [латекса] B [/ латекса].

[латекс] A = \ left [\ begin {array} {cc} 4 & 1 \\ 3 & 2 \ end {array} \ right] \ text {and} B = \ left [\ begin {array} {cc} 5 & 9 \\ 0 & 7 \ end {array} \ right] [/ latex]

Решение

Добавьте соответствующие записи.Добавьте запись в строке 1, столбце 1, [latex] {a} _ {11}, \ text {} [/ latex] матрицы [latex] A [/ latex] к записи в строке 1, столбце 1, [ латекс] {b} _ {11} [/ латекс], из [латекса] B [/ латекса]. Продолжайте шаблон, пока не будут добавлены все записи.

[латекс] \ begin {массив} {l} A + B = \ left [\ begin {array} {cc} 4 & 1 \\ 3 & 2 \ end {array} \ right] + \ left [\ begin {array} {cc} 5 & 9 \\ 0 & 7 \ end {array} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {ccc} 4 + 5 & & 1 + 9 \\ 3 + 0 & & 2 + 7 \ end {array} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {cc} 9 & 10 \\ 3 & 9 \ end {array} \ right] \ hfill \ end { array} [/ latex]

Пример 4: Нахождение разности двух матриц

Найдите разницу между [латексом] A [/ латексом] и [латексом] B [/ латексом].

[латекс] A = \ left [\ begin {array} {cc} -2 & 3 \\ 0 & 1 \ end {array} \ right] \ text {and} B = \ left [\ begin {array} {cc} 8 & 1 \\ 5 & 4 \ end {array} \ right] [/ latex]

Решение

Мы вычитаем соответствующие элементы каждой матрицы.

[латекс] \ begin {array} {l} AB = \ left [\ begin {array} {rr} \ hfill -2 & \ hfill 3 \\ \ hfill 0 & \ hfill 1 \ end {array} \ right] — \ left [\ begin {array} {rr} \ hfill 8 & \ hfill 1 \\ \ hfill 5 & \ hfill 4 \ end {array} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} { rrr} \ hfill -2-8 & \ hfill & \ hfill 3-1 \\ \ hfill 0-5 & \ hfill & \ hfill 1-4 \ end {array} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {rrr} \ hfill -10 & \ hfill & \ hfill 2 \\ \ hfill -5 & \ hfill & \ hfill -3 \ end {array} \ right] \ hfill \ end {array} [/ latex ]

Пример 5: Нахождение суммы и разности двух матриц 3 x 3

Даны [латекс] A [/ латекс] и [латекс] B: [/ латекс]

1. Найдите сумму.
2. Найдите разницу.

[латекс] A = \ left [\ begin {array} {rrr} \ hfill 2 & \ hfill -10 & \ hfill -2 \\ \ hfill 14 & \ hfill 12 & \ hfill 10 \\ \ hfill 4 & \ hfill -2 & \ hfill 2 \ end {array} \ right] \ text {and} B = \ left [\ begin {array} {rrr} \ hfill 6 & \ hfill 10 & \ hfill -2 \\ \ hfill 0 & \ hfill -12 & \ hfill — 4 \\ \ hfill -5 & \ hfill 2 & \ hfill -2 \ end {array} \ right] [/ latex]

Решение

1. Добавьте соответствующие записи.

   [латекс] \ begin {массив} {l} \ hfill \\ A + B = \ left [\ begin {array} {rrr} \ hfill 2 & \ hfill -10 & \ hfill -2 \\ \ hfill 14 & \ hfill 12 & \ hfill 10 \\ \ hfill 4 & \ hfill -2 & \ hfill 2 \ end {array} \ right] + \ left [\ begin {array} {rrr} \ hfill 6 & \ hfill 10 & \ hfill -2 \\ \ hfill 0 & \ hfill -12 & \ hfill -4 \\ \ hfill -5 & \ hfill 2 & \ hfill -2 \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill 2 + 6 & \ hfill -10 + 10 & \ hfill -2-2 \\ \ hfill 14 + 0 & \ hfill 12-12 & \ hfill 10-4 \\ \ hfill 4-5 & \ hfill -2 + 2 & \ hfill 2-2 \ end { массив} \ right] \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill 8 & \ hfill 0 & \ hfill -4 \\ \ hfill 14 & \ hfill 0 & \ hfill 6 \\ \ hfill -1 & \ hfill 0 & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} [/ latex]

2. Вычтите соответствующие записи.

   [латекс] \ begin {массив} {l} \ hfill \\ AB = \ left [\ begin {array} {rrr} \ hfill 2 & \ hfill -10 & \ hfill -2 \\ \ hfill 14 & \ hfill 12 & \ hfill 10 \\ \ hfill 4 & \ hfill -2 & \ hfill 2 \ end {array} \ right] — \ left [\ begin {array} {rrr} \ hfill 6 & \ hfill 10 & \ hfill -2 \\ \ hfill 0 & \ hfill -12 & \ hfill -4 \\ \ hfill -5 & \ hfill 2 & \ hfill -2 \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill 2-6 & \ hfill -10-10 & \ hfill -2 + 2 \\ \ hfill 14-0 & \ hfill 12 + 12 & \ hfill 10 + 4 \\ \ hfill 4 + 5 & \ hfill -2-2 & \ hfill 2 + 2 \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill -4 & \ hfill -20 & \ hfill 0 \\ \ hfill 14 & \ hfill 24 & \ hfill 14 \\ \ hfill 9 & \ hfill -4 & \ hfill 4 \ end {array} \ right] \ hfill \ end {array} [/ latex]

Попробуйте 1

Добавить матрицу [латекс] A [/ латекс] и матрицу [латекс] B [/ латекс].

[латекс] A = \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 6 \\ \ hfill 1 & \ hfill 0 \\ \ hfill 1 & \ hfill -3 \ end {array} \ right] \ text {и} B = \ left [\ begin {array} {rr} \ hfill 3 & \ hfill -2 \\ \ hfill 1 & \ hfill 5 \\ \ hfill -4 & \ hfill 3 \ end {array} \ right] [/ латекс]

Матрицы сложения и вычитания — ChiliMath

В этом уроке я подготовил семь (7) рабочих примеров, чтобы проиллюстрировать базовый подход к тому, как легко складывать или вычитать матрицы.

Если вы знаете, как складывать и вычитать действительные числа, эта тема должна быть действительно легкой.Единственное, что требуется для «легального» выполнения операций сложения или вычитания в «мире» матриц, — это убедиться, что данные матрицы должны иметь одинаковый размер или размерность.

Что означает, что данная матрица имеет одинаковый размер или размерность?

Предположим, нам даны матрицы A и B. Они имеют одинаковый размер или размер, потому что у них одинаковое количество строк и столбцов.

Мы можем описать размер или размерность матрицы, используя следующий стандартный формат:

количество строк x количество столбцов

Позвольте мне показать вам несколько примеров…

Последняя матрица размером 5 x 5 также считается «квадратной матрицей», поскольку количество строк и количество столбцов равны.Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что все квадратные матрицы имеют обратные, но первое требование к матрице, чтобы иметь обратную матрицу, состоит в том, что она должна быть сначала квадратной матрицей.

Ознакомьтесь с моим отдельным руководством о том, как найти обратную матрицу 2 × 2.

Я должен подчеркнуть, что для того, чтобы сложить или вычесть две заданные матрицы, они должны иметь одинаковый размер или размер. В противном случае мы заключаем, что сумма (сложение) или разность (вычитание) двух матриц, имеющих разные размеры или размеры, не определена!

Теперь давайте посмотрим на общее правило того, как складывать и вычитать матрицы одинаковых размеров или размеров.

Правила сложения и вычитания матриц одинакового размера или измерения

Предположим, что матрицы A и B имеют две строки и два столбца (2 × 2) с некоторыми произвольными элементами или записями…

«Формулы» для сложения и вычитания матриц показаны ниже…

• Добавьте матрицы , добавив их соответствующие записи

• Вычесть матрицы путем вычитания их соответствующих записей

Давайте поработаем над некоторыми проблемами.

Примеры сложения и вычитания матриц

Пример 1 : Выполните указанную операцию для A + C.

Обратите внимание, что матрицы A и C имеют одинаковый «размер» или «размерность», потому что их количество строк и столбцов одинаково. Оба могут быть описаны как матрица 3 x 3 . Это говорит мне о том, что найти их сумму — это нормально.

Добавлю соответствующие записи и упрощу.

Вот как это просто!

Пример 2 : Выполните указанную операцию для B + F.

Обратите внимание, что матрица B имеет размерность 2 × 3 , а матрица F имеет размерность 2 × 2 .

Поскольку количество строк и столбцов не совпадает, сумма матриц B и F не существует или не определена . Я остановлюсь здесь. Это наш ответ, хотите верьте, хотите нет.

Пример 3 : Выполните указанную операцию для E-B.

Последние два примера показали вам, как складывать матрицы. На этот раз мы поговорим о вычитании матриц.Помните, что процесс сложения и вычитания матриц очень похож. Если вы забыли, просмотрите приведенную выше «формулу».

В этом примере нам нужно найти разницу между матрицей E и матрицей B.

Однако, похоже, это невозможно, поскольку они имеют различных размеров или . Матрица E имеет размер 3 × 2, а матрица B — 2 × 3.

Поскольку я не могу вычесть по входам, из-за того, что записи двух матриц не имеют прямого соответствия, я должен утверждать, что НЕ возможно найти их различие.Следовательно, наш ответ: undefined .

Это не вопрос с подвохом. Учителя иногда «добавляют» это в смесь, чтобы проверить, понимаете ли вы концепцию, согласно которой можно складывать или вычитать только матрицы с одинаковыми размерами или размерами. Не расстраивайтесь, я сам попал в эту «ловушку». Надеюсь, теперь, когда вы знаете, вы будете осторожны в следующий раз, когда столкнетесь с такой проблемой.

Пример 4 : Выполните указанную операцию для F-D.

При быстром просмотре я вижу, что можно найти разницу между матрицами F и D, потому что обе имеют одинаковое количество строк и столбцов.Большой!

Для начала я вычту соответствующие записи F и D. Мое единственное предостережение — будьте очень осторожны при вычитании действительных чисел. Обычно здесь возникают общие ошибки. Помните, что два соседних отрицательных знака оказываются положительными.

Неплохо, правда?

Пример 5 : Выполните указанную операцию для C-A.

Две заданные матрицы C и A имеют одинаковые размеры или размеры (обе матрицы 3 × 3). Это позволяет нам выполнять операцию вычитания.

Вычитая по входу, я получил…

Пример 6 : Выполните указанную операцию для (A + C) + (C-A).

Это отличный пример «многоступенчатой» задачи, которая включает в себя сложение и вычитание матриц. Цель состоит в том, чтобы выполнить указанную операцию над каждой круглой скобкой, а затем добавить их вместе.

Чтобы пропустить некоторые шаги, просмотрите, как мы решили для (A + C) в примере 1 и C-A в примере 5.

Пока у нас есть эти частичные ответы…

Итак, последний шаг — сложить их вместе, чтобы получить требуемый ответ.

Как видите, сложение и вычитание матриц очень просто. Я надеюсь, что вы приобрели некоторую уверенность и знания о том, как с этим справиться.

Пример 7 : Выполните указанную операцию для (A + C) + (C-A).

Это та же проблема, что и в примере 6. Но я хочу решить ее немного иначе, чтобы продемонстрировать тот факт, что есть другие способы решения определенной проблемы. Хотя метод, примененный в примере 6, вполне приемлем, этот «альтернативный» подход имеет гораздо больше смысла, поскольку он очень прост.

Поехали…

Если вы рассматриваете выражение (A + C) + (C-A) как , объединяющее похожие или похожие термины, проблема типа , то имеет смысл быстро упростить исходную задачу, даже не занимаясь сложением и вычитанием матриц.

Обратите внимание, что я могу объединить C-термины как 2C.

Теперь, члены A должны сокращаться, потому что они имеют противоположные знаки.

Наша исходная задача сводится к 2C, что составляет вдвое или вдвое больше матрицы C .

Это означает, что я собираюсь умножить каждый элемент матрицы C на 2. На самом деле это тема моего другого урока по алгебре, посвященного скалярному умножению матрицы.

С

, то 2C решается с помощью…

Окончательный ответ, полученный с помощью этого метода, точно такой же, как в примере 6. Легко, правда?

Возможно, вас заинтересует:

Скалярное умножение

Умножение матриц

Матрицы сложения и вычитания

Сложение матриц — MathsTips.com

В этой статье мы сделаем сложение матриц.Сложение между двумя матрицами возможно тогда и только тогда, когда они имеют одинаковый порядок или размеры, то есть они должны иметь одинаковое количество строк и столбцов. Добавление, если матрица возможна путем добавления элемента другой матрицы, если они имеют тот же порядок.

Предположим, у Mohan есть два магазина в точках A и B. Каждый магазин продает мужскую и женскую обувь трех разных ценовых категорий. Количество, продаваемое каждым магазином, представлено в виде матриц, приведенных ниже:

Магазин 1:

Магазин 2:

Предположим, Мохан хочет узнать общий объем продаж обуви в каждой ценовой категории.Таким образом, это может быть представлено в матричной форме как

Эта новая матрица представляет собой сумму двух вышеуказанных матриц. Итак, сумма двух матриц получается сложением соответствующих элементов данных матриц.

Таким образом, if — это матрица 2 * 2 и еще одна матрица 2 * 2. Затем мы определяем

В общем случае, если матрица и матрица — две матрицы одного порядка, скажем, m * n.

Таким образом, сумма двух матриц A и B определяется как матрица, где для всех значений i и j.

Свойства сложения матриц

1. Коммутативный закон

Это означает, что если, — матрицы одного порядка, скажем m * n, то A + B = B + A
Таким образом, A + B =

В + А =

2. Ассоциативное право

Это означает, что 3 матрицы, то есть, являются матрицами одного порядка, скажем, m * n, затем (A + B) + C = A + (B + C).

Таким образом, (A + B) + C = +
= + = A + (B + C)

1. Две матрицы должны быть одного порядка (количество строк = количество столбцов).
2. Добавьте соответствующий элемент других матриц.

Добавление матрицы заказа 2 * 2

Пример 1: Дано и найдите A + B.

Решение:

Добавление матрицы заказа 3 * 3

Пример 2: и найдите A + B.

Решение:

Упражнение

1. Позвольте и найти A + b.
2. Позвольте и найти A + B.
3. Позвольте и найти A + B.
4. Позвольте и и Покажите, что A + B = B + A.{-1}) \} \\ & + \ det B. \ end {split}

   Добавление матрицы

   Марко Табога, доктор философии

   Эта лекция знакомит с одной из основных алгебраических операций — сложением матриц. что может быть выполнено на матрицах.

   Определение

   Две матрицы могут быть сложены вместе тогда и только тогда, когда они имеют одинаковые измерение. Их сумма получается суммированием каждого элемента одной матрицы с соответствующий элемент другой матрицы.

   Ниже приводится формальное определение.

   В следующем примере показано, как выполняется сложение матриц.

   Помните, что векторы-столбцы и векторы-строки также являются матрицами. Как Следовательно, их можно суммировать таким же образом, как показано следующим пример.

   Свойства матричной добавки

   Дополнение матрицы обладает свойствами, аналогичными тем, которыми обладает более привычное сложение действительных чисел.

   Предложение (коммутативное имущество) Матричное сложение коммутативно, что для любые матрицы а также а также таким образом, чтобы вышеупомянутые дополнения были содержательно определены.

   Проба

   Это непосредственное следствие факта что свойство коммутативности применяется к суммам скаляров и, следовательно, к поэлементные суммы, которые выполняются при выполнении матричного сложения.

   Предложение (ассоциативное имущество) Матричное сложение ассоциативно, что для любые матрицы , а также таким образом, чтобы вышеупомянутые дополнения были содержательно определены.

   Проба

   Это непосредственное следствие факта что ассоциативное свойство применяется к суммам скаляров и, следовательно, к поэлементные суммы, которые выполняются при выполнении матричного сложения.

   Решенные упражнения

   Ниже вы можете найти несколько упражнений с объясненными решениями.

   Упражнение 1

   Позволять а также быть матрицы определены byFind их сумма.

   Решение

   Упражнение 2

   Позволять быть следующим матрица: Определить то матрица в виде следует: Computewhere это транспонирование .

   Решение

   Упражнение 3

   Позволять быть матрица определена byShow что сумма и его транспонирование представляет собой симметричную матрицу.

   Решение

   Как цитировать

   Укажите как:

   Табога, Марко (2017).