Средние степенные: Степенные средние.
Степенные средние.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьСредние величины играют исключительно большую роль в статистике. Средние величины представляют собой наиболее распространенную форму сводных величин. Они дают общую количественную характеристику элементов массового процесса. Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдаемые значения признака. В сущности, средняя величина характеризует однородную совокупность одним числом. Например: средняя температура воздуха в аудитории.
Средняя обладает тем хорошим свойством, что в ней погашаются отклонения отдельных величин от основного типа.
Средняя величина – обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.
Условиями применения средних величин являются: наличие качественно однородной совокупности и достаточно большой ее объем.
Пример. Рабочие бригады имеют следующую месячную заработную плату (табл. 5.1):
Таблица 5.1
Заработная плата рабочих
Рабочий | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Всего: 10 | |
Зарплата, грн. | 493 | 561 | 609 | 718 | 1070 | 850 | 1203 | 894 | 901 | 1251 | Всего: 8550 |
Требуется определить среднюю месячную зарплату рабочих бригады:
Средняя зарплата рабочего составляет 855 грн.
Существуют две категории средних величин: степенные средние (к ним относятся средняя арифметическая, средняя геометрическая и др.), а также структурные средние (мода и медиана). Выбор того или иного вида средней производится в зависимости от цели исследований, экономической сущности усредняемого показателя и характера имеющихся исходных данных.
Общая формула степенной средней имеет вид:
(5.1)
процесс осреденения индивидуальных значений;
х – величина, для которой вычисляется средняя – осредняемый признак;
m – показатель степени средней;
n — количество наблюдений (объем совокупности).
Подставляя различные значения т, получают различные формы средних величин.
Средняя арифметическая (при т = 1) используется для осреднения прямых значений признаков путем их суммирования. Ее логическая формула имеет вид:
Ее логическая формула имеет вид:
(5.2)
Если данные не сгруппированы, применяется средняя арифметическая простая:
, (5.3)
где х – отдельные значения признака;
п – объем совокупности.
По формуле средней арифметической простой вычисляются также средние в хронологическом ряду, если интервалы времени, за которое приводятся значения признаков, равны.
Если в хронологическом ряду приведены моментные показатели, то для вычисления cредней они заменяются полусуммами значений на начало и конец периода. Если моментов более двух и интервалы между ними равны, то средняя вычисляется по формуле
, (5.4)
где п – число моментов времени.
Если данные сгруппированы, то используют среднюю арифметическую взвешенную:
или , (5.5)
где fi – частота, di – частость i-й группы.
При этом а
Осреднению подлежат не только отдельные значения вариант, но и их групповые средние , тогда весом будет частота (частость) каждой группы:
(5.6)
Вычисленная таким способом средняя из групповых средних называется общей.
Весом может быть также абсолютная величина, логически связанная с осредняемым показателем. Выбор весов основывается на логической формуле показателя. Поскольку средняя величина вычисляется из расчета на единицу совокупности, то вес всегда будет находиться в знаменателе логической формулы. Например, при определении средней суммы затрат на одно рекламное объявление весом будет количество рекламных объявлений. При вычислении средней суммы затрат на одного рекламодателя весом будет количество рекламодателей.
При вычислении средней суммы затрат на одного рекламодателя весом будет количество рекламодателей.
Средняя арифметическая имеет определенные математические свойства, раскрывающие ее сущность. Так, сумма отклонений отдельных вариант от средней равна нулю, а сумма квадратов таких отклонений приближается к минимуму. Эти два свойства лежат в основе изучения вариации признаков.
Если отдельные значения вариант увеличить (уменьшить) на одну и ту же величину А или в k раз, то средняя изменится соответственно.
Например, если денежные вклады граждан в сбербанк скорректировать на уровень инфляции, составляющий 1,2, то средний размер вклада увеличится соответственно в 1,2 раза.
Средняя не изменится при пропорциональном изменении всех весов, но ее размер изменится, если произойдут структурные сдвиги.
Например, при неизменной курсовой стоимости акций отдельных эмитентов средняя стоимость акций может увеличиться за счет увеличения доли «дорогих» акций в общем количестве их продажи.
Указанные свойства средней используют в случае осреднения признаков порядковой (ранговой) шкалы. Для 3-х бальной шкалы варианты признака можно оцифровать порядковыми рангами R = 1, 2, 3 или центрированными R0 = — 1, 0, 1.
Средний центрированный балл
(5.7)
Аналитические возможности среднего центрированного балла шире, чем среднего порядкового, т.к. может принимать положительные или отрицательные значения и свидетельствует о положительной или отрицательной оценке явления. Кроме того, поскольку средний центрированный балл не зависит от размерности шкалы, его используют для сравнения оценок разных явлений.
Пример. В таблице 5.2 приведены данные об отношении населения к приватизации земли. Определим уровень поддержки приватизации земли населением.
Табл. 5.2
Отношение населения к приватизации земли
Отношение к приватизации | Доля ответов, % | Ранги | |
Rj | R0 | ||
Полностью поддерживаю | 32 | 3 | 1 |
Частично поддерживаю | 47 | 2 | 0 |
Не поддерживаю | 21 | 1 | -1 |
Итого | 100 | – | – |
Следовательно, уровень поддержки приватизации земли положительный, но пока невысокий.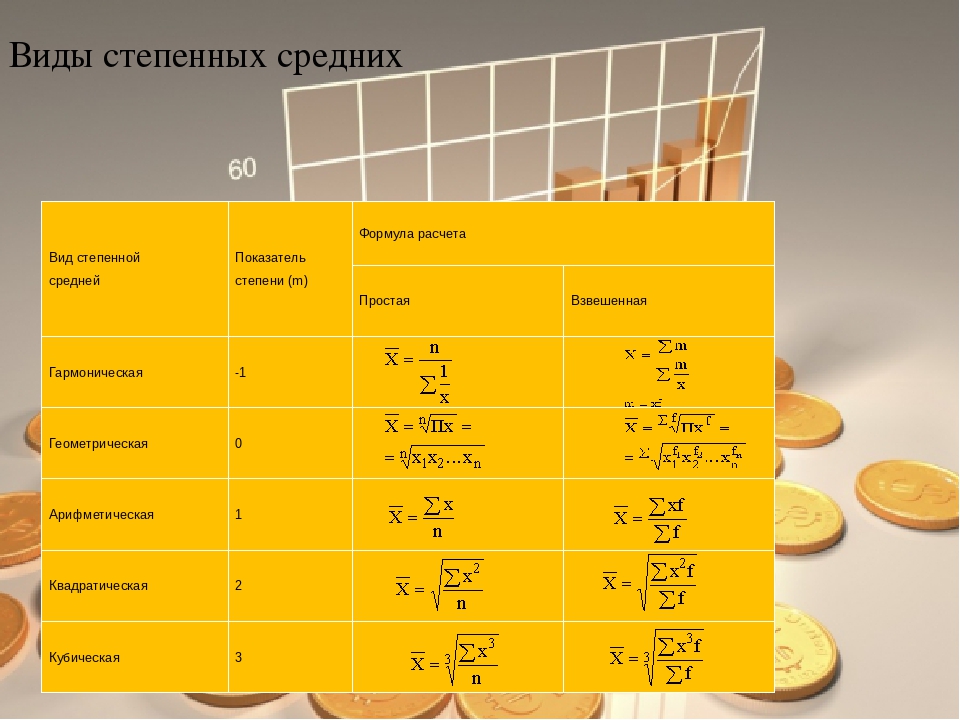
Средняя гармоническая (т = – 1) используется для осреднения индивидуальных значений признаков из обратных величин путем их суммирования. Для несгруппированных данных используется средняя гармоническая простая
(5.8)
Если данные сгруппированы, то используют среднюю гармоническую взвешенную
, (5.9)
где wi – объем значений признака, т.е.
Пример. Определить среднюю цену единицы продукции, если известны
(табл. 5.3) следующие данные:
Таблица 5.3
Данные о стоимости продукции
Продукция | Цена, грн., хi | Сумма реализации, тыс. | Частота случаев, fi = wi / xi |
А | 30 | 600 | 20 |
Б | 20 | 1000 | 50 |
В | 35 | 350 | 10 |
ИТОГО: |
| 1950 | 80 |
Средняя цена единицы продукции равна сумме реализации деленной на количество реализованных единиц. Сумма реализации (числитель) – известна, а количество реализованной продукции (знаменатель) – неизвестна. В таком случае, среднюю цену единицы продукции определяют по формуле средней гармонической:
В таком случае, среднюю цену единицы продукции определяют по формуле средней гармонической:
.
Если бы для расчета мы использовали среднюю арифметическую простую, то получили бы неверный результат:
.
Очевидно, что среднюю гармоническую взвешенную целесообразно использовать в тех случаях, когда отсутствует информация о значении знаменателя логической формулы, т.е. отсутствуют веса (когда статистическая информация не содержит конкретных частот по отдельным вариантам совокупности, а представлена только как их произведение).
Рассчитывать среднюю гармоническую взвешенную можно и в том случае, когда отдельные значения вариантов не указаны, а известны только итоги (суммарные значения числителя и знаменателя) логической формулы.
Средняя геометрическая (т = 0) определяется как произведение относительных величин динамики xij , рассчитанных как отношение i-го значения показателя к предыдущему (i – 1).
Формула средней геометрической простой
(5.10)
где — символ произведения;
– число осредняемых величин.
Средняя квадратическая (т = 2) используется для характеристики вариации и будет рассматриваться в следующей лекции (тема 6).
Вопрос о том, какой вид средней необходимо применить, решается в каждом конкретном случае путем анализа изучаемой совокупности, определяется материальным содержанием изучаемого явления, а также исходя из осмысления результатов исследований. В статистике правильную характеристику совокупности можно получить при использовании только определенного вида средней, установить которую помогает анализ. Для правильного выбора вида средней величины необходимо составить логическую схему.
Пример. Имеется цех, в котором работает 100 человек. Необходимо определить среднюю зарплату одного рабочего. Среднюю зарплату определим по логической формуле:
Случаи использования различных средних величин.
1. Средняя арифметическая простая используется в том случае, если числитель и знаменатель исследуемой системы приведен в исходных данных.
2. Средняя арифметическая взвешенная используется в том случае, если знаменатель исследуемой системы (логической схемы) известен, а числитель – нет.
3. Средняя гармоническая используется в том случае, если числитель исследуемой схемы приведен в исходных данных, а знаменатель – нет.
4. Средняя квадратическая используется только лишь при определении показателей вариации.
5. Средняя геометрическая используется только лишь при расчете среденегодового темпа роста.
6. Структурные средние используются, преимущественно при определении спроса и предложения.
Следует учесть, что разные виды средних величин на одном и том же исходном материале имеют неодинаковые значения.
Пример. Бригада из пяти человек выпускает детали. При этом каждый рабочий выпускает в следующем количестве (табл.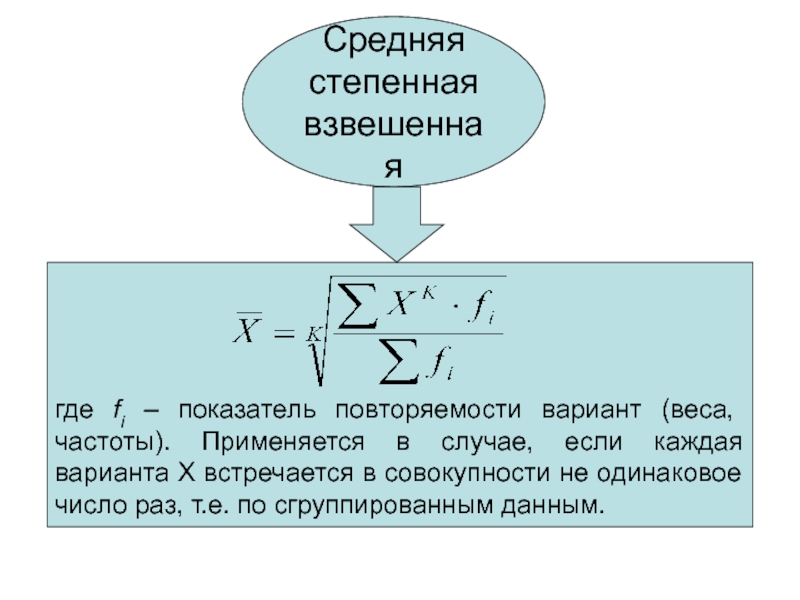 5.4):
5.4):
Таблица 5.4
Выпуск деталей рабочими
Рабочий | Выпуск деталей (хi) |
1 | 10 |
2 | 8 |
3 | 11 |
4 | 14 |
5 | 7 |
ВСЕГО: 5 | 50 |
Определим средний выпуск деталей одним рабочим, используя различные виды средних.
среднеарифметическая
среднеквадратическая
среднегармоническая
среднегеометрическая
В общем виде соотношения между средними имеет вид:
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
11.Степенные средние и область их применения.
Средняя величина — это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.
Существует 2 класса средних величин: степенные и структурные.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
где X – значения отдельных
статистических величин или середин
группировочных интервалов; m —
показатель степени, от значения которого
зависят следующие виды
степенных средних величин: при
m = -1 средняя
гармоническая; при
m = 0 средняя
геометрическая; при
m = 1 средняя
арифметическая; при
m = 2 средняя
квадратическая; при
m = 3 средняя
кубическая.
Средняя арифметическая — это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:
где X — значения величин, для которых необходимо рассчитать среднее значение; N — общее количество значений X (число единиц в изучаемой совокупности). Средняя арифметическая взвешенная имеет следующий вид:
где f — количество величин с одинаковым значением X (частота).
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в
виде интервалов, то для расчетов
используют середины интервалов X, которые
определяются как полусумма верхней и
нижней границ интервала. А если у
интервала X остутствует нижнияя или
верхняя граница (открытый интервал), то
для ее нахождения применяют размах
(разность между верхней и нижней границей)
соседнего интервала X. Средняя
гармоническая применяется,
когда исходные данные не содержат частот
f по отдельным значениям X, а представлены
как их произведение Xf. Обозначив Xf=w,
выразим f=w/X, и, подставив эти обозначения
в формулу средней арифметической
взвешенной, получим формулу средней
гармонической взвешенной:
Средняя
гармоническая применяется,
когда исходные данные не содержат частот
f по отдельным значениям X, а представлены
как их произведение Xf. Обозначив Xf=w,
выразим f=w/X, и, подставив эти обозначения
в формулу средней арифметической
взвешенной, получим формулу средней
гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Средняя квадратическая
применяется в тех случая, когда исходные
значения X могут быть как положительными,
так и отрицательными, например при
расчете средних отклонений.
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Средние показатели
Наиболее распространенной формой статистических показателей, используемых в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака статистической совокупности. Средние величины являются как бы «представителями» всего ряда наблюдений. Определить среднюю можно во многих случаях через исходное соотношение средней (ИСС) или ее логическую формулу:
.
Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:
Числитель исходного соотношения средней представляет собой ее
определяющий показатель. Для средней заработной платы таким определяющим
показателем является фонд заработной платы. Для каждого показателя,
используемого в социально-экономическом анализе, можно составить только одно
истинное исходное соотношение для расчета средней.
Для средней заработной платы таким определяющим
показателем является фонд заработной платы. Для каждого показателя,
используемого в социально-экономическом анализе, можно составить только одно
истинное исходное соотношение для расчета средней.
Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n-1.
Понятие и виды средних величин
Средняя величина — это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.
Существует 2 класса средних величин: степенные и структурные .
К структурным средним относятся мода и медиана,
но наиболее часто применяются степенные
средние различных видов.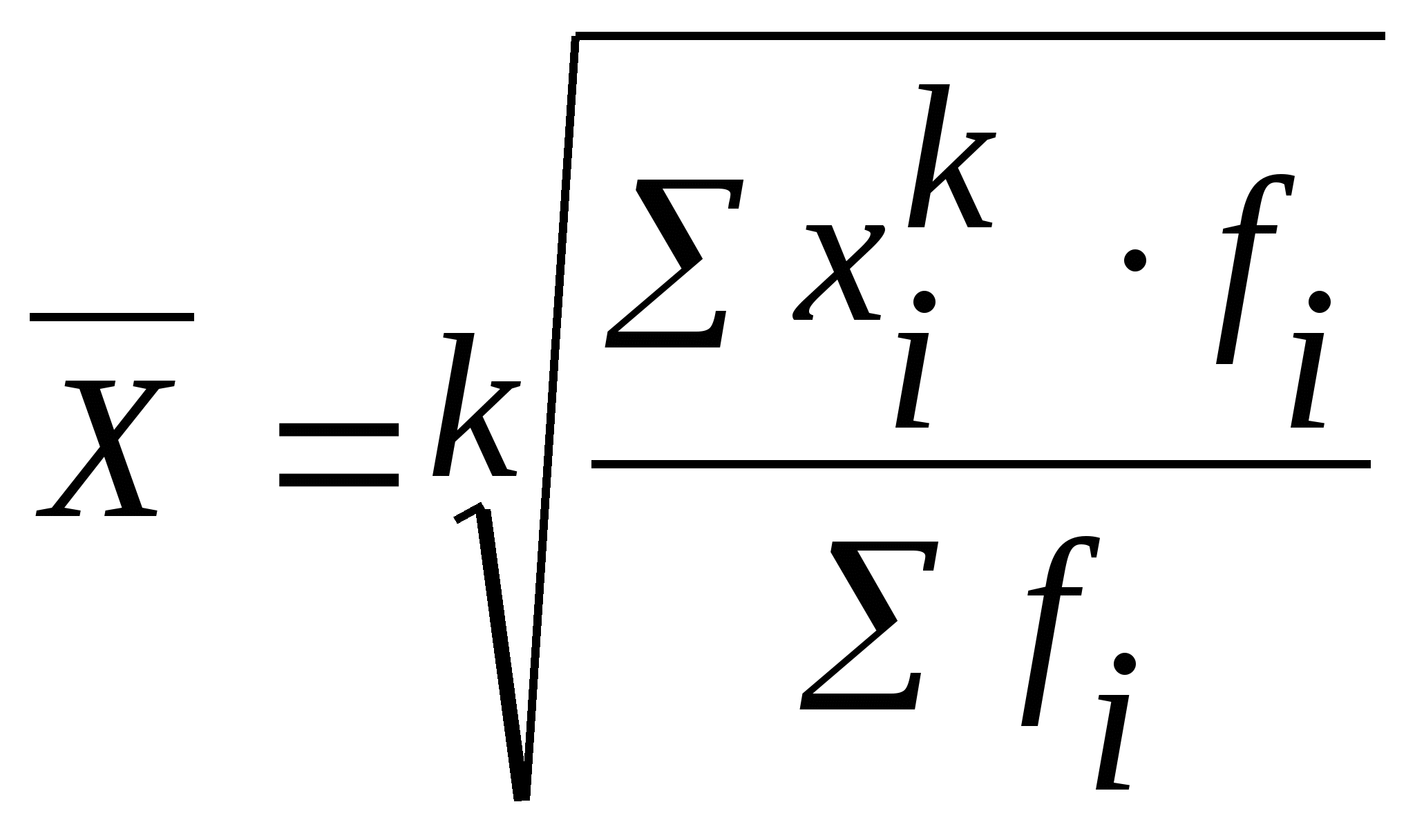
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле средней степенной (при различной величине k (m)):
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
где x- средняя величина исследуемого явления;
xi – i -й вариант усредняемого признака ;
fi – вес i-го варианта.
где X – значения отдельных статистических величин или середин группировочных интервалов;
m — показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая.
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Средняя арифметическая – начальный момент первого порядка, математическое ожидание значений случайной величины при большом числе испытаний;
Средняя арифметическая — это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:
или
где X — значения величин, для которых необходимо рассчитать
среднее значение; N — общее количество значений X (число единиц в изучаемой
совокупности).
Средняя арифметическая взвешенная имеет следующий вид:
где f — количество величин с одинаковым значением X (частота).
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ
интервала. А если у интервала X отсутствует нижняя или верхняя граница
(открытый интервал), то для ее нахождения применяют размах (разность между
верхней и нижней границей) соседнего интервала X.
А если у интервала X отсутствует нижняя или верхняя граница
(открытый интервал), то для ее нахождения применяют размах (разность между
верхней и нижней границей) соседнего интервала X.
Функция СРЗНАЧ вычисляет среднее (арифметическое) своих аргументов.
Функция СРЗНАЧА вычисляет среднее арифметическое значений, заданных в списке аргументов. Помимо чисел в расчете могут участвовать текст и логические значения, такие как ИСТИНА и ЛОЖЬ.
Средняя гармоническая
Средняя гармоническая для определения средней суммы обратных величин;
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким
образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны
частоты f, а известно w=Xf.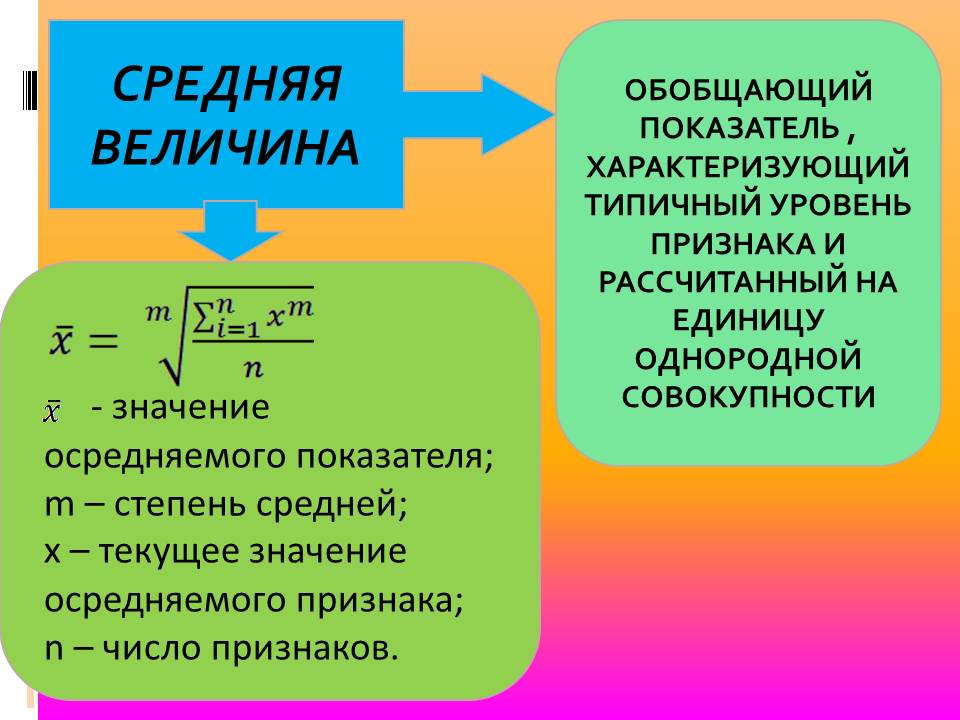 В тех случаях, когда все w=1, то есть индивидуальные
значения X встречаются по 1 разу, применяется формула средней гармонической
простой:
В тех случаях, когда все w=1, то есть индивидуальные
значения X встречаются по 1 разу, применяется формула средней гармонической
простой:
или
Функция СРГАРМ возвращает среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная к среднему арифметическому обратных величин.
Среднее гармоническое всегда меньше среднего геометрического, которое всегда меньше среднего арифметического.
Средняя геометрическая
Средняя геометрическая для оценки средних темпов роста случайной величин, нахождения значения признака, равноудаленного от минимального и максимального значения;
Средняя геометрическая применяется при
определении средних относительных изменений. Геометрическая средняя величина
дает наиболее точный результат осреднения, если задача стоит в нахождении
такого значения X, который был бы равноудален как от максимального, так и от
минимального значения X.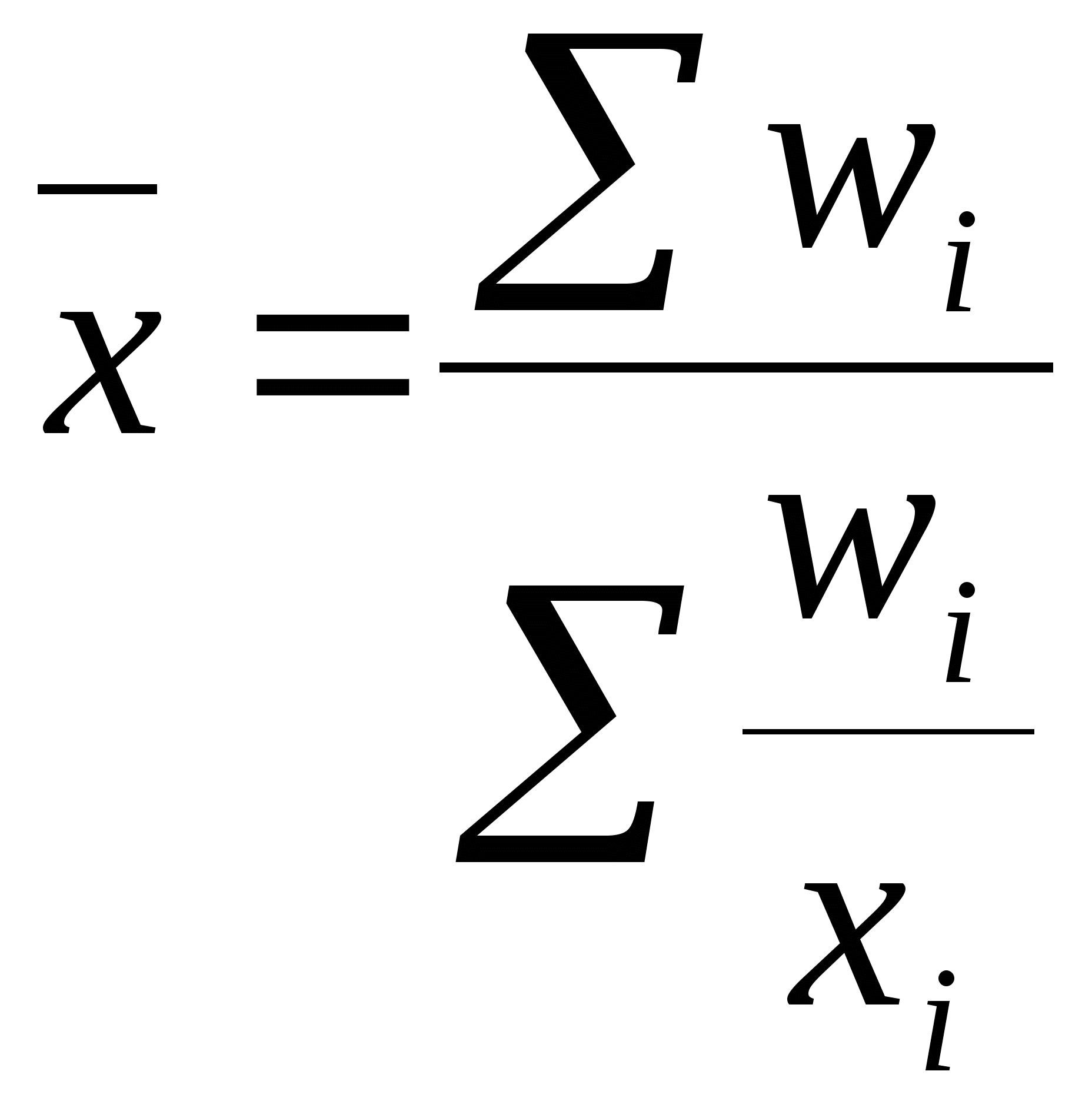
Функция СРГЕОМ возвращает среднее геометрическое значений массива или интервала положительных чисел.
Средняя квадратическая
Средняя квадратическая – начальный момент второго порядка.
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X.
Средняя кубическая
Средняя кубическая– начальный момент третьего порядка.
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
в начало
средняя арифметическая, средняя квадратическая, средняя гармоническая.
 — Студопедия
— СтудопедияСредние величины открыли ученые Петте и Кетле. Они определили, что постоянные величины действуют одинаково на каждое изучаемое явление. Эти величины похожи друг на друга и создают общие для всех закономерности.
Следствием их изучения явилось выделение средних величин в качестве основного приема статичтического анализа.
Математическая статистика выводит средние из формул степенной средней:
— среднее значение исследуемого явления.
x— значение признака (варианта).
n— число признаков.
m— показатель степени средней.
В зависимости от значения показателя степени m различают следуещие виды степенных средних:
При m = — 1 — среднее гармоническое (xгар )
При m = 0 — среднее геометрическое (xг )
При m = 1 — среднее арифметическое (xар )
При m = 2 — среднее квадратическое(xкв )
При m = 3 — среднее кубическое (xкуб )
Виды средних величин
1.
средняя арифметическая простая применяется, когда перечислены все значения усредненного признака:
x — значение признака
n — кол-во единиц обладающих данным признаком.
2.среднее арифметическое взвешенное применяется, когда задан «вес признака»( кол-во единиц, обладающих одинаковым признаком)
x— значение признака, f— вес признака
3.средняя гармоническая простая.
4.средняя гармоническая взвешенная применяется, когда задан объем признака – это суммарное значение признака по всей совокупности или по группам.
x — значение признака.
w — объем признака.
5.средняя геометрическая простая.
x— значение признака.
k— кол-во осредняемых величин.
6.средняя геометрическая взвешенная.
7.среднее хронологическое применяется в рядах динамики
x1 — начальный уровень ряда
x n — конечный уровень ряда
n — число уровней в ряду
8.средняя квадратическая простая
9.
средняя квадратическая взвешенная
10.средняя кубическая простая
11.средняя кубическая взвешенная
Содержание дисциплины «Статистика» : Кафедра МЭО : АлтГТУ
Кафедра «Международные экономические отношения»
Модуль 1Тема 1 Основные понятия и категории статистики
Статистика как общественная наука и отрасль практической деятельности. Предмет статистики, его особенности. Теоретическая основа статистики. Взаимосвязь статистики с другими науками. Основные разделы статистической науки. Задачи статистики. Современная организация статистики в РФ. Международные статистические организации. Предмет теории статистики. Статистическая совокупность, единица совокупности. Признак. Классификация и вариация признаков. Понятие статистического показателя.
Предмет статистики, его особенности. Теоретическая основа статистики. Взаимосвязь статистики с другими науками. Основные разделы статистической науки. Задачи статистики. Современная организация статистики в РФ. Международные статистические организации. Предмет теории статистики. Статистическая совокупность, единица совокупности. Признак. Классификация и вариация признаков. Понятие статистического показателя.
Тема 2 Этапы статистического исследования
Понятие статистического исследования. Основные этапы статистического исследования. Понятие о статистическом наблюдении. Роль статистического наблюдения в создании первичной информационной базы статистики, его задачи. Виды статистического наблюдения. Сплошное и несплошное наблюдение. Текущее и прерывное наблюдение. Непосредственное наблюдение. Документальное наблюдение. Опросы, их назначение, способы проведения. Программа наблюдения. Статистические формуляры. Организационные вопросы наблюдения (место, время, способ, срок и критический момент наблюдения).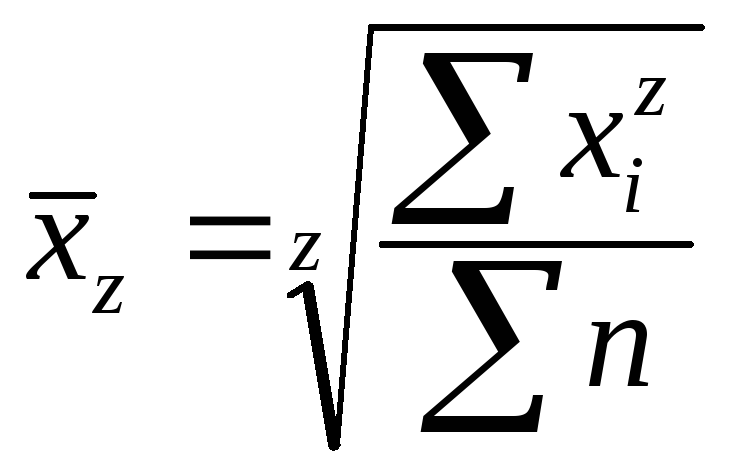 Оценка качества результатов статистического наблюдения. Ошибки наблюдений. Государственная отчетность. Специально организованное наблюдение.
Оценка качества результатов статистического наблюдения. Ошибки наблюдений. Государственная отчетность. Специально организованное наблюдение.
Тема 3 Статистическая сводка и группировка данных
Сводка материалов наблюдения как метод агрегирования и представления статистической информации. Организация и техника сводки. Группировка как научная основа сводки. Задачи и виды группировок. Особенности группировок по атрибутивным и количественным признакам. Определение количества групп и интервалов группировки. Простые, сложные, комбинированные группировки. Ряды распределения как особый вид группировок. Вторичная группировка. Важнейшие группировки и классификации, применяемые в социально-экономической статистике.
Модуль 2Тема 4 Абсолютные и относительные статистические показатели
Классификация, цель, структура, возможности применения статистических показателей. Абсолютные величины как непосредственные характеристики изучаемых явлений, получаемых в процессе статистического наблюдения и сводки. Виды абсолютных величин. Понятие об относительных величинах, их назначение. Формы выражения относительных величин, их выбор. Виды относительных величин. Относительные показатели планового задания, выполнения плана и динамики, их взаимосвязь. Относительные показатели динамики – базисные и цепные. Относительные показатели структуры и координации. Относительные показатели интенсивности и сравнения.
Виды абсолютных величин. Понятие об относительных величинах, их назначение. Формы выражения относительных величин, их выбор. Виды относительных величин. Относительные показатели планового задания, выполнения плана и динамики, их взаимосвязь. Относительные показатели динамики – базисные и цепные. Относительные показатели структуры и координации. Относительные показатели интенсивности и сравнения.
Тема 5 Формирование и применение статистических таблиц. Формирование и применение графических методов в статистике.
Статистические таблицы как метод представления результатов статистического наблюдения и сводки. Элементы таблиц. Правила построения статистических таблиц. Виды статистических таблиц. Статистические графики как средство научного обобщения, представления и анализа статистической информации. Основные элементы графика. Виды графического изображения статистических данных. Графики, диаграммы и картограммы.
Модуль 3Тема 6 Средние величины
Правила и условия применения средних величин. Закон больших чисел и средние величины. Соотношения между средними величинами и индивидуальными значениями изучаемых признаков. Виды средних величин. Общая средняя и групповые средние. Степенные средние и структурные средние величины. Арифметическая, гармоническая, геометрическая, квадратическая и кубическая средние. Простые и взвешенные средние величины. Особенности расчета средней арифметической в интервальных вариационных рядах. Математические свойства средней арифметической. Выбор формы средней величины. Мода, медиана.
Закон больших чисел и средние величины. Соотношения между средними величинами и индивидуальными значениями изучаемых признаков. Виды средних величин. Общая средняя и групповые средние. Степенные средние и структурные средние величины. Арифметическая, гармоническая, геометрическая, квадратическая и кубическая средние. Простые и взвешенные средние величины. Особенности расчета средней арифметической в интервальных вариационных рядах. Математические свойства средней арифметической. Выбор формы средней величины. Мода, медиана.
Тема 7 Методы оценки разброса исходных данных
Показатели вариации. Понятие о вариации значений признака и задачи ее статистического изучения. Абсолютные показатели вариации: размах вариации, среднее линейное, квадратическое отклонение, дисперсия, их назначение, методы расчета. Свойства среднего квадратического отклонения. Виды дисперсий и правило их сложения. Дисперсия альтернативного признака. Относительные показатели вариации. Анализ вариационных рядов.
Учебно-методические материалы по дисциплине
Основная литература
1. Статистика [Электронный ресурс]: электронный учебник / под.ред. М.Г. Назарова.- Электронные данные.- М.: КНОРУС, 2008. – 1 эл. опт. диск (CD-ROM): цв., зв. – 2 экз.
2. Елисеева, Ирина Ильинична. Общая теория статистики: учеб. для вузов /И.И. Елисеева, М.М. Юзбашев.- М.: Финансы и статистика, 2004.-481 с. (16 экз.)
Дополнительная литература
3. Елисеева, И.И. Общая теория статистики: учеб. для вузов /И.И. Елисеева, М.М. Юзбашев; под ред. И.И. Елисеевой.- М.: Финансы и статистика, 2005.-656 с. (7 экз.)
4. Книга, Алла Стефановна. Статистика [Текст]: учебное пособие /А.С. Книга.- Барнаул, изд-во Алт.гос.тех.ун-та, 2010 (2006) -147 с. (1 экз.+ 7 экз.)
5. Курникова, Е.Л. Международные системы информации по макроэкономической статистике: [Текст]: учебный материал/ Е.Л. Курникова. – М.: Издательство «МГИМО-Университет», 2006. – 101 с. (1 экз., каф.МЭО)
– 101 с. (1 экз., каф.МЭО)
6. Нестеров, Л.И, Организация статистики за рубежом [Текст] / Л.И,Нестеров. – М.: ИПЦ: «Статистика России», 2006. – 155 с. (1 экз., каф. МЭО)
7. Основы международной статистики [Текст]: Учебник / Под. общ. ред. д-ра экон. наук Ю.Н. Иванова. – М.: ИНФРА-М, 2010. – 621 с. (22 экз.)
8. Социальная статистика: учеб. для вузов по направлению и специальности «Статистика» / [Н.В. Бурова и др.]; под ред И.И. Елисеевой.-М.: Финансы и статистика, 2003.-480 с. (10 экз.)
9. Социально-экономическая статистика: практикум [Текст]: учеб. пособие для вузов по специальности «Статистика» и др. экон. специальностям / [Н.М. Гореева и др.]; под ред. С.А. Орехова. — М.: Эксмо, 2007. — 382, [1] с.- (1 экз.)
10. Социально-экономическая статистика: практикум: учеб. пособие / [В.Н. Салин и др.]; под ред. В.Н. Салина, Е.П. Шпаковской.-М.: Финансы и статистика, 2004.-192 с.
11. Теория статистики: учеб. для экон. специальностей вузов /Р. А. Шмойлова [и др.]; под ред. Р.А. Шмойловой.-М.: Финансы и статистика, 2004.-656 с. (10 экз.)
А. Шмойлова [и др.]; под ред. Р.А. Шмойловой.-М.: Финансы и статистика, 2004.-656 с. (10 экз.)
12. Экономическая статистика: учеб. для вузов по направлению 080100 / [Алексеев А. Р. и др.]; под ред. Ю.Н. Иванова.-М.: Инфра — М, 2006.-736 с. (3 экз.)
Программное обеспечение и Интернет-ресурсы
13. Евростат http://www.eurostat.ec.europa.eu
14. Министерство промышленности и торговли http://www.minpromtorg.gov.ru
15. Министерство экономического развития РФ http://www.economy.gov.ru
16. Правительство РФ http://www.gov.ru
17. Справочная правовая система «Консультант Плюс» http://www.consultant.ru
18. Федеральная служба государственной статистики РФ http://www.gks.ru
Методические указания студентам
19. Баранова, Е.В. Методические указания к выполнению расчетного задания по дисциплине «Статистика» для студентов направления «Экономика» / Е.В. Баранова. — Барнаул, АлтГТУ, 2010.- 24 с. {n}x_{i}}}}
{n}x_{i}}}}
Средние степеней 1, 0, −1 и 2 имеют собственные имена:
- A1(x1,…,xn)=m=x1+x2+⋯+xnn{\displaystyle A_{1}(x_{1},\ldots ,x_{n})=m={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}} называется средним арифметическим;
(иначе говоря: среднее арифметическое n чисел, является их сумма, деленная на n)
- A0(x1,…,xn)=g=x1x2⋯xnn{\displaystyle A_{0}(x_{1},\ldots ,x_{n})=g={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}} называется средним геометрическим;
(иначе говоря: среднее геометрическое n чисел, является корень n-ой степени из произведения этих чисел)
- A−1(x1,…,xn)=h=n1x1+1×2+⋯+1xn{\displaystyle A_{-1}(x_{1},\ldots ,x_{n})=h={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}} называется средним гармоническим.
 {2}}{n}}}} называется средним квадратичным.
{2}}{n}}}} называется средним квадратичным.
Неравенство о средних
Неравенство о средних утверждает, что для d1>d2{\displaystyle d_{1}>d_{2}}
Ad1(x1,…,xn)≥Ad2(x1,…,xn){\displaystyle A_{d_{1}}(x_{1},\ldots ,x_{n})\geq A_{d_{2}}(x_{1},\ldots ,x_{n})},причем равенство достигается только в случае равенства всех аргументов x1=…=xn{\displaystyle x_{1}=\ldots =x_{n}}.
Для доказательства неравенства о средних достаточно показать, что частная производная Ad(x1,…,xn){\displaystyle A_{d}(x_{1},\ldots ,x_{n})} по d{\displaystyle d} неотрицательна и обращается в ноль только при x1=…=xn{\displaystyle x_{1}=\ldots =x_{n}} (а далее, например, применить формулу конечных приращений).
Неравенство о среднем арифметическом, геометрическом и гармоническом
Частным случаем неравенства о средних является неравенство о среднем арифметическом, геометрическом и гармоническом
max{x1,…,xn}≥x1+…+xnn≥(x1⋅…⋅xn)1/n≥n1x1+…+1xn≥min{x1,…,xn},{\displaystyle \max\{x_{1},\ldots ,x_{n}\}\geq {\frac {x_{1}+\ldots +x_{n}}{n}}\geq \left(x_{1}\cdot \ldots \cdot x_{n}\right)^{1/n}\geq {\frac {n}{{\frac {1}{x_{1}}}+\ldots +{\frac {1}{x_{n}}}}}\geq \min\{x_{1},\ldots ,x_{n}\},}где каждое из равенств достигается только при x1=…=xn{\displaystyle x_{1}=\ldots =x_{n}}.
См. также
МощностьRMS в сравнении со средней мощностью
ВОПРОС:
Должен ли я использовать единицы среднеквадратичного значения мощности для определения или описания мощности переменного тока, связанной с моим сигналом, системой или устройством?
Ответ:
Это зависит от того, как вы определяете среднеквадратичную мощность.
Вы не хотите рассчитывать среднеквадратичное значение сигнала мощности переменного тока. Это приводит к физически бессмысленному результату.
Вы действительно используете среднеквадратичные значения напряжения и / или тока для расчета средней мощности, что дает значимые результаты.
Обсуждение:
Сколько мощности рассеивается при подаче синусоидального напряжения 1 В (среднеквадратичное значение) на резистор 1 Ом?
Это хорошо понятно 1 , и здесь нет никаких противоречий.
Теперь давайте посмотрим, как это соотносится со значением, полученным при расчете среднеквадратичной мощности.
На рисунке 1 показан график синусоиды 1 В.Размах амплитуды составляет 1 В среднеквадратичное значение × 2 √2 = 2,828 В с изменением от +1,414 В до -1,414 В. 2
Рисунок 1. График синусоиды 1 В (среднеквадратичное значение).Рисунок 2 представляет собой график мощности, рассеиваемой этой синусоидой 1 В (среднеквадратичное значение) на резисторе 1 Ом (P = V 2 / R), который показывает:
Рис. 2. График мощности, рассеиваемой синусоидой 1 В (среднеквадратичное значение) на резисторе 1 Ом.- Кривая мгновенной мощности имеет смещение 1 Вт и колеблется от 0 Вт до 2 Вт.
- Среднеквадратичное значение этого сигнала мощности равно 1.225 Вт.
- Одним из методов вычисления этого числа является уравнение 2 3 :
- Это можно проверить, используя более подробную формулу 4 в MATLAB ® или Excel.

- Среднее значение этого сигнала мощности составляет 1 Вт. Это очевидно при осмотре; форма сигнала колеблется симметрично выше и ниже 1 Вт. Это же значение получается при вычислении среднего числового значения точек данных формы сигнала.
- Среднее значение мощности соответствует мощности, рассчитанной с использованием среднеквадратичного значения напряжения.
Мощность, рассеиваемая синусоидальным среднеквадратичным значением 1 В на резисторе 1 Ом, составляет 1 Вт, а не 1,225 Вт. Таким образом, именно средняя мощность дает правильное значение, и, следовательно, именно средняя мощность имеет физическое значение. Среднеквадратичная мощность (как определено здесь) не имеет очевидного полезного значения (не имеет очевидного физического / электрического значения), кроме как величина, которую можно рассчитать как упражнение.
Выполнение того же анализа с использованием синусоидального тока 1 А среднеквадратичного значения через резистор 1 Ом — тривиальное упражнение. Результат тот же.
Результат тот же.
Источники питания для интегральных схем (ИС) обычно являются источниками постоянного тока, поэтому среднеквадратичная мощность не является проблемой для питания ИС. Для постоянного тока среднее и среднеквадратичное значение такие же, как и для постоянного тока. Важность использования средней мощности, в отличие от среднеквадратичной мощности, как определено в этом документе, относится к мощности, связанной с изменяющимися во времени напряжением и током, то есть шумом, радиочастотными сигналами и генераторами.
Используйте среднеквадратичное значение напряжения и / или среднеквадратичного значения тока для расчета средней мощности, что дает значимые значения мощности.
1 Мощность, рассеиваемая напряжением на резисторе, является фундаментальным соотношением, которое легко выводится из закона Ома (V = IR) и основных определений напряжения (энергия / единица заряда) и тока (единица заряда / времени). Напряжение × ток = энергия / время = мощность
2 Размах амплитуды синусоиды — это среднеквадратичное значение, умноженное на 2√2. Для синусоидального напряжения V p-p = V rms × 2√2, где V p-p — размах напряжения, а V rms — среднеквадратичное значение напряжения.Это хорошо известная связь, описанная в бесчисленных учебниках, а также здесь: en.wikipedia.org/wiki/Root_mean_square.
Для синусоидального напряжения V p-p = V rms × 2√2, где V p-p — размах напряжения, а V rms — среднеквадратичное значение напряжения.Это хорошо известная связь, описанная в бесчисленных учебниках, а также здесь: en.wikipedia.org/wiki/Root_mean_square.
3 Это адаптировано из среднеквадратичного значения, рассчитанного из постоянного значения смещения постоянного тока плюс отдельное среднеквадратичное значение переменного тока, а также из примечания по применению «Улучшите измерения среднеквадратичного значения переменного тока с помощью цифрового мультиметра» от Keysight.
4 Стандартное определение в учебнике — это один из примеров более подробной формулы.
15.5: Питание в цепи переменного тока
Цели обучения
К концу раздела вы сможете:
- Опишите, как можно записать среднюю мощность от цепи переменного тока в терминах пикового тока и напряжения, а также среднеквадратичных значений тока и напряжения
- Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности
Элемент схемы рассеивает или производит мощность в соответствии с \ (P = IV \), где I — ток через элемент, а \ (V \) — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность \ (p (t) = i (t) v (t) \) также зависит от времени. График \ (p (t) \) для различных элементов схемы показан на рисунке \ (\ PageIndex {1} \). Для резистора \ (i (t) \) и \ (v (t) \) синфазны и, следовательно, всегда имеют один и тот же знак. Для конденсатора или катушки индуктивности относительные знаки \ (i (t) \) и \ (v (t) \) меняются в течение цикла из-за разницы фаз. Следовательно, \ (p (t) \) в одни моменты времени положительно, а в другие — отрицательно, что указывает на то, что емкостные и индуктивные элементы вырабатывают энергию в одни моменты и поглощают ее в другие.
Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность \ (p (t) = i (t) v (t) \) также зависит от времени. График \ (p (t) \) для различных элементов схемы показан на рисунке \ (\ PageIndex {1} \). Для резистора \ (i (t) \) и \ (v (t) \) синфазны и, следовательно, всегда имеют один и тот же знак. Для конденсатора или катушки индуктивности относительные знаки \ (i (t) \) и \ (v (t) \) меняются в течение цикла из-за разницы фаз. Следовательно, \ (p (t) \) в одни моменты времени положительно, а в другие — отрицательно, что указывает на то, что емкостные и индуктивные элементы вырабатывают энергию в одни моменты и поглощают ее в другие.
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. То, что нас почти всегда интересует, — это усредненная по времени мощность, которую мы называем средней мощностью .T \ sin \ omega t \, \ cos \, \ omega t \, dt = 0. \ nonumber \]
Следовательно, средняя мощность, связанная с элементом схемы, равна
.\ [\ boxed {P _ {\ mathrm {ave}} = \ frac {1} {2} I_ {0} V_ {0} \ cos \ phi.} \ Label {eq5} \]
В инженерных приложениях \ (\ cos \ phi \) известен как коэффициент мощности , который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за отсутствия напряжения и тока. фазы.{2} R. \ label {eq10} \]
Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения. Оба уравнения \ ref {eq5} и \ ref {eq10} верны для средней мощности, но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна \ (110 \ sqrt {2} \, V = 156 \, V \).Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, установленный на бытовой розетке, будет показывать 110 В.
Для конденсатора и катушки индуктивности \ (\ phi = \ pi / 2 \) и \ (- \ pi / 2 \, rad \), соответственно. Поскольку \ (\ cos \, \ pi / 2 = cos (- \ pi / 2) = 0 \), мы находим из уравнения \ ref {eq5}, что средняя мощность, рассеиваемая любым из этих элементов, равна \ (P_ {ave } = 0 \). Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода.Это поведение проиллюстрировано на графиках на рисунках \ (\ PageIndex {1b} \) и \ (\ PageIndex {1c} \), которые показывают, что \ (p (t) \) колеблется синусоидально около нуля. 2}} = \ dfrac {R} {Z}.{-6} F \) и \ (R = 5.00 \, \ Omega \).
2}} = \ dfrac {R} {Z}.{-6} F \) и \ (R = 5.00 \, \ Omega \).
- Какое действующее значение напряжения на генераторе?
- Какое сопротивление цепи?
- Какова средняя выходная мощность генератора?
Стратегия
Среднеквадратичное значение напряжения — это амплитуда напряжения, умноженная на \ (1 / \ sqrt {2} \). Импеданс цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по формуле \ ref {eq30}, потому что у нас есть импеданс цепи \ (Z \), среднеквадратичное напряжение \ (V_ {rms} \) и сопротивление \ (R \).2 / R \), где В заменяет действующее значение напряжения.
Упражнение \ (\ PageIndex {1A} \)
Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
- Ответ
\ (v (t) = (10.
 0 \, V) \, \ sin \, 90 \ pi t \)
0 \, V) \, \ sin \, 90 \ pi t \)
Упражнение \ (\ PageIndex {1B} \)
Покажите, что среднеквадратичные значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток равен \ (I_ {rms} \), выражаются как \ (I_ {rms} R, \, I_ {rms} X_C \) и \ (I_ {rms} X_L \) соответственно.Определите эти значения для компонентов схемы RLC по формуле \ ref {eq5}.
- Ответ
2,00 В; 10,01 В; 8.01 В
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (by 4.0).
Пиковая мощность в сравнении со средней мощностью — что это такое и как ее измерить?
Чем мы можем вам помочь?
Отправьте нам свою информацию, и мы поможем вам как можно быстрее.
Имя *
Фамилия *
Компания *
Электронное письмо *
Телефон
Страна * — Выберите -AfghanistanAlbaniaAlgeriaAndorraAngolaAntiguaArgentinaArmeniaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBhutanBoliviaBosniaBotswanaBrazilBruneiBulgariaBurkinaBurundiCambodiaCameroonCanada — AlbertaCanada — Британский ColumbiaCanada — ManitobaCanada — Новый BrunswickCanada — Ньюфаундленд и LabradorCanada — Нова ScotiaCanada — OntarioCanada — Принц Эдвард IslandCanada — QuebecCanada — SaskatchewanCape VerdeCentral Африканский RepublicChadChileChinaColombiaComorosCongoCosta RicaCroatiaCubaCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFijiFinlandFranceGabonGambiaGeorgiaGermanyGhanaGreeceGrenadaGuatemalaGuineaGuyanaHaitiHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsraelItalyJamaicaJapanJordanKazakhstanKenyaKiribatiKuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall I slandsMauritaniaMauritiusMexicoMicronesiaMoldovaMonacoMongoliaMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNew ZealandNicaraguaNigerNigeriaNorth KoreaNorwayOmanPakistanPalauPanamaPapua Новый GuineaParaguayPeruPhilippinesPolandPortugalQatarRepublic из MontenegroRomaniaRussian FederationRwandaSamoaSan MarinoSao Томе и PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth KoreaSpainSri LankaSudanSurinameSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzania, Объединенная Республика ofThailandTogoTongaTrinidadTunisiaTurkeyTurkmenistanTuvaluUgandaUkraineUnited Арабская EmiratesUnited KingdomUnited StatesUruguayUzbekistanVanuatuVenezuelaVietnamYemenZambiaZimbabwe
Состояния * — Выберите -AlabamaAlaskaArizonaArkansasCaliforniaColoradoConnecticutDelawareDistrict из ColumbiaFloridaGeorgiaGuamHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaNorthern Marianas IslandsOhioOklahomaOregonPennsylvaniaPuerto RicoRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyoming
Состояния * — Выбрать — 北海道 青森 県 岩手 県 宮城 宮城 県 秋田 県 福島 県 茨城 県 栃 木 県 県 埼 玉 県 千葉 県 東京 都 神奈川 県 新潟 県 富山 県 石川 県 県 長野 県 県滋 賀 県 京都 府 大阪 府兵 庫 県 奈良 山 県 鳥取 県 島 根 広 島 県 山口 県 徳 島 県 愛媛 県 高
Я хочу получать новости о продуктах, обучающие веб-семинары и новости
Сообщение(* Обязательное поле)
Мощность | Физика
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте мощность, рассчитав изменения энергии во времени.

- Изучите энергопотребление и расчеты стоимости потребляемой энергии.
Что такое сила?
Рис. 1. Эта мощная ракета космического корабля «Индевор» работала и потребляла энергию с очень высокой скоростью. (кредит: НАСА)
Сила — это слово вызывает в воображении множество образов: профессиональный футболист, отталкивающий своего противника, драгстер, ревущий от стартовой линии, вулкан, выбрасывающий лаву в атмосферу, или взрывающаяся ракета, как на рисунке 1.
Эти образы силы объединяет быстрое выполнение работы, что соответствует научному определению мощности ( P ) как скорости выполнения работы.
Мощность
Мощность — это скорость выполнения работы.
[латекс] \ displaystyle {P} = \ frac {W} {t} \\ [/ latex]
В системе СИ для мощности используется ватт, (Вт), где 1 ватт равен 1 джоуль в секунду (1 Вт = 1 Дж / с).
Поскольку работа — это передача энергии, мощность — это также скорость, с которой энергия расходуется. Например, лампочка мощностью 60 Вт потребляет 60 Дж энергии в секунду. Большая мощность означает большой объем работы или энергии, выработанный за короткое время. Например, когда мощный автомобиль быстро разгоняется, он выполняет большой объем работы и потребляет большое количество топлива за короткое время.
Например, лампочка мощностью 60 Вт потребляет 60 Дж энергии в секунду. Большая мощность означает большой объем работы или энергии, выработанный за короткое время. Например, когда мощный автомобиль быстро разгоняется, он выполняет большой объем работы и потребляет большое количество топлива за короткое время.
Расчет мощности по энергии
Пример 1. Расчет мощности для подъема по лестнице
Какова выходная мощность для женщины весом 60,0 кг, которая преодолевает лестничный пролет высотой 3,00 м за 3,50 с, начиная с состояния покоя, но имея конечную скорость 2?00 м / с? (См. Рисунок 2.)
Рис. 2. Когда эта женщина бежит наверх, начиная с отдыха, она превращает химическую энергию, исходную из пищи, в кинетическую энергию и гравитационную потенциальную энергию. Ее выходная мощность зависит от того, как быстро она это сделает.
Стратегия и концепция
Работа, переходящая в механическую энергию, равна Вт = KE + PE. Внизу лестницы мы принимаем как KE, так и PE g как исходный ноль; таким образом, [латекс] W = \ text {KE} _ {\ text {f}} + \ text {PE} _ {\ text {g}} = \ frac {1} {2} mv _ {\ text {f} } ^ 2 + mgh \\ [/ latex], где h — высота лестницы по вертикали. 2 \ right) \ left (3.00 \ text {m} \ right)} {3.50 \ text {s}} \\\ text {} & = & \ frac {120 \ text {J} +1764 \ text {J} } {3.50 \ text {s}} \\\ text {} & = & 538 \ text {W} \ end {array} \\ [/ latex]
2 \ right) \ left (3.00 \ text {m} \ right)} {3.50 \ text {s}} \\\ text {} & = & \ frac {120 \ text {J} +1764 \ text {J} } {3.50 \ text {s}} \\\ text {} & = & 538 \ text {W} \ end {array} \\ [/ latex]
Обсуждение
Женщина выполняет 1764 Дж работы, чтобы подняться по лестнице, по сравнению со всего лишь 120 Дж, чтобы увеличить свою кинетическую энергию; таким образом, большая часть ее мощности требуется для подъема, а не для ускорения.
Поразительно, что полезная выходная мощность этой женщины чуть меньше 1 лошадиных сил (1 л.с. = 746 Вт)! Люди могут генерировать больше, чем лошадиные силы с помощью мышц ног в течение коротких периодов времени, быстро превращая доступный в крови сахар и кислород в объем работы.(Лошадь может выделять 1 л.с. в течение нескольких часов подряд.) Как только кислород истощается, выходная мощность снижается, и человек начинает быстро дышать, чтобы получить кислород для метаболизма большего количества пищи — это известно как этап аэробных упражнений . Если бы женщина поднималась по лестнице медленно, то ее выходная мощность была бы намного меньше, хотя объем выполняемой работы был бы таким же.
Если бы женщина поднималась по лестнице медленно, то ее выходная мощность была бы намного меньше, хотя объем выполняемой работы был бы таким же.
Установление соединений: расследование на вынос — измерение номинальной мощности
Определите собственную номинальную мощность, измерив время, необходимое вам, чтобы подняться по лестнице.Мы проигнорируем выигрыш в кинетической энергии, так как приведенный выше пример показал, что это была небольшая часть выигрыша в энергии. Не ожидайте, что ваша мощность будет больше 0,5 л.с.
Примеры силы
Рис. 3. Огромное количество электроэнергии вырабатывается угольными электростанциями, такими как эта в Китае, но еще большее количество энергии идет на передачу тепла в окружающую среду. Здесь большие градирни необходимы для передачи тепла так же быстро, как оно производится.Передача тепла характерна не только для угольных электростанций, но является неизбежным следствием выработки электроэнергии из любого топлива — ядерного, угля, нефти, природного газа и т.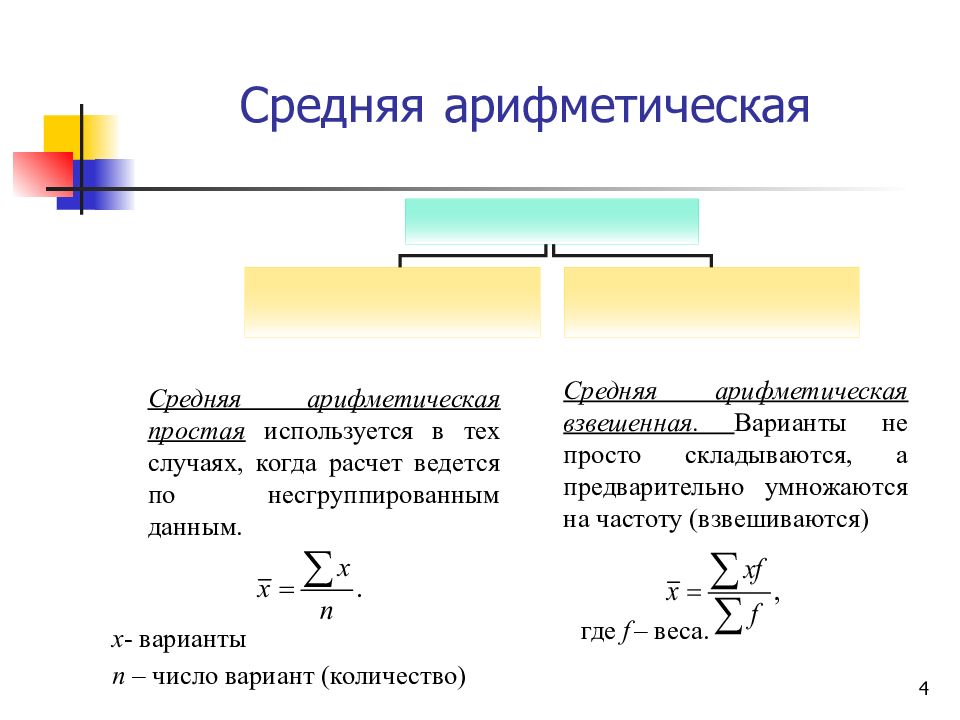 п. (Источник: Kleinolive, Wikimedia Commons)
п. (Источник: Kleinolive, Wikimedia Commons)
Примеры силы ограничены только воображением, потому что видов столько же, сколько форм работы и энергии. (См. Некоторые примеры в Таблице 1.) Солнечный свет, достигающий поверхности Земли, несет максимальную мощность около 1,3 киловатт на квадратный метр (кВт / м 2 ).Крошечная часть этого сохраняется на Земле в течение длительного времени. Наш уровень потребления ископаемого топлива намного превышает скорость его хранения, поэтому они неизбежно будут исчерпаны. Сила подразумевает, что энергия передается, возможно, меняя форму. Невозможно полностью преобразовать одну форму в другую, не потеряв часть ее в виде тепловой энергии. Например, лампа накаливания мощностью 60 Вт преобразует в свет всего 5 Вт электроэнергии, а 55 Вт рассеивается в тепловую энергию.
Кроме того, обычная электростанция преобразует только 35-40% топлива в электричество. Оставшаяся часть превращается в огромное количество тепловой энергии, которая должна рассеиваться в виде теплопередачи так же быстро, как и создается. Электростанция, работающая на угле, может производить 1000 мегаватт; 1 мегаватт (МВт) — это 10 6 Вт электроэнергии. Но электростанция потребляет химическую энергию в размере около 2500 МВт, создавая передачу тепла в окружающую среду в размере 1500 МВт. (См. Рисунок 3.)
| Таблица 1. Выходная или потребляемая мощность | |
|---|---|
| Объект или явление | Мощность в ваттах |
| Сверхновая (в пике) | 5 × 10 37 |
| Галактика Млечный Путь | 10 37 |
| Пульсар Крабовидной туманности | 10 28 |
| Солнце | 4 × 10 26 |
| Извержение вулкана (максимальное) | 4 × 10 15 |
| Молния | 2 × 10 12 |
| Атомная электростанция (полная передача электроэнергии и тепла) | 3 × 10 9 |
| Авианосец (полезная и теплопроводная) | 10 8 |
| Драгстер (общая полезная и теплопередающая) | 2 × 10 6 |
| Автомобиль (общий полезный и теплоотдача) | 8 × 10 4 |
| Футболист (общий полезный и теплопередающий) | 5 × 10 3 |
| Сушилка для белья | 4 × 10 3 |
| Человек в состоянии покоя (вся теплопередача) | 100 |
| Обычная лампа накаливания (общая полезная и теплопередающая) | 60 |
| Сердце, человек в состоянии покоя (общая полезная и теплоотдача) | 8 |
| Часы электрические | 3 |
| Карманный калькулятор | 10 −3 |
Мощность и энергопотребление
Обычно нам приходится платить за энергию, которую мы используем.Стоимость энергии для электроприбора интересно и легко оценить, если известны его потребляемая мощность и затраченное время. Чем выше уровень энергопотребления и чем дольше прибор используется, тем выше его стоимость. Уровень потребляемой мощности [латекс] P = \ frac {W} {t} = \ frac {E} {t} \\ [/ latex], где E — энергия, поставляемая электроэнергетической компанией. Таким образом, энергия, потребляемая за время т , составляет
E = Pt.
В счетах за электроэнергию указано количество использованной энергии в единицах киловатт-часов (кВт⋅ч) , , которое является произведением мощности в киловаттах и времени в часах. Этот блок удобен тем, что потребление электроэнергии на уровне киловатт в течение нескольких часов является типичным.
Пример 2. Расчет затрат на электроэнергию
Какова стоимость эксплуатации компьютера мощностью 0,200 кВт, 6 часов в день в течение 30 дней, если стоимость электроэнергии составляет 0,120 доллара США за кВт⋅ч?
Стратегия
Стоимость основана на потребленной энергии; таким образом, мы должны найти E из E = Pt , а затем рассчитать стоимость.Поскольку электрическая энергия выражается в кВт⋅ч, в начале такой задачи удобно преобразовать единицы в кВт и часы.
Решение
Энергопотребление в кВт⋅ч составляет
[латекс] \ begin {array} {lll} E & = & Pt = (0.200 \ text {kW}) (6.00 \ text {h / d}) (30.0 \ text {d}) \\\ text {} & = & 36.0 \ text {кВт} \ cdot \ text {h} \ end {array} \\ [/ latex]
, а стоимость просто равна
. Стоимость= (36,0 кВт⋅ч) (0,120 доллара США за кВт perч) = 4,32 доллара США в месяц.
Обсуждение
Стоимость использования компьютера в этом примере не является ни чрезмерной, ни незначительной. Понятно, что стоимость — это сочетание силы и времени. Когда и то и другое высокое, например, кондиционер летом, стоимость высока.
Мотивация к экономии энергии стала более убедительной из-за ее постоянно растущей цены. Вооружившись знанием того, что потребляемая энергия является продуктом мощности и времени, вы можете оценить затраты для себя и сделать необходимые оценочные суждения о том, где экономить энергию.Нужно уменьшить либо мощность, либо время. Наиболее рентабельно ограничить использование мощных устройств, которые обычно работают в течение длительного времени, например водонагревателей и кондиционеров. Сюда не входят устройства с относительно высокой мощностью, такие как тостеры, потому что они работают всего несколько минут в день. Он также не будет включать электрические часы, несмотря на то, что они используются круглосуточно, потому что они являются устройствами с очень низким энергопотреблением. Иногда для выполнения той же задачи можно использовать устройства с большей эффективностью, то есть устройства, потребляющие меньше энергии.Одним из примеров является компактная люминесцентная лампа, которая дает в четыре раза больше света на ватт потребляемой мощности, чем ее собрат с лампами накаливания.
Современная цивилизация зависит от энергии, но нынешние уровни потребления и производства энергии не являются устойчивыми. Вероятность связи между глобальным потеплением и использованием ископаемого топлива (с сопутствующим производством углекислого газа) привела к сокращению использования энергии, а также к переходу на неископаемые виды топлива. Несмотря на то, что энергия в изолированной системе является сохраняемой величиной, конечным результатом большинства преобразований энергии является перенос тепла в окружающую среду, которое больше не используется для выполнения работы.Как мы обсудим более подробно в Термодинамике, способность энергии производить полезную работу «деградировала» при преобразовании энергии.
Сводка раздела
- Мощность — это скорость выполнения работы или в форме уравнения для средней мощности P для работы Вт , выполненной за время t , [латекс] P = \ frac {W} {t} \\ [/ латекс]
- Единицей измерения мощности в системе СИ является ватт (Вт), где [латекс] 1 \ text {W} = 1 \ frac {\ text {J}} {\ text {s}} \\ [/ latex].
- Мощность многих устройств, таких как электродвигатели, также часто выражается в лошадиных силах (л.с.), где 1 л.с. = 746 Вт.
Концептуальные вопросы
- Большинство электроприборов имеют мощность в ваттах. Зависит ли этот рейтинг от того, как долго прибор включен? (В выключенном состоянии это устройство с нулевой ваттностью.) Объясните в терминах определения мощности.
- Объясните в терминах определения мощности, почему потребление энергии иногда указывается в киловатт-часах, а не в джоулях.Какая связь между этими двумя энергетическими единицами?
- Искра статического электричества, которую вы можете получить от дверной ручки в холодный и сухой день, может нести несколько сотен ватт мощности. Объясните, почему вы не пострадали от такой искры.
Задачи и упражнения
- Пульсар в Крабовидной туманности (см. Рис. 4) — это остаток сверхновой, которая произошла в 1054 году нашей эры. Используя данные из таблицы 1, вычислите приблизительный коэффициент, на который мощность этого астрономического объекта снизилась после его взрыва.
Рис. 4. Крабовидная туманность (предоставлено ESO, через Wikimedia Commons)
- Предположим, что звезда в 1000 раз ярче нашего Солнца (то есть излучающая в 1000 раз большую мощность) внезапно становится сверхновой. Используя данные из Таблицы 1: (a) Во сколько раз увеличивается его выходная мощность? (б) Во сколько раз ярче, чем вся наша галактика Млечный Путь, сверхновая? (c) Основываясь на ваших ответах, обсудите, возможно ли наблюдать сверхновые в далеких галактиках. Отметим, что существует порядка 10 11 наблюдаемых галактик, средняя яркость которых несколько меньше нашей собственной галактики.
- Человек в хорошем физическом состоянии может выдавать 100 Вт полезной мощности в течение нескольких часов подряд, возможно, задействуя механизм, приводящий в действие электрогенератор. Пренебрегая любыми проблемами эффективности генератора и практическими соображениями, такими как время отдыха: (а) Сколько человек потребуется, чтобы запустить электрическую сушилку для одежды мощностью 4,00 кВт? (б) Сколько людей потребуется, чтобы заменить большую электростанцию, вырабатывающую 800 МВт?
- Сколько стоит эксплуатация 3.Электрические часы 00-Вт на год при стоимости электроэнергии 0,0900 $ за кВт · ч?
- Большой бытовой кондиционер может потреблять 15,0 кВт электроэнергии. Какова стоимость эксплуатации этого кондиционера 3,00 часа в день в течение 30,0 дней, если стоимость электроэнергии составляет 0,110 доллара США за кВт · ч?
- (a) Какова средняя потребляемая мощность в ваттах прибора, потребляющего 5,00 кВт · ч энергии в день? (б) Сколько джоулей энергии устройство потребляет в год?
- (a) Какова средняя полезная выходная мощность человека, который делает 6.00 × 10 6 Дж полезной работы за 8.00 ч? (b) Работая с такой скоростью, сколько времени потребуется этому человеку, чтобы поднять 2000 кг кирпичей 1,50 м на платформу? (Работу по поднятию тела можно не выполнять, потому что здесь она не считается полезным результатом.)
- Драгстер весом 500 кг разгоняется до конечной скорости 110 м / с за 400 м (около четверти мили) и сталкивается со средней силой трения 1200 Н. Какова его средняя выходная мощность в ваттах и лошадиных силах, если это занимает 7,30 с?
- (а) Сколько времени займет автомобиль массой 850 кг с полезной мощностью 40 л.с.0 л.с. (1 л.с. = 746 Вт) для достижения скорости 15,0 м / с без учета трения? (b) Сколько времени займет это ускорение, если при этом автомобиль также преодолеет холм высотой 3,00 м?
- (a) Найдите полезную выходную мощность двигателя лифта, который поднимает груз массой 2500 кг на высоту 35,0 м за 12,0 с, если он также увеличивает скорость в состоянии покоя до 4,00 м / с. Обратите внимание, что общая масса уравновешенной системы составляет 10 000 кг, так что только 2500 кг поднимается в высоту, но все 10 000 кг ускоряются. (б) Сколько это стоит, если электричество стоит 0 долларов.0900 за кВт · ч?
- (a) Каково доступное энергосодержание в джоулях батареи, которая работает с электрическими часами мощностью 2,00 Вт в течение 18 месяцев? (b) Как долго батарея, которая может обеспечивать 8,00 × 10 4 Дж, может работать с карманным калькулятором, потребляющим энергию со скоростью 1,00 × 10 −3 Вт?
- (a) Сколько времени потребуется самолету массой 1,50 × 10 5 кг с двигателями мощностью 100 МВт, чтобы достичь скорости 250 м / с и высоты 12,0 км, если сопротивление воздуха будет незначительным? (б) Если это действительно занимает 900 с, какова мощность? (c) Учитывая эту мощность, какова средняя сила сопротивления воздуха, если самолет занимает 1200 с? (Подсказка: вы должны найти расстояние, которое самолет преодолеет за 1200 с при постоянном ускорении.)
- Рассчитайте выходную мощность, необходимую для 950-килограммового автомобиля, чтобы преодолеть уклон 2,00 ° с постоянной скоростью 30,0 м / с, столкнувшись с сопротивлением ветра и трением в сумме 600 Н. Явно покажите, как вы выполняете шаги, указанные в Стратегиях решения проблем в области энергетики. .
- (a) Рассчитайте мощность на квадратный метр, приходящуюся от Солнца в верхние слои атмосферы Земли. (Возьмем выходную мощность Солнца равной 4,00 × 10 26 Вт.) [/ Latex] (b) Часть этой мощности поглощается и отражается атмосферой, так что максимум 1.30 кВт / м 2 достигает поверхности Земли. Вычислите площадь в км 2 коллекторов солнечной энергии, необходимых для замены электростанции, вырабатывающей 750 МВт, если коллекторы преобразуют в электричество в среднем 2,00% максимальной мощности. (Такая малая эффективность преобразования связана с самими устройствами и тем фактом, что солнце находится прямо над головой лишь на короткое время.) При тех же предположениях, какая площадь потребуется для удовлетворения энергетических потребностей Соединенных Штатов (1,05 × 10 20 J)? Энергетические потребности Австралии (5.4 × 10 18 Дж)? Энергетические потребности Китая (6,3 × 10 19 Дж)? (Эти значения энергопотребления взяты с 2006 г.)
Глоссарий
мощность: скорость выполнения работы
ватт: (Вт) единица мощности СИ, с [латексом] 1 \ text {W} = \ frac {\ text {J}} {\ text {s}} \\ [/ latex]
лошадиных сил: более старая несистемная единица мощности, с 1 л.с. = 746 Вт
киловатт-час: блок кВт · час, используемый в основном для выработки электроэнергии, предоставляемой электроэнергетическими компаниями
Избранные решения проблем и упражнения
1.2 × 10 −10
3. (а) 40; (б) 8 миллионов
5. 149 долларов США
7. (а) 208 Вт; (б) 141 с
9. (а) 3,20 с; (б) 4,04 с
11. (а) 9,46 × 10 7 Дж; (б) 2,54 л
13. Определить известные: м = 950 кг, угол наклона θ = 2,00º, v = 3,00 м / с, f = 600 Н
Выявление неизвестных: мощность P автомобиля, сила F , что автомобиль применяется к дороге
Решение для неизвестных: [латекс] P = \ frac {W} {t} = \ frac {Fd} {t} = F \ left (\ frac {d} {t} \ right) = Fv \\ [/ latex ], Где F параллелен наклону и должна противодействовать силам сопротивления и силе тяжести: [латекс] F = f + w = 600 \ text {N} + mg \ sin \ theta \\ [/ latex] .4 \ text {W} \ end {array} \\ [/ latex]
Около 28 кВт (или около 37 л.с.) приемлемо для автомобиля, чтобы преодолевать небольшой уклон.
Расчет средней мощности, рассеиваемой в цепи переменного тока
Расчет средней мощности, рассеиваемой в цепи переменного токаСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Electrical Engineering Stack Exchange — это сайт вопросов и ответов для профессионалов в области электроники и электротехники, студентов и энтузиастов.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 11к раз
\ $ \ begingroup \ $Это вопрос из очень важного задания, над которым я работаю: «Нагрузка приводится в действие источником переменного тока.В конкретное время напряжение на нагрузке составляет 120 cos (wt + 50), а ток через нагрузку составляет 20 sin (wt-10). Рассчитайте среднюю мощность в ваттах, рассеиваемую нагрузкой ».
Мои рабочие: Сначала я конвертирую ток в косинус, чтобы получить 20cos (wt-100)
.Тогда я использую формулу \ $ \ P = | Vrms || Irms | cos (\ theta v — \ theta i) \ $ что дает мне -1039,2 Вт
Я предположил, что вопрос был задан для реальной мощности, поскольку это мощность, рассеиваемая в резисторе, и это единственное уравнение, приведенное в литературе.Онлайн-калькулятор дал мне комплексное число, действительная часть которого в два раза больше, чем я нашел. Это правильно? Отрицательная мощность в резисторе? Где я ошибся?
Создан 02 ноя.
IanIan311 золотой знак11 серебряных знаков66 бронзовых знаков
\ $ \ endgroup \ $ \ $ \ begingroup \ $Онлайн-калькулятор дал мне комплексное число, действительная часть которого в два раза больше, чем я нашел.
Будьте осторожны с онлайн-калькуляторами и ожидаемыми данными. Многие формулы переменного тока предполагают среднеквадратичные значения.
Предполагая, что напряжение и ток, указанные в вашей задаче, равны , а не RMS, вы все сделали правильно.
$ P_ {avg} = \ frac {1} {\ sqrt {2}} V_o \ cdot \ frac {1} {\ sqrt {2}} I_o \ cos {150} \\ P_ {avg} = \ frac {120 \ cdot 20} {2} * \ hspace {2pt} \ text {-}. 866 \\ P_ {avg} = — 1039,2 \ hspace {2pt} \ text {W}
$Создан 02 ноя.
\ $ \ endgroup \ $ \ $ \ begingroup \ $Отрицательная мощность резистора? Где я ошибся?
Нагрузка не является резистором.Если бы это был резистор, не было бы разницы фаз между сигналами тока и напряжения.
В общем случае отрицательная мощность возможна — это означает, что в нагрузке есть источник питания, и она передает мощность обратно вашему источнику, а не забирает энергию от него.
Так что я не думаю, что вы подошли к проблеме неправильно.
Создан 02 ноя.
ФотонФотон11k33 золотых знака140140 серебряных знаков268268 бронзовых знаков
\ $ \ endgroup \ $ 2 \ $ \ begingroup \ $Ну, как вы написали данную информацию у нас:
$$ \ text {P} = \ frac {\ hat {\ text {V}} _ {\ space \ text {load}}} {\ sqrt {2}} \ cdot \ frac {\ hat {\ text { I}} _ {\ space \ text {load}}} {\ sqrt {2}} \ cdot \ cos \ left (\ varphi _ {\ space \ text {load}} \ right) \ tag1 $$
Где:
$$ \ varphi _ {\ space \ text {load}} = \ left | \ arg \ left (\ underline {\ text {V}} _ {\ space \ space \ text {load}} \ right) — \ arg \ left (\ underline {\ text {I}} _ {\ space \ space \ text {load}} \ right) \ right | \ tag2 $$
Используя приведенные значения, получаем:
- $$ \ hat {\ text {V}} _ {\ space \ text {load}} = 120 \ tag3 $$
- $$ \ hat {\ text {I}} _ {\ space \ text {load}} = 20 \ tag4 $$
- $$ \ varphi _ {\ space \ text {load}} = \ left | \ arg \ left (120e ^ {\ frac {50 \ pi i} {180}} \ right) — \ arg \ left (20e ^ { — \ frac {5 \ pi i} {9}} \ right) \ right | = \ frac {5 \ pi} {6} \ tag5 $$
Итак:
$$ \ text {P} = \ frac {120} {\ sqrt {2}} \ cdot \ frac {20} {\ sqrt {2}} \ cdot \ cos \ left (\ frac {5 \ pi} { 6} \ right) = — 600 \ sqrt {3} \ приблизительно-1039.23048 \ space \ text {W} \ tag6 $$
ответ дан 6 мар ’18 в 12:55
JanJan3,35688 серебряных знаков1515 бронзовых знаков
\ $ \ endgroup \ $ \ $ \ begingroup \ $При вычислении комплексной мощности действительная часть комплексной мощности представляет собой среднюю рассеиваемую мощность.S = P + jQ P = Vrms Irms cos (Φ) где cosΦ — коэффициент мощности схемы, поэтому вычисления могут быть простыми.
Создан 06 мая 2020, 17:05 как и другие.
\ $ \ endgroup \ $Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками ac или задайте свой вопрос.
Электротехнический стек Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Нормализованная мощность против средней мощности
Когда дело доходит до анализа производительности между поездками и наблюдения за прогрессом тренировки, следует ли вам сосредоточиться на нормированной мощности или средней мощности?
Тренировка по триатлону с использованием измерителя мощности открывает множество показателей на велосипеде и анализа после поездки, но выбор того, на чем следует сосредоточиться, может быть непростым.Один из наиболее важных способов оценки ваших результатов — это посмотреть, сколько мощности вы можете выдержать в течение заданной продолжительности поездки или расстояния. Это поможет вам оценить прогресс в тренировках и установить цели для ваших соревнований по триатлону, чтобы вы могли уверенно бегать на велосипеде.
Но следует ли вам сосредоточиться на средней мощности или нормализованной мощности (NP)?
Связано: 7 ключевых терминов по обучению измерителю мощности
Что такое средняя мощность?
Прежде чем мы рассмотрим нормализованную мощность, давайте проясним, как работает средняя мощность.На протяжении всей поездки на вашем головном устройстве постоянно рассчитывается средняя мощность. Это просто общая мощность вашей поездки, разделенная на продолжительность поездки.
На первый взгляд, усреднение звучит как отличный способ отработать усилия, которые вы прикладываете во время тренировки, и может быть полезно, когда речь идет о поездках с высокой повторяемостью. Для FTP-теста в помещении, стабильной, плоской гонки на время или повторяющихся циклов одного и того же курса он отлично работает.
СРЕДНЯЯ МОЩНОСТЬ часто не отражает интенсивность, которую вы ощущаете во время езды.
Но есть большая проблема, когда дело доходит до более разнообразного катания на открытом воздухе по разным маршрутам, особенно по холмам.Это потому, что средняя мощность включает в себя все восстановления между интервалами или спусками с нулевым ваттом, а также подходы с большим усилием или тяжелые подъемы.
В результате получается несколько упрощенная цифра, которая часто не отражает реальную интенсивность, которую вы чувствуете во время езды. Это затрудняет сравнение силовой тренировки с тренировкой, чтобы увидеть, улучшились ли вы.
Что такое нормализованная мощность?
Нормализованная мощность — это показатель, разработанный TrainingPeaks. Вы могли заметить, что NP рядом со средней мощностью в ваших данных после поездки, будь то в TrainingPeaks или на другой онлайн-платформе для обучения.
Одна из вещей, которая отталкивает спортсменов от Нормализованной мощности, — это то, насколько она варьируется по сравнению со средней мощностью. Иногда он приближается к вашему среднему, иногда кажется неприятным — обычно выше. Итак, почему на это стоит обратить внимание?
Короче говоря, нормализованная мощность дает сопоставимые данные о поездке, и это делает ее одной из самых важных показателей в вашем арсенале тренировок измерителя мощности.
Используя алгоритм, описанный Training Peaks как «немного сложный», NP компенсирует буквальные взлеты и падения во время езды, чтобы лучше отразить общие усилия, которые вы приложили.Идея состоит в том, что рассчитанная цифра — это мощность, которую вы могли бы поддерживать, если бы поездка была идеально устойчивой.
Нормализованная мощность и средняя мощность
Чтобы сравнить значения средней и нормализованной мощности, давайте рассмотрим пример часового подъема на вашем FTP с последующим обратным спуском на холостом ходу.
При средней мощности огромные усилия при подъёме с высокой интенсивностью в некоторой степени сводятся на нет всеми данными о нулевой мощности, записанными при обратном спуске с холма.Ваше среднее значение упадет прямо вниз, поэтому данные на самом деле не отражают ваши усилия.
С другой стороны, NP достаточно умен, чтобы знать, что вы много работали, и дает цифру, которая более точно отражает это.
Нормализованная мощность значительно упрощает сравнение ваших результатов от одного заезда к следующему.
Именно по этой причине TrainingPeaks использует NP, а не среднюю мощность для расчета вашей оценки тренировочного стресса (TSS) — общего напряжения, которое вы body — на каждую велосипедную сессию.
Таким образом, использование нормализованной мощности не только позволяет вам лучше понять вашу тренировочную нагрузку, но также значительно упрощает сравнение ваших результатов от одной поездки к другой.
Это особенно полезно при преодолении различных трасс, условий и местности. Наблюдение за увеличением NP при одинаковой продолжительности езды и воспринимаемых усилий свидетельствует об улучшении силы и физической формы без необходимости придерживаться одного и того же скучного маршрута. Это также позволяет вам отточить силу ваших ворот для гонок.
Все это делает Нормализованную мощность лучшим показателем, когда дело доходит до того, на какую метрику следует обращать внимание при анализе триатлона на велосипеде.
Пиковая мощность и средняя мощность в нс и субнс Лазеры
Существенным и хорошо известным различием между лазерами и обычными некогерентными источниками света является способность концентрировать лазерное излучение в виде коротких импульсов с длительностью до нескольких единиц. фемтосекунды, содержащие потенциально всего несколько оптических циклов.Технически вы можете управлять некогерентным светодиодным источником, используя импульсы тока, что позволяет излучать световые импульсы в наносекундном диапазоне. Однако каждый импульс имел бы максимальную мощность (то есть пиковую мощность), равную средней мощности того же устройства, если бы применялось постоянное смещение. Только лазерные резонаторы могут концентрировать накопленную энергию в активных материалах таким образом, чтобы достигать пиковой мощности на порядки выше, чем их средняя мощность, вплоть до исключительного уровня PW, о котором недавно сообщалось в исследовательских публикациях.Чрезвычайно высокие уровни пиковой мощности, достигаемые импульсными лазерными источниками, являются одной из основных причин их успеха во многих приложениях, появившихся в последние десятилетия. Следовательно, точная оценка пиковой мощности лазера с учетом других рабочих параметров, таких как средняя мощность, длительность импульса и частота повторения, является фундаментальной для выбора наилучшего варианта для конкретного применения среди различных коммерческих альтернатив. В принципе, вычислить пиковую мощность довольно просто, учитывая фактический временной профиль лазерного импульса.Предполагая последовательность непрерывно повторяющихся, периодических, прямоугольных импульсов с частотой повторения fR, длительностью импульса tP и средней мощностью PAV, расчет энергии EP импульса и пиковой мощности PP является тривиальным, а энергия импульса обеспечивается соотношением между средней мощностью и частотой повторения. и пиковая мощность, обеспечиваемая соотношением энергии и длительности импульса:
Конечно, это простое соотношение справедливо для лазерных импульсов с квадратным или плоским временным профилем, что довольно редко встречается на практике.Обычно временные профили лазерных импульсов более точно аппроксимируются функциями колоколообразной формы, такими как профиль Гаусса или профиль Sech3, причем последний актуален в основном для ультракоротких импульсов, полученных в режиме пассивной синхронизации мод. В этом случае следует переопределить длительность импульса как общепринятый параметр полной ширины на полувысоте (FWHM). Поскольку концентрация энергии в гауссовом импульсе с длительностью tP на полувысоте немного отличается от прямоугольного импульса с равной длительностью импульса, необходимо изменить формулу выше:
Обязательно более гладкие передний и задний фронты гауссова импульса немного уменьшаются (в 0 раз.94) пиковая мощность для данной энергии импульса или средней мощности. Дело в том, что ситуация может еще больше усложниться, когда в картину войдут лазеры, излучающие импульсы длительностью несколько наносекунд или субнаносекунд. Обычно гауссова форма импульса является отличным приближением для реального профиля импульса DPSS-лазеров с модуляцией добротности, хотя она точна только для лазеров, работающих в одиночной продольной моде (SLM). Большинство имеющихся в продаже лазеров с модуляцией добротности основаны на нескольких продольных модах, которые колеблются в одно и то же время с постоянной интерференцией.Этот эффект виден при регистрации оптических импульсов с помощью достаточно быстрых фотодиодов и цифровых осциллографов, демонстрирующих модуляцию амплитуды, наложенную на форму гауссова импульса. Период и глубина модуляции зависят от количества продольных мод, колеблющихся вместе. Для импульсов длительностью в десятки наносекунд резонаторы поддерживают такое количество режимов, что модуляция усредняется и практически не видна. Тем не менее, для субнаносекундного режима остается лишь несколько режимов, что приводит к глубокой модуляции огибающей импульса и сильному отклонению от идеальной гауссовой формы.Определение полной ширины полумаксимальной длительности импульса становится сомнительным, и следует использовать более точное статистическое определение, дающее возможность поправочного коэффициента для пиковой мощности выше 1 (потенциально коэффициент 1,5 может быть разумным предположением).
Рисунок 1: сравнение различных формы импульсов, нормированных по энергии. | Рисунок 2: Средняя мощность и длительность импульса как функция частоты повторения для лазера WedgeHF компании Bright Solutions. |
Рассматривая, например, кривые характеристик стандартного HF-лазера Wedge от Bright Solutions на длине волны 1064 нм, средняя мощность на частоте 100 кГц составляет 4,6 Вт, а длительность импульса составляет около 2,5 нс, что дает пиковую мощность ~ 18 кВт.
При более низкой частоте повторения длительность импульса лазера Wedge HF короче, а энергия импульса выше, что дает более высокую пиковую мощность. Поэтому, например, на частоте 10 кГц, с импульсами ~ 700 пс и средней мощностью ~ 1.8 Вт, пиковая мощность увеличивается до ~ 260 кВт. Для более подробного сравнения различных промышленных лазерных источников на 1 мкм в таблице ниже приведены пиковая мощность и другие критические параметры.
Из приведенной выше таблицы очевидно преимущество в пиковой мощности, достигаемое за счет более коротких длительностей импульсов, даже при гораздо более низких уровнях средней мощности. Указанные в таблице модели лазеров имеют одинаковое качество луча (M 2 <1,5 для всех).Следовательно, они могут быть сфокусированы на аналогичных размерах пятна, и соответствующие значения пиковой плотности мощности изменяются пропорционально заявленным пиковым мощностям.
Позвольте одному из наших менеджеров по продукции ответить на любые вопросы или помочь в выборе подходящего лазера, позвонив нам по телефону 636.272.7227 или свяжитесь с нами здесь!
.
 , грн., wi
, грн., wi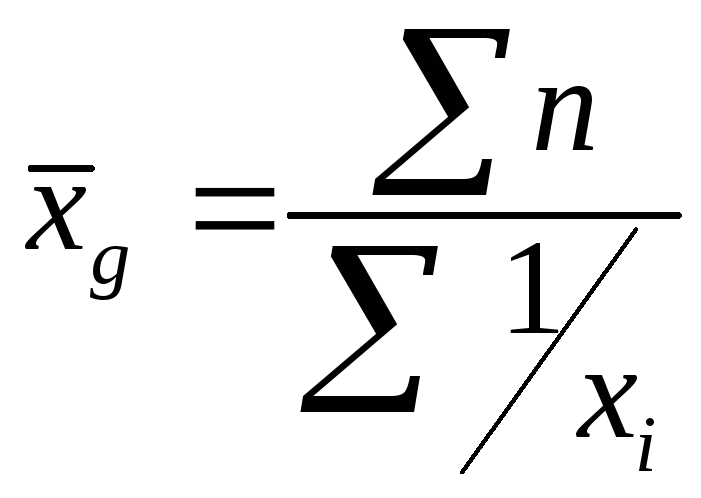 {2}}{n}}}} называется средним квадратичным.
{2}}{n}}}} называется средним квадратичным.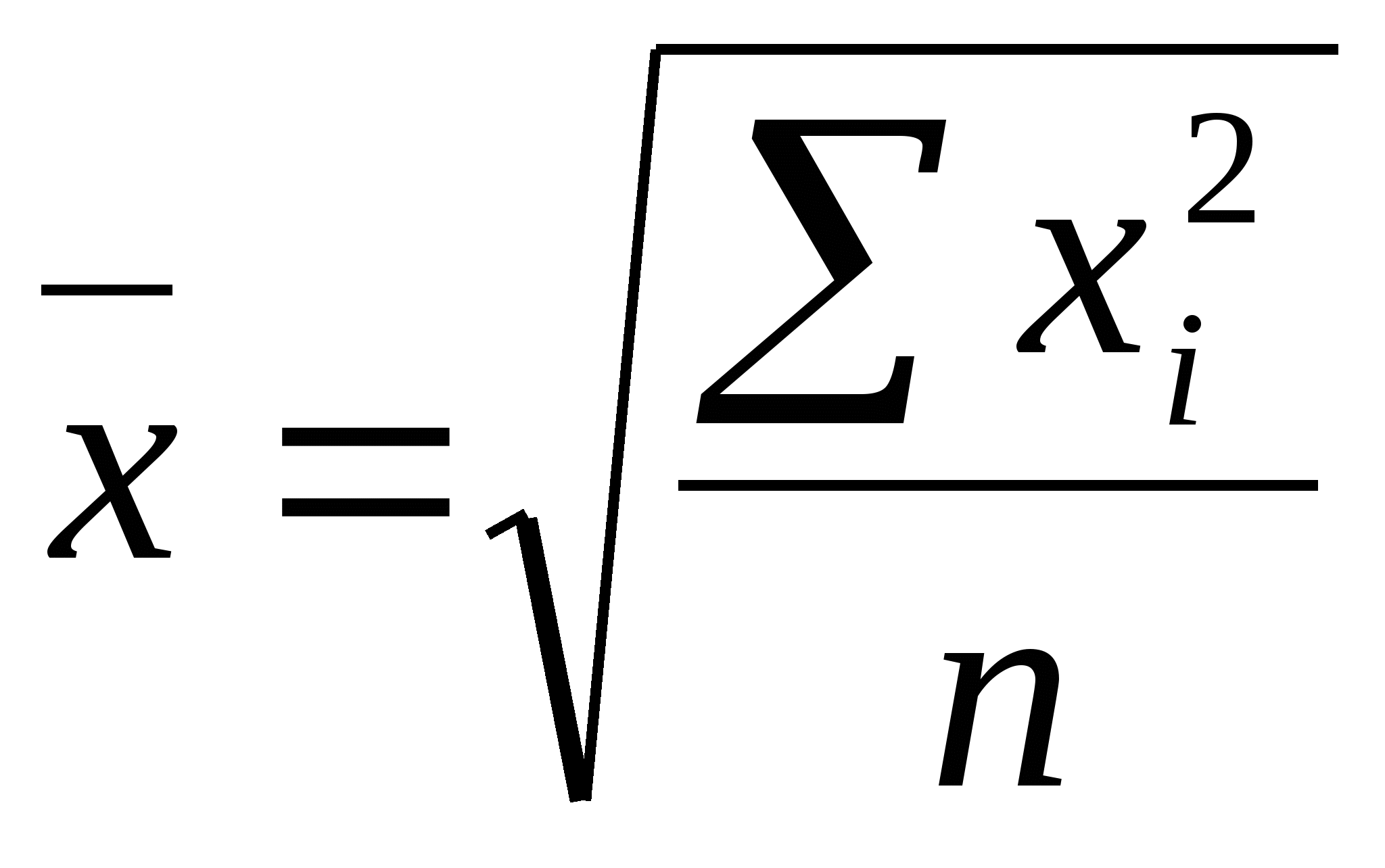
 0 \, V) \, \ sin \, 90 \ pi t \)
0 \, V) \, \ sin \, 90 \ pi t \)