Среднее статистическое: СТАТИСТИЧЕСКОЕ СРЕДНЕЕ — это… Что такое СТАТИСТИЧЕСКОЕ СРЕДНЕЕ?
СТАТИСТИЧЕСКОЕ СРЕДНЕЕ — это… Что такое СТАТИСТИЧЕСКОЕ СРЕДНЕЕ?
- СТАТИСТИЧЕСКОЕ СРЕДНЕЕ
СТАТИСТИЧЕСКОЕ СРЕДНЕЕ, в статистике — число, результат вычислений, которое дает типичное представление обо всем множестве чисел. Эта величина представляет собой АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ от этих чисел. Для получения представления о типичных величинах некоторого множества чисел определяют также модус (наиболее часто встречающееся число) и промежуточное число, приходящееся на середину диапазона значений всех чисел и разделяющее его на верхнюю и нижнюю части.
Научно-технический энциклопедический словарь.
- СТАТИСТИЧЕСКАЯ МЕХАНИКА
- СТАТИЧЕСКОЕ ЭЛЕКТРИЧЕСТВО
Смотреть что такое «СТАТИСТИЧЕСКОЕ СРЕДНЕЕ» в других словарях:
статистическое среднее — statistinis vidurkis statusas T sritis fizika atitikmenys: angl.

Среднее значение статической деформации, при которой происходило утомление образца до разрушения — Среднее статистическое значение статической деформации отдельного образца, к которой относятся усталостная выносливость образца Источник … Словарь-справочник терминов нормативно-технической документации
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — один из осн. разделов матем. статистики … Физическая энциклопедия
среднее — 3.3 среднее (mean): Среднее значение для (выбранного) времени усреднения результатов измерений анемометром. Источник: ГОСТ Р ИСО 1 … Словарь-справочник терминов нормативно-технической документации
среднее выходное качество — 2.7.4 среднее выходное качество Ожидаемый средний уровень качества выходящей продукции после контроля при данном значении входного уровня качества.
 Примечания 1 На практике могут быть использованы различные определения среднего выходного качества … Словарь-справочник терминов нормативно-технической документации
Примечания 1 На практике могут быть использованы различные определения среднего выходного качества … Словарь-справочник терминов нормативно-технической документациисреднее процесса
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — раздел статистического вывода , предназначенный для оценивания характеристик (параметров) генеральной совокупности по результатам выборочного исследования. С.О. параметров генеральной совокупности возможно, если выборка извлечена с использованием … Социология: Энциклопедия
ГОСТ Р 50779.11-2000: Статистические методы. Статистическое управление качеством. Термины и определения
 11 2000: Статистические методы. Статистическое управление качеством. Термины и определения оригинал документа: 3.4.3 (верхняя и нижняя) границы регулирования Граница на контрольной карте, выше которой верхняя граница,… … Словарь-справочник терминов нормативно-технической документации
11 2000: Статистические методы. Статистическое управление качеством. Термины и определения оригинал документа: 3.4.3 (верхняя и нижняя) границы регулирования Граница на контрольной карте, выше которой верхняя граница,… … Словарь-справочник терминов нормативно-технической документацииГОСТ Р ИСО 16269-6-2005: Статистические методы. Статистическое представление данных. Определение статистических толерантных интервалов — Терминология ГОСТ Р ИСО 16269 6 2005: Статистические методы. Статистическое представление данных. Определение статистических толерантных интервалов оригинал документа: 3.1.2 толерантная граница (tolerance limit): Граница толерантного интервала.… … Словарь-справочник терминов нормативно-технической документации
ОЦЕНИВАНИЕ СТАТИСТИЧЕСКОЕ — один из основных разделов статистики математич. (см.), посвященный оцениванию по случайным наблюдениям тех или иных характеристик из распределения. В социологич. исследованиях чаще всего используются два вида О.
 с. точечное и интервальное.… … Российская социологическая энциклопедия
с. точечное и интервальное.… … Российская социологическая энциклопедия
Среднее статистическое — Энциклопедия по машиностроению XXL
Рассмотрим процесс нестационарного совместного тепломассообмена в каплях или пузырях, имеющих средний статистический радиус [51]. В этом случае система уравнений (3.3). (3.4) в дисперсной фазе принимает вид [c.32]В разреженных газах средняя статистическая длина / свободного пробега отдельной молекулы между двумя столкновениями с другими молекулами становится сравнимой с размерами сосуда, в котором находится газ. Следовательно, величина / начинает оказывать влияние на физические процессы, происходящие в газе. [c.236]
Мы уже видели, что величина максимальных напряжений вблизи очага концентрации, выраженная через теоретический коэффициент концентрации ад, еще не характеризует полностью роль местных напряжений в усталостном разрушении.

Полимеры получают из мономеров — веществ, каждая молекула которых способна образовывать одно или несколько составных звеньев. Так как полимеры представляют собой смеси молекул с различной длиной цепи, то под молекулярной массой полимера понимают ее среднее статистическое значение. Молекулярная масса полимеров может достигать значений в несколько миллионов. [c.201]
Слоистый материал, расчет 16 Слоистых пластин теория 34 Случайная функция 86, 246 Состояние чистого натяжения 334 Соответствия принцип ИО Среднее статистическое 87 Старения зффекты 129 Статистическая изотропия 246
 556]
556]
Среднее статистическое значение величины оценки определенного направления исследований (в баллах) М [c.98]
Каждый вид энергии имеет определенный характер взаимодействия между частицами и телами в соответствующих полях. Следует отметить некоторые особенности механической и тепловой энергии и их взаимодействия. Механическая энергия, т. е. энергия свободно движущейся частицы или системы, может возникать не только при механических, но и электрических, магнитных, гравитационных и других факторах. Тепловое взаимодействие хотя и представляет в своей основе как бы механическое взаимодействие между хаотически движущимися частицами (атомами, молекулами), однако, являясь результатом совокупного действия многих частиц, оно относится к качественно иному виду взаимодействия, осуществляемому как среднее статистическое взаимодействие систем, характеризующихся различным тепловым состоянием.
Средние статистические значения потери точности АУб положения, вызванные динамической нагрузкой, жесткость направляющих /С Б, постоянная времени Гш и время Tib переходного процесса в режимах Б4° и 5 иллюстрируются данными табл.
Особенность ускоренных испытаний состоит в том, что они характеризуют сопротивление усталости всего объёма материала, участвующего в деформации, и дают поэтому средние статистические характеристики. Между тем [c.90]
На рис. 1-8,а показана элементарная кристаллическая решетка твердого раствора замещения хрома в железе. Отдельные узлы решетки железа замещены ионами хрома- Ионы обоих металлов располагаются в узлах кристаллической решетки в произвольном порядке, со средней статистической равномерностью. [c.16]
Значительно реже применяется метод относительных оценок, когда определяются среднее статистическое значение величины оценки и коэффициент удельного веса данного решения. Это объясняется ограниченным количеством специалистов по тем или иным конкретным вопросам.
Закон теплоотдачи при свободной конвекции изменяется при достаточно больших значениях числа Gr независимо от размеров тела. Физически это изменение связано с тем, что ламинарный характер течения около поверхности нагрева в целом нарушается и возникает так называемая тепловая турбулентность. Пр и этом режиме течения около поверхности существует вязкий слой, с внешней стороны которого срываются турбулентные вихри. Характер движения жидкости становится в среднем (статистически) одинаковым для различных частей поверхности теплообмена, и коэффициент теплоотдачи перестает зависеть от размеров тела. Это описывается формулой
Физически это изменение связано с тем, что ламинарный характер течения около поверхности нагрева в целом нарушается и возникает так называемая тепловая турбулентность. Пр и этом режиме течения около поверхности существует вязкий слой, с внешней стороны которого срываются турбулентные вихри. Характер движения жидкости становится в среднем (статистически) одинаковым для различных частей поверхности теплообмена, и коэффициент теплоотдачи перестает зависеть от размеров тела. Это описывается формулой
Если обозначить среднее статистическое значение абсолютной величины поперечной скорости, зависящей от структуры турбулентности, то можно определить т так [c.234]
Цепи,-образованные между углеродными атомами, могут быть линейными, представляющими собой спиралевидные сложные системы. Связи атомов углерода между собой могут давать также сетчатую или пространственную конфигурацию полимера. Длина цепи определяется коэффициентом полимеризации п, который представляет собой среднюю, статистическую величину и, чем острее пик распределения этой величины, тем стабильнее свойства данного полимера. [c.13]
[c.13]
На рис. 4 представлено устройство для подсчета среднего статистического значения —медианы выборки деталей, элементов в лабораторных и цеховых условиях. [c.434]
| Таблица П4.2 Средняя статистическая точность координат и углового положения осей отверстий, полученных на операции сверления, мм |
Средняя статистическая точность операций строгания при отклонениях формы и углового положения технологической базы, не превышающих 10 % отклонений линейных размеров [c.273]
В противоположность феноменологическому пути изучения физических явлений известен молекулярно-кинетический путь. Он состоит в изучении физических явлений в соответствии с изучением молекулярного строения вещества. Путь этот проложен Дж. Максвеллом и Л. Больцманом. Макроскопические движения вещества изучаются совместно с молекулярными движениями в нем. Так как в микромире молекулярные движения вследствие взаимных столкновений между молекулами происходят хаотично, то невозможно изучать их движения индивидуально, а следует рассматривать их только в среднем — статистически. Поэтому к изучению их должны быть применены статистические методы. Такие методы в полной мере развиваются в курсе статистической физики.
[c.5]
Он состоит в изучении физических явлений в соответствии с изучением молекулярного строения вещества. Путь этот проложен Дж. Максвеллом и Л. Больцманом. Макроскопические движения вещества изучаются совместно с молекулярными движениями в нем. Так как в микромире молекулярные движения вследствие взаимных столкновений между молекулами происходят хаотично, то невозможно изучать их движения индивидуально, а следует рассматривать их только в среднем — статистически. Поэтому к изучению их должны быть применены статистические методы. Такие методы в полной мере развиваются в курсе статистической физики.
[c.5]
Средние статистические данные [c.136]
Рабочая площадь поршня штока амортизатора определяется в зависимости от зарядного начального давления р q, которое устанавливается по средним статистическим данным. [c.282]
Таким образом, метод Гиббса рассматривает макроскопические свойства тела как свойства ансамбля, состоящего из колоссального числа отдельных атомных объектов, поведение которых полностью описывается законами классической механики. Гиббс выясняет, какие свойства будет иметь такой ансамбль. При этом Гиббс выяснил громадную роль понятия вероятности в этих проблемах теории строения вещества и показал, что оно позволяет осуществить очень глубокий анализ макроскопических, в частности, термодинамических свойств. Он показал связь этих свойств со средними статистическими свойствами ансамблей из атомных объектов.
[c.8]
Гиббс выясняет, какие свойства будет иметь такой ансамбль. При этом Гиббс выяснил громадную роль понятия вероятности в этих проблемах теории строения вещества и показал, что оно позволяет осуществить очень глубокий анализ макроскопических, в частности, термодинамических свойств. Он показал связь этих свойств со средними статистическими свойствами ансамблей из атомных объектов.
[c.8]
Использовались также среднее гармоническое и среднее статистическое Мс от и Л/ц [c.172] Приводимые в различных источниках значения [рт] и [pmv] представляют собой средние статистические данные, относящиеся к определенным конструкциям. [c.310]
Эргодический процесс является прежде всего стационарным случайным процессом. Стационарность предполагает независимость функций плотности распределения вероятностей от сдвига по времени. Вследствие этого для стационарных случайных процессов все моменты распределения также не зависят от начала отсчета времени. Стационарность является необходимым, но не достаточным условием эргодичности случайного процесса. Для того чтобы стационарный процесс был эргодическим, нужно, чтобы характеристики, полученные усреднением по одной реализации, не отличались от аналогичных характеристик, полученных усреднением по другим реализациям. Свойство эргодичности существенным образом облегчает анализ акустических сигналов. По-, скольку для них в этом случае средние статистические величины равны средним по времени, все функции плотности распределения вероятностей могут быть получены не по совокупности реализаций, а лишь по одной из них. Так, функция р(х), не зависящая от времени t в силу стационарности процесса, равна относительному времени пребывания сигнала п(О между уровнями а и ж -f Ад , а функция корре.чяции равна среднему по времени произведению
[c.14]
Вследствие этого для стационарных случайных процессов все моменты распределения также не зависят от начала отсчета времени. Стационарность является необходимым, но не достаточным условием эргодичности случайного процесса. Для того чтобы стационарный процесс был эргодическим, нужно, чтобы характеристики, полученные усреднением по одной реализации, не отличались от аналогичных характеристик, полученных усреднением по другим реализациям. Свойство эргодичности существенным образом облегчает анализ акустических сигналов. По-, скольку для них в этом случае средние статистические величины равны средним по времени, все функции плотности распределения вероятностей могут быть получены не по совокупности реализаций, а лишь по одной из них. Так, функция р(х), не зависящая от времени t в силу стационарности процесса, равна относительному времени пребывания сигнала п(О между уровнями а и ж -f Ад , а функция корре.чяции равна среднему по времени произведению
[c.14]
Характерной особенностью нароста является его нестабильность и неоднородность. Нарост непрерывно изменяет свою форму и размеры и систематически частично или полностью срывается с режущего элемента, так что следует говорить о его форме, размерах и действительном времени существования лищь исходя из средних статистических данных. В условиях непрерывного резания срыв нароста или его части наступает после накопления на режущем элементе определенного для данных условий количества заторможенных слоев металла при прохождении соответствующего пути резания.
[c.165]
Нарост непрерывно изменяет свою форму и размеры и систематически частично или полностью срывается с режущего элемента, так что следует говорить о его форме, размерах и действительном времени существования лищь исходя из средних статистических данных. В условиях непрерывного резания срыв нароста или его части наступает после накопления на режущем элементе определенного для данных условий количества заторможенных слоев металла при прохождении соответствующего пути резания.
[c.165]
Анализ таблицы показывает, что при исследованных скоростных и нагрузочных режимах АСССН обеспечивает существенное повышение точности положения ползуна относительно направляющих. Вычисленные средние статистические значения Апредельные верхнее бУтах и нижнее 6случайные отклонения приведены в табл. 5. [c.42]
Концевые лопатки РК ДРОС изготовлены методом центробежного литья в кокиль [44]. В качестве основного материала применен литейный сплав АЛ4 (или АЛ4М). Центробежным литьем в ЛПИ изготовлено более 60 типов модельных лопаток различной конфигурации с высотой 15—125 мм и толщиной тонких кромок до 0,3 мм. Группы отливок после термообработки подвергаются выборочному контролю качества структуры металла, прочностных характеристик и травлению на предмет обнаружения микротрещин. Средние статистические показатели испытаний образцов лопаток из сплава АЛ4 = 180 -4-200 МПа без термообработки и Од = 220 250 МПа после термообработки по режиму Т1 [44].
[c.122]
Группы отливок после термообработки подвергаются выборочному контролю качества структуры металла, прочностных характеристик и травлению на предмет обнаружения микротрещин. Средние статистические показатели испытаний образцов лопаток из сплава АЛ4 = 180 -4-200 МПа без термообработки и Од = 220 250 МПа после термообработки по режиму Т1 [44].
[c.122]
ЭРГСДЙЧЕСКАЯ ГИПОТЕЗА в статистической физике—предположение, что средние по времени значения физ. величин, характеризующих систему, равны их средним статистическим. Предложена Л. Больцманом в 1887 для обоснования статистической физики. [c.625]
Размеры каждого канала можно определить в долях от периметра уплотнения В, ширины уплотняющей поверхности I и средней статистической высоты микронеровностей /г 5, = = = Г// б/ = S,/i. Тогда под знаком суммы в уравнении (28) оста» нутся только безразмерные величины и их совокупность можно [c.90]
Одним из самых распространенных методов определения эффективных характеристик среды является метод теории случайных функций. В качестве модели, адекватной широкому классу композиционных материалов, является представление материальных тензоров как случайных макрооднородных полей. В этом методе тензор модулей упругости считается случайной функцией, представимой в виде суммы статистически среднего тензора модулей упрут ости и тензора, описывающего флуктуационные добавки. Принимается гипотеза эргодичности среднее по объему совпадает со средним статистическим. Допущение о малости флук— 1уаций позволяет пренебречь корреляционными функциями высших порядков и получить выражения для эффективных характеристик в корреляционном приближении, предложенном впервые в работе [33].
[c.19]
В качестве модели, адекватной широкому классу композиционных материалов, является представление материальных тензоров как случайных макрооднородных полей. В этом методе тензор модулей упругости считается случайной функцией, представимой в виде суммы статистически среднего тензора модулей упрут ости и тензора, описывающего флуктуационные добавки. Принимается гипотеза эргодичности среднее по объему совпадает со средним статистическим. Допущение о малости флук— 1уаций позволяет пренебречь корреляционными функциями высших порядков и получить выражения для эффективных характеристик в корреляционном приближении, предложенном впервые в работе [33].
[c.19]
At p — среднее статистическое случайной величины а — среднее квадратичное отклонение — параметр, характеризующий степень разброса случайной величины к относительно среднего значения, [c.36]
В этом методе тензор модулей упругости считается случайной функцией, представимой в виде суммы статистически среднего тензора модулей упругости и тензора, описывающего флюктуаци-онные добавки. Как правило, принимается гипотеза эргодичности среднее по объему совпадает со средним статистическим. (Правда, здесь объем, по которому совершается осреднение, связан с характерным размером неоднородности, и поэтому средние величины, вообще говоря, зависят от координат).
[c.89]
Как правило, принимается гипотеза эргодичности среднее по объему совпадает со средним статистическим. (Правда, здесь объем, по которому совершается осреднение, связан с характерным размером неоднородности, и поэтому средние величины, вообще говоря, зависят от координат).
[c.89]
Программы нагружения А, В, С, D показаны на рнс. 3.11, который дает представление об эмпирических распределениях параметра ф. Здесь показаны 95 %-ные доверительные интервалы для этой величины, а также средние статистические значения. Кружками обозначены средние значеиня, полученные в нредположеиии, что справедливо линейное правило суммирования, а все образцы испытывают вплоть до достижения предельного состояния. Квадраты соответствуют аналогичным n niij- [c.88]
Экспериментальные данные по микрогеометрии поверхностей дают основание предположить, что для каждой поверхности можно указать такой характерный размер L (меньший или равный номинальному размеру поверхности), начиная с которого микрогеометрия будет статистически одинакова на любом участке поверхности.
 Размер L предполагается достаточно большим, чтобы можно было провести определение средних статистических характеристик микрогеометрии. При этом граница поверхности реальных твердых тел в сечении моделируется набором клиньев с одинаковым углом 2а при вершине обеих поверхностей, но с различными ординатами вершин (где индекс поверхности i = 1,2, номер клина ] i. .. N), Возможны также и другие модели шероховатых поверхностей [6,15]. Обозначим через абсциссы вершин шероховатостей. Введем неподвижную систему отсчета так, чтобы ось ординат была параллельна возвышениям неровностей, а ось абсцисс параллельна направлению относительного их перемеш,ения. Возвышения неровностей второй поверхности в начальный момент времени будем отсчитывать от некоторой прямой, проведенной на расстоянии от оси абсцисс и жестко связанной со второй поверхностью, так что величина /г = йо (1 — е) будет текущим абсолютным расстоянием между поверхностями. По мере сближения двух контактируюш,их поверхностей е увеличивается, а h уменьшается (рис.
Размер L предполагается достаточно большим, чтобы можно было провести определение средних статистических характеристик микрогеометрии. При этом граница поверхности реальных твердых тел в сечении моделируется набором клиньев с одинаковым углом 2а при вершине обеих поверхностей, но с различными ординатами вершин (где индекс поверхности i = 1,2, номер клина ] i. .. N), Возможны также и другие модели шероховатых поверхностей [6,15]. Обозначим через абсциссы вершин шероховатостей. Введем неподвижную систему отсчета так, чтобы ось ординат была параллельна возвышениям неровностей, а ось абсцисс параллельна направлению относительного их перемеш,ения. Возвышения неровностей второй поверхности в начальный момент времени будем отсчитывать от некоторой прямой, проведенной на расстоянии от оси абсцисс и жестко связанной со второй поверхностью, так что величина /г = йо (1 — е) будет текущим абсолютным расстоянием между поверхностями. По мере сближения двух контактируюш,их поверхностей е увеличивается, а h уменьшается (рис. 13). Начало отсчета совместим с началом участка длины L, и пусть L будет одинаково для обеих поверхностей. При-
[c.46]
13). Начало отсчета совместим с началом участка длины L, и пусть L будет одинаково для обеих поверхностей. При-
[c.46]Пример изменения вида функции распределения частиц по раз.ме-рам в процессе приготовления островковой пленки дает работа [26[. В ней изучались островковые пленки Аи на стеклянной и углеродной подложках и было установлено, что с увеличением толщины осадка d плотность островков возрастает, проходит через максил1ум при d 0,4 нм, после чего уменьшается. В области толщин d нормальному закону. Это можно объяснить возникновением и быстрым ростом новых зародышей на подложке. Ситуация резко изменяется, когда пленка становится толще 0,7 нм. При этом наблюдается резкое увеличение D, сопровождаемое переходом от нормального к логарифмически нормальному распределению частиц по размерам, что указывает на включение и последующее преобладание процесса коалес-ценции островков. [c.10]
При изучении диффузии водорода через поликристалличе-ские образцы наблюдают, таким образом, средне-статистическую величину проницаемости из проницаемостей различно ориентированных кристаллов и проницаемости межкристалличе-ских прослоек. [c.119]
[c.119]
Результаты расчетов по методу Мопте-Карло являются осреднениями некоторого множества случайных величин. Как и всякие средние статистические величины, результаты метода Монте-Карло подвержены флуктуациям, тем большим, чем меньше число осредняемых величин. Точность метода растет обратно пропорционально корню квадратному из числа розыгрышей. Поэтому для получения большой точности может потребоваться практически неприемлемый объем вычислений. На результаты метода Монте-Карло следует смотреть как на результаты эксперимента, всегда подверженные определенному разбросу, обусловленному ошибками измерений. [c.228]
С увеличением числа циклов до разрушения (уменьшением нагрузки) относительно долговечностей, соответствующих экстремумам плотности трещин, последняя также, как и в области ма-лыхЛ р, падает, что, по-видимому, объясняется снижением уровня циклических пластических деформаций [4] и уменьшением длин трещин /, средняя статистическая величина которых в зависимости от условий и уровня нагружения приведена на рис. 2, б. Общая совокупность их длин для всех рассмотренных условий нагружения, как показали результаты статистической обработки, подчиняется нормальному закону распределения. Из рис. 2, следует, что характер изменения величин Г аналогичен характеру изменения у (рис. 2, а), причем максимальные значения I и у соответствуют одним и тем же долговечностям для одинаковых режимов нагружения. При этом наибольшие длины трещин к моменту разрушения наблюдаются в условиях одночастотного на-7 гружения и нагружения с временными выдержками, а дри двухчастотном нагружении они хотя и имеют несколько меньшую величину, но последняя и изменяется с числом циклов в меньшей степени, чем для указанных выше режимов.
[c.40]
2, б. Общая совокупность их длин для всех рассмотренных условий нагружения, как показали результаты статистической обработки, подчиняется нормальному закону распределения. Из рис. 2, следует, что характер изменения величин Г аналогичен характеру изменения у (рис. 2, а), причем максимальные значения I и у соответствуют одним и тем же долговечностям для одинаковых режимов нагружения. При этом наибольшие длины трещин к моменту разрушения наблюдаются в условиях одночастотного на-7 гружения и нагружения с временными выдержками, а дри двухчастотном нагружении они хотя и имеют несколько меньшую величину, но последняя и изменяется с числом циклов в меньшей степени, чем для указанных выше режимов.
[c.40]
Как найти среднее арифметическое число в Excel
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
- Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:h2 и нажимаем ВВОД.
- В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому.
 С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3). - Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:h2). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)
Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
Как мы узнали средневзвешенную цену?
Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Статистические функции Excel, которые необходимо знать
Функции категории Статистические предназначены в первую очередь для анализа диапазонов ячеек в Excel. С помощью данных функций Вы можете вычислить наибольшее, наименьшее или среднее значение, подсчитать количество ячеек, содержащих заданную информацию, и т.д.
Данная категория содержит более 100 самых различных функций Excel, большая часть из которых предназначена исключительно для статистических расчетов и обычному рядовому пользователю покажется темным лесом. Мы же в рамках этого урока рассмотрим самые полезные и распространенные функции данной категории.
В рамках данной статьи мы не будем затрагивать такие популярные статистические функции Excel, как СЧЕТ и СЧЕТЕСЛИ, для них подготовлен отдельный урок.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
НАИБОЛЬШИЙ()
Возвращает n-ое по величине значение из массива числовых данных. Например, на рисунке ниже мы нашли пятое по величине значение из списка.
Например, на рисунке ниже мы нашли пятое по величине значение из списка.
Чтобы убедиться в этом, можно отсортировать числа в порядке возрастания:
НАИМЕНЬШИЙ()
Возвращает n-ое наименьшее значение из массива числовых данных. Например, на рисунке ниже мы нашли четвертое наименьшее значение из списка.
Если отсортировать числа в порядке возрастания, то все станет гораздо очевидней:
МЕДИАНА()
Статистическая функция МЕДИАНА возвращает медиану из заданного массива числовых данных. Медианой называют число, которое является серединой числового множества. Если в списке нечетное количество значений, то функция возвращает то, что находится ровно по середине. Если же количество значений четное, то функция возвращает среднее для двух чисел.
Например, на рисунке ниже формула возвращает медиану для списка, состоящего из 14 чисел.
Если отсортировать значения в порядке возрастания, то все становится на много понятней:
МОДА()
Возвращает наиболее часто встречающееся значение в массиве числовых данных.
Если отсортировать числа в порядке возрастания, то все становится гораздо понятней:
Статистическая функция МОДА на данный момент устарела, точнее, устарела ее форма записи. Вместо нее теперь используется функция МОДА.ОДН. Форма записи МОДА также поддерживается в Excel для совместимости.
Как известно, категория Статистические в Excel содержит более 100 самых разноплановых функций. Но, как показывает практика, львиная доля этих функций практически не применяется, а особенно начинающими пользователями. В этом уроке мы постарались познакомить Вас только с самыми популярными статистическими функциями Excel, которые Вы рано или поздно сможете применить на практике. Надеюсь, что данный урок был для Вас полезен. Удачи Вам и успехов в изучении Excel.
Оцените качество статьи. Нам важно ваше мнение:
Проводится сплошное статистическое наблюдение за деятельностью субъектов малого и среднего предпринимательства за 2020 год во всех субъектах РФ
В первом полугодии 2021 года в соответствии с Федеральным законом от 24. 07.2007 № 209-ФЗ «О развитии малого и среднего предпринимательства в Российской Федерации» Федеральной службой государственной статистики (далее – Росстат) проводится сплошное статистическое наблюдение за деятельностью субъектов малого и среднего предпринимательства (далее — сплошное наблюдение) за 2020 год во всех субъектах Российской Федерации. Сплошное наблюдение – это экономическая перепись малого бизнеса, проводимая Росстатом один раз в пять лет.
07.2007 № 209-ФЗ «О развитии малого и среднего предпринимательства в Российской Федерации» Федеральной службой государственной статистики (далее – Росстат) проводится сплошное статистическое наблюдение за деятельностью субъектов малого и среднего предпринимательства (далее — сплошное наблюдение) за 2020 год во всех субъектах Российской Федерации. Сплошное наблюдение – это экономическая перепись малого бизнеса, проводимая Росстатом один раз в пять лет.
Экономическая перепись малого бизнеса позволит сформировать полную и объективную информационную основу для успешной реализации государственной политики по развитию малого и среднего предпринимательства (далее МСП) и выполнения задач, обозначенных Президентом Российской Федерации по повышению роли малого и среднего бизнеса в экономике России.
Кроме того, итоги сплошного наблюдения позволят сформировать информацию, необходимую для проведения оценки эффективности деятельности органов местного самоуправления и органов исполнительной власти субъектов Федерации в сфере развития МСП в соответствии с Указами Президента России.
Участие в экономической переписи малого бизнеса в соответствии с законодательством РФ является обязательным. На основе информации, полученной в ходе экономической переписи, будут приниматься государственные решения и программы поддержки.
Для участия в переписи необходимо до 1 апреля 2021 года заполнить анкету в электронном виде с помощью портала Госуслуг (при наличии подтвержденной учетной записи), интернет-сайта Росстата (при наличии электронной цифровой подписи), операторов электронного документооборота.
Анкеты разработаны отдельно для малых предприятий и индивидуальных предпринимателей, их заполнение не займет много времени. Росстат гарантирует полную конфиденциальность предоставленной информации – все полученные сведения будут использованы исключительно в обобщенном виде.
При возникновении вопросов можно обратиться в территориальный орган статистики Новосибирская по ссылке: https://novosibstat.gks.ru/folder/98192 и к помощи специалистов:
— по юридическим лицам: Горшкова Светлана Олеговна, 8 (383) 223-86-15;
— по индивидуальным предпринимателям: Донец Любовь Михайловна, тел. 8 (383) 223-75-20.
8 (383) 223-75-20.
Информация о проведении экономической переписи малого бизнеса уже опубликована на официальных сайтах: Правительство Новосибирской области: https://www.nso.ru/news/44267 , Министерство промышленности, торговли и развития предпринимательства Новосибирской области: https://minrpp.nso.ru/news/4334 , Малое и среднее предпринимательство: https://msp.nso.ru/news/2279 .
Сплошное статистическое наблюдение малого и среднего бизнеса за 2020 год
Весной 2021 года в соответствии с Федеральным Законом от 24 июля 2007 г. № 209-ФЗ «О развитии малого и среднего предпринимательства в Российской Федерации» Росстат проводит экономическую перепись малого бизнеса. Она проходит 1 раз в 5 лет, и участие в ней является обязательным для всех малых, микропредприятий и индивидуальных предпринимателей.
Анкеты разработаны отдельно для малых предприятий (в том числе и микропредприятий) – форма № МП-сп «Сведения об основных показателях деятельности малого предприятия за 2020 год» и отдельно для индивидуальных предпринимателей – форма № 1-предприниматель «Сведения о деятельности индивидуального предпринимателя за 2020 год».
В электронном виде анкету можно будет заполнить:
с 15 января по 1 апреля 2021 года
- на сайте Росстата (при наличии электронной подписи) – https://websbor.gks.ru/online/;
- у операторов электронного документооборота.
с 1 марта по 1 мая 2021 года
- на Едином портале государственных услуг (gosuslugi.ru)
(для юридических лиц – при наличии подтвержденной учетной записи и электронной подписи;
для индивидуальных предпринимателей – при наличии подтвержденной учетной записи).
Если анкета заполнена на бумажном бланке, то ее необходимо до 1 апреля 2021 года передать лично или отправить по почте в отдел государственной статистике по месту деятельности предприятия. Направляемая анкета должна быть заверена подписью и печатью юридического лица или индивидуального предпринимателя, а также содержать информацию об адресе электронной почты и номере телефона исполнителя.
Росстат гарантирует конфиденциальность предоставленной Вами информации. Все сведения будут использоваться в обобщенном виде.
Если у Вас возникнут вопросы или понадобится помощь специалиста, обратитесь по телефонам горячей линии 89885502770, 89188994530 или в районный (городской) отдел государственной статистики
Вся актуальная информация о проведении сплошного наблюдения размещена на тематической странице «Сплошное статистическое наблюдение малого и среднего бизнеса за 2020 год» на сайте Ростовстата: https://rostov.gks.ru/folder/97305
Характеристики выборки и генеральной совокупности
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использованию статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой. Число объектов N из генеральной совокупности и из выборки n называются соответственно объемом генеральной совокупности N и объемом выборки n.
Статистическое описание и вероятностные модели применяются к физическим, экономическим, социологическим, биологическим процессам, обладающим тем свойством, что хотя результат отдельного измерения физической величины X не может быть предсказан с достаточной точностью, но значение некоторой функции от множества результатов повторных измерений может быть предсказан с существенно лучшей точностью. Такая функция называется статистикой. Часто точность предсказания некоторой статистики возрастает с возрастанием объема выборки.
Наиболее известные статистики – относительная частота, выборочные средние, дисперсия. Когда возрастает объем выборки n, многие выборочные статистики сходятся по вероятности к соответствующим параметрам теоретического распределения величины X. Поэтому каждую выборку рассматривают как выборку из теоретически бесконечной генеральной совокупности, распределение признака в которой совпадает с теоретическим распределением вероятности случайной величины. Во многих случаях теоретическая генеральная совокупность есть идеализация действительной совокупности, из которой получена выборка.
Различные значения наблюдаемого признака, встречающегося в совокупности, называются вариантами. Частоты вариантов выражают доли (удельные веса) элементов совокупности с одинаковыми значениями признака. Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующим им частотами.
Значения, находящиеся в середине вариационного ряда, принято делить на собственно средние и структурные средние. Собственно среднее — это арифметическое среднее. Структурные средние — мода и медиана. Кроме того, чтобы охарактеризовать структуру вариационного ряда, используют квартили, квинтили, децили и процентили. Теперь обо всём по порядку.
Среднее арифметическое значение генеральной совокупности находят по формуле:
(1)
где
— число единиц генеральной совокупности,
— значение j-го наблюдения.
Если величина выборки X может принимать значения с вероятностями соответственно , то средним значением величины X для выборки (её математическим ожиданием E(x) ,будет
или
или же (2)
для негруппированных выборок и
(3)
для группированных выборок, где
— число единиц выборки,
— число классов,
— значение i-го класса,
— частота i-го класса.
Пример 1. В таблице даны значения средней температуры воздуха в населённом пункте N в 2014 году:
| Месяц | |
| 1 | -2,3 |
| 2 | -4,0 |
| 3 | 2,0 |
| 4 | 9,0 |
| 5 | 10,0 |
| 6 | 19,4 |
| 7 | 19,9 |
| 8 | 17,1 |
| 9 | 14,9 |
| 10 | 7,3 |
| 11 | 2,2 |
| 12 | -0,3 |
Найти среднюю температуру воздуха.
Решение. Найдём среднюю температуру воздуха как среднее значение для негруппированной выборки:
Пример 2. В таблице – данные о группировке сельских хозяйств по урожайности зерновых:
Урожайность зерновых в центнерах с га |
Число сельских хозяйств – абсолютное |
Удельный вес сельских хозяйств – в процентах |
до 5,0 |
4244 |
6,2 |
5,1-10,0 |
10446 |
15,2 |
10,1-15,0 |
18956 |
27,5 |
15,1-20,0 |
20207 |
29,3 |
20,1-25,0 |
8159 |
11,9 |
25,1-30,0 |
4145 |
6,0 |
30,1-35,0 |
1316 |
1,9 |
35,1-40,0 |
792 |
1,2 |
40,1-45,0 |
183 |
0,3 |
45,1-50,0 |
182 |
0,3 |
50,1-55,0 |
161 |
0,2 |
Всего |
68791 |
100,0 |
Найти среднюю урожайность зерновых.
Решение. Так как имеем только группированные данные и неизвестна средняя урожайность каждой группы, как приближенные значения к средней каждой группы примем центры интервалов:
Центры интервалов |
||
2,5 |
4222 |
10610,0 |
7,5 |
10446 |
78345,0 |
12,5 |
18956 |
236950,0 |
17,5 |
20207 |
363622,5 |
22,5 |
8159 |
183577,5 |
27,5 |
4145 |
113987,5 |
32,5 |
1316 |
42770,0 |
37,5 |
792 |
29700,0 |
42,5 |
183 |
7777,5 |
47,5 |
182 |
8645,0 |
52,5 |
161 |
8452,5 |
Всего |
68791 |
1074437,5 |
Найдём требуемую в условии задачи среднюю урожайности зерновых:
Итак, средняя урожайность по выборке составляет 15,6 центнеров с га.
Модой называют значение, которое в вариационном ряду встречается чаще других. Моду можно найти на гистограмме как самый высокий столбец.
Например, в выборке, значения которой 20, 50, 60, 70, 80, 20, 20, 75, 70, 20, 80, 20, 50, 60, модой является 20.
Медианой называют значение, которое находится в середине вариационного ряда. Первая половина элементов выборки меньше этого значения, а вторая половина — больше.
Если в выборке нечётное число элементов, то за медиану принимают собственно серединное значение. Например, в выборке, значения которой 14, 15, 18, 21, 27, медианой является 18.
Если в выборке чётное число элементов, то медиану находят, выбирая два значения, которые находятся в середине и вычисляя их среднее арифметическое. Например, есть выборка 11, 14, 15, 18, 21, 27. Медиану находят так: (15+18)/2 = 16,5.
По аналогии с медианой, которая делит значения выборки на две части, вводят понятие квартилей, которые делят вариационный ряд на 4 равные части.
Децили делят вариационный ряд уже на 10 одинаковых частей, а квинтили — на 5. Процентили делят вариационный ряд на 100 равных частей.
Дисперсией величины называется среднее значение квадрата отклонения величины от её среднего значения. Дисперсию генеральной совокупности рассчитывают по формуле:
(4)
Дисперсию выборки рассчитывают по формуле:
(5)
для негруппированных выборок и
(6)
для группированных выборок.
Пример 3. В таблице – данные о возрасте жителей административной территории Т в 2013 году. Не будем приводить эту таблицу из-за её громоздкости. Отметим лишь, что в таблице дана численность каждого из возрастов (по одному году, например, 33 года, 40 лет, 65 лет и т.д.) в группах от 0 лет по 94 года (включительно) и численность всей возрастной группы в интервале 95-99 лет, а также численность жителей старше 100 лет.
Требуется найти средний возраст жителей административной территории и дисперсию среднего возраста.
Решение. Найдём средний возраст. Так как данные в таблице являются данными генеральной совокупности, находим средний возраст генеральной совокупности:
В таблице – данные о числе жителей каждого возраста, исключение же – жители в возрасте 95-99 лет и старше 100 лет. Поэтому рассчитали центр интервала возрастной группы 95-99 лет: 97 лет и в расчётах использовали его.
Так как число жителей старше 100 лет относительно небольшое, чтобы упростить расчёты, нижнюю границу интервала приняли за значение признака.
Итак, средний возраст жителей административной территории Т – 38,2 года
Найдём теперь его дисперсию:
Пример 4. Найти дисперсию урожайности зерновых в сельских хозяйствах, используя данные примера 2.
Решение. Средняя урожайность по выборке составляет 15,6 центнеров с га. Чтобы найти дисперсию, создадим дополнительную таблицу.
Центры интервалов |
Число хозяйств |
|||
2,5 |
4244 |
-13,1 |
172,1 |
730412,3 |
7,5 |
10446 |
-8,1 |
65,9 |
688558,6 |
12,5 |
18956 |
-3,1 |
9,7 |
184391,3 |
17,5 |
20207 |
1,9 |
3,5 |
71505,7 |
22,5 |
8159 |
6,9 |
47,3 |
386328,5 |
27,5 |
4165 |
11,9 |
141,2 |
585113,6 |
32,5 |
1316 |
16,9 |
285,0 |
375024,0 |
37,5 |
792 |
21,9 |
478,8 |
379196,9 |
42,5 |
183 |
26,9 |
722,6 |
132234,9 |
47,5 |
182 |
31,9 |
1016,4 |
184986,0 |
52,5 |
161 |
36,9 |
1360,2 |
218995,1 |
Всего |
68791 |
— |
— |
393679,1 |
Теперь у нас есть всё, чтобы найти дисперсию:
Пример 5. Найти дисперсию температуры в населённом пункте N в 2009 году, используя данные примера 1.
Решение. Данная выборка – негруппированная, найдём дисперсию температуры для негруппированной выборки:
Стандартное отклонение равно положительному корню из дисперсии. Стандартное отклонение генеральной совокупности находят по формуле
(7)
Стандартное отклонение выборки находят по формуле
. (9)
для негруппированных выборок и
(10)
для группированных выборок.
Погрешности выборки характеризуют, насколько значительная ошибка допущена при замещении генеральной совокупности выборкой. Сколь бы тщательно ни подбирали выборку, параметр генеральной совокупности и оценка выборки Т всегда будут отличаться. Их разница является погрешность выборки .
Среднюю стандартную погрешность выборки находят по формуле
(11)
Средняя стандартная погрешность выборки характеризует рассеяние средних арифметических выборки по отношению к средним генеральной совокупности: чем больше погрешность, тем дальше среднее арифметическое выборки может находиться от среднего генеральной совокупности. В свою очередь, чем меньше погрешность, тем ближе к среднему генеральной совокупности находится среднее выборки. При увеличении числа наблюдений n стандартная погрешность уменьшается.
Стандартную погрешность называют также абсолютной погрешностью средней величины и нередко записывают .
Пример 6. Найти стандартную погрешность средней урожайности сельских хозяйств и интервал оценки, используя результаты примеров 2 и 4.
Решение. В примере 2 найдена средняя урожайность зерновых, равная 15,6 центнеров с га. В примере 4 найдена дисперсия урожайности, равная 57,2. Найдём стандартное отклонение урожайности:
Найдём теперь стандартную погрешность:
Интервал оценки средней урожайности:
Всё по теме «Математическая статистика»
средних статистических значений — среднее значение, мода, медиана
В статистике среднее значение определяется как число, которое измеряет центральную тенденцию данного набор чисел. Существует ряд различных средних значений, включая, помимо прочего, в: среднее значение, медиана, режим и диапазон.
Среднее
Среднее — это то, что большинство людей обычно называют средним.Среднее значение относится к число, которое вы получаете, когда суммируете заданный набор чисел, а затем делите эту сумму по общему количеству в наборе. Среднее также правильнее называть арифметическим. иметь в виду.
Дан набор из n элементов от 1 до n
Среднее значение находится путем сложения всех и и последующего деления на общее количество. номер, n
Это можно обобщить следующей формулой:
Средний пример проблем
Пример 1
Найдите среднее значение набора чисел ниже
Решение
Первый шаг — подсчитать, сколько чисел есть в наборе, который мы будем звоните n
Следующим шагом будет сложение всех чисел в наборе
.Последний шаг — найти фактическое среднее значение путем деления суммы на n
.Среднее также можно найти для сгруппированных данных, но прежде, чем мы рассмотрим этот пример, позвольте сначала определим частоту.
Частота в статистике означает то же самое, что и в повседневном употреблении этого слова. Частота элемент в наборе относится к тому, сколько таких элементов есть в наборе. В частота может быть от 0 до максимально возможного числа. Если вам говорят, что частота элемент a равен 3, это означает, что в наборе 3 a s.
Пример 2
Найдите среднее значение для набора возрастов в таблице ниже
.| Возраст (лет) | Частота |
|---|---|
| 10 | 0 |
| 11 | 8 |
| 12 | 3 |
| 13 | 2 |
| 14 | 7 |
Решение
Первый шаг — найти общее количество возрастов, которое мы назовем n .Поскольку подсчитывать все возрасты будет утомительно, мы можем найти n , сложив частоты:
Далее нам нужно найти сумму всех возрастов. Мы можем сделать это двумя способами: мы можем сложите каждый индивидуальный возраст, что будет долгим и утомительным процессом; или мы можем используйте частоту, чтобы ускорить работу.
Поскольку мы знаем, что частота показывает, сколько людей этого возраста есть, мы можем просто умножить каждый возраст на его частоту, а затем сложить все эти продукты.
Последний шаг — найти среднее значение путем деления суммы на n
.Среднее по совокупности и среднее по выборке
в Введение в раздел статистики, мы определили генеральную совокупность и выборку при этом образец является частью генеральной совокупности.
В статистике есть два вида средних значений: среднее значение по совокупности и среднее по выборке. Население среднее — истинное среднее для всей совокупности набора данных, в то время как выборочное среднее это среднее значение небольшой выборки населения. Эти разные средства появляются часто как по статистике, так и по вероятности, и их не следует путать друг с другом.
Среднее значение населения представлено греческой буквой μ (произносится как mu ), в то время как Среднее значение выборки представлено как x 12 (произносится как x столбец ).Общая количество элементов в популяции представлено числом N , в то время как количество Элементы в выборке представлены номерами n . Это приводит к корректировке формула, которую мы привели выше для вычисления среднего.
Среднее значение выборки обычно используется для оценки среднего значения совокупности, когда совокупность означает неизвестно.Это потому, что они имеют одинаковое ожидаемое значение.
Медиана
Медиана определяется как число в середине заданного набора чисел, расположенных в порядке возрастания. Когда дан набор чисел, медиана — это число, расположенное точно в середине списка, когда вы размещаете числа из от самого низкого до самого высокого. Медиана также является мерой среднего.На более высоком уровне В статистике медиана используется как мера дисперсии. Медиана важна, потому что он описывает поведение всего набора чисел.
Пример 3
Найдите медиану в наборе чисел, приведенном ниже
Решение
Из определения медианы мы можем сказать, что первый шаг — это переставить данный набор чисел в порядке возрастания, т.е.е. из от самого низкого до самого высокого
Затем мы проверяем набор, чтобы найти то число, которое находится точно посередине.
Давайте попробуем еще один пример, чтобы подчеркнуть кое-что интересное, что часто происходит, когда решение для медианы.
Пример 4
Найдите медиану данных
Решение
Как и в предыдущем примере, мы начинаем с изменения порядка данных, начиная с от наименьшего к наибольшему.
Затем мы проверяем данные, чтобы найти число, которое находится точно посередине.
Как видно из вышеизложенного, мы получаем два числа ( 4 и 5 ). посередине. Мы можем найти медиану, найдя среднее значение этих двух чисел. следующим образом:
Режим
Режим определяется как элемент, который наиболее часто встречается в данном наборе элементы.Используя определение частоты, данное выше, можно также определить режим как элемент с наибольшей частотой в заданном наборе данных.
Для данного набора данных может быть более одного режима. Пока эти элементы все имеют одинаковую частоту, и эта частота самая высокая, все они модальные элементы набора данных.
Пример 5
Найдите режим следующего набора данных.
Решение
Mode = 3 и 15
Режим для сгруппированных данных
Как мы видели в разделе о данных, сгруппированные данные делятся на классы. У нас есть определяется режим как элемент, который имеет самую высокую частоту в данном наборе данных. В сгруппированных данных мы можем найти два типа режима: модальный класс или класс с самая высокая частота и сама мода, которую мы вычисляем из модального класса, используя формула ниже.
где
- L — нижний предел модального класса
- f 1 — частота модального класса
- f 0 — частота класса перед модальным классом в таблица частот
- f 2 — частота класса после модального класса в таблица частот
- h — интервал классов модального класса
Пример 6
Найдите модальный класс и фактический режим набора данных ниже
| Число | Частота |
|---|---|
| 1–3 | 7 |
| 4–6 | 6 |
| 7–9 | 4 |
| 10–12 | 2 |
| 13–15 | 2 |
| 16–18 | 8 |
| 19 — 21 | 1 |
| 22–24 | 2 |
| 25–27 | 3 |
| 28 — 30 | 2 |
Решение
Модальный класс = 10 — 12
где
- L = 10
- f 1 = 9
- f 0 = 4
- f 2 = 2
- ч = 3
следовательно,
Решение вышеуказанного с помощью порядок операций:
Диапазон определяется как разница между наибольшим и наименьшим числом в заданный набор данных.
Пример 7
Найдите диапазон набора данных ниже
Решение
средних статистических значений — среднее значение, медиана и мода
Как я уже упоминал несколько раз, Data Science состоит из трех основных столпов: кодирования, статистики и бизнеса.Чтобы добиться успеха, вы должны хорошо разбираться во всех трех. В этой новой серии я хочу помочь вам изучить наиболее важные части Статистика . Это первый шаг — и в этом эпизоде мы познакомимся с самой основной статистической концепцией: статистическими средними величинами.
3 столпа: статистика, кодирование, бизнесСтатистика. Для чего это?
Несколько недель назад я наткнулся на отличную статью Натана Яу о визуализации данных. Он пишет о dataviz, но мне нравится, как он ставит важность статистики в начале статьи:
«Данные — это отображение реальной жизни. Это абстракция , и невозможно инкапсулировать все в электронную таблицу, что приводит к неопределенности в числах. Насколько хорошо образец представляет всю совокупность? Насколько вероятно, что набор данных представляет истину? Насколько вы доверяете цифрам? Статистика — это игра, в которой вы выясняете эти неопределенности и делаете оценочные суждения на основе ваших расчетов ».
Статистика — это «сжатие» большого количества информации в несколько чисел, чтобы наш мозг мог ее легче обрабатывать.
Например:
Более 500 миллионов человек проживают в 28 странах Европейского Союза. Если мы хотим сравнить зарплаты в разных странах, мы не будем сравнивать каждую из зарплат по отдельности. Это чепуха. Мы посчитаем и сравним средних зарплат вместо . Это полезная абстракция.
Однако, если вы будете следить за этой серией статей о статистике, вы также увидите, что описание всего набора данных только одним числом может часто приводить к неверным результатам.Взять среднюю зарплату — это круто, но это не позволяет нам увидеть, например, диапазон данных. В одной стране разница между самыми бедными и богатыми людьми может быть намного больше, чем в другой, и это тоже может быть важно знать.
Хороший специалист по данным всегда может найти те несколько чисел, которые описывают его данные самым простым, но все же наиболее значимым образом. Присоединяйтесь ко мне, и я покажу вам набор статистических инструментов, необходимых, чтобы быть лучшим в этом!
Средние статистические данные
Начнем с простого! Статистические средние.Это простая для понимания концепция, и она очень часто используется. Смысл использования средних значений — получить центральное значение набора данных. Конечно, есть несколько способов решить, какое значение является наиболее важным… Вот почему у нас есть более одного среднего типа.
Три наиболее распространенных статистических средних:
- Среднее значение
- Среднее значение
- Режим
Среднее значение
На обиходе слово « среднее » относится к значению, которое в статистике мы называем «средним арифметическим ». «При вычислении среднего арифметического мы берем набор, складываем все его элементы, затем делим полученное значение на количество элементов. Например, среднее арифметическое этого списка: [1,2,6,9] равно (1 + 2 + 6 + 9) /4=4,5 .
Это математика для средней школы, поэтому я предполагаю, что вы в любом случае очень хорошо знаете этот расчет.
Примечание: называть «среднее арифметическое» «средним» неправильно. Слово «средний» может относиться к любому из средних типов — мода и медиана также являются средними.Если вы слышите, что кто-то неправильно использует «среднее» в кафе, не исправляйте его … но на совещании по анализу данных (или особенно на собеседовании), пожалуйста, придерживайтесь «среднего арифметического».
Примечание 2: «Но, Томи, в заголовке этого раздела вы написали« Среднее », а не« Среднее арифметическое ». Что здесь происходит?» Ладно, ты прав. Мы не говорим «среднее арифметическое» на совещаниях по данным. Мы просто говорим «среднее арифметическое». Но мы думаем «среднее арифметическое». Единственная причина этого в том, что мы ленивы.И, честно говоря, это не лучшая практика, потому что есть и другие типы средств (например, среднее геометрическое или среднее гармоническое. Подробнее: здесь). Итог:
- «Среднее». Хорошо.
- «Среднее арифметическое». Идеально.
А вот и наиболее часто используемая метафора, показывающая важность медианы!
В комнате сидят десять рабочих. Их годовая зарплата:
| Рабочий № 1 | 15 €.000 |
| Рабочий № 2 | € 18.000 |
| Рабочий № 3 | € 18.000 |
| Рабочий № 4 | € 18.000 |
| Рабочий № 5 | € 18.000 |
| Рабочий № 6 | € 19.000 |
| Рабочий № 7 | € 20.000 |
| Рабочий № 8 | € 22.000 |
| Рабочий № 9 | € 22.000 |
| Рабочий № 10 | € 22 .000 |
Что такое центральное значение их зарплаты?
Давайте сначала попробуем среднее арифметическое! Результат — 19 200 евро.
Достаточно ли это «сжатое значение» информации в таблице выше? Можно ли сказать, что все эти 10 рабочих зарабатывают около 19 200 евро в год? Я бы сказал: да, 19 200 долларов — это не так уж и далеко от 15 000 или 22 000 евро.
Но вот беда: рабочий № 10 уходит домой, а вместо него входит генеральный директор компании. Она зарабатывает 100 евро.000 в год.
| Рабочий № 1 | € 15.000 |
| Рабочий № 2 | € 18.000 |
| Рабочий № 3 | € 18.000 |
| Рабочий № 4 | € 18.000 |
| Рабочий № 5 | € 18.000 |
| Рабочий № 6 | € 19.000 |
| Рабочий № 7 | € 20.000 |
| Рабочий № 8 | € 22.000 |
| Рабочий № 9 | € 22.000 |
| Генеральный директор | 100 000 евро |
Теперь среднее арифметическое изменилось на 27 000 евро. Достаточно ли это значение, чтобы описать среднюю зарплату? Ну не совсем. 9 из 10 человек зарабатывают менее 27 000 евро в год, поэтому утверждение о том, что 27 000 евро — это хорошая центральная величина, не является правильным.
Теперь генеральный директор уходит домой, и входит Билл Гейтс.
| Рабочий № 1 | € 15.000 |
| Рабочий № 2 | 18 евро.000 |
| Рабочий № 3 | € 18.000 |
| Рабочий № 4 | € 18.000 |
| Рабочий № 5 | € 18.000 |
| Рабочий № 6 | € 19.000 |
| Рабочий № 7 | € 20.000 |
| Рабочий № 8 | € 22.000 |
| Рабочий № 9 | € 22.000 |
| Билл Гейтс | 1.000.000.000 € |
Среднее арифметическое составляет € 100.017.000! Все в комнате зарабатывают 100 миллионов евро в год !? Даже не близко.
Когда есть экстремальные значения — или на языке статистики: выбросов — в наборе данных, среднее арифметическое больше не является достаточно хорошим представлением данных.
Вот тогда-то и вступает в игру медиана ! Вы можете получить медианное значение набора, просто расположив все его элементы от наименьшего к наибольшему, а затем взяв среднее значение. Вот пример:
sample_data = [9,11,5,7,1]
Какое среднее значение в этом списке? Сначала отсортируйте его в порядке возрастания: [1,5,7,9,11] .Затем возьмите среднее значение списка. В данном случае это 7 . Это медиана.
Примечание: среднее значение этого списка sample_data составляет 6,6 , что довольно близко к медиане.
Но что происходит, когда у нас есть список с четным числом элементов? Давайте еще раз посмотрим на наших сотрудников:
| Рабочий № 1 | € 15.000 |
| Рабочий № 2 | € 18.000 |
| Рабочий № 3 | 18.000 |
| Рабочий № 4 | € 18.000 |
| Рабочий № 5 | € 18.000 |
| Рабочий № 6 | € 19.000 |
| Рабочий № 7 | € 20.000 |
| Рабочий № 8 | 22000 евро |
| Рабочий № 9 | 22000 евро |
| Рабочий № 10 | 22000 евро |
К счастью, эти данные уже отсортированы, поэтому нам просто нужно выбрать среднее значение. .Это Рабочий № 5 или Рабочий № 6? Ответ: это среднее из двух, так что 18 500 евро. Общее правило заключается в том, что если у вас есть список с четным числом элементов, вы можете рассчитать медианное значение:
- сортировка списка
- с использованием среднего двух средних элементов.
Каково среднее значение, когда приходит генеральный директор? Точно так же: 18 500 евро.
А когда войдет Билл Гейтс? То же: 18 500 евро.
Теперь вы можете видеть, что в этих двух последних случаях медиана была лучшим центральным значением для всего набора данных, чем среднее арифметическое.
Примечание: даже если бы это было так, медиана сама по себе не является достаточно хорошим числом для описания набора данных с выбросами, главным образом потому, что, глядя на медианное значение, мы даже не подозреваем, что Билл Гейтс находится в комнате, тоже. А в реальных задачах науки о данных вы хотите знать о «Билле Гейтсе» в комнатах. Я вернусь к этой проблеме в следующих нескольких статьях.
Режим
Третий известный средний тип — Mode. Определение простое: режим — это элемент, который чаще всего встречается в списке.Теоретически это полезно, когда числовые значения в вашем наборе данных используются как категориальные значения. Но, честно говоря, мы его редко используем; и даже когда мы это делаем, мы на самом деле не называем это режимом. Мы просто говорим: самый частый элемент в списке.
Тем не менее, я хотел добавить его в список, потому что, вы знаете … если вас спросят во время собеседования, по крайней мере, теперь вы будете знать, что ответить. 🙂
Что использовать? Среднее, медиана или мода?
На этот вопрос нет однозначного ответа.Исходя из моего опыта, среднее значение и медиана будут использоваться одинаково часто, а режим почти никогда … Но когда использовать какой? Это действительно зависит от конкретного случая. Есть несколько практических правил, но, как я уже упоминал выше, я не вижу смысла использовать только одно число для описания набора данных … так что давайте вернемся к этому вопросу, когда мы узнаем больше о дисперсии, стандартном отклонении и т. Д. стандартная ошибка, про разные дистрибутивы и прочее — в следующих статьях!
А теперь…
Проверьте себя!
Хорошо, теперь, когда вы знаете все три известных типа средних — мода, медиана и среднее — пора проверить себя! Это задание фактически использовалось несколько лет назад на собеседованиях с младшими аналитиками данных …
Возьмем дистрибутив, который смещен вправо.Вот оно на графике:
В этом наборе данных есть элементы от 1 до 20. Каждый элемент встречается более одного раза. (Например, у нас есть около ста 1 значений, около ста сорока 2 значений и так далее … и в конце списка у нас есть около десяти 19 значений и одно или два 20 значений.)
Ось x отмечает различные элементы списка: числа от 1 до 20. Ось y показывает количество появлений каждого из этих элементов.
Задача:
Нарисуйте вертикальную линию на диаграмме, где вы оцениваете режим, среднее и медианное значения.В каком порядке значения слева направо?
Решение
Решение таково: режим <медиана <среднее значение.
Поскольку у вас нет данных, вы не можете рассчитать точные значения, чтобы получить этот ответ. Но вы можете сделать две вещи:
- Вы можете создать собственные образцы данных, которые приведут к аналогичной диаграмме со смещением вправо. Вот очень простой пример:
[1,1,2,2,2,3,3,4,5,6]. Если рассчитать режим (2), среднее значение (2.9) и медианы (2,5) для этого набора данных образца, вы уже будете знать ответ на исходный вопрос: режим <медиана <среднее. - Вы тоже можете придумать решение! Во-первых, попытайтесь выяснить взаимосвязь между модой и медианой. Представьте, что мы отрезаем правую часть оси абсцисс. Режим будет 4, и, поскольку эта часть диаграммы почти симметрична, медиана тоже будет около 4.
Вернем правую часть диаграммы.Теперь у нас есть много значений, превышающих 8, и эти значения увеличивают среднее значение — при этом режим не меняется. Таким образом, отношение между модой и медианой — это мода <медиана.
А как насчет медианы и среднего? Мы уже знаем, что среднее значение более чувствительно к экстремальным значениям. Таким образом, одно или два 20 значений в конце списка будут влиять на среднее значение, но, вероятно, не изменят значение медианы (как в примере Билла Гейтса). Это означает, что медиана <среднее. Итого: режим <медиана <среднее значение.
Заключение
3 наиболее распространенных статистических средних: среднее арифметическое, медиана и мода. Вы всегда будете использовать среднее и медианное значение, поэтому хорошо рассчитывать их!
Это был наш первый маленький шаг в открытии великой вселенной статистики для науки о данных! Следующий шаг — понять статистическую изменчивость.
Ура,
Томи Местер
Среднее значение, Медиана, Режим и Диапазон
Purplemath
Среднее, медиана и мода — это три вида «средних».В статистике есть много «средних», но я думаю, что это три наиболее распространенных, и, безусловно, те три, с которыми вы, скорее всего, столкнетесь на курсах, предшествующих статистике, если эта тема вообще возникнет.
«Среднее» — это «среднее», к которому вы привыкли, когда вы складываете все числа, а затем делите их на количество чисел. «Медиана» — это «среднее» значение в списке чисел. Чтобы найти медиану, ваши числа должны быть перечислены в числовом порядке от наименьшего к наибольшему, поэтому вам, возможно, придется переписать свой список, прежде чем вы сможете найти медиану.«Режим» — это значение, которое встречается чаще всего. Если ни один номер в списке не повторяется, то для списка нет режима.
MathHelp.com
«Диапазон» списка чисел — это просто разница между наибольшим и наименьшим значениями.
Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:
13, 18, 13, 14, 13, 16, 14, 21, 13
Среднее значение — это обычное среднее значение, поэтому я сложу, а затем разделю:
(13 + 18 + 13 + 14 + 13 + 16 + 14 + 21 + 13) ÷ 9 = 15
Обратите внимание, что в данном случае среднее значение не является значением из исходного списка.Это обычный результат. Вы не должны предполагать, что ваше среднее значение будет одним из ваших исходных чисел.
Медиана — это среднее значение, поэтому сначала мне придется переписать список в числовом порядке:
13, 13, 13, 13, 14, 14, 16, 18, 21
В списке девять чисел, поэтому средним будет (9 + 1) ÷ 2 = 10 ÷ 2 = 5-е число:
13, 13, 13, 13, 14, 14, 16, 18, 21
13, 13, 13, 13, 14, 14, 16, 18, 21
Итак, медиана равна 14.
Режим — это число, которое повторяется чаще, чем любое другое, поэтому 13 — это режим.
Наибольшее значение в списке — 21, наименьшее — 13, поэтому диапазон составляет 21–13 = 8.
означает: 15
медиана: 14
режим: 13
диапазон: 8
Примечание. Формула места для определения медианы: «([количество точек данных] + 1) ÷ 2», но вам необязательно использовать эту формулу.Вы можете просто рассчитывать с обоих концов списка, пока не встретитесь в середине, если хотите, особенно если ваш список короткий. В любом случае будет работать.
Партнер
Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:
1, 2, 4, 7
Среднее значение является обычным средним:
(1 + 2 + 4 + 7) ÷ 4 = 14 ÷ 4 = 3.5
Медиана — это среднее число. В этом примере числа уже перечислены в числовом порядке, поэтому мне не нужно переписывать список. Но нет «среднего» числа, потому что есть четное количество чисел. Из-за этого медиана списка будет средним (то есть обычным средним) двух средних значений в списке. Средние два числа — 2 и 4, поэтому:
.(2 + 4) ÷ 2 = 6 ÷ 2 = 3
Итак, медиана этого списка равна 3, а значение, которого нет в списке вообще.
Режим — это номер, который повторяется чаще всего, но все числа в этом списке появляются только один раз, поэтому режима нет.
Наибольшее значение в списке — 7, наименьшее — 1, а их разница — 6, поэтому диапазон равен 6.
среднее: 3,5
медиана: 3
режим: нет
диапазон: 6
Все значения в списке выше были целыми числами, но среднее значение в списке было десятичным.Получение десятичного значения для среднего (или для медианы, если у вас четное количество точек данных) совершенно нормально; не округляйте свои ответы, чтобы попытаться сопоставить формат других чисел.
Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:
8, 9, 10, 10, 10, 11, 11, 11, 12, 13
Среднее значение является обычным средним, поэтому я сложу и разделю:
(8 + 9 + 10 + 10 + 10 + 11 + 11 + 11 + 12 + 13) ÷ 10 = 105 ÷ 10 = 10.5
Медиана — это среднее значение. В списке из десяти значений это будет (10 + 1) ÷ 2 = 5,5-е значение; формула напоминает мне с этой «точкой пять», что мне нужно усреднить пятое и шестое числа, чтобы найти медиану. Пятое и шестое числа — это последние 10 и первые 11, поэтому:
(10 + 11) ÷ 2 = 21 ÷ 2 = 10,5
Режим — это номер, который повторяется чаще всего. В этом списке два значения, которые повторяются трижды; а именно 10 и 11, каждое повторяется трижды.
Наибольшее значение — 13, наименьшее — 8, поэтому диапазон 13-8 = 5.
среднее: 10,5
медиана: 10,5
режимы: 10 и 11
диапазон: 5
Как видите, два средних значения (в данном случае среднее и медиана) могут иметь одно и то же значение. Но это , а не , как обычно, и вы должны , а не этого ожидать.
Примечание. В зависимости от вашего текста или преподавателя, приведенный выше набор данных может рассматриваться как не имеющий режима, а не как имеющий два режима, потому что ни один отдельный номер не повторялся чаще, чем любой другой. Я видел книги, в которых говорится об этом; похоже, что нет единого мнения относительно «правильного» определения «режима» в приведенном выше случае. Поэтому, если вы не уверены, как вам следует ответить на «режим» в приведенном выше примере, спросите своего инструктора до следующего теста.
Единственная сложная часть нахождения среднего, медианного значения и моды — это точное определение того, какое «среднее» является каким. Просто запомните следующее:
означает: обычное значение «средний»
медиана: среднее значение
режим: чаще всего
(Выше я использовал термин «средний» довольно случайно. Техническое определение того, что мы обычно называем «средним», технически называется «средним арифметическим»: сложение значений и последующее деление на количество значений.Поскольку вам, вероятно, больше знакомо понятие «среднее», чем «мера центральной тенденции», я использовал более удобный термин.)
Учащийся получил следующие оценки на своих тестах: 87, 95, 76 и 88. Он хочет в целом 85 или выше. Какую минимальную оценку он должен получить за последний тест, чтобы достичь этого среднего?
Минимальная оценка — это то, что мне нужно найти.Чтобы найти среднее значение всех его оценок (известных и неизвестных), мне нужно сложить все оценки, а затем разделить их на количество оценок. Поскольку у меня еще нет оценок за последний тест, я буду использовать переменную для обозначения этого неизвестного значения: « x ». Затем вычисление для нахождения желаемого среднего:
(87 + 95 + 76 + 88 + x ) ÷ 5 = 85
Умножая на 5 и упрощая, получаем:
87 + 95 + 76 + 88 + x = 425
346 + х = 425
x = 79
Ему нужно набрать не менее 79 баллов на последнем тесте.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении медианы. Попробуйте выполнить указанное упражнение или введите свое собственное. Или попробуйте ввести любой список чисел, а затем выбрать вариант — среднее, медианное, режим и т. Д. — из того, что предлагает вам виджет. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)
URL: https://www.purplemath.com/modules/meanmode.htm
Калькулятор статистического среднего для среднего, медианы, режима и диапазона
Пример набора данных
Чтобы показать, как рассчитать среднее значение, медианное значение, режим и диапазон, я буду использовать следующий набор данных:
36, 3, 8 , 12, 15, 18, 22, 34, 8, 25, 17, 13, 23
Как рассчитать среднее значение?
Среднее значение — это среднее значение всех чисел в наборе данных.Чтобы вычислить среднее значение набора чисел, вы складываете все числа вместе, а затем делите эту сумму на количество элементов в наборе.
| Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 |
| Набор данных содержит 13 чисел |
| Среднее = (36 + 3 + 8 + 12 + 15 + 18 + 22 + 34 + 8 + 25 + 17 + 13 + 23) ÷ 13 |
| Среднее = 234 ÷ 13 |
| Среднее = 18 |
Как сделать Вы вычисляете медиану?
Медиана — это среднее число в наборе данных после сортировки набора данных от наименьшего к наибольшему.Чтобы вычислить медиану набора данных, вы подсчитываете количество элементов, а затем сортируете элементы от наименьшего к наибольшему. Затем, для нечетных элементов, вы добавляете 1 к количеству элементов, а затем делите на 2, чтобы получить позицию среднего числа. В нашем примере набора данных медиана — это 7-е число в отсортированном списке, то есть число 17.
| Набор данных с нечетными номерами: 36, 3, 8, 12, 15, 18, 22, 34, 8 , 25, 17, 13, 23 | |||||||||||||
| Количество элементов в наборе 13 | |||||||||||||
| Среднее положение = ((count + 1) ÷ 2) | |||||||||||||
| Среднее положение = ((13 + 1) ÷ 2 ) | |||||||||||||
| Среднее положение = (14 ÷ 2) | |||||||||||||
| Среднее положение = 7 | |||||||||||||
| Счетчик | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Набор данных | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 | 9008 8
| Медиана = 17 (7-е число в отсортированном наборе данных) | |||||||||||||
Обратите внимание, что для даже элементов вы найдете среднее из двух средних чисел.Первая средняя позиция будет равна количеству элементов, разделенных на 2 минус 1. Вторая средняя позиция будет первой средней позицией плюс 1. Затем вы складываете два средних числа вместе и делите на 2, чтобы найти среднее. Из нашего измененного набора данных примера это дает вам среднее значение 16, что является средним значением для 6-го и 7-го элементов (15 и 17).
| Набор данных с четными номерами: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13 | ||||||||||||
| Количество элементов в наборе: 12 | ||||||||||||
| 1-й средний Позиция = (count ÷ 2) — 1 | ||||||||||||
| 1-я средняя позиция = (12 ÷ 2) — 1 = 6 | ||||||||||||
| 1-я средняя позиция = 15 | ||||||||||||
| 2-я средняя позиция = 1-я средняя позиция + 1 | ||||||||||||
| 2-е среднее положение = 6 + 1 = 7 | ||||||||||||
| 2-е среднее число = 17 | ||||||||||||
| Среднее значение средних чисел = (15 + 17) ÷ 2 = 16 | ||||||||||||
| Счетчик | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Набор данных | 3 | 8 | 8 | 12 | 13 | 15 | 9 0438 17 | 18 | 22 | 25 | 34 | 36 |
| Медиана = 16 (среднее из 15 и 17) | ||||||||||||
Как рассчитать режим?
Режим — это номер в наборе данных, который наиболее часто повторяется в наборе.Чтобы найти режим, вы просто подсчитываете, сколько раз каждый уникальный номер появляется в наборе данных. Чаще всего появляется номер режима. В нашем примере набора данных чаще всего встречается номер 8. Следовательно, режим набора данных — 8.
| Пример набора данных: 36, 3, 8, 12, 15, 18, 22, 34 , 8, 25, 17, 13, 23 | |||||||||||||
| Сортированный набор данных | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 |
| Режим = 8 (8 встречается чаще всего) | |||||||||||||
Обратите внимание, что набор данных может иметь более 1 режима.Например, если вышеупомянутый набор данных включает еще 3, тогда набор будет иметь два режима: 3 и 8. Набор данных, имеющий два режима, называется бимодальным набором , тогда как набор данных, имеющий более двух режимов, называется называется мультимодальным набором .
Как рассчитать диапазон?
Диапазон — это разница между наибольшим числом в наборе и наименьшим числом в наборе. Чтобы найти диапазон, вы сортируете диапазон от наименьшего к наибольшему, чтобы определить минимальное и максимальное значения.Затем вы вычитаете минимальное значение из максимального, чтобы найти диапазон. В нашем примере установлено минимальное значение 3, а максимальное — 36, в результате получается диапазон 33 (36 — 3).
| Пример набора данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 | |||||||||||||
| Сортированный набор данных | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 |
| Диапазон = 33 (разница между максимумом 36 и минимумом 3) | |||||||||||||
Среднее статистическое — Среднее — Измерьте центральную тенденцию в статистике
Среднее статистическое дает важную информацию о имеющемся наборе данных, и как единое число может дать много информации об эксперименте и природе данные.
Примеры
Концепция статистического среднего имеет очень широкий диапазон применимости в статистике для ряда различных типов экспериментов.
Например, если простой маятник используется для измерения ускорения свободного падения, имеет смысл взять набор значений и затем усреднить окончательный результат. Это устраняет случайные ошибки в эксперименте и обычно дает более точное значение, чем проведенный один эксперимент.
Среднее статистическое значение также дает хорошее представление об интерпретации статистических данных.
Например, средняя продолжительность жизни в Японии выше, чем в Бразилии, что говорит о том, что в среднем люди в Японии, вероятно, будут жить дольше. По этому поводу можно сделать много жизнеспособных выводов, например, что это связано с лучшими медицинскими учреждениями в Японии, но правда в том, что мы не узнаем этого, пока не измерим.
Точно так же средний рост людей в России выше, чем в Китае, а это означает, что в среднем вы обнаружите, что русские выше китайцев.
Среднее статистическое значение является мерой центральной тенденции и дает нам представление о том, где, по-видимому, сгруппированы данные.
Например, средние оценки, полученные учащимися в тесте, необходимы для правильной оценки успеваемости учащегося в этом тесте. Если учащийся набрал низкий процент, но намного опережает средний, это означает, что тест сложный и, следовательно, его успеваемость хорошая, что просто процент не сможет сказать.
Различные статистические средства
Существуют различные виды статистических средств или мер центральной тенденции для точек данных.У каждого своя полезность. Среднее арифметическое, среднее геометрическое, медиана и мода являются одними из наиболее часто используемых мер статистического среднего. Они имеют смысл в разных ситуациях и должны использоваться в зависимости от распределения и характера данных.
Например, среднее арифметическое часто используется в научных экспериментах, среднее геометрическое используется в финансах для расчета сложных величин, медиана используется в качестве надежного среднего в случае искаженных данных с большим количеством выбросов, а режим часто используется в определение наиболее часто встречающихся данных, например, во время выборов.
Что в среднем? Введение в статистические меры Учебное пособие
Три способа сказать «средний»
В новостях
21 октября 2010 года не менее уважаемая газета, чем New York Times, опубликовала статью с заголовком: «Средний долг колледжа вырос до 24 000 долларов в 2009 году» (см. Статью). Ух ты! Студенты действительно ждут этого после окончания учебы, не так ли? Ну и дела — не могу поверить, средний долг составляет 24 тысячи долларов.Но ждать. Что означает «средний долг колледжа»? Является ли средний долг большинством студентов? Или что-то еще? Этот урок направлен на то, чтобы понять, что люди имеют в виду, когда говорят о «среднем».
Задний план
Когда вы узнали о среднем значении, медиане и моде, вы должны были хотя бы немного раньше знакомиться со средними значениями по алгебре в старших классах. Я думаю, вы раньше не видели этих концепций, не бойтесь! Мы их сейчас рассмотрим.
означает — это то, о чем мы обычно думаем, когда думаем о среднем значении.Среднее значение рассчитывается путем сложения всех значений в нашем наборе и последующего деления на количество добавленных значений.
Пример
Если мы хотим найти среднее значение чисел 3, 1, 2, 1, 8, мы сначала складываем их.
3 + 1 + 2 + 1 + 8 = 15
Затем мы делим на 5, поскольку это 5 чисел.
15/5 = 3.
Медиана
— это в некотором смысле среднее число.Чтобы найти медиану, мы сначала перечисляем числа в порядке возрастания, а затем выбираем средний элемент в списке.
Пример
Используя значения выше, сначала записываем их по порядку:
1 1 2 3 8
Теперь выбираем значение в середине списка:
2
Наконец, режим
— это просто самое распространенное значение в списке.Это можно найти путем подсчета количества раз, когда каждое значение появляется в списке, а затем выбора значения, которое появляется чаще всего.
Пример
Смотрим на наш старый список
1 1 2 3 8
мы выбираем наиболее часто встречающееся число, поэтому
1
потому что 1 появляется дважды, а остальные — только один раз.
Источник: www.nytimes.com 21 октября 2010 г. «Средний долг колледжа вырос до 24 000 долларов в 2009 г.»
Особые случаи
Две медианы?
Итак, чтобы найти медиану набора чисел, мы просто перечисляем числа по порядку и выбираем среднее.Но что нам делать в такой ситуации:
5 3 2 6 1 8 7 4
Перечисление их по порядку дает нам
1 2 3 4 5 6 7 8
Но здесь нет среднего числа, потому что список имеет четную длину.
Когда это происходит, мы выбираем два средних числа, в данном случае 4 и 5, и вычисляем их среднее значение. Итак (4 + 5) / 2 = 9/2 = 4,5.
Нет очевидного режима?
Иногда, когда имеется много точек данных и только несколько значений, которые они могут принимать, мы обнаруживаем, что ни одно значение не является наиболее распространенным.Часто существует связь между двумя или более значениями. Например, рассмотрим следующий список.
4 3 2 3 4 3 2 1 1 2 3 3 4 2 4 4 2
Каждое из значений 2, 3 и 4 появляется по пять раз каждое.
В таких случаях, когда действительно нет четкого выбора режима, будет достаточно одного из наиболее распространенных значений или ни одного, в зависимости от контекста. Если такие связи обнаруживаются в статистических исследованиях, они, скорее всего, будут отмечены и даже могут быть значительными.
Так что в среднем?
Назад к новостям
Возвращаясь к статье о студенческой задолженности, мы видим, что термин «средний» может иметь одно из нескольких значений. Когда печатается в подобных новостях, «средний» обычно означает «средний», и мы только что узнали, что «средний» — это неустойчивый показатель центральной тенденции. На среднее может повлиять присутствие выбросов в наборе данных, так что если бы пара школ сообщила об аномально высоком или аномально низком уровне студенческого долга, это повлияло бы на всю статистику студенческого долга.Давайте посмотрим, как это могло произойти.
Изготовленный пример
В следующем списке представлены фиктивные данные о десяти разных студенческих долгах. Студенты просто пронумерованы от 1 до 10.
1) 9 243
2) 9 343 9000 3
3) 10,554
4) 91 234
5) 96,115
6) 9 544
7) 8,332
8) 7 214
9) 7 895
10) 10 908
Среднее значение этих чисел получается путем сложения их всех и деления на 10, и оно составляет около 26 038 долларов.Но когда мы смотрим на список, мы не видим цифр, близких к 26 000 долларов. Вместо этого мы видим, что большинство долгов составляет от 7 000 до 10 000 долларов, а у двух крайне неудачливых студентов долги достигают 100 000 долларов.
Что это говорит нам?
Что мы можем извлечь из этого? Несмотря на то, что среднее из этих чисел действительно составляет 26000 долларов (и было бы технически правильным, если бы оно было опубликовано в газетной статье), мы видим, что 80% студентов в списке фактически должны менее половины этой суммы.
Лучшим показателем центральной тенденции в этом случае может быть выбор медианы. Переставляя числа от наименьшего к наибольшему, получаем
.1) 7 214
2) 7 895
3) 8,332
4) 9 243
5) 9 343
6) 9 544
7) 10,554
8) 10 908
9) 91 234
10) 96,115
Поскольку количество значений четное, мы выбираем два средних и берем их среднее значение: (9 243 доллара + 9 343 доллара) / 2 = 9 293 доллара.Эта величина кажется гораздо более точной характеристикой «среднего» студенческого долга.
Среднее значение, мода и медиана — Меры центральной тенденции — Когда использовать с различными типами переменных и асимметричных распределений
Введение
Мера центральной тенденции — это одно значение, которое пытается описать набор данных путем определения центрального положения в этом наборе данных. Таким образом, меры центральной тенденции иногда называют мерами центрального расположения.Они также относятся к категории сводной статистики. Среднее значение (часто называемое средним), скорее всего, является мерой центральной тенденции, с которой вы наиболее знакомы, но есть и другие, такие как медиана и мода.
Среднее значение, медиана и мода — все это действительные меры центральной тенденции, но в разных условиях некоторые меры центральной тенденции становятся более подходящими для использования, чем другие. В следующих разделах мы рассмотрим среднее значение, режим и медиану, а также узнаем, как их вычислить и при каких условиях они наиболее подходят для использования.
Среднее (арифметическое)
Среднее (или среднее) является наиболее популярным и хорошо известным показателем центральной тенденции. Его можно использовать как с дискретными, так и с непрерывными данными, хотя чаще всего он используется с непрерывными данными (типы данных см. В нашем руководстве по типам переменных). Среднее значение равно сумме всех значений в наборе данных, деленной на количество значений в наборе данных. Итак, если у нас есть \ (n \) значения в наборе данных, и они имеют значения \ (x_1, x_2, \)… \ (, x_n \), выборочное среднее, обычно обозначаемое \ (\ overline {x} \ ) (произносится как «x bar»), это:
$$ \ overline {x} = {{x_1 + x_2 + \ dots + x_n} \ over {n}} $$
Эта формула обычно записывается слегка иным образом, используя греческую заглавную букву \ (\ сумма \), произносимую «сигма», что означает «сумма… «:
$$ \ overline {x} = {{\ sum {x}} \ over {n}} $$
Возможно, вы заметили, что приведенная выше формула относится к среднему значению выборки. Итак, почему мы назвали его выборочным средним? Это связано с тем, что в статистике выборки и совокупности имеют очень разные значения, и эти различия очень важны, даже если в случае среднего они рассчитываются одинаково. Признать, что мы вычисляют среднее значение генеральной совокупности, а не среднее значение выборки, мы используем строчную греческую букву «му», обозначаемую как \ (\ mu \):
$$ \ mu = {{\ sum {x}} \ over {n }} $$
Среднее значение — это, по сути, модель вашего набора данных.Это наиболее распространенное значение. Однако вы заметите, что среднее значение не всегда является одним из фактических значений, которые вы наблюдали в своем наборе данных. Однако одним из его важных свойств является то, что он сводит к минимуму ошибку в предсказании любого значения в вашем наборе данных. То есть это значение, которое вызывает наименьшее количество ошибок среди всех других значений в наборе данных.
Важным свойством среднего является то, что оно включает каждое значение в вашем наборе данных как часть расчета.Кроме того, среднее значение является единственной мерой центральной тенденции, при которой сумма отклонений каждого значения от среднего всегда равна нулю.
Когда не использовать среднее значение
Среднее значение имеет один главный недостаток: оно особенно подвержено влиянию выбросов. Это значения, которые необычны по сравнению с остальным набором данных, будучи особенно маленькими или большими по числовому значению. Например, рассмотрим заработную плату персонала на заводе ниже:
| Персонал | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Заработная плата | 15k | 18k | 16k | 14k | 15k | 15k | 12k | 17k | 90k | 95k |
Средняя зарплата для этих десяти сотрудников составляет 30 долларов.7к. Однако проверка необработанных данных показывает, что это среднее значение может быть не лучшим способом точно отразить типичную зарплату рабочего, поскольку у большинства рабочих зарплата находится в диапазоне от 12 до 18 тысяч долларов. Среднее значение искажается двумя большими зарплатами. Поэтому в этой ситуации мы хотели бы лучше измерить центральную тенденцию. Как мы узнаем позже, взятие медианы было бы лучшим измерителем центральной тенденции в этой ситуации.
Другой случай, когда мы обычно предпочитаем медиану среднему (или режиму), — это когда наши данные искажены (т.е., частотное распределение для наших данных искажено). Если мы рассмотрим нормальное распределение — поскольку это наиболее часто оценивается в статистике — когда данные совершенно нормальные, среднее значение, медиана и мода идентичны. Более того, все они представляют собой наиболее типичное значение в наборе данных. Однако по мере того, как данные становятся искаженными, среднее значение теряет способность обеспечивать наилучшее центральное расположение данных, поскольку искаженные данные уводят его от типичного значения. Однако медиана лучше всего сохраняет это положение, и на нее не так сильно влияют искажения значений.Это объясняется более подробно в разделе «Перекошенное распределение» далее в этом руководстве.
Медиана
Медиана — это средний балл для набора данных, упорядоченных по порядку величины. На медианное значение меньше влияют выбросы и искаженные данные. Для вычисления медианы предположим, что у нас есть данные ниже:
Нам сначала нужно переставить эти данные по порядку величины (сначала наименьшие):
Наша средняя отметка — средняя отметка — в данном случае 56 (выделено на смелый).Это средний балл, потому что до него 5 баллов и 5 баллов после него. Это нормально работает, когда у вас нечетное количество баллов, но что происходит, когда у вас четное количество баллов? Что, если бы у вас было всего 10 баллов? Что ж, вам просто нужно взять два средних значения и усреднить результат. Итак, если мы посмотрим на пример ниже:
Мы снова переставим эти данные по порядку величины (сначала наименьшие):
Только теперь нам нужно взять 5-й и 6-й баллы в нашем наборе данных и усреднить их, чтобы получить медианное значение. из 55.5.
Mode
Этот режим является наиболее частой оценкой в нашем наборе данных. На гистограмме он представляет собой самый высокий столбец на гистограмме или гистограмме. Поэтому иногда вы можете рассматривать этот режим как самый популярный вариант. Пример режима представлен ниже:
Обычно режим используется для категориальных данных, где мы хотим знать, какая категория является наиболее распространенной, как показано ниже:
. транспортным средством в этом конкретном наборе данных является автобус.Однако одна из проблем с режимом заключается в том, что он не уникален, поэтому он оставляет нас с проблемами, когда у нас есть два или более значений, которые имеют самую высокую частоту, например, ниже:
Теперь мы застряли в том, какое Режим лучше всего описывает центральную тенденцию данных. Это особенно проблематично, когда у нас есть непрерывные данные, потому что у нас, скорее всего, не будет ни одного значения, которое встречается чаще, чем другое. Например, измерьте вес 30 человек (с точностью до 0.1 кг). Насколько вероятно, что мы найдем двух или более человек с точно одинаковым весом (например, 67,4 кг)? Ответ, вероятно, очень маловероятен — многие люди могут быть близки, но с такой небольшой выборкой (30 человек) и большим диапазоном возможных весов вы вряд ли найдете двух людей с точно таким же весом; то есть с точностью до 0,1 кг. Вот почему режим очень редко используется с непрерывными данными.
Другая проблема режима заключается в том, что он не дает нам очень точного измерения центральной тенденции, когда наиболее распространенная метка находится далеко от остальных данных в наборе данных, как показано на диаграмме ниже:
На приведенной выше диаграмме режим имеет значение 2.Однако мы ясно видим, что режим не является репрезентативным для данных, которые в основном сосредоточены в диапазоне значений от 20 до 30. Было бы неверно использовать этот режим для описания основной тенденции этого набора данных.
Асимметрия распределения, среднее и медиана
Мы часто проверяем, нормально ли распределены наши данные, потому что это общее предположение, лежащее в основе многих статистических тестов. Пример нормально распределенного набора данных представлен ниже:
Если у вас есть нормально распределенная выборка, вы можете законно использовать как среднее, так и медианное значение в качестве меры центральной тенденции.Фактически, в любом симметричном распределении среднее значение, медиана и мода равны. Однако в этой ситуации среднее значение широко предпочтительнее как лучший показатель центральной тенденции, потому что это показатель, который включает в себя все значения в наборе данных для его расчета, и любое изменение любого из баллов повлияет на значение иметь в виду. Это не относится к медиане или моде.
Однако, когда наши данные перекошены, например, как в приведенном ниже наборе данных со смещением вправо:
Мы обнаруживаем, что среднее значение перетаскивается в прямом направлении от перекоса.В этих ситуациях медиана обычно считается наилучшим представителем центрального расположения данных. Чем более искажено распределение, тем больше разница между медианной и средним значением и тем больше внимания следует уделять использованию медианы, а не среднего. Классическим примером приведенного выше распределения со смещением вправо является доход (зарплата), когда более высокие заработки дают ложное представление о типичном доходе, если выражаются как среднее, а не медианное значение.
Если вы имеете дело с нормальным распределением и тесты на нормальность показывают, что данные ненормальны, обычно вместо среднего используется медиана.Однако это скорее практическое правило, чем строгое руководство. Иногда исследователи хотят сообщить среднее значение асимметричного распределения, если медиана и среднее значение не сильно отличаются (субъективная оценка), и если это позволяет провести более легкое сравнение с предыдущими исследованиями.
Сводная информация о том, когда использовать среднее, медиану и моду
Воспользуйтесь следующей сводной таблицей, чтобы узнать, как лучше всего измерить центральную тенденцию по отношению к различным типам переменных.
| Тип переменной | Лучший показатель центральной тенденции |
| Номинальный | Режим |
| Порядковый | Медиана |
| Интервал / отношение (без перекоса) | Среднее значение |
| Интервал / отношение (перекос) | Медиана |
Для ответов на часто задаваемые вопросы о показателях центральной тенденции перейдите на следующую страницу.


 Примечания 1 На практике могут быть использованы различные определения среднего выходного качества … Словарь-справочник терминов нормативно-технической документации
Примечания 1 На практике могут быть использованы различные определения среднего выходного качества … Словарь-справочник терминов нормативно-технической документации 11 2000: Статистические методы. Статистическое управление качеством. Термины и определения оригинал документа: 3.4.3 (верхняя и нижняя) границы регулирования Граница на контрольной карте, выше которой верхняя граница,… … Словарь-справочник терминов нормативно-технической документации
11 2000: Статистические методы. Статистическое управление качеством. Термины и определения оригинал документа: 3.4.3 (верхняя и нижняя) границы регулирования Граница на контрольной карте, выше которой верхняя граница,… … Словарь-справочник терминов нормативно-технической документации с. точечное и интервальное.… … Российская социологическая энциклопедия
с. точечное и интервальное.… … Российская социологическая энциклопедия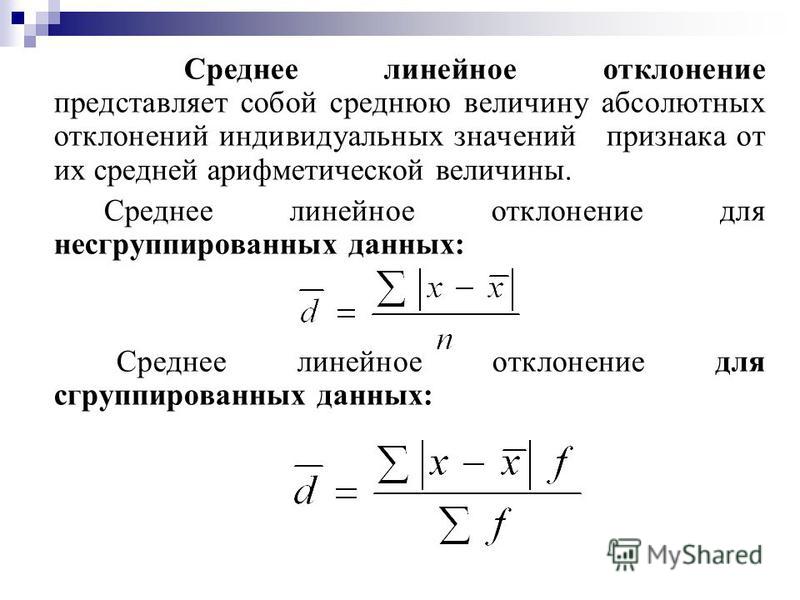 С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).