Способы нахождения определителя матрицы: теоремы и примеры нахождения определителей

Содержание

теоремы и примеры нахождения определителей

Содержание:

В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:

$$\left| \begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right|=a_{11} \cdot a_{22}-a_{12} \cdot a_{21}$$

Пример

Задание. Вычислить определитель второго порядка $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$

Решение. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=11 \cdot 5-(-2) \cdot 7=55+14=69$

Ответ. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=69$

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.

$$\left| \begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$

$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

Слишком сложно?

Методы вычисления определителей не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.

Решение. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$

$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$

Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:

$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$

Пример

Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ с помощью правила Саррюса.

Решение.

$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$

Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Пример

Задание. Разложив по первой строке, вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$

Решение. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right| \leftarrow=a_{11} \cdot A_{11}+a_{12} \cdot A_{12}+a_{13} \cdot A_{13}=$

$1 \cdot(-1)^{1+1} \cdot \left| \begin{array}{cc}{5} & {6} \\ {8} & {9}\end{array}\right|+2 \cdot(-1)^{1+2} \cdot \left| \begin{array}{cc}{4} & {6} \\ {7} & {9}\end{array}\right|+3 \cdot(-1)^{1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$

Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Пример

Задание. Вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$

Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.

$$\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4-4 \cdot 1} & {5-4 \cdot 2} & {6-4 \cdot 3} \\ {7-7 \cdot 1} & {8-7 \cdot 2} & {9-7 \cdot 3}\end{array}\right|=$$

$$=\left| \begin{array}{rrr}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {-6} & {-12}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {2 \cdot(-3)} & {2 \cdot(-6)}\end{array}\right|=0$$

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Пример

Задание. Вычислить определитель $\left| \begin{array}{llll}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|$ , разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:

$$\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=\left| \begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \\ {5-5} & {4-0} & {3-5} & {2-10} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|$$

Полученный определитель разложим по элементам первого столбца:

$$\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=0+0+1 \cdot(-1)^{3+1} \cdot \left| \begin{array}{rrr}{8} & {-2} & {-12} \\ {4} & {-2} & {-8} \\ {4} & {2} & {0}\end{array}\right|+0$$

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. {2+2} \cdot \left| \begin{array}{ll}{2} & {4} \\ {4} & {8}\end{array}\right|=$$

$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$

Ответ. $\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=0$

Замечание

Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель $\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_{11}$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:

$$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {2} & {-5} & {3} & {0} \\ {-1} & {4} & {2} & {-3}\end{array}\right|$$

Далее получим нули в первом столбце, кроме элемента $a_{11}$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

$$\Delta=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):

$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {3} & {-1} & {2} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:

$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {-10} & {-10} \\ {0} & {0} & {-1} & {-9}\end{array}\right|$$

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:

$$\Delta=-10 \left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {-1} & {-9}\end{array}\right|=$$

$$=-10 \cdot \left| \begin{array}{cccc}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {0} & {-8}\end{array}\right|=(-10) \cdot 1 \cdot(-1) \cdot 1 \cdot(-8)=-80$$

Ответ. $\Delta=-80$

Теорема Лапласа

Теорема

Пусть $\Delta$ — определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k \leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|$

Решение. Выберем в данном определителе пятого порядка две строки — вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

$$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=\left| \begin{array}{cc}{1} & {-1} \\ {4} & {-5}\end{array}\right| \cdot(-1)^{2+4+2+4} \cdot \left| \begin{array}{ccc}{2} & {0} & {5} \\ {3} & {1} & {1} \\ {1} & {2} & {1}\end{array}\right|+$$

$$+\left| \begin{array}{ll}{1} & {2} \\ {4} & {0}\end{array}\right| \cdot(-1)^{2+4+2+5} \cdot \left| \begin{array}{rrr}{2} & {0} & {4} \\ {3} & {1} & {0} \\ {1} & {2} & {-2}\end{array}\right|+\left| \begin{array}{cc}{-1} & {2} \\ {-5} & {0}\end{array}\right| \cdot(-1)^{2+4+5} \cdot \left| \begin{array}{ccc}{2} & {3} & {0} \\ {3} & {2} & {1} \\ {1} & {1} & {2}\end{array}\right|=$$

$$=-23+128+90=195$$

Ответ. $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$

Читать дальше: обратная матрица.

Определитель матрицы 2×2, 3×3, 4×4…

Определитель (детерминант) квадратной матрицы A — это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.

Обозначения

Пусть $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$

Свойства определителя

Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$
Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$
Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14
$\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (две первые строки пропорциональны)
или
$\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (два первых столбца пропорциональны)
Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$ $R_{1} +R_{2} =R_{3}$ или
$ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$ $C_{1}+C_{3}=C_{2}$
При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 16
В определителе
$\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, можно вынести множитель 3 из первой строки $(R_{1})$, тогда получаем:
$3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, затем выносим 2 из третьего столбца $(C_{3})$:
$6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$
При вычислении определителя можно прибавлять (отнимать) строки к другим строкам и столбцы к другим столбцам; определитель матрицы при этом не меняется.
Пример 17
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$
Пример 18
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$
При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент.
Пример 19
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$
Пример 20
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$
Определитель матрицы равен определителю транспонированной матрицы.
Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.

Минор матрицы

Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.

Пример 21
$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

Один из миноров матрицы A есть $\begin{vmatrix} 1 & 4\\ 5 & 3 \end{vmatrix}$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)

Другим минором является $\begin{vmatrix} 1 & 2 \\ 6 & 1 \end{vmatrix}$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)

Пример 22
$B=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix} $

Один из миноров матрицы B есть $ \begin{vmatrix} 1 & 7 & 9\\ 8 & 3 & 2\\ 8 & 1 & 4 \end{vmatrix}$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)

Другим минором является $\begin{vmatrix} 1 & 7 \\ 8 & 3 \end{vmatrix}$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)

Пусть $A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & .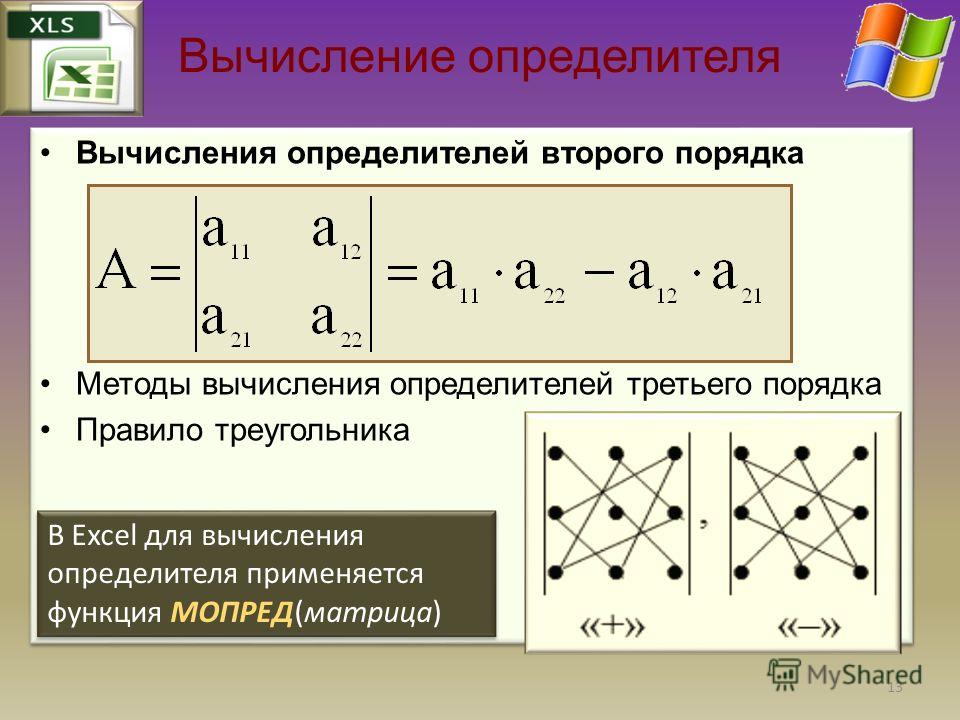 & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{pmatrix}$

Можно определить минор $\Delta_{i,j}$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_{i,j}$ квадратной матрицы A. Такой минор называется дополнительным.

Пример 23
$ A = \begin{pmatrix} 4 & 7\\ 2 & 9 \end{pmatrix}$

Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_{2,1}$.

Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем

Минор, дополнительный к элементу 2, есть $\Delta_{2,1} = 7$.

Пример 24
$B=\begin{pmatrix} 1 & 4 & 2\\ 5 & 3 & 7\\ 6 & 2 & 1\\ \end{pmatrix}$

Нужно найти минор, дополнительный к элементу 7. Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_{2,3}$.

Мы должны вычеркнуть строку 2 и столбец 3 из матрицы B, после чего мы получаем

Минор, дополнительный к элементу 7, — это $\Delta_{2,3}= \begin{vmatrix} 1 & 4\\ 6 & 2 \end{vmatrix}$

Пример 25
$C=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix}$

Нужно найти минор, дополнительный к элементу 5. Так как данный элемент находится в строке 1, столбце 2, видно, что это $a_{1,2}$.

Мы должны вычеркнуть строку 1 и столбец 2 из матрицы C, после чего мы получаем

Минор, дополнительный к элементу 5, — это $\Delta_{1,2}= \begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$

Алгебраическое дополнение элемента матрицы

Пусть $A=\begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . {7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ соответствует элементу $a_{2,5}$.

Порядок определителя

Порядок определителя матрицы равен числу ее строк и столбцов.

Пример 26
$\begin{vmatrix} 1 & 4\\ 6 & 2\\ \end{vmatrix}$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)

Пример 27
$\begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)

Вычисление определителя матрицы

Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений.

$\left| A\right| = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & .

{4}\cdot\Delta_{1,3}=$ $a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}+a_{1.3}\cdot\Delta_{1,3}$

$\Delta_{1,1}= \begin{vmatrix} a_{2,2} & a_{2,3}\\ a_{3,2} & a_{3,3} \end{vmatrix} = a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2}$

$\Delta_{1,2}= \begin{vmatrix} a_{2,1} & a_{2,3}\\ a_{3,1} & a_{3,3} \end{vmatrix} = a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1}$

$\Delta_{1,3}= \begin{vmatrix} a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{vmatrix} = a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1}$

$\left| A\right| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot(a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1,2}\cdot a_{2.1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$

Упростить получение последней формулы можно следующим образом.

Начнем с того, что перепишем первые две строки под определителем как показано ниже.

$\begin{vmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\ \color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\ \color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} a_{1,1} & \color{red}{a_{1,2}} & \color{red}{a_{1,3}}\\ a_{2,1} & a_{2,2} & \color{red}{a_{2,3}}\\ \end{array}$

Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты:

$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}}$

$\begin{vmatrix} \color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\ \color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\ \color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm} \begin{array}{ccc} \color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\ \color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\ \end{array}$

Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты:

$\color{blue}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$

Вычитая вторую сумму из первой, получаем формулу определителя:

$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$

Пример 30
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{pmatrix}$

$\begin{vmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 1 & 4 & 3\\ 2 & 1 & 5\\ \end{array}$

$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 -(3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $ 1 + 12 + 60 -(9 + 10 + 8)=73-27=46$

Пример 31
$A=\begin{pmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{pmatrix}$

$\begin{vmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 3 & 5 & 1\\ 1 & 4 & 2\\ \end{array} $

$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 -(1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$

Элементы матрицы могут быть обозначены буквами. {2} \end{vmatrix}= $

$\begin{vmatrix} a-c & b-c \\ (a-c)(a+c) & (b-c)(b+c) \end{vmatrix}=$ $(a-c)(b-c)\begin{vmatrix} 1 & 1\\ a+c & b+c \end{vmatrix}=$

$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$

Вычисление определителя матрицы 4×4

Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.

Но сначала надо использовать свойства определителей:

Проверим, не выполняется ли одно из условий того, что определитель равен 0.
Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.

В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение — это определитель матрицы 3×3, который считается по уже известной формуле.

Пример 33
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 0 & 0 & 0 & 0\\ 2 & 3 & 1 & 8 \end{vmatrix}$

Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.

Пример 34
$\begin{vmatrix} 1 & 3 & 1 & 2\\ 5 & 8 & 5 & 3\\ 0 & 4 & 0 & 0\\ 2 & 3 & 2 & 8 \end{vmatrix}$
Замечаем, что $C_{1}$ равно $C_{3}$, следовательно, определитель равен 0.

Пример 35
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 10 & 16 & 18 & 4\\ 2 & 3 & 1 & 8 \end{vmatrix}$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.

Пример 36
$\begin{vmatrix} \color{red}{4} & 3 & 2 & 2\\ 0 & 1 & -3 & 3\\ 0 & -1 & 3 & 3\\ 0 & 3 & 1 & 1 \end{vmatrix}$

Поскольку в столбце 1 только один элемент отличен от нуля, применяем общую формулу, используя этот столбец. Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.

=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot(-3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$

Пример 37
$\begin{vmatrix} 4 & 3 & 2 & 2\\ 0 & 1 & 0 & -2\\ 1 & -1 & 3 & 3\\ 2 & 3 & 1 & 1 \end{vmatrix}$

Чтобы изменить строку так, чтобы в ней стало больше нулей, нужно совершать операции со столбцами, и наоборот. Выбираем строку или столбец, содержащий элемент 1, поскольку из него можно получить любое число простым умножением. {2+2}\cdot \begin{vmatrix} 4 & 2 & 8\\ 1 & 3 & 1\\ 2 & 1 & 7 \end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$

Пример 38
$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 3 & 3 & 3 & 3\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

Можно вынести множитель 3 из строки 3:
$3\cdot \begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

Поскольку в строке 3 все элементы равны 1, легко обратить получить нули.

$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1 \end{vmatrix}$ $ \xlongequal{C_{1} — C_{4},C_{2}-C_{4},C_{3}-C_{4}} \begin{vmatrix} -1 & -4 & 1 & 2\\ 3 & 4 & 2 & -1\\ 0 & 0 & 0 & \color{red}{1}\\ -2 & 3 & 1 & 1 \end{vmatrix}$ $=1\cdot(-1)^{3+4}\cdot$ $=(-1)\cdot \begin{vmatrix} -1 & -4 & 1\\ 3 & 4 & 2 \\ -2 & 3 & 1\\ \end{vmatrix}$
$=-((-1)\cdot 4\cdot 1 +3 \cdot 3\cdot1 + (-2)\cdot (-4)\cdot 2$ $- (1\cdot 4\cdot (-2) + 2\cdot 3\cdot (-1) + 1\cdot (-4)\cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47$

Пример 39
$\begin{vmatrix} 2 & 5 & 1 & 4\\ 4 & 1 & 6 & 3\\ 5 & 3 & 7 & 2\\ 1 & 0 & 2 & 4 \end{vmatrix}$

Здесь мы можем использовать единицу из последней строки и обратить остальные элементы первого столбца в нули. {4+1}\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}$

Выносим общий множитель -1 из столбца 2 и еще раз -1 из столбца 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 — (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3\cdot 1)]=$ $-(180+12+117-24-195-54)=36$

Пример 40
$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$

Мы видим элемент 1 в столбце 3, так что мы можем обратить остальные элементы строки 2 в нули.

$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 & 1 & 2 & -1\\ 0 & 0 & \color{red}{1} & 0 \\ -1 & -4 & 3 & -2\\ -1 & -2 & 2 & -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 & 1 & -1\\ -1 & -4 & -2\\ -1 & -2 & -1 \end{vmatrix}$

Выносим общий множитель -1 из строки 2 и еще раз -1 из строки 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $-[2\cdot 4\cdot 1 + 1\cdot 2\cdot (-1)+ 1\cdot 1\cdot 2 — ((-1)\cdot 4\cdot 1 + 2\cdot 2\cdot 2 + 1\cdot 1\cdot 1)]=$ $-(8-2+2+4-8-1)=-3$

Пример 41
$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3\\ \end{vmatrix}$

Заметим, что все строки и все столбцы состоят из одних и тех же элементов, но в разном порядке. В таком случае мы можем сложить все строки или все столбцы.

$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{L_{1}+L_{2}+L_{3}+L_{4}} \begin{vmatrix} 10 & 10 & 10 & 10\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix} =$ $10\cdot \begin{vmatrix} 1 & 1 & 1 & 1\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{C_{1} — C_{4},C_{2}-C_{4},C_{3}-C_{4}}10\cdot \begin{vmatrix} 0 & 0 & 0 & \color{red}{1}\\ -1 & 1 & 2 & 2\\ 2 & 3 & 1 & 1\\ 1 & -1 & -2 & 3 \end{vmatrix}=$

$=10\cdot1\cdot(-1)^{1+4}$

$ = (-10)\cdot \begin{vmatrix} -1 & 1 & 2\\ 2 & 3 & 1\\ 1 & -1 & -2 \end{vmatrix}=$ $(-10)\cdot((-1)\cdot 3\cdot (-2) +2 \cdot (-1)\cdot2 + 1\cdot 1\cdot 1$ $-(2\cdot 3\cdot 1 + 1\cdot (-1)\cdot (-1) + (-2)\cdot1\cdot2))$ $= -10\cdot(6 -4 +1 -6 — 1 + 4) =0$

Вычисление определителей 2-го и 3-го порядков.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$

Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$

— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число

$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}. 2+5x+4=0:$

$D=25-16=9$

$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$

Ответ: $x_1=-4;\,\,\, x_2=-1.$

{jumi[*4]}

3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$

Решение.

$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$

$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$

Ответ: $0.$

3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$

Решение.

$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$

$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$

$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha). T=\det A.$

2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.

3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.

4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.

5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.

6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).

Примеры:

3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. $

Доказательство.

$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$

$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$

$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$

$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$

$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. {3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$

$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$

$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$

$=8a+15b+12c-19d.$

Ответ: $8a+15b+12c-19d.$

{jumi[*4]}

3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$

Решение.

Вычислим этот определитель с помощью приведения определителя к треугольному виду:

$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два

$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394. 2.$

Вычислить определители, используя подходящее разложение по строке или столбцу.

3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$

Ответ: $-14.$

3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$

Ответ: $4.$

3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$

Ответ: $2a-8b+c+5d.$

3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$

Ответ: $665.$

{jumi[*4]}

Математика онлайн

Решение математики онлайн

Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.

Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.

Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.

О калькуляторах

По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.

Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]

Преимущества

1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.

2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.

3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.

4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.

5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.

Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.

Определитель матрицы.

Навигация по странице:

Определитель матрицы или детерминант матрицы — это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.

Определение.

Определителем матрицы n×n будет число:

det(A) =	Σ	(-1)^{N(α₁,α₂,…,α_n)}·a_α₁1·a_α₂2·…·a_{α_nn}
	(α₁,α₂,…,α_n)

где (α₁,α₂,…,α_n) — перестановка чисел от 1 до n, N(α₁,α₂,…,α_n) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n.

Обозначение

Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).

Свойства определителя матрицы

Определитель матрицы с двумя равными строками (столбцами) равен нулю.
Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
При транспонировании значение определителя матрицы не меняется:
det(A) = det(A^T)
Определитель обратной матрицы:
det(A^-1) = det(A)^-1
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
Общий множитель в строке (столбце) можно выносить за знак определителя:
a₁₁a₁₂. ..a_1na₂₁a₂₂…a_2n….k·a_i1k·a_i2…k·a_in….a_n1a_n2…a_nn = k·a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….a_i1a_i2…a_in….a_n1a_n2…a_nn
Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:
B = k·A => det(B) = kⁿ·det(A)
где A матрица n×n, k — число.
Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
a₁₁a₁₂…a_1na₂₁a₂₂. ..a_2n….b_i1 + c_i1b_i2 + c_i2…b_in + c_in….a_n1a_n2…a_nn = a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….b_i1b_i2…b_in….a_n1a_n2…a_nn + a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….c_i1c_i2…c_in….a_n1a_n2…a_nn
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Определитель произведения матриц равен произведению определителей этих матриц:
det(A·B) = det(A)·det(B)

Методы вычисления определителя матрицы

Вычисление определителя матрицы 1×1

Правило:

Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:

∆ = |a₁₁| = a₁₁

Вычисление определителя матрицы 2×2

Правило:

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ =

= a₁₁·a₂₂ — a₁₂·a₂₁

Пример 1.

Найти определитель матрицы A

A =

	5	7
	-4	1

Решение:

det(A) =

= 5·1 — 7·(-4) = 5 + 28 = 33

Вычисление определителя матрицы 3×3

Правило треугольника для вычисления определителя матрицы 3-тего порядка

Правило:

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.


+		–

∆ =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ — a₁₃·a₂₂·a₃₁ — a₁₁·a₂₃·a₃₂ — a₁₂·a₂₁·a₃₃

Правило Саррюса для вычисления определителя матрицы 3-тего порядка

Правило:

∆ =

a₁₁	a₁₂	a₁₃	a₁₁	a₁₂
a₂₁	a₂₂	a₂₃	a₂₁	a₂₂
a₃₁	a₃₂	a₃₃	a₃₁	a₃₂

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ — a₁₃·a₂₂·a₃₁ — a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Пример 2.

Найти определитель матрицы A = 571-410203

Решение:

det(A) = 571-410203 = 5·1·3 + 7·0·2 + 1·(-4)·0 — 1·1·2 — 5·0·0 — 7·(-4)·3 = 15 + 0 + 0 — 2 — 0 + 84 = 97

Вычисление определителя матрицы произвольного размера

Разложение определителя по строке или столбцу

Правило:

Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	— разложение по i-той строке
	j = 1

Правило:

Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	— разложение по j-тому столбцу
	i = 1

При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример 3.

Найти определитель матрицы A

A =

2	4	1
0	2	1
2	1	1

Решение: Вычислим определитель матрицы разложив его по первому столбцу:

= 2·(-1)¹⁺¹· 2111 + 0·(-1)²⁺¹· 4111 + 2·(-1)³⁺¹· 4121 =

= 2·(2·1 — 1·1) + 2·(4·1 — 2·1) = 2·(2 — 1) + 2·(4 — 2) = 2·1 + 2·2 = 2 + 4 = 6

Пример 4.

Найти определитель матрицы A

A = 2411020021134023

Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):

det(A) = 2411020021134023 = — 0· 411113023 + 2· 211213423 — 0· 241213403 + 0· 241211402 =

= 2·(2·1·3 + 1·3·4 + 1·2·2 — 1·1·4 — 2·3·2 — 1·2·3) = 2·(6 +12 + 4 — 4 — 12 — 6) = 2·0 = 0

Приведение определителя к треугольному виду

Правило:

Используя свойства определителя для элементарных преобразований над строками и столбцами 8 — 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.

Пример 5.

Найти определитель матрицы A приведением его к треугольному виду

A = 2411021021134023

Решение:

det(A) = 2411021021134023

Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:

det(A) = 241102102 — 21 — 41 — 13 — 14 — 2·20 — 4·22 — 1·23 — 1·2 = 241102100-3020-801

Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):

det(A) = — 2141012000-3200-81

Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:

det(A) = — 214 + 1·81012 + 0·8000-3 + 2·8200-8 + 1·81 = — 211210120001320001 = -2·1·13·1 = -26

Теорема Лапласа

Теорема:

Пусть ∆ — определитель n-ого порядка.

Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

Присоединяйтесь

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]

Определитель 4 порядка. Калькулятор

Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.

Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.

Пример 1. Вычислить определитель методом разложения.

Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются — выделено красным)

В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников

Найденные значения подставляем в выходной детерминант

Результат легко проверить с помощью матричного калькулятора YukhymCALC . Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.

Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных

Результаты совпадают, следовательно вычисления проведены верно.

Пример 2. Вычислить определитель матрицы четвертого порядка.

Решение.

Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде

Далее переходим к отысканию определителей по правилу треугольников

Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем

Результат проверяем матричным калькулятором YukhymCALC . Правильность расчетов подтверждается следующим рисунком

Метод возведения определителя к треугольному виду

Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.

Пример 3. Найти определитель матрицы сведением к треугольному виду

Решение.

Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим

Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем

Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. В результате элементарных преобразований определитель примет вид

Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе

По свойству, определитель треугольной матрицы равен произведению диагональных элементов.

По желанию можно проверить результат матричным калькулятором.

В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.

Рассмотрим более сложный.

Пример 4.

Найти определитель матрицы 4-го порядка

Решение.

Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант

Для удобства вычислений, меняем третью строчку со вторым местами..

По свойству определителей любая замена строк местами ведет к изменению знака определителя. Учитываем это в некотором множителе k=-1.

От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим

Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.

Результат будет следующим

От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.

Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления

Проверка матричным калькулятором подтверждает правильность производимых вычислений.

Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений. В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.

Определители квадратных матриц

К оглавлению

I. Определитель матрицы первого порядка

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент а₁₁:

II. Определитель матрицы второго порядка

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Например, пусть

III. Определитель матрицы третьего порядка

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Пример. Вычислить определитель третьего порядка:

Решение.

Замечание. Вычисление определителей четвертого и более высокого порядка приводит к большим вычислениям, так как

· для нахождения определителя первого порядка мы находим одно слагаемое, состоящее из одного сомножителя,

· для нахождения определителя второго порядка нужно вычислить алгебраическую сумму из двух слагаемых, где каждое слагаемое состоит из произведения двух сомножителей,

· для нахождения определителя третьего порядка нужно вычислить алгебраическую сумму из шести слагаемых, где каждое слагаемое состоит из произведения трех сомножителей,

· для нахождения определителя четвертого порядка нужно вычислить алгебраическую сумму из двадцати четырех слагаемых, где каждое слагаемое состоит из произведения четырех сомножителей и т. д.

Определить количество слагаемых в алгебраической сумме, можно вычислив факториал:

Вычисление определителя четвертого порядка приводит к большим вычислениям. Поэтому в этом случае используют искусственные методы, о которых мы остановимся позже.

IV. Примеры для самостоятельного решения

А. Вычислить определитель второго порядка:

Б. Вычислить определитель третьего порядка:

В. Решить уравнение:

К оглавлению

Определитель квадратной матрицы

6.4 — Определитель квадратной матрицы

Определитель — это действительное число, связанное с каждой квадратной матрицей. я еще не нашел хорошего Английское определение того, что такое определитель. Все, что я могу найти, либо определяет его в терминах математическая формула или предлагает некоторые из ее применений. Есть даже определение определитель, определяющий его через самого себя.

Определитель квадратной матрицы A обозначается «det A» или | А |.Последнее выглядит как абсолютное значение A, но вам придется применять контекст. Если вертикальные линии расположены вокруг матрица, значит определитель.

Строка ниже показывает два способа записи определителя.

3	1	=	от		3	1
5	2	=	от		5	2

Определитель матрицы 2×2

Определитель матрицы 2×2 находится так же, как операция поворота.Это произведение элементов главной диагонали на минус произведение элементов вне главной диагонали.

Свойства определителей

Определитель — действительное число, а не матрица.
Определитель может быть отрицательным числом.
Он вообще не связан с абсолютным значением, за исключением того, что они оба используют вертикальные линии.
Определитель существует только для квадратных матриц (2×2, 3×3, … п×п). Определитель матрицы 1 × 1 — это единственное значение в определителе.
Матрица, обратная матрице, будет существовать, только если определитель не равен нулю.

Расширение с использованием миноров и кофакторов

Определение определителя, которое у нас есть, относится только к матрице 2×2. Существует ярлык для матрицу 3×3, но я твердо верю, что вы должны изучить способ, который будет работать для всех размеров, а не только частный случай для матрицы 3×3.

Метод называется расширением с использованием миноров и кофакторов. Прежде чем мы сможем использовать их, мы должны определить их.

Несовершеннолетние

Минором для любого элемента является определитель, который получается, когда строка и столбец тот элемент находится в удалении.

Обозначение M _ij используется для обозначения минора элемента в строке i и столбце j. Таким образом, M ₂₁ будет означать минор для элемента в строке 2, столбце 1.

Рассмотрим определитель 3×3, показанный ниже. Я включил заголовки, чтобы вы можете оставить строки и столбцы прямыми, но обычно вы не включаете те.Мы собираемся найти некоторых несовершеннолетних.

	С ₁	С ₂	С ₃
Р ₁	1	3	2
Р ₂	4	1	3
Р ₃	2	5	2

Поиск минора для R

₂ C ₁

Минор — это определитель, который остается при удалении строки и столбца элемента, для которого вы пытаетесь найти минор. Это означает, что мы должны удалить строку 2 и столбец 1, а затем найти определитель.

	С ₂	С ₃
Р ₁	3	2	= 3(2) — 5(2) = 6 — 10 = -4
Р ₃	5	2	= 3(2) — 5(2) = 6 — 10 = -4

Как видите, минор для строки 2 и столбца 1 равен M ₂₁ = -4.

Попробуем еще.

Поиск минора для R

₃ C ₂

На этот раз мы удалим строку 3 и столбец 2.

	С ₁	С ₃
Р ₁	1	2	= 1(3) — 4(2) = 3 — 8 = -5
Р ₂	4	3	= 1(3) — 4(2) = 3 — 8 = -5

Таким образом, минор для строки 3 столбца 2 равен M ₃₂ = -5.

Матрица миноров

Когда вы просто пытаетесь найти определитель матрицы, это излишество. Но есть одно чрезвычайно полезное приложение для него, и оно даст нам практику поиск несовершеннолетних.

Матрица миноров – это квадратная матрица, в которой каждый элемент является минором для числа в этой позиции.

Вот общая матрица миноров для определителя 3×3.

	С ₁	С ₂	С ₃
Р ₁	М ₁₁	М ₁₂	М ₁₃
Р ₂	М ₂₁	М ₂₂	М ₂₃
Р ₃	М ₃₁	М ₃₂	М ₃₃

Найдем матрицу миноров для нашего исходного определителя. Здесь определитель.

	С ₁	С ₂	С ₃
Р ₁	1	3	2
Р ₂	4	1	3
Р ₃	2	5	2

Вот работа по поиску каждого минора в матрице миноров.

	С ₁	С ₂	С ₃
Р ₁	= 2 — 15 = -13	= 8 — 6 = 2	= 20 — 2 = 18
Р ₂	= 6 — 10 = -4	= 2 — 4 = -2	= 5 — 6 = -1
Р ₃	= 9 — 2 = 7	= 3 — 8 = -5	= 1 — 12 = -11

Наконец, вот матрица миноров. Опять же, вам не нужно ставить ярлыки для строки и столбцов там, но это может вам помочь.

	С ₁	С ₂	С ₃
Р ₁	-13	2	18
Р ₂	-4	-2	-1
Р ₃	7	-5	-11

Кофакторы

Кофактор для любого элемента является либо минором, либо противоположным минору, в зависимости от того, где находится элемент в исходном определителе. Если ряд и столбец элемента в сумме должен быть четным числом, тогда кофактор — это то же, что минор. Если строка и столбец элемента в сумме являются нечетными число, то кофактор напротив минора.

Ооо, понял? Нечетные знаки меняются, четные — это один и тот же знак. Дежавю. Мы говорили об этом начиная с раздела 3.2 о многочленах.

Таблица знаков

Вместо того, чтобы складывать строку и столбец элемента, чтобы увидеть, нечетное или четное, многие люди предпочитают использовать диаграмму знаков.Знаковая диаграмма либо + или — для каждого элемента в матрице. Первый элемент (строка 1, столбец 1) всегда + и он чередуется оттуда.

Примечание: + не означает положительное значение, а — отрицательное. + означает то же самое знак как минор, а — означает противоположность минора. Подумайте об этом дополнение и вычитание, а не положительное или отрицательное.

Вот таблица знаков для определителя 2×2.

Вот таблица знаков для определителя 3×3.

	С ₁	С ₂	С ₃
Р ₁	+	—	+
Р ₂	—	+	—
Р ₃	+	—	+

Матрица кофакторов

Опять же, если все, что вы пытаетесь сделать, это найти определитель, вам не нужно пройти через эту большую работу.

Матрица кофакторов — это матрица, полученная заменой каждого элемента матрица своим кофактором. Это матрица миноров с измененными знаками на элементах в — позициях.

	С ₁	С ₂	С ₃
Р ₁	-13	-2	18
Р ₂	4	-2	1
Р ₃	7	5	-11

Расширение для поиска определителя

Вот шаги, которые нужно пройти, чтобы найти определитель.

Выберите любую строку или столбец в матрице. Неважно, какой ряд или какой столбец, который вы используете, ответ будет одинаковым для любой строки. Есть несколько рядов или столбцы, которые проще, чем другие, но мы вернемся к этому позже.
Умножить каждый элемент в этой строке или столбце по его кофактору и добавить. Результатом является определитель.

Расширим нашу матрицу по первой строке.

Из таблицы знаков мы видим, что 1 находится в положительном положении, 3 — в отрицательном. положение и 2 находится в положительном положении.Ставя + или — перед элемента, он заботится о корректировке знака при переходе от минора к кофактору.

+ 1	1	3	— 3	4	3	+ 2	4	1
+ 1	5	2	— 3	2	2	+ 2	2	5

= 1 (2 — 15) — 3 (8 — 6) + 2 (20 — 2)
= 1 (-13) — 3 (2) + 2 (18)
= -13 — 6 + 36
= 17

Определитель этой матрицы равен 17.

Как я уже говорил ранее, на самом деле не имеет значения, какую строку или столбец вы используете.

Попробуем еще раз, но на этот раз расширим второй столбец. Как усилие чтобы сэкономить время, миноры для этого столбца (из матрицы миноров) были равны 2, -2 и -5. Исходными элементами были 3, 1 и 5. 3 и 5 отрицательные. позиции.

определитель = — 3 ( 2 ) + 1 ( -2 ) — 5 ( -5 ) = -6 -2 + 25 = 17

Разверните любую строку или любой столбец, вы получите 17.

Но диагонали делать нельзя.Если попробуем главную диагональ, получится

+ 1 (-13) + 1 (-2) + 2 (-11) = -13 -2 — 22 = -37

Некоторые строки или столбцы лучше других

Выберите строку или столбец с наибольшим количеством нулей.
Поскольку каждый минор или кофактор умножается на элемент в матрице, выбор строки или столбца с большим количеством нулей означает, что вы будете умножение на много нулей. Умножение на ноль совсем не занимает много времени. На самом деле, если элемент равен нулю, вы не нужно найти даже несовершеннолетнего или кофактор.
Выберите строку или столбец с наибольшим количеством чисел (или переменных).
Элементы в строке или столбце, которые вы расширяете, не используются для поиска несовершеннолетние. Единственное место, где они умножаются, это один раз, в расширении. Если вы выберете строку или столбец с наименьшие числа, то каждый минор будет произведением больших чисел.
Если вы выберете строку или столбец, в которых есть переменные, вы только имеют умножить на переменные один раз, во время расширения.

Обратная матрица (повторно)

На этот раз рассмотрим наш первоначальный определитель в виде матрицы.

1	3	2
4	1	3
2	5	2

Найдите матрицу миноров , как описано выше.

-13	2	18
-4	-2	-1
7	-5	-11

Превратите его в матрицу кофакторов , изменив знаки на соответствующих элементы на основе таблицы знаков.

-13	-2	18
4	-2	1
7	5	-11

Найдите сопряженное путем транспонирования матрицы кофакторов.

Чтобы транспонировать матрицу, нужно поменять местами строки и столбцы. то есть ряды стать столбцами и столбцы становятся строками. Транспонирование матрицы можно найти с помощью TI-82. или калькулятор ТИ-83, введя название матрицы и выбрав Матрица, Math, а затем вариант 2, буква T с надстрочным индексом, например [A] ^T .

-13	4	7
-2	-2	5
18	1	-11

Наконец, разделите сопряженное к матрице на определитель матрицы.В этой задаче определитель равен 17, поэтому мы разделим каждый элемент на 17. Результирующая матрица — это , обратная исходной матрицы.

-13/17	17.04.	17/7
-2/17	-2/17	17/5
18/17	1/17	-11/17

Обратная матрица находится путем деления сопряженной матрицы матрица на определитель матрицы. Не пытайтесь это сделать на своем калькулятор, так как калькулятор не позволит вам разделить матрицу на скаляр. Вместо этого вам придется умножать на обратный определитель.

Если вы проверите это на своем калькуляторе, вы можете убедиться, что обратное на самом деле является присоединенным, деленным на определитель.

Поскольку обратное — это сопряженное, деленное на определителя, мы можем понять, почему обратное не существует, если определитель равен нулю. Это приведет к делению на ноль, который не определен.

Определители больших заказов

Найдем определитель системы 4×4.

	С ₁	С ₂	С ₃	С ₄
Р ₁	3	2	0	1
Р ₂	4	0	1	2
Р ₃	3	0	2	1
Р ₄	9	2	3	1

Выберите строку или столбец с наибольшим количеством нулей. В данном случае это второй столбец.

Для каждого элемента в исходной матрице его минор будет определителем 3×3. Нам придется расширить каждый из них на используя три определителя 2 × 2.

Вот почему мы хотим расширить второй столбец. Несовершеннолетние умножаются по их элементам, так что если элемент в исходной матрице равен 0, он не действительно имеет значение, что такое минор, и мы можем сэкономить много времени, не имея найти его. Во втором столбце вам не нужно будет находить двух несовершеннолетних потому что соответствующий им элемент во втором столбце равен нулю.

— 2	4	1	2	+ 0		— 0		+ 2	3	0	1
	3	2	1		?		?		4	1	2
	9	3	1						3	2	1

Мы могли бы заполнить эти два средних минора, но так как они умножаются на 0, на самом деле не имеет значения, что они собой представляют. На самом деле, вы могли бы так же легко пропустить их.

Теперь осталось найти два определителя 3×3.

В первом определителе 3×3, нулей нет, поэтому выберите строку или столбец с наибольшими числами. Тот будет столбец 1, поэтому расширьте его по первому столбцу.

Уведомление 4 находится в положительном положении. Таблицы знаков начинаются с каждого новый определитель. Положение числа в исходной матрице не имеет значение только его положение в текущей матрице.

4	1	2
3	2	1	=	+ 4	2	1	— 3	1	2	+ 9	1	2
9	3	1			3	1		3	1		2	1

= 4 (2 — 3) — 3 (1 — 6) + 9 (1 — 4) = 4 (-1) — 3 (-5) + 9 (-3) ) = -4 + 15 — 27 = -16

Рассмотрим другую матрицу 3×3. В этой строке стоит 0 1 и столбец 2. Любой из них был бы хорошим выбором для расширения, но поскольку в строке 1 числа немного больше, мы будем расширяться по первой строке.

3	0	1
4	1	2	=	+ 3	1	2	— 0	?	?	+ 1	4	1
3	2	1			2	1		?	?		3	2

= 3 (1 — 4) — 0 (не имеет значения) + 1 (8 — 3) = 3 (-3) + 1 (5) = -9 + 5 = -4

Когда пойдете искать определитель, помните, что там были элементы из исходная матрица 4 × 4, умноженная на каждый из этих определителей 3 × 3. Первый был -2, а второй +2.

Определитель = -2 (-16) + 2 (-4) = 32 — 8 = 24

Наихудший сценарий

Чтобы найти определитель 3×3 без нулей, нужно найти три определителя 2×2.

Чтобы найти определитель 4×4 без нулей, нужно найти четыре определителя 3×3, каждый из которых затем становится тремя определителями 2×2, всего получается двенадцать определителей 2×2.

Чтобы найти определитель 5×5 без нулей, нужно найти пять определителей 4×4, каждый из которых затем становится четырьмя определителями 3×3, каждый из которых становится тремя определителями 2×2 в сумме из шестидесяти определителей 2×2.

Использование калькулятора

После этой последней проблемы вы должны спросить себя, нет ли более легкого пути. Ну да, есть, если в определителе нет переменных. Вы можете воспользоваться калькулятором.

Обозначение, которое использует калькулятор TI-82 или TI-83, — это обозначение Det A. Итак, после входа в матрицу в одну из доступных матриц на калькуляторе, введите DET, выбрав Матрица, Математика и выбрав вариант 1. Затем введите имя матрицы, которую вы используете.

Вам не нужно использовать круглые скобки (если у вас нет TI-83), но вы можете, если вы хотите найти определитель произведения «det ([A]*[B])» или определитель транспонированного «det ([A] ^T )» как в отличие от транспонирования определителя «(det [A]) ^T» . Кстати, калькулятор не найдет транспонирование определителя, потому что в детерминант является скаляром (действительным числом) и калькулятор знает только, как найти транспонирование матрицы. Транспонирование скаляр это что скаляр.

Треугольные матрицы

Вам очень понравится находить определители этих матриц.

Верхняя треугольная матрица: Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо над ней. То есть все ненулевые значения находятся в верхнем треугольнике. Все, что ниже диагонали является нулем.
Нижняя треугольная матрица: Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо ниже нее.; То есть все ненулевые значения находятся в нижнем треугольнике. Все, что выше диагонали равен нулю.
Диагональная матрица: Матрица, в которой все ненулевые элементы находятся на главной диагонали. Все выключено главная диагональ равна нулю.

Определитель треугольной матрицы или диагональной матрицы равен произведению элементов главной диагонали.

Элементарные операции со строками

Можно было выполнить три элементарные операции со строками, которые вернули бы эквивалентная система.С определителями, поскольку определитель транспонирования совпадает с определителя матрицы, элементарные операции со строками можно применять и к столбцам.

Выполняя сокращение строк (используя поворот на 1, если хотите), вы можете поместить матрицу в треугольная форма. Как только он будет в треугольной форме, все, что вам нужно сделать, это умножить на элементы на главной диагонали и у вас есть определитель.

Рассмотрим каждую из трех элементарных операций над строками.

Если поменять местами две строки или два столбца в определителе, результирующий определитель будет отличаются только знаком.То есть, если вы поменяете местами строки или столбцы, результирующий определитель будет напротив исходного определителя.
Если вы умножаете строку или столбец на ненулевую константу, определитель умножается на эту та же ненулевая константа.
Если вы умножаете строку или столбец на ненулевую константу и добавляете ее к другой строке или столбцу, заменив эту строку или столбец, определитель не изменится.

Эта последняя операция эквивалентна повороту на единицу!

Предупреждение: если ваша точка опоры — это число, отличное от единицы, то вы умножаете каждую строку, которую вы изменение поворотным элементом.Итак, если вы повернетесь на 3 и поменяете две строки, то в результате определитель будет в 3*3=9 раз больше исходного определителя.

Пока вы вращаетесь на одной из них, все будет в порядке.

Вам не нужно помещать матрицу в редуцированную строчно-эшелонную форму или даже в строчно-эшелонную форму. Вы можете остановить сокращение в любой момент и расширить его, используя миноры и кофакторы. Что я предложить является сводным, где есть один, а затем расширить.

Определители, равные нулю

Определитель матрицы будет равен нулю, если

Вся строка равна нулю.
Две строки или столбца равны.
Строка или столбец постоянно кратны другой строке или столбцу.

Помните, что матрица обратима, неособа, тогда и только тогда, когда определитель не равен нулю. Итак, если определитель равен нулю, матрица вырожденная и не имеет обратной.

Определитель матрицы

Определитель — это специальное число , которое можно вычислить по матрице.

Матрица должна быть квадратной (одинаковое количество строк и столбцов), как эта:

Матрица
(у нее 2 строки и 2 столбца)

Вычислим определитель этой матрицы:

3×6 − 8×4
= 18 − 32
= −14

Полегче, а? Вот еще пример:

Пример:

Символ для определителя представляет собой две вертикальные линии с каждой стороны, например:

|Б| = 1×4 − 2×3
= 4 − 6
= −2

(Примечание: это тот же символ, что и абсолютное значение. )

Для чего это?

Определитель помогает нам найти обратную матрицу, рассказывает нам о матрице то, что полезно в системах линейных уравнений, исчислении и многом другом.

Вычисление определителя

Прежде всего, матрица должна быть в квадрате (т.е. иметь такое же количество строк, как и столбцов). Тогда это просто арифметика.

Для матрицы 2×2

Для матрицы 2×2 (2 строки и 2 столбца):

Определитель:

|А| = ad − bc
«Определитель A равен a, умноженному на d минус b, умноженному на c»

Легко вспомнить, когда думаешь о кресте:

Синий положительный (+реклама),
Красный отрицательный (−bc)

Пример: найти определитель

Отвечать:

|С|= 4×8 − 6×3

= 32 − 18

= 14

Для матрицы 3×3

Для матрицы 3×3 (3 строки и 3 столбца):

Определитель:

|А| = a(ei − fh) − b(di − fg) + c(dh − eg)
«Определитель A равен . .. и т. д.»

Может показаться сложным, но есть шаблон :

Чтобы вычислить определитель матрицы 3×3 :

Умножьте на на определитель матрицы 2×2 , который равен не в строке или столбце .
Аналогично для b и для c
Просуммируйте их, но помните минус перед b

В виде формулы (помните, что вертикальные черточки || означают «определяющее число») :

«Определитель числа A равен a, умноженному на определитель числа … и т. д.»

Пример:

|Д| = 6×(−2×7 − 5×8) − 1×(4×7 − 5×2) + 1×(4×8 − (−2×2))

= 6×(−54) − 1×(18) + 1×(36)

= −306

Для матриц 4×4 и выше

Шаблон продолжается для матриц 4×4:

плюс определитель матрицы, который равен , а не в в строке или столбце,
минус b , умноженный на определитель матрицы, который равен , а не в строке или столбце b ,
плюс c умноженный на определитель матрицы, который равен , а не в строке или столбце c ,
минус d , умноженный на определитель матрицы, который равен , а не в строке или столбце d ,

В виде формулы:

Обратите внимание на шаблон +-+- (+a. .. −b… +c… −d…). Это важно помнить.

Паттерн продолжается для матриц 5×5 и выше. Обычно для этого лучше всего использовать матричный калькулятор!

Не единственный способ

Этот метод расчета называется «расширение Лапласа», и мне он нравится, потому что его легко запомнить. Но есть и другие методы (чтобы вы знали).

Резюме

Для матрицы 2×2 определитель равен ad — bc
Для матрицы 3×3 умножьте a на определитель матрицы 2×2 , то есть , а не в строке или столбце a , аналогично для b и c , но помните, что b имеет отрицательный знак!
Шаблон продолжается для больших матриц: умножьте a на определитель матрицы , который равен , а не в строке или столбце a , продолжайте таким же образом по всей строке, но помните + — + — шаблон.

718 2390 2391 2392 8477 719 2393 8478 8479 8480

Определитель матрицы 3×3 (общий и сокращенный метод)

Как мы видели на прошлых уроках, чтобы определить, что является определителем матрицы, нам нужно вернуться к нашему определению матрицы. Помните, мы узнали, что матрица — это упорядоченный список чисел, заключенных в прямоугольные скобки.Этот список также можно назвать прямоугольным массивом, и он обеспечивает упорядоченный способ отображения «списка» информационных элементов. Если вы хотите рассмотреть определение матрицы более подробно, вы можете вернуться к нашему уроку о записи матриц.

Матрица описывает линейное преобразование или линейную карту, которая является своего рода транскрипцией между двумя типами алгебраических структур, таких как векторные поля. Таким образом, мы можем решать системы линейных уравнений, представляя линейную систему в виде матрицы.Матричное представление линейной системы выполняется с использованием всех переменных коэффициентов, найденных в системе, и их использования в качестве записей элементов для построения прямоугольного массива расширенной матрицы соответствующего размера. В такой матрице результаты каждого уравнения системы будут располагаться справа от вертикальной линии, представляющей знак равенства.

Зная это, этот урок будет посвящен процессу вычисления определителя матрицы 3×3 и двум возможным методам его использования.

Что такое определитель матрицы

Используя знание того, что матрица представляет собой массив, содержащий информацию о линейном преобразовании, и что этот массив может быть согласован с коэффициентами каждой переменной в системе уравнений, мы можем описать функцию определителя: определитель будет масштабироваться линейное преобразование из матрицы, это позволит нам получить обратную матрицу (если она есть) и поможет в решении систем линейных уравнений, создав условия, в которых мы можем ожидать определенных результатов или характеристик от система (в зависимости от определителя и типа линейной системы мы можем знать, можем ли мы ожидать уникальное решение, более одного решения или вообще ни одного решения для системы).

Но есть условие для получения определителя матрицы, матрица должна быть квадратной, чтобы его вычислить. Следовательно, упрощенное определение состоит в том, что определитель — это значение, которое можно вычислить из квадратной матрицы, чтобы облегчить решение систем линейных уравнений, связанных с такой матрицей. Определитель неквадратной матрицы не существует, математически определяются только определители квадратных матриц.

Определитель матрицы может быть обозначен просто как det A, det(A) или |A|.Это последнее обозначение исходит из обозначения, которое мы непосредственно применяем к матрице, определитель которой мы получаем. Другими словами, мы обычно записываем матрицы и их определители очень похожим образом:

Уравнение 1: Разница между записью матрицы и определителя

Обратите внимание на разницу, матрица записана в прямоугольных скобках, а определитель матрицы имеет свои компоненты, окруженные двумя прямыми линиями.

Сегодняшний урок будет посвящен процессу вычисления определителя матрицы 3×3 с использованием свойств определителя матрицы, которые были кратко рассмотрены на прошлых уроках.Помните, что мы полностью рассмотрим эту тему в следующем уроке под названием: свойства определителей. Тем не менее, важно помнить об этих свойствах при выполнении расчетов упражнений в последнем разделе этого урока.

Как найти определитель матрицы 3×3

Существует два метода нахождения определителя матрицы 3×3: общий метод и сокращенный метод. Как бы ни звучали названия каждого из них, общий метод является «формальным» методом для математического использования, следуя всем правилам и производя некоторые вычисления детерминанта второстепенной матрицы по пути, чтобы найти окончательное решение.В то время как сокращенный метод — это скорее хитрый трюк, который мы можем использовать для упрощения вычислений, по-прежнему стараясь не забывать числа, порядок их умножения и некоторые перестановки элементов в матрице.

После того, как вы познакомитесь с обоими методами нахождения определителя матрицы 3×3, вы всегда сможете выбрать тот, который подходит вам лучше всего, и использовать его в своих исследованиях, но помните, что важно знать оба метода на случай, если вас когда-нибудь спросят чтобы сравнить результаты от них.

Итак, давайте без дальнейших промедлений определим определитель матрицы 3×3 A, как показано ниже, чтобы мы могли наблюдать, как его можно вычислить обоими методами:

Уравнение 2: Определитель матрицы A

Общий метод
Общий метод получения определителя матрицы 3×3 состоит в разбиении матрицы на вторичные матрицы меньших размеров в процессе, называемом «расширение первой строки». Что делает этот процесс, так это использует элементы из первой строки матрицы 3×3 и использует их как множители в сумме умножений, где перераспределяется большая матрица.
Давайте шаг за шагом рассмотрим, как вычислить определитель матрицы 3×3:
1. Сначала вы берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которым принадлежит ваш первый выбранный элемент.
  Взяв за основу определитель матрицы 3×3, показанный в уравнении 2, мы строим первую часть результата этой операции, выбирая первый элемент первой строки и столбца (который является константой «а»), а затем умножаем его на матрица, составленная из четырех элементов, не принадлежащих ни к одной из строк столбца, в котором находится «а».Умножьте «а» на полученную вторичную матрицу 2×2, и это будет первый член решения.
2. Второй член начинается со второго элемента верхней строки (константа «b»), сопровождаемого отрицательным знаком, который теперь будет умножать вторичную матрицу 2×2, которая снова получается из четырех элементов в матрице, которые не принадлежат либо в столбец строки, в которой находится «b».
3. Повторяем первый шаг, но теперь уже с третьим элементом из верхней строки матрицы.
Итак, определитель формулы матрицы 3×3 для общего метода:
Уравнение 3: Уравнение для определителя матрицы 3×3 с помощью общего метода
Процесс называется расширением первой строки, потому что, как вы можете видеть в уравнении 3, все элементы из первой строки исходной матрицы 3×3 остаются основными факторами в расширении, для которого необходимо найти решение. Все матрицы 2×2 в расширении — это то, что мы называем «вторичными матрицами», и их можно легко решить, используя уравнение, изученное на уроке по матрице 2×2.
Итак, принимая во внимание формулу определителя квадратной матрицы размерностью 2×2, мы видим, что уравнение 3 дает:
Уравнение 4: Уравнение для определителя матрицы 3×3 с помощью общего метода (часть 2)
В этот момент вы, возможно, заметили, что нахождение определителя матрицы больше 2×2 становится долгим испытанием, но логика процесса остается той же, и поэтому сложность аналогична, единственный ключевой момент — отслеживать операции вы работаете, даже больше с еще большими матрицами, чем 3×3.
Сокращенный метод
Сокращенный метод определения определителя матрицы 3×3 — это хитрый прием, облегчающий вычисление определителя большой матрицы путем непосредственного умножения и сложения (или вычитания) всех элементов необходимым образом без необходимости пройти через матричное разложение первой строки и без вычисления определителей вторичных матриц.
Весь процесс вычисления определителя матрицы 3×3 с использованием сокращенного метода можно увидеть в приведенном ниже уравнении:
Уравнение 5. Упрощенный метод получения определителя матрицы 3×3.
Теперь давайте объясним метод быстрого доступа:
При вычислении определителя матрицы nxn (в данном случае матрицы 3×3), как показано выше, обратите внимание, что мы сначала переписываем матрицу, сопровождаемую повторением двух ее первых столбцов, теперь записанных снаружи справа.
Тогда значение определителя будет результатом вычитания между сложением произведений всех умножений вниз-вправо и умножений вниз-влево. Проще говоря, будет в общей сложности три полных диагонали, идущих из верхнего левого угла в нижний правый, и еще один набор из трех полных диагоналей, идущих из верхнего правого угла в нижний левый.
Мы перемножим элементы каждой диагонали вместе, а затем сложим их с результатами, полученными от других диагоналей.Есть кое-что, что нужно иметь в виду, все умножения диагоналей, идущие сверху слева вниз справа, имеют внутренний положительный знак, в то время как все умножения диагоналей, идущие сверху справа вниз, имеют внутренний отрицательный знак, умноженный на них к ним, и поэтому при сложении результатов всех умножений получится вычитание, подобное показанному в уравнении 5.
Хотя этот метод проще в выполнении, чем общий метод, его немного сложно объяснить из-за того, что все умножения и сложения выполняются одновременно, поэтому мы рекомендуем вам использовать уравнение 5 в качестве руководства и уделять пристальное внимание к видео, где демонстрируются примеры этого метода.
В последнем разделе этого урока мы рассмотрим набор из трех различных матриц 3×3 и их определители. Мы рекомендуем вам сравнить процессы для обоих методов, чтобы лучше понять их.

Определитель большой матрицы

Процесс вычисления определителя матрицы большего размера, чем 3×3, следует той же логике, что мы видели до сих пор. Используя общий метод на матрице A 4×4, где ее первая (верхняя) строка соответствует элементам a, b, c и d, мы вычисляем определитель матрицы следующим образом:

Уравнение 6: Определитель матрицы 4×4

Мы еще раз расширили определитель по его первой строке и получили вторичные матрицы, которые в данном случае являются матрицами 3×3, каждую из которых можно разложить и разбить на матрицы 2×2.Шаблон в процессе повторяется, вы можете продолжать работать таким же образом с еще большими квадратными матрицами, и он всегда будет работать, но если вам больше нравится метод быстрого доступа, то вас ждет удовольствие, поскольку метод работает точно так же. как и в случае с матрицами 3×3, это просто увеличивает количество элементов, с которыми вы работаете, но логика и перестановка точно такие же (умножение из верхнего левого угла в нижний правый имеет положительный знак, умножение из верхнего правого угла в нижний левый имеет положительный знак). внутренний отрицательный знак).

Вы рады видеть, как сокращенный метод работает на больших матрицах? Мы рекомендуем вам попробовать это самостоятельно, чтобы вы могли увидеть весь процесс. Вы всегда можете вернуться и решить ту же матрицу, используя общий метод, и доказать, что ваш результат верен.

Упражнения на вычисление определителя матрицы 3×3

В следующих упражнениях мы решим определитель предоставленной в каждом случае матрицы 3×3 соответствующим методом, а в конце сравним полученные результаты.

Обратите внимание, что матрицы A, B и C, представленные в обоих разделах упражнений выше, абсолютно одинаковы. Это было сделано специально, чтобы вы могли сравнить результаты обоих методов и посмотреть, как они дают одинаковые значения.

В завершение этого урока мы хотели бы порекомендовать вам эту статью о том, как вычислять определители, и еще одну о определителе квадратной матрицы, где вы найдете намного больше примеров, чем те, что приведены здесь.

Мы надеемся, что этот урок был интересным и полезным, увидимся в следующем!

Определитель матрицы – объяснение и примеры

Определитель матрицы является скалярной величиной огромной важности.С помощью определителя матриц мы можем найти полезную информацию о линейных системах, решить линейные системы, найти , обратную матрицы, и использовать ее в исчислении. Давайте взглянем на определение определителя:

Определитель матрицы — это скалярная величина, которая получается в результате определенных операций с элементами матрицы.

В этом уроке мы рассмотрим определитель, как найти определитель, формулу определителя матриц $2\times 2$ и $3\times 3$, а также примеры, поясняющие наше понимание определителей . Давайте начнем!

Что такое определитель матрицы?

Определитель матрицы — это одно постоянное значение (или скалярное значение), которое сообщает нам определенные сведения о матрице. Значение определителя получается в результате определенных операций, которые мы делаем с элементами матрицы.

Существует $ 3 $ способов, которыми мы обозначаем определитель матрицы . Посмотрите на картинку ниже:

С левой стороны находится Матрица $ A $.Вот так мы пишем матрицу.

В правой части $ 3 $ обозначения для определителей матриц. Мы можем обозначить определитель матрицы $A$, написав $det(A)$, $| А | $, или поместив все элементы матрицы внутрь двух вертикальных полос (как показано). Все эти обозначения $ 3 $ обозначают определитель матрицы .

Как найти определитель матрицы

Так как же найти определитель матрицы?

Прежде всего, мы можем вычислить определитель только для квадратных матриц!

Для неквадратных матриц нет определителя.

Теперь есть формула (алгоритм) для нахождения определителя любой квадратной матрицы. Это выходит за рамки данного урока. Вместо этого мы рассмотрим нахождение определителей матриц $ 2 \times 2 $ и матриц $ 3 \ x 3 $. Формулу можно расширить, чтобы найти определитель матрицы $ 4 \× 4 $, но это слишком сложно и беспорядочно!

Ниже мы рассмотрим формулы для матриц $ 2 \times 2 $ и матриц $ 3 \times 3 $ и посмотрим, как вычислить определитель таких матриц.

Формула определителя матрицы

В этом разделе мы найдем определитель матриц $ 2 \times 2 $ и $ 3 \times 3 $.

Определитель матрицы 2 x 2

Рассмотрим матрицу $ 2 \times 2 $, показанную ниже:

$ A = \begin{bmatrix} { a } & { b } \\ { c } & { d } \ end {bmatrix} $

Формула для определителя матрицы $ 2 \times 2 $ показана ниже:

$ det( A ) = | А | = \begin{vmatrix} { a } & { b } \\ { c } & { d } \end {vmatrix} = ad – bc $

Примечание. Мы использовали $ 3 $ различных обозначений для обозначения определителя этого matrix

Чтобы найти определитель матрицы $ 2 \times 2 $, мы берем произведение верхнего левого элемента и нижнего правого элемента и вычитаем из него произведение верхнего правого элемента и нижнего левого элемента. Вход.

Вычислим определитель матрицы $ B $, показанной ниже:

$ B = \begin{bmatrix} { 1 } & { 3 } \\ { – 3 } & { 2 } \end {bmatrix} $

Используя по только что изученной формуле мы можем найти определитель:

$ det( B ) = | Б | = \begin{vmatrix} { 1 } & { 3 } \\ { – 3 } & { 2 } \end {vmatrix} $

$ = ( 1 ) ( 2 ) – ( 3 ) ( – 3 ) $

$ = 2 + 9 $

$ = 11 $

Определитель матрицы $ B $ равен $ 11 $.

Определитель матрицы 3 x 3

Теперь, когда мы узнали, как найти определитель матрицы $ 2 \times 2 $, это пригодится при нахождении определителя матрицы $ 3 x 3 $. Рассмотрим матрицу $ B $, показанную ниже:

$ B = \begin{bmatrix} {a} & {b} & {c} \\ {d} & {e} & {f} \\ {g} & {h } & { i } \end {bmatrix} $

Формула для определителя матрицы $ 3 x 3 $ показана ниже:

$ det( B ) = | Б | = a \begin{vmatrix} {e} & {f} \\ {h} & {i} \end{vmatrix} — b \begin{vmatrix} {d} & {f} \\ {g} & {i } \end{vmatrix} + c \begin{vmatrix} { d } & { e } \\ { g } & { h } \end{vmatrix} $

Примечание:

Возьмем $ a $ и умножьте его на определитель матрицы $ 2 \times 2 $, который равен , а не в строке и столбце $ a $
Затем мы вычтем произведение $ b $ и определителя $ 2 \ умножить на 2 $ матрицу, которая равна , а не в строке и столбце $ b $
Наконец, мы добавляем произведение $ c $ и определитель матрицы $ 2 \times 2 $, которая равна , а не в строку и столбец $ c $

Используя формулу определителя матрицы $ 2 \times 2 $, мы можем дополнительно свести эту формулу к следующему виду:

$ det( B ) = | Б | = a (ei – fh) – b (di – fg) + c (dh – eg) $

Если вы не можете запомнить эту формулу (я знаю, это сложно!), просто запомните пункты $3$, описанные выше. .Кроме того, запомните знаки скалярных величин, на которые вы умножаете каждый определитель. $a$ положительное, $b$ отрицательное и $c$ положительное.

Теперь рассмотрим матрицу $ 3 \times 3 $, показанную ниже:

$ B = \begin{bmatrix} { 1 } & { 2 } & { – 1 } \\ { 0 } & { 3 } & { – 4 } \\ { – 1 } & { 2 } & { 1 } \end {bmatrix} $

Давайте вычислим определитель этой матрицы, используя только что изученную формулу. Показано ниже:
$ B = \begin{bmatrix} { 1 } & { 2 } & { – 1 } \\ { 0 } & { 3 } & { – 4 } \\ { – 1 } & { 2 } & { 1 } \end {bmatrix} $
$ det( B ) = | Б | = 1 [ ( 3 )( 1 ) – ( – 4 )( 2 ) ] – 2 [ ( 0 )( 1 ) – ( – 4 )( – 1 ) ] + (-1) [ ( 0 )( 2 ) – ( 3 )( – 1 ) ] $
$ = 1 [ 3 + 8 ] – 2 [ 0 – 4 ] + (-1) [ 0 + 3 ] $
$ = 1 [ 11 ] – 2[ – 4 ] – 1[ 3 ] $
$ = 11 + 8 – 3 $
$ = 16 $

Определитель матрицы $ 3 \times 3 $ $ B $ равен $ 16 $.

Давайте рассмотрим больше примеров, чтобы лучше понять детерминанты! Пример 1 С | $.

Решение

Нам нужно найти определитель матрицы $ 2 \times 2 $, показанной выше. Воспользуемся формулой и найдем определитель. Ниже показано:

$ det( C ) = | С | = \begin{vmatrix} { – 9 } & { – 2 } \\ { 3 } & { – 1 } \end {vmatrix} $

$ = ( – 9 ) ( – 1 ) – ( – 2 ) ( 3 ) $

$ = 9 + 6 $

$ = 15 $

пример 2 & { 2 } \end {vmatrix} = 34 $.

Решение
Нам уже известен определитель, и нам нужно найти элемент $ x $. Подставим это в формулу и решим для $ x $:
$ \begin{vmatrix} { 1 } & { x } \\ { 8 } & { 2 } \end {vmatrix} = 34 $
$ ( 1 ) ( 2 ) – ( x ) ( 8 ) = 34 $
$ 2 – 8x = 34 $
$ -8x = 34 – 2 $
$ – 8x = 32 $
$ x = – 4 $
Пример 3
Вычислите определитель матрицы $ D $, показанной ниже: \end {bmatrix} $
Решение
Мы будем использовать формулу для вычисления определителя матрицы $D$. Ниже показано:
$ det( D ) = | Д | = \begin{vmatrix} { 6 } & { 2 } \\ { – 12 } & { – 4 } \end {vmatrix} $
$ = ( 6 ) ( – 4 ) – ( 2 ) ( – 12 ) $
$ = -24+24$
$ = 0$
Определитель этой матрицы равен 0$!
Это особый тип матрицы. Это необратимая матрица, известная как сингулярная матрица . Чтобы узнать больше, проверьте здесь.
Практические вопросы
Найдите определитель приведенной ниже матрицы:
$ A = \begin{bmatrix} – 5 & – 10 \\ 3 & – 1 \end{bmatrix} $
Найти $ y $ по заданному $ \begin{vmatrix} { 1 } & { 3 } & { – 1 } \\ { 5 } & { 0 } & { y } \\ { – 1 } & { 2 } & { 3 } \end {vmatrix} = – 60 $
Ответы
Дана матрица $ A $, матрица $ 2 \times 2 $.Нам нужно найти его определитель. Мы делаем это, применяя формулу. Процесс показан ниже:
$ det( A ) = | А | = \begin{vmatrix} { – 5 } & { – 10 } \\ { 3 } & { – 1 } \end {vmatrix} $
$ = ( – 5 ) ( – 1 ) – ( – 10 ) ( 3 ) $
$ = 5 + 30 $
$ = 35 $
Нам уже дан определитель и нужно найти элемент $ y $. Подставим его в формулу для определителя матрицы $3\times 3$ и решим для $y$:
$\begin{vmatrix} { 1 } & { 3 } & { – 1 } \\ { 5 } & { 0 } & { y } \\ { – 1 } & { 2 } & { 3 } \ end {vmatrix} = – 60 $
$ 1 [ ( 0 )( 3 ) – ( y )( 2 ) ] – 3 [ ( 5 )( 3 ) – ( y )( – 1 ) ] + (-1) [ ( 5 )( 2 ) – ( 0 )( – 1 ) ] = – 60$
$ 1 [- 2y ] – 3 [ 15 + y ] + (-1) [ 10 ] = – 60 $
$ – 2y – 45 – 3y – 10 = – 60 $
$ – 5y – 55 = – 60 $
$ – 5y = – 60 + 55 $
$ – 5y = – 5 $
$ y = 1 $
Предыдущий урок | Главная страница | Следующий урок
Определитель матрицы 3×3 — ChiliMath
Стандартная формула для нахождения определителя матрицы 3×3 представляет собой разбивку более мелких задач на определитель 2×2 , с которыми очень легко справиться.Если вам нужно освежить знания, ознакомьтесь с другим моим уроком о том, как найти определитель 2 × 2. Предположим, нам дана квадратная матрица A, где
Определитель матрицы A вычисляется как
Вот ключевые моменты:
Обратите внимание, что элементы верхней строки, а именно a, b и c, служат скалярными множителями соответствующей матрицы 2 на 2.
Скаляр a умножается на матрицу 2×2 оставшихся элементов, созданную при рисовании вертикальных и горизонтальных отрезков, проходящих через a.
Тот же процесс применяется для построения матриц 2×2 для скалярных множителей b и c.
Определитель матрицы 3 x 3 (анимированный)
Примеры нахождения определителя матрицы 3×3
Пример 1: Найдите определитель приведенной ниже матрицы 3×3.
Приведенная ниже установка поможет вам найти соответствие между общими элементами формулы и элементами реальной задачи.
Применение формулы,
Пример 2: Оцените определитель матрицы 3 × 3 ниже.
Будьте очень осторожны при подстановке значений в нужные места в формуле. Распространенные ошибки возникают, когда учащиеся проявляют небрежность на начальном этапе подстановки значений.
Кроме того, не торопитесь, чтобы убедиться, что ваши арифметические расчеты также верны. В противном случае единственная ошибка где-то в расчетах приведет к неправильному ответу в конце.
С тех пор,
наш расчет определителя становится…
Пример 3: Найдите определитель матрицы 3×3 ниже.
Наличие нуля (0) в первой строке должно значительно упростить наши вычисления. Помните, что элементы в первой строке действуют как скалярные множители. Следовательно, умножение нуля на что-либо приведет к исчезновению всего выражения.
Вот снова настройка, чтобы показать соответствующее числовое значение каждой переменной в формуле.
Используя формулу, мы имеем…
Практика с рабочими листами
Вас также может заинтересовать:
Определители матрицы 2×2
Определитель матрицы | Как найти определитель — видео и расшифровка урока
Как найти определитель матрицы
Как уже упоминалось, прежде чем мы сможем найти определитель матрицы, нам нужно иметь квадратную матрицу. То есть матрица должна быть порядка 2 х 2, или 3 х 3, или 4 х 4, или n х n вообще.Ключевая формула для нахождения определителя матрицы: ad-bc . Эта формула применима непосредственно к матрицам 2 x 2, но мы также будем использовать ее при вычислении определителей в матрицах большего размера. Наконец, есть несколько сокращений, которые могут помочь нам быстро найти определитель матрицы в определенных ситуациях.
Определитель матрицы 2 x 2
Самый простой случай для определителей – это вопрос о нахождении определителя матрицы 2 x 2. Как уже упоминалось, для матрицы 2 x 2
$$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix},\\ det(A) = |A| = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad — bc $$
Другими словами, просто возьмите произведение верхнего левого и нижнего правого элементов и вычтите произведение из верхней правой и нижней левой записей.Давайте посмотрим на пример.
Пример
Найдите определитель $$D = \begin{pmatrix} 3 & 8 \\ 4 & 6 \end{pmatrix}\\ \begin{vmatrix} 3 & 8 \\ 4 & 6 \end{vmatrix } = 3\cdot 6 — 8\cdot 4 = 18 — 32 = -14. $$
Здесь показано, как найти определитель матрицы 2 x 2. Просто подставьте значения в формулу и оцените! Обратите внимание, что здесь определитель отрицательный — это нормально, определитель может быть любым скалярным значением. Если он равен нулю, то мы кое-что знаем об этой матрице (во-первых, она не имеет обратной).
Определитель матрицы 3 x 3
Чтобы найти определитель матрицы 3 x 3, все немного сложнее. Для общей матрицы 3 x 3 мы имеем
$$B = \begin{pmatrix} a & b & c\\ d & e & f\\ g & h & i \end{pmatrix}\\ det(B ) = |В| = \begin{vmatrix} a & b & c\\ d & e & f\\ g & h & i \end{vmatrix} = a\begin{vmatrix} e & f\\ h & i \end{vmatrix} — b\begin{vmatrix} d & f\\ g & i \end{vmatrix} +c \begin{vmatrix} d & e\\ g & h \end{vmatrix} \\ =a(ei-fh)- b(di — fg) + c(dh-eg) $$
Пример
Хотя мы могли бы использовать данную формулу, ее сложно запомнить, поэтому обычно проще продолжить разбивку во второй строке.Давайте посмотрим на этот процесс более внимательно. Обратите внимание, что в этом процессе мы берем коэффициенты из исходной матрицы и умножаем их на определитель матрицы 2 x 2, состоящей из элементов, которые равны , а не в строке или столбце этого коэффициента.
Первый член определителя.
Второй член определителя.
Третий член определителя.
Теперь обратите внимание, что в формуле также меняется знак операции. Сначала сложение, потом вычитание, потом сложение. Знак члена зависит от положения этого коэффициента в матрице:
$$\begin{pmatrix} + & — & +\\ — & + & -\\ + & — & + \end{pmatrix} $ $
Итак, мы можем выбрать в любой строке или в любом столбце для наших коэффициентов, если мы убедимся, что знаки этих коэффициентов в формуле правильные. Это важно, потому что иногда предпочтительнее выбрать одну строку или столбец, а не другую.
Формула определителя
Используя общую форму матрицы, мы можем получить формулу определителя, которую можно использовать и для матриц большего размера. Рассмотрим матрицу 4 x 4:
$$E = \begin{pmatrix} a & b & c & d\\ e & f & g & h\\ i & j & k & l\\ m & n & o & p \end{pmatrix} $$
Чтобы найти det(E) , мы поступаем так же, как и с 3 x 3, выбирая коэффициенты из одной строки или столбца и составляя меньшие матрицы из элементов , а не . в строке и столбце этого коэффициента.
$$det(E) = \begin{vmatrix} a & b & c & d\\ e & f & g & h\\ i & j & k & l\\ m & n & o & p \end{ vmatrix}\\ = a\begin{vmatrix} f & g & h\\ j & k & l\\ n & o & p \end{vmatrix} — b \begin{vmatrix} e & g & h\\ i & k & l\\ m & o & p \end{vmatrix} + c \begin{vmatrix} e & f & h\\ i & j & l\\ m & n & p \end{vmatrix} — d \ begin{vmatrix} e & f & g\\ i & j & k\\ m & n & o \end{vmatrix} \\ = a \bigg[ f \begin{vmatrix} k & l\\ o & p \ end{vmatrix} — g\begin{vmatrix} j & l\\ n & p \end{vmatrix} + h\begin{vmatrix} j & k\\ n & o \end{vmatrix} \bigg] — b\ bigg[e \begin{vmatrix} k & l\\ o & p \end{vmatrix} — g \begin{vmatrix} i & l\\ m & p \end{vmatrix} + h \begin{vmatrix} i & k \\ m & o \end{vmatrix}\bigg] \\ + c \bigg[e \begin{vmatrix} j & l\\ n & p \end{vmatrix} — f \begin{vmatrix} i & l \\ m & p \end{vmatrix} + h \begin{vmatrix} i & j\\ m & n \end{vmatrix}\bigg] — d \bigg[ e \begin{vmatrix} j & k\\ n & о \end{vmatrix} — f \begin{vmatrix} i & k\\ m & o \end{vmatrix} + g \begin{vmatrix} i & j\\ m & n \end{vmatrix}\bigg]\\ = a \big[ f(kp-lo) — g(jp-ln)+ h(jo-kn) \big] — b \big[ e (kp-lo) — g (ip-lm) + h (io-km) \big]\\ + c \big[e (jp-ln)- f (ip-lm) + h (in-jm)\big] — d \big [ e (jo-kn) — f (io-km) + g (in-jm) \big] $$
Как мы видим, вывод формулы определителя для большей матрицы очень быстро становится громоздким. В большинстве вычислений для матриц размером более 3 x 3 гораздо предпочтительнее использовать программное обеспечение или калькулятор для выполнения таких операций, как поиск определителей.
Свойства определителя
Есть несколько важных свойств определителя, которые необходимо знать перед углубленной работой с матрицами. Вот наиболее распространенные и важные правила определения:
det(I) = 1 . Определитель единичной матрицы равен 1.
.
Перестановка двух строк (или двух столбцов) в матрице изменит знак определителя (с положительного на отрицательный и наоборот).
При умножении строки матрицы на константу определитель также умножается на эту константу.
Добавление или вычитание строки (или кратной строки) с другой строкой , а не изменяет определитель.
Если в матрице две одинаковые строки, то ее определитель равен нулю.
Если в строке матрицы все нули, то ее определитель равен нулю.
Если определитель матрицы равен нулю, то говорят, что матрица сингулярна . Сингулярная матрица не имеет обратной.
Определитель треугольной матрицы является произведением стержней (то есть элементов на диагонали).
Это последнее свойство определителя позволяет нам быстро найти определитель некоторых матриц большего размера. Если мы сможем с помощью операций со строками преобразовать эту матрицу в треугольную матрицу, отслеживая при этом влияние операций на определитель, мы сможем найти определитель, просто умножая по диагонали и отменяя все изменения, сделанные нашими операциями со строками. , если есть.
Резюме урока
Матрица содержит строки и столбцы значений, организованных в виде прямоугольного массива. порядок матрицы — это количество строк и столбцов, которые она имеет. Другими словами, матрица с 91 476 m 91 477 строк и 91 476 n 91 477 столбцов называется 91 424 91 476 m 91 477 x 91 476 n 91 477 матрицей 91 425 , а ее порядок равен 91 476 m 91 477 x 91 476 n 91 477 . Чтобы матрица имела определитель, она должна быть квадратной, поэтому матрица должна иметь порядок n x n , чтобы иметь определитель.
Определитель матрицы всегда является скалярной величиной, а не другой матрицей или вектором.
Чтобы найти определитель матрицы 2 x 2 {eq}\begin{pmatrix} a & b\\ c & d \end{pmatrix} {/eq}, используйте формулу ad — bc .
Чтобы найти определитель матрицы 3 x 3, выберите строку или столбец и используйте ее элементы в качестве коэффициентов.
При нахождении определителя матрицы 3 x 3 каждый из коэффициентов умножается на определитель матрицы 2 x 2, содержащей элементы, которые равны , а не в строке или столбце этого коэффициента.Эти произведения объединяются с помощью попеременного сложения и вычитания. Чтобы найти определитель большей матрицы, можно использовать тот же процесс, но он становится громоздким. Лучший способ найти определитель большей матрицы — это, как правило, программное обеспечение или калькулятор.
Матрица с двумя одинаковыми строками или строкой нулей имеет определитель, равный нулю.
Матрица с нулевым определителем называется сингулярной и не имеет обратной.
Определитель треугольной матрицы — это произведение точек опоры или элементов по диагонали.
Операции со строками могут изменять определитель матрицы. Например, умножение строки на скаляр или перестановка двух строк влияет на определитель матрицы — отслеживайте эти изменения, если нужно отменить их в конце.
Вычисление определителя матрицы Пошаговое решение математических задач

Мы знаем, что не каждая система линейных уравнений имеет единственное решение. Иногда система из n уравнений с n переменными не имеет решения или бесконечное множество решений.В этом разделе мы вводим определитель матрица. В следующем разделе мы увидим, что определитель можно использовать определить, имеет ли система уравнений единственное решение.
Каждой квадратной матрице A соответствует действительное число, называемое определителем А, пишется |А|.
Определитель матрицы A 2 x 2,

определяется как
ПРИМЕЧАНИЕ Обратите внимание, что матрицы заключены в квадратные скобки, а определители обозначаются вертикальными чертами. Кроме того, матрица представляет собой массив чисел, но ее определитель — одно число.
ОЦЕНКА A 2 X 2 ОПРЕДЕЛИТЕЛЬ

Если
, затем
ОПРЕДЕЛИТЕЛЬ А 3 Х 3 МАТРИЦА
Определитель матрицы A 3 x 3,

определяется как
Простой метод вычисления определителей 3 X 3 находится путем перестановки и факторизуя условия, данные выше, чтобы получить

Каждая из величин в скобках представляет определитель 2 X 2 матрица, которая является частью матрицы 3 x 3, остающейся, когда строка и столбец множитель исключается, как показано ниже.
Эти определители матриц 2 X 2 называются минорами элемента в матрица 3х3. Символ M _ij представляет определитель матрица, которая получается при удалении строки i и столбца j. Следующий список дает некоторые миноры из матрицы выше.
В матрице 4 x 4 минорами являются определители матриц 3 x 3, а n x Матрица n имеет миноры, которые являются определителями (n — 1) X (n — 1) матрицы.
Чтобы найти определитель матрицы 3 X 3 или больше, сначала выберите любую строку или столбец. Затем необходимо умножить минор каждого элемента в этой строке или столбце. на + l или — 1, в зависимости от того, является ли сумма номеров строк и столбцов числа четные или нечетные. Произведение минора на число + 1 или — l равно называется кофактором .
КОФАКТОР Пусть M _ij будет минором элемента au в матрице n x n . Кофактор а _и , написано A _ij , это:

Наконец, определитель матрицы n x n находится следующим образом.
ПОИСК ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
Умножьте каждый элемент в любой строке или столбце матрицы на его коэффициент. То сумма этих произведений дает значение определителя. Процесс формирования эта сумма произведений называется расширением по данной строке или столбцу.
ПОИСК КОФАКТОР ЭЛЕМЕНТА
Для матрицы
найдите кофактор каждого из следующих элементов.
(a) 6
Поскольку 6 находится в первой строке и первом столбце матрицы, i = 1 и j = 1.
Кофактор равен (-1) ¹⁺¹ * (-6) = 1 * (-6) = -6.
(b) 3
Здесь i = 2 и j = 3.
Кофактор равен (-1) ²⁺³ * 10 = (-1) * 10 = -10.
(c) 8
Имеем i = 2 и j = l.

Кофактор равен (-1) ²⁺¹ * (-8) = (-1) * (-8) = 8.

ОЦЕНКА ОПРЕДЕЛИТЕЛЯ 3 X 3
Оценка
расширяется вторым столбцом.

Чтобы найти этот определитель, сначала найдите миноры каждого элемента во втором столбец.

Теперь найдите кофактор каждого из этих миноров.
Определитель находится путем умножения каждого кофактора на соответствующий ему элемент в матрице и нахождение суммы этих произведений.
ПРЕДОСТЕРЕЖЕНИЕ: Будьте очень внимательны и следите за всеми отрицательными знаками при оценивающие детерминанты.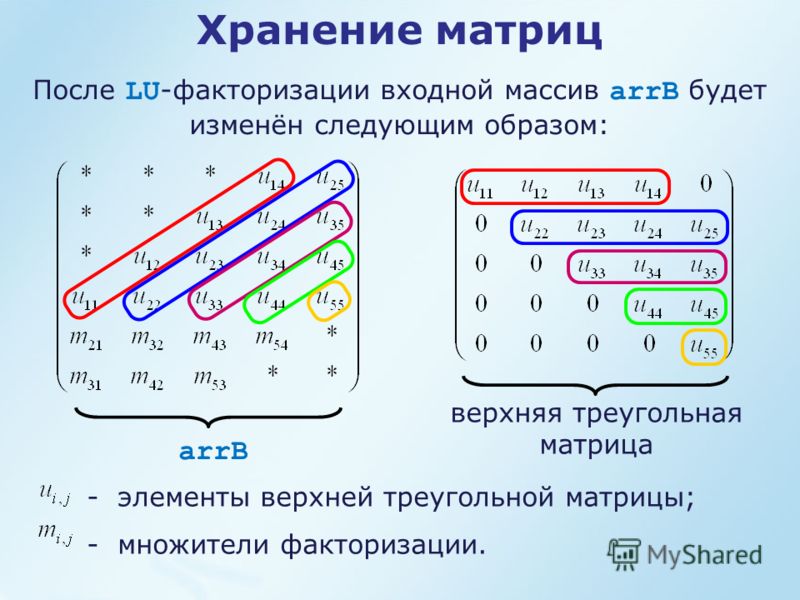 Работайте осторожно, записывая каждый шаг, как в Примеры.Пропуск шагов часто приводит к ошибкам в этих вычислениях.
Точно такой же ответ можно найти, используя любую строку или столбец матрицы. Одна из причин, по которой в примере 3 использовался столбец 2, заключается в том, что он содержит элемент 0, так что не особо надо было вычислять М ₃₂ и А ₃₂ выше. Быстро понимаешь, что нули могут быть очень полезны при работе с детерминанты.
Вместо вычисления (-1) ^i+j для заданного элемента выполняется следующее можно использовать доски для разметки знаков:

Знаки чередуются для каждой строки и столбца, начиная с + в первой строка, позиция первого столбца.Таким образом, эти массивы знаков могут быть воспроизведены как нужный. Если мы разложим матрицу 3 X 3, например, вокруг строки 3, первый второстепенный будет иметь связанный с ним знак +, второй второстепенный знак — и третий минор + знак. Таким образом, эти массивы знаков могут быть расширены для определителей матриц 5 X 5, 6 X 6 и более крупных матриц.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ 4 X 4
Вычисление
Разложение по младшим по четвертой строке дает
Каждый из четырех определителей в примере 4 должен оцениваться путем расширения три несовершеннолетних, требующих большой работы, чтобы получить окончательное значение.Всегда ищите строку или столбец с наибольшим количеством нулей, чтобы упростить работу. В следующем разделе мы ввести несколько свойств, облегчающих вычисление определителей. К счастью, определители больших матриц можно быстро вычислить. легко с помощью компьютера или некоторых калькуляторов.

.

РубрикаРазное