Событие достоверное пример: Достоверные события — Теория вероятности
Событие достоверное — Энциклопедия по машиностроению XXL
Случайные события называются несовместными, если они не могут появиться одновременно. Случайные события образуют полную группу попарно несовместных событий, если при каждом испытании должно появиться одно и только одно из них, т. е. хотя бы одно из них обязательно должно произойти и каждые два из них несовместны. В дальнейшем случайные события будем называть событиями. Достоверным называется такое событие, которое в результате испытания непременно должно произойти. Невозможным называется событие, которое в результате испытания не может произойти. Несколько событий при данном испытании называются равновозможными, если из-за симметрии испытания нет основания считать какое-либо из них более (менее) возможным, чем любое другое. [c.5]Интеграл (14) выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу [а,Ь), в котором заключены все ее возможные значения.

Такое событие достоверно, и, следовательно, вероятность его равна единице. [c.64]
Наоборот, если все случаи из всего числа возможных случаев N благоприятствуют возникновению ожидаемого события (п=Ы), то такое событие достоверно и его вероятность равна единице [c.9]
События А1,…,Ап образуют совокупность единственно возможных событий, если событие +. .. достоверно. [c.585]
В справедливости этого положения можно убедиться непосредственно. Для вывода же этого положения из теоремы сложения вероятностей достаточно заметить, что появление одного из единственно возможных событий представляет событие достоверное, вероятность которого равна единице ( 2).
Функция распределения F x) является неубывающей функцией своего аргумента, т. е. F x2)>F xi) при X2>Xi. Поскольку хсобытие невозможное, а л функция распределения равна нулю, т. е. F(—oo)=P(J[c.69]
е. F(—oo)=P(J[c.69]
Если все испытания приводят к одному и тому же конечному состоянию, то это состояние является достоверным. Поэтому вероятность достоверного события равна единице.
Определение вероятности процента деталей в партии, имеющих погрешности, значения которых лежат в каком-либо заданном интервале. Ветви теоретической кривой нормального распределения (см. рис. 4.3, б) уходят в бесконечность, асимптотически приближаясь к оси абсцисс. Площадь, ограниченная кривой нормального распределения и осью абсцисс, равна вероятности того, что случайная величина (например, погрешность размера) лежит в интервале от —оо до — -оо. Эта вероятность как вероятность достоверного события, равная 1 (или 100 %), определяется интегралом [c.91]
Из условия, что вероятность пройти частице без соударения путь л = О равна единице, как вероятность достоверного события (w (х) = 1), находим константу интегрирования С — 1 при л О
 26]
26]
В отличие от неслучайных событий, о которых нам может быть точно известно, появятся они или не появятся, мы никогда не можем сказать этого о событиях случайных. Частота появления случайного события определяется его вероятностью. Однако вероятностная оценка может быть достаточно надежной, и мы можем опираться на нее даже при предсказании самых важных для нас событий часто не менее уверенно, чем тогда, когда имеем дело с достоверными сведениями о событиях.
Резонно поставить вопрос какой должна быть вероятность события, чтобы его наступление можно было считать достоверным Разумеется, ответ на этот вопрос носит в значительной мере субъективный характер и зависит главным образом от степени важности ожидаемого события. Поясним это двумя примерами. [c.30]
Таким образом, можно назвать практически достоверными события, вероятность которых отличается от единицы на 10 -10 » , а практически невозможными те, вероятность которых меньше 10 -10-7. [c.30]
[c.30]
Представленные примеры иллюстрируют достоверность описания закономерности событий в вершине усталостной трещины за счет ротаций объемов материала в полуцикле разгрузки. Это приводит к созданию разнообразных профилей усталостных бороздок на разных этапах роста трещины и эффекта пластического затупления вершины трещины при нерегулярном нагружении, что приводит к созданию более сложной конфигурации профиля бороздки. [c.178]
К физике тогда вообще относились с большим недоверием. Считалось, что физические науки… обращены на то, чтобы опровергнуть повествование о сотворении мира, потопе и о других достоверных событиях, о которых священные книги сохранили для нас память . [c.112]
Из выражений (9.63) и (9.64) видно, что отказ элемента является достоверным событием и Р- (п) = 1 при или прп п = = (хд — + 1, а вероятность безотказной работы i — (п) = = 1 при Ug С Хп, т. е. на интервале [1, к ), и Д- п) = О при п > ко- Графики i — (и) и Р- (п) представлены на рис. 39, 40 соответственно.
[c.171]
39, 40 соответственно.
[c.171]
Событие, которому благоприятствуют все я возможных случаев или которому благоприятствует всё поле, имеющее меру 6, называется достоверным. Вероятность достоверного события равна единице. [c.280]
Невозможному событию т = 0) соответствует вероятность 0, достоверному (благоприятствуют все п возможных случаев) вероятность 1. Вероятность случайного события заключена между 0 и 1.
Нижний предел — оо не следует трактовать в буквальном смысле. В частности, для нашего примера с давлением нижним пределом может быть только некоторое положительное значение. Так как невероятному событию отвечает F(x)=0, а достоверному Р х) = , для функции распределения всегда справедливо следующее неравенство [c.59]
Достоверность события понимается здесь теоретически, т. е. как абсолютная достоверность. В обыденной жизни и технике достоверными считаются события (измерения, заключения), вероятность которых достаточно велика, но отнюдь не абсолютна.
С целью формализации процесса отбора принято выбрасывать из ряда наблюдений такие, вероятность которых очень мала и составляет менее 0,003. События подобной достоверности можно считать практически невозможными. Иначе говоря, в достоверную часть включаются все те наблюдения, доверительная вероятность которых /)>0,997. Этой вероятности отвечает интервал Зо. Итак, наблюдение бракуется, если его отклонение ет среднего больше Зо
ДОСТОВЕРНЫЕ, НЕВОЗМОЖНЫЕ И ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ СОБЫТИЙ [c.9]
Основной недостаток имеющихся разработок по надежности машин и других изделий, по нашему мнению, заключается в том, что при анализе сложных объектов (машин) соединяются вместе достоверные, невозможные и случайные события, т. е. не учитываются специфические особенности современных техниче-
[c.27]
е. не учитываются специфические особенности современных техниче-
[c.27]
Вероятность достоверного события равна единице Р (достоверное событие) = 1. [c.6]
Используем теперь исходное условие, согласно которому известно, что в результате залпа, произведенного стрелками А, В и С, в мишени обнаружено только две пробоины. Из этого условия следует, что промах одного из трех стрелков является достоверностью и следовательно, исключается случай попадания всех трех стрелков в цель. Обозначим Wfj — математическую вероятность события, при котором стрелки А и В попадают в цель, а стрелок С не попадает, при условии, что промах одного из стрелков является достоверностью. Математическая вероятность IVp, величину которой требуется определить по условию задачи, будет больше Wq во столько раз, во сколько единица больше суммы (И х+ -1- Wg -j- Wf.y так как промах одного из стрелков является достоверностью, а математическое ожидание достоверности равно единице.
Различают понятие единственно возможных событий, если шявление в результате испытания одного н только одного из них является событием достоверным (при бросании монеты единственно возможным событием является появился герб , появилась цифра ). [c.131]
Для общего случая, считая, что случайная величина может принять любое звачение (событие достоверно), площадь, ограниченная кривой распределения
Событие называется достоверным, еслиР(А) = 1. Событие.4 называется невозможным, если Р(Л) = 0. Вероятность любого события А заключена между нулем и единицей [c.100]
Вероятность выражается в долях единицы или в процентах. Расс.мотрим некоторый энергетический уровень в валентной зоне. Если он занят электроном. то/ =1, и вероятность превращается в достоверность. Если же он не занят, то эта вероятность / =0 сумма вероятностей обоих событий занят , не занят равна единице. Но вероятность того, что энергетический уровень в валентной зоне не занят электроном, есть вероятность нахождения на этом уровне дырки /р. Таким образом,/р=1, если / =0, а сумма этих вероятностейОтсюда можно найти выражение дляу . Отняв от единицы выражение (3.2), получим соотношение
[c.52]
Но вероятность того, что энергетический уровень в валентной зоне не занят электроном, есть вероятность нахождения на этом уровне дырки /р. Таким образом,/р=1, если / =0, а сумма этих вероятностейОтсюда можно найти выражение дляу . Отняв от единицы выражение (3.2), получим соотношение
[c.52]
Критерии прочностной надежности, запасы прочности. Основной количественной характеристико надежности является вероятность безотказности изделия. Вероятностью события называется число, характеризующее возможность появления события. Вероятность достоверного события принимают равной единице, вероятность невозможного события — равной нулю. [c.9]
Вычислить вероятности событий можно лишь в том случае, когда известно, сколько событий какого типа возможно. В приведенном примере с урной нужно знать число содержащихся в ней белых (п ) и число черных и красных (тгь) шаров. Часто мы этого не знаем и решаем обратную задачу — по частоте появления шаров того или иного цвета в описанном выше опыте определяем вероят ность появления белого, черного или красного. Пусть мы проделали А/ испытаний, т.е. /V раз доставали шар из урны, каждь1й раз записывали его цвет и возвращали обратно в урну. Пусть при этом мы К раз вытащили белый шар, тогда К/Ы называется частотой появления белого шара. Основной закон теории вероятностей — закон больших чисел — утверждает, что при достаточно бол1 шом числе испытаний Ы частота появления события (с вероятностью, близкой к достоверности) как угодно мало отличается от вероятности этого события, иначе говоря, если
[c.28]
Пусть мы проделали А/ испытаний, т.е. /V раз доставали шар из урны, каждь1й раз записывали его цвет и возвращали обратно в урну. Пусть при этом мы К раз вытащили белый шар, тогда К/Ы называется частотой появления белого шара. Основной закон теории вероятностей — закон больших чисел — утверждает, что при достаточно бол1 шом числе испытаний Ы частота появления события (с вероятностью, близкой к достоверности) как угодно мало отличается от вероятности этого события, иначе говоря, если
[c.28]
Для оценки точности и достоверности измерений неровностей поверхности в данной теории эвристически рекомендуют определенный способ использования формулы (59). Он заключается в том, что при определении числа Пд в формулу (59) подставляют среднее значение Л47 и дисперсию DR тех параметров шероховатости (Ra, Rq, опорная линия профиля на уровне и), для которых они определены методами теории случайных функций. Профилограммы шероховатости поверхности при этом интерпретируют как реализации стационарной эргодической случайной функции у (х, ш) с нормальным распределением вероятностей. Переменная X означает вектор пространственных координат, меняющихся в области Т евклидова пространства R , а переменная ш — элементарное случайное событие из некоторого вероятностного пространства.
[c.74]
Переменная X означает вектор пространственных координат, меняющихся в области Т евклидова пространства R , а переменная ш — элементарное случайное событие из некоторого вероятностного пространства.
[c.74]
Метод Дельфи, как и большинство методов коллективной экспертизы, не лишен недостатков. Так, данным методом не предусмотрена оценка надежности предсказания даты наступления будущих событий. Будущее состояние науки и техники в значительной мере определяется развитием таких областей, как экономика, социология, политика, поэтому только научный и технический состав экспертов не всегда может дать достаточно достоверные предсказания. В связи с этим в ряде прогностических фирм США были предприняты дальнейшие разработки метода Дельфи, которые не изменяя его основы, направлены на расширение возможностей метода и увеличение эффективности его использования. Предлагаемые усовершенствования метода Дельфи касаются вопросов отбора экспертов, способов [c.77]
Новые значения вероятностей использовались затем для определения новых вероятных сроков наступления событий с прежними уровнями достоверности р (0,1 0,5 0,9). На основе построенных графиков наступления событий можно определить события как предп1е-ствующие, так и последующие (ряс. 17).
[c.82]
На основе построенных графиков наступления событий можно определить события как предп1е-ствующие, так и последующие (ряс. 17).
[c.82]
Наряду со всем тем, что делалось В. И. Лениным в первые годы Советской власти в области развития радио, одной из серьезных его забот было стремление обеспечить скорейшую и достоверную информацию населения Республики о принятых партией и правительством постановлениях и других важных событиях внутренней и международной жизни. Выполняя эти указания Владимира Ильича, Наркомпочтель, начиная с 1918 г., организовал систематические передачи по радио подобных материалов. В городах страны и на крупных железнодорожных станциях появились информационные плакаты с надписью Радио из Москвы . [c.300]
Трактованию численной ошибки вероятности в дальнейшем будет посвящено много примеров. Сейчас ограничимся указанием, что событие считается достоверным, [c.58]
Следует отметить, что математическая вероятность всегда имеет значение правильной дроби, так как по смыслу число благоприятных случаев всегда меньше общего числа рав-новозмошных случаев. Если число благоприятных случаев равно числу равновозможных, имеет место достоверность события, характеризуемая W =i.
[c.91]
Если число благоприятных случаев равно числу равновозможных, имеет место достоверность события, характеризуемая W =i.
[c.91]
Урок 33. вероятность события. сложение вероятностей — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Глоссарий по теме
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Её ещё называют статистической вероятностью события.
Равновозможные события — такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9. сс.242-261.
изуч. математики. — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9. сс.242-261.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Рассмотрим пример:
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
Варианты ответов:
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Определение.
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
- Процесс доставания предмета из коробки является испытанием.
- Результат доставания предмета из корзины является событием.
- Событие «вынутый предмет окажется клубком» является достоверным событием.
- События «вынутый предмет не окажется клубком» или «вынутый предмет окажется красным клубком» являются невозможными событиями.

- Событие «вынутый предмет окажется зеленым клубком» является вероятным событием.
А={вынутый предмет оказался клубком}.
В={вынутый предмет не оказался клубком.
С={вынутый предмет оказался зеленым клубком}.
D ={вынутый предмет оказался красным клубком}.
2. Определим еще несколько важных понятий теории вероятностей
Определение
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω= {w 1, w 2, w 3, w 4, w 5, w6}, где wi— выпадение i очков.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Например:
- A – сдал экзамен по математике;
- Ᾱ – не сдал экзамен по математике.
Определение.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Пример .
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпало два «орла»
— Выпало две «решки»
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Определение.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.
Статистическая вероятность события рассчитывается опытным путем.
Пример.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов. Тогда вероятностью события А называется число
Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
2 .Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Например:
- Пусть А — идет дождь, B — идет снег, тогда А + В – «идет снег или дождь»
- При 3-х выстрелах по мишени события: А0 – «попаданий нет», А1 – «одно попадание», А2 – «два попадания», тогда А=А0+А1+А2 — «произошло не больше двух попаданий»
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅D — из урны вынули два белых шара
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅- из урны вынули два шара: белый и не белый
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Решение:
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.
Теория вероятности | Математика, которая мне нравится
Возникновение теории вероятностей относится к XVII веку и связано с комбинаторными задачами азартных игр. Первым руководством по теории вероятностей был трактат Гюйгенса “О расчетах в азартной игре” (1657 г.). Предмет его тот же, что и в предшествовавших работах Ферма и Паскаля: игральные кости и карточные игры. В 1713 г. вышла книга Якоба Бернулли “Искусство предположений” уже после смерти автора. Занимались задачами теории вероятностей П. Л. Чебышев, А.А. Марков, А.Н. Колмогоров и др.
Л. Чебышев, А.А. Марков, А.Н. Колмогоров и др.
Основной объект теории вероятностей — случайность или неопределенность, связанная с незнанием. Однако увеличение наших знаний требует и развития теории вероятностей. Дело в том, что точных, детерминированных количественных законов почти не существует. Так, закон о зависимости давления газа от его температуры — есть на самом деле результат вероятностного характера о числе соударений частиц о стенки сосуда и их скоростях. Просто в области обычных температур и давлений случайные отклонения, которые тут имеют место, с большой вероятностью очень малы и не регистрируются нашими приборами. Иначе обстоит дело при изучении более редких потоков частиц, скажем, космического излучения, хотя качественной разницы между этими двумя примерами нет.
Известен также принцип неопределенности, в силу которого для любой пары физических характеристик, связанных этим принципом, фиксация одной из них делает невозможным точное определение другой.
Вопрос в том, когда следует применять методы теории вероятностей, а когда нет, для изучения данного явления. Это определяется степенью точности, с которой изучается явление, и сведениями о его природе, которыми мы располагаем.
Основные понятия
Опыт, эксперимент, наблюдение явления называются испытаниями. Примеры испытаний: бросание монеты, извлечение шара из урны, бросание игральной кости. Примеры событий: выпадение герба или цифры, взятие белого или черного шара, появление того или иного числа очков на брошенной игральной кости. Для обозначения событий используются заглавные буквы латинского алфавита: и т.д.
Определение. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример. Испытание: однократное бросание игральной кости. Событие — появление четырех очков. Событие — появление четного числа очков. События и — совместные.
События и — совместные.
Определение. Два события называются несовместными, если появление одного из них исключает появления другого в одном и том же испытании.
Пример. Испытание: однократное бросание игральной кости. Событие — появление четырех очков. Событие — появление двух очков.
Определение. Два события и называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит.
Пример. Испытание: бросание монеты. Событие — выпадение герба, событие — выпадение решки.
Определение. Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти.
Пример. Испытание: извлечение шара из урны, в которой все шары белые. Событие — вынут белый шар — достоверное; событие — вынут черный шар — невозможное.
Определение. Событие называется случайным, если оно объективно может наступить или не наступить в данном испытании.
Пример. Событие — выпадение шести очков при бросании игральной кости — случайное.
Определение. Суммой событий называется событие , состоящее в наступлении по крайней мере одного из событий или .
Пример. Испытание: стрельба двух стрелков (каждый делает по одному выстрелу). Событие — попадает в мишень первый стрелок, событие — попадает в мишень второй стрелок. Суммой событий и будет событие — попадает в мишень по крайней мере один стрелок.
Аналогично суммой конечного числа событий называется событие , состоящее в наступлении хотя бы одного из событий .
Из определения суммы событий непосредственно следует, что . Справедливо также и сочетательное свойство. Однако , а не , как в алгебре.
Определение. Произведением событий называется событие , состоящее в том, что в результате испытания произошли и событие и событие .
Аналогично произведением конечного числа событий называется событие , состоящее в том, что в результате испытания произошли все указанные события.
Пример. В предыдущем примере произведением событий и будет событие , состоящее в попадании в мишень двумя стрелками.
Из определения произведения событий непосредственно следует, что . Справедливы также сочетательный и дистрибутивный законы. Однако (а не ).
Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытаний, т.е. событий.
Определение. Говорят, что совокупность испытаний образует полную группу событий для данного испытания, если ее результатом обязательно становится хотя бы одно из них.
Пример. Полными группами событий являются: выпадение герба и выпадение решки при одном бросании монеты; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости; попадание в цель и промах при одном выстреле.
Рассмотрим полную группу попарно несовместных событий , связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий равновозможно, т.е. условия испытания не создают преимущества в появлении какого-либо события перед другими возможными.
Определение. События , образующие полную группу попарно несовместных и равновозможных событий, будем называть элементарными событиями.
Пример. Пусть — событие, состоящее в том, что при одном бросании кости выпадает грань с цифрой i. Тогда события образуют полную группу попарно несовместных событий. Так как кость предполагается однородной и симметричной, то события являются равновозможными, т.е. элементарными.
Определение. Событие называется благоприятствующим событию , если наступление события влечет за собой наступление события .
Пример. Пусть при бросании игральной кости события и — появление соответственно двух, четырех и шести очков и — событие, состоящее в появлении четного числа очков; события благоприятствуют событию .
Определение (классическое определение вероятности). Вероятностью события называется отношение числа элементарных событий, благоприятствующих событию , к числу всех элементарных событий, т.е.
Пример. Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие — выпадение герба и событие — выпадение решки образуют полную группу несовместных и равновозможных событий для данного испытания. Событию благоприятствует лишь одно событие — само . Поэтому .
Пример. Найдем вероятность того, что при бросании игральной кости выпадет четное число очков (событие ). Число элементарных событий здесь 6. Число благоприятствующих элементарных событий 3 (выпадение 2, 4 и 6). Поэтому .
Из классического определения вероятности следует:
1. вероятность достоверного события равна единице;
2. верояность невозможного события равна нулю;
3. вероятность случайного события есть положительное рациональное число, заключенное между нулем и единицей, т.е. ;
вероятность случайного события есть положительное рациональное число, заключенное между нулем и единицей, т.е. ;
4. элементарные события являются равновероятными, т.е. обладают одной и той же вероятностью.
Задачи.
1. В классе учится человек, среди них отличников. Ответьте на следующие вопросы.
1) Наудачу выбирают одного ученика. Какова вероятность, что он будет отличником?
2) Наудачу выбирают учеников. Какова вероятность, что среди них будет ровно отличников?
2. Калиф-Аист забыл волшебное слово “мутабор” и произносит слова наудачу. Ответьте на следующие вопросы для случаев, когда Калиф делает одну попытку и 10 попыток.
1) Какова вероятность, что он угадает, если он помнит длину заветного слова и все его буквы?
2) Какова вероятность, что он угадает, если он все верно помнит про все буквы заветного слова, кроме буквы “р”, про которую не уверен, одна она в слове или их там две?
3) Какова вероятность, что он угадает, если он помнит, что в слове не было никаких букв, кроме “м”, “у”, “т”, “а”, “б”, “о”, “р”, и помнит длину слова (входили ли эти буквы в слово и по скольку раз, он не помнит)?
4) Какова вероятность того, что Калиф произнесет слово, в котором будет сочетание букв “табу”, если он помнит длину слова и все входящие в него буквы?
Комбинаторика и теория вероятностей : Теория вероятностей
Что нужно знать, чтобы определять вероятности событийВсе события, за которыми люди наблюдают или сами создают их, делятся на:
- достоверные события;
- невозможные события;
- случайные события.

 Появление
бракованного изделия является случайным событием, более редким, чем
производство годных изделий.
Появление
бракованного изделия является случайным событием, более редким, чем
производство годных изделий. Пример №1:
В среднем из 2000 садовых насосов, поступивших в продажу, 14 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение:
Число вариантов выбора насосов: n = 2000. Число вариантов выбора исправных насосов: m = 2000 — 14 = 1986.
Искомая вероятность:
Ответ: 0,993.
Пример №2:
Фабрика выпускает сумки. В среднем на 120 качественных сумок приходится девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение:Число вариантов выбора сумок: n = 120 + 9 = 129.
Число вариантов выбора качественной сумки: m = 120.
Искомая вероятность:
Ответ: 0,93.
Пример №3:
В группе 30 студентов. Трём студентам следует направиться на кафедру информатики, чтобы взять и принести компьютер и проектор. Вычислить
вероятность того, что это сделают три определённых студента. Решение. Число возможных событий рассчитываем, используя
формулу
Вычислить
вероятность того, что это сделают три определённых студента. Решение. Число возможных событий рассчитываем, используя
формулуВероятность того, что на кафедру отправятся три определённых студента:
Случайные события и случайные величины
Вероятностные закономерности проявляются только в массовых явлениях, т.е. когда один и тот же объект изменяет свое состояние многократно или когда множество одинаковых объектов однократно изменяют свое состояние одинаковым образом.
Массовые явления и процессы характерны неоднократным повторением при постоянных условиях некоторых событий.
Событием в теории вероятностей называется явление, происходящее при реализации какого-либо комплекса условий, который может быть воспроизведен сколь угодно большое число раз.
Массовые явления всегда являются результатом большого, иногда бесконечно большого числа испытаний.
Испытание – это воспроизведение комплекса условий какого – либо события.
Событие, которое всегда происходит в результате испытаний, называется достоверным.
Событие, которое никогда не происходит в результате испытаний, называется невозможным.
Событие, которое иногда происходит в результате испытаний, называется случайным.
Например: выпадение «орла» или «решки» при подбрасывании монеты является событием; само подбрасывание – это испытание; падение монеты – достоверное событие; ее вылет в космос – невозможное событие; выпадение «орла» (или «решки») – случайное событие.
Невозможные и достоверные события детерминированы (предопределены) их причинами. Случайные события обусловлены игнорированием слабых (несущественных) связей или незнанием связей сильных. Т.о., по крайней мере в макромире, случайность является результатом незнания всех причин явления.
Если результаты случайных событий поддаются количественной оценке, то их характеризуют при помощи случайных величин.
Случайная величина – это переменная, принимающая в результате испытаний то или иное числовое значение.
Имеется два вида случайных величин: дискретные и непрерывные.
Дискретной называется такая случайная величина, которая принимает конечное или бесконечное счетное множество значений.
Это означает, что всем элементам данного множества могут быть сопоставлены натуральные числа или они могут быть выписаны в последовательности X1, X2 … Xn.
Примером дискретной случайной величины является размер обуви жителей некоторого города.
Непрерывной случайной величиной называется такая переменная, которая может принимать любое значение в некотором интервале.
Поэтому число значений непрерывной случайной величины всегда бесконечно. Например, рост жителей некоторого города.
Поскольку в технике большинство явлений и процессов характеризуется количественными параметрами, которые изменяются случайным образом, то поэтому случайные величины и являются основными объектами изучения и управления.
Основные понятия теории вероятностей — презентация онлайн
1. Тема урока:
«ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИВЕРОЯТНОСТЕЙ»
Что такое событие?
• Событие – это результат испытания.

Из урны наудачу берут один шар.
Извлечение шара из урны есть
испытание.
Появление шара определенного цвета –
событие.
Событие, которое происходит всегда,
называют достоверным.
Событие, которое не может произойти,
называется невозможным.
Пример.
Пусть из урны, содержащей
только черные шары, вынимают шар.
Тогда появление черного шара –
достоверное событие;
Появление белого
шара – невозможное событие.
Непредсказуемые события называются
случайными .
В жизни мы постоянно сталкиваемся с тем, что
некоторое событие может произойти, а может и не
произойти.
Пример.
После опубликования результатов
розыгрыша лотереи событие –
выигрыш, либо происходит, либо не
происходит.
5. Типы событий
СОБЫТИЯСЛУЧАЙНЫЕ
ДОСТОВЕРНЫЕ
НЕВОЗМОЖНЫЕ
событие, которое может
произойти или не
произойти в результате
некоторого испытания
событие, которое
обязательно
произойдет в
результате данного
испытания
событие, которое не
может произойти
в результате
данного
испытания
0
Р (А) = 1
Р (А) = 0
6.
 Распредели события по их типам СЛУЧАЙНЫЕ
Распредели события по их типам СЛУЧАЙНЫЕДОСТОВЕРНЫЕ
НЕВОЗМОЖНЫЕ
1. После зимы наступает весна.
2. После ночи приходит утро.
3. Камень падает вниз.
4. Вода становится теплее при нагревании
5. Выиграть приз в спортлото
6. Бутерброд падает маслом вниз
7. В школе отменили занятия.
8. Поэт пользуется велосипедом
9. В доме живет кошка.
10. З0 февраля день рождения у моего друга
11. При подбрасывании кубика выпадает 7 очков.
12. Человек рождается старым и становится с каждым днем моложе.
Два события, которые в данных условиях могут
происходить одновременно, называются
совместными, а те, которые не могут
происходить одновременно, — несовместными.
Пример.
Брошена монета. Появление
«герба» исключает появление
надписи. События «появился герб»
и «появилась надпись» несовместные.
Равновозможными называются события,
когда в их наступлении нет преимуществ.
Пример.
Пусть бросают игральную кость.

В силу симметрии кубика можно
считать, что появление любой из
цифр 1, 2, 3, 4, 5 или 6 одинаково
возможно (равновероятно).
Единственно возможными называются
события, когда при рассмотрении группы
событий может произойти только одно из них.
Пример.
Если полную группу образуют только два
несовместных события, то они называются
противоположными.
Пример.
ВИДЫ СЛУЧАЙНЫХ СОБЫТИЙ
НЕСОВМЕСТНЫЕ
СОВМЕСТНЫМИ
ПОЯВЛЕНИЕ ОДНОГО СОБЫТИЯ В
ЕДИНИЧНОМ ИСПЫТАНИЕ ИСКЛЮЧАЕТ
ПОЯВЛЕНИЕ ДРУГОГО
Два события, которые в данных
условиях могут происходить
одновременно
ЕДИНСТВЕННО
ВОЗМОЖНОЕ
ПРИ РАССМОТРЕНИИ ГРУППЫ
СОБЫТИЙ МОЖЕТ ПРОИЗОЙТИ
ТОЛЬКО ОДНО ИЗ НИХ
РАВНОВОЗМОЖНЫЕ
СОБЫТИЯ ИМЕЮТ РАВНЫЕ
ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ
ПРОТИВОПОЛОЖНЫЕ
Если полную группу образуют
только два несовместных события
Классическое определение вероятности.
Вероятностью события А при проведении
некоторого испытания называют отношение
числа тех исходов, в результате которых
наступает событие А, к общему числу всех
(равновозможных между собой) исходов этого
испытания.

13. ИСХОД
ИСХОДОМ (элементарнымсобытием) называется один из
взаимоисключающих друг друга
вариантов, которым может
завершиться случайный
эксперимент
ИСХОДЫ
ОДНОЗНАЧНЫЕ
Предполагают
единственный
результат того или
иного события:
смена дня и ночи,
времени года
НЕОДНОЗНАЧНЫЕ
Предполагают
несколько различных
результатов того или
иного события: выигрыш
в Спортлото; результаты
спортивных игр
15. Благоприятный исход — желаемый исход
Благоприятный исход — желаемыйисход
Примеры:
Бросаете монету. Хочу, чтобы выпала решка,
=> благоприятный исход = выпала
решка. Значит выпадение орла –
неблагоприятный исход.
Сдаю экзамен. Из 20 билетов 10 знаю на
отлично, 5 на хорошо, 3 на
удовлетворительно и 2 не знаю. Хочу сдать
на хорошо. Тогда благоприятный исход =
сдать на хорошо. А какова вероятность сдать
на хорошо?
Ответ: 5/20=1/4.

16. БРОСАЮТ МОНЕТУ (это испытание)
ВОЗМОЖНЫЕ ИСХОДЫВЫПАЛ
«орел»
ВЫПАЛА
«решка»
Вероятность
каждого
исхода
1
P
2
.
Правила вычисления вероятностей
1) Вероятность элементарного события (события,
которое соответствует единственному исходу из N
равновозможных) равна 1/N.
2)Вероятность невозможного события равна 0.
3)Вероятность достоверного события равна 1.
4) Вероятность любого события заключена в пределах от
0 до 1: 0 Р(А) 1.
5) Вероятность события, противоположного событию А
(события, заключающегося в том , что событие А не
наступает), равна 1- Р(А).
Алгоритм нахождения вероятности
случайного события.
Для нахождения вероятности случайного события А
при проведении некоторого испытания следует найти:
1) число N всех возможных исходов данного испытания;
2) количество N(A) тех исходов, в которых наступает
событие А;
3) частное
события А.

, оно и будет равно вероятности
Принято вероятность события А обозначать так: Р(А).
Значит
Пример.
На завод привезли партию из 1000 подшипников. Случайно в
эту партию попало 30 подшипников, не удовлетворяющих
стандарту. Определить вероятность Р(А) того, что взятый
наудачу подшипник окажется стандартным.
Решение.
Благоприятное событие А: подшипник
окажется стандартным.
Количество всех возможных исходов
N = 1000.
Количество благоприятных исходов
N(A)=1000-30=970.
Значит:
Ответ: 0.97.
Пример
Монета бросается два раза. Какова вероятность того, что:
герб выпадет хотя бы один раз?
Решение:
Благоприятное событие А: герб выпадет хотя бы один раз.
Кол-во всех возможных исходов N = 2 ∙ 2 = 4.
Кол-во благоприятных исходов N(A)={ГГ, ГР, РГ} = 3.
Значит:
Ответ: 0.75.
.
Правила вычисления вероятности
произведения событий
Произведением событий А и В называют событие А*В, состоящее в
наступлении обоих этих событий
Если события А и В независимы (они происходят в разных
испытаниях, и исход одного испытания не может влиять на исход
другого), то вероятность того, что наступят оба этих события, равна
Р(А)*Р(В):
Р(А*В)=Р(А)*Р(В)
Например, вероятность выпадения двух шестерок при двукратном
бросании кубика равна: 1/6*1/6=1/36.

Пример.
Найдем вероятность того, что при подбрасывании двух костей
суммарное число очков окажется равным 5.
Решение:
Благоприятное событие А: в сумме выпало 4 очка.
Количество всех возможных исходов:
1-я кость — 6 вариантов
2-я кость — 6 вариантов
N=6∙6=36.
Кол-во благоприятных исходов N(A)= {1 + 4, 2 + 3, 3 + 2, 4 + 1}=4
Значит:
Ответ:
.
Правила вычисления вероятности
суммы событий
Суммой событий А и В называют событие А+В, состоящее в
наступлении хотя бы одного из этих событий.
Если А и В несовместны, то Р(А+В)=Р(А)+Р(В)
Для произвольных событий А и В вероятность суммы этих
событий равна сумме их вероятностей без вероятности их
совместного события:
P( А В) P( А) P( В) P( АВ).
24. ВЕРОЯТНОСТИ СУММЫ И ПРОИЗВЕДЕНИЯ СОБЫТИЙ
P A B P A P BP A B P A P B
Сумма вероятностей противоположных
событий равна 1:
P A P A 1
25. ПРИМЕР
Вероятность, что при бросании игральнойкости выпадет либо 3 очка, либо 4 очка.

P A B P A P B
1 1 1
6 6 3
26. ПРИМЕР
Вероятность, того что молодой человеквыиграет в лотерею 0, 01. А вероятность
того, что он в этот же вечер познакомится с
красивой девушкой 0,4. С какой
вероятностью произойдут оба события?
P A B P A P B
0,01 0,4 0,004
27. СОВМЕСТНЫЕ СОБЫТИЯ
События A и B совместные (зависимые), вероятностьсуммы двух совместных событий равна сумме
вероятностей этих событий, уменьшенной на
вероятность их произведения:
P A B P A P B P A B
В ящике лежат 6 красных и 6 синих шаров. Наудачу
вынимают 8 шаров. Определите вероятность события А все выбранные шары красные.
Решение: Р(А) = 0, т.к. это событие А — невозможное.
Ответ: 0.
Научная конференция проводится 3 дня. Всего запланировано 50
докладов: в первый день – 30 докладов, а остальные распределены
поровну между вторым и третьим днями. Порядок докладов
определяется жеребьевкой. Какова вероятность, что доклад
профессора М.
 окажется запланированным на последний день
окажется запланированным на последний деньконференции?
Решение:
Благоприятное событие А: доклад
профессора М. окажется запланированным
на последний день конференции.
Кол-во всех возможных исходов N = 50.
Кол-во благоприятных исходов N(A)=(50-30):2=10.
Значит:
Ответ: 0.2.
Перед началом первого тура чемпионата по теннису разбивают
на игровые пары случайным образом с помощью жребия. Всего
в чемпионате участвует 46 теннисистов, среди которых 19
участников из России, в том числе Ярослав Исаков. Найдите
вероятность того, что в первом туре Ярослав Исаков будет
играть с каким – либо теннисистом из России.
Решение:
Благоприятное событие А: в первом туре Ярослав
Исаков будет играть с каким – либо теннисистом
из России
Кол-во всех возможных исходов N = 45.
Кол-во благоприятных исходов N(A)=18.
Значит:
Ответ: 0.4.
.
Задача
Фабрика выпускает сумки. В среднем из 180 сумок восемь
сумок со скрытыми дефектами.
 Найдите вероятность того, что
Найдите вероятность того, чтокупленная сумка окажется качественной. Результат округлите до
сотых.
Решение:
N(A) = 180-8 = 172 сумки качественные,
N = 180 всего сумок
P(A) = 172/180 = 0,955…≈ 0,96
Ответ: 0,96.
Задача
.
В таблице приведены результаты диагностической работы
по математике в 9-х классах. Какова вероятность того, что оценка
выбранной наугад работы будет выше, чем среднее по школе
значение оценки?
Оценки
«2»
«3»
«4»
«5»
Число
учащихся
7
20
15
8
Решение:
7+20+15+8 = 50 – всего учащихся
(2*7+3*20+4*15+5*8):50 = 3,48 ≈ 3 – среднее по школе значение оценки.
15+8=23 – количество девятиклассников, получивших оценку выше
средней по школе.
Р = 23/50 = 0,46.
Ответ: 0,46.
Задача
.
Ваня забыл последние 2 цифры пароля для входа на сайт, но
помнит, что они различны и образуют двузначное число, меньшее 30.
С учетом этого он набирает наугад 2 цифры.
 Найти вероятность того,
Найти вероятность того,что это будут нужные цифры.
Решение:
Подсчитаем количество всех возможных двузначных чисел с
разными цифрами, меньшее 30, которые может набрать абонент:
10
20
12
21
13
23
14
24
15
25
16
26
17
27
18
28
19
29
Таких чисел 18. Так как только одно число правильное,
то искомая вероятность Р=1/18.
Ответ: 1/18.
Задача
Студент при подготовке к экзамену не успел выучить один из тех
25 билетов, которые будут предложены на экзамене. Какова
вероятность того, что студенту достанется на экзамене выученный
билет?
Решение:
N = 25 – количество билетов
N(A) = 25-1 = 24 – количество выученных
билетов
P(A)= 24/25 = 0,96 – искомая вероятность.
Ответ: 0,96.
В коробке имеется 3 кубика: чёрный, красный и белый.
Вытаскивая кубики наугад, мы ставим их последовательно
друг за другом. Какова вероятность того, что в результате
получится последовательность: красный, чёрный, белый?
Решение:
Сколько всего возможно результатов опыта? n=6
Пусть Ч – черный кубик, К – красный кубик, Б – белый
кубик, тогда
ЧКБ, ЧБК, БЧК, БКЧ, КЧБ, КБЧ.

P ( А)
1
Ответ:
6
m 1
1.
n 6
Домашнее задание:
1. Монета бросается 3 раза подряд. Найти вероятность
событий: А- число выпадений герба больше числа
выпадений решки; В- выпадает два герба; С- результаты
всех бросаний одинаковы.
2. Из урны, в которой находится 3 белых, 4 чёрных и 5
красных шаров, наудачу вынимается один шар. Какова
вероятность событий: А- появление белого шара; В –
появление чёрного шара; С- появление жёлтого шара; Dпоявление красного шара.
Вероятность несовместных событий
Факт 1.
Случайное событие – это событие, которое при данных условиях может произойти, а может не произойти.
Например, событие “при бросании игральной кости выпало 3 или 4 очка”. Напомним, что игральная кость – это кубик с шестью гранями, на которых написаны числа от 1 до 6.
Предположим, что мы проводим некоторое испытание (эксперимент), например, бросаем игральную кость. Результатом нашего испытания может быть одно из шести событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков. Такие события называются элементарными событиями (то есть это “простейшие” события, которые в совокупности образуют все множество исходов нашего эксперимента).
Результатом нашего испытания может быть одно из шести событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков. Такие события называются элементарными событиями (то есть это “простейшие” события, которые в совокупности образуют все множество исходов нашего эксперимента).
Например, событие “при бросании игральной кости выпало 3 или 4 очка” не является элементарным, оно состоит из двух элементарных событий “при бросании игральной кости выпало 3 очка” и “при бросании игральной кости выпало 4 очка”.
Если сложить вероятности всех возможных элементарных событий у некоторого эксперимента, то получится \(1\).
Два события мы будем называть равновероятными (равновозможными), если вероятности наступления любого из них одинаковы. Например, при бросании игральной кости вероятности любого из событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, одинаковы. Или, например, при подбрасывании монеты вероятности событий “выпадет орел” и “выпадет решка” также одинаковы.
Примером неравновероятных событий могут послужить два события: “при бросании игральной кости выпадет 1 очко” и “при бросании игральной кости выпадет нечетное количество очков”. Почему? В первом случае нам удовлетворяет только исход, когда кубик упадет кверху гранью, на которой написано 1; во втором случае нам подходит целых три исхода: он может выпасть кверху гранью с 1, с 3 или с 5.
Факт 2.
Если при проведении некоторого эксперимента возможны \(N\) равновероятных элементарных событий, то вероятность события \(A\) : \[P(A)=\dfrac mN,\] где \(m\) – количество “подходящих” элементарных событий.
Вероятность обозначается буквой \(P\).
На рисунке схематично изображено множество всех возможных равновероятных (одинаковые по размеру круги) исходов у некоторого эксперимента, которые не пересекаются:
Таким образом, под такой вероятностью можно понимать часть, которую составляют “подходящие” исходы от всех возможных исходов.
Давайте рассмотрим несколько примеров, в которых используется данная формула.
Пример 1.
Найдите вероятность того, что при бросании игральной кости выпадет 3 очка.
Решение. Всего при бросании игральной кости возможны шесть исходов (в данном случае, элементарные события), которые мы описывали ранее. Как мы уже говорили, вероятности наступления каждого из этих исходов одинаковы. Следовательно, \(N=6\). Подходит нам только один исход: когда выпадет 3 очка. Следовательно, \(m=1\).
Таким образом, вероятность нашего события равна \(\dfrac16\).
Вообще говоря, вероятность любого из исходов: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, равна \(\frac16\).
Пример 2.
Найдите вероятность того, что при бросании двух игральных костей в сумме выпадет 4 очка.
Решение. Для начала нужно найти количество всех возможных исходов у нашего эксперимента. Предположим, на первом кубике выпало 1. k\) элементарных исходов.
k\) элементарных исходов.
Теперь давайте подумаем, сколько из них нам подходит. Чтобы в сумме на обоих кубиках было 4 очка, нужно, чтобы:
– на первом кубике выпало 1, на втором 3 очка;
– на первом кубике выпало 2, а на втором 2 очка;
– на первом кубике выпало 3, а на втором 1 очко.
Таким образом, нам подходит только три исхода.
Следовательно, вероятность равна \(\dfrac3{36}=\dfrac1{12}\).
Пример 3.
Торт разделен на 9 кусков, которые условно пронумерованы числами от 1 до 9. Найдите вероятность того, что Маша возьмет кусок с номером 6.
Решение. Маша может взять любой из девяти кусков, следовательно, у нашего эксперимента всего девять исходов. Подходящий нам исход только один – Маша должна взять кусок с номером 6. Следовательно, вероятность равна \(\dfrac19\).
Пример 4.
В соревнованиях по толканию ядра участвуют 8 спортсменов из Аргентины, 6 спортсменов из Бразилии, 5 спортсменов из Парагвая и 6 — из Уругвая. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Аргентины.
Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Аргентины.
Решение. Заметим, что вероятность того, что спортсмен, выступающий последним, окажется из Аргентины, такая же, как вероятность, что он будет выступать первым, вторым, третьим и т.п. Всего претендентов на последнее место \(8+6+5+6=25\) спортсменов. Нам удовлетворяют лишь \(8\) из Аргентины.
Следовательно, вероятность равна отношению количества удовлетворяющих
исходов к количеству всех: \(\dfrac8{25}\).
Пример действительного входного события (слева) и соответствующего…
Время, в котором мы живем, часто называют информационным веком. Однако его также можно охарактеризовать как век постоянной информационной перегрузки. Нигде это не присутствует в большей степени, чем в Интернете, который служит бесконечным источником новостных статей, сообщений в блогах и сообщений в социальных сетях. Конечно, эта перегрузка еще больше в профессиях, связанных с созданием или извлечением информации и знаний, таких как журналисты, юристы, исследователи, клерки или медицинские работники.Объем доступных документов и взаимосвязанность их содержания являются одновременно и благом, и проклятием для современного потребителя информации. С одной стороны, они предоставляют почти безграничную информацию, но, с другой стороны, их потребление и понимание требует времени, которое многие из нас не могут выделить. В результате возросла популярность автоматизированных методов извлечения, агрегирования и суммирования, хотя они далеки от того, чтобы быть всеобъемлющими. Когда мы, люди, сталкиваемся с переизбытком информации, мы склонны искать закономерности, которые наводят порядок в хаосе.В новостях мы можем найти знакомых политических деятелей или знаменитостей, тогда как мы можем искать выразительные симптомы в медицине или прецеденты в законе. Другими словами, мы ищем известные сущности в качестве ориентиров, а затем исследуем содержание по линиям их отношений с другими сущностями.
Конечно, эта перегрузка еще больше в профессиях, связанных с созданием или извлечением информации и знаний, таких как журналисты, юристы, исследователи, клерки или медицинские работники.Объем доступных документов и взаимосвязанность их содержания являются одновременно и благом, и проклятием для современного потребителя информации. С одной стороны, они предоставляют почти безграничную информацию, но, с другой стороны, их потребление и понимание требует времени, которое многие из нас не могут выделить. В результате возросла популярность автоматизированных методов извлечения, агрегирования и суммирования, хотя они далеки от того, чтобы быть всеобъемлющими. Когда мы, люди, сталкиваемся с переизбытком информации, мы склонны искать закономерности, которые наводят порядок в хаосе.В новостях мы можем найти знакомых политических деятелей или знаменитостей, тогда как мы можем искать выразительные симптомы в медицине или прецеденты в законе. Другими словами, мы ищем известные сущности в качестве ориентиров, а затем исследуем содержание по линиям их отношений с другими сущностями. К сожалению, этот подход не отражен в текущих моделях документов, которые не обеспечивают аналогичного внимания к сущностям. В результате извлечение сущностно-ориентированных знаний и отношений из потока текстовой информации становится более трудным, чем должно быть, а включение внешних источников знаний затруднено.В этой диссертации мы представляем неявные сети сущностей как всеобъемлющую модель документа, которая устраняет этот недостаток и обеспечивает целостное представление коллекций документов и потоков документов. Основываясь на предпосылке моделирования отношений совпадения между терминами и сущностями как первоклассными гражданами, мы исследуем, как результирующая сетевая структура способствует эффективному и действенному поиску сущностей, и демонстрируем извлечение сложных отношений сущностей, а также их обобщение.Мы показываем, что неявная сетевая модель полностью совместима с динамическими потоками документов. Кроме того, мы вводим методы агрегирования документов, которые чувствительны к контексту упоминаний сущностей и могут использоваться для различения различных отношений сущностей.
К сожалению, этот подход не отражен в текущих моделях документов, которые не обеспечивают аналогичного внимания к сущностям. В результате извлечение сущностно-ориентированных знаний и отношений из потока текстовой информации становится более трудным, чем должно быть, а включение внешних источников знаний затруднено.В этой диссертации мы представляем неявные сети сущностей как всеобъемлющую модель документа, которая устраняет этот недостаток и обеспечивает целостное представление коллекций документов и потоков документов. Основываясь на предпосылке моделирования отношений совпадения между терминами и сущностями как первоклассными гражданами, мы исследуем, как результирующая сетевая структура способствует эффективному и действенному поиску сущностей, и демонстрируем извлечение сложных отношений сущностей, а также их обобщение.Мы показываем, что неявная сетевая модель полностью совместима с динамическими потоками документов. Кроме того, мы вводим методы агрегирования документов, которые чувствительны к контексту упоминаний сущностей и могут использоваться для различения различных отношений сущностей. Помимо отношений отдельных объектов, мы вводим сетевые темы как новый и масштабируемый метод для извлечения тем из коллекций и потоков документов. Наконец, мы объединяем идеи, полученные с помощью этих приложений, в универсальной модели гиперграфического документа, которая устраняет разрыв между неструктурированным текстом и структурированными источниками знаний.
Помимо отношений отдельных объектов, мы вводим сетевые темы как новый и масштабируемый метод для извлечения тем из коллекций и потоков документов. Наконец, мы объединяем идеи, полученные с помощью этих приложений, в универсальной модели гиперграфического документа, которая устраняет разрыв между неструктурированным текстом и структурированными источниками знаний.
События JavaScript
HTML-события — это «вещей» , которые происходят с элементами HTML.
Когда JavaScript используется на страницах HTML, JavaScript может «реагировать» на эти события.
HTML-события
Событием HTML может быть действие браузера или пользователя.
Вот несколько примеров событий HTML:
- Завершена загрузка HTML-страницы
- Поле ввода HTML было изменено
- Была нажата кнопка HTML
Часто, когда происходят события, вы можете захотеть что-то сделать.
JavaScript позволяет выполнять код при обнаружении событий.
HTML позволяет добавлять атрибуты обработчика событий с кодом JavaScript к элементам HTML.
С одинарными кавычками:
< элемент событие = ‘ какой-то JavaScript ‘ >
С двойными кавычками:
< элемент событие = » какой-то JavaScript » >
В следующем примере атрибут onclick (с кодом) добавляется к <кнопка> элемент:
Пример
В приведенном выше примере код JavaScript изменяет содержимое элемент с.
В следующем примере код изменяет содержимое
свой собственный элемент (с использованием this .innerHTML ):
Пример
Код JavaScript часто состоит из нескольких строк. Чаще можно увидеть атрибуты событий, вызывающие функции:
Чаще можно увидеть атрибуты событий, вызывающие функции:
Общие события HTML
Вот список некоторых распространенных HTML-событий:
| Событие | Описание |
|---|---|
| сменный | Элемент HTML был изменен |
| по клику | Пользователь щелкает элемент HTML |
| при наведении мыши | Пользователь наводит указатель мыши на элемент HTML |
| onmouseout | Пользователь отводит указатель мыши от элемента HTML |
| нажатие клавиши | Пользователь нажимает клавишу клавиатуры |
| под нагрузкой | Браузер завершил загрузку страницы |
Список намного длиннее: W3Schools JavaScript Reference HTML DOM Events.
Обработчики событий JavaScript
Обработчики событий могут использоваться для обработки и проверки пользовательского ввода, действий пользователя, и действия браузера:
- Действия, которые следует выполнять каждый раз при загрузке страницы
- Что нужно сделать, когда страница закрыта
- Действие, которое должно выполняться, когда пользователь нажимает кнопку
- Содержимое, которое должно быть проверено, когда пользователь вводит данные
- И еще.
 ..
..
Можно использовать множество различных методов, позволяющих JavaScript работать с событиями:
- Атрибуты событий HTML могут напрямую выполнять код JavaScript
- Атрибуты событий HTML могут вызывать функции JavaScript
- Вы можете назначать свои собственные функции обработчика событий элементам HTML
- Вы можете запретить отправку или обработку событий
- И многое другое …
Вы узнаете намного больше о событиях и обработчиках событий в главах HTML DOM.
События | Документация API jQuery
Прикрепить обработчик к событию для элементов.
Привяжите обработчик события к событию JavaScript «размытие» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «изменить» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «щелчок» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «contextmenu» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «dblclick» или вызовите это событие для элемента.
Прикрепите обработчик к одному или нескольким событиям для всех элементов, которые соответствуют селектору, сейчас или в будущем, на основе определенного набора корневых элементов.
Удалить обработчики событий, ранее прикрепленные с помощью .live() к элементам.
Привязать обработчик события к событию JavaScript «ошибка».
Текущий элемент DOM в фазе всплытия событий.
Необязательный объект данных, передаваемый методу события при привязке текущего выполняющегося обработчика.
Элемент, к которому был присоединен вызываемый в данный момент обработчик событий jQuery.
Возвращает информацию о том, вызывалось ли когда-либо событие event.preventDefault() для этого объекта события.
Возвращает значение, вызывавшееся когда-либо для этого объекта события.
Возвращает ли событие.stopPropagation() когда-либо вызывался для этого объекта события.
Указывает, была ли нажата клавиша META при запуске события.
Пространство имен, указанное при запуске события.
Положение мыши относительно левого края документа.
Положение мыши относительно верхнего края документа.
При вызове этого метода действие по умолчанию для события не будет запущено.
Другой элемент DOM, участвующий в событии, если он есть.
Последнее значение, возвращенное обработчиком событий, запущенным этим событием, если только значение не было неопределенным.
Предотвращает выполнение остальных обработчиков и предотвращает всплытие события вверх по дереву DOM.
Предотвращает всплытие события в дереве DOM, предотвращая уведомление родительских обработчиков о событии.
Элемент DOM, инициировавший событие.
Разница в миллисекундах между временем, когда браузер создал событие, и 1 января 1970 года.
Описывает характер события.
Для событий клавиш или мыши это свойство указывает конкретную клавишу или кнопку, которая была нажата.
Привяжите обработчик событий к событию JavaScript «фокус» или вызовите это событие для элемента.
Привязать обработчик события к событию focusin.
Привязать обработчик события к событию JavaScript focusout.
Привязать один или два обработчика к совпадающим элементам, которые будут выполняться, когда указатель мыши входит и покидает элементы.
Приостанавливает или прекращает выполнение события готовности jQuery.
Принимает функцию и возвращает новую, которая всегда будет иметь определенный контекст.
Объект, похожий на обещание (или «затем»), который разрешается, когда документ готов.
Привяжите обработчик события к событию JavaScript «keydown» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «нажатие клавиши» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «keyup» или вызовите это событие для элемента.
Прикрепите обработчик событий для всех элементов, соответствующих текущему селектору, сейчас и в будущем.
Привязать обработчик события к событию «загрузка» JavaScript.
Привяжите обработчик события к событию JavaScript «mousedown» или вызовите это событие для элемента.
Привяжите обработчик событий, который будет запускаться, когда мышь входит в элемент, или активируйте этот обработчик для элемента.
Привяжите обработчик события, который будет запускаться, когда мышь покидает элемент, или активируйте этот обработчик на элементе.
Привяжите обработчик события к событию JavaScript «mousemove» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «mouseout» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «mouseover» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «mouseup» или вызовите это событие для элемента.
Прикрепите функцию обработчика событий для одного или нескольких событий к выбранным элементам.
Прикрепить обработчик к событию для элементов. Обработчик выполняется не более одного раза для каждого элемента каждого типа события.
Укажите функцию для выполнения при полной загрузке DOM.
Привяжите обработчик события к событию JavaScript «изменение размера» или вызовите это событие для элемента.
Привяжите обработчик события к событию JavaScript «прокрутки» или вызовите это событие для элемента.
Привязать обработчик события к событию JavaScript «выбрать» или вызвать это событие для элемента.
Привяжите обработчик события к событию JavaScript «отправить» или вызовите это событие для элемента.
Привязать два или более обработчика к совпадающим элементам, чтобы они выполнялись попеременно.
Выполнить все обработчики и варианты поведения, прикрепленные к соответствующим элементам для данного типа события.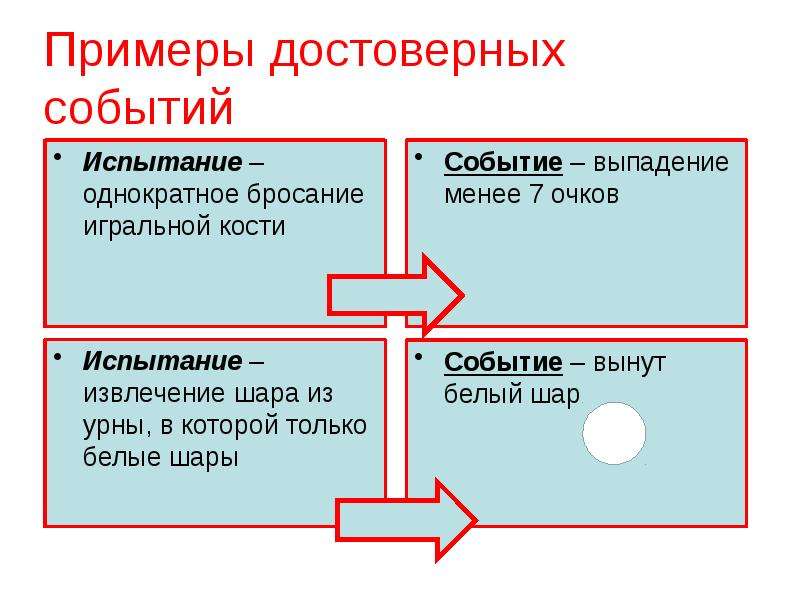
Выполнить все обработчики, прикрепленные к элементу для события.
Удалить ранее прикрепленный обработчик событий из элементов.
Удалить обработчик из события для всех элементов, соответствующих текущему селектору, на основе определенного набора корневых элементов.
Привязать обработчик события к событию «выгрузка» JavaScript.
| |||
приспособления[] | список | Файловые вложения для события. В настоящее время поддерживаются только вложения Google Диска. Чтобы изменить вложения, для параметра запроса Максимум 25 вложений на событие, | |
вложения[].идентификатор файла | струна | ID вложенного файла. Только для чтения. Для файлов Google Диска это идентификатор соответствующей записи ресурса | |
вложения[].fileUrl | струна | URL-ссылка на вложение. Для добавления вложенных файлов Google Диска используйте тот же формат, что и в свойстве Требуется при добавлении вложения. | доступный для записи |
вложения[].iconLink | струна | URL-ссылка на значок вложения. Только для чтения. | |
вложения[].mimeType | струна | Тип интернет-носителя (MIME-тип) вложения. | |
вложения[].title | струна | Заголовок вложения. | |
участниковПропущено | логическое значение | Возможно, участники были исключены из представления события. При извлечении события это может быть связано с ограничением, заданным параметром запроса При извлечении события это может быть связано с ограничением, заданным параметром запроса maxAttendee .При обновлении события это можно использовать только для обновления ответа участника. По желанию. Значение по умолчанию — Ложь. | доступный для записи |
участников[] | список | Участники мероприятия. Дополнительные сведения о планировании мероприятий с другими пользователями календаря см. в руководстве «Мероприятия с посетителями». Учетные записи служб должны использовать делегирование полномочий на уровне домена для заполнения списка участников. | доступный для записи |
посетителей[].additionalGuests | целое число | Количество дополнительных гостей. По желанию. По умолчанию 0. По желанию. По умолчанию 0. | доступный для записи |
участники[].displayName | струна | Имя участника, если доступно. По желанию. | доступный для записи |
участников[].электронная почта | струна | Адрес электронной почты участника, если он доступен. Это поле должно присутствовать при добавлении участника. Это должен быть действительный адрес электронной почты в соответствии с RFC5322. Требуется при добавлении участника. | доступный для записи |
участники[].id | струна | Идентификатор профиля посетителя, если он доступен. | |
участников[].опционально | логическое значение | Является ли это необязательным участником. По желанию. Значение по умолчанию — Ложь. | доступный для записи |
участники[].organizer | логическое значение | Является ли участник организатором мероприятия. Только для чтения. Значение по умолчанию — Ложь. | |
участников[].ресурс | логическое значение | Является ли участник ресурсом. Можно установить только при первом добавлении участника на мероприятие. Последующие модификации игнорируются. По желанию. Значение по умолчанию — Ложь. По желанию. Значение по умолчанию — Ложь. | доступный для записи |
участники[].responseStatus | струна | Статус ответа участника. Возможные значения:
| доступный для записи |
участники[].self | логическое значение | Представляет ли эта запись календарь, в котором появляется эта копия события. Только для чтения. Значение по умолчанию — Ложь. Только для чтения. Значение по умолчанию — Ложь. | |
идентификатор цвета | струна | Цвет события. Это идентификатор, относящийся к записи в разделе event определения цветов (см. конечную точку цветов). По желанию. | доступный для записи |
Данные конференции | вложенный объект | Информация о конференции, например сведения о конференции Google Meet.Чтобы создать новую информацию о конференции, используйте поле createRequest . Чтобы сохранить изменения, не забудьте установить для параметра запроса conferenceDataVersion значение 1 для всех запросов на изменение событий. | доступный для записи |
конференцияData.conferenceId | струна | ID конференции. Может использоваться разработчиками для отслеживания конференций, не должен отображаться для пользователей. Значение ID формируется по-разному для каждого типа конференц-решения:
 | |
конференцияData.conferenceSolution | вложенный объект | Решение для проведения конференций, например Google Meet. Отключено для конференции с неудачным запросом на создание. Требуется либо | |
Данные конференции.конференцияSolution.iconUri | струна | Значок этого решения, видимый пользователю. | |
конференцияData.conferenceSolution.key | вложенный объект | Ключ, который может однозначно идентифицировать решение конференции для данного события. | |
конференцияData.conferenceSolution.ключ.тип | струна | Тип решения конференции. Если клиент сталкивается с незнакомым или пустым типом, он все равно должен отображать точки входа. Однако он должен запрещать модификации. Возможные значения:
| |
конференцияData.conferenceSolution.name | струна | Имя этого решения, видимое пользователю. Не локализовано. | |
конференцияData.createRequest | вложенный объект | Запрос на создание новой конференции и ее присоединение к событию.Данные генерируются асинхронно. Чтобы увидеть, присутствуют ли данные, проверьте поле состояния . Требуется либо | |
конференцияData.createRequest.conferenceSolutionKey | вложенный объект | Решение для проведения конференций, например Hangouts или Google Meet. | |
конференцияData.createRequest.conferenceSolutionKey.type | струна | Тип решения конференции. Если клиент сталкивается с незнакомым или пустым типом, он все равно должен отображать точки входа. Однако он должен запрещать модификации. Возможные значения:
| |
конференцияData.createRequest.requestId | струна | Уникальный идентификатор, созданный клиентом для этого запроса. Клиенты должны повторно генерировать этот идентификатор для каждого нового запроса. Если предоставленный идентификатор совпадает с предыдущим запросом, запрос игнорируется. | |
Данные конференции.createRequest.статус | вложенный объект | Статус запроса на создание конференции. | |
конференцияData.createRequest.status.statusCode | струна | Текущий статус запроса на создание конференции. Только для чтения. Только для чтения.Возможные значения:
| |
конференцияData.entryPoints[] | список | Информация об отдельных точках входа в конференцию, например URL-адреса или номера телефонов. Все они должны принадлежать одной конференции. Требуется либо | |
конференцияData.entryPoints[].accessCode | струна | Код доступа для доступа к конференции. Максимальная длина составляет 128 символов. При создании новых данных конференции заполните только те поля { Дополнительно. | |
конференцияData.entryPoints[].entryPointType | струна | Тип точки входа в конференцию. Возможные значения:
| |
Данные конференции. | струна | Метка для URI. Виден конечным пользователям. Не локализовано. Максимальная длина составляет 512 символов. примеров:
| |
Данные конференции.входные точки[].meetingCode | струна | Код встречи для доступа к конференции. Максимальная длина составляет 128 символов. При создании новых данных конференции заполните только те поля { Дополнительно. | |
конференцияData.entryPoints[].пароль | струна | Пароль для доступа к конференции. Максимальная длина составляет 128 символов. При создании новых данных конференции заполните только те поля { | |
ConferenceData.entryPoints[].password | струна | Пароль для доступа к конференции. Максимальная длина составляет 128 символов. Максимальная длина составляет 128 символов. При создании новых данных конференции заполните только те поля { Дополнительно. | |
конференцияData.entryPoints[].pin | струна | PIN-код для доступа к конференции. Максимальная длина составляет 128 символов. При создании новых данных конференции заполните только те поля { Дополнительно. | |
конференцияData.entryPoints[].uri | струна | URI точки входа. Максимальная длина 1300 символов. Формат:
| |
ConferenceData.notes | струна | Дополнительные примечания (например, инструкции от администратора домена, юридические уведомления) для отображения пользователю.Может содержать HTML. Максимальная длина 2048 символов. По желанию. | |
конференцияДанные.подпись | струна | Подпись данных конференции. Генерируется на стороне сервера. Отменено для конференции с неудачным запросом на создание. Опционально для конференции с отложенным запросом на создание. | |
создано | дата-время | Время создания события (как метка времени RFC3339). Только для чтения. Только для чтения. | |
создатель | объект | Создатель события. Только для чтения. | |
создатель.displayName | струна | Имя создателя, если доступно. | |
создатель.электронная почта | струна | Адрес электронной почты создателя, если он доступен. | |
создатель.id | струна | Идентификатор профиля создателя, если он доступен. | |
создатель.я | логическое значение | Соответствует ли создатель календарю, в котором появляется эта копия события. Только для чтения. Значение по умолчанию — Ложь. | |
описание | струна | Описание события.Может содержать HTML. По желанию. | доступный для записи |
конец | вложенный объект | (эксклюзивное) время окончания события. Для повторяющегося события это время окончания первого экземпляра. | |
дата окончания | дата | Дата в формате «гггг-мм-дд», если это событие на целый день. | доступный для записи |
end.dateTime | дата-время | Время в виде комбинированного значения даты и времени (отформатировано в соответствии с RFC3339). Смещение часового пояса требуется, если часовой пояс явно не указан в timeZone . | доступный для записи |
конечный часовой пояс | струна | Часовой пояс, в котором указано время.(В формате имени базы данных часовых поясов IANA, например, «Европа/Цюрих».) Для повторяющихся событий это поле является обязательным и указывает часовой пояс, в котором повторяемость расширяется. Для одиночных событий это поле является необязательным и указывает пользовательский часовой пояс для начала/окончания события. | доступный для записи |
endTimeUnspecified | логическое значение | Действительно ли время окончания не указано.Время окончания по-прежнему предоставляется из соображений совместимости, даже если для этого атрибута установлено значение True. Значение по умолчанию — Ложь. | |
Etag | etag | ETag ресурса. | |
тип события | струна | Определенный тип события. Только для чтения. Возможные значения:
| |
расширенные свойства | объект | Расширенные свойства события. | |
расширенные свойства.private | объект | Свойства, которые являются частными для копии события, отображаемой в этом календаре. | доступный для записи |
extendedProperties.private.(key) | струна | Имя частного свойства и соответствующее значение. | |
extendedProperties.shared | объект | Свойства, которые являются общими для копий мероприятия в календарях других посетителей. | доступный для записи |
extendedProperties.shared.(key) | струна | Имя общего свойства и соответствующее значение. | |
гаджет | объект | Гаджет, продлевающий это событие. Гаджеты устарели; вместо этого эта структура используется только для возврата метаданных календаря дней рождения. | |
гаджет. | струна | Режим отображения гаджета. Устарело. Возможные значения:
| доступный для записи |
гаджет.высота | целое число | Высота гаджета в пикселях. Высота должна быть целым числом больше 0. Необязательно. Устарело. | доступный для записи |
gadget.iconLink | струна | URL значка гаджета. Схема URL должна быть HTTPS. Устарело. Устарело. | доступный для записи |
гаджет.ссылка | струна | URL гаджета. Схема URL должна быть HTTPS. Устарело. | доступный для записи |
гаджет.предпочтения | объект | Настройки. | доступный для записи |
гаджет.настройки.(ключ) | струна | Имя предпочтения и соответствующее значение. | |
гаджет.название | струна | Название гаджета. Устарело. Устарело. | доступный для записи |
тип гаджета | струна | Тип гаджета. Устарело. | доступный для записи |
ширина гаджета | целое число | Ширина гаджета в пикселях.Ширина должна быть целым числом больше 0. Необязательно. Устарело. | доступный для записи |
guestCanInviteOthers | логическое значение | Могут ли участники, кроме организатора, приглашать других участников на мероприятие. По желанию. Значение по умолчанию — Истина. | доступный для записи |
guestCanModify | логическое значение | Могут ли участники, кроме организатора, изменять событие. По желанию. Значение по умолчанию — Ложь. По желанию. Значение по умолчанию — Ложь. | доступный для записи |
гостейCanSeeOtherGuests | логическое значение | Могут ли другие посетители, кроме организатора, видеть участников мероприятия. По желанию. Значение по умолчанию — Истина. | доступный для записи |
HangoutLink | струна | Абсолютная ссылка на Google Hangout, связанную с этим событием.Только для чтения. | |
htmlСсылка | струна | Абсолютная ссылка на это событие в веб-интерфейсе Календаря Google. Только для чтения. | |
iCalUID | струна | Уникальный идентификатор события, определенный в RFC5545. Он используется для уникальной идентификации событий в календарных системах и должен указываться при импорте событий с помощью метода импорта. Обратите внимание, что | |
идентификатор | струна | Непрозрачный идентификатор события. При создании новых одиночных или повторяющихся событий вы можете указать их идентификаторы. Предоставляемые идентификаторы должны соответствовать следующим правилам: При создании новых одиночных или повторяющихся событий вы можете указать их идентификаторы. Предоставляемые идентификаторы должны соответствовать следующим правилам:
Если вы не укажете идентификатор, он будет автоматически сгенерирован сервером. Обратите внимание, что | доступный для записи |
вид | струна | Тип ресурса (« календарь#событие «). | |
местоположение | струна | Географическое положение события в произвольной форме. По желанию. | доступный для записи |
заблокирован | логическое значение | Является ли это заблокированной копией события, в которой нельзя внести изменения в основные поля события «сводка», «описание», «местоположение», «начало», «конец» или «повторение». Значение по умолчанию — Ложь. Только для чтения. Значение по умолчанию — Ложь. Только для чтения. | |
органайзер | объект | Организатор мероприятия. Если организатор также является участником, это указывается отдельной записью в поле участников с полем организатор , для которого установлено значение True. Чтобы изменить организатора, используйте операцию перемещения. Только для чтения, за исключением случаев импорта события. | доступный для записи |
органайзер.отображаемое имя | струна | Имя организатора, если имеется. | доступный для записи |
организатор. | струна | Адрес электронной почты организатора, если имеется. Это должен быть действительный адрес электронной почты в соответствии с RFC5322. | доступный для записи |
организатор.id | струна | Идентификатор профиля организатора, если он доступен. | |
органайзер.сам | логическое значение | Соответствует ли организатор календарю, в котором появляется эта копия события. Только для чтения. Значение по умолчанию — Ложь. | |
originalStartTime | вложенный объект | Для экземпляра повторяющегося события это время, когда это событие должно начаться в соответствии с данными повторения в повторяющемся событии, указанном в recurringEventId. Он однозначно идентифицирует экземпляр в серии повторяющихся событий, даже если экземпляр был перемещен в другое время. Неизменный. Он однозначно идентифицирует экземпляр в серии повторяющихся событий, даже если экземпляр был перемещен в другое время. Неизменный. | |
originalStartTime.date | дата | Дата в формате «гггг-мм-дд», если это событие на целый день. | доступный для записи |
originalStartTime.dateTime | дата-время | Время в виде комбинированного значения даты и времени (отформатировано в соответствии с RFC3339).Смещение часового пояса требуется, если часовой пояс явно не указан в timeZone . | доступный для записи |
originalStartTime. | струна | Часовой пояс, в котором указано время. (В формате имени базы данных часовых поясов IANA, например, «Европа/Цюрих».) Для повторяющихся событий это поле является обязательным и указывает часовой пояс, в котором повторяемость расширяется.Для одиночных событий это поле является необязательным и указывает пользовательский часовой пояс для начала/окончания события. | доступный для записи |
частныйКопия | логическое значение | Если установлено значение True, распространение событий отключено. Обратите внимание, что это не то же самое, что свойства частного события. По желанию. Неизменный. Значение по умолчанию — Ложь. | |
повторение[] | список | Список строк RRULE, EXRULE, RDATE и EXDATE для повторяющегося события, как указано в RFC5545. Обратите внимание, что строки DTSTART и DTEND не разрешены в этом поле; время начала и окончания события указывается в полях Обратите внимание, что строки DTSTART и DTEND не разрешены в этом поле; время начала и окончания события указывается в полях start и end . Это поле опущено для одиночных событий или экземпляров повторяющихся событий. | доступный для записи |
идентификатор повторяющегося события | струна | Для экземпляра повторяющегося события это идентификатор повторяющегося события, которому принадлежит этот экземпляр.Неизменный. | |
напоминания | объект | Информация о напоминаниях о событии для аутентифицированного пользователя. | |
напоминания. | список | Если в событии не используются напоминания по умолчанию, здесь перечислены напоминания, относящиеся к событию, или, если они не установлены, это означает, что для этого события не установлены напоминания.Максимальное количество напоминаний о переопределении — 5. | доступный для записи |
напоминания.переопределения[].метод | струна | Метод, используемый этим напоминанием. Возможные значения:
Требуется при добавлении напоминания. | доступный для записи |
напоминания.переопределяет[].минуты | целое число | Количество минут до начала события, когда должно срабатывать напоминание. Допустимые значения находятся в диапазоне от 0 до 40320 (4 недели в минутах). Требуется при добавлении напоминания. | доступный для записи |
напоминания.useDefault | логическое значение | Применяются ли к событию напоминания календаря по умолчанию. | доступный для записи |
последовательность | целое число | Порядковый номер согласно iCalendar. | доступный для записи |
источник | объект | Источник, из которого было создано событие. Например, веб-страница, сообщение электронной почты или любой документ, идентифицируемый по URL-адресу со схемой HTTP или HTTPS.Может быть просмотрен или изменен только создателем события. | |
источник.название | струна | Название источника; например, название веб-страницы или тема электронной почты. | доступный для записи |
источник.url | струна | URL-адрес источника, указывающего на ресурс. Схема URL должна быть HTTP или HTTPS. Схема URL должна быть HTTP или HTTPS. | доступный для записи |
начало | вложенный объект | (включительно) время начала события. Для повторяющегося события это время начала первого экземпляра. | |
дата начала | дата | Дата в формате «гггг-мм-дд», если это событие на целый день. | доступный для записи |
начало.датаВремя | дата-время | Время в виде комбинированного значения даты и времени (отформатировано в соответствии с RFC3339). Смещение часового пояса требуется, если часовой пояс явно не указан в timeZone . | доступный для записи |
начальный часовой пояс | струна | Часовой пояс, в котором указано время.(В формате имени базы данных часовых поясов IANA, например, «Европа/Цюрих».) Для повторяющихся событий это поле является обязательным и указывает часовой пояс, в котором повторяемость расширяется. Для одиночных событий это поле является необязательным и указывает пользовательский часовой пояс для начала/окончания события. | доступный для записи |
статус | струна | Статус события. По желанию. Возможные значения:
| доступный для записи |
резюме | струна | Название события. | доступный для записи |
прозрачность | струна | Блокирует ли событие время в календаре. По желанию. Возможные значения:
| доступный для записи |
обновленный | дата-время | Время последней модификации события (как метка времени RFC3339).Только для чтения. | |
видимость | струна | Видимость события. По желанию. Возможные значения:
| доступный для записи |
Events API для управления событиями и календарями
{
"мета": {
"код": "200"
},
"календарь": {
"id": "1473327868906",
"количество_событий": 33,
"link_short": "http:\/\/cal.ае\/эоадью",
"link_long": "https://www.addevent.com\/calendar\/pg261852"
},
"Мероприятия": [{
"id": "125163",
"title": "Название события",
"eventname": "Название события",
"description": "Описание события",
"location": "1600 Amphitheatre Pkwy, Mountain View, CA 94043",
"организатор": "Томас Скотт",
"organizer_email": "thomas@example. ком",
"date_start": "12\/21\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1640077200,
"дата_конец": ноль,
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1640084400,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример.орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt.
ком",
"date_start": "12\/21\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1640077200,
"дата_конец": ноль,
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1640084400,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример.орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt. to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200
}, {
"id": "125162",
"title": "Название события",
"eventname": "Название события",
"description": "Описание события",
"location": "1600 Amphitheatre Pkwy, Mountain View, CA 94043",
"организатор": "Томас Скотт",
"organizer_email": "thomas@example.ком",
"date_start": "12\/14\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1639472400,
"date_end": "12\/14\/2021",
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1639479600,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример.
to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200
}, {
"id": "125162",
"title": "Название события",
"eventname": "Название события",
"description": "Описание события",
"location": "1600 Amphitheatre Pkwy, Mountain View, CA 94043",
"организатор": "Томас Скотт",
"organizer_email": "thomas@example.ком",
"date_start": "12\/14\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1639472400,
"date_end": "12\/14\/2021",
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1639479600,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример. орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt.to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200 }],
"пейджинг": {
"предыдущий": "",
"далее": "https:\/\/www.addevent.com\/api\/v1\/oe\/events\/list\/?token=USER-TOKEN-ID&page=2"
}
}
орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt.to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200 }],
"пейджинг": {
"предыдущий": "",
"далее": "https:\/\/www.addevent.com\/api\/v1\/oe\/events\/list\/?token=USER-TOKEN-ID&page=2"
}
}
sched — Планировщик событий — Документация по Python 3.10.1
Исходный код: Lib/sched.py
Модуль sched определяет класс, реализующий событие общего назначения. планировщик:
планировщик:
- класс
график.планировщик( timefunc=time.монотонный , delayfunc=time.sleep ) Класс планировщика
0после каждого событие запускается, чтобы позволить другим потокам работать в многопоточном режиме. Приложения.Изменено в версии 3.3: параметры timefunc и delayfunc являются необязательными.
Изменено в версии 3.3: планировщик
классаможно безопасно использовать в многопоточных среды.
Пример:
>>> расписание импорта, время
>>> с = план.планировщик (время.время, время.сна)
>>> def print_time(a='default'):
... print("Из print_time", time.time(), а)
...
>>> определение print_some_times():
... печать (время.время())
... s.enter(10, 1, время печати)
... s.enter(5, 2, время_печати, аргумент=('позиционный',))
... s.enter(5, 1, print_time, kwargs={'a': 'ключевое слово'})
... s.run()
... печать (время.время())
...
>>> print_some_times()
930343690.257
От print_time 930343695.274 позиционный
От времени печати 930343695.275 ключевое слово
От print_time 930343700.273 по умолчанию
930343700.276
Объекты планировщика
экземпляры планировщика имеют следующие методы и атрибуты:
- Планировщик
.enterabs( время , приоритет , действие , аргумент=() , kwargs={} ) Запланировать новое событие. Аргумент time должен быть совместим с числовым типом.
 с возвращаемым значением функции timefunc , переданной в конструктор.События, запланированные на одно и то же время , будут выполняться в порядке их приоритет . Меньшее число представляет более высокий приоритет.
с возвращаемым значением функции timefunc , переданной в конструктор.События, запланированные на одно и то же время , будут выполняться в порядке их приоритет . Меньшее число представляет более высокий приоритет.Выполнение события означает выполнение
action(*argument, **kwargs). аргумент представляет собой последовательность, содержащую позиционные аргументы для действия . kwargs — это словарь, содержащий аргументы ключевого слова для действия .Возвращаемое значение — это событие, которое можно использовать для последующей отмены события. (см.
cancel()).Изменено в версии 3.3: аргумент параметр является необязательным.
Изменено в версии 3.3: kwargs добавлен параметр.
- Планировщик
.введите( задержка , приоритет , действие , аргумент=() , kwargs={} ) Запланировать событие на задержку еще на единиц времени.
 Помимо относительного времени,
другие аргументы, эффект и возвращаемое значение такие же, как и для
Помимо относительного времени,
другие аргументы, эффект и возвращаемое значение такие же, как и для введите абс().Изменено в версии 3.3: аргумент параметр является необязательным.
Изменено в версии 3.3: kwargs добавлен параметр.
- Планировщик
.отмена( событие ) Удалить событие из очереди. Если событие не является событием, очередь, этот метод вызовет ошибку
ValueError.
- Планировщик
.пустой() Вернуть
True, если очередь событий пуста.
- Планировщик
.запустить( блокировка = True ) Запустить все запланированные события. Этот метод будет ждать (используя
delayfunc()функция, переданная конструктору) для следующего события, затем выполнить ее и т. д.
до тех пор, пока не закончатся запланированные события.
д.
до тех пор, пока не закончатся запланированные события.Если блокировка имеет значение false, выполняются запланированные события, срок действия которых истекает в ближайшее время. (если есть), а затем вернуть крайний срок следующего запланированного звонка в планировщик (если есть).
Либо действие , либо delayfunc может вызвать исключение. В любом случае, планировщик будет поддерживать согласованное состояние и распространять исключение. Если исключение вызвано действием , событие не будет предпринято в будущих вызовах до
запустить().Если последовательность событий выполняется дольше, чем время, доступное до следующее событие, планировщик просто отстанет. Никакие события не будут удалены; вызывающий код отвечает за отмену событий, которые больше не уместно.
Изменено в версии 3.3: добавлен параметр блокировки .
- Планировщик
.очередь Атрибут только для чтения, возвращающий список предстоящих событий в том порядке, в котором они будет запущен.
 Каждое событие отображается в виде именованного кортежа с
следующие поля: время, приоритет, действие, аргумент, kwargs.
Каждое событие отображается в виде именованного кортежа с
следующие поля: время, приоритет, действие, аргумент, kwargs.
Узнайте, как установить SLO — советы SRE
Уравнение SLI представляет собой количество хороших событий, деленное на общее количество допустимых событий, умноженное на 100, чтобы сохранить однородный процент.
Давайте посмотрим на SLI, которые мы хотим измерить для критического пути пользователя «Оформить заказ». Представьте путь, который проходят ваши клиенты, чтобы купить товар в магазине. Сначала они тратят время на просмотр, изучение товаров, добавление товара в корзину (возможно, оставляют его там, чтобы подумать над ним еще немного), а затем, наконец, когда они готовы, решают оформить заказ. Если вы зайдете так далеко со своим клиентом, вы можете предположить, что вам удалось завоевать его бизнес, поэтому абсолютно необходимо, чтобы клиентов могли оформить заказ .
Вот SLI, которые следует учитывать для этого пути пользователя.
Availability SLI
Мы хотим, чтобы функция проверки нашего сервиса была доступна для наших пользователей, поэтому мы выберем доступность SLI. То, что мы ищем, — это метрика, которая скажет нам, насколько хорошо наш сервис работает с точки зрения доступности. В этом случае мы хотим отслеживать, сколько пользователей пытались проверить и сколько из этих запросов были успешными, поэтому количество успешных запросов является «хорошей» метрикой.Важно подробно описать, что именно мы собираемся измерять и где мы планируем это измерять, поэтому SLI доступности должен выглядеть примерно так:
Доля запросов HTTP GET для /checkout_service/response_counts, не имеющих статуса 5XX ( 3XX и 4XX исключены) измерено в сервисной сетке Istio.
Почему исключены коды состояния 3XX и 4XX? Мы не хотим подсчитывать события, которые не указывают на сбой в нашей службе, потому что они будут сбрасывать наши сигналы SLI, поэтому мы исключаем перенаправления 3XX и ошибки клиента 4XX из нашего «общего» значения.
Latency SLI
Вы также должны убедиться, что подтверждение заказа будет возвращено покупателю в течение приемлемого периода времени. Для этого установите SLI задержки, который измеряет, сколько времени занимает успешный ответ. Здесь мы установим значение 500 мс для возврата ответа, предполагая, что это приемлемый порог для бизнеса. Таким образом, SLI задержки будет выглядеть следующим образом:
Доля HTTP-запросов GET для /checkout_service/response_counts, которые не имеют статуса 5XX (за исключением 3XX и 4XX), которые отправляют весь свой ответ в течение 500 мс, измеренная в сервисной сетке Istio.
Шаг 3. Определите целевые показатели SLO и период измерения SLO
Когда у нас есть SLI, пришло время установить SLO. Целевые показатели уровня обслуживания являются целевыми индикаторами уровня обслуживания в течение определенного временного окна. Это помогает измерить, соответствует ли надежность службы в течение определенного периода времени, например месяца, квартала или года, ожиданиям большинства ее пользователей.
Например, если в течение одного календарного месяца поступило 10 000 HTTP-запросов и только 9 990 из них вернули успешный ответ в соответствии с SLI, это соответствует 9 990/10 000 или 99.Доступность 9% в этом месяце.
Важно установить достижимую цель, чтобы предупреждения были значимыми. Обычно при выборе SLO лучше всего исходить из исторических тенденций и исходить из того, что если достаточное количество людей довольны сервисом сейчас, то, вероятно, у вас все в порядке. В конце концов, было бы идеально сопоставить эти цифры с желаемыми целями, которые ваш бизнес может захотеть от вас достичь.
Мы можем сказать, что наш SLO будет 99,9%, согласно тенденциям исторических данных.Затем пришло время поместить эти слова в настоящие осязаемые информационные панели и оповещения.
Шаг 4. Создание консолей SLI, SLO и бюджета ошибок
Как инженеры, мы должны иметь возможность видеть состояние службы в любое время, а это означает, что нам необходимо создавать панели мониторинга. Для мониторинга, ориентированного на клиента, нам нужны графики SLI, SLO и бюджетов ошибок.
Для мониторинга, ориентированного на клиента, нам нужны графики SLI, SLO и бюджетов ошибок.
Большинство систем мониторинга работают очень похожим образом, поэтому вам решать, какую из них использовать.Основные компоненты, как правило, одинаковы. Разбивка SLI Checkout Availability на общие поля мониторинга, скорее всего, будет выглядеть так:
Приложив много усилий, вы сможете рассчитать правильные определения, необходимые для создания графиков SLI и SLO. Но этот процесс может быть довольно утомительным, особенно если вам нужно создать несколько сервисов и SLO. К счастью, компонент мониторинга служб Cloud Operations может автоматически генерировать эти графики. Поскольку в этом примере мы используем интеграцию сервисной сетки Istio, возможность наблюдения в системе становится еще более доступной.Вот как настроить панель мониторинга с помощью Service Monitoring:
1. Перейдите на страницу Monitoring в Cloud Console и выберите Services
2. Поскольку мы используем Istio, наши сервисы автоматически доступны для Cloud Monitoring, так что вам просто нужно для выбора кассового сервиса.



 ..
..
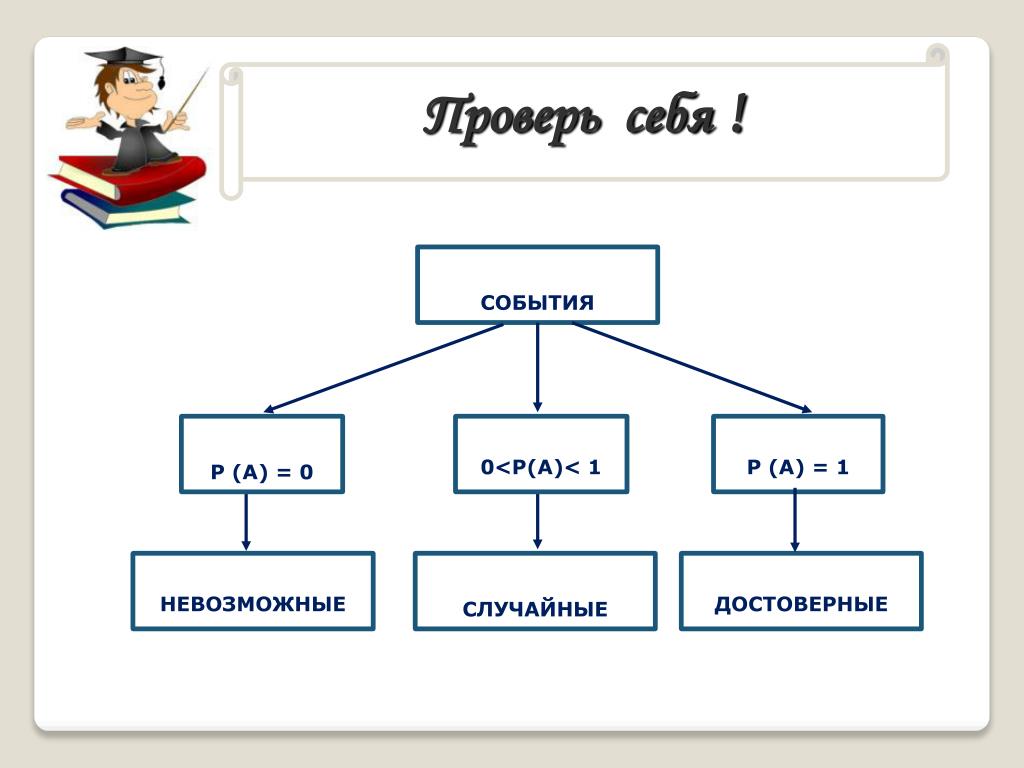 google.com)
google.com)
 google.com)
google.com)
 точки входа[].label
точки входа[].label  Должны отображаться только заполненные поля.
Должны отображаться только заполненные поля. Должны отображаться только заполненные поля.
Должны отображаться только заполненные поля.

 дисплей
дисплей  Одно различие в их семантике заключается в том, что в повторяющихся событиях все вхождения одного события имеют разные идентификаторы
Одно различие в их семантике заключается в том, что в повторяющихся событиях все вхождения одного события имеют разные идентификаторы  электронная почта
электронная почта  timeZone
timeZone  переопределения[]
переопределения[] 

 Другие поля могут быть пустыми.
Другие поля могут быть пустыми.


 ком",
"date_start": "12\/21\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1640077200,
"дата_конец": ноль,
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1640084400,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример.орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt.
ком",
"date_start": "12\/21\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1640077200,
"дата_конец": ноль,
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1640084400,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример.орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt.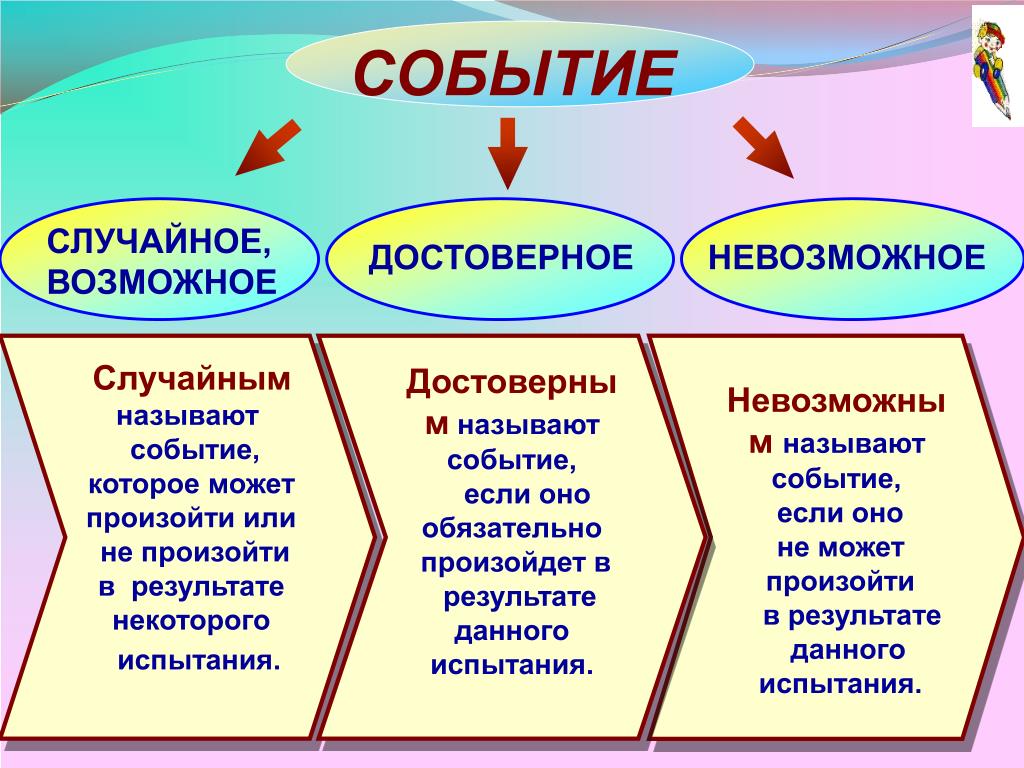 to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200
}, {
"id": "125162",
"title": "Название события",
"eventname": "Название события",
"description": "Описание события",
"location": "1600 Amphitheatre Pkwy, Mountain View, CA 94043",
"организатор": "Томас Скотт",
"organizer_email": "thomas@example.ком",
"date_start": "12\/14\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1639472400,
"date_end": "12\/14\/2021",
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1639479600,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример.
to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200
}, {
"id": "125162",
"title": "Название события",
"eventname": "Название события",
"description": "Описание события",
"location": "1600 Amphitheatre Pkwy, Mountain View, CA 94043",
"организатор": "Томас Скотт",
"organizer_email": "thomas@example.ком",
"date_start": "12\/14\/2021",
"date_start_time": "09:00:00",
"date_start_ampm": "AM",
"date_start_unix": 1639472400,
"date_end": "12\/14\/2021",
"date_end_time": "11:00:00",
"date_end_ampm": "AM",
"date_end_unix": 1639479600,
"all_day_event": "ложь",
"date_format": "ММ\/ДД\/ГГГГ",
"timezone": "Америка\/Лос-Анджелес",
"напоминание": "60",
"правило": "",
"updated_times": "0",
"rsvp_require": "истина",
"rsvp_template_id": "",
"rsvp_seat_limited": "истина",
"rsvp_seat_limit": "50",
"rsvp_seats_left": "45",
"rsvp_inactive": "ложь",
"rsvp_notify": "электронная почта@пример. орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt.to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200 }],
"пейджинг": {
"предыдущий": "",
"далее": "https:\/\/www.addevent.com\/api\/v1\/oe\/events\/list\/?token=USER-TOKEN-ID&page=2"
}
}
орг",
"rsvp_count": "8",
"rsvp_attn_going": "5",
"rsvp_attn_maybe": "2",
"rsvp_attn_cantgo": "1",
"цвет": "2",
"пользовательские_данные": "",
"link_short": "https://evt.to\/iaaehuuw",
"link_long": "https://www.addevent.com\/event\/xh5112744",
"дата_создания": 1640077200,
"date_modified": 1640077200 }],
"пейджинг": {
"предыдущий": "",
"далее": "https:\/\/www.addevent.com\/api\/v1\/oe\/events\/list\/?token=USER-TOKEN-ID&page=2"
}
}

 с возвращаемым значением функции timefunc , переданной в конструктор.События, запланированные на одно и то же время , будут выполняться в порядке их приоритет . Меньшее число представляет более высокий приоритет.
с возвращаемым значением функции timefunc , переданной в конструктор.События, запланированные на одно и то же время , будут выполняться в порядке их приоритет . Меньшее число представляет более высокий приоритет. Помимо относительного времени,
другие аргументы, эффект и возвращаемое значение такие же, как и для
Помимо относительного времени,
другие аргументы, эффект и возвращаемое значение такие же, как и для  д.
до тех пор, пока не закончатся запланированные события.
д.
до тех пор, пока не закончатся запланированные события. Каждое событие отображается в виде именованного кортежа с
следующие поля: время, приоритет, действие, аргумент, kwargs.
Каждое событие отображается в виде именованного кортежа с
следующие поля: время, приоритет, действие, аргумент, kwargs.