Сколько корней имеет квадратное уравнение: Сколько корней имеет квадратное уравнение? Вы точно уверены, что 2 ? | Математика не для всех
Сколько корней имеет квадратное уравнение? Вы точно уверены, что 2 ? | Математика не для всех
Подписывайтесь на канал в Яндекс. Дзен или на канал в телеграм «Математика не для всех», чтобы не пропустить интересующие Вас материалы. Также есть группы в VK, Одноклассниках и Facebook : всё для математического просвещения!
Сколько корней имеет квадратное уравнение? Менее умудренные математики ответят, что может иметь два, один или вообще не иметь корней. Другие же отметят, что квадратное уравнение в любом случае имеет два корня (комплексных с ненулевой мнимой частью), даже если его дискриминант меньше нуля, а в случае равенства дискриминанту нуля — два совпадающих корня. Но что, если я скажу, квадратный трехчлен может иметь 4 (!!!) разных корня? Как пелось в песне: «Не спешите нас хоронить, а у нас еще здесь дела. ..«. И моё дело — рассказать, как такое возможно. Поехали!
..«. И моё дело — рассказать, как такое возможно. Поехали!
Теорема Безу известна большинству тех, кто знал математику хотя бы на «хорошо». В школьном курсе (в 7-8 классе) она формулировалась таким образом:
Таким образом, если многочлен делится без остатка на выражение (x-a), то число а — является корнем многочлена, а также корнем уравнения P(x)=0.
Вот как это выглядит на самом простом примере:
Но не всё так однозначно. В школьной математике теорема Безу формулируется без уточнения над каким кольцом чисел она применяется. Этот важный факт и приведет нас к неожиданному результату.
Что такое кольцо?
Под кольцом понимается любая алгебраическая структура (будем говорить для простоты «множество») в котором определены операции умножения и обратимого сложения, а также некоторые свойства, такие как коммутативность и ассоциативность сложения, наличие нейтрального элемента относительно сложения (наличие 0), наличие обратного элемента относительно сложения (наличие -a) дистрибутивность
В общем случае наличие нейтрального элемента относительно умножения (наличие 1) и коммутативность относительно умножения (a x b = b x a) не требуется.Если эти условия выполняются, такое кольцо называется коммутативным с единицей.
Школьная математика (если не залезать в комплексные числа) «живет» над кольцом вещественных чисел (которое, кроме того, является и полем, но эту уже другая история). Вот пример множества, не являющегося кольцом:
Очевидно, что если рассмотреть множество целых чисел, то есть добавить к натуральным 0 и отрицательные числа, то полученное множество можно будет назвать кольцом, более того сразу коммутативным кольцом с единицей. Так же дела обстоят и с множеством вещественных чисел. Ведь и там и там есть нейтральные элементы (0 и 1) и все остальные требования выполняются (например, 3 + (-3) = 0, 3*4=4*3 и т.д.).
Мои статьи про числа: про натуральные и про вещественные.
Подведем итог первой части, исправив школьный пробел: теорема Безу верна, если коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей. По-простому: если коэффициенты — это любые числа из обычного курса математики, то квадратное уравнение имеет 2 корня и его можно разложить в виде (x-x1)*(x-x2).
По-простому: если коэффициенты — это любые числа из обычного курса математики, то квадратное уравнение имеет 2 корня и его можно разложить в виде (x-x1)*(x-x2).
Однако, бывают и другие коммутативные кольца, где всё не так однозначно и корней может быть больше. Поговорим об этом во второй частиИсточник: https://www.mirf.ru/wp-content/uploads/2018/04/The_One_Ring_1510632814498.jpg
Источник: https://www.mirf.ru/wp-content/uploads/2018/04/The_One_Ring_1510632814498.jpg
**************************************************************************
Путеводитель по каналу «Математика не для всех» — здесь собрано больше 100 статей на самые разнообразные темы: как для новичков, так и для более начитанных математиков! Например, почитайте про самое маленькое число, которое когда-либо использовалось учеными.
Второй проект — канал «Русский язык не для всех»
Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием. ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.
ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.
**************************************************************************
Решение квадратных уравнений
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь —
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравненияКогда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]
\\ \end{align}\]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант.
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.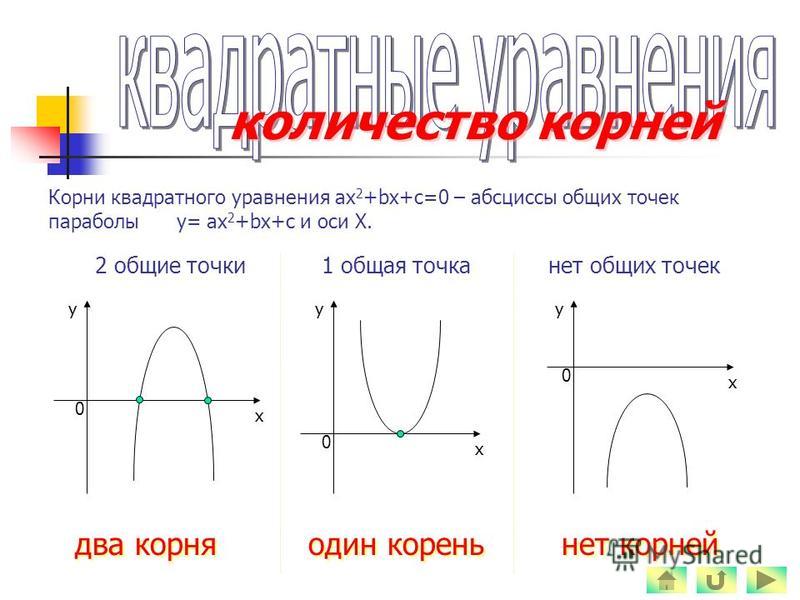
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Смотрите также:
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Метод коэффициентов, часть 1
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: строительные бригады
Математика
Муниципальное Бюджетное Общеобразовательное Учреждение Камбарская средняя общеобразовательная школа № 3
КОНСПЕКТ УРОКА ПО АЛГЕБРЕ
«КВАДРАТНЫЕ УРАВНЕНИЯ»
Подготовила
Учитель математики
Шляпникова Елена Ивановна
г. Камбарка
Камбарка
2015
Урок-соревнование по теме: «Квадратные уравнения» , 8 класс.
Цели: образовательные: повторение, обобщение и систематизация материала темы,
контроль усвоения знаний и умений;
развивающие: развитие математического и общего кругозора, мышления и речи,
внимания и памяти;
воспитательные: воспитание интереса к математике, активности, умения общаться.
Подготовка к уроку: класс делиться на группы по 4 человека.
Ход урока.
Добрый день!
Сегодня на уроке мы должны показать свои знания. Проводя упорные «тренировки» на предыдущих занятиях по решению квадратных уравнений, сегодня мы узнаем, кто из вас «возьмет больший вес». Условно вес штанги будет определяться в количестве баллов полученных за решение заданий.
(Класс делится на команды по
4 человека. )
)
Каждый этап соревнования оценивается баллами: за каждое верно выполненное задание – 1 балл. Если во время какого-то этапа команда выполняет быстрее всех задание, то она может взять дополнительное задание, за которое может получить дополнительные баллы.
Дополнительные задания:
1) (х² + 1 )/ 2 – 2х = -1 2) (х² — 3 )/2 – 6х = 5
3) (х² — 4 )/3 + 4х = 3 4) (х² — х )/3 = ( 2х – 4 )/ 5
І. Разминка: (мах 3 балла)
Команды отвечают по очереди на вопросы ( по одному каждой команде )
- Дайте определение квадратного уравнения.
- Какие квадратные уравнения называются неполными?
- Какие квадратные уравнения называются приведенными?
- По какой формуле вычисляется дискриминант квадратного уравнения?
- Если дискриминант меньше нуля, сколько корней имеет квадратное уравнение?
- Если дискриминант больше нуля, сколько корней имеет квадратное уравнение?
- Если дискриминант равен нулю, сколько корней имеет квадратное уравнение?
- Сформулировать теорему Виета.
 Что
позволяет сделать эта теорема?
Что
позволяет сделать эта теорема? - Сформулировать теорему обратную теореме Виета. Что позволяет сделать эта теорема?
ІІ. «4-й лишний» (мах 3 балла)
Найти лишнее уравнение в каждой группе
1 группа
1) х2-4=0
2) х2-6х+1=0
3) х2-121=0
4) х2-9х=0
2 группа
1) х2-6х=0
2) х2+3х=0
3) 4х2+5х=0
4) 3х2=0
3 группа
1) 9х2+х-4=0
2) 7х2-6х=0
3) х2-3х-7=0
4) х2-4х+2=0
ІІІ. «Торопись, да не ошибись» (мах 4 балла)
Члены команд на листочках выполняют задания:
1) 49 = 14х + 2х²
2) х² — 4х = 5
3) 2х² — 8 = 0
4) ( х – 2 ) х = 0
5) х² — 9 = 0
6) 35 х² + 2х — 1 = 0
7) х – 5 = 0.
а ) среди данных уравнений укажите номера тех, которые являются полными, приведенными, неполными;
б ) в уравнении №5 запишите значения коэффициентов а, в, с;
в ) найдите сумму и произведение корней уравнения №2;
г ) решите уравнение №6.
ІV. Конкурс капитанов + «Цепочка» (мах 2 балла)
Капитаны решают уравнение:
(х + 1)² + ( 1 + х )5 = 14
Одновременно с конкурсом капитанов проводится эстафета «Цепочка»: сидящие за партами решают уравнение, в котором дискриминант находит первый ученик, первый корень – второй ученик, второй корень – третий ученик.
5 х² — 4х – 1 = 0
V. «Найди ошибку» ( мах 7 баллав)
Каждая команда должна в данных уравнениях найти ошибку:
1) 2 х² — 3х – 2 = 0 2) 2у – 9у² + 10 = 0
Д = (-3)² — 4∙2∙(-2) = 9 + 16 = 25 Д = (-9)² — 4∙2∙10 = 81 – 80 = 1
х1 = = = у1 = = = 2,5
х2 = = = -2 у2 = = = 2
3) 9 х² — 14х + 5 = 0 4) 12 х² — 4х – 1 = 0
Д = (-7)² — 5∙9 =49 – 45 = 4 Д = (-2)² — 12∙(-1) = 4 + 12 = 16
х1 = = = 1 х1 = = =
х2 = = = 1 х2 = = = 0
5) х² + 11х – 12 = 0 6) х² + х – 56 = 0 7) х² — 49 = 0
х1 + х2 = 11 х1 = 12 х1 + х2 = -1 х1 = -7 х² =
49
х1 ∙ х2 = — 12 х2 = -1 х1 ∙ х2 = -56 х2 = 8 х = 7
VІ. «Тише едешь, дальше будешь» ( мах 5
баллов, за задачу 2 балла)
«Тише едешь, дальше будешь» ( мах 5
баллов, за задачу 2 балла)
Команде дается задание, которое она должна выполнить за 7 мин.
1) Решить уравнение х² = 12 – 11х
2) Решить уравнение 2 х² — 3х + 2 = 0
3) Уравнение х² + bх + 24 = 0 имеет корень х = 8. Найдите b и второй корень.
4) Решить задачу: В прямоугольном треугольнике один из катетов на 3 см меньше гипотенузы, а другой – на 6 см меньше гипотенузы. Найти гипотенузу и площадь треугольника.
В конце урока пока жюри подводит итоги, выполняются задания из рубрики «Это интересно»
1. Если в квадратном уравнении ах² + bх + с = 0 сумма коэффициентов а + b + с = 0,
то х = 1 и х = с/а
Например, 5х² — 7х + 2 = 0 ; а + b + с = 5 — 7 + 2 = 0 следовательно, х = 1 и х = 2/5
2. Если в том же уравнении а — b + с = 0, то х = -1 и х = -с/а
Например, 3х² + 2х –
1 = 0 ; а — b + с = 3 – 2 + (-1) = 0 следовательно, х = -1 и х = ⅓.
Используя теоремы, найти корни уравнения: 1978 х² + 1984х + 6 = 0
Жюри подводит итоги и называет победителей- чья команда смогла поднять самую тяжелую штангу.
Задание на дом: 1. Используя теоремы, записанные в конце урока, решить уравнения:
а) 345х² + 137х – 208 = 0; б) 132х² — 247х + 115 = 0.
2. № 650 (а), 654(а,б)
Приложения
Вопросы
- Дайте определение квадратного уравнения.
- Какие квадратные уравнения называются неполными?
- Какие квадратные уравнения называются приведенными?
- По какой формуле вычисляется дискриминант квадратного уравнения?
- Если дискриминант меньше нуля, сколько корней имеет квадратное уравнение?
- Если дискриминант больше нуля, сколько корней имеет квадратное уравнение?
- Если дискриминант равен нулю, сколько корней имеет квадратное уравнение?
- Сформулировать теорему Виета.
 Что
позволяет сделать эта теорема?
Что
позволяет сделать эта теорема? - Сформулировать теорему обратную теореме Виета. Что позволяет сделать эта теорема?
«4-й лишний»
Найти лишнее уравнение в каждой группе
1 группа
1) х2-4=0
2) х2-6х+1=0
3) х2-121=0
4) х2-9х=0
2 группа
1) х2-6х=0
2) х2+3х=0
3) 4х2+5х=0
4) 3х2=0
3 группа
1) 9х2+х-4=0
2) 7х2-6х=0
3) х2-3х-7=0
4) х2-4х+2=0
«Торопись, да не ошибись»
1) 49 = 14х + 2х²
2) х² — 4х = 5
3) 2х² — 8 = 0
4) ( х – 2 ) х = 0
5) х² — 9 = 0
6) 35 х² + 2х — 1 = 0
7) х – 5 = 0.
а ) среди данных уравнений укажите номера тех, которые являются полными-
приведенными-
неполными-
б ) в уравнении №5 запишите значения коэффициентов а= , в= , с= ;
в ) найдите сумму и произведение корней уравнения №2; х1+х2= х1 х2=
г ) решите уравнение №6.
Конкурс капитанов + «Цепочка»
Капитанам решить уравнение (х+1)2+5 (1+х)=14
Остальные ребята решают по цепочке уравнение 5х2-4х-1=0
1-й выписать коэффициенты
Вычислить дискриминант Д=
2-й найти один корень х1=
3-й найти второй корень х2=
«Найди ошибку»
1) 2 х² — 3х – 2 = 0 2) 2у – 9у² + 10 = 0
Д = (-3)² — 4∙2∙(-2) = 9 + 16 = 25 Д = (-9)² — 4∙2∙10 = 81 – 80 = 1
х1 = = = у1 = = = 2,5
х2 = = = -2 у2 = = = 2
3) 9 х² — 14х + 5 = 0 4) 12 х² — 4х – 1 = 0
Д = (-7)² — 5∙9 =49 – 45 = 4 Д = (-2)² — 12∙(-1) = 4 + 12 = 16
х1 = = = 1 х1 = = =
х2 = = = 1 х2 = = = 0
5) х² + 11х – 12 = 0 6) х² + х – 56 = 0 7) х² — 49 = 0
х1 + х2 = 11 х1 = 12 х1 + х2 = -1 х1 = -7 х² = 49
х1 ∙ х2 = — 12 х2 = -1 х1 ∙ х2 = -56 х2 = 8 х = 7
«Тише едешь, дальше будешь»
1) Решить уравнение х² = 12 – 11х
2) Решить уравнение 2 х² — 3х + 2 = 0
3) Уравнение х² + bх + 24 =
0 имеет корень х = 8. Найдите b и второй корень.
Найдите b и второй корень.
4) Решить задачу: В прямоугольном треугольнике один из катетов на 3 см меньше гипотенузы, а другой – на 6 см меньше гипотенузы. Найти гипотенузу и площадь треугольника.
Использованная литература
- Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2002.
Как решать квадратные уравнения? Формулы и Примеры
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:
Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:
- если D < 0, корней нет;
- если D = 0, есть один корень;
- если D > 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x2 — 2x + 6 = 0
- x2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.
- 2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Запоминаем!
У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.
Пример 1. Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: |
|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. |
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax2 + c = 0, при b = 0;
- ax2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax
2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.
Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.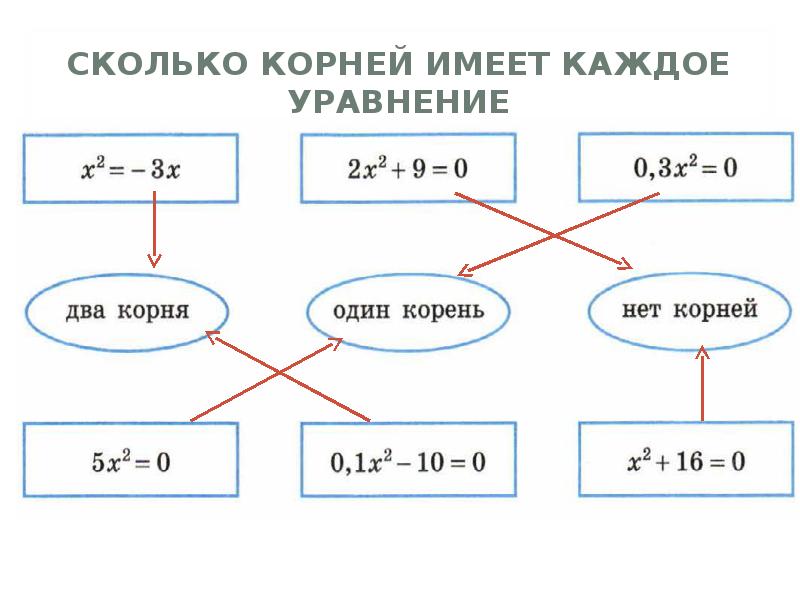
Пример 1. Решить −6x2 = 0.
Как решаем:
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
−6x2 = 0
x2 = 0
x = √0
x = 0
Ответ: 0.
Как решить уравнение ax
2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:
- перенесем c в правую часть: ax2 = — c,
- разделим обе части на a: x2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.
Если — c/а > 0, то корни уравнения x2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
| В двух словах |
|---|
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению х2= -c/a, которое:
|
Пример 1. Найти решение уравнения 8x2 + 5 = 0.
Как решать:
- Перенесем свободный член в правую часть:
8x2 = — 5
- Разделим обе части на 8:
x2 = — 5/8
- В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x2 + 5 = 0 не имеет корней.
Как решить уравнение ax
2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x2 + 0,125x = 0
Как решать:
- Вынести х за скобки
х(0,5x + 0,125) = 0
- Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
- Решить линейное уравнение:
0,5x = 0,125,
х = 0,125/0,5 - Разделить:
х = 0,25
- Значит корни исходного уравнения — 0 и 0,25.
Ответ: х = 0 и х = 0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2). |
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
Выглядит она так:
где D = b2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
, .
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b2−4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.
Как решаем:
- Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
х = — 28/2(-4)
х = 3,5
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x2 = 0.
Как решаем:
- Произведем равносильные преобразования. Умножим обе части на −1
54 — 6x2 = 0 | *(-1)
6x2 — 54 = 0
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6x2 = 54
х2 = 9
х = ±√9
х1 = 3, х2 = — 3
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x2— х = 0.
Как решаем:
- Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ = 1
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x2— 10 = 39.
Как решаем:
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x2— 10 = 39
x2= 39 + 10
x2= 49
х = ±√49
х₁ = 7, х₂ = −7
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x2— 4x+94 = 0.
Как решаем:
- Найдем дискриминант по формуле
D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112
- Дискриминант отрицательный, поэтому корней нет.
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.
Рассмотрим, как появилась эта формула.
Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2— 4ac = 4n2 — 4ac = 4(n2— ac) и подставим в формулу корней:
Для удобства вычислений обозначим выражение n2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n2— ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n2— ac;
- если D1< 0, значит действительных корней нет;
- если D1= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
- если же D1> 0, значит можно найти два действительных корня по формуле
Формула Виета
youtube.com/embed/LKGtbQZzBuo»/>
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. |
Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0. |
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Пифагора: x2 − 6x + 8 = 0.
Как решаем:
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
- Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6.
 А значения 4 и 2 подходят обоим равенствам:
А значения 4 и 2 подходят обоим равенствам: - Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x2 — 4 x — 6 = 0, чем 1100x2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x2— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x2— 3x + 7 = 0 перейти к решению 2x2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
- x₁ + x₂ = — b/a,
- x₁* x₂ = c/a.
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
Формула корней квадратного уравнения
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!
С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!Список вопросов теста
Вопрос 1
Сколько корней имеет квадратное уравнение, если:
Варианты ответов
Вопрос 2
Решите уравнение x2 — 3x + 2 = 0.
Варианты ответов
Вопрос 3
Сколько корней имеет квадратное уравнение?
Варианты ответов
- 1 корень
- 2 корня
- 3 корня
- 4 корня
- не имеет корней
Вопрос 4
Найдите корни квадратного уравнения 5x2 + 15x +102 = 0.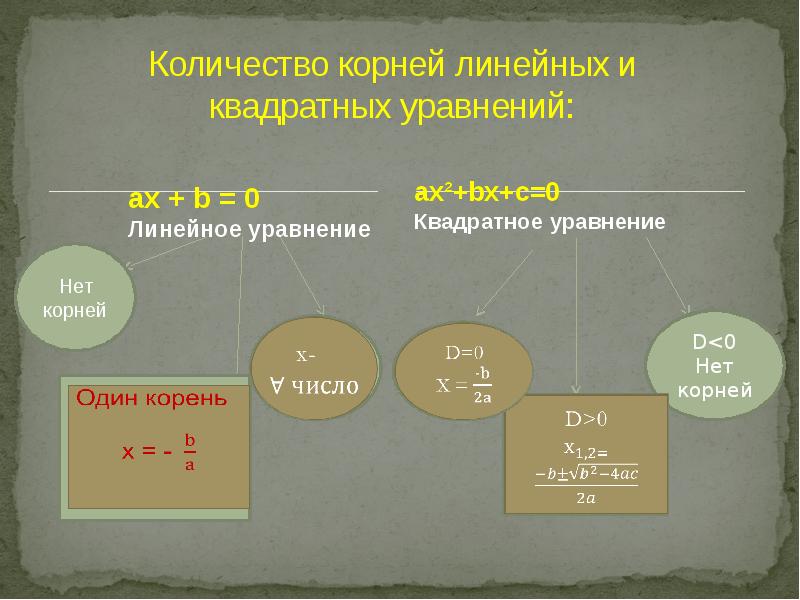
Варианты ответов
- 5
- -12
- 37
- -0,5
- не имеет корней
Вопрос 5
Найдите корни квадратного уравнения 4x2 + 4x + 1 = 0.
Варианты ответов
- -0,5
- 4
- 0,25
- -8
- нет корней
Вопрос 6
Найдите корни уравнения 5x2 — 8x — 4 = 0.
Варианты ответов
- 2
- -0,4
- 0,5
- -4
- -2
- нет корней
Вопрос 7
По какой формуле вычисляется дискриминант квадратного уравнения?
Варианты ответов
Вопрос 8
При каких значениях х принимают равные значения двучлены 8x2 — 10x и 4x — 5.
Варианты ответов
Вопрос 9
При каком значении трёхчлен 16a2 — 8a + 2 принимает значение равное 1.
Варианты ответов
- 0,25
- 0
- 2
- -8
- нет корней
Вопрос 10
Решите уравнение (x — 1)(x + 5) = 7.
Варианты ответов
- 2
- -6
- 5
- -1
- нет корней
Уравнения онлайн.
 Решение линейных уравнений с примерами 9 0 решение
Решение линейных уравнений с примерами 9 0 решениеКвадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:
Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
n} \)
7) a n > 1, если a > 1, n > 0
8) a n 1, n
9) a n > a m , если 0В практике часто используются функции вида y = a x , где a — заданное положительное число, x — переменная. Такие функции называют показательными . Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \(a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \(a \neq 1\), не имеет корней, если \(b \leq 0\), и имеет корень при любом b > 0.3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = a x при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = a x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.График функции у = a x при 0 Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если хПоказательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \(a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \(a \neq 1\) равны тогда и только тогда, когда равны их показатели.
{x-2} = 1 \)
x — 2 = 0
Ответ х = 2Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \(3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1Приложение
Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.
=Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.
Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы.
Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой.
Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ.
Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий.
Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции.
Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета.
Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории.
В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность.
Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их.
Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи.
Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы.
Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители.
Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение.
В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах.
Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы.
Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная.
Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов.
Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц.
Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач.
C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами.
Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Как определить корни уравнения. Как находить корень уравнения
Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях.
В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
Навигация по странице.
Что такое уравнение?
Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения :
Определение.
Уравнение – это равенство, содержащее неизвестное число, которое надо найти.
Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p , t , u и т.п., но наиболее часто используются буквы x , y и z .
Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.
Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8 , y=3 и т.
п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3 , z−2=5 , 3·t=9 , 8:x=2 .
Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18 и x+3·(x+2·(x−2))=3 . Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9 , также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8 , 7−3=z+1 или 3·x−4=2·(x+12) .
Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений , изучающиеся в школе.
В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ).
При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
Определение.
Уравнением называют равенство, содержащее переменную, значение которой нужно найти.
Например, уравнение x+3=6·x+7 – уравнение с переменной x , а 3·z−1+z=0 – уравнение с переменной z .
На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.
Определение.
Уравнения с одной, двумя, тремя и т.д. переменными – это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.
Например, уравнение 3,2·x+0,5=1 – это уравнение с одной переменной x , в свою очередь уравнение вида x−y=3 – это уравнение с двумя переменными x и y . И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27 .
Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x , y и z .
Что такое корень уравнения?
С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.
Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a в уравнение a+1=5 подставить число 2 , то получится неверное числовое равенство 2+1=5 . Если же мы в это уравнение подставим вместо a число 4 , то получится верное равенство 4+1=5 .
На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.
Определение.
Корень уравнения – это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.
Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.
Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5 . Согласно озвученному определению корня уравнения, число 4 есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5 , а число 2 не является его корнем, так как ему отвечает неверное равенство вида 2+1=5 .
На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.
Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5 имеет корень 4 , а уравнение 0·x=5 не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x , мы получим неверное равенство 0=5 .
Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4 имеет единственный корень 6 , корнями уравнения x 2 =9 являются два числа −3 и 3 , уравнение x·(x−1)·(x−2)=0 имеет три корня 0 , 1 и 2 , а решением уравнения x=x является любое число, то есть, оно имеет бесконечное множество корней.
Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества в фигурных скобках. Например, если корнями уравнения являются числа −1 , 2 и 4 , то пишут −1 , 2 , 4 или {−1, 2, 4} . Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x , и корнями этого уравнения являются числа 3 и 5 , то можно записать x=3 , x=5 , также переменной часто добавляют нижние индексы x 1 =3 , x 2 =5 , как бы указывая номера корней уравнения.
Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N , целых чисел Z , действительных чисел R . Например, если корнем уравнения с переменной x является любое целое число, то пишут , а если корнями уравнения с переменной y является любое действительное число от 1 до 9 включительно, то записывают .
Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.
Определение.
Решением уравнения с двумя, тремя и т.д. переменными называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.
Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7 . Подставим в него вместо x число 1 , а вместо y число 2 , при этом имеем равенство 1+2=7 .
Очевидно, оно неверное, поэтому, пара значений x=1 , y=2 не является решением записанного уравнения. Если же взять пару значений x=4 , y=3 , то после подстановки в уравнение мы придем к верному равенству 4+3=7 , следовательно, эта пара значений переменных по определению является решением уравнения x+y=7 .
Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.
Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7 . Решение этого уравнения x=4 , y=3 кратко можно записать как (4, 3) .
Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений .
Список литературы.
- Математика . 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
- Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения.
Это число может варьироваться от нуля до бесконечности.
Что подразумевается под уравнением и его корнем?
Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.
Поиск всех возможных корней уравнения является его решением. То есть нужно выполнить ряд математических действий, которые его упрощают. А потом приводят к равенству, в котором содержится только неизвестная и какое-либо число.В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо.
А в ответе такого уравнения нужно записать, что решений нет.
Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
О линейном уравнении
Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.
Алгоритм преобразований:
- перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
- разделить обе части получившегося равенства на коэффициент «а».
Общий вид решения такой:х = -в/а .
Из него ясно, что ответом будет одно число. То есть всего один корень.
Квадратное уравнение
Его общий вид: а * х 2 + в * х + с = 0 .
Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 — 4 а * с . После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.
Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант
В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:
х 1,2 = (-в ± √Д) / (2 * а) .
Здесь всегда получится два ответа. Это связано с тем, что в исходной формуле стоит знак «плюс/минус». Он существенно изменяет значение неизвестной.При равенстве «Д» нулю корень уравнения — это единственное число.
Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:
х = (-в) / (2 * а).
При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.
Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.
Формулы для расчета корней квадратного уравнения, не использующие дискриминант
Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:
х 2 + в * х + с = 0.
Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:
х 1 + х 2 = -в
и
х 1 * х 2 = с.Оно решается за счет того, что из первого выводится выражение для одного из корней.
И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
К этому варианту всегда можно прийти от общего вида квадратного уравнения.
Достаточно только разделить все коэффициенты на «а».
Как быть, если нужно узнать наименьшее значение корня?
Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.
Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:
2 х 5 + 2 х 4 — 3 х 3 — 3 х 2 + х + 1 = 0.
Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.
В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 .
Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.
После множителя (х + 1) будет стоять (2 х 4 — 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.
Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.
Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.
Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».
Нужно вернуться к введенному обозначению. х 1,2 = ± 1, х 3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.
В качестве заключения
Напоминание: все уравнения нужно проверять на то, подходит ли корень.
Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.
Если х = -1, то получается такой же результат. Корень тоже подходящий.
Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.
Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.
Вывод: надо помнить о проверке и внимательно подходить к решению.
Если есть две величины, а между ними стоит знак равенства, то это пример, который называют уравнением. Высчитав неизвестное, мы узнаем корень. Чтобы рассекретить это неизвестное, придется потрудиться над вычислением.
Понятнее будет, если возьмем в работу конкретное уравнение: x+10=16-2х. Оно относится к линейным, составляют его свободные члены и неизвестное х.Разносим эти составляющие в разные стороны от знака равенства. Теперь уравнение приобрело такой вид: 2х + х = 16 – 10 или 3х = 6; х = 2. Результат: Х = 2. Немного больший запас знаний нужно для вычисления корня в примере, где искомое в квадрате. Это уравнение квадратное и отличие его от линейного в том, что результатов может быть 1 или 2 или обнаружится, что корней 0. Чтобы понять лучше, решим уравнение: Х, возведенный в квадрат, умножить на 3 + 3Х = 90. Делаем так, чтобы справа образовался 0: Х2 х 3 + 3Х -90 = 0. Числа перед Х – коэффициенты 1, 3, 3. Требуется определение дискриминанта: возводим в квадрат 3 – второй коэффициент и отнимаем произведение 1 и 3. В итоге получим 6 – значит, доведя до конца расчет, обнаружим, что у этого уравнения корней 2. Если бы дискриминант выражался числом отрицательным, то изощряться в вычислении корней было бы нерационально – их просто нет. В случае если D=0, корень только 1. Теперь все-таки выполним расчет, чтобы определить эти 2 корня. Для подсчета 1 корня ко второму коэффициенту со знаком – прибавляем корень из D и делим это на удвоенный первый коэффициент: -3 + квадратный корень из 16, делим на 2.
Выйдет 1/2. Вычисление второго аналогично, только корень из D вычитаем. Имеем в результате – 3 целых и 1/2.
Сложнее квадратного уравнение кубическое. Вид у него такой: х3-3х2-4х+20=0. Подбираем число, на которое можно поделить свободный член, чтобы слева появился 0. Делители для 20 – это ±1, ±2, ±4, ±5, ± 10, ± 20. Получается, что это делитель 5, он же и один из искомых корней. Остается решить квадратное уравнение и все корни известны.
Вот и все премудрости. Нет ничего сложного, но чтобы было совсем просто, можно воспользоваться онлайн-калькулятором.
Уравнения в математике так же важны, как глаголы в русском языке. Без умения находить корень уравнения сложно утверждать, что ученик усвоил курс алгебры. К тому же для каждого их вида существуют свои особенные пути решения.
Что это такое?
Уравнение — это два произвольных выражения, содержащих переменные величины, между которыми поставлен знак равенства. Причем количество неизвестных величин может быть произвольным.
Минимальное количество — одна.
Решить его — это значит узнать, есть ли корень уравнения. То есть число, которое превращает его в верное равенство. Если его нет, то ответом является утверждение, что «корней нет». Но может быть и противоположное, когда ответом является множество чисел.
Какие виды уравнений существуют?
Линейное. Оно содержит переменную, степень которой равна единице.
- Квадратное. Переменная стоит со степенью 2, или преобразования приводят к появлению такой степени.
- Уравнение высшей степени.
- Дробно-рациональное. Когда переменная величина оказывается в знаменателе дроби.
- С модулем.
- Иррациональное. То есть такое, которое содержит алгебраический корень.
Как решается линейное уравнение?
Оно является основным. К такому виду стремятся привести все остальные. Так как у него найти корень уравнения достаточно просто.
- Сначала нужно выполнить возможные преобразования, то есть раскрыть скобки и привести подобные слагаемые.
- Перенести все одночлены с переменной величиной в левую часть равенства, оставив свободные члены в правой.
- Привести подобные члены в каждой части решаемого уравнения.
- В получившемся равенстве в левой его половине будет стоять произведение коэффициента и переменной, а в правой — число.
- Осталось найти корень уравнения, разделив число справа, на коэффициент перед неизвестной.
Как найти корни квадратного уравнения?
Сначала его нужно привести к стандартному виду, то есть раскрыть все скобки, привести подобные слагаемые и перенести все одночлены в левую часть. В правой части равенства должен остаться только ноль.
- Воспользуйтесь формулой для дискриминанта. Возведите в квадрат коэффициент перед неизвестной со степенью «1». Перемножьте свободный одночлен и число перед переменной в квадрате с числом 4. Из полученного квадрата вычтите произведение.
- Оцените значение дискриминанта. Он отрицательный — решение закончено, так как у него корней нет.
Равен нулю — ответом будет одно число. Положительный — два значения у переменной.
Как решить кубическое уравнение?
Сначала найдите корень уравнения x. Он определяется методом подбора из чисел, которые являются делителями свободного члена. Этот способ удобно рассмотреть на конкретном примере. Пусть уравнение имеет вид: х 3 — 3х 2 — 4х + 12 = 0.
Его свободный член равен 12. Тогда делителями, которые требуется проверить, будут положительные и отрицательные числа: 1, 2, 3, 4, 6 и 12. Перебор можно закончить уже на числе 2. Оно дает верное равенство в уравнении. То есть его левая часть оказывается равной нулю. Значит число 2 — это первый корень кубического уравнения.
Теперь необходимо разделить исходное уравнение на разность переменной и первого корня. В конкретном примере это (х — 2). Несложное преобразование приводит числитель к такому разложению на множители: (х — 2)(х + 2)(х — 3). Одинаковые множители числителя и знаменателя сокращаются, а оставшиеся две скобки при раскрытии дают простое квадратное уравнение: х 2 — х — 6 = 0.
Здесь найдите два корня уравнения по принципу, описанному в предыдущем разделе. Ими оказываются числа: 3 и -2.
Итого, у конкретного кубического уравнения получилось три корня: 2, -2 и 3.
Как решаются системы линейных уравнений?
Здесь предложен метод исключения неизвестных. Он заключается в том, чтобы выразить одну неизвестную через другую в одном уравнении и подставить это выражение в другое. Причем решением системы из двух уравнений с двумя неизвестными всегда является пара переменных величин.
Если в них переменные обозначены буквами х 1 и х 2 , то можно из первого равенства вывести, к примеру, х 2 . Потом оно подставляется во второе. Проводится необходимое преобразование: раскрытие скобок и приведение подобных членов. Получается простое линейное уравнение, корень которого вычислить легко.
Теперь возвратитесь к первому уравнению и найдите корень уравнения x 2 , используя получившееся равенство. Эти два числа являются ответом.
Для того чтобы быть уверенным в полученном ответе, рекомендуется всегда делать проверку.
Ее не обязательно записывать.
Если решается одно уравнение, то каждый из его корней нужно подставить в исходное равенство и получить одинаковые числа в обеих его частях. Все сошлось — решение верное.
При работе с системой корни необходимо подставлять в каждое решение и выполнять все возможные действия. Получается верное равенство? Значит решение правильное.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен.
Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16Итак, дискриминант положительный, поэтому уравнение имеет два различных корня.
Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом.
Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов.
Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи.
Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю.
Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Дискриминанты и определение числа действительных корней квадратного уравнения
Что такое дискриминант?
Дискриминант — это величина, вычисляемая по квадратному уравнению. Он использует его, чтобы «различать» корни (или решения) квадратного уравнения.
Квадратное уравнение имеет вид: ax 2 + bx + c
Дискриминант, D = b 2 — 4ac
Примечание.
.Это выражение внутри квадратного корня квадратной формулы
Дискриминант бывает в трех случаях;
Корпус 1:
b 2 — 4ac> 0
Если дискриминант больше нуля, это означает, что квадратное уравнение имеет два действительных, различных (разных) корня .
Пример
х 2 — 5х + 2 = 0
а = 1, б = -5, в = 2
Дискриминант, D = b 2 — 4ac
= (-5) 2 — 4 * (1) * (2)
= 17
Следовательно, квадратное уравнение
имеет два действительных различных корня.х 2 — 5х + 2.
Корпус 2:
b 2 — 4ac <0
Если дискриминант больше нуля, это означает, что квадратное уравнение не имеет действительных корней .

Пример
3x 2 + 2x + 1 = 0
а = 3, б = 2, с = 1
Дискриминант, D = b 2 — 4ac
= (2) 2 — 4 * (3) * (1)
= — 8
Следовательно, у квадратного уравнения 3x 2 + 2x + 1 нет действительных корней.
Корпус 3:
b 2 — 4ac = 0
Если дискриминант равен нулю, это означает, что квадратное уравнение имеет два действительных идентичных корня .
Пример
х 2 + 2х + 1 = 0
а = 1, б = 2, с = 1
Дискриминант, D = b 2 — 4ac
= (2) 2 — 4 * (1) * (1)
= 0
Следовательно, есть два действительных идентичных корня квадратного уравнения x 2 + 2x + 1.
Сводка
Квадратное уравнение: ax 2 + bx + c
Определитель D = b 2 — 4ac
D> 0 означает два реальных, различных корня.

D = 0 означает два настоящих одинаковых корня /
D <0 означает отсутствие реальных корней.
Теперь попробуйте эти (будьте осторожны со знаками минус)
вопросов
Q1.х 2 — 7x + 2 = 0
Q2. — 3x 2 + 2x — 1 = 0
Q3. 9x 2 — 12x + 4 = 0
Q4. — х 2 + х + 1 = 0
ответы
Q1. D = 41 означает два реальных, различных корня.
Q2. D = -16, означает отсутствие настоящих корней.
Q3. D = 0 означает два настоящих одинаковых корня.
Q4. D = 5 означает два реальных, различных корня.
Как узнать, сколько решений имеет квадратное уравнение?
Квадратное уравнение — это уравнение, которое выглядит так:
x 2 + 4x — 2 = 0.
В общем виде это записывается как ax 2 + bx + c = 0, где a, b и c — все числа, а x — наша неизвестная переменная.
В приведенном выше примере у нас будет a = 1, b = 4 и c = -2.
Чтобы найти количество решений, мы разделим квадратное уравнение на 3 случая.
Случай 1: 2 уникальных решения — например, x 2 + 5x + 6 = 0. Имеет решения x = 2 и x = 3.
Случай 2: повторное решение 1 — например, x 2 + 4x + 4 = 0.Имеет решение x = 2.
Случай 3: Нет решений — например, x 2 + 2x + 4 = 0. Не имеет решений.
Но как мы узнаем, в каком мы деле? Для этого мы взглянем на квадратную формулу, которую вы, надеюсь, уже видели. Для справки, это дает решение общей квадратной оси 2 + bx + c = 0 как:
x = [- b ± √ ( b 2 — 4 ac )] / 2 a
, где ± означает, что два решения равны
x = [- b + √ ( b 2 — 4 ac )] / 2 a и
x = [- b — √ ( b 2 — 4 ac )] / 2 a.

В случае 1 это даст два отдельных ответа для x. В случае 2 оба ответа будут одинаковыми.
Однако в случае 3 вы, скорее всего, получите ошибку! Эта ошибка возникает из-за того, что мы не можем извлечь квадратный корень из отрицательного числа *. Это означает, что если мы в случае 3, то участок √ ( b 2 — 4 ac ) является частью, которая вызывает проблемы! Как я уже сказал, мы не можем извлечь квадратный корень из отрицательного числа, поэтому, если b 2 -4 ac отрицательное, у нас есть ошибка и нет решения.
Это ключ к знанию того, сколько решений у нас есть:
Если b 2 -4 ac положительно (> 0), то у нас есть 2 решения.
Если b 2 — 4 ac равно 0, то у нас есть только одно решение, поскольку формула сокращается до x = [- b ± 0] / 2 a. Итак, x = -b / 2 a , что дает только одно решение.
Наконец, если b 2 -4 ac меньше 0, у нас нет решений.
Пример:
Сколько решений у x 2 — 3x + 2 = -1?
1) Переставьте, чтобы соответствовать общей формуле: x 2 — 3x + 3 = 0. Итак, a = 1, b = -3 и c = 3.
2) Используйте формулу: b 2 — 4ac = (-3) 2 — 4 (1) (3) = 9-12 = -3.
3) Поскольку b 2 — 4ac <0, у нас нет решений.
Вот и все! Пожалуйста, свяжитесь с нами, если вам потребуется дополнительная помощь.
* Для заинтересованных / продвинутых студентов: Технически вы МОЖЕТЕ извлечь квадратный корень из отрицательного числа. Это выходит за рамки курса GCSE, поэтому, если после этого вас что-то смущает, не волнуйтесь! Но прежде всего я объясню, почему вам этого еще никто не сказал.
Представьте, что я попросил вас дать мне ответ на 7 ÷ 3, но вы могли использовать только целые числа.
Уравнение 7 ÷ 3 равно 2,33 …, но это не целое число! Так что не существует целочисленных решений.Если бы я позволил вам использовать дроби, вы могли бы сказать мне, что 7 ÷ 3 равно 7/3 или 2 и 1/3.
Та же идея применима и к проблеме здесь. У нас есть только действительные числа (то есть дроби, десятичные дроби, целые числа и «иррациональные» числа, такие как пи), чтобы справиться с вопросом, и если вас попросят извлечь квадратный корень из отрицательного числа, реальных решений не будет. !
Решение действительно существует в «Мнимых» числах. Вы еще не знаете об этих числах (точно так же, как сначала не знали о дробях).Вы узнаете об этом больше на A level Further Maths или, возможно, в университете, но если это звучит интересно, пожалуйста, проверьте их через Google.
Если b 2 — 4ac <0, то "Реальных" решений нет.
Однако для экзамена GCSE, сказав, что нет никаких решений, будет достаточно!
Найти корни квадратного уравнения с помощью дискриминанта
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.
Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Квадратное уравнение — Формула, примеры
Квадратные уравнения представляют собой алгебраические выражения второй степени и имеют форму ax 2 + bx + c = 0.
Слово « Quadratic » происходит от слова « Quad », что означает квадрат.Другими словами, квадратное уравнение — это «уравнение степени 2 ». Есть много сценариев, в которых используется квадратное уравнение. Знаете ли вы, что при запуске ракеты ее путь описывается квадратным уравнением? Кроме того, квадратное уравнение находит множество приложений в физике, технике и астрономии.
Квадратные уравнения — это уравнения второй степени относительно x, которые имеют два ответа на x. Эти два ответа для x также называются корнями квадратных уравнений и обозначаются как (α, β).Мы узнаем больше о корнях квадратного уравнения в нижеследующем содержании.
Что такое квадратное уравнение?
Квадратное уравнение — это алгебраическое выражение второй степени по x. Квадратное уравнение в его стандартной форме имеет вид ax 2 + bx + c = 0, где a, b — коэффициенты, x — переменная, а c — постоянный член.
Первым условием для того, чтобы уравнение было квадратным уравнением, является коэффициент при x 2 является ненулевым членом (a 0).Для записи квадратного уравнения в стандартной форме сначала записывается член x 2 , затем член x и, наконец, постоянный член. Числовые значения a, b, c обычно не записываются как дроби или десятичные дроби, а записываются как целые значения.
Далее в реальных математических задачах квадратные уравнения представлены в различных формах: (x — 1) (x + 2) = 0, -x 2 = -3x + 1, 5x (x + 3) = 12x, x 3 = х (х 2 + х — 3).Все эти уравнения необходимо преобразовать в стандартную форму квадратного уравнения перед выполнением дальнейших операций.
Формула квадратного уравнения
Квадратичная формула — это простейший способ найти корни квадратного уравнения. Существуют определенные квадратные уравнения, которые нелегко разложить на множители, и здесь мы можем удобно использовать эту квадратную формулу, чтобы найти корни как можно быстрее.
Корни квадратного уравнения также помогают найти сумму корней и произведение корней квадратного уравнения.Два корня в формуле корней квадратного уравнения представлены как одно выражение. В качестве альтернативы можно использовать положительный знак и отрицательный знак для получения двух различных корней уравнения.
Квадратичная формула = [-b ± √ (b² — 4ac)] / 2a
Важные формулы для решения квадратных уравнений
Следующий список важных формул полезен при решении квадратных уравнений.
- Квадратное уравнение в его стандартной форме имеет вид ax 2 + bx + c = 0
- Дискриминант квадратного уравнения D = b 2 — 4ac
- При D> 0 корни действительны и различны.2 \).
- Для положительных значений a (a> 0) квадратичное выражение f (x) = ax 2 + bx + c имеет минимальное значение при x = -b / 2a.
- Для отрицательного значения a (a <0) квадратичное выражение f (x) = ax 2 + bx + c имеет максимальное значение при x = -b / 2a.
- Для a> 0 диапазон квадратного уравнения ax 2 + bx + c = 0 равен [b 2 — 4ac / 4a, ∞)
- Для a <0 диапазон квадратного уравнения ax 2 + bx + c = 0 равен: (∞, — (b 2 — 4ac) / 4a]
Доказательство квадратичной формулы
Рассмотрим произвольное квадратное уравнение: ax 2 + bx + c = 0, a ≠ 0
Чтобы определить корни этого уравнения, действуем следующим образом:
ax 2 + bx = -c ⇒ x 2 + bx / a = -c / a
Теперь представим левую часть в виде полного квадрата, введя новый член (b / 2a) 2 с обеих сторон:
x 2 + bx / a + (b / 2a) 2 = -c / a + (b / 2a) 2
Левая часть теперь представляет собой идеальный квадрат:
(x + b / 2a) 2 = -c / a + b 2 / 4a 2 ⇒ (x + b / 2a) 2 = (b 2 — 4ac) / 4a 2
Это хорошо для нас, потому что теперь мы можем извлекать квадратные корни, чтобы получить:
x + b / 2a = ± √ (b 2 — 4ac) / 2a
x = (-b ± √ (b 2 — 4ac)) / 2a
Таким образом, завершив квадраты, мы смогли выделить x и получить два корня уравнения.
Корни квадратного уравнения
Корнями квадратного уравнения являются два значения x, которые получаются путем решения квадратного уравнения. Корни квадратного уравнения обозначаются символами alpha (α) и beta (β). Эти корни квадратного уравнения также называются нулями уравнения. Здесь мы узнаем больше о том, как определить природу корней квадратного уравнения без фактического нахождения корней уравнения.А также проверьте формулы, чтобы найти сумму и произведение корней уравнения.
Природа корней квадратного уравнения
Природу корней квадратного уравнения можно узнать, фактически не находя корни (α, β) уравнения. Это возможно, если взять значение дискриминанта, которое является частью формулы для решения квадратного уравнения. Величина b 2 — 4ac называется дискриминантом квадратного уравнения и обозначается буквой «D».На основе значения дискриминанта можно предсказать природу корней квадратного уравнения.
Дискриминант: D = b
2 — 4ac
- D> 0, корни действительные и различные
- D = 0, корни действительные и равные.
- D <0, корни не существуют или корни мнимые.
Связь между коэффициентами и корнями квадратного уравнения
Коэффициент при x 2 , член x и постоянный член квадратного уравнения ax 2 + bx + c = 0 полезны для более подробного изучения свойств корней квадратного уравнения.Сумму и произведение корней квадратного уравнения можно вычислить непосредственно из уравнения, фактически не находя корни квадратного уравнения. Сумма корней квадратного уравнения равна минусу коэффициента при x, деленного на коэффициент при x 2 . Произведение корня уравнения равно постоянному члену, деленному на коэффициент при x 2 . Для квадратного уравнения ax 2 + bx + c = 0 сумма и произведение корней выглядят следующим образом.
- Сумма корней: α + β = -b / a = — Коэффициент x / Коэффициент x 2
- Произведение корней: αβ = c / a = Постоянный член / Коэффициент x 2
Квадратное уравнение также может быть составлено для заданных корней уравнения.
Если α, β, являются корнями квадратного уравнения, то квадратное уравнение выглядит следующим образом.
x 2 — (α + β) x + αβ = 0
Методы решения квадратных уравнений
Квадратное уравнение можно решить, чтобы получить два значения x или два корня уравнения.Существует четыре различных метода нахождения корней квадратного уравнения. Четыре метода решения квадратных уравнений заключаются в следующем.
- Факторизация квадратного уравнения
- Формульный метод поиска корней
- Способ заполнения квадрата
- Графический метод поиска корней
Давайте подробно рассмотрим каждый из вышеперечисленных методов, чтобы понять, как использовать эти методы, их приложения и способы их использования.
Факторизация квадратного уравнения
Факторизация квадратного уравнения выполняется в несколько шагов. Для общей формы квадратного уравнения ax 2 + bx + c = 0 нам нужно сначала разделить средний член на два члена так, чтобы произведение членов было равно постоянному члену.
Далее, мы можем взять общие термины из доступного термина, чтобы окончательно получить требуемые коэффициенты. Для понимания факторизации общий вид квадратного уравнения может быть представлен следующим образом.
- x 2 + (a + b) x + ab = 0
- x 2 + ax + bx + ab = 0
- х (х + а) + Ь (х + а)
- (х + а) (х + b) = 0
Давайте разберемся с факторизацией на примере ниже.
- x 2 + 5x + 6 = 0
- x 2 + 2x + 3x + 6 = 0
- х (х + 2) + 3 (х + 2) = 0
- (х + 2) (х + 3) = 0
Таким образом, два полученных фактора квадратного уравнения — это (x + 2) и (x + 3).
Квадратичная формула для поиска корней
Квадратные уравнения, которые нельзя решить методом факторизации, можно решить с помощью формулы. В формуле решения квадратного уравнения используются члены стандартной формы квадратного уравнения. С помощью приведенной ниже формулы мы можем получить два корня x, сначала используя положительный знак в формуле, а затем используя отрицательный знак.
С помощью этой формулы можно решить любое квадратное уравнение.
Помимо вышеупомянутых двух методов решения квадратных уравнений, существует еще один важный метод решения квадратного уравнения.Метод завершения квадрата квадратного уравнения также полезен для нахождения корней уравнения. Этот метод включает в себя многочисленные алгебраические вычисления и поэтому был объяснен как отдельная тема.
Способ заполнения квадрата
Метод завершения квадрата квадратного уравнения заключается в алгебраическом возведении в квадрат и упрощении, чтобы получить требуемые корни уравнения. Рассмотрим квадратное уравнение ax 2 + bx + c = 0, a ≠ 0. Чтобы определить корни этого уравнения, мы упростим его следующим образом:
- топор 2 + bx + c = 0
- топор 2 + bx = -c
- x 2 + bx / a = -c / a
Теперь представим левую часть в виде полного квадрата, введя новый член (b / 2a) 2 с обеих сторон:
- x 2 + bx / a + (b / 2a) 2 = -c / a + (b / 2a) 2
- (x + b / 2a) 2 = -c / a + b 2 / 4a 2
- (x + b / 2a) 2 = (b 2 — 4ac) / 4a 2
- x + b / 2a = + √ (b 2 — 4ac) / 2a
Теперь, используя этот метод завершения квадрата, мы можем консолидировать значения корней уравнения.
После упрощения и извлечения квадратного корня два возможных корня квадратного уравнения равны x = (-b + √ (b 2 — 4ac)) / 2a. Здесь знак «+» дает один корень, а знак «-» — другой корень квадратного уравнения. Как правило, этого подробного метода избегают, и для получения требуемых корней используется только формула.
Построение квадратного уравнения
График квадратного уравнения ax 2 + bx + c = 0 может быть получен путем представления квадратного уравнения в виде функции y = ax 2 + bx + c.Далее, решая и подставляя значения для x, мы можем получить значения y, мы можем получить множество точек. Эти точки могут быть представлены на оси координат, чтобы получить график в форме параболы для квадратного уравнения.
Точка, где график пересекает горизонтальную ось x, является решением квадратного уравнения. Эти точки также можно получить алгебраически, приравняв значение y к 0 в функции y = ax 2 + bx + c и решив относительно x.
2 + b_2x + c_2 = 0 \).2 \)
Максимальное и минимальное значение квадратичного выражения
Максимальное и минимальное значение квадратного уравнения ax 2 + bx + c = 0 можно увидеть на графиках ниже. Для положительных значений a (a> 0) квадратичное выражение имеет минимальное значение при x = -b / 2a, а для отрицательного значения a (a <0) квадратичное выражение имеет максимальное значение при x = -b / 2а.
Максимальное и минимальное значения квадратичных выражений дополнительно помогают найти диапазон квадратичного выражения: диапазон квадратичных выражений также зависит от значения a.Для положительных значений a (a> 0) диапазон составляет [f (-b / 2a), ∞), а для отрицательных значений a (a <0) диапазон составляет (-∞, f (-b / 2а)].
- Для a> 0, диапазон: [f (-b / 2a), ∞)
- Для a <0, диапазон: (-∞, f (-b / 2a)]
Решение квадратного уравнения — Советы и хитрости
Некоторые из приведенных ниже советов и приемов по квадратным уравнениям помогают упростить решение квадратных уравнений.
- Квадратные уравнения обычно решаются путем факторизации.Но в тех случаях, когда она не может быть решена путем факторизации, используется формула.
- Корни квадратного уравнения также называют нулями уравнения.
- Для квадратных уравнений, имеющих отрицательные значения дискриминанта, корни представляются с помощью комплексных чисел.
- Сумму и произведение корней квадратного уравнения можно использовать для нахождения высших алгебраических выражений, включающих эти корни.
Связанные темы
Часто задаваемые вопросы о квадратном уравнении
Что такое квадратное уравнение?
Квадратное уравнение в математике — это уравнение второй степени вида ax² + bx + c = 0.Здесь a, b — коэффициенты, c — постоянный член, а x — переменная. Поскольку переменная x имеет вторую степень, у этого квадратного уравнения есть два корня или ответ. Корни квадратного уравнения могут быть найдены либо путем факторизации, либо с помощью формулы.
Что такое квадратичная формула?
Квадратичная формула для решения квадратного уравнения ax² + bx + c = 0: x = [-b ± √ (b² — 4ac)] / 2a. Здесь мы получаем два значения x, применяя в этой формуле символы плюс и минус.Следовательно, два возможных значения x: [-b + √ (b² — 4ac)] / 2a и [-b — √ (b² — 4ac)] / 2a.
Как применить квадратичную формулу?
Значения a, b и c применяются к квадратной формуле x = [-b ± √ (b² — 4ac)] / 2a, чтобы получить два корня квадратного уравнения.
Что является определяющим в квадратичной формуле?
Величина b² — 4ac называется определителем и обозначается как D. Определитель является частью формулы корней квадратного уравнения. Определители помогают нам определить природу корней квадратного уравнения, фактически не находя корни квадратного уравнения.
Каковы некоторые реальные применения квадратных уравнений
Квадратные уравнения используются для нахождения нулей параболы и ее оси симметрии.
Есть много реальных приложений квадратных уравнений. Например, его можно использовать в задачах на время бега, чтобы оценить скорость, расстояние или время во время путешествия на машине, поезде или самолете. Квадратные уравнения описывают взаимосвязь между количеством и ценой товара. Точно так же расчеты спроса и затрат также считаются задачами квадратных уравнений.Также можно отметить, что спутниковая тарелка или телескоп-рефлектор имеет форму, которая определяется квадратным уравнением.
Чем квадратные уравнения отличаются от линейных?
Линейная степень — это уравнение с одной степенью и одной переменной, а квадратное уравнение — это уравнение с двумя степенями и одной переменной. Линейное уравнение имеет вид ax + b = 0, а квадратное уравнение имеет форму ax² + bx + c = 0. Линейное уравнение имеет один корень, а квадратное уравнение имеет два корня или два ответа.Кроме того, квадратное уравнение является продуктом двух линейных уравнений.
Как упростить квадратное уравнение?
Первым шагом в процессе упрощения квадратного уравнения является преобразование его в стандартную форму ax² + bx + c = 0.
Кроме того, его можно упростить, найдя его множители в процессе факторизации. Также для уравнения, которое трудно разложить на множители, оно решается с помощью формулы. Кроме того, есть несколько других способов упростить квадратное уравнение.
Каковы четыре способа решения квадратного уравнения?
Четыре способа решения квадратного уравнения заключаются в следующем.
- Метод факторизации
- Метод формул
- Метод заполнения квадратов
- Метод построения графика
Как решить квадратное уравнение факторингом?
Квадратное уравнение может быть решено путем факторизации с помощью последовательности из трех шагов. Сначала разделите средний член таким образом, чтобы произведение разделенных членов было равно произведению первого и последнего членов.Предположим, квадратное уравнение имеет вид x² + (a + b) x + ab = 0, и его можно разделить как x² + ax + bx + ab = 0. В качестве второго шага возьмите общий член из первые два и последние два срока.
x (x + a) + b (x + a) = 0, (x + a) (x + b) = 0. Наконец, приравняйте каждый из множителей к нулю и получите значения x. x + a = 0 и x + b = 0, и, следовательно, мы можем получить x = -a и x = -b
Как решить квадратное уравнение, заполнив квадрат?
Квадратное уравнение, решаемое методом завершения квадрата по формуле (a + b) ² = a²
Как найти значение дискриминанта?
Значение дискриминанта в квадратном уравнении может быть найдено из переменных и постоянных членов стандартной формы квадратного уравнения ax² + bx + c = 0.Значение дискриминанта составляет D = b² — 4ac, и он помогает предсказать природу корней квадратного уравнения без фактического нахождения корней уравнения.
Как решить квадратные уравнения с помощью графиков?
Квадратное уравнение решается аналогично линейному уравнению с помощью построения графиков. Возьмем квадратное уравнение ax² + bx + c = 0 как y = ax² + bx + c. Здесь мы берем набор значений x и y и строим график.
Эти две точки, где этот график пересекает ось x, являются возможными решениями этого квадратного уравнения.
Как узнать природу корней квадратного уравнения?
Дискриминант помогает предсказать природу корней квадратного уравнения. Определитель квадратного уравнения ax² + bx + c = 0 равен b² — 4ac. Дискриминант обозначается как D = b² — 4ac. Если D> 0, корни действительны и различны, при D = 0 корни равны, а при D <0 корни являются мнимыми комплексными числами.
Насколько важен дискриминант в определении природы корней квадратного уравнения?
Дискриминант очень нужен, чтобы легко определить природу корней квадратного уравнения.Без дискриминанта определение природы корней уравнения — долгий процесс, поскольку нам сначала нужно решить уравнение, чтобы найти оба корня. Следовательно, дискриминант является важной и необходимой величиной, которая помогает легко определить природу корней квадратного уравнения.
Когда квадратные уравнения имеют равные корни?
У данного квадратного уравнения равные корни, если дискриминант равен нулю.
Для квадратного уравнения вида ax² + bx + c = 0 дискриминант равен D = b² — 4ac = 0.Здесь оба корня равны и каждый имеет значение x = -b / 2a.
Каковы значения детерминантов в формуле квадратного уравнения?
Определитель (D = b² — 4ac) полезен для предсказания природы корней квадратного уравнения. Для D> 0 корни действительные и различные, для D = 0 корни действительные и равные, а для D <0 корни не существуют или корни являются мнимыми комплексными числами. С помощью этого определителя и с наименьшими вычислениями мы можем выяснить природу корней квадратного уравнения.
Сколько корней имеет квадратное уравнение?
Это уравнение второй степени относительно x, отсюда получается два корня. Мы можем получить эти корни квадратного уравнения, используя формулу корней квадратного уравнения. Один корень можно получить, используя положительный знак, и мы можем получить другой корень, применив отрицательный знак в формуле.
Как решить квадратное уравнение, не используя квадратичную формулу?
Есть два метода, альтернативных квадратичной формуле.
Один метод — решить квадратное уравнение путем факторизации, а другой — путем заполнения квадратов. Всего существует три метода нахождения корней квадратного уравнения.
Как квадратная формула используется для решения квадратного уравнения?
Формула алгебры (a + b) ² = a² + 2ab + b² используется для решения квадратного уравнения и вывода квадратной формулы. Эта алгебраическая формула используется для управления квадратным уравнением и вывода квадратной формулы для нахождения корней уравнения.
Квадраты: многочлены второй степени
10
Решение квадратного уравнения с множителем
Двойной корень
Квадратичное неравенство
Сумма корней и произведение корней
КВАДРАТИКА — ДРУГОЕ НАЗВАНИЕ многочлена 2-й степени. 2 — самый высокий показатель степени.
1. Какой вид имеет полиномиальная функция 2-й степени?
y = ax 2 + bx + c
2.
Какой вид имеет квадратное уравнение?
топор 2 + bx + c = 0
3. Что мы подразумеваем под корнем квадратичного?
Решение квадратного уравнения.
4. Сколько корней всегда у квадратичной?
Два, реальные или сложные.
5. График квадратичной всегда имеет форму, называемую -?
Парабола.
6. Каковы три метода решения квадратного уравнения,
6. То есть нахождения корней?1. Факторинг. 2. Завершение квадрата.
3. Квадратичная формула.
Начнем с метода факторинга. В следующей теме мы представим как Завершение квадрата, так и формулу квадратного уравнения.
7. Если произведение множителей равно 0 — если ab = 0 — то что вы можете
7.сделать вывод о факторах a , b ?Либо a = 0, либо b = 0.
Пример 1. Решение по факторингу.
f ( x ) = x 2 −2 x −3. Найдите корни f ( x ) и нарисуйте график y = f ( x ).
Решение . x 2 −2 x −3 = ( x + 1) ( x — 3).
Следовательно, корни — это −1 и 3. (См. Урок 37 по алгебре.) Это точки пересечения графа размером x .
Прерывание y является постоянным членом −3.
В каждом полиноме пересечение y является постоянным членом, потому что постоянный член — это значение y , когда x = 0.
Пример 2. Двойной корень
f ( x ) = x 2 −10 x + 25. Найдите корни
f ( x ) и нарисуйте график y = f ( x ).Решение . x 2 −10 x + 25 =
( x — 5) ( x — 5) = ( x — 5) 2 .Два корня равны, их 5, 5. 5 называется двойным корнем. (См. Урок алгебры 37, вопрос 4.)
При двойном корне график не пересекает ось x . Это просто трогает.
Двойной корень возникает, когда квадратичный является трехчленом полного квадрата: x 2 ± 2 ax + a 2 ; то есть, когда квадратичная величина является квадратом бинома: ( x ± a ) 2 .
Пример 3. Сколько действительных корней, т.е. корней, которые являются действительными числами, имеет квадратичный элемент каждого графа?
Ответ . График а) имеет два действительных корня. Он имеет два перехватчика x .
График б) не имеет реальных корней. У него нет x -перехватов. Оба корня сложные.
График c) имеет два действительных корня. Но они двойной корень.
Пример 4.Квадратичное неравенство.
Решите это неравенство:
x 2 — 4 x — 5
Для этого осмотрите график
y = x 2 — 4 x — 5.
Решение . Для каких значений x эта квадратичная величина будет отрицательной? То есть где график под осью x ?
График отрицательный между корнями, которые равны -1 и 5.Решение неравенства равно −1 x. Мы также можем заметить, что квадратичная функция будет иметь положительные значения — график будет выше оси x — слева и справа от корней:
x 9 1036 x> 5.
В то время как квадратичный будет иметь значение 0 в корнях.
Мы рассмотрели три возможности:
Этот квадратичный равен , равному 0 в двух корнях.
Это на меньше, чем 0 между двумя корнями.
Это на больше, чем 0 слева и справа от двух корней.
Эти три возможности, которые верны для любого действительного числа, имеют причудливое название Закона трихотомии. Любое число должно быть либо равно, меньше или больше 0.
Закон трихотомии также принимает такую форму:
Для любых действительных чисел a, b , либо a = b , a b, либо a > b .
Однако мы должны знать, какая из этих возможностей верна. Для любых двух чисел мы должны знать их относительный порядок. Это заложено в значении «числа».
Задача 1. Нарисуйте график y = x 2 — 2 x −8. То есть покажите перехваты x и y .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).x 2 −2 x — 8 = ( x + 2) ( x — 4). Следовательно, корни равны −2, 4. Пересечение y является постоянным членом −8.
Задача 2. Нарисуйте график
.y = x 2 + 4 x + 4.
x 2 + 4 x + 4 = ( x + 2) 2 .В −2 есть двойной корень. Перехват y — постоянный член, 4.
Проблема 3.
а) Чтобы решить это квадратное неравенство —
x 2 + 2 x — 3> 0
—проверьте график
y = x 2 + 2 x — 3.
Квадратичное значение будет положительным — выше оси x — для значений x слева и справа от корня.Решение:
x x> 1.б) Решите это квадратное неравенство:
x 2 + 2 x — 3
−3 х
Квадратичный будет отрицательным между корнями.
Проблема 4. Квадратичная имеет следующие корни. Запишите каждую квадратичную как произведение линейных множителей.
а) 3, 4 ( x — 3) ( x — 4)
б) −3, −4 ( x + 3) ( x + 4)
в) — р , с ( x + r ) ( x — s )
г) 3+, 3 — ( x — 3 -) ( x −3 +)
Сумма корней и произведение корней
Теорема.
В квадратичной системе со старшим коэффициентом 1:
Сумма корней равна отрицательному коэффициента x ;
произведение корней — постоянный член.
То есть, если
x 2 + bx + c = 0,
и корни r и s , затем
r + s = — б , RS = с . Ибо, если корни равны r и s , то квадратичный равен
( x — r ) ( x — s ) = x 2 — rx — sx + rs = x 2 — ( r + s ) x + rs . Коэффициент при x равен — ( r + s ), что является отрицательным значением суммы корней. Постоянный член — рупий , который является их произведением.
Пример 5. Построить квадратичную с корнями 2 и 3.
Решение . Сумма корней равна 5, их произведение равно 6, следовательно, квадратичный равен x 2 — 5 x + 6.
Сумма корней равна минус коэффициента x . Произведение корней — постоянный член.
Пример 6. Построить квадратичную с корнями 2 +, 2 -.
Решение . Сумма корней равна 4. Их произведение — разность двух квадратов: 2 2 — () 2 = 4 — 3 = 1.
Таким образом, квадратичный равен x 2 — 4 x + 1.
Пример 7. Построить квадратичный, корни которого равны 2 + 3 i , 2 — 3 i , где i — комплексная единица.
Решение . Сумма корней равна 4. Произведение снова является разностью двух квадратов: 4 — 9 i 2 = 4 + 9 = 13.
Квадратичный с этими корнями равен
.x 2 — 4 x + 13.
Задача 5. Построить квадратичную с корнями −3, 4.
Сумма корней равна 1. Их произведение равно −12. Следовательно, квадратичное значение равно x 2 — x — 12.
Задача 6. Построить квадратичную с корнями 3 +, 3 -.
Сумма корней равна 6. Их произведение равно 9 — 3 = 6.
Следовательно, квадратичный равен x 2 — 6 x + 6.Задача 7. Построить квадрат, корни которого равны 2 + i , 2 — i .
Сумма корней равна 4. Их произведение равно 4 — ( i ) 2 = 4 + 5 = 9.
Следовательно, квадратичный равен x 2 — 4 x + 9.*
В более общем смысле, для любого коэффициента x 2 , то есть, если квадратичный равен
топор 2 + bx + c ,
и корни r и s , затем
r + s = – б
а, RS = c
a. Когда a = 1, мы имеем теорему выше.
Следующая тема: Завершение квадрата
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Все знаки указывают на дискриминант
Все знаки указывают на дискриминант
У вас когда-нибудь был один из этих Magic 8 Balls? Они выглядят как комично негабаритные шары для пула, но в них встроено плоское окно, так что вы можете видеть, что находится внутри 20-гранного кубика, плавающего в отвратительной непрозрачной синей слизи.
Предположительно, бильярдный шар обладает прогностическими способностями; все, что вам нужно сделать, это задать ему вопрос, встряхнуть, и медленно, мистическим образом, как покрытая нефтью печать, выходящая из разлива нефти, игральная кость поднимется к маленькому окошку и откроет ответ на ваш вопрос.
Квадратное уравнение содержит своего рода Magic 8 Ball. Выражение b 2 — 4 ac под знаком радикала называется дискриминантом , и оно может фактически определить для вас, сколько решений имеет данное квадратное уравнение, если вы не хотите на самом деле вычислять их.Учитывая, что квадратное уравнение, которое невозможно сформулировать, требует много работы для решения (квадратная формула изобилует тоннами арифметики, а для завершения квадратного метода требуется целая куча шагов), часто бывает полезно заглянуть в загадочную загадку, чтобы сделать убедитесь, что уравнение даже имеет любых вещественных числовых решений, прежде чем вы потратите какое-либо время на их поиски.
Talk the Talk
Дискриминант — это выражение b 2 — 4 ac , которое определено для любого квадратного уравнения ax 2 + bx + c = 0.По знаку выражения можно определить, сколько действительных чисел имеет квадратное уравнение.
Вот как работает дискриминант. Дано квадратное уравнение ax 2 + bx + c = 0, подставьте коэффициенты в выражение b 2 — 4 ac , чтобы увидеть, какие результаты:
- Если вы получите положительное число, квадратичная функция будет иметь два уникальных решения.
- Если вы получите 0, у квадратичного будет ровно одно решение — двойной корень.
- Если вы получите отрицательное число, у квадратичного не будет реальных решений, только два мнимых. (Другими словами, решения будут содержать числа i , о которых вы узнали в «Борьбе с радикалами».
)
Дискриминант не является магическим. Это просто показывает, насколько важен этот радикал в формуле корней квадратного уравнения. Если, например, его подкоренное выражение равно 0, то вы получите
единственное решение. Если, однако, b 2 — 4 ac отрицательно, то внутри квадратного корня в квадратной формуле будет отрицательное значение, что означает только мнимые решения.
Пример 4 : Не вычисляя их, определите, сколько реальных решений имеет уравнение 3 x 2 — 2 x = -1.
Решение : Установите квадратное уравнение равным 0, прибавив 1 к обеим сторонам.
У вас есть проблемы
Задача 4: Не вычисляя их, определите, сколько реальных решений имеет уравнение 25 x 2 -40 x + 16 = 0.
Установите a = 3, b = -2 и c = 1 и оцените дискриминант.
- b 2 — 4 ac
- = (- 2) 2 — 4 (3) (1)
- = 4-12
- = -8
Поскольку дискриминант отрицательно, квадратное уравнение не имеет вещественных числовых решений, только два мнимых.
Выдержки из Полное руководство для идиотов по алгебре 2004 У. Майкла Келли. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Эту книгу можно приобрести на Amazon.com и Barnes & Noble.
Квадратные уравнения
Пример квадратного уравнения :
Функция создает красивые кривые, подобные этой:
Имя
Название Quadratic происходит от «квадрата», что означает квадрат, потому что переменная возводится в квадрат (например, x 2 ).
Его также называют «уравнением степени 2» (из-за «2» на x )
Стандартная форма
Стандартная форма квадратного уравнения выглядит так:
- a , b и c — известные значения. a не может быть 0.
- « x » — это переменная или неизвестно (мы еще не знаем).
Вот несколько примеров:
2x 2 + 5x + 3 = 0 В этом случае a = 2 , b = 5 и c = 3 x 2 — 3x = 0 Это немного сложнее:
- Где а ? Ну a = 1 , так как мы обычно не пишем «1x 2 »
- б = −3
- А где c ? Ну c = 0 , поэтому не показан.
5x — 3 = 0 Ой! Это , а не квадратное уравнение: оно отсутствует x 2
(другими словами a = 0 , что означает, что оно не может быть квадратичным)Поиграйте с этим
Поиграйте с «Проводником квадратного уравнения», чтобы увидеть:
- график функции и
- решения (так называемые «корни»).
Скрытые квадратные уравнения!
Как мы видели ранее, Стандартная форма квадратного уравнения —
Но иногда квадратное уравнение так не выглядит!
Например:
Скрытый в стандартной форме a, b и c x 2 = 3x — 1 Перенести все термины в левую часть x 2 — 3x + 1 = 0 a = 1, b = −3, c = 1 2 (w 2 — 2w) = 5 Развернуть (снять скобки),
и переместить 5 влево2 Вт 2 — 4 Вт — 5 = 0 a = 2, b = −4, c = −5 z (z − 1) = 3 Разверните и переместите 3 влево z 2 — z — 3 = 0 а = 1, b = -1, с = -3 Как их решить?
« решений » квадратного уравнения — это где равно нулю .
Их еще называют « корней », иногда « нулей »
Обычно существует 2 решения (как показано на этом графике).
И есть несколько разных способов найти решения:
Или мы можем использовать специальную Квадратичную формулу :Просто введите значения a, b и c и выполняйте вычисления.
Сейчас мы рассмотрим этот метод более подробно.
О квадратичной формуле
Плюс / Минус
Прежде всего, что это за плюс / минус, который выглядит как ±?
± означает, что есть ДВА ответа:
x = −b + √ (b 2 — 4ac) 2a
x = −b — √ (b 2 — 4ac) 2a
Вот пример с двумя ответами:
Но не всегда так получается!
- Представьте, что кривая «просто касается» оси x.
- Или представьте, что кривая настолько высока , что даже не пересекает ось x!
Вот тут-то нам и помогает «Дискриминант» …
Дискриминант
Вы видите b 2 — 4ac в приведенной выше формуле? Он называется Дискриминант , потому что он может «различать» возможные типы ответов:
- когда b 2 — 4ac положительный, мы получаем два Реальных решения
- , когда он равен нулю, мы получаем только ОДНО реальное решение (оба ответа одинаковы)
- при отрицательном значении получаем пару Комплексных решений
Комплексные решения? Давайте поговорим о них после того, как мы увидим, как использовать формулу.
Использование квадратичной формулы
Просто введите значения a, b и c в квадратную формулу и произведите вычисления.
Пример: Решить 5x
2 + 6x + 1 = 0Коэффициенты: a = 5, b = 6, c = 1
Квадратичная формула: x = −b ± √ (b 2 — 4ac) 2a
Вставьте a, b и c: x = −6 ± √ (6 2 — 4 × 5 × 1) 2 × 5
Решить: x = −6 ± √ (36−20) 10
х = −6 ± √ (16) 10
х = −6 ± 4 10
х = -0.
2 или -1
Ответ: x = −0,2 или x = −1
И мы их видим на этом графике.
Чек -0,2 : 5 × ( −0,2 ) 2 + 6 × ( −0,2 ) + 1
= 5 × (0,04) + 6 × (−0,2) + 1
= 0,2 — 1,2 + 1
= 0Чек -1 : 5 × ( −1 ) 2 + 6 × ( −1 ) + 1
= 5 × (1) + 6 × (−1) + 1
= 5-6 + 1
= 0Вспоминая формулу
Добрый читатель предложил спеть это к «Pop Goes the Weasel»:
♫ «x равно минус b ♫ «Вокруг тутового куста плюс или минус квадратный корень Обезьяна погналась за лаской из квадрата b минус четыре a c Обезьяна думала, что все было весело ВСЕ более двух а « Поп! идет ласка » Попробуйте спеть несколько раз, и она застрянет у вас в голове!
Или вы можете вспомнить эту историю:
х = −b ± √ (b 2 — 4ac) 2a
«Негативный мальчик думал« да »или« нет »о том, чтобы пойти на вечеринку,
на вечеринке он разговаривал с квадратным мальчиком, но не с четырьмя классными цыпочками.
В 2 часа ночи все было кончено. «Комплексные решения?
Когда Дискриминант (значение b 2 — 4ac ) отрицателен, мы получаем пару Комплексных решений … что это означает?
Это означает, что наш ответ будет включать в себя мнимые числа. Вау!
Пример: Решить 5x
2 + 2x + 1 = 0Коэффициенты равны : a = 5, b = 2, c = 1
Обратите внимание, что дискриминант отрицательный: b 2 — 4ac = 2 2 — 4 × 5 × 1
= −16Используйте квадратичную формулу : x = −2 ± √ (−16) 10
√ (−16) = 4 i
(где i — мнимое число √ − 1)Итак: x = −2 ± 4 и 10
Ответ: x = −0.
2 ± 0,4 и
График не пересекает ось абсцисс. Вот почему мы пришли к комплексным числам.
В некотором смысле это проще: нам не нужно больше вычислений, мы оставляем его как -0,2 ± 0,4 i .
Пример: Решить x
2 — 4x + 6,25 = 0Коэффициенты равны : a = 1, b = −4, c = 6,25
Обратите внимание, что дискриминант отрицательный: b 2 — 4ac = (−4) 2 — 4 × 1 × 6.25
= −9Используйте квадратичную формулу : x = — (- 4) ± √ (−9) 2
√ (−9) = 3 i
(где i — мнимое число √ − 1)Итак: x = 4 ± 3 i 2
Ответ: x = 2 ± 1,5 i
График не пересекает ось абсцисс.
Вот почему мы пришли к комплексным числам.
НО перевернутое зеркальное отображение нашего уравнения действительно пересекает ось x на уровне 2 ± 1,5 (примечание: отсутствует i ).
Просто интересный факт для вас!
Сводка
- Квадратное уравнение в стандартной форме: ax 2 + bx + c = 0
- Квадратные уравнения могут быть разложены на множители
- Квадратичная формула: x = −b ± √ (b 2 — 4ac) 2a
- Когда Дискриминант ( b 2 −4ac ) равен:
- положительный, есть 2 реальных решения
- ноль, есть одно реальное решение
- отрицательный, есть 2 комплексных решения
360, 361, 1201, 1202, 2333, 2334, 3894, 3895, 2335, 2336
.

 Если эти условия выполняются, такое кольцо называется коммутативным с единицей.
Если эти условия выполняются, такое кольцо называется коммутативным с единицей.


 Что
позволяет сделать эта теорема?
Что
позволяет сделать эта теорема? Что
позволяет сделать эта теорема?
Что
позволяет сделать эта теорема?

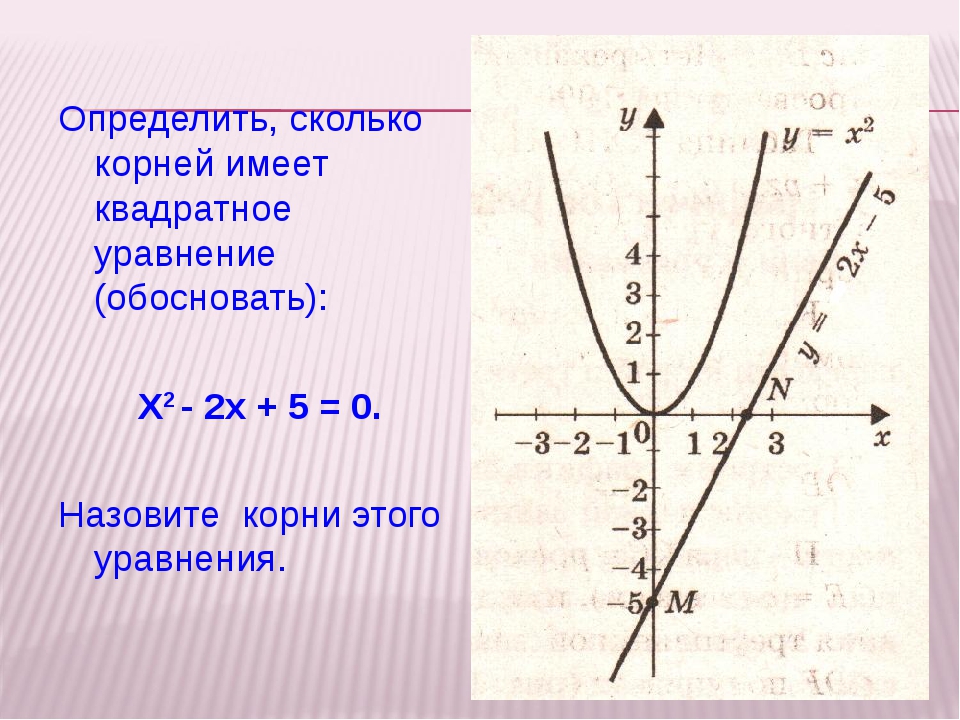


 А значения 4 и 2 подходят обоим равенствам:
А значения 4 и 2 подходят обоим равенствам:
 n} \)
n} \)
 {x-2} = 1 \)
{x-2} = 1 \)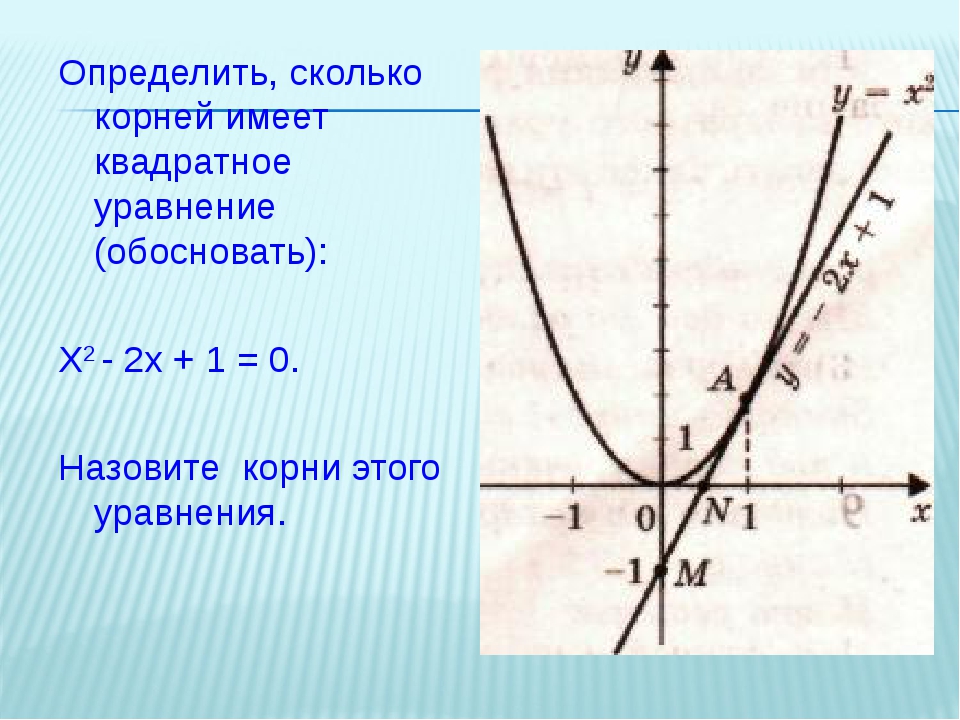 Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.
Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы.
Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой.
Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой.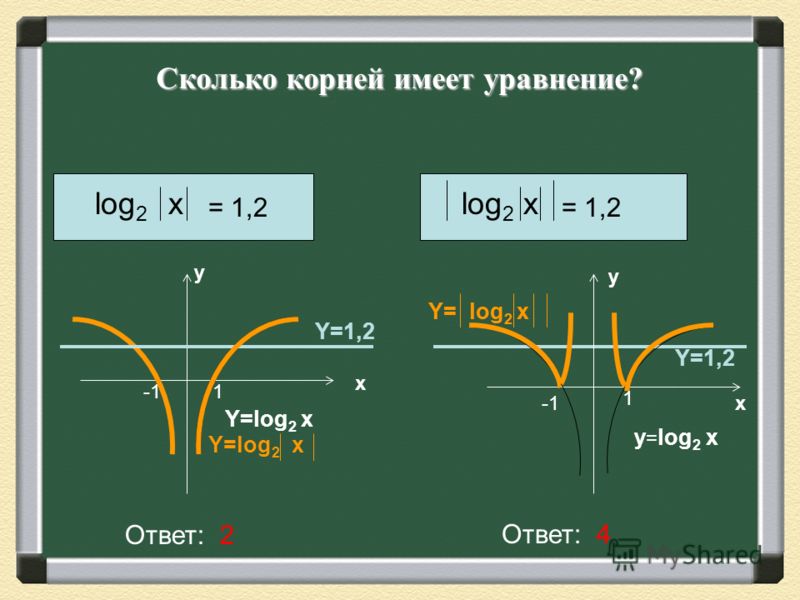 Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ.
Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ.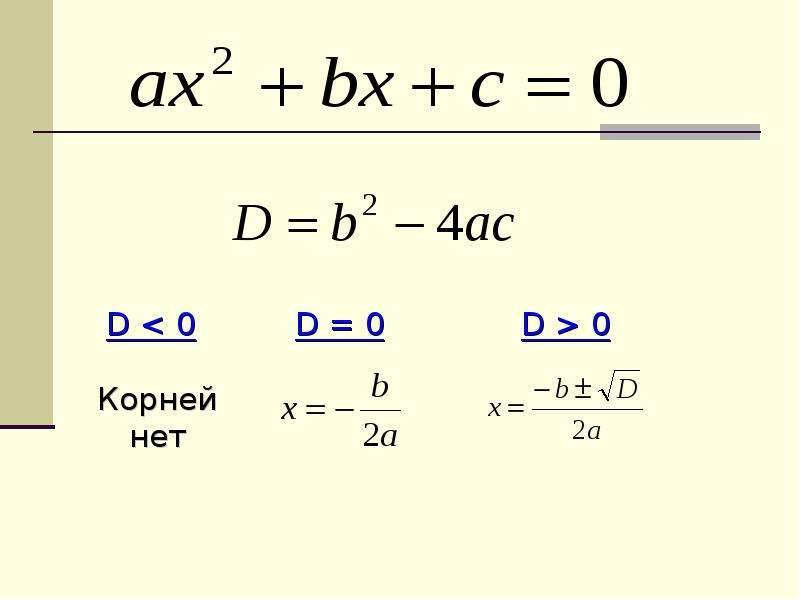 Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий.
Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции.
Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета.
Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории.
Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность.
В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их.
Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи.
Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы.
Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители.
Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение.
Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах.
В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах.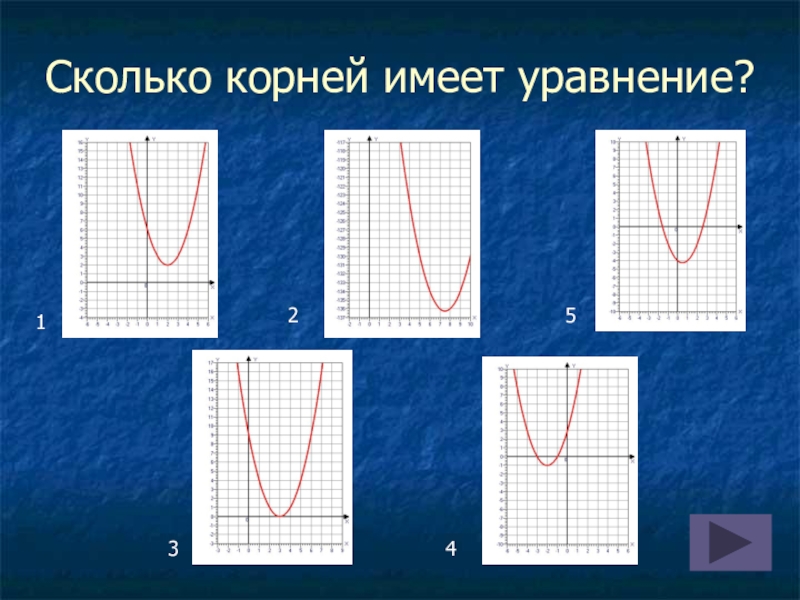 Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы.
Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная.
Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов.
Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц.
Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
 C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами.
C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами. В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней. п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.
п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
. При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
При этом в определение уравнения внедряется слово «переменная», и оно становится таким: Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.
Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.

 Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают . Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
 Это число может варьироваться от нуля до бесконечности.
Это число может варьироваться от нуля до бесконечности. А в ответе такого уравнения нужно записать, что решений нет.
А в ответе такого уравнения нужно записать, что решений нет. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:
Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»: И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый. Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.
Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Может быть, он посторонний? Стоит выполнить проверку предложенного примера. Разносим эти составляющие в разные стороны от знака равенства. Теперь уравнение приобрело такой вид: 2х + х = 16 – 10 или 3х = 6; х = 2. Результат: Х = 2.
Немного больший запас знаний нужно для вычисления корня в примере, где искомое в квадрате. Это уравнение квадратное и отличие его от линейного в том, что результатов может быть 1 или 2 или обнаружится, что корней 0. Чтобы понять лучше, решим уравнение: Х, возведенный в квадрат, умножить на 3 + 3Х = 90. Делаем так, чтобы справа образовался 0: Х2 х 3 + 3Х -90 = 0. Числа перед Х – коэффициенты 1, 3, 3. Требуется определение дискриминанта: возводим в квадрат 3 – второй коэффициент и отнимаем произведение 1 и 3. В итоге получим 6 – значит, доведя до конца расчет, обнаружим, что у этого уравнения корней 2. Если бы дискриминант выражался числом отрицательным, то изощряться в вычислении корней было бы нерационально – их просто нет. В случае если D=0, корень только 1. Теперь все-таки выполним расчет, чтобы определить эти 2 корня. Для подсчета 1 корня ко второму коэффициенту со знаком – прибавляем корень из D и делим это на удвоенный первый коэффициент: -3 + квадратный корень из 16, делим на 2.
Разносим эти составляющие в разные стороны от знака равенства. Теперь уравнение приобрело такой вид: 2х + х = 16 – 10 или 3х = 6; х = 2. Результат: Х = 2.
Немного больший запас знаний нужно для вычисления корня в примере, где искомое в квадрате. Это уравнение квадратное и отличие его от линейного в том, что результатов может быть 1 или 2 или обнаружится, что корней 0. Чтобы понять лучше, решим уравнение: Х, возведенный в квадрат, умножить на 3 + 3Х = 90. Делаем так, чтобы справа образовался 0: Х2 х 3 + 3Х -90 = 0. Числа перед Х – коэффициенты 1, 3, 3. Требуется определение дискриминанта: возводим в квадрат 3 – второй коэффициент и отнимаем произведение 1 и 3. В итоге получим 6 – значит, доведя до конца расчет, обнаружим, что у этого уравнения корней 2. Если бы дискриминант выражался числом отрицательным, то изощряться в вычислении корней было бы нерационально – их просто нет. В случае если D=0, корень только 1. Теперь все-таки выполним расчет, чтобы определить эти 2 корня. Для подсчета 1 корня ко второму коэффициенту со знаком – прибавляем корень из D и делим это на удвоенный первый коэффициент: -3 + квадратный корень из 16, делим на 2. Выйдет 1/2. Вычисление второго аналогично, только корень из D вычитаем. Имеем в результате – 3 целых и 1/2.
Выйдет 1/2. Вычисление второго аналогично, только корень из D вычитаем. Имеем в результате – 3 целых и 1/2. Минимальное количество — одна.
Минимальное количество — одна.
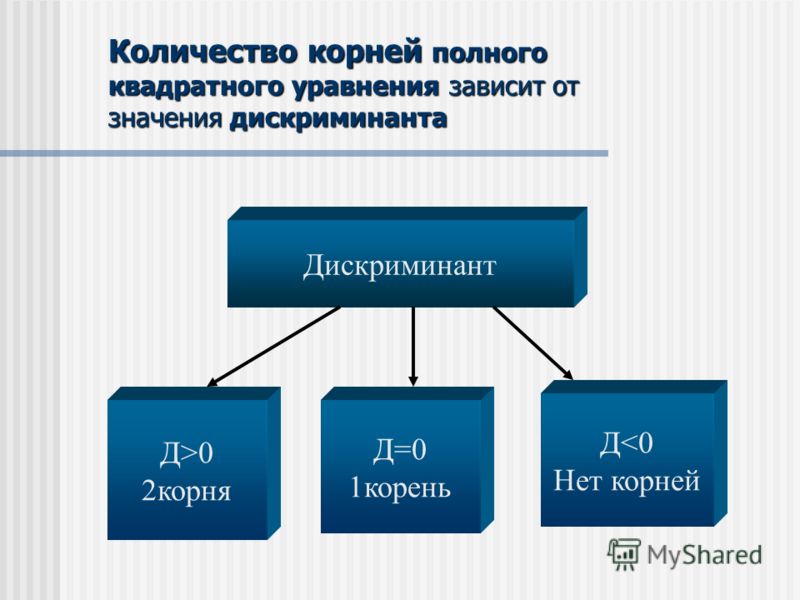 Равен нулю — ответом будет одно число. Положительный — два значения у переменной.
Равен нулю — ответом будет одно число. Положительный — два значения у переменной.
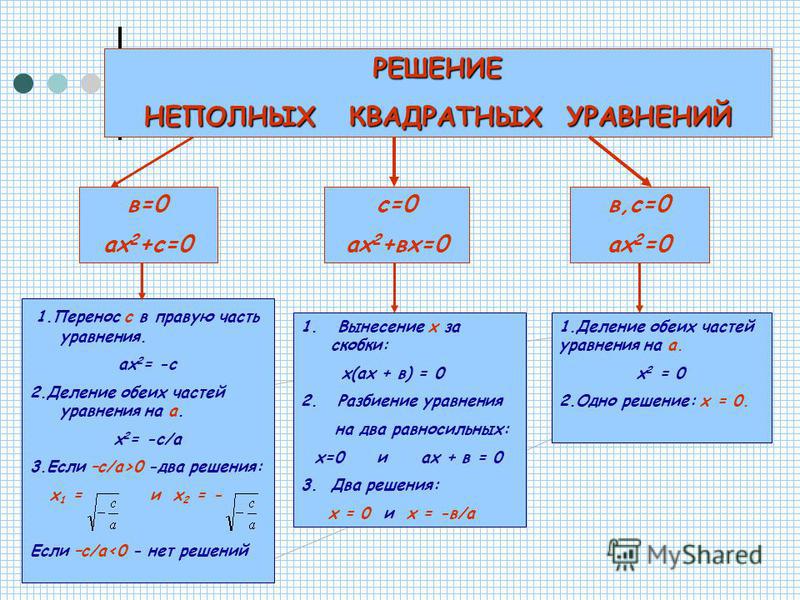 Ее не обязательно записывать.
Ее не обязательно записывать. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант . Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение: Наконец, если D
Наконец, если D Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его: Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Отсюда находятся корни. В заключение разберем несколько таких уравнений: Это выражение внутри квадратного корня квадратной формулы
Это выражение внутри квадратного корня квадратной формулы

 В приведенном выше примере у нас будет a = 1, b = 4 и c = -2.
В приведенном выше примере у нас будет a = 1, b = 4 и c = -2.

 Уравнение 7 ÷ 3 равно 2,33 …, но это не целое число! Так что не существует целочисленных решений.Если бы я позволил вам использовать дроби, вы могли бы сказать мне, что 7 ÷ 3 равно 7/3 или 2 и 1/3.
Уравнение 7 ÷ 3 равно 2,33 …, но это не целое число! Так что не существует целочисленных решений.Если бы я позволил вам использовать дроби, вы могли бы сказать мне, что 7 ÷ 3 равно 7/3 или 2 и 1/3.  Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Слово « Quadratic » происходит от слова « Quad », что означает квадрат.Другими словами, квадратное уравнение — это «уравнение степени 2 ». Есть много сценариев, в которых используется квадратное уравнение. Знаете ли вы, что при запуске ракеты ее путь описывается квадратным уравнением? Кроме того, квадратное уравнение находит множество приложений в физике, технике и астрономии.
Слово « Quadratic » происходит от слова « Quad », что означает квадрат.Другими словами, квадратное уравнение — это «уравнение степени 2 ». Есть много сценариев, в которых используется квадратное уравнение. Знаете ли вы, что при запуске ракеты ее путь описывается квадратным уравнением? Кроме того, квадратное уравнение находит множество приложений в физике, технике и астрономии. Первым условием для того, чтобы уравнение было квадратным уравнением, является коэффициент при x 2 является ненулевым членом (a 0).Для записи квадратного уравнения в стандартной форме сначала записывается член x 2 , затем член x и, наконец, постоянный член. Числовые значения a, b, c обычно не записываются как дроби или десятичные дроби, а записываются как целые значения.
Первым условием для того, чтобы уравнение было квадратным уравнением, является коэффициент при x 2 является ненулевым членом (a 0).Для записи квадратного уравнения в стандартной форме сначала записывается член x 2 , затем член x и, наконец, постоянный член. Числовые значения a, b, c обычно не записываются как дроби или десятичные дроби, а записываются как целые значения. Корни квадратного уравнения также помогают найти сумму корней и произведение корней квадратного уравнения.Два корня в формуле корней квадратного уравнения представлены как одно выражение. В качестве альтернативы можно использовать положительный знак и отрицательный знак для получения двух различных корней уравнения.
Корни квадратного уравнения также помогают найти сумму корней и произведение корней квадратного уравнения.Два корня в формуле корней квадратного уравнения представлены как одно выражение. В качестве альтернативы можно использовать положительный знак и отрицательный знак для получения двух различных корней уравнения.


 Если α, β, являются корнями квадратного уравнения, то квадратное уравнение выглядит следующим образом.
Если α, β, являются корнями квадратного уравнения, то квадратное уравнение выглядит следующим образом. Далее, мы можем взять общие термины из доступного термина, чтобы окончательно получить требуемые коэффициенты. Для понимания факторизации общий вид квадратного уравнения может быть представлен следующим образом.
Далее, мы можем взять общие термины из доступного термина, чтобы окончательно получить требуемые коэффициенты. Для понимания факторизации общий вид квадратного уравнения может быть представлен следующим образом. С помощью этой формулы можно решить любое квадратное уравнение.
С помощью этой формулы можно решить любое квадратное уравнение. После упрощения и извлечения квадратного корня два возможных корня квадратного уравнения равны x = (-b + √ (b 2 — 4ac)) / 2a. Здесь знак «+» дает один корень, а знак «-» — другой корень квадратного уравнения. Как правило, этого подробного метода избегают, и для получения требуемых корней используется только формула.
После упрощения и извлечения квадратного корня два возможных корня квадратного уравнения равны x = (-b + √ (b 2 — 4ac)) / 2a. Здесь знак «+» дает один корень, а знак «-» — другой корень квадратного уравнения. Как правило, этого подробного метода избегают, и для получения требуемых корней используется только формула. 2 + b_2x + c_2 = 0 \).2 \)
2 + b_2x + c_2 = 0 \).2 \)

 Есть много реальных приложений квадратных уравнений. Например, его можно использовать в задачах на время бега, чтобы оценить скорость, расстояние или время во время путешествия на машине, поезде или самолете. Квадратные уравнения описывают взаимосвязь между количеством и ценой товара. Точно так же расчеты спроса и затрат также считаются задачами квадратных уравнений.Также можно отметить, что спутниковая тарелка или телескоп-рефлектор имеет форму, которая определяется квадратным уравнением.
Есть много реальных приложений квадратных уравнений. Например, его можно использовать в задачах на время бега, чтобы оценить скорость, расстояние или время во время путешествия на машине, поезде или самолете. Квадратные уравнения описывают взаимосвязь между количеством и ценой товара. Точно так же расчеты спроса и затрат также считаются задачами квадратных уравнений.Также можно отметить, что спутниковая тарелка или телескоп-рефлектор имеет форму, которая определяется квадратным уравнением. Кроме того, его можно упростить, найдя его множители в процессе факторизации. Также для уравнения, которое трудно разложить на множители, оно решается с помощью формулы. Кроме того, есть несколько других способов упростить квадратное уравнение.
Кроме того, его можно упростить, найдя его множители в процессе факторизации. Также для уравнения, которое трудно разложить на множители, оно решается с помощью формулы. Кроме того, есть несколько других способов упростить квадратное уравнение. x (x + a) + b (x + a) = 0, (x + a) (x + b) = 0. Наконец, приравняйте каждый из множителей к нулю и получите значения x. x + a = 0 и x + b = 0, и, следовательно, мы можем получить x = -a и x = -b
x (x + a) + b (x + a) = 0, (x + a) (x + b) = 0. Наконец, приравняйте каждый из множителей к нулю и получите значения x. x + a = 0 и x + b = 0, и, следовательно, мы можем получить x = -a и x = -b Эти две точки, где этот график пересекает ось x, являются возможными решениями этого квадратного уравнения.
Эти две точки, где этот график пересекает ось x, являются возможными решениями этого квадратного уравнения. Для квадратного уравнения вида ax² + bx + c = 0 дискриминант равен D = b² — 4ac = 0.Здесь оба корня равны и каждый имеет значение x = -b / 2a.
Для квадратного уравнения вида ax² + bx + c = 0 дискриминант равен D = b² — 4ac = 0.Здесь оба корня равны и каждый имеет значение x = -b / 2a. Один метод — решить квадратное уравнение путем факторизации, а другой — путем заполнения квадратов. Всего существует три метода нахождения корней квадратного уравнения.
Один метод — решить квадратное уравнение путем факторизации, а другой — путем заполнения квадратов. Всего существует три метода нахождения корней квадратного уравнения. Какой вид имеет квадратное уравнение?
Какой вид имеет квадратное уравнение?
 Два корня равны, их 5, 5. 5 называется двойным корнем. (См. Урок алгебры 37, вопрос 4.)
Два корня равны, их 5, 5. 5 называется двойным корнем. (См. Урок алгебры 37, вопрос 4.)


 В квадратичной системе со старшим коэффициентом 1:
В квадратичной системе со старшим коэффициентом 1: 


 Предположительно, бильярдный шар обладает прогностическими способностями; все, что вам нужно сделать, это задать ему вопрос, встряхнуть, и медленно, мистическим образом, как покрытая нефтью печать, выходящая из разлива нефти, игральная кость поднимется к маленькому окошку и откроет ответ на ваш вопрос.
Предположительно, бильярдный шар обладает прогностическими способностями; все, что вам нужно сделать, это задать ему вопрос, встряхнуть, и медленно, мистическим образом, как покрытая нефтью печать, выходящая из разлива нефти, игральная кость поднимется к маленькому окошку и откроет ответ на ваш вопрос.
 )
)




 2 или -1
2 или -1
 2 ± 0,4 и
2 ± 0,4 и 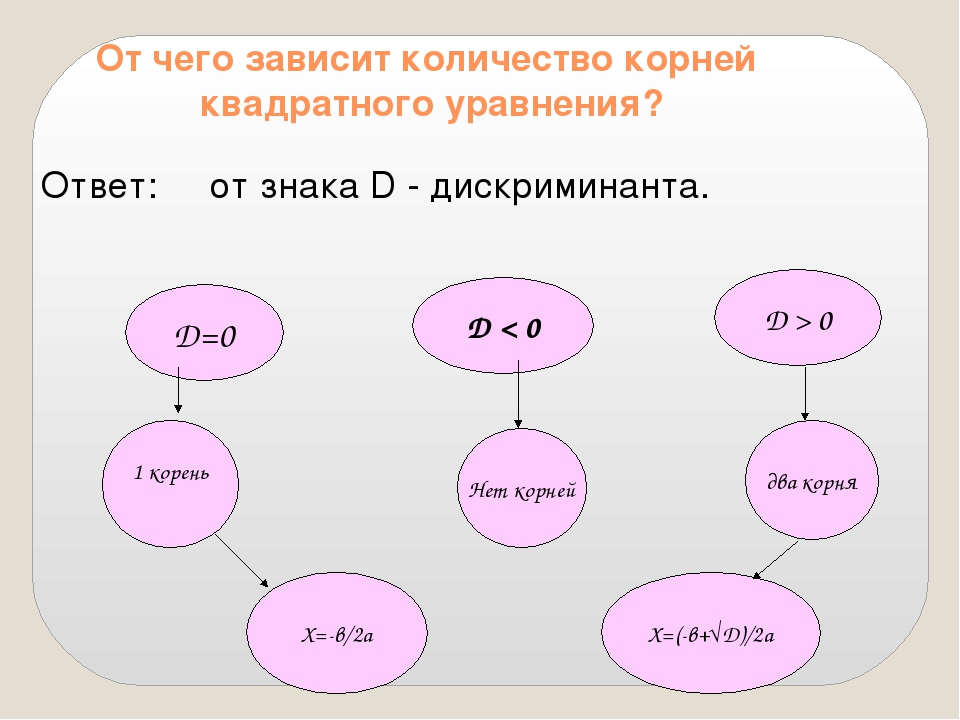 Вот почему мы пришли к комплексным числам.
Вот почему мы пришли к комплексным числам.