Систем уравнений виды: определение, виды, примеры решения, что это такое

Содержание

определение, виды, примеры решения, что это такое

Статья знакомит с таким понятием, как определение системы уравнений и ее решением. Будут рассмотрены часто встречающиеся случаи решений систем. Приведенные примеры помогут подробно пояснить решение.

Определение системы уравнений

Чтобы перейти к определению системы уравнений, необходимо обратить внимание на два момента: вид записи и ее смысл. Чтобы понять это, нужно подробно остановиться на каждом из видов, тогда сможем прийти к определению систем уравнений.

Например, возьмем два уравнения 2·x+y=−3 и x=5, после чего объединим фигурной скобкой такого плана:

2·x+y=-3,x=5.

Уравнения, объединенные фигурной скобкой, считаются записями систем уравнений. Они задают множества решений уравнений данной системы. Каждое решение должно являться решением всех заданных уравнений.

Другими словами это означает, что любые решения первого уравнения будут решениями всех уравнений, объединенных системой.

Определение 1

Системы уравнений – это некоторое количество уравнений, объединенных фигурной скобкой, имеющих множество решений уравнений, которые одновременно являются решениями для всей системы.

Основные виды систем уравнений

Видов уравнений достаточно много, как систем уравнений. Для того, чтобы было удобно решать и изучать их, подразделяют на группы по определенным характеристикам. Это поможет в рассмотрении систем уравнений отдельных видов.

Для начала уравнения классифицируются по количеству уравнений. Если уравнение одно, то оно является обычным уравнением, если их более, тогда имеем дело с системой, состоящей из двух или более уравнений.

Другая классификация затрагивает число переменных. Когда количество переменных 1, говорят, что имеем дело с системой уравнений с одной неизвестной, когда 2 – с двумя переменными. Рассмотрим пример

x+y=5,2·x-3·y=1

Очевидно, что система уравнений включает в себя две переменные х и у.

При записи таких уравнений считается число всех переменных, имеющихся в записи. Их наличие в каждом уравнении необязательно. Хотя бы одно уравнение должно иметь одну переменную. Рассмотрим пример системы уравнений

2x=11,x-3·z2=0,27·x+y-z=-3

Данная система имеет 3 переменные х, у, z. Первое уравнение имеет явный х и неявные у и z. Неявные переменные – это переменные, имеющие 0 в коэффициенте. Второе уравнение имеет х и z, а у неявная переменная. Иначе это можно записать таким образом

2x+0·y+0·z=11

А другое уравнение x+0·y−3·z=0.

Третья классификация уравнений – это вид. В школе проходят простые уравнения и системы уравнений, начиная с систем двух линейных уравнений с двумя переменными. Имеется в виду, что система включает в себя 2 линейных уравнения. Для примера рассмотрим

2·x-y=1,x+2·y=-1и -3·x+y=0.5,x+223·y=0

Это основные простейшие линейные уравнения. Далее можно столкнуться с системами, содержащими 3 и более неизвестных.

В 9 классе решают уравнения с двумя переменными и нелинейные. В целых уравнениях повышается степень для увеличения сложности. Такие системы называют системами нелинейных уравнений с определенным количеством уравнений и неизвестных. Рассмотрим примеры таких систем

x2-4·x·y=1,x-y=2 и x=y3x·y=-5

Обе системы с двумя переменными и обе являются нелинейными.

При решении можно встретить дробно-рациональные уравнения. Например

x+y=3,1x+1y=25

Могут называть просто системой уравнений без уточнения, каких именно. Редко уточняют сам вид системы.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Старшие классы переходят к изучению иррациональных, тригонометрических и показательных уравнений. Например,

x+y-x·y=5,2·x·y=3, x+y=5·π2,sin x+cos 2y=-1,y-log3x=1,xy=312.

Высшие учебные заведения изучают и исследуют решения систем линейных алгебраических уравнений (СЛАУ). Левая часть таких уравнений содержит многочлены с первой степенью, а правая – некоторые числа. Отличие от школьных в том, что количество переменных и количество уравнений может быть произвольным, чаще всего несовпадающим.

Решение систем уравнений

Определение 2

Решение системы уравнений с двумя переменными

– это пара переменных, которая при подстановке обращает каждое уравнение в верное числовое неравенство, то есть является решением для каждого уравнения данной системы.

К примеру, пара значений х=5 и у=2 являются решением системы уравнений x+y=7,x-y=3. Потому как при подстановке уравнения обращаются в верные числовые неравенства 5+2=7 и 5−2=3. Если подставить пару х=3 и у=0, тогда система не будет решена, так как подстановка не даст верное уравнение, а именно, мы получим 3+0=7.

Сформулируем определение для систем, содержащих одну и более переменных.

Определение 3

Решение системы уравнений с одной переменной – это значение переменной, которая является корнем уравнений системы, значит, все уравнения будут обращены в верные числовые равенства.

Рассмотрим на примере системы уравнений с одной переменной t

t2=4,5·(t+2)=0

Число -2 – решение уравнения, так как (−2)·2=4, и 5·(−2+2)=0 являются верными числовыми равенствами. При t=1 система не решена, так как при подстановке получим два неверных равенства 12=4 и 5·(1+2)=0.

Определение 4

Решение системы с тремя и более переменными называют тройку, четверку и далее значений соответственно, которые обращают все уравнения системы в верные равенства.

Если имеем значения переменных х=1, у=2, z=0, то подставив их в систему уравнений 2·x=2,5·y=10,x+y+z=3, получим 2·1=2, 5·2=10 и 1+2+0=3. Значит, эти числовые неравенства верные. А значения (1, 0, 5) не будут решением, так как, подставив значения, второе из них будет неверное, как и третье: 5·0=10, 1+0+5=3.

Системы уравнений могут не иметь решений вовсе или иметь бесконечное множество. В этом можно убедиться при углубленном изучении данной тематики. Можно прийти к выводу, что системы уравнений – это пересечение множеств решений всех ее уравнений. Раскроем несколько определений:

Определение 5

Несовместной называют систему уравнений, когда она не имеет решений, в противном случае ее называют совместной.

Определение 6

Неопределенной называют систему, когда она имеет бесконечное множество решений, а определенной при конечном числе решений либо при их отсутствии.

Такие термины редко применяются в школе, так как рассчитаны для программ высших учебных заведений. Знакомство с равносильными системами углубит имеющиеся знания по решению систем уравнений.

Основные типы систем уравнений

Цели:

Систематизировать основные типы систем уравнений. Рассмотреть способы их решения.
Побуждать учеников к самоконтролю, взаимоконтролю, самоанaлизу своей учебной деятельности.

Оборудование: доска, экран, проектор.

Ход урока

I. Организационный момент. Сообщение темы и целей урока.

II. Повторение и закрепление пройденного материала.

ответы на вопросы по домашнему заданию. Разбор нерешенных задач.
контроль усвоения материала.

Самостоятельная работа. На экране или на оборотной стороне доски заранее заготовлены задания. Два ученика решают у доски. Проверка ведется фронтально, но пары обмениваются тетрадями и проводят взаимопроверку.

1 вариант

Сумма двух чисел равна 30, а их произведение равно 216. Найдите эти числа.
Гипотенуза прямоугольного треугольника равна 20 см, а его периметр равен 48 см. Найдите катеты.

2 вариант

Сумма двух чисел равна 40, а их произведение равно 364. Найдите эти числа.
Гипотенуза прямоугольного треугольника равна 25 см, а его периметр равен 60 см. Найдите катеты.

III. Изучение нового материала.

Система уравнений, в которой хотя бы одно из уравнений не является линейным, называется системой нелинейных уравнений.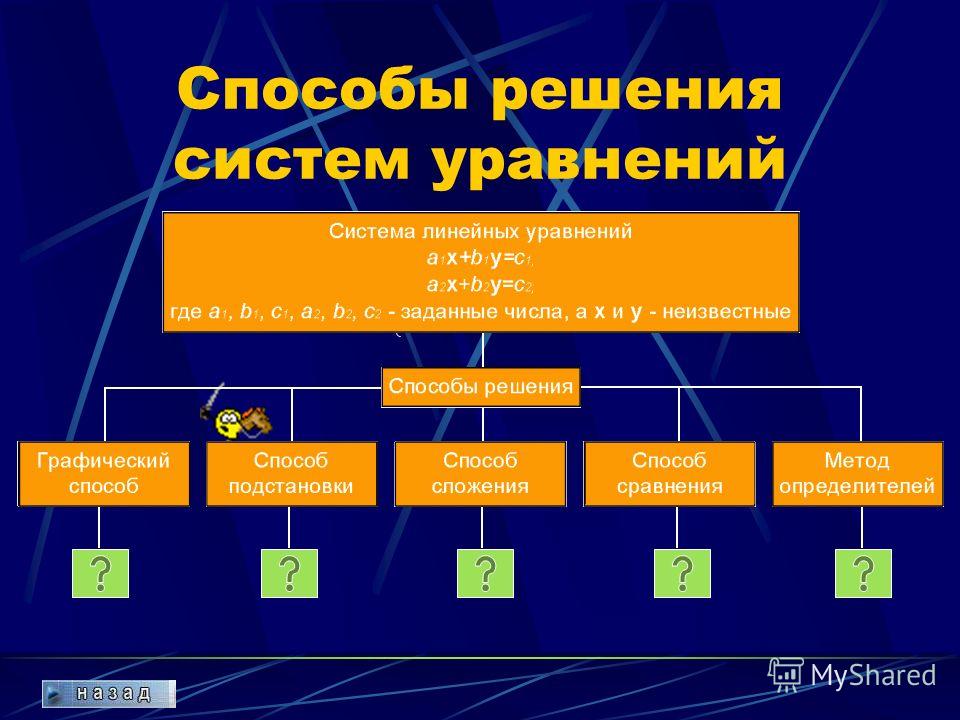 Существуют способы решения любой системы линейных уравнений. Для систем нелинейных уравнений универсальных способов не существует.

Основной подход к решению систем нелинейных уравнений состоит в том, что с помощью тех или иных преобразований получают линейное уравнение, содержащее неизвестные. Это уравнение позволяет выразить одну неизвестную через другие и затем использовать для решения способ подстановки.

Остановимся на самых распространенных системах нелинейных уравнений.

А) Системы, содержащие одно линейное уравнение.

Такие системы решаются способом подстановки. Из линейного уравнения одна из неизвестных выражается через другую и подставляется в оставшееся уравнение. Затем это уравнение с одной неизвестной решается, потом определяется и вторая неизвестная.

Пример 1. Решить систему уравнений:

Так как в системе второе уравнение является линейным, то выразим из него неизвестную у=-(х+8) и подставим в первое уравнение: х²+(х+8)2+6х-2(х+8)=0 или х²+10х+24=0. Отсюда, (-6;-2), (-4;-4).

Б) Системы, которые с помощью замен сводятся к линейным.

Решить систему уравнений

Введем замены неизвестных: и= и v= . Получим систему линейных уравнений

Эта система имеет единственное решение: и=1, v=1. Возвращаясь к неизвестным х, у, получим систему линейных уравнений:

Система имеет единственное решение: х=1, у=1.

В) Однородные системы.

Системы уравнений, у которых левая часть одного из уравнений является однородным многочленом, а правая часть равна нулю или у которых левые части двух уравнений являются однородными многочленами, а правые части равны числам, не равным нулю, называются однородными системами уравнений.

Решить систему уравнений

Первое уравнение этой системы является однородным. Решаем его относительно неизвестной у, считая х постоянной величиной, и получим: у=-х и у=. Подставим полученное соотношение во второе уравнение. При у=-х имеем: х²-х(-х)-(-х)²+3х+7(-х)+3=0 или х² – 4х+3=0. Тогда х₁=1, у₁=-1, х₂=3, у₂=-3. В случае у= получаем: х²-х- ( )²+3х+7+3=0 или х² +26х+12=0. Тогда х_3,4=-13; у_3,4=. Система имеет четыре решения.

Г) Симметричные системы.

Система уравнений называется симметричной, если при замене х на у, а у на х уравнения системы меняются. Для решения симметричных систем в качестве новых переменных используют простейшие симметричные выражения: и=х+у, v=ху. Способ замены неизвестных.

Решить систему уравнений

Система уравнений является симметричной, так как при замене х на у, а у на х получаем систему

которая с точностью до перестановки слагаемых и сомножителей совпадает с исходной.

Введем новые неизвестные: и=х+у, v=ху. Тогда х²+у²=(х+у)²-2ху=и2-2v и исходная система будет иметь вид

Сложив уравнения системы, получим квадратное уравнение: и²+и-12=0, откуда и₁=-4, и₂=3. Тогда v₁=9, v₂=2. Возвращаясь, получаем

Решив их, получим для первой системы — отсутствие решений, для второй – (1;2) и (2;1).

Во многих случаях, система не являющаяся симметричной, с помощью соответствующих замен неизвестных может быть сведена к таковой.

Решить систему уравнений

Введем замены неизвестных: и=х+у и v= . Получим систему линейных уравнений

и₁=1, и₂=. Тогда v₁=-, v₂=1. Возвращаясь, получаем

Решив их, получим для первой системы — (-1;2), для второй – ().

В заключение темы заметим, что при анализе или решении линейных или нелинейных систем уравнений можно использовать графические методы, иногда встречаются и системы двух уравнений с тремя неизвестными, которые мы рассмотрим на следующих уроках.

IV. Контрольные вопросы.

Как решаются системы, содержащие линейные уравнения?
Дайте определение однородной системы уравнений.
Как решаются однородной системы уравнений?
Дайте определение симметричной системы уравнений.
Как решаются симметричные системы уравнений?

V. Задания на уроках и на дом.

(на экране проецируется через проектор).

VI. Подведение итогов урока.

Системы уравнений. Понятие системы уравнений.

Свойства систем уравнений. Линейные системы уравнений с двумя неизвестными. Основные методы решения систем уравнений

Понятие системы уравнений.
Система уравнений — набор уравнений с несколькими неизвестными. Решение системы уравнений — совокупность значений неизвестных, обращающих каждое из уравнений системы в тождество. Решить систему уравнений — найти все её решения или доказать, что их нет. Система не имеющая решений решений, называется несовместной. Равносильные системы — системы, множества решений которых совпадают. Все несовместимые системы — равносильны.
Свойства систем уравнений:

Линейные системы уравнений с двумя неизвестными:
Линейные системы уравнений с двумя переменными — это система вида:
		Прямые — графики уравнений системы пересекаются в одной точке. Система имеет единственное решение:
		Прямые — графики уравнений системы — параллельны. Система не имеет решений.
		Прямые — графики уравнений системы совпадают. Система имеет бесконечно много решений:
Основные методы решения систем уравнений:
Графический метод:
1. Построить в одной системе координат графики обоих уравнений:
2. Найти координаты точек пересечения графиков.
Метод подстановки:
1. Выразить одну переменную через другую в одном из уравнений.
2. Подставить это выражение в другое уравнение и получить уравнение с одной переменной.
3. Найти корни уравнения с одной переменной.
4. Подставить найденные корни в выражение для первой переменной и получить ее значение.
Метод сложения (вычитания):
1. Сложить почленно уравнения системы, предварительно умножив каждое из уравнений на такой множитель:
2. Найти корни уравнения с одной переменной.
3. Подставить найденные корни в любое из уравнений системы и получить уравнение с одной неизвестной.
4. Найти корни этого уравнения.
Метод введения новых переменных:
1. Вместо исходных переменных x и y ввести такие новые переменные: чтобы система с ними стала проще.
2. Решить систему с новыми переменными.
3. Найти значения исходных переменных.

Методы решения систем рациональных уравнений. Алгебра, 9 класс: уроки, тесты, задания.

1.	Метод сложения (линейные уравнения) Сложность: лёгкое
2.	Метод подстановки (линейные уравнения) Сложность: лёгкое
3.	Корни квадратного уравнения, теорема Виета Сложность: лёгкое
4.	Метод подстановки (линейное и квадратное) Сложность: лёгкое
5.	Метод алгебраического сложения Сложность: среднее
6.	Способ сложения Сложность: среднее
7.	Пары чисел, которые являются решением системы уравнений Сложность: среднее
8.	Графический метод (парабола и прямая) Сложность: среднее
9.	Графический метод (гипербола и прямая) Сложность: среднее
10.	Графический метод (элементарные функции) Сложность: среднее
11.	Система квадратных уравнений Сложность: среднее
12.	Система уравнений (линейное и квадратное) I Сложность: среднее
13.	Система уравнений (линейное и квадратное) II Сложность: среднее
14.	Система уравнений (линейное и квадратное) III Сложность: среднее
15.	Задача на составление системы уравнений Сложность: среднее
16.	Система рациональных уравнений Сложность: среднее
17.	Система, состоящая из рационального и квадратного уравнений Сложность: среднее
18.	Система, состоящая из рационального и линейного уравнений Сложность: среднее
19.	Система рациональных уравнений, вводится одна новая переменная Сложность: среднее
20.	Система, состоящая из рациональных уравнений Сложность: среднее
21.	Система, состоящая из квадратного и рационального уравнений Сложность: среднее
22.	Система линейных уравнений Сложность: среднее
23.	Система, состоящая из квадратного и рационального уравнений, метод умножения Сложность: среднее
24.	Пары чисел, которые являются решением системы уравнений Сложность: среднее
25.	Графический метод (окружность и парабола) Сложность: сложное

Решение системы линейных уравнений методом Гаусса с нахождением общего решения

Вообще говоря, на сайте уже есть один калькулятор, решающий СЛАУ методом Гаусса — Решение системы линейных алгебраических уравнений методом Гаусса. Он даже расписывает решение пошагово.

Однако, у него есть некоторые недостатки, которые будет решать новый калькулятор из этой статьи:

Во-первых, предыдущий калькулятор выдает решение в формате с плавающей запятой, тогда как во многих задачниках ответ обычно дается в виде дроби.

Во-вторых, предыдущий калькулятор только определяет факт наличия бесконечного множества решений (неопределенная система), но не выдает решение в общем виде.

В-третьих, предыдущий калькулятор работает только в случае когда число уравнений совпадает с числом неизвестных, и таким образом, не может решать недоопределенных (число неизвестных больше числа уравнений) и переопределенных систем (число неизвестных меньше числа уравнений).

Что касается, второго и третьего пунктов, то универсальность метода Гаусса состоит в том, что на самом деле он годится для систем линейных уравнений с любым числом уравнений и неизвестных, просто это не было использовано.

Описание самого метода Гаусса можно посмотреть по ссылке выше, а под калькулятором подробнее рассмотрены разные случаи (виды систем).

Сам калькулятор, помимо нахождения единственного решения, может находить и общее решение в случае неопределенной системы уравнений.
Матрица уравнений из случая 2 ниже (совместная неопределенная система линейных уравнений) использована в нем в качестве входных данных по умолчанию:

Решение системы линейных уравнений методом Гаусса для любого числа уравнений и неизвестных

1 2 -3 5 1 1 3 -13 22 -1 3 5 1 -2 5 2 3 4 -7 4

СЛАУ в матричном виде

Количество решений

Коэффициенты решения

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить close

content_copy Ссылка save Сохранить extension Виджет

1. Совместная определенная система линейных уравнений (имеющая одно решение)

Пример: пусть дана система линейных уравнений

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Откуда обратным ходом находим единственное решение:

Система совместна и определена.

2. Совместная неопределенная система линейных уравнений (имеющая бесконечное множество решений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

В результате приходим к системе:

Последние два уравнения верны при любых значениях переменных:

поэтому их можно отбросить.

Чтобы найти решения оставшихся двух уравнений, x1 и x2 можно выразить через x3 и x4.

При этом сами x3 и x4 могут принимать любые значения

Полученная эквивалентная система совместна, но неопределена. Формулы:
;
при произвольных x3 и x4 описывают бесконечное множество решений заданной системы.

3. Несовместная система линейных уравнений (не имеющая решений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Полученная эквивалентная система несовместна, так как последнее уравнение:

не может быть удовлетворено никакими значениями неизвестных.
Эта система несовместна, т. е. не имеет решения.

4. Переопределенная система линейных уравнений (число неизвестных меньше числа уравнений)

Пример: пусть дана система линейных уравнений

После приведения матрицы к трапециевидной форме методом Гаусса получим

Как видим, в данном случае «лишнее» уравнение можно просто отбросить. Также в результате преобразований можно получить одинаковые строки, «лишние» из которых тоже можно отбросить — после чего задача сводится к случаям 1 или 2.

5. Недоопределенная система линейных уравнений (число неизвестных больше числа уравнений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Полученная эквивалентная система имеет вид:

Как видно, в ней отсутствуют уравнения, дающие однозначные значения для x3 и x4, что равносильно появлению уравнений вида:

которые можно отбросить.

Таким образом этот случай сводится к случаю 2 с бесконечным множеством решений, которые описываются следующими формулами:

I.

5. Исследование неоднородных систем линейных алгебраических уравнений

(схема 18)

Пусть задана неоднородная система линейных алгебраических уравнений размерности m×n.

Матрицаназывается расширенной матрицей системы, если наряду с коэффициентами при неизвестных, она содержит столбец свободных членов. Следовательно, размерность равна m×(n+1).

Исследование любой системы линейных алгебраических уравнений начинается с преобразования ее расширенной матрицы методом Гаусса, который основан на следующих элементарных преобразованиях:

– перестановка строк матрицы;

– умножение строк матрицы на действительное отличное от руля число;

– поэлементное сложение строк матрицы;

– вычеркивание нулевой строки;

– транспонирование матрицы (в этом случае преобразования производятся по столбцам).

Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений.

Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют.

На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема.

Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть

Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными.

Если r=n, то система имеет единственное решение (является совместной определенной), ее матрица элементарными преобразованиями приводится к треугольному виду. Такую систему можно решить также методом Крамера и с помощью обратной матрицы.

Если r<n (количество переменных в системе больше количества уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций.

1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n—r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид:

. (1.10)

2. Из коэффициентов при базисных переменных составить минор (базисный минор), который должен быть отличен от нуля.

3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля.

4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением.

5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений.

6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных.

Заметим, что количество базисных наборов переменных системы (1. 10) равно числу сочетаний из n элементов по r элементов C_n^r. Так как каждому базисному набору переменных соответствует свое базисное решение, следовательно, количество базисных решений у системы также равно C_n^r.

Пусть строки матрицы обозначены соответственно l₁;l₂;…;l_n. Строка l называется линейной комбинацией строк l₁;l₂;…;l_n матрицы, если она равна сумме произведений этих строк на произвольные действительные числа, то есть ,.

Однородная система уравнений всегда совместна, так как имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная система n линейных уравнений с n переменными имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель ∆ был равен нулю. Это означает, что ранг r ее главной матрицы меньше числа n неизвестных (r<n). В этом случае исследование однородной системы уравнений на общее и частные решения проводится аналогично исследованию неоднородной системы. Решения однородной системы уравнений обладают важным свойством: если известны два различных решения однородной системы линейных алгебраических уравнений, то их линейная комбинация также является решением этой системы. Нетрудно убедиться в справедливости следующей теоремы.

Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений

Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:

Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования:

Так как r(A)=2 и , то по теореме 1. 3 (Кронекера-Капелли) заданная система линейных алгебраических уравнений совместна. Количество переменных n=2, т.е. r<n, значит, система является неопределённой. Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов переменных: {x₁;x₂}, {x₁;x₃}, {x₁;x₄}, {x₂;x₃}, {x₂;x₄}, {x₃;x₄}. Рассмотрим один из них {x₁;x₂}. Тогда систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.

Вспомогательные определители

По формулам (1.6) имеем

Данное выражение базисных переменных через свободные представляет собой общее решение системы:

При конкретных значениях свободных переменных из общего решения получаем частное решение системы. Например, частное решение соответствует значениям свободных переменных x₃=x₄=17. При x₃=0 x₄=0 получаем базисное решение системы

Вопросы для самопроверки

Система линейных алгебраических уравнений — это… Что такое Система линейных алгебраических уравнений?

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

(1)

Система линейных уравнений от трёх переменных определяет набор плоскостей.

Точка пересечения является решением.

Здесь — количество уравнений, а — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c₁⁽¹⁾ = c₁⁽²⁾, c₂⁽¹⁾ = c₂⁽²⁾, …, c_n⁽¹⁾ = c_n⁽²⁾.

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма

Система линейных уравнений может быть представлена в матричной форме как:

или:

Здесь — это матрица системы, — столбец неизвестных, а — столбец свободных членов. Если к матрице приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Эквивалентные системы линейных уравнений

Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Система линейных алгебраических уравнений

эквивалентна системе

где — невырожденная матрица.

В частности, если сама матрица — невырожденная, и для неё существует обратная матрица , то решение системы уравнений можно формально записать в виде

Методы решения

Прямые (или точные) методы позволяют найти решение за определённое количество шагов. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

Прямые методы

Итерационные методы

Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения

эквивалентного начальной системе линейных алгебраических уравнений. При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

Среди итерационных методов можно отметить самые популярные:

См. также

Примечания

↑ В рамках данной статьи коэффициенты системы, свободные члены и неизвестные считаются действительными числами, хотя они могут быть комплексными или даже сложными математическими объектами с условием, что для них определены операции умножения и сложения.
↑ Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
↑ Вержбицкий В. М. Основы численных методов. — М.: Высшая школа, 2009. — С. 80—84. — 840 с. — ISBN 9785060061239

Ссылки

11.

1: Системы линейных уравнений — две переменные

Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, то есть сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает от продажи своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов необходимо произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.

Введение в системы уравнений

Чтобы исследовать такие ситуации, как ситуация с производителем скейтборда, нам необходимо признать, что мы имеем дело с более чем одной переменной и, вероятно, более чем с одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных. Но даже в этом случае это не гарантирует уникального решения.

В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

\ [\ begin {align *} 2x + y & = 15 \\ 3x – y & = 5 \ end {align *} \]

Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. В этом примере упорядоченная пара \ ((4,7) \) является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы поиска такого решения, если оно существует.

\ [\ begin {align *} 2 (4) + (7) & = 15 \ text {True} \\ 3 (4) — (7) & = 5 \ text {True} \ end {align *} \ ]

Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. Непротиворечивая система уравнений имеет по крайней мере одно решение. Согласованной системой считается , независимая система , если она имеет единственное решение, такое как пример, который мы только что исследовали. Две линии имеют разные уклоны и пересекаются в одной точке на плоскости.Согласованной системой считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые точки пересечения y . Другими словами, линии совпадают, поэтому уравнения представляют одну и ту же линию. Каждая точка на линии представляет пару координат, удовлетворяющую системе. Таким образом, существует бесконечное количество решений.

Другой тип системы линейных уравнений — это несовместимая система , в которой уравнения представляют собой две параллельные линии.Линии имеют одинаковый наклон и разные точки пересечения y- . Для обеих линий нет общих точек; следовательно, у системы нет решения.

ВИДЫ ЛИНЕЙНЫХ СИСТЕМ

Существует три типа систем линейных уравнений с двумя переменными и три типа решений.

Независимая система имеет ровно одну пару решений \ ((x, y) \). Точка пересечения двух линий — единственное решение.
Несогласованная система не имеет решения.Обратите внимание, что две линии параллельны и никогда не пересекутся.
У зависимой системы бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.

На рисунке \ (\ PageIndex {2} \) сравниваются графические представления каждого типа системы.

Рисунок \ (\ PageIndex {2} \)

Для системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением.

Подставьте упорядоченную пару в каждое уравнение системы.
Определите, являются ли истинные утверждения результатом подстановки в обоих уравнениях; в таком случае заказанная пара является решением.

Пример \ (\ PageIndex {1} \): определение того, является ли упорядоченная пара решением системы уравнений

Определите, является ли упорядоченная пара \ ((5,1) \) решением данной системы уравнений.

\ [\ begin {align *} x + 3y & = 8 \\ 2x − 9 & = y \ end {align *} \]

Решение

Подставляем упорядоченную пару \ ((5,1) \) в оба уравнения.

\ [\ begin {align *} (5) +3 (1) & = 8 \\ 8 & = 8 \ text {True} \\ 2 (5) −9 & = (1) \\ 1 & = 1 \ text {True} \ end {align *} \]

Упорядоченная пара \ ((5,1) \) удовлетворяет обоим уравнениям, поэтому она является решением системы.

Анализ

Мы можем ясно увидеть решение, построив график каждого уравнения. Поскольку решение представляет собой упорядоченную пару, удовлетворяющую обоим уравнениям, это точка на обеих прямых и, следовательно, точка пересечения двух прямых.См. Рисунок \ (\ PageIndex {3} \).

Рисунок \ (\ PageIndex {3} \)

Упражнение \ (\ PageIndex {1} \)

Определите, является ли упорядоченная пара \ ((8,5) \) решением следующей системы.

\ [\ begin {align *} 5x − 4y & = 20 \\ 2x + 1 & = 3y \ end {align *} \]

Ответ: Не выход.

Решение систем уравнений с помощью построения графиков

Существует несколько методов решения систем линейных уравнений.Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив систему уравнений на одном и том же наборе осей.

Пример \ (\ PageIndex {2} \): решение системы уравнений с двумя переменными с помощью построения графика

Решите следующую систему уравнений, построив график. Определите тип системы.

\ [\ begin {align *} 2x + y & = −8 \\ x − y & = −1 \ end {align *} \]

Решение

Решите первое уравнение относительно \ (y \).

\ [\ begin {align *} 2x + y & = −8 \\ y & = −2x − 8 \ end {align *} \]

Решите второе уравнение относительно \ (y \).

\ [\ begin {align *} x − y & = −1 \\ y & = x + 1 \ end {align *} \]

Изобразите оба уравнения на том же наборе осей, как на рисунке \ (\ PageIndex {4} \).

Рисунок \ (\ PageIndex {4} \)

Кажется, что линии пересекаются в точке \ ((- 3, −2) \). Мы можем убедиться, что это решение системы, подставив упорядоченную пару в оба уравнения.

\ [\ begin {align *} 2 (−3) + (- 2) & = −8 \\ −8 & = −8 \ text {True} \\ (−3) — (- 2) & = — 1 \\ −1 & = −1 \ text {True} \ end {align *} \]

Решением системы является упорядоченная пара \ ((- 3, −2) \), поэтому система независима.

Упражнение \ (\ PageIndex {2} \)

Решите следующую систему уравнений, построив график.

\ [\ begin {align *} 2x − 5y & = −25 \\ −4x + 5y & = 35 \ end {align *} \]

Ответ: Решением системы является упорядоченная пара \ ((- 5,3) \).
Рисунок \ (\ PageIndex {5} \)

Вопросы и ответы

Можно ли использовать построение графиков, если система несовместима или зависима?

Да, в обоих случаях мы можем построить график системы для определения типа системы и решения. Если две линии параллельны, система не имеет решения и непоследовательна. Если две линии идентичны, система имеет бесконечное количество решений и является зависимой системой.

Решение систем уравнений подстановкой

Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод.Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную. Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.

Как: решить систему двух уравнений с двумя переменными, используя метод подстановки.

Решите одно из двух уравнений относительно одной из переменных через другую.
Подставьте выражение для этой переменной во второе уравнение, затем решите для оставшейся переменной.
Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
Проверьте решение в обоих уравнениях.

Пример \ (\ PageIndex {3} \): решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем подстановки.

\ [\ begin {align *} −x + y & = −5 \\ 2x − 5y & = 1 \ end {align *} \]

Решение

Сначала мы решим первое уравнение относительно \ (y \).

\ [\ begin {align *} −x + y & = — 5 \\ y & = x − 5 \ end {align *} \]

Теперь мы можем подставить выражение \ (x − 5 \) вместо \ (y \) во втором уравнении.

\ [\ begin {align *} 2x − 5y & = 1 \\ 2x − 5 (x − 5) & = 1 \\ 2x − 5x + 25 & = 1 \\ −3x & = −24 \\ x & = 8 \ end {align *} \]

Теперь мы подставляем \ (x = 8 \) в первое уравнение и решаем относительно \ (y \).

\ [\ begin {align *} — (8) + y & = −5 \\ y & = 3 \ end {align *} \]

Наше решение — \ ((8,3) \).

Проверьте решение, подставив \ ((8,3) \) в оба уравнения.

\ [\ begin {align *} −x + y & = −5 \\ - (8) + (3) & = −5 \ text {True} \\ 2x − 5y & = 1 \\ 2 (8) −5 (3) & = 1 \ text {True} \ end {align *} \]

Упражнение \ (\ PageIndex {3} \)

Решите следующую систему уравнений путем подстановки.

\ [\ begin {align *} x & = y + 3 \\ 4 & = 3x − 2y \ end {align *} \]

Ответ: \ ((- 2, −5) \)

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Да, но этот метод работает лучше всего, если одно из уравнений содержит коэффициент \ (1 \) или \ (- 1 \), чтобы нам не приходилось иметь дело с дробями.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — метод сложения. В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения умножением, чтобы одна переменная была исключена сложением.

Как: решить систему уравнений, используя метод сложения.

Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
Напишите одно уравнение над другим, выровняв соответствующие переменные. Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную.Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
Решите полученное уравнение для оставшейся переменной.
Подставьте это значение в одно из исходных уравнений и решите вторую переменную.
Проверьте решение, подставив значения в другое уравнение.

Пример \ (\ PageIndex {4} \): решение системы методом сложения

Решите данную систему уравнений сложением.

\ [\ begin {align *} x + 2y & = −1 \\ −x + y & = 3 \ end {align *} \]

Решение

Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент при \ (x \) во втором уравнении, \ (- 1 \), противоположен коэффициенту при \ (x \) в первом уравнении, \ (1 \). Мы можем сложить два уравнения, чтобы исключить \ (x \), не умножая его на константу.

Теперь, когда мы исключили \ (x \), мы можем решить полученное уравнение для \ (y \).

\ [\ begin {align *} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align *} \]

Затем мы подставляем это значение вместо \ (y \) в одно из исходных уравнений и решаем относительно \ (x \).

\ [\ begin {align *} −x + y & = 3 \\ −x + \ dfrac {2} {3} & = 3 \\ −x & = 3− \ dfrac {2} {3} \\ — x & = \ dfrac {7} {3} \\ x & = — \ dfrac {7} {3} \ end {align *} \]

Решение этой системы — \ (\ left (- \ dfrac {7} {3}, \ dfrac {2} {3} \ right) \).

Проверьте решение в первом уравнении.

\ [\ begin {align *} x + 2y & = −1 \\ \ left (- \ dfrac {7} {3} \ right) +2 \ left (\ dfrac {2} {3} \ right) & = \\ — \ dfrac {7} {3} + \ dfrac {4} {3} & = — \ dfrac {3} {3} \\ −1 & = −1 \; \; \; \; \; \; \; \; \ text {True} \ end {align *} \]

Анализ

Мы получаем важное представление о системах уравнений, глядя на графическое представление. См. Рисунок \ (\ PageIndex {6} \), чтобы увидеть, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.

Рисунок \ (\ PageIndex {6} \)

Пример \ (\ PageIndex {5} \): Использование метода сложения, когда требуется умножение одного уравнения

Решите данную систему уравнений методом сложения.

\ [\ begin {align *} 3x + 5y & = −11 \\ x − 2y & = 11 \ end {align *} \]

Решение

Добавление этих уравнений в представленном виде не устраняет переменную. Однако мы видим, что в первом уравнении есть \ (3x \), а во втором уравнении есть \ (x \).Итак, если мы умножим второе уравнение на \ (- 3 \), члены x прибавятся к нулю.

\ [\ begin {align *} x − 2y & = 11 \\ −3 (x − 2y) & = — 3 (11) \; \; \; \; \; \; \; \; \ text {Умножаем обе части на} −3. \\ −3x + 6y & = −33 \; \; \; \; \; \; \; \; \; \ text {Используйте свойство дистрибутива. } \ end {align *} \]

А теперь добавим их.

\ [\ begin {align *} 3x + 5y & = -11 \\ \ underline {-3x + 6y} & = \ underline {-33} \\ 11y & = -44 \\ y & = -4 \ end {align *} \]

На последнем этапе мы подставляем \ (y = −4 \) в одно из исходных уравнений и решаем относительно \ (x \).

\ [\ begin {align *} 3x + 5y & = −11 \\ 3x + 5 (−4) & = −11 \\ 3x − 20 & = −11 \\ 3x & = 9 \\ x & = 3 \ end {align *} \]

Наше решение — упорядоченная пара \ ((3, −4) \). См. Рисунок \ (\ PageIndex {7} \). Проверьте решение в исходном втором уравнении.

\ [\ begin {align *} x − 2y & = 11 \\ (3) −2 (−4) & = 3 + 8 \\ & = 11 \; \; \; \; \; \; \; \; \; \; \ text {True} \ end {align *} \]

Рисунок \ (\ PageIndex {7} \)

Упражнение \ (\ PageIndex {4} \)

Решите систему уравнений сложением.

\ [\ begin {align *} 2x − 7y & = 2 \\ 3x + y & = −20 \ end {align *} \]

Ответ: \ ((- 6, −2) \)

Пример \ (\ PageIndex {6} \): использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными сложением.

\ [\ begin {align *} 2x + 3y & = −16 \\ 5x − 10y & = 30 \ end {align *} \]

Решение

Одно уравнение имеет \ (2x \), а другое — \ (5x \).Наименьшее общее кратное — \ (10x \), поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Удалим \ (x \), умножив первое уравнение на \ (- 5 \), а второе уравнение на \ (2 \).

\ [\ begin {align *} −5 (2x + 3y) & = −5 (−16) \\ −10x − 15y & = 80 \\ 2 (5x − 10y) & = 2 (30) \\ 10x −20y & = 60 \ end {align *} \]

Затем мы складываем два уравнения.

Подставляем \ (y = −4 \) в исходное первое уравнение.

\ [\ begin {align *} 2x + 3 (−4) & = — 16 \\ 2x − 12 & = −16 \\ 2x & = −4 \\ x & = — 2 \ end {align *} \ ]

Решение: \ ((- 2, −4) \).Проверьте это в другом уравнении.

\ [\ begin {align *} 5x − 10y & = 30 \\ 5 (−2) −10 (−4) & = 30 \\ −10 + 40 & = 30 \\ 30 & = 30 \ end {align *} \]

См. Рисунок \ (\ PageIndex {8} \).

Рисунок \ (\ PageIndex {8} \)

Пример \ (\ PageIndex {7} \): Использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными сложением.

\ [\ begin {align *} \ dfrac {x} {3} + \ dfrac {y} {6} & = 3 \\ \ dfrac {x} {2} — \ dfrac {y} {4} & = 1 \ end {align *} \]

Решение

Сначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.

\ [\ begin {align *} 6 \ left (\ dfrac {x} {3} + \ dfrac {y} {6} \ right) & = 6 (3) \\ 2x + y & = 18 \\ 4 \ left (\ dfrac {x} {2} — \ dfrac {y} {4} \ right) & = 4 (1) \\ 2x − y & = 4 \ end {align *} \]

Теперь умножьте второе уравнение на \ (- 1 \), чтобы мы могли исключить переменную x .

\ [\ begin {align *} −1 (2x − y) & = −1 (4) \\ −2x + y & = −4 \ end {align *} \]

Добавьте два уравнения, чтобы исключить переменную \ (x \), и решить полученное уравнение.

\ [\ begin {align *} 2x + y & = 18 \\ −2x + y & = −4 \\ 2y & = 14 \\ y & = 7 \ end {align *} \]

Подставим \ (y = 7 \) в первое уравнение.

\ [\ begin {align *} 2x + (7) & = 18 \\ 2x & = 11 \\ x & = \ dfrac {11} {2} \\ & = 7.5 \ end {align *} \]

Решение: \ (\ left (\ dfrac {11} {2}, 7 \ right) \). Проверьте это в другом уравнении.

\ [\ begin {align *} \ dfrac {x} {2} — \ dfrac {y} {4} & = 1 \\ \ dfrac {\ dfrac {11} {2}} {2} — \ dfrac { 7} {4} & = 1 \\ \ dfrac {11} {4} — \ dfrac {7} {4} & = 1 \\ \ dfrac {4} {4} & = 1 \ end {align *} \ ]

Упражнение \ (\ PageIndex {5} \)

Решите систему уравнений сложением.

\ [\ begin {align *} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align *} \]

Ответ: \ ((10, −4) \)

Выявление несовместимых систем уравнений, содержащих две переменные

Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать эти методы для выявления несовместимых систем. Напомним, что несовместимая система состоит из параллельных линий с одинаковым наклоном, но с разными точками пересечения по оси Y.Они никогда не пересекутся. При поиске решения несовместимой системы мы получим ложное утверждение, например \ (12 = 0 \).

Пример \ (\ PageIndex {8} \): решение несовместимой системы уравнений

Решите следующую систему уравнений.

\ [\ begin {align *} x & = 9−2y \\ x + 2y & = 13 \ end {align *} \]

Решение

Мы можем подойти к этой проблеме двумя способами. Поскольку одно уравнение для \ (x \) уже решено, наиболее очевидным шагом является использование подстановки.

\ [\ begin {align *} x + 2y & = 13 \\ (9−2y) + 2y & = 13 \\ 9 + 0y & = 13 \\ 9 & = 13 \ end {align *} \]

Ясно, что это утверждение противоречит тому, что \ (9 ≠ 13 \). Следовательно, у системы нет решения.

Второй подход заключается в том, чтобы сначала манипулировать уравнениями так, чтобы они оба были в форме пересечения наклона. Мы манипулируем первым уравнением следующим образом.

\ [\ begin {align *} x & = 9−2y \\ 2y & = −x + 9 \\ y & = — \ dfrac {1} {2} x + \ dfrac {9} {2} \ end { выровнять *} \]

Затем мы преобразуем второе уравнение в форму пересечения наклона.

\ [\ begin {align *} x + 2y & = 13 \\ 2y & = −x + 13 \\ y & = — \ dfrac {1} {2} x + \ dfrac {13} {2} \ end { выровнять *} \]

Сравнивая уравнения, мы видим, что они имеют одинаковый наклон, но разные \ (y \) — точки пересечения. Следовательно, линии параллельны и не пересекаются.

\ [\ begin {align *} y & = — \ dfrac {1} {2} x + \ dfrac {9} {2} \\ y & = — \ dfrac {1} {2} x + \ dfrac {13} {2} \ end {align *} \]

Анализ

Запись уравнений в форме пересечения наклона подтверждает, что система несовместима, потому что все линии в конечном итоге будут пересекаться, если они не параллельны.Параллельные линии никогда не пересекаются; таким образом, у этих двух линий нет общих точек. Графики уравнений в этом примере показаны на рисунке \ (\ PageIndex {9} \).

Рисунок \ (\ PageIndex {9} \)

Упражнение \ (\ PageIndex {6} \)

Решите следующую систему уравнений с двумя переменными.

\ [\ begin {align *} 2y − 2x & = 2 \\ 2y − 2x & = 6 \ end {align *} \]

Ответ: Нет решения. Это противоречивая система.

Выражение решения системы зависимых уравнений, содержащих две переменные

Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют одну и ту же линию. Зависимые системы имеют бесконечное количество решений, потому что все точки на одной линии также находятся на другой линии. После использования замены или добавления результирующее уравнение будет тождественным, например \ (0 = 0 \).

Пример \ (\ PageIndex {9} \): поиск решения зависимой системы линейных уравнений

Найдите решение системы уравнений с помощью метода сложения .

\ [\ begin {align *} x + 3y & = 2 \\ 3x + 9y & = 6 \ end {align *} \]

Решение

С помощью метода сложения мы хотим исключить одну из переменных, добавив уравнения. В этом случае давайте сосредоточимся на удалении \ (x \). Если мы умножим обе части первого уравнения на \ (- 3 \), то мы сможем исключить переменную x.

\ [\ begin {align *} x + 3y & = 2 \\ (−3) (x + 3y) & = (−3) (2) \\ −3x − 9y & = −6 \ end {align * } \]

Теперь сложите уравнения.

Мы видим, что будет бесконечное количество решений, удовлетворяющих обоим уравнениям.

Анализ

Если бы мы переписали оба уравнения в форме пересечения наклона, мы могли бы знать, как будет выглядеть решение перед добавлением. Давайте посмотрим, что происходит, когда мы преобразуем систему в форму с пересечением наклона.

\ [\ begin {align *} x + 3y & = 2 \\ 3y & = −x + 2 \\ y & = — \ dfrac {1} {3} x + \ dfrac {2} {3} \\ 3x + 9y & = 6 \\ 9y & = — 3x + 6 \\ y & = — \ dfrac {3} {9} x + \ dfrac {6} {9} \\ y & = — \ dfrac {1} {3 } x + \ dfrac {2} {3} \ end {align *} \]

См. Рисунок \ (\ PageIndex {10} \).Обратите внимание, что результаты такие же. Общее решение системы: \ (\ left (x, — \ dfrac {1} {3} x + \ dfrac {2} {3} \ right) \).

Рисунок \ (\ PageIndex {10} \)

Упражнение \ (\ PageIndex {7} \)

Решите следующую систему уравнений с двумя переменными.

\ [\ begin {align *} y − 2x & = 5 \\ −3y + 6x & = −15 \ end {align *} \]

Ответ: Система зависима, поэтому существует бесконечное количество решений вида \ ((x, 2x + 5) \).

Использование систем уравнений для исследования прибыли

Используя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме производства скейтбордов в начале раздела.Функция дохода производителя скейтборда — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением \ (R = xp \), где \ (x \) = количество и \ (p \) = цена. Функция дохода показана оранжевым цветом на рисунке \ (\ PageIndex {11} \).

Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как аренда и заработная плата, и переменные затраты, такие как коммунальные услуги. Функция стоимости показана синим цветом на рисунке \ (\ PageIndex {11} \).Ось \ (x \) представляет количество в сотнях единиц. Ось \ (y \) представляет затраты или доход в сотнях долларов.

Рисунок \ (\ PageIndex {11} \)

Точка пересечения двух линий называется точкой безубыточности. Из графика видно, что если произведено \ (700 \) единиц, то стоимость составит \ (3300 долларов США \), а выручка также составит \ (3300 долларов США \). Другими словами, компания разоряется, даже если они производят и продают \ (700 \) единиц. Они не зарабатывают и не теряют деньги.

Заштрихованная область справа от точки безубыточности представляет объемы, от которых компания получает прибыль.Заштрихованная область слева представляет объемы, по которым компания терпит убытки. Функция прибыли — это функция дохода за вычетом функции затрат, записываемая как \ (P (x) = R (x) −C (x) \). Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.

Пример \ (\ PageIndex {10} \): поиск точки безубыточности и функции прибыли с помощью замены

Учитывая функцию затрат \ (C (x) = 0,85x + 35,000 \) и функцию дохода \ (R (x) = 1.55x \), найдите точку безубыточности и функцию прибыли.

Решение

Запишите систему уравнений, используя \ (y \) вместо обозначения функций.

\ [\ begin {align *} y & = 0,85x + 35,000 \\ y & = 1,55x \ end {align *} \]

Подставьте выражение \ (0.85x + 35,000 \) из первого уравнения во второе уравнение и решите относительно \ (x \).

\ [\ begin {align *} 0,85x + 35,000 & = 1,55x \\ 35,000 & = 0,7x \\ 50,000 & = x \ end {align *} \]

Затем мы подставляем \ (x = 50,000 \) либо в функцию затрат, либо в функцию дохода.

\ (1,55 (50 000) = 77 500 \)

Точка безубыточности равна \ ((50,000,77,500) \).

Функция прибыли находится по формуле \ (P (x) = R (x) −C (x) \).

\ [\ begin {align *} P (x) & = 1,55x- (0,85x + 35,000) \\ & = 0,7x-35,000 \ end {align *} \]

Функция прибыли равна \ (P (x) = 0,7x − 35,000 \).

Анализ

Стоимость производства \ (50 000 \) единиц составляет \ (77 500 долларов США \), а выручка от продажи \ (50 000 \) единиц также составляет \ (77 500 долларов США \).Чтобы получить прибыль, бизнес должен произвести и продать более \ (50 000 \) единиц. См. Рисунок \ (\ PageIndex {12} \).

Рисунок \ (\ PageIndex {12} \)

Из графика на рисунке \ (\ PageIndex {13} \) видно, что функция прибыли имеет отрицательное значение до тех пор, пока \ (x = 50,000 \) не пересечет график \ (x \) — ось. Затем график переходит в положительные \ (y \) — значения и продолжает движение по этому пути, поскольку функция прибыли представляет собой прямую линию. Это показывает, что точка безубыточности для предприятий наступает, когда функция прибыли равна \ (0 \).Область слева от точки безубыточности представляет собой убыточную операцию.

Рисунок \ (\ PageIndex {13} \)

Пример \ (\ PageIndex {11} \): запись и решение системы уравнений с двумя переменными

Стоимость билета в цирк составляет \ (25 долларов США) для детей и \ (50 долларов США) для взрослых. В определенный день посещаемость цирка составляет \ (2,000 \), а общий доход от ворот составляет \ (70,000 $ \). Сколько детей и сколько взрослых купили билеты?

Решение

Пусть \ (c \) = количество детей и \ (a \) = количество присутствующих взрослых.

Общее количество человек \ (2,000 \). Мы можем использовать это, чтобы написать уравнение количества людей в цирке в тот день.

\ (с + а = 2,000 \)

Доход от всех детей можно найти, умножив \ (25,00 $ \) на количество детей \ (25c \). Доход от всех взрослых можно найти, умножив \ ($ 50.00 \) на количество взрослых \ (50a \). Общий доход составляет \ (70 000 долларов США). Мы можем использовать это, чтобы написать уравнение дохода.

\ (25c + 50a = 70,000 \)

Теперь у нас есть система линейных уравнений с двумя переменными.

\ (с + а = 2,000 \)

\ (25c + 50a = 70,000 \)

В первом уравнении коэффициент при обеих переменных равен \ (1 \). Мы можем быстро решить первое уравнение для \ (c \) или \ (a \). Будем решать относительно \ (a \).

\ [\ begin {align *} c + a & = 2,000 \\ a & = 2,000 − c \ end {align *} \]

Подставьте выражение \ (2,000 − c \) во второе уравнение для a и решите относительно \ (c \).

\ [\ begin {align *} 25c + 50 (2,000-c) & = 70,000 \\ 25c + 100,000-50c & = 70,000 \\ -25c & = -30,000 \\ c & = 1,200 \ end {align *} \]

Подставьте \ (c = 1,200 \) в первое уравнение, чтобы найти \ (a \).

\ [\ begin {align *} 1,200 + a & = 2,000 \\ a & = 800 \ end {align *} \]

Мы обнаружили, что \ (1200 \) детей и \ (800 \) взрослых купили билеты в цирк в тот день.

Упражнение \ (\ PageIndex {8} \)

Билеты в цирк стоят \ (4 доллара США) для детей и (12 долларов США) для взрослых. Если было куплено \ (1650 \) билетов на питание на общую сумму \ (14 200 долларов \), сколько детей и сколько взрослых купили билеты на питание?

Ответ: \ (700 \) детей, \ (950 \) взрослых

Медиа

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с системами линейных уравнений.

Ключевые концепции

Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. См. Пример \ (\ PageIndex {1} \).
Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений или несовместимые с отсутствием решения.
Один из методов решения системы линейных уравнений с двумя переменными — построение графиков. В этом методе мы строим уравнения на одном и том же наборе осей. См. Пример \ (\ PageIndex {2} \).
Другой метод решения системы линейных уравнений — подстановка. В этом методе мы решаем одну переменную в одном уравнении и подставляем результат во второе уравнение. См. Пример \ (\ PageIndex {3} \).
Третий метод решения системы линейных уравнений — это сложение, в котором мы можем исключить переменную, добавив противоположные коэффициенты соответствующих переменных.См. Пример \ (\ PageIndex {4} \).
Часто бывает необходимо умножить одно или оба уравнения на константу, чтобы упростить исключение переменной при сложении двух уравнений. См. Пример \ (\ PageIndex {5} \), Пример \ (\ PageIndex {6} \) и Пример \ (\ PageIndex {7} \).
Любой метод решения системы уравнений приводит к ложному утверждению для несовместимых систем, потому что они состоят из параллельных линий, которые никогда не пересекаются. См. Пример \ (\ PageIndex {8} \).
Решение системы зависимых уравнений всегда будет верным, потому что оба уравнения описывают одну и ту же линию. См. Пример \ (\ PageIndex {9} \).
Системы уравнений могут использоваться для решения реальных задач, которые включают более одной переменной, например, относящиеся к выручке, затратам и прибыли. См. Пример \ (\ PageIndex {10} \) и Пример \ (\ PageIndex {11} \).

Системы линейных уравнений: две переменные

Результаты обучения

Решайте системы уравнений путем построения графиков, подстановок и сложений.
Определите несовместимые системы уравнений, содержащие две переменные.
Выразите решение системы зависимых уравнений, содержащей две переменные, в стандартных обозначениях.

(предоставлено Thomas Sørenes)

Введение в системные решения

Чтобы исследовать такие ситуации, как ситуация с производителем скейтборда, нам необходимо признать, что мы имеем дело с более чем одной переменной и, вероятно, более чем с одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных. Но даже в этом случае это не гарантирует уникального решения.

[латекс] \ begin {align} 2x + y & = 15 \\ [1 мм] 3x-y & = 5 \ end {align} [/ latex]

Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. В этом примере упорядоченная пара [латекс] (4,7) [/ латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы поиска такого решения, если оно существует.

[латекс] \ begin {align} 2 \ left (4 \ right) + \ left (7 \ right) & = 15 && \ text {True} \\ [1 мм] 3 \ left (4 \ right) — \ left (7 \ right) & = 5 && \ text {True} \ end {align} [/ latex]

Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. Согласованная система уравнений имеет по крайней мере одно решение. Согласованной системой считается , независимая система , если она имеет единственное решение, такое как пример, который мы только что исследовали.Две линии имеют разные уклоны и пересекаются в одной точке на плоскости. Согласованной системой считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые точки пересечения y . Другими словами, линии совпадают, поэтому уравнения представляют одну и ту же линию. Каждая точка на линии представляет пару координат, удовлетворяющую системе. Таким образом, существует бесконечное количество решений.

Общее примечание: типы линейных систем

Существует три типа систем линейных уравнений с двумя переменными и три типа решений.

Независимая система имеет ровно одну пару решений [latex] \ left (x, y \ right) [/ latex]. Точка пересечения двух линий — единственное решение.
Несогласованная система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекутся.
Зависимая система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.

Ниже приводится сравнение графических представлений каждого типа системы.

Практическое руководство. Для данной системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением.

Подставьте упорядоченную пару в каждое уравнение системы.
Определите, являются ли истинные утверждения результатом подстановки в обоих уравнениях; в таком случае заказанная пара является решением.

Пример: определение того, является ли упорядоченная пара решением системы уравнений

Определите, является ли упорядоченная пара [латекс] \ left (5,1 \ right) [/ latex] решением данной системы уравнений.

[латекс] \ begin {align} x + 3y & = 8 \\ 2x-9 & = y \ end {align} [/ latex]

Показать решение

Подставьте упорядоченную пару [латекс] \ left (5,1 \ right) [/ latex] в оба уравнения.

[латекс] \ begin {align} \ left (5 \ right) +3 \ left (1 \ right) & = 8 \\ [1mm] 8 & = 8 && \ text {True} \\ [3mm] 2 \ left (5 \ right) -9 & = \ left (1 \ right) \\ [1 мм] 1 & = 1 && \ text {True} \ end {align} [/ latex]

Упорядоченная пара [латекс] \ left (5,1 \ right) [/ latex] удовлетворяет обоим уравнениям, поэтому это решение системы.

Анализ решения

Попробуй

Определите, является ли упорядоченная пара [латекс] \ left (8,5 \ right) [/ latex] решением следующей системы.

[латекс] \ begin {align} 5x-4y & = 20 \\ 2x + 1 & = 3y \ end {align} [/ latex]

Решение систем уравнений с помощью построения графиков

Существует несколько методов решения систем линейных уравнений. Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив систему уравнений на одном и том же наборе осей.

Пример: решение системы уравнений с двумя переменными с помощью построения графиков

Решите следующую систему уравнений, построив график. Определите тип системы.

[латекс] \ begin {align} 2x + y & = — 8 \\ x-y & = — 1 \ end {align} [/ latex]

Показать решение

Решите первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {align} 2x + y & = — 8 \\ y & = — 2x-8 \ end {align} [/ latex]

Решите второе уравнение для [латекс] y [/ латекс].

[латекс] \ begin {align} x-y & = — 1 \\ y & = x + 1 \ end {align} [/ latex]

Изобразите оба уравнения на одном и том же наборе осей:

Линии пересекаются в точке [латекс] \ влево (-3, -2 \ вправо) [/ латекс].Мы можем убедиться, что это решение системы, подставив упорядоченную пару в оба уравнения.

[латекс] \ begin {align} 2 \ left (-3 \ right) + \ left (-2 \ right) & = — 8 \\ [1 мм] -8 = -8 && \ text {True} \\ [ 3 мм] \ left (-3 \ right) — \ left (-2 \ right) & = — 1 \\ [1 мм] -1 & = — 1 && \ text {True} \ end {align} [/ latex]

Решением системы является упорядоченная пара [латекс] \ left (-3, -2 \ right) [/ latex], поэтому система независима.

Попробуй

Решите следующую систему уравнений, построив график.

[латекс] \ begin {собрано} 2x — 5y = -25 \\ -4x + 5y = 35 \ end {собрано} [/ latex]

Показать решение

Решением системы является упорядоченная пара [латекс] \ left (-5,3 \ right) [/ latex].

Вопросы и ответы

Можно ли использовать построение графиков, если система непоследовательна или зависима?

Да, в обоих случаях мы можем построить график системы для определения типа системы и решения. Если две линии параллельны, система не имеет решения и непоследовательна.Если две линии идентичны, система имеет бесконечное количество решений и является зависимой системой.

Попробуй

Постройте три разные системы с помощью онлайн-графического инструмента. Отнесите каждое решение к категории непротиворечивых или несовместимых. Если система непротиворечива, определите, является ли она зависимой или независимой. Возможно, вам будет проще построить каждую систему по отдельности, а затем очистить свои записи, прежде чем строить следующую.
1)
[латекс] 5x-3y = -19 [/ latex]
[латекс] x = 2y-1 [/ латекс]

2)
[латекс] 4x + y = 11 [/ latex]
[латекс] -2y = -25 + 8x [/ latex]

3)
[латекс] y = -3x + 6 [/ latex]
[латекс] — \ frac {1} {3} y + 2 = x [/ latex]

Показать решение

Одно решение — последовательное, независимое
Нет решений, непоследовательные, ни зависимые, ни независимые
Множество решений — последовательные, зависимые

Решение систем уравнений подстановкой

Как: дана система двух уравнений с двумя переменными, решите ее с помощью метода подстановки.

Решите одно из двух уравнений относительно одной из переменных через другую.
Подставьте выражение для этой переменной во второе уравнение, затем решите для оставшейся переменной.
Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
Проверьте решение в обоих уравнениях.

Пример: решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {align} -x + y & = — 5 \\ 2x-5y & = 1 \ end {align} [/ latex]

Показать решение

Сначала мы решим первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {align} -x + y & = — 5 \\ y & = x — 5 \ end {align} [/ latex]

Теперь мы можем заменить выражение [latex] x — 5 [/ latex] на [latex] y [/ latex] во втором уравнении.

[латекс] \ begin {align} 2x — 5y & = 1 \\ 2x — 5 \ left (x — 5 \ right) & = 1 \\ 2x — 5x + 25 & = 1 \\ -3x & = — 24 \\ x & = 8 \ end {align} [/ latex]

Теперь мы подставляем [latex] x = 8 [/ latex] в первое уравнение и решаем относительно [latex] y [/ latex].

[латекс] \ begin {align} — \ left (8 \ right) + y & = — 5 \\ y & = 3 \ end {align} [/ latex]

Наше решение — [латекс] \ left (8,3 \ right) [/ latex].

Проверьте решение, подставив [latex] \ left (8,3 \ right) [/ latex] в оба уравнения.

[латекс] \ begin {align} -x + y & = — 5 \\ — \ left (8 \ right) + \ left (3 \ right) & = — 5 && \ text {True} \\ [3mm] 2x — 5y & = 1 \\ 2 \ left (8 \ right) -5 \ left (3 \ right) & = 1 && \ text {True} \ end {align} [/ latex]

Попробуй

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {align} x & = y + 3 \\ 4 & = 3x — 2y \ end {align} [/ latex]

Показать решение

[латекс] \ влево (-2, -5 \ вправо) [/ латекс]

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Да, но этот метод работает лучше всего, если одно из уравнений содержит коэффициент 1 или –1, чтобы нам не приходилось иметь дело с дробями.

Следующее видео длится ~ 10 минут и представляет собой мини-урок по использованию метода подстановки для решения системы линейных уравнений.Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы подытожить решение для каждого примера.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — это метод сложения , этот метод также называется методом исключения . В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю.Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения умножением, чтобы одна переменная была исключена сложением.

Как: решить систему уравнений методом сложения.

Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
Напишите одно уравнение над другим, выровняв соответствующие переменные.Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
Решите полученное уравнение для оставшейся переменной.
Подставьте это значение в одно из исходных уравнений и решите вторую переменную.
Проверьте решение, подставив значения в другое уравнение.

Пример: решение системы методом сложения

Решите данную систему уравнений сложением.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \ end {align} [/ latex]

Показать решение

Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент [латекс] x [/ латекс] во втором уравнении, –1, противоположен коэффициенту [латекс] x [/ латекс] в первом уравнении, 1.Мы можем сложить два уравнения, чтобы исключить [latex] x [/ latex] без умножения на константу.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \\ \ hline 3y & = 2 \ end {align} [/ latex]

Теперь, когда мы удалили [latex] x [/ latex], мы можем решить полученное уравнение для [latex] y [/ latex].

[латекс] \ begin {align} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align} [/ latex]

Затем мы подставляем это значение для [latex] y [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} -x + y & = 3 \\ -x + \ frac {2} {3} & = 3 \\ -x & = 3- \ frac {2} {3} \\ -x & = \ frac {7} {3} \\ x & = — \ frac {7} {3} \ end {align} [/ latex]

Решение этой системы — [латекс] \ left (- \ frac {7} {3}, \ frac {2} {3} \ right) [/ latex].

Проверьте решение в первом уравнении.

[латекс] \ begin {align} x + 2y & = — 1 \\ \ left (- \ frac {7} {3} \ right) +2 \ left (\ frac {2} {3} \ right) & = \\ — \ frac {7} {3} + \ frac {4} {3} & = \\ \ — \ frac {3} {3} & = \\ -1 & = — 1 && \ text {True} \ end {align} [/ латекс]

Анализ решения

Мы получаем важное представление о системах уравнений, глядя на графическое представление.Посмотрите на график ниже, чтобы увидеть, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.

Пример: использование метода сложения, когда требуется умножение одного уравнения

Решите данную систему уравнений методом сложения .

[латекс] \ begin {align} 3x + 5y & = — 11 \\ x — 2y & = 11 \ end {align} [/ latex]

Показать решение

Добавление этих уравнений в представленном виде не устраняет переменную.Однако мы видим, что в первом уравнении есть [latex] 3x [/ latex], а во втором уравнении — [latex] x [/ latex]. Итак, если мы умножим второе уравнение на [latex] -3, \ text {} [/ latex], термины x прибавятся к нулю.

[латекс] \ begin {align} x — 2y & = 11 \\ -3 \ left (x — 2y \ right) & = — 3 \ left (11 \ right) && \ text {Умножаем обе стороны на} -3 \ \ -3x + 6y & = — 33 && \ text {Использовать свойство распределения}. \ end {align} [/ latex]

А теперь добавим их.

[латекс] \ begin {align} 3x + 5y & = — 11 \\ −3x + 6y & = — 33 \\ \ hline 11y & = — 44 \\ y & = — 4 \ end {align} [/ latex]

На последнем этапе мы подставляем [latex] y = -4 [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} 3x + 5y & = — 11 \\ 3x + 5 \ left (-4 \ right) & = — 11 \\ 3x — 20 & = — 11 \\ 3x & = 9 \\ x & = 3 \ end {align} [/ latex]

Наше решение — упорядоченная пара [латекс] \ left (3, -4 \ right) [/ latex]. Проверьте решение в исходном втором уравнении.

[латекс] \ begin {align} x — 2y & = 11 \\ \ left (3 \ right) -2 \ left (-4 \ right) & = 3 + 8 \\ & = 11 && \ text {True} \ конец {align} [/ latex]

Попробуй

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x — 7y & = 2 \\ 3x + y & = — 20 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (-6, -2 \ вправо) [/ латекс]

Пример: использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} 2x + 3y & = — 16 \\ 5x — 10y & = 30 \ end {align} [/ latex]

Показать решение

Одно уравнение имеет [латекс] 2x [/ латекс], а другое — [латекс] 5x [/ латекс].Наименьшее общее кратное — [latex] 10x [/ latex], поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Давайте удалим [latex] x [/ latex], умножив первое уравнение на [latex] -5 [/ latex], а второе уравнение на [latex] 2 [/ latex].

[латекс] \ begin {align} -5 \ left (2x + 3y \ right) & = — 5 \ left (-16 \ right) \\ -10x — 15y & = 80 \\ [3 мм] 2 \ left (5x — 10y \ right) & = 2 \ left (30 \ right) \\ 10x — 20y & = 60 \ end {align} [/ latex]

Затем мы складываем два уравнения.

[латекс] \ begin {align} -10x-15y & = 80 \\ 10x-20y & = 60 \\ \ hline -35y & = 140 \\ y & = — 4 \ end {align} [/ latex]

Подставьте [латекс] y = -4 [/ latex] в исходное первое уравнение.

[латекс] \ begin {align} 2x + 3 \ left (-4 \ right) & = — 16 \\ 2x — 12 & = — 16 \\ 2x & = — 4 \\ x & = — 2 \ end {align} [ / латекс]

Решение: [латекс] \ left (-2, -4 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} 5x — 10y & = 30 \\ 5 \ left (-2 \ right) -10 \ left (-4 \ right) & = 30 \\ -10 + 40 & = 30 \\ 30 & = 30 \ end {align} [/ latex]

Пример: использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} \ frac {x} {3} + \ frac {y} {6} & = 3 \\ [1 мм] \ frac {x} {2} — \ frac {y} {4 } & = 1 \ end {align} [/ latex]

Показать решение

Сначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.

[латекс] \ begin {align} 6 \ left (\ frac {x} {3} + \ frac {y} {6} \ right) & = 6 \ left (3 \ right) \\ [1 мм] 2x + y & = 18 \\ [3 мм] 4 \ left (\ frac {x} {2} — \ frac {y} {4} \ right) & = 4 \ left (1 \ right) \\ [1 мм] 2x-y & = 4 \ end {align} [/ latex]

Теперь умножьте второе уравнение на [latex] -1 [/ latex], чтобы мы могли исключить x .

[латекс] \ begin {align} -1 \ left (2x-y \ right) & = — 1 \ left (4 \ right) \\ [1 мм] -2x + y & = — 4 \ end {align} [/ латекс]

Сложите два уравнения, чтобы исключить x , и решите полученное уравнение относительно y .

[латекс] \ begin {align} 2x + y & = 18 \\ −2x + y & = — 4 \\ \ hline 2y & = 14 \\ y & = 7 \ end {align} [/ latex]

Подставьте [латекс] y = 7 [/ латекс] в первое уравнение.

[латекс] \ begin {align} 2x + \ left (7 \ right) & = 18 \\ 2x & = 11 \\ x & = \ frac {11} {2} \\ & = 7.5 \ end {align} [/ latex]

Решение: [латекс] \ left (\ frac {11} {2}, 7 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} \ frac {x} {2} — \ frac {y} {4} & = 1 \\ [1 мм] \ frac {\ frac {11} {2}} {2} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {11} {4} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {4} {4} & = 1 \ end {align} [/ latex]

Попробуй

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (10, -4 \ вправо) [/ латекс]

В следующем видео мы представляем больше примеров того, как использовать метод сложения (исключения) для решения системы двух линейных уравнений.

Классифицируйте решения по системам

Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать эти методы для выявления несовместимых систем. Напомним, что несовместимая система состоит из параллельных линий, которые имеют одинаковый наклон, но разные точки пересечения [latex] y [/ latex]. Они никогда не пересекутся. При поиске решения несовместимой системы мы получим ложное утверждение, например [latex] 12 = 0 [/ latex].

Пример: решение несовместимой системы уравнений

Решите следующую систему уравнений.

[латекс] \ begin {gather} & x = 9 — 2y \\ & x + 2y = 13 \ end {gather} [/ latex]

Показать решение

Мы можем подойти к этой проблеме двумя способами. Поскольку одно уравнение для [латекс] x [/ латекс] уже решено, наиболее очевидным шагом является использование замены.

[латекс] \ begin {align} x + 2y & = 13 \\ \ left (9 — 2y \ right) + 2y & = 13 \\ 9 + 0y & = 13 \\ 9 & = 13 \ end {align} [/ latex]

Ясно, что это утверждение противоречит тому, что [латекс] 9 \ ne 13 [/ латекс].Следовательно, у системы нет решения.

[латекс] \ begin {собрано} x = 9 — 2y \\ 2y = -x + 9 \\ y = — \ frac {1} {2} x + \ frac {9} {2} \ end {собрано} [ / латекс]

Затем мы преобразуем второе уравнение в форму пересечения наклона.

[латекс] \ begin {собрано} x + 2y = 13 \\ 2y = -x + 13 \\ y = — \ frac {1} {2} x + \ frac {13} {2} \ end {собрано} [ / латекс]

Сравнивая уравнения, мы видим, что они имеют одинаковый наклон, но разные точки пересечения y .Следовательно, линии параллельны и не пересекаются.

[латекс] \ begin {gather} y = — \ frac {1} {2} x + \ frac {9} {2} \\ y = — \ frac {1} {2} x + \ frac {13} {2 } \ end {gather} [/ latex]

Анализ решения

Запись уравнений в форме пересечения наклона подтверждает, что система несовместима, потому что все линии в конечном итоге будут пересекаться, если они не параллельны. Параллельные линии никогда не пересекаются; таким образом, у этих двух линий нет общих точек. Графики уравнений в этом примере показаны ниже.

Попробуй

Решите следующую систему уравнений с двумя переменными.

[латекс] \ begin {собрано} 2y — 2x = 2 \\ 2y — 2x = 6 \ end {собрано} [/ latex]

Показать решение

Нет решения. Это противоречивая система.

Выражение решения системы зависимых уравнений, содержащих две переменные

Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют собой одну и ту же линию.Зависимые системы имеют бесконечное количество решений, потому что все точки на одной линии также находятся на другой линии. После использования замены или добавления результирующее уравнение будет идентичным, например [латекс] 0 = 0 [/ латекс].

Пример: поиск решения зависимой системы линейных уравнений

Найдите решение системы уравнений с помощью метода сложения .

[латекс] \ begin {собрано} x + 3y = 2 \\ 3x + 9y = 6 \ end {собрано} [/ latex]

Показать решение

С помощью метода сложения мы хотим исключить одну из переменных, добавив уравнения.В этом случае давайте сосредоточимся на удалении [латекс] х [/ латекс]. Если мы умножим обе части первого уравнения на [latex] -3 [/ latex], то мы сможем исключить переменную [latex] x [/ latex].

[латекс] \ begin {align} x + 3y & = 2 \\ \ left (-3 \ right) \ left (x + 3y \ right) & = \ left (-3 \ right) \ left (2 \ right) \\ -3x — 9y & = — 6 \ end {align} [/ latex]

Теперь сложите уравнения.

[латекс] \ begin {align} −3x − 9y & = — 6 \\ + 3x + 9y & = 6 \\ \ hline 0 & = 0 \ end {align} [/ latex]

Мы видим, что будет бесконечное количество решений, удовлетворяющих обоим уравнениям.

Анализ решения

[латекс] \ begin {align} \ begin {gather} x + 3y = 2 \\ 3y = -x + 2 \\ y = — \ frac {1} {3} x + \ frac {2} {3} \ конец {собрано} \ hspace {2cm} \ begin {gather} 3x + 9y = 6 \\ 9y = -3x + 6 \\ y = — \ frac {3} {9} x + \ frac {6} {9} \ \ y = — \ frac {1} {3} x + \ frac {2} {3} \ end {gather} \ end {align} [/ latex]

Посмотрите на график ниже.Обратите внимание, что результаты такие же. Общее решение системы — [латекс] \ left (x, — \ frac {1} {3} x + \ frac {2} {3} \ right) [/ latex].

Написание общего решения

В предыдущем примере мы представили анализ решения следующей системы уравнений:

[латекс] \ begin {собрано} x + 3y = 2 \\ 3x + 9y = 6 \ end {собрано} [/ latex]

После небольшой алгебры мы обнаружили, что эти два уравнения в точности совпадают. Затем мы записали общее решение как [latex] \ left (x, — \ frac {1} {3} x + \ frac {2} {3} \ right) [/ latex].Зачем нам писать решение именно так? В некотором смысле это представление о многом говорит нам. Он говорит нам, что x может быть любым, x — x . Это также говорит нам, что y будет зависеть от x , точно так же, как когда мы пишем правило функции. В этом случае, в зависимости от того, что вы указали для x , y будет определено в терминах x как [латекс] — \ frac {1} {3} x + \ frac {2} {3} [ /латекс].

Другими словами, существует бесконечно много пар ( x , y ), которые удовлетворяют этой системе уравнений, и все они попадают на линию [латекс] f (x) — \ frac {1} {3} x + \ frac {2} {3} [/ латекс].

Попробуй

Решите следующую систему уравнений с двумя переменными.

[латекс] \ begin {собрано} y — 2x = 5 \\ -3y + 6x = -15 \ end {собрано} [/ latex]

Показать решение

Система зависима, поэтому существует бесконечно много решений вида [латекс] \ left (x, 2x + 5 \ right) [/ latex].

Использование систем уравнений для исследования прибыли

Используя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме производства скейтбордов в начале раздела.Функция выручки производителя скейтбордов — это функция, используемая для расчета суммы денег, поступающей в бизнес. Это может быть представлено уравнением [латекс] R = xp [/ latex], где [latex] x = [/ latex] количество и [latex] p = [/ latex] цена. Функция дохода показана оранжевым цветом на графике ниже.

Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как аренда и заработная плата, и переменные затраты, такие как коммунальные услуги.Функция стоимости показана синим цветом на графике ниже. Ось x представляет количество в сотнях единиц. Ось y представляет собой стоимость или доход в сотнях долларов.

Точка пересечения двух линий называется точкой безубыточности . Из графика видно, что если произведено 700 единиц, стоимость составит 3300 долларов, а выручка также составит 3300 долларов. Другими словами, компания сломается, даже если произведет и продаст 700 единиц. Они не зарабатывают и не теряют деньги.

Заштрихованная область справа от точки безубыточности представляет объемы, от которых компания получает прибыль. Заштрихованная область слева представляет объемы, по которым компания терпит убытки. Функция прибыли — это функция дохода за вычетом функции затрат, записываемая как [латекс] P \ left (x \ right) = R \ left (x \ right) -C \ left (x \ right) [/ latex]. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.

Пример: определение точки безубыточности и функции прибыли с помощью подстановки

Дана функция стоимости [латекс] C \ left (x \ right) = 0.85x + 35 {,} 000 [/ latex] и функция дохода [latex] R \ left (x \ right) = 1,55x [/ latex], найдите точку безубыточности и функцию прибыли.

Показать решение

Напишите систему уравнений, используя [latex] y [/ latex], чтобы заменить обозначение функции.

[латекс] \ begin {align} y & = 0,85x + 35 {,} 000 \\ y & = 1,55x \ end {align} [/ latex]

Подставьте выражение [latex] 0.85x + 35 {,} 000 [/ latex] из первого уравнения во второе уравнение и решите относительно [latex] x [/ latex].

[латекс] \ begin {собрано} 0.85x + 35 {,} 000 = 1,55x \\ 35 {,} 000 = 0,7x \\ 50 {,} 000 = x \ end {в собранном виде} [/ latex]

Затем мы подставляем [латекс] x = 50 {,} 000 [/ latex] либо в функцию стоимости, либо в функцию дохода.

[латекс] 1,55 \ слева (50 {,} 000 \ справа) = 77 {,} 500 [/ латекс]

Точка безубыточности — [латекс] \ left (50 {,} 000,77 {,} 500 \ right) [/ latex].

Функция прибыли находится по формуле [латекс] P \ left (x \ right) = R \ left (x \ right) -C \ left (x \ right) [/ latex].

[латекс] \ begin {align} P \ left (x \ right) & = 1.55x- \ left (0.85x + 35 {,} 000 \ right) \\ & = 0.7x — 35 {,} 000 \ end {align} [/ latex]

Функция прибыли [латекс] P \ left (x \ right) = 0,7x — 35 {,} 000 [/ latex].

Анализ решения

Стоимость производства 50 000 единиц составляет 77 500 долларов США, а выручка от продажи 50 000 единиц также составляет 77 500 долларов США. Чтобы получить прибыль, бизнес должен произвести и продать более 50 000 единиц.

Из графика ниже видно, что функция прибыли имеет отрицательное значение до тех пор, пока [latex] x = 50 {,} 000 [/ latex] не пересечет ось x .Затем график переходит в положительные значения y и продолжает движение по этому пути, поскольку функция прибыли представляет собой прямую линию. Это показывает, что точка безубыточности для предприятий наступает, когда функция прибыли равна 0. Область слева от точки безубыточности представляет работу с убытками.

Написание системы линейных уравнений для ситуации

Редко можно получить уравнения, которые четко моделируют поведение, с которым вы сталкиваетесь в бизнесе, скорее, вы, скорее всего, столкнетесь с ситуацией, для которой вы знаете ключевую информацию, как в приведенном выше примере.Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему.

Как сделать: в ситуации, которая представляет собой систему линейных уравнений, напишите систему уравнений и найдите решение.

Определите входные и выходные данные каждой линейной модели.
Определите наклон и пересечение y каждой линейной модели.
Найдите решение, установив две линейные функции равными другой и решив для x , или найдите точку пересечения на графике.

А теперь давайте попробуем применить эти ключевые факторы на практике. В следующем примере мы определяем, сколько разных типов билетов продано, учитывая информацию об общей выручке и количестве билетов, проданных на мероприятие.

Пример: запись и решение системы уравнений с двумя переменными

Стоимость билета в цирк составляет 25 долларов для детей и 50 долларов для взрослых. В определенный день посещаемость цирка составляет 2000 человек, а общий доход от ворот составляет 70 000 долларов.Сколько детей и сколько взрослых купили билеты?

Показать решение

Пусть c = количество детей и a = количество взрослых, посещающих школу.

Общее количество человек — 2000 человек. Мы можем использовать это, чтобы написать уравнение количества людей в цирке в тот день.

[латекс] c + a = 2 {,} 000 [/ латекс]

Доход от всех детей можно найти, умножив 25 долларов США на количество детей, [латекс] 25c [/ латекс]. Доход от всех взрослых можно найти, умножив 50 долларов.00 по количеству взрослых, [латекс] 50а [/ латекс]. Общий доход составляет 70 000 долларов. Мы можем использовать это, чтобы написать уравнение дохода.

[латекс] 25c + 50a = 70 {,} 000 [/ латекс]

Теперь у нас есть система линейных уравнений с двумя переменными.

[латекс] \ begin {собрано} c + a = 2,000 \\ 25c + 50a = 70 {,} 000 \ end {собрано} [/ latex]

В первом уравнении коэффициент обеих переменных равен 1. Мы можем быстро решить первое уравнение для [латекса] c [/ латекса] или [латекса] a [/ латекса].Решим за [латекс] [/ latex].

[латекс] \ begin {собрано} c + a = 2 {,} 000 \\ a = 2 {,} 000-c \ end {собрано} [/ latex]

Подставьте выражение [latex] 2 {,} 000-c [/ latex] во второе уравнение для [latex] a [/ latex] и решите относительно [latex] c [/ latex].

[латекс] \ begin {align} 25c + 50 \ left (2 {,} 000-c \ right) & = 70 {,} 000 \\ 25c + 100 {,} 000 — 50c & = 70 {,} 000 \ \ -25c & = — 30 {,} 000 \\ c & = 1 {,} 200 \ end {align} [/ latex]

Подставьте [latex] c = 1 {,} 200 [/ latex] в первое уравнение для решения относительно [latex] a [/ latex].

[латекс] \ begin {align} 1 {,} 200 + a & = 2 {,} 000 \\ a & = 800 \ end {align} [/ latex]

Мы обнаружили, что 1200 детей и 800 взрослых купили в тот день билеты в цирк.

Попробуй

Билеты в цирк стоят 4 доллара для детей и 12 долларов для взрослых. Если было куплено 1650 билетов на питание на общую сумму 14 200 долларов, сколько детей и сколько взрослых купили билеты на питание?

Иногда система уравнений может помочь в принятии решения. В следующем примере мы помогаем ответить на вопрос: «Какая компания по аренде грузовиков предоставит наилучшую стоимость?»

Пример: построение системы линейных моделей для выбора компании по аренде грузовиков

Джамал выбирает между двумя компаниями по аренде грузовиков.Первый, Keep on Trucking, Inc., взимает предоплату в размере 20 долларов, затем 59 центов за милю. Второй, Move It Your Way, требует предоплаты в размере 16 долларов США, затем 63 цента за милю. Когда компания Keep on Trucking, Inc. станет лучшим выбором для компании Jamal?

Показать решение

Двумя важными величинами в этой задаче являются стоимость и количество пройденных миль. Поскольку нам нужно рассмотреть две компании, мы определим две функции.

Пример: решение проблемы химической смеси

У химика есть 70 мл 50% раствора метана.Сколько 80% раствора она должна добавить, чтобы окончательный раствор состоял из 60% метана?

Показать решение

Мы воспользуемся следующей таблицей, чтобы помочь нам решить эту проблему со смесью:

	Количество	Часть	Всего
Начало
Добавить
Финал

Начнем с 70 мл раствора, и неизвестное количество может быть x .Часть представляет собой проценты или концентрацию раствора 0,5 для начала, 0,8 для доп.

	Количество	Часть	Всего
Начало	70 мл	0,5
Добавить	[латекс] х [/ латекс]	0,8
Финал	[латекс] 70 + x [/ латекс]	0,6

Добавьте столбец суммы, чтобы получить окончательную сумму.Часть этого количества составляет 0,6, потому что мы хотим, чтобы окончательный раствор содержал 60% метана.

	Количество	Часть	Всего
Начало	70 мл	0,5	35
Добавить	[латекс] х [/ латекс]	0,8	[латекс] 0,8x [/ латекс]
Финал	[латекс] 70 + x [/ латекс]	0,6	[латекс] 42 + 0,6x [/ латекс]

Умножьте сумму на часть, чтобы получить общую сумму.обязательно распределить по последнему ряду: [латекс] (70 + х) 0,6 [/ латекс].

Если мы сложим начало и добавим записи в столбце «Итого», мы получим окончательное уравнение, которое представляет общую сумму и ее концентрацию.

[латекс] \ begin {align} 35 + 0,8x & = 42 + 0,6x \\ 0,2x & = 7 \\ \ frac {0,2} {0,2} x & = \ frac {7} {0,2} \\ x & = 35 \ конец {align} [/ latex]

35 мл 80% раствора необходимо добавить к 70 мл 50% раствора, чтобы получить 60% раствор метана.

Тот же процесс можно использовать, если к начальной и конечной сумме привязана цена, а не процент.

Ключевые понятия

Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо.
Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений или несовместимые с отсутствием решения.
Один из методов решения системы линейных уравнений с двумя переменными — построение графиков. В этом методе мы строим уравнения на одном и том же наборе осей.
Другой метод решения системы линейных уравнений — подстановка. В этом методе мы решаем одну переменную в одном уравнении и подставляем результат во второе уравнение.
Третий метод решения системы линейных уравнений — это сложение, в котором мы можем исключить переменную, добавив противоположные коэффициенты соответствующих переменных.
Часто бывает необходимо умножить одно или оба уравнения на константу, чтобы упростить исключение переменной при сложении двух уравнений.
Любой метод решения системы уравнений приводит к ложному утверждению для несовместимых систем, потому что они состоят из параллельных линий, которые никогда не пересекаются.
Решение системы зависимых уравнений всегда будет верным, потому что оба уравнения описывают одну и ту же линию.
Системы уравнений могут использоваться для решения реальных задач, которые включают более одной переменной, например, относящиеся к выручке, затратам и прибыли.

Глоссарий

метод сложения алгебраический метод, используемый для решения систем линейных уравнений, в котором уравнения складываются таким образом, чтобы исключить одну переменную, позволяя решить полученное уравнение для оставшейся переменной; затем используется подстановка для решения первой переменной

точка безубыточности точка, в которой функция затрат пересекает функцию дохода; где прибыль равна нулю

согласованная система система, для которой существует единое решение для всех уравнений в системе, и это независимая система, или если существует бесконечное количество решений, и это зависимая система

функция затрат функция, используемая для расчета затрат на ведение бизнеса; обычно состоит из двух частей: постоянных затрат и переменных затрат

зависимая система система линейных уравнений, в которой два уравнения представляют одну и ту же линию; существует бесконечное количество решений зависимой системы

несовместимая система система линейных уравнений без общего решения, потому что они представляют собой параллельные линии, которые не имеют общей точки или прямой

независимая система система линейных уравнений с ровно одной парой решений [латекс] \ left (x, y \ right) [/ latex]

функция прибыли функция прибыли записывается как [латекс] P \ left (x \ right) = R \ left (x \ right) -C \ left (x \ right) [/ latex], выручка минус затраты

функция дохода функция, которая используется для расчета дохода, записывается просто как [латекс] R = xp [/ latex], где [latex] x = [/ latex] количество, а [latex] p = [/ latex] цена.

метод подстановки алгебраический метод, используемый для решения систем линейных уравнений, в которых одно из двух уравнений решается для одной переменной, а затем подставляется во второе уравнение для решения для второй переменной

система линейных уравнений набор из двух или более уравнений с двумя или более переменными, которые должны рассматриваться одновременно.

Системы линейных уравнений

Линейное уравнение — это уравнение для линии .

Линейное уравнение не всегда имеет вид y = 3,5 — 0,5x ,

Также может иметь вид y = 0,5 (7 — x)

Или как y + 0,5x = 3,5

Или как y + 0,5x — 3,5 = 0 и больше.

(Примечание: это одно и то же линейное уравнение!)

A Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.

Пример: Вот два линейных уравнения:

Вместе они представляют собой систему линейных уравнений.

Сможете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)

Попробуем построить и решить реальный пример:

Пример: вы против лошади

Это гонка!

Можно бегать 0,2 км каждую минуту.

Лошадь может бегать 0.5 км каждую минуту. Но оседлать лошадь нужно за 6 минут.

Как далеко вы можете уйти, прежде чем лошадь вас поймает?

Мы можем составить два уравнения ( d = расстояние в км, t = время в минутах)

Вы бежите со скоростью 0,2 км каждую минуту, поэтому d = 0,2 т
Лошадь бежит со скоростью 0,5 км в минуту, но мы берем на ее время 6: d = 0,5 (t − 6)

Итак, у нас есть система уравнений (это линейных ):

Решаем на графике:

Вы видите, как лошадь стартует через 6 минут, а потом бежит быстрее?

Кажется, тебя поймают через 10 минут… тебе осталось всего 2 км.

В следующий раз беги быстрее.

Итак, теперь вы знаете, что такое система линейных уравнений.

Давайте продолжим узнавать о них больше ….

Решение

Существует множество способов решения линейных уравнений!

Давайте посмотрим на другой пример:

Пример: Решите эти два уравнения:

На этом графике показаны два уравнения:

Наша задача — найти место пересечения двух линий.

Ну, мы видим, где они пересекаются, так что это уже решено графически.

А теперь давайте решим это с помощью алгебры!

Хммм … как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:

x + y — (−3x + y) = 6 — 2

А теперь упростим:

х + у + 3х — у = 6-2

4x = 4

х = 1

Итак, теперь мы знаем, что линии пересекаются в точке x = 1 .

И мы можем найти совпадающее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одинаковое значение при x = 1). Воспользуемся первым (второй можете попробовать сами):

х + у = 6

1 + у = 6

г = 5

И решение:

x = 1 и y = 5

И график показывает, что мы правы!

Линейные уравнения

В линейных уравнениях допускаются только простые переменные. Нет x ², y ³, √x и т. Д. :

Линейное против нелинейного

Размеры

Линейное уравнение может быть в двух измерениях … (например, x и y )
… или в 3-х измерениях … (получается самолет)
… или 4 размера …
… или больше!

Общие переменные

Чтобы уравнения «работали вместе», они разделяют одну или несколько переменных:

Система уравнений состоит из двух или более уравнений в одной или нескольких переменных

Множество переменных

Таким образом, Система уравнений может иметь много уравнений и много переменных.

Пример: 3 уравнения с 3 переменными

2x	+	y	–	2z	=	3
х	–	y	–	z	=	0
х	+	y	+	3z	=	12

Может быть любая комбинация:

2 уравнения с 3 переменными,
6 уравнений в 4 переменных,
9000 уравнений в 567 переменных,
и др.

Решения

Когда количество уравнений равно , то же , что и количество переменных, , вероятно, будет решением. Не гарантировано, но вероятно.

На самом деле есть только три возможных случая:

Нет раствор
Одно решение
Бесконечно много решений

Когда нет решения , уравнения называются «несовместимыми» .

Одно или бесконечно много решений называются «согласованными»

Вот диаграмма для 2 уравнений с 2 переменными :

Независимая

«Независимый» означает, что каждое уравнение дает новую информацию.
В противном случае это «Иждивенец» .

Также называется «линейная независимость» и «линейная зависимость»

Пример:

Эти уравнения «Зависимые» , потому что они на самом деле то же уравнение , только умноженное на 2.

Итак, второе уравнение не дало новой информации .

Где верны уравнения

Уловка состоит в том, чтобы найти где все уравнений истинны одновременно .

Верно? Что это значит?

Пример: вы против лошади

Линия «ты» истинна по всей ее длине (но больше нигде).

В любом месте этой строки d равно 0.2т

при t = 5 и d = 1 уравнение верно (d = 0,2t? Да, поскольку 1 = 0,2 × 5 верно)
при t = 5 и d = 3 уравнение неверно (верно ли d = 0,2t? Нет, поскольку 3 = 0,2 × 5 неверно )

Точно так же «конская» линия верна по всей длине (но больше нигде).

Но только в точке, где они пересекают (при t = 10, d = 2), они оба являются истинными .

Значит, они должны быть правдой одновременно …

… поэтому некоторые люди называют их «Одновременные линейные уравнения»

Решить с помощью алгебры

Для их решения принято использовать алгебру.

Вот пример «Лошади», решенный с помощью алгебры:

Пример: вы против лошади

Система уравнений:

В этом случае кажется, что проще всего установить их равными друг другу:

d = 0.2т = 0,5 (т − 6)

Начать с : 0,2t = 0,5 (t — 6)

Расширить 0,5 (t − 6) : 0,2t = 0,5t — 3

Вычтем 0,5t с обеих сторон: −0,3t = −3

Разделим обе части на −0,3 : t = −3 / −0,3 = 10 минут

Теперь мы знаем , когда тебя поймают!

Зная t , можно вычислить d : d = 0,2t = 0,2 × 10 = 2 км

И наше решение:

t = 10 минут и d = 2 км

Алгебра против графиков

Зачем использовать алгебру, если графики настолько просты? Потому что:

Более 2 переменных не могут быть решены с помощью простого графика.

Итак, алгебра приходит на помощь двумя популярными методами:

Решение заменой
Решение путем исключения

Мы увидим каждую с примерами по 2 переменным и 3 переменным. Вот и …

Решение заменой

Это шаги:

Напишите одно из уравнений в стиле «переменная = …»
Заменить (т.е. заменить) эту переменную в другое уравнение (а).
Решите другое уравнение (а)
(при необходимости повторить)

Вот пример с 2 уравнениями с 2 переменными :

Пример:

Мы можем начать с любого уравнения и любой переменной .

Воспользуемся вторым уравнением и переменной «y» (это выглядит как простейшее уравнение).

Напишите одно из уравнений в стиле «переменная =»… «:

Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 — x . Теперь наши уравнения выглядят так:

Теперь замените «y» на «8 — x» в другом уравнении:

3x + 2 (8 — x) = 19
у = 8 — х

Решите, используя обычные методы алгебры:

Развернуть 2 (8 − x) :

3x + 16 — 2x = 19
у = 8 — х

Тогда 3x − 2x = x :

И на последок 19−16 = 3

Теперь мы знаем, что такое x , мы можем поместить его в уравнение y = 8 — x :

И ответ:

х = 3
у = 5

Примечание: поскольку — это решение, уравнения «непротиворечивы»

Проверка: почему бы вам не проверить, работают ли x = 3 и y = 5 в обоих уравнениях?

Решение подстановкой: 3 уравнения с 3 переменными

ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .

Это несложно, сделать … это займет у просто много времени !

Пример:

х + г = 6
г — 3у = 7
2x + y + 3z = 15

Мы должны аккуратно выровнять переменные, иначе мы потеряем из виду, что делаем:

х			+	z	=	6
	–	3 года	+	z	=	7
2x	+	y	+	3z	=	15

WeI может начать с любого уравнения и любой переменной.Воспользуемся первым уравнением и переменной «x».

Напишите одно из уравнений в стиле «переменная = …»:

x					=	6 — z
	–	3 года	+	z	=	7
2x	+	y	+	3z	=	15

Теперь замените «x» на «6 — z» в других уравнениях:

(К счастью, есть только одно уравнение с x в нем)

	х					=	6 — z
		–	3 года	+	z	=	7
2 (6-z)		+	y	+	3z	=	15

Решите, используя обычные методы алгебры:

2 (6 − z) + y + 3z = 15 упрощается до y + z = 3 :

х					=	6 — z
	–	3 года	+	z	=	7
		y	+	z	=	3

Хорошо.Мы достигли некоторого прогресса, но пока не достигли этого.

Теперь повторите процесс , но только для последних 2 уравнений.

Напишите одно из уравнений в стиле «переменная = …»:

Выберем последнее уравнение и переменную z:

х					=	6 — z
	–	3 года	+	z	=	7
				z	=	3 — х лет

Теперь замените «z» на «3 — y» в другом уравнении:

х					=	6 — z
	–	3 года	+	3 — х лет	=	7
				z	=	3 года

Решите, используя обычные методы алгебры:

−3y + (3 − y) = 7 упрощается до −4y = 4 , или другими словами y = −1

х			=	6 — z
	y		=	-1
		z	=	3 года

Почти готово!

Зная, что y = −1 , мы можем вычислить, что z = 3 − y = 4 :

х			=	6 — z
	y		=	-1
		z	=	4

И зная, что z = 4 , мы можем вычислить, что x = 6 − z = 2 :

x			=	2
	y		=	-1
		z	=	4

И ответ:

х = 2
у = -1
г = 4

Проверка: проверьте сами.

Мы можем использовать этот метод для 4 или более уравнений и переменных … просто повторяйте одни и те же шаги снова и снова, пока она не будет решена.

Заключение: Замена работает хорошо, но требует много времени.

Решение методом исключения

Уничтожение может быть быстрее … но должно быть аккуратным.

«Исключить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.

По идее, мы можем смело :

умножить уравнение на константу (кроме нуля),
прибавить (или вычесть) уравнение к другому уравнению

Как в этих примерах:

ПОЧЕМУ мы можем складывать уравнения друг в друга?

Представьте себе два действительно простых уравнения:

х — 5 = 3
5 = 5

Мы можем добавить «5 = 5» к «x — 5 = 3»:

х — 5 + 5 = 3 + 5
х = 8

Попробуйте сами, но используйте 5 = 3 + 2 в качестве второго уравнения

Он по-прежнему будет работать нормально, потому что обе стороны равны (для этого стоит знак =!)

Мы также можем поменять местами уравнения, чтобы первое могло стать вторым и т. Д., Если это поможет.

Хорошо, время для полного примера. Давайте использовать 2 уравнения с 2 переменными , пример из предыдущего:

Пример:

Очень важно, чтобы все было в порядке:

3x	+	2 года	=	19
х	+	y	=	8

Сейчас… наша цель — исключить переменную из уравнения.

Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.

Умножьте второе уравнение на 2:

3x	+	2 года	=	19
2 x	+	2 л	=	16

Вычтем второе уравнение из первого уравнения:

x			=	3
2x	+	2 года	=	16

Ура! Теперь мы знаем, что такое x!

Затем мы видим, что во втором уравнении есть «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:

Умножьте второе уравнение на ½ (т.е.е. разделить на 2):

х			=	3
x	+	y	=	8

Вычтем первое уравнение из второго уравнения:

х			=	3
		y	=	5

Готово!

И ответ:

x = 3 и y = 5

А вот график:

Синяя линия — это где 3x + 2y = 19 истинно

Красная линия — это место, где x + y = 8 истинно

При x = 3, y = 5 (где линии пересекаются) они равны , оба истинны. Это и есть ответ.

Вот еще один пример:

Пример:

2x — y = 4
6x — 3y = 3

Разложите аккуратно:

2x	–	y	=	4
6x	–	3 года	=	3

Умножьте первое уравнение на 3:

6x	–	3 года	=	12
6x	–	3 года	=	3

Вычтем второе уравнение из первого уравнения:

0	–	0	=	9
6x	–	3 года	=	3

0-0 = 9 ???

Что здесь происходит?

Все просто, решения нет.

На самом деле это параллельные линии:

И на последок:

Пример:

2x — y = 4
6x — 3y = 12

Аккуратно:

2x	–	y	=	4
6x	–	3 года	=	12

Умножьте первое уравнение на 3:

6x	–	3 года	=	12
6x	–	3 года	=	12

Вычтем второе уравнение из первого уравнения:

0	–	0	=	0
6x	–	3 года	=	3

0 — 0 = 0

Ну, это на самом деле ИСТИНА! Ноль действительно равен нулю…

… это потому, что на самом деле это одно и то же уравнение …

… так что существует бесконечное количество решений

Это одна строка:

Итак, теперь мы рассмотрели пример каждого из трех возможных случаев:

Нет раствор
Одно решение
Бесконечно много решений

Решение методом исключения: 3 уравнения с 3 переменными

Прежде чем мы начнем со следующего примера, давайте рассмотрим улучшенный способ решения задач.

Следуйте этому методу, и мы с меньшей вероятностью ошибемся.

Прежде всего удалите переменные в порядке :

Сначала удалите x с (из уравнений 2 и 3, по порядку)
, затем исключите y (из уравнения 3)

Вот как мы их устраняем:

У нас есть «форма треугольника»:

Теперь начните снизу и вернитесь к (так называемая «обратная подстановка»)
(введите z , чтобы найти y , затем z и y , чтобы найти x ):

И решаемся:

ТАКЖЕ, мы обнаружим, что легче выполнить расчетов в уме или на бумаге для заметок, чем всегда работать в рамках системы уравнений:

Пример:

х + у + г = 6
2y + 5z = −4
2x + 5y — z = 27

Аккуратно написано:

х	+	y	+	z	=	6
		2 года	+	5z	=	−4
2x	+	5лет	–	z	=	27

Сначала удалите x из 2-го и 3-го уравнения.

Во втором уравнении нет x … переходите к третьему уравнению:

Вычтите 2 раза 1-е уравнение из 3-го уравнения (просто проделайте это в уме или на бумаге для заметок):

И получаем:

х	+	y	+	z	=	6
		2 года	+	5z	=	−4
		3 года	–	3z	=	15

Затем удалите y из 3-го уравнения.

Мы, , могли бы вычесть 1½ раза 2-е уравнение из 3-го уравнения (потому что 1½ раза 2 равно 3) …

… но мы можем избежать дробей , если мы:

умножьте третье уравнение на 2 и
умножьте второе уравнение на 3

и , затем выполняют вычитание … вот так:

И в итоге получаем:

х	+	y	+	z	=	6
		2 года	+	5z	=	−4
				z	=	-2

Теперь у нас есть «треугольник»!

Теперь вернемся снова вверх «с обратной заменой»:

Мы знаем z , поэтому 2y + 5z = −4 становится 2y − 10 = −4 , тогда 2y = 6 , поэтому y = 3 :

х	+	y	+	z	=	6
		y			=	3
				z	=	-2

Тогда x + y + z = 6 становится x + 3−2 = 6 , поэтому x = 6−3 + 2 = 5

x			=	5
	y		=	3
		z	=	-2

И ответ:

x = 5
y = 3
z = −2

Проверка: проверьте сами.

Общий совет

Когда вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто выполняете шаги, и ответы появляются.

Но иногда замена может дать более быстрый результат.

Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
Устранение проще для больших ящиков

И всегда полезно сначала просмотреть уравнения, чтобы увидеть, есть ли простой ярлык… так что опыт помогает.

Типы систем уравнений

Согласованные и несовместимые системы

Набор решений системы уравнений состоит из всех решений этой системы. Есть три возможности для решения, установленного для системы.

1.) Система имеет конечное число решений.

2.) Система имеет бесконечное количество решений.

3.) В системе нет решений.

Системы уравнений делятся на две категории: согласованные системы и несовместимые системы. 2 = 1

y = x — 2

. система не имеет точек пересечения.Отсюда следует, что у системы нет решения, и это несовместимая система.

Несогласованная система

Независимые и зависимые системы

Теперь давайте сделаем еще один шаг в классификации наших типов систем. Как мы уже говорили, система непротиворечива, если у нее есть хотя бы одно решение. Мы можем дополнительно классифицировать эти согласованные системы. Когда система имеет ровно одно решение, мы говорим, что система независимая .Наш первоначальный пример партии попал бы в эту категорию, потому что система имеет только одно решение. Таким образом, эта система непротиворечива и независима.

Когда в системе бесконечно много решений, мы называем систему зависимой . Вам может быть интересно, что значит для системы бесконечное множество решений. Чтобы продемонстрировать это явление, рассмотрим следующую систему:

3 x — 5 y = 12

6 x — 10 y = 24

Зависимая система

Когда мы строим график этой системы, как показано на изображении выше, мы видим, что два уравнения имеют один и тот же график.Из-за этого графики везде пересекаются. Поскольку множество решений состоит из всех точек пересечения графиков уравнений в системе, мы видим, что существует бесконечное число решений этой системы. Таким образом, можно сказать, что эта система последовательна и зависима.

Краткое содержание урока

Система уравнений — это группа из двух или более уравнений с одинаковыми переменными. Решение системы уравнений — это значения переменных, которые делают все уравнения в системе истинными.Решение системы также является точкой пересечения графиков уравнений в системе. Набор решений системы уравнений состоит из всех решений этой системы.

Есть три возможности для набора решений системы. Может быть конечное количество решений, бесконечное количество решений или никаких решений. Когда в системе есть хотя бы одно решение, мы называем его согласованным , а когда в системе нет решения, мы называем его несогласованным .Кроме того, когда система согласована и имеет ровно одно решение, мы называем ее независимой , а когда система согласована и имеет бесконечно много решений, мы называем ее зависимой .

Системы линейных уравнений: построение графиков

Системы линейных уравнений: Графики (стр. 2 из 7)

Разделы: Определения, Решение с помощью построения графиков, Подстановка, Исключение / добавление, Исключение Гаусса.

Когда вы решаете системы уравнений (линейных или иных), вы, с точки зрения связанных графических линий уравнений, находите любые точки пересечения этих линий.

Для линейных систем уравнений с двумя переменными тогда существует три возможных типа решений систем, которые соответствуют трем различным типам графиков двух прямых линий.

Эти три случая показаны ниже:

Первый график выше, «Случай 1» показывает две отдельные непараллельные линии, которые пересекаются в ровно один балл.Это называется «независимой» системой уравнения, и решением всегда будет какая-то точка x , y .

Независимый система: одна точка решения	Чемодан 2	Чемодан 3

Второй график выше, «Дело 2 «показывает две четкие параллельные линии.Поскольку параллельные прямые никогда не пересекайся, тогда не может быть пересечения; то есть для системы уравнений, отображаемых в виде параллельных линий, решения не может быть. Это называется «несовместной» системой уравнений, и она не имеет решения.

Независимый система: одно решение и одна точка пересечения	Несоответствующий система: нет решения и нет точки пересечения	Чемодан 3

Третий график выше, «Дело 3 «, отображается только одна линия.На самом деле это та же линия, нарисованная дважды. Эти «две» линии, фактически являясь одной и той же линией, «пересекаются» в каждой точке по их длине. Это называется «зависимым» система, а «решение» — это вся линия.

Независимый система: одно решение и одна точка пересечения	Несоответствующий система: нет решения и нет точки пересечения	Зависимые система: решение — вся строка

Это показывает, что система уравнений может иметь одно решение (конкретная точка x , y ), никакого решения или бесконечное решение (все решения уравнение).У вас никогда не будет системы с двумя или тремя решениями; он всегда будет один, ни одного или бесконечно много.

Вероятно, это первый метод, который вы увидите для решение систем уравнений будет «решением с помощью построения графиков». Предупреждение: вы должны относиться к этим проблемам с недоверием. Единственный способ найти решение на графике — ЕСЛИ вы нарисуете очень аккуратная система осей, IF вы рисуете очень аккуратные линии, IF решение оказывается точкой с хорошими аккуратными целочисленными координатами, и IF линии не близки к параллельности. Авторские права © Элизабет Стапель 2003-2011 Все права защищены

Например, если линии пересекаются под небольшим углом, это может быть практически невозможно чтобы сказать, где пересекаются линии.

А если точки пересечения нет аккуратная пара целых чисел, все ставки отключены.

(Можете ли вы сказать, посмотрев, что отображаемое решение имеет координаты
из (–4,3, –0,95)? Нет? Тогда вы понимаете мою точку зрения.)

С положительной стороны, так как они будут вынуждены чтобы дать вам красивые изящные решения для «решения путем построения графиков» проблем, вы сможете получить все правильные ответы , если вы построите график очень аккуратно .Например:

Решите следующие проблемы система с помощью графиков.

Я знаю, что мне нужен аккуратный график, поэтому Я возьму свою линейку и начну. Сначала я решу каждое уравнение для « y =», так что я могу легко построить график:

2 x — 3 y = –2
2 x + 2 = 3 y
(2/3) x + (2/3) = y

4 x + y = 24
y = –4 x + 24

Вторую линию будет легко построить используя только наклон и точку пересечения, но мне понадобится Т-диаграмма для первой линии.

x	y = (2/3) x + (2/3)	y = –4 x + 24
–4	–8/3 + 2/3 = –6/3 = –2	16 + 24 = 40
–1	–2/3 + 2/3 = 0	4 + 24 = 28
2	4/3 + 2/3 = 6/3 = 2	–8 + 24 = 16
5	10/3 + 2/3 = 12/3 = 4	–20 + 24 = 4
8	16/3 + 2/3 = 18/3 = 6	–32 + 24 = –8

(Иногда можно заметить перекресток прямо на Т-графике.Вы понимаете суть обоих приведенных выше уравнений? Проверьте заштрихованный серым ряд выше.)

Теперь, когда у меня есть некоторые моменты, я аккуратно возьму линейку и график и поищу перекресток:

Даже если бы перекресток не заметил точки на Т-графике, я, конечно, вижу это на картинке.

решение: ( x , y ) = (5, 4)

<< Предыдущий Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >>

Цитируйте эту статью как:

Стапель, Елизавета.«Системы линейных уравнений: построение графиков». Purplemath . Доступна с
https://www.purplemath.com/modules/systlin2.htm . Дата обращения [Дата] [Месяц] 2016 г.

Системы линейных уравнений, примеры решений, изображения и практические задачи.Система просто ..

Что такое система уравнений?

Отвечать
Система уравнений просто означает «более одного уравнения». Система линейных уравнений — это не более 1 строки, см. Рисунок:
Хорошо, так что же такое
решение системы уравнений? Отвечать
Решение — это место, где уравнения «встречаются» или пересекаются.Красная точка — это решение системы.
Сколько решений могут иметь системы линейных уравнений?
Отвечать
Может быть нулевое решение, одно решение или бесконечное количество решений — каждый случай подробно описан ниже. Примечание. Хотя системы линейных уравнений могут иметь 3 или более уравнений, мы собираемся обратиться к наиболее распространенному случаю — стержню с ровно 2 линиями.
Вариант I: 1 Решение
Это наиболее распространенная ситуация, когда линии пересекаются ровно в одной точке.
Дело 2: Нет решений
Это происходит только тогда, когда линии параллельны. Как видите, параллельные линии никогда не встретятся.
Пример стержня, у которого нет решения:
Строка 1: $$ y = 5x + 13 $$
Строка 2: $$ y = 5x + 12 $$
Случай III: Бесконечные решения
Это самый редкий случай, и он возникает только тогда, когда у вас есть та же строка
Рассмотрим, например, две строки ниже (y = 2x + 1 и 2y = 4x + 2).Эти два уравнения — одна и та же линия.
Пример системы с бесконечным числом решений:
Строка 1: y = 2x + 1
Строка 2: 2y = 4x + 2
Как мы можем найти решения систем уравнений?
Найти решение систем линейных уравнений можно любым из следующих способов:
Решение систем линейных уравнений
А система линейные уравнения представляет собой просто набор из двух или более линейных уравнений.
В двух переменных ( Икс а также у ) , график системы двух уравнений представляет собой пару прямых на плоскости.
Есть три возможности:
Линии пересекаются в нулевых точках. (Линии параллельны.)
Линии пересекаются ровно в одной точке. (Большинство случаев.)
Прямые пересекаются в бесконечном множестве точек.(Два уравнения представляют собой одну и ту же линию.)
Нулевые решения:
у знак равно — 2 Икс + 4 у знак равно — 2 Икс — 3
Одно решение:
у знак равно 0.5 Икс + 2 у знак равно — 2 Икс — 3
Бесконечно много решений:
у знак равно — 2 Икс — 4 у + 4 знак равно — 2 Икс
Существует несколько различных методов решения систем линейных уравнений:
Графический метод . Это полезно, когда вам просто нужен приблизительный ответ или вы уверены, что пересечение происходит в целочисленных координатах. Просто нарисуйте две линии и посмотрите, где они пересекаются!
См. Второй график выше. Решение — это место пересечения двух линий, точка ( — 2 , 1 ) .
Метод замены . Сначала решите одно линейное уравнение для у с точки зрения Икс . Затем замените это выражение на у в другом линейном уравнении. Вы получите уравнение в Икс . Решите это, и у вас будет Икс -координата перекрестка. Затем подключите Икс к любому уравнению, чтобы найти соответствующее у -координат.(Если проще, вы можете начать с решения уравнения для Икс с точки зрения у , тоже — такая же разница!)
Пример 1:
Решите систему { 3 Икс + 2 у знак равно 16 7 Икс + у знак равно 19
Решите второе уравнение относительно у .
у знак равно 19 — 7 Икс
Заменять 19 — 7 Икс для у в первом уравнении и решите относительно Икс .
3 Икс + 2 ( 19 — 7 Икс ) знак равно 16 3 Икс + 38 — 14 Икс знак равно 16 — 11 Икс знак равно — 22 Икс знак равно 2
Заменять 2 для Икс в у знак равно 19 — 7 Икс и решить для у .
у знак равно 19 — 7 ( 2 ) у знак равно 5
Решение ( 2 , 5 ) .
Метод линейной комбинации , иначе Метод сложения , иначе Метод исключения. Сложить (или вычесть) одно уравнение, кратное другому уравнению (или из него), таким образом, чтобы либо Икс -термы или у -условия аннулируются.Затем решите для Икс (или же у , в зависимости от того, что осталось) и подставьте обратно, чтобы получить другую координату.
Пример 2:
Решите систему { 4 Икс + 3 у знак равно — 2 8 Икс — 2 у знак равно 12
Умножьте первое уравнение на — 2 и добавьте результат ко второму уравнению.
— 8 Икс — 6 у знак равно 4 8 Икс — 2 у знак равно 12 _ — 8 у знак равно 16
Решить для у .
у знак равно — 2
Замена для у в любом из исходных уравнений и решите относительно Икс .
4 Икс + 3 ( — 2 ) знак равно — 2 4 Икс — 6 знак равно — 2 4 Икс знак равно 4 Икс знак равно 1
Решение ( 1 , — 2 ) .
РубрикаРазное
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Биосфера
Глобальное потепление
Защита биосферы
Климат
Климатические пояса
Обитатели океанов
Океан
Полезно знать
Потепление
Природа
Разное
Человек и природа
Экология
Экология России
2019 © Все права защищены. Карта сайта

Систем уравнений виды: определение, виды, примеры решения, что это такое

определение, виды, примеры решения, что это такое

Определение системы уравнений

Основные виды систем уравнений

Решение систем уравнений

Основные типы систем уравнений

Системы уравнений. Понятие системы уравнений.

Понятие системы уравнений.

Свойства систем уравнений:

Линейные системы уравнений с двумя неизвестными:

Основные методы решения систем уравнений:

Методы решения систем рациональных уравнений. Алгебра, 9 класс: уроки, тесты, задания.

Решение системы линейных уравнений методом Гаусса с нахождением общего решения

Решение системы линейных уравнений методом Гаусса для любого числа уравнений и неизвестных

1. Совместная определенная система линейных уравнений (имеющая одно решение)

2. Совместная неопределенная система линейных уравнений (имеющая бесконечное множество решений)

3. Несовместная система линейных уравнений (не имеющая решений)

4. Переопределенная система линейных уравнений (число неизвестных меньше числа уравнений)

5. Недоопределенная система линейных уравнений (число неизвестных больше числа уравнений)

I.

Система линейных алгебраических уравнений — это… Что такое Система линейных алгебраических уравнений?

Матричная форма

Эквивалентные системы линейных уравнений

Методы решения

Прямые методы

Итерационные методы

См. также

Примечания

Ссылки

11.

Введение в системы уравнений

Решение систем уравнений с помощью построения графиков

Решение систем уравнений подстановкой

Решение систем уравнений с двумя переменными методом сложения

Выявление несовместимых систем уравнений, содержащих две переменные

Выражение решения системы зависимых уравнений, содержащих две переменные

Использование систем уравнений для исследования прибыли

Ключевые концепции

Системы линейных уравнений: две переменные

Результаты обучения

Введение в системные решения

Общее примечание: типы линейных систем

Практическое руководство. Для данной системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением.

Пример: определение того, является ли упорядоченная пара решением системы уравнений

Анализ решения

Попробуй

Решение систем уравнений с помощью построения графиков

Пример: решение системы уравнений с двумя переменными с помощью построения графиков

Попробуй

Вопросы и ответы

Можно ли использовать построение графиков, если система непоследовательна или зависима?

Попробуй

Решение систем уравнений подстановкой

Как: дана система двух уравнений с двумя переменными, решите ее с помощью метода подстановки.

Пример: решение системы уравнений с двумя переменными подстановкой

Попробуй

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Решение систем уравнений с двумя переменными методом сложения

Как: решить систему уравнений методом сложения.

Пример: решение системы методом сложения

Анализ решения

Пример: использование метода сложения, когда требуется умножение одного уравнения

Попробуй

Пример: использование метода сложения, когда требуется умножение обоих уравнений

Пример: использование метода сложения в системах уравнений, содержащих дроби

Попробуй

Классифицируйте решения по системам

Пример: решение несовместимой системы уравнений

Анализ решения

Попробуй

Выражение решения системы зависимых уравнений, содержащих две переменные

Пример: поиск решения зависимой системы линейных уравнений

Анализ решения

Написание общего решения

Попробуй

Пример: определение точки безубыточности и функции прибыли с помощью подстановки

Анализ решения

Написание системы линейных уравнений для ситуации

Как сделать: в ситуации, которая представляет собой систему линейных уравнений, напишите систему уравнений и найдите решение.